Изучение зависимостей площадей и периметров в четырехугольниках

  • Авторы
  • Руководители
  • Файлы работы
  • Наградные документы

Хакверди Елиз Уналовна 1

1Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа №30»

Берговина Ю.Д. 1

1Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа №30»

Автор работы награжден дипломом победителя III степени

Диплом школьникаСвидетельство руководителя

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

С понятием периметр и площадь я познакомилась в 3 классе. Эти важные понятия необходимы человеку на протяжении всей его жизни. Деятельность строителей, инженеров, земледельцев и представителей других профессий немыслима без прочных знаний по этой теме.

Актуальность темы. Понятия «площади» и «периметра» необходимы человеку в окружающей жизни постоянно, например – сделать ремонт в доме или красиво оформить клумбу на даче. И то и другое понятие связывают стороны многоугольников. Знание зависимостей между этими величинами очень важно для современного человека.

Цель проекта: установить некоторые зависимости между площадью и периметром, увидеть их применение в практических ситуациях.

Задачи:повторить понятия по теме исследования, а именно: «площадь фигуры» и «периметр фигуры»; провести необходимые исследования и опыты; сделать выводы о зависимости площадей и периметров; рассмотреть практическое применение полученных результатов.

Основнаячасть

Определение предмета исследования. Что нужно выяснить:

Как связаны периметры и площади прямоугольников? 

Зависит ли площадь прямоугольника от его периметра?

Какой прямоугольник имеет наибольшую площадь при заданном периметре?

Если известен периметр прямоугольника, то нельзя ли однозначно установить его площадь?

Что можно сказать о зависимости площади квадрата от его периметра?

Проблема.

Никаких зависимостей связывающих площади и периметры фигур мы пока не изучили.

Вот, самый простой пример, который задает проблему: «Есть два участка земли 80 м на 100 м и 50 м на 160 м. Вроде, площадь одинаковая – 8000 м 2, а первый участок выгоднее купить, чем второй, забор то на 60 м короче строить». С точки зрения математики, все ясно, а вот логически – странно, периметр это замкнутая воображаемая нить, и то, что внутри нее не должно меняться, как ее не крути. Почему есть разница в периметрах? Так все-таки, есть ли какие-то зависимости, или площадь и периметр никак не зависят друг от друга?

Гипотеза.Предполагаем, что некоторые зависимости существуют. С изменением длины одной из сторон прямоугольника при заданном периметре изменится и площадь этого прямоугольника. Можно даже предположить, что если площадь больше, то периметр больше. Если у одной фигуры больше периметр, чем у второй, то её площадь больше, меньше или по-разному?

Мы уже знаем: 

Периметр – величина, равная сумме длин всех сторон многоугольника.

Площадь фигуры – величина, показывающая сколько места занимает фигура на плоскости.

Свойства площадей нам тоже известны:

Равные фигуры имеют равные площади.

Площадь всей фигуры равна сумме площадей ее частей.

За единицу площади принимают площадь квадрата, сторона которого равна единичному отрезку.

Проверка гипотезы.

Исследования начнем с простой и хорошо знакомой нам фигуры – прямоугольника.

Исследование №1.   

Заполним таблицу, считая площадь одной клеточки равной 1 см 2

Таблица №1

№

Фигуры

Площадь

(S, см 2)

Периметр

(Р, см)

1

  

1

4

2

  

2

6

3

  

3

8

4

  

4

10

5

  

4

8

6

  

5

12

7
 

6

14

8

  

6

10

9

  

7

16

10

  

8

12

11
 

8

18

12

  

9

20

13

  

9

12

14

  

10

22

15

  

10

14

Исследуя результаты измерений, делаем вывод, что не всегда увеличение площади означает, что периметр тоже увеличивается, например фигуры №3 и №5 или фигуры №4 и №8, или фигуры №6 и №10 и №13. Если периметры равны, то площади могут быть различны. (Приложение 1, стр.14-16)

Мы заметили, если периметр одного прямоугольника больше, то и его площадь больше чем у других, например фигуры №2 и №3 или фигуры №4 и №6. Однако, если периметр одного прямоугольника больше, то его площадь не всегда больше, например фигуры №6 и №8.

При одинаковом периметре и площади бывают разные! Отчего же так происходит?

Продолжим наблюдения. 

Исследование №2.                

Таблица №2

№ фигуры

1 сторона (длина, см)

2 сторона (ширина, см)

Площадь

(S, см 2)

Периметр

(Р, см)

1

1

100

100

202

2

2

50

100

104

3

4

25

100

58

4

5

20

100

50

5

10

10

100

40

6

20

5

100

50

7

25

4

100

58

8

50

2

100

104

9

100

1

100

202

Замечаем, что при равных площадях периметры не равны, самый маленький периметр из всех прямоугольников с равными площадями – у квадрата. Вот какое замечательное свойство у квадрата! Оказывается, что среди всех прямоугольников одинаковой площади у квадрата самый маленький периметр!

Какой же из всех прямоугольников заданного периметра имеет наибольшую площадь? Решение этой задачи было известно ещё математикам Древней Греции. Оно изложено в книге Евклида.

Исследование №3.                

Таблица №3

№ фигуры

1 сторона (длина, см)

2 сторона (ширина, см)

Площадь (S, см 2)

Периметр (Р, см)

1

1

49

49

100

2

2

48

96

100

3

5

45

225

100

4

10

40

400

100

5

20

30

600

100

6

25

25

625

100

Очевидно, можно сделать вывод, что при одинаковом периметре, самая выгодная площадь у квадрата. Запомним это замечательное свойство квадрата, заключать в своих границах наибольшую площадь при постоянном периметре. Отчего же возникают такие зависимости, в чем причина? Чтобы лучше разобраться в этом вопросе, проведем опыт.

Опыт.

Я взяла четырехугольник – квадрат. Измерила его стороны, вычислила площадь и периметр. Разрезала фигуру пополам и составила новую фигуру (Приложение 2, стр.17).  Результаты измерений занесла в таблицу №4.

Таблица №4

№ фигуры

1 сторона (длина, см)

2 сторона (ширина, см)

Площадь

(S, см 2)

Периметр

(Р, см)

1

8

8

64

32

2

16

4

64

40

Таблица №5

1 фигура

  

2 фигура

  

Количество квадратиков не изменилось. Наблюдаем, что происходит со сторонами, когда периметр увеличивается. У фигуры появились дополнительные стороны, которые стали границами, это дополнительные 8+8=16 см, и исчезла граница 4+4=8 см. Итого: 16-8=8 см. Вот и дополнительные 8 см. Периметр увеличится.

Практические задачи.

А что можно сказать о зависимости площади квадрата от его периметра?

Задача №1. Если известен периметр квадрата, то можно ли однозначно установить его площадь?

Решим задачу для квадрата, периметр которого равен 40 см. Можно, поскольку по известному периметру можно вычислить сторону квадрата. А вычислив его сторону, можно потом вычислить площадь по этой найденной стороне.

1) 40 : 4 = 10 (см) – одна сторона

2) 10 • 10 = 100 (см 2) – площадь

Площадь квадрата однозначно зависит от его периметра, поскольку каждому значению периметра квадрата соответствует единственное значение площади.

Задача №2. Начертите какой-нибудь квадрат. Как надо изменить его стороны, чтобы построить квадрат, площадь которого была бы: 1) в 4 раза больше? 2) в 9 раз больше? 3) в 16 раз больше?

Проверим решение построением (Приложение 3, стр.18). 

Таблица №6

№

Фигуры

Вывод

1

  

Стороны увеличить в 2 раза

2

  

Стороны увеличить в 3 раза

3

  

Стороны увеличить в 4 раза

Задача №3. Начертите три прямоугольника, у одного из которых стороны имеют длину 7 см и 3 см, у второго соответственно 8 см и 2 см, а у третьего – 9 см и 1 см. Вычислите периметр и площадь каждого из этих прямоугольников. Сравните получившиеся периметры между собой и получившиеся площади между собой.

Проиллюстрируем на примере.

Первый прямоугольник: Р = (7 + 3) • 2 = 20 (см), S = 7 • 3= 21 (см 2).


Второй прямоугольник: Р = (8 + 2) • 2 = 20 (см), S = 8 • 2 = 16 (см 2).


Третий прямоугольник: Р = (9 + 1) • 2 = 20 (см), S = 9 • 1 = 9 (см 2).


Периметры прямоугольников равны, а площадь первого прямоугольника больше площади второго прямоугольника и площадь второго – больше площади третьего: 21 > 16 > 9 . Если известен периметр прямоугольника, то нельзя однозначно установить его площадь. Площадь прямоугольника не будет однозначно зависеть от его периметра.

А, что можно сказать о зависимости периметра квадрата от длины его стороны?

Задача №4. Может ли периметр квадрата не измениться, если длина стороны квадрата изменилась? Могут ли получиться разные значения периметра квадрата при одном и том же значении длины его стороны?

Таблица №7

Длина стороны квадрата α, см

1

2

3

4

5

Периметр квадрата Р, см

4

8

12

16

20

Из таблицы видно, что с изменением стороны квадрата изменяется и периметр. Периметр квадрата однозначно зависит от длины его стороны, поскольку периметр квадрата – 4 • α, то есть при изменении значения α, изменится значение выражения. Если изменить длину стороны квадрата, то это обязательно приведёт к изменению его периметра, то есть Р зависит от а. 

Если длина стороны квадрата увеличивается, то его периметр тоже увеличивается.
Если длина стороны квадрата уменьшается, то его периметр тоже уменьшается.

Заключение

Практические результаты и выводы, полученные мною, могут быть использованы при подготовке домашних заданий и в бытовых вопросах, постоянно возникающих в жизни. Мои исследования помогли узнать о том, что по известному периметру прямоугольника нельзя однозначно установить его площадь.
Потому, что у прямоугольников с одинаковым периметром могут быть разные площади, как выяснилось выше.
 Я выяснила, что площадь квадрата однозначно зависит от его периметра, поскольку каждому значению периметра квадрата соответствует единственное значение площади.

Основные выводы.

Если периметры прямоугольников равны, то площади могут быть различны. 

Не всегда увеличение площади прямоугольников означает, что периметр тоже увеличивается.

Если площади прямоугольников равны, то периметры могут быть различны.

Из всех прямоугольников с равными площадями наименьший периметр имеет квадрат.

Из всех прямоугольников с равными периметрами наибольшую площадь имеет квадрат.

Площадь квадрата однозначно зависит от его периметра.

Основные выводы я разместила на памятках-закладках (Приложение 4.1 и 4.2, стр.19-20)

Списокиспользованныхисточниковилитературы

А. Г. Мерзляк. Математика: 5 кл.: учебник для общеобразовательных организаций / А. Г. Мерзляк, В. Б. Полонский, М. С. Якир. −  2-е изд., перераб. — М.: Вентана-Граф, 2018

М.И. Моро, М.А. Бантова, Г.В. Бельтюкова, Математика — 4 класс, учебник для общеобразовательных организаций, в двух частях, М: Просвещение, 2018 г.-148 с.

3. Я.И. Перельман, Занимательная геометрия, Изд.: Терра-Книжный клуб, 2008 г., 384 стр.

4. Я.И. Перельман: Занимательная геометрия на вольном воздухе и дома , Издательство: Центрополиграф, 2017 г.

5. М.Г. Нефедова, Рабочая тетрадь по математике, Периметр и площадь — 3-4 классы. М: Издательство «Экзамен», 2014 г.- 46 стр.

6. М.И. Башмаков, М.Г. Нефедова, Математика, 3 класс, учебник, АСТ-Астрель, Москва, 2010 г.

7. О.В. Узорова, М.Г. Нефедова: Математика. 4 класс. Простые и составные задачи площади и периметра, Тренинговая тетрадь, ФГОС: издательства АСТ, 2015 г.

Приложение 4.1

Приложение 4.2

 

Просмотров работы: 6856

Площадь и периметр прямоугольника — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Подготовила учитель математики:
Смирнова В.И.
МБОУ « средняя
общеобразовательная школа №6»,
г. Сосновый Бор, Ленинградской
области

2.

Распутайте клубок28
+
53
=
81
28
х
4
=
112
18
х
7
=
112
—
59
=
53
28
+
=
154
126
126
:10
-180
24
24
*80
*20
:5
*5
:10
-180
24
24
*80
*20
*5
:5
2400

5. Вычисли недостающую величину

длина
12 см
ширина
5 см
периметр
площадь

6. Вычисли недостающую величину

длина
12 см
ширина
5 см
периметр
34 см
площадь

7. Вычисли недостающую величину

длина
12 см
ширина
5 см
периметр
34 см
площадь
60 см2

8. Вычисли недостающую величину

длина
12 см
3 дм
ширина
5 см
6 см
периметр
34 см
площадь
60 см2

9. Вычисли недостающую величину

длина
12 см
3 дм
ширина
5 см
6 см
периметр
34 см
72 см
площадь
60 см2

10. Вычисли недостающую величину

длина
12 см
3 дм
ширина
5 см
6 см
периметр
34 см
72 см
площадь
60 см2
180 см2

11.

Вычисли недостающую величинудлина
12 см
3 дм
ширина
5 см
6 см
периметр
34 см
72 см
площадь
60 см2
180 см2
15 см
60 см2

12. Вычисли недостающую величину

длина
12 см
3 дм
15 см
ширина
5 см
6 см
4 см
периметр
34 см
72 см
площадь
60 см2
180 см2
60 см2

13. Вычисли недостающую величину

длина
12 см
3 дм
15 см
ширина
5 см
6 см
4 см
периметр
34 см
72 см
38 см
площадь
60 см2
180 см2
60 см2

14. Вычисли недостающую величину

длина
12 см
3 дм
15 см
ширина
5 см
6 см
4 см
8 см
периметр
34 см
72 см
38 см
36 см
площадь
60 см2
180 см2
60 см2

15. Вычисли недостающую величину

длина
12 см
3 дм
15 см
10 см
ширина
5 см
6 см
4 см
8 см
периметр
34 см
72 см
38 см
36 см
площадь
60 см2
180 см2
60 см2

16.

Вычисли недостающую величинудлина
12 см
3 дм
15 см
10 см
ширина
5 см
6 см
4 см
8 см
периметр
34 см
72 см
38 см
36 см
площадь
60 см2
180 см2
60 см2
80 см2

17. Найти площади изображенных фигур

Найти площади изображенных
фигур
Найти площади изображенных
фигур

20. Исследовательская работа по теме: «Сравнение фигур, их периметров и площадей»

3)
2)
1)
5)
4)
7)
6)
Запишите номера фигур, согласно заданию:
Равные фигуры
Фигуры, имеющие равные площади
Фигуры, имеющие равные периметры
1) Найдите:
а) равные прямоугольники;
б) прямоугольники, имеющие одинаковую площадь;
в) прямоугольники, имеющие одинаковый периметр.
2) Подумайте, можно ли утверждать, что:
а) если прямоугольники имеют одинаковую площадь, то они равны;
б) если прямоугольники имеют одинаковый периметр, то они равны;
в) если прямоугольники имеют одинаковую площадь, то их периметры
равны;
г) если один из прямоугольников имеет большую площадь, то он имеет и
больший периметр;
д) если площадь одного прямоугольника меньше площади другого, то
первый прямоугольник можно полностью расположить внутри второго.
3) Подумайте, какие из следующих утверждений (высказываний) истинны,
а какие – ложны:
а) равные фигуры имеют одинаковую площадь;
б) фигуры, имеющие одинаковую площадь, равны
в) если фигуры не равны, то их площади тоже не равны;
г) фигуры, имеющие разные площади, не могут быть равны.
Отвечая тем самым на эти вопросы, вы сами подвели итог своей
исследовательской работы.

English     Русский Правила

Могут ли они быть равны?

Возраст от 11 до 14 лет

Уровень задачи

У нас было много решений этой задачи, так что молодцы все, кто ответил!

Дэвид, Ной, Феликс, Том, Эми и Лаура из Бристольской гимназии вместе работали над этой задачей. Дэвид говорит:

Мы обнаружили, что прямоугольник 6 на 3 работает, потому что 6+3+6+3=18 и 6×3=18, поэтому площадь и периметр равны.

Лора и Эми говорят:

Мы систематически работали над перечислением всех возможных прямоугольников, т.е. 1×1 1×2 1×3 1×4 … и решить, есть ли падежи с 1, 2 или 3

2×1 2×2 2×3 2×4. ..
3×1 3×2 3×3 3×4…

Мы заметили диагональный узор, в котором периметр становится меньше площади.
Мы все еще работаем над решением!

Молодцы Гурав из Индии, Радха из Станхоупа, Кирсти из колледжа да Винчи и Кейтлин из начальной школы Маршфилда, которые правильно нашли прямоугольники с одинаковой площадью и периметром, такие как 4×4 и 3×6.

Ханна из школы Leicester Girls High сделала несколько хороших заметок о четных и нечетных числах:

Я понял, что по крайней мере одно из значений длины или ширины прямоугольника должно быть четным. Периметр всегда будет четным, потому что длина умножается на 2, что делает его четным, и прибавляется к ширине, которая была умножена на 2, что также делает его четным. Но если и длина, и ширина нечетны, то площадь будет нечетной, а это означает, что периметр не может быть таким же, как область.

Щелкните здесь, чтобы узнать, как Декстер из школы Уилсона использовал диаграммы для понимания различных прямоугольников и как он также использовал алгебру, чтобы найти примеры прямоугольников, у которых периметр равен площади.

 

Люси из Бельгии визуально заметила, что происходит с прямоугольниками с целым числом длин сторон:

Каждый квадрат по краям составляет одну единицу периметра, за исключением четырех угловых квадратов. Они составляют две единицы периметра, но только одну единицу площади. Это означает, что периметр на 4 больше, чем площадь, и в середине должны быть квадраты, которые будут учитываться только для площади, а не для периметра.

Бхавик из школы для мальчиков королевы Елизаветы также рассматривал прямоугольники с целым числом длин сторон и пришел к такому же выводу. Щелкните здесь, чтобы увидеть его очень четкое объяснение того, почему может быть только два таких прямоугольника, площадь которых равна периметру.

 

Натан из начальной школы Рашмора попытался использовать алгебру, которую продолжили Вики из Фарнборо-Хилл, Элиза и Жаклин из Колледжа Шевалье, Австралия, и Том. Вики заметила, что для прямоугольника x на y площадь равна периметру, если: $$ \begin{align*} xy &= 2x+2y \\ xy-2y &= 2x \\ y(x -2) &= 2х\\ у &= \frac {2x}{x-2} \end{align*} $$

 

Затем Нихарика посмотрела на возможные значения x и y из этого уравнения: $$ \begin{align*} y &= \frac {2x}{x-2} \text{ and }  x ,y> 0 \\ \Rightarrow x-2 & > 0 \\ x&> 2 \end{align*} $$ Этих прямоугольников бесконечное множество.

 

Подстановка различных значений x и y и проверка правильности ответов — хороший навык решения задач — молодцы Кристоф и Мимас, которые сделали это. Также Шашанк из Индии нарисовал график возможных x и y значения:


Эстер прокомментировала это:

Хотя вы всегда можете подставить число в формулу, которую я использовал, $2x+2y=xy$, конечный результат не всегда является целым числом.
На самом деле единственными прямоугольниками с целыми длинами сторон являются прямоугольник 3×6 и квадрат 4×4.
Любые другие числа, подставленные в формулу как x , дадут десятичный вывод для y .
Например, если вы введете 5 как x , ваше значение для y будет 10/3.
 

Молодцы ученица 2BE класса мисс Джеррард из средней школы Перта, которая заметила некоторые интересные связи между площадью и периметром:

Мы все нашли 2 прямоугольника, которые сработали довольно быстро. Это были квадрат со сторонами 4 (A=P=16) и прямоугольник со сторонами 3 и 6 (A=P=18).

 

Затем мы решили попробовать использовать десятичные дроби, чтобы посмотреть, сможем ли мы найти что-нибудь еще, поскольку мы застряли. Один из нас обнаружил, что прямоугольник со сторонами 10 и 2,5 работает, так как он дает нам площадь и периметр 25.

 

После того, как мы нашли этот прямоугольник, кому-то еще в классе удалось обнаружить закономерность, связывающую числа. Начните с квадрата со сторонами 4 на 4.

Затем посмотрите на прямоугольник со стороной 3 и шириной 6.

Разница между длинами 3 и 4 равна 1, разница между ширинами 4 и 6 равна 2

Чтобы перейти от 3 к следующей длине, нужно разделить разницу между 4 и 3 пополам и вычесть ее из 3, чтобы получить 2,5.

Чтобы перейти от 6 к следующей ширине, удвойте разницу между 4 и 6 и прибавьте ее к 6, чтобы получить 10.

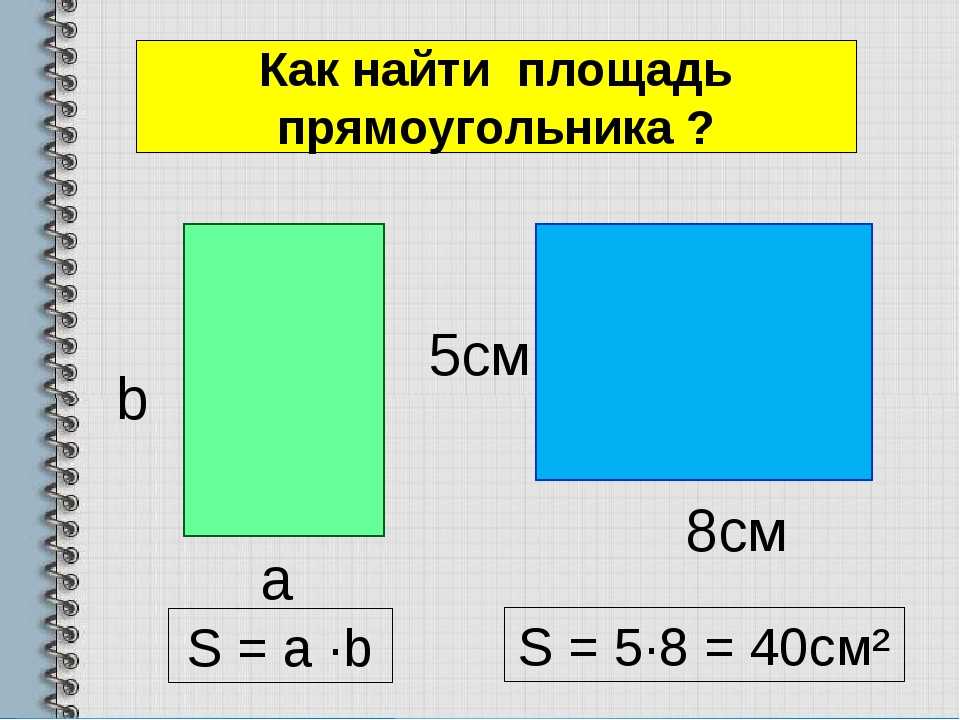
Мы обнаружили, что если вы продолжите делить разницу длин пополам и вычитать это, а также удваивать ширину и прибавлять, вы можете найти гораздо больше прямоугольников с одинаковым периметром и площадью:

$4$ на $4$

$3$ на $6 $

$2\frac{1}{2}$ на $10$

$2\frac{1}{4}$ на $18$

$2\frac{1}{8}$ на $34$

. .

Вы все молодцы.


Вычисление периметра прямоугольников (примеры вопросов)

Решение задач с прямоугольным периметром — это навык, который имеет много интересных практических применений. Например, мы можем использовать расчеты периметра для таких ситуаций, как требования к ограждению вокруг игрового поля, размеры рамы картины, расстояния вокруг пешеходной дорожки или размеры большого окна. Вычисление периметра прямоугольников — полезный навык, потому что он часто используется в нашей повседневной жизни.

Примеры вопросов о периметре прямоугольников

Давайте вспомним, что периметр — это расстояние вокруг внешней стороны двухмерной формы. Может быть полезно визуализировать периметр в виде ограждения, окружающего парк или задний двор. Когда мы вычисляем периметр, мы, по сути, вычисляем общее расстояние вокруг этой двумерной формы.

Расчет задач периметра можно выполнять разными способами, но наиболее эффективная стратегия — просто использовать формулу периметра.

Чему равен периметр прямоугольника?

Формула периметра прямоугольника гласит, что P = (L + W) × 2, где P представляет периметр, L представляет длину, а W представляет ширину. Когда вам даны размеры прямоугольной формы, вы можете просто подставить значения L и W в формулу, чтобы найти периметр. Например, если прямоугольник ниже представляет собой сад, который нуждается в кирпичной рамке, мы можем использовать формулу периметра, чтобы определить, сколько футов кирпичной бордюры нам нужно всего.

Формула периметра прямоугольника

Формула утверждает, что P = (L + W) × 2, поэтому давайте подставим 14 футов для L и 6 футов для W. Теперь у нас есть P = (14 + 6) × 2, что упрощается до 40 или 40 футов.

Использование формулы периметра экономит нам немного времени, избегая альтернативной стратегии, которая заключалась бы в суммировании длин каждой стороны отдельно. 14 + 6 + 14 + 6 даст правильный ответ, но эта стратегия обычно занимает больше времени, поэтому рекомендуется использовать формулу.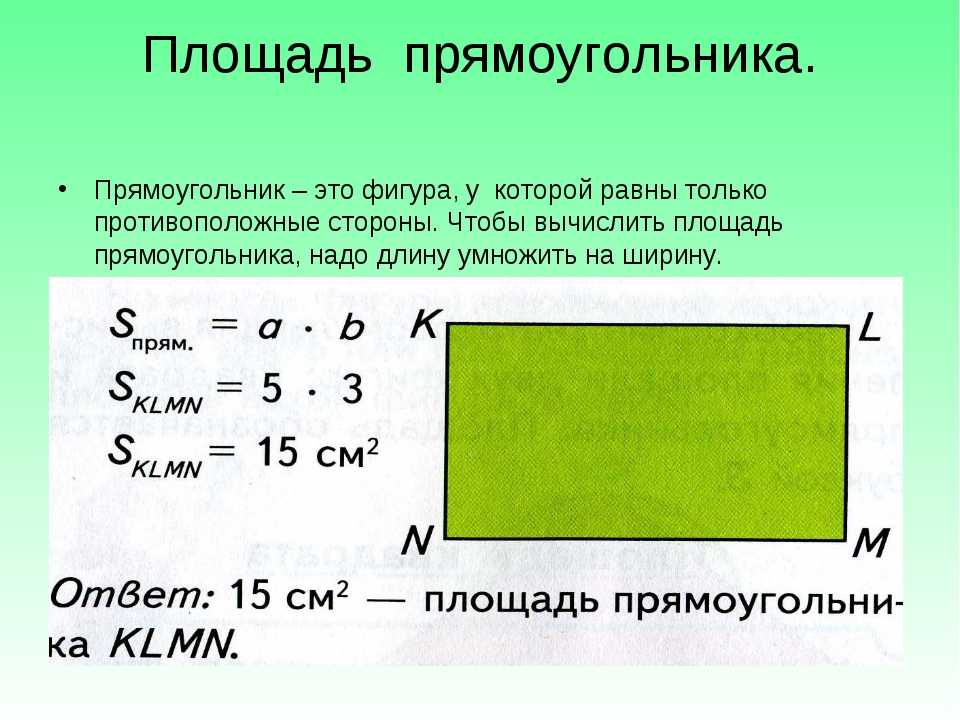

Однако не во всех задачах периметра можно получить длину и ширину таким простым способом. На самом деле, некоторые задачи о периметре дадут вам одно измерение, а также площадь прямоугольника. Чтобы решить такую ​​проблему периметра, нам нужно пересмотреть наше понимание площади. Помните, чтобы вычислить площадь прямоугольника, мы просто умножаем длину на ширину. Прямоугольник размером 3,5 см на 4 см будет иметь площадь 14 см 2 , потому что 3,5 × 4 = 14. Давайте воспользуемся этим знанием площади и применим его к задаче периметра.

Например, предположим, что вам нужно обрамить большое прямоугольное окно площадью 35 квадратных футов и длиной 7 футов. Давайте используем то, что мы знаем о вычислении площади, чтобы найти периметр.

Мы знаем, что площадь поверхности находится путем умножения длины на ширину. Это означает, что семь умножить на что-то равно 35, 7 × ? = 35. Мы можем найти недостающую длину стороны, разделив 35 на 7, что равно 5. Теперь мы можем применить формулу периметра, потому что мы знаем, что длина равна 7 футам, а ширина 5 футам.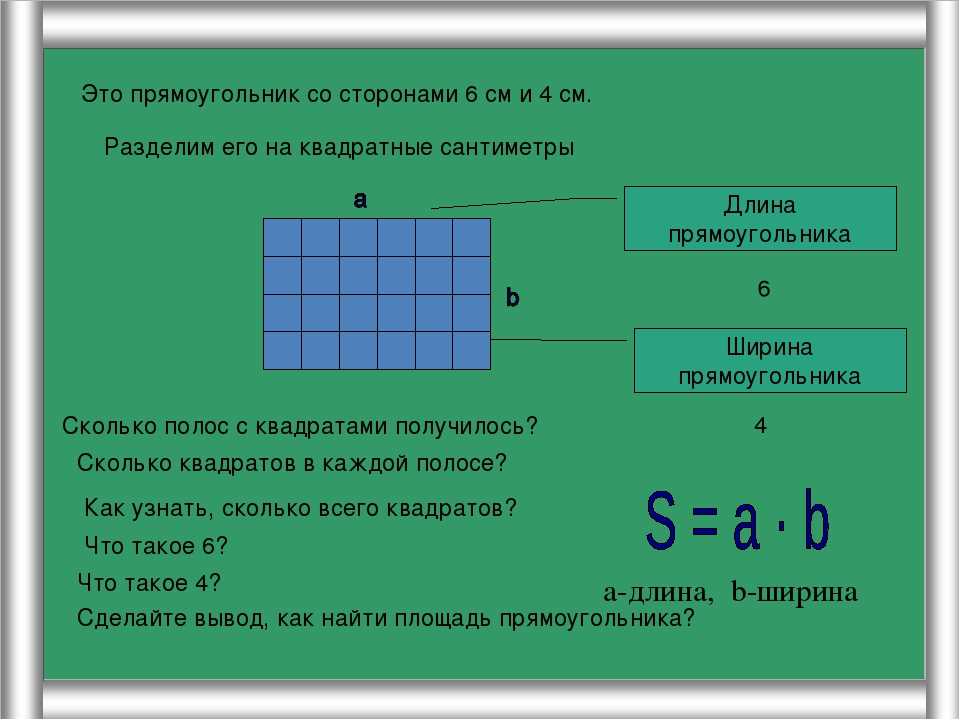

P = (L + W) × 2 становится P = (7 + 5) × 2, что упрощается до 24 или 24 футов.

Теперь, когда мы рассмотрели формулу периметра и ее различные приложения, рассмотрим следующий вопрос. Есть ли у прямоугольника площадью 20 квадратных футов более одного возможного варианта периметра? Если вы сказали да, то вы правы. Прямоугольники с ограниченной площадью, например 20 квадратных футов, могут иметь различные периметры. Например, прямоугольник площадью 20 квадратных футов может иметь размеры 1 фут × 20 футов, 2 фута × 10 футов или 4 фута × 5 футов. Все эти варианты будут давать разные периметры, хотя все они имеют одинаковую площадь. . Давайте докажем эту концепцию, рассчитав периметр трех только что упомянутых возможных прямоугольников: 1 фут × 20 футов, 2 фута × 10 футов и 4 фута × 5 футов.

1 фут × 20 футов: P = (Д + Ш) × 2 = (1 + 20) × 2 = 42 фута
2 фута × 10 футов = Д + Ш × 2 = (2 + 10) × 2 = 24 футов
4 фута × 5 футов = Д + Ш × 2 = 4 + 5 × 2 = 18 футов
*Также важно отметить, что формула P = (Д + Ш) × 2 применима только к прямоугольникам. Эта формула будет работать только для четырехугольников, у которых два набора конгруэнтных сторон.

Периметр прямоугольника Примеры вопросов

Вот несколько примеров вопросов, касающихся площади прямоугольника.

Вопрос №1:

 
Какая формула используется для вычисления периметра прямоугольника?

\(Периметр=4+(длина+ширина)\)

\(Периметр=\frac{(\text{длина}×\текст{ширина})}{2}\)

\(Периметр=( длина+ширина)×4 \)

\(Периметр=(длина+ширина)×2 \)

Показать ответ

Ответ:

Прямоугольник имеет две равные длины и две равные ширины. Чтобы найти периметр или расстояние вокруг прямоугольника, нам нужно сложить длины всех четырех сторон. Это можно сделать эффективно, просто добавив длину и ширину, а затем умножив эту сумму на два, поскольку каждой длины по две. \(Периметр=(длина+ширина)×2\) — это формула для периметра.

Скрыть ответ

Вопрос №2:

 
Вычислите периметр данного прямоугольника.

22 фута

44 фута

86,5 футов

108,75 футов

Показать ответ

Ответ:

Мы можем рассчитать периметр прямоугольника с помощью Formula \ (Perimeter =. ×2\). Мы видим, что длина равна 14,5 футам, а ширина — 7,5 футам, поэтому наша формула принимает вид \(Периметр=(14,5+7,5)×2\), что упрощается до 44. Периметр прямоугольника равен 44 футам.

Скрыть Ответ

Вопрос №3:

 
Определите периметр прямоугольника, если его площадь 64 м 2 , а длина 16 м. (

40 метров

45 метров

30 метров

38 метров

Показать Ответ

Ответ:

Для того, чтобы определить ширину прямоугольника, сначала нужно определить метр. Площадь прямоугольника вычисляется путем умножения \(длина×ширина\), поэтому мы можем использовать следующее уравнение, чтобы найти недостающее значение (w).

Площадь = l × w
64 м 2 =16 × w

Разделите обе стороны на 16, чтобы найти w.

w = 4 или 4 м

Теперь, когда мы знаем длину и ширину, мы можем использовать формулу \(Периметр=(длина+ширина)×2\), чтобы найти периметр. Подставив 16 м в длину и 4 м в ширину, мы получим следующее: \(Периметр=(16 м+4 м)×2\), что упрощается до 40 м. Периметр прямоугольника 40 метров.

Скрыть ответ

Вопрос № 4:

 
Стороны прямоугольной песочницы в парке Санниленд имеют длину 15 и 8,5 футов. Определить периметр песочницы.

47 футов

42 фута

46,5 футов

49,5 футов

Показать ответ

Ответ:

Ответ:

2\). Мы знаем, что длина равна 15 футам, а ширина — 8,5 футам, поэтому мы можем подставить эти значения в формулу, чтобы найти периметр. Теперь наша формула принимает вид \(Периметр=(15+8,5)×2\), что упрощается до 47 или 47 футов.

Скрыть ответ

Вопрос № 5:

 
Глория проектирует сад для своего заднего двора. Она знает, что хочет иметь 24 квадратных фута в саду, но она гибка в отношении размеров. Она хочет поставить забор вокруг сада, но забор (за метр) может быть довольно дорогим, поэтому она хочет сравнить варианты. Вариант А состоит в том, чтобы построить сад размером 8 футов на 3 фута. Вариант Б – построить сад размером 6 футов на 4 фута. Какой вариант потребует меньшего количества ограждений и, следовательно, меньшей стоимости?

Вариант А дешевле

Вариант Б дешевле

Показать ответ

Ответ:

Вариант А имеет длину 8 футов и ширину 3 фута.