Методический материал для проведения зачета по теме электричество.
Просмотр содержимого документа
«Методический материал для проведения зачета по теме электричество.»
ВАРИАНТ 1
ЧАСТЬ А Выберите один верный ответ.
На рисунке показана зависимость сопротивления проводника площадью сечения 1 мм2 от его длины. Чему равно удельное электрическое сопротивление вещества, из которого сделан проводник?
20 Ом мм2/м
5 Оммм2/м
0,5 Оммм2/м
0,2 Оммм2/м
Как изменится сила тока, проходящего через проводник, если увеличить в 2 раза напряжение между его концами, а площадь сечения проводника уменьшить в 2 раза?
не изменится 2) уменьшится в 2 раза
увеличится в 2 раза 4) увеличится в 4 раза
На участке цепи, изображенном на рисунке, сопротивление каждого резистора равно 3 Ом.
 Общее сопротивление участка равно
Общее сопротивление участка равно
12 0м
5 Ом
3,5 Ом
2 Ом
В цепи, изображенной на рисунке амперметр показывает силу тока 1 А. К каким точкам нужно подключить вольтметр, чтобы его показания были равны 4 В?
АБ
БВ
БГ
АВ
Три резистора сопротивлениями R1 = 10 Ом, R2 = 6 Ом и R3 = 3 Ом соединены в цепь как показано на рисунке. На каком резисторе выделится наибольшее количество теплоты
на первом
на втором
на всех одинаково
ЭДС источника равна 8В, внешнее сопротивление 3 Ом, внутреннее сопротивление 1 Ом.
 Сила тока в полной цепи равна
Сила тока в полной цепи равна
32 А
25 А
2 А
0,5 А
ЧАСТЬ В
Используя условие задачи, установите соответствия величин из левого столбца таблицы с их изменениями в правом столбце.
В цепи, изображенной на рисунке, ползунок реостата передвинули вниз. При этом…
Величина Изменение
сила тока 1) увеличивается
Б. электродвижущая сила 2) уменьшается
напряжение 3) не изменяется
на резисторе
Г. сопротивление реостата
Решите задачи.
В электроприборе за 15 мин электрическим током совершена работа 9 кДж.

Электрическая цепь состоит из двух резисторов сопротивлением по 4 Ом соединенных последовательно, источника тока с ЭДС 30 В и внутренним сопротивлением 2 Ом. Определить силу тока в цепи.
ЧАСТЬ С
Решите задачу.
Температура однородного медного цилиндрического проводника длиной 10 м в течение 57 с повысилась на 10 К. Определить напряжение, которое было приложено к проводнику в это время. Изменением сопротивления проводника и рассеянием тепла при его нагревании пренебречь.
ВАРИАНТ 2
ЧАСТЬ А Выберите один верный ответ.
На рисунке показана зависимость сопротивления проводника длиной 1 м от его площади сечения. Чему равно удельное электрическое сопротивление вещества, из которого сделан проводник?
20 Оммм2/м
5 Оммм2/м
0,5 Оммм2/м
0,2 Оммм2/м
Как изменится сила тока, проходящего через проводник, если уменьшить в 2 раза напряжение между его концами, а длину проводника увеличить в 2 раза?
не изменится
уменьшится в 2 раза
увеличится в 2 раза
уменьшится в 4 раза
На участке цепи, изображенном на рисунке, сопротивление каждого резистора равно 4 Ом.
 Общее сопротивление участка равно
Общее сопротивление участка равно
16 0м
10 Ом
3 Ом
1 Ом
В цепи, изображенной на рисунке амперметр показывает силу тока 2 А. К каким точкам нужно подключить вольтметр, чтобы его показания были равны 2 В?
АБ
АВ
БВ
БГ
Три резистора сопротивлениями R1 = 10 Ом, R2 = 6 Ом и R3 = 3 Ом соединены в цепь как показано на рисунке. На каком резисторе выделится наибольшее количество теплоты?
на первом
на втором
на третьем
на всех одинаково
Сила тока в полной цепи 8 А, внешнее сопротивление 4 Ом, внутреннее сопротивление 1 Ом.
 ЭДС источника равна
ЭДС источника равна
40В
33В
3 В
0,5 В
ЧАСТЬ В
Используя условие задачи, установите соответствия величин из левого столбца таблицы с их изменениями в правом столбце.
В цепи, изображенной на рисунке, ползунок реостата передвинули вверх. При этом…
Величина Изменение
А. напряжение на | 1) увеличивается |
резисторе | |
Б. внутреннее | 2) уменьшается |
сопротивление | |
В. | 3) не изменяется |
Г. сопротивление | |
резистора |
Решите задачи.
Каково напряжение на резисторе сопротивлением 360 Ом, если за 12 мин электрическим током была совершена работа 450 Дж?
Электрическая цепь состоит из двух резисторов сопротивлением по 10 Ом каждый соединенных параллельно, источника тока с ЭДС 24 В и внутренним сопротивлением 1 Ом. Определить силу тока в цепи.
ЧАСТЬ С
К однородному медному цилиндрическому проводнику длиной 10 м приложили разность потенциалов 1 В. Определите промежуток времени, в течение которого температура проводника повысится на 10 К. Изменением сопротивления проводника и рассеянием тепла при его нагревании пренебречь.

ВАРИАНТ 3
ЧАСТЬ А
Выберите один верный ответ.
На рисунке показана зависимость сопротивления проводника площадью сечения 1 мм
40 Ом мм2/м
10 Ом мм2/м
0,5 Ом мм2/м
0,1 Ом мм2/м
Как изменится сила тока, проходящего через проводник, если уменьшить в 2 раза напряжение между его концами, а площадь сечения проводника увеличить в 2 раза?
не изменится
уменьшится в 2 раза
увеличится в 2 раза
увеличится в 4 раза
На рисунке изображены графики зависимости силы тока в четырех проводниках от напряжения на их концах.
 Сопротивление какого проводника равно 1 Ом?
Сопротивление какого проводника равно 1 Ом?
проводника 1
проводника 2
проводника 3
проводника 4
На участке цепи, изображенном на рисунке, сопротивление каждого резистора равно 3 Ом. Общее сопротивление участка равно
12 Ом
6 Ом
4 Ом
3 Ом
5. В цепи, изображенной на рисунке амперметр показывает силу тока 2 А. К каким точкам нужно подключить вольтметр, чтобы его показания были равны 20 В?
Три резистора сопротивлениями R1 = 3 Ом, R2 = 6 Ом и R3 = 9 Ом соединены в цепь как показано на рисунке. На каком резисторе выделится наименьшее количество теплоты?
на первом
на втором
на третьем
на всех одинаково
Сила тока в полной цепи 6 А, внешнее сопротивление 2 Ом, внутреннее сопротивление 1 Ом.
 ЭДС источника равна
ЭДС источника равна
18 В
13 В
3 В
0,5 В
ЧАСТЬ В
Используя условие задачи, установите соответствия величин из левого столбца таблицы с их изменениями в правом столбце.
В цепи, изображенной на рисунке, ползунок реостата передвинули вниз. При этом…
Изменение
увеличивается
уменьшается
не изменяется
Величина
напряжение на резисторе
Б. внутреннее сопротивление
сила тока
Г. сопротивление резистора
Решите задачи.
В электроприборе с сопротивлением 2,5 Ом электрическим током за 15 мин совершена работа 9 кДж. Определите силу тока в цепи.
Электрическая цепь состоит из двух резисторов сопротивлением 15 Ом и 23 Ом соединенных последовательно, источника тока с ЭДС 100 В и внутренним сопротивлением 2 Ом. Определить силу тока в цепи.
ЧАСТЬ С
Решите задачу.
К однородному медному цилиндрическому проводнику на 15 с приложили разность потенциалов 1 В. Какова длина проводника, если его температура при этом повысилась на 10 К? Изменением сопротивления проводника и рассеянием тепла при его нагревании пренебречь.
ВАРИАНТ 4
ЧАСТЬ А
Выберите один верный ответ.
На рисунке показана зависимость сопротивления проводника длиной 1 м от его площади сечения.
 Чему равно удельное электрическое сопротивление вещества, из которого сделан проводник?
Чему равно удельное электрическое сопротивление вещества, из которого сделан проводник?
10 Оммм2/м
2,5 Ом мм2/м
0,1 Оммм2/м
0,05 Оммм2/м
Как изменится сила тока, проходящего через проводник, если увеличить в 2 раза напряжение между его концами, а длину проводника уменьшить в 2 раза?
не изменится
уменьшится в 2 раза
увеличится в 2 раза
увеличится в 4 раза
На рисунке изображены графики зависимости силы тока в четырех проводниках от напряжения на их концах. Сопротивление какого проводника меньше 1 Ом?
проводника 1
проводника 2
проводника 3
проводника 4
На участке цепи, изображенном на рисунке, сопротивление каждого резистора равно 2 Ом.
 Общее сопротивление участка равно
Общее сопротивление участка равно
8 Ом
5 Ом
4 Ом
1 Ом
В цепи, изображенной на рисунке амперметр показывает силу тока 2 А. К каким точкам нужно подключить вольтметр, чтобы его показания были равны 6 В?
Три резистора сопротивлениями R, = 10 Ом, R, = 6 Ом и R, = 3 Ом соединены в цепь как показано на рисунке. На каком резисторе выделится наименьшее количество теплоты?
на первом
на втором
на третьем
на всех одинаково
7. Электрическая цепь состоит из источника с ЭДС 3 В и внутренним сопротивлением 1 Ом. Внешнее сопротивление 2 Ом. Сила тока в цепи равна
9 А
7 А
1,5 А
1 А
ЧАСТЬ В
Используя условие задачи, установите соответствия величин из левого столбца таблицы с их изменениями в правом столбце.

В цепи, изображенной на рисунке, ползунок реостата передвинули вверх. При этом…
Решите задачи.
В резисторе сопротивлением 360 Ом при напряжении 15 В электрическим током была совершена работа 450 Дж. За какое время была совершена работа?
Электрическая цепь состоит из двух резисторов сопротивлением по 4 Ом соединенных параллельно, источника тока с ЭДС16 В и внутренним сопротивлением 2 Ом. Определить силу тока в цепи.
ЧАСТЬ С
Решите задачу.
К однородному медному цилиндрическому проводнику длиной 40 м приложили разность потенциалов 10 В. Каким будет изменение температуры проводника через 15 с? Изменением сопротивления проводника и рассеянием тепла при его нагревании пренебречь.
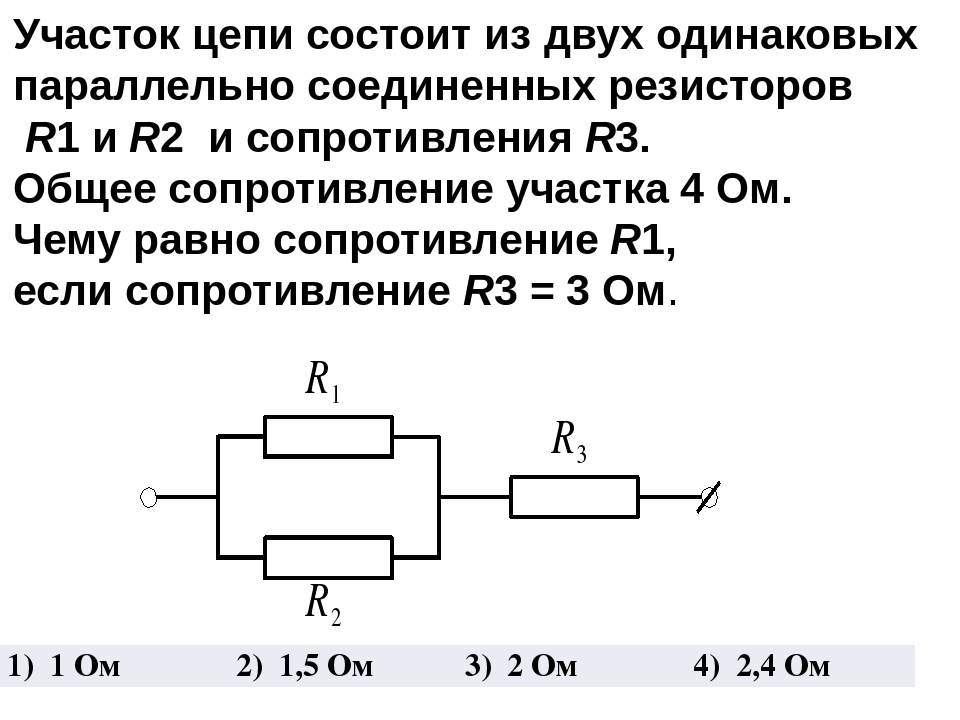
1. Нарисовать схему соединения резисторов R1 =2 Ом, R2 =4 Ом, R3 = 6 Ом, при котором общее сопротивление цепи = 3 Ом? 2
Приложение
5.
Вариант 1
1. Нарисовать схему соединения резисторов R1 =2 Ом, R2 =4 Ом, R3 = 6 Ом, при котором общее сопротивление цепи = 3 Ом?
2 . После того, как один из проводов данной цепи перерезали, показания амперметра (при том же напряжении на концах цепи) уменьшилось в 2 раза. Перечеркните на схеме
перерезанный провод.
10 Ом
20 Ом
30 Ом
3. Электрическая цепь состоит из двух резисторов сопротивлением по 4 Ом,
амперметра и источника тока с ЭДС 30 В и внутренним сопротивлением 2 Ом.
Нарисовать схему соединения этих элементов цепи, при котором амперметр показывает 3 А.
4. Лампа Л1 имеет мощность 60 Вт. Какова мощность лампы Л2 ?
25 В
100 В
5.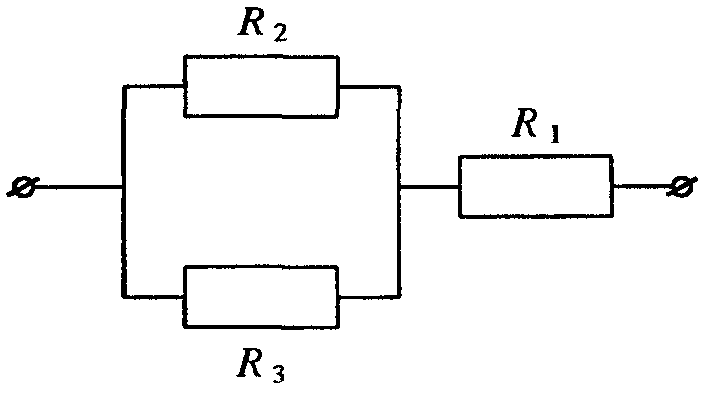 Два
нагревательных элемента имеют
сопротивления R1 =
100 Ом, R2 =
400 Ом . За какое время в первом элементе
выделится такое же количество теплоты,
как во втором за 1 час?
Два
нагревательных элемента имеют
сопротивления R1 =
100 Ом, R2 =
400 Ом . За какое время в первом элементе
выделится такое же количество теплоты,
как во втором за 1 час?
R1
R2
Вариант 2
1. Нарисовать схему соединения резисторов R1=3 Ом, R2=4 Ом и R3=12 Ом, при котором общее сопротивление цепи равно 6 Ом.
2. После того как один из проводов данной цепи перерезали, показание амперметра (при том же напряжении на концах цепи) уменьшилось в 2 раза. Перечеркните на схеме перерезанный провод.
10 Ом
5 Ом
10 Ом
3. Электрическая цепь состоит из двух
резисторов сопротивлением по 4 Ом,
амперметра и источника тока с ЭДС 12В и
внутренним сопротивлением 2 Ом.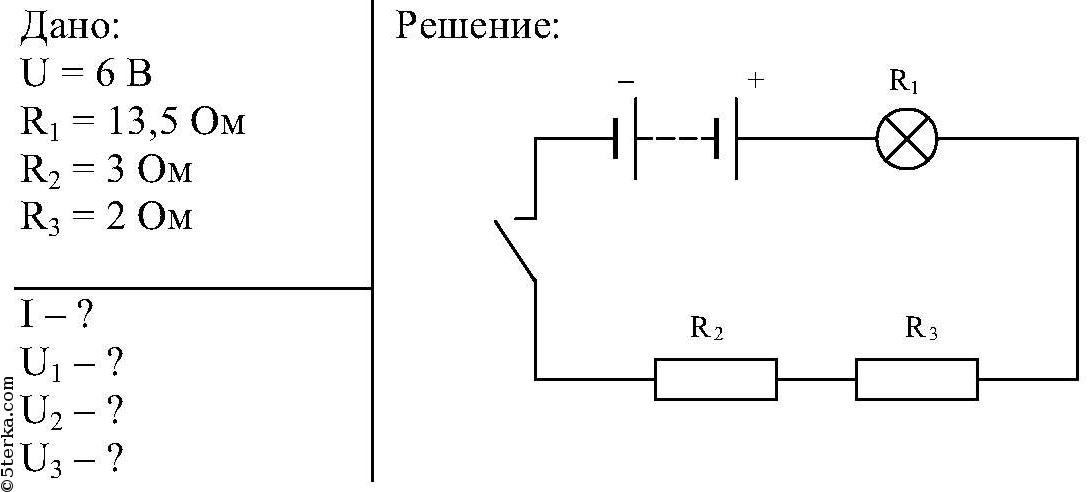 Нарисовать
схему соединения этих элементов цепи,
при котором амперметр показывает 3 А.
Нарисовать
схему соединения этих элементов цепи,
при котором амперметр показывает 3 А.
4. Лампа Л1 имеет мощность 60 Вт. Какова мощность лампы Л2?
1 А
2.5 А
5. Два нагревательных элемента имеют сопротивления R1=100 Ом, R2=400 Ом. За какое время в первом элементе выделится такое же количество теплоты, как во втором за 1 час?
R1 R2
Вариант 3
1. Нарисовать схему соединения трех одинаковых резисторов сопротивлением 4 Ом каждый, при котором общее сопротивление цепи равно 6 Ом.
2. После того как один из проводов данной цепи перерезали, показание амперметра (при том же напряжении на концах цепи) уменьшилось в 2 раза. Перечеркните на схеме перерезанный провод.
. 8 Ом
12 Ом
24 Ом
+ —
3.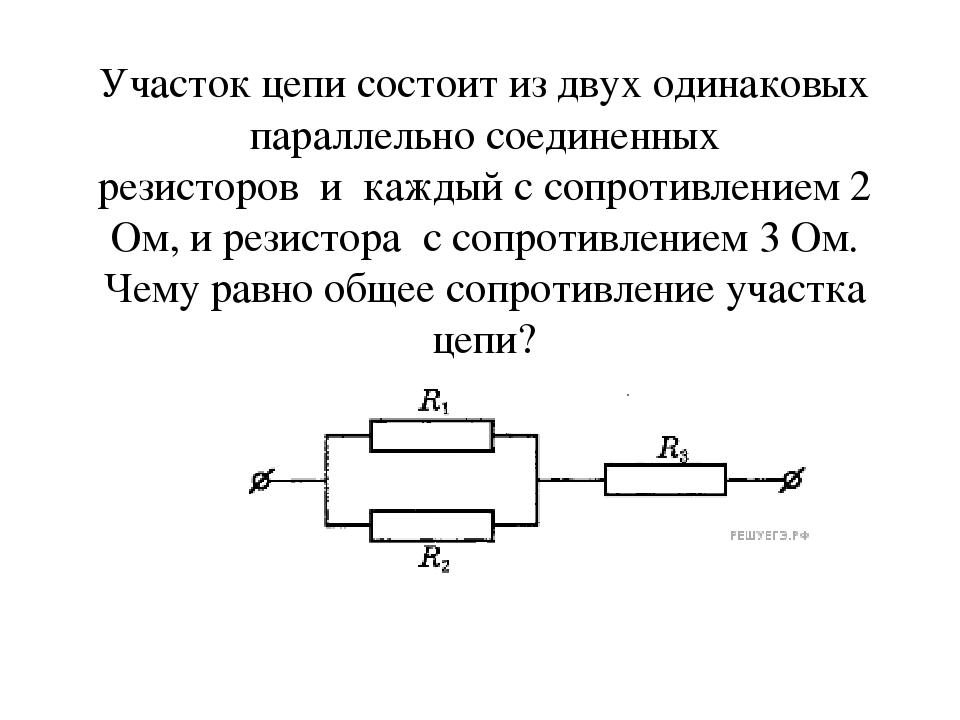 ЭДС источника тока 100 В, внутреннее
сопротивление
ЭДС источника тока 100 В, внутреннее
сопротивление
2 Ом. Найти показание амперметра.
15 Ом
23 Ом
4. Сопротивление ламп Л1 и Л2 равны соответственно R1=150 Ом, R2=30 Ом. Сравнить мощности ламп.
5. Какое количество теплоты выделится в резисторе сопротивлением 50 Ом за 5 мин?
50 В
25 Ом 50 Ом
Вариант 4
Нарисовать схему соединения резисторов R1=1 Ом, R2=2 Ом, R3=3 Ом, R4=4 Ом, при котором общее сопротивление цепи равно 7 Ом.
2. После того как один из проводов данной цепи перерезали, показание амперметра (при том же напряжении на концах цепи) уменьшилось в 2 раза. Перечеркните на схеме перерезанный провод.
24 Ом
4 Ом 6 Ом
24 Ом
3.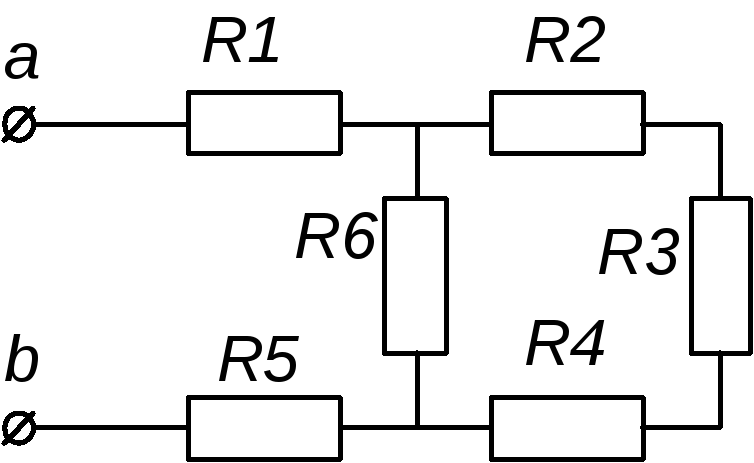 Электрическая цепь состоит из двух
резисторов сопротивлением по 20 Ом,
амперметра и источника тока с ЭДС 24 В и
внутренним сопротивлением 2 Ом. Нарисовать
схему соединения этих элементов цепи,
при котором амперметр показывает 1 А.
Электрическая цепь состоит из двух
резисторов сопротивлением по 20 Ом,
амперметра и источника тока с ЭДС 24 В и
внутренним сопротивлением 2 Ом. Нарисовать
схему соединения этих элементов цепи,
при котором амперметр показывает 1 А.
4. Мощность первой лампы 100 Вт, мощность второй 200 Вт. Найти мощность третьей лампы.
1 А
100 В
5. Нагревательный элемент электрической плитки состоит из двух одинаковых спиралей. При последовательном соединении спиралей вода в кастрюле закипает через 20 мин. Сколько времени потребуется для закипания того же количества воды при параллельном соединении спиралей?
Закон ома для полной цепи
Закон Ома для полной цепи
 Внутреннее сопротивление источника тока r = 0,1 R1. Определить, во сколько раз изменятся показания амперметра и напряжение на клеммах источника при замыкании ключа К?
Внутреннее сопротивление источника тока r = 0,1 R1. Определить, во сколько раз изменятся показания амперметра и напряжение на клеммах источника при замыкании ключа К?Решение
1. При разомкнутом ключе К закон Ома для полной цепи записывается следующим образом
. (1)
2. При замыкании ключа сопротивление нагрузки изменится
. (2)
3. Закон Ома в этом случае примет вид
. (3)
4. Отношение токов определится как
. (4)
5. Падение напряжения на клеммах источника при разомкнутом ключе
. (5)
6. Падение напряжения после замыкания ключа
. (6)
7. Отношение напряжений на клеммах источника
. (7)
2.3.2. Батарея замкнутая на сопротивлениеR1 = 10 Ом, даёт ток силой I1 = 3 А; замкнутая на сопротивлениеR2 = 20 Ом, она даёт ток силой I2 = 1,6 А. Определите ЭДС источника и её внутреннее сопротивление r.
Определите ЭДС источника и её внутреннее сопротивление r.Решение
1. Запишем дважды уравнение закона Ома для полной цепи
(1)
2. Выразим из первого уравнения системы (1) величину и подставим во второе уравнение
, (2)
3. Разрешим полученное уравнение относительно внутреннего сопротивления источника r
. (3)
4. Значение величины можно получить из любого уравнения системы (1) при подстановки в него r из уравнения (3)
.
2.3.3. Батареи с ЭДС 1 = 20 В, 2 = 30 В и внутренними сопротивлениями соответственно r1 = 4 Ом, r2 = 6 Ом соединены параллельно и согласно. Каковы должны быть параметры и r эквивалентного источника, которым можно заменить соединение?Решение
1.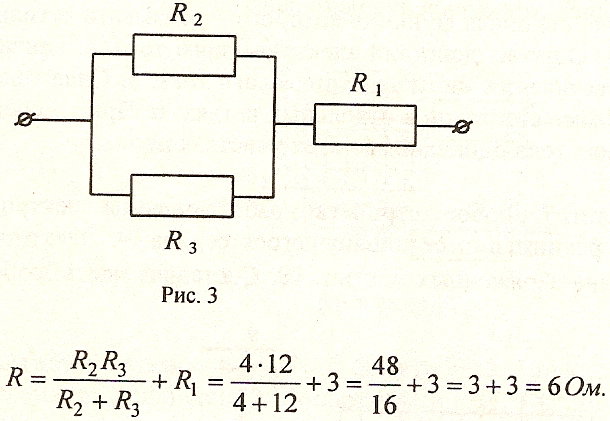 Определим силу тока, протекающего через источники при их совместном включении
Определим силу тока, протекающего через источники при их совместном включении
. (1)
2. Сила тока, который может быть получен от двух источников при их совместной работе I0 = I1 + I2 = 5 A
3. Общее внутреннее сопротивление
. (2)
4. Определим далее эквивалентную ЭДС
. (3)
Таким образом, эквивалентный источник должен иметь ЭДС = 12 В и внутреннее сопротивление r = 2,4 Ом.
2.3.4. Две батареи с одинаковым внутренним сопротивлением соединены так, что ЭДС образовавшегося источника напряжения равна . ЭДС одной из батарей 3/2. Нарисуйте все возможные схемы соединений. Для каждого варианта соединений определите ЭДС второй батареи.
Решение
1. Один из вариантов включение источников последовательно и встречно, когда ЭДС второго источника равна 2 = 0,5, а 1 = . В этом случае общая ЭДС определится как . Внутренне сопротивление такого включения источников будет равно 2r. 2. Возможно и параллельное согласное включение источников, общее сопротивление которых будет равно r/2. Падение напряжения на источниках будет одинаковым и равным . Сила тока через общую шину определится как
В этом случае общая ЭДС определится как . Внутренне сопротивление такого включения источников будет равно 2r. 2. Возможно и параллельное согласное включение источников, общее сопротивление которых будет равно r/2. Падение напряжения на источниках будет одинаковым и равным . Сила тока через общую шину определится как. (1)
Сила тока через первый источник
. (2)
Сила тока через второй источник
. (3)
Электродвижущая сила второго источника
. (4)
3. Следующий способ отличается от предыдущего тем, что источники включены встречно. Чтобы получить в результате батарею с ЭДС, равной , необходимо, чтобы у второго элемента ЭДС была равна /2. Как и в предыдущем случае сила тока будет определяться уравнением (1), потому что внутренние сопротивления включены параллельно. Сила тока через первый источник будет определяться как
. (5)
(5)Ток через второй источник
. (6)
Электродвижущая сила второго элемента должна составлять
. (7)
2.3.5. Три одинаковые батареи соединены параллельно и подключены к внешнему сопротивлению. Как изменится сила тока через это сопротивление, если полярность одной из батарей поменять на обратную?Решение
1. Отметим сразу что, в связи с идентичностью элементов в обоих случаях их параллельного включения суммарное внутреннее сопротивление будет в три раза меньше, чем у одного источника, при этом при согласном включении сила тока через внешнее сопротивление R определится уравнением
. (1)
2. Проанализируем ситуацию при встречном включении одного из источников тока. Результирующий ток определится как. (2)
3. Отношение сил токов
. (3)
2.3. 6. Что покажет вольтметр, если в цепи, изображённой на рисунке, если источники одинаковы, ЭДС каждого из них =1,5 В, внутреннее сопротивление r = 2 Ом? Чему будет равна сила тока в цепи?
6. Что покажет вольтметр, если в цепи, изображённой на рисунке, если источники одинаковы, ЭДС каждого из них =1,5 В, внутреннее сопротивление r = 2 Ом? Чему будет равна сила тока в цепи?Решение
1. Будем считать, что вольтметр обладает бесконечно большим сопротивлением, в этом случае сила тока в цепи определится соотношением
. (1)
2. Поскольку все три элемента в данной схеме включения работают в режиме короткого замыкания, и ток I0, по сути является током короткого замыкания, то в указанных на схеме точках разность потенциалов будет равна нулю, т.е. UV =0.
2.3.7. Определите заряд конденсатора С ёмкостью С = 4 мкФ в стационарном режиме, если R1 = R2 = R3 = R= 100 Ом. Источник тока обладает ЭДС = 300 В и нулевым внутренним сопротивлением.
Решение
1. Сопротивления R2 и R3 включены параллельно, поэтому их можно представить эквивалентным одним сопротивлением величиной
. (1)2. Определим силу тока в цепи
. (2)
3. Падение напряжения на сопротивлении R1 будет равно разности потенциалов на обкладках конденсатора, который для постоянного тока обладает бесконечным сопротивлением
. (3)
4. Заряд конденсатора определим из уравнения энергии
. (4)
2.3.8. Два вертикально расположенных стержня, имеющие длину L = 1 м и диаметр d = 1 см сопротивление на единицу длины = 110 5 Омм, подсоединены через идеальный амперметр к источнику ЭДС = 1,5 В и внутренним сопротивлением r0 = 0,05 Ом. Полосок касается сопротивление R = 0,1 Ом, которое в поле тяжести g начинает соскальзывать вдоль них из верхней точки вниз без нарушения контакта, как показано на рисунке. В пренебрежении эффектами, связанными с магнитным полем, определить какое значение тока I покажет амперметр через время = 0,5 с после начала движения? Силу трения не учитывать
Полосок касается сопротивление R = 0,1 Ом, которое в поле тяжести g начинает соскальзывать вдоль них из верхней точки вниз без нарушения контакта, как показано на рисунке. В пренебрежении эффектами, связанными с магнитным полем, определить какое значение тока I покажет амперметр через время = 0,5 с после начала движения? Силу трения не учитыватьРешение
1. Запишем кинематические уравнения движения сопротивления, считая, что на него действует только сила тяжести и движение происходит по вертикальной оси с нулевой начальной скоростью
, (1)
и определим расстояние которое пройдёт сопротивление за время
. (2)
2. Определим электрическое сопротивление одного отрезка стержня длиной
. (3)
3. Электрическая схема установки, таким образом представит собой три последовательно включенных внешних сопротивления: R0 = R + 2r и внутреннее сопротивление источника r0. Закон Ома для полной цепи в этом случае запишется так
Закон Ома для полной цепи в этом случае запишется так
. (4)
2.3.9. Два гальванических элемента с 1 =1,5 В и 2 = 4,5 В соединены одноимёнными полюсами. Внутреннее сопротивление первого источника r1 в два раза меньше внутреннего сопротивления второго элемента r2, т.е. r2 = 2 r1. Каковы при этом включении элементов будут показания вольтметра?Решение
1. Если считать, что вольтметр обладает бесконечным сопротивлением, то разность электродвижущих сил источников тока будет равна сумме падений напряжения на их внутренних сопротивлениях
. (1)
2. С другой стороны второй элемент является внешней нагрузкой для первого элемента
, (2)
где U показания вольтметра.
3. Выразим из последнего уравнения силу тока в цепи
. (3)
4. Подставим значение силы тока в уравнение (1)
, (4)
откуда
. (5)
2.3.10. Источник тока обладает внутренним сопротивлением r = 1 Ом, ёмкость конденсатора С = 10 мкФ, R1 = 5 Ом, R2 = 10 Ом. До замыкания ключа вольтметр показывает напряжение U1 = 10 В, а после замыкания U2 = 8 В. Определить заряд конденсатора и величину сопротивления R3.Решение
1. При разомкнутом ключе ток в цепи отсутствует, поэтому вольтметр будет демонстрировать величину ЭДС, U1 = = 10 В.
2. Запишем далее уравнение общего сопротивления цепи, считая что конденсатор для постоянного тока в стационарном режиме представляет бесконечное сопротивление
, (1)
с другой стороны
. (2)
(2)
3. Определим величину сопротивления R3
. (3)
4. Определим падение напряжения на сопротивлении R3, которое включено параллельно конденсатору
. (4)
5. Заряд, прошедший через конденсатор
. (5)
2.3.11. Идеальный источник тока с = 100 В включен в цепь, состоящую из конденсаторов С3 = С4 = 1 мкФ, С1 = 2 мкФ, С2 =4 мкФ и сопротивления R. Определить падение напряжения на конденсаторах С1 и С2.Решение
1. При подключении схемы к источнику в цепи потечёт ток до момента полной зарядки всех конденсаторов. После того как конденсаторы зарядятся ток прекращается, т.к. электрические ёмкости представляют для постоянного тока разрыв цепи.
2. Все обкладки конденсаторов, соединённые с сопротивлением будут иметь одинаковый потенциал, при этом пары конденсаторов С1 + С3 и С2 + С4 включены с источником тока последовательно.
3. Падение напряжения на конденсаторах определится уравнением
. (1)
4. Заряд конденсаторов определится как
. (2)
5. Выразим из последнего уравнения величину U2, подставим её в уравнение (1) и разрешим его относительно U1
, (3)
, (4)
. (5)
6. Определим далее величину U2 из уравнения (1)
. (6)
2.3.12. Электрическая схема состоит из двух конденсаторов С1 = 2 мкФ и С2 = 4 мкФ и трёх сопротивлений R1 = 200 Ом, R2 = R3 = 100 Ом.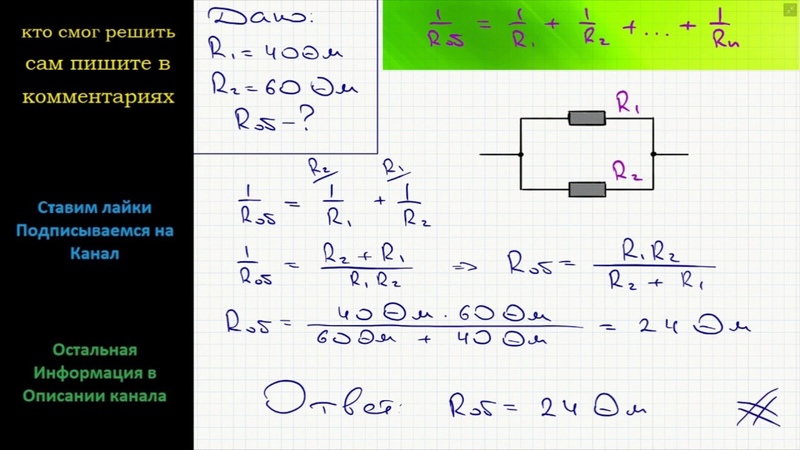 В цепь включён идеальный источник тока с = 100 В. Определить падение напряжения на конденсаторах U1, U2 и их заряд Q1, Q2.
В цепь включён идеальный источник тока с = 100 В. Определить падение напряжения на конденсаторах U1, U2 и их заряд Q1, Q2.Решение
1. Падение напряжения U1 на конденсаторе С1 равно разности потенциалов между точками цепи 1 и 3, а напряжение на С2 определяется разностью потенциалов между точками 2 и 4
, . (1)
2. После зарядки конденсаторов цепь будет представлять собой три последовательно соединённых сопротивления
=400 Ом. (2)
3. Определим силу тока в цепи
. (3)
4. Определим величину напряжений U1, U2 которые, как следует из уравнений (1) будут равны сумме падений напряжения на сопротивлениях U1 = UR1 + UR2, U2 = UR3 + UR4
, (4)
, (5)
5. Заряд конденсаторов определим, используя взаимосвязь падения напряжения заряда и ёмкости
Заряд конденсаторов определим, используя взаимосвязь падения напряжения заряда и ёмкости
(6)
2.3.13. Два последовательно соединённых конденсатора С1 = 2 мкФ и С2 = 4 мкФ замкнуты на источник тока с = 20 В, параллельно которому включено сопротивление R = 20 Ом. Ток короткого замыкания источника IКЗ в три раза превышает рабочий стационарный ток в цепи I. Определить падение напряжения на каждом из конденсаторов.Решение
1. При последовательном соединении конденсаторов через них протекает одинаковый зарядный ток, поэтому заряд на их обкладках будет одинаковым, т.е. Q1 = Q2
. (1)
2. Падение напряжения на конденсаторах можно представить в виде суммы
. (2)
3. Выразим далее величину U2 из уравнения (1) подставим её в уравнение (2) и определим падение напряжения на С1 и С2
, (3)
5.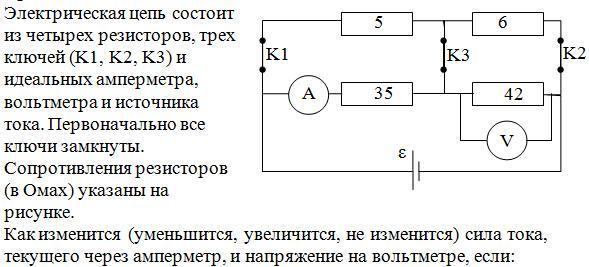 Определим далее внутреннее сопротивление источника тока и величину U0
Определим далее внутреннее сопротивление источника тока и величину U0
. (4)
6. Подставим далее величину U0 в уравнения (3)
. (5)
Правила Кирхгофа
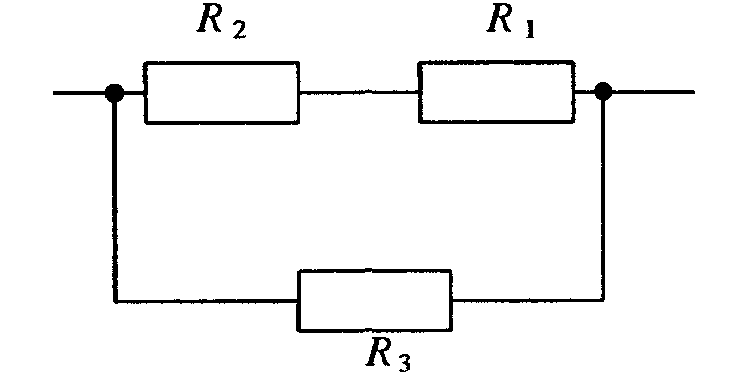
2.4.1. Определить силу токов во всех участках цепи, если источники тока обладают ЭДС: 1 = 10 B, 2 = 20 В, их внутренние сопротивления соответственно равны: r1 = 2 Ом, r2 = 3 Ом. Источники нагружены на внешнее сопротивление R = 100 Ом.
Решение
1. Задачу целесообразно решать, используя правила Кирхгофа, которые удобны при расчетах параметров разветвлённых цепей. В общем виде математические выражения правил имеют вид:
. (1)
2. В соответствие с первым правилом алгебраическая сумма сил токов в любом из узлов должна быть равна нулю
В соответствие с первым правилом алгебраическая сумма сил токов в любом из узлов должна быть равна нулю
. (2)
3. Выделим два замкнутых контура, содержащих источники тока (направление обхода контуров показано пунктиром) и запишем для них второе правило Кирхгофа
. (3)
4. Таким образом, приходим к системе трёх алгебраических уравнений с тремя неизвестными величинами
(4)
5. Выразим из второго и третьего уравнений системы (4) силы тока I1 и I2
, (5)
и подставим эти значения в первое уравнение системы с целью его решения относительно силы тока I
, (6)
, (7)
, (8)
. (9)
6. Определим далее значение сил токов I1 и I2
(10)
7. Знак минус для тока I1 показывает, что направление тока выбрано неправильно, ток будет течь в обратном направлении.
Знак минус для тока I1 показывает, что направление тока выбрано неправильно, ток будет течь в обратном направлении.
8. Проверим правильность решения путём анализа баланса токов по уравнению (1)
. (11)
2.4.2. Электрическая цепь состоит из резисторов R1 = R2 = 10 Ом и трёх идеальных источников тока, причём 1 = 10 В, 2 = 14 В. При каком значении ЭДС третьего источника 3 ток через сопротивление R3не потечёт?Решение
1. Выберем направление токов, выделим два контура и запишем уравнения правил Кирхгофа в соответствии с уравнениями (1) предыдущей задачи
(1)
2. Так как по условию задачи I3 = 0, то I1 = I2, уравнения (1) при этом примут вид
(2)
3. Поделим почленно последние уравнения друг на друга и полученное соотношение разрешим относительно 3
Поделим почленно последние уравнения друг на друга и полученное соотношение разрешим относительно 3
,
,
. (3)
2.4.3. Схема состоит из трёх идеальных источников ЭДС, два из которых заданы: 1 = 10 В, 2 = 8 В, и трёх сопротивлений два из которых тоже известны: R1 = 100 Ом, R2 = 80 Ом. Определить при каком значении 3ток через сопротивление R3ток течь не будет.Решение
1.Выберем узел схемы для которого запишем уравнение первого правила Кирхгофа
. (1)
2. Выделим два замкнутых контура и совершим их обход в указанных пунктирной линией направлениях по второму правилу Кирхгофа
. (2)
(2)
3. По условию задачи I3 =0, поэтому уравнения (1) и (2) можно переписать следующим образом
. (3)
4. Поделим почленно последние два уравнения системы (3) друг на друга
,
. (4)
5. Определим из уравнения (4) значение 3
,
. (5)
2.4.4. Две аккумуляторные батареи (1 = 8 В, r1 = 2Ом; 2 = 6 В, r2 = 1,5 Ом) включены параллельно и согласно. Параллельно источникам тока подсоединено сопротивление R = 10 Ом. Определить силу тока текущего через сопротивление.Решение
1. Выберем узел, для которого запишем уравнение первого правила Кирхгофа
. (1)
(1)
2. Выделим два контура, показанные на схеме пунктирными линиями и составим для них уравнения второго правила Кирхгофа
. (2)
3. Из уравнений (2) выразим токи I1 и I2 и подставим полученные значения в уравнение (1)
, (3)
, (4)
. (5)
4. Определим из уравнения (5) силу тока, протекающего через сопротивление R
, (6)
. (7)
5. Определим далее токи через источники тока
. (8)
Знак «минус» показывает, что направление тока I1 выбрано неверно.
2.4.5. Определить силу тока I3в резисторе R3и падение напряжения U3, если: 1 = 4 В, 2 = 3 В, R1 = 2 Ом, R2 = 6 Ом,R3 = 1 Ом. Источники считать идеальными, их внутренним сопротивлением пренебречь.
Источники считать идеальными, их внутренним сопротивлением пренебречь.Решение
1. Запишем три уравнения в соответствии с правилами Кирхгофа
. (1)
2. Выразим из первого уравнения системы (1) силу тока I1
, (2)
и подставим полученное значение во второе уравнение
, (3)
. (4)
3. Разрешим третье уравнение системы (1) относительно силы тока I2
. (5)
4. Подставим значение I2 из уравнения (5) в уравнение (4)
. (6)
5. Уравнение (6) содержит одну неизвестную искомую величину I3
. (7)
. (8)
Таким образом, ток через сопротивление R3 равен нулю, это значит, что падение напряжения на этом резисторе тоже равно нулю.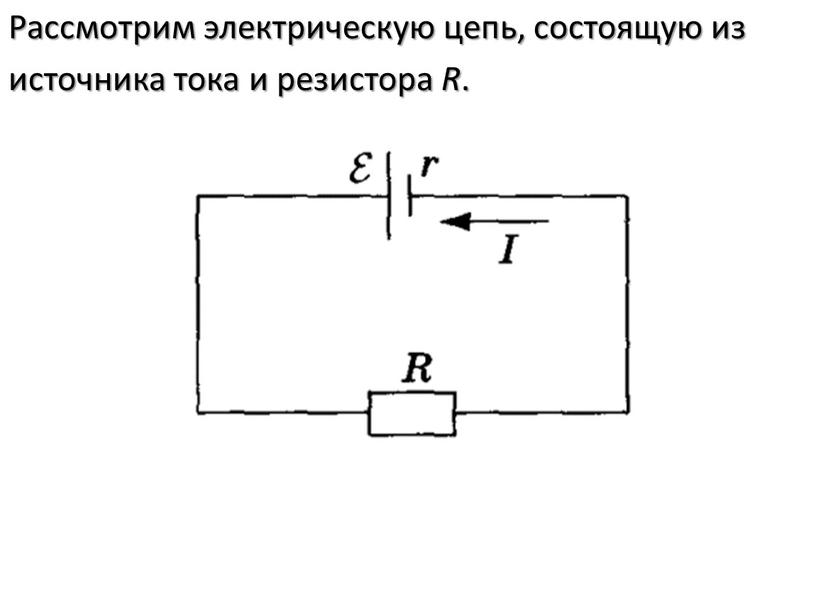
2.4.6. Три источника с ЭДС 1 = 12 В, 2 = 5 В и 3 = 10 В с одинаковым внутренним сопротивлением r = 1 Ом соединены между собой одноимёнными полюсами. Пренебрегая сопротивлением соединительных проводов, определить силы токов, протекающих через источники.
Решение1. Выберем один из узлов и выделим два замкнутых контура, для которых запишем три уравнения первого и второго правила Кирхгофа
. (1)
2. Подставим в последние два уравнения системы (1) заданные числовые значения и сведём её к виду
. (2)
3. Выразим значения сил токов I1 и I3
, (3)
и подставим эти значения в первое уравнение системы (2)
, (4)
следовательно
. (5)
(5)
Решение
1. Запишем для данной цепи уравнения Кирхгофа, рассматривая баланс токов в узле А и баланс напряжений для выбранных контуров
(1)
2. Подставим численные значения заданных по условию задачи величин
(2)
3. Выразим из первого уравнения системы (2) силу тока I3 и подставим это значение в третье уравнение
, (3)
, (4)
. (5)
(5)
4. Образуем новую систему алгебраических уравнений из второго уравнения системы (2) и уравнения (5)
. (6)
5. Выразим далее из второго уравнения системы (6) силу ток I1 и подставим в первое уравнение
. (7)
6. Определим остальные две силы тока, воспользовавшись ранее записанными соотношениями между ними
. (8)
. (9)
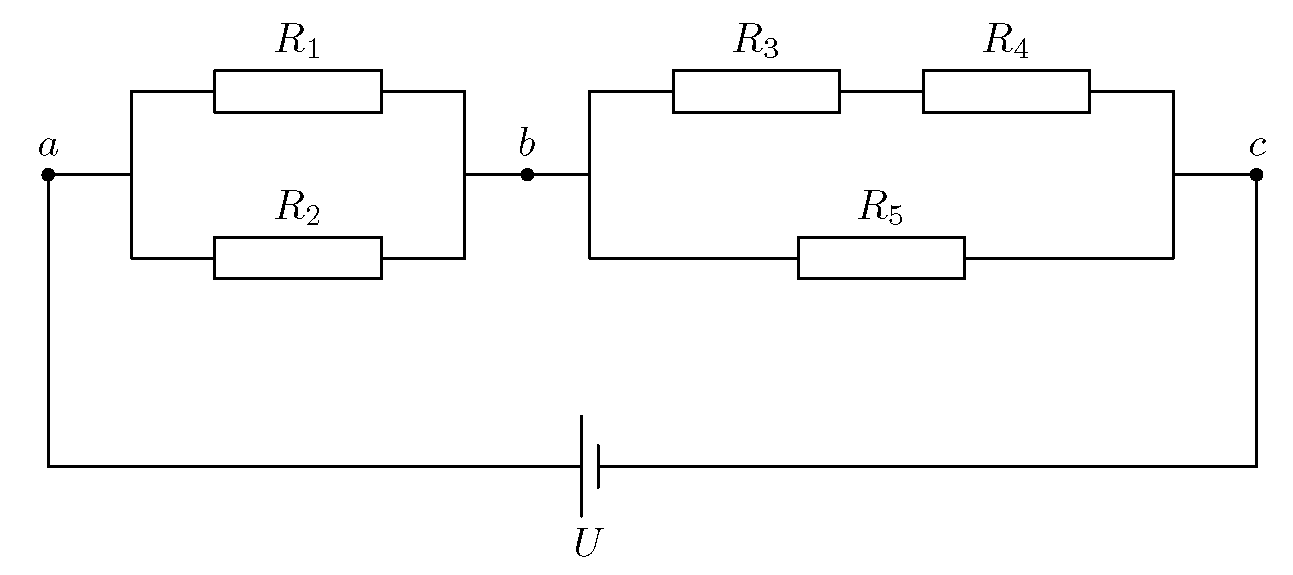
2.4.8.Определить силы токов, текущих в каждой ветви цепи, если: 1 = 6,5 В, 2 = 3,9 В; R1 = R2 = R3 = R4 = R5 = 10 Ом.Решение
1. Для определения искомых величин токов необходимо составить шесть уравнений: три уравнения баланса токов и три уравнения баланса напряжений. Выберем для баланса токов три узла, а для баланса напряжений выделим три замкнутых контура.
Выберем для баланса токов три узла, а для баланса напряжений выделим три замкнутых контура.
2. Составим уравнения баланса токов для узлов a, b и с
. (1)
3. Для обозначенных на схеме цепи пунктирными линиями замкнутых контуров 1, 2 и 3 составим уравнения баланса напряжений, направление обхода показаны стрелками
. (2)
4. С учётом одинаковой величины всех сопротивлений R = 10 Ом последнюю систему уравнений можно переписать следующим образом
(3)
5. Совместное решение системы алгебраических уравнений (4)
(4)
методом подстановки позволяет прийти к следующим значениям сил токов
(5)
Отрицательные значения сил токов, полученные в результате решения, показывают, что их направление было изначально выбрано неверно и следует поменять на обратное.
2. 5. Нелинейные элементы в цепях постоянного тока
5. Нелинейные элементы в цепях постоянного тока
2.5.1. Определить величину силы тока через идеальный источник (r = 0, = 10 В) при включении его в схему двумя способами, если R1 = R2 = R3 = R4 = 10 Ом, а диод идеальный, т.е. обладает в прямом направлении нулевым сопротивлением, а в обратном направлении бесконечно большим сопротивлением.
Решение
1. В первом случае (левая схема) диод будет представлять собой бесконечно большое сопротивление, т.е., по сути, разрыв цепи. Во втором случае (правая схема) сопротивление диода будет мало. Таким образом эквивалентные схемы цепей можно преобразовать следующим образом.
2. В случае большого сопротивления цепи резисторы R3 и R4 оказываются включенными последовательно, их общее сопротивление R3,4 = 20 Ом, которое, в свою очередь включено параллельно резистору R2. (1)
(1)
3. Определим эквивалентное сопротивление правой цепи
. (2)
4. Сила тока в первом случае включения источника тока
. (3)
5. При открытом диоде, когда он обладает весьма малым сопротивлением схему тоже можно последовательно преобразовать, при этом, (4)
, (5)
. (6)
6. Сила тока при открытом диоде составит
. (7)
2.5.2. Определить силу тока, протекающего через идеальный диод, если он включен в диагональ симметричного моста, составленного из сопротивлений R1= 10 кОм,R2= 15 кОм,R3= 30 кОмR4 = 25 кОм. Мостик подключен к идеальному источнику тока с = 200 B.Решение
1.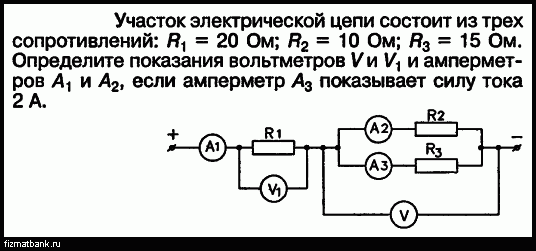 Предположим, что диод заперт, т.е. между точками а и b бесконечно большое сопротивление. В этом случае общее сопротивление схемы определится уравнением
Предположим, что диод заперт, т.е. между точками а и b бесконечно большое сопротивление. В этом случае общее сопротивление схемы определится уравнением
. (1)
2. Сила тока через источник определится как
. (2)
3. Эквивалентная схема цепи в этом случае может быть представлена в виде последовательного соединения сопротивлений R1,4 и R2,3, которые, в свою очередь, включены параллельно источнику тока, (1)
. (2)
4. Падение напряжения на элементах эквивалентной схемы
, (3)
, (4)
, (5)
. (6)
5. Разность потенциалов между точками включения диода составляет U = 12 В, при такой полярности в узловых точках диод должен быть открыт и должен представлять собой весьма малое сопротивление. Другими словами эквивалентная схема цепи будет представлять собой параллельное включение сопротивлений R1, R2 и R3,R4, которые образуют последовательную цепь. Общее сопротивление цепи в этом случае определится как
Общее сопротивление цепи в этом случае определится как. (7)
6. Сила тока через источник
. (8)
7. Составим систему уравнений Кирхгофа для баланса токов в узлах a и b, дополнив их двумя уравнениями закона Ома для участка цепи
(9)
8. Подставив в уравнения (5) и (6) заданные значения сопротивлений, преобразуем их к виду
. (10)
9. Подставим значение силы тока I1 из уравнения (10) в уравнение (1) системы (9)
. (11)
10. Сила тока I1 из уравнений (10) определится как
. (12)
11. Далее подставим значение силы тока I2 из уравнения (10) в уравнение (4) системы (9)
. (13)
12. Определим далее силу тока I2, воспользовавшись для этого уравнениями (10)
.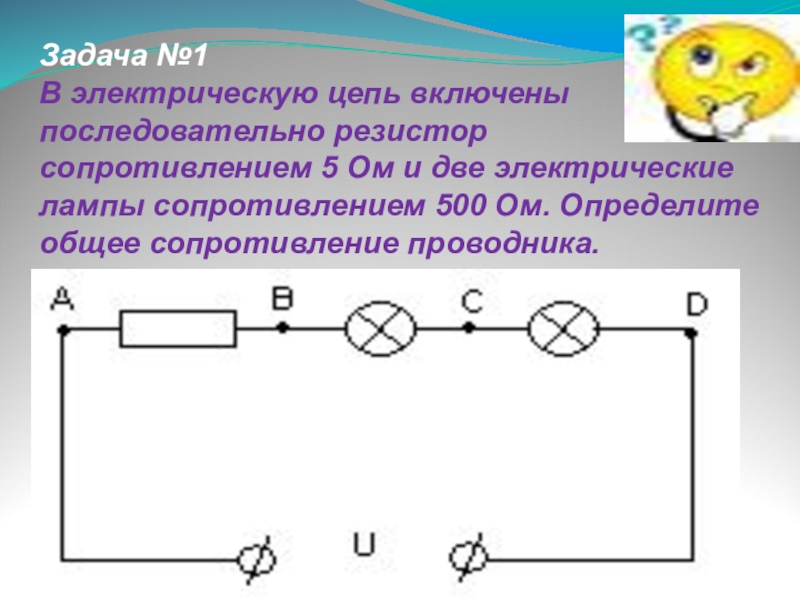 (14)
(14)
13. Из уравнения (4) системы (9) найдём искомую величину силы тока через диод
. (15)
2.5.3. Фотоэлемент включён в диагональ моста, составленного из четырёх резисторов R1 = 100 кОм, R2= 400 кОм, R3= 200 кОм, R4 = 300 кОм. Идеальный источник тока с ЭДС = 1 кВ включен в другую диагональ моста. Определить напряжение на фотоэлементе, если через него течёт ток силой ID = 10 мА.Решение 1.Поскольку через фотоэлемент от анода к катоду течёт, заданный по условию задачи ток силой ID = 10 мА, то он открыт и представляет собой малое сопротивление. Эквивалентная схема цепи в этом случае может быть представлена в виде параллельного включения сопротивлений R1, R2, и R3, R4, которые в свою очередь соединены последовательно.
2. Определим эквивалентное сопротивление всей цепи
. (1)
3. Найдём величину силы тока через источник I0
. (2)
4. Составим систему из пяти (по количеству неизвестных величин) алгебраических уравнений на основе первого правила Кирхгофа и условий равенства потенциалов узлов a и b
(3)
5. Запишем уравнения (4), (5) с учётом заданных величин резисторов
. (4)
6. Перепишем уравнение (2) системы (3) с учётом уравнений (4)
. (5)
7. Определим из уравнения (2) системы (3) значение силы тока I1
. (6)
8. Найдём падение напряжений на резисторах R1 и R2
. (7)
. (8)
9. Напряжение на фотоэлементе: .
Делитель напряжения — Основы электроники
Делитель напряжения это цепь или схема соединения резисторов, применяемая для получения разных напряжений от одного источника питания.
Рассмотрим цепь из двух последовательно соединенных резисторов с разными сопротивлениями (рис. 1).
Рисунок 1. Последовательная цепь есть простейший делитель напряжения.
Согласно закону Ома если приложить к такой цепи напряжение, то падение напряжения на этих резисторах будет тоже разным.
UR1=I*R1;
UR2=I*R2.
Схема, изображенная на рисунке 1, и есть простейший делитель напряжения на резисторах. Обычно делитель напряжения изображают, как это показано на рисунке 2.
Рисунок 2. Классическая схема делителя напряжения.
Для примера разберем простейший делитель напряжения, изображенный на рисунке 2. В нем R1 = 2 кОм, R2 = 1 кОм и напряжение источника питания, оно же и есть входное напряжения делителя Uвх = 30 вольт. Напряжение в точке А равно полному напряжению источника, т. е. 30 вольт. Напряжение Uвых, то есть в точке В равно напряжению на R2.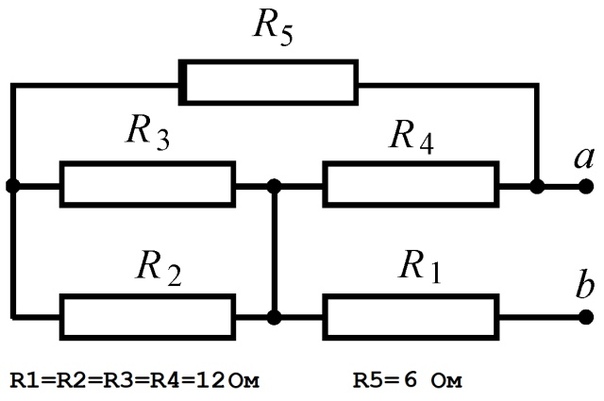 Определим напряжение Uвых.
Определим напряжение Uвых.
Общий ток в цепи равен:
(1)
Для нашего примера I=30 В/ (1 кОм + 2 кОм) = 0,01 А = 10 мА.
Напряжение на R2 будет равно:
(2)
Для нашего примера UR2 = 0,01 А*1000 Ом = 10 В.
Выходное напряжение можно вычислить вторым способом, подставив в выражение (2) значение тока (1), тогда получим:
(3)
UR2 = 30 В*1 кОм/(1 кОм + 2 кОм) = 10 В.
Второй способ применим для любого делителя напряжения, состоящего из двух и более резисторов, включенных последовательно. Напряжение в любой точке схемы можно вычислить с помощью калькулятора за один прием, минуя вычисление тока.
Делитель напряжения из двух последовательно включенных резисторов с равными сопротивлениями
Если делитель напряжения состоит из двух одинаковых резисторов, то приложенное напряжение делится на них пополам.
Uвых = Uвх/2
Делитель напряжения из трех последовательно включенных резисторов с равными сопротивлениями
На рисунке 3 изображен делитель напряжения, состоящий из трех одинаковых резисторов сопротивлением в 1 кОм каждый. Вычислим напряжение в точках А и В относительно точки Е.
Вычислим напряжение в точках А и В относительно точки Е.
Рисунок 3. Делитель напряжения из трех резисторов.
Общее сопротивление R= R1+R2+R3 = 1 кОм + 1 кОм + 1 кОм = 3 кОм
Напряжение в точке А относительно точки Е будет равно:
Тгда Ua-e =30 В/(1 кОм + 1 кОм + 1 кОм)*1 кОм = 10 В.
Напряжение в точке В относительно точки Е будет равно:
Тгда Ub-e =30 В/(1 кОм + 1 кОм + 1 кОм)*(1 кОм + 1 кОм) = 20 В.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Электрические схемы — Студопедия
1. B 15 № 1404. Как изменится сопротивление участка цепи АВ, изображенного на рисунке, если ключ К разомкнуть?
Сопротивление каждого резистора равно 4 Ом.
1) уменьшится на 4 Ом
2) уменьшится на 2 Ом
3) увеличится на 2 Ом
4) увеличится на 4 Ом
Решение.
До размыкания ключа, изображенные на рисунке вертикально сопротивления закорочены, схема представляет собой просто резистор R.
Если разомкнуть ключ, «вертикальные» сопротивления перестанут быть закороченным и схема станет представлять собой последовательно соединение резистора R с двумя параллельно соединенными резисторами R. Следовательно сопротивление участка цепи после размыкания ключа будет равно:
.
Таким образом, сопротивление участка цепи увеличится на 2 Ом.
Правильный ответ: 3.
2. B 15 № 1408. На фотографии — электрическая цепь.
Показания вольтметра даны в вольтах.Чему будут равны показания вольтметра, если его подключить параллельно резистору 2 Ом? Вольтметр считать идеальным.
1) 0,3 В
2) 0,6 В
3) 1,2 В
4) 1,8 В
Решение.
Согласно закону Ома, сила тока, сопротивление проводника и напряжение между его концами связаны соотношением . Поскольку резистор 1 Ом и резистор 2 Ом подключены последовательно, сила тока, текущего через них, совпадает. Следовательно, идеальный вольтметр, подключенный параллельно к резистору 2 Ом, покажет напряжение
.
Правильный ответ: 3.
3. B 15 № 1409. На рисунке показан участок цепи постоянного тока.
Каково сопротивление этого участка, если ?
1) 7 Ом
2) 2,5 Ом
3) 2 Ом
4) 3 Ом
Решение.
Участок представляет собой последовательное соединение резистора r и двух параллельно соединенных резисторов 3r. Следовательно, сопротивление этого участка равно .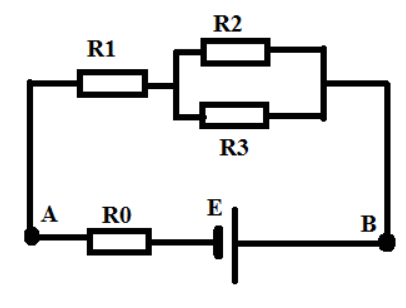
Правильный ответ: 2.
4. B 15 № 1410. На фотографии — электрическая цепь.
Показания включенного в цепь амперметра даны в амперах. Какое напряжение покажет идеальный вольтметр, если его подключить параллельно резистору 3 Ом?
1) 0,8 В
2) 1,6 В
3) 2,4 В
4) 4,8 В
Решение.
Согласно закону Ома, сила тока, сопротивление проводника и напряжение между его концами связаны соотношением . Все резисторы подключены последовательно, а значит, через них всех течет одинаковый ток силой 0,8 A. Таким образом, идеальный вольтметр, подключенный параллельно к резистору 3 Ом, покажет напряжение
Правильный ответ: 3.
5. B 15 № 1411. На участке цепи, изображенном на рисунке, сопротивление каждого из резисторов равно R.
Полное сопротивление участка при замкнутом ключе К равно
1)
2) R
3) 2R
4) 3R
Решение.
После замыкания ключа правая половина схемы окажется закороченной, получившаяся схема будет эквивалента двум подключенным параллельно резисторам.
Полное сопротивление участка при замкнутом ключе К равно: .
Правильный ответ: 1.
6. B 15 № 1412. На участке цепи, изображенном на рисунке, сопротивление каждого из резисторов равно R.
Полное сопротивление участка при замкнутом ключе К равно:
1)
2) R
3) 2R
4) 3R
Решение.
После замыкания ключа левая половина схемы окажется закороченной, получившаяся схема будет эквивалента просто одному резистору.
Полное сопротивление участка при замкнутом ключе К равно R.
Правильный ответ: 2.
7. B 15 № 1413. На участке цепи, изображенном на рисунке, сопротивление каждого из резисторов равно R.
Полное сопротивление участка при замкнутом ключе K равно:
1)
2) R
3) 2R
4) 3R
Решение.
После замыкания ключа схема будет представлять собой параллельное сопротивление резистора с двумя последовательно соединенными резисторами.
Полное сопротивление участка при замкнутом ключе K равно:
.
Правильный ответ: 1.
8. B 15 № 1414. На участке цепи, изображенном на рисунке, сопротивление каждого из резисторов равно R.
Полное сопротивление участка при замкнутом ключе K равно:
1)
2) R
3) 2R
4) 3R
Решение.
После замыкания ключа правая половина схемы окажется закороченной, получившаяся схема будет эквивалента двум подключенным последовательно резисторам.
Полное сопротивление участка при замкнутом ключе K равно: .
Правильный ответ: 3.
9. B 15 № 1415. На участке цепи, изображенном на рисунке, сопротивление каждого из резисторов равно R.
Полное сопротивление участка при замкнутом ключе К равно:
1) 0
2) R
3) 2R
4) 3R
Решение.
После замыкания ключа клеммы окажутся закороченными.
Полное сопротивление участка при замкнутом ключе К равно 0.
Правильный ответ: 1.
10. B 15 № 1417. Участок цепи состоит из трех последовательно соединенных резисторов, сопротивления которых равны r, 2r и 3r Сопротивление участка уменьшится в 1,5 раза, если убрать из него:
1) первый резистор
2) второй резистор
3) третий резистор
4) первый и второй резисторы
Решение.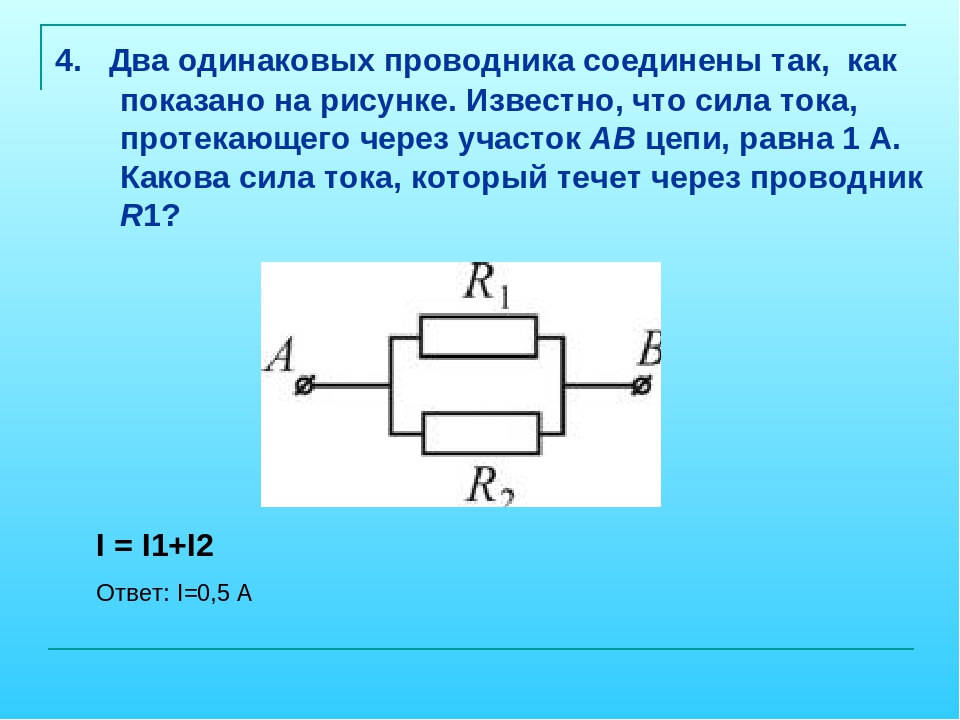
Участок цепи, состоящий из трех последовательно соединенных резисторов с сопротивлениями r, 2r и 3r, имеет сопротивление . Чтобы уменьшить это сопротивление в 1,5 раза, то есть сделать его равным:
,
необходимо убрать сопротивление 2r. Следовательно, нужно убрать второй резистор.
Правильный ответ: 2.
11. B 15 № 1419. На рисунке показан участок цепи постоянного тока, содержащий 3 резистора.
Если сопротивление каждого резистора 21 Ом, то сопротивление всего участка цепи:
1) 63 Ом
2) 42 Ом
3) 14 Ом
4) 7 Ом
Решение.
Участок цепи представляет собой два последовательно соединенных резистора, к которым параллельно подсоединен еще один. Следовательно, сопротивление всего участка равно:
.
Правильный ответ: 3.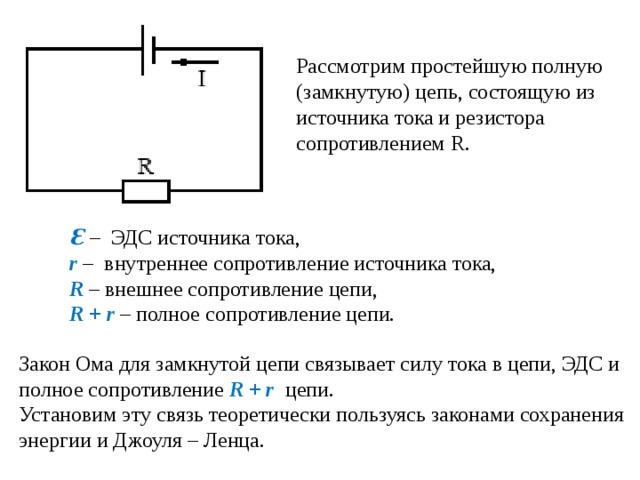
12. B 15 № 1421. На участке цепи, изображенном на рисунке, сопротивление каждого из резисторов равно R.
Полное сопротивление участка при замкнутом ключе К равно:
1) 0
2)
3)
4)
Решение.
1 способ:
После замыкания ключа левая половина схемы окажется закороченной, получившаяся схема будет эквивалента просто одному резистору.
Полное сопротивление участка при замкнутом ключе К равно R.
Правильный ответ: 2.
2 способ:
Рассмотрим левую половинку схемы после замыкания ключа. Она представляет собой параллельное соединение резистора с сопротивлением R и соединительного провода с пренебрежимо малым сопротивлением. Поэтому по правилу подсчета общего сопротивления параллельно соединенных проводников получаем, что сопротивление левой половинки равно .
Таким образом, сопротивление левой половинки схемы равно нулю. Отсюда сразу получаем, что полное сопротивление схемы после замыкания ключа равно .
13. B 15 № 1422. На участке цепи, изображенном на рисунке, сопротивление каждого из резисторов равно R.
Полное сопротивление участка при замкнутом ключе К равно:
1)
2) R
3) 2R
4) 0
Решение.
После замыкания ключа схема будет эквивалента параллельному соединению двух резисторов.
Полное сопротивление участка при замкнутом ключе К равно: .
Правильный ответ: 1.
14. B 15 № 1423. На участке цепи, изображенном на рисунке, сопротивление каждого из резисторов равно R.
Полное сопротивление участка при замкнутом ключе К равно:
1)
2) R
3) 2R
4) 0
Решение.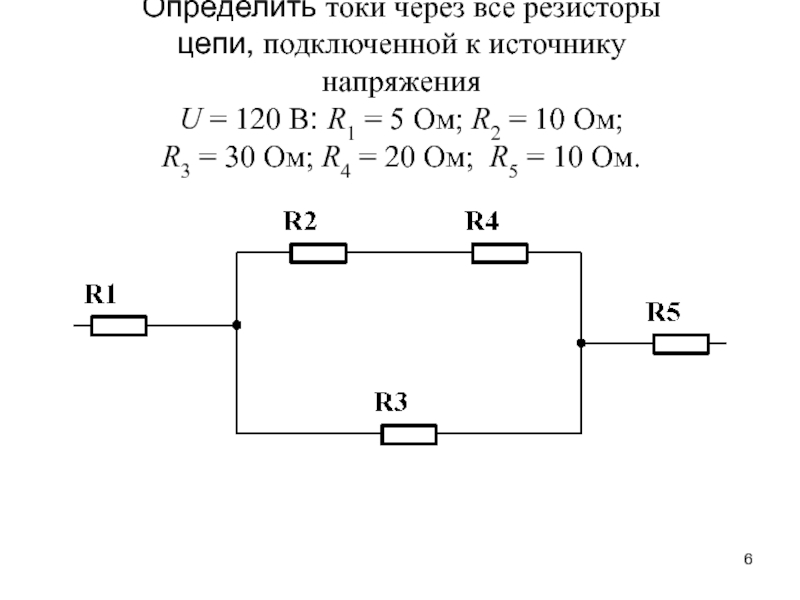
После замыкания ключа левая половина схемы окажется закороченной, получившаяся схема будет эквивалента просто одному резистору.
Полное сопротивление участка при замкнутом ключе К равно R.
Правильный ответ: 2.
15. B 15 № 1424. На участке цепи, изображенном на рисунке, сопротивление каждого из резисторов равно R.
Полное сопротивление участка при замкнутом ключе К равно:
1)
2) R
3) 2R
4) 3R
Решение.
После замыкания ключа левая половина схемы окажется закороченной, получившаяся схема будет эквивалента последовательному соединению трех резисторов.
Полное сопротивление участка при замкнутом ключе К равно: .
Правильный ответ: 4.
16. B 15 № 1425. На участке цепи, изображенном на рисунке, сопротивление каждого из резисторов равно R.
B 15 № 1425. На участке цепи, изображенном на рисунке, сопротивление каждого из резисторов равно R.
Полное сопротивление участка при замкнутом ключе К равно:
1)
2) R
3) 2R
4) 0
Решение.
После замыкания ключа схема будет эквивалента последовательному соединению двух пар параллельно соединенных резисторов.
Полное сопротивление участка при замкнутом ключе К равно:
.
Правильный ответ: 2.
17. B 15 № 1426. Рассчитайте общее сопротивление электрической цепи, представленной на рисунке.
1) 6 Ом
2) 4 Ом
3) 3 Ом
4) 0,25 Ом
Решение.
Электрическая цепь представляет собой последовательное соединение резистора 1 Ом с параллельно соединенными резисторами 2 Ом и еще одним резистором 1 Ом. Сопротивление такой схемы равно:
Сопротивление такой схемы равно:
.
Правильный ответ: 3.
18. B 15 № 1427. Сопротивление цепи на рисунке равно:
1) 11 Ом
2) 6 0м
3) 4 Ом
4) 1 0м
Решение.
Электрическая цепь представляет собой последовательное соединение резистора 2 Ом с параллельно соединенными резисторами 6 Ом и 3 Ом. Сопротивление такой схемы равно:
.
Правильный ответ: 3.
19. B 15 № 1436. Каким будет сопротивление участка цепи (см. рисунок), если ключ К замкнуть?
(Каждый из резисторов имеет сопротивление R.):
1) 2R
2) 0
3) 3R
4) R
Решение.
После замыкания ключа клеммы окажутся закороченными.
Полное сопротивление участка при замкнутом ключе К равно 0.
20. B 15 № 3230. На рисунке представлена электрическая цепь. Амперметр и вольтметр считайте идеальными. Вольтметр показывает напряжение 2 В. Амперметр показывает силу тока
B 15 № 3230. На рисунке представлена электрическая цепь. Амперметр и вольтметр считайте идеальными. Вольтметр показывает напряжение 2 В. Амперметр показывает силу тока
1) 0,2 А
2) 0,5 А
3) 0,8 А
4) 1,2 А
Решение.
Реостат, два резистора с сопротивлениями 4 Ом и 6 Ом и амперметр подключены последовательно, а значит, через них течет одинаковый ток. Используя закон Ома для участка цепи, определим силу тока, текущего через резистор с сопротивлением 4 Ом: . Именно такую силу тока и показывает амперметр.
21. B 15 № 3231. На рисунке представлена электрическая цепь. Вольтметр показывает напряжение 2 В. Считая амперметр и вольтметр идеальными, определите показания амперметра.
1) 0,2 А
2) 0,5 А
3) 0,8 А
4) 1,2 А
Решение.
Реостат, два резистора с сопротивлениями 4 Ом и 10 Ом и амперметр подключены последовательно, а значит, через них течет одинаковый ток. Используя закон Ома для участка цепи, определим силу тока, текущего через резистор с сопротивлением 10 Ом: Именно такую силу тока и показывает амперметр.
22. B 15 № 3232. На рисунке представлена электрическая цепь. Амперметр и вольтметр считайте идеальными. Вольтметр показывает напряжение 12 В. Амперметр показывает силу тока
1) 0,2 А
2) 0,5 А
3) 0,8 А
4) 1,2 А
Решение.
Реостат, два резистора с сопротивлениями 4 Ом и 6 Ом и амперметр подключены последовательно, а значит, через них течет одинаковый ток. Вольтметр подключен к участку цепи, представляющему собой последовательное соединение двух резисторов. Общее сопротивление этого участка цепи равно . Используя закон Ома, определим силу тока, текущего через резисторы: . Именно такую силу тока и показывает амперметр.
Используя закон Ома, определим силу тока, текущего через резисторы: . Именно такую силу тока и показывает амперметр.
23. B 15 № 3233. На рисунке представлена электрическая цепь. Амперметр и вольтметр считайте идеальными. Вольтметр показывает напряжение 12 В. Амперметр показывает силу тока
1) 0,2 А
2) 0,5 А
3) 0,8 А
4) 1,2 А
Решение.
Реостат, три резистора с сопротивлениями 4 Ом, 5 Ом и 6 Ом и амперметр подключены последовательно, а значит, через них течет одинаковый ток. Вольтметр подключен к участку цепи, представляющему собой последовательное соединение трёх резисторов. Общее сопротивление этого участка цепи равно
Используя закон Ома, определим силу тока, текущего через резисторы: . Именно такую силу тока и показывает амперметр.
24. B 15 № 3331. Каково сопротивление изображённого на рисунке участка цепи, если сопротивление каждого резистораr?
B 15 № 3331. Каково сопротивление изображённого на рисунке участка цепи, если сопротивление каждого резистораr?
1)
2)
3) 4r
4)
Решение.
Участок цепи представляет собой три последовательно соединенных резистора, к которым параллельно подсоединен еще один такой же резистор. Следовательно, сопротивление всего участка равно
.
25. B 15 № 3332. Два резистора включены в электрическую цепь параллельно, как показано на рисунке. Значения силы тока в резисторах , . Для сопротивлений резисторов справедливо соотношение
1)
2)
3)
4)
Решение.
При параллельном соединении напряжения на резисторах совпадают. Согласно закону Ома для участка цепи: Следовательно,
.
26. B 15 № 3379. На рисунке приведена фотография электрической цепи, собранной учеником для исследования зависимости силы тока, проходящего через резистор, от напряжения на нем. Для того чтобы через резистор протекал ток силой 1 А, напряжение на нем должно быть равно:
Для того чтобы через резистор протекал ток силой 1 А, напряжение на нем должно быть равно:
1) 0,2 В
2) 3,4 В
3) 5,7 В
4) 7,6 В
Решение.
Из рисунка можно определить показания амперметра и вольтметра. Однако предварительно надо вспомнить определение цены деления измерительного прибора. Цену деления можно определить, разделив расстояние между ближайшими цифрами на шкале на число делений между ними. Например, для вольтметра имеем: .
На фотографии видно, что при напряжении на резисторе в 4,3 В сила тока через него равна 0,75 А. Напряжение на резисторе и сила тока через него пропорциональны, согласно закону Ома, . Следовательно, для того чтобы через резистор тек ток силой 1 А, необходимо приложить к нему напряжение .
27. B 15 № 3381.
Ученик собрал электрическую цепь, изображенную на рисунке. Какая энергия выделится во внешней части цепи при протекании тока в течение 10 мин? Необходимые данные указаны на схеме. Амперметр считать идеальным.
Какая энергия выделится во внешней части цепи при протекании тока в течение 10 мин? Необходимые данные указаны на схеме. Амперметр считать идеальным.
1) 600 Дж
2) 21 600 Дж
3) 36 кДж
4) 3600 Дж
Решение.
Согласно закону Джоуля-Ленца, энергия выделяющаяся за время при протекании через сопротивление величиной тока равна . На схеме ученика резисторы 2 Ом и 4 Ом соединены последовательно, а значит, их общее сопротивление равно Ом. Сила тока равна 1 А. Таким образом, во внешней цепи за 10 минут выделится .
28. B 15 № 3394.
Участок цепи состоит из двух одинаковых параллельно соединенных резисторов и , каждый с сопротивлением 2 Ом, и резистора с сопротивлением 3 Ом.
Общее сопротивление участка цепи равно:
1) 1 Ом
2) 2 Ом
3) 31 Ом
4) 4 Ом
Решение.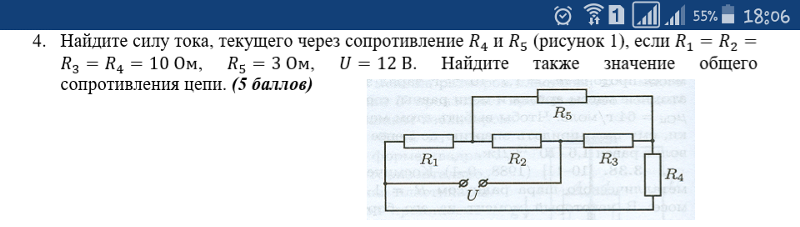
Сначала найдем общее сопротивление двух параллельно соединенных резисторов и : Ом. Резистор подсоединен к ним последовательно. Следовательно общее сопротивление участка цепи равно Ом.
29. B 15 № 3421.
Два резистора включены в электрическую цепь последовательно. Как соотносятся показания идеальных вольтметров, изображенных на рисунке:
1)
2)
3)
4)
Решение.
Через идеальный вольтметр не течет ток, он имеет бесконечное сопротивление, а потому не влияет на величины токов и напряжений в сети. При последовательном соединении, через резисторы течет одинаковый ток. Согласно закону Ома, сила тока через проводник и напряжение, приложенное к нему связаны соотношением . Таким образом, показания вольтметров связаны соотношением: .
30. B 15 № 3422.
B 15 № 3422.
Схема электрической цепи показана на рисунке. Когда ключ К разомкнут, идеальный вольтметр показывает 8 В. При замкнутом ключе вольтметр показывает 7 В. Сопротивление внешней цепи равно 3,5 Ом. Чему равно ЭДС источника тока?
1) 7 В
2) 8 В
3) 15 В
4) 24,5 В
Решение.
Поскольку показания вольтметра, подсоединенного к источнику меняются при замыкании ключа, это означает, что источник не идеальный, и его внутренне сопротивление отлично от нуля. Показания во втором случае меньше, так как через источник начинает течь ток, и часть напряжения падает на внутреннем сопротивлении. В первом же случае, тока в сети нет. Более точно говоря, ток был, пока происходила зарядка конденсатора, но после того, как конденсатор зарядился, ток прекратился. А значит, в первом случае, вольтметр показывает ЭДС источника.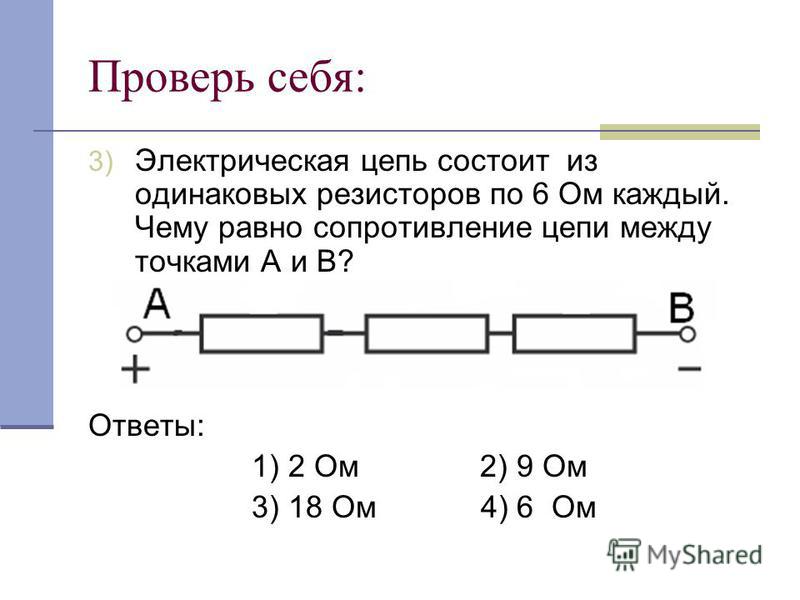 Она равна 8 В.
Она равна 8 В.
31. B 15 № 3424.
На рисунке изображена схема электрической цепи. Что произойдет с общим сопротивлением цепи при замыкании ключа К? Сопротивление цепи
1) увеличится при любых значениях и
2) уменьшится при любых значениях и
3) уменьшится, только если
4) увеличится, только если
Решение.
При замыкании ключа два резистора окажутся подключенными параллельно. При параллельном соединении двух резисторов общее сопротивлении всегда меньше, чем сопротивление любого из них. Проверим это, например для сопротивления , для второго проверяется аналогично. Рассмотрим разность:
Правильный ответ: 2.
32. B 15 № 3471. На рисунке приведена электрическая цепь. Чему равна работа электрического тока за 5 мин протекания тока на участке цепи, к которому подключен вольтметр?
1) 6300 Дж
2) 630 Дж
3) 10,5 Дж
4) 0,3 Дж
Решение.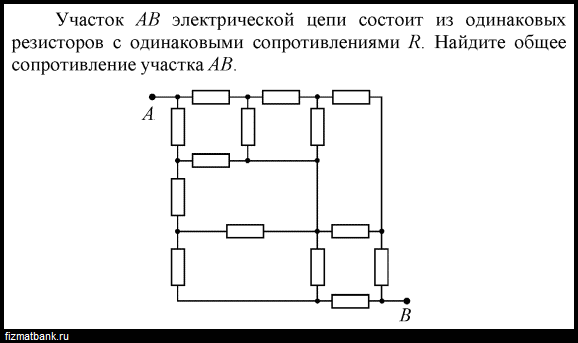
Работа тока за время связана с напряжением и силой тока соотношением . Из рисунка видно, что напряжение равно , а сила тока . Следовательно, работа тока равна .
Правильный ответ: 2.
33. B 15 № 3522. Чему равно сопротивление электрической цепи между точками и , если каждый из резисторов имеет сопротивление ?
1)
2)
3)
4)
Решение.
Поскольку все резисторы одинаковые, из симметрии схемы заключаем, что потенциалы точек и равны , а значит, ток по вертикальной перемычке по закону Ома, не потечет (так как напряжение на ней равно нулю: ) и ее можно выбросить из рассмотрения и не учитывать при подсчете общего сопротивления (так как что с ней, что без нее, ток течет всегда одинаково). Этот факт можно понять еще следующим образом. Предположим, что ток течет по перемычке вниз, «перевернем» всю схему вокруг горизонтальной оси, ток в перемычке теперь будет течь вверх, но сама схема не поменялась, значит в ней ток должен быть такой же, как до переворота. Единственный вариант удовлетворить этому требованию, потребовать, чтобы ток в перемычке был равен нулю.
Единственный вариант удовлетворить этому требованию, потребовать, чтобы ток в перемычке был равен нулю.
Таким образом, мы переходим к более простой схеме, ее общее сопротивление можно легко посчитать, используя правила для последовательного и параллельного подключения проводников: .
Если бы сопротивления были бы разными, то приведенные здесь аргументы потеряли бы силу и пришлось бы искать общее сопротивление первоначальной схемы, используя законы Кирхгофа.
Правильный ответ: 4.
34. B 15 № 3529.
Какое из неравенств верно отображает соответствие между мощностями, выделяющимися на резисторах ; ; ; ?
1)
2)
3)
4)
Решение.
Сперва заметим, что полные сопротивления верхней и нижней ветвей схемы совпадают: .
Следовательно, ток разделится между этими ветвями ровно пополам.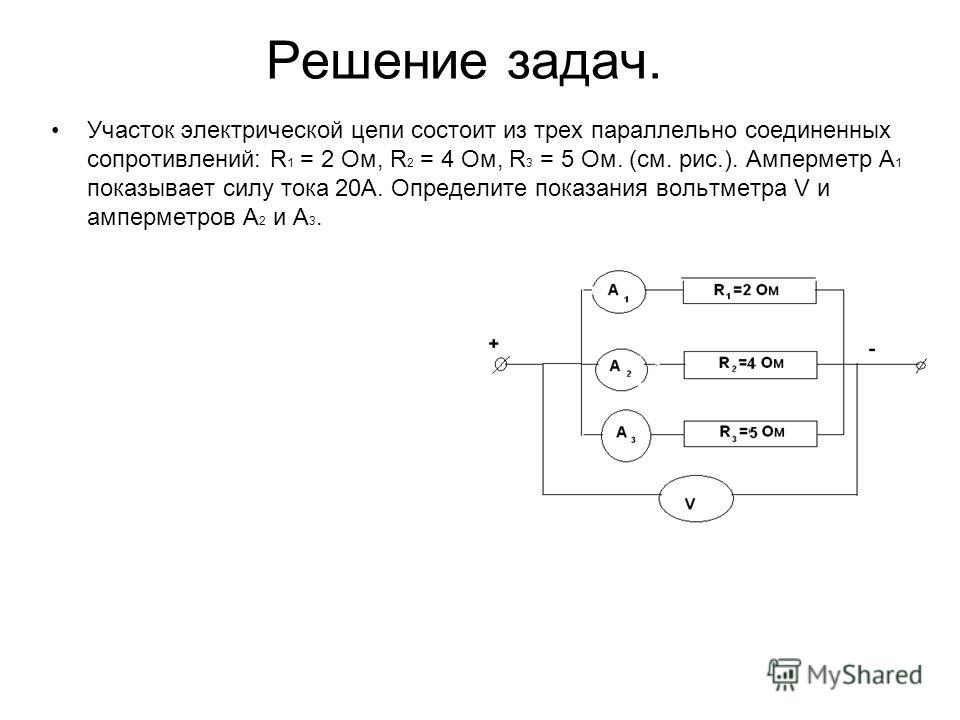 Таким образом, через все сопротивления течет одинаковый ток. Мощность, выделяющаяся на резисторе, связана с силой тока, текущего через него и величиной сопротивления соотношением .
Таким образом, через все сопротивления течет одинаковый ток. Мощность, выделяющаяся на резисторе, связана с силой тока, текущего через него и величиной сопротивления соотношением .
Следовательно, чем меньше сопротивление, тем меньше выделяющаяся на нем мощность. Поскольку , заключаем, что .
Правильный ответ: 3.
35. B 15 № 3537.
Источник тока имеет ЭДС , внутреннее сопротивление , , . Какой силы ток течет через источник?
1) 1 А
2) 2 А
3) 4 А
4) 1,63 А
Решение.
Определим сперва полное сопротивление нагрузки в цепи. Нагрузка представляет собой параллельно соединенные резисторы и , к которым последовательно подключен резистор , следовательно, общее сопротивление нагрузки равно . По закону Ома для полной цепи, сила тока равна .
Правильный ответ: 2.
36. B 15 № 3538.
B 15 № 3538.
Источник тока имеет ЭДС , внутреннее сопротивление , , . Какой силы ток течет через источник?
1) 1 А
2) 2 А
3) 4 А
4) 1,63 А
Решение.
Определим сперва полное сопротивление нагрузки в цепи. Нагрузка представляет собой параллельно соединенные резисторы , и , следовательно, общее сопротивление нагрузки находится следующим образом: . По закону Ома для полной цепи, сила тока равна .
Правильный ответ: 3.
37. B 15 № 3587. На рисунке показана схема электрической цепи. Через какой резистор течет наибольший ток?
1) 1
2) 2
3) 3
4) 4
Решение.
Схема представляет собой параллельное соединение резисторов №2, №3 и №4, к которым последовательно подключен резистор №1. При последовательном подключении сила тока одинаковая. При параллельном соединении сила тока делится между резисторами таким образом, чтобы напряжения на всех резисторах было одинаково. Следовательно, максимальный ток течет через резистор №1.
При параллельном соединении сила тока делится между резисторами таким образом, чтобы напряжения на всех резисторах было одинаково. Следовательно, максимальный ток течет через резистор №1.
Правильный ответ: 1.
38. B 15 № 3603. На рисунке показана схема электрической цепи. Через какой резистор течет наименьший ток?
1) 1
2) 2
3) 3
4) 4
Решение.
Схема представляет собой параллельное соединение резисторов №2 и №3, к которым последовательно подключены резисторы №1 и №4. При последовательном подключении сила тока одинаковая. При параллельном соединении сила тока делится между резисторами таким образом, чтобы напряжения на всех резисторах было одинаково. Таким образом, сразу можно заключить, что через резисторы №1 и №4 течет больший ток, чем через резисторы №2 и №3. По закону Ома напряжение на резисторе связано с текущим через него током соотношением: . А значит, для параллельно подключенных резисторов имеем: . Следовательно, минимальный ток течет через резистор №3.
А значит, для параллельно подключенных резисторов имеем: . Следовательно, минимальный ток течет через резистор №3.
Правильный ответ: 3.
39. B 15 № 3794. Сопротивление каждого резистора в цепи, показанной на рисунке, равно 100 Ом. Участок подключён к источнику постоянного напряжения выводами и . Напряжение на резисторе равно 12 В. Напряжение между выводами схемы равно
1) 12 В
2) 18 В
3) 24 В
4) 36 В
Решение.
Резисторы , и подключены последовательно. Следовательно, через них течет одинаковый ток. Поскольку их сопротивления совпадают, заключаем, используя закон Ома для участка цепи, что напряжения на всех этих трех резисторах одинаковые и равны 12 В. При последовательном подключении напряжения складываются. Таким образом, к участку цепи, включающему сопротивления , , приложено напряжение
.
Но это и есть напряжение между выводами схемы .
Правильный ответ: 4.
40. B 15 № 5365. На рисунке показана схема участка электрической цепи. По участку АВ течёт постоянный ток А. Какое напряжение показывает идеальный вольтметр, если сопротивление Ом?
1) 1В
2) 2 В
3) 0
4) 4 В
Решение.
Идеальный вольтметр покажет напряжение на резисторе которое по закону Ома равно Верхний участок цепи и нижний участок цепи в параллельном участке имеют одинаковое сопротивление, поэтому сила тока в этих участках одинаковая и Тогда
Правильный ответ указан под номером 2.
41. B 15 № 5400. На рисунке показана схема участка электрической цепи. По участку АВ течёт постоянный ток А. Какое напряжение показывает идеальный вольтметр, если сопротивление Ом?
1) 1В
2) 2 В
3) 3 B
4) 0
Решение.
Идеальный вольтметр покажет напряжение на резисторе которое по закону Ома равно Верхний участок цепи и нижний участок цепи в параллельном участке имеют одинаковое сопротивление, поэтому сила тока в этих участках одинаковая и Тогда
Правильный ответ указан под номером 3.
42. B 15 № 6049. На рисунке изображена схема участка электрической цепи, состоящего из трёх резисторов R1 , R2 , R3 . На каком из следующих рисунков приведена электрическая схема этого участка цепи, эквивалентная заданной?
1) 1
2) 2
3) 3
4) 4
Решение.
Представим, что мы изгибаем провода схемы, так чтобы получился один из приведённых выше рисунков. При таких преобразованиях получим, что приведённая схема эквивалентна схеме, указнной под номером 3.
Правильный ответ указан под номером: 3.
43. B 15 № 6084.
На рисунке изображена схема участка электрической цепи, состоящего из трёх резисторов R1, R2 , R3 . На каком из следующих рисунков приведена электрическая схема этого участка цепи, эквивалентная заданной?
1) 1
2) 2
3) 3
4) 4
Решение.
Представим, что мы изгибаем провода схемы, так чтобы получился один из приведённых выш
Тепловое действие электрического тока» — КиберПедия
(2ч)
Реши задачи:
1. Найдите общую силу тока в цепи, состоящей из пяти параллельно соединённых проводников, сопротивления которых соответственно равны R1= 2 Ом, R2=R3= R4 =9 Ом, R5=5 Ом, если ЭДС источника равна 24 В, его внутреннее сопротивление 2 Ом.
Дано: Схема: Решение:
Найти
2. В электроприборе за 15 мин электрическим током силой 2 А совершена работа 9 кДж. Определите сопротивление прибора.
В электроприборе за 15 мин электрическим током силой 2 А совершена работа 9 кДж. Определите сопротивление прибора.
Дано: СИ: Решение:
Найти:
3. Какое количество теплоты выделится в реостате, сопротивление которого 6 Ом, если за 5 мин через него проходит электрический заряд, равный 600 Кл?
Дано: СИ: Решение:
Найти:
4. КПД источника тока равен 60%. Мощность, выделяющаяся во внешней цепи, равна 20 Вт. Найти количество теплоты, выделившееся в источнике тока за 5 мин.
Дано: СИ: Решение:
Найти:
Оценка _____ подпись преподавателя ________________/Л.С. Тишкина/
Дата «___» _________20____г
Задание 29 по теме
«Собственная и примесная проводимости полупроводников. Полупроводниковый диод. Транзистор»
(2ч)
Реши:
1. Какими носителями электрического заряда создаётся ток в полупроводниках?
Какими носителями электрического заряда создаётся ток в полупроводниках?
А. Только электронами. Б. Только ионами. В Электронами и ионами. Г. Электронами и «дырками»
2. Каким типом проводимости обладают полупроводниковые материалы без примесей?
А. В основном электронной. Б. В основном дырочной. В. В равной степени электронной и дырочной. Г. Ионной.
3. В четырехвалентный кремний добавили первый раз трёхвалентный индий, а во второй раз пятивалентный фосфор. Каким типом проводимости в основном будет обладать полупроводники в каждом случае?
А. В первом случае – дырочной, во втором – электронной. Б. В первом случае – электронной, во втором – дырочной. В. В обоих случаях электронной. Г. В обоих случаях дырочной.
4. Какими типами проводимости в основном обладают полупроводниковые материалы с донорными примесями?
А. В основном электронной. Б. В основном дырочной. В. В равной степени электронной и дырочной. Г. Ионной.
5. Каково основное свойство р-n-перехода?
А. Уменьшение сопротивления при нагревании. Б. Уменьшение сопротивления при освещении. В. Односторонняя проводимость. Г. Среди ответов А-В нет правильного.
Уменьшение сопротивления при нагревании. Б. Уменьшение сопротивления при освещении. В. Односторонняя проводимость. Г. Среди ответов А-В нет правильного.
6. Какой основной проводимостью может обладать база транзистора?
А. Только электронной. Б. Только дырочной. В. Электронно-дырочной. Г. Может электронной, может дырочной.
Оценка _____ подпись преподавателя ________________/Г.С. Акатова/
Дата «___» _________20____г
Задание 30
Самостоятельная работа по теме «Постоянный электрический ток»
(3ч)
ВАРИАНТ 1
ЧАСТЬ А Выберите один верный ответ.
1. На рисунке показана зависимость сопротивления проводника площадью сечения 1 мм2 от его длины. Чему равно удельное электрическое сопротивление вещества, из которого сделан проводник?
1) 20 Ом*мм2/м 2) 5 Ом*мм2/м 3) 0,5 Ом*мм2/м 4) 0,2 Ом* мм2/м
2. Как изменится сила тока, проходящего через проводник, если увеличить в 2 раза напряжение между его концами, а площадь сечения проводника уменьшить в 2 раза?
Как изменится сила тока, проходящего через проводник, если увеличить в 2 раза напряжение между его концами, а площадь сечения проводника уменьшить в 2 раза?
1) не изменится 2) уменьшится в 2 раза
3) увеличится в 2 раза 4) увеличится в 4 раза
3. На рисунке изображены графики зависимости силы тока в четырех проводниках от напряжения на их концах. Сопротивление какого проводника равно 4 Ом?
1) проводника 1 2) проводника 2 3) проводника 3 4) проводника 4
4. На участке цепи, изображенном на рисунке, сопротивление каждого резистора равно 3Ом. Общее сопротивление участка равно
1) 12 0м 2) 5 Ом 3) 3,5 Ом 4) 2 Ом
5. В цепи, изображенной на рисунке амперметр показывает силу тока 1 А.К каким точкам нужно подключить вольтметр, чтобы его показания были равны 4 В?
1) АБ 2) БВ 3) БГ 4) АВ
6. В цепи, изображенной на рисунке амперметр показывает силу тока 1 А.К каким точкам нужно подключить вольтметр, чтобы его показания были равны 4 В?
В цепи, изображенной на рисунке амперметр показывает силу тока 1 А.К каким точкам нужно подключить вольтметр, чтобы его показания были равны 4 В?
1) АБ 2) БВ 3) БГ 4) АВ
7. ЭДС источника равна 8В, внешнее сопротивление 3 Ом, внутреннее сопротивление 1 Ом. Сила тока в полной цепи равна
1) 32 А 2) 25 А 3) 2 А 4) 0,5 А
ЧАСТЬ В
8. Используя условие задачи, установите соответствия величин из левого столбца таблицы с их изменениями в правом столбце.
В цепи, изображенной на рисунке, ползунок реостата передвинули вниз. При этом…
Величина Изменение
А. сила тока 1) увеличивается
Б. электродвижущая сила 2) уменьшается
В. напряжение на резисторе 3) не изменяется
Г. сопротивление реостата
Решите задачи.
9. В электроприборе за 15 мин электрическим током совершена работа 9 кДж. Сила тока в цепи 2 А. Определите сопротивление прибора.
Определите сопротивление прибора.
Дано: СИ: Решение:
Найти:
10. Электрическая цепь состоит из двух резисторов сопротивлением по 4 Ом соединенных последовательно, источника тока с ЭДС 30 В и внутренним сопротивлением 2 Ом. Определить силу тока в цепи.
Дано: Решение:
Найти:
ЧАСТЬ С
Решите задачу.
11. Температура однородного медного цилиндрического проводника длиной 10 м в течение 57 с повысилась на 10 К. Определить напряжение, которое было приложено к проводнику в это время. Изменением сопротивления проводника и рассеянием тепла при его нагревании пренебречь.
Дано: Решение:
Найти:
Оценка _____ подпись преподавателя ________________/Л.С. Тишкина/
ВАРИАНТ 2
ЧАСТЬ А Выберите один верный ответ.
1. На рисунке показана зависимость сопротивления проводника длиной 1 м от его площади сечения. Чему равно удельное электрическое сопротивление вещества, из которого сделан проводник?
Чему равно удельное электрическое сопротивление вещества, из которого сделан проводник?
1) 20 Ом*мм2/м 2) 5 Ом*мм2/м 3) 0,5 Ом*мм2/м 4) 0,2 Ом*мм2/м
2. Как изменится сила тока, проходящего через проводник, если уменьшить в 2 раза напряжение между его концами, а длину проводника увеличить в 2 раза?
1) не изменится 2) уменьшится в 2 раза 3) увеличится в 2 раза 4) уменьшится в 4 раза
3. На рисунке изображены графики зависимости силы тока в четырех проводниках от напряжения на их концах. Сопротивление какого проводника равно 1,5 Ом?
1) проводника 1 2) проводника 2 3) проводника 3 4) проводника 4
4. На участке цепи, изображенном на рисунке, сопротивление каждого резистора равно 4 Ом. Общее сопротивление участка равно
1) 16 Ом 2) 10 Ом 3) 3 Ом 4) 1 Ом
5. В цепи, изображенной на рисунке амперметр показывает силу тока 2 А. К каким точкам нужно подключить вольтметр, чтобы его показания были равны 2 В?
К каким точкам нужно подключить вольтметр, чтобы его показания были равны 2 В?
1) АБ 2) АВ 3) БВ 4) БГ
6. Три резистора сопротивлениями R1=10 Ом, R2=6 Ом и R3=3 Ом соединены в цепь как показано на рисунке. На каком резисторе выделится наибольшее количество теплоты?
1) на первом 2) на втором 3) на третьем 4) на всех одинаково
7. Сила тока в полной цепи 8 А, внешнее сопротивление 4 Ом, внутреннее сопротивление 1 Ом. ЭДС источника равна
1) 40 В 2) 33 В 3) 3В 4) 0,5 В
ЧАСТЬ В
8. Используя условие задачи, установите соответствия величин из левого столбца таблицы с их изменениями в правом столбце.
В цепи, изображенной на рисунке, ползунок реостата передвинули вверх. При этом…
Величина Изменение
А. напряжение на резисторе 1) увеличивается
Б. внутреннее сопротивление 2) уменьшается
В. сила тока 3) не изменяется
сила тока 3) не изменяется
Г. сопротивление резистора
Решите задачи.
9. Каково напряжение на резисторе сопротивлением 360 Ом, если за 12 мин электрическим током была совершена работа 450 Дж?
Дано: СИ: Решение:
Найти:
10. Электрическая цепь состоит из двух резисторов сопротивлением по 10 Ом каждый соединенных параллельно, источника тока с ЭДС 24 В и внутренним сопротивлением 1 Ом. Определить силу тока в цепи.
Дано: Решение:
Найти:
ЧАСТЬ С
Решите задачу.
11. К однородному медному цилиндрическому проводнику длиной 10 м приложили разность потенциалов 1 В. Определите промежуток времени, в течение которого температура проводника повысится на 10 К. Изменением сопротивления проводника и рассеянием тепла при его нагревании пренебречь.
Дано: Решение:
Найти:
Оценка _____ подпись преподавателя ________________/Л. С. Тишкина/
С. Тишкина/
ВАРИАНТ 3
ЧАСТЬ А Выберите один верный ответ.
1. На рисунке показана зависимость сопротивления проводника площадью сечения 1 мм2 от его длины. Чему равно удельное электрическое сопротивление вещества, из которого сделан проводник?
1) 40 Ом*мм2/м 2) 10 Ом*мм2/м 3) 0,5 Ом*мм2/м 4) 0,1 Ом*мм2/м
2. Как изменится сила тока, проходящего через проводник, если уменьшить в 2 раза напряжение между его концами, а площадь сечения проводника увеличить в 2 раза?
1) не изменится 2) уменьшится в 2 раза 3) увеличится в 2 раза 4) увеличится в 4 раза
3. На рисунке изображены графики зависимости силы тока в четырех проводниках от напряжения на их концах. Сопротивление какого проводника равно 1 Ом?
1) проводника 1 2) проводника 2 3) проводника 3 4) проводника 4
4. На участке цепи, изображенном на рисунке, сопротивление каждого резистора равно 3 Ом. Общее сопротивление участка равно
На участке цепи, изображенном на рисунке, сопротивление каждого резистора равно 3 Ом. Общее сопротивление участка равно
1) 12 Ом 2) 6 Ом 3) 4 Ом 4) 3 Ом
5. В цепи, изображенной на рисунке амперметр показывает силу тока 2 А.К каким точкам нужно подключить вольтметр, чтобы его показания были равны 20 В?
1) АБ 2) БВ 3) ВГ 4) АВ
6. Три резистора сопротивлениями R1=3Ом, R2=6 Ом и R3=9Ом соединены в цепь как показано на рисунке. На каком резисторе выделится наименьшее количество теплоты?
1) на первом 2) на втором 3) на третьем 4) на всех одинаково
7. Сила тока в полной цепи 6 А, внешнее сопротивление 2 Ом, внутреннее сопротивление 1 Ом. ЭДС источника равна
1) 18 В 2) 13 В 3) 3 В 4) 0,5 В
ЧАСТЬ В
8. Используя условие задачи, установите соответствия величин из левого столбца таблицы с их изменениями в правом столбце.
Используя условие задачи, установите соответствия величин из левого столбца таблицы с их изменениями в правом столбце.
В цепи, изображенной на рисунке, ползунок реостата передвинули вниз. При этом…
Величина Изменение
А. напряжение на резисторе 1) увеличивается
Б. внутреннее сопротивление 2) уменьшается
В. Сила тока 3) не изменяется
Г. сопротивление резистора
Решите задачи.
9. В электроприборе с сопротивлением 2,5 Ом электрическим током за 15 мин совершена работа 9кДж. Определите силу тока в цепи.
Дано: СИ: Решение:
Найти:
10. Электрическая цепь состоит из двух резисторов сопротивлением 15 Ом и 23 Ом соединенных последовательно, источника тока с ЭДС 100 В и внутренним сопротивлением 2 Ом. Определить силу тока в цепи.
Дано: Решение:
Найти:
ЧАСТЬ С
Решите задачу.
11. К однородному медному цилиндрическому проводнику на 15 с приложили разность потенциалов 1 В. Какова длина проводника, если его температура при этом повысилась на 10 К? Изменением сопротивления проводника и рассеянием тепла при его нагревании пренебречь.
Дано: Решение:
Найти:
Оценка _____ подпись преподавателя ________________/Л.С. Тишкина/
ВАРИАНТ 4
ЧАСТЬ А Выберите один верный ответ
1. На рисунке показана зависимость сопротивления проводника длиной 1 м от его площади сечения. Чему равно удельное электрическое сопротивление вещества, из которого сделан проводник?
1) 10 Ом*мм2/м 2) 2,5 Ом*мм2/м 3) 0,1 Ом*мм2/м 4) 0,05 Ом*мм2/м
2. Как изменится сила тока, проходящего через проводник, если увеличить в 2 раза напряжение между его концами, а длину проводника уменьшить в 2 раза?
1) не изменится 2) уменьшится в 2 раза 3) увеличится в 2 раза 4) увеличится в 4 раза
3. На рисунке изображены графики зависимости силы тока в четырех проводниках от напряжения на их концах. Сопротивление какого проводника меньше 1 Ом?
На рисунке изображены графики зависимости силы тока в четырех проводниках от напряжения на их концах. Сопротивление какого проводника меньше 1 Ом?
1) проводника 1 2) проводника 2 3) проводника 3 4) проводника 4
4. На участке цепи, изображенном на рисунке, сопротивление каждого резистора равно 2 Ом. Общее сопротивление участка равно
1) 8 Ом 2) 5 Ом 3) 4 Ом 4) 1 Ом
5. В цепи, изображенной на рисунке амперметр показывает силу тока 2 А. К каким точкам нужно подключить вольтметр, чтобы его показания были равны 6 В?
1) АБ 2) АВ 3) БВ 4) БГ
6. Три резистора сопротивлениями R1 = 10 Ом, R2 = 6 Ом и R3 = 3 Ом соединены в цепь как показано на рисунке. На каком резисторе выделится наименьшее количество теплоты?
1) на первом 2) на втором 3) на третьем 4) на всех одинаково
7. Электрическая цепь состоит из источника с ЭДС 3 В и внутренним сопротивлением 1 Ом. Внешнее сопротивление 2 Ом. Сила тока в цепи равна
Электрическая цепь состоит из источника с ЭДС 3 В и внутренним сопротивлением 1 Ом. Внешнее сопротивление 2 Ом. Сила тока в цепи равна
А 2) 7 А 3) 1,5 А 4) 1 А
ЧАСТЬ В
8. Используя условие задачи, установите соответствия величин из левого столбца таблицы с их изменениями в правом
В цепи, изображенной на рисунке, ползунок реостата передвинули вверх. При этом…
Величина Изменение
А. сила тока 1) увеличивается
Б.электродвижущая сила 2) уменьшается
В.напряжение на резисторе 3) не изменяется
Г. сопротивление реостата
Решите задачи.
9. В резисторе сопротивлением 360 Ом при напряжении 15 В электрическим током была совершена работа 450 Дж. За какое время была совершена работа?
Дано: Решение:
Найти:
10. Электрическая цепь состоит из двух резисторов сопротивлением по 4 Ом соединенных параллельно, источника тока с ЭДС16 В и внутренним сопротивлением 2 Ом.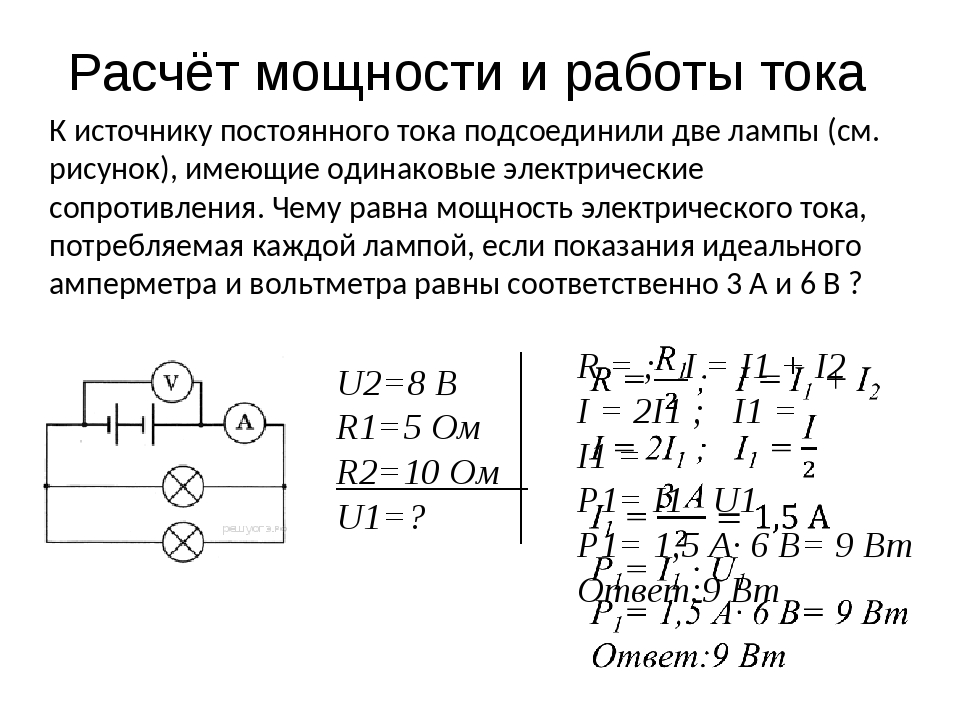 Определить силу тока в цепи.
Определить силу тока в цепи.
Дано: Решение:
Найти:
ЧАСТЬ С
Решите задачу.
11. К однородному медному цилиндрическому проводнику длиной 40 м приложили разность потенциалов 10 В. Каким будет изменение температуры проводника через 15 с? Изменением сопротивления проводника и рассеянием тепла при его нагревании пренебречь.
Дано: Решение:
Найти:
Оценка _____ подпись преподавателя ________________/Л.С. Тишкина/
Дата «___» _________20____г
Задание 31 по теме
«Опыт Эрстеда. Взаимодействие проводников с токами. Электродвигатель. Электроизмерительные приборы»
(2ч)
Реши задачи:
1.С какой силой действует магнитное поле индукцией 20 мТл на проводник, в котором сила тока 40 А, если длина активной части проводника 0,1 м? Линии индукции поля и ток взаимно перпендикулярны.
Дано: СИ: Решение:
Найти
2.По двум прямолинейным проводникам, находящимся на расстоянии 5 см друг от друга, протекают токи 10А и 5А в противоположных направлениях. Определите силу, с которой первый проводник будет действовать на второй .
Дано: Решение:
Найти
3.В проводнике с длиной активной части 8 см сила тока равна 50 А. Он находится в однородном магнитной поле индукцией 20 мТл. Какую работу совершил источник тока, если проводник переместился на 10 см перпендикулярно линиям индукции?
Дано: СИ: Решение:
Найти:
4. Электрон движется в однородном магнитном поле индукцией 4 мТл. Найти период обращения электрона, если его масса равна кг, заряд — Кл.
Дано: СИ: Решение:
Найти:
Оценка _____ подпись преподавателя ________________/Л.С. Тишкина/
Дата «___» _________20____г
Задание 32
Преобразование химической энергии в электрическую.
 Химические источники электрической энергии (аккумуляторы)
Химические источники электрической энергии (аккумуляторы)Гальванические элементы являются источниками постоянного напряжения. Электрическая энергия, получаемая в этом случае, образуется в результате химических реакций, происходящих внутри элемента. В гальванических элементах во время работы происходит движение ионов и оседание на электродах элемента, выделившегося из электролита вещества.
Аккумулятором называется прибор, обладающий способностью накапливать и сохранять в течении некоторого времени электрическую энергию в результате химических процессов.
В отличие от аккумулятора в гальваническом
элементе получающееся химическое
соединения не могут быть вторично
разложены и приведены в первоначальное
состояние током постоянного источника.
Повторные заряд и разряд аккумулятора
не только не вредят ему, но даже улучшают
его свойства, т. к. в работе участвуют
все более глубокие слои пластин
электродов.
к. в работе участвуют
все более глубокие слои пластин
электродов.
В зависимости от состава электролита и материала пластин аккумуляторы могут быть кислотными и щелочными.
Простейший кислотный аккумулятор
состоит из двух цинковых пластин
(электродов), погруженных в электролит,
которым служит вода с небольшим
добавлением серной кислоты. Постоянный
ток постоянного источника, проходя
через электролит, разлагает его на
составные части. Внутри электролита
возникает движение положительных ионов
водорода к пластине, соединенной с
отрицательным зажимом источника тока,
и отрицательных ионов кислорода — к
пластине, соединенной с положительным
зажимом источника тока. В результате
электролиза окисляется свинец на
положительном электроде и образуется
губчатый свинец на отрицательном
электроде. Таким образом, электрическая
энергия преобразуется в химическую и
аккумулятор становится заряженным.
Химическая энергия может сохраняться
определенное время и при надобности
легко переходит в электрическую.
В щелочных аккумуляторах электролитом служит раствор едкого калия в воде. Внутреннее сопротивление аккумуляторов очень мало по сравнению с внутренним сопротивлением гальванических элементов. Это дает возможность считать напряжение на зажимах аккумуляторной батареи примерно равным ее ЭДС.
В отключенном состоянии заряженный аккумулятор теряет часть запасенной им емкости, происходит саморазряд, который увеличивается с повышением температуры и плотности электролита.
Работу аккумулятора характеризует его отдача по емкости и отдача по энергии. Отдача по емкости — это отношение емкости при разряде к емкости при заряде. Отдача по энергии — это отношение энергии, полученной от аккумулятора при его работе, к энергии, затраченной на заряд аккумулятора.
Контрольные вопросы
1. В каких единицах выражается ЭДС, напряжение и ток?
2. От чего зависит сопротивление металлического проводника?
3. Сформулируйте закон Ома для замкнутой
электрической цепи и для ее участка.
Сформулируйте закон Ома для замкнутой
электрической цепи и для ее участка.
4. В чем состоит различие между замкнутой цепью и ее участком?
5. Каково соотношение между ЭДС и напряжением на зажимах источника энергии?
6. Что называется коротким замыканием, каковы его последствия и как его предотвратить?
7. Сформулируйте первый и второй законы Кирхгофа.
8. Как определяется общее сопротивление при последовательном, параллельном и смешанном соединении потребителей энергии?
9. Чему равна работа и мощность электрического тока и в каких единицах они выражаются?
10. Как рассчитать поперечное сечение провода?
11. Сформулируйте закон Джоуля — Ленца.
12. Какое сопротивление называется нелинейным?
13. Что называется электрической проводимостью?
14. Каково практическое применение
тепловых действий электрического тока?
Каково практическое применение
тепловых действий электрического тока?
Задачи
Элементы электрических и магнитных цепей
Как изменится сопротивление проволочного резистора: а) при увеличении его длины в 2 раза; б) при уменьшении площади поперечного сечения провода в 3 раза; в) при одновременном увеличении длины в 4 раза, а диаметра провода в 2 раза?
Для двух резисторов была выбрана проволока одной и той же длины, изготовленная из одного материала. При каком соотношении диаметров проволок сопротивление одного из резисторов будет: а) в 3 раза меньше; б) в 4 раза больше; в) в 10 раз больше сопротивления другого резистора?
Определить минимальный диаметр медной проволоки длиной 100 м, если ее сопротивление не должно превышать 1 Ом. Чему равно сопротивление 1 м медной проволоки диаметром 2 мм?
Найти сопротивление вольфрамовой нити длиной 70 м и диаметром 0,1· мм.
 Каково
сечение вольфрамовой проволоки, если
ее сопротивление составляет 0,5 Ом на
каждый метр длины?
Каково
сечение вольфрамовой проволоки, если
ее сопротивление составляет 0,5 Ом на
каждый метр длины?Определить сопротивление резистора, обмотка которого выполнена из нихромового провода диаметром 0,1 мм, намотанного в один виток к витку на керамический каркас длиной 10 мм и диаметром 4 мм, как изменится сопротивление при двухрядной намотке?
Решение.
, ,
Длина одного витка соответствует длине окружности каркаса, число же витков при плотной намотке проволоки равно отношению длины каркаса к диаметру проволоки:
При двухрядной намотке, если пренебречь расположением первого ряда (т. е. его толщиной), длина проволоки будет в 2 раза больше, т. е. R = 314 Ом.
При измерениях было установлено, что проволочный резистор, изготовлены из проволоки длиной 100 м и диаметром 0,6 мм, имел сопротивление 50 Ом.
 Из какого
материала или сплава был изготовлен
резистор?
Из какого
материала или сплава был изготовлен
резистор?Сопротивление электрической лампы с номинальными параметрами 60 Вт и 220 В при температуре 293 К (т. е. в нагретом состоянии) равно 62 Ом. Найти температуру накаленной вольфрамовой нити при номинальном напряжении, приняв температурный коэффициент равным 5•10-3 1/К во всем диапазоне температур.
Решение.
Сопротивление нити в нагретом состоянии определяется по ее номинальным параметрам
. Зная сопротивление накаленной нити можно определить ее перегрев:
и температуру:
Определить сопротивление медного резистора при температурах Т1 = 323;338;353 К, если при первоначальной температуре Т0 = 293К его сопротивление было равно 50 Ом.
Каков температурный коэффициент сопротивления резистора, если при изменении температуры среды на 100 К его сопротивление изменилось на 500 Ом? Номинальное значение сопротивления 1 кОм.

Сопротивление резистора при температуре Т1 = 323 К составляет 270 Ом, а при температуре Т2 = 353 К достигает 293 Ом. Найти температурный коэффициент резистора и его номинальное сопротивление при температуре 293 К. Из какого материала изготовлен резистор?
Чему равна емкость плоского конденсатора с круглыми пластинами диаметром 10 мм, если расстояние между пластинами 0,01 мм, а относительная диэлектрическая проницаемость диэлектрика ε = 2,4? Из какого материала выполнен диэлектрик?
Определить энергию электрического поля конденсатора емкостью 10 мкФ при напряжении между пластинами 220 В. Какую работу необходимо совершить источнику напряжения, чтобы перезарядить конденсатор до того же напряжения, но противоположного знака?
Как изменится индуктивность катушки: а) при увеличении числа витков в 2 раза; б) при уменьшении относительной магнитной проницаемости в З раза; в) при одновременном увеличении числа витков и длины катушки в 2 раза?
Какова индуктивность обмотки, имеющей 450 витков, если ток 0,5 А создает в ней магнитный поток 5•10-5 Вб? Определить ток, необходимый для создания в этой катушке магнитного потока 5•10-4 Вб.

Расчет электрических цепей
Определить ток резистора, к которому приложено напряжение 42 В, если его сопротивление 10; 20; 100 кОм; 1 МОм. Рассчитать сопротивление резистора. к которому приложено напряжение 15 В, а ток равен 0,1 А; 10мА и 10мкА.
Какое наибольшее напряжение можно приложить к резистору сопротивлением 33 Ом, если ток не должен превышать 3 А? Найти наибольшее значение напряжения, если мощность не должна превышать в этом же резисторе 150 Вт.
Каково напряжение на выводах источника электроэнергии подключенного к потребителям сопротивлением 41 Ом через двухпроводную линию из медного провода сечением 1,5 мм2 и общей длиной 500 м, если ток в цепи равен 2,7 А?
Определить длину нихромовой проволоки сечением 0,55 мм2, необходимой для намотки резистора, рассчитанного на мощность 750 Вт, при подключении его к источнику напряжением 220 В.

Для регулирования тока и напряжения потребителя сопротивлением Rн=100 Ом последовательно с ним включают переменный резистор Rр сопротивлением от 0 до 200 Ом. В каких пределах можно регулировать ток и напряжение потребителя, подключенного к сети напряжением 42 В?
Решение.
Общее сопротивление цепи:
ток в цепи:
Максимальный ток в цепи будет при R=0, т. е. , а максимальное напряжение
Минимальный ток в цепи будет при полном сопротивлении резистора
а наименьшее напряжение
К источнику электроэнергии Uпит = 220 В подключены параллельно четыре потребителя сопротивлениями соответственно 100; 150; 80 и 750 Ом.
 Определить мощность и
ток каждого потребителя, а так же
мощность и ток источника.
Определить мощность и
ток каждого потребителя, а так же
мощность и ток источника.В резисторе при приложенном напряжении 42 В выделяемая мощность равна 50 Вт. Какова выделяемая в резисторе мощность при напряжениях 127, 220 В?
Линия передачи электроэнергии подключена к источнику напряжением 460 В. Определить мощность потерь в линии, если ток линии 200 А, а сопротивление потребителя 2,2 Ом. Найти сопротивление линии.
В схеме замещения параметры активного двухполюсника
(источника) соответствуют ,
а сопротивление пассивного двухполюсника (потребителя)
Rн=20 Ом. Определить ток цепи, мощности, потребляемые :
двухполюсниками, если Rл и Rиз можно пренебречь.
В
Четырехполюсник
линии передачи используются соединительные
алюминиевые провода сечением 10 мм2, длиной 120 м
к
Активный двухполюсник
Пассивный двухполюсник
аждый. Определить падение напряжения
на
Определить падение напряжения
нас
Рис. к задачам 1.23, 1.24
оединительной линии, если схема передачисоответствует рисунку, Rвн=0,5 Ом; Rн=24 Ом.
Рассчитать напряжение на выводах источника с ЭДС 120 В, если внутреннее сопротивление источника по сравнению с сопротивлением потребителя: а) в 5 раз больше; б) равно; в) в 5 раз меньше.
Источник электроэнергии с ЭДС 24 В и внутренним сопротивлением 2 Ом подключен к потребителю сопротивлением 48 Ом. Найти: а) ток цепи; б) падение напряжения на внешнем участке цепи; в) падение напряжения на внутреннем участке; г) кпд работы источника.
Генератор постоянного тока независимого возбуждения имеет напряжение на выводах 230 В при токе 60 А. Сопротивление цепи якоря генератора (внутреннее сопротивление) равно 0,05 Ом. Определить напряжение на выводах генератора, если ток потребителя уменьшится в 2 раза.

Какая мощность расходуется в соединительных проводах. если напряжение и ток потребителя составляет соответственно 112 В и 5 А? Потребитель подключен к источнику с ЭДС 115 В и внутренним сопротивлением Rвн = 0,5 Ом.
В электрической цепи, схема замещения которой приведена на рисунке показание вольтметра при разомкнутом ключе К было 25 В.
Когда ключ замкнут, показание амперметра составляет 10 А.
ОК
пределить ЭДС источника, его внутреннее сопротивление,напряжение
И мощность потребителя сопротивлением 2,4 Ом.
Решение.
При разомкнутом ключе, если пренебречь внутреннимсопротивлением вольтметра, его показание
соответствует ЭДС источника ε = 25 В.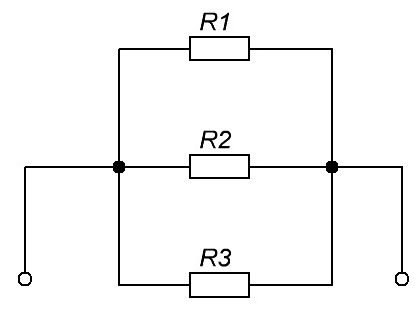
Внутреннее сопротивление можно
найти используя закон Ома для полной цепи:
Рис. к задаче 1.29
Напряжение потребителя: Мощность потребителя:
Определить величину и направление тока в электрической цепи, схема замещения которой приведена на рисунке, если напряжение на выводах цепи равно 2 В. Остальные параметры цепи следующие: R1=2Ом и R2=4Ом.
+ ε1 ε2 ε3
Рис. к задаче 1.30
—В электрической цепи, схема замещения
которой представлена на рисунке узловое
напряжение равно 10 В. Определить токи во всех
ветвях цепи и сопротивление R2, если: ε1 = 12 В;
ε2 = 13 В; R1 = 1
Ом; R3 = 2 Ом.
У
Рис. к задаче 1.31
казать на схеме направление узлового напряжения.Определить значение тока I1 в ветви с ЭДС ε1 и сопротивлением R1 электрической цепи, схема замещения которой соответствует рисунку. Известны следующие параметры цепи: ε1 = 15 В; ε2 = 5В; ε3 = 12 В, ε4 = 9 В; R1 = R2 = R3 = R4 = 2 Ом.
Решение.
Составим три исходных расчетных уравнений, используя уравнение состояния данной цепи:
Подставляя исходные значения ЭДС и сопротивлений резисторов можно записать:
Выразим токи I2 и I3 через ток I1, используя приведенные
уравнения:
О
Рис. к задаче 1.32
к задаче 1.32
Два резистора с сопротивлениями 19,5 и 30 Ом
подключены последовательно к источнику постоянного напряжения с ε = 100 В и r = 0,5 Ом. Определить ток цепи и напряжение каждого резистора.
Два потребителя с сопротивлениями 25 и 30 Ом соединены последовательно и подключены к источнику с ЭДС ε = 110 В. Определить ток цепи и погрешность от пренебрежения сопротивлением соединительных проводов Rпр = 0,5 Ом и внутреннего сопротивления источника Rвн = 0,8 Ом.
Источник постоянного тока с ЭДС 230 В и внутренним сопротивлением r = 0,4 Ом подключен к двум последовательно соединенным потребителям. Сопротивление одного из них 4,4 Ом, а напряжение на нем 110 В. Найти напряжение на выводах источника и ток в цепи.
Общий ток цепи, состоящий из двух параллельно соединенных резисторов сопротивлением 210 и 70 Ом, равен 80 мА.
 Найти токи каждого резистора и
эквивалентное сопротивление цепи.
Найти токи каждого резистора и
эквивалентное сопротивление цепи.Цепь состоит из двух параллельно соединенных резисторов сопротивлением 10 Ом каждый; по одному из резисторов проходит ток 1 А. Чему будет равен этот ток при обрыве цепи другого резистора, если внутреннее сопротивление источника 1 Ом?
Определить сопротивление резистора, который необходимо включить параллельно с резистором, имеющим сопротивление 15 кОм, при условии, чтобы эквивалентное сопротивление всей цепи составляло 10 кОм.
При параллельном подключении к нагрузке резистора сопротивлением 5,1 кОм общее сопротивление цепи равно 3 кОм. Чему будет равно эквивалентное сопротивление цепи, если к нагрузке подключить параллельно резистор 1; 3; 7,5 кОм?
Цепь постоянного тока состоит из четырех резисторов с проводимостями 0,02; 0,03; 0,01; 0,04 См. Определить эквивалентное сопротивление их параллельного и последовательного соединений.

Одна цепь состоит из резисторов, соединенных последовательно, а другая — соединенных параллельно, причем количество резисторов и их сопротивления одинаковы. В каком случае эквивалентное сопротивление будет больше?
Найти эквивалентные сопротивления цепей, если сопротивления резисторов одинаковы: . Найти токи резистора R1, если ЭДС источника 15 В, а внутренним сопротивлением можно пренебречь.
а ) б)
Рис. к задаче 1.42
В электрической цепи, схема замещения которой приведена на рис. б) к задаче 1.42, сопротивление резисторов равны: R1 = 50 Ом; R2 = 120 Ом; R3 = 200 Ом. Определить мощность, выделяемую в резисторе R1, ток резистора R2, если приложенное к цепи напряжение равно 110 В.
Найти эквивалентное сопротивление цепи, используя правила преобразования электрических схем, если R1= R5 = 5 Ом; R2 = 7 Ом; R4 = 15 Ом; R6 = 6 Ом; R3=R7=R9=10 Ом; R8=4 Ом; R10 = R11 = 20 Ом.
 Чему равен ток цепи,
если источник имеет ε = 120 В и r =1 Ом?
Чему равен ток цепи,
если источник имеет ε = 120 В и r =1 Ом?
Рис. к задаче 1.43
Определить токи ветвей электрической цепи, схема замещения которой приведена на рисунке. Сопротивления резисторов одинаковы и равны R = 15 Ом, напряжение питания U = 120 В. Как изменится ток источника при замыкании ключа К?
а в с
Рис. к задаче 1.45
Kd
Решение.
В рассматриваемой цепи нет последовательного или параллельного соединения резисторов. В схеме замещения имеются соединения в виде треугольников и звезды. В данном случае удобно преобразовать треугольник с вершинами a, b, c в эквивалентную звезду. В результате получаем схему:
U П о формулам:
получаем:
Э квивалентное сопротивление цепи определяется из выражения
a
О
U
бщий ток цепиНапряжение между узлами о и d равно
Следовательно, токи ветвей bd и сd равны 4 А. Рис.б
Рис.б
Возвращаясь к исходной схеме можно найти напряжение ; ; .
Следовательно, токи ветвей треугольника .
В результате замыкания ключа схема замещения цепи имеет вид ,приведенный на рис.б.
Эквивалентное сопротивление цепи и ток .Токи ветвей в данном случае .
Таким образом, при замыкании ключа токи цепи не меняются.
В электрической цепи, схема замещения которой соответствует рисунку к задаче 1.45, сопротивления ветвей равны: Rab = 5 Ом; Rac = 15 Ом; Rbc = 20 Ом; Rbd = 10 Ом; Rcd = 8 Ом. Найти эквивалентное сопротивление и ток в цепи в положениях замыкания и размыкания ключа К при напряжении питания U = 110 В.
Для электрической цепи, схема которой приведена на рисунке, сопротивления резисторов равны: R1 = 20 Ом; R2 = 200 Ом; R3 = 200 Ом; R4 = 100 Ом; R5 = 140 Ом; R6 = 60 Ом.
 Определить эквивалентное сопротивление
и ток цепи при напряжении питания U =
120 B.
Определить эквивалентное сопротивление
и ток цепи при напряжении питания U =
120 B.
a
U
Рис. к задаче 1.47
Начертить схему: а) последовательного; б) параллельного присоединения четырех резисторов к источнику постоянного тока.
Потребитель, сопротивление которого равно 10 Ом, подключен к источнику с ЭДС 15 В и внутренним сопротивлением 0,5 Ом. Насколько возрастет ток потребителя, если параллельно потребителю подключить еще один источник питания с такими же параметрами?
Какое количество источников с ЭДС 1,5 В и внутренним сопротивлением 0,5 Ом необходимо для создания тока 1,4 А в потребителе сопротивлением 1 Ом? Решить задачу для последовательного и параллельного соединения источников.

Решение.
При последовательном соединении источников для создания тока 1,4 А необходимо п источников. Закон Ома для цепи постоянного тока при последовательном соединении п одинаковых источников . Решая это уравнение, находим: 1,4+0,7п=1,5п и п=2 (округление в большую сторону).
При параллельном соединении количество источников определяется также на основании закона Ома: , 1,4=1,5п/(0,5+п). Решая это уравнение находим п=7.
И
Рис. к задаче 1.51
сточником питания цепи постоянного тока является батарея, схема которой представлена на рисунке. Определить ЭДС и внутреннее сопротивление батареи, а так же ток потребителя сопротивлением 7 Ом, если ЭДС и внутреннее сопротивление каждого элемента равны 1,5 В и 0,5 Ом.
Цепь постоянного тока, состоящая из последовательного соединения трех резисторов R1 = 50 Ом; R2 = 40 Ом; R3 = 75 Ом, подключена к источнику напряжения 110 В.
 Определить, как изменится
ток в цепи, если параллельно третьему
резистору подключен резистор
сопротивлением 125 Ом.
Определить, как изменится
ток в цепи, если параллельно третьему
резистору подключен резистор
сопротивлением 125 Ом.
Определить ток питания электрической цепи, a b
если его ЭДС 120 В. Сопротивление резисторов
R1 = R7 = 50 M; R2 = R6 = 4 Ом;
R3 = R4 = R5 = 2 Ом. Найти общую мощность цепи.
Д
Рис. к задаче 1.54
ва источника питания ЭДС 60 В и 75 В включены в дифференциальную схему, как показано на рисунке. Найти ток общей ветви, если сопротивление резисторов R1 = 3 Ом; R3 = 5 Ом.
Р
R3
ешение. На примере данной задачи рассмотрим
основные методы расчета цепей постоянного
тока.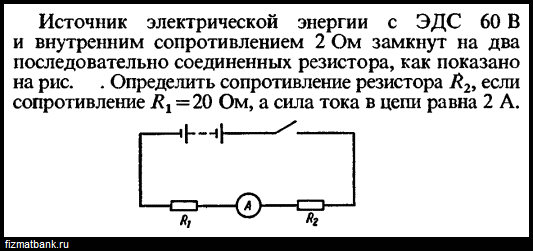
1) МЕТОД НАЛОЖЕНИЯ
Для нахождения токов ветвей, создаваемых источниками ЭДС ε1 , проводим расчет вспомогательных схем.
Эквивалентное сопротивление:
Токи ветвей:
Учитывая направление токов определяем искомые токи, как алгебраические суммы:
; ; .
2) ИСПОЛЬЗОВАНИЕ ЗАКОНОВ КИРХГОФА.
Задаваясь направлениями токов, указанными на рисунке, составляем уравнения для одного узла и двух контуров цепи:
или
Исключая один из токов , получаем систему из двух уравнений:
Решением этой системы являются значения
токов I1 =
27,6A; I2 = 26,6A; I3 = 1A.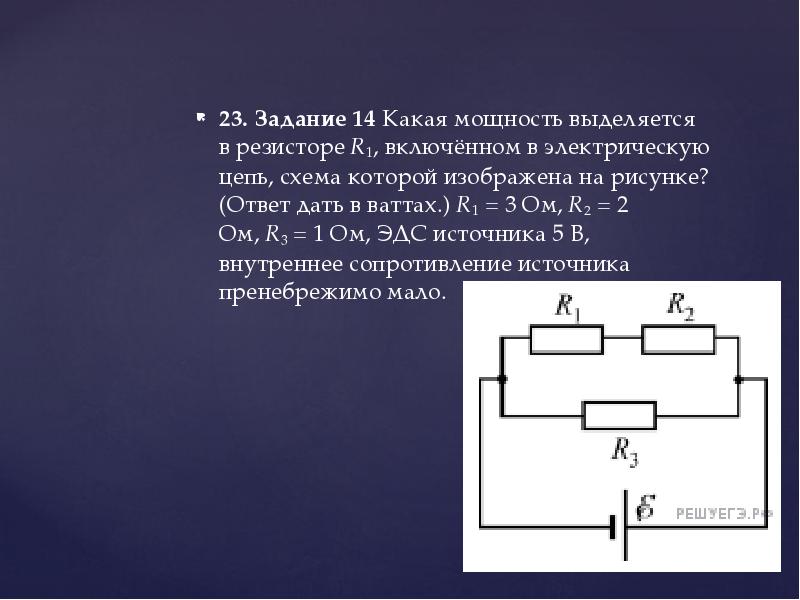
3) МЕТОД КОНТУРНЫХ ТОКОВ.
В ыделяем на исходной схеме два контура и составляем для них уравнения по второму закону Кирхгофа: или
П осле преобразований получаем: ε1
Решением системы уравнений являются значения токов:
4) МЕТОД УЗЛОВЫХ НАПРЯЖЕНИЙ.
Воспользовавшись формулой , находим напряжение между узлами 1 и 2
.
Токи ветвей соответственно равны
5) МЕТОД ЭКВИВАЛЕНТНОГО ИСТОЧНИКА.
Вначале выделяем ветвь 1, заметив остальную часть цепи по отношению к ней в виде эквивалентного источника и , где
,
Следовательно, ток ветви 1 по закону Ома равен
Аналогичные соотношения можно записать и для ветви 2:
;
ε1
Для контроля правильности расчета можно воспользоваться балансом мощностей:Используя методы наложения, контурных токов
и узловых напряжений, определить токи ветвей
в цепи, если ε = 15 В, а R
= 5 Ом.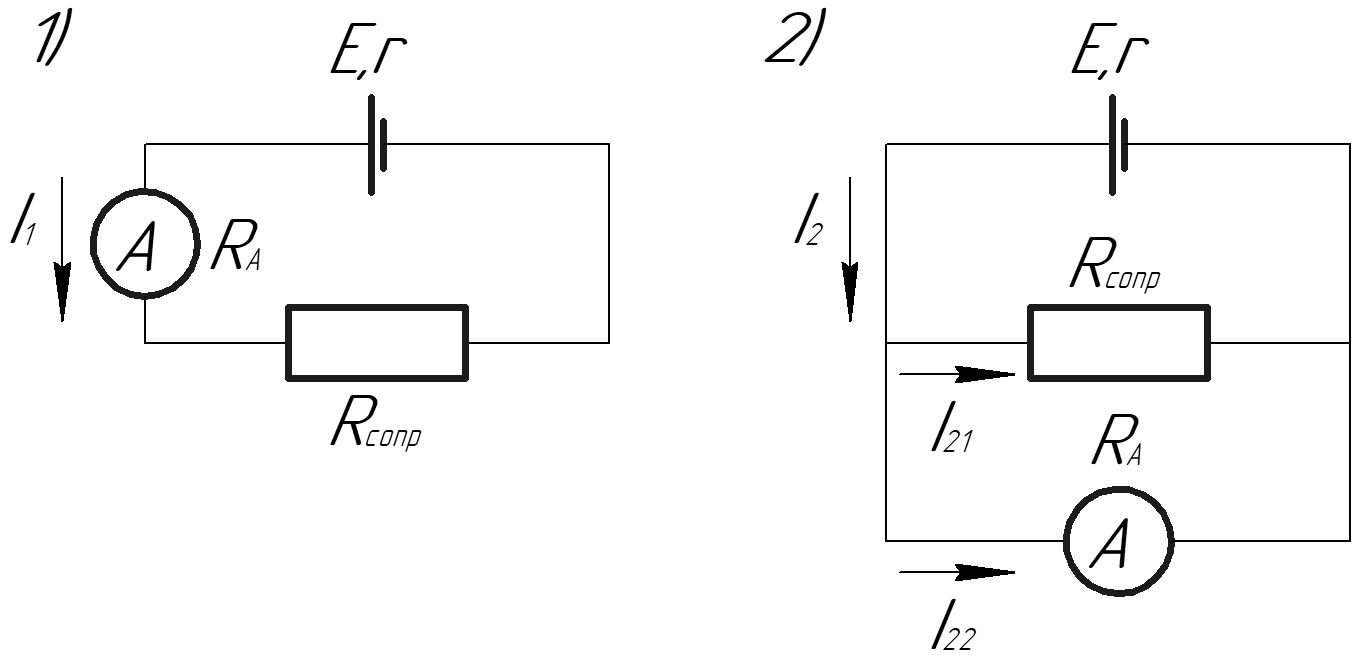 Составить
Составить
уравнение баланса мощностей.
Рис. к задаче 1.55
Используя методы наложения, контурных токов и
у зловых напряжений, определить токи ветвей в цепи, если ε = 30 В, а R = 5 Ом. Составить уравнение баланса мощностей.
I1
I2
1
Рис. к задаче 1.57
Рис. к задаче 1. 56
В электрической цепи, схема которой приведена на рисунке, известны два втекающих тока I1 = 4 A и I2 = 2 A, а также параметры
ε1 = 10 В; ε2 = 18 В и R1 = 2 Ом; R2 = 3 Ом;
R3 = 5 Ом.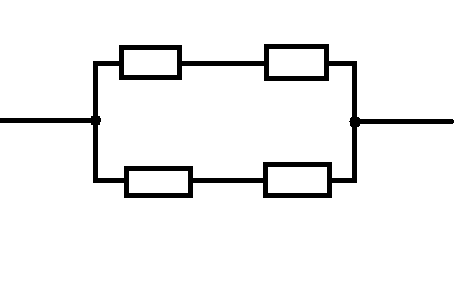
Определить токи всех резисторов цепи.
П
ε5
рименяя один из методов расчета сложных цепей, найти
все токи в электрической цепи. Параметры элементов цепи
равны ε1 = 30 В, ε2 = 8 В, ε5 = 16 В, и R1 = 2 Ом;
Рис. к задаче 1.58
Ом.3
Определить как распределяются токи в цепи представленной на рисунке, если ε1 = 14 В; ε2 = 20 В; R1 = 3 Ом; R2 = 3 Ом; R3 = 4 Ом; R4 = 2 Ом; R3 = 60м.
Рис. к задаче 1.59
Определить как распределяются токи в цепи, если R1 = 3 Ом; R2 = 4 Ом; R3 = 6 Ом; ε1 = 27 В; ε2 = 24 В;
ε1 +
—
Рис. к задаче 1.60
к задаче 1.60
Решение упражнений на стр. 32
Решения упражнений
1. An электрическая схема представлена ниже.
Какое эквивалентное сопротивление эта схема?
2 + 3 = рэнд
6 + 6 = 12 Вт
1 / Rp = 1 / R 1 + 1 / R экв
1 / Rp = 1/4 + 1/12
Rp = 3 Вт
Rt = 3 + 6 = 9 Вт
2.An электрическая схема представлена ниже.
Какой номинал резистора R 3 ?
Я 1 = Я 2 + Я 3 потому что в этом случае I1 — это полный ток.
2 = 1,5 + я 3
I 3 = 0,5 А
Если V 2 = 90 В, то V 3 = 90 В, потому что параллельное напряжение постоянно.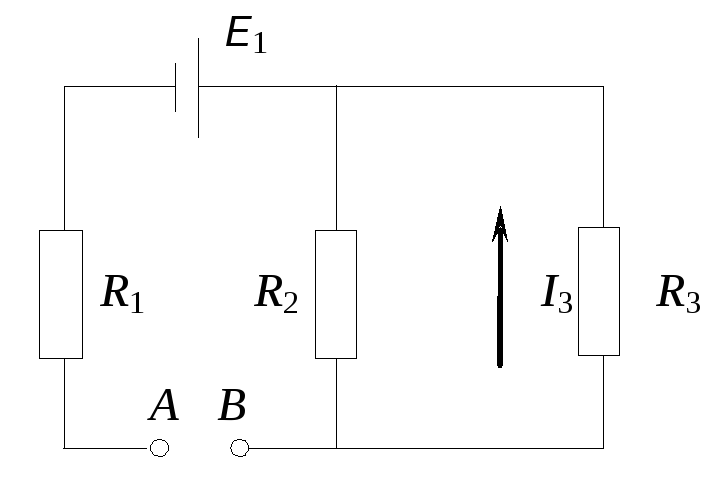
R 3 = V 3 / I 3 = 90 / 0,5 = 180 Вт
3. А последовательно-параллельная электрическая схема проиллюстрирована ниже.
Найдите R t .
4 и 3 рандов находятся последовательно, поэтому R eq1 = R 4 + R 3 = 10 + 20 = 30 Вт.
рэнд 2 и рэнд 1 работают параллельно, поэтому
1 / R экв2 = 1 / R 2 + 1 / R eq1
1 / R экв2 = 1 / 15+ 1/30
R экв2 = 10 Вт.
Rt = 5 руб. + R eq2 + R 1 = 10 + 10 + 10 = 30 Вт.
4. А
последовательно-параллельная электрическая схема проиллюстрирована ниже.
Какая разница потенциалов на выводе резистора R 1 ?
Первое обнаруженное общее сопротивление: 1 / R экв. = 1 / R 1 + 1 / ( 2 + 3 ) 1 / R экв. = 1/30 + 1 / (5 + 10) |
= 10 Вт.
рупий т = 4 рупий + R экв = 20 + 10 = 30 Вт.
I т = V / R = 12/30 = 0,40 A
В 4 = IR 4 = 0,40 (20) = 8 В
В 1 = V t V 4 = 12 8 = 4 V
5. А
последовательно-параллельный электрический показан ниже.
А
последовательно-параллельный электрический показан ниже.
Какая сила тока течет от источника питания, I s ?
R 2 и R 3 испытывают одинаковое напряжение, поэтому V 2 = I 2 R 2 = (0.5) 75 = 37,5 В и
I = V 3 / R 3 = 37,5 / 100 = 0,375 A
Так общий ток = 0,5 + 0,375 = 0,875 А
6. Следующая электрическая схема состоит из блока питания, пять резисторов (R 1 , R 2 , R 3 , R 4 и R 5 ) и амперметр.
Амперметр показывает 0,25 А.
а.Какая разница потенциалов (напряжение), В т , через клеммы блока питания?
1 / R eq1 = 1 / ( 1 + 2 ) + 1/ 3
1 / R eq1 = 1 / (20 + 40) + 1/30
р экв1 = 20 Вт.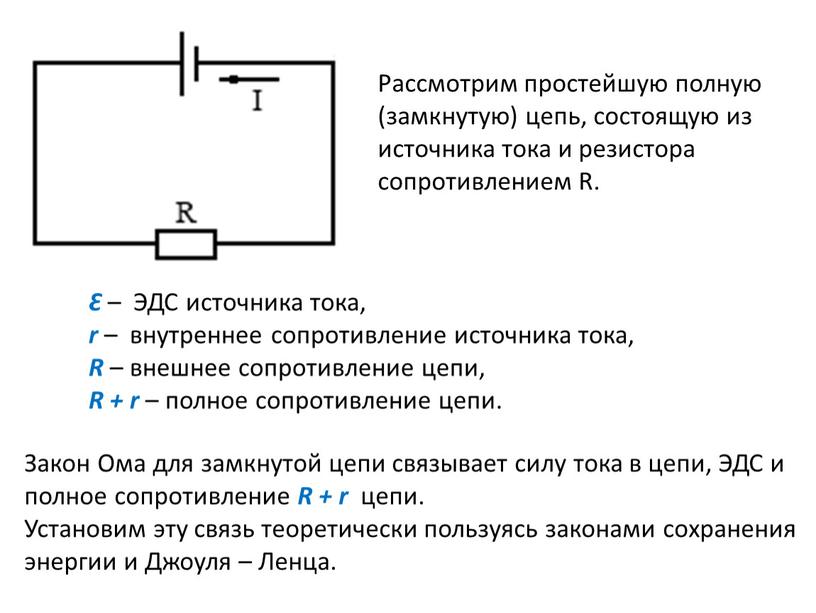
1 / R экв2 = 1/ 4 + 1/ 5
1 / R экв2 = 1/40 + 1/120
R экв2 = 30 Вт.
Rt = рэнд (экв1) + R экв2 = 20 + 30 = 50 Вт.
Вт = IRt = 0,25 (50) = 12,5 В
г. Какая разница потенциалов на R 3 ?
Vp = V 3 = I t R eq1 = 0,25 (20) = 5 В
г. Что равна разности потенциалов на R 1 ?
Я 1 = Вп / ( 1 + 2 ) = 5 / (20 + 40) = 0.0833A
В 1 = I 1 R 1 = 0,0833 (20) = 1,67 В
г. Какой ток протекает через R 5 ?
В 5 = Вт В 3 = 12,5 — 5 = 7,5 В
Я 5 = V 5 / R 5 = 7,5 / 120 = 0,0625 A
7. An
электрическая схема представлена ниже.
An
электрическая схема представлена ниже.
Какова сила тока I в резисторах R 2 и R 3 ?
R экв. = 1 / R 4 + 1 / ( 2 + R 3 )
р экв = 1/10 + 1 / (3 + 7)
р экв = 5 Вт.
РТ = R 1 + R экв = 7 + 5 = 12 Вт.
Это = Vt / Rt = 6/12 = 0,5 А
ток, протекающий через R 2 и R 3 , будет таким же, как и то, что сверху (поскольку R — это то же самое), поэтому будет 0,5 / 2 = 0,25A
8. Следующая электрическая схема состоит из источника питания пять резисторов (R 1 , R 2 , R 3 , R 4 и R 5 ) и два амперметра и.
Какая разница потенциалов (напряжение) на выводах резисторов R 3 ?
R 2 и R 3 получают 1,5 0,75 = 0,75
A.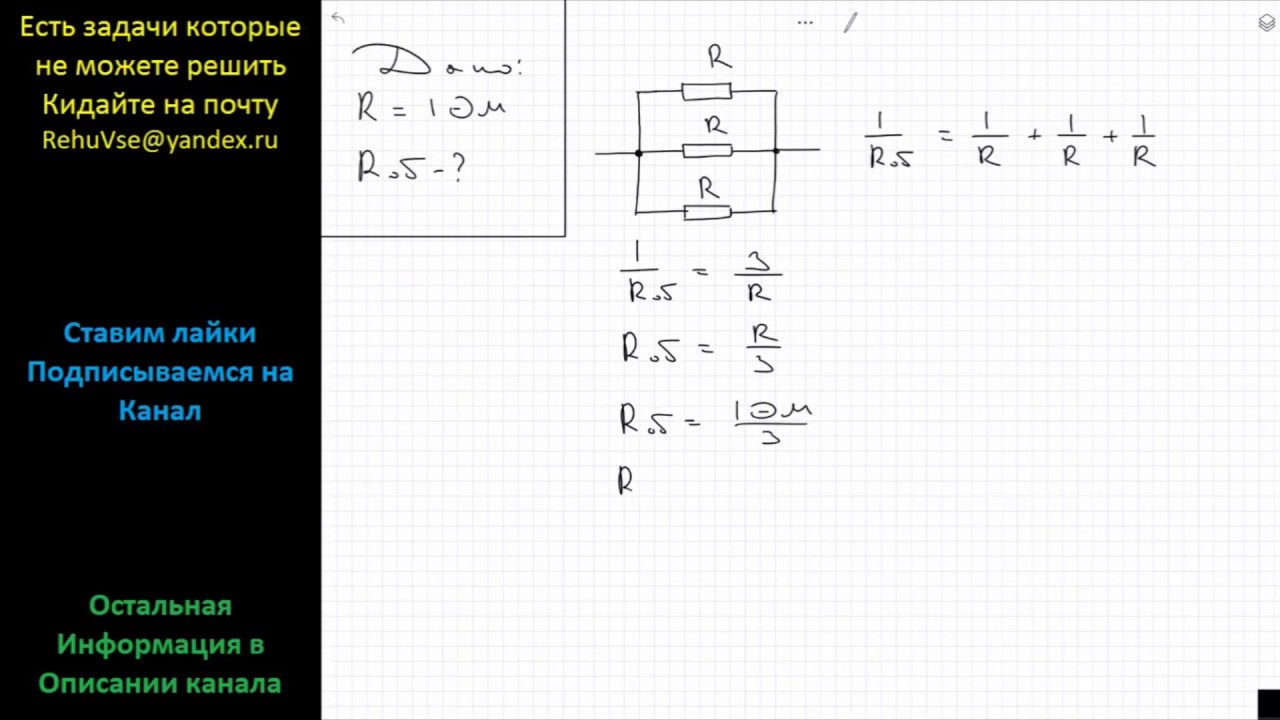 (тот же ток!) Это означает, что 2 R + 3 = 4 RR.
(тот же ток!) Это означает, что 2 R + 3 = 4 RR.
Так R 3 = 20 10 = 10 W.
9.Следующая схема состоит из источник питания, два амперметра и, вольтметр и три резистора (R 1 , 2 и 3 ).
Суммарная сила тока I т составляет 20 А. Сила тока I 3 составляет 12 А. разность потенциалов (напряжение) В 1 на выводах резистора R 1 составляет 5 В.
Какое сопротивление резистора R 3 ?
I 1 = It- I 3 = 20-12 = 8 A = I 2
В 2 = I 2 R 2 = 8 (5) = 40 В.
В 1 + V 2 = V 3
5 + 40 = В 3 = 45 В
Р 3 =
V 3 / I 3 = 45/12 = 3. 75 Вт.
75 Вт.
10. Источник с разностью потенциалов 30 В подключено к схеме, показанной ниже.
Какая сила тока I в цепи?
В 2 = I 2 R 2 = 1 (10) = 10 В
В 3 = Vt V 2 = 30 10 = 20 V
Это = V 3 / R 3 = 20/10 = 2 A
11.Следующие электрические Схема состоит из источника питания, четырех резисторов ( R 1 , R 2 , R 3 и R 4 ) и вольтметр В 4 ( В с = В итого ).
Какова сила тока ( I 3 ) через R 3 ?
В 2 и 3 = 100 60 = 40 В
I 3 = V 2 и 3 / (R 2 + R 3 ) = 40 / (10 + 30) = 1. 0 А
0 А
12. Как можно подключить один резистор 25 Вт и два резистора по 100 Вт чтобы их общее сопротивление было 75 Вт?
Поместите два резистора по 100 Вт параллельно. (поэтому Req = 50 Вт) и соедините новую ветвь последовательно с 25 Вт.
13. Как можно подключить четыре резистора 1,0 Вт и один резистор 2,0 Вт дать комбинированное сопротивление 1,5 Вт?
14.Четыре одинаковых резисторы подключаются, как показано. Если общее напряжение составляет 12 В, найдите напряжение на каждом резисторе.
R 1 имеет полное 12 В.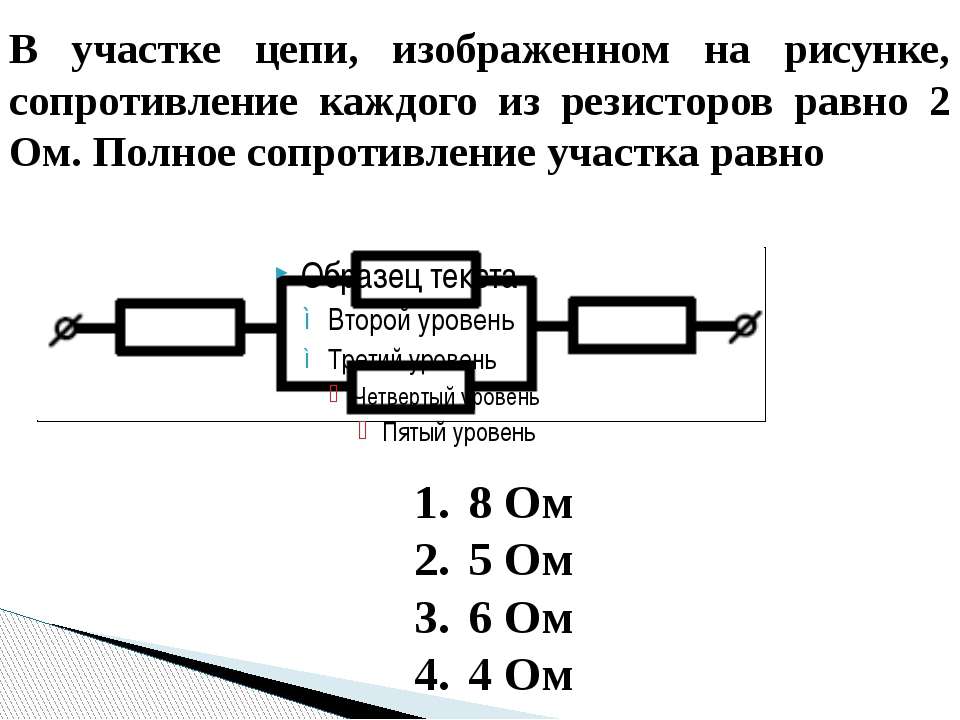 Это ни с чем не связано.
Это ни с чем не связано.
R 2 имеет вдвое больше сопротивление R 3 и R 4 комбинированные (запутались? Просто назначьте любое значение (например, 1 Ом на все 4 одинаковых резистора и разобраться), так что он будет иметь вдвое большее напряжение. 12 = 2х + х; х = 4 В.
Вывод В 2 = 2х = 8В; V 3 и V 4 = 4 В.
10.3: Последовательные и параллельные резисторы
Цели обучения
К концу раздела вы сможете:
- Определите термин эквивалентное сопротивление
- Рассчитайте эквивалентное сопротивление резисторов, соединенных последовательно
- Рассчитайте эквивалентное сопротивление резисторов, включенных параллельно
В книге «Ток и сопротивление» мы описали термин «сопротивление» и объяснили основную конструкцию резистора.По сути, резистор ограничивает поток заряда в цепи и представляет собой омическое устройство, где \ (V = IR \). В большинстве схем имеется более одного резистора. Если несколько резисторов соединены вместе и подключены к батарее, ток, подаваемый батареей, зависит от эквивалентного сопротивления цепи.
В большинстве схем имеется более одного резистора. Если несколько резисторов соединены вместе и подключены к батарее, ток, подаваемый батареей, зависит от эквивалентного сопротивления цепи.
Эквивалентное сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения. Самыми простыми комбинациями резисторов являются последовательное и параллельное соединение (Рисунок \ (\ PageIndex {1} \)).В последовательной цепи выходной ток первого резистора течет на вход второго резистора; следовательно, ток одинаков в каждом резисторе. В параллельной схеме все выводы резистора на одной стороне резисторов соединены вместе, а все выводы на другой стороне соединены вместе. В случае параллельной конфигурации каждый резистор имеет одинаковое падение потенциала на нем, и токи через каждый резистор могут быть разными в зависимости от резистора.Сумма отдельных токов равна току, протекающему по параллельным соединениям.
серии
Считается, что резисторывключены последовательно, когда ток течет через резисторы последовательно. Рассмотрим рисунок \ (\ PageIndex {2} \), на котором показаны три последовательно включенных резистора с приложенным напряжением, равным \ (V_ {ab} \).Поскольку заряды проходят только по одному пути, ток через каждый резистор одинаков. Эквивалентное сопротивление набора резисторов при последовательном соединении равно алгебраической сумме отдельных сопротивлений.
Рисунок \ (\ PageIndex {2} \): (a) Три резистора, последовательно подключенные к источнику напряжения. (b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения. На рисунке \ (\ PageIndex {2} \) ток, исходящий от источника напряжения, протекает через каждый резистор, поэтому ток через каждый резистор одинаков. Ток в цепи зависит от напряжения, подаваемого источником напряжения, и сопротивления резисторов. Для каждого резистора происходит падение потенциала, равное потере электрической потенциальной энергии, когда ток проходит через каждый резистор. Согласно закону Ома, падение потенциала \ (V \) на резисторе при протекании через него тока рассчитывается по формуле \ (V = IR \), где \ (I \) — ток в амперах (\ (A \)), а \ (R \) — сопротивление в Ом \ ((\ Omega) \).N V_i = 0. \]
Ток в цепи зависит от напряжения, подаваемого источником напряжения, и сопротивления резисторов. Для каждого резистора происходит падение потенциала, равное потере электрической потенциальной энергии, когда ток проходит через каждый резистор. Согласно закону Ома, падение потенциала \ (V \) на резисторе при протекании через него тока рассчитывается по формуле \ (V = IR \), где \ (I \) — ток в амперах (\ (A \)), а \ (R \) — сопротивление в Ом \ ((\ Omega) \).N V_i = 0. \]
Это уравнение часто называют законом петли Кирхгофа, который мы рассмотрим более подробно позже в этой главе. На рисунке \ (\ PageIndex {2} \) сумма падения потенциала каждого резистора и напряжения, подаваемого источником напряжения, должна равняться нулю:
\ [\ begin {align *} V — V_1 — V_2 — V_3 & = 0, \\ [4pt] V & = V_1 + V_2 + V_3, \\ [4pt] & = IR_1 + IR_2 + IR_3, \ end { выровнять *} \]
Решение для \ (I \)
\ [\ begin {align *} I & = \ frac {V} {R_1 + R_2 + R_3} \\ [4pt] & = \ frac {V} {R_ {S}}. N R_i.\ label {серия эквивалентных сопротивлений} \]
N R_i.\ label {серия эквивалентных сопротивлений} \]
Одним из результатов подключения компонентов в последовательную цепь является то, что если что-то происходит с одним компонентом, это влияет на все остальные компоненты. Например, если несколько ламп подключены последовательно и одна лампа перегорела, все остальные лампы погаснут.
Пример \ (\ PageIndex {1} \): эквивалентное сопротивление, ток и мощность в последовательной цепи
Батарея с напряжением на клеммах 9 В подключена к цепи, состоящей из четырех последовательно соединенных резисторов \ (20 \, \ Omega \) и одного \ (10 \, \ Omega \) (Рисунок \ (\ PageIndex {3 } \)).Предположим, что батарея имеет незначительное внутреннее сопротивление.
- Рассчитайте эквивалентное сопротивление цепи.
- Рассчитайте ток через каждый резистор.
- Рассчитайте падение потенциала на каждом резисторе.
- Определите общую мощность, рассеиваемую резисторами, и мощность, отдаваемую аккумулятором.

Стратегия
В последовательной цепи эквивалентное сопротивление представляет собой алгебраическую сумму сопротивлений.2R \), а общая мощность, рассеиваемая резисторами, равна сумме мощности, рассеиваемой каждым резистором. Мощность, подаваемая батареей, можно найти с помощью \ (P = I \ epsilon \).
Решение
- Эквивалентное сопротивление — это алгебраическая сумма сопротивлений (уравнение \ ref {серия эквивалентных сопротивлений}): \ [\ begin {align *} R_ {S} & = R_1 + R_2 + R_3 + R_4 + R_5 \\ [4pt ] & = 20 \, \ Omega + 20 \, \ Omega + 20 \, \ Omega + 20 \, \ Omega + 10 \, \ Omega = 90 \, \ Omega.2 (10 \, \ Omega) = 0,1 \, W, \ nonumber \] \ [P_ {рассеивается} = 0,2 \, W + 0,2 \, W + 0,2 \, W + 0,2 \, W + 0,1 \, W = 0,9 \, W, \ nonumber \] \ [P_ {источник} = I \ epsilon = (0,1 \, A) (9 \, V) = 0,9 \, W. \ nonumber \]
Значение
Есть несколько причин, по которым мы будем использовать несколько резисторов вместо одного резистора с сопротивлением, равным эквивалентному сопротивлению цепи.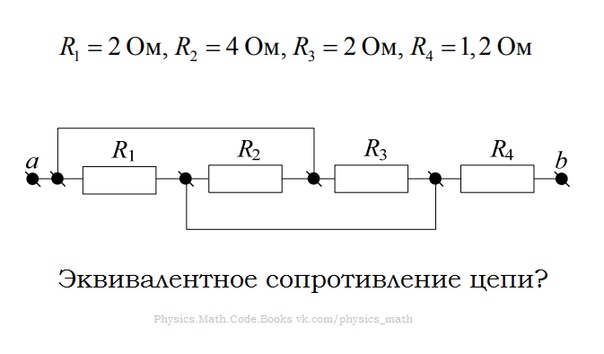 Возможно, резистора необходимого размера нет в наличии, или нам нужно отводить выделяемое тепло, или мы хотим минимизировать стоимость резисторов.Каждый резистор может стоить от нескольких центов до нескольких долларов, но при умножении на тысячи единиц экономия затрат может быть значительной.
Возможно, резистора необходимого размера нет в наличии, или нам нужно отводить выделяемое тепло, или мы хотим минимизировать стоимость резисторов.Каждый резистор может стоить от нескольких центов до нескольких долларов, но при умножении на тысячи единиц экономия затрат может быть значительной.
Упражнение \ (\ PageIndex {1} \)
Некоторые гирлянды миниатюрных праздничных фонарей закорачиваются при перегорании лампочки. Устройство, вызывающее короткое замыкание, называется шунтом, который позволяет току течь по разомкнутой цепи. «Короткое замыкание» похоже на протягивание куска проволоки через компонент. Луковицы обычно сгруппированы в серии по девять луковиц.Если перегорает слишком много лампочек, в конце концов открываются шунты. Что вызывает это?
- Ответ
Эквивалентное сопротивление девяти последовательно соединенных лампочек составляет 9 R . Ток равен \ (I = V / 9 \, R \). Если одна лампочка перегорит, эквивалентное сопротивление равно 8 R , и напряжение не изменится, но ток возрастет \ ((I = V / 8 \, R \).
 Чем больше лампочек перегорят, ток станет равным. В конце концов, ток становится слишком большим, что приводит к перегоранию шунта.№ Р_и. \]
Чем больше лампочек перегорят, ток станет равным. В конце концов, ток становится слишком большим, что приводит к перегоранию шунта.№ Р_и. \]- Одинаковый ток течет через каждый резистор последовательно.
- Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его. Общее падение потенциала на последовательной конфигурации резисторов равно сумме падений потенциала на каждом резисторе.
Параллельные резисторы
На рисунке \ (\ PageIndex {4} \) показаны резисторы, включенные параллельно, подключенные к источнику напряжения. Резисторы включены параллельно, когда один конец всех резисторов соединен непрерывным проводом с незначительным сопротивлением, а другой конец всех резисторов также соединен друг с другом непрерывным проводом с незначительным сопротивлением.Падение потенциала на каждом резисторе одинаковое. Ток через каждый резистор можно найти с помощью закона Ома \ (I = V / R \), где напряжение на каждом резисторе постоянно.
Рисунок \ (\ PageIndex {4} \): Два резистора, подключенных параллельно источнику напряжения.(b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения. Например, автомобильные фары, радио и другие системы подключены параллельно, так что каждая подсистема использует полное напряжение источника и может работать полностью независимо. То же самое и с электропроводкой в вашем доме или любом здании.
Например, автомобильные фары, радио и другие системы подключены параллельно, так что каждая подсистема использует полное напряжение источника и может работать полностью независимо. То же самое и с электропроводкой в вашем доме или любом здании.Ток, протекающий от источника напряжения на рисунке \ (\ PageIndex {4} \), зависит от напряжения, подаваемого источником напряжения, и эквивалентного сопротивления цепи. В этом случае ток течет от источника напряжения и попадает в соединение или узел, где цепь разделяется, протекая через резисторы \ (R_1 \) и \ (R_2 \). По мере того, как заряды проходят от батареи, некоторые проходят через резистор \ (R_1 \), а некоторые — через резистор \ (R_2 \).Сумма токов, текущих в переход, должна быть равна сумме токов, текущих из перехода:
\ [\ sum I_ {in} = \ sum I_ {out}.
 {- 1}.{-1}. \ label {10.3} \]
{- 1}.{-1}. \ label {10.3} \]Это соотношение приводит к эквивалентному сопротивлению \ (R_ {P} \), которое меньше наименьшего из отдельных сопротивлений. Когда резисторы подключены параллельно, от источника течет больше тока, чем протекает для любого из них по отдельности, поэтому общее сопротивление ниже.
Пример \ (\ PageIndex {2} \): Анализ параллельной цепи
Три резистора \ (R_1 = 1,00 \, \ Omega \), \ (R_2 = 2,00 \, \ Omega \) и \ (R_3 = 2,00 \, \ Omega \) подключены параллельно.Параллельное соединение подключается к источнику напряжения \ (V = 3,00 \, V \).
- Какое эквивалентное сопротивление?
- Найдите ток, подаваемый источником в параллельную цепь.
- Рассчитайте токи в каждом резисторе и покажите, что в сумме они равны выходному току источника.
- Рассчитайте мощность, рассеиваемую каждым резистором.
- Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.

Стратегия
(a) Общее сопротивление для параллельной комбинации резисторов определяется с помощью уравнения \ ref {10.3}. (Обратите внимание, что в этих расчетах каждый промежуточный ответ отображается с дополнительной цифрой.)
(b) Ток, подаваемый источником, можно найти из закона Ома, заменив \ (R_ {P} \) на полное сопротивление \ (I = \ frac {V} {R_ {P}} \).
(c) Отдельные токи легко вычислить по закону Ома \ (\ left (I_i = \ frac {V_i} {R_i} \ right) \), поскольку каждый резистор получает полное напряжение.{-1} = 0,50 \, \ Omega. \ Nonumber \] Общее сопротивление с правильным количеством значащих цифр равно \ (R_ {eq} = 0,50 \, \ Omega \). Как и предполагалось, \ (R_ {P} \) меньше наименьшего индивидуального сопротивления.
- Полный ток можно найти из закона Ома, заменив полное сопротивление \ (R_ {P} \). Это дает \ [I = \ frac {V} {R_ {P}} = \ frac {3.00 \, V} {0.50 \, \ Omega} = 6.00 \, A. \ nonumber \] Текущий I для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см.
 предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.- Отдельные токи легко вычислить по закону Ома, так как каждый резистор получает полное напряжение. Таким образом, \ [I_1 = \ frac {V} {R_1} = \ frac {3.00 \, V} {1.00 \, \ Omega} = 3.00 \, A. \ nonumber \] Аналогично, \ [I_2 = \ frac {V } {R_2} = \ frac {3.00 \, V} {2.00 \, \ Omega} = 1.50 \, A \ nonumber \] и \ [I_3 = \ frac {V} {R_3} = \ frac {3.00 \, V } {2.00 \, \ Omega} = 1.50 \, A. \ nonumber \] Общий ток — это сумма отдельных токов: \ [I_1 + I_2 + I_3 = 6.2} {2.00 \, \ Omega} = 4.50 \, W. \ nonumber \]
- Общую мощность также можно рассчитать несколькими способами. Выбор \ (P = IV \) и ввод общей текущей доходности \ [P = IV = (6.00 \, A) (3.00 \, V) = 18.00 \, W. \ nonumber \]
Значение
Общая мощность, рассеиваемая резисторами, также 18,00 Вт:
\ [P_1 + P_2 + P_3 = 9,00 \, W + 4,50 \, W + 4,50 \, W = 18,00 \, W.
 \ nonumber \]
\ nonumber \]Обратите внимание, что общая мощность, рассеиваемая резисторами, равна мощности, подаваемой от источника.
Упражнение \ (\ PageIndex {2A} \)
Рассмотрим одну и ту же разность потенциалов \ ((V = 3,00 \, V) \), приложенную к одним и тем же трем последовательно включенным резисторам. Будет ли эквивалентное сопротивление последовательной цепи больше, меньше или равно трем резисторам, включенным параллельно? Будет ли ток в последовательной цепи выше, ниже или равен току, обеспечиваемому тем же напряжением, приложенным к параллельной цепи? Как мощность, рассеиваемая последовательно резистором, будет сравниваться с мощностью, рассеиваемой параллельно резисторами?
- Решение
Эквивалент последовательной схемы будет \ (R_ {eq} = 1.00 \, \ Omega + 2.00 \, \ Omega + 2.00 \, \ Omega = 5.00 \, \ Omega \), что выше эквивалентного сопротивления параллельной цепи \ (R_ {eq} = 0.50 \, \ Omega \ ). Эквивалентный резистор любого количества резисторов всегда выше, чем эквивалентное сопротивление тех же резисторов, соединенных параллельно.
 Ток через последовательную цепь будет \ (I = \ frac {3.00 \, V} {5.00 \, \ Omega} = 0.60 \, A \), что меньше суммы токов, проходящих через каждый резистор в параллельная цепь, \ (I = 6.00 \, А \). Это неудивительно, поскольку эквивалентное сопротивление последовательной цепи выше. Ток при последовательном соединении любого количества резисторов всегда будет ниже, чем ток при параллельном соединении тех же резисторов, поскольку эквивалентное сопротивление последовательной цепи будет выше, чем параллельной цепи. Мощность, рассеиваемая последовательно включенными резисторами, будет равна \ (P = 1,800 \, Вт \), что ниже мощности, рассеиваемой в параллельной цепи \ (P = 18.00 \, Вт \).
Ток через последовательную цепь будет \ (I = \ frac {3.00 \, V} {5.00 \, \ Omega} = 0.60 \, A \), что меньше суммы токов, проходящих через каждый резистор в параллельная цепь, \ (I = 6.00 \, А \). Это неудивительно, поскольку эквивалентное сопротивление последовательной цепи выше. Ток при последовательном соединении любого количества резисторов всегда будет ниже, чем ток при параллельном соединении тех же резисторов, поскольку эквивалентное сопротивление последовательной цепи будет выше, чем параллельной цепи. Мощность, рассеиваемая последовательно включенными резисторами, будет равна \ (P = 1,800 \, Вт \), что ниже мощности, рассеиваемой в параллельной цепи \ (P = 18.00 \, Вт \).
Упражнение \ (\ PageIndex {2B} \)
Как бы вы использовали реку и два водопада для моделирования параллельной конфигурации двух резисторов? Как разрушается эта аналогия?
- Решение
Река, текущая в горизонтальном направлении с постоянной скоростью, разделяется на две части и течет через два водопада.
 Молекулы воды аналогичны электронам в параллельных цепях. Количество молекул воды, которые текут в реке и падает, должно быть равно количеству молекул, которые текут над каждым водопадом, точно так же, как сумма тока через каждый резистор должна быть равна току, текущему в параллельном контуре.Молекулы воды в реке обладают энергией благодаря своему движению и высоте. Потенциальная энергия молекул воды в реке постоянна из-за их одинаковой высоты. Это аналогично постоянному изменению напряжения в параллельной цепи. Напряжение — это потенциальная энергия на каждом резисторе.
Молекулы воды аналогичны электронам в параллельных цепях. Количество молекул воды, которые текут в реке и падает, должно быть равно количеству молекул, которые текут над каждым водопадом, точно так же, как сумма тока через каждый резистор должна быть равна току, текущему в параллельном контуре.Молекулы воды в реке обладают энергией благодаря своему движению и высоте. Потенциальная энергия молекул воды в реке постоянна из-за их одинаковой высоты. Это аналогично постоянному изменению напряжения в параллельной цепи. Напряжение — это потенциальная энергия на каждом резисторе.При рассмотрении энергии аналогия быстро разрушается. В водопаде потенциальная энергия преобразуется в кинетическую энергию молекул воды. В случае прохождения электронов через резистор падение потенциала преобразуется в тепло и свет, а не в кинетическую энергию электронов.
Суммируем основные характеристики резисторов параллельно:
- Эквивалентное сопротивление находится по формуле \ ref {10.
 3} и меньше любого отдельного сопротивления в комбинации.
3} и меньше любого отдельного сопротивления в комбинации. - Падение потенциала на каждом параллельном резисторе одинаковое.
- Параллельные резисторы не получают суммарный ток каждый; они делят это. Ток, поступающий в параллельную комбинацию резисторов, равен сумме токов, протекающих через каждый резистор, включенный параллельно.
В этой главе мы представили эквивалентное сопротивление резисторов, соединенных последовательно, и резисторов, соединенных параллельно. Как вы помните, в разделе «Емкость» мы ввели эквивалентную емкость конденсаторов, соединенных последовательно и параллельно. Цепи часто содержат как конденсаторы, так и резисторы. В таблице \ (\ PageIndex {1} \) приведены уравнения, используемые для эквивалентного сопротивления и эквивалентной емкости для последовательных и параллельных соединений.
Таблица \ (\ PageIndex {1} \): Сводка по эквивалентному сопротивлению и емкости в последовательной и параллельной комбинациях Комбинация серий Параллельная комбинация Эквивалентная емкость \ [\ frac {1} {C_ {S}} = \ frac {1} {C_1} + \ frac {1} {C_2} + \ frac {1} {C_3} +.  N R_i \ nonumber \]
N R_i \ nonumber \]\ [\ frac {1} {R_ {P}} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} +. . . \ nonumber \] Сочетания последовательного и параллельного
Более сложные соединения резисторов часто представляют собой просто комбинации последовательного и параллельного соединения. Такие комбинации обычны, особенно если учитывать сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинации последовательного и параллельного соединения могут быть уменьшены до одного эквивалентного сопротивления, используя метод, показанный на рисунке \ (\ PageIndex {5} \).Различные части могут быть идентифицированы как последовательные или параллельные соединения, уменьшенные до их эквивалентных сопротивлений, а затем уменьшенные до тех пор, пока не останется единственное эквивалентное сопротивление.
Рисунок \ (\ PageIndex {5} \): (а) Исходная схема из четырех резисторов. (b) Шаг 1: резисторы \ (R_3 \) и \ (R_4 \) включены последовательно, и эквивалентное сопротивление равно \ (R_ {34} = 10 \, \ Omega \) (c) Шаг 2: сокращенная схема показывает, что резисторы \ (R_2 \) и \ (R_ {34} \) включены параллельно, с эквивалентным сопротивлением \ (R_ {234} = 5 \, \ Omega \).(d) Шаг 3: приведенная схема показывает, что \ (R_1 \) и \ (R_ {234} \) включены последовательно с эквивалентным сопротивлением \ (R_ {1234} = 12 \, \ Omega \), которое является эквивалентное сопротивление \ (R_ {eq} \). (e) Уменьшенная схема с источником напряжения \ (V = 24 \, V \) с эквивалентным сопротивлением \ (R_ {eq} = 12 \, \ Omega \). Это приводит к току \ (I = 2 \, A \) от источника напряжения. Процесс занимает больше времени, чем труден. Здесь мы отмечаем эквивалентное сопротивление как \ (R_ {eq} \).
Процесс занимает больше времени, чем труден. Здесь мы отмечаем эквивалентное сопротивление как \ (R_ {eq} \).Обратите внимание, что резисторы \ (R_3 \) и \ (R_4 \) включены последовательно. Их можно объединить в одно эквивалентное сопротивление.
 {- 1} = 5 \, \ Omega.\ nonumber \]
{- 1} = 5 \, \ Omega.\ nonumber \]Этот шаг процесса сокращает схему до двух резисторов, показанных на рисунке \ (\ PageIndex {5d} \). Здесь схема сводится к двум резисторам, которые в данном случае включены последовательно. Эти два резистора можно уменьшить до эквивалентного сопротивления, которое является эквивалентным сопротивлением цепи:
\ [R_ {eq} = R_ {1234} = R_1 + R_ {234} = 7 \, \ Omega + 5 \ Omega = 12 \, \ Omega. \ nonumber \]
Основная цель этого анализа схемы достигнута, и теперь схема сведена к одному резистору и одному источнику напряжения.
Теперь мы можем проанализировать схему. Ток, обеспечиваемый источником напряжения, равен \ (I = \ frac {V} {R_ {eq}} = \ frac {24 \, V} {12 \, \ Omega} = 2 \, A \). Этот ток проходит через резистор \ (R_1 \) и обозначается как \ (I_1 \). Падение потенциала на \ (R_1 \) можно найти с помощью закона Ома:
\ [V_1 = I_1R_1 = (2 \, A) (7 \, \ Omega) = 14 \, V. \ nonumber \]
Глядя на рисунок \ (\ PageIndex {5c} \), это оставляет \ (24 \, V — 14 \, V = 10 \, V \) отбрасывать через параллельную комбинацию \ (R_2 \) и \ ( R_ {34} \).
 Ток через \ (R_2 \) можно найти по закону Ома:
Ток через \ (R_2 \) можно найти по закону Ома:\ [I_2 = \ frac {V_2} {R_2} = \ frac {10 \, V} {10 \, \ Omega} = 1 \, A. \ nonumber \]
Резисторы \ (R_3 \) и \ (R_4 \) включены последовательно, поэтому токи \ (I_3 \) и \ (I_4 \) равны
.\ [I_3 = I_4 = I — I_2 = 2 \, A — 1 \, A = 1 \, A. \ nonumber \]
Используя закон Ома, мы можем найти падение потенциала на двух последних резисторах. Потенциальные капли равны \ (V_3 = I_3R_3 = 6 \, V \) и \ (V_4 = I_4R_4 = 4 \, V \).2 (4 \, \ Omega) = 4 \, W, \\ [4pt] P_ {рассеивается} & = P_1 + P_2 + P_3 + P_4 = 48 \, W. \ end {align *} \]
Полная энергия постоянна в любом процессе. Следовательно, мощность, подаваемая источником напряжения, составляет
\ [\ begin {align *} P_s & = IV \\ [4pt] & = (2 \, A) (24 \, V) = 48 \, W \ end {align *} \]
Анализ мощности, подаваемой в схему, и мощности, рассеиваемой резисторами, является хорошей проверкой достоверности анализа; они должны быть равны.

Пример \ (\ PageIndex {3} \): объединение последовательных и параллельных цепей
На рисунке \ (\ PageIndex {6} \) показаны резисторы, подключенные последовательно и параллельно.Мы можем рассматривать \ (R_1 \) как сопротивление проводов, ведущих к \ (R_2 \) и \ (R_3 \).
- Найдите эквивалентное сопротивление цепи.
- Какое падение потенциала \ (V_1 \) на резисторе \ (R_1 \)?
- Найдите ток \ (I_2 \) через резистор \ (R_2 \).
- Какая мощность рассеивается \ (R_2 \)?
Стратегия
(a) Чтобы найти эквивалентное сопротивление, сначала найдите эквивалентное сопротивление параллельного соединения \ (R_2 \) и \ (R_3 \). Затем используйте этот результат, чтобы найти эквивалентное сопротивление последовательного соединения с \ (R_1 \).

(b) Ток через \ (R_1 \) можно найти с помощью закона Ома и приложенного напряжения. Ток через \ (R_1 \) равен току от батареи. Падение потенциала \ (V_1 \) на резисторе \ (R_1 \) (которое представляет собой сопротивление в соединительных проводах) можно найти с помощью закона Ома.{-1} = 5.10 \, \ Omega. \ Nonumber \] Общее сопротивление этой комбинации занимает промежуточное положение между значениями чистой серии и чисто параллельной (\ (20.0 \, \ Omega \) и \ (0.804 \, \ Omega \) ), соответственно).
- Ток через \ (R_1 \) равен току, обеспечиваемому батареей: \ [I_1 = I = \ frac {V} {R_ {eq}} = \ frac {12.0 \, V} {5.10 \, \ Omega} = 2.35 \, A. \ nonumber \] Напряжение на \ (R_1 \) равно \ [V_1 = I_1R_1 = (2.35 \, A) (1 \, \ Omega) = 2.35 \, V. \ nonumber \] Напряжение, приложенное к \ (R_2 \) и \ (R_3 \), меньше напряжения, подаваемого батареей, на величину \ (V_1 \).Когда сопротивление провода велико, это может существенно повлиять на работу устройств, представленных \ (R_2 \) и \ (R_3 \).

- Чтобы найти ток через \ (R_2 \), мы должны сначала найти приложенное к нему напряжение. Напряжение на двух параллельных резисторах одинаково: \ [V_2 = V_3 = V — V_1 = 12.0 \, V — 2.35 \, V = 9.65 \, V. \ nonumber \] Теперь мы можем найти ток \ (I_2 \) через сопротивление \ (R_2 \) по закону Ома: \ [I_2 = \ frac {V_2} {R_2} = \ frac {9.65 \, V} {6.00 \, \ Omega} = 1.2 (6.00 \, \ Omega) = 15.5 \, W. \ nonumber \]
Значение
Анализ сложных схем часто можно упростить, сведя схему к источнику напряжения и эквивалентному сопротивлению. Даже если вся схема не может быть сведена к одному источнику напряжения и одному эквивалентному сопротивлению, части схемы могут быть уменьшены, что значительно упрощает анализ.
Упражнение \ (\ PageIndex {3} \)
Учитывайте электрические цепи в вашем доме.Приведите хотя бы два примера схем, в которых для эффективной работы необходимо использовать комбинацию последовательных и параллельных схем.

- Решение
Все цепи верхнего освещения параллельны и подключены к основному источнику питания, поэтому при перегорании одной лампочки все верхнее освещение не гаснет. У каждого верхнего света будет как минимум один переключатель, включенный последовательно с источником света, так что вы можете включать и выключать его.
В холодильнике есть компрессор и лампа, которая загорается при открытии двери.Обычно для подключения холодильника к стене используется только один шнур. Цепь, содержащая компрессор, и цепь, содержащая цепь освещения, параллельны, но есть переключатель, включенный последовательно со светом. Термостат управляет переключателем, включенным последовательно с компрессором, чтобы контролировать температуру холодильника.
Практическое применение
Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор.
 Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение IR в проводах также может быть значительным и может проявляться из-за тепла, выделяемого в шнуре.
Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение IR в проводах также может быть значительным и может проявляться из-за тепла, выделяемого в шнуре.Например, когда вы роетесь в холодильнике и включается мотор, свет холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
Что происходит в этих сильноточных ситуациях, показано на рисунке \ (\ PageIndex {7} \). Устройство, обозначенное символом \ (R_3 \), имеет очень низкое сопротивление, поэтому при его включении течет большой ток. Этот увеличенный ток вызывает большее падение IR в проводах, обозначенных \ (R_1 \), снижая напряжение на лампочке (которое составляет \ (R_2 \)), которое затем заметно гаснет.
Рисунок \ (\ PageIndex {7} \): Почему свет тускнеет при включении большого прибора? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение IR в проводах и снижает напряжение на свету.
Стратегия решения проблем: последовательные и параллельные резисторы
- Нарисуйте четкую принципиальную схему, пометив все резисторы и источники напряжения. Этот шаг включает список известных значений проблемы, так как они отмечены на вашей принципиальной схеме.
- Точно определите, что необходимо определить в проблеме (определите неизвестные). Письменный список полезен.
- Определите, подключены ли резисторы последовательно, параллельно или в комбинации последовательно и параллельно.Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
- Используйте соответствующий список основных функций для последовательных или параллельных подключений, чтобы найти неизвестные.
 Есть один список для серий и другой для параллельных.
Есть один список для серий и другой для параллельных. - Проверьте, являются ли ответы разумными и последовательными.
Пример \ (\ PageIndex {4} \): объединение последовательных и параллельных цепей
Два резистора, соединенных последовательно \ ((R_1, \, R_2) \), соединены с двумя резисторами, включенными параллельно \ ((R_3, \, R_4) \).Последовательно-параллельная комбинация подключается к батарее. Каждый резистор имеет сопротивление 10,00 Ом. Провода, соединяющие резисторы и аккумулятор, имеют незначительное сопротивление. Через резистор \ (R_1 \) проходит ток 2,00 А. Какое напряжение подается от источника напряжения?
Стратегия
Используйте шаги предыдущей стратегии решения проблем, чтобы найти решение для этого примера.
Решение
Рисунок \ (\ PageIndex {8} \): Чтобы найти неизвестное напряжение, мы должны сначала найти эквивалентное сопротивление цепи.- Нарисуйте четкую принципиальную схему (Рисунок \ (\ PageIndex {8} \)).

- Неизвестно напряжение аккумулятора. Чтобы определить напряжение, подаваемое батареей, необходимо найти эквивалентное сопротивление.
- В этой схеме мы уже знаем, что резисторы \ (R_1 \) и \ (R_2 \) включены последовательно, а резисторы \ (R_3 \) и \ (R_4 \) включены параллельно. Эквивалентное сопротивление параллельной конфигурации резисторов \ (R_3 \) и \ (R_4 \) последовательно с последовательной конфигурацией резисторов \ (R_1 \) и \ (R_2 \).{-1} = 5,00 \, \ Омега. \ nonumber \] Эта параллельная комбинация включена последовательно с двумя другими резисторами, поэтому эквивалентное сопротивление схемы равно \ (R_ {eq} = R_1 + R_2 + R_ {34} = (25.00 \, \ Omega \). поэтому напряжение, подаваемое батареей, равно \ (V = IR_ {eq} = 2,00 \, A (25,00 \, \ Omega) = 50,00 \, V \).
- Один из способов проверить соответствие ваших результатов — это рассчитать мощность, подаваемую батареей, и мощность, рассеиваемую резисторами. Мощность, обеспечиваемая аккумулятором, равна \ (P_ {batt} = IV = 100.
 2R_4 \\ [4pt] & = 40.00 \, W + 40.00 \, W + 10.00 \, W + 10.00 \, W = 100. \, W. \ end {align *} \]
2R_4 \\ [4pt] & = 40.00 \, W + 40.00 \, W + 10.00 \, W + 10.00 \, W = 100. \, W. \ end {align *} \]Поскольку мощность, рассеиваемая резисторами, равна мощности, выделяемой батареей, наше решение кажется последовательным.
Значение
Если проблема имеет комбинацию последовательного и параллельного соединений, как в этом примере, ее можно уменьшить поэтапно, используя предыдущую стратегию решения проблемы и рассматривая отдельные группы последовательных или параллельных соединений.При нахождении \ (R_ {eq} \) для параллельного соединения необходимо с осторожностью относиться к обратному. Кроме того, единицы и числовые результаты должны быть разумными. Эквивалентное последовательное сопротивление должно быть больше, а эквивалентное параллельное сопротивление, например, должно быть меньше. Мощность должна быть больше для одних и тех же устройств, подключенных параллельно, по сравнению с последовательными и так далее.
Авторы и авторство
Сэмюэл Дж.
 Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами.Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами.Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
резисторов последовательно и параллельно
Цели обучения
К концу этого раздела вы сможете:
- Нарисуйте цепь с резисторами, включенными параллельно и последовательно.
- Вычислите падение напряжения тока на резисторе, используя закон Ома.
- Сравните способ расчета общего сопротивления для резисторов, включенных последовательно и параллельно.
- Объясните, почему полное сопротивление параллельной цепи меньше наименьшего сопротивления любого из резисторов в этой цепи.
- Рассчитайте общее сопротивление цепи, которая содержит смесь резисторов, подключенных последовательно и параллельно.
Большинство схем имеет более одного компонента, называемого резистором , который ограничивает поток заряда в цепи.
 Мера этого предела расхода заряда называется сопротивлением . Простейшие комбинации резисторов — это последовательное и параллельное соединение, показанное на рисунке 1.Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от того, как они подключены.
Мера этого предела расхода заряда называется сопротивлением . Простейшие комбинации резисторов — это последовательное и параллельное соединение, показанное на рисунке 1.Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от того, как они подключены.Рис. 1. (а) Последовательное соединение резисторов. (б) Параллельное соединение резисторов.
Когда резисторы в серии ? Резисторы включены последовательно всякий раз, когда поток заряда, называемый током , должен проходить через устройства последовательно. Например, если ток течет через человека, держащего отвертку, в землю, тогда R 1 на Рисунке 1 (a) может быть сопротивлением вала отвертки, R 2 сопротивлением ее ручки , R 3 сопротивление тела человека и R 4 сопротивление его обуви.На рисунке 2 показаны резисторы, последовательно подключенные к источнику напряжения .
 Кажется разумным, что полное сопротивление является суммой отдельных сопротивлений, учитывая, что ток должен проходить через каждый резистор последовательно. (Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев обувь с резиновыми подошвами с высоким сопротивлением. прибор, который уменьшил бы рабочий ток.)
Кажется разумным, что полное сопротивление является суммой отдельных сопротивлений, учитывая, что ток должен проходить через каждый резистор последовательно. (Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев обувь с резиновыми подошвами с высоким сопротивлением. прибор, который уменьшил бы рабочий ток.)Рис. 2. Три резистора, подключенных последовательно к батарее (слева), и эквивалентное одиночное или последовательное сопротивление (справа).
Чтобы убедиться, что последовательно соединенные сопротивления действительно складываются, давайте рассмотрим потерю электроэнергии, называемую падением напряжения , в каждом резисторе на рис. 2. Согласно закону Ома падение напряжения В на резистор, когда через него протекает ток, рассчитывается по формуле V = IR , где I равно току в амперах (A), а R — сопротивление в омах (Ω).
 Другой способ представить это: В, — это напряжение, необходимое для протекания тока I через сопротивление R . Таким образом, падение напряжения на R 1 составляет В 1 = IR 1 , что на R 2 составляет В 2 = IR 2 , и что через R 3 составляет V 3 = IR 3 .Сумма этих напряжений равна выходному напряжению источника; то есть
Другой способ представить это: В, — это напряжение, необходимое для протекания тока I через сопротивление R . Таким образом, падение напряжения на R 1 составляет В 1 = IR 1 , что на R 2 составляет В 2 = IR 2 , и что через R 3 составляет V 3 = IR 3 .Сумма этих напряжений равна выходному напряжению источника; то естьВ = В 1 + В 2 + В 3 .
Это уравнение основано на сохранении энергии и сохранении заряда. Электрическая потенциальная энергия может быть описана уравнением PE = qV , где q — электрический заряд, а V — напряжение. Таким образом, энергия, подаваемая источником, составляет кв / , а энергия, рассеиваемая резисторами, составляет
.
qV 1 + qV 2 + qV 3 .
Установление связей: законы сохранения
Вывод выражений для последовательного и параллельного сопротивления основан на законах сохранения энергии и сохранения заряда, согласно которым общий заряд и полная энергия постоянны в любом процессе. Эти два закона непосредственно участвуют во всех электрических явлениях и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.
Эти энергии должны быть равны, потому что в цепи нет другого источника и другого назначения для энергии.Таким образом, qV = qV 1 + qV 2 + qV 3 . Заряд q аннулируется, давая V = V 1 + V 2 + V 3 , как указано. (Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, так как нет емкости для хранения заряда, нет места для утечки заряда и заряд сохраняется.
 ) Теперь подстановка значений для отдельных напряжений дает
) Теперь подстановка значений для отдельных напряжений даетV = IR 1 + IR 2 + IR 3 = I ( R 1 + R 2 + R 3 ).
Обратите внимание, что для эквивалентного сопротивления одной серии R с , мы имеем
В = ИК с .
Это означает, что полное или эквивалентное последовательное сопротивление R с трех резисторов составляет R с = R 1 + R 2 + R 3 .Эта логика действительна в общем для любого количества резисторов, включенных последовательно; таким образом, полное сопротивление R с последовательного соединения составляет
R с = R 1 + R 2 + R 3 +…,
, как предлагается.
 Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого, а последовательно соединенные сопротивления просто складываются.
Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого, а последовательно соединенные сопротивления просто складываются.Пример 1. Расчет сопротивления, тока, падения напряжения и рассеиваемой мощности: анализ последовательной цепи
Предположим, что выходное напряжение батареи на рисунке 2 равно 12.0 В, а сопротивления равны R 1 = 1,00 Ом, R 2 = 6,00 Ом и R 3 = 13,0 Ом. а) Каково полное сопротивление? (б) Найдите ток. (c) Рассчитайте падение напряжения на каждом резисторе и покажите, как они складываются, чтобы равняться выходному напряжению источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия и решение для (а)Общее сопротивление — это просто сумма отдельных сопротивлений, определяемая следующим уравнением:
[латекс] \ begin {array} {lll} {R} _ {\ text {s}} & = & {R} _ {1} + {R} _ {2} + {R} _ {3} \ \ & = & 1.
Стратегия и решение для (b) 00 \ text {} \ Omega + 6.00 \ text {} \ Omega + 13.0 \ text {} \ Omega \\ & = & 20.0 \ text {} \ Omega \ end {array} \\ [/ latex].
00 \ text {} \ Omega + 6.00 \ text {} \ Omega + 13.0 \ text {} \ Omega \\ & = & 20.0 \ text {} \ Omega \ end {array} \\ [/ latex].Ток определяется по закону Ома, В = IR . Ввод значения приложенного напряжения и общего сопротивления дает ток для цепи:
[латекс] I = \ frac {V} {{R} _ {\ text {s}}} = \ frac {12.0 \ text {V}} {20.0 \ text {} \ Omega} = 0.60 \ text {A }\\[/латекс].
Стратегия и решение для (c)Напряжение — или IR падение — в резисторе определяется законом Ома.Ввод текущего значения и значения первого сопротивления дает
.В 1 = IR 1 = (0,600 A) (1,0 Ом) = 0,600 В.
Аналогично
В 2 = IR 2 = (0,600 A) (6,0 Ом) = 3,60 В
и
V3 = IR 3 = (0,600 A) (13,0 Ом) = 7,80 В.
Обсуждение для (c)Три капли IR добавляют к 12.
 0 В, прогноз:
0 В, прогноз:В 1 + В 2 + В 3 = (0,600 + 3,60 + 7,80) В = 12,0 В.
Стратегия и решение для (d)Самый простой способ рассчитать мощность в ваттах (Вт), рассеиваемую резистором в цепи постоянного тока, — это использовать закон Джоуля , P = IV , где P — электрическая мощность. В этом случае через каждый резистор протекает одинаковый полный ток.Подставляя закон Ома В = IR в закон Джоуля, мы получаем мощность, рассеиваемую первым резистором, как
P 1 = I 2 R 1 = (0,600 A) 2 (1,00 Ом) = 0,360 Вт
Аналогично
P 2 = I 2 R 2 = (0,600 A) 2 (6,00 Ом) = 2,16 Вт
и
P 3 = I 2 R 3 = (0.{2}} {R} \\ [/ latex], где В, — это падение напряжения на резисторе (а не полное напряжение источника).
Стратегия и решение для (e) Будут получены такие же значения.
Будут получены такие же значения.Самый простой способ рассчитать выходную мощность источника — использовать P = IV , где В, — напряжение источника. Это дает
P = (0,600 A) (12,0 В) = 7,20 Вт.
Обсуждение для (е)Обратите внимание, что по совпадению общая мощность, рассеиваемая резисторами, также равна 7.20 Вт, столько же, сколько мощность, выдаваемая источником. То есть
P 1 + P 2 + P 3 = (0,360 + 2,16 + 4,68) W = 7,20 Вт
Мощность — это энергия в единицу времени (ватт), поэтому для сохранения энергии требуется, чтобы выходная мощность источника была равна общей мощности, рассеиваемой резисторами.
Основные характеристики резисторов серии
- Последовательные сопротивления добавить: R с = R 1 + R 2 + R 3 +….

- Одинаковый ток течет через каждый резистор последовательно.
- Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его.
На рис. 3 показаны резисторы параллельно , подключенные к источнику напряжения. Резисторы включены параллельно, когда каждый резистор подключен непосредственно к источнику напряжения путем соединения проводов с незначительным сопротивлением. Таким образом, к каждому резистору приложено полное напряжение источника. Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения (при условии, что источник напряжения не перегружен).Например, автомобильные фары, радиоприемник и т. Д. Подключены параллельно, так что они используют полное напряжение источника и могут работать полностью независимо. То же самое и в вашем доме, или в любом другом здании. (См. Рисунок 3 (b).)
Рис. 3. (a) Три резистора, подключенных параллельно батарее, и эквивалентное одиночное или параллельное сопротивление.
 (б) Электроснабжение в доме. (Источник: Dmitry G, Wikimedia Commons)
(б) Электроснабжение в доме. (Источник: Dmitry G, Wikimedia Commons)Чтобы найти выражение для эквивалентного параллельного сопротивления R p , давайте рассмотрим протекающие токи и их связь с сопротивлением.Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, равны [латекс] {I} _ {1} = \ frac {V} {{R} _ {1}} \\ [/ latex] , [латекс] {I} _ {2} = \ frac {V} {{R} _ {2}} \\ [/ latex] и [латекс] {I} _ {3} = \ frac {V} {{R} _ {3}} \\ [/ латекс]. Сохранение заряда подразумевает, что полный ток I , производимый источником, является суммой этих токов:
I = I 1 + I 2 + I 3 .
Подстановка выражений для отдельных токов дает
[латекс] I = \ frac {V} {{R} _ {1}} + \ frac {V} {{R} _ {2}} + \ frac {V} {{R} _ {3}} = V \ left (\ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ frac {1} {{R} _ {3}} \ справа) \\ [/ латекс].

Обратите внимание, что закон Ома для эквивалентного одиночного сопротивления дает
[латекс] I = \ frac {V} {{R} _ {p}} = V \ left (\ frac {1} {{R} _ {p}} \ right) \\ [/ latex].
Члены в круглых скобках в последних двух уравнениях должны быть равны. Обобщая для любого количества резисторов, общее сопротивление R p параллельного соединения связано с отдельными сопротивлениями на
[латекс] \ frac {1} {{R} _ {p}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ гидроразрыв {1} {{R} _ {\ text {.} 3}} + \ text {.} \ Text {…} \\ [/ latex]
Это соотношение приводит к общему сопротивлению R p , которое меньше наименьшего из отдельных сопротивлений. (Это видно в следующем примере.) При параллельном подключении резисторов от источника течет больше тока, чем протекает по любому из них по отдельности, поэтому общее сопротивление ниже.
Пример 2. Расчет сопротивления, тока, рассеиваемой мощности и выходной мощности: анализ параллельной цепи
Пусть выходное напряжение батареи и сопротивления в параллельном соединении на рисунке 3 будут такими же, как и в ранее рассмотренном последовательном соединении: В = 12.
Стратегия и решение для (а) 0 В, R 1 = 1,00 Ом, R 2 = 6,00 Ом и R 3 = 13,0 Ом. а) Каково полное сопротивление? (б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, как они складываются, чтобы равняться общему выходному току источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
0 В, R 1 = 1,00 Ом, R 2 = 6,00 Ом и R 3 = 13,0 Ом. а) Каково полное сопротивление? (б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, как они складываются, чтобы равняться общему выходному току источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.Общее сопротивление для параллельной комбинации резисторов определяется с помощью следующего уравнения.Ввод известных значений дает
[латекс] \ frac {1} {{R} _ {p}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ frac {1} {{R} _ {3}} = \ frac {1} {1 \ text {.} \ text {00} \ text {} \ Omega} + \ frac {1} {6 \ text {. } \ text {00} \ text {} \ Omega} + \ frac {1} {\ text {13} \ text {.} 0 \ text {} \ Omega} \\ [/ latex].
Таким образом,
[латекс] \ frac {1} {{R} _ {p}} = \ frac {1.
 00} {\ text {} \ Omega} + \ frac {0 \ text {.} \ Text {1667}} {\ текст {} \ Omega} + \ frac {0 \ text {.} \ text {07692}} {\ text {} \ Omega} = \ frac {1 \ text {.} \ text {2436}} {\ text { } \ Omega} \\ [/ латекс].
00} {\ text {} \ Omega} + \ frac {0 \ text {.} \ Text {1667}} {\ текст {} \ Omega} + \ frac {0 \ text {.} \ text {07692}} {\ text {} \ Omega} = \ frac {1 \ text {.} \ text {2436}} {\ text { } \ Omega} \\ [/ латекс].(Обратите внимание, что в этих расчетах каждый промежуточный ответ отображается с дополнительной цифрой.Мы должны перевернуть это, чтобы найти полное сопротивление R p . Это дает
[латекс] {R} _ {\ text {p}} = \ frac {1} {1 \ text {.} \ Text {2436}} \ text {} \ Omega = 0 \ text {.} \ Text { 8041} \ text {} \ Omega \\ [/ latex].
Полное сопротивление с правильным количеством значащих цифр составляет R p = 0,804 Ом
Обсуждение для (а)R p , как и предполагалось, меньше наименьшего индивидуального сопротивления.
Стратегия и решение для (b)Полный ток можно найти из закона Ома, заменив полное сопротивление R p .
 Это дает
Это дает[латекс] I = \ frac {V} {{R} _ {\ text {p}}} = \ frac {\ text {12.0 V}} {0.8041 \ text {} \ Omega} = \ text {14} \ text {.} \ text {92 A} \\ [/ latex].
Обсуждение для (б)Ток I для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. Предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
Стратегия и решение для (c)Отдельные токи легко вычислить по закону Ома, так как каждый резистор получает полное напряжение. Таким образом,
[латекс] {I} _ {1} = \ frac {V} {{R} _ {1}} = \ frac {12.0 \ text {V}} {1.00 \ text {} \ Omega} = 12.0 \ text {A} \\ [/ латекс].
Аналогично
[латекс] {I} _ {2} = \ frac {V} {{R} _ {2}} = \ frac {12.0 \ text {V}} {6.00 \ text {} \ Omega} = 2 \ text {.} \ text {00} \ text {A} \\ [/ latex]
и
[латекс] {I} _ {3} = \ frac {V} {{R} _ {3}} = \ frac {\ text {12} \ text {.
Обсуждение для (c) } 0 \ text {V}} {\ text {13} \ text {.} \ Text {0} \ text {} \ Omega} = 0 \ text {.} \ Text {92} \ text {A} \\ [/ latex].
} 0 \ text {V}} {\ text {13} \ text {.} \ Text {0} \ text {} \ Omega} = 0 \ text {.} \ Text {92} \ text {A} \\ [/ latex].Общий ток складывается из отдельных токов:
I 1 + I 2 + I 3 = 14,92 A.
Это соответствует сохранению заряда.{2}} {13.0 \ text {} \ Omega} = 11.1 \ text {W} \\ [/ latex].
Обсуждение для (д)Мощность, рассеиваемая каждым резистором параллельно, значительно выше, чем при последовательном подключении к одному и тому же источнику напряжения.
Стратегия и решение для (e)Общую мощность также можно рассчитать несколькими способами. Выбрав P = IV и введя полный ток, получим
P = IV = (14,92 A) (12,0 В) = 179 Вт.
Обсуждение для (е)Общая мощность, рассеиваемая резисторами, также 179 Вт:
P 1 + P 2 + P 3 = 144 Вт + 24,0 Вт + 11,1 Вт = 179 Вт
Это соответствует закону сохранения энергии.
Общее обсуждение
Обратите внимание, что и токи, и мощность при параллельном подключении больше, чем для тех же устройств, подключенных последовательно.
Основные характеристики резисторов, включенных параллельно- Параллельное сопротивление определяется из [latex] \ frac {1} {{R} _ {\ text {p}}} = \ frac {1} {{R} _ {1}} + \ frac {1} { {R} _ {2}} + \ frac {1} {{R} _ {3}} + \ text {…} \\ [/ latex], и оно меньше любого отдельного сопротивления в комбинации.
- Каждый резистор, включенный параллельно, имеет то же полное напряжение, что и источник. (В системах распределения электроэнергии чаще всего используются параллельные соединения для питания бесчисленных устройств, обслуживаемых одинаковым напряжением, и для того, чтобы они могли работать независимо.)
- Параллельные резисторы не получают суммарный ток каждый; они делят это.
Сочетания последовательного и параллельного
Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного.
 Они обычно встречаются, особенно если учитывать сопротивление провода. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно. Комбинации последовательного и параллельного подключения можно уменьшить до одного эквивалентного сопротивления, используя методику, показанную на рисунке 4.Различные части идентифицируются как последовательные или параллельные, уменьшаются до их эквивалентов и далее уменьшаются до тех пор, пока не останется единственное сопротивление. Процесс занимает больше времени, чем труден.
Они обычно встречаются, особенно если учитывать сопротивление провода. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно. Комбинации последовательного и параллельного подключения можно уменьшить до одного эквивалентного сопротивления, используя методику, показанную на рисунке 4.Различные части идентифицируются как последовательные или параллельные, уменьшаются до их эквивалентов и далее уменьшаются до тех пор, пока не останется единственное сопротивление. Процесс занимает больше времени, чем труден.Рис. 4. Эта комбинация из семи резисторов имеет как последовательные, так и параллельные части. Каждый из них идентифицируется и уменьшается до эквивалентного сопротивления, а затем уменьшается до тех пор, пока не будет достигнуто одно эквивалентное сопротивление.
Самая простая комбинация последовательного и параллельного сопротивления, показанная на рисунке 4, также является наиболее поучительной, поскольку она используется во многих приложениях.
 Например, R 1 может быть сопротивлением проводов от автомобильного аккумулятора к его электрическим устройствам, которые подключены параллельно. R 2 и R 3 могли быть стартером и светом салона. Ранее мы предполагали, что сопротивление провода незначительно, но, когда это не так, оно имеет важные последствия, как показывает следующий пример.
Например, R 1 может быть сопротивлением проводов от автомобильного аккумулятора к его электрическим устройствам, которые подключены параллельно. R 2 и R 3 могли быть стартером и светом салона. Ранее мы предполагали, что сопротивление провода незначительно, но, когда это не так, оно имеет важные последствия, как показывает следующий пример.Пример 3. Расчет сопротивления,
IR Падение, ток и рассеиваемая мощность: объединение последовательных и параллельных цепейНа рис. 5 показаны резисторы из двух предыдущих примеров, подключенные другим способом — комбинацией последовательного и параллельного.Мы можем считать R 1 сопротивлением проводов, ведущих к R 2 и R 3 . (а) Найдите полное сопротивление. (b) Что такое падение IR в R 1 ? (c) Найдите текущие I 2 через R 2 .
 (d) Какую мощность рассеивает R 2 ?
(d) Какую мощность рассеивает R 2 ?Рис. 5. Эти три резистора подключены к источнику напряжения, так что R 2 и R 3 параллельны друг другу, и эта комбинация последовательно с R 1 .
Стратегия и решение для (а)Чтобы найти полное сопротивление, отметим, что R 2 и R 3 находятся параллельно, и их комбинация R p находится последовательно с R 1 . Таким образом, общее (эквивалентное) сопротивление этой комбинации составляет
.R общ = R 1 + R p .
Сначала находим R p , используя уравнение для параллельных резисторов и вводя известные значения:
[латекс] \ frac {1} {{R} _ {\ text {p}}} = \ frac {1} {{R} _ {2}} + \ frac {1} {{R} _ {3 }} = \ frac {1} {6 \ text {.
 } \ text {00} \ text {} \ Omega} + \ frac {1} {\ text {13} \ text {.} 0 \ text {} \ Omega} = \ frac {0.2436} {\ text {} \ Омега} \\ [/ латекс].
} \ text {00} \ text {} \ Omega} + \ frac {1} {\ text {13} \ text {.} 0 \ text {} \ Omega} = \ frac {0.2436} {\ text {} \ Омега} \\ [/ латекс].Инвертирование дает
[латекс] {R} _ {\ text {p}} = \ frac {1} {0,2436} \ text {} \ Omega = 4.11 \ text {} \ Omega \\ [/ latex].
Таким образом, общее сопротивление равно
.R общ = R 1 + R p = 1,00 Ом + 4,11 Ом = 5,11 Ом.
Обсуждение для (а)Общее сопротивление этой комбинации является промежуточным между значениями чистой серии и чистой параллели (20.0 Ом и 0,804 Ом соответственно), найденные для тех же резисторов в двух предыдущих примерах.
Стратегия и решение для (b)Чтобы найти падение IR в R 1 , отметим, что полный ток I протекает через R 1 . Таким образом, его падение IR составляет
В 1 = ИК 1
Мы должны найти I , прежде чем сможем вычислить V 1 .
 Полный ток I находится с помощью закона Ома для схемы. То есть
Полный ток I находится с помощью закона Ома для схемы. То есть[латекс] I = \ frac {V} {{R} _ {\ text {tot}}} = \ frac {\ text {12.0} \ text {V}} {5.11 \ text {} \ Omega} = 2.35 \ text {A} \\ [/ latex].
Вводя это в выражение выше, получаем
В 1 = IR 1 = (2,35 А) (1,00 Ом) = 2,35 В.
Обсуждение для (б)Напряжение, приложенное к R 2 и R 3 , меньше полного напряжения на величину В 1 .Когда сопротивление провода велико, это может существенно повлиять на работу устройств, представленных R 2 и R 3 .
Стратегия и решение для (c)Чтобы найти ток через R 2 , мы должны сначала найти приложенное к нему напряжение. Мы называем это напряжение В p , потому что оно приложено к параллельной комбинации резисторов.
 Напряжение, приложенное как к R 2 , так и к R 3 , уменьшается на величину В 1 , и поэтому оно составляет
Напряжение, приложенное как к R 2 , так и к R 3 , уменьшается на величину В 1 , и поэтому оно составляетV p = V — V 1 = 12.0 В — 2,35 В = 9,65 В.
Теперь ток I 2 через сопротивление R 2 находится по закону Ома:
[латекс] {I} _ {2} = \ frac {{V} _ {\ text {p}}} {{R} _ {2}} = \ frac {9.65 \ text {V}} {6.00 \ текст {} \ Omega} = 1,61 \ text {A} \\ [/ latex].
Обсуждение для (c)Ток меньше 2,00 А, которые протекали через R 2 , когда он был подключен параллельно батарее в предыдущем примере параллельной цепи.
Стратегия и решение для (d)Мощность, рассеиваемая R 2 , равна
P 2 = ( I 2 ) 2 R 2 = (1,61 A) 2 (6,00 Ом) = 15,5 Вт
Обсуждение для (д)Мощность меньше 24,0 Вт, рассеиваемых этим резистором при параллельном подключении к источнику 12,0 В.

Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор.Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение IR в проводах также может быть значительным.
Например, когда вы роетесь в холодильнике, и мотор включается, свет холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
То, что происходит в этих сильноточных ситуациях, показано на рисунке 6. Устройство, представленное R 3 , имеет очень низкое сопротивление, поэтому при его включении протекает большой ток. Этот увеличенный ток вызывает большее падение IR в проводах, представленных R 1 , уменьшая напряжение на лампе (которое составляет R 2 ), которое затем заметно гаснет.

Рис. 6. Почему свет тускнеет при включении большого прибора? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение напряжения в проводах и снижает напряжение на свету.
Проверьте свое понимание
Можно ли любую произвольную комбинацию резисторов разбить на последовательную и параллельную? Посмотрите, сможете ли вы нарисовать принципиальную схему резисторов, которые нельзя разбить на комбинации последовательно и параллельно.
Решение Нет, существует множество способов подключения резисторов, которые не являются комбинациями последовательного и параллельного, включая петли и переходы. В таких случаях правила Кирхгофа, которые будут включены в Правила Кирхгофа, позволят вам проанализировать схему. Стратегии решения проблем для последовательных и параллельных резисторов- Нарисуйте четкую принципиальную схему, обозначив все резисторы и источники напряжения.
 Этот шаг включает список известных проблем, поскольку они отмечены на вашей принципиальной схеме.
Этот шаг включает список известных проблем, поскольку они отмечены на вашей принципиальной схеме. - Точно определите, что необходимо определить в проблеме (определите неизвестные). Письменный список полезен.
- Определите, подключены ли резисторы последовательно, параллельно или в комбинации последовательно и параллельно.Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
- Используйте соответствующий список основных функций для последовательных или параллельных подключений, чтобы найти неизвестные. Есть один список для серий и другой для параллельных. Если ваша проблема представляет собой комбинацию последовательного и параллельного соединения, сокращайте ее поэтапно, рассматривая отдельные группы последовательных или параллельных соединений, как это сделано в этом модуле и примерах. Особое примечание: при нахождении R необходимо соблюдать осторожность.

- Проверьте, являются ли ответы разумными и последовательными. Единицы и числовые результаты должны быть разумными. Общее последовательное сопротивление должно быть больше, а общее параллельное сопротивление, например, должно быть меньше. Мощность должна быть больше для одних и тех же устройств, подключенных параллельно, по сравнению с последовательными и так далее.
Сводка раздела
Концептуальные вопросы
1. Переключатель имеет переменное сопротивление, близкое к нулю в замкнутом состоянии и очень большое в разомкнутом, и он включен последовательно с устройством, которым он управляет.Объясните влияние переключателя на рисунке 7 на ток в разомкнутом и замкнутом состоянии.
Рисунок 7. Выключатель обычно включается последовательно с источником сопротивления и напряжения. В идеале, переключатель имеет почти нулевое сопротивление в замкнутом состоянии, но имеет чрезвычайно большое сопротивление в разомкнутом состоянии. (Обратите внимание, что на этой диаграмме скрипт E представляет напряжение (или электродвижущую силу) батареи.
 )
)2. Какое напряжение на разомкнутом переключателе на Рисунке 7?
3. На разомкнутом переключателе есть напряжение, как на Рисунке 7.Почему же тогда мощность, рассеиваемая разомкнутым переключателем, мала?
4. Почему мощность, рассеиваемая замкнутым переключателем, как на Рисунке 7, мала?
5. Студент в физической лаборатории по ошибке подключил электрическую лампочку, батарею и выключатель, как показано на рисунке 8. Объясните, почему лампа горит, когда выключатель разомкнут, и гаснет, когда он замкнут. (Не пытайтесь — батарея сильно разряжается!)
Рис. 8. Ошибка подключения: включите этот переключатель параллельно устройству, обозначенному [латекс] R [/ латекс].(Обратите внимание, что на этой диаграмме скрипт E представляет напряжение (или электродвижущую силу) батареи.)
6. Зная, что сила удара зависит от величины тока, протекающего через ваше тело, вы бы предпочли, чтобы он был включен последовательно или параллельно с сопротивлением, таким как нагревательный элемент тостера, если он потрясен им? Объяснять.

7. Были бы ваши фары тусклыми при запуске двигателя автомобиля, если бы провода в вашем автомобиле были сверхпроводящими? (Не пренебрегайте внутренним сопротивлением батареи.) Объяснять.
8. Некоторые гирлянды праздничных огней соединены последовательно для экономии затрат на проводку. В старой версии использовались лампочки, которые при перегорании прерывали электрическое соединение, как выключатель. Если одна такая лампочка перегорит, что случится с остальными? Если такая цепочка работает от 120 В и имеет 40 одинаковых лампочек, каково нормальное рабочее напряжение каждой? В более новых версиях используются лампы, которые при перегорании замыкаются накоротко, как замкнутый выключатель. Если одна такая лампочка перегорит, что случится с остальными? Если такая цепочка работает от 120 В и в ней осталось 39 идентичных лампочек, каково тогда рабочее напряжение каждой?
9.Если две бытовые лампочки мощностью 60 и 100 Вт подключить последовательно к бытовой электросети, какая из них будет ярче? Объяснять.

10. Предположим, вы проводите физическую лабораторию, которая просит вас вставить резистор в цепь, но все прилагаемые резисторы имеют большее сопротивление, чем запрошенное значение. Как бы вы соединили доступные сопротивления, чтобы попытаться получить меньшее запрошенное значение?
11. Перед Второй мировой войной некоторые радиостанции получали питание через «шнур сопротивления», который имел значительное сопротивление.Такой резистивный шнур снижает напряжение до желаемого уровня для ламп радиоприемника и т.п., и это экономит расходы на трансформатор. Объясните, почему шнуры сопротивления нагреваются и расходуют энергию при включенном радио.
12. У некоторых лампочек есть три уровня мощности (не включая ноль), получаемые от нескольких нитей накала, которые индивидуально переключаются и соединяются параллельно. Какое минимальное количество нитей необходимо для трех режимов мощности?
Задачи и упражнения
Примечание.
 Можно считать, что данные, взятые из цифр, имеют точность до трех значащих цифр.
Можно считать, что данные, взятые из цифр, имеют точность до трех значащих цифр.1. (a) Каково сопротивление десяти последовательно соединенных резисторов сопротивлением 275 Ом? (б) Параллельно?
2. (a) Каково сопротивление последовательно соединенных резисторов 1,00 × 10 2 Ом, 2,50 кОм и 4,00 кОм? (б) Параллельно?
3. Какое наибольшее и наименьшее сопротивление можно получить, соединив резисторы на 36,0 Ом, 50,0 Ом и 700 Ом?
4. Тостер на 1800 Вт, электрическая сковорода на 1400 Вт и лампа на 75 Вт подключены к одной розетке в цепи 15 А, 120 В.(Три устройства работают параллельно, если подключены к одной розетке.) а) Какой ток потребляет каждое устройство? (b) Перегорит ли эта комбинация предохранитель на 15 А?
5. Обычно фара мощностью 30,0 Вт и стартер мощностью 2,40 кВт подключаются параллельно в систему на 12,0 В. Какую мощность потребляли бы одна фара и стартер при последовательном подключении к батарее 12,0 В? (Не обращайте внимания на любое другое сопротивление в цепи и любое изменение сопротивления в двух устройствах.
 )
)6.(a) Для батареи 48,0 В и резисторов 24,0 Ом и 96,0 Ом найдите для каждого из них ток и мощность при последовательном соединении. (b) Повторите, когда сопротивления включены параллельно.
7. Ссылаясь на пример комбинирования последовательных и параллельных цепей и рисунок 5, вычислите I 3 следующими двумя различными способами: (a) из известных значений I и I 2 ; (б) используя закон Ома для R 3 . В обеих частях явно показано, как вы следуете шагам, описанным в Стратегии решения проблем для последовательных и параллельных резисторов выше.
Рис. 5. Эти три резистора подключены к источнику напряжения, так что R 2 и R 3 параллельны друг другу, и эта комбинация последовательно с R 1 .
8. Ссылаясь на рисунок 5: (a) Вычислите P 3 и обратите внимание на его сравнение с P 3 , найденным в первых двух примерах задач в этом модуле.
 (b) Найдите общую мощность, отдаваемую источником, и сравните ее с суммой мощностей, рассеиваемых резисторами.
(b) Найдите общую мощность, отдаваемую источником, и сравните ее с суммой мощностей, рассеиваемых резисторами.9. Обратитесь к Рисунку 6 и обсуждению затемнения света при включении тяжелого прибора. (a) Учитывая, что источник напряжения составляет 120 В, сопротивление провода составляет 0,400 Ом, а номинальная мощность лампы составляет 75,0 Вт, какая мощность будет рассеиваться лампой, если при включении двигателя через провода пройдет в общей сложности 15,0 А? Предположите незначительное изменение сопротивления лампы. б) Какая мощность потребляет двигатель?
Рис. 6. Почему свет тускнеет при включении большого прибора? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение напряжения в проводах и снижает напряжение на свету.
10. Линия электропередачи на 240 кВ, имеющая 5,00 × 10 2 , подвешена к заземленным металлическим опорам с помощью керамических изоляторов, каждый из которых имеет сопротивление 1,00 × 10 9 Ом (рисунок 9 (a)).
 Какое сопротивление на землю у 100 изоляторов? (b) Рассчитайте мощность, рассеиваемую 100 из них. (c) Какая часть мощности, переносимой линией, это? Ясно покажите, как вы выполняете шаги, описанные в Стратегии решения проблем для последовательных и параллельных резисторов выше.
Какое сопротивление на землю у 100 изоляторов? (b) Рассчитайте мощность, рассеиваемую 100 из них. (c) Какая часть мощности, переносимой линией, это? Ясно покажите, как вы выполняете шаги, описанные в Стратегии решения проблем для последовательных и параллельных резисторов выше.Рис. 9. Высоковольтная (240 кВ) линия электропередачи 5,00 × 10 2 подвешена к заземленной металлической опоре электропередачи. Ряд керамических изоляторов обеспечивает сопротивление 1,00 × 10 9 Ом каждый.
11. Покажите, что если два резистора R 1 и R 2 объединены, и один намного больше другого ( R 1 >> R 2 ): (a ) Их последовательное сопротивление почти равно большему сопротивлению R 1 .(b) Их параллельное сопротивление почти равно меньшему сопротивлению R 2 .
12. Необоснованные результаты Два резистора, один из которых имеет сопротивление 145 Ом, подключены параллельно, чтобы получить общее сопротивление 150 Ом.
 а) Каково значение второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения являются необоснованными или непоследовательными?
а) Каково значение второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения являются необоснованными или непоследовательными?13. Необоснованные результаты Два резистора, один из которых имеет сопротивление 900 кОм, соединены последовательно, чтобы получить общее сопротивление 0.500 МОм. а) Каково значение второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения являются необоснованными или непоследовательными?
Глоссарий
- серия:
- последовательность резисторов или других компонентов, включенных в цепь один за другим
- резистор:
- компонент, обеспечивающий сопротивление току, протекающему по электрической цепи
- сопротивление:
- вызывает потерю электроэнергии в цепи
- Закон Ома:
- соотношение между током, напряжением и сопротивлением в электрической цепи: В = IR
- напряжение:
- электрическая потенциальная энергия на единицу заряда; электрическое давление, создаваемое источником питания, например аккумулятором
- падение напряжения:
- потеря электроэнергии при прохождении тока через резистор, провод или другой компонент
- ток:
- поток заряда через электрическую цепь мимо заданной точки измерения
- Закон Джоуля:
- соотношение между потенциальной электрической мощностью, напряжением и сопротивлением в электрической цепи, определяемое по формуле: [latex] {P} _ {e} = \ text {IV} [/ latex]
- параллельно:
- подключение резисторов или других компонентов в электрической цепи таким образом, что каждый компонент получает одинаковое напряжение от источника питания; часто изображается на диаграмме в виде лестницы, где каждый компонент находится на ступеньке лестницы
Избранные решения проблем и упражнения
1.
 (а) 2,75 кОм (б) 27,5 Ом
(а) 2,75 кОм (б) 27,5 Ом3. (а) 786 Ом (б) 20,3 Ом
5. 29,6 Вт
7. (а) 0,74 А (б) 0,742 А
9. (а) 60,8 Вт (б) 3,18 кВт
11. (a) [латекс] \ begin {array} {} {R} _ {\ text {s}} = {R} _ {1} + {R} _ {2} \\ \ Rightarrow {R} _ {\ text {s}} \ приблизительно {R} _ {1} \ left ({R} _ {1} \ text {>>} {R} _ {2} \ right) \ end {array} \\ [/ латекс]
(b) [латекс] \ frac {1} {{R} _ {p}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2} } = \ frac {{R} _ {1} + {R} _ {2}} {{R} _ {1} {R} _ {2}} \\ [/ latex],
так что
[латекс] \ begin {array} {} {R} _ {p} = \ frac {{R} _ {1} {R} _ {2}} {{R} _ {1} + {R} _ {2}} \ приблизительно \ frac {{R} _ {1} {R} _ {2}} {{R} _ {1}} = {R} _ {2} \ left ({R} _ {1 } \ text {>>} {R} _ {2} \ right) \ text {.} \ end {array} \\ [/ latex]
13. (a) –400 кОм (b) Сопротивление не может быть отрицательным. (c) Считается, что последовательное сопротивление меньше, чем у одного из резисторов, но должно быть больше, чем у любого из резисторов.

Сопротивление в параллельной цепи
Сопротивление в параллельной цепи
В примерной схеме, рис. 3-44, два резистора подключены параллельно через 5-вольтовую батарею.Каждый имеет значение сопротивления 10 Ом. Формируется полная цепь, состоящая из двух параллельных путей, и ток течет, как показано.Рисунок 3-44. — Два равных резистора, включенных параллельно.
Вычисление отдельных токов показывает, что через каждое сопротивление проходит половина ампера. Полный ток, протекающий от батареи к переходу резисторов и возвращающийся от резисторов к батарее, равен 1 амперам.Общее сопротивление цепи можно рассчитать, используя
значений полного напряжения (E T ) и полного тока (I T ).ПРИМЕЧАНИЕ. С этого момента в примерах задач будут использоваться сокращения и символы для электрических величин.
Дано:
Решение:
Это вычисление показывает, что полное сопротивление составляет 5 Ом; половину номинала любого из двух резисторов.
Поскольку полное сопротивление параллельной цепи меньше, чем у любого из отдельных резисторов, общее сопротивление параллельной цепи не является суммой значений отдельных резисторов, как это было в случае последовательной цепи.Общее сопротивление параллельно подключенных резисторов также называется ЭКВИВАЛЕНТНЫМ СОПРОТИВЛЕНИЕМ. ( рэнд рэндов). Термины полное сопротивление и эквивалентное сопротивление используются как синонимы.
Есть несколько методов, используемых для определения эквивалентного сопротивления параллельных цепей. Лучший метод для данной схемы зависит от количества и номинала резисторов. Для схемы, описанной выше, где все резисторы имеют одинаковое значение, используется следующее простое уравнение:
Это уравнение действительно для любого количества параллельных резисторов с РАВНЫМ ЗНАЧЕНИЕМ.Пример. Параллельно подключены четыре резистора на 40 Ом. Каково их эквивалентное сопротивление?
Дано:
Решение:
На Рис. 3-45 показаны два резистора разной величины, включенные параллельно. Поскольку показан полный ток, можно рассчитать эквивалентное сопротивление.
3-45 показаны два резистора разной величины, включенные параллельно. Поскольку показан полный ток, можно рассчитать эквивалентное сопротивление.Рисунок 3-45. — Пример схемы с неравнопараллельными резисторами.
Дано:
Решение:
Эквивалентное сопротивление цепи, показанной на рисунке 3-45, меньше, чем у любого из двух резисторов (R 1 , R 2 ).Важно помнить, что эквивалентное сопротивление параллельной цепи всегда меньше, чем сопротивление любой ветви.Эквивалентное сопротивление можно найти, если вам известны отдельные значения сопротивления и напряжение источника. Вычисляя ток каждой ветви, складывая токи ответвления для вычисления общего тока и разделив напряжение источника на общий ток, можно найти общий ток. Этот метод хоть и эффективен, но довольно длительный. Более быстрый способ найти эквивалентное сопротивление — использовать общую формулу для параллельных резисторов:
Если вы примените общую формулу к схеме, показанной на рисунке 3-45, вы получите такое же значение для эквивалентного сопротивления (2 Ом), что и было полученный в предыдущем расчете, в котором использовались напряжение источника и полный ток.
Дано:
Решение:
Преобразуйте дроби к общему знаменателю.
Поскольку обе стороны являются взаимными (делятся на одну), игнорируйте обратную функцию.
Формула, которую вы дали для одинаковых резисторов, подключенных параллельно
, является упрощением общей формулы для параллельных резисторов
Существуют и другие упрощения общей формулы для параллельных резисторов, которые можно использовать для расчета общей суммы или эквивалентное сопротивление в параллельной цепи.ВЗАИМНЫЙ МЕТОД. — Этот метод основан на взятии обратной величины для каждой стороны уравнения. Это представляет собой общую формулу для резисторов, включенных параллельно:
Эта формула используется для вычисления эквивалентного сопротивления ряда неравных параллельных резисторов. При решении этих задач вы должны найти наименьший общий знаменатель. Если вы не знаете, как найти наименьший общий знаменатель, освежите его в математике, том 1, NAVEDTRA 10069 (серия).
Пример: три резистора подключены параллельно, как показано на рисунке 3-46. Значения резистора: R 1 = 20 Ом, R 2 = 30 Ом, R 3 = 40 Ом. Какое эквивалентное сопротивление? (Используйте обратный метод.)
Рисунок 3-46. — Пример параллельной схемы с разными резисторами ответвления.
Дано:
Решение:ПРОДУКТ ПРЕВЫШАЕТ СУММУ. — Удобный метод определения эквивалентного или полного сопротивления двух параллельных резисторов — использовать следующую формулу.
Это уравнение, называемое формулой произведения на сумму, используется настолько часто, что его следует сохранить в памяти.Пример. Какое эквивалентное сопротивление резистора 20 Ом и резистора 30 Ом, подключенных параллельно, как показано на рисунке 3-47?
Рисунок 3-47. — Параллельная схема с двумя неравными резисторами.
Дано:
Решение:
Четыре равных резистора подключены параллельно, каждый резистор имеет омическое значение 100 Ом, каково эквивалентное сопротивление?Три резистора, соединенных параллельно, имеют номиналы 12 кОм, 20 кОм и 30 кОм.
 Какое эквивалентное сопротивление?
Какое эквивалентное сопротивление?Два резистора, соединенных параллельно, имеют номиналы 10 кОм и 30 кОм. Какое эквивалентное сопротивление?
резисторов в последовательной и параллельной комбинации сетей
ПОСЛЕДОВАТЕЛЬНЫЕ И ПАРАЛЛЕЛЬНЫЕ СОЧЕТАНИЯ РЕЗИСТОРОВ
Последовательные и параллельные резисторы
Резисторы могут быть подключены отдельно или параллельно. Некоторые схемы резисторов состоят из комбинации последовательных и параллельных цепей для создания более сложных схем.Эти схемы обычно известны как схемы со смешанными резисторами. Несмотря на то, что эти цепи имеют комбинированные последовательные и параллельные цепи, нет никаких изменений в методе расчета эквивалентного сопротивления. Основные правила отдельных сетей, такие как «одинаковый ток протекает через последовательно подключенные резисторы» и «одинаковое напряжение на резисторах, подключенных параллельно», применимы к смешанным схемам.
Пример схемы смешанных резисторов показан ниже
Он состоит из четырех резисторов R1, R2, R3 и R4 в смешанной комбинации резисторов.
 Напряжение питания равно V, а общий ток, протекающий в цепи, равен I. Ток, протекающий через резисторы R2 и R3, равен I1, а ток, протекающий через резистор R4, равен I2.
Напряжение питания равно V, а общий ток, протекающий в цепи, равен I. Ток, протекающий через резисторы R2 и R3, равен I1, а ток, протекающий через резистор R4, равен I2.Здесь резисторы R2 и R3 соединены последовательно. Следовательно, применяя правило последовательно соединенных резисторов, эквивалентное сопротивление R2 и R3 дается как
R A = R2 + R3
Здесь R A — эквивалентное сопротивление R2 и R3.
Теперь резисторы R2 и R3 можно заменить одним резистором R A .Полученная схема показана ниже.
Теперь резисторы R A, и R4 соединены параллельно. Следовательно, при применении правила параллельной комбинации резисторов эквивалентное сопротивление R A, и R4 равно
R B = R A * R4 / (R A + R4)
Здесь R B — эквивалентное сопротивление R A и R4.
Теперь мы можем заменить резисторы R A, и R4 на один резистор R B.
 После замены резисторов полученная схема показана ниже.
После замены резисторов полученная схема показана ниже.Теперь схема состоит всего из двух резисторов. Здесь также последовательно соединены резисторы R1 и R B . Следовательно, применяя правило последовательно включенных резисторов, полное эквивалентное сопротивление цепи определяется как
R EQ = R1 + R B
Здесь R EQ — полное эквивалентное сопротивление цепи. Теперь резисторы R1 и R B можно заменить одним резистором R EQ .
Окончательная эквивалентная схема для вышеуказанной сложной схемы показана ниже.
Хотя они выглядят сложными, схемы смешанных резисторов могут быть сведены к простой схеме, состоящей только из одного источника напряжения и одного резистора, следуя простым правилам подключения резисторов последовательно и резисторов параллельно.
Вернуться к списку
Последовательные и параллельные резисторы Пример
Рассчитаем эквивалентное сопротивление для схемы ниже, состоящей из 7 резисторов R1 = 4 Ом, R2 = 4 Ом, R3 = 8 Ом, R4 = 10 Ом, R5 = 4 Ом, R6 = 2 Ом и R7 = 2 Ом.
 Напряжение питания 5 В.
Напряжение питания 5 В.Теперь резисторы R 6 и R 7 соединены последовательно. Если эквивалентное сопротивление последовательно соединенных R 6 и R 7 равно R a , то
R a = R 6 + R 7 = 2 + 2 = 4 Ом
Результирующая схема сводится к показанной ниже.
В приведенной выше схеме резисторы R a и R 5 соединены параллельно.Следовательно, эквивалентное сопротивление R a и R 5 составляет
R b = (R a * R 5 ) / (R a + R 5 ) = (4 * 4) / (4 + 4) = 2 Ом.
Тогда упрощенная схема показана ниже.
В этой схеме последовательно соединены резисторы R 4 и R b .
R c = R 4 + R b = 10 + 2 = 12 Ом.
Теперь мы можем заменить резисторы R 4 и R b на резистор R c , как показано ниже.

В приведенной выше схеме резисторы R 2 и R 3 соединены последовательно. Если R d эквивалентно сопротивлению R 2 и R 3 , тогда
R d = R 2 + R 3 = 4 + 8 = 12 Ом.
Эквивалентная схема:
Здесь параллельно соединены резисторы R c и R d .Пусть R p будет эквивалентным сопротивлением R c и R d параллельно. потом
R p = (R c * R d ) / (R c + R d ) = (12 * 12) / (12 + 12) = 6 Ом.
Результирующая схема
Здесь резисторы R1 и Rp соединены последовательно. Пусть R EQ будет эквивалентным сопротивлением этой комбинации. потом
R EQ = R1 + Rp = 4 + 6 = 10 Ом.
Это эквивалентное сопротивление цепи. Следовательно, данную схему можно окончательно перерисовать как
Ток в цепи можно рассчитать по закону Ома.

I = V / R EQ = 5/10 = 0,5 А
Вернуться к списку
Резисторные сети
Вычислим эквивалентное сопротивление для схемы сложного резистора.
Схема ниже состоит из десяти резисторов от R1 до R10, соединенных последовательно и параллельно.
Значения сопротивления, указанные в цепи, указаны в Ом (Ом), а напряжение питания — в Вольтах (В).
Здесь последовательно соединены резисторы R 9 и R 10 . Пусть R A — эквивалентное сопротивление этой комбинации.
Следовательно, R A = R9 + R10 = 3 + 3 = 6 Ом.
Схема после замены R9 и R10 на R A есть
В этой схеме параллельно соединены резисторы R8 и R A, .Тогда эквивалентное сопротивление R8 и R A равно
R B = (R8 * R A ) / (R8 + R A ) = (6 * 6) / (6 + 6) = 3 Ом.
Теперь заменив R8 и R A на R B , мы получим следующую схему.

В этой схеме последовательно соединены резисторы R7 и R B .
R C = R7 + R B = 9 + 3 = 12 Ом.
Эквивалентная схема после замены R7 и R B на R C :
Понятно, что резисторы R6 и Rc соединены параллельно.Если R D является эквивалентным сопротивлением этой комбинации, то
R D = (R6 * Rc) / (R6 + Rc) = (12 * 12) / (12 + 12) = 6 Ом.
Схема с R D , заменяющая R6 и Rc, является
Теперь резисторы R4 и R D соединены последовательно. Если R E эквивалентно сопротивлению R4 и R D , тогда
R E = R4 + R D = 6 + 6 = 12 Ом.
Результирующая сокращенная схема после замены R4 и R D на R E выглядит следующим образом:
В этой схеме параллельно соединены резисторы R5 и R E .
Пусть R F будет эквивалентным сопротивлением R5 и R E параллельно.

Тогда R F = (R5 * R E ) / (R5 + R E ) = (12 * 12) / (12 + 12) = 6 Ом.
Упрощенная схема показана ниже.
Здесь резисторы R2 и R3 включены последовательно. Если R G является эквивалентом этой комбинации, то
R G = R2 + R3 = 4 + 2 = 6 Ом.
После замены R2 и R3 на R G схема будет преобразована в
Резисторы R F и R G включены параллельно.
Пусть R T будет эквивалентом этой комбинации.
Тогда R T = (R F * R G ) / (R F + R G ) = (6 * 6) / (6 + 6) = 3 Ом.
Теперь резисторы R1 и R T стоят последовательно. Если R EQ — полное эквивалентное сопротивление цепи, то R EQ = R1 + R T = 3 + 3 = 6 Ом.
Наконец, приведенную выше сложную схему можно перерисовать следующим образом
Полный ток в цепи можно рассчитать по закону Ома.

I = V1 / R EQ = 6/6 = 1 А.
Следовательно, любая сложная резистивная цепь, состоящая из числа резисторов, соединенных в комбинации как последовательной, так и параллельной комбинаций, может быть уменьшена, сначала идентифицируя простые параллельные ветви резистора и ветви последовательного резистора.Рассчитывается эквивалентное сопротивление этих простых ветвей, и ветви заменяются эквивалентным резистором. Этот процесс снижает сложность схемы. Продолжая этот процесс, мы можем заменить сложную резистивную цепь одним резистором.
Существуют некоторые сложные резистивные схемы, которые нельзя свести к простым схемам, просто применяя правила последовательного резистивного сочетания и параллельного резистивного сочетания. Такие схемы, как аттенюаторы T-Pad и некоторые сложные резистивные мостовые схемы, являются примерами таких сложных резистивных схем.Чтобы упростить эти сложные резистивные схемы, следует использовать другой подход.
Некоторые сложные резистивные цепи можно уменьшить, используя закон Кирхгофа по току и закон Кирхгофа по напряжению.

Найти токи и напряжения в сложной резистивной цепи, просто используя закон Ома, может быть невозможно. Для таких цепей будут полезны правила Кирхгофа для цепей.
Законы Кирхгофа для цепей основаны на концепции сохранения тока и энергии в цепи.Есть два закона Кирхгофа. Первый — это закон тока Кирхгофа, который касается тока в узле, а второй — закон напряжения Кирхгофа, который касается напряжения в замкнутой цепи.
Текущий закон Кирхгофа гласит: «Ток, входящий в узел, равен току, выходящему из узла, потому что ему некуда идти, и ток в узле не теряется».
Проще говоря, Закон Кирхгофа по току гласит, что сумма токов, входящих в узел, равна сумме токов, выходящих из цепи.
Закон Кирхгофа о напряжении гласит, что «полное напряжение в замкнутом контуре равно сумме всех падений напряжения в этом контуре».
Проще говоря, закон Кирхгофа утверждает, что направленная алгебраическая сумма напряжений в замкнутом контуре равна нулю.
С помощью этих двух законов можно рассчитать значения токов и напряжений в любой сложной цепи.

Тем не менее, у нас могут быть сложные резистивные схемы, в которых трудно определить эквивалентное сопротивление, в таких ситуациях мы будем использовать преобразование резисторов по схеме звезда-треугольник, чтобы упростить схемы резисторов.
Вернуться к списку
Последовательные и параллельные резисторы
Резисторы могут быть подключены отдельно друг от друга либо последовательно, либо параллельно. Некоторые схемы резисторов состоят из комбинации последовательных и параллельных цепей для создания более сложных схем. Эти схемы обычно известны как схемы со смешанными резисторами. Несмотря на то, что эти цепи имеют комбинированные последовательные и параллельные цепи, нет никаких изменений в методе расчета эквивалентного сопротивления.Основные правила отдельных сетей, такие как «одинаковый ток протекает через последовательно подключенные резисторы» и «одинаковое напряжение на резисторах, подключенных параллельно», применимы к смешанным схемам.
Пример схемы смешанных резисторов показан ниже
Он состоит из четырех резисторов R1, R2, R3 и R4 в смешанной комбинации резисторов.
 Напряжение питания равно V, а общий ток, протекающий в цепи, равен I. Ток, протекающий через резисторы R2 и R3, равен I1, а ток, протекающий через резистор R4, равен I2.
Напряжение питания равно V, а общий ток, протекающий в цепи, равен I. Ток, протекающий через резисторы R2 и R3, равен I1, а ток, протекающий через резистор R4, равен I2.Здесь резисторы R2 и R3 соединены последовательно. Следовательно, применяя правило последовательно соединенных резисторов, эквивалентное сопротивление R2 и R3 дается как
.R A = R2 + R3
Здесь RA — эквивалентное сопротивление R2 и R3
Теперь резисторы R2 и R3 можно заменить одним резистором RA. Полученная схема показана ниже.
Теперь резисторы RA и R4 соединены параллельно. Следовательно, при применении правила параллельной комбинации резисторов эквивалентное сопротивление RA и R4 равно
.R B = R A × R4 / (R A + R4)
Здесь RB — эквивалентное сопротивление RA и R4
Теперь мы можем заменить резисторы RA и R4 одним резистором RB.После замены резисторов полученная схема показана ниже.
Сейчас схема состоит всего из двух резисторов.
. Здесь также последовательно соединены резисторы R1 и RB. Следовательно, применяя правило последовательно включенных резисторов, общее эквивалентное сопротивление цепи составляет
Здесь также последовательно соединены резисторы R1 и RB. Следовательно, применяя правило последовательно включенных резисторов, общее эквивалентное сопротивление цепи составляетR EQ = R1 + R B
Здесь R EQ — полное эквивалентное сопротивление цепи. Теперь резисторы R1 и R B можно заменить одним резистором R EQ .
Окончательная эквивалентная схема для вышеуказанной сложной схемы показана ниже.
Несмотря на то, что они выглядят сложными, схемы смешанных резисторов могут быть сведены к простой схеме, состоящей только из одного источника напряжения и одного резистора, следуя простым правилам последовательного включения резисторов и параллельного включения резисторов.
Последовательные и параллельные резисторы Пример
Рассчитаем эквивалентное сопротивление для приведенной ниже схемы, состоящей из 7 резисторов R1 = 4 Ом, R2 = 4 Ом, R3 = 8 Ом, R4 = 10 Ом, R5 = 4 Ом, R6 = 2 Ом и R7 = 2 Ом.
 Напряжение питания 5 В.
Напряжение питания 5 В.Теперь резисторы R6 и R7 соединены последовательно. Если эквивалентное сопротивление серий R6 и R7in равно Ra, то
Ra = R6 + R7 = 2 + 2 = 4 Ом
Результирующая схема сокращается до показанной ниже.
В приведенной выше схеме резисторы Ra и R5 соединены параллельно. Следовательно, эквивалентное сопротивление Ra и R5 равно
.R b = ( R a × R 5 ) / ( R + R 5 ) = (4 × 4) / (4 + 4) = 2 Ом.
Далее упрощенная схема показана ниже.
В этой схеме резисторы R4 и R b включены последовательно.
Rc = R4 + R b = 10 + 2 = 12 Ом.
Теперь мы можем заменить резисторы R4 и R b на резистор Rc, как показано ниже.
В приведенной выше схеме резисторы R2 и R3 снова включены последовательно. Если Rd эквивалентно сопротивлению R2 и R3, тогда
.Rd = R2 + R3 = 4 + 8 = 12 Ом.

Схема замещения
Здесь резисторы Rc и Rd соединены параллельно. Пусть Rp будет эквивалентным сопротивлением Rc и Rd, включенных параллельно. Тогда
R p = (R c × R d ) / (R c + R d ) = (12 × 12) / (12 + 12) = 6 Ом.
В результате получается схема
Здесь резисторы R1 и Rp соединены последовательно. Пусть R EQ будет эквивалентным сопротивлением этой комбинации.
Затем
R EQ = R1 + Rp = 4 + 6 = 10 Ом.
Это эквивалентное сопротивление цепи. Следовательно, данную схему можно окончательно перерисовать как
Ток в цепи можно рассчитать по закону Ома
I = V / R EQ = 5/10 = 0,5 A
Сетевой резистор
Рассчитаем эквивалентное сопротивление для цепи сложного резистора.
Схема ниже состоит из десяти резисторов от R1 до R10, соединенных последовательно и параллельно.

Значения сопротивлений, указанных в цепи, указаны в Ом (Ом), а напряжение питания — в Вольтах (В).
Здесь последовательно соединены резисторы R9 и R10. Пусть R A — эквивалентное сопротивление этой комбинации.
Следовательно, R A = R9 + R10 = 3 + 3 = 6 Ом.
Цепь после замены R9 и R10 на R A —
В этой схеме резисторы R8 и R8 A и соединены параллельно.Тогда эквивалентное сопротивление R8 и R A равно
R B = (R8 × R A ) / (R8 + R A ) = (6 × 6) / (6 + 6) = 3 Ом.
Теперь заменив R8 и R A на R B , мы получим следующую схему.
В этой схеме резисторы R7 и R B включены последовательно.
R C = R7 + R B = 9 + 3 = 12 Ом.
Эквивалентная схема после замены R7 и R B на R C составляет
Понятно, что резисторы R6 и Rc соединены параллельно.
 Если R D является эквивалентным сопротивлением этой комбинации, то
Если R D является эквивалентным сопротивлением этой комбинации, тоR D = (R6 × Rc) / (R6 + Rc) = (12 × 12) / (12 + 12) = 6 Ом.
Схема с R¬D, заменяющим R6 и Rc —
Теперь резисторы R4 и RD соединены последовательно. Если RE эквивалентное сопротивление R4 и RD, тогда
R E = R4 + R D = 6 + 6 = 12 Ом.
Результирующая сокращенная схема после замены R4 и R D на R E составляет
В этой схеме параллельно соединены резисторы R5 и R E .
Пусть R F будет эквивалентным сопротивлением R5 и R E , включенных параллельно.
Затем
R F = (R5 × R E ) / (R5 + R E ) = (12 × 12) / (12 + 12) = 6 Ом.
Упрощенная схема показана ниже.
Здесь резисторы R2 и R3 включены последовательно. Если RG является эквивалентом этой комбинации, то
R G = R2 + R3 = 4 + 2 = 6 Ом.

После замены R2 и R3 на RG схема будет преобразована в
Резисторы RF и RG включены параллельно.
Пусть R T будет эквивалентом этой комбинации.
Тогда R T = (R F × R G ) / (R F + R G ) = (6 × 6) / (6 + 6) = 3 Ом.
Теперь резисторы R1 и RT включены последовательно. Если REQ — полное эквивалентное сопротивление цепи, то REQ = R1 + RT = 3 + 3 = 6 Ом.
Наконец, указанная выше сложная схема может быть перерисована следующим образом:
Полный ток в цепи можно рассчитать по закону Ома
I = V1 / R EQ = 6/6 = 1 А
Следовательно, любая сложная резистивная цепь, состоящая из числа резисторов, подключенных в комбинации как последовательной, так и параллельной комбинаций, может быть уменьшена, сначала идентифицируя простые параллельные ветви резистора и ветви последовательного резистора.Рассчитывается эквивалентное сопротивление этих простых ветвей, и ветви заменяются эквивалентным резистором.
 Этот процесс снижает сложность схемы. Продолжая этот процесс, мы можем заменить сложную резистивную цепь одним резистором.
Этот процесс снижает сложность схемы. Продолжая этот процесс, мы можем заменить сложную резистивную цепь одним резистором.Существуют некоторые сложные резистивные схемы, которые нельзя свести к простым схемам, просто применяя правила последовательных резистивных комбинаций и параллельных резистивных комбинаций. Такие схемы, как аттенюаторы T-Pad и некоторые сложные резистивные мостовые схемы являются примерами таких сложных резистивных схем.Чтобы упростить эти сложные резистивные схемы, следует использовать другой подход.
Некоторые сложные резистивные цепи можно уменьшить, используя закон Кирхгофа по току и закон Кирхгофа по напряжению.
Найти токи и напряжения в сложной резистивной цепи, просто используя закон Ома, может быть невозможно. Для таких цепей будут полезны правила Кирхгофа для цепей.
Законы Кирхгофа для цепей основаны на концепции сохранения тока и энергии в цепи.Есть два закона Кирхгофа. Первый — это закон тока Кирхгофа, который касается тока в узле, а второй — закон напряжения Кирхгофа, который касается напряжения в замкнутой цепи.

Закон Кирхгофа о течениях гласит, что «ток, входящий в узел, равен току, выходящему из узла, потому что ему некуда идти, и ток не теряется в узле».
Проще говоря, Закон Кирхгофа по току гласит, что сумма токов, входящих в узел, равна сумме токов, выходящих из цепи.
Закон Кирхгофа о напряжении гласит, что «полное напряжение в замкнутом контуре равно сумме всех падений напряжения в этом контуре».
Проще говоря, закон Кирхгофа утверждает, что направленная алгебраическая сумма напряжений в замкнутом контуре равна нулю.
С помощью этих двух законов можно рассчитать значения токов и напряжений в любой сложной цепи.
Тем не менее, у нас могут быть некоторые сложные резистивные схемы, в которых трудно определить эквивалентное сопротивление, в таких ситуациях мы будем использовать преобразование резисторов по схеме звезда-треугольник, чтобы упростить схемы резисторов.
Резисторы в параллельных цепях — Закон Ома — Национальная редакция 5 по физике
1555g5wi9fm.0.0.0.1:0.1.0.$0.$1.$0″> Когда резисторы подключены параллельно, мы можем рассчитать общее параллельное сопротивление (R T ), используя соотношение;\ [\ frac {1} {{{R_T}}} = \ frac {1} {{{R_1}}} + \ frac {1} {{{R_2}}} + \ frac {1} {{ {R_3}}} \]
Давайте воспользуемся теми же тремя значениями сопротивления, что и в предыдущем примере, и рассчитаем общее сопротивление при параллельном соединении резисторов.
Схема с батареей 6 В, двумя резисторами 10 Ом и резистором 20 Ом, включенными параллельно.Общее сопротивление RT находится с помощью соотношения;
\ [\ frac {1} {{{R_T}}} = \ frac {1} {{{R_1}}} + \ frac {1} {{{R_2}}} + \ frac {1} {{ {R_3}}} \]
1555g5wi9fm.0.0.0.1:0.1.0.$0.$1.$6″> \ [\ frac {1} {{{R_T}}} = \ frac {1} {{10}} + \ frac {1} {{20}} + \ frac {1 } {{10}} \]\ [\ frac {1} {{{R_T}}} = \ frac {5} {{20}} \]
\ [\ frac {{{R_T}}} {1} = \ frac {{20}} {5} \]
\ [{R_T} = 4 \]
Общее сопротивление равно \ (4 \ Omega \)
Подсказка 1
Параллельно общее сопротивление всегда меньше, чем сопротивление наименьшего номинала.
Подсказка 2
При выполнении вышеуказанного расчета попробуйте использовать кнопки дроби на калькуляторе. Если у вас нет кнопки дроби, превратите дроби в десятичные, например;
1555g5wi9fm.0.0.0.1:0.1.0.$0.$1.$15″> \ [\ frac {1} {{20}} = 1 \ div 20 = 0,05 \] Серияи параллельные схемы
Что такое электрическая схема?
Для того, чтобы электроны текли, им нужна замкнутая цепь. Электрическая цепь обеспечивает полный, замкнутый путь для электричества.Части цепи состоят из нагрузки или сопротивления; провода; и переключатель. Источником энергии может быть батарея, термопара, фотоэлемент или электрический генератор. Нагрузка — это часть схемы, которая использует энергию. Нагрузка схемы всегда оказывает некоторое сопротивление потоку электронов. В результате энергия преобразуется в тепло, свет или механическую энергию. Переключатель электрической цепи служит для предотвращения потока электронов. Это называется обрыв цепи
.Есть два типа электрических цепей: последовательная и параллельная.
Цепь серииПоследовательная цепь, есть только один путь для прохождения электронов (см.
 Изображение последовательной цепи). Основным недостатком последовательной цепи является то, что при обрыве цепи вся цепь разомкнута и ток не течет. Примером из серии могут стать огни на многих недорогих елках. Если погаснет один свет, погаснут все.
Изображение последовательной цепи). Основным недостатком последовательной цепи является то, что при обрыве цепи вся цепь разомкнута и ток не течет. Примером из серии могут стать огни на многих недорогих елках. Если погаснет один свет, погаснут все.Параллельная цепь
В параллельной цепи разные части электрической цепи находятся в нескольких разных ветвях.Электроны могут течь по нескольким путям. Если есть разрыв в одной ветви цепи, электроны все еще могут течь в других ветвях (см. Изображение параллельной цепи). Ваш дом подключен к параллельной схеме, поэтому, если одна лампочка погаснет, другая останется включенной.
Электрические цепи в вашем доме
У себя дома вы заметите, что большинство розеток имеют 3 штыря. К розетке подключены три провода. Два провода идут параллельно друг другу и имеют разность потенциалов 120 вольт в США, в Европе разность потенциалов составляет 220 вольт.Третий провод подключен к земле.
 Провод, который соединен с землей, обеспечивает кратчайший путь электронов к Земле. Этот третий провод не несет тока. Провод — это просто средство защиты от короткого замыкания. Короткое замыкание — это случай, когда электричество проходит по более короткому пути в цепи. Эти цепи имеют меньшее сопротивление и, следовательно, больший ток. Если провод с высоким потенциалом соприкоснется с другой металлической поверхностью устройства, все устройство будет потреблять ток, что приведет к поражению человека, касающегося его.Заземляющий провод, имеющий более короткую цепь, обеспечивает функцию безопасности, поэтому вместо тока, протекающего через прибор, он будет течь на землю.
Провод, который соединен с землей, обеспечивает кратчайший путь электронов к Земле. Этот третий провод не несет тока. Провод — это просто средство защиты от короткого замыкания. Короткое замыкание — это случай, когда электричество проходит по более короткому пути в цепи. Эти цепи имеют меньшее сопротивление и, следовательно, больший ток. Если провод с высоким потенциалом соприкоснется с другой металлической поверхностью устройства, все устройство будет потреблять ток, что приведет к поражению человека, касающегося его.Заземляющий провод, имеющий более короткую цепь, обеспечивает функцию безопасности, поэтому вместо тока, протекающего через прибор, он будет течь на землю.Элементы безопасности цепей — предохранители и автоматические выключатели
Ваш дом позволяет использовать только определенное количество электроэнергии одновременно. В зависимости от проводки в некоторых домах может подаваться до 150 ампер за один раз. Это делится на множество цепей.
Недостаток предохранителей Средняя цепь в доме — 15 или 20 ампер.Более сильный ток, протекающий по проводам, приведет к их нагреву и может вызвать пожар. Поэтому необходимо иметь устройства, которые будут останавливать поток электронов, когда ток становится слишком высоким. Предохранитель — обычное устройство во многих домах. Внутри предохранителя находится крошечная полоска металла. Когда ток, протекающий через него, будет слишком большим, это приведет к расплавлению тонкой полоски, что приведет к разрыву цепи.
Средняя цепь в доме — 15 или 20 ампер.Более сильный ток, протекающий по проводам, приведет к их нагреву и может вызвать пожар. Поэтому необходимо иметь устройства, которые будут останавливать поток электронов, когда ток становится слишком высоким. Предохранитель — обычное устройство во многих домах. Внутри предохранителя находится крошечная полоска металла. Когда ток, протекающий через него, будет слишком большим, это приведет к расплавлению тонкой полоски, что приведет к разрыву цепи.состоит в том, что после сгорания предохранителя их необходимо заменить.Лучшее решение — использовать так называемый автоматический выключатель. У автоматического выключателя есть переключатель, который размыкается при слишком высоком токе. Это предотвращает протекание тока. Переключатель можно замкнуть вручную после уменьшения количества потребляемого тока. Например, когда вы включаете в своем доме слишком много электронных устройств, мощность которых превышает 15 ампер, автоматический выключатель отключается.


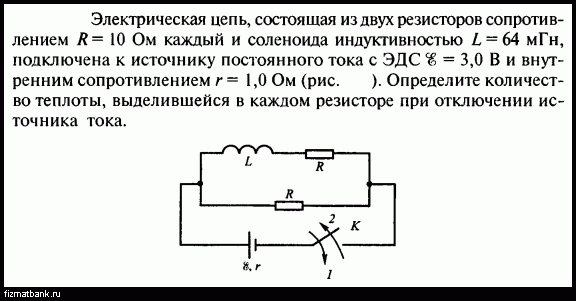 Общее сопротивление участка равно
Общее сопротивление участка равно Сила тока в полной цепи равна
Сила тока в полной цепи равна
 Общее сопротивление участка равно
Общее сопротивление участка равно ЭДС источника равна
ЭДС источника равна
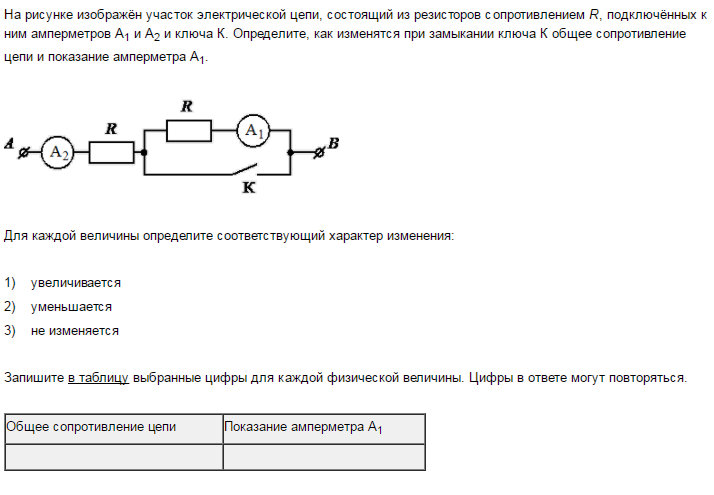
 Сопротивление какого проводника равно 1 Ом?
Сопротивление какого проводника равно 1 Ом?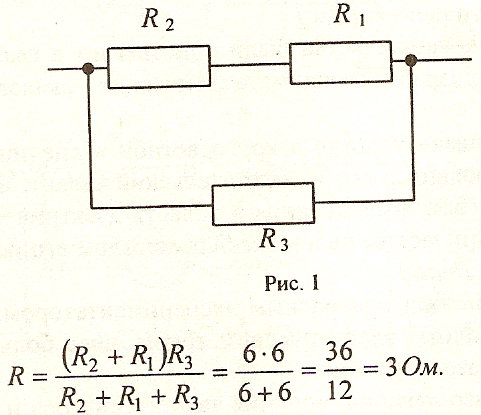 ЭДС источника равна
ЭДС источника равна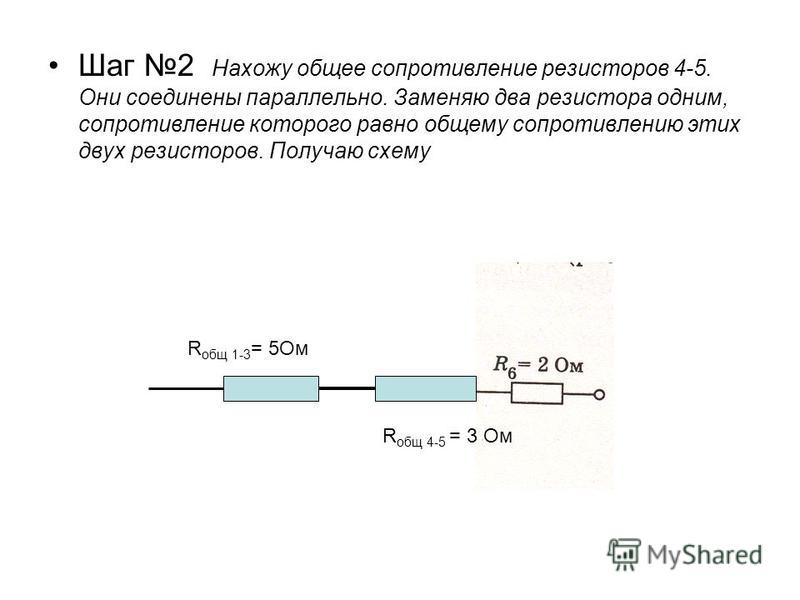 Чему равно удельное электрическое сопротивление вещества, из которого сделан проводник?
Чему равно удельное электрическое сопротивление вещества, из которого сделан проводник? Общее сопротивление участка равно
Общее сопротивление участка равно
 Каково
сечение вольфрамовой проволоки, если
ее сопротивление составляет 0,5 Ом на
каждый метр длины?
Каково
сечение вольфрамовой проволоки, если
ее сопротивление составляет 0,5 Ом на
каждый метр длины? Из какого
материала или сплава был изготовлен
резистор?
Из какого
материала или сплава был изготовлен
резистор?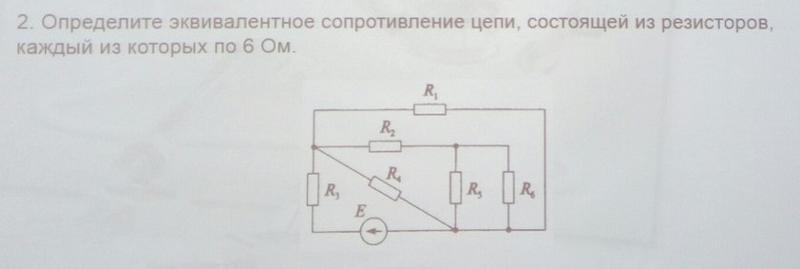

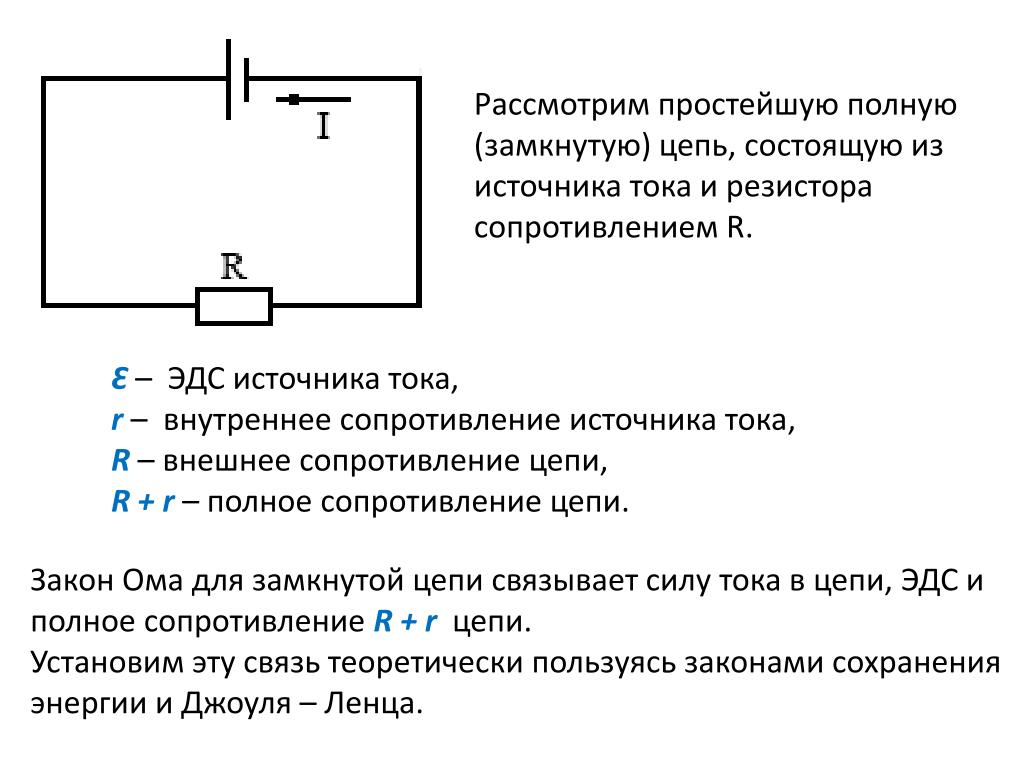
 Определить мощность и
ток каждого потребителя, а так же
мощность и ток источника.
Определить мощность и
ток каждого потребителя, а так же
мощность и ток источника.
 Найти токи каждого резистора и
эквивалентное сопротивление цепи.
Найти токи каждого резистора и
эквивалентное сопротивление цепи.
 Чему равен ток цепи,
если источник имеет ε = 120 В и r =1 Ом?
Чему равен ток цепи,
если источник имеет ε = 120 В и r =1 Ом? Определить эквивалентное сопротивление
и ток цепи при напряжении питания U =
120 B.
Определить эквивалентное сопротивление
и ток цепи при напряжении питания U =
120 B.
 Определить, как изменится
ток в цепи, если параллельно третьему
резистору подключен резистор
сопротивлением 125 Ом.
Определить, как изменится
ток в цепи, если параллельно третьему
резистору подключен резистор
сопротивлением 125 Ом.
 Чем больше лампочек перегорят, ток станет равным. В конце концов, ток становится слишком большим, что приводит к перегоранию шунта.№ Р_и. \]
Чем больше лампочек перегорят, ток станет равным. В конце концов, ток становится слишком большим, что приводит к перегоранию шунта.№ Р_и. \]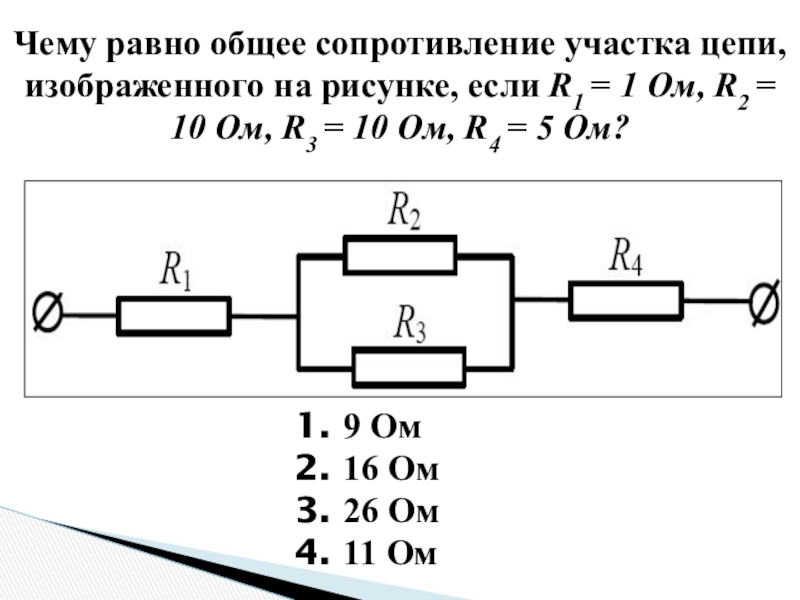 Например, автомобильные фары, радио и другие системы подключены параллельно, так что каждая подсистема использует полное напряжение источника и может работать полностью независимо. То же самое и с электропроводкой в вашем доме или любом здании.
Например, автомобильные фары, радио и другие системы подключены параллельно, так что каждая подсистема использует полное напряжение источника и может работать полностью независимо. То же самое и с электропроводкой в вашем доме или любом здании. {- 1}.{-1}. \ label {10.3} \]
{- 1}.{-1}. \ label {10.3} \]
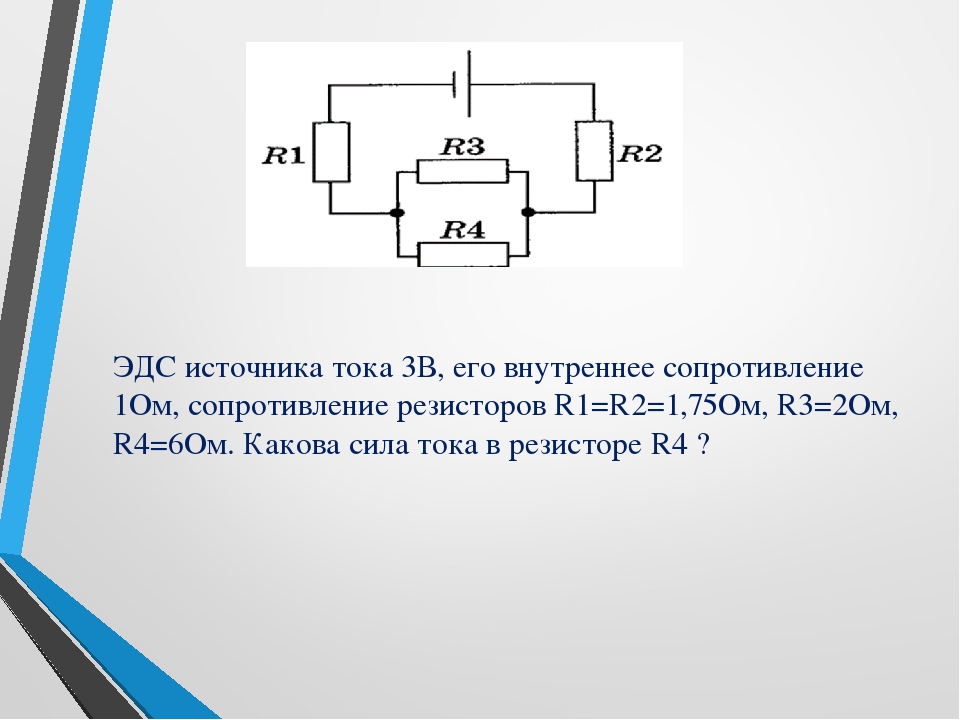 предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.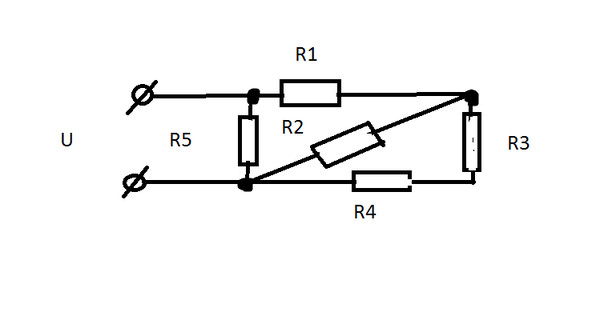 \ nonumber \]
\ nonumber \] Ток через последовательную цепь будет \ (I = \ frac {3.00 \, V} {5.00 \, \ Omega} = 0.60 \, A \), что меньше суммы токов, проходящих через каждый резистор в параллельная цепь, \ (I = 6.00 \, А \). Это неудивительно, поскольку эквивалентное сопротивление последовательной цепи выше. Ток при последовательном соединении любого количества резисторов всегда будет ниже, чем ток при параллельном соединении тех же резисторов, поскольку эквивалентное сопротивление последовательной цепи будет выше, чем параллельной цепи. Мощность, рассеиваемая последовательно включенными резисторами, будет равна \ (P = 1,800 \, Вт \), что ниже мощности, рассеиваемой в параллельной цепи \ (P = 18.00 \, Вт \).
Ток через последовательную цепь будет \ (I = \ frac {3.00 \, V} {5.00 \, \ Omega} = 0.60 \, A \), что меньше суммы токов, проходящих через каждый резистор в параллельная цепь, \ (I = 6.00 \, А \). Это неудивительно, поскольку эквивалентное сопротивление последовательной цепи выше. Ток при последовательном соединении любого количества резисторов всегда будет ниже, чем ток при параллельном соединении тех же резисторов, поскольку эквивалентное сопротивление последовательной цепи будет выше, чем параллельной цепи. Мощность, рассеиваемая последовательно включенными резисторами, будет равна \ (P = 1,800 \, Вт \), что ниже мощности, рассеиваемой в параллельной цепи \ (P = 18.00 \, Вт \). Молекулы воды аналогичны электронам в параллельных цепях. Количество молекул воды, которые текут в реке и падает, должно быть равно количеству молекул, которые текут над каждым водопадом, точно так же, как сумма тока через каждый резистор должна быть равна току, текущему в параллельном контуре.Молекулы воды в реке обладают энергией благодаря своему движению и высоте. Потенциальная энергия молекул воды в реке постоянна из-за их одинаковой высоты. Это аналогично постоянному изменению напряжения в параллельной цепи. Напряжение — это потенциальная энергия на каждом резисторе.
Молекулы воды аналогичны электронам в параллельных цепях. Количество молекул воды, которые текут в реке и падает, должно быть равно количеству молекул, которые текут над каждым водопадом, точно так же, как сумма тока через каждый резистор должна быть равна току, текущему в параллельном контуре.Молекулы воды в реке обладают энергией благодаря своему движению и высоте. Потенциальная энергия молекул воды в реке постоянна из-за их одинаковой высоты. Это аналогично постоянному изменению напряжения в параллельной цепи. Напряжение — это потенциальная энергия на каждом резисторе. 3} и меньше любого отдельного сопротивления в комбинации.
3} и меньше любого отдельного сопротивления в комбинации. N R_i \ nonumber \]
N R_i \ nonumber \] Процесс занимает больше времени, чем труден. Здесь мы отмечаем эквивалентное сопротивление как \ (R_ {eq} \).
Процесс занимает больше времени, чем труден. Здесь мы отмечаем эквивалентное сопротивление как \ (R_ {eq} \).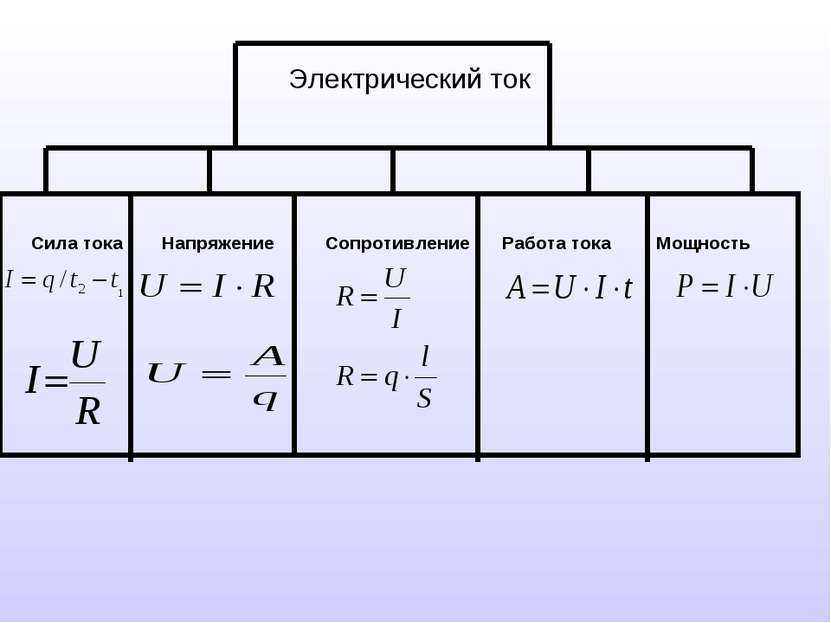 {- 1} = 5 \, \ Omega.\ nonumber \]
{- 1} = 5 \, \ Omega.\ nonumber \] Ток через \ (R_2 \) можно найти по закону Ома:
Ток через \ (R_2 \) можно найти по закону Ома:



 Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение IR в проводах также может быть значительным и может проявляться из-за тепла, выделяемого в шнуре.
Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение IR в проводах также может быть значительным и может проявляться из-за тепла, выделяемого в шнуре.
 Есть один список для серий и другой для параллельных.
Есть один список для серий и другой для параллельных.
 2R_4 \\ [4pt] & = 40.00 \, W + 40.00 \, W + 10.00 \, W + 10.00 \, W = 100. \, W. \ end {align *} \]
2R_4 \\ [4pt] & = 40.00 \, W + 40.00 \, W + 10.00 \, W + 10.00 \, W = 100. \, W. \ end {align *} \] Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами.Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами.Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).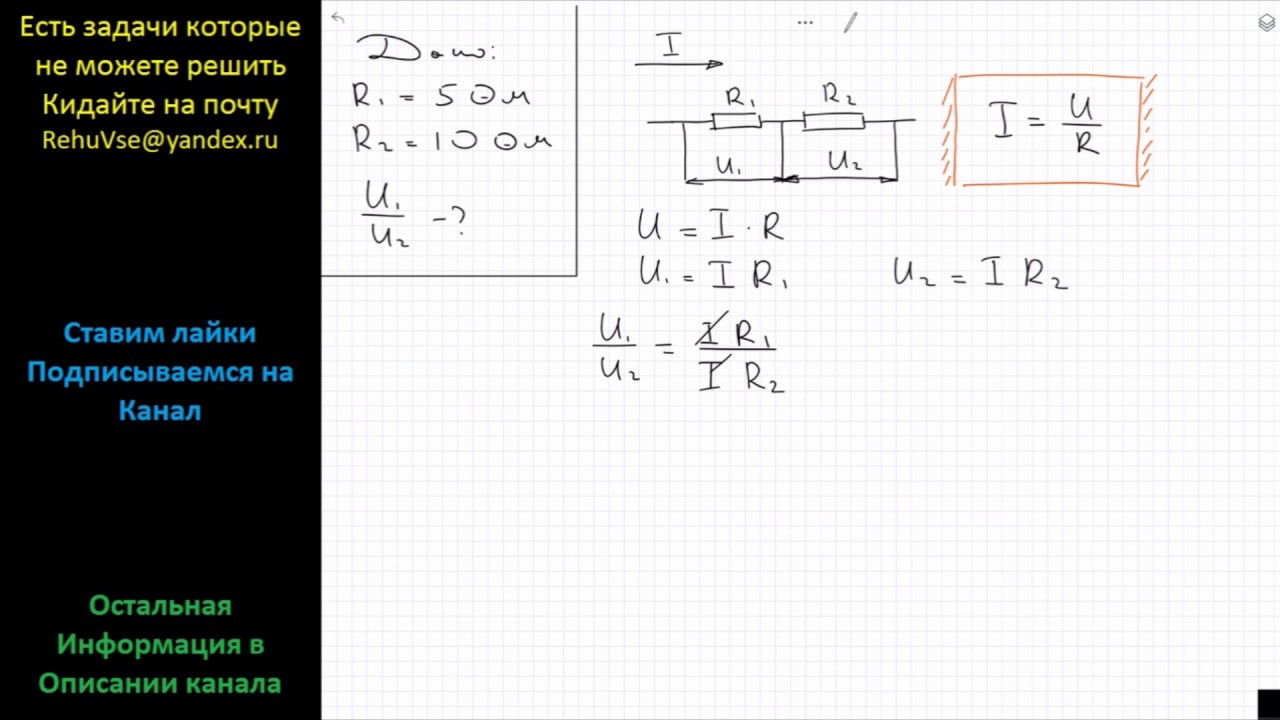 Мера этого предела расхода заряда называется сопротивлением . Простейшие комбинации резисторов — это последовательное и параллельное соединение, показанное на рисунке 1.Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от того, как они подключены.
Мера этого предела расхода заряда называется сопротивлением . Простейшие комбинации резисторов — это последовательное и параллельное соединение, показанное на рисунке 1.Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от того, как они подключены. Кажется разумным, что полное сопротивление является суммой отдельных сопротивлений, учитывая, что ток должен проходить через каждый резистор последовательно. (Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев обувь с резиновыми подошвами с высоким сопротивлением. прибор, который уменьшил бы рабочий ток.)
Кажется разумным, что полное сопротивление является суммой отдельных сопротивлений, учитывая, что ток должен проходить через каждый резистор последовательно. (Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев обувь с резиновыми подошвами с высоким сопротивлением. прибор, который уменьшил бы рабочий ток.)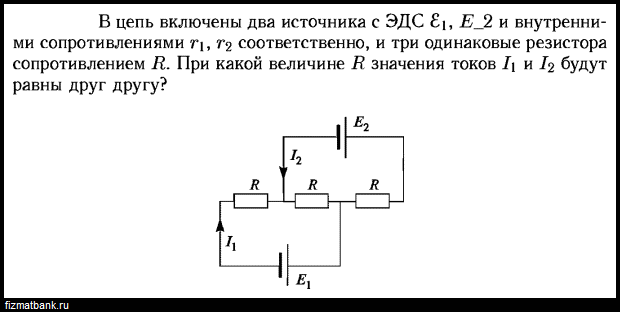 Другой способ представить это: В, — это напряжение, необходимое для протекания тока I через сопротивление R . Таким образом, падение напряжения на R 1 составляет В 1 = IR 1 , что на R 2 составляет В 2 = IR 2 , и что через R 3 составляет V 3 = IR 3 .Сумма этих напряжений равна выходному напряжению источника; то есть
Другой способ представить это: В, — это напряжение, необходимое для протекания тока I через сопротивление R . Таким образом, падение напряжения на R 1 составляет В 1 = IR 1 , что на R 2 составляет В 2 = IR 2 , и что через R 3 составляет V 3 = IR 3 .Сумма этих напряжений равна выходному напряжению источника; то есть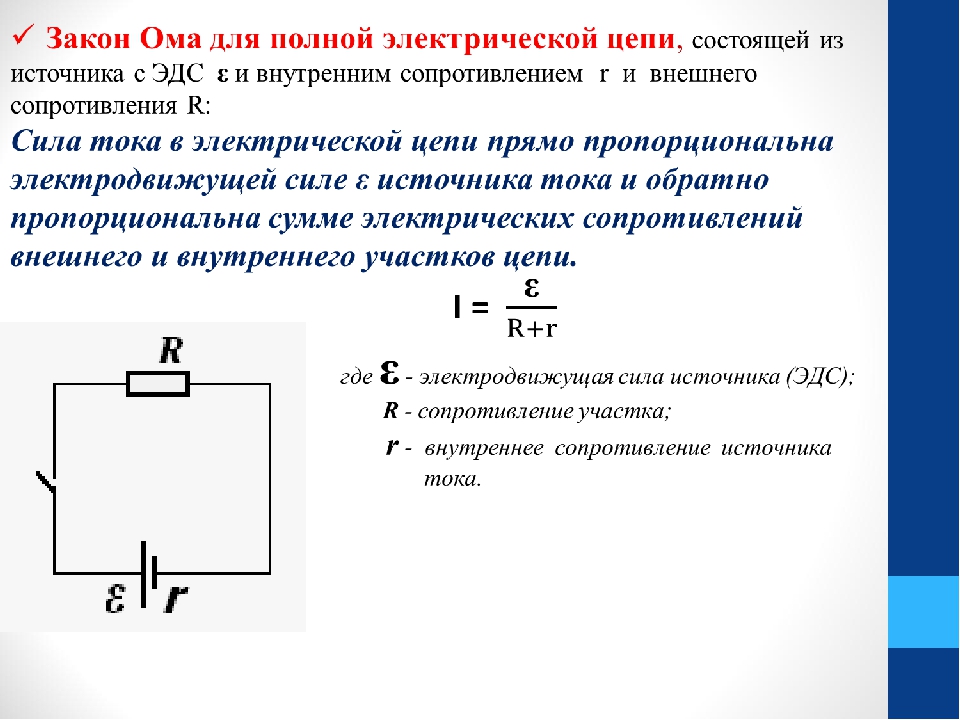
 ) Теперь подстановка значений для отдельных напряжений дает
) Теперь подстановка значений для отдельных напряжений дает Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого, а последовательно соединенные сопротивления просто складываются.
Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого, а последовательно соединенные сопротивления просто складываются.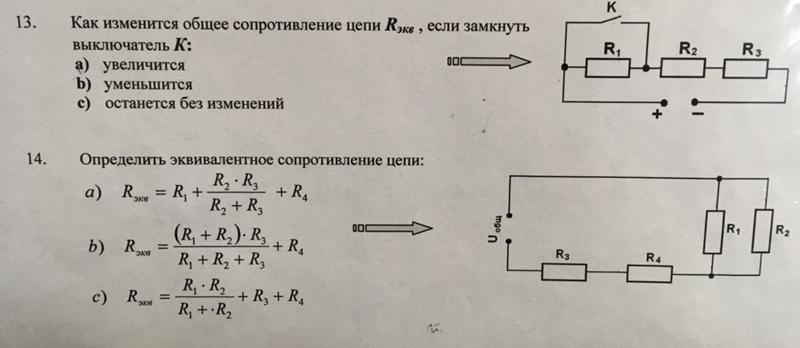 00 \ text {} \ Omega + 6.00 \ text {} \ Omega + 13.0 \ text {} \ Omega \\ & = & 20.0 \ text {} \ Omega \ end {array} \\ [/ latex].
00 \ text {} \ Omega + 6.00 \ text {} \ Omega + 13.0 \ text {} \ Omega \\ & = & 20.0 \ text {} \ Omega \ end {array} \\ [/ latex]. 0 В, прогноз:
0 В, прогноз: Будут получены такие же значения.
Будут получены такие же значения.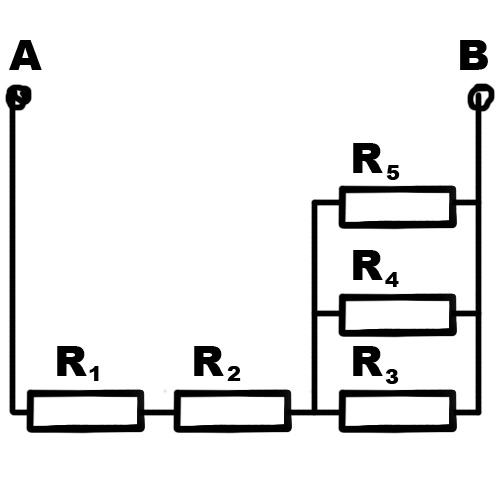
 (б) Электроснабжение в доме. (Источник: Dmitry G, Wikimedia Commons)
(б) Электроснабжение в доме. (Источник: Dmitry G, Wikimedia Commons)
 0 В, R 1 = 1,00 Ом, R 2 = 6,00 Ом и R 3 = 13,0 Ом. а) Каково полное сопротивление? (б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, как они складываются, чтобы равняться общему выходному току источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
0 В, R 1 = 1,00 Ом, R 2 = 6,00 Ом и R 3 = 13,0 Ом. а) Каково полное сопротивление? (б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, как они складываются, чтобы равняться общему выходному току источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами. 00} {\ text {} \ Omega} + \ frac {0 \ text {.} \ Text {1667}} {\ текст {} \ Omega} + \ frac {0 \ text {.} \ text {07692}} {\ text {} \ Omega} = \ frac {1 \ text {.} \ text {2436}} {\ text { } \ Omega} \\ [/ латекс].
00} {\ text {} \ Omega} + \ frac {0 \ text {.} \ Text {1667}} {\ текст {} \ Omega} + \ frac {0 \ text {.} \ text {07692}} {\ text {} \ Omega} = \ frac {1 \ text {.} \ text {2436}} {\ text { } \ Omega} \\ [/ латекс].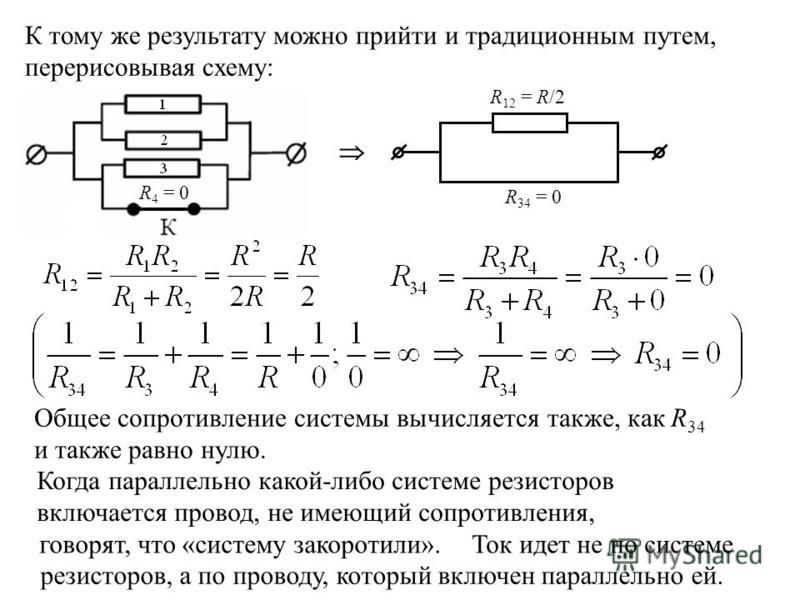 Это дает
Это дает } 0 \ text {V}} {\ text {13} \ text {.} \ Text {0} \ text {} \ Omega} = 0 \ text {.} \ Text {92} \ text {A} \\ [/ latex].
} 0 \ text {V}} {\ text {13} \ text {.} \ Text {0} \ text {} \ Omega} = 0 \ text {.} \ Text {92} \ text {A} \\ [/ latex].
 Они обычно встречаются, особенно если учитывать сопротивление провода. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно. Комбинации последовательного и параллельного подключения можно уменьшить до одного эквивалентного сопротивления, используя методику, показанную на рисунке 4.Различные части идентифицируются как последовательные или параллельные, уменьшаются до их эквивалентов и далее уменьшаются до тех пор, пока не останется единственное сопротивление. Процесс занимает больше времени, чем труден.
Они обычно встречаются, особенно если учитывать сопротивление провода. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно. Комбинации последовательного и параллельного подключения можно уменьшить до одного эквивалентного сопротивления, используя методику, показанную на рисунке 4.Различные части идентифицируются как последовательные или параллельные, уменьшаются до их эквивалентов и далее уменьшаются до тех пор, пока не останется единственное сопротивление. Процесс занимает больше времени, чем труден. Например, R 1 может быть сопротивлением проводов от автомобильного аккумулятора к его электрическим устройствам, которые подключены параллельно. R 2 и R 3 могли быть стартером и светом салона. Ранее мы предполагали, что сопротивление провода незначительно, но, когда это не так, оно имеет важные последствия, как показывает следующий пример.
Например, R 1 может быть сопротивлением проводов от автомобильного аккумулятора к его электрическим устройствам, которые подключены параллельно. R 2 и R 3 могли быть стартером и светом салона. Ранее мы предполагали, что сопротивление провода незначительно, но, когда это не так, оно имеет важные последствия, как показывает следующий пример. (d) Какую мощность рассеивает R 2 ?
(d) Какую мощность рассеивает R 2 ?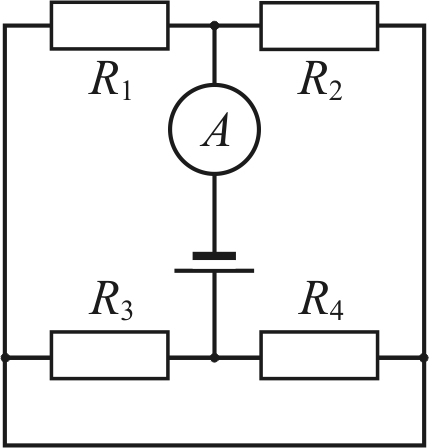 } \ text {00} \ text {} \ Omega} + \ frac {1} {\ text {13} \ text {.} 0 \ text {} \ Omega} = \ frac {0.2436} {\ text {} \ Омега} \\ [/ латекс].
} \ text {00} \ text {} \ Omega} + \ frac {1} {\ text {13} \ text {.} 0 \ text {} \ Omega} = \ frac {0.2436} {\ text {} \ Омега} \\ [/ латекс]. Полный ток I находится с помощью закона Ома для схемы. То есть
Полный ток I находится с помощью закона Ома для схемы. То есть Напряжение, приложенное как к R 2 , так и к R 3 , уменьшается на величину В 1 , и поэтому оно составляет
Напряжение, приложенное как к R 2 , так и к R 3 , уменьшается на величину В 1 , и поэтому оно составляет

 Этот шаг включает список известных проблем, поскольку они отмечены на вашей принципиальной схеме.
Этот шаг включает список известных проблем, поскольку они отмечены на вашей принципиальной схеме.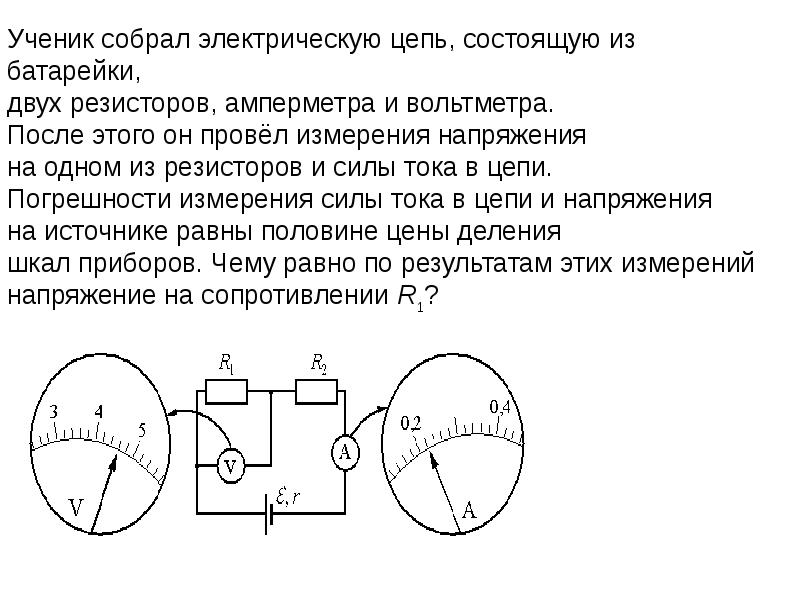
 )
)

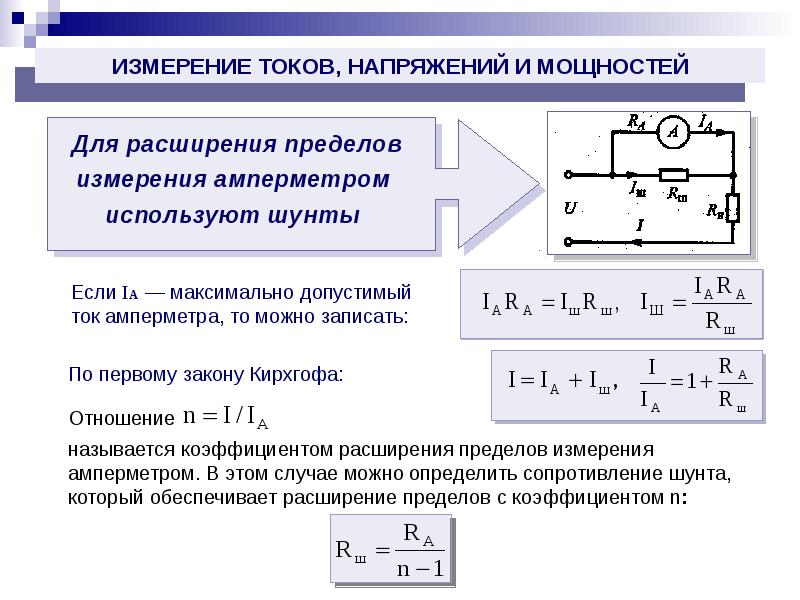 Можно считать, что данные, взятые из цифр, имеют точность до трех значащих цифр.
Можно считать, что данные, взятые из цифр, имеют точность до трех значащих цифр.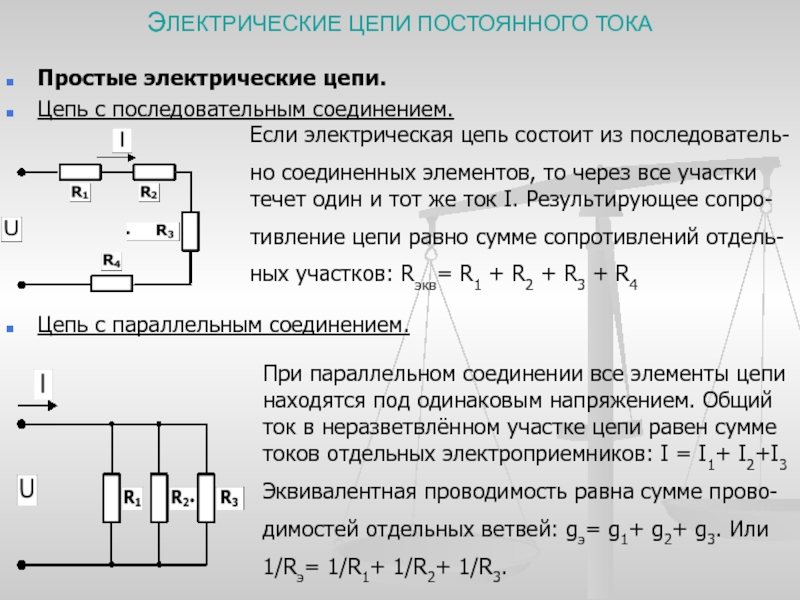 )
) (b) Найдите общую мощность, отдаваемую источником, и сравните ее с суммой мощностей, рассеиваемых резисторами.
(b) Найдите общую мощность, отдаваемую источником, и сравните ее с суммой мощностей, рассеиваемых резисторами. Какое сопротивление на землю у 100 изоляторов? (b) Рассчитайте мощность, рассеиваемую 100 из них. (c) Какая часть мощности, переносимой линией, это? Ясно покажите, как вы выполняете шаги, описанные в Стратегии решения проблем для последовательных и параллельных резисторов выше.
Какое сопротивление на землю у 100 изоляторов? (b) Рассчитайте мощность, рассеиваемую 100 из них. (c) Какая часть мощности, переносимой линией, это? Ясно покажите, как вы выполняете шаги, описанные в Стратегии решения проблем для последовательных и параллельных резисторов выше. а) Каково значение второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения являются необоснованными или непоследовательными?
а) Каково значение второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения являются необоснованными или непоследовательными? (а) 2,75 кОм (б) 27,5 Ом
(а) 2,75 кОм (б) 27,5 Ом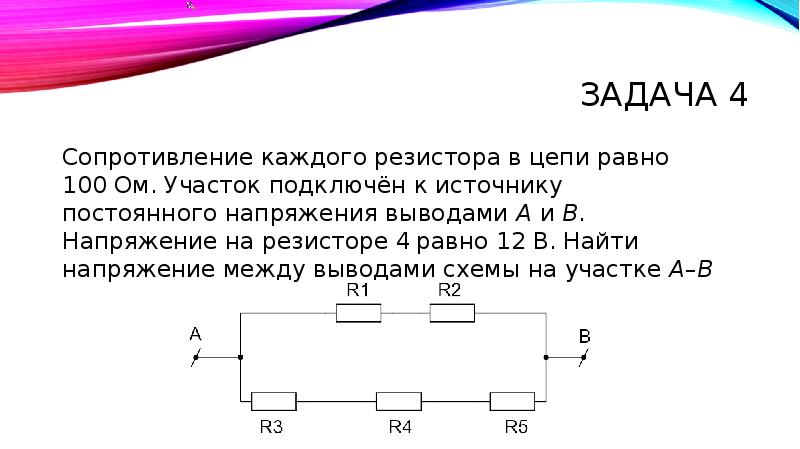
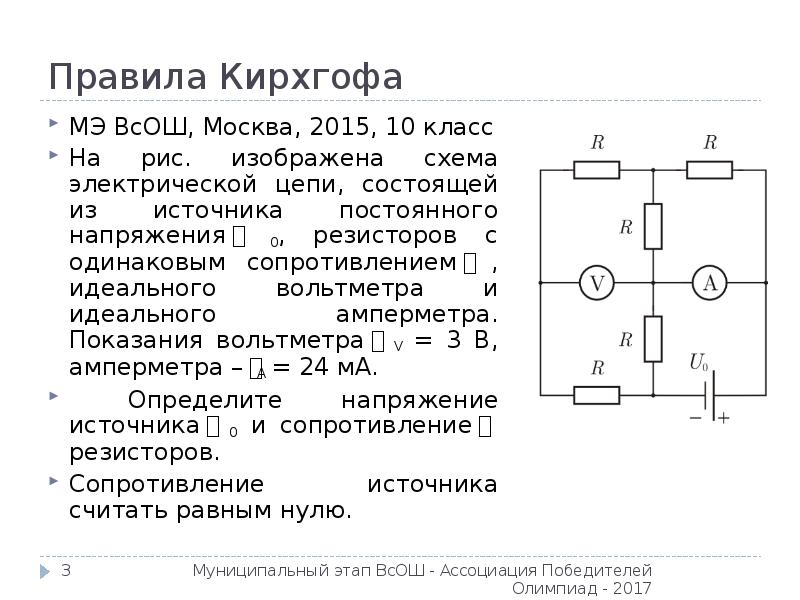
 3-45 показаны два резистора разной величины, включенные параллельно. Поскольку показан полный ток, можно рассчитать эквивалентное сопротивление.
3-45 показаны два резистора разной величины, включенные параллельно. Поскольку показан полный ток, можно рассчитать эквивалентное сопротивление.

 Какое эквивалентное сопротивление?
Какое эквивалентное сопротивление? Напряжение питания равно V, а общий ток, протекающий в цепи, равен I. Ток, протекающий через резисторы R2 и R3, равен I1, а ток, протекающий через резистор R4, равен I2.
Напряжение питания равно V, а общий ток, протекающий в цепи, равен I. Ток, протекающий через резисторы R2 и R3, равен I1, а ток, протекающий через резистор R4, равен I2. После замены резисторов полученная схема показана ниже.
После замены резисторов полученная схема показана ниже.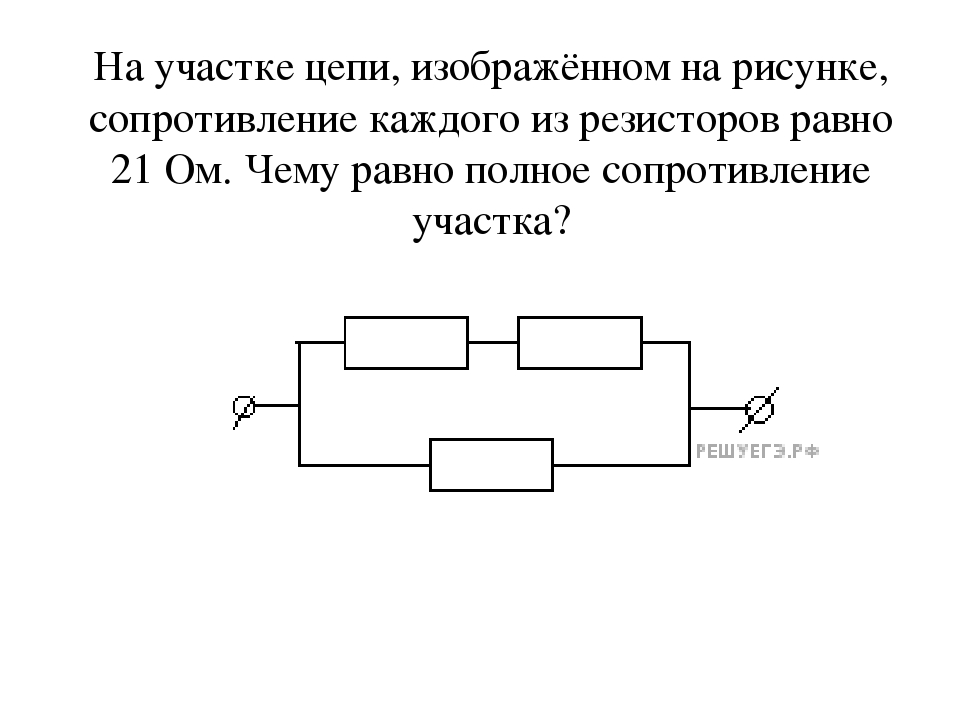 Напряжение питания 5 В.
Напряжение питания 5 В.






 Напряжение питания равно V, а общий ток, протекающий в цепи, равен I. Ток, протекающий через резисторы R2 и R3, равен I1, а ток, протекающий через резистор R4, равен I2.
Напряжение питания равно V, а общий ток, протекающий в цепи, равен I. Ток, протекающий через резисторы R2 и R3, равен I1, а ток, протекающий через резистор R4, равен I2.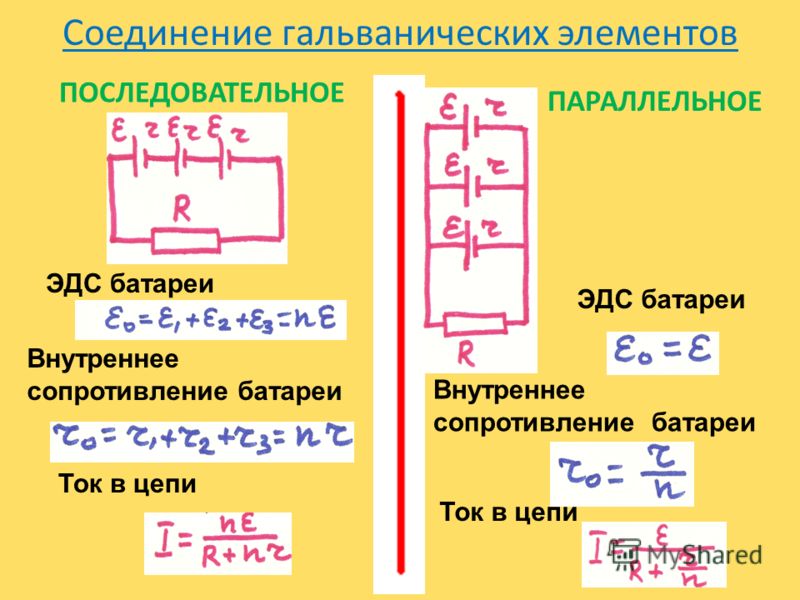 Здесь также последовательно соединены резисторы R1 и RB. Следовательно, применяя правило последовательно включенных резисторов, общее эквивалентное сопротивление цепи составляет
Здесь также последовательно соединены резисторы R1 и RB. Следовательно, применяя правило последовательно включенных резисторов, общее эквивалентное сопротивление цепи составляет Напряжение питания 5 В.
Напряжение питания 5 В.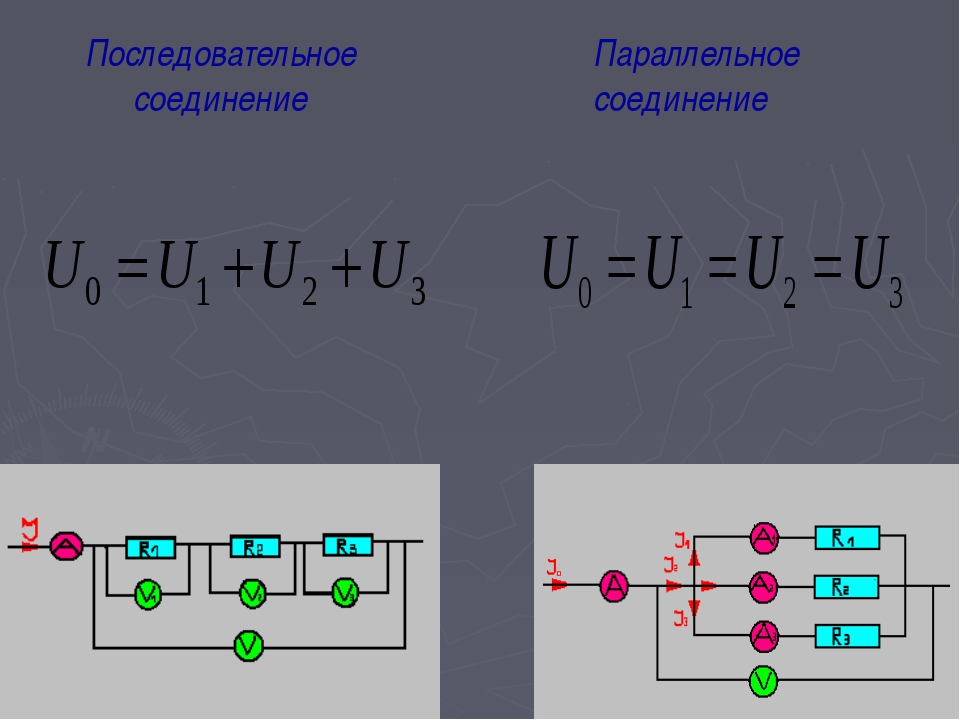

 Если R D является эквивалентным сопротивлением этой комбинации, то
Если R D является эквивалентным сопротивлением этой комбинации, то
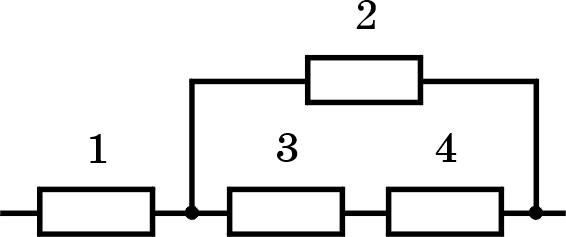 Этот процесс снижает сложность схемы. Продолжая этот процесс, мы можем заменить сложную резистивную цепь одним резистором.
Этот процесс снижает сложность схемы. Продолжая этот процесс, мы можем заменить сложную резистивную цепь одним резистором.
 Изображение последовательной цепи). Основным недостатком последовательной цепи является то, что при обрыве цепи вся цепь разомкнута и ток не течет. Примером из серии могут стать огни на многих недорогих елках. Если погаснет один свет, погаснут все.
Изображение последовательной цепи). Основным недостатком последовательной цепи является то, что при обрыве цепи вся цепь разомкнута и ток не течет. Примером из серии могут стать огни на многих недорогих елках. Если погаснет один свет, погаснут все. Провод, который соединен с землей, обеспечивает кратчайший путь электронов к Земле. Этот третий провод не несет тока. Провод — это просто средство защиты от короткого замыкания. Короткое замыкание — это случай, когда электричество проходит по более короткому пути в цепи. Эти цепи имеют меньшее сопротивление и, следовательно, больший ток. Если провод с высоким потенциалом соприкоснется с другой металлической поверхностью устройства, все устройство будет потреблять ток, что приведет к поражению человека, касающегося его.Заземляющий провод, имеющий более короткую цепь, обеспечивает функцию безопасности, поэтому вместо тока, протекающего через прибор, он будет течь на землю.
Провод, который соединен с землей, обеспечивает кратчайший путь электронов к Земле. Этот третий провод не несет тока. Провод — это просто средство защиты от короткого замыкания. Короткое замыкание — это случай, когда электричество проходит по более короткому пути в цепи. Эти цепи имеют меньшее сопротивление и, следовательно, больший ток. Если провод с высоким потенциалом соприкоснется с другой металлической поверхностью устройства, все устройство будет потреблять ток, что приведет к поражению человека, касающегося его.Заземляющий провод, имеющий более короткую цепь, обеспечивает функцию безопасности, поэтому вместо тока, протекающего через прибор, он будет течь на землю.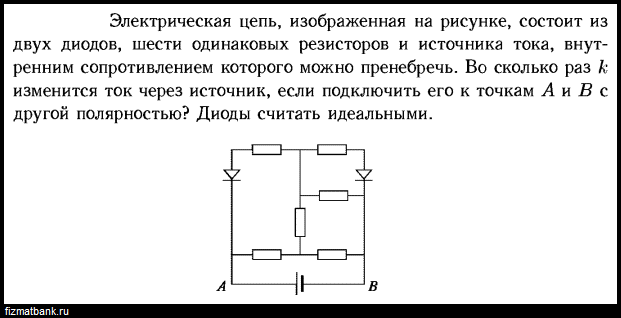 Средняя цепь в доме — 15 или 20 ампер.Более сильный ток, протекающий по проводам, приведет к их нагреву и может вызвать пожар. Поэтому необходимо иметь устройства, которые будут останавливать поток электронов, когда ток становится слишком высоким. Предохранитель — обычное устройство во многих домах. Внутри предохранителя находится крошечная полоска металла. Когда ток, протекающий через него, будет слишком большим, это приведет к расплавлению тонкой полоски, что приведет к разрыву цепи.
Средняя цепь в доме — 15 или 20 ампер.Более сильный ток, протекающий по проводам, приведет к их нагреву и может вызвать пожар. Поэтому необходимо иметь устройства, которые будут останавливать поток электронов, когда ток становится слишком высоким. Предохранитель — обычное устройство во многих домах. Внутри предохранителя находится крошечная полоска металла. Когда ток, протекающий через него, будет слишком большим, это приведет к расплавлению тонкой полоски, что приведет к разрыву цепи.
Leave A Comment