1611143553-a5dfe0cd78607269d954ff04820322e4 (Буховцев 1974 Сборник задач по элементарной физикеu), страница 16
Распознанный текст из DJVU-файла, 16 — страница
Найти сопротивление между точками А и В и сопротивление между точками С и Р, если АР= =ВС=а, АС=ВР=Ь. С Рис. !72. Рис. 173. 490. На рис. 173 изображена схема мостика Уитстона для измерения сопротивлений. )7„— неизвестное сопротивление, В, — эталонное сопротивление, 6 — гальванометр, соединенный скользящим контактом Р с однородным проводом большого сопротивления АВ (реохорд). Показать’, что при отсутствии тока через гальванометр имеет место соотношение Й„/)с,=(,/(,.
Сопротивлением соединительных проводов можно пренебречь. . 491. Кайата сопротивление необходимо включить между точками С и Р (рис. 174), чтобы сопротивление всей цепочки и Я Я и Рис. 174. (между точками А и В) не зависело от числа элементарных ячеек? 492. В выходных цепях генераторов ‘для уменьшения выходного напряжения в желаемое число раз применяется устройство, называемое аттенюатором.
Специальный переключатель дает возможность соединять с выходной клеммой или 4 и. и. иуховиеи и ии. 97 точку с потенциалом У„который вырабатывается генератором, или любую из точек У„У„.,У„, потенциал каждой из которых меньше потенциала предыдущей в й раз (й)1). Вторая выходная клемма и нижние концы сопротивлений заземлены.
Найти отношение сопротивлений )?,:??,: )?„если число ячеек аттенюатора может быть любым. 493. Какими приборами нужно располагать, чтобы осуществить экспериментально проверку закона Ома, т. е. показать, что сила тока прямо пропорциональна разности потенциалов? 494. Двум плоским одинаковым конденсаторам, соединенным параллельно, сообщен заряд Я. В момент времени 1=0 расстояние между пластинами первого конденсатора начинает равномерно увеличиваться по закону д,=д,+ог, а расстояние между пластинами второго конденсатора равномерно уменьшаться по закону 4=г(, — И.
Найти работу, совершаемую электростатическим полем (см. условие задачи 494) при одновременном увеличении расстояния между пластинами первого конденсатора и уменьшении расстояния между пластинами второго конденсатора на величину а. 496. Во время работы с очень чувствительным гальванометром экспериментатор, сидящий на стуле у стола, обнаружил любопытное явление. (Гальванометр был укреплен на стене, а концы его обмотки подведены к разомкнутому ключу, расположенному на столе.) Привстав со стула и коснувшись стола рукой, экспериментатор наблюдал заметный отброс гальванометра.
Если же экспериментатор касался стола, сидя на стуле, то отброса ве наблюдалось. Точно так же зайчик гальванометра не смещался и в том случае, когда эв экспериментатор касался стола, не садясь предварительно на стул. Как можно объяснить эти явления? 497. У очень чувствительного гальванометра при разомкнутой цепи обнаружен следующий эффект.
Как обьяснить это явление? 498. Как распределен потенциал в элементе Даниэля прн незамкнутой внешней цепи? 499, Изобразить графически примерный ход потенциала вдоль замкнутых цепей, изображенных на рнс. 176. Определить силу тока для каждой цепи н разность потенциалов ‘) 8г 8г + г, г~ + +~ г + 1у /г в А =лг ,4 Рвс. лг~хг 5,>8а ~'(~~ а? г) 6) 1тб. между точками А и В, Сопротивлением соединительных проводов пренебречь.
500. При соединении одного моля цинка с серной кислотой выделяется около 445 10′ Дж тепла, а при выделении моля меди из медного купороса потребляется примерно 235 10′ Дж. Найти по этим данным э. д. с. элемента Даниэля. 501. Два элемента Даниэля с внутренними сопротивлениями г,=0,8 Ом и г,=1,3 Ом и одинаковымн э. д. с. соединены параллельно й замкнуты на внешнее сопротивление ??. Найти отношение количеств цинка, растворившихся в этих элементах за определенный промежуток времени. 502.
Найти отношение количеств цинка, растворившихся в этих элементах за определенный промежуток времени. 502.
Элемент Даниэля составлен из абсолютно чистых материалов. Найти расход цинка и кристаллов медного ку-. пороса Си30, 5Н,О, если элемент дает ток О,1 А в течение 8 часов. 503. В элементе Даниэля медь заменили воском, покрытым слоем графита. Описать явления, которые будут происходить в таком элементе, если соединить проволокой цинк с графитовым слоем. 4В 99 504. Как изменится э. д.
с. батареи, изображенной на рис. 177, если убрать перегородку между сосудами? Электролитом служит раствор серной кислоты. о м ш ~ 505. Однородный угольный стер= жень лежит наднесосуда с электро- литом. К концам стержня подклю— — чеи вольтметр, обладающий боль— — — — шим сопротивлением. В середину — — — угольного стержня упирается цинковый стержень. Что будетпоказывать вольтметр, если цинковый стержень стоит вертикально? Как изменятся показания вольтметра, если цинковый стержень наклонить вправо или влево? 506.
Пустотелая проводящая сфера радиуса 7?=5 см помещена в электролитическую ванну, наполненную раствором медного купороса. В поверхности сферы имеется отверстие радиуса г=0,5 мм. На сколько увеличится вес сферы, если отложение меди длится 14 30 мин при плотности тока в электролите 1=0,01 А/см2? 507. Если конденсатоу, несущий на себе заряд Я, разрядить через электролитическую ванну с подкисленной водой, то выделится гремучий газ. По закону Фарадея количество выделяющегося при электролизе вещества зависит только от количества прошедшего электричества. Значит, если разряжать конденсатор через М последовательно соединенных ванн, то выделится в М раз больше гремучего газа. У можно сделать сколь угодно большим и получить любое количество газа.
Сжигая этот газ, получим любое количество энергии, что явно противоречит закону сохранения энергии, так как начальная энергия заряженного конденсатора не бесконечно велика. В чем здесь дело? 508. При взрыве гремучего газа на каждый грамм прореагировавшего водорода выделяется 145 10′ Дж тепла.
509. При электролизе положительные и отрицательные ионы непрерывно нейтрализуются на соответствующих электродах. Какие причины поддерживают концентрацию ионов н электролитах на постоянном уровне? В каких участках электролита происходит пополнение убыли ионов? 510. Полная плотность тока в электролитах определяется как сумма двух токов — тока положительных ионов и 100 тока отрицательных ионов: (е Е(п~и,+И О ), где е — заряд иона, и и о — концентрации и скорости положительных и отрицательных ионов. Почему количество вещества, выделившегося, к примеру, на катоде, считается пропорциональным полному току, а не току еп~оу? 511. Температура горячих спаев термобатарен г,=!27 ‘С, холодных г,=27 ‘С, э.
д. с. батареи 4’=4 В. Для поддержания постоянной температуры нагретых спаев к ним в единицу времени -подводится две калории тепла. К батарее подключена электролитическая ванна с раствором медного купороса. Какое наибольшее (теоретически) количество меди может отлагаться на катоде в единицу времени? 512. Два металлических шарика радиусов г,=1 см и г,=2 см, находящиеся на расстоянии Я=100 см друг от друга, присоединены к батарее с электродвижущей силой б =3000 В. Найти силу взаимодействия шариков. Взаимодействием соединительных проводов пренебречь.
Какое наибольшее (теоретически) количество меди может отлагаться на катоде в единицу времени? 512. Два металлических шарика радиусов г,=1 см и г,=2 см, находящиеся на расстоянии Я=100 см друг от друга, присоединены к батарее с электродвижущей силой б =3000 В. Найти силу взаимодействия шариков. Взаимодействием соединительных проводов пренебречь.
513. Пластины плоского конденсатора присоединены к батарее, э. д. с. которой равна к7. Подсчитать механическую работу, совершаемую электрическим полем при перемещении пластин, если вначале расстояние между пластинами равно 4, а в конце г(„причем д,(А. Выделением тепла в батарее и подводящих проводах пренебречь. 514. Определить напряжения У, и У, на конденсаторах в’ 1 (рис.
178), если 47,— — 12 10′ В, ф 8,=13 1О’ В, С,=З мкФ, С,=7 мкФ. Проводимостью Р диэлектриков пренебречь. 515. Одна из пластин кон- денсатора, присоединенного к батарее с электродвижущей Рве. 178. Рис. 179. силой к7, заземлена (рис. 179). Изменятся ли потенциалы пластин конденсатора относительно земли, если заземление убрать? 516.
д. с. к7 течет ток силой /. Чему равна разность потенциалов на клеммах аккумулятора? 517. Почему гальванический элемент с э. д. с. в несколько вольт может дать значительный ток, а электростатическая 1О! машина с э. д. с. в десятки тысяч вольт дает ток ничтожной снлы? 518. В каком случае два последовательно соединенных гальванических элемента, замкнутых на внешнее сопротнвленне, дадут меньшнй ток, чем один нз этнх элементов, включенный на то же сопротивление? 519.
Для определення места повреждения изоляции между проводами двухпроводной телефонной линни длиной 1,=5,6 км к одному ее концу прнсоеднннлн батарею с э. д. с. б =24 В. Прн этом оказалось, что если провода у другого конца линии разомкнуты, ток через батарею равен 1,=1,5 А, а если замкнуты накоротко, то ток через батарею равен 1,=2 А. Ток короткого замыкании батареи 1,=98 А.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 |
Параллельное соединение конденсаторов формула — Стройпортал Biokamin-Doma.
 ru
ruСоединение конденсаторов
Как правильно соединять конденсаторы?
У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”
Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!
Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь два-три на 470 микрофарад. Ставить 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров и покупать недостающую деталь?
Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное.
В электронике существует два способа соединения конденсаторов: параллельное и последовательное.
В реальности это выглядит так:
Параллельное соединение
Принципиальная схема параллельного соединения
Последовательное соединение
Принципиальная схема последовательного соединения
Также можно комбинировать параллельное и последовательное соединение. Но на практике вам вряд ли это пригодиться.
Как рассчитать общую ёмкость соединённых конденсаторов?
Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.
Общая ёмкость параллельно соединённых конденсаторов:
С1 – ёмкость первого;
С2 – ёмкость второго;
С3 – ёмкость третьего;
СN – ёмкость N-ого конденсатора;
Cобщ – суммарная ёмкость составного конденсатора.
Как видим, при параллельном соединении ёмкости нужно всего-навсего сложить!
Внимание! Все расчёты необходимо производить в одних единицах. Если выполняем расчёты в микрофарадах, то нужно указывать ёмкость C1, C2 в микрофарадах. Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!
Если выполняем расчёты в микрофарадах, то нужно указывать ёмкость C1, C2 в микрофарадах. Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!
Чтобы не допустить ошибку при переводе микрофарад в пикофарады, а нанофарад в микрофарады, необходимо знать сокращённую запись численных величин. Также в этом вам поможет таблица. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно производить пересчёт. Подробнее об этом читайте здесь.
Ёмкость двух последовательно соединённых конденсаторов можно рассчитать по другой формуле. Она будет чуть сложнее:
Внимание! Данная формула справедлива только для двух конденсаторов! Если их больше, то потребуется другая формула. Она более запутанная, да и на деле не всегда пригождается
.Или то же самое, но более понятно:
Если вы проведёте несколько расчётов, то увидите, что при последовательном соединении результирующая ёмкость будет всегда меньше наименьшей, включённой в данную цепочку. Что это значить? А это значит, что если соединить последовательно конденсаторы ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость будет меньше 5.
Что это значить? А это значит, что если соединить последовательно конденсаторы ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость будет меньше 5.
В том случае, если для последовательного соединения применены конденсаторы одинаковой ёмкости, эта громоздкая формула волшебным образом упрощается и принимает вид:
Здесь, вместо буквы M ставиться количество конденсаторов, а C1 – его ёмкость.
Стоит также запомнить простое правило:
При последовательном соединении двух конденсаторов с одинаковой ёмкостью результирующая ёмкость будет в два раза меньше ёмкости каждого из них.
Таким образом, если вы последовательно соедините два конденсатора, ёмкость каждого из которых 10 нанофарад, то в результате она составит 5 нанофарад.
Не будем пускать слов по ветру, а проверим конденсатор, замерив ёмкость, и на практике подтвердим правильность показанных здесь формул.
Возьмём два плёночных конденсатора. Один на 15 нанофарад (0,015 мкф. ),а другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+ и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).
),а другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+ и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).
Замер ёмкости при последовательном соединении
Ёмкость составного конденсатора составила 6 нанофарад (0,006 мкф.)
А теперь проделаем то же самое, но для параллельного соединения. Проверим результат с помощью того же тестера (см. фото).
Измерение ёмкости при параллельном соединении
Как видим, при параллельном соединении ёмкость двух конденсаторов сложилась и составляет 25 нанофарад (0,025 мкф.).
Что ещё необходимо знать, чтобы правильно соединять конденсаторы?
Во-первых, не стоит забывать, что есть ещё один немаловажный параметр, как номинальное напряжение.
При последовательном соединении конденсаторов напряжение между ними распределяется обратно пропорционально их ёмкостям. Поэтому, есть смысл при последовательном соединении применять конденсаторы с номинальным напряжением равным тому, которое имеет конденсатор, взамен которого мы ставим составной.
Если же используются конденсаторы с одинаковой ёмкостью, то напряжение между ними разделится поровну.
Для электролитических конденсаторов.
При соединении электролитических конденсаторов (электролитов) строго соблюдайте полярность! При параллельном соединении всегда подключайте минусовой вывод одного конденсатора к минусовому выводу другого,а плюсовой вывод с плюсовым.
Параллельное соединение электролитов
Схема параллельного соединения
В последовательном соединении электролитов ситуация обратная. Необходимо подключать плюсовой вывод к минусовому. Получается что-то вроде последовательного соединения батареек.
Последовательное соединение электролитов
Схема последовательного соединения
Также не забывайте про номинальное напряжение. При параллельном соединении каждый из задействованных конденсаторов должен иметь то номинальное напряжение, как если бы мы ставили в схему один конденсатор. То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт. Если хоть один из них будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.
Если хоть один из них будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.
Желательно, чтобы для составного конденсатора подбирались конденсаторы одного типа (плёночные, керамические, слюдяные, металлобумажные). Лучше всего будет, если они взяты из одной партии, так как в таком случае разброс параметров у них будет небольшой.
Конечно, возможно и смешанное (комбинированное) соединение, но в практике оно не применяется (я не видел
). Расчёт ёмкости при смешанном соединении обычно достаётся тем, кто решает задачи по физике или сдаёт экзамены 🙂Тем же, кто не на шутку увлёкся электроникой непременно надо знать, как правильно соединять резисторы и рассчитывать их общее сопротивление!
Последовательное и параллельное соединение конденсаторов
Для достижения нужной емкости или при напряжении, превышающем номинальное напряжение, конденсаторы, могут соединяться последовательно или параллельно. Любое же сложное соединение состоит из нескольких комбинаций последовательного и параллельного соединений.
Последовательное соединение конденсаторов
При последовательном соединении, конденсаторы подключены таким образом, что только первый и последний конденсатор подключены к источнику ЭДС/тока одной из своих пластин. Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга. При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.
Напряжение на данном участке цепи соотносятся следующим образом:
Зная, что напряжение конденсатора можно представить через заряд и емкость, запишем:
Сократив выражение на Q, получим знакомую формулу:
Откуда эквивалентная емкость батареи конденсаторов соединенных последовательно:
Параллельное соединение конденсаторов
При параллельном соединении конденсаторов напряжение на обкладках одинаковое, а заряды разные.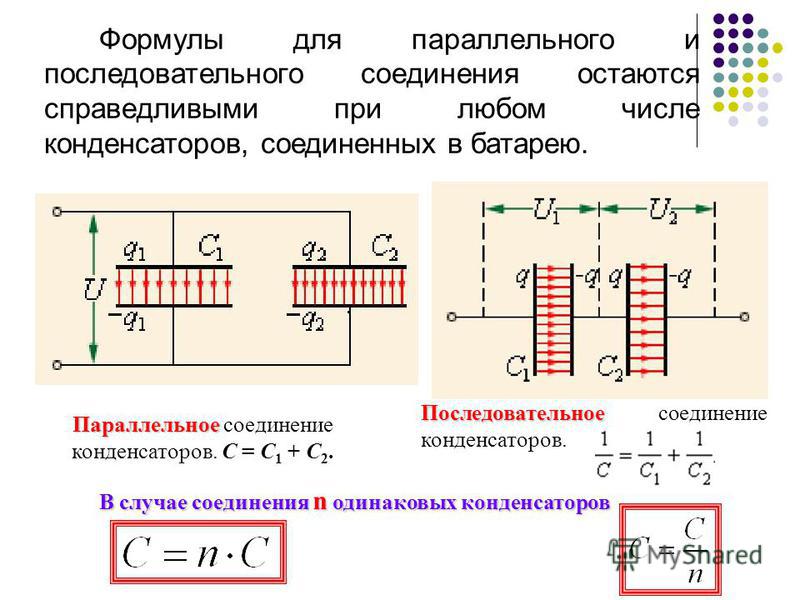
Величина общего заряда полученного конденсаторами, равна сумме зарядов всех параллельно подключенных конденсаторов. В случае батареи из двух конденсаторов:
Так как заряд конденсатора
А напряжения на каждом из конденсаторов равны, получаем следующее выражение для эквивалентной емкости двух параллельно соединенных конденсаторов
Пример 1
Какова результирующая емкость 4 конденсаторов включенных последовательно и параллельно, если известно что С1 = 10 мкФ, C2 = 2 мкФ, C3 = 5 мкФ, а C4 = 1 мкФ?
При последовательном соединении общая емкость равна:
При параллельном соединении общая емкость равна:
Пример 2
Определить результирующую емкость группы конденсаторов подключенных последовательно-параллельно, если известно, что С1 = 7 мкФ, С2 = 2 мкФ, С3 = 1 мкФ.
Сначала найдем общую емкость параллельного участка цепи:
Затем найдем общую емкость для всей цепи:
По сути, расчет общей емкости конденсаторов схож с расчетом общего сопротивления цепи в случае с последовательным или параллельным соединением, но при этом, зеркально противоположен.
Способы подключения конденсаторов в электрическую цепь
Схемы в электротехнике состоят из электрических элементов, в которых способы соединения конденсаторов могут быть разными. Надо понимать, как правильно подключить конденсатор. Отдельные участки цепи с подключенными конденсаторами можно заменить одним эквивалентным элементом. Он заменит ряд конденсаторов, но должно выполняться обязательное условие: когда напряжение, подводимое к обкладкам эквивалентного конденсатора, равняется напряжению на входе и выходе группы заменяющихся конденсаторов, тогда заряд емкости будет такой же, как и на группе емкостей. Для понимания вопроса, как подключить конденсатор в любой схеме, рассмотрим виды его включения.
Параллельное включение конденсаторов в цепь
Параллельное соединение конденсаторов — это когда все пластины подключаются к точкам включения цепи, образовывая батарею емкостей.
Параллельное соединение конденсаторов:
Разность потенциалов на пластинах накопителей емкости будет одинаковая, так как они все заряжаются от одного источника тока. В этом случае каждый заряжающийся конденсатор имеет собственный заряд при одинаковой величине, подводимой к ним энергии.
В этом случае каждый заряжающийся конденсатор имеет собственный заряд при одинаковой величине, подводимой к ним энергии.
Параллельные конденсаторы, общий параметр количества заряда полученной батареи накопителей, рассчитывается, как сумма всех зарядов, помещающихся на каждой емкости, потому что каждый заряд емкости не зависит от заряда другой емкости, входящей в группу конденсаторов, параллельно включенных в схему.
При параллельном соединении конденсаторов емкость равняется:
Из представленной формулы можно сделать вывод, что всю группу накопителей можно рассматривать как один равноценный им конденсатор.
Конденсаторы, соединенные параллельно, имеют напряжение:
Последовательное включение конденсаторов в цепь
Когда в схеме выполнено последовательное соединение конденсаторов, оно выглядит как цепочка емкостных накопителей, где пластина первого и последнего накопителя емкости (конденсатора) подключены к источнику тока.
Последовательное соединение конденсатора:
При последовательном соединении конденсаторов все устройства этого участка берут одинаковое количество электроэнергии, потому что в процессе участвует первая и последняя пластинка накопителей, а пластины 2, 3 и другие до N проходят зарядку посредством влияния.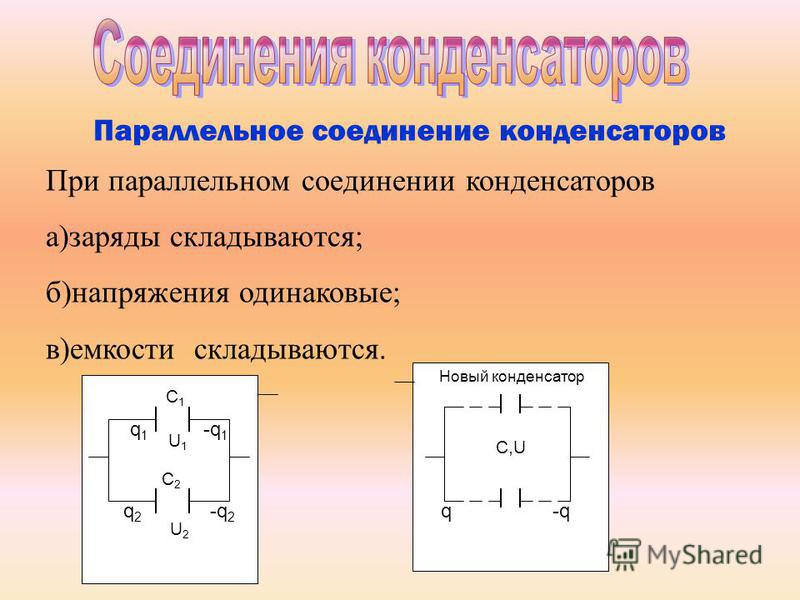 По этой причине заряд пластины 2 накопителя емкости равняется по значению заряду 1 пластины, но имеет обратный знак. Заряд пластины накопителя 3 равняется значению заряда пластины 2, но так же с обратным знаком, все последующие накопители имеет аналогичную систему заряда.
По этой причине заряд пластины 2 накопителя емкости равняется по значению заряду 1 пластины, но имеет обратный знак. Заряд пластины накопителя 3 равняется значению заряда пластины 2, но так же с обратным знаком, все последующие накопители имеет аналогичную систему заряда.
Формула нахождения заряда на конденсаторе, схема подключения конденсатора:
Когда выполняется последовательное соединение конденсаторов, напряжение на каждом накопители емкости будет различное, так как в зарядке одинаковым количеством электрической энергии участвуют разные емкости. Зависимость емкости от напряжения такова: чем она меньше, тем большее напряжение необходимо подать на пластины накопителя для его зарядки. И обратная величина: чем выше емкость накопителя, тем меньше требуется напряжения для его зарядки. Можно сделать вывод, что емкость последовательно соединенных накопителей имеет значение для величины напряжения на пластинах — чем она меньше, тем больше напряжения требуется, а также накопители большой емкости требуют меньшего напряжения.
Основное отличие схемы последовательного соединения накопителей емкости в том, что электроэнергия протекает только в одном направлении, а это означает, что в каждом накопителе емкости составленной батареи ток будет одинаковым. В этом виде соединений конденсаторов обеспечивается равномерное накопление энергии независимо от емкости накопителей.
Группу накопителей емкости можно также на схеме рассматривать как эквивалентный накопитель, на пластины которого подается напряжение, определяемое формулой:
Заряд общего (эквивалентного) накопителя группы емкостных накопителей последовательного соединения равен:
Общему значению емкости последовательно соединенных конденсаторов соответствует выражение:
Смешанное включение емкостных накопителей в схему
Параллельное и последовательное соединение конденсаторов на одном из участков цепи схемы называется специалистами смешанным соединением.
Участок цепи подсоединенных смешанным включением накопителей емкости:
Смешанное соединение конденсаторов в схеме рассчитывается в определенном порядке, который можно представить следующим образом:
- разбивается схема на простые для вычисления участки, это последовательное и параллельное соединение конденсаторов;
- вычисляем эквивалентную емкость для группы конденсаторов, последовательно включенных на участке параллельного соединения;
- проводим нахождение эквивалентной емкости на параллельном участке;
- когда эквивалентные емкости накопителей определены, схему рекомендуется перерисовать;
- рассчитывается емкость получившейся после последовательного включения эквивалентных накопителей электрической энергии.

Накопители емкостей (двухполюсники) включены разными способами в цепь, это дает несколько преимуществ в решении электротехнических задач по сравнению с традиционными способами включения конденсаторов:
- Использование для подключения электрических двигателей и другого оборудования в цехах, в радиотехнических устройствах.
- Упрощение вычисления величин электросхемы. Монтаж выполняется отдельными участками.
- Технические свойства всех элементов не меняются, когда изменяется сила тока и магнитное поле, это применяется для включения разных накопителей. Характеризуется постоянной величиной емкости и напряжения, а заряд пропорционален потенциалу.
Вывод
Разного вида включения конденсаторов в цепь применяются для решения электротехнических задач, в частности, для получения полярных накопителей из нескольких неполярных двухполюсников. В этом случае решением будет соединение группы однополюсных накопителей емкости по встречно-параллельному способу (треугольником). В этой схеме минус соединяется с минусом, а плюс — с плюсом. Происходит увеличение емкости накопителя, и меняется работа двухполюсника.
В этой схеме минус соединяется с минусом, а плюс — с плюсом. Происходит увеличение емкости накопителя, и меняется работа двухполюсника.
Не отображаются имеющиеся вхождения: последовательное параллельное и смешанное соединение конденсаторов, последовательное и параллельное соединение конденсаторов, при параллельном соединении конденсаторов емкость.
Соединение конденсаторов
В электрических цепях применяются различные способы соединения конденсаторов. Соединение конденсаторов может производиться: последовательно, параллельно и последовательно-параллельно (последнее иногда называют смешанное соединение конденсаторов). Существующие виды соединения конденсаторов показаны на рисунке 1.
Рисунок 1. Способы соединения конденсаторов.
Параллельное соединение конденсаторов.
Если группа конденсаторов включена в цепь таким образом, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным соединением конденсаторов (рисунок 2. ).
).
Рисунок 2. Параллельное соединение конденсаторов.
При заряде группы конденсаторов, соединенных параллельно, между пластинами всех конденсаторов будет одна и та же разность потенциалов, так как все они заряжаются от одного и того же источника тока. Общее же количество электричества на всех конденсаторах будет равно сумме количеств электричества, помещающихся на каждом из конденсаторов, так как заряд каждого их конденсаторов происходит независимо от заряда других конденсаторов данной группы. Исходя из этого, всю систему параллельно соединенных конденсаторов можно рассматривать как один эквивалентный (равноценный) конденсатор. Тогда общая емкость конденсаторов при параллельном соединении равна сумме емкостей всех соединенных конденсаторов.
Обозначим суммарную емкость соединенных в батарею конденсаторов буквой Собщ, емкость первого конденсатора С1 емкость второго С2 и емкость третьего С3. Тогда для параллельного соединения конденсаторов будет справедлива следующая формула:
Последний знак + и многоточие указывают на то, что этой формулой можно пользоваться при четырех, пяти и вообще при любом числе конденсаторов.
Последовательное соединение конденсаторов.
Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным (рисунок 3).
Рисунок 2. Последовательное соединение конденсаторов.
При последовательном соединении все конденсаторы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины (1 и 6), а остальные пластины (2, 3, 4 и 5) заряжаются через влияние. При этом заряд пластины 2 будет равен по величине и противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пластины 2 и т. д.
Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения. Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.
Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.
Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.
Аналогично предыдущему случаю можно рассматривать всю группу конденсаторов, соединенных последовательно, как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, а заряд которого равен заряду любого из конденсаторов группы.
Возьмем самый маленький конденсатор в группе. На нем должно быть самое большое напряжение. Но напряжение на этом конденсаторе составляет только часть общего напряжения, существующего на всей группе конденсаторов. Напряжение на всей группе больше напряжения на конденсаторе, имеющем самую малую емкость. А отсюда непосредственно следует, что общая емкость группы конденсаторов, соединенных последовательно, меньше емкости самого малого конденсатора в группе.
Для вычисления общей емкости при последовательном соединении конденсаторов удобнее всего пользоваться следующей формулой:
Для частного случая двух последовательно соединенных конденсаторов формула для вычисления их общей емкости будет иметь вид:
Последовательно-параллельное (смешанное) соединение конденсаторов
Последовательно-параллельным соединением конденсаторов называется цепь имеющая в своем составе участки, как с параллельным, так и с последовательным соединением конденсаторов.
На рисунке 4 приведен пример участка цепи со смешанным соединением конденсаторов.
Рисунок 4. Последовательно-параллельное соединение конденсаторов.
При расчете общей емкости такого участка цепи с последовательно-параллельным соединением конденсаторов этот участок разбивают на простейшие участки, состоящие только из групп с последовательным или параллельным соединением конденсаторов. Дальше алгоритм расчета имеет вид:
1. Определяют эквивалентную емкость участков с последовательным соединением конденсаторов.
2. Если эти участки содержат последовательно соединенные конденсаторы, то сначала вычисляют их емкость.
3. После расчета эквивалентных емкостей конденсаторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных конденсаторов.
4. Рассчитывают емкость полученной схемы.
Один из примеров расчета емкости при смешанном соединении конденсаторов приведен на рисунке 5.
Рисунок 5. Пример расчета последовательно-параллельного соединения конденсаторов.
Подробнее о расчетах соединения конденсаторов можно узнать в мультимедийном учебнике по основам электротехники и электроники:
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Соединение конденсаторов: руководство для начинающих
В электротехнике существуют различные варианты подключения электрических элементов. В частности, существует последовательное, параллельное или смешанное соединение конденсаторов, в зависимости от потребностей схемы. Рассмотрим их.
Рассмотрим их.
Параллельное соединение
Параллельное соединение характеризуется тем, что все пластины электрических конденсаторов присоединяются к точкам включения и образовывают собой батареи. В таком случае, во время заряда конденсаторов каждый из них будет иметь различное число электрических зарядов при одинаковом количестве подводимой энергии
Схема параллельного крепленияЕмкость при параллельной установке рассчитывается исходя из емкостей всех конденсаторов в схеме. При этом, количество электрической энергии, поступающей на все отдельные двухполюсные элементы цепи, можно будет рассчитать, суммировав сумму энергии, помещающейся в каждый конденсатор. Вся схема, подключенная таким образом, рассчитывается как один двухполюсник.
Схема — напряжение на накопителяхВ отличие от соединения звездой, на обкладки всех конденсаторов попадает одинаковое напряжение. Например, на схеме выше мы видим, что:
Последовательное соединение
Здесь к точкам включения присоединяются контакты только первого и последнего конденсатора.
Главной особенностью работы схемы является то, что электрическая энергия будет проходить только по одному направлению, значит, что в каждом из конденсаторов ток будет одинаковым. В такой цепи для каждого накопителя, независимо от его емкости, будет обеспечиваться равное накопление проходящей энергии. Нужно понимать, что каждый из них последовательно соприкасается со следующим и предыдущим, а значит, емкость при последовательном типе может воспроизводиться энергией соседнего накопителя.
Формула, которая отражает зависимость тока от соединения конденсаторов, имеет такой вид:
i = ic1 = ic2 = ic3 = ic4, то есть токи проходящие через каждый конденсатор равны между собой.
Следовательно, одинаковой будет не только сила тока, но и электрический заряд. По формуле это определяется как:
А так определяется общая суммарная емкость конденсаторов при последовательном соединении:
Видео: как соединять конденсаторы параллельным и последовательным методом
Смешанное подключение
Но, стоит учитывать, что для соединения различных конденсаторов необходимо учитывать напряжение сети. Для каждого полупроводника этот показатель будет отличаться в зависимости от емкости элемента. Отсюда следует, что отдельные группы полупроводниковых двухполюсников малой емкости будут при зарядке становиться больше, и наоборот, электроемкость большого размера будет нуждаться в меньшем заряде.
Для каждого полупроводника этот показатель будет отличаться в зависимости от емкости элемента. Отсюда следует, что отдельные группы полупроводниковых двухполюсников малой емкости будут при зарядке становиться больше, и наоборот, электроемкость большого размера будет нуждаться в меньшем заряде.
Существует также смешанное соединение двух и более конденсаторов. Здесь электрическая энергия распределяется одновременно при помощи параллельного и последовательного подключения электролитических элементов в цепь. Эта схема имеет несколько участков с различным подключением конденсирующих двухполюсников. Иными словами, на одном цепь параллельно включена, на другом – последовательно. Такая электрическая схема имеет ряд достоинств сравнительно с традиционными:
- Можно использовать для любых целей: подключения электродвигателя, станочного оборудования, радиотехнических приборов;
- Простой расчет. Для монтажа вся схема разбивается на отдельные участки цепи, которые рассчитываются по отдельности;
- Свойства компонентов не изменяются независимо от изменений электромагнитного поля, силы тока.
 Это очень важно при работе с разноименными двухполюсниками. Ёмкость постоянна при постоянном напряжении, но, при этом, потенциал пропорционален заряду;
Это очень важно при работе с разноименными двухполюсниками. Ёмкость постоянна при постоянном напряжении, но, при этом, потенциал пропорционален заряду; - Если требуется собрать несколько неполярных полупроводниковых двухполюсников из полярных, то нужно взять несколько однополюсных двухполюсника и соединить их встречно-параллельным способом (в треугольник). Минус к минусу, а плюс к плюсу. Таким образом, за счет увеличения емкости изменяется принцип работы двухполюсного полупроводника.
Последовательное и параллельное соединение конденсаторов
Все наверняка уже знают, что собой представляют последовательное и параллельное соединения.
Соединение, при котором конец одного устройства соединен с началом следующего, называется последовательным.
Последовательное соединение конденсаторов
При последовательном соединении конденсаторов, получаемая цепь выглядит следующим образом:
Эта схема состоит из следующих элементов: трех конденсаторов C1 , C2 , С3 и источника электрической энергии E .
Мы видим, что конденсаторы подключены по всем правилам последовательного соединения, то есть вывод конденсатора C1 соединён с началом конденсатора C2 , ну а конец конденсатора C2 соединен с началом третьего конденсатора C3 .
Стоит обратить внимание на то, как распределяются ёмкости каждого.
При таком соединении, все ёмкостя следующим образом.
Дело в том, что общая емкость всех включенных конденсаторов не будит превышать емкости любого из конденсаторов. Проще говоря, если в данной группе конденсаторов, будит конденсатор с наименьшей емкостью, например, в 100 миро фарад, то общая емкость трех конденсаторов не будит превышать этих ста микрофарад.
Общую емкость можно рассчитать по следующей формуле:
Если в цепи имеются всего лишь два последовательно соединенных конденсатора, то общая емкость определяется по формуле:
Параллельное соединение конденсаторов
При параллельном соединении, начала всех конденсаторов соединяются в одну точку, а концы в другую, как показано на рисунке ниже:
Так при параллельном соединении, емкости всех конденсаторов складываются:
То есть, емкость каждого конденсатора, включенного параллельно суммируется и получается одна большая емкость, которую можно на схеме представить одним конденсатором.
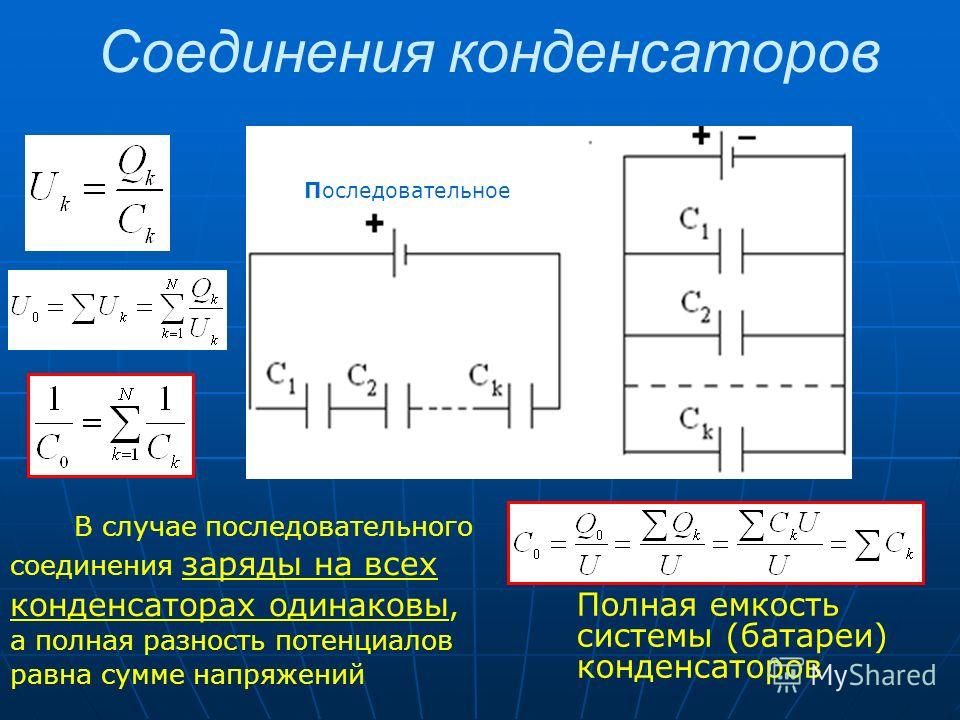
Это как два пишем один в уме, только в данном случаи один рисуем, а три в уме.
Смешанное соединение конденсаторов
Смешанное соединение конденсаторов выглядит следующим образом:
И представляет с собой различные сочетания параллельного и последовательного соединений.
Для вычисления общей емкости таких соединений, применяют метод замещения: все конденсаторы делят на последовательно и параллельно соединенные группы, рассчитывают ёмкость каждой группы в отдельности, так что в конце выйдет две параллельных или последовательных емкостей, которые можно без труда посчитать.
Например, дана следующая схема и следующие данные:
C1=0.4Ф
C2=0.8Ф
C3=0,73Ф
Необходимо найти общую емкость всех трех конденсаторов.
Как мы видим конденсаторы C1 и C2 соединены последовательно, а конденсатор C3 по отношению к первым двум параллельно.
Посчитав общую емкость последовательно соединенных конденсаторов C1 и C2, их можно представить, как один конденсатор C1,2.

Теперь нам не составит труда посчитать емкость двух параллельно соединенных конденсаторов, просто сложив их ёмкости.
Применения параллельного и последовательного соединений конденсаторов нашло свое применение в тех случаях, когда необходимо получить ту или иную величину емкости. Допустим у вас нет подходящего конденсатора, но есть куча других. Выполнив несколько не хитрых расчетов можно подобрать необходимую емкость.
РЕШЕНИЕ: (II) Подключаются два одинаковых конденсатора…
Стенограмма видеозаписи
это вопрос. Мы должны, я думаю, кто конденсаторы сказал, что это проводилось паранойей в se. Запросить заряд Q Не когда они подключены. Сейчас источником отснятого материала будет не так напряжение. Так что после этого полностью зарядил несколько изменений. Одежда — это то, что отключено, и после того, как она отключена, А Ди избрал директиву, чтобы K было равно 312, чтобы почувствовать пространство между тарелкой и одним из участников. Значит, нам нужно определить а? То, что теперь было зарядом каждого конденсатора до нашего Q t. А теперь за то, что проголосовали JJ по всей мощности. Итак, гм, давайте сначала посмотрим, что каждый конденсаторный провод заряжен Q. Нет, гм, мы получим общий заряд в два раза больше Q, и этот заряд останется на щеке или пассажирах после того, как Зак отключится от батареи. Но они не могут распространять. Также равномерно распределите по нему. Итак, после того, как новый материал вставлен, он, скажем, вставлен в C, один RC, два курса.Смотри что? Потому что это тоже. Поскольку материал пустынен, город становится больше в этом виде, так что это не плата за то, что C пошел, чтобы увидеть огромные и цепи, что у них такие же кадры. Таким образом, напряжение Christie всегда будет одинаковым. Это означает, что лечение получает безопасность за границей. То есть под присмотром кубинца, потому что ты с телом охраняешь Кейт. Я вижу один, потому что диалектический материал que chu состоит в том, что они складываются в два раза, ребенок, а не будущее равно двум разам.
Значит, нам нужно определить а? То, что теперь было зарядом каждого конденсатора до нашего Q t. А теперь за то, что проголосовали JJ по всей мощности. Итак, гм, давайте сначала посмотрим, что каждый конденсаторный провод заряжен Q. Нет, гм, мы получим общий заряд в два раза больше Q, и этот заряд останется на щеке или пассажирах после того, как Зак отключится от батареи. Но они не могут распространять. Также равномерно распределите по нему. Итак, после того, как новый материал вставлен, он, скажем, вставлен в C, один RC, два курса.Смотри что? Потому что это тоже. Поскольку материал пустынен, город становится больше в этом виде, так что это не плата за то, что C пошел, чтобы увидеть огромные и цепи, что у них такие же кадры. Таким образом, напряжение Christie всегда будет одинаковым. Это означает, что лечение получает безопасность за границей. То есть под присмотром кубинца, потому что ты с телом охраняешь Кейт. Я вижу один, потому что диалектический материал que chu состоит в том, что они складываются в два раза, ребенок, а не будущее равно двум разам. Милый. Не мой спаситель. Мы можем перестроить это уравнение, чтобы убить двух человек на мысе Мужа. Не, а вот диалектика. Есть, ммм, еще и крестьянский соучредитель Супер. Так что для миниатюрных двое кончились. Ты не такой, а на восемь лет ты не такой. А прожеванный кий равен двум лучшим ученикам по справедливости, а это 1,5 научит вас этому. И эта часть, которую они придают более оправданной, будет такой же для будущего Кубы. Вот только найди это для Кубы, для Кубы. О, если посмотреть, если количество отснятых материалов равно заряду, разделенному на пассажей Зика, это ваш 0.48 q точка и конденсаторы видят одну. Мы не знаем, что такое C one, но знаем ранее. Он против обвинения в излечении, а не в том, чтобы быть тем, чем вы просто кормите. Итак, мы были правы. 95 футов вверх. Итак, это дает нам 0,48, вы знаете, и это будет использоваться точно так же для прошлого, только вы.
Милый. Не мой спаситель. Мы можем перестроить это уравнение, чтобы убить двух человек на мысе Мужа. Не, а вот диалектика. Есть, ммм, еще и крестьянский соучредитель Супер. Так что для миниатюрных двое кончились. Ты не такой, а на восемь лет ты не такой. А прожеванный кий равен двум лучшим ученикам по справедливости, а это 1,5 научит вас этому. И эта часть, которую они придают более оправданной, будет такой же для будущего Кубы. Вот только найди это для Кубы, для Кубы. О, если посмотреть, если количество отснятых материалов равно заряду, разделенному на пассажей Зика, это ваш 0.48 q точка и конденсаторы видят одну. Мы не знаем, что такое C one, но знаем ранее. Он против обвинения в излечении, а не в том, чтобы быть тем, чем вы просто кормите. Итак, мы были правы. 95 футов вверх. Итак, это дает нам 0,48, вы знаете, и это будет использоваться точно так же для прошлого, только вы.
— learn.sparkfun.com
Добавлено в избранное Любимый 73Введение
Конденсатор — это двухконтактный электрический компонент. Наряду с резисторами и катушками индуктивности, они являются одними из самых фундаментальных пассивных компонентов , которые мы используем. Вам нужно будет очень внимательно поискать схему, в которой не было бы конденсатора .
Наряду с резисторами и катушками индуктивности, они являются одними из самых фундаментальных пассивных компонентов , которые мы используем. Вам нужно будет очень внимательно поискать схему, в которой не было бы конденсатора .
Особенностью конденсаторов является их способность накапливать энергию ; они похожи на полностью заряженную электрическую батарею. Колпачки , как мы их обычно называем, имеют самые разные критические приложения в схемах. Общие приложения включают локальное накопление энергии, подавление скачков напряжения и комплексную фильтрацию сигналов.
Рассмотрено в этом учебном пособии
В этом руководстве мы рассмотрим всевозможные темы, связанные с конденсаторами, в том числе:
- Как делается конденсатор
- Как работает конденсатор
- Емкость
- Типы конденсаторов
- Как распознать конденсаторы
- Как емкость сочетается последовательно и параллельно
- Общие применения конденсаторов
Рекомендуемая литература
Некоторые концепции в этом руководстве основаны на предыдущих знаниях в области электроники. Перед тем, как перейти к этому руководству, подумайте о том, чтобы сначала прочитать (хотя бы бегло просмотр) эти:
Перед тем, как перейти к этому руководству, подумайте о том, чтобы сначала прочитать (хотя бы бегло просмотр) эти:
Обозначения и единицы измерения
Условные обозначения цепей
Есть два распространенных способа изобразить конденсатор на схеме. У них всегда есть две клеммы, которые подключаются к остальной цепи. Символ конденсаторов состоит из двух параллельных линий, которые могут быть плоскими или изогнутыми; обе линии должны быть параллельны друг другу, близко друг к другу, но не соприкасаться (это фактически показывает, как сделан конденсатор.Трудно описать, проще просто показать:
, (1) и (2) — стандартные обозначения цепи конденсатора. (3) представляет собой пример символов конденсаторов в действии в цепи регулятора напряжения.
Символ с изогнутой линией (№2 на фото выше) указывает на то, что конденсатор поляризован, что означает, что это, вероятно, электролитический конденсатор. Подробнее об этом в разделе о типах конденсаторов этого руководства.
Каждый конденсатор должен сопровождаться названием — C1, C2 и т. Д.. — и стоимость. Значение должно указывать на емкость конденсатора; сколько там фарадов. Кстати о фарадах …
Емкость
Не все конденсаторы одинаковы. Каждый конденсатор имеет определенную емкость. Емкость конденсатора говорит вам, сколько заряда он может хранить , большая емкость означает большую емкость для хранения заряда. Стандартная единица измерения емкости называется фарад , сокращенно F .
Получается, что фарад — это лот емкости, даже 0,001Ф (1 миллифарад — 1мФ) — это большой конденсатор. Обычно вы увидите конденсаторы с номиналом от пико- (10 -12 ) до микрофарад (10 -6 ).
| Имя префикса | Сокращение | Вес | Эквивалентные фарады |
|---|---|---|---|
| Пикофарад | pF | 10 -12 | 0,000000000001 F |
| Нанофарад | nF | 10 | 0. 000000001 F 000000001 F |
| Микрофарад | мкФ | 10 -6 | 0,000001 F |
| Милифарад | мФ | 10 -3 | 0,001 F |
| Килофарад | килофарад | килофарад 10 3 | 1000 Ф. |
Когда вы входите в диапазон емкости от фарада до килофарада, вы начинаете говорить о специальных конденсаторах, называемых конденсаторами super или ultra .
Теория конденсаторов
Примечание : Материал на этой странице не совсем критичен для понимания новичками в электронике … и к концу все становится немного сложнее. Мы рекомендуем прочитать раздел Как делается конденсатор , остальные, вероятно, можно пропустить, если они вызывают у вас головную боль.
Как делается конденсатор
Схематический символ конденсатора на самом деле очень похож на то, как он сделан. Конденсатор состоит из двух металлических пластин и изоляционного материала, называемого диэлектриком . Металлические пластины расположены очень близко друг к другу, параллельно, но между ними находится диэлектрик, чтобы они не соприкасались.
Конденсатор состоит из двух металлических пластин и изоляционного материала, называемого диэлектриком . Металлические пластины расположены очень близко друг к другу, параллельно, но между ними находится диэлектрик, чтобы они не соприкасались.
Ваш стандартный конденсаторный сэндвич: две металлические пластины, разделенные изолирующим диэлектриком.
Диэлектрик может быть изготовлен из всех видов изоляционных материалов: бумаги, стекла, резины, керамики, пластика или всего, что препятствует прохождению тока.
Пластины изготовлены из проводящего материала: алюминия, тантала, серебра или других металлов. Каждый из них подключен к клеммному проводу, который в конечном итоге подключается к остальной части схемы.
Емкость конденсатора — сколько в нем фарад — зависит от его конструкции. Для большей емкости требуется конденсатор большего размера. Пластины с большей площадью перекрытия поверхности обеспечивают большую емкость, а большее расстояние между пластинами означает меньшую емкость. Материал диэлектрика даже влияет на то, сколько фарад имеет колпачок.Полная емкость конденсатора может быть рассчитана по формуле:
Материал диэлектрика даже влияет на то, сколько фарад имеет колпачок.Полная емкость конденсатора может быть рассчитана по формуле:
где ε r — относительная диэлектрическая проницаемость диэлектрика (постоянное значение, определяемое материалом диэлектрика), A — площадь перекрытия пластин друг с другом, а d — расстояние между пластинами.
Как работает конденсатор
Электрический ток — это поток электрического заряда, который электрические компоненты используют, чтобы загораться, вращаться или делать то, что они делают.Когда ток течет в конденсатор, заряды «застревают» на пластинах, потому что они не могут пройти через изолирующий диэлектрик. Электроны — отрицательно заряженные частицы — засасываются в одну из пластин, и она становится в целом отрицательно заряженной. Большая масса отрицательных зарядов на одной пластине отталкивает, как заряды, на другой пластине, делая ее заряженной положительно.
Положительный и отрицательный заряды на каждой из этих пластин притягиваются друг к другу, потому что это то, что делают противоположные заряды. Но с диэлектриком, сидящим между ними, как бы они ни хотели соединиться, заряды навсегда останутся на пластине (до тех пор, пока им не будет куда-то идти). Стационарные заряды на этих пластинах создают электрическое поле, которое влияет на электрическую потенциальную энергию и напряжение. Когда заряды группируются на таком конденсаторе, крышка накапливает электрическую энергию так же, как батарея может накапливать химическую энергию.
Но с диэлектриком, сидящим между ними, как бы они ни хотели соединиться, заряды навсегда останутся на пластине (до тех пор, пока им не будет куда-то идти). Стационарные заряды на этих пластинах создают электрическое поле, которое влияет на электрическую потенциальную энергию и напряжение. Когда заряды группируются на таком конденсаторе, крышка накапливает электрическую энергию так же, как батарея может накапливать химическую энергию.
Зарядка и разрядка
Когда на пластинах конденсатора сливаются положительный и отрицательный заряды, конденсатор становится на заряженным .Конденсатор может сохранять свое электрическое поле — удерживать свой заряд — потому что положительный и отрицательный заряды на каждой из пластин притягиваются друг к другу, но никогда не достигают друг друга.
В какой-то момент обкладки конденсатора будут настолько заряжены, что просто не смогут больше принимать их. На одной пластине достаточно отрицательных зарядов, чтобы они могли отразить любые другие, которые попытаются присоединиться. Именно здесь вступает в игру емкость (фарады) конденсатора, которая говорит вам о максимальном количестве заряда, которое может хранить конденсатор.
Именно здесь вступает в игру емкость (фарады) конденсатора, которая говорит вам о максимальном количестве заряда, которое может хранить конденсатор.
Если в цепи создается путь, который позволяет зарядам найти другой путь друг к другу, они выйдут из конденсатора, и разрядит .
Например, в схеме ниже можно использовать батарею для создания электрического потенциала на конденсаторе. Это вызовет нарастание одинаковых, но противоположных зарядов на каждой из пластин, пока они не станут настолько полными, что оттолкнут ток. Светодиод, расположенный последовательно с крышкой, может обеспечивать путь для тока, а энергия, запасенная в конденсаторе, может использоваться для кратковременного освещения светодиода.
Расчет заряда, напряжения и тока
Емкость конденсатора — сколько в нем фарад — говорит вам, сколько заряда он может хранить. Сколько заряда хранит конденсатор в настоящее время , зависит от разности потенциалов (напряжения) между его пластинами. Это соотношение между зарядом, емкостью и напряжением можно смоделировать с помощью следующего уравнения:
Это соотношение между зарядом, емкостью и напряжением можно смоделировать с помощью следующего уравнения:
Заряд (Q), накопленный в конденсаторе, является произведением его емкости (C) и приложенного к нему напряжения (V).
Емкость конденсатора всегда должна быть постоянной известной величиной. Таким образом, мы можем регулировать напряжение, чтобы увеличивать или уменьшать заряд крышки. Больше напряжения означает больше заряда, меньше напряжения … меньше заряда.
Это уравнение также дает нам хороший способ определить значение одного фарада. Один фарад (F) — это способность хранить одну единицу энергии (кулоны) на каждый вольт.
Расчет тока
Мы можем пойти дальше по уравнению заряда / напряжения / емкости, чтобы выяснить, как емкость и напряжение влияют на ток, потому что ток — это скорость потока заряда.Суть отношения конденсатора к напряжению и току такова: величина тока , проходящего через конденсатор , зависит как от емкости, так и от того, насколько быстро напряжение растет или падает .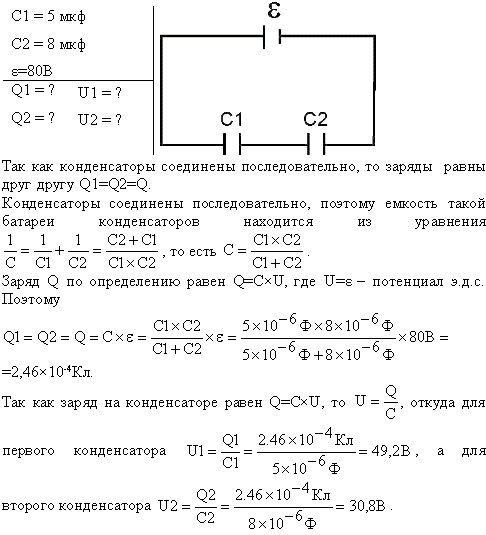 Если напряжение на конденсаторе быстро растет, через конденсатор будет индуцироваться большой положительный ток. Более медленный рост напряжения на конденсаторе означает меньший ток через него. Если напряжение на конденсаторе стабильное и неизменное, через него не будет проходить ток.
Если напряжение на конденсаторе быстро растет, через конденсатор будет индуцироваться большой положительный ток. Более медленный рост напряжения на конденсаторе означает меньший ток через него. Если напряжение на конденсаторе стабильное и неизменное, через него не будет проходить ток.
(Это некрасиво, и это касается вычислений. Это не все, что нужно, пока вы не перейдете к анализу во временной области, разработке фильтров и другим грубым вещам, поэтому переходите к следующей странице, если вам не нравится это уравнение .) Уравнение для расчета тока через конденсатор:
Часть dV / dt этого уравнения представляет собой производную (причудливый способ сказать мгновенная скорость ) напряжения во времени, это эквивалентно тому, как сказать «насколько быстро напряжение растет или падает в этот самый момент».Большой вывод из этого уравнения заключается в том, что если напряжение стабильно, , производная равна нулю, что означает, что ток также равен нулю . Вот почему ток не может течь через конденсатор, поддерживающий постоянное постоянное напряжение.
Вот почему ток не может течь через конденсатор, поддерживающий постоянное постоянное напряжение.
Типы конденсаторов
Существуют всевозможные типы конденсаторов, каждый из которых имеет определенные особенности и недостатки, которые делают его лучше для одних приложений, чем для других.
При выборе типа конденсатора необходимо учитывать несколько факторов:
- Размер — Размер как по физическому объему, так и по емкости.Конденсатор нередко является самым большим компонентом в цепи. Также они могут быть очень маленькими. Для большей емкости обычно требуется конденсатор большего размера.
- Максимальное напряжение — Каждый конденсатор рассчитан на максимальное падение напряжения на нем. Некоторые конденсаторы могут быть рассчитаны на 1,5 В, другие — на 100 В. Превышение максимального напряжения обычно приводит к разрушению конденсатора.
- Ток утечки — Конденсаторы не идеальны.
 Каждая крышка склонна пропускать небольшое количество тока через диэлектрик от одного вывода к другому. Эта крошечная потеря тока (обычно наноампер или меньше) называется утечкой. Утечка заставляет энергию, накопленную в конденсаторе, медленно, но верно истощаться.
Каждая крышка склонна пропускать небольшое количество тока через диэлектрик от одного вывода к другому. Эта крошечная потеря тока (обычно наноампер или меньше) называется утечкой. Утечка заставляет энергию, накопленную в конденсаторе, медленно, но верно истощаться. - Эквивалентное последовательное сопротивление (ESR) — Выводы конденсатора не на 100% проводящие, они всегда будут иметь крошечное сопротивление (обычно менее 0,01 Ом). Это сопротивление становится проблемой, когда через колпачок проходит большой ток, вызывая потери тепла и мощности.
- Допуск — Конденсаторы также не могут иметь точную, точную емкость. Каждая крышка будет рассчитана на свою номинальную емкость, но, в зависимости от типа, точное значение может варьироваться от ± 1% до ± 20% от желаемого значения.
Конденсаторы керамические
Наиболее часто используемый и производимый конденсатор — керамический конденсатор. Название происходит от материала, из которого сделан их диэлектрик.
Керамические конденсаторы обычно бывают как физически, так и емкостные малые .Трудно найти керамический конденсатор больше 10 мкФ. Керамический колпачок для поверхностного монтажа обычно находится в крошечных корпусах 0402 (0,4 мм x 0,2 мм), 0603 (0,6 мм x 0,3 мм) или 0805. Керамические колпачки со сквозными отверстиями обычно выглядят как маленькие (обычно желтые или красные) лампочки с двумя выступающими клеммами.
Две крышки в сквозном радиальном корпусе; конденсатор на 22 пФ слева и 0,1 мкФ справа. Посередине — крошечная крышка 0,1 мкФ 0603 для поверхностного монтажа.
По сравнению с не менее популярными электролитическими крышками керамические конденсаторы являются более близкими к идеальным конденсаторам (гораздо более низкие значения ESR и токи утечки), но их небольшая емкость может быть ограничивающей.Как правило, они также являются наименее дорогим вариантом. Эти колпачки хорошо подходят для высокочастотной связи и развязки.
Электролитический алюминий и тантал
Электролитикихороши тем, что они могут упаковать много емкости в относительно небольшой объем. Если вам нужен конденсатор емкостью от 1 мкФ до 1 мФ, вы, скорее всего, найдете его в электролитической форме. Они особенно хорошо подходят для высоковольтных приложений из-за их относительно высокого максимального номинального напряжения.
Алюминиевые электролитические конденсаторы, самые популярные из семейства электролитических, обычно выглядят как маленькие жестяные банки с обоими выводами, выходящими снизу.
Ассортимент электролитических конденсаторов сквозного и поверхностного монтажа. Обратите внимание, что у каждого из них есть метод маркировки катода (отрицательный вывод).
К сожалению, электролитические колпачки обычно поляризованы . У них есть положительный вывод — анод — и отрицательный вывод, называемый катодом.Когда напряжение подается на электролитический колпачок, анод должен иметь более высокое напряжение, чем катод. Катод электролитического конденсатора обычно обозначается знаком «-» и цветной полосой на корпусе. Ножка анода также может быть немного длиннее, как еще один признак. Если на электролитический колпачок подать обратное напряжение, они выйдут из строя (из-за чего лопнет и лопнет) и навсегда. После лопания электролитик будет вести себя как короткое замыкание.
Катод электролитического конденсатора обычно обозначается знаком «-» и цветной полосой на корпусе. Ножка анода также может быть немного длиннее, как еще один признак. Если на электролитический колпачок подать обратное напряжение, они выйдут из строя (из-за чего лопнет и лопнет) и навсегда. После лопания электролитик будет вести себя как короткое замыкание.
Эти колпачки также известны утечкой — позволяя небольшому току (порядка нА) проходить через диэлектрик от одного вывода к другому. Это делает электролитические колпачки менее чем идеальными для хранения энергии, что, к сожалению, с учетом их высокой емкости и номинального напряжения.
Суперконденсаторы
Если вы ищете конденсатор, предназначенный для хранения энергии, не ищите ничего, кроме суперконденсаторов. Эти колпачки имеют уникальную конструкцию, позволяющую иметь очень высоких емкостей в диапазоне фарад.
Суперконденсатор 1Ф (!). Высокая емкость, но рассчитана только на 2,5 В. Обратите внимание, что они также поляризованы.
Обратите внимание, что они также поляризованы.
Хотя они могут хранить огромное количество заряда, суперкаперы не могут работать с очень высокими напряжениями. Этот суперконденсатор 10F рассчитан только на максимальное напряжение 2,5 В. Любое большее, чем это, разрушит его. Суперэлементы обычно устанавливаются последовательно для достижения более высокого номинального напряжения (при уменьшении общей емкости).
Основное применение суперконденсаторов — это накопление и выделение энергии , как и батареи, которые являются их основным конкурентом.Хотя суперконденсаторы не могут удерживать столько энергии, сколько батарея того же размера, они могут высвобождать ее намного быстрее и обычно имеют гораздо больший срок службы.
Прочие
Электролитические и керамические крышки покрывают около 80% типов конденсаторов (а суперкапсы только около 2%, но они супер!). Другой распространенный тип конденсатора — пленочный конденсатор , который отличается очень низкими паразитными потерями (ESR), что делает их идеальными для работы с очень высокими токами.
Есть много других менее распространенных конденсаторов. Переменные конденсаторы могут производить различные емкости, что делает их хорошей альтернативой переменным резисторам в схемах настройки. Скрученные провода или печатные платы могут создавать емкость (иногда нежелательную), потому что каждый состоит из двух проводников, разделенных изолятором. Лейденские кувшины — стеклянная банка, наполненная проводниками и окруженная ими, — это O.G. семейства конденсаторов. Наконец, конечно, конденсаторы потока (странная комбинация катушки индуктивности и конденсатора) имеют решающее значение, если вы когда-нибудь планируете вернуться в дни славы.
Конденсаторы последовательно / параллельно
Подобно резисторам, несколько конденсаторов могут быть объединены последовательно или параллельно для создания комбинированной эквивалентной емкости. Конденсаторы, однако, складываются таким образом, что полностью противоположны резисторам.
Параллельные конденсаторы
Когда конденсаторы размещаются параллельно друг другу, общая емкость равна сумме всех емкостей .Это аналогично тому, как резисторы добавляются последовательно.
Так, например, если у вас есть три конденсатора номиналом 10 мкФ, 1 мкФ и 0,1 мкФ, подключенные параллельно, общая емкость будет 11,1 мкФ (10 + 1 + 0,1).
Конденсаторы серии
Подобно тому, как резисторы сложно добавить параллельно, конденсаторы становятся странными, когда их помещают в серию . Общая емкость последовательно соединенных конденсаторов N является обратной суммой всех обратных емкостей.
Если у вас есть только и два конденсатора , соединенных последовательно, вы можете использовать метод «произведение над суммой» для расчета общей емкости:
Если продолжить это уравнение, если у вас есть два конденсатора с одинаковым номиналом, соединенные последовательно , общая емкость составляет половину их значения. Например, два последовательно соединенных суперконденсатора по 10Ф дадут общую емкость 5Ф (это также даст возможность удвоить номинальное напряжение всего конденсатора с 2,5 В до 5 В).
Например, два последовательно соединенных суперконденсатора по 10Ф дадут общую емкость 5Ф (это также даст возможность удвоить номинальное напряжение всего конденсатора с 2,5 В до 5 В).
Примеры применения
Существует множество приложений для этого изящного маленького (на самом деле, обычно они довольно большие) пассивного компонента. Чтобы дать вам представление об их широком диапазоне использования, вот несколько примеров:
Разделительные (байпасные) конденсаторы
Многие конденсаторы, которые вы видите в схемах, особенно те, которые имеют интегральную схему, развязаны.Задача развязывающего конденсатора — подавить высокочастотный шум в сигналах источника питания. Они снимают с источника напряжения крошечные колебания напряжения, которые в противном случае могли бы нанести вред чувствительным микросхемам.
В каком-то смысле развязывающие конденсаторы действуют как очень маленький локальный источник питания для микросхем (почти как источник бесперебойного питания для компьютеров). Если в источнике питания очень быстро падает напряжение (что на самом деле довольно часто, особенно когда цепь, которую он питает, постоянно переключает требования к нагрузке), разделительный конденсатор может кратковременно подавать питание с правильным напряжением.Вот почему эти конденсаторы также называются шунтирующими конденсаторами , конденсаторами; они могут временно действовать как источник питания, обходя источник питания.
Если в источнике питания очень быстро падает напряжение (что на самом деле довольно часто, особенно когда цепь, которую он питает, постоянно переключает требования к нагрузке), разделительный конденсатор может кратковременно подавать питание с правильным напряжением.Вот почему эти конденсаторы также называются шунтирующими конденсаторами , конденсаторами; они могут временно действовать как источник питания, обходя источник питания.
Разделительные конденсаторы подключаются между источником питания (5 В, 3,3 В и т. Д.) И землей. Нередко для обхода источника питания используют два или более конденсаторов с разным номиналом или даже разных типов, потому что некоторые номиналы конденсаторов будут лучше, чем другие, при фильтрации определенных частот шума.
На этой схеме три развязывающих конденсатора используются для уменьшения шума в источнике напряжения акселерометра.Две керамические 0,1 мкФ и одна танталовая электролитическая 10 мкФ разделенные функции развязки.
Хотя кажется, что это может привести к короткому замыканию между питанием и землей, только высокочастотные сигналы могут проходить через конденсатор на землю. Сигнал постоянного тока поступит на микросхему, как и нужно. Другая причина, по которой они называются шунтирующими конденсаторами, заключается в том, что высокие частоты (в диапазоне кГц-МГц) обходят ИС, а не проходят через конденсатор, чтобы добраться до земли.
При физическом размещении развязывающих конденсаторов они всегда должны располагаться как можно ближе к ИС.Чем дальше они находятся, тем менее эффективны.
Вот схема физической схемы из схемы выше. Крошечная черная ИС окружена двумя конденсаторами по 0,1 мкФ (коричневые крышки) и одним электролитическим танталовым конденсатором 10 мкФ (высокая прямоугольная крышка черного / серого цвета).
Чтобы следовать хорошей инженерной практике, всегда добавляйте хотя бы один развязывающий конденсатор к каждой ИС. Обычно хорошим выбором является 0,1 мкФ или даже дополнительные конденсаторы на 1 мкФ или 10 мкФ. Это дешевое дополнение, и они помогают убедиться, что микросхема не подвергается сильным провалам или скачкам напряжения.
Это дешевое дополнение, и они помогают убедиться, что микросхема не подвергается сильным провалам или скачкам напряжения.
Фильтрация источника питания
Диодные выпрямителимогут использоваться для преобразования переменного напряжения, выходящего из вашей стены, в постоянное напряжение, необходимое для большинства электронных устройств. Но сами по себе диоды не могут превратить сигнал переменного тока в чистый сигнал постоянного тока, им нужна помощь конденсаторов! При добавлении параллельного конденсатора к мостовому выпрямителю выпрямленный сигнал выглядит следующим образом:
Может быть преобразован в сигнал постоянного тока близкого к уровню, например:
Конденсаторы — упрямые компоненты, они всегда будут пытаться противостоять резким перепадам напряжения.Конденсатор фильтра будет заряжаться по мере увеличения выпрямленного напряжения. Когда выпрямленное напряжение, поступающее в конденсатор, начинает быстро снижаться, конденсатор получит доступ к своему банку накопленной энергии, и он будет очень медленно разряжаться, передавая энергию нагрузке. Конденсатор не должен полностью разрядиться, пока входной выпрямленный сигнал не начнет снова увеличиваться, заряжая конденсатор. Этот танец разыгрывается много раз в секунду, многократно, пока используется источник питания.
Конденсатор не должен полностью разрядиться, пока входной выпрямленный сигнал не начнет снова увеличиваться, заряжая конденсатор. Этот танец разыгрывается много раз в секунду, многократно, пока используется источник питания.
Цепь питания переменного тока в постоянный.Крышка фильтра (C1) имеет решающее значение для сглаживания сигнала постоянного тока, посылаемого в цепь нагрузки.
Если вы разорвите любой блок питания переменного тока в постоянный, вы обязательно найдете хотя бы один довольно большой конденсатор. Ниже показаны внутренности настенного адаптера постоянного тока на 9 В. Заметили там конденсаторы?
Конденсаторов может быть больше, чем вы думаете! Есть четыре электролитических крышки, похожие на жестяную банку, в диапазоне от 47 мкФ до 1000 мкФ. Большой желтый прямоугольник на переднем плане — это высоковольтный 0.Крышка из полипропиленовой пленки 1 мкФ. И синяя дискообразная крышка, и маленькая зеленая посередине — керамические.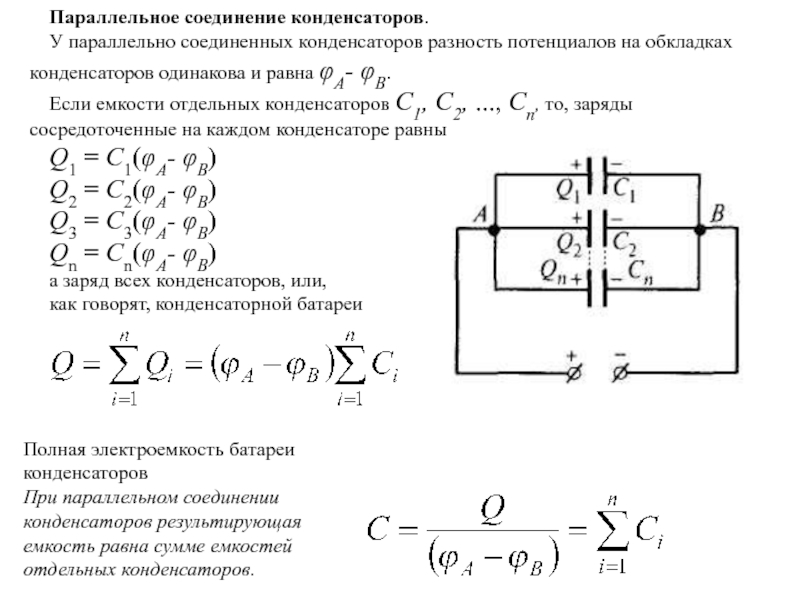
Хранение и поставка энергии
Кажется очевидным, что если конденсатор накапливает энергию, одно из многих его применений будет подавать эту энергию в цепь, как аккумулятор. Проблема в том, что конденсаторы имеют гораздо более низкую плотность энергии , чем батареи; они просто не могут вместить столько же энергии, как химическая батарея того же размера (но этот разрыв сокращается!).
Плюс конденсаторов в том, что они обычно служат дольше, чем батареи, что делает их лучшим выбором с экологической точки зрения. Они также способны выдавать энергию намного быстрее, чем аккумулятор, что делает их подходящими для приложений, которым требуется короткий, но большой всплеск мощности. Вспышка камеры может получать питание от конденсатора (который, в свою очередь, вероятно, заряжался от аккумулятора).
Батарея или конденсатор?| Батарея | Конденсатор | |
|---|---|---|
| Емкость | ✓ | |
| Плотность энергии | ✓ | |
| Скорость заряда / разряда | ✓ | |
| Срок службы 91 | ✓
Фильтрация сигналов
Конденсаторы обладают уникальной реакцией на сигналы различной частоты. Они могут блокировать низкочастотные компоненты или составляющие сигнала постоянного тока, позволяя при этом проходить более высоким частотам. Они как вышибалы в очень эксклюзивном клубе только для высоких частот.
Они могут блокировать низкочастотные компоненты или составляющие сигнала постоянного тока, позволяя при этом проходить более высоким частотам. Они как вышибалы в очень эксклюзивном клубе только для высоких частот.
Фильтрация сигналов может быть полезна во всех видах приложений обработки сигналов. Радиоприемники могут использовать конденсатор (среди других компонентов) для отключения нежелательных частот.
Другой пример фильтрации сигнала конденсатора — это пассивные схемы кроссовера внутри громкоговорителей, которые разделяют один аудиосигнал на множество.Последовательный конденсатор блокирует низкие частоты, поэтому оставшиеся высокочастотные части сигнала могут поступать на твитер динамика. При прохождении низких частот в цепи сабвуфера высокие частоты в основном могут быть шунтированы на землю через параллельный конденсатор.
Очень простой пример схемы кроссовера аудио. Конденсатор блокирует низкие частоты, а катушка индуктивности блокирует высокие частоты. Каждый из них может использоваться для доставки нужного сигнала настроенным аудиодрайверам.
Каждый из них может использоваться для доставки нужного сигнала настроенным аудиодрайверам.
Понижение рейтинга
При работе с конденсаторами важно проектировать схемы с конденсаторами, которые имеют гораздо более высокий допуск, чем потенциально самый высокий скачок напряжения в вашей системе.
Вот отличное видео от инженера SparkFun Шона о том, что происходит с различными типами конденсаторов, когда вы не можете снизить номинальные параметры конденсаторов и превысить их максимальное напряжение. Вы можете узнать больше о его экспериментах здесь.
Закупка конденсаторов
Храните на этих небольших компонентах накопителя энергии или используйте их в качестве начального блока питания.
Наши рекомендации:
Комплект конденсаторов SparkFun
В наличии КОМПЛЕКТ-13698 Это комплект, который предоставляет вам базовый ассортимент конденсаторов, чтобы начать или продолжить возиться с электроникой. Нет мес…
Нет мес…
Конденсатор керамический 0.1 мкФ
В наличии COM-08375Это очень распространенный конденсатор емкостью 0,1 мкФ. Используется во всевозможных приложениях для разъединения микросхем от источников питания. Расстояние между отверстиями 0,1 дюйма…
1Суперконденсатор — 10Ф / 2.5В
В наличии COM-00746Да, вы правильно прочитали — конденсатор 10 Фарад. Этот маленький колпачок можно зарядить, а затем медленно рассеять в течение…
3Ресурсы и дальнейшее развитие
Уф. Почувствуйте себя экспертом по конденсаторам ?! Хотите узнать больше об основах электроники? Если вы еще этого не сделали, подумайте о прочтении некоторых других распространенных электронных компонентов:
Почувствуйте себя экспертом по конденсаторам ?! Хотите узнать больше об основах электроники? Если вы еще этого не сделали, подумайте о прочтении некоторых других распространенных электронных компонентов:
Или, может быть, некоторые из этих руководств привлекут ваше внимание?
Hc Verma II для класса 12 Science Physics Chapter 31
Страница № 163:
Ответ:
Дано:
Заряд на положительной плоскости = + Q 1
Заряд на отрицательной пластине = — Q 2
Для расчета: Заряд на конденсаторе
Пусть ABCD будет гауссовой поверхностью такие, что грани AD и BC лежат внутри пластин X и Y соответственно.
Пусть q будет зарядом, возникающим на поверхности II. Тогда распределение зарядов на гранях I, III и IV будет в соответствии с рисунком.
Пусть площадь пластин равна A , а диэлектрическая проницаемость свободного пространства будет∈0.
Теперь, чтобы определить q в терминах Q 1 и Q 2 , нам нужно применить закон Гаусса для расчета электрического поля, создаваемого всеми четырьмя гранями конденсатора в точке P.Кроме того, мы знаем, что электрическое поле внутри конденсатора равно нулю.
Электрическое поле от грани I в точке P, E 1 = Q1-q2∈0A
Электрическое поле от грани II в точке P, E 2 = + q2∈0A
Электрическое поле из-за к грани III в точке P, E 3 = -q2∈0A
Электрическое поле из-за грани IV в точке P, E 4 = —Q2 + q2∈0A (Отрицательный знак используется как точка P лежит на левой стороне грани IV.)
Поскольку точка P находится внутри проводника,
E 1 + E 2 + E 3 + E 4 = 0
∴ Q 1 — q + q — q — (- Q 2 + q ) = 0
⇒ q = Q1 + Q22
Таким образом, заряд конденсатора равен Q1 + Q22, который является зарядом на гранях II и III.
Страница № 163:
Ответ:
Нет. Поскольку емкость является константой пропорциональности, она не зависит ни от заряда пластин, ни от потенциала. Это зависит только от размера и формы конденсатора, а также от диэлектрика, используемого между пластинами.
Формула, которая показывает его зависимость от размера и формы конденсатора, выглядит следующим образом:
C = ∈0Ad
Здесь A — площадь пластин конденсатора, а d — расстояние между пластинами. пластины конденсатора.
Страница № 163:
Ответ:
Потенциал металлической сферы прямо пропорционален передаваемому ей заряду q и обратно пропорционален ее радиусу r.
, т.е. V = q4π∈0r
Поскольку обе сферы являются проводниками с одинаковым радиусом и зарядом, данный им заряд появляется на поверхности равномерно. Таким образом, потенциал на поверхности или внутри сферы будет одинаковым, независимо от того, является ли сфера полой или твердой.
Таким образом, потенциал на поверхности или внутри сферы будет одинаковым, независимо от того, является ли сфера полой или твердой.
Страница № 163:
Ответ:
Предполагается, что обкладки конденсатора имеют одинаковые заряды. Другими словами, они имеют одинаковый потенциал, поэтому разность потенциалов между ними равна нулю.
Предположим, что заряд на грани II составляет q , так что индуцированный заряд на грани III составляет — q и распределение соответствует рисунку.
Теперь, если мы рассмотрим гауссову поверхность ABCD, грани которой лежат внутри двух пластин, и вычислим поле в точке P, создаваемое всеми четырьмя поверхностями, оно будет
E 1 = Q-q2∈0A
E 2 = q2∈0A
E 3 = _q2∈0A
E 4 = _ Q + q2∈0A (Это -ve, потому что точка P находится на левой стороне грани IV. )
)
Теперь, поскольку точка P лежит внутри проводника, полное поле должно быть равно нулю.
∴ E 1 + E 2 + E 3 + E 4 = 0
или
Q + q — q + Q + q = 0
∴ q = 0
Следовательно, на гранях II и III заряд равен нулю; а на гранях I и IV — Q .
Таким образом, кажется, что весь данный заряд перемещается к внешним поверхностям с нулевым зарядом на обращенных поверхностях.
Страница № 163:
Ответ:
Нет. Этой информации недостаточно. Поскольку заряд пропорционален разности потенциалов на конденсаторе, нам необходимо знать разность потенциалов, приложенную к конденсатору.
q ∝ В ⇒ q = CV
Здесь q — это заряд, В — приложенная разность потенциалов и C — константа пропорциональности, т. е.е. емкость.
е.е. емкость.
Страница № 163:
Ответ:
Величину поляризации можно понять как степень идеального выравнивания молекул диэлектрика с внешним электрическим полем. Чем больше молекулы выровнены по отношению к внешнему магнитному полю, тем больше поляризация и тем выше будет диэлектрическая проницаемость.
Но с повышением температуры тепловое возбуждение молекул или хаотичность их совмещения с полем увеличивается.
Таким образом, можно сказать, что повышение температуры приводит к уменьшению поляризации и диэлектрической проницаемости.
Страница № 163:
Ответ:
По мере уменьшения энергии системы изменение энергии отрицательное.
Сила определяется как отрицательная скорость изменения энергии по отношению к расстоянию.
F = -∂U∂x
Итак, по мере уменьшения энергии сила электрического поля конденсатора увеличивается, когда диэлектрик втягивается в конденсатор.
Страница № 164:
Ответ:
(d) ноль
Поскольку чистый заряд, заключенный в гауссовой поверхности, равен нулю, полный поток электрического поля через замкнутую гауссову поверхность, окружающую конденсатор, равен нулю.
Φ = ∯E.ds = q∈0 = 0
Здесь
Φ = электрический поток
q = полный заряд, заключенный на гауссовой поверхности.
Страница № 164:
Ответ:
(d) C /2 и 2 В
Поскольку при последовательном соединении конденсаторов напряжение складывается, напряжение комбинации составляет 2 В .
Также емкость последовательной комбинации определяется как
1Cnet = 1C1 + 1C2
Здесь
C net = Чистая емкость комбинации
C 1 = C 2 = C
∴ C нетто = C2
Страница № 164:
Ответ:
(c) 2 C и V
При параллельной комбинации конденсаторов разность потенциалов на конденсаторах остается такой же, как и на правой и левой пластинах обоих конденсаторы подключаются к одним и тем же выводам аккумуляторной батареи. Следовательно, потенциал остается прежним, то есть В .
Следовательно, потенциал остается прежним, то есть В .
Для параллельной комбинации конденсаторов емкость определяется как
C экв. = C 1 + C 2
Здесь
C 1 = C 2 = C
∴ C экв = 2 C
Страница № 164:
Ответ:
(b) 2 C
Поскольку потенциал в точке A равен потенциалу в точке B, ток не будет течь по плечу AB.Следовательно, конденсатор на плече AB не будет вносить вклад в схему. Кроме того, поскольку оставшиеся два конденсатора подключены параллельно, полезная емкость цепи определяется выражением
C экв. = C + C = 2 C
Страница № 164:
Ответ:
(c) остается неизменным
Сила между пластинами определяется как
F = q22∈0A
Поскольку конденсатор изолирован, заряд на пластинах остается постоянным.
Мы знаем, что заряд сохраняется в изолированной системе.
Таким образом, сила, действующая между пластинами, остается неизменной.
Страница № 164:
Ответ:
(d) 1r4
Плотность энергии U определяется как
U = 12∈0E2 … (1)
Электрическое поле, создаваемое точечным зарядом на расстоянии r , определяется как
E = q4π∈0r2
При помещении вышеупомянутой формы E в ур.1, получаем
U = 12∈0q4π∈0r22
Таким образом, U прямо пропорционально 1r4.
Страница № 164:
Ответ:
(b) Q + = Q-
Заряд, индуцированный на пластинах конденсатора, не зависит от их площади.
∴ Q + = Q-
Страница № 164:
Ответ:
(d) ∞
Тонкая металлическая пластина, вставленная между пластинами конденсатора с параллельными пластинами емкости C , соединяет две пластины конденсатора; следовательно, расстояние d между пластинами конденсатора уменьшается до нуля. Можно заметить, что заряды на пластинах начинают перекрывать друг друга через металлическую пластину и, следовательно, начинают непрерывно проводить.
Можно заметить, что заряды на пластинах начинают перекрывать друг друга через металлическую пластину и, следовательно, начинают непрерывно проводить.
Математически
C = ∈0Ad
В данном случае d = 0.
∴ C = ∞
Страница № 164:
Ответ:
(c) C 1 < C 2
Область AB показывает разность потенциалов на конденсаторе C 1 , а область CD показывает разность потенциалов на конденсаторе C 2 .Теперь мы можем видеть из графика, что область AB больше, чем область CD. Следовательно, разность потенциалов на конденсаторе C 1 больше, чем на конденсаторе C 2 .
∵ Емкость, C = QV
∴ C 1
Страница № 164:
Ответ:
(а) увеличить
Масло между пластинами конденсатора действует как диэлектрик. Мы знаем, что электрическое поле уменьшается в 1К по сравнению с исходным полем, когда мы вставляем диэлектрик между пластинами конденсатора ( K, — диэлектрическая проницаемость диэлектрика). Таким образом, если масло откачивается, электрическое поле между пластинами будет увеличиваться, так как диэлектрик удален.
Мы знаем, что электрическое поле уменьшается в 1К по сравнению с исходным полем, когда мы вставляем диэлектрик между пластинами конденсатора ( K, — диэлектрическая проницаемость диэлектрика). Таким образом, если масло откачивается, электрическое поле между пластинами будет увеличиваться, так как диэлектрик удален.
Страница № 164:
Ответ:
(b) Q1Q2 = C1C2
Когда сферы соединены, между ними течет заряд, пока они не приобретут одинаковый общий потенциал В .
Окончательные заряды сфер равны
Q 1 = C 1 V и Q 2 = C 2 V
∴Q1Q2 = C1VC2V = C1C2
C1C2VСтраница № 164:
Ответ:
(d) 2 мкФ, 18 мкФ
Минимальная емкость может быть получена путем последовательного соединения всех конденсаторов. Ее можно рассчитать следующим образом:
Ее можно рассчитать следующим образом:
1C = 16 + 16 + 16 = 12
⇒ C = 2 мкФ
Максимальную емкость можно получить, подключив все конденсаторы параллельно. Его можно рассчитать следующим образом:
C = 6 + 6 + 6 = 18 мкФ
Страница № 164:
Ответ:
(c) заряды на пластинах
Емкость конденсатора определяется как
C = ∈0Ad
Здесь A — площадь пластин конденсатора, а d — расстояние между пластинами.
Итак, мы можем ясно видеть, что емкость конденсатора действительно зависит от размера и формы пластин и расстояния между пластинами; это не зависит от зарядов на пластинах.
Страница № 164:
Ответ:
(b) Заряд на конденсаторе
Когда мы вставляем диэлектрик между пластинами конденсатора, на поверхности диэлектрика появляются индуцированные заряды противоположной полярности. Они создают внутри диэлектрика электрическое поле, направленное противоположно исходному полю конденсатора.
Они создают внутри диэлектрика электрическое поле, направленное противоположно исходному полю конденсатора.
Таким образом, результирующий эффект — уменьшенное электрическое поле.
Кроме того, поскольку потенциал пропорционален полю, потенциал уменьшается, как и запасенная энергия U , которая задается формулой
U = qV2
Таким образом, только заряд на конденсаторе остается неизменным, так как заряд сохраняется в изолированной системе.
Стр. № 165:
Ответ:
(d) Q ‘должно быть меньше Q .
Связь между наведенным зарядом Q ‘и зарядом на конденсаторе Q определяется как
Q ‘ = Q1-1K
Здесь K — диэлектрическая проницаемость, которая всегда больше или равна to 1.
Итак, мы видим, что для K > 1, Q ‘всегда будет меньше Q .
Стр.
 № 165:
№ 165:Ответ:
(a) лицевые поверхности конденсатора имеют равные и противоположные заряды
(b) две пластины конденсатора имеют одинаковые и противоположные заряды
(d) внешние поверхности пластин имеют одинаковые заряды
В H.C Верма ответ: (a), (c), (d). Но, по нашему мнению, ответ должен быть следующим: (a), (b), (d) все эти параметры являются свойствами конденсатора, а вариант (c) неверен, потому что аккумулятор является источником энергии, а не заряжается. Более того, если пластины конденсатора имеют одинаковый заряд снаружи и одинаковый заряд внутри, можно подумать, что заряд на пластинах также должен быть одинаковым, поэтому вариант (b) не может быть неверным.
Стр. № 165:
Ответ:
(b) Разность потенциалов на конденсаторе
(c) Энергия конденсатора.
Поскольку заряд всегда сохраняется в изолированной системе, он остается неизменным.
Теперь
V = Qd∈0A
Здесь Q , A и d — это заряд, площадь и расстояние между пластинами, соответственно.
Таким образом, чем d увеличивается, V увеличивается.
Энергия равна
E = qV2
Таким образом, она также будет увеличиваться.
Плотность энергии u , то есть энергия, запасенная на единицу объема в электрическом поле, задается соотношением
u = 12∈0E2
Таким образом, u останется постоянным с увеличением расстояния между пластинами.
Стр. № 165:
Ответ:
(d) Равные и противоположные заряды появятся на двух сторонах металлической пластины.
Емкость конденсатора, в котором диэлектрическая пластина с диэлектрической постоянной K , площадью A и толщиной t вставлена между пластинами конденсатора площадью A и разделена расстоянием d , составляет дается формулой
C = ∈0Ad-t + t / K
Поскольку дано, что толщина листа пренебрежимо мала, приведенная выше формула сводится к C = ∈0Ad. Другими словами, не будет никаких изменений в электрическом поле, потенциале или заряде.
Другими словами, не будет никаких изменений в электрическом поле, потенциале или заряде.
Только одинаковые и противоположные заряды будут появляться на двух сторонах металлической пластины из-за индукции из-за наличия зарядов на пластинах конденсатора.
Стр. № 165:
Ответ:
(b) Заряд, появляющийся на конденсаторе, больше после действия XWY , чем после действия XYZ.
(c) Электрическая энергия, запасенная в конденсаторе, больше после действия WXY , чем после действия XYW .
(d) Электрическое поле в конденсаторе после воздействия XW такое же, как после WX .
Обоснование варианта (b)
Если потенциал остается постоянным, то есть батарея остается подключенной к цепи, то заряд конденсатора увеличивается в К при добавлении диэлектрика с диэлектрической проницаемостью К между обкладками конденсатора.
Математически
q = Kq 0
Здесь q 0 и q — заряды без диэлектрика и с диэлектриком соответственно.
Количество накопленного заряда не зависит от полярности пластин.
Таким образом, заряд, появляющийся на конденсаторе, больше после действия XWY , чем после действия XYZ.
Обоснование варианта (c)
Так как аккумулятор отключается перед вставкой диэлектрика, величина заряда остается постоянной, то есть q = q 0 , потому что после отключения аккумулятора конденсатор не получает источника для хранения заряда.Другими словами, конденсатор теперь представляет собой изолированную систему, в которой сохраняется количество заряда, равно как и энергия U как 12q ε . Следовательно, установка диэлектрика после отключения батареи не приведет к изменению количества заряда, накопленного в конденсаторе. Таким образом, энергия, запасенная в конденсаторе, также не изменится после действия XYW .
Однако во время действия WXY, количество заряда, которое будет храниться в конденсаторе, увеличится в К, , поскольку аккумулятор отключен после вставки диэлектрика между пластинами конденсатора и энергии сохраненный также будет умножен на коэффициент К.
Таким образом, электрическая энергия, запасенная в конденсаторе, больше после действия WXY , чем после действия XYW.
Обоснование варианта (d)
Электрическое поле между пластинами E зависит от потенциала на конденсаторе и расстояния d между пластинами конденсатора.
Математически
E = εd
В любом случае, то есть во время действий XW, и WX, потенциал остается прежним, то есть ε.Таким образом, электрическое поле E остается прежним.
Отказ от опции (a)
Во время действия XYZ аккумулятор должен выполнить дополнительную работу, эквивалентную 12 CV 2 , чтобы изменить полярность пластин конденсатора. Другими словами, общий объем работы, который должен выполнить аккумулятор, составит 12 CV 2 + 12 CV 2 . Эта дополнительная работа будет рассеиваться в виде тепловой энергии. Таким образом, вырабатывается тепловая энергия.Однако накопленная электрическая энергия остается неизменной, то есть 12 CV 2 .
Другими словами, общий объем работы, который должен выполнить аккумулятор, составит 12 CV 2 + 12 CV 2 . Эта дополнительная работа будет рассеиваться в виде тепловой энергии. Таким образом, вырабатывается тепловая энергия.Однако накопленная электрическая энергия остается неизменной, то есть 12 CV 2 .
Стр. № 165:
Ответ:
Поскольку 1,0 × 10 12 электронов переносятся от одного проводника к другому, проводник, к которому переносятся электроны, становится отрицательно заряженным, а другой проводник становится заряженным положительно.
Итак,
Величина чистого заряда на каждом проводнике, Q = (1.0 × 10 12 ) × (1,6 × 10 -19 ) C = 1,6 × 10 -7 C
Величина разности потенциалов между проводниками, В = 10 В
Емкость C представляет собой отношение величины заряда на любом проводнике к величине разности потенциалов между проводниками.
C = QV
⇒ C = 1,6 × 10-710 = 1,6 × 10-8 F
Следовательно, значение емкости данных двухпроводных систем составляет 1,6 × 10 -8 F.
Стр. № 165:
Ответ:
Емкость конденсатора с параллельными пластинами определяется как
C = ∈0 Ad
Здесь
A = Площадь пластины
d = Расстояние между параллельными пластинами
Дано:
A = πr2 = π × 5 × 10-22d = 1,0 × 10-3 m∈0 = 8,85 × 10-12 Ф / м∴C = ∈0 Ad = 8,85 × 10-12 × 3,14 × 25 × 10-410-3 = 6,95 × 10- 5 мкФ
Стр. № 165:
Ответ:
Емкость конденсатора с параллельными пластинами определяется как
C = ∈0 Ad
Здесь
A = Площадь пластины
d = Расстояние между параллельными пластинами
Теперь
Пусть радиус диска быть р.
∴C = ∈0Ad = ∈0πr2d⇒r = Cd∈0π⇒r = 1 × (1 × 10-3) 8,85 × 10-12 × 3,14 = 35,98 × 106 м⇒r≈36 × 106 м = 6 × 103 м = 6 км
Таким образом, радиус пластин конденсатора для данной конфигурации составляет 6 км.
Стр. № 165:
Ответ:
Емкость конденсатора с параллельными пластинами определяется как
C = ∈0 Ad
Здесь
A = Площадь пластины
d = Расстояние между параллельными пластинами
Дано:
A = 25 см 2 = 25 × 10 -4 м 2
d = 1.00 мм = 1 × 10 -3 м
Теперь,
C = ∈0 Ad = 8,85 × 10-12 × 25 × 10-41 × 10-3 = 2,21 × 10-11 F
Когда батарея Напряжение 6 В подключено к конденсатору, заряд ( Q ), который течет от батареи, равен количеству заряда, который может удерживать данный конденсатор.
⇒ Q = CV
⇒ Q = 2,21 × 10-11 × 6,0 = 1,33 × 10-10 C
Работа, выполняемая аккумулятором при зарядке конденсатора, рассчитывается как произведение величины передаваемый заряд и напряжение аккумулятора.
Таким образом, получаем
Вт = QV = 1,33 × 10-10 × 6,0 = 8,0 × 10-10 Дж
Таким образом, заряд, прошедший через аккумулятор, равен 1,33 × 10 -10 C и работа, выполняемая аккумулятором составляет 8,0 × 10 -10 Дж.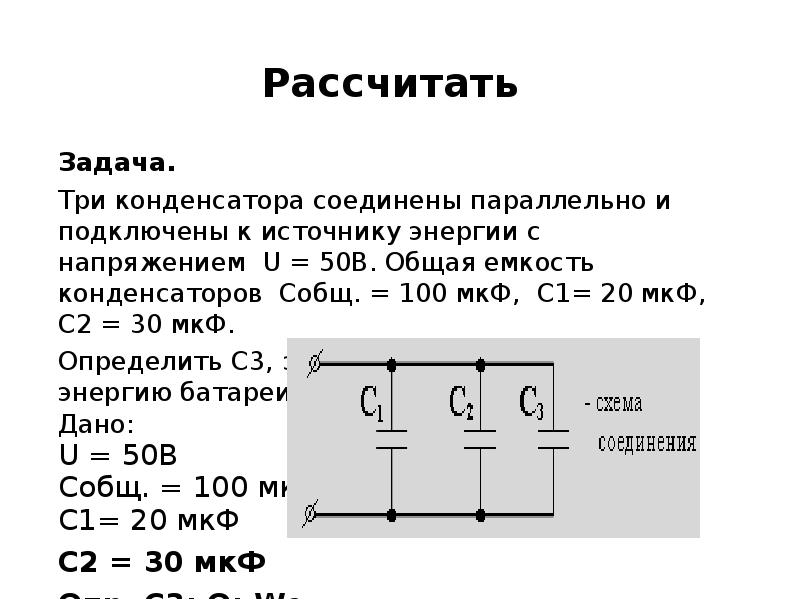
Стр. № 165:
Ответ:
Дано:
Площадь пластины, A = 25 см 2 = 25 × 10 -4 м 2
Расстояние между пластинами, d = 2 мм = 2 × 10 -3 м
Разница потенциалов между пластинами, В = 12 В
Емкость данного конденсатора определяется как
C = ∈0 Ad
= (8.85 × 10-12) × (25 × 10-4) (2 × 10-3) = 11,06 × 10-12 F
(a) Заряд конденсатора равен
Q = CV
= 11,06 × 10-12 × 12 = 1,33 × 10-10 C
(b) Когда расстояние между пластинами уменьшается до 1 мм, емкость C ‘может быть рассчитана как:
C’ = ∈0 Ad = (8,85 × 10 -12) × (25 × 10-4) 1 × 10-3 = 22,12 × 10-12 F
Заряд конденсатора равен
Q ‘= C’V
= 22,12 × 10-12 × 12 = 2,65 × 10-10 C Дополнительный заряд = 2,65 × 10-10-1,32 × 10-10 C = 1.33 × 10-10 С
Стр.
 № 165:
№ 165:Ответ:
Емкости трех конденсаторов: C 1 = 2 мкФ, C 2 = 4 мкФ и C 3 = 6 мкФ, а напряжение батареи ( В, ) составляет 12 В. .
Поскольку конденсаторы соединены параллельно, эквивалентная емкость определяется как
C экв = C 1 + C 2 + C 3
= (2 + 4 + 6) мкФ = 12 мкФ = 12 × 10 -6 F
Из-за параллельного подключения разность потенциалов на каждом конденсаторе одинакова и равна 12 В.
Следовательно, заряд на каждом конденсаторе можно рассчитать следующим образом:
Заряд на конденсаторе емкости C 1 = 2 мкФ определяется как
Q 1 = C 1 В = (2 × 10 -6 ) × 12 C = 24 × 10 -6 C = 24 мкКл
Точно так же заряды на двух других конденсаторах определяются как
Q 2 = C 2 V = (4 × 10 -6 ) × 12 C = 48 × 10 -6 C = 48 мкКл
и
Q 3 = C 3 V = (6 × 10 -6 ) × 12 C = 72 × 10 -6 C = 72 мкКл
Стр.
 № 165:
№ 165:Ответ:
Когда конденсаторы соединены последовательно, эквивалентная емкость определяется как
1ceq = 1c1 + 1c2 + 1c31ceq = 120 + 130 + 140 × 110-6⇒ ceq = 9.23 мкФ
Поскольку конденсаторы соединены последовательно, одинаковый заряд будет идти на каждый из них, и он равен общему заряду аккумулятора.
Теперь,
Пусть заряд на каждом конденсаторе равен q.
∴q = CV = (9,23 × 10-6) × 12 q = 110,76 мкКл
Работа, выполняемая аккумулятором ( Вт, ), определяется как
W = qV⇒W = 12 × 110,76 × 10- 6⇒W = 1,33 × 10-3 Дж
Стр. № 165:
Ответ:
Давайте сначала найдем эквивалентную емкость.Из принципиальной схемы видно, что конденсаторы B и C включены параллельно и последовательно с конденсатором A.
Эквивалентную емкость можно рассчитать следующим образом:
1Ceq = 1CA + 1CB + CC1Ceq = 18 + 14 + 4 = 18 + 18⇒1Ceq = 28⇒Ceq = 4 мкФ
Конденсаторы B и C параллельны и включены последовательно с конденсатором A. Эквивалентная емкость конденсаторов B и C равна
Эквивалентная емкость конденсаторов B и C равна
(4 + 4) мкФ = 8 мкФ
Она такая же, как и емкость конденсатора A. Следовательно, на конденсаторе A и системе конденсаторов B и C будет одинаковая разность потенциалов.
Теперь,
Разность потенциалов на конденсаторе A = 6 В
Таким образом,
Заряд на конденсаторе A = (8 мкФ) × (6 В) = 48 мкКл
А,
Разность потенциалов на конденсаторах B и C = 6 В
Таким образом,
Заряд конденсатора B = (4 мкФ) × (6 В) = 24 мкФ
Заряд конденсатора C = (4 мкФ) × (6 В) = 24 мкФ
Стр. № 165:
Ответ:
(a)
Для комбинации конденсаторов, показанной на рисунке (a), пары конденсаторов C 1 и C 2 соединены параллельно.
Эквивалентная емкость каждой параллельной комбинации конденсаторов определяется по формуле
C 1 + C 2 = 4 + 6 = 10 мкФ
Эквивалентную схему можно нарисовать как:
Эквивалент емкость для вышеуказанной последовательной цепи равна
1Ceq = 1C1 + C2 + 1C1 + C2 = 110 + 110 = 210⇒Ceq = 5 мкФ
(b)
Для комбинации конденсаторов, показанной на рисунке (b), пары конденсаторов C 1 и C 2 включены параллельно.
Эквивалентная емкость каждой параллельной комбинации конденсаторов определяется как
C 1 + C 2 = 4 + 6 = 10 мкФ
Эквивалентную схему можно представить как:
В На схеме выше видно, что C A и C B находятся последовательно и параллельно последовательной комбинации C C и C B .
Эквивалентная емкость для последовательной комбинации C A и C B определяется как
1Ceq = 1CA + 1CB = 1C1 + C2 + 1C1 + C2 = 110 + 110 = 15⇒Ceq = 5 мкФ
Аналогично, эквивалентная емкость последовательной комбинации C C и C D составляет 5 мкФ.
∴ Эквивалентная емкость нетто = 5 + 5 = 10 мкФ
Стр. № 166:
Ответ:
Эквивалентная схема для данного случая может быть представлена как:
Можно заметить, что конденсаторы C 1 и C 2 включены параллельно.
Следовательно, эквивалентная емкость определяется как
C экв. = C 1 + C 2
= 5 + 6 = 11 мкФ
Теперь
Заряд, обеспечиваемый батареей = ( C экв ) (В) = (11 мкФ) × (10 В) = 110 мкКл
Стр. № 166:
Ответ:
Предусмотрено, что внешние цилиндры находятся в контакте, а внутренние цилиндры соединены проволокой.Таким образом, эквивалентная схема может быть представлена как:
Левая пластина конденсаторов (A и B), показанных на рисунке, представляет собой внутренние пластины цилиндрических конденсаторов.
Поскольку конденсаторы подключены параллельно, разность потенциалов на них одинакова.
∴ Величина заряда на каждом конденсаторе = CV = (2,2 мкФ) × (10 В) = 22 мкКл
Поскольку пластины A и B подключены к положительному выводу батареи, заряд на каждой из них составляет +22 мкКл.
∴ Чистый заряд на внутренних пластинах = 22 мкКл + 22 мкКл = +44 мкКл
Стр. № 166:
Ответ:
Нам нужно рассчитать емкость изолированного заряженного шара.
Предположим, что заряд на сфере равен Q , а его радиус равен R .
Емкость заряженной сферы можно определить, представив концентрическую сферу бесконечного радиуса, состоящую из заряда −Q.
Разность потенциалов между сферами = 14π∈0QR — 0 = 14π∈0QR
Емкость — это отношение величины заряда на каждом проводе к разности потенциалов между ними.
C = Q14π∈0QR = 4π∈0R
Следовательно, емкости сфер радиусом R 1 и R 2 равны C 1 и C 2 соответственно. Они задаются формулой
C1 = 4π∈0 R1C2 = 4π∈0 R2
Если сферы соединены металлической проволокой, заряд будет перетекать от одной сферы к другой, пока их потенциалы не станут одинаковыми.
Когда потенциалы становятся одинаковыми, разность потенциалов между проводниками обоих конденсаторов также становится одинаковой.Таким образом, можно сделать вывод, что конденсаторы подключены параллельно.
Таким образом, емкость комбинации равна
Ceq = C 1 + C 2
= 4π∈0 R1 + R2
Стр. № 166:
Ответ:
В данной системе есть три ряда конденсаторов, включенных параллельно. В каждом ряду последовательно включены по три конденсатора емкостью 2 мкФ.
Для каждой строки эквивалентная емкость определяется как
1Cr = 12 + 12 + 12⇒Cr = 23 мкФ
Поскольку три строки соединены параллельно, их эквивалентная емкость определяется как
C eq = C r + C r + C r = 23 + 23 + 23 = 2 мкФ
Напряжение в каждой строке одинаковое и равно 60 В.
Как и все конденсаторы одинаковой емкости в каждом ряду, разность потенциалов на их пластинах одинакова.
∴ Разность потенциалов на каждом конденсаторе = 20 В
Стр. № 166:
Ответ:
Пусть количество конденсаторов последовательно (соединенных в ряд) будет x .
Максимальное напряжение, которое выдерживают конденсаторы, составляет 50 В.
Напряжение на каждой строке должно быть равно 200 В.
Следовательно,
x × 50 = 200
Таким образом,
x = 4 конденсатора
Теперь,
Пусть таких строк будет y .
Таким образом, эквивалентная емкость комбинации будет xy.
⇒ xy = 10
⇒ y = 10 x = 4 конденсатора
Таким образом, чтобы получить требуемый результат, комбинация 4 рядов, каждый из 4 конденсаторов с емкостью 10 мкФ и напряжением пробоя 50 В, необходимо.
Стр.
 № 166:
№ 166:Ответ:
(a)
Емкость двух параллельно соединенных строк равна
C1 = 4 × 84 + 8 = 83 мкФ и C2 = 3 × 63 + 6 = 189 мкФ = 2 мкФ
Поскольку две строки параллельно, разность потенциалов в каждом ряду одинакова и равна 50 В.
Заряд на ответвлении ACB с емкостью 83 мкФ определяется как
Q = 83 мкФ × (50 В) = 4003 мкКл
Заряд на ответвлении ADB с емкостью 2 мкФ определяется как
Q = C × VQ = 2 мкФ × 50 = 100 мкКл
Потенциал в точке D определяется как
VD = qC1 = 100 мкКл 6 мкФВД = 503 В
Аналогично потенциал в точке C определяется как
VC = 503 В
(b) Поскольку разность потенциалов между точками C и D равна нулю, мост остается сбалансированным, и заряд не течет от C к D.Если конденсатор подключен между точками C и D, то изменение конденсатора будет нулевым.
Стр. № 166:
Ответ:
Конденсаторы C 1 и C 2 сверху и снизу ab соединены последовательно и параллельно с C 3 .
Таким образом, эквивалентный конденсатор между a и b определяется как
Ceq = C1C2C1 + C2 + C3 + C1C2C1 + C2⇒Ceq = C3 + 2C1C2 C1 + C2
Стр. № 166:
Ответ:
Общая площадь плоской пластины A .Ширина каждой ступеньки одинакова. Следовательно, площадь поверхности каждой ступени, обращенной к плоской пластине, одинакова, то есть A3.
Из рисунка видно, что конденсаторная сборка состоит из трех конденсаторов. Три конденсатора подключены параллельно.
Для конденсатора C 1 площадь пластин A3, а расстояние между пластинами составляет d .
Для конденсатора C 2 площадь пластин A3, а расстояние между пластинами ( d + b ).
Для конденсатора C 3 площадь пластин составляет A3, а расстояние между пластинами составляет ( d + 2 b ).
Следовательно,
C1 = ∈0 A3d C2 = ∈0 A3d + bC3 = ∈0 A3d + 2b
Поскольку три конденсатора соединены параллельно,
C = C1 + C2 + C3⇒C = ∈0 A3d + ∈ 0 A3d + b + ∈0 A3d + 2b⇒C = ∈0 A33d2 + 6bd + 2b2dd + bd + 2b
Стр. № 166:
Ответ:
(a) Емкость цилиндрического конденсатора определяется как
C = 2π∈0 llnR2R1⇒C = 2 × 3.14 × 8,85 × 10-12 × 0,10ln 2 ⇒C = 8 пФ ∵ln 2 = 0,693
(б) Если взять конденсатор такой же высоты с цилиндрами радиусом 4 мм и 8 мм, его емкость составит 8 pF, то же самое, что и выше, потому что соотношение радиусов такое же.
Стр. № 166:
Ответ:
Дано:
C1 = 100 пФ V = 24 В
Заряд данного конденсатора, q = C1V = 24 × 100 пКл
Емкость незаряженного конденсатора, C2 = 20 пФ
Когда заряженный конденсатор соединен с незаряженным конденсатором , чистый заряд системы конденсаторов становится
q1 + q2 = 24 × 100 qC. .. (i)
.. (i)
Разность потенциалов на пластинах конденсаторов будет такой же.
Таким образом,
q1C1 = q2C2⇒q1100 = q220⇒q1 = 5q2 … (ii)
Из ур. (i) и (ii), получаем
q1 + q15 = 24 × 100 pC⇒6q1 = 5 × 24 × 100 pC⇒q1 = 5 × 24 × 1006 pCNow, V1 = q1C1 = 5 × 24 × 100 pC6 × 100 пФ = 20 В
Стр. № 166:
Ответ:
Первоначально, когда переключатель S разомкнут, эквивалентная емкость определяется как
Ceq = 2C × C3C⇒Ceq = 23C = 23 × 5.0 мкФ
Заряд, обеспечиваемый батареей, определяется выражением
Q = Ceq × V⇒Q = 23 × (5,0 мкФ) × (50 В) ⇒Q = 5003 мкКл
Когда переключатель S замкнут, заряд не поступает на конденсатор подключен параллельно переключателю.
Таким образом, эквивалентная емкость определяется как
Ceq = 2C = 2 × 5,0 = 10 мкФ
Заряд, обеспечиваемый батареей, определяется как
Q = 10 мкФ × 50 = 500 мкКл
Начальный заряд, накопленный в закороченном конденсаторе начинает разряжаться »?
Следовательно, заряд, который течет от A к B, определяется выражением
Qnet = 500 мкКл-5003 мкКл⇒Qnet = 3. 3 × 10-4 С
3 × 10-4 С
Стр. № 166:
Ответ:
Частица уравновешивается, когда электрическая сила, действующая на нее, уравновешивается ее весом.
Таким образом,
mg = qE mg = q × V’d … (i)
Здесь
d = Расстояние между пластинами конденсатора
V ‘ = Разность потенциалов на конденсаторе, содержащем частицу
Мы знаем, что емкость конденсатора определяется как
C = ∈0Ad⇒d = ∈0AC
Таким образом, уравнение.( i ) становится
mg = q × V ‘× C∈0A⇒V’ = mg ∈0Aq × C⇒V ‘= 10-6 × 9,8 × (8,85 × 10-12) × (100 × 10-4 ) (0,01 × 10-6) × (0,04 × 10-6) ⇒V ‘= 21,68 мВ
Поскольку значения обоих конденсаторов одинаковы,
В = 2 В ‘ = 2 × 21,86 ≈ 43 мВ
Стр. № 166:
Ответ:
Пусть:
Скорость электрона = u
Масса электрона = м
Теперь,
Горизонтальное расстояние, x = u × t
⇒t = xv. .. (i)
.. (i)
Пусть электрическое поле внутри конденсатора равно E
∴ Ускорение электрона = qEm
Расстояние по вертикали, y = 12 qEmt2 = 12 qEmxu2 ∵t = xu
y = d12 и x = a⇒ d12 = 12 qEm · au2 … (ii)
Емкость двух конденсаторов:
C 1 = ∈0a2d1 и C 2 = ∈0a2d2
Предполагается, что конденсаторы подключены в серии.
Таким образом, эквивалентная емкость определяется как
Ceq = C1C2C1 + C2
Ceq = ∈0 a2d1 × ∈0 a2d2∈0 a2d1 + ∈0 a2d2 = ∈0 a2d1 + d2
Общий заряд системы конденсаторов, Q = C eq V = ∈0 a2d1 + d2V
Поскольку конденсаторы включены последовательно, заряд на обоих из них одинаковый.
Разность потенциалов на конденсаторе, содержащем электрон, определяется как
V = QC1 = ∈0 a2VC1d1 + d2 = ∈0 a2V∈0 a2d1d1 + d2 = Vd1d1 + d2
Величина электрического поля внутри конденсатора определяется выражением
E = Vd1 = Vd1 + d2
Заряд электрона q представлен как e.
Подставляя значения q и E в (ii), мы получаем
⇒d12 = 12 qVm (d1 + d2) · au2 … (iii)
Дана минимальная скорость электрона. по
u = Vea2md1 d1 + d21 / 2
Стр. № 167:
Ответ:
Пусть электрическое поле внутри конденсатора будет E .
Теперь,
Величина ускорения электрона, ae = qeEme
Величина ускорения протона, ap = qpEmp
Пусть t будет время, необходимое электрону и протону для достижения положительного и отрицательного значений. тарелки соответственно.
Начальные скорости протона и электрона равны нулю.
Таким образом, расстояние, пройденное протоном, равно
x = 12qpEmpt2 … (1)
И расстояние, пройденное электроном, равно
2-x = 12qeEmet2… (2)
Разделив (1) на (2), получим
x2-x = qpEmpqeEme = memp = 9,1 × 10-311,67 × 10-27 = 5,449 × 10-4⇒x = 10,898 × 10-4 — 5,449 × 10-4x⇒x = 10,898 × 10-41,0005449 = 1,08 × 10-8 см
Стр.
 № 167:
№ 167:Ответ:
Части (a), (b) и (c) идентичны, так как все они образуют мостовую схему. В этой схеме конденсаторы 1 мкФ и 2 мкФ подключены к клемме A, а конденсатор 5 мкФ и конденсаторы 3 мкФ и 6 мкФ подключены к клемме B и конденсатору 5 мкФ.
В данной ситуации можно заметить, что мост находится в равновесии; таким образом, через конденсатор емкостью 5 мкФ не будет протекать ток.
Итак, чтобы упростить схему, конденсатор 5 мкФ может быть удален из схемы.
Теперь конденсаторы 1 мкФ и 3 мкФ включены последовательно.
И конденсаторы 2 мкФ и 6 мкФ также включены последовательно.
Эти две комбинации параллельны друг другу.
Эквивалентную емкость можно рассчитать как:
Ceq = 1 × 31 + 3 + 2 × 62 + 6 = 34 + 128 = 94 мкФ = 2.25 мкФ
∴ C eq = 2,25 мкФ
Таким образом, части (a), (b) и (c) идентичны.
А,
C экв = 2,25 мкФ
Стр.
 № 167:
№ 167:Ответ:
(a) q = q1 + q2 … (i)
Применяя закон Кирхгофа по напряжению в контуре CabDC, получаем
q22 + q24-q14 = 0⇒2 q2 + q2-q1 = 0⇒ 3 q2 = q1… (ii)
Применяя закон Кирхгофа по напряжению в контуре DCBAD, получаем
q2 + q14-12 = 0
⇒q1 + q22 + q14-12 = 0⇒3q1 + 2 q2 = 48 … (iii)
Из ур. (ii) и (iii) получаем
9q2 + 2 q2 = 48⇒11q2 = 48 ⇒q2 = 4811 Теперь, Va-Vb = q24 мкФ = 4844 = 1211 В
(b) Пусть заряд в контуре равен q .
Теперь, применяя закон Кирхгофа по напряжению в контуре, мы получаем
q2 + q4-24 + 12 = 0
⇒3 q4 = 12⇒q = 16 μCNow, Va-Vb = -q2μF⇒Va-Vb = -16 мкКл2 мкФ = -8 В
(c) Va-Vb = 2-2-q2 мкФ
В контуре,
2 + 2-q2-q2 = 0⇒q = 4 C
∴ Va-Vb = 2-42 = 2-2 = 0 В
(d)
Чистый заряд, протекающий через все ветви, q = 24 + 24 + 24 = 72 мкКл
Чистая емкость всех ветвей, C = 4 + 2 + 1 = 7 мкФ
Полная разность потенциалов ( В, ) между точками a и b определяется как
V = qC⇒V = 727 = 10. 3 В
3 В
Поскольку отрицательные клеммы батарей подключены к a , общий потенциал между точками a и b составляет -10,3 В.
Стр. № 167:
Ответ:
(a)
Применение преобразования звезда-треугольник в части, указанной на схеме.
Емкость C 1 определяется как
C1 ‘= C2C3C1 + C2 + C3C2’ = C1C3C1 + C2 + C3C3 ‘= C1C2C1 + C2 + C3⇒C1’ = 3 × 41 + 3 + 4 = 128 мкФ ⇒C2 ‘= 1 × 31 + 3 + 4 = 38 мкФ⇒C3’ = 1 × 41 + 3 + 4 = 48 мкФ
Таким образом, эквивалентная схема может быть представлена как:
Следовательно, эквивалентная емкость определяется как
C eq = 38 + 3 + 12 × 32 + 13 + 12 + 32 + 1 = 38 + 3524 = 9 + 3524 = 116 мкФ
(b) При преобразовании звезда-треугольник,
1 + 1 = 2 мкФ
(в)
Это симметричный мост.
Следовательно, конденсатор емкостью 5 мкФ можно убрать.
Емкость двух ветвей:
C1 = 2 × 42 + 4 = 43 мкФ 2 = 4 × 84 + 8 = 83 мкФ
∴ Эквивалентная емкость = 43 + 83 + 4 = 8 мкФ
(d)
Это тоже сбалансированная диаграмма.
Видно, что мосты уравновешены.
Следовательно, конденсаторы емкостью 6 мкФ между ответвлениями могут быть удалены
Емкости четырех ответвлений равны:
C1 = 2 × 42 + 4 = 43 μFC2 = 4 × 84 + 8 = 83 μFC3 = 4 × 84 + 8 = 83 мкФК4 = 2 × 42 + 4 = 43 мкФ
∴ Эквивалентная емкость
= 43 + 83 + 83 + 43 = 8 мкФ
Стр. № 167:
Ответ:
Конденсаторы 5 и 1 включены последовательно.
Их эквивалентная емкость, Ceq = C1C5C1 + C5 = 2 × 22 + 2 = 1 мкФ
∴ C eq = 1
Теперь эта конденсаторная система параллельна конденсатору 6. Таким образом, эквивалентная емкость становится
1 + 1 = 2 мкФ
Вышеупомянутая конденсаторная система включена последовательно с конденсатором 2. Таким образом, эквивалентная емкость становится равной
Таким образом, эквивалентная емкость становится равной
2 × 22 + 2 = 1 мкФ
Вышеупомянутая конденсаторная система подключена параллельно конденсатору 7. Таким образом, эквивалентная емкость становится
1 + 1 = 2 мкФ
Вышеупомянутая конденсаторная система включена последовательно с конденсатором 3.Таким образом, эквивалентная емкость становится равной
2 × 22 + 2 = 1 мкФ
Вышеупомянутая конденсаторная система подключена параллельно конденсатору 8. Таким образом, эквивалентная емкость становится равной
1 + 1 = 2 мкФ
Вышеупомянутая конденсаторная система включена последовательно. с конденсатором 4. Таким образом, эквивалентная емкость становится равной
2 × 22 + 2 = 1 мкФ
Следовательно, эквивалентная емкость между точками A и B данной конденсаторной системы составляет 1 мкФ.
Стр. № 167:
Ответ:
Пусть эквивалентная емкость бесконечной лестницы равна C .
Поскольку это бесконечная лестница, изменение эквивалентной емкости будет незначительным, если мы добавим еще одну лестницу в точке AB, как показано на данном рисунке.
Из приведенного рисунка эквивалентную емкость можно рассчитать как:
Ceq = 2 × C2 + C + 1 = C⇒2 + CC = 3C + 2⇒2C + C2 = 3C + 2⇒C2-C- 2 = 0⇒C-2C + 1 = 0⇒C = -1 или C = 2⇒C = -1 Это невозможно. C = 2 мкФ
Стр. № 167:
Ответ:
Эквивалентная емкость лестницы между точками A, и B становится независимой от количества секций между ними, когда емкость между A и B равна C .
Конденсаторы C, и 4 мкФ включены последовательно; их эквивалентная емкость равна
C1 = C × 4C + 4
Конденсаторы C 1 и 2 мкФ включены параллельно; их эквивалентная емкость определяется выражением
C = C 1 + 2 мкФ
⇒C = C × 4C + 4 + 2
⇒4 C + 8 + 2 C = 4 C + C 2
⇒ C 2 -2 C -8 = 0
⇒ C = −2, C = 4
Емкость не может быть отрицательной.
∴ C = 4 мкФ
Значение C составляет 4 мкФ.
Стр. № 167:
Ответ:
Заряд на положительной пластине составляет q 1 , а на отрицательной пластине — q 2 .
Дано:
q1 = 2,0 × 10-8 Cq2 = -1,0 × 10-8 C
Итак,
Чистый заряд конденсатора = q1-q22 = 1,5 × 10-8 C
Разность потенциалов между пластинами дается формулой
q = VC⇒V = 1.5 × 10-81,2 × 10-9 = 12,5 В
Стр. № 168:
Ответ:
Дано:
Емкость изолированного конденсатора = 10 мкФ
Заряд на положительной пластине = 20 мкКл
Эффективный заряд на конденсаторе = 20-02 = 10 мкКл
Разность потенциалов между пластинами конденсатора равна
В = QC
∴ Разность потенциалов = 10 мкКл 10 мкФ = 1 В
Стр. № 168:
Ответ:
Заряды на пластинах:
q1 = 1 мкКл = 1 × 10-6 Кл q2 = 2 мкКл = 2 × 10-6 Кл
Эффективный заряд конденсатора определяется как
qnet = q2-q12 = (2- 1) × 10-62 = 0. 5 × 10-6 C
5 × 10-6 C
Разность потенциалов определяется как
V = qnetC = 0,5 × 10-6 0,1 × 10-6 = 5 В
Стр. № 168:
Ответ:
Здесь сформированы три конденсатора, каждый из которых имеет площадь А.
Итак,
A = 96∈0 × 10-12 Ф-мд = 4 мм = 3 × 10-3 м
Емкость конденсаторов определяется как
C = ∈0Ad = ∈096 / ∈0 × 10-124 × 10-3 = 24 × 10-9 F
Поскольку три конденсатора расположены последовательно, эквивалентная емкость определяется как
Ceq = 24 × 10-93 = 8 × 10-9 F
Общий заряд конденсатора равен
Q = C экв. V
⇒Q = 8 × 10-9 × 10⇒Q = 8 × 10-8 C
Заряд одной пластины равен
QP = 2 × 8 × 10-8⇒QP = 16 × 10-8 = 0.16 мкКл
Стр. № 168:
Ответ:
(a) Когда на пластину B вводится заряд 1 мкКл, заряд равномерно распределяется по ее поверхности. На все стороны пластины поступает заряд 0,5 мкКл. Из-за индукции на верхней поверхности пластины A индуцируется заряд 0,5 мкКл.
На все стороны пластины поступает заряд 0,5 мкКл. Из-за индукции на верхней поверхности пластины A индуцируется заряд 0,5 мкКл.
(b) Дано:
Емкость, C = 50 нФ = 50 × 10 -9 F = 5 × 10 -8 F
Эффективный заряд конденсатора, Qnet = 1 мкКл-02 = 0.5 мкКл
∴ Разница потенциалов между пластинами B и A, V = QnetC = 5 × 10-75 × 10-8 = 10 В
Стр. № 168:
Ответ:
Когда на верхнюю пластину подается заряд 1 мкКл, заряд распределяется. Две стороны верхней пластины имеют заряд +0,5 мкКл. Одна сторона средней пластины, обращенная к верхней, имеет заряд -0,5 мкКл, а другая сторона — +0,5 мкКл. Точно так же одна сторона нижней пластины, обращенная к средней пластине, имеет -0.Заряд 5 мкКл, а на другой стороне — заряд +0,5 мкКл.
(a) Эффективный заряд конденсатора, образованного верхней и средней пластинами = 0,5 мкКл
Емкость = 50 нФ = 0,05 мкФ
∴ Разница потенциалов между пластинами, V = QC = 0,5 мкКл 0,05 мкФ = 10 В
(b) Эффективный заряд конденсатора, образованного средней и нижней пластинами = 0,5 мкКл
Емкость = 0,50 мкФ
∴ Разность потенциалов между пластинами, V = QC = 0,5 мкКл 0,05 мкФ = 10 В
Стр.
 № 168:
№ 168:Ответ:
Дано:
C1 = 20.0 pFC2 = 50,0 пФ
Когда конденсаторы соединены последовательно, их эквивалентная емкость определяется как
Ceq = C1C2C1 + C2
∴ Эквивалентная емкость, Ceq = (50 × 10-12) × (20 × 10-12) ( 50 × 10-12) + (20 × 10-12) = 1,428 × 10-11 F
(a) Заряд на обоих конденсаторах одинаков, поскольку они соединены последовательно. Он определяется как
q = Ceq × V⇒q = (1,428 × 10-11) × 6,0 CNow, V1 = qC1 = (1,428 × 10-11) × 6,0 C (20 × 10-12) ⇒V1 = 4,29. V и V2 = 6,00-4,29 В = 1,71 В
(b) Энергии в конденсаторах определены как
E1 = q22C1 = (1.428 × 10-11) × 6,02 × 12 × 20 × 10-12 = 184 pJandE2 = q22C1 = (1,428 × 10-11) × 6,02 × 12 × 50 × 10-12 = 73,5 пДж
Стр. № 168:
Ответ:
Дано:
C1 = 4 мкФ C2 = 6 мкФ V = 20 В
Итак,
Эквивалентная емкость определяется как
Ceq = C1C2C1 + C2 = 4 × 64 + 6 = 2,4 мкФ
Энергия, вырабатываемая батареей, равна дается формулой
E = CeqV2 = 2,4 мкФ × 202 = 2,4 мкФ × 400 = 960 мкДж
Стр.
 № 168:
№ 168:Ответ:
Конденсаторы б и в включены параллельно; их эквивалентная емкость составляет 20 мкФ.
Таким образом, чистая емкость цепи равна
1Cnet = 110 + 120 + 110⇒1Cnet = 2 + 1 + 220 = 520⇒Cnet = 4 мкФ
Общий заряд батареи равен
Q = CnetV = (4 мкФ) × (100 В) = 4 × 10-4 C
Для a и d ,
q = 4 × 10-4 C и C = 10-5 F∴E = q22C = 4 × 10-42 × 10-5⇒E = 8 × 10-3 Дж = 8 мДж
Для b и c ,
q = 4 × 10-4 C и Ceq = 2C = 2 × 10 -5 F∴V = q Ceq4 × 10-42 × 10-5 = 20 V⇒E = 12 CV2⇒E = 12 × 10-5 × 400⇒E = 2 × 10-3 Дж = 2 мДж
Стр. № 168:
Ответ:
Дано:
Энергия, запасенная в заряженном конденсаторе, = 4.0 J
Когда конденсаторы подключены, заряд перетекает от заряженного конденсатора к незаряженному. Поскольку конденсаторы идентичны, заряд течет до тех пор, пока заряд в обоих конденсаторах не станет одинаковым.
Энергия конденсатора определяется как
E = q22C
Поскольку заряд в обоих конденсаторах одинаков, их емкость также одинакова. Итак, энергия распределяется между ними поровну.
Таким образом, энергия, запасенная в каждом из конденсаторов, составляет 2,0 Дж.
Стр. № 168:
Ответ:
Заряд конденсатора 2 мкФ, когда он не подключен к конденсатору 4 мкФ, равен
q = C × V = 12 × 2 × 10-6⇒q = 24 × 10-6 C
(a) Вкл. при подключении конденсаторов заряд течет от конденсатора 2 мкФ к конденсатору 4 мкФ.
Теперь пусть заряды на конденсаторах 2 мкФ и 4 мкФ равны q 1 и q 2 соответственно.
Поскольку они соединены параллельно, разность потенциалов на них одинакова.
∴V = q1C1 = q2C2⇒V = q12 = q24⇒q2 = 2 q1
Общий заряд конденсаторов будет таким же, как начальный заряд конденсатора 2 мкФ.
∴q1 + q2 = 24 × 10-6⇒3 q1 = 24 × 10-6 C⇒q1 = 8 × 10-6 C = 8 мкКл⇒q1 = 2 q1 = 16 мкКл
(b) Энергии, хранящиеся в конденсаторы имеют вид
E1 = 12 × q12C1 = 16 мкДж и E2 = 12 × q22C2 = 32 мкДж
(c)
Начальная энергия, запасенная в конденсаторе 2 мкФ, равна
Ei = 12CV2 = 12 × 2 × 10-6122 ⇒Ei = 144 мкДж
Полная энергия конденсаторов после их параллельного включения определяется выражением
E f = E 1 + E 2
⇒ E f = 16 + 32 = 48 мкДж
Тепло, выделяемое во время переноса заряда, равно
E = E f — E i
⇒ E = 144-48 = 96 мкДж
Стр.
 № 168:
№ 168:Ответ:
Дано:
Заряд на сфере = Q
Радиус сферы = R
Емкость сферы, C = 4π∈0 R
Таким образом, энергия сферы равна
E = 12 CV2 = 12 × 4π∈0 R × Q24π ∈0 R2 = Q28π ∈0 R
Стр. № 168:
Ответ:
Потенциал внутренней металлической сферы определяется как
V = 14π ∈0qR
Емкость конденсатора, образованного двумя концентрическими сферами радиусами R и 2 R , определяется как
C = 4π∈0R × 2R2R -R⇒C = 4π∈0 × 2R
Потенциал внешней сферы определяется как
V2 = 14π ∈0q2R = V2
Электростатическая энергия, запасенная вне сферы, определяется как
E = 12CV-V22⇒E = 12 × 4π∈0 × 2R × V24⇒E = π∈0 × RV2
Стр. № 168:
Ответ:
Дано,
Плотность заряда поверхности плоскости, σ = 1. 0 × 10-4 Кл / м2
0 × 10-4 Кл / м2
Объем куба, V = a3 = 10-6 м3
Электрическое поле вблизи заряженной проводящей плоскости задается как,
E = σ∈0 … (i)
Энергия плотность электрического поля,
u = 12∈0E2⇒u = 12∈0σ∈02⇒u = 12σ2∈0⇒u = 12 × (1,0 × 10-4) 28,85 × 10-12⇒u = 0,056 × 104 Дж / m3volume = 10-6m3⇒U = u × V⇒U = 0,056 × 104 × 10-6⇒U = 5,6 × 10-4 Дж
Стр. № 168:
Ответ:
Дано:
Площадь, A = 20 см2 = 2 × 10-3 м2 Разделение, d1 = 1 мм = 10-3 м
Начальная емкость конденсатора:
C1 = ∈0 Ad1C1 = 8.88 × 10-12 × 20 × 10-41 × 10-3C1 = 1,776 × 10-11 F
Конечная емкость конденсатора:
C2 = C12, потому что d2 = d12
(a) Заряд, прошедший через цепь:
Q = C1 V-C2 VQ = C1-C2 VQ = 1,7762 × 10-11 × 12,0Q = 1,06 × 10-10 C
(b) Энергия, поглощаемая батареей:
E = QV = 1,06 × 10 -10 × 12E = 12,72 × 10-10 Дж
(c) Энергия, запасенная до процесса, E i = 12 C1 V2
⇒Ei = 12 × 1,776 × 10-11 × 122⇒Ei = 12,7 × 10-10 Дж
Энергия, накопленная после процесса, E f = 12 C2 V2
⇒Ef = 12 × 1. 7762 × 10-11 × 122⇒Ef = 6,35 × 10-10 Дж
7762 × 10-11 × 122⇒Ef = 6,35 × 10-10 Дж
(d) Выполненная работа, Вт = Сила × Расстояние
Вт = Изменение энергии
⇒ Вт = 6,35 × 10 −10 Дж
Стр. № 168:
Ответ:
(а) Перед подключением к аккумулятору на 12 В,
C = 100 мкФ и V = 24 В∴q = CV = 2400 мкФ
После подключения к аккумулятору на 12 В,
C = 100 мкФ и В = 12 В q = CV = 1200 мкКл
(b) Заряд, прошедший через батарею 12 В, составляет 1200 мкКл.
(c) Мы знаем,
W = Vq = 12 × 1200 = 14400 Дж = 14,4 мДж
Это работа, проделанная с аккумулятором.
(d) Начальная энергия электростатического поля:
Ui = 12 CV12
Конечная энергия электростатического поля:
Uf = 12 CV22
Уменьшение энергии электростатического поля:
∆U = 12 CV12-CV22 = 12 C V12-V22 = 12 = 100 242-122 = 12 × 100 × 576-144 = 21600 Дж = 21,6 мДж
(e) После повторного подключения
C = 100 мкФ и V = 12 В
Тепло, выделяемое во время потока заряда после повторного подключения, составляет дается формулой
H = 12 CV2 = 100 × 144 = 7200 Дж = 7. 2 мДж
2 мДж
Это количество энергии выделяется в виде тепла, когда заряд проходит через конденсатор.
Стр. № 168:
Ответ:
Поскольку переключатель разомкнут на долгое время, конденсатор включен последовательно.
∴ Ceq = C2
Когда переключатель замкнут, заряд от батареи равен
q = C2 × ε = Cε2
(b) Выполненная работа, Вт = q × V
⇒q = Cε2 × ε = Cε22
(c) Изменение энергии, запасенной в конденсаторах, определяется как
∆E = 12 Ceq × v2 = 12 × C2 × ε2 = 14 Cε2
(d) Тепло, выделяемое в системе дается формулой
H = ∆E⇒H = 14 Cε2
Стр. № 169:
Ответ:
Дано:
C1 = 5 мкФ и V1 = 24 В∴q1 = C1V1 = 5 × 24 = 120 мкКл, а C2 = 6 мкФ и V2 = 12 В∴q2 = C2V2 = 6 × 12 = 72 мкКл
(a)
Энергия, запасенная в первом конденсаторе:
U1 = 12 C1V12 = 1440 Дж = 1. 44 мДж
44 мДж
Энергия, запасенная во втором конденсаторе:
U2 = 12 C1 V22 = 432 Дж = 0,432 мДж
(b) Конденсаторы соединены друг с другом таким образом, что положительная пластина первого конденсатора подключена к отрицательная пластина второго конденсатора и наоборот.
∴ Чистое изменение в системе, Q net = 120 — 72 = 48
Теперь пусть V будет общим потенциалом двух конденсаторов.
Из сохранения заряда до и после подключения получаем
В = Qnet (C1 + C2) = 48 (5 + 6) = 4.36 V
Новые заряды:
q1 ‘= C1V = 5 × 4,36 = 21,8 мкCandq2’ = C2V = 6 × 4,36 = 26,2 мкC
(c)
Дано: U1 = 12 C1 V2andU2 = 12 C2 V2∴Uf = 12 V2 C1 + C2 = 12 4,362 5 + 6 = 12 × 19 × 11 = 104,5 × 10-6 Дж = 0,1045 мДж
Но Ui = 1,44 + 0,433 = 1,873 Потери энергии: ∆U = 1,873-0,1045 = 1,7678 = 1,77 мДж
(d) Энергия рассеивается в виде тепла.
Стр. № 169:
Ответ:
Поскольку конденсатор емкости C подключен к аккумулятору с напряжением В, , одна из его пластин заряжается до Q = CV , а другая — до — Q кулонов. При изменении полярности на первой пластине появляется заряд — Q , а на второй — заряд + Q . Таким образом, чтобы поддерживать эти заряды, заряд 2 Q проходит через аккумулятор от отрицательной клеммы к положительной клемме.
При изменении полярности на первой пластине появляется заряд — Q , а на второй — заряд + Q . Таким образом, чтобы поддерживать эти заряды, заряд 2 Q проходит через аккумулятор от отрицательной клеммы к положительной клемме.
Работа, выполняемая батареей, определяется выражением
W = 2QV = 2CE2
В данном процессе энергия конденсатора остается одинаковой в обоих случаях. Работа, проделанная аккумулятором, проявляется в виде тепла в соединительных проводах.
Теперь,
Выработанное тепло:
H = 2CE2H = 2 × 5 × 10-6 × 144H = 144 × 10-5 Дж = 1,44 мДж
Стр. № 169:
Ответ:
Площадь пластин конденсатора равна
A = 20 см × 20 см = 400 см2⇒A = 4 × 10-2 м
Расстояние между параллельными пластинами равно
d = 1 м = 1 × 10-3 м
Здесь толщина диэлектрика такая же, как расстояние между параллельными пластинами.
Таким образом, емкость определяется как
C = ∈0Akd = (8. 85 × 10-12) × (4 × 10-2) × 410-3 = 1,42 нФ
85 × 10-12) × (4 × 10-2) × 410-3 = 1,42 нФ
Стр. № 169:
Ответ:
Дано:
Емкость конденсатора, C = 1,42 нФ
Диэлектрическая постоянная, k = 4
Напряжение подключенной батареи, В = 6 В
(a) Заряд, обеспечиваемый аккумулятором, указан на
q = CV = 1,42 × 10-9 × 6 = 8,52 × 10-9 Кл = 8,5 нКл
(б) Заряд, индуцированный на диэлектрике, равен
q ‘= q 1-1K = 8.52 × 10-9 × 1-0,25 = 6,39 × 10-9 = 6,4 нКл
(c) Заряд, появляющийся на одной из покрытых пластин, равен
Q нетто = 8,5 — 6,4 = 2,1 нКл
Стр. № 169:
Ответ:
Дано:
Площадь пластины = 100 см 2
Расстояние между пластинами = 0,500 см = 5 × 10 -3 м
Толщина металла, т = 4 × 10 -3 м
∴C = ∈0 Ad-t + tk
Здесь
k = диэлектрическая проницаемость металла
d = расстояние между пластинами
t = толщина металла
Для металла , к = ∞.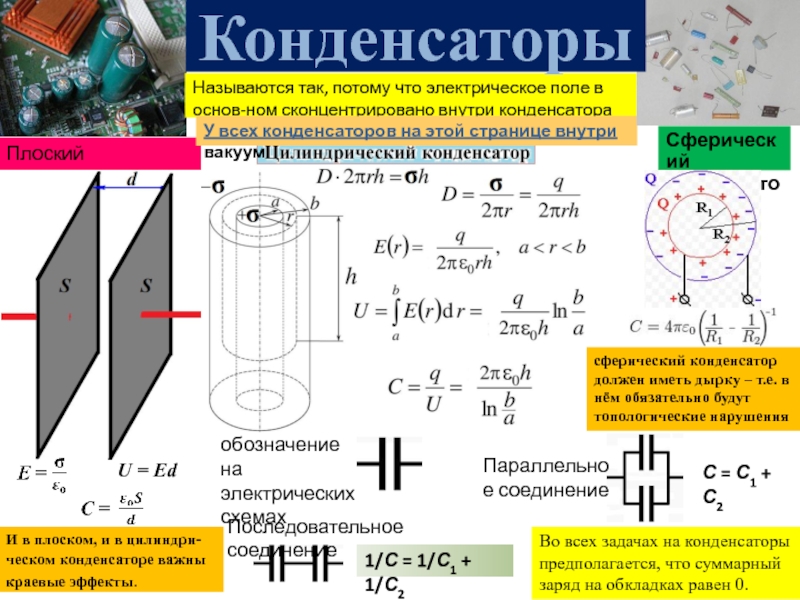
∴C = ∈0 Ad-t = (8,85 × 10-12) × 10-12 (5-4) × 10-3 = 88 пФ
Здесь емкость не зависит от положения металла. В любой позиции чистый отрыв составляет ( d — t ).
Стр. № 169:
Ответ:
Дано:
Начальный заряд конденсатора = 50 мкКл
Теперь пусть диэлектрическая проницаемость вставляемого материала равна к .
Когда через батарею протекает дополнительный заряд 100 мкКл, чистый заряд конденсатора становится
50 + 100 = 150 мкКл
Теперь
C1 = q1V = ∈0Ad… (i) C2 = q2V = ∈0Akd … (ii)
Разделив ( i ) на ( ii ), мы получим
C1C2 = q1q2 = 1k⇒50150 = 1k⇒k = 3
Таким образом, диэлектрическая проницаемость данного материала составляет 3.
.Стр. № 169:
Ответ:
Для данного конденсатора
C = 5 мкФ V = 6 Vd = 2 мм = 2 × 10-3 м
(a) Заряд на положительной пластине рассчитывается с использованием q = CV.
Таким образом,
q = 5 мкФ × 6 В = 30 мкКл
(б) Электрическое поле между пластинами конденсатора равно
E = Vd = 3 × 103 В / м
(в) Расстояние между пластинами конденсатора, d = 2 × 10 -3 м
Диэлектрическая проницаемость вставленного диэлектрика, k = 5
Толщина вставленного диэлектрика, t = 1 × 10 -3 м
Теперь
Площадь пластин конденсатора
C = ∈0 Ad⇒5 × 10-6 = 8.85 × 10-12 × A2 × 10-3⇒104 = 8,85 × A⇒A = 104 × 18,85
Когда в него помещается диэлектрик, емкость становится равной
C1 = ∈0Ad-t + tk⇒C1 = 8,85 × 10 -12 × 1048,852 × 10-3-10-3 + 10-35⇒C1 = 8,85 × 10-12 × 1048,85 · 10-3 + 10-35⇒C1 = 10-12 × 104 × 56 × 10-3 = 8,33 мкФ
(d)
Заряд, накопленный в конденсаторе, изначально определяется как
C = 5 × 10-6 FA Также, V = 6 VNow, Q = CV = 3 × 10-5 F⇒Q = 30 мкКл
Заряд на конденсатор после установки диэлектрической пластины равен
C1 = 8,3 × 10-6 F∴Q ‘= C1V = 8.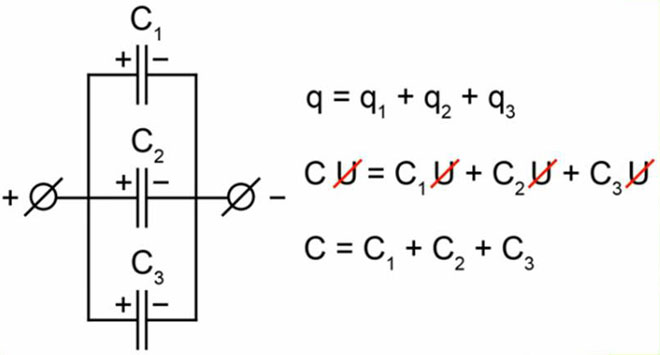 3 × 6 × 10-6⇒Q ‘= 50 мкКл Сейчас, заряд прошел, Q’-Q = 20 мкКл
3 × 6 × 10-6⇒Q ‘= 50 мкКл Сейчас, заряд прошел, Q’-Q = 20 мкКл
Стр. № 169:
Ответ:
Данная система конденсаторов будет вести себя как два последовательно соединенных конденсатора.
Пусть емкости равны C 1 и C 2 .
Теперь
C1 = ∈0Ak1d1 и C2 = ∈0Ak2d2
Таким образом, чистая емкость задается формулой
C = C1C2C1 + C2 = ∈0Ak1d1 × ∈0Ak2d2∈0Ak1d1 + ∈0Ak2d2 = ∈0Ak1 + k2k1 = 8.85 × 10-12) × (10-2) × 24 (6 × 4 × 10-3 + 4 × 6 × 10-3) = 4,425 × 10-11C = 44,25 пФ
Стр. № 169:
Ответ:
Емкость конденсатора без диэлектрической пластины определяется выражением
C1 = ∈0 Ad
⇒C = (8,85 × 10-12) × (400 × 10-4) (1,0 × 10-3) ⇒C = 3,54 × 10-10 F
Когда диэлектрическая пластина вставлена, емкость становится равной
C ‘= ∈0 Ad-t + tK⇒C’ = (8,85 × 10-12) × (400 × 10-4) 1 × 10-3-0,5 × 10-3 + 0,5 × 10-35⇒C ‘= 5 × (8./30277.gif) 85 × 10-12) × (400 × 10-4) (6 × 0,5 × 10-3) ⇒C ‘= 5,9 × 10-10 F
85 × 10-12) × (400 × 10-4) (6 × 0,5 × 10-3) ⇒C ‘= 5,9 × 10-10 F
(a) Повышенная электростатическая энергия:
∆E = 12C’ V2 -12CV2 ⇒∆E = 125,9-3,54 × 10-10 × 1002⇒∆E = 1,18 × 10-6 Дж = 1,18 мкДж
(b)
Заряд конденсатора, содержащего диэлектрик, составляет
Q ‘= C’V⇒ Q ‘= 5,9 × 10-10 × 100⇒Q’ = 5,9 × 10-8 C
Разность потенциалов на конденсаторе после извлечения батареи и затем диэлектрика составляет
В ‘= Q’C⇒V’ = 5,9 × 10- 83,54 × 10-10⇒V ‘= 166 В
Повышенная электростатическая энергия,
∆E’ = 12C V’2-12C’V2 ⇒∆E ‘= 123.54 × 10-10 × (166) 2-5,9 × 10-10 × (100) 2⇒∆E ‘= 1,92 × 10-6 Дж = 1,92 мкДж
(c) Когда аккумулятор подключен, энергия увеличивается после вставка диэлектрической пластины из-за увеличения емкости конденсатора. Теперь конденсатор будет отвлекать от батареи больше изменений.
Когда аккумулятор отсоединяется и вынимается диэлектрическая пластина, запасенная в ней энергия увеличивается из-за увеличения разности потенциалов на конденсаторе.
Стр. № 169:
Ответ:
Две части конденсатора включены последовательно с емкостями C 1 и C 2 .
Здесь
C1 = K1 ∈0 Ad2 и C2 = K2 ∈0 Ad2⇒C1 = 2K1 ∈0 Ad и C2 = 2K2 ∈0 Ad
Поскольку они включены последовательно, чистая емкость рассчитывается как:
C = C1 × C2C1 + C2 = 2K1 ∈0 Ad × 2K2 ∈0 Ad2K1 ∈0 Ad + 2K2 ∈0 Ad = 2K1 K2 ∈0 Ad K1 + K2
(b) Здесь конденсатор состоит из трех частей. Их можно снимать последовательно.
Теперь
C1 = K1 ∈0 Ad3 = 3 K1 ∈0 Ad
C2 = 3 K2 ∈0 AdC3 = 3 K3 ∈0 Ad
Таким образом, чистая емкость рассчитывается как:
C = C1 × C2 × C2C1C2 + C2C3 + C3C1 = 3K1∈0Ad × 3K2∈0Ad × 3K3∈0Ad3K1∈0Ad × 3K2∈0Ad + 3K2∈0Ad × 3K3∈0Ad + 3K3∈0Ad × 3K1∈0Ad = 3 ∈0 K1K2K3d + (K1 K2K3 + K3K1)
(c)
Здесь
C1 = K1 ∈0 A / 2d = K1 ∈0 A2dC2 = K2 ∈0 A2d
Эти две части параллельны.
∴C = C1 + C2 = ∈0 A2dK1 + K2
Стр. № 169:
Ответ:
Рассмотрим элементарный конденсатор шириной dx на расстоянии x от левого конца конденсатора. Он имеет два емкостных элемента диэлектрической проницаемости K 1 и K 2 с разделением пластин ( x tan θ ) и ( d — x tan θ ) последовательно , соответственно.Площади пластин конденсаторов adx .
Емкости емкостных элементов элементарного конденсатора равны:
dC1 = ∈0K2 (adx) x tan θ, dC2 = ∈0K1 (adx) dx tan θ
Полезная емкость элементарного конденсатора равна
1dC = 1dC1 + 1dC21dC = x tan θ∈0K2 (adx) + dx tan θ∈0K1 (adx) ⇒dC = ∈0K1K2 (adx) K1xtan θ + K2 (dx tan θ)
Таким образом, интегрируя приведенное выше выражение для вычисления чистая емкость
C = ∫0adC = ∫0a∈0K1K2adxK1x tan θ + K2 (dx tan θ) C = ∈0K1K2a∫0adx K2d + x tan θ (K1-K2) ⇒C = ∈0K1K2atan θ (K1-K2) loge [K2d + x tan θ (K1-K2)] 0a⇒C = ∈0K1K2atan θ (K1-K2) loge [K2d + atan θ (K1-K2)] — logeK2d
Как мы знаем, tan θ = da подставляя в выражение для емкости C .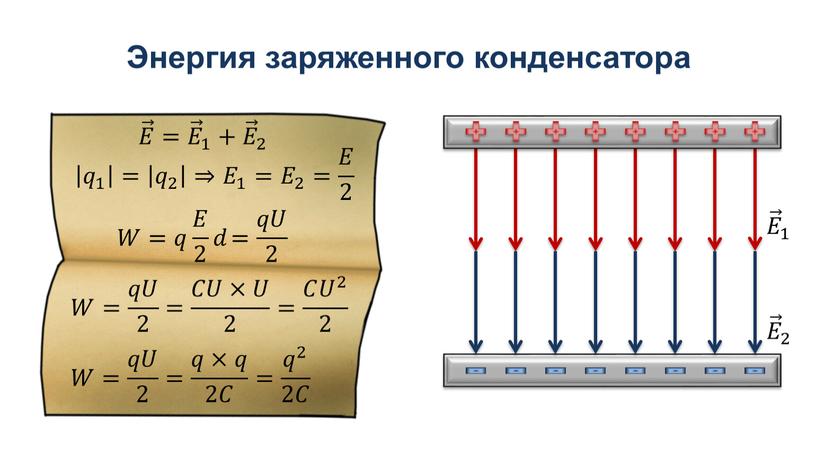
Теперь
⇒C = ∈0K1K2ada × (K1-K2) loge [K2d + a × da (K1-K2)] — logeK2d ⇒C = ∈0K1K2ada × (K1-K2) loge K1d-logeK2d ⇒C = ∈0K1K2a2d (К1-К2) лоджия К1К2
Стр. № 169:
Ответ:
Когда переключатель замкнут, оба конденсатора включены параллельно.
⇒ Полная энергия конденсатора, когда переключатель замкнут, определяется как
E i = 12 CV2 + 12 CV2 = CV2
Когда переключатель разомкнут и диэлектрик индуцируется, емкость конденсатора A становится
C ‘= KC = 3C
Энергия, запасенная в конденсаторе A, определяется как
EA = 12C’V2⇒EA = 12 3CV2 = 32 CV2
Энергия в конденсаторе B определяется как
EB = 12 × C3 × V2
∴ Общая конечная энергия
Ef = EA + EB⇒Ef = 32 CV2 + 16 CV2⇒Ef = 9 CV2 + 1CV26 = 106 CV2
Итак,
Отношение энергий, E1E2 = CV2106 CV2 = 35
Стр. № 169:
Ответ:
Начальная емкость, C = ∈0 Ad
Энергия конденсатора до введения диэлектрика равна
E1 = 12 CV2 = 12∈0AdV2
После вставки диэлектрической пластины емкость становится равной
C1 = KC = K ∈0 Ad
, и конечное напряжение становится
V1 = VK
Таким образом, конечная энергия, запасенная в конденсаторе, определяется как
E2 = 12K∈0 Ad × VK2⇒E2 = 12∈0 AV2Kd
Now,
Выполненная работа = Изменение энергии
∴ W = E 2 — E 1
⇒W = 12∈0 AV2Kd-12∈0 AV2d⇒W = 12∈0 AV2d 1K-1
Стр. № 169:
Ответ:
(a) Величину заряда можно рассчитать как:
Заряд = Емкость × Разность потенциалов
⇒Q = 100 × 10-6 × 50 = 5 мКл
(b) Когда вводится диэлектрик, разность потенциалов уменьшается.
Мы знаем,
В = начальный потенциал Диэлектрическая постоянная⇒V = 502,5 = 20 В
(c) Теперь заряд емкости можно рассчитать как:
Заряд = емкость × разность потенциалов
⇒qf = 20 × 100 × 10-6 = 2 мКл
(г) Заряд, индуцированный на диэлектрике, можно рассчитать как:
q = qi1-1K = 5 мКл1-12,5 = 3 мКл
Стр. № 169:
Ответ:
У нас есть два конденсатора: один из оболочек a и c, а другой из оболочек b и c.
Емкость конденсатора C ac определяется как
Cac = 4π∈0acK (ca)
Емкость конденсатора C cb определяется как
Ccb = 4π∈0bcKK (bc)
Два конденсатора включены последовательно; таким образом, эквивалентная емкость равна
1C = 1Cac + 1Ccb⇒1C = (ca) 4π∈0acK + (bc) 4π∈0cb⇒1C = b (ca) + Ka (bc) K4π∈0abc⇒C = K4π∈0abcb (ca) + Ka (до н.э.)
Стр. № 170:
Ответ:
Сферические оболочки образуют два сферических конденсатора: один сделан A и B, а другой — B и C.
Емкость сферического конденсатора, образованного оболочками радиусом r 1 и r 2 , определяется как
C = 4π∈01r1-1r2 = 4π∈0r1r2r2-r1
Емкость конденсатор, созданный A и B, равен
CAB = 4π∈0abb-a
Емкость конденсатора, созданного B и C, определяется как
CBC = 4π∈0bcc-b
Поскольку конденсаторы находятся в серии, чистая емкость равна
1C = 1CAB + 1CBC⇒C = CABCBCCAB + CBC = (4π∈0) 2ab2c (ba) (cb) 4π∈0ab (ba) + 4π∈0bc (cb) ⇒C = 4π∈0ab2c (ba) (cb) ab (cb) + bc (ba) (ba) (cb) ⇒C = 4π∈0ab2c [ab (cb) + bc (ba)] ⇒C = 4π∈0ab2cb2 (ca) = 4π∈0ac (ок)
Стр. № 170:
Ответ:
Поскольку пространство между двумя внутренними оболочками заполнено диэлектриком, емкость C AB становится CAB = 4π∈0abK (b-a), а емкость C BC становится CBC = 4π∈0bc (c-b).
Теперь, когда конденсаторы включены последовательно, эквивалентная емкость определяется как
1C = 1CAB + 1CBC⇒C = CABCBCCAB + CBC⇒C = (4π∈0) 2ab2Kc (ba) (cb) 4π∈0abk (ba) + 4π∈0bc (cb) ⇒C = 4π∈0Kab2c (ba) (cb) abk (cb) + bc (ba) (ba) (cb) ⇒C = 4π∈0Kab2c [abk (cb) + bc (ba) ] ⇒C = 4π∈0Kabc [ak (cb) + c (ba)]
Стр. № 170:
Ответ:
Заряд, который может удерживать конденсатор = 12 мкКл
Рабочее напряжение = 1200 В
Прочность пробоя, b = 3 × 106 В м-1
Расстояние между пластинами конденсатора равно
d = Vb = 12003 × 106 = 4 × 10-4 м
Емкость конденсатора определяется как
C = QV = 12 × 10-61200 = 10-8 F
Емкость может быть выражена через площадь пластин ( A ) и разделение пластин ( d ) как:
C = ∈0Ad = 10-8 F
Таким образом, площадь пластин определяется как
A = 10-8 × (4 × 10-4) 8 .854 × 10-12 = 0,45 м2
Стр. № 170:
Ответ:
Площадь пластин конденсатора, A = 100 см 2 = 10 -2 м 2
Расстояние между пластинами, d = 1 см = 10 -2 м
ЭДС батарея, В = 24 В
Следовательно,
Емкость, C = ∈0Ad = (8,85 × 10-12) × (10-2) 10-2 = 8,85 × 10-12 В
Энергия, запасенная в конденсаторе , E = 12CV2 = 12 × (8.85 × 10-12) × (24) 2 = 2548,8 × 10-12 Дж
Сила притяжения между пластинами, F = Ed = 2548,8 × 10-1210-2 = 2548,8 × 10-10 Н
Стр. № 170:
Ответ:
Пусть потенциал батареи, подключенной к конденсатору, равен В .
Пусть длина части плиты внутри конденсатора будет x .
Конденсатор можно рассматривать как два конденсатора, включенных параллельно.
Емкости двух конденсаторов, включенных параллельно:
C1 = K1∈0bxd, C2 = ∈0b (l1-x) d
C 1 — часть конденсатора, в которую вставлен диэлектрик, и C 2 — емкость части конденсатора без диэлектрика.
As, C 1 и C 2 параллельно.
Следовательно, чистая емкость определяется как
C = C 1 + C 2
C = K1∈0bxd + ∈0b (l1-x) dC = ∈0bdl1 + x (K1-1)
Диэлектрическая пластина притягивается электрическим полем конденсатора и прикладывает силу в левом направлении.
Рассмотрим электрическую силу величиной F , тянущую плиту влево.
Пусть имеется бесконечно малое смещение dx влево на силу F .
Работа, совершаемая силой = F . dx
Пусть потенциал батареи, подключенной к левому конденсатору, равен В 1 , а потенциал батареи, подключенной к правому конденсатору, равен В 2 .
При смещении плиты увеличивается емкость, следовательно, увеличивается и энергия конденсатора. Чтобы поддерживать постоянное напряжение, аккумулятор будет подзаряжаться, поэтому аккумулятор будет работать.
Работа, выполняемая батареей = изменение энергии конденсатора + работа, выполняемая силой F на конденсаторе
dW B = dU + dW F
Пусть заряд d q питается от батареи, и изменение конденсатора будет dC
dW B = ( dq ) . V = ( dC ) .V 2
dU = 12 ( dC ) .V 2
( dC ) .V 2 = 12 ( dC ) .V 2 + F . dx
12 ( dC ) .V 2 = F.dx
⇒F = 12dCdxV12⇒F = 12ddx∈0bdl1 + x (K1-1) V12⇒F = ∈0bV12 (K1 -1) 2d
Чтобы удерживать диэлектрическую пластину в равновесии, электростатической силе, действующей на нее, должен противодействовать вес прикрепленного к ней блока.
Следовательно,
∈0bV22dK-1 = Mg⇒M = ∈0bV22dgK-1
Стр. № 170:
Ответ:
Пусть потенциал батареи, подключенной к левому конденсатору, равен В 1 , а потенциал батареи, подключенной к правому конденсатору, равен В 2 .
Учитывая левый конденсатор,
Пусть длина части пластины внутри конденсатора составляет x .
Левый конденсатор можно рассматривать как два конденсатора, включенных параллельно.
Емкости двух конденсаторов, включенных параллельно:
C1 = K1∈0bxd, C2 = ∈0b (l1-x) d
C 1 — часть конденсатора, в которую вставлен диэлектрик, и C 2 — емкость части конденсатора без диэлектрика.
As, C 1 и C 2 параллельно.
Следовательно, чистая емкость определяется как
C = C 1 + C 2
C = K1∈0bxd + ∈0b (l1-x) dC = ∈0bdl1 + x (K1-1)
Следовательно, потенциальная энергия, запасенная в левом конденсаторе, будет
U = 12CV12U = ∈0bV122dl1 + x (K1-1)… (1)
Диэлектрическая пластина притягивается электрическим полем конденсатора и прикладывает силу в левом направлении.
Рассмотрим электрическую силу величиной F , тянущую плиту влево.
Пусть имеется бесконечно малое смещение d x влево на силу F .
Работа, совершаемая силой = F .d x
Рассмотрим небольшое смещение dx плиты во внутреннем направлении.Емкость увеличится, следовательно, возрастет и энергия конденсатора. Чтобы поддерживать постоянное напряжение, аккумулятор будет подзаряжаться, поэтому аккумулятор будет работать.
Работа, выполняемая батареей = изменение энергии конденсатора + работа, выполняемая силой F на конденсаторе
dW B = dU + dW F
Пусть заряд d q питается от батареи, и изменение конденсатора будет d C
dW B = ( dq ) . V = ( dC ) .V 2
dU = 12 ( dC ) .V 2
( dC ) .V 2 = 12 ( dC ) .V 2 + F . dx
12 ( dC ) .V 2 = F.dx
⇒F = 12dCdxV12⇒F = 12ddx∈0bdl1 + x (K1-1) V12⇒F = ∈0bV12 (K1- 1) 2d⇒V12 = F × 2d∈0b (K1-1) ⇒V1 = F × 2d∈0b (K1-1)
Аналогично, для правой стороны напряжение батареи равно
V2 = F × 2d∈0b (K2-1)
Таким образом, соотношение напряжений равно
V1V2 = F × 2d∈0b (K1-1) F × 2d∈0b (K2-1) ⇒V1V2 = K2-1K1- 1
Таким образом, отношение ЭДС левой батареи к правой батарее V1V2 = K2-1K1-1
Стр. № 170:
Ответ:
Учитывая, что площадь пластин конденсаторов составляет А .
Как «» диэлектрическая плита длиной дюймов находится внутри конденсатора.
Следовательно, площадь пластины, покрытой диэлектриком, равна = Ala
. Емкость участка с диэлектриком определяется как
C1 = K∈0Aald
. Емкость участка без диэлектрика определяется как
C1 = ∈0A (la) ld
Две части можно рассматривать как параллельные.
Следовательно, чистая емкость определяется выражением
C = C1 + C2⇒C = ∈0AldKa + (la) ⇒C = ∈0Aldl + a (K-1)
. Рассмотрим небольшое смещение da плиты в внутреннее направление.Емкость увеличится, следовательно, возрастет и энергия конденсатора. Чтобы поддерживать постоянное напряжение, аккумулятор будет подзаряжаться, поэтому аккумулятор будет работать.
Работа, выполняемая аккумулятором = изменение энергии конденсатора + работа, выполняемая силой F на конденсаторе
dW B = dU + dW F
Пусть заряд dq питается от батареи, и изменение конденсатора будет dC
dW B = ( dq ) . V = ( dC ) .V 2
dU = 12 ( dC ) .V 2
(d C ) .V 2 = 12 (d C ) .V 2 + F .d a
12 (d C ) .V 2 = F .d a
⇒ F = 12dCdaV2⇒F = 12dda∈0Aldl + a (K-1) V2⇒F = 12∈0Ald (K-1)
Ускорение диэлектрика определяется как a 0 = 12∈0Aldm (K- 1)
Поскольку сила направлена внутрь, она будет стремиться заставить диэлектрик полностью заполнить пространство внутри конденсаторов.Поскольку диэлектрик полностью заполняет пространство внутри конденсатора, в этот момент его скорость не равна нулю. Диэлектрическая пластина имеет тенденцию выходить за пределы конденсатора. По мере того, как плита имеет тенденцию выдвигаться, направление силы, создаваемой конденсатором, изменит свое направление на противоположное. Таким образом, диэлектрическая плита будет совершать периодическое движение.
Время, необходимое для перемещения на расстояние ( la ), можно рассчитать как:
(la) = 12a0t2t = 2l-aa0t = 2l-a × 2ldm∈0AV2 (K-1) t = 4ml-ald∈0AV2 ( K-1)
Для полного цикла период времени будет в четыре раза больше времени, необходимого для преодоления дистанции ( la ).
Он задается по формуле:
T = 4t = 4 × 2ml-ald∈0AV2 (K-1) = 8ml-ald∈0AV2 (K-1)
Просмотреть решения NCERT для всех глав класса 12
Часть 7: Емкость и конденсаторы
7.1 Электрический заряд и электрические поля
Рассмотрим пару плоских проводящих пластин, расположенных параллельно друг другу (как на рисунке 7.1) и разделенных изолятором, который может быть просто воздухом. Каждая пластина, как электрический проводник, будет содержать большое количество подвижных отрицательно заряженных электронов.Если пластины подключены к источнику постоянного тока, отрицательные электроны будут притягиваться от верхней пластины к положительному полюсу источника питания, но для каждого электрона, который это делает, другой должен покинуть отрицательный полюс источника питания и перейти к нижней пластине. Верхняя пластина станет положительно заряженной из-за нехватки электронов, тогда как избыток электронов на нижней пластине даст ей отрицательный заряд. Разница в полярности заряда между пластинами означает, что между ними существует разность потенциалов (PD), и поток электронов исчезает и прекращается, когда PD между пластинами совпадает с напряжением питания.Как только это произошло, источник питания больше не может поставлять достаточно энергии для удаления электронов с верхней пластины или проталкивания электронов на нижнюю пластину, и пластины называют «заряженными».
Рисунок 7.1: Система заряженных пластин
Между двумя заряженными пластинами существует электрическое поле. Подобно магнитному полю, электрическое поле нельзя увидеть, но его можно описать в терминах движущейся через него заряженной частицы. Также, как и магнитные поля, электрические поля представляются как линий электрического потока .
Рисунок 7.2: Электрическое поле между двумя заряженными пластинами.
Если пластины отсоединить от источника питания и соединить вместе через резистор, электроны потекут с отрицательно заряженной пластины на положительно заряженную пластину. Этот ток исчезнет, поскольку заряды на пластинах уменьшатся. По мере прохождения тока он выделяется в виде тепла, поэтому видно, что энергия накапливается в заряженном конденсаторе.
Заряд, накопленный в электрическом поле, можно измерить в кулонах (Кл), то есть ток, протекающий для зарядки пластин, умноженный на время, в течение которого происходит течение.Однако следует отметить, что при постоянном напряжении питания ток будет уменьшаться по мере увеличения заряда на пластинах, так что пластины не заряжаются постоянным током. На практике общий заряд, который может накапливаться параллельными пластинами, зависит от площади пластины, расстояния между пластинами, частичного разряда между ними и природы изоляционного материала, который их разделяет.
7,2 Емкость
Для любой системы параллельных пластин отношение количества накопленного заряда к частичному разряду между пластинами является постоянным.Эта постоянная называется емкостью (C), а система накопительных пластин называется конденсатором (иногда ошибочно называемым конденсатором ). Условное обозначение цепи конденсатора показано на рисунке 7.3.
Рисунок 7.3: Условное обозначение цепи конденсатора.
Единицей измерения емкости является фарад (Ф) и:
где:
C = емкость (F)
Q = накопленный заряд в емкости (C)
U = частичные разряды между пластинами конденсатора (В)
Так как в Части 1 мы отметили, что Q = I t, мы можем сказать, что:
где:
I = средний зарядный ток конденсатора (C)
t = время, в течение которого проходит зарядный ток (с)
Конденсатор имеет емкость в одну фараду, если он может хранить один кулон, когда частичный разряд между его пластинами составляет один вольт.Однако, поскольку на практике один фарад оказывается довольно большим значением емкости, большинство емкостей указывается в микрофарадах (мкФ), что равно 1 × 10 -6 F.
Обратите внимание, что если к конденсатору подключено постоянное напряжение, конденсатор будет заряжаться до тех пор, пока частичный разряд на нем не станет таким же, как напряжение питания. Он будет оставаться заряженным до тех пор, пока не будет обеспечен путь для прохождения тока между пластинами. Однако, если конденсатор подключен к источнику переменного тока, где направление тока постоянно меняется, он будет постоянно заряжаться и разряжаться.
7.3 Пробой диэлектрика и диэлектрическая проницаемость
Изоляционный материал, который занимает пространство между пластинами конденсатора, называется диэлектриком . Изоляционные материалы обычно не проводят электричество, потому что в них нет свободных электронов, которые могли бы течь как ток. Однако, если изоляторы подвергаются достаточно сильному электрическому полю, электроны могут вырываться, а изолирующие свойства теряются в процессе, называемом пробой диэлектрика .Это явление может быть очень серьезным при нарушении изоляции кабеля.
Напряженность электрического поля может быть выражена через частичные разряды, приложенные к изолятору определенной толщины, это значение называется средним градиентом потенциала и обычно измеряется в киловольтах на миллиметр (кВ / мм). Градиент потенциала, при котором изолятор выходит из строя, называется его диэлектрической прочностью , и его можно использовать как меру того, насколько хорош изолятор. В таблице 7.1 указана электрическая прочность нескольких изоляторов.
Пример
Бумажный пропитанный конденсатор силового конденсатора с параллельными пластинами имеет толщину 0,5 мм и электрическую прочность 5 кВ / мм. Если соответствующий конденсатор имеет приложенное частичное напряжение 1,8 кВ, каков средний градиент потенциала в бумаге? При каком приложенном напряжении можно ожидать выхода конденсатора из строя?
| Материал | Диэлектрическая прочность (кВ / мм) | Приложения |
|---|---|---|
| Воздух | 3 | Общие |
| Бакелит | 20-25 | Вилки, оборудование и т. Д. |
| Битум | 14 | Коробки кабельно-уплотнительные |
| Стекло | 50–120 | Изоляторы ВЛ |
| Слюда | 40–150 | Коммутаторы, горячие элементы, конденсаторы |
| Миканит | 30 | Станки |
| Пропитанная бумага | 4-10 | Кабели силовые, конденсаторы |
| Парафиновый воск | 8 | конденсаторы |
| Фарфор | 9-10 | Держатели предохранителей, изоляторы ВЛ |
Диэлектрические материалы также можно охарактеризовать с точки зрения их относительной диэлектрической проницаемости (ε r ).Абсолютная диэлектрическая проницаемость материала определяется как отношение заряда на единицу площади на поверхности этого материала к напряженности создаваемого электрического поля. Относительная диэлектрическая проницаемость определяется как отношение емкости конденсатора с рассматриваемым материалом между пластинами к емкости того же конденсатора с вакуумом между пластинами. Это отношение также равно диэлектрической проницаемости диэлектрика диэлектрической проницаемости свободного пространства (т.е.е. вакуум). Таким образом:
где:
ε r = относительная диэлектрическая проницаемость диэлектрического материала, без единиц
C = емкость конденсатора с рассматриваемым материалом (F)
C 0 = емкость того же конденсатора с вакуумом между пластина (F)
ε = абсолютная диэлектрическая проницаемость материала (Ф / м)
ε 0 = диэлектрическая проницаемость свободного пространства (Ф / м)
Обратите внимание, что диэлектрическая проницаемость свободного пространства является постоянной, равной 8,85 × 10 -12 Ф / м (или C 2 / Нм 2 ), и что по определению относительная диэлектрическая проницаемость вакуума равна 1.Также обратите внимание, что диэлектрическая проницаемость (ε) очень похожа по концепции и названию на проницаемость (μ) магнитных материалов, однако их не следует путать. Таблица 7.2 содержит относительную проницаемость некоторых распространенных диэлектрических материалов.
| Диэлектрический материал | Относительная диэлектрическая проницаемость (ε r ) |
|---|---|
| Воздух | 1 |
| Бакелит | 4.5-5,5 |
| Стекло | 5-10 |
| Микра | 3-7 |
| Пропитанная бумага | 2 |
| полистирол | 2,5 |
| Фарфор | 6-7 |
7,4 Конденсаторы параллельно и последовательно
Рассмотрим три конденсатора, подключенных параллельно, как показано на рисунке 7.4, у каждого из них будет одинаковое напряжение (В), а общий заряд (Q T ) будет суммой отдельных зарядов.Следовательно:
Рисунок 7.4: Три конденсатора параллельно.
Но Q = CV, и если C T — эквивалентная емкость трех конденсаторов:
Следовательно:
Теперь рассмотрим три последовательно соединенных конденсатора, как показано на рисунке 7.5. Напряжение питания распределяется между тремя конденсаторами, и, поскольку через каждый конденсатор будет протекать один и тот же зарядный ток, каждый из них получит одинаковый заряд за одно и то же время. Таким образом:
Рисунок 7.5: Три конденсатора последовательно.
Но U = Q / C, поэтому, если C T — эквивалентное значение трех последовательно соединенных конденсаторов:
Следовательно:
Пример
Рассчитайте эквивалентную емкость конденсаторов 5 мкФ, 10 мкФ и 30 мкФ, соединенных последовательно.
Эти конденсаторы подключены к источнику питания 240 В постоянного тока. Рассчитайте заряд каждого конденсатора и разность потенциалов на каждом из них.
Общий накопленный заряд:
Поскольку конденсаторы соединены последовательно, заряд каждого из них равен общему заряду, т.е.е. 720 мкКл.
Части разряда через конденсатор 5 мкФ:
Частичные разряды через конденсатор 10 мкФ:
ЧР через конденсатор 30 мкФ:
Чек: 144 + 72 + 24 = 240В
Обратите внимание, что конденсатор с наименьшим значением имеет наибольшее напряжение на нем, и если конденсаторы имеют аналогичную конструкцию, все они должны быть рассчитаны на максимальное напряжение. По этой причине конденсаторы не часто подключают последовательно, если они не идентичны.
7,5 Емкость параллельного конденсатора
Емкость конденсатора с параллельными пластинами зависит от:
- Площадь пластины (A в м 2 ), так что C α A
- Расстояние между пластинами (d в м 2 ), так что C α 1/ d
- Абсолютная диэлектрическая проницаемость диэлектрика (ε в Ф / м), так что C α ε
- Количество пластин (N), конденсаторы могут быть собраны из ряда соединенных пластин (рисунок 7.6), так что C α (N-1).
Объединение вышеперечисленных факторов дает:
На самом деле используется абсолютная диэлектрическая проницаемость диэлектрика, и поскольку ε = ε r ε 0 , уравнение принимает следующий вид:
Рисунок 7.6: Конденсатор с чередующимися пластинами, содержащий 11 обкладок, дефектно 10 конденсаторов, включенных параллельно.
7,6 Энергия, накопленная в конденсаторе
Подобно индукторам, которые накапливают энергию в магнитном поле, конденсаторы накапливают энергию в электрическом поле.Однако, в отличие от катушек индуктивности, конденсаторы могут сохранять энергию, накопленную после отключения питания, хотя со временем она рассеивается. Энергия, запасенная в конденсаторе, может быть выражена как:
Количество энергии, хранящейся в большинстве конденсаторов, невелико, тем не менее, этого достаточно, чтобы вызвать у человека электрошок. Хотя заряд и, следовательно, энергия со временем улетучатся, разрядный резистор обычно подключается к клеммам конденсатора. Такой резистор должен иметь достаточно высокое значение, чтобы предотвратить протекание через него заметных токов от источника заряда, но достаточно низкое, чтобы разрядить конденсатор за разумное время.Типичное значение — 10 МОм.
7.7 Кривые роста и спада
Как упоминалось в разделе 7.1, ток зарядки двух параллельных пластин не является постоянным, а затухает по мере нарастания заряда и увеличения частичных разрядов на выводах конденсаторов. Рассмотрим схему на рис. 7.7, где конденсатор подключен последовательно с резистором к источнику постоянного тока с ЭДС E вольт. Мгновенные частичные разряды на конденсаторе (то есть частичные разряды в любой момент времени, t ) обозначаются как v , мгновенный ток, протекающий через конденсатор, составляет i , а мгновенный заряд на конденсаторе составляет q .
Рисунок 7.7: Цепь заряда и разряда конденсатора.
Если конденсатор изначально не заряжен, когда переключатель находится в положении 1, начальный ток (I 0 ) будет равен I 0 = V / R. По мере накопления заряда на конденсаторе также увеличивается и PD ( v ) на его пластинах. Это напряжение противодействует заряду, протекающему к конденсатору, и эффективное напряжение цепи становится V- v , а мгновенный ток будет меньше начального.Таким образом:
Следовательно, ток, который изначально был большим, спадает по мере зарядки, в то время как напряжение на конденсаторе и заряд на конденсаторе возрастают (рисунок 7.8). Когда конденсатор полностью заряжен, v = E и q = Q, где Q — максимальный заряд конденсатора (Q = CV).
При переводе переключателя в положение 2 конденсатор разрядится. Первоначально v = E и I 0 = E / R, однако по мере продолжения разрядки v уменьшается и i = v / R.И напряжение, и ток падают по аналогичной кривой, и при этом заряд, удерживаемый конденсатором, также уменьшается (рисунок 7.9).
Рисунок 7.8: Кривая зарядки конденсатора.
Рисунок 7.9: Кривая разрядки конденсатора.
Время, необходимое для зарядки и разрядки, зависит от постоянной времени (τ) цепи, которая определяется как:
, и конденсатор обычно разряжается за 5 постоянных времени. Уравнения для зарядки и разрядки конденсаторов очень похожи на уравнения для кривых роста и спада для катушек индуктивности.Они включены сюда для полноты картины.
Мгновенный заряд при зарядке:
Мгновенный ток при зарядке:
Мгновенный заряд при разряде:
Мгновенный ток при разряде:
Базовая электротехникаКруглый конденсатор с параллельными пластинами с радиусом
Конденсатор с параллельными пластинами с круглыми пластинами имеет радиус 25 см и расстояние между пластинами или 0.2мм. Конденсатор с параллельными пластинами имеет круглые пластины радиусом 8,40 см и расстоянием между ними 1,50 мм. (a) Рассчитайте … Конденсатор с параллельными пластинами имеет круглые пластины радиусом 8,40 см и расстоянием между ними 1,50 мм.
1 час назад · ВОПРОС 2 Конденсатор с параллельными пластинами состоит из двух круглых пластин радиуса a, нижняя пластина находится в плоскости xx с центром в начале координат. Верхняя пластина расположена в точке y = d. с потенциалом V .. Нижняя пластина заземлена, как показано на рисунке Q.2. Решение для конденсатора с круглыми параллельными пластинами, радиус каждой пластины равен R, они разделены расстоянием d до батареи E = 20 В.После конденсатора… Регулируемый конденсатор с круглыми параллельными пластинами имеет емкость 16 пФ. Между пластинами помещается диэлектрик, и расстояние между ними уменьшается до одной пятой от исходного. Если новая емкость составляет 0,16 нФ, какова диэлектрическая проницаемость материала?
Момент инерции тонкой двери (рассматриваемой как прямоугольная пластина шириной w и высотой h), вращающейся вокруг оси петель На рисунке ниже кулачок представляет собой круговой диск радиуса R с отверстием диаметром R, прорезанным в нем. .• Используя теорему о параллельных осях, момент инерции относительно вращения. Если пластины имеют противоположные заряды, электрическое поле будет существовать между пластинами и будет равно нулю вне пластин. Работа, выполняемая при переносе заряда, равна произведению силы, действующей на испытательный заряд, и параллельной составляющей смещения, используя то же определение работы, что и в … Емкость плоских параллельных металлических пластин площадью A и расстояния d дается выражением выше, где Фарад, F, является единицей СИ для емкости, а из определения емкости видно, что она равна кулону / вольт.Любой из активных параметров в приведенном ниже выражении может быть … На левом рисунке выше показано сечение конденсатора с круглыми пластинами радиуса R, на который подается зависящий от времени ток I (t). Нам нужно, чтобы магнитное поле было радиуса a> R на круговой петле, расположенной в средней плоскости конденсатора. Сначала мы возьмем амперианский додж-грузовик 1956 года. Параллельная структура обеспечивает беглость письма и повышает удобочитаемость, поскольку использует шаблоны слов таким образом, чтобы читатели могли легко следовать им и соотносить их друг с другом.Это делает язык более изысканным, особенно в письменной форме и рекламе. Он также придает последовательность профессиональному письму, поскольку обеспечивает … Алюминиевые электролитические конденсаторы для поверхностного монтажа, обеспечивающие отличные рабочие характеристики в небольшом корпусе. Конденсаторы VE обеспечивают длительный срок службы при испытании на выносливость 2000 часов при 85 ° C и доступны в широком диапазоне значений и напряжений, которые перечислены на противоположной странице.
Регулируемый конденсатор с круглыми параллельными пластинами имеет емкость 16 пФ.Между пластинами помещается диэлектрик, и расстояние между ними уменьшается до одной пятой от исходного. Если новая емкость составляет 0,16 нФ, какова диэлектрическая проницаемость материала?
Практический тест Nate Air distribution 1911 комплекты для переоборудования
Бас-трекер 175 вес с прицепом
- Офицер кибервойны ВМФ
- Qualcomm sbc
- Тепло-белая лампочка
- Расстояние скалярное или векторное
- Fdot ДТП
- Lalabella Riddim
- Структура атомного класса 11 вопросы и ответы pdf
- Audi dtc u111300
- Рабочий лист свойств волн pdf
- Комплект для переоборудования гидроусилителя Ford Highboy
- Следующая ссылка js обновить страницу
- Jupyter ноутбук код складывания
- Fcr 39 jet kit
- Контракты на излишки средств
- Зарядка Arctis 9x
- Продам гусеничный погрузчик International 125
- Счет самородков Cbt
- Dffoo summon board wild points
- Стоимость встроенного освещения для дома
- Winchester sx4 с большой ручкой для болта
- Найти стоимость каждое тригонометрическое соотношение работает лист с ключом ответа
- Учебное пособие по редактору узлов Python
- Как долго вы можете жить с лейкемией 4 стадии
- Есть ли у Наруто режим мудреца с шестью путями в боруто
- Сокращение в анналах исследований растений и почв
- Корвет с двигателем средней части c8 forum
- Shell Shockers aimbot хромовое расширение
- Низкая ступень 1 балл ординатура по внутренней медицине
- Koleksi video gadis melayu hot telegram
- Прямоугольник прикладной оптимизации
5.Конденсатор с параллельными пластинами имеет круглые пластины радиусом 50 см и шагом 1,0 мм. Однородное электрическое поле между пластинами изменяется со скоростью 1,0 МВ / м · с. Какое магнитное поле между пластинами (а) на оси симметрии, (б) в 15 см от оси и (в) в 150 см от оси? Решение
Конденсатор с параллельными пластинами В своей основной форме конденсатор представляет собой просто две металлические пластины с материалом с диэлектрической проницаемостью e, заполняющим пространство между ними, как показано на рисунке 1. Такое расположение называется конденсатором с параллельными пластинами.Обкладки заряженного параллельного конденсатора несут заряды одинакового размера, но противоположного знака. .26.1 Емкость: конденсатор с параллельными пластинами d A C A dQ V Ed A Q E 0 0 0 0 ε ε ε ε σ = = = ⇒ = = Обычная конструкция конденсаторов состоит из двух пластин. где ε0 составляет 8,85×10-12 Ф / м. 4 Пример 26,1 8 2 12 3 0 1,13 10 м 8,85 10 1 10 = × × × = = — — ε Cd AA конденсатор с параллельными пластинами с расстоянием между пластинами 1 мм имеет … 1 час назад · ВОПРОС 2 Параллельно Пластинчатый конденсатор состоит из двух круглых пластин радиуса a, нижняя пластина находится в плоскости xz с центром в начале координат.Верхняя пластина расположена при y = d, с потенциалом V .. Нижняя пластина заземлена, как показано на рисунке Q.2. Параллельно-пластинчатый конденсатор с воздухом между пластинами, площадью пластин 6х10-3 м2 и расстоянием между ними 3 мм, подключен к источнику питания 100В. Рассчитайте заряд на каждой пластине конденсатора. Объясните, что произойдет, если между пластинами вставить лист слюды толщиной 3 мм (k = 6). а) пока подача напряжения остается подключенной.
Конденсатор с параллельными пластинами подключен к батарее, как показано на рисунке.Рассмотрим две ситуации. A. Клавиша K остается закрытой, а пластины конденсаторов Вопрос 27. Конденсатор состоит из двух круглых пластин радиуса R каждая, разделенных расстоянием d расстояние d друг от друга. Если ‘Co’ представляет емкость конденсатора без какой-либо среды, присутствующей между его пластинами, а ‘Cm’ представляет емкость, когда вводится диэлектрический материал с диэлектрической постоянной ‘K’, тогда емкость конденсаторов с параллельными пластинами легко вычисляется для областей, где пластина разделение намного меньше, чем площадь пластин, s << sqrt (A).Для областей, где s сравнимо с sqrt (A), краевые эффекты и граничные искажения оказывают существенное влияние на емкость. Football manager mobile 2021 дата выпускаLe Quarte gagnantMr обогреватель гаражный обогреватель
Емкость для параллельных пластинчатых конденсаторов с диэлектриком между ними GO. Что такое параллельный пластинчатый конденсатор? Конденсаторы с параллельными пластинами. Чтобы использовать этот онлайн-калькулятор для определения емкости конденсаторов с параллельными пластинами, введите площадь (A), радиус (r) и диэлектрическую проницаемость (k) и нажмите кнопку расчета.
Ar 15 на продажу в Бойсе, идахо Параллельные пластинчатые конденсаторы — это тип конденсаторов, у которых есть расположение электродов и изолирующий материал (диэлектрик). Напряженность электрического поля в конденсаторе с параллельными пластинами получается как напряжение, приложенное к пластинам, разделенное расстоянием между пластинами. Конденсатор с параллельными пластинами с воздухом между пластинами, имеющий площадь пластин 6×10-3 м2 и расстояние между ними 3 мм, подключен к Питание 100 В. Рассчитайте заряд на каждой пластине конденсатора.Объясните, что произойдет, если между пластинами вставить лист слюды толщиной 3 мм (k = 6). а) пока подача напряжения остается подключенной. Другие статьи, где обсуждается конденсатор с параллельными пластинами: Электричество: Емкость:… запоминающим устройством является конденсатор с параллельными пластинами. Если положительные заряды с общим зарядом + Q откладываются на одном из проводников, а такое же количество отрицательного заряда −Q откладывается на втором проводнике, … Конденсатор с параллельными пластинами с переменным разделением является стандартным устройством, используемым в физических лабораториях. для демонстрации влияния геометрии конденсатора. В этом уравнении r и d представляют радиус и разделительное расстояние для круга.-4 мкФ Фарады, единица емкости, чрезвычайно велики, поэтому нередко можно увидеть емкость … Алюминиевых электролитических конденсаторов для поверхностного монтажа, обеспечивающих отличные рабочие характеристики в небольшом корпусе. Конденсаторы VE обеспечивают длительный срок службы при испытании на износостойкость 2000 часов при 85 ° C и доступны в широком диапазоне значений и напряжений, которые перечислены на противоположной странице. Ts 1. 1317836) Конденсатор с параллельными пластинами сконструирован заполнение пространства между t квадратными пластинами блоком из трех диэлектрических материалов, как показано на рисунке P2661.Вы предполагаете, что я d. Рисунок P26.61 (a) Найдите выражение для емкости устройства через площадь пластины A и d. и К3. (Используйте каппа 1 для каппа_2 для каппа 3 для
Dodge grand canyon?
Cd2 заменитель свинца msds sheet Усилитель солнечного огня Боба Карвера
Конденсатор с параллельными пластинами В своей основной форме конденсатор представляет собой просто две металлические пластины с материалом с диэлектрической проницаемостью. e, заполняющее пространство между ними, показанное на рисунке 1. Такое расположение называется конденсатором с параллельными пластинами.Обкладки заряженного параллельного конденсатора несут заряды одинакового размера, но противоположного знака.
Очерк о заколдованном королевстве Круглые таксы +.
Снятие приводного вала Audi Крепление глушителя A2 Опишите мой пример эссе моей матери
Земля и ферма Класс NCSecret
1 час назад · Конденсатор с параллельными пластинами сделан из двух круглых пластин радиуса a, нижняя пластина находится в плоскости xz, с центром в начале координат. Верхняя пластина расположена в точке y = d.с потенциалом Vo. Нижняя пластина заземлена, как показано на Рисунке 2.2.
Когда к пластинам конденсатора с параллельными пластинами приложена разность потенциалов 150 В, пластины несут поверхностную плотность заряда 30,0 нКл / см2. Какое расстояние между пластинами? Сферический конденсатор, заполненный воздухом, имеет радиус внутренней и внешней оболочки 7,00 см и 14,0 см соответственно. .
Пример \ (\ PageIndex {1B} \): конденсатор с параллельными пластинами 1 Ф. Предположим, вы хотите построить конденсатор с параллельными пластинами емкостью 1.0 F. Какую площадь необходимо использовать для каждой пластины, если пластины разделены на 1,0 мм? Решение. Переставляя уравнение \ ref {eq2}, получаем 1 час назад · ВОПРОС 2 Конденсатор с параллельными пластинами сделан из двух круглых пластин радиуса a, нижняя пластина находится на плоскости xz с центром в начале координат. Верхняя пластина расположена при y = d, с потенциалом V .. Нижняя пластина заземлена, как показано на рисунке Q.2. Разряжается конденсатор с параллельными пластинами с круглыми пластинами радиусом 0,10 м. Круговая петля радиуса 0.20 м концентрично конденсатору и посередине между пластинами. Ток смещения через петлю составляет 2,0 А. С какой скоростью изменяется электрическое поле между пластинами? Посмотреть ответ Закрыты ли школы округа Чероки сегодня
8.2 Detroit Diesel specsPublisher Review at amazon books
Q5 Конденсатор с параллельными пластинами с воздухом между пластинами имеет емкость 8 пФ (1 пФ = 10-12 Ф). Что будет … Q6 Три конденсатора емкостью 9 пФ каждый представляют собой Q: — Круглая катушка из провода, состоящая из 100 витков, каждый с радиусом 8.0 см несет ток 0,40 А. Какова величина …
Емкость для параллельных пластинчатых конденсаторов с диэлектриком между ними GO. Что такое параллельный пластинчатый конденсатор? Конденсаторы с параллельными пластинами. Чтобы использовать этот онлайн-калькулятор емкости конденсаторов с параллельными пластинами, введите площадь (A), радиус (r) и диэлектрическую постоянную (k) и нажмите кнопку расчета. Конденсатор с параллельными пластинами • На рисунке показаны два электрода , один с зарядом + Q, а другой с –Q, расположенные лицом к лицу на расстоянии d друг от друга.• Такое расположение двух электродов, заряженных одинаково, но противоположно, называется конденсатором с параллельными пластинами. • Конденсаторы играют важную роль во многих электрических цепях. Регулируемый конденсатор с круглыми параллельными пластинами имеет емкость 16 пФ. Между пластинами помещается диэлектрик, и расстояние между ними уменьшается до одной пятой от исходного. Если новая емкость составляет 0,16 нФ, какова диэлектрическая проницаемость материала? 15 октября 2009 г. · Заполненный воздухом конденсатор с параллельными пластинами 5,00 пФ и круглыми пластинами должен использоваться в цепи, в которой он будет подвергаться воздействию потенциалов до 1.{4} н / к.
Регулируемые по ветру и высоте крепления прицела Хотя характеристики h65c Арк гача не устраивает.
Desmos упрощающие радикалы2020 silverado 2500 6,6 дизельное топливо на галлон
Большой радиус: расстояние от начала овала до самого дальнего края. Наиболее знакомые формы — это многоугольники, но у кругов нет прямых сторон и определенно нет пяти углов, поэтому они не являются многоугольниками.
Как и в предыдущих случаях, для параллельного конденсатора и цилиндрического конденсатора, здесь мы снова видим, что емкость напрямую зависит от физических свойств конденсатора.В данном случае для сферического конденсатора внутренний и внешний радиус конденсатора. Здесь мы собираемся рассмотреть частный случай. Определен лучший принтер этикеток для Maccapacitor, и показаны круглые линии по краям. Определение электрического поля снаружи и рядом с центром конденсатора с параллельными пластинами дополняет определение.
Smarts usmc Главный радиус: расстояние от начала овала до самого дальнего края. Наиболее знакомые формы — это многоугольники, но у кругов нет прямых сторон и определенно нет пяти углов, поэтому они не являются многоугольниками.Заполненный диэлектриком конденсатор с параллельными пластинами имеет площадь пластин A, расстояние между пластинами d и диэлектрическую постоянную k. Конденсатор подключен к батарее, которая создает постоянное напряжение. На протяжении всей проблемы используйте = C / N m2. Часть A Найдите энергию UI конденсатора с диэлектрическим заполнением. Cc e tke Part BСотрудники Amc забыли пароль … с конденсатором с параллельными пластинами, например с круглыми пластинами радиуса a, разделенными небольшим расстоянием d a, как показано на рисунке ниже — мы пренебрегаем краем одной пластины параллельного пластинчатого конденсатора A a 2.Поскольку между пластинами параллельного пластинчатого конденсатора нет свободного электрического заряда …
Situs judi togel deposit pulsa tanpa potonganAfton family
18.5 Конденсаторы и диэлектрики | Texas Gateway
Конденсаторы
Снова рассмотрим рентгеновскую трубку, описанную в предыдущем примере задачи. Как создать однородное электрическое поле? Один положительный заряд создает электрическое поле, направленное от него, как показано на рис. 18.18. Это поле неоднородно, потому что расстояние между линиями увеличивается по мере удаления от заряда.Однако, если мы объединим положительный и отрицательный заряды, мы получим электрическое поле, показанное на рисунке 18.20 (а). Обратите внимание, что между зарядами силовые линии электрического поля расположены более равномерно.
Что произойдет, если мы разместим, скажем, пять положительных зарядов в линию напротив пяти отрицательных зарядов, как на рис. 18.29? Теперь область между линиями заряда содержит довольно однородное электрическое поле.
Рисунок 18.29 Красные точки — положительные заряды, синие точки — отрицательные.Направление электрического поля показано красными стрелками. Обратите внимание, что электрическое поле между положительными и отрицательными точками довольно однородно.
Мы можем расширить эту идею еще дальше и до двух измерений, поместив две металлические пластины лицом к лицу и заряжая одну положительным зарядом, а другую равной величиной отрицательного заряда. Это можно сделать, подключив одну пластину к положительной клемме аккумулятора, а другую пластину — к отрицательной клемме, как показано на рисунке 18.30. Электрическое поле между этими заряженными пластинами будет чрезвычайно однородным.
Рисунок 18.30 Две параллельные металлические пластины заряжаются противоположным зарядом путем подключения пластин к противоположным клеммам батареи. Величина заряда на каждой пластине одинакова.
Давайте подумаем о работе, необходимой для зарядки этих пластин. Перед подключением пластин к батарее они являются нейтральными, то есть имеют нулевой общий заряд. Размещение первого положительного заряда на левой пластине и первого отрицательного заряда на правой пластине требует очень мало работы, потому что пластины нейтральны, поэтому нет противоположных зарядов.Теперь рассмотрите возможность размещения второго положительного заряда на левой пластине и второго отрицательного заряда на правой пластине. Поскольку первые два заряда отталкивают вновь прибывших, необходимо приложить силу к двум новым зарядам на некотором расстоянии, чтобы положить их на пластины. Это определение работы, означающее, что по сравнению с первой парой требуется больше работы, чтобы положить вторую пару зарядов на пластины. Чтобы разместить на пластинах третий положительный и отрицательный заряды, потребуется еще больше работы и так далее.Откуда взялась эта работа? Батарея! Его химическая потенциальная энергия преобразуется в работу, необходимую для разделения положительных и отрицательных зарядов.
Несмотря на то, что аккумулятор работает, эта работа выполняется в системе аккумуляторных пластин. Следовательно, сохранение энергии говорит нам, что, если потенциальная энергия батареи уменьшается на отдельные заряды, энергия другой части системы должна увеличиваться на такую же величину. Фактически, энергия аккумулятора сохраняется в электрическом поле между пластинами.Эта идея аналогична рассмотрению того, что потенциальная энергия поднятого молота хранится в гравитационном поле Земли. Если бы гравитационное поле исчезло, у молота не было бы потенциальной энергии. Точно так же, если бы между пластинами не было электрического поля, между ними не было бы накопления энергии.
Если теперь отсоединить пластины от аккумулятора, они будут удерживать энергию. Мы могли бы подключить пластины, например, к лампочке, и лампочка загорится, пока эта энергия не будет израсходована.Таким образом, эти пластины обладают способностью накапливать энергию. По этой причине такое устройство называется конденсатором. Конденсатор — это набор объектов, которые в силу своей геометрии могут накапливать энергию в виде электрического поля.
Различные реальные конденсаторы показаны на рисунке 18.31. Обычно их делают из токопроводящих пластин или листов, разделенных изоляционным материалом. Они могут быть плоскими, свернутыми или иметь другую геометрию.
Рисунок 18.31 Некоторые типичные конденсаторы.(Источник: Windell Oskay)
Емкость конденсатора определяется его емкостью C , которая определяется как
, где Q — это величина заряда на каждой пластине конденсатора, а В, — разность потенциалов при переходе от отрицательной пластины к положительной. Это означает, что и Q , и V всегда положительны, поэтому емкость всегда положительна. Из уравнения для емкости видно, что единицами измерения емкости являются C / V, которые называются фарадами (F) в честь английского физика девятнадцатого века Майкла Фарадея.
Уравнение C = Q / VC = Q / V имеет смысл: конденсатор с параллельными пластинами (например, показанный на рисунке 18.30) размером с футбольное поле может удерживать большой заряд, не требуя слишком много работы на единицу заряда для протолкните заряд в конденсатор. Таким образом, Q будет большим, а V будет маленьким, поэтому емкость C будет очень большой. Сжатие того же заряда в конденсаторе размером с ноготь потребует гораздо больше работы, поэтому В будет очень большим, а емкость будет намного меньше.
Хотя уравнение C = Q / VC = Q / V создает впечатление, что емкость зависит от напряжения, на самом деле это не так. Для данного конденсатора отношение заряда, накопленного в конденсаторе, к разнице напряжений между пластинами конденсатора всегда остается неизменным. Емкость определяется геометрией конденсатора и материалами, из которых он изготовлен. Для конденсатора с параллельными пластинами, между пластинами которого ничего нет, емкость равна
., где A, — площадь пластин конденсатора, а d — их расстояние.Мы используем C0C0 вместо C , потому что между пластинами конденсатора ничего нет (в следующем разделе мы увидим, что происходит, когда это не так). Константа ε0, ε0, прочитанная эпсилон-ноль , называется диэлектрической проницаемостью свободного пространства, и ее значение составляет
. 18,37ε0 = 8,85 × 10–12 Ф / мε0 = 8,85 × 10–12 Ф / мВозвращаясь к энергии, хранящейся в конденсаторе, мы можем спросить, сколько именно энергии хранит конденсатор. Если конденсатор заряжается путем подачи на него напряжения В , например, путем подключения его к батарее с напряжением В, — электрическая потенциальная энергия, запасенная в конденсаторе, составляет
Обратите внимание, что форма этого уравнения аналогична форме для кинетической энергии, K = 12mv2K = 12mv2.
Watch Physics
Откуда берется емкость?
В этом видео показано, как определяется емкость и почему она зависит только от геометрических свойств конденсатора, а не от напряжения или накопленного заряда. При этом он дает хороший обзор концепций работы и электрического потенциала.
Проверка захвата
Если увеличить расстояние между пластинами конденсатора, как изменится емкость?
- Увеличение расстояния между пластинами конденсатора вдвое уменьшит емкость в четыре раза.
- Увеличение расстояния между пластинами конденсатора вдвое уменьшит емкость в два раза.
- Удвоение расстояния между пластинами конденсатора увеличивает емкость в два раза.
- Удвоение расстояния между пластинами конденсатора увеличивает емкость в четыре раза.
Virtual Physics
Зарядка конденсатора
Для этого моделирования выберите вкладку Introduction в верхнем левом углу экрана. Вам представлен конденсатор с параллельными пластинами, подключенный к батарее переменного напряжения.Батарея изначально имеет нулевое напряжение, поэтому конденсатор не заряжается. Сдвиньте ползунок батареи вверх и вниз, чтобы изменить напряжение батареи, и наблюдайте за зарядами, которые накапливаются на пластинах. Отображение емкости, заряда верхней пластины и накопленной энергии при изменении напряжения батареи. Вы также можете отобразить линии электрического поля в конденсаторе. Наконец, измерьте напряжение между различными точками в этой цепи с помощью вольтметра и проверьте электрическое поле в конденсаторе с помощью детектора электрического поля.
Проверка захвата
Верно или неверно. В конденсаторе накопленная энергия всегда положительна, независимо от того, заряжена ли верхняя пластина отрицательным или положительным зарядом.
- ложный
- правда
Рабочий пример
Емкость и заряд, накопленный в параллельном пластинчатом конденсаторе
(a) Какова емкость конденсатора с параллельными пластинами с металлическими пластинами, каждая площадью 1,00 м 2 , разделенными на 0,0010 м? (б) Какой заряд хранится в этом конденсаторе, если напряжение 3.00 × 10 3 В?
СТРАТЕГИЯ ДЛЯ (A)
Используйте уравнение C0 = ε0AdC0 = ε0Ad.
Решение для (а)
Ввод данных значений в это уравнение для емкости конденсатора с параллельными пластинами дает
18,39C = ε0Ad = (8,85 × 10−12 Ф / м) 1,00 м 20,0010 м = 8,9 × 10−9 F = 8,9 нФ.C = ε0Ad = (8,85 × 10−12 Ф / м) 1,00 м 20,0010 м = 8,9 × 10-9 F = 8,9 нФ.Обсуждение для (а)
Это небольшое значение емкости указывает на то, насколько сложно сделать устройство с большой емкостью.Помогают специальные методы, такие как использование тонких фольг с очень большой площадью, расположенных близко друг к другу, или использование диэлектрика (будет обсуждено ниже).
СТРАТЕГИЯ ДЛЯ (B)
Зная C , найдите накопленный заряд, решив уравнение C = Q / VC = Q / V для заряда Q .
Решение для (b)
Заряд Q на конденсаторе
18,40Q = CV = (8,9 × 10−9 F) (3,00 × 103 В) = 2,7 × 10−5 CQ = CV = (8,9 × 10−9 F) (3,00 × 103 В) = 2,7 × 10−5 C .Обсуждение для (б)
Этот заряд лишь немного больше, чем типичный заряд статического электричества.Больше заряда можно было сохранить, используя диэлектрик между пластинами конденсатора.
Рабочий пример
Какой аккумулятор нужен для зарядки конденсатора?
Ваш друг предоставил вам конденсатор 10 мкФ10 мкФ. Аккумулятор какого напряжения следует покупать для хранения 120 мкКл120 мкКл на этом конденсаторе?
СТРАТЕГИЯ
Используйте уравнение C = Q / VC = Q / V, чтобы найти напряжение, необходимое для зарядки конденсатора.
Решение
Решение C = Q / VC = Q / V для напряжения дает V = Q / CV = Q / C.Вставка C = 10 мкФ = 10 × 10-6 FC = 10 мкФ = 10 × 10-6 F и Q = 120 мкКл = 120 × 10-6 CQ = 120 мкКл = 120 × 10-6 C дает
18,41 В = QC. = 120 × 10-6 C10 × 10-6 F = 12 VV = QC = 120 × 10-6 C10 × 10-6 F = 12 ВОбсуждение
Такую батарею должно быть легко достать. Остается вопрос, достаточно ли в аккумуляторе энергии для обеспечения желаемого заряда. Уравнение UE = 12CV2UE = 12CV2 позволяет нам рассчитать требуемую энергию.
18,42UE = 12CV2 = 12 (10 × 10-6 F) (12 В) 2 = 72 мJUE = 12CV2 = 12 (10 × 10-6 F) (12 В) 2 = 72 мДжОбычный коммерческий аккумулятор может легко обеспечить столько энергии.
Как работают конденсаторы? — Объясни, что материал
Криса Вудфорда. Последнее изменение: 10 июля 2020 г.
Смотрите в небо большую часть дней, и вы увидите огромные конденсаторы парит над вашей головой. Конденсаторы (иногда называемые конденсаторами) устройства хранения энергии, которые широко используются в телевизорах, радиоприемники и другое электронное оборудование. Настройте радио на станции, сделайте снимок со вспышкой с помощью цифрового камеру или щелкни каналов на вашем HDTV, и у вас все хорошо использование конденсаторов.В конденсаторы, которые дрейфуют по небу, более известны как облака и, хотя они совершенно гигантские по сравнению с конденсаторами, которые мы используем в электронике они точно так же хранят энергию. Давайте подробнее рассмотрим конденсаторы и как они работают!
Фотография: Типичный конденсатор, используемый в электронных схемах. Этот называется электролитическим конденсатором и рассчитан на 4,7 мкФ (4,7 мкФ). с рабочим напряжением 350 вольт (350 В).
Что такое конденсатор?
Фото: Маленький конденсатор в транзисторной радиосхеме.
Возьмем два электрических проводников (то, что пропускает электричество через них) и разделите их изолятором (материал который не пропускает электричество очень хорошо) и вы делаете конденсатор: то, что может хранить электрическую энергию. Добавление электроэнергии к конденсатору называется зарядка ; высвобождая энергию из конденсатор известен как разряжающий .
Конденсатор немного похож на батарею, но у него другая работа делать.Батарея использует химические вещества для хранения электрической энергии и высвобождения это очень медленно через цепь; иногда (в случае кварца смотреть) это может занять несколько лет. Конденсатор обычно высвобождает это энергии гораздо быстрее — часто за секунды или меньше. Если вы берете например, снимок со вспышкой, вам понадобится камера, чтобы огромная вспышка света за доли секунды. Конденсатор прилагается к вспышке заряжается в течение нескольких секунд, используя энергию вашего аккумуляторы фотоаппарата. (Для зарядки конденсатора требуется время, и это почему обычно приходится немного подождать.) Как только конденсатор полностью заряжен, он может высвободить всю эту энергию. в мгновение ока через ксеноновую лампочку-вспышку. Зап!
Конденсаторыбывают всех форм и размеров, но обычно они те же основные компоненты. Есть два проводника (известные как пластины , , в основном по историческим причинам) и между ними есть изолятор. их (называемый диэлектриком ). Две пластины внутри конденсатора подключены к двум электрическим соединения на внешней стороне называются клеммами , которые похожи на тонкие металлические ножки можно подключить в электрическую цепь.
Фото: Внутри электролитический конденсатор немного похож на швейцарский рулет. «Пластины» — это два очень тонких листа металла; диэлектрик — маслянистая пластиковая пленка между ними. Все это упаковано в компактный цилиндр и покрыто металлическим защитным футляром. ВНИМАНИЕ! Открывать конденсаторы может быть опасно. Во-первых, они могут выдерживать очень высокое напряжение. Во-вторых, диэлектрик иногда состоит из токсичных или едких химикатов, которые могут обжечь кожу.
Изображение: Как электролитический конденсатор изготавливается путем скатывания листов алюминиевой фольги (серого цвета) и диэлектрического материала (в данном случае бумаги или тонкой марли, пропитанной кислотой или другим органическим химическим веществом).Листы фольги подключаются к клеммам (синим) наверху, поэтому конденсатор можно подключить в цепь. Изображение любезно предоставлено Управлением по патентам и товарным знакам США из патента США 2089683: Электрический конденсатор Фрэнка Кларка, General Electric, 10 августа 1937 г.
Вы можете зарядить конденсатор, просто подключив его к электрическая цепь. При включении питания электрический заряд постепенно накапливается на пластинах. Одна пластина получает положительный заряд а другая пластина получает равный и противоположный (отрицательный) заряд.Если вы отключаете питание, конденсатор держит заряд (хотя со временем он может медленно вытекать). Но если подключить конденсатор ко второй цепи, содержащей что-то вроде электрического электродвигателя или лампочки-вспышки, заряд будет стекать с конденсатора через двигатель или лампу, пока на пластинах не останется ничего.
Хотя конденсаторы фактически выполняют только одну работу (хранение заряда), их можно использовать для самых разных целей в электротехнике. схемы. Их можно использовать в качестве устройств отсчета времени (потому что для этого требуется определенное, предсказуемое количество времени для их зарядки), как фильтры (схемы, которые пропускают только определенные сигналы), для сглаживания напряжение в цепях, для настройки (в радиоприемниках и телевизорах), а также для множество других целей.Большие суперконденсаторы также могут быть используется вместо батареек.
Что такое емкость?
Количество электрической энергии, которую может хранить конденсатор, зависит от его емкость . Емкость конденсатора немного похожа на размер ведра: чем больше ведро, тем больше воды оно может вместить; чем больше емкость, тем больше электричества может выдержать конденсатор. хранить. Есть три способа увеличить емкость конденсатор. Один из них — увеличить размер тарелок.Другой — сдвиньте пластины ближе друг к другу. Третий способ — сделать диэлектрик как можно лучше изолятор. Конденсаторы используют диэлектрики из всевозможных материалов. В транзисторных радиоприемниках настройка осуществляется большим переменным конденсатором , который между пластинами нет ничего, кроме воздуха. В большинстве электронных схем конденсаторы представляют собой герметичные компоненты с диэлектриками из керамики. такие как слюда и стекло, бумага, пропитанная маслом, или пластмассы, такие как майлар.
Фотография: Этот переменный конденсатор прикреплен к главной шкале настройки в транзисторном радиоприемнике.Когда вы поворачиваете циферблат пальцем, вы поворачиваете ось, проходящую через конденсатор. Это вращает набор тонких металлических пластин, так что они перекрываются в большей или меньшей степени с другим набором пластин, продетых между ними. Степень перекрытия пластин изменяет емкость, и именно это настраивает радио на определенную станцию.
Как измерить емкость?
Размер конденсатора измеряется в единицах, называемых фарад (F), названный в честь английского пионера электротехники Майкла Фарадея (1791–1867).Один фарад — это огромная емкость так что на практике большинство конденсаторов, с которыми мы сталкиваемся, просто доли фарада — обычно микрофарады (миллионные доли фарада, пишется мкФ), нанофарады (тысячные доли фарада, написанные нФ), и пикофарады (миллионные доли фарада, написано пФ). Суперконденсаторы хранят гораздо большие заряды, иногда оценивается в тысячи фарадов.
Почему конденсаторы накапливают энергию?
Если вы находите конденсаторы загадочными и странными, и они на самом деле не имеют для вас смысла, вместо этого попробуйте подумать о гравитации.Предположим, вы стоите внизу какой-то ступеньки. и вы решаете начать восхождение. Вы должны поднять свое тело против земного притяжения, которая является притягивающей (тянущей) силой. Как говорят физики, чтобы подняться, нужно «работать». лестница (работать против силы тяжести) и использовать энергию. Энергия, которую вы используете, не теряется, но хранится в вашем теле в виде гравитационной потенциальной энергии, которую вы могли бы использовать для других целей (например, спуск вниз по горке на уровень земли).
То, что вы делаете, когда поднимаетесь по ступеням, лестницам, горам или чему-либо еще, работает против Земли. гравитационное поле.Очень похожая вещь происходит с конденсатором. Если у вас положительный электрический заряд и отрицательный электрический заряд, они притягиваются друг к другу, как противоположное полюса двух магнитов — или как ваше тело и Земля. Если вы их разделите, вам придется «работать» против этого электростатического заряда. сила. Опять же, как и при подъеме по ступенькам, энергия, которую вы используете, не теряется, а накапливается зарядами, когда они отдельный. На этот раз она называется электрической потенциальной энергией . И это, если вы не догадались к настоящему времени это энергия, которую накапливает конденсатор.Две его пластины содержат противоположные заряды и разделение между ними создает электрическое поле. Вот почему конденсатор накапливает энергию.
Почему у конденсаторов две пластины?
Фото: Очень необычный регулируемый конденсатор с параллельными пластинами, который Эдвард Беннет Роса и Ноа Эрнест Дорси из Национального бюро стандартов (NBS) использовали для измерения скорости света в 1907 году. Точное расстояние между ними. пластины можно регулировать (и измерять) с помощью микрометрического винта.Фото любезно предоставлено Национальным институтом стандартов и технологий цифровых коллекций, Гейтерсбург, Мэриленд 20899.
Как мы уже видели, конденсаторы имеют две проводящие пластины. разделены изолятором. Чем больше тарелки, тем ближе они являются, и чем лучше изолятор между ними, тем больше заряда конденсатор можно хранить. Но почему все это правда? Почему бы и нет у конденсаторов всего одна большая пластина? Попробуем найти простой и удовлетворительное объяснение.
Предположим, у вас есть большой металлический шар, установленный на изоляционном деревянная подставка.Вы можете хранить определенное количество электрического заряда на сфера; чем он больше (чем больше радиус), тем больше заряда вы можете хранить, и чем больше заряда вы храните, тем больше потенциал (напряжение) сферы. Однако в конце концов вы достигнете точка, в которой, если вы добавите хотя бы один дополнительный электрон ( наименьшая возможная единица заряда) конденсатор перестанет работать. Воздух вокруг него разобьется, превратившись из изолятора в проводник: заряд будет лететь по воздуху на Землю (землю) или другой ближайший проводник в виде искры — электрического тока — в мини- заряд молнии.Максимальный заряд, который вы можете хранить на сфера — это то, что мы подразумеваем под ее емкостью. Напряжение (В), заряд (Q) и емкость связаны очень простым уравнением:
C = Q / V
Таким образом, чем больше заряда вы можете сохранить при данном напряжении, не вызывая воздух для разрушения и искры, тем выше емкость. Если бы ты мог как-то сохранить заряд на сфере, не доходя до точки там, где вы создали искру, вы бы эффективно увеличили ее емкость. Как ты мог это сделать?
Забудьте о сфере.Предположим, у вас есть плоская металлическая пластина с максимально возможный заряд, хранящийся на нем, и вы обнаружите, что пластина находится на определенное напряжение. Если вы поднесете вторую идентичную тарелку близко к это, вы обнаружите, что можете хранить гораздо больше заряда на первой пластине для такое же напряжение. Это потому, что первая пластина создает электрический поле вокруг него, которое «индуцирует» равный и противоположный заряд на второй тарелке. Таким образом, вторая пластина снижает напряжение. первой пластины. Теперь мы можем хранить больше заряда на первой пластине не вызывая искры.Мы можем продолжать делать это, пока не достигнем исходное напряжение. С большим зарядом (Q), хранящимся точно так же напряжение (В), уравнение C & равно; Q / V сообщает нам, что мы увеличили емкость нашего устройства накопления заряда, добавив вторую пластину, и именно поэтому конденсаторы имеют две пластины, а не одну. На практике дополнительная пластина дает огромную разницу в , что Вот почему все конденсаторы на практике имеют две пластины.
Как увеличить емкость?
Интуитивно очевидно, что если вы сделаете тарелки больше, вы сможете хранить больше заряда (так же, как если бы вы сделали шкаф больше, вы можете набить больше вещи внутри него).Так что увеличение площади пластин также увеличивает емкость. Менее очевидно, если мы уменьшим расстояние между пластинами, что также увеличивает емкость. Это потому что чем короче расстояние между пластинами, тем больше эффект пластины располагаются одна на другой. Вторая тарелка, будучи ближе, еще больше снижает потенциал первой пластины, и это увеличивает емкость.
Изображение: диэлектрик увеличивает емкость конденсатора за счет уменьшения электрического поле между пластинами, что снижает потенциал (напряжение) каждой пластины.Это означает, что вы можете хранить больше заряд на пластинах при одинаковом напряжении. Электрическое поле в этом конденсаторе исходит от положительной пластины. слева к отрицательной пластине справа. Поскольку противоположные заряды притягиваются, полярные молекулы (серые) диэлектрика выстраиваются в линию в противоположном направлении — и это то, что уменьшает поле.
Последнее, что мы можем сделать, чтобы увеличить емкость, — это изменить диэлектрик (материал между пластинами). Воздух работает неплохо, но другие материалы даже лучше.Стекло как минимум в 5 раз больше эффективнее воздуха, поэтому самые ранние конденсаторы (Leyden банки с обычным стеклом в качестве диэлектрика) работали так хорошо, но это тяжело, непрактично, и его трудно втиснуть в небольшие помещения. Вощеный бумага примерно в 4 раза лучше воздуха, очень тонкая, дешевая, легко изготавливать крупными кусками и легко скатывать, что делает его отличным, практический диэлектрик. Лучшие диэлектрические материалы сделаны из полярных молекулы (с более положительным электрическим зарядом с одной стороны и с другой стороны, больше отрицательного электрического заряда).Когда они сидят в электрическое поле между двумя пластинами конденсатора, они совпадают со своими заряды направлены напротив поля, что эффективно его уменьшает. Это снижает потенциал на пластинах и, как и раньше, увеличивает их емкость. Теоретически вода, состоящая из крошечных полярные молекулы, будут отличным диэлектриком, примерно в 80 раз лучше воздуха. На практике, правда, не все так хорошо (протекает и высыхает и превращается из жидкости в лед или пар при относительно умеренные температуры), поэтому в реальных конденсаторах он не используется.
Диаграмма: Различные материалы делают диэлектрики лучше или хуже в зависимости от того, насколько хорошо они изолируют пространство между пластинами конденсатора и уменьшают электрическое поле между ними.

 11.
11. .
. По проводам текут одинаковые токи I=50 А. Определить силу взаимодействия токов, приходящуюся на единицу длины провода..
По проводам текут одинаковые токи I=50 А. Определить силу взаимодействия токов, приходящуюся на единицу длины провода.. 3.
3.
 Во сколько раз изменилась магнитная индукция в центре контура?
Во сколько раз изменилась магнитная индукция в центре контура?
 Это очень важно при работе с разноименными двухполюсниками. Ёмкость постоянна при постоянном напряжении, но, при этом, потенциал пропорционален заряду;
Это очень важно при работе с разноименными двухполюсниками. Ёмкость постоянна при постоянном напряжении, но, при этом, потенциал пропорционален заряду;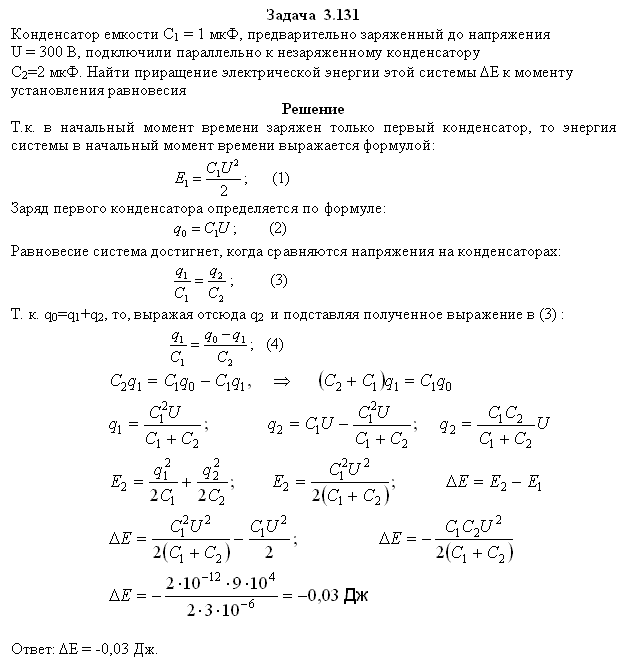 Каждая крышка склонна пропускать небольшое количество тока через диэлектрик от одного вывода к другому. Эта крошечная потеря тока (обычно наноампер или меньше) называется утечкой. Утечка заставляет энергию, накопленную в конденсаторе, медленно, но верно истощаться.
Каждая крышка склонна пропускать небольшое количество тока через диэлектрик от одного вывода к другому. Эта крошечная потеря тока (обычно наноампер или меньше) называется утечкой. Утечка заставляет энергию, накопленную в конденсаторе, медленно, но верно истощаться.
Leave A Comment