Перевод десятичного числа в двоичное — Мегаобучалка
Может потребоваться перевести десятичное число в двоичное. Один из способов – это деление на два и формирование двоичного числа из остатков. Например, нужно получить из числа 77 его двоичную запись:
77 / 2 = 38 (1 остаток)
38 / 2 = 19 (0 остаток)
19 / 2 = 9 (1 остаток)
9 / 2 = 4 (1 остаток)
4 / 2 = 2 (0 остаток)
2 / 2 = 1 (0 остаток)
1 / 2 = 0 (1 остаток)
Собираем остатки вместе, начиная с конца: 1001101. Это и есть число 77 в двоичном представлении. Проверим:
1001101 = 1*26 + 0*25 + 0*24 + 1*23 + 1*22 + 0*21 + 1*20 = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77
Восьмеричная система счисления
Итак, современное «железо понимает» лишь двоичную систему счисления. Однако человеку трудно воспринимать длинные записи нулей и единиц с одной стороны, а с другой – переводит числа из двоичной в десятичную систему и обратно, достаточно долго и трудоемко.
В восьмеричной системе счисления используется восемь знаков-цифр (от 0 до 7). Каждой цифре соответствуют набор из трех цифр в двоичной системе счисления:
000 – 0
001 – 1
010 – 2
011 – 3
100 – 4
101 – 5
110 – 6
111 – 7
Для преобразования двоичного числа в восьмеричное достаточно разбить его на тройки и заменить их соответствующими им цифрами из восьмеричной системы счисления. Разбивать на тройки нужно начинать с конца, а недостающие цифры в начале заменить нулями. Например:
1011101 = 1 011 101 = 001 011 101 = 1 3 5 = 135
Т.е число 1011101 в двоичной системе счисления равно числу 135 в восьмеричной системе счисления. Или 10111012 = 1358.
Обратный перевод. Допустим, требуется перевести число 1008 (не заблуждайтесь! 100 в восьмеричной системе – это не 100 в десятичной) в двоичную систему счисления.
1008 = 1 0 0 = 001 000 000 = 001000000 = 10000002
Перевод восьмеричного числа в десятичное можно осуществить по уже знакомой схеме:
6728 = 6 * 82 + 7 * 81 + 2 * 80 = 6 * 64 + 56 + 2 = 384 + 56 + 2 = 44210
1008 = 1 * 82 + 0 * 81 + 0 * 80 = 6410
Шестнадцатеричная система счисления
Шестнадцатеричная система счисления, так же как и восьмеричная, широко используется в компьютерной науке из-за легкости перевода в нее двоичных чисел. При шестнадцатеричной записи числа получаются более компактными.
В шестнадцатеричной системе счисления используются цифры от 0 до 9 и шесть первых латинских букв – A (10), B (11), C (12), D (13), E (14), F (15).
При переводе двоичного числа в шестнадцатеричное, первое разбивается на группы по четыре разряда, начиная с конца. В случае, если количество разрядов не делится нацело, то первая четверка дописывается нулями впереди.
Например:
10001100101 = 0100 1100 0101 = 4 C 5 = 4C5
Если потребуется, то число 4C5 можно перевести в десятичную систему счисления следующим образом (C следует заменить на соответствующее данному символу число в десятичной системе счисления – это 12):
4C5 = 4 * 162 + 12 * 161 + 5 * 16
Максимальное двухразрядное число, которое можно получить с помощью шестнадцатеричной записи — это FF.
FF = 15 * 161 + 15 * 160 = 240 + 15 = 255
255 – это максимальное значение одного байта, равного 8 битам: 1111 1111 = FF. Поэтому с помощью шестнадцатеричной системы счисления очень удобно кратко (с помощью двух цифр-знаков) записывать значения байтов. Внимание! Состояний у 8-ми битного байта может быть 256, однако максимальное значение – 255. Не забывайте про 0 – это как раз 256-е состояние.
Системы счисления. Перевод чисел
Перевод чисел
В десятичную систему счисления
Из двоичной
101,012 = = 1 * 22 + 0 * 21 + 1 * 20 + 0 * 2-1 + 1 * 2-2 = = 4 + 0 + 1 + 0 + 1/4 = = 5,2510
Из восьмеричной
253,318 = = 2 * 82 + 5 * 81 + 3 * 80 + 3 * 8-1 + 1 * 8-2 = = 128 + 40 + 3 + 3/8 + 1/64 = = 171 + 0,375 + 0,015625 = = 171,39062510
Из шестнадцатеричной
42D16 == 4 * 16
Из десятичной системы счисления
При переводе целых чисел из десятичной системы счисления последовательно выполняют деление этого числа и получаемых целых частных на основание выбранной системы счисления. Деление выполняют до тех пор, пока частное не будет равно нулю.
Деление выполняют до тех пор, пока частное не будет равно нулю.
Число получают путем «сбора» остатков, начиная с конца.
В двоичную
34 / 2 = 17 (0)17 / 2 = 8 (1)8 / 2 = 4 (0)4 / 2 = 2 (0)2 / 2 = 1 (0)1 / 2 = 0 (1)
В восьмеричную
472 / 8 = 59 (0)59 / 8 = 7 (3)7 / 8 = 0 (7)
47210 = 7308
В шестнадцатеричную
924 / 16 = 57 (12)57 / 16 = 3 (9)3 / 16 = 0 (3)
92410 = 39C16
Перевод десятичных дробей из десятичной системы счисления
Дробь в десятичной системе счисления последовательно умножают на основание выбранной системы счисления пока не получиться нулевая дробная часть или достигнута требуемая точность. При каждом последующем умножении целая часть отбрасывается.
В двоичную дробь
0,225 * 2 = 0,450,45 * 2 = 0,90,9 * 2 = 1,80,8 * 2 = 1,60,6 * 2 = 1,20,2 * 2 = 0,40,4 * 2 = 0,80,8 * 2 = 1,6…
0,22510 = 0,00111001…2
В восьмеричную дробь
0,225 * 8 = 1,80,8 * 8 = 6,40,4 * 8 = 3,20,2 * 8 = 1,60,6 * 8 = 4,8…
0,22510 = 0,16314…8
0,225 * 16 = 3,60,6 * 16 = 9,60,6 * 16 = 9,6…
0,22510 = 0,699…16
Арифметические операции в двоичной системе счисления
В двоичной системе счисления арифметические операции выполняются по тем же правилам, что и в десятичной системе счисления, т.к. они обе являются позиционными (наряду с восьмеричной, шестнадцатеричной и др. ).
).
Сложение
Сложение одноразрядных двоичных чисел выполняется по следующим правилам:
0 + 0 = 01 + 0 = 10 + 1 = 11 + 1 = 10
В последнем случае, при сложении двух единиц, происходит переполнение младшего разряда, и единица переносится в старший разряд. Переполнение возникает в случае, если сумма равна основанию системы счисления (в данном случае это число 2) или больше его (для двоичной системы счисления это не актуально).
Сложим для примера два любых двоичных числа:
1101+ 101 —— 10010
Вычитание
Вычитание одноразрядных двоичных чисел выполняется по следующим правилам:
0 — 0 = 01 — 0 = 10 — 1 = (заем из старшего разряда) 11 — 1 = 0
Пример:
1110- 101 —- 1001
Умножение
Умножение одноразрядных двоичных чисел выполняется по следующим правилам:
0 * 0 = 01 * 0 = 00 * 1 = 01 * 1 = 1
Пример:
1110* 10——+ 0000 1110 —— 11100
Деление
Деление выполняется так же как в десятичной системе счисления:
1110 | 10 |—-10 | 111—- 11 10—- 10 10—- 0
Простая информатика — Система счисления
Система счисления – это способ записи чисел.
В позиционных системах счисления количество, обозначаемое цифрой в числе, зависит от ее позиции, а в непозиционных – нет. Например:
11 – здесь первая единица обозначает десять, а вторая – 1.
II – здесь обе единицы обозначают единицу.
345, 259, 521 – здесь цифра 5 в первом случае обозначает 5, во втором – 50, а в третьем – 500.
XXV, XVI, VII – здесь, где бы ни стояла цифра V, она везде обозначает пять единиц. Другими словами, величина, обозначаемая знаком V, не зависит от его позиции.
Сложение, умножение и другие математические операции в позиционных системах счисления выполнить легче, чем в непозиционных, т.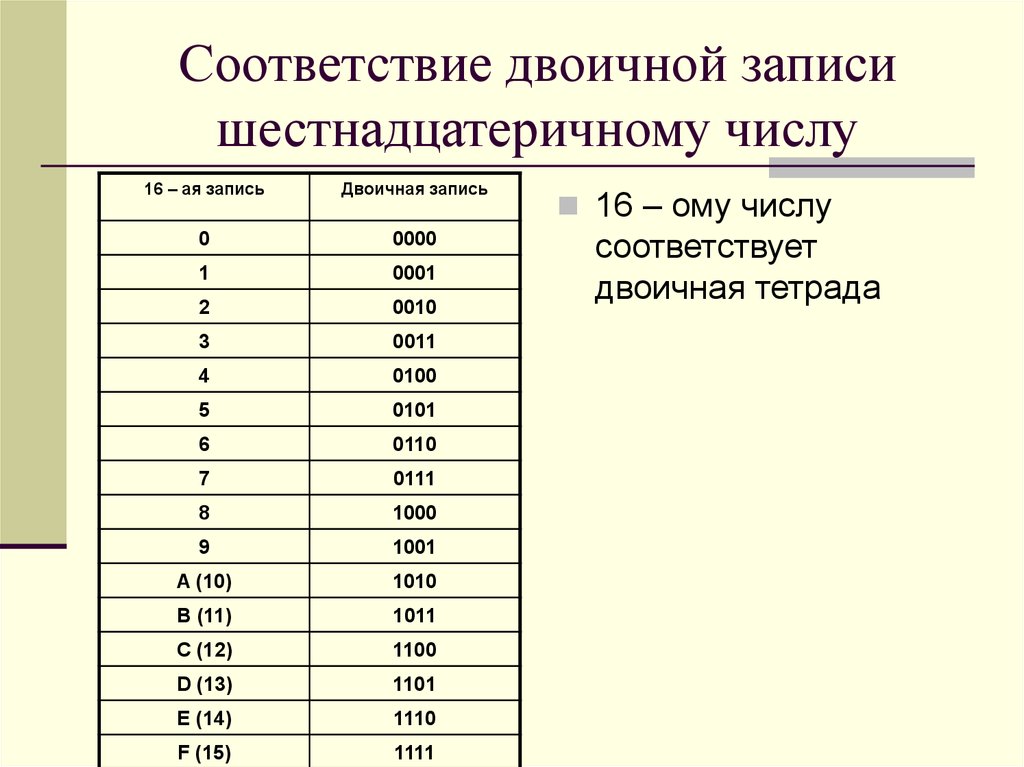 к. математические операции осуществляются по несложным алгоритмам (например, умножение в столбик, сравнение двух чисел).
к. математические операции осуществляются по несложным алгоритмам (например, умножение в столбик, сравнение двух чисел).
В мире наиболее распространены позиционные системы счисления. Помимо знакомой всем с детства десятичной (где используется десять цифр от 0 до 9), в технике широкое распространение нашли такие системы счисление как двоичная (используются цифры 0 и 1), восьмеричная и шестнадцатеричная.
Следует отметить, важную роль нуля. «Открытие» этой цифры в истории человечества сыграло большую роль в формировании позиционных систем счисления.
Основание системы счисления – это количество знаков, которое используется для записи цифр.
Разряд — это позиция цифры в числе. Разрядность числа — количество цифр, из которых состоит число (например, 264 — трехразрядное число, 00010101 — восьмиразрядное число). Разряды нумеруются справа на лево (например, в числе 598 восьмерка занимает первый разряд, а пятерка — третий).
Итак, в позиционной системе счисления числа записываются таким образом, что каждый следующий (движение справа на лево) разряд больше другого на степень основания системы счисления. (придумать схему)
(придумать схему)
Одно и тоже число (значение) можно представить в различных системах счисления. Представление числа при этом различно, а значение остается неизменным.
Двоичная система счисления
В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.)
Чтобы научиться понимать числа в двоичной системе счисления, сначала рассмотрим, как формируются числа в привычной для нас десятичной системе счисления.
В десятичной системе счисления мы располагаем десятью знаками-цифрами (от 0 до 9). Когда счет достигает 9, то вводится новый разряд (десятки), а единицы обнуляются и счет начинается снова. После 19 разряд десятков увеличивается на 1, а единицы снова обнуляются. И так далее. Когда десятки доходят до 9, то потом появляется третий разряд – сотни.
Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две знака-цифры: 0 и 1.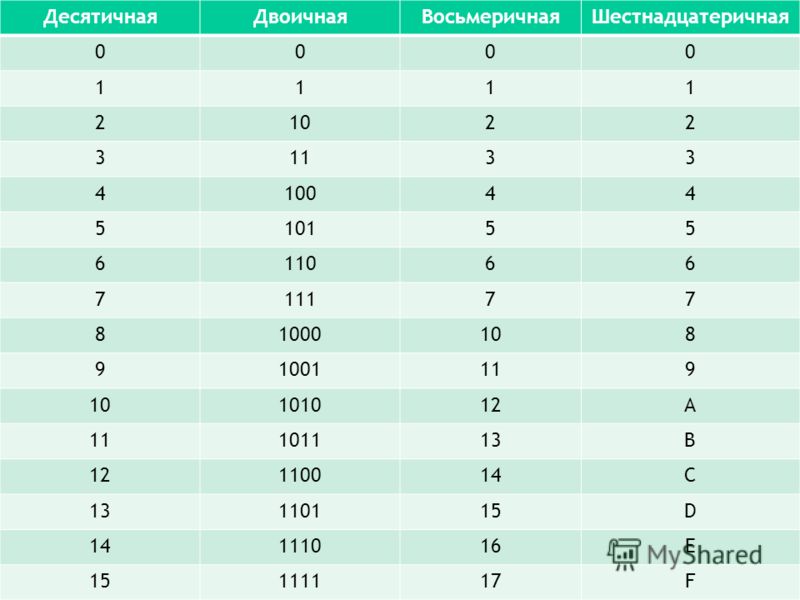 Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.
Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.
Попробуем считать в двоичной системе:
0 – это ноль
1 – это один (и это предел разряда)
10 – это два
11 – это три (и это снова предел)
100 – это четыре
101 – пять
110 – шесть
111 – семь и т.д.
Перевод чисел из двоичной системы счисления в десятичную
Не трудно заметить, что в двоичной системе счисления длины чисел с увеличением значения растут быстрыми темпами. Как определить, что значит вот это: 10001001? Непривычный к такой форме записи чисел человеческий мозг обычно не может понять сколько это. Неплохо бы уметь переводить двоичные числа в десятичные.
В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и т.д. Например:
1476 = 1000 + 400 + 70 + 6
Можно пойти еще дальше и разложить так:
1476 = 1 * 103 + 4 * 102 + 7 * 101 + 6 * 100
Посмотрите на эту запись внимательно. Здесь цифры 1, 4, 7 и 6 — это набор цифр из которых состоит число 1476. Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.
Здесь цифры 1, 4, 7 и 6 — это набор цифр из которых состоит число 1476. Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.
Аналогично можно разложить и любое двоичное число. Только основание здесь будет 2:
10001001 = 1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20
Если посчитать сумму составляющих, то в итоге мы получим десятичное число, соответствующее 10001001:
1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20 = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137
Т.е. число 10001001 по основанию 2 равно числу 137 по основанию 10. Записать это можно так:
100010012 = 13710
Почему двоичная система счисления так распространена?
Дело в том, что двоичная система счисления – это язык вычислительной техники. Каждая цифра должна быть как-то представлена на физическом носителе. Если это десятичная система, то придется создать такое устройство, которое может быть в десяти состояниях. Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания.
Каждая цифра должна быть как-то представлена на физическом носителе. Если это десятичная система, то придется создать такое устройство, которое может быть в десяти состояниях. Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания.
Перевод десятичного числа в двоичное
Может потребоваться перевести десятичное число в двоичное. Один из способов – это деление на два и формирование двоичного числа из остатков. Например, нужно получить из числа 77 его двоичную запись:
77 / 2 = 38 (1 остаток)
38 / 2 = 19 (0 остаток)
19 / 2 = 9 (1 остаток)
9 / 2 = 4 (1 остаток)
4 / 2 = 2 (0 остаток)
2 / 2 = 1 (0 остаток)
1 / 2 = 0 (1 остаток)
Собираем остатки вместе, начиная с конца: 1001101. Это и есть число 77 в двоичном представлении. Проверим:
1001101 = 1*26 + 0*25 + 0*24 + 1*23 + 1*22 + 0*21 + 1*20 = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77
Восьмеричная система счисления
Итак, современное «железо понимает» лишь двоичную систему счисления. Однако человеку трудно воспринимать длинные записи нулей и единиц с одной стороны, а с другой – переводит числа из двоичной в десятичную систему и обратно, достаточно долго и трудоемко. В результате, часто программисты используют другие системы счисления: восьмеричную и шестнадцатеричную. И 8 и 16 являются степенями двойки, и преобразовывать двоичное число в них (так же как и выполнять обратную операцию) очень легко.
Однако человеку трудно воспринимать длинные записи нулей и единиц с одной стороны, а с другой – переводит числа из двоичной в десятичную систему и обратно, достаточно долго и трудоемко. В результате, часто программисты используют другие системы счисления: восьмеричную и шестнадцатеричную. И 8 и 16 являются степенями двойки, и преобразовывать двоичное число в них (так же как и выполнять обратную операцию) очень легко.
В восьмеричной системе счисления используется восемь знаков-цифр (от 0 до 7). Каждой цифре соответствуют набор из трех цифр в двоичной системе счисления:
000 – 0
001 – 1
010 – 2
011 – 3
100 – 4
101 – 5
110 – 6
111 – 7
Для преобразования двоичного числа в восьмеричное достаточно разбить его на тройки и заменить их соответствующими им цифрами из восьмеричной системы счисления. Разбивать на тройки нужно начинать с конца, а недостающие цифры в начале заменить нулями. Например:
1011101 = 1 011 101 = 001 011 101 = 1 3 5 = 135
Т.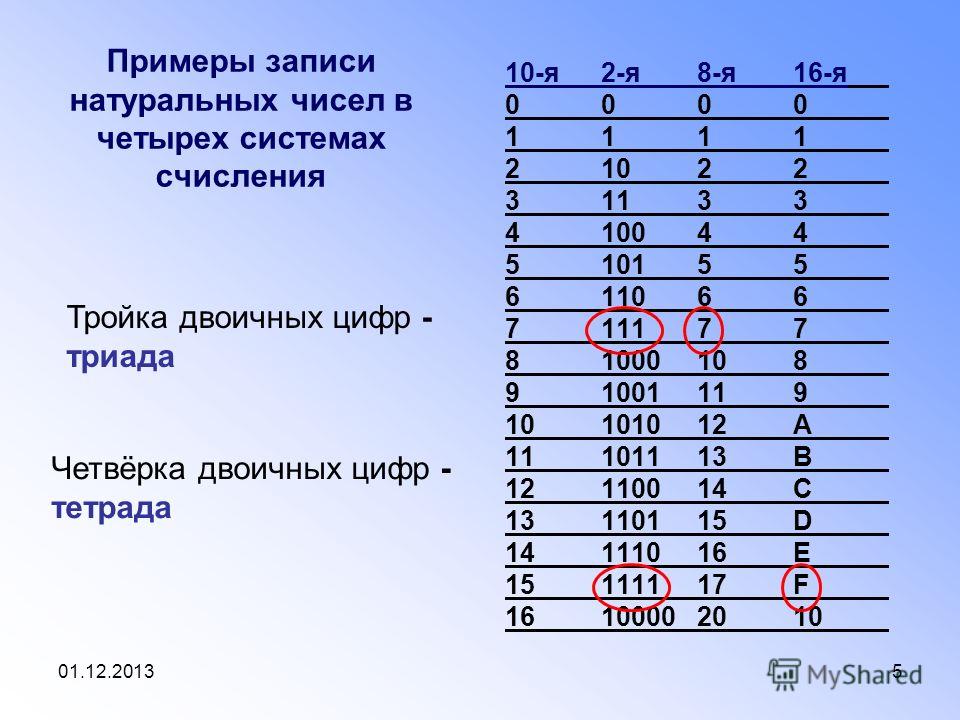 е число 1011101 в двоичной системе счисления равно числу 135 в восьмеричной системе счисления. Или 10111012 = 1358.
е число 1011101 в двоичной системе счисления равно числу 135 в восьмеричной системе счисления. Или 10111012 = 1358.
Обратный перевод. Допустим, требуется перевести число 1008 (не заблуждайтесь! 100 в восьмеричной системе – это не 100 в десятичной) в двоичную систему счисления.
1008 = 1 0 0 = 001 000 000 = 001000000 = 10000002
Перевод восьмеричного числа в десятичное можно осуществить по уже знакомой схеме:
6728 = 6 * 82 + 7 * 81 + 2 * 80 = 6 * 64 + 56 + 2 = 384 + 56 + 2 = 44210
1008 = 1 * 82 + 0 * 81 + 0 * 80 = 6410
Шестнадцатеричная система счисления
Шестнадцатеричная система счисления, так же как и восьмеричная, широко используется в компьютерной науке из-за легкости перевода в нее двоичных чисел. При шестнадцатеричной записи числа получаются более компактными.
В шестнадцатеричной системе счисления используются цифры от 0 до 9 и шесть первых латинских букв – A (10), B (11), C (12), D (13), E (14), F (15).
При переводе двоичного числа в шестнадцатеричное, первое разбивается на группы по четыре разряда, начиная с конца. В случае, если количество разрядов не делится нацело, то первая четверка дописывается нулями впереди. Каждой четверке соответствует цифра шестнадцатеричной системе счисления:
Например:
10001100101 = 0100 1100 0101 = 4 C 5 = 4C5
Если потребуется, то число 4C5 можно перевести в десятичную систему счисления следующим образом (C следует заменить на соответствующее данному символу число в десятичной системе счисления – это 12):
4C5 = 4 * 162 + 12 * 161 + 5 * 160 = 4 * 256 + 192 + 5 = 1221
Максимальное двухразрядное число, которое можно получить с помощью шестнадцатеричной записи — это FF.
FF = 15 * 161 + 15 * 160 = 240 + 15 = 255
255 – это максимальное значение одного байта, равного 8 битам: 1111 1111 = FF. Поэтому с помощью шестнадцатеричной системы счисления очень удобно кратко (с помощью двух цифр-знаков) записывать значения байтов. Внимание! Состояний у 8-ми битного байта может быть 256, однако максимальное значение – 255. Не забывайте про 0 – это как раз 256-е состояние
Внимание! Состояний у 8-ми битного байта может быть 256, однако максимальное значение – 255. Не забывайте про 0 – это как раз 256-е состояние
преобразовать двоичное число 1011101 в шестнадцатеричное
Как записать 1011101 в шестнадцатеричное (с основанием 16)?
1011101 равно 5d в шестнадцатеричной форме
| ||||||||||||||||
Преобразование из/в десятичные, шестнадцатеричные, восьмеричные и двоичные числа. Калькулятор преобразования двоичной базы.
Здесь вы можете найти ответ на такие вопросы, как: преобразовать двоичное число 1011101 в шестнадцатеричное или преобразование двоичного в шестнадцатеричное.
| Декабрь | Шестнадцатеричный | Октябрь | Бункер |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 2 | 2 | 10 |
| 3 | 3 | 3 | 11 |
| 4 | 4 | 4 | 100 |
| 5 | 90 008 55 | 101 | |
| 6 | 6 | 6 | 110 |
| 7 | 7 | 7 | 111 |
| 8 | 8 90 009 | 10 | 1000 |
| 9 | 9 | 11 | 1001 |
| А | 12 | 1010 | |
| 11 | В | 13 | 1011 | 9001 0
| 12 | С | 14 | 1100 |
| 13 | D | 15 | 1101 |
| 14 | E | 16 | 1110 |
| 15 | F | 17 | 1111 |
| Декабрь | 9 0069 ШестнадцатеричныйОктябрь | Корзина | |
|---|---|---|---|
| 16 | 10 | 20 | 10000 |
| 17 | 11 | 21 | 10001 |
| 18 | 12 | 22 | 10010 |
| 19 | 13 | 23 | 10011 |
| 20 | 14 | 24 | 10100 |
| 21 | 15 | 25 | 10101 |
| 22 | 16 | 26 | 10110 |
| 23 | 1 7 | 27 | 10111 |
| 24 | 18 | 30 | 11000 |
| 25 | 19 | 31 | 11001 | 26 | 1A | 32 | 11010 |
| 27 | 1B | 33 | 11011 |
| 28 | 1С | 34 | 11100 |
| 29 | 1D | 35 9 0009 | 11101 |
| 30 | 1Е | 36 | 11110 |
| 31 | 1F | 37 | 11111 |
| Декабрь | Шестнадцатеричный | Октябрь | Бункер |
|---|---|---|---|
| 32 | 20 | 40 | 100000 |
| 33 | 21 | 41 | 100001 |
| 34 | 22 | 900 08 42100010 | |
| 35 | 23 | 43 | 100011 |
| 36 | 24 | 44 | 100100 |
| 37 | 25 | 45 | 100101 |
| 38 | 26 | 46 90 009 | 100110 |
| 39 | 27 | 47 | 100111 |
| 40 | 28 | 50 | 101000 |
| 41 | 29 | 51 | 101001 |
| 42 | 2А | 52 | 101010 |
| 43 | 2B | 53 | 101011 |
| 44 | 2C | 54 | 10110 0 |
| 45 | 2D | 55 | 101101 |
| 46 | 2E | 56 | 101 110 |
| 47 | 2F | 57 | 101111 |
| Декабрь | Шестнадцатеричный | Октябрь | Корзина |
|---|---|---|---|
| 48 | 30 | 60 | 110000 |
| 49 | 31 | 61 | 110001 9000 9 |
| 50 | 32 | 62 | 110010 |
| 51 | 33 | 63 | 110011 |
| 52 | 34 | 64 | 110100 |
| 53 | 35 | 65 | 110101 |
| 54 | 36 | 66 | 110110 |
| 55 | 37 | 67 | 110111 900 09 |
| 56 | 38 | 70 | 111000 |
| 57 | 39 | 71 | 111001 90 009 |
| 58 | 3А | 72 | 111010 |
| 59 | 3B | 73 | 111011 |
| 60 | 3C 9000 9 | 74 | 111100 |
| 61 | 3D | 75 | 111101 |
| 62 | 3Е | 76 | 111110 |
| 63 | 3F | 77 | 111111 |
| Декабрь | Шестнадцатеричный | 9 Октябрь0070 | Корзина |
|---|---|---|---|
| 64 | 40 | 100 | 1000000 |
| 65 9000 9 | 41 | 101 | 1000001 |
| 66 | 42 | 102 | 100001 0 |
| 67 | 43 | 103 | 1000011 |
| 68 | 44 | 104 | 1000100 |
| 69 | 45 | 105 | 1000101 |
| 70 | 46 | 106 | 1000110 |
| 71 90 009 | 47 | 107 | 1000111 |
| 72 | 48 | 110 | 1001 000 |
| 73 | 49 | 111 | 1001001 |
| 74 | 4A | 112 | 100101 0 |
| 75 | 4Б | 113 | 1001011 |
| 76 | 4C | 114 | 1001100 |
| 77 90 009 | 4D | 115 | 1001101 |
| 78 | 4E | 116 | 1001 110 |
| 79 | 4F | 117 | 1001111 |
| Декабрь | Hex | Октябрь | Корзина |
|---|---|---|---|
| 80 | 50 | 120 | 1010000 |
| 81 | 51 | 121 | 1010001 | 90 010
| 82 | 52 | 122 | 1010010 |
| 83 | 53 | 123 | 1010011 |
| 84 | 54 | 124 | 1010100 |
| 85 | 55 | 1 25 | 1010101 |
| 86 | 56 | 126 | 1010110 |
| 87 | 57 | 127 | 1010111 | 90 010
| 88 | 58 | 130 | 1011000 |
| 89 | 59 | 131 | 1011001 |
| 90 | 5A | 132 | 1011010 |
| 91 | 5B | 1 33 | 1011011 |
| 92 | 5С | 134 | 1011100 |
| 93 | 5D | 135 | 1011101 | 90 010
| 94 | 5E | 136 | 1011110 |
| 95 | 5F | 137 | 1011111 |
| Dec | Hex | Oct | Bin |
|---|---|---|---|
| 96 | 60 90 009 | 140 | 1100000 |
| 97 | 61 | 141 | 1100001 |
| 98 | 62 | 142 9000 9 | 1100010 |
| 99 | 63 | 143 | 1100011 |
| 100 9 0009 | 64 | 144 | 1100100 |
| 101 | 65 | 145 | 1100101 |
| 66 | 146 | 1100110 | |
| 103 | 67 | 147 | 1100111 |
| 104 | 68 | 150 90 009 | 1101000 |
| 105 | 69 | 151 | 1101001 |
| 10 6 | 6А | 152 | 1101010 |
| 107 | 6B | 153 | 1101011 |
| 6С | 154 | 1101100 | |
| 109 | 6D | 155 | 1101101 |
| 110 | 6E | 156 | 1101110 |
| 111 | 6F | 157 | 1101111 |
| Декабрь | Hex | Oct | Bin |
|---|---|---|---|
| 112 | 70 | 160 | 1110000 | 90 010
| 113 | 71 | 161 | 1110001 |
| 114 | 72 | 162 | 1110010 |
| 115 | 73 | 163 | 1110011 |
| 116 | 74 | 164 | 1 110100 |
| 117 | 75 | 165 | 1110101 |
| 118 | 76 | 166 | 11101 10 |
| 119 | 77 | 167 | 1110111 |
| 120 | 78 | 170 | 1111000 |
| 121 | 79 | 171 | 1111001 |
| 122 | 7А | 172 | 90 008 1111010|
| 123 | 7B | 173 | 1111011 |
| 124 | 7C | 174 | 1111100 |
| 125 | 7Д | 175 | 1111101 |
| 126 | 7E | 176 | 1111110 |
| 127 | 7F | 177 | 1111111 |
| Декабрь | Шестнадцатеричный 9007 0 | Октябрь | Ячейка |
|---|---|---|---|
| 128 | 80 | 200 | 10000000 |
| 129 | 81 9000 9 | 201 | 10000001 |
| 130 | 82 | 202 | 10000010 |
| 131 | 83 | 203 | 10000011 |
| 132 | 84 | 204 | 10000100 |
| 133 | 85 | 205 | 10000101 |
| 134 | 86 | 206 | 10000110 |
| 135 9000 9 | 87 | 207 | 10000111 |
| 136 | 88 | 210 | 10001000 |
| 137 | 89 | 211 9 0009 | 10001001 |
| 138 | 8А | 212 | 10001010 |
| 139 | 8Б | 213 | 10001011 |
| 140 | 8C | 214 | 10001100 |
| 8D | 215 | 10001101 | |
| 142 | 8E | 216 | 10001110 |
| 143 | 8F | 217 | 10001111 |
| Декабрь | Шестнадцатеричный | Октябрь | Bin 90 070 |
|---|---|---|---|
| 144 | 90 | 220 | 10010000 |
| 145 | 91 | 221 | 9000 8 10010001|
| 146 | 92 | 222 | 10010010 |
| 147 | 93 | 223 | 10010011 |
| 148 | 94 | 224 | 10010100 |
| 149 | 95 | 225 | 10010101 |
| 150 | 96 | 226 | 10010110 |
| 151 | 97 | 227 | 10010111 |
| 152 | 98 | 230 | 10011000 |
| 153 | 99 | 231 | 10011001 90 009 |
| 154 | 9A | 232 | 10011010 |
| 155 | 9B 90 009 | 233 | 10011011 |
| 156 | 9C | 234 | 10011100 |
| 157 | 9D 9000 9 | 235 | 10011101 |
| 158 | 9E | 236 | 10011110 |
| 159 | 9F | 237 | 10011111 |
| Декабрь | Шест.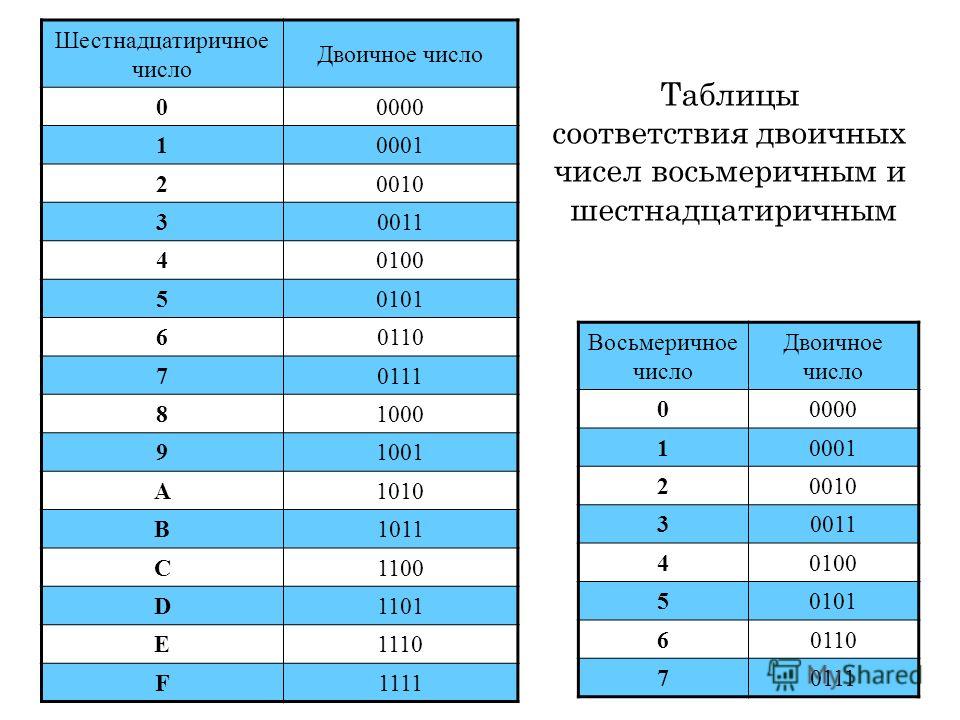 160 160 | А0 | 240 | 10100000 |
|---|---|---|---|---|
| 161 | A1 | 241 | 10100001 | |
| 162 | А2 | 242 | 10100010 | |
| 163 | A3 | 243 | 10100011 | |
| 164 | A4 9 0009 | 244 | 10100100 | |
| 165 | A5 | 245 | 10100101 | 90 010|
| 166 | А6 | 246 | 10100110 | |
| 167 | A7 | 247 | 10100111 | |
| 168 | А8 | 250 | 10101000 | |
| 169 | A9 | 251 | 10101001 | |
| 170 | АА | 252 | 10101010 | |
| 171 | АВ | 253 | 10 101011 | |
| 172 | AC | 254 | 10101100 | |
| 173 | AD | 255 | 10101101 | |
| 174 | АЕ | 256 | 10101110 | |
| 175 | AF | 257 | 10101111 |
| Hex | Oct | Bin | |
|---|---|---|---|
| 192 | C0 | 300 | 1100000 0 |
| 193 | C1 | 301 | 11000001 |
| 194 | C2 | 302 | 90 008 11000010|
| 195 | С3 | 303 | 11000011 |
| 196 | C4 | 304 | 11000100 |
| 197 | C5 | 305 | 11000101 |
| 198 | C6 | 90 008 30611000110 | |
| 199 | C7 | 307 | 11000111 |
| 200 | C8 | 310 | 11001000 |
| 201 | C9 | 311 | 11001001 |
| 202 | СА | 312 | 1100101 0 |
| 203 | СВ | 313 | 11001011 |
| 204 | СС 9 0009 | 314 | 11001100 |
| 205 | CD | 315 | 11001101 |
| 206 | CE 9 0009 | 316 | 11001110 |
| 207 | CF | 317 | 11001111 |
| Дек | He x | Окт | Корзина |
|---|---|---|---|
| 208 | D0 | 320 | 11010000 | 209 | D1 | 321 | 11010001 |
| 210 | D2 | 322 | 11010010 900 09 |
| 211 | D3 | 323 | 11010011 |
| 212 | D4 | 324 | 11010100 |
| 213 | D5 | 325 | 11010101 |
| 214 | D6 | 326 | 1 1010110 |
| 215 | D7 | 327 | 11010111 |
| 216 | D8 | 330 | 110110 00 |
| 217 | D9 | 331 | 11011001 |
| 218 | DA | 332 | 11011010 |
| 219 | БД | 333 | 11011011 |
| 220 | ДК | 334 | 11011100 |
| 221 | ДД | 335 | 11011101 |
| 222 | DE | 336 90 009 | 11011110 |
| 223 | ДФ | 337 | 11011111 |
| Декабрь | Шестнадцатеричный | Октябрь | 900 69 Корзина|
|---|---|---|---|
| 224 | E0 | 340 | 11100000 |
| 225 | E 1 | 341 | 11100001 |
| 226 | E2 | 342 | 11100010 |
| 227 | Е3 | 343 | 11100011 |
| 228 | E4 | 344 | 11100100 |
| 229 | E5 | 3 45 | 11100101 |
| 230 | E6 | 346 | 11100110 |
| Е7 | 347 | 11100111 | |
| 232 | E8 | 350 | 11101000 |
| 233 | Е9 | 351 | 11101001 |
| 234 | EA | 352 | 11101010 |
| 235 | EB 9 0009 | 353 | 11101011 |
| 236 | ЕС | 354 | 11101100 | 90 010
| 237 | ЭД | 355 | 11101101 |
| 238 | EE | 356 | 11101110 |
| 239 | ЭФ | 357 | 11101111 |
| Декабрь | Шестнадцатеричный | Октябрь | Бункер |
|---|---|---|---|
| 240 | F0 | 360 | 11110000 |
| 241 | F1 | 361 9000 9 | 11110001 |
| 242 | F2 | 362 | 11110010 |
| 243 | F3 | 363 | 11110011 |
| 244 | F4 | 364 | 11110100 |
| 245 | F5 | 365 | 111101 01 |
| 246 | F6 | 366 | 11110110 |
| 247 | F7 | 367 | 11110111 |
| 248 | F8 | 370 | 11111000 |
| 249 | F9 | 371 | 11111001 |
| 250 | FA | 372 | 11111010 |
| 251 | FB | 373 900 09 | 11111011 |
| 252 | FC | 374 | 11111100 |
| 25 3 | ФД | 375 | 11111101 |
| 254 | FE | 376 | 11111110 |
| FF | 377 | 11111111 |
Преобразователь базы чисел
Пожалуйста, дайте ссылку на эту страницу! Просто щелкните правой кнопкой мыши на изображении выше, затем выберите «Скопировать адрес ссылки», а затем вставьте его в HTML-код.
- 3736 восьмеричное в десятичное
- 35840 десятичное в шестнадцатеричное
- 11110101001 двоичное в восьмеричное восьмеричное
- 3640 восьмеричное в двоичное
- 1984 десятичное в восьмеричное
- 4A шестнадцатеричное в восьмеричное
- 110010000000 двоичный код в шестнадцатеричный
- 560 восьмеричный в двоичный
двоичный 1011101 шестнадцатеричный | работа, решение
Как написать 1011101 в шестнадцатеричном формате?
1011101 записывается как 5d в шестнадцатеричном формате
Преобразование из/в десятичное в двоичное. Преобразование двоичного числа. Возможно, вы обратились к нам в поисках ответов на такие вопросы, как: Двоичный 1011101 в шестнадцатеричном формате | работа, решение или двоичное преобразование в шестнадцатеричное. Используйте калькулятор ниже, чтобы преобразовать в / из основных базовых систем.
Чтобы использовать этот калькулятор, просто введите значение в любом поле слева.
С помощью этого конвертера вы можете получить ответы на такие вопросы, как:
- Что такое 1011101 в двоичном формате?
- Что такое 1011101 в шестнадцатеричном формате?
- Что такое 1011101 в восьмеричной системе?
- Как преобразовать 1011101 в двоичный файл?
- Как преобразовать 1011101 в двоичный файл? И так далее.
Преобразование десятичной системы в двоичную, включая шестнадцатеричную и восьмеричную
| 9 декабря0070 | Hex | Oct | Bin |
|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 2 | 2 | 2 | 10 |
| 3 | 3 | 3 | 11 |
| 4 | 4 | 900 08 4100 | |
| 5 | 5 | 5 | 101 |
| 6 | 6 | 6 | 110 |
| 7 | 7 | 7 | 111 |
| 8 | 8 | 10 | 1000 |
| 9 | 9 0008 911 | 1001 | |
| 10 | А | 12 | 1010 |
| 11 | Б | 13 | 1011 |
| 12 | C | 14 | 1100 |
| 13 | D | 15 | 1101 |
| 14 | E | 16 | 1110 |
| 15 | F | 17 | 9 0008 1111
| Декабрь | Шестнадцатеричный | Октябрь | Корзина |
|---|---|---|---|
| 16 | 10 | 20 | 10000 |
| 17 | 11 | 21 | 10001 |
| 18 | 12 | 22 | 10010 9000 9 |
| 19 | 13 | 23 | 10011 |
| 20 | 14 | 9000 8 2410100 | |
| 21 | 15 | 25 | 10101 |
| 22 | 16 9000 9 | 26 | 10110 |
| 23 | 17 | 27 | 10111 |
| 24 | 18 | 30 | 11000 |
| 19 | 31 | 11001 | |
| 26 | 1A | 32 | 9000 8 11010|
| 27 | 1Б | 33 | 11011 |
| 28 | 1С | 34 | 9 0008 11100|
| 29 | 1D | 35 | 11101 |
| 30 | 1E | 36 | 11110 |
| 31 | 9 0008 1F37 | 11111 |
| Декабрь | Шестнадцатеричный | Октябрь | Корзина |
|---|---|---|---|
| 32 | 20 | 40 | 100000 |
| 33 | 21 | 41 | 100001 |
| 34 | 22 | 42 | 100010 |
| 35 | 23 | 43 | 100011 |
| 36 | 24 | 44 | 100100 |
| 37 | 25 | 45 | 9 0008 100101|
| 38 | 26 | 46 | 100110 |
| 39 | 27 | 47 | 100111 |
| 40 | 28 | 50 | 101000 |
| 41 | 29 | 51 | 101001 |
| 42 | 2A | 52 | 101010 |
| 43 | 2B | 53 | 10101 1 |
| 44 | 2C | 54 | 101100 |
| 45 | 2D | 55 | 101 101 |
| 46 | 2E | 56 | 101110 |
| 47 | 2F | 57 | 101111 |
| Hex | Oct | Bin | |
|---|---|---|---|
| 48 | 30 | 60 | 110000 9000 9 |
| 49 | 31 | 61 | 110001 |
| 50 | 32 | 62 | 110010 |
| 51 | 33 | 63 | 110011 |
| 52 | 34 | 64 | 110100 |
| 53 | 35 | 65 | 110101 |
| 54 | 36 | 66 | 110110 900 09 |
| 55 | 37 | 67 | 110111 |
| 56 | 38 | 70 | 111000 90 009 |
| 57 | 39 | 71 | 111001 |
| 58 | 3A | 72 | 111010 |
| 59 | 3B 9000 9 | 73 | 111011 |
| 60 | 3C | 74 | 111100 |
| 61 | 3D | 75 | 111101 |
| 62 | 3E | 76 | 111110 |
| 63 | 3F | 77 | 111111 |
Примеры базовых преобразований
- 111110011101001 в десятичное число
- 25244 в двоичное число
- 1111001001010111 в десятичное число
- 10010100011010 в десятичную
- 51324 в двоичную
- 51886 в двоичную
- 1101000100110001 в десятичную
- 4 9736 в двоичном формате
Отказ от ответственности
Несмотря на то, что мы прилагаем все усилия для обеспечения точности информации, представленной на этом веб-сайте, мы не даем никаких гарантий в отношении этой информации.

Leave A Comment