Контрольные работы по геометрии (8 класс)
Контрольные работы по геометрии 8 класс к учебнику «Геометрия 7-9» Л .С. Атанасян и др
Просмотр содержимого документа
«Контрольные работы по геометрии (8 класс)»
Контрольные работы по геометрии 8 класс Учебник « Геометрия 8» Атанасян Л. С.
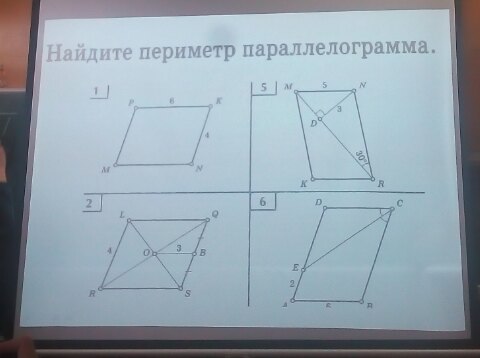
Контрольная работа № 1. «Многоугольники» | ||
1 вариант. 1). Диагонали прямоугольника ABCD пересекается в точке О, ABO = 36°. Найдите AOD. 2). Найдите углы прямоугольной трапеции, если один из ее углов равен 20°. 3). Стороны параллелограмма относятся как 1 : 2, а его периметр равен 30 см. Найдите стороны параллелограмма. 4). В равнобокой трапеции сумма углов при большем основании равна 96°. Найдите углы трапеции. 5).* Высота ВМ, проведенная из вершины угла ромба ABCD образует со стороной АВ угол 30°, АМ = 4 см. Найдите длину диагонали BD ромба, если точка М лежит на стороне AD. | 2 вариант. 1). Диагонали прямоугольника MNKP пересекаются в точке О,MON= 64°. Найдите ОМР. 2). Найдите углы равнобокой трапеции, если один из ее углов на 30° больше второго. 3). Стороны параллелограмма относятся как 3 : 1, а его периметр равен 4). В прямоугольной трапеции разность углов при одной из боковых сторон равна 48°. Найдите углы трапеции. 5).* Высота ВМ, проведенная из вершины угла ромба ABCD образует со стороной АВ угол 30°, длина диагонали АС равна 6 см. | |
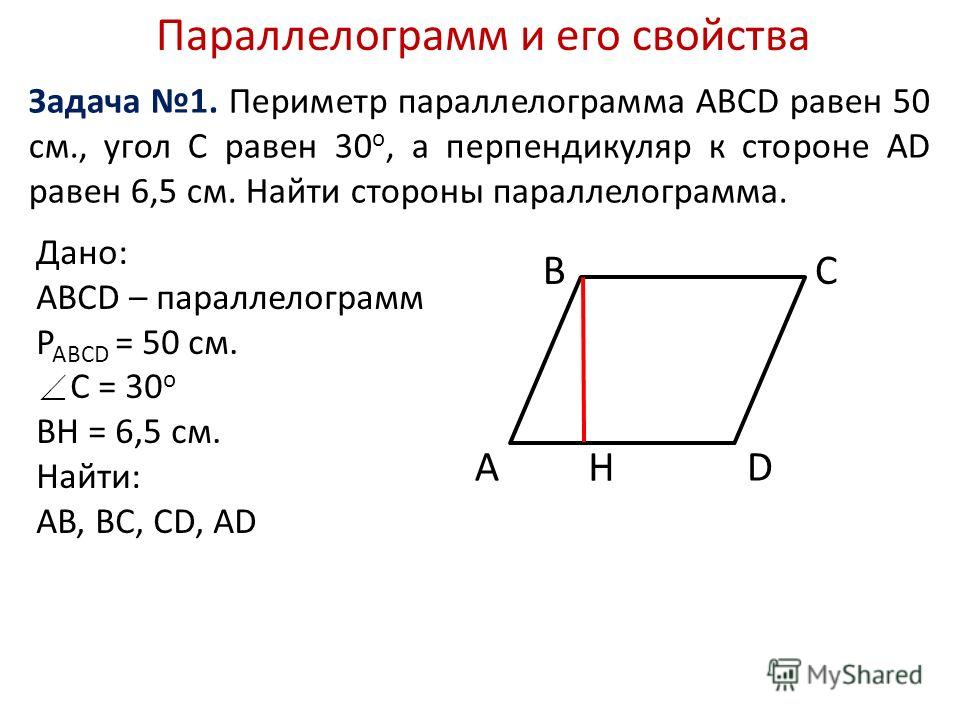
Контрольная работа № 2. «Площади» | ||
1 вариант. 1). Сторона треугольника равна 5 см, а высота, проведенная к ней, в два раза больше стороны. Найдите площадь треугольника. 2). Катеты прямоугольного треугольника равны 6 и 8 см. Найдите гипотенузу и площадь треугольника. 3). Найдите площадь и периметр ромба, если его диагонали равны 8 и 10 см. 4).* В прямоугольной трапеции АВСК большая боковая сторона равна 3см, угол К равен 45°, а высота СН делит основание АК пополам. Найдите площадь трапеции. | 2 вариант. 1). Сторона треугольника равна 12 см, а высота, проведенная к ней, в три раза меньше высоты. Найдите площадь треугольника. 2). 3). Диагонали ромба равны 10 и 12 см. Найдите его площадь и периметр. 4).* В прямоугольной трапеции ABCD большая боковая сторона равна 8 см, угол А равен 60°, а высота ВН делит основание AD пополам. Найдите площадь трапеции. | |
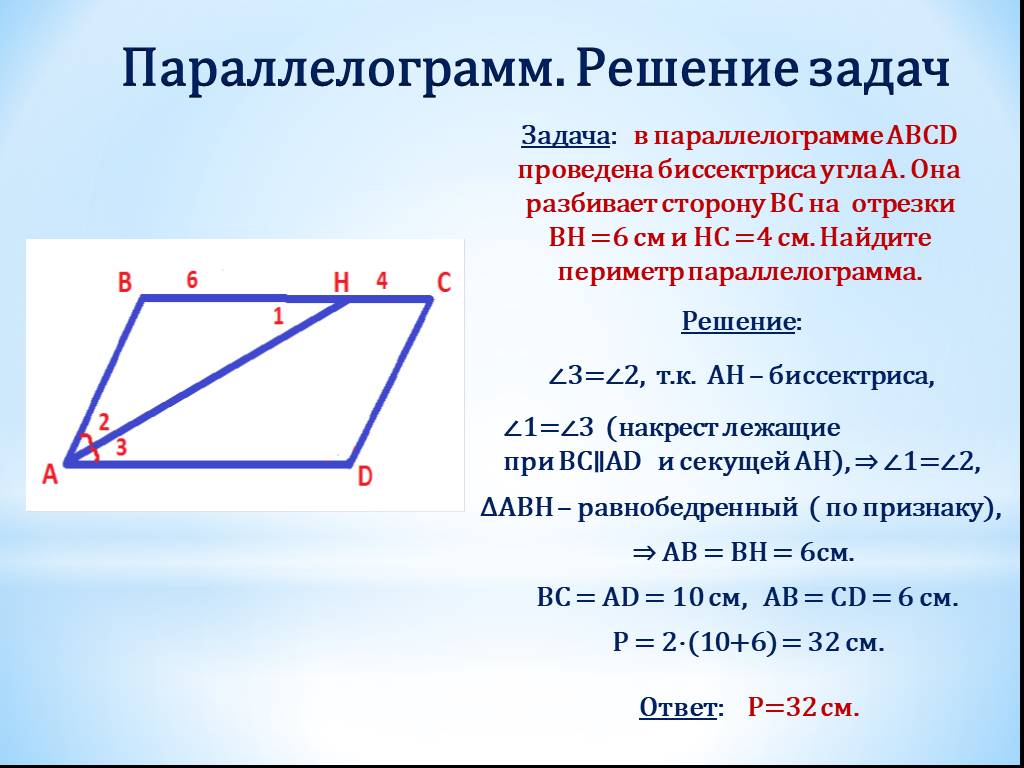
Контрольная работа № 3. « Подобие треугольников» | ||
1 вариант. 1). По рис. A = B, СО = 4, DO = 6, АО = 5. Найти: а). ОВ; б). АС : BD; в). . 2 ). В треугольнике ABC сторона АВ = 4 см, ВС = 7 см, АС = 6 см, а в треугольнике MNK сторона МК = 8 см, MN =12 см, KN = 14 см. 3). Прямая пересекает стороны треугольника ABC в точках М и К соответственно так, что МК || АС, ВМ : АМ = 1 : 4. Найдите периметр треугольника ВМК, если периметр треугольника ABC равен 25 см. 4). В трапеции ABCD (AD и ВС основания) диагонали пересекаются в точке О, AD = 12 см, ВС = 4 см. Найдите площадь треугольника ВОС, если площадь треугольника AOD равна 45 см2. | 2 вариант. 1). По рис. РЕ || NK, MP = 8, MN 2). В ∆ АВС АВ = 12 см, ВС = 18 см, В = 70 0, а в ∆ МNК МN = 6 см, NК = 9 см, N = 70 0. 3). Отрезки АВ и CD пересекаются в точке О так, что ACO = BDO, АО : ОВ = 2:3. Найдите периметр треугольника АСО, если периметр треугольника 4). В трапеции ABCD ( AD и ВС основания) диагонали пересекаются в точке О, = 32 см2, = 8 см2. Найдите меньшее основание трапеции, если большее из них равно 10 см. | |
Контрольная работа № 4. «Прямоугольный треугольник» | |
1 вариант. 1). Средние линии треугольника относятся как 2 : 2 : 4, а периметр треугольника равен 45 см. 2). Медианы треугольника ABC пересекаются в точке О. Через точку О проведена прямая, параллельная стороне АС и пересекающая стороны АВ и ВС в точках Е и F соответственно. Найдите EF, если сторона АС равна 15 см. 3). В прямоугольном треугольнике ABC (C = 90° ) АС = 5 см, ВС = 5 см. Найдите угол В и гипотенузу АВ. 4). В треугольнике ABC A = , 5). В трапеции ABCD продолжения боковых сторон пересекаются в точке К, причем точка В — середина отрезка АК. Найдите сумму оснований трапеции, если AD = 12 см. | 2 вариант. 1). Стороны треугольника относятся как 4 : 5 : 6, а периметр треугольника, образованного его средними линиями, равен 30 см. 2). Медианы треугольника MNK пересекаются в точке О. Через точку 3). В прямоугольном треугольнике РКТ (T = 90° ), РТ = 7см, КТ = 1 см. Найдите угол К и гипотенузу КР. 4). В треугольнике ABC A = , C = , высота ВН равна 4 см. Найдите АС. 5). В трапеции MNKP продолжения боковых сторон пересекаются в точке Е, причем ЕК = КР. Найдите разность оснований трапеции, если NK = 7 |
Контрольная работа № 5. | |
1 вариант. 1). АВ и АС — отрезки касательных, проведенных к окружности радиуса 9 см. Найдите длины отрезков АС и АО, если АВ = 12 см. 2). По рисунку АВ : BC = 11 : 12.Найти: BCA, BAC. 3). Хорды MN и РК пересека- ются в точке Е так, что ME = 12 см, NE = 3 см, РЕ = КЕ. Найдите РК. 4). Окружность с центром О и радиусом 16 см описана около треугольника ABC так, что угол OAB равен 30°, угол OCB равен 45°. Найдите стороны АВ и ВС треугольника. | 2 вариант. 1). MN и МК — отрезки касательных, проведенных к окружности радиуса 5 см. Найти: BOC, ABC. 3). Хорды АВ и CD пересека – ются в точке F так, что AF = 4 см, ВF = 16 см, CF = DF. Найдите CD. 4). Окружность с центром О и радиусом 12 см описана около треугольника MNK так, что угол MON равен 120°, угол NOK равен 90°. Найдите стороны MN и NK треугольника. |
№6. Итоговая аттестация
[PDF] Вариант 1 Найдите тупой угол параллелограмма, если его
Вариант 1 1. Найдите тупой угол параллелограмма, если его острый угол равен Ответ дайте в градусах.
.
2. Один угол параллелограмма больше другого на . Найдите больший угол. Ответ дайте в градусах. 3. Периметр параллелограмма равен 64. Одна сторона параллелограмма на 11 больше другой. Найдите меньшую сторону параллелограмма. 4. Две стороны параллелограмма относятся как , а периметр его равен 40. Найдите большую сторону параллелограмма. 5. Найдите диагональ прямоугольника, две стороны которого равны 8 и 15.
6. Найдите диагональ прямоугольника, если его периметр равен 108, а периметр одного из треугольников, на которые диагональ разделила прямоугольник, равен 95. 7. Найдите меньшую диагональ ромба, стороны которого равны 27, а острый угол равен .
8. Найдите большую диагональ ромба, сторона которого равна угол равен .
, а острый
9. В ромбе угол равен . Найдите угол . Ответ дайте в градусах. 10.Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.
11.Средняя линия трапеции равна 49, а меньшее основание равно 41.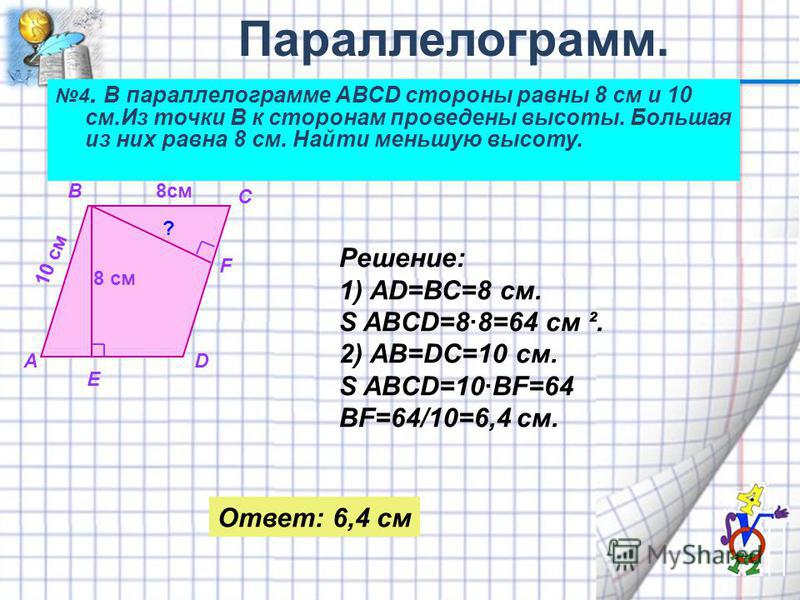 Найдите большее основание трапеции.
Найдите большее основание трапеции.
12.Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 70 и 39. Найдите среднюю линию этой трапеции.
13.В равнобедренной трапеции основания равны 32 и 52, острый угол равен . Найдите ее периметр. 14.Основания равнобедренной трапеции равны 21 и 33. Косинус острого угла трапеции равен . Найдите боковую сторону. 15.Большее основание равнобедренной трапеции равно 25. Боковая сторона равна 10. Синус острого угла равен . Найдите меньшее основание. 16.Основания равнобедренной трапеции равны 43 и 7. Высота трапеции равна 27. Найдите тангенс острого угла.
Вариант 2 1. Найдите тупой угол параллелограмма, если его острый угол равен Ответ дайте в градусах.
.
2. Один угол параллелограмма больше другого на . Найдите больший угол. Ответ дайте в градусах. 3. Периметр параллелограмма равен 22. Одна сторона параллелограмма на 4 больше другой. Найдите меньшую сторону параллелограмма. 4. Две стороны параллелограмма относятся как , а периметр его равен 80. Найдите большую сторону параллелограмма. 5. Найдите диагональ прямоугольника, две стороны которого равны 20 и 15.
4. Две стороны параллелограмма относятся как , а периметр его равен 80. Найдите большую сторону параллелограмма. 5. Найдите диагональ прямоугольника, две стороны которого равны 20 и 15.
6. Найдите диагональ прямоугольника, если его периметр равен 50, а периметр одного из треугольников, на которые диагональ разделила прямоугольник, равен 45. 7. Найдите меньшую диагональ ромба, стороны которого равны 48, а острый угол равен .
8. Найдите большую диагональ ромба, сторона которого равна угол равен .
, а острый
9. В ромбе угол равен . Найдите угол . Ответ дайте в градусах. 10.Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.
11.Средняя линия трапеции равна 21, а меньшее основание равно 13. Найдите большее основание трапеции.
12.Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 90 и 49. Найдите среднюю линию этой трапеции.
13.В равнобедренной трапеции основания равны 67 и 107, острый угол равен . Найдите ее периметр. 14.Основания равнобедренной трапеции равны 23 и 43. Косинус острого угла трапеции равен . Найдите боковую сторону. 15.Большее основание равнобедренной трапеции равно 12. Боковая сторона равна 5. Синус острого угла равен 0,8. Найдите меньшее основание. 16.Основания равнобедренной трапеции равны 43 и 23. Высота трапеции равна 20. Найдите тангенс острого угла.
Вариант 3 1. Найдите тупой угол параллелограмма, если его острый угол равен Ответ дайте в градусах.
.
2. Один угол параллелограмма больше другого на . Найдите больший угол. Ответ дайте в градусах. 3. Периметр параллелограмма равен 48. Одна сторона параллелограмма на 10 больше другой. Найдите меньшую сторону параллелограмма. 4. Две стороны параллелограмма относятся как , а периметр его равен 80. Найдите большую сторону параллелограмма. 5. Найдите диагональ прямоугольника, две стороны которого равны 10 и
6. Найдите диагональ прямоугольника, если его периметр равен 106, а периметр одного из треугольников, на которые диагональ разделила прямоугольник, равен 93.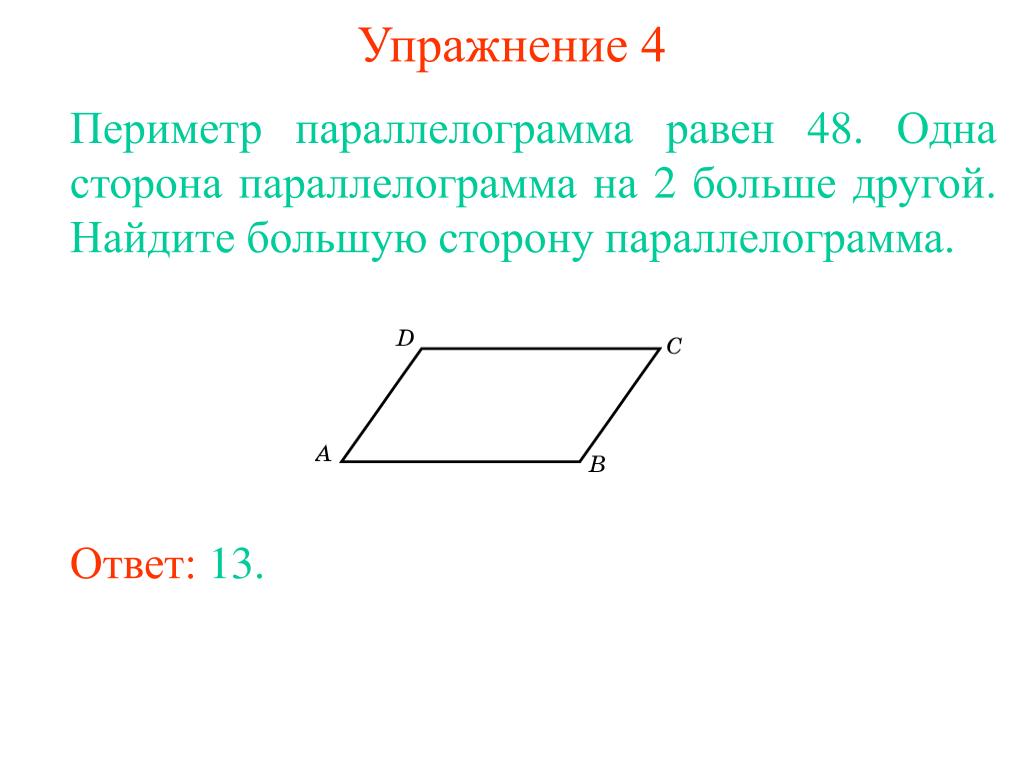 7. Найдите меньшую диагональ ромба, стороны которого равны 17, а острый угол равен .
7. Найдите меньшую диагональ ромба, стороны которого равны 17, а острый угол равен .
8. Найдите большую диагональ ромба, сторона которого равна угол равен .
, а острый
.
9. В ромбе угол равен . Найдите угол . Ответ дайте в градусах. 10.Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.
11.Средняя линия трапеции равна 34,5, а меньшее основание равно 27. Найдите большее основание трапеции.
12.Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 32 и 20. Найдите среднюю линию этой трапеции.
13.В равнобедренной трапеции основания равны 42 и 67, острый угол равен . Найдите ее периметр. 14.Основания равнобедренной трапеции равны 26 и 32. Косинус острого угла трапеции равен . Найдите боковую сторону. 15.Большее основание равнобедренной трапеции равно 26. Боковая сторона равна 18. Синус острого угла равен .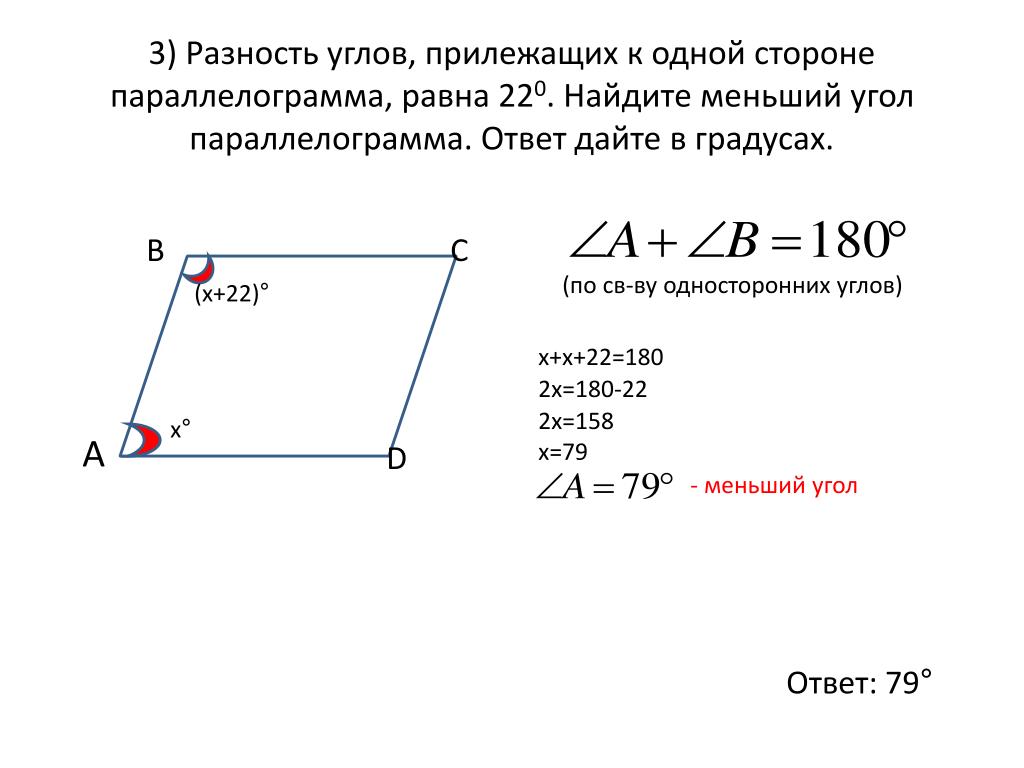 Найдите меньшее основание. 16.Основания равнобедренной трапеции равны 35 и 21. Высота трапеции равна 2,8. Найдите тангенс острого угла.
Найдите меньшее основание. 16.Основания равнобедренной трапеции равны 35 и 21. Высота трапеции равна 2,8. Найдите тангенс острого угла.
Вариант 4 1. Найдите тупой угол параллелограмма, если его острый угол равен Ответ дайте в градусах.
.
2. Один угол параллелограмма больше другого на . Найдите больший угол. Ответ дайте в градусах. 3. Периметр параллелограмма равен 20. Одна сторона параллелограмма на 2 больше другой. Найдите меньшую сторону параллелограмма. 4. Две стороны параллелограмма относятся как , а периметр его равен 20. Найдите большую сторону параллелограмма. 5. Найдите диагональ прямоугольника, две стороны которого равны 20 и 21.
6. Найдите диагональ прямоугольника, если его периметр равен 28, а периметр одного из треугольников, на которые диагональ разделила прямоугольник, равен 26. 7. Найдите меньшую диагональ ромба, стороны которого равны 37, а острый угол равен .
8. Найдите большую диагональ ромба, сторона которого равна угол равен .
, а острый
9.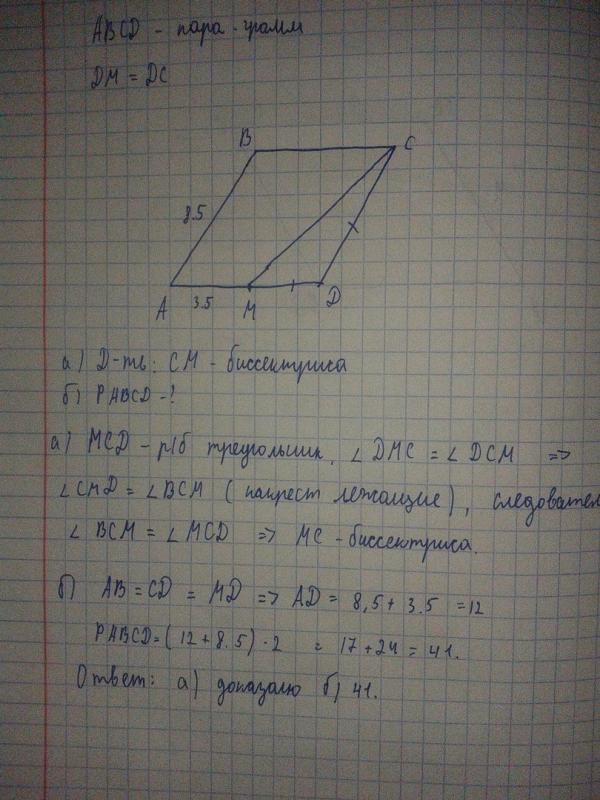 В ромбе угол равен . Найдите угол . Ответ дайте в градусах. 10.Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.
В ромбе угол равен . Найдите угол . Ответ дайте в градусах. 10.Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.
11.Средняя линия трапеции равна 37,5, а меньшее основание равно 29. Найдите большее основание трапеции.
12.Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 86 и 47. Найдите среднюю линию этой трапеции.
13.В равнобедренной трапеции основания равны 57 и 92, острый угол равен . Найдите ее периметр. 14.Основания равнобедренной трапеции равны 25 и 29. Косинус острого угла трапеции равен . Найдите боковую сторону. 15.Большее основание равнобедренной трапеции равно 18. Боковая сторона равна 10. Синус острого угла равен . Найдите меньшее основание. 16.Основания равнобедренной трапеции равны 35 и 16. Высота трапеции равна 3,8. Найдите тангенс острого угла.
Вариант 5 1. Найдите тупой угол параллелограмма, если его острый угол равен Ответ дайте в градусах.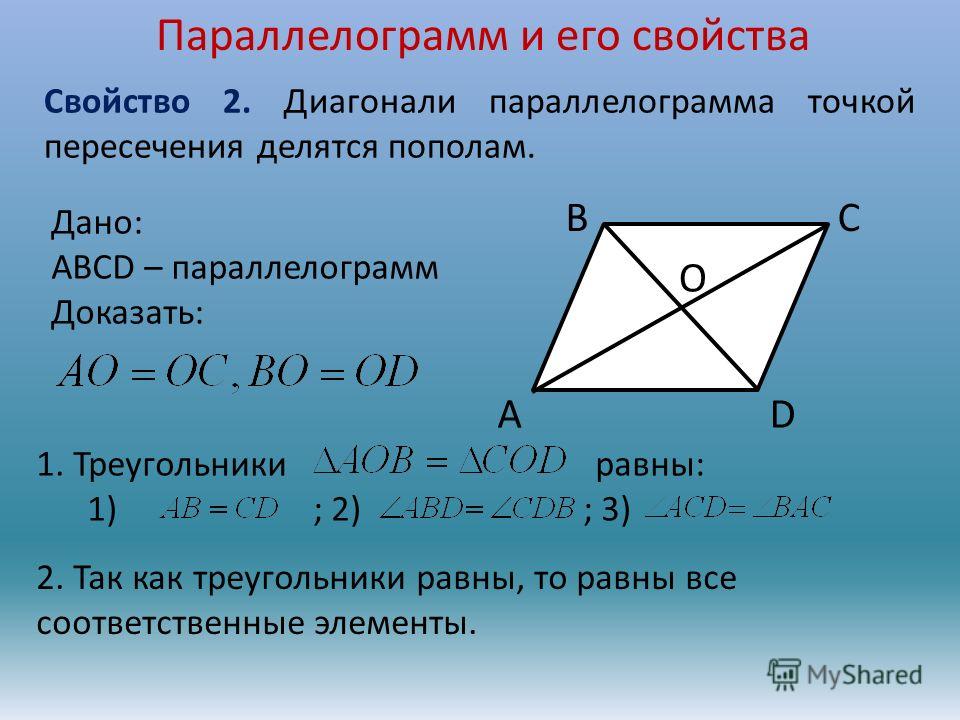
.
2. Один угол параллелограмма больше другого на . Найдите больший угол. Ответ дайте в градусах. 3. Периметр параллелограмма равен 88. Одна сторона параллелограмма на 35 больше другой. Найдите меньшую сторону параллелограмма. 4. Две стороны параллелограмма относятся как , а периметр его равен 24. Найдите большую сторону параллелограмма. 5. Найдите диагональ прямоугольника, две стороны которого равны 6 и
6. Найдите диагональ прямоугольника, если его периметр равен 104, а периметр одного из треугольников, на которые диагональ разделила прямоугольник, равен 91. 7. Найдите меньшую диагональ ромба, стороны которого равны 29, а острый угол равен .
8. Найдите большую диагональ ромба, сторона которого равна острый угол равен .
,а
.
9. В ромбе угол равен . Найдите угол . Ответ дайте в градусах. 10.Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.
11.Средняя линия трапеции равна 47, а меньшее основание равно 23.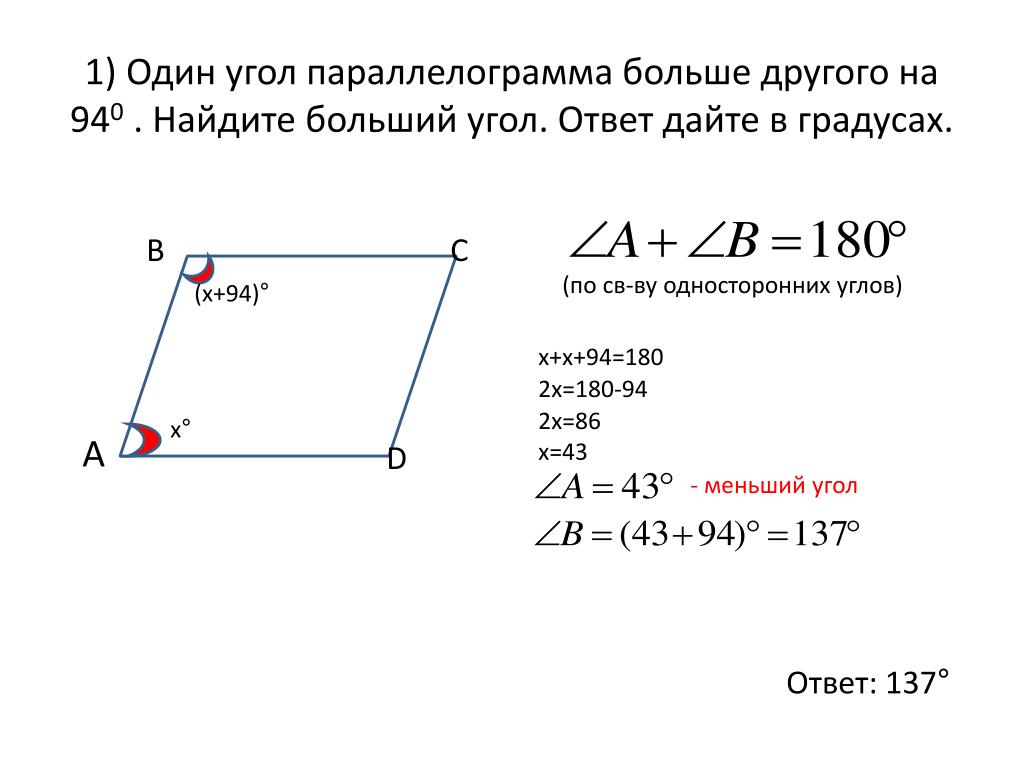 Найдите большее основание трапеции.
Найдите большее основание трапеции.
12.Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 84 и 46. Найдите среднюю линию этой трапеции.
13.В равнобедренной трапеции основания равны 12 и 22, острый угол равен . Найдите ее периметр. 14.Основания равнобедренной трапеции равны 29 и 31. Косинус острого угла трапеции равен . Найдите боковую сторону. 15.Большее основание равнобедренной трапеции равно 56. Боковая сторона равна 36. Синус острого угла равен . Найдите меньшее основание. 16.Основания равнобедренной трапеции равны 26 и 9. Высота трапеции равна 2,125. Найдите тангенс острого угла.
Вариант 6 1. Найдите тупой угол параллелограмма, если его острый угол равен Ответ дайте в градусах.
.
2. Один угол параллелограмма больше другого на . Найдите больший угол. Ответ дайте в градусах. 3. Периметр параллелограмма равен 90. Одна сторона параллелограмма на 37 больше другой. Найдите меньшую сторону параллелограмма.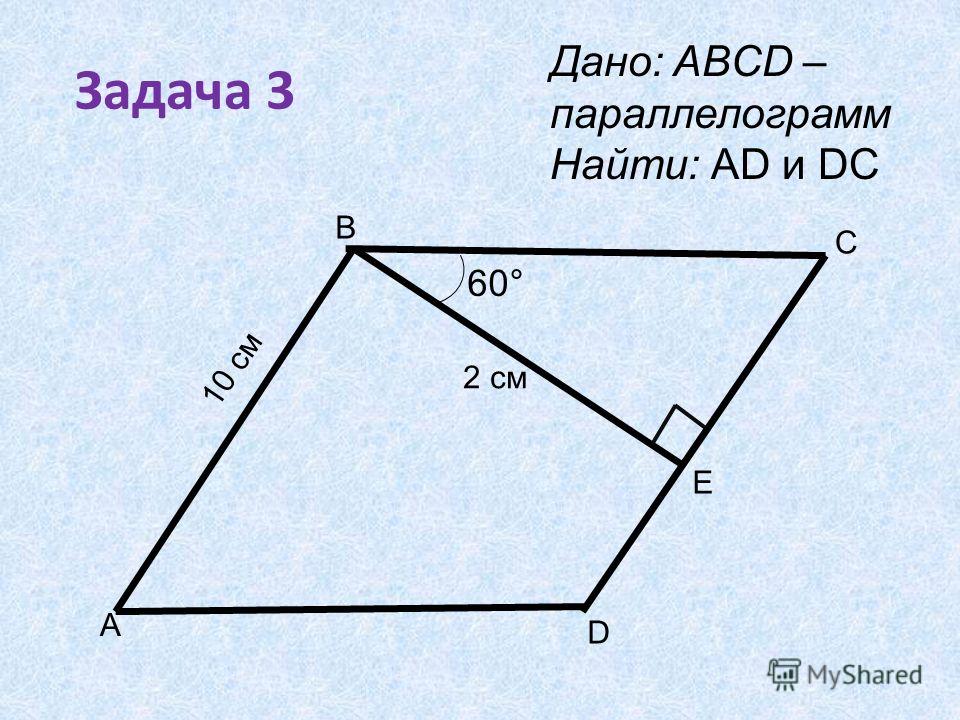 4. Две стороны параллелограмма относятся как , а периметр его равен 40. Найдите большую сторону параллелограмма. 5. Найдите диагональ прямоугольника, две стороны которого равны 6 и .
4. Две стороны параллелограмма относятся как , а периметр его равен 40. Найдите большую сторону параллелограмма. 5. Найдите диагональ прямоугольника, две стороны которого равны 6 и .
6. Найдите диагональ прямоугольника, если его периметр равен 46, а периметр одного из треугольников, на которые диагональ разделила прямоугольник, равен 41. 7. Найдите меньшую диагональ ромба, стороны которого равны 36, а острый угол равен .
8. Найдите большую диагональ ромба, сторона которого равна угол равен .
, а острый
9. В ромбе угол равен . Найдите угол . Ответ дайте в градусах. 10.Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.
11.Средняя линия трапеции равна 53, а меньшее основание равно 45. Найдите большее основание трапеции.
12.Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 34 и 21. Найдите среднюю линию этой трапеции.
13.В равнобедренной трапеции основания равны 23 и 41, острый угол равен . Найдите ее периметр. 14.Основания равнобедренной трапеции равны 20 и 22. Косинус острого угла трапеции равен . Найдите боковую сторону. 15.Большее основание равнобедренной трапеции равно 25. Боковая сторона равна 15. Синус острого угла равен . Найдите меньшее основание. 16.Основания равнобедренной трапеции равны 45 и 23. Высота трапеции равна 33. Найдите тангенс острого угла.
Две стороны параллелограмма находятся в соотношении 53. Если его периметр равен 64 см, найдите длины его сторон…
Перейти к
- Параллелограммы. Упражнение 16А.
- Параллелограммы. Упражнение 16B.
- Рациональное число
- Экспоненты
- Квадраты и квадратные корни
- Кубы и кубические корни
- Игра с числами
- Операции над алгебраическими выражениями
- Факторизация
- Линейные уравнения
- Процент
- Доходы и расходы
- Сложные проценты
- Прямые и обратные пропорции
- Время и работа
- Полигоны
- Параллелограммы
- Построение четырехугольников
- Площадь трапеции и многоугольника
- Трехмерные фигуры
- Объем и площадь поверхности твердых тел
- Обработка данных
- Введение в координатную геометрию
- Линейные графики и линейные графики
- Круговые диаграммы
- Вероятность
Главная >
Решения RS Aggarwal
Класс 8
Математика
>
Глава 16 — Параллелограммы
>
Параллелограммы. Упражнение 16А.
>
Вопрос 4
Упражнение 16А.
>
Вопрос 4
Вопрос 4 Параллелограммы Упражнение 16A
Две стороны параллелограмма относятся как 5:3. Если его периметр равен 64 см, найдите
длин его сторон.
Ответ:
Учитывая, что две стороны параллелограмма относятся как 5:3, пусть x является общим кратным.
Также учитывая, что его периметр равен 64 см
Но мы знаем, что периметр = 2 (длина + ширина) = 2(5x + 3x)
64 = 2(5x + 3x)
64 = 2(8x)
64 = 16x
x = 64/16 = 4
5x=20
3x=12
Следовательно, стороны равны 20 и 12
Связанные вопросы
ABCD — параллелограмм, в котором ∠A=110°. Найдите величину каждого из углов ∠B, ∠C и ∠D.
Два смежных угла параллелограмма равны. Какова мера каждого из этих углов?
Какова мера каждого из этих углов?
Сумма двух противоположных углов параллелограмма равна 130°. Найдите величину каждого из его углов.
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Параллелограммы Упражнение 16A
Параллелограммы Упражнение 16B
Главы
Рациональные числа
Экспоненты
квадратов и квадратных корней
кубиков и корней кубов
Игра с числами
Операции по алгебраическим выражениям
Фактор
Линейные уравнения
Процент
Прибыль
Компонентные интересы
Direct и Ingers. и работа
и работа
Многоугольники
Параллелограммы
Построение четырехугольников
Площадь трапеции и многоугольника
Трехмерные фигуры
Объем и площадь поверхности твердых тел
Обработка данных
Введение в координатную геометрию
Линейные графики и линейные графики
Круговые диаграммы
Вероятность 9003
Курсы
Быстрые ссылки
Условия и политика
Условия и политика
2022 © Quality Tutorials Pvt Ltd Все права защищены
Периметр параллелограмма — формула, определение, примеры, применение
Периметр параллелограмма — это длина непрерывной линии, образованной его границей. Его единица такая же, как и у его сторон. Четырехугольник – это замкнутая фигура, состоящая из четырех отрезков. Четырехугольник называется параллелограммом, если его противоположные стороны параллельны и имеют одинаковую длину. Некоторыми примерами параллелограмма являются ромб, прямоугольник и квадрат. Вот некоторые свойства параллелограмма. Простыми словами можно сказать, что периметр параллелограмма равен сумме всех его четырех сторон.
Вот некоторые свойства параллелограмма. Простыми словами можно сказать, что периметр параллелограмма равен сумме всех его четырех сторон.
- Противоположные стороны равны.
- Противоположные углы равны.
- диагоналей делят друг друга пополам.
- Каждые два соседних угла являются дополнительными.
В этой статье мы узнаем, как найти периметр параллелограмма, используя некоторые формулы. Мы также поймем приложения формул периметра параллелограмма. Мы рассмотрим концепцию с помощью нескольких решенных примеров для лучшего понимания концепции.
| 1. | Что такое периметр параллелограмма? |
| 2. | Периметр формулы параллелограмма |
| 3. | Периметр формулы параллелограмма со сторонами |
| 4. | Периметр формулы параллелограмма с одной стороной и диагоналями |
5. | Периметр основания параллелограмма, высота и угол |
| 6. | Найдите периметр параллелограмма |
| 7. | Часто задаваемые вопросы о периметре параллелограмма |
Что такое периметр параллелограмма?
Периметр параллелограмма равен длине его контура и, следовательно, равен сумме всех его сторон. Но мы всегда можем не знать все стороны параллелограмма. Вместо этого нам могут дать другую информацию о параллелограмме и попросить найти его периметр. Итак, у нас есть разные формулы для нахождения периметра параллелограмма с использованием разных его компонентов. В следующем разделе давайте рассмотрим его различные формулы, чтобы найти периметр параллелограмма.
Периметр формулы параллелограмма
Периметр параллелограмма можно найти в следующих случаях:
- Когда известны две смежные стороны.
- Когда известны одна сторона и диагонали.

- Когда известны основание, высота и любой угол.
Вот формулы для нахождения периметра параллелограмма в каждом из этих случаев:
- P = 2 (a + b), где a, b — смежные стороны параллелограмма
- P = 2a + √(2x 2 + 2y 2 — 4a 2 ), где a — сторона a параллелограмма, а x, y — его диагонали.
- P = 2a + 2h / sinθ, где a — сторона параллелограмма, h — высота, а θ — угол параллелограмма.
Но как вывести все эти формулы? Теперь выведем приведенные формулы для нахождения периметра параллелограмма.
Периметр формулы параллелограмма со сторонами
Как обсуждалось ранее, периметр параллелограмма равен сумме длин всех его сторон. Мы знаем, что противоположные стороны параллелограмма равны. Рассмотрим параллелограмм, у которого две смежные стороны равны «а» и «b» (тогда и две другие смежные стороны будут только «а» и «b»).
Тогда периметр параллелограмма равен a + b + a + b (или) 2a + 2b (или) 2 (a + b).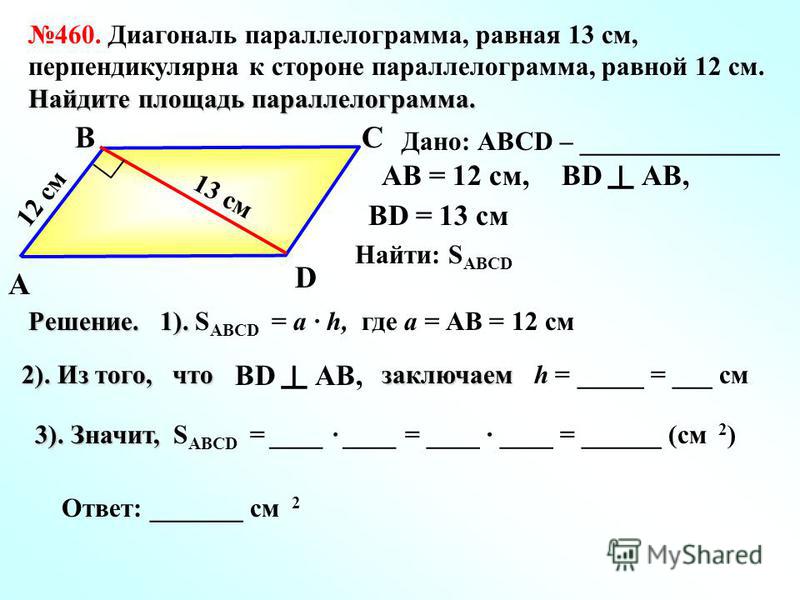 Таким образом, периметр (P) параллелограмма со сторонами a и b равен
Таким образом, периметр (P) параллелограмма со сторонами a и b равен
Р = 2 (а + б) ед.
Формула периметра параллелограмма с одной стороной и диагоналями
Рассмотрим параллелограмм со сторонами ‘a’ и ‘b’ и диагоналями ‘x’ и ‘y’. Предположим, что значения стороны «а» и диагоналей «х» и «у» даны, но значение «b» не задано, и нас просят найти периметр параллелограмма.
Применение закона косинусов для треугольника ABD,
x 2 = A 2 + B 2 — 2AB COS ombad
Применение косинусного правила для ADC Triangle,
Y 2 = A 2 + B 2 — 2 2 + B 2 — 2 2 + B 2 — 2 . Складывая два приведенных выше уравнения,
x 2 + y 2 = 2a 2 + 2b 2 — 2ab (cos ∠BAD + cos ∠ADC) …. (1)
Мы знаем, что любые два смежных угла параллелограмма (это свойство параллелограмма) являются дополнительными. Так
Так
∠BAD + ∠ADC = 180°
∠BAD = 180° — ∠ADC
Применение cos с обеих сторон,
cos ∠BAD = cos (180° — ∠ADC) = — 2 cos 9003ADC Это в (1),
x 2 + y 2 = 2a 2 + 2b 2 — 2Ab ( — COS ϪADC + COS тийдк)
x 2 + y 2 2 2 2 2 2 2 . = 2a 2 + 2b 2 — 2ab (0)
x 2 + y 2 = 2a 2 + 2b 2
Мы получили отношение между сторонами и диагоналями параллелограмма. Теперь мы решим это для «b», так как нам не известна длина «b».
2b 2 = x 2 + y 2 — 2a 2
B 2 = (x 2 + Y 2 — 2A . 2A — 2A — 2A — 2 — 2 4 — 2 — 2 — 2 — 2 — 2 4 — 2 . √ [(x 2 + y 2 — 2a 2 ) / 2]
Теперь мы знаем стороны параллелограмма («a» и «b») и, следовательно, можем использовать формулу из предыдущего сечение, чтобы найти его периметр (P).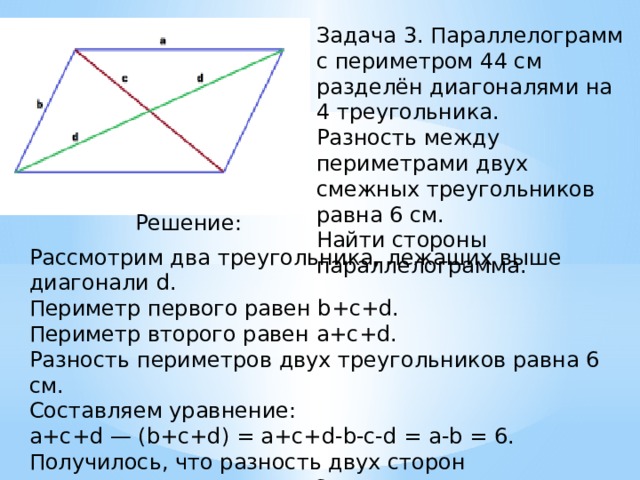
P = 2a + 2b
P = 2a + 2 √ [(x 2 + y 2 — 2a 2 ) / 2]
P = 2a + 904 + √ 2[2] y 2 — 2a 2 )
P = 2a + √(2x 2 + 2y 2 — 4a 2 )
Периметр параллелограмма с основанием, высотой и углом
Рассмотрим параллелограмм, одна из сторон которого равна «a», соответствующая ему высота равна «h», а один из углов при вершине равен «θ». Предположим, что неизвестная сторона параллелограмма равна «b». Сначала мы найдем «b», а затем найдем периметр.
Применение sin к треугольнику BEC,
sin θ = h/b
b = h / sin θ
Таким образом, периметр (P) параллелограмма равен
P = 2a + 2b
3
3
3 P = 2a + 2h / sin θ
Здесь θ не обязательно должен быть определенным углом параллелограмма. Это может быть любой угол при вершине, потому что любые два смежных угла параллелограмма являются дополнительными и sin θ = sin (180 ° — θ) для любого θ.
Найдите периметр параллелограмма
Давайте посмотрим на применение формул периметра параллелограмма в этом разделе. Мы рассмотрим некоторые из решенных примеров, чтобы понять, как найти периметр, используя формулы, обсуждавшиеся в разделах выше.
Пример 1: Найдите периметр параллелограмма, смежные стороны которого равны 5 единицам и 9 единицам.
Решение: Смежные стороны данного параллелограмма равны a = 5 единицам и b = 9 единицам. Тогда его периметр (P) равен
Р = 2 (а + б)
Р = 2 (5 + 9) = 2 (14) = 28 единиц.
Пример 2: Найдите периметр параллелограмма, если одна из его сторон равна 7 единицам, а диагонали равны 8 единицам и 10 единицам.
Решение: Используя формулу, когда даны сторона и диагонали параллелограмма, получаем P = 2a + √(2x 2 + 2y 2 — 4a 2 ). Здесь a = 7, x = 8, y = 10. Подставляя эти значения в формулу, имеем
P = 2a + √(2x 2 + 2y 2 — 4a 2 )
= 2 × 7 + √ (2 (8) 2 + 2 (10) 2 — 4 (7) 2 )
9000 2 — 4 (7) 2 ) 2 — 4 (7) . 14 + √(2 × 64 + 2 × 100 — 4 × 49)
14 + √(2 × 64 + 2 × 100 — 4 × 49)
= 14 + √(128 + 200 — 196)
= 14 + √(132)
= 14 + 11,49
(9200049 единиц) округляется до двух знаков после запятой)Важные замечания по периметру параллелограмма
- Периметр параллелограмма равен сумме всех его четырех сторон.
- У нас есть три формулы для нахождения периметра параллелограмма со сторонами a, b; диагонали x, y и угол θ.
- P = 2 (a + b), где a, b — смежные стороны параллелограмма
- P = 2a + √(2x 2 + 2y 2 — 4a 2 ), где a — сторона a параллелограмма, а x, y — его диагонали.
- P = 2a + 2h / sinθ, где a — сторона параллелограмма, h — высота, а θ — угол параллелограмма.
☛ Статьи по теме:
- Формула параллелограмма
- Формулы периметра
- Разница между площадью и периметром
Периметр параллелограмма Примеры
Пример 1: Чему равен периметр параллелограмма со стороной 8 дюймов и диагоналями 10 дюймов и 12 дюймов? Округлите ответ до двух знаков после запятой.

Решение:
Сторона данного параллелограмма равна a = 8 дюймов.
Пусть другая сторона равна ‘b’ дюймов.
Его диагонали равны x = 10 дюймов и y = 12 дюймов. 2 года 2 — 4a 2 )
P = 2(8) + √(2(10) 2 + 2(12) 2 — 4(8) 2 90 290 265 3,1 ≥ Ответ: Периметр данного параллелограмма = 31,23 дюйма.
Пример 2: Каков периметр параллелограмма, одна из сторон которого равна 15 ярдам, соответствующая ему высота равна 20 ярдам, а один из углов при вершине равен 30 градусам?
Решение:
Одна из сторон данного параллелограмма равна а = 15 ярдам.
Его высота h = 20 ярдов.
Один угол при вершине равен θ = 30°.
Его периметр (P) равен
P = 2a + 2h / sin θ
P = 2(15) + (2 × 20) / (sin 30°) = 110 ярдов
Ответ: Периметр данного параллелограмма = 110 ярдов.

Пример 3: Периметр параллелограмма равен 48 см, а одна из его сторон равна 16 см. Найдите длину другой стороны.
Решение: Дано: периметр (P) = 48 см, а сторона а = 16 см. Чтобы найти длину другой стороны b параллелограмма, воспользуемся формулой периметра параллелограмма P = 2(a + b).
P = 2(a + b)
⇒ 48 = 2 (16 + b)
⇒ 16 + b = 48/2
⇒ b = 24 — 16
⇒ b = 8 см
3 :
Другая сторона параллелограмма равна 8 см.
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами Cuemath.
Записаться на бесплатный пробный урок
Практические вопросы по периметру параллелограмма
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о периметре параллелограмма
Что такое периметр параллелограмма?
Периметр параллелограмма равен сумме всех его сторон. Таким образом, периметр параллелограмма со сторонами «а» и «b» равен a + a + b + b (или) 2a + 2b единиц. Это наиболее часто используемая формула для нахождения периметра параллелограмма.
Таким образом, периметр параллелограмма со сторонами «а» и «b» равен a + a + b + b (или) 2a + 2b единиц. Это наиболее часто используемая формула для нахождения периметра параллелограмма.
По какой формуле найти периметр параллелограмма?
У нас есть разные формулы для нахождения периметра параллелограмма в зависимости от доступной информации.
- Периметр параллелограмма, смежные стороны которого равны ‘a’ и ‘b’, равен 2a + 2b.
- Периметр параллелограмма, одна из сторон которого равна а, а диагонали равны х и у, равен 2а + √(2x 2 + 2y 2 — 4a 2 ).
- Периметр параллелограмма, у которого основание равно «a», высота равна «h», а один из углов при вершине равен «θ», равен 2a + 2h / sin θ.
Что такое периметр параллелограмма с использованием диагоналей?
Мы не можем найти периметр параллелограмма только по диагоналям, но если мы знаем еще и одну из сторон, то можем ее найти. Периметр параллелограмма, одна из сторон которого равна а, а диагонали равны х и у, равен 2а + √(2x 2 + 2y 2 — 4a 2 ).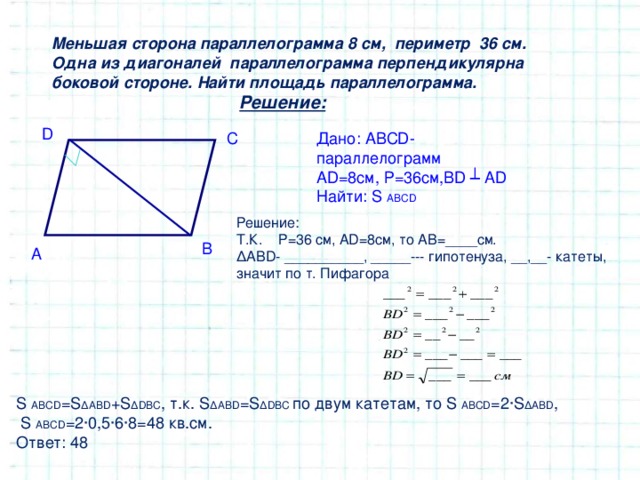
Что такое периметр параллелограмма с использованием основания и высоты?
Мы не можем найти периметр параллелограмма, если известны только основание и высота, но если мы также знаем угол при вершине, то мы можем его найти. Периметр параллелограмма, основание которого равно «а», высота равна «h» и один из углов при вершине равен «θ», равен 2a + 2h/sin θ.
Как найти периметр параллелограмма?
Периметр параллелограмма получается простым сложением всех его сторон. Поскольку противоположные стороны параллелограмма равны, достаточно знать две его смежные стороны, чтобы найти периметр. Но нам не всегда могут быть даны две смежные стороны, вместо этого нам может быть предоставлена некоторая другая информация об этом, чтобы найти его периметр.
- Если даны смежные стороны параллелограмма ‘a’ и ‘b’, то примените формулу 2a + 2b, чтобы найти его периметр.
- Если одна из сторон параллелограмма равна «а», а его диагонали равны «х» и «у», то примените формулу 2а + √(2x 2 + 2y 2 — 4a 2 ), чтобы найти его периметр.



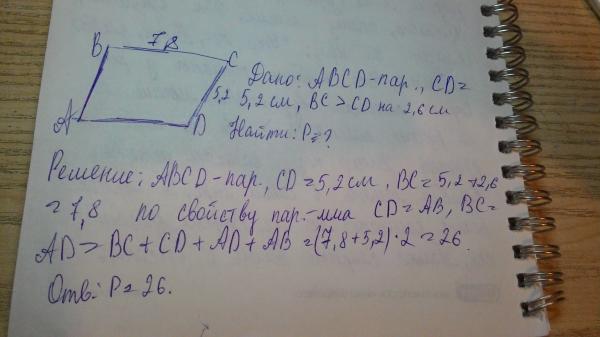 Найдите AM, если точка М лежит на продолжении стороны AD.
Найдите AM, если точка М лежит на продолжении стороны AD. Один из катетов прямоугольного треугольника равен 12 см, а гипотенуза 13 см. Найдите второй катет и гипотенузу треугольника.
Один из катетов прямоугольного треугольника равен 12 см, а гипотенуза 13 см. Найдите второй катет и гипотенузу треугольника.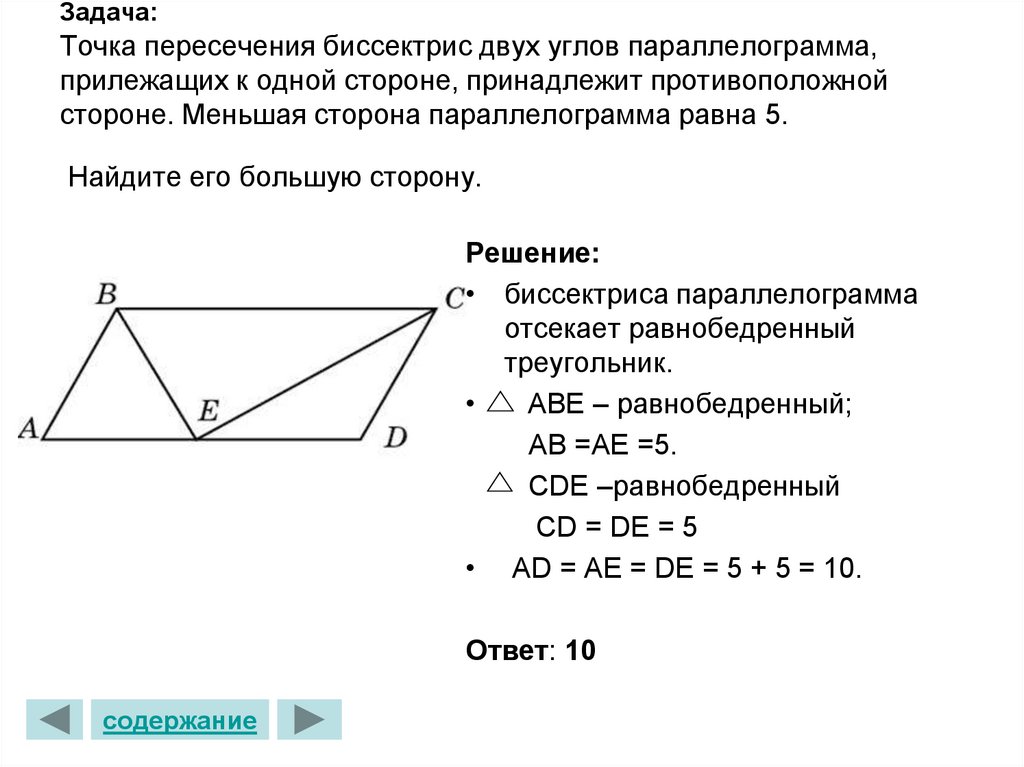 Найдите углы треугольника MNK
Найдите углы треугольника MNK Найдите сторону АС и угол С треугольника АВС, если МК = 7 см, К = 60 0.
Найдите сторону АС и угол С треугольника АВС, если МК = 7 см, К = 60 0.
 Найдите средние линии треугольника.
Найдите средние линии треугольника. «Окружность»
«Окружность» Найдите MN и МК, если МО = 13 см.
Найдите MN и МК, если МО = 13 см.


Leave A Comment