Уравнения и неравенства с-13 1 уравнения высших степеней
УРАВНЕНИЯ И НЕРАВЕНСТВА.
С-13.1 Уравнения высших степеней
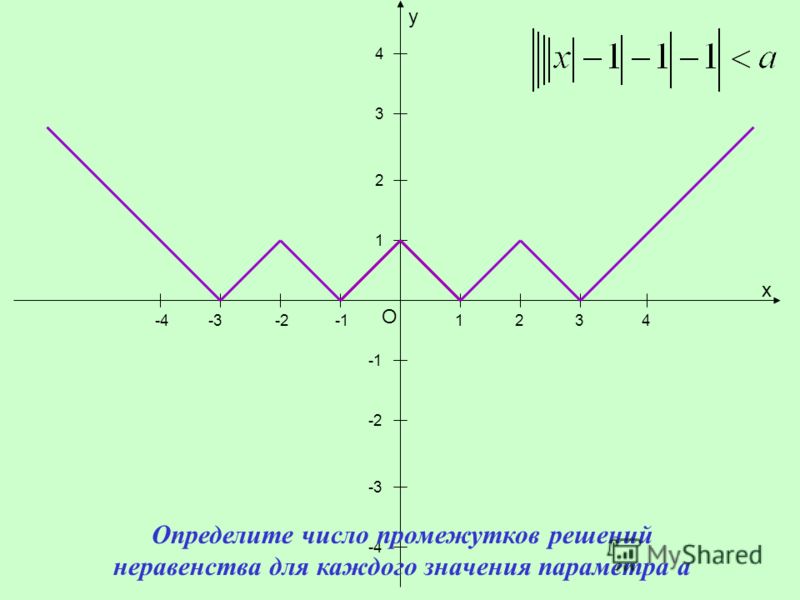
1. Дана функция . а) Решите уравнение ; б) решите неравенство .
2. Дана функция . а) Решите уравнение ; б) выясните, при каких вещественных уравнение имеет единственное решение.
3*. Решите уравнение, представив левую часть в виде произведения квадратных трехчленов: .
4*. Решите неравенство .
С-13.2. Рациональные уравнения и неравенства
1. а) Решите уравнение . б) Решите неравенство .
2. а) .
б) .
3. а) .
б) .
4. а) .
б) .
С-13.3. Системы уравнений. Однородные и симметрические системы
Решите системы уравнений:
1.
2.
3.
4.
5.
С-13.4. Простейшие уравнения и неравенства с параметром. Аналитические методы
1. Решите уравнение с параметром : .
2. Решите неравенство с параметром : .
3. Решите неравенство с параметром : .
4. При каких значениях параметра а неравенство выполнено для всех ?
С-13.5. Уравнения и неравенства с параметром. Графические методы. Плоскость .
1. Решите неравенство с параметром : .
2. Выясните, сколько корней имеет уравнение в зависимости от .
3. При каких значениях а множество решений неравенства содержит отрезок ?
4. Дано неравенство с параметром . а) Выясните, при каких значениях а неравенство имеет решение. б) Выясните, при каких значениях а все решения этого неравенства положительны. в) Решите это неравенство.
С-13.6. Иррациональные уравнения
Решите уравнения:
1.
2.
3.
4.
5.
6.
7.
С-13.7. Иррациональные неравенства
1. Дана функция . а) Решите уравнение .
б) Решите неравенство .
2.
3.
4.
5.
С-13.8. Иррациональные уравнения и неравенства с параметрами
1. Решите уравнение (аналитически).
Решите уравнение (аналитически).
2. а) Найдите количество корней уравнения в зависимости от параметра ; б) решите уравнение для найденных значений ; в) выясните, при каких значениях параметра решение неравенства является лучом; г) решите неравенство .
3. Найдите все значения а, при которых уравнение имеет решение на отрезке .
4. При всех неотрицательных значениях параметра а решите неравенство .
С-13.9.Показательные уравнения
Решите уравнения:
1)
2)
3)
4)
5)
6)
7)
С-13.10. Логарифмические уравнения
Решите уравнения:
1.
2.
3.
4.
5.
6.
7.
С-13.11. Логарифмические неравенства
Решите неравенства:
1.
2.
3.
4.
5.
6.
7.
С-13.12. Логарифмические уравнения и неравенства с параметрами.
Множества на плоскости.
1. а) Изобразите множество точек, задаваемое неравенством .
б) При каких неравенство имеет решения?
в) При каких решение неравенства содержит отрезок длиной больше 1?
г) Решите неравенство .
2. Найдите, при каких неравенство не имеет решений. Решите неравенство для всех вещественных значений a.
С-13.13. Тригонометрические уравнения
1. а) Решите уравнение .
б) Найдите, при каком а уравнение имеет решение.
Решите уравнения:
2.
3.
4.
5.
6.
7.
С-13.14. Тригонометрические неравенства
Решите неравенства:
1.
2.
3.
С-13.15. Смешанные уравнения и неравенства. Отбор корней в тригонометрическом уравнении.
1.
2.
3.
4.
Контрольная работа
Иррациональные уравнения и неравенства
I. Решите уравнения:
1.
2.
3.
4.
5.
II. Решите неравенства:
1.
2.
3.
4.
III.
1. Найдите, при каких уравнение имеет единственное решение.
2. Решите неравенство для всех вещественных значений a.
Контрольная работа
Логарифмические и показательные уравнения и неравенства
I. Решите уравнения:
1.
2.
3.
4.
5.
6.
II. Решите неравенства:
1.
2.
3.
4.
III.
1. Найдите, при каких неравенство не имеет решений.
2. Решите неравенство для всех вещественных значений a.
Контрольная работа: Уравнения и неравенства
1. Решите неравенство:
2. Решите неравенство:
3. Решите уравнение . Для каждого значения параметра a укажите количество корней этого уравнения на отрезке
4. Решите уравнение:
5. Решите неравенство:
6. а) Решите неравенство ;
б) выясните, при каком значении параметра a неравенство не имеет решений;
в) решите неравенство при всех значениях параметра a.
При каких значениях параметра а число корней уравнения равно числу корней уравнений ? 15. Найдите все значения параметра а, при каждом из которых уравнение имеет ровно 8 решений.
ПРИЛОЖЕНИЕ 2практические работы
Практическая работа №1
«Определение типа задач с параметром и выстраивание схемы поиска решения»
Классифицируйте задачи по типу ограничений, накладываемых на параметр, поставив в соответствующем столбце знак «+».
Укажите возможные варианты решения (аналитический, функционально-графический способы).
№
Задание
Классификация задач по типу ограничений, накладываемых на параметр
Варианты решения
нахождение решения для любого значения параметра или значений из указанного множества
определение всех значений параметра при указанном количестве решений
нахождение количества решений в зависимости от значений параметра
определение всех значений параметра, при которых множество решений удовлетворяет заданным условиям
1.
При каких целых значениях параметра а уравнение ах2+2ах+х=1-а будет иметь целые корни?
2.
При каких значениях параметра а уравнение 13 EMBED Equation.3 1415 имеет три решения?
3.
Найдите все значения параметра а, при которых прямые
4х-3у-а=0 и 5х-ау+8=0 пересекаются в точке с отрицательными координатами.
4.
Для каждого значения параметра а определите число решений уравнения 13 EMBED Equation.3 1415.
5.
Для каждого положительного параметра а решите неравенство 13 EMBED Equation.3 1415.
6.
При каких значениях параметра а уравнение ах-1=13 EMBED Equation.3 1415имеет единственное решение?
7.
Определить при каких значениях параметра а решение системы уравнений 13 EMBED Equation.3 1415 удовлетворяет условиям х > 1, у
8.
Сколько корней имеет уравнение 13 EMBED Equation.3 1415 в зависимости от значений параметра а?
9.
Найдите все значения х, которые удовлетворяют неравенству
(2а-х)х2
10.
При каких значениях параметра а система 13 EMBED Equation.3 1415 имеет бесконечно много решений?
Практическая работа №2
«Решение задач с параметром с выбором рационального способа решения»
Уровни
№
Задание
Уровень А
1.
При каких а каждый корень уравнения 3(х+а) =6-а удовлетворяет условию х13 EMBED Equation.3 1415?
2.
Сколько решений в зависимости от параметра а имеет уравнение 13 EMBED Equation.3 1415?
3.
При каких значениях параметра а уравнение 3х2+5х-а=0 имеет два различных корня?
4.
Решите уравнение с параметром (х-1)13 EMBED Equation.3 1415.
5.
При каких значениях параметра а система уравнений 13 EMBED Equation.3 1415 не имеет решения?
Уровень В
6.
При каких значениях параметра а уравнение 3х4+4х3-12х2-а=0 имеет не менее трёх корней?
7.
Определите количество корней уравнения cos2x(sinx-a)=0 на промежутке 13 EMBED Equation.3 1415.
8.
Найдите все значения параметра а, при каждом из которых уравнение 13 EMBED Equation. 3 1415 имеет ровно 4 различных корня на отрезке 13 EMBED Equation.3
3 1415 имеет ровно 4 различных корня на отрезке 13 EMBED Equation.3
9.
Решите неравенство с параметром (а+1)13 EMBED Equation.3 1415
10.
При каком значении параметра а сумма квадратов корней уравнения х2+ х13 EMBED Equation.3 1415принимает наименьшее значение?
Уровень С
11.
Найдите все значения х, которые удовлетворяют неравенству
(2а-3)х2+2>(7а-5)х-6а при любых значениях параметра а13 EMBED Equation.3 1415.
12.
Для каждого значения параметра p определите число корней уравнения13 EMBED Equation.3 1415
13.
При каких значениях параметра а уравнение 13 EMBED Equation.3 1415 имеет решения?
14.
Известно, что уравнение (2а+3)х2+ах+3х=0 имеет хотя бы один корень. При каких значениях параметра а число корней уравнения равно числу корней уравнений 13 EMBED Equation.3 1415?
15.
Найдите все значения параметра а, при каждом из которых уравнение 13 EMBED Equation.3 1415 имеет ровно 8 решений.
Практическая работа №3
«Решение задач с модулем и параметром с выбором рационального способа решения»
Уровни
№
Задание
Уровень А
1.
Решите уравнение с параметром 13 EMBED Equation.3 1415
2.
Решите неравенство с параметром 13 EMBED Equation.3 1415
3.
При каких значениях параметра а уравнение 13 EMBED Equation.3 1415имеет 3 различных решения?
4.
При каких значениях параметра а система уравнений13 EMBED Equation.3 1415 имеет единственное решение?
Уровень В
5.
Решите уравнение с параметром 13 EMBED Equation.3 1415
6.
Решите неравенство с параметром 13 EMBED Equation.3 1415
· х.
7.
Решите уравнение с параметром 13 EMBED Equation.3 1415.
8.
При каких значениях параметра а система неравенств13 EMBED Equation.3 1415 имеет одно решение?
Уровень С
9.
Решите уравнение с параметром 13 EMBED Equation.3 1415
10
При каких значениях параметра а уравнение 3а(х-2)2-213 EMBED Equation. 3 1415+5=0 имеет 4 различных решения?
3 1415+5=0 имеет 4 различных решения?
11.
При каких значениях параметра а система неравенств13 EMBED Equation.3 1415 имеет одно решение? Для всех таких значений а найдите это решение.
12.
При каких значениях параметра а система уравнений 13 EMBED Equation.3 1415 имеет одно решение?
Практическая работа №4
«Конструирование задач с параметром»
Уровень А.
Используя рисунок, составьте уравнение и неравенство с параметром:
13 SHAPE \* MERGEFORMAT 1415
Используя рисунок, составьте задачу с параметром:
13 SHAPE \* MERGEFORMAT 1415
Уровень В.
Используя рисунок, составьте уравнение и неравенство с параметром:
13 SHAPE \* MERGEFORMAT 1415
2. Используя рисунок, составьте задачу с параметром:
Уровень С. Составьте две задачи с параметром, используя алгоритм
конструирования.
х
0
1
1
у
y = f (х)
х
0
1
1
у
y = f (х)
х
0
1
1
у
y = f (х)
y = h(х)
у
х
0
1
1
y = f (х)
y = h(х)
Root EntryEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation Native
Задание с4 Уметь решать различные задачи с параметрами.
6
1. Для каждого значения параметра решите уравнение:
1) (а²-1)х — (2а²+а-3) = 0, где а — параметр.
;
2. Найдите значения параметра р, при которых уравнение (1-р)х² + 2рх – р – 2 = 0 имеет два различных положитель-
ных корня.
3. Найдите значения параметра р, при которых уравнение рх² + 2(р-1)х + р – 3 = 0 имеет два различных отрицатель-
ных корня.
4. Найдите значения параметра р, при которых уравнение (1-р)х² + 2(р-3)х + 4 – р = 0 имеет корни разных знаков.
5. При каких значениях параметра а оба корня уравнения ах² + 4 ах + 1 – 2а + 4а² = 0 меньше чем -1?
6. При каких значениях параметра а один корень уравнения ах² + х + 1 = 0 больше 2, а другой корень меньше чем 2?
7. При каких значениях параметра а оба корня уравнения х² — ах + 2 = 0 лежат на промежутке (0; 3)?
8. Найдите значение параметра а, при которых 1 лежит между корнями уравнения 2ах² — 2х – 3а – 2 = 0.
9. Найдите значение параметра а, при которых уравнение (а-1)х² — 2ах + 2 – 3а = 0 имеет единственное решение,
10. При каких значениях параметра р все корни уравнения (2-р)х² — 3рх + 2р = 0 больше чем 0,5?
11. При каких значениях параметра а корни уравнения х² — 2ах + а² — а = 0 расположены на отрезке [-2;6]?
12. Найдите значения параметра а, при которых один корень уравнения (а-2)х² — 2(а+3)х + 4а = 0 меньше чем 2,
а другой корень больше чем 3.
13. При каких значениях параметра а уравнения х² + ах + 1 = 0 и х² + х + а = 0 имеют общий корень?
14. При каких значениях параметра а уравнения (1-а)х² + 2х – 4а = 0 и ах² — 4х + 4а = 0 равносильны?
15. Найдите все значения параметра р, при которых уравнениеимеет четыре различных
действительных корня.
16. Найдите все значения параметра а, при каждом из которых уравнение имеет единственное
решение.
17. При каких значениях параметра а уравнение имеет два различных решения?
18. При каких значениях параметра р уравнение имеет два различных корня?
19. При каких значениях параметра с уравнение
имеет единственное решение?
При каких значениях параметра с уравнение
имеет единственное решение?
20. Найдите значения параметра а, при которых уравнение имеет два различных корня.
21. Найдите значения параметра с, при котором уравнение имеет единственный корень.
22. Найдите все значения параметра р, при которых уравнение 4Sin3x – 3Cos6x = p не имеет корней.
23. При каких значениях параметра с уравнение 2Cos2x – Cos4x = c имеет хотя бы один корень?
24. При каких значениях параметра а уравнение не имеет корней?
25. Найдите все значения параметра а, при которых уравнение имеет один корень.
26. При каких значениях параметра а уравнение имеет два действительных корня?
Задание с4 Задачи с параметрами.
27. При каких значениях параметра а система уравнений имеет единственное решение?
28. Найдите все значения параметра а, при которых уравнение имеет единственное решение.
29. Найдите все значения параметра р, при которых уравнение имеет одно решение.
30. При каких значениях параметра а уравнение имеет решения?
31. При каких а уравнение имеет решение?
32. При каких значениях а найдутся такие значения х , что числа в указанном порядке обра-
зуют арифметрическую прогрессию?
33. Найдите все значения параметра р, при которых найдутся такие значения х, что числа
в указанном порядке образуют некоторую арифметическую прогрессию.
34. Найдите все значения параметра а, при которых уравнение имеет единственное решение.
35. Найдите значения параметра р, при которых уравнение имеет единственное решение.
36. Для каждого значения параметра а решите неравенство:
37. При каких значениях параметра а данное неравенство выполняется при любых действительных значениях х?
1) (а + 4 ) х² — 2aх
+ 2а – 6 < 0 ; 2 ) ( a²
— 1 ) x²
+ 2 ( a
– 1 ) x
+ 2 > 0.
38. Найдите все значения параметра р, при которых значение многочлена f(x) = (p² — 1)x² + 2(p – 1)x + 1 положительно
при любых действительных х.
39. При каком наименьшем целом значении р функция f(x) = -x³ + x² — 5x + 2 убывает на все числовой прямой?
40. При каком наименьшем целом р функция возрастает на всей числовой прямой?
41. При каком значении а, для всех х таких, что хε (1;2) выполняется неравенство х² + ах + а² + 6а < 0?
42. Найдите все значения параметра а, для которых неравенство х² — ах + а > 0 верно при всех х, удовлетворяющих
неравенству .
43. При каких значениях параметра а каждое решение неравенства х² — 3х + 2 < 0 будет содержаться среди решений
неравенства ах² — ( 3а + 1)х + 3 ≥ 0.
44. Найдите значения параметра а, при которых область определения данной функции f(x) совпадаете со множеством
всех действительных чисел:
45. Найдите все значения параметра а, при которых область определения функции содержит
пять целых чисел.
46. Найдите все значения параметра а, при которых область определения функции содержит
отрезок длиной 4, состоящий из отрицательных чисел.
47. Найдите значения параметра а, при которых область определения функции содержит
отрезок длины 3, состоящий из положительных чисел.
2-2kx + 2k + 2 <0. $Не соответствует решению в моей книге. Возможно, я неправильно понял вопрос или мое решение неверно. Или в книге это неправильно сказано.
Я правильно понял вопрос? Если да, то мое решение правильное?
Большое спасибо.
Диапазон значений неравенства параметров.
Вот что я сделал:
Имеем следующее неравенство:
$$ 5c-3a \ leq b \ leq 4c-a. \ Quad \ quad (E_0) $$
Поскольку $ b> 0 $, то можно разделить на $ b $:
$$ \ dfrac {5c-3a} {b} \ leq 1 \ leq \ dfrac {4c-a} {b}. \ quad (1) $$
\ quad (1) $$
Далее $ (1) $ можно увидеть как:
$$ \ dfrac {5c-3a} {b} \ leq 1 \ leq \ dfrac {5c-3a + 2a-c} {b}, $$ или же $$ \ dfrac {5c-3a} {b} \ leq 1 \ leq \ dfrac {5c-3a} {b} + \ dfrac {2a-c} {b}, $$ или же $$ 0 \ leq 1- \ dfrac {5c-3a} {b} \ leq \ dfrac {2a-c} {b}. \ Quad (2) $$
С помощью $ (2) $ мы можем заключить, что: $ \ dfrac {2a-c} {b} \ geq0 $ и поскольку $ b> 0 $, то $ 2a-c \ geq0 $.
В итоге имеем: $$ \ dfrac {c} {a} \ leq2. \ Quad \ quad (E_1) $$
Теперь вернемся к $ (E_0) $ и разделим его на $ a $, получим:
$$ 5 \ dfrac {c} {a} -3 \ leq \ dfrac {b} {a} \ leq 4 \ dfrac {c} {a} -1.\ quad (3) $$
Используя $ (E_1) $, мы получаем верхнюю границу: $$ \ dfrac {b} {a} \ leq 4 \ dfrac {c} {a} -1 \ leq7. $$
Теперь пора использовать логарифмическое неравенство, чтобы получить нижнюю оценку.
У нас:
$$ c \ log b \ geq a + c \ log c. $$
Сначала разделим его на $ c $, получим:
$$ \ log b \ geq \ dfrac {a} {c} + \ log c. $$
Мы снова используем $ (E_1) $, чтобы увидеть, что: $ \ log \ dfrac {b} {c} \ geq \ dfrac {a} {c} \ geq \ dfrac {1} {2}> 0. $ (I это необходимо, чтобы гарантировать, что $ \ log \ dfrac {b} {c}> 0 $).Затем это полезно разделить на $ \ log \ dfrac {b} {c} $ с обеих сторон. Затем
$$ \ dfrac {c} {a} \ geq \ dfrac {1} {\ log \ dfrac {b} {c}}. $$
Вернувшись к $ (3) $ и используя левую часть, мы получим:
$$ — 3 + 5 \ dfrac {c} {a} \ geq -3+ \ dfrac {5} {\ log \ dfrac {b} {c}}. \ Quad (4) $$
Теперь разделите $ (E_0) $ на $ c $ и примените журнал (мы о правой части), вы получите:
$$ \ log \ dfrac {b} {c} \ leq \ log (4- \ dfrac {a} {c}). $$
Что эквивалентно (с использованием $ (E_1) $)
$$ \ log \ dfrac {b} {c} \ leq \ log (4- \ dfrac {a} {c}) \ leq \ log \ dfrac {7} {2}.
$Теперь используйте $ (4) $, чтобы получить:
$$ — 3 + 5 \ dfrac {c} {a} \ geq -3+ \ dfrac {5} {\ log \ dfrac {b} {c}} \ geq -3+ \ dfrac {5} {\ log \ dfrac {7} {2}}. \ quad (E_2) $$
\ quad (E_2) $$
Вывод:
$$ — 3+ \ dfrac {5} {\ log \ dfrac {7} {2}} \ leq \ dfrac {b} {a} \ leq 7. $$ $$ 0.99 \ leq \ dfrac {b} {a} \ leq 7. $$
Изменить: $ \ log $ — натуральный логарифм. Раньше я неправильно рассчитывал.
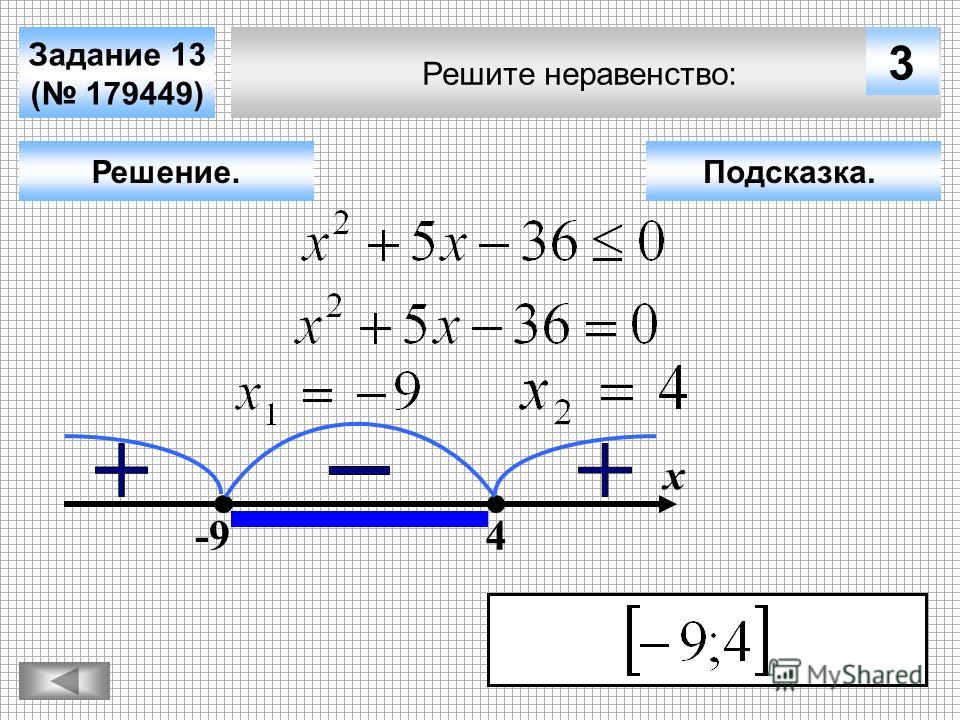
Решение квадратичных неравенств
Решения квадратичных неравенств
Квадратичное неравенство Математическое утверждение, которое связывает квадратное выражение как меньшее или большее, чем другое.является математическим утверждением, которое связывает квадратное выражение как меньшее или большее, чем другое. Некоторые примеры квадратных неравенств, решаемых в этом разделе, приведены ниже.
| x2−2x − 11≤0 | 2×2−7x + 3> 0 | 9 − x2> 0 |
Решением квадратного неравенства является действительное число, которое при замене переменной дает истинное утверждение.
Пример 1
Являются ли −3, −2 и −1 решениями x2 − x − 6≤0?
Решение:
Замените данное значение на x и упростите.
x2 − x − 6≤0x2 − x − 6≤0x2 − x − 6≤0 (−3) 2 — (- 3) −6≤0 (−2) 2 — (- 2) −6≤0 (- 1) 2 — (- 1) −6≤09 + 3−6≤04 + 2−6≤01 + 1−6≤06≤0✗0≤0 ✓ − 4≤0 ✓
Ответ: −2 и −1 — решения, −3 — нет.
Квадратичные неравенства могут иметь бесконечно много решений, одно решение или ни одного решения.Если существует бесконечно много решений, изобразите набор решений на числовой прямой и / или выразите решение, используя обозначение интервалов. Построив график функции, определенной как f (x) = x2 − x − 6, найденной в предыдущем примере, мы имеем
Результат вычисления любого значения x будет отрицательным, нулевым или положительным.
f (−3) = 6 Положительный f (x)> 0 f (−2) = 0 Zerof (x) = 0 f (−1) = — 4 Отрицательный f (x) <0
Значения в домене функции, разделяющие области, дающие положительные или отрицательные результаты, называются критическими числами. Значения в домене функции, которые разделяют области, дающие положительные или отрицательные результаты.. В случае квадратичной функции критическими числами являются корни, иногда называемые нулями. Например, f (x) = x2 − x − 6 = (x + 2) (x − 3) имеет корни −2 и 3. Эти значения ограничивают области, где функция положительна (выше оси x ). или отрицательный (ниже оси x ).
Следовательно, x2 − x − 6≤0 имеет решения, где −2≤x≤3, используя обозначение интервала [−2,3]. Кроме того, x2 − x − 6≥0 имеет решения, где x≤ − 2 или x≥3, используя обозначение интервала (−∞, −2] ∪ [−3, ∞).
Пример 2
По графику f определите решения для f (x)> 0:
Решение:
Из графика мы видим, что корни равны −4 и 2. График функции лежит выше оси x (f (x)> 0) между этими корнями.
Из-за строгого неравенства набор решений закрашен открытой точкой на каждой из границ.Это означает, что эти критические числа фактически не включены в набор решений. Этот набор решений можно выразить двумя способами:
{x | −4 В этом учебнике мы продолжим представлять ответы в интервальной нотации. Ответ: (−4,2) Попробуй! По графику f определите решения для f (x) <0: Ответ: (−∞, −4) ∪ (2, ∞) Далее мы описываем технику, используемую для решения квадратичных неравенств без построения графика параболы. Знаки плюс указывают на то, что функция положительна для региона. Отрицательные знаки указывают на то, что функция отрицательная по региону.Границы — это критические числа, в данном случае −2 и 3. Знаковые диаграммы полезны, когда подробное изображение графика не требуется, и они широко используются в математике более высокого уровня. Шаги по решению квадратного неравенства с одной переменной описаны в следующем примере. Решите: −x2 + 6x + 7≥0. Решение: Важно отметить, что это квадратное неравенство имеет стандартную форму с нулем на одной стороне неравенства. Шаг 1 : Определите критические числа. Для квадратного неравенства в стандартной форме критическими числами являются корни. Поэтому установите функцию равной нулю и решите. −x2 + 6x + 7 = 0− (x2−6x − 7) = 0− (x + 1) (x − 7) = 0x + 1 = 0 или x − 7 = 0x = −1x = 7 Критические числа -1 и 7. Шаг 2 : Создайте знаковую диаграмму. Поскольку критические числа ограничивают области, в которых функция является положительной или отрицательной, нам нужно проверить только одно значение в каждой области.В этом случае критические числа делят числовую прямую на три области, и мы выбираем тестовые значения x = −3, x = 0 и x = 10. Тестовые значения могут отличаться. Фактически, нам нужно только определить знак (+ или -) результата при вычислении f (x) = — x2 + 6x + 7 = — (x + 1) (x − 7). f (−3) = — (- 3 + 1) (- 3−7) = — (- 2) (- 10) = — Отрицательное f (0) = — (0 + 1) (0−7) = — (1) (- 7) = + Положительный f (10) = — (10 + 1) (10−7) = — (11) (3) = — Отрицательный Поскольку результат оценки −3 был отрицательным, мы помещаем отрицательные знаки над первой областью.Результат оценки на 0 был положительным, поэтому мы помещаем положительные знаки над средней областью. Наконец, результат оценки 10 был отрицательным, поэтому мы помещаем отрицательные знаки над последней областью, и диаграмма знаков готова. Шаг 3 : Используйте табличку с знаками, чтобы ответить на вопрос. В этом случае нас просят определить, где f (x) ≥0, где функция положительна или равна нулю. На диаграмме знаков мы видим, что это происходит, когда значения x находятся между -1 и 7 включительно. Используя обозначение интервалов, заштрихованная область выражается как [−1,7]. График не требуется; однако для полноты он представлен ниже. Действительно, функция больше или равна нулю, выше или на оси x для значений x в указанном интервале. Ответ: [−1,7] Решить: 2×2−7x + 3> 0. Решение: Начните с определения критических чисел, в данном случае корней f (x) = 2×2−7x + 3. 2×2−7x + 3 = 0 (2x − 1) (x − 3) = 02x − 1 = 0 или x − 3 = 02x = 1x = 3x = 12 Критические числа — 12 и 3. Из-за строгого неравенства> мы будем использовать открытые точки. Затем выберите тестовое значение в каждой области и определите знак после оценки f (x) = 2×2−7x + 3 = (2x − 1) (x − 3).Здесь мы выбираем тестовые значения −1, 2 и 5. f (−1) = [2 (−1) −1] (- 1−3) = (-) (-) = + f (2) = [2 (2) −1] (2−3) = (+) (-) = — f (5) = [2 (5) −1] (5−3) = (+) (+) = + И мы можем заполнить табличку знаков. Вопрос просит нас найти значения x , которые дают положительные результаты (больше нуля). Поэтому заштрихуйте области со знаком «+» над ними. Это набор решений. Ответ: (−∞, 12) ∪ (3, ∞) Иногда квадратичная функция не учитывается.В этом случае мы можем использовать формулу корней квадратного уравнения. Решите: x2−2x − 11≤0. Решение: Найдите критические числа. x2−2x − 11 = 0 Определите a , b и c для использования в формуле корней квадратного уравнения. Здесь a = 1, b = −2 и c = −11. Подставьте соответствующие значения в формулу корней квадратного уравнения, а затем упростите. x = −b ± b2−4ac2a = — (- 2) ± (−2) 2−4 (1) (- 11) 2 (1) = 2 ± 482 = 2 ± 432 = 1 ± 23 Следовательно, критические числа 1−23≈ − 2,5 и 1 + 23≈4,5. Используйте закрытую точку на номере, чтобы указать, что эти значения будут включены в набор решений. Здесь мы будем использовать тестовые значения −5, 0 и 7. f (−5) = (- 5) 2−2 (−5) −11 = 25 + 10−11 = + f (0) = (0) 2−2 (0) −11 = 0 + 0−11 = −f (7) = (7) 2−2 (7) −11 = 49−14−11 = + После заполнения знаковой диаграммы закрасьте значения, в которых функция отрицательна, как указано в вопросе (f (x) ≤0). Ответ: [1-23,1 + 23] Попробуй! Решите: 9 − x2> 0. Ответ: (−3,3) Возможно, нет критических чисел. Решите: x2−2x + 3> 0. Решение: Чтобы найти критические числа, решите, x2−2x + 3 = 0 Подставляем a = 1, b = −2 и c = 3 в формулу корней квадратного уравнения, а затем упрощаем. x = −b ± b2−4ac2a = — (- 2) ± (−2) 2−4 (1) (3) 2 (1) = 2 ± −82 = 2 ± 2i22 = 1 + i2 Поскольку решения нереальны, мы заключаем, что настоящих корней нет; следовательно, нет критических чисел. В этом случае график не имеет пересечений x и полностью находится выше или ниже оси x . Мы можем протестировать любое значение, чтобы создать знаковую диаграмму. Здесь мы выбираем x = 0. f (0) = (0) 2−2 (0) + 3 = + Поскольку тестовое значение дало положительный результат, знаковая диаграмма выглядит следующим образом: Ищем значения, при которых f (x)> 0; знаковая диаграмма подразумевает, что любое действительное число для x удовлетворяет этому условию. Ответ: (−∞, ∞) Функция из предыдущего примера изображена на графике ниже. Мы видим, что он не имеет точек пересечения x и всегда находится выше оси x (положительное значение). Если бы вопрос заключался в решении x2−2x + 3 <0, то ответом было бы отсутствие решения. Функция никогда не бывает отрицательной. Попробуй! Решить: 9×2−12x + 4≤0. Ответ: Одно решение, 23. Найдите область: f (x) = x2−4. Решение: Напомним, что аргумент функции извлечения квадратного корня должен быть неотрицательным. Следовательно, область состоит из всех действительных чисел для x , таких что x2−4 больше или равно нулю. x2−4≥0 Должно быть ясно, что x2−4 = 0 имеет два решения x = ± 2; это критические значения.Выберите тестовые значения в каждом интервале и оцените f (x) = x2−4. f (−3) = (- 3) 2−4 = 9−4 = + f (0) = (0) 2−4 = 0−4 = −f (3) = (3) 2−4 = 9 −4 = + Оттенок в x -значениях, дающих положительный результат. Ответ: Домен: (−∞, −2] ∪ [2, ∞) Определите, является ли данное значение решением. По графику f определите набор решений. f (x) ≤0; f (x) ≥0; f (x) ≥0; f (x) ≤0; f (x)> 0; f (x) <0; f (x)> 0; f (x) <0; f (x) ≥0; f (x) <0; Используйте преобразования, чтобы построить график следующего, а затем определить набор решений. Используйте знаковую диаграмму для решения и построения графика набора решений.Представляйте ответы, используя интервальную нотацию. Найдите область определения функции. Компания по производству робототехники определила, что ее недельная прибыль в тысячах долларов моделируется формулой P (n) = — n2 + 30n − 200, где n представляет количество единиц, которые она производит и продает.Сколько единиц должна произвести и продать компания, чтобы сохранить прибыльность. (Подсказка: прибыльность возникает, когда прибыль больше нуля.) Высота в футах снаряда, выпущенного прямо в воздух, определяется выражением h (t) = — 16t2 + 400t, где t представляет время в секундах после выстрела. В какие промежутки времени снаряд находится на глубине менее 1000 футов? Округлить до ближайшей десятой доли секунды. Всегда ли знаковая диаграмма для любой данной квадратичной функции чередуется? Объясните и проиллюстрируйте свой ответ несколькими примерами. Изучите и обсудите другие методы решения квадратного неравенства. Объясните разницу между квадратным уравнением и квадратным неравенством. Как мы можем определить и решить каждую из них? Какова геометрическая интерпретация каждого из них? (−∞, −1) ∪ (1, ∞) (−∞, 1) ∪ (1, ∞) [−3, −1] [−2,2] (−∞, −4) ∪ (−2, ∞) (−∞, −12] ∪ [6, ∞) (-14,52) −53 (−∞, 12) ∪ (12, ∞) (−∞, −32] ∪ [32, ∞) [-52,52] (−∞, −22) ∪ (22, ∞) (−∞, −23] ∪ [1, ∞) (−∞, −2−6) ∪ (−2 + 6, ∞) [2−22,2 + 22] (−∞, −5] ∪ [5, ∞) (−∞, −23] ∪ [1, ∞) Компания должна производить и продавать более 10 единиц и менее 20 единиц каждую неделю. (Вы можете сначала прочитать Введение в неравенство и устранение неравенств.) В алгебре у нас есть вопросы о неравенстве, например: Какое возможное количество голов забил Алекс? Как мы их решаем? Уловка состоит в том, чтобы разбить решение на две части: Превратите английский в алгебру. Затем используйте алгебру для решения. Превратить английский в алгебру помогает: Мы также должны записать , что на самом деле требуется для , чтобы мы знали, куда мы идем и когда мы приехали! Лучший способ узнать это — на примере, поэтому давайте попробуем наш первый пример: Какое возможное количество голов забил Алекс? Письма о назначении: Мы знаем, что Алекс забил на 3 гола больше, чем Сэм, поэтому: A = S + 3 А мы знаем, что вместе они забили меньше 9 голов: S + A <9 Нас спрашивают, сколько голов мог бы забить Алекс: A Начать с: S + A <9 A = S + 3, поэтому: S + (S + 3) <9 Упростить: 2S + 3 <9 Вычтем 3 с обеих сторон: 2S <9-3 Упростить: 2S <6 Разделите обе стороны на 2: S <3 Сэм забил менее 3 голов, что означает, что Сэм мог забить 0, 1 или 2 гола. Алекс забил на 3 гола больше, чем Сэм, поэтому Алекс мог забить 3, 4 или 5 голов . Чек: Сколько может быть девочек-щенков? Письма о назначении: Мы знаем, что есть 8 щенков, поэтому: g + b = 8, что может быть преобразовано в б = 8 — г Мы также знаем, что девочек больше, чем мальчиков, поэтому: г> б У нас спрашивают количество щенков девочек: г Решить: Начать с: g> b b = 8 — g , поэтому: g> 8 — g Добавьте g к обеим сторонам: g + g> 8 Упростить: 2g> 8 Разделите обе стороны на 2: г> 4 Итак, девочек может быть 5, 6, 7 или 8. Может ли родиться 8 девочек? Тогда бы вообще не было мальчиков, и вопрос по этому поводу не ясен (иногда вопросы такие). Чек Быстрый пример: Он проезжает 25 км, а затем 20 км. Его средняя скорость бега составляет половину его средней скорости езды на велосипеде. Джо завершает гонку менее чем за 2,5 часа, что мы можем сказать о его средней скорости? Письма о назначении: Формулы: Нас спрашивают о его средних скоростях: с и 2 с Гонка делится на две части: Джо завершает забег менее чем за 2,5 часа Решить: Начать с: 25 2 с + 20 с <2½ Умножить все члены на 2 с: 25 + 40 <5 с Упростить: 65 <5s Разделите обе стороны на 5: 13 Поменять местами: с> 13 Значит, его средняя скорость бега больше 13 км / ч, а его средняя скорость езды на велосипеде больше 26 км / ч В этом примере мы можем использовать сразу два неравенства: В какое время скорость будет от 10 до 15 м / с? Письма: Формула: У нас спрашивают время t , когда v находится между 5 и 15 м / с: 10 10 <20 - 10 т <15 Решить: Начать с: 10 <20 - 10 т <15 Вычтем 20 из каждого: 10-20 <20-10t - 20 <15-20 Упростить: −10 <−10t <−5 Разделим каждое на 10: −1 <−t <−0.5 Изменить знаки и отменить неравенства: 1> t> 0,5 Лучше сначала показать меньшее число Таким образом, скорость составляет от 10 м / с до 15 м / с между 0,5 и 1 секундой позже. И достаточно жесткий пример , чтобы закончить: Сделайте набросок: мы не знаем размеров столов, только их площадь, они могут подходить идеально или нет! Письма о назначении: Формула для периметра: 2 (Ш + Д) , и мы знаем, что это 16 м Мы также знаем, что площадь прямоугольника равна ширине, умноженной на длину: Площадь = Ш × Д И площадь должна быть больше или равна 7: Нас спрашивают о возможных значениях W и L Решим: Начать с: Ш × Д ≥ 7 Заменитель L = 8 — W: W × (8 — W) ≥ 7 Expand: 8W — W 2 ≥ 7 Переместите все термины в левую часть: W 2 — 8W + 7 ≤ 0 Это квадратное неравенство.Ее можно решить разными способами, здесь мы решим ее, заполнив квадрат: Переместите числовой член — 7 в правую часть неравенства: W 2 — 8W ≤ −7 Заполните квадрат в левой части неравенства и уравновесите его, прибавив такое же значение к
правая часть неравенства: W 2 — 8W + 16 ≤ −7 + 16 Упростить: (W — 4) 2 ≤ 9 Извлеките квадратный корень из обеих частей неравенства: −3 ≤ W — 4 ≤ 3 Да, у нас есть два неравенства, потому что 3 2 = 9 И (−3) 2 = 9 Добавьте 4 к обеим сторонам каждого неравенства: 1 ≤ W ≤ 7 Таким образом, ширина должна быть между 1 м и 7 м (включительно), а длина — 8 — ширина . Чек: Похоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, разговариваете по мобильному телефону). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы сможете прокручивать их, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана. В предыдущем разделе мы решили уравнения, содержащие абсолютные значения.В этом разделе мы хотим рассмотреть неравенства, содержащие абсолютные значения. Нам нужно будет рассмотреть два отдельных случая. Как и в случае с уравнениями, давайте начнем с довольно простого случая. Это говорит о том, что независимо от того, что такое \ (p \), оно должно находиться на расстоянии не более 4 от начала координат. Это означает, что \ (p \) должно быть где-то в диапазоне Мы могли бы получить аналогичное неравенство с <и получить аналогичный результат. В общем, здесь используются следующие формулы: Обратите внимание, что требует, чтобы значение \ (b \) было положительным, так же как мы сделали с уравнениями. Давайте взглянем на пару примеров. На самом деле особо нечего делать, кроме как ввести формулу. Как и в случае с уравнениями, \ (p \) просто представляет все, что находится внутри столбцов абсолютных значений.Итак, с этим первым у нас есть Итак, это не что иное, как довольно простое двойное неравенство, которое нужно решить, так что давайте сделаем это. Обозначение интервала для этого решения — \ (\ left ({- 3,7} \ right) \). Здесь особо нечего делать. Обозначение интервала: \ (\ left [{- \ frac {1} {3}, — \ frac {1} {9}} \ right] \). Нам нужно быть немного осторожнее с решением двойного неравенства с этим, но в остальном оно почти идентично предыдущим двум частям. На последнем этапе не забудьте поменять направление неравенств, так как мы разделили все на отрицательное число.Обозначение интервала для этого решения \ (\ left [{- 1,4} \ right] \). Давайте снова начнем с простого числового примера. Это говорит о том, что каким бы ни был \ (p \), он должен находиться на расстоянии не менее 4 от начала координат, и поэтому \ (p \) должен находиться в одном из следующих двух диапазонов: Перед тем, как дать общее решение, нам нужно разобраться с типичной ошибкой, которую допускают учащиеся при решении задач такого типа. Многие студенты пытаются объединить их в одно двойное неравенство следующим образом: Хотя это может показаться логичным, мы не можем достаточно подчеркнуть, что ЭТО НЕПРАВИЛЬНО !! Вспомните, что говорит двойное неравенство. В двойном неравенстве требуется, чтобы оба неравенства выполнялись одновременно. Двойное неравенство выше означало бы, что \ (p \) — это число, которое одновременно меньше -4 и больше 4.Это просто не имеет смысла. Нет числа, которое бы этому соответствовало. Эти решения нужно записать в виде двух неравенств. Вот их общая формула. Опять же, нам потребуется , чтобы было положительным числом \ (b \). Опять же, \ (p \) представляет количество внутри столбцов абсолютных значений, поэтому все, что нам нужно сделать здесь, это вставить формулу, а затем решить два линейных неравенства. Обозначения интервалов для них — \ (\ left ({- \ infty, — 2} \ right) \) или \ (\ left ({5, \ infty} \ right) \). Давайте просто подключим формулы и перейдем сюда, Обозначения интервалов для них: \ (\ left ({- \ infty, — \ frac {{13}} {6}} \ right] \) или \ (\ left [{- \ frac {7} {6} , \ infty} \ right) \). Опять же, здесь особо нечего делать. Обратите внимание, что при делении на отрицательное число нам пришлось изменить направление неравенств! Обозначение интервалов для этих решений — \ (\ left ({2, \ infty} \ right) \) или \ (\ left ({- \ infty, — \ frac {4} {3}} \ right) \). Хорошо, теперь нам нужно быстро взглянуть на то, что происходит, если \ (b \) равно нулю или отрицательно.Мы сделаем это с помощью набора примеров и начнем с нуля. Эти четыре примера, кажется, охватывают все наши базы. Теперь мы знаем, что \ (\ left | p \ right | \ ge 0 \) и поэтому не может быть меньше нуля. Следовательно, в этом случае нет решения, поскольку невозможно, чтобы абсолютное значение было строго меньше нуля (, т.е. отрицательное значение). Это почти то же самое, что и предыдущая часть. Мы по-прежнему не можем иметь абсолютное значение меньше нуля, однако оно может быть равно нулю.Так что решение будет только в том случае, если , и мы знаем, как решить эту проблему из предыдущего раздела. В этом случае давайте еще раз напомним, что неважно, что такое \ (p \), у нас гарантированно будет \ (\ left | p \ right | \ ge 0 \). Это означает, что независимо от того, что такое \ (x \), мы можем быть уверены, что \ (\ left | {2x — 4} \ right | \ ge 0 \) будет истинным, поскольку абсолютные значения всегда будут положительными или нулевыми. Решением в этом случае являются все действительные числа или все возможные значения \ (x \). В обозначениях неравенства это будет \ (- \ infty Эта часть почти идентична предыдущей, за исключением того, что на этот раз обратите внимание, что мы не хотим, чтобы абсолютное значение когда-либо было равно нулю. Итак, нас не волнует, какое значение принимает абсолютное значение, если оно не равно нулю. Это означает, что нам просто нужно избегать значений \ (x \), для которых мы получаем Решением в этом случае являются все действительные числа, кроме \ (x = 3 \). А теперь давайте быстро разберем примеры с отрицательными числами. Обратите внимание, что мы работаем с ними парами, потому что на этот раз, в отличие от предыдущего набора примеров, решения будут одинаковыми для каждого. Оба (все четыре?) Из них будут использовать тот факт, что независимо от того, что такое \ (p \), у нас гарантированно будет \ (\ left | p \ right | \ ge 0 \). Другими словами, абсолютные значения всегда положительны или равны нулю. Хорошо, если абсолютные значения всегда положительны или равны нулю, они не могут быть меньше или равны отрицательному числу. Следовательно, ни для одного из них нет решения. В этом случае, если абсолютное значение положительное или нулевое, оно всегда будет больше или равно отрицательному числу. Тогда решением для каждого из них будут все действительные числа. Хотя необходимо, чтобы вы могли решить многочлен
неравенства «вручную», было бы очень удобно использовать
TI-89 для проверки вашей работы или создания практических задач.К сожалению, в руководстве TI-89 указано, что команда решения может
использоваться только для решения линейных
неравенства. Однако есть способ «обмануть» решение
команда на решение полиномиальных и рациональных неравенств. (В
Пользовательские функции ниже основаны на методе, описанном
Цзинхуан Тиан из муниципального колледжа Рио-Саладо, Темпе, Аризона, в мае
2002 Учитель математики (Том 95, № 5, стр.
384-5).) Задача 44 на странице A8 текста Ларсена: «Решите неравенство 2x 2 + 1 <9x - 3 и постройте график
решения на реальной линии.« Во-первых, вы можете использовать команду «решить (», чтобы решить
связанное уравнение. Для этого после выбора
NewProb в меню «F6 — Очистить» выберите «1:
решить («из меню» F2 — Алгебра «. Затем введите соответствующее уравнение «2x 2 + 1 = 9x — 3″
и решите его относительно x. Решения делят числовую прямую на три области,
x <1/2, 1/2 Вы можете использовать «|» ключ для замены значения, как показано
справа.(Я выбрал x = 0 из левой области, x
= 1 из средней области и x = 5 из правой
область, край. Расчет «2x 2 + 1 <9x - 3 | x
= 0 "прокручивается за пределы экрана. Поскольку неравенство
верно при x = 1, решение неравенства 1/2 Самый простой способ решить подобные проблемы на TI-89 — это
создать пользовательскую функцию для выполнения этой работы.Как только эта функция
Созданный, он останется в памяти калькулятора. Функция
это: Определить решение pi (f, x, s) = решить (sign (factor (f, x)) = s, x) Вот как создать эту функцию в вашем TI-89: После запуска нового
проблема, нажмите У каждой функции есть имя.Я выбрал имя
Solvepi, что означает «решить полиномиальные неравенства».
(Это очень хорошая идея, чтобы имена функций
мнемоника.) Введите имя, нажав <2nd> Затем введите параметры функции, которые являются значениями,
вы предоставляете, когда вызываете функцию.Эта функция имеет
три параметра: «f», выражение для оценки, «x»,
переменная, используемая в выражении, и «s», которая принимает
значение 1 (для «>») или -1 (для «<»). Чтобы войти в
параметры, введите "(" <альфа> «f, x,», <альфа> «s)» Наконец, необходимо ввести тело функции.Первый,
введите «=», затем нажмите Чтобы получить функцию «знак («, вы можете выбрать математическое меню
нажав <2nd> Вы можете нажать <КАТАЛОГ>, затем «S» и использовать
клавиши со стрелками для прокрутки вниз до «знак («, или вы
можно ввести функцию, нажав <2nd> Вы можете получить функцию «коэффициент («, нажав Чтобы завершить тело функции, введите Чтобы решить неравенство «2x 2 + 1 <9x - 3»,
вы можете выбрать имя функции из VAR-LINK
меню (нажмите <2nd> Функция принимает три параметра: Как работает функция Solvepi? В нашем конкретном курсе мы обычно не решаем рациональные
неравенства, но метод, описанный Тианом, приводит к следующему
определяемая пользователем функция: работает для решения неравенств вида n / d> 0 (s = 1) и n / d <0 (s = -1).Вы можете поэкспериментировать с этим, если вы
подобно. Если Если Если решение содержит параметры и Если параметр не отображается ни при каких условиях, он
означает, что параметр может принимать любое комплексное значение. Результат Параметры, введенные Имена переменных Решение квадратичных неравенств
 Для этого мы используем знаковую диаграмму — модель функции, использующую числовую линию и знаки (+ или -) для обозначения областей в домене, где функция является положительной или отрицательной. который моделирует функцию с помощью числовой линии, представляющей ось x , и знаков (+ или -), указывающих, где функция является положительной или отрицательной. Например,
Для этого мы используем знаковую диаграмму — модель функции, использующую числовую линию и знаки (+ или -) для обозначения областей в домене, где функция является положительной или отрицательной. который моделирует функцию с помощью числовой линии, представляющей ось x , и знаков (+ или -), указывающих, где функция является положительной или отрицательной. Например, Пример 3
 Здесь мы оцениваем, используя факторизованную форму.
Здесь мы оцениваем, используя факторизованную форму. Пример 4

Пример 5

Пример 6
Пример 7

Основные выводы
Тематические упражнения
Часть A: Решения квадратичных неравенств


Часть B: Решение квадратичных неравенств

Часть C: Обсуждение

ответов
Решение вопросов со словами о неравенстве
Сэм и Алекс играют в одной футбольной команде.
В прошлую субботу Алекс забил на 3 гола больше, чем Сэм, но вместе они забили меньше 9 голов. Превращение английского в алгебру
Сэм и Алекс играют в одной футбольной команде.
В прошлую субботу Алекс забил на 3 гола больше, чем Сэм, но вместе они забили меньше 9 голов. Решить:

Еще много примеров!
Пример: Из 8 щенков девочек больше, чем мальчиков.
Пример: Джо участвует в гонке, в которой он должен ехать на велосипеде и бегать.
1.
 Велоспорт
Велоспорт 2. Работает
Пример: скорость
v м / с шара, брошенного прямо в воздух, определяется как v = 20 — 10t , где t — время в секундах.
,
поэтому поменяйте местами: 0,5
Пример: прямоугольная комната вмещает не менее 7 столов, каждый из которых имеет площадь 1 квадратный метр.Периметр комнаты 16 м.
Какой может быть ширина и длина комнаты?
Алгебра — Абсолютные неравенства
Показать мобильное уведомление Показать все заметки Скрыть все заметки Раздел 2-15: Неравенства абсолютных значений
Неравенства с участием
<и \ (\ le \)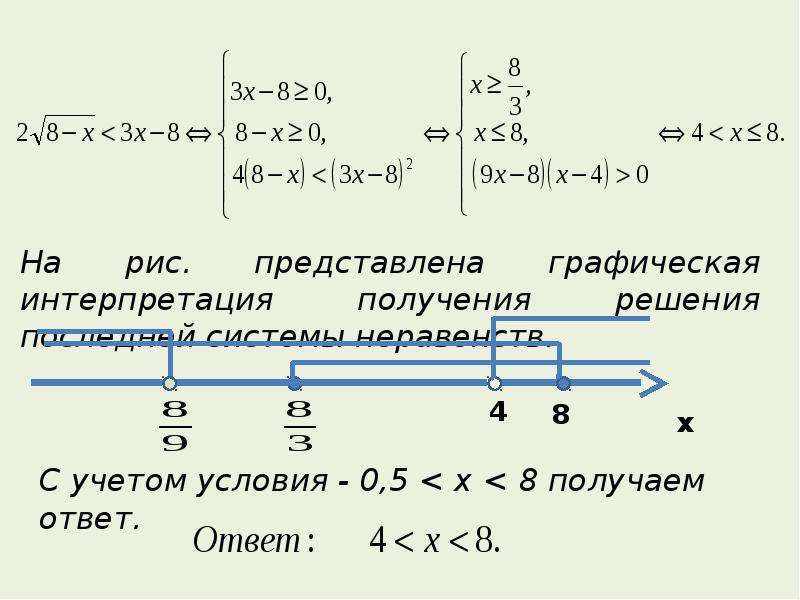 \ [- 4 \ le p \ le 4 \]
\ [- 4 \ le p \ le 4 \]
Показать все решения Скрыть все решения
a \ (\ left | {2x — 4} \ right | Показать решение
b \ (\ left | {9m + 2} \ right | \ le 1 \) Показать решение
c \ (\ left | {3 — 2z} \ right | \ le 5 \) Показать решение
Неравенства с участием> и \ (\ ge \)
 Приведем пару примеров.
Приведем пару примеров.
Показать все решения Скрыть все решения
a \ (\ left | {2x — 3} \ right |> 7 \) Показать решение
b \ (\ left | {6t + 10} \ right | \ ge 3 \) Показать решение
c \ (\ left | {2 — 6y} \ right |> 10 \) Показать решение
Показать все решения Скрыть все решения
Показать обсуждение
a \ (\ left | {3x + 2} \ right | Показать решение
b \ (\ left | {x — 9} \ right | \ le 0 \) Показать решение
c \ (\ left | {2x — 4} \ right | \ ge 0 \) Показать решение
d \ (\ left | {3x — 9} \ right |> 0 \) Показать решение
Показать все решения Скрыть все решения
Показать обсуждение
a \ (\ left | {4x + 15} \ right | Показать решение
b \ (\ left | {2x — 9} \ right | \ ge — 8 \) и \ (\ left | {2x — 9} \ right |> — 8 \) Показать решение Решение линейных неравенств
Решение линейных неравенств
Введение:
Полиномиальные неравенства Подход №1 — Использование «решить (»
Подход № 2 — Создание пользовательской функции
Чтобы использовать функцию для решения неравенства, выполните следующие действия.
шаги: FAQ:
Рациональное неравенство Определить solveri (n, d, x, s) =
решить (знак (множитель (n, x) / множитель (d, x)) = s, x)
, последнее обновление 26 ноября 2006 г., автор: JL
Stanbrough Решатель уравнений и систем — MATLAB решает
решает не может найти решение и ReturnConditions — это false , решить функция внутренне вызывает числовой решатель vpasolve , который пытается найти числовое решение.Для полинома
уравнения и системы без символьных параметров, числовой решатель возвращает все
решения. Для неполиномиальных уравнений и систем без символических параметров
числовой решатель возвращает только одно решение (если решение существует). решить не может найти решение и ReturnConditions — это true , решить возвращает пустое решение с предупреждением. Если нет решений
существует, решить возвращает пустое решение без предупреждения. ReturnConditions равно true , solution возвращает
параметры в решении и условия, при которых
решения верны. Если ReturnConditions равно false ,
функция решает либо выбирает значения
параметры и возвращает соответствующие результаты или возвращает параметризованные
решения без выбора конкретных значений. В последнем случае решает также выдает предупреждение с указанием значений параметров в возвращенном
решения. решения может содержать
параметры из входных уравнений в дополнение к введенным параметрам
по решить . решить сделать
не появляются в рабочем пространстве MATLAB. Доступ к ним должен осуществляться с помощью
выходной аргумент, который их содержит. В качестве альтернативы можно использовать
параметры в рабочем пространстве MATLAB используют syms для
инициализировать параметр.Например, если параметр — k ,
используйте syms k . параметры и условия являются
не допускается в качестве входных данных для решения .

Leave A Comment