Для какого из приведенных чисел истинно высказывание число 100 и не число четное: Для какого из приведённых чисел ложно высказывание: НЕ ( число <10) ИЛИ НЕ (число чётное)?...

Каталог заданий ОГЭ. Задания 2. Значение логического выражения.

ГИА по информатике 2 задание. Задание на умение
определять значение логического выражения.

Задание 1. Для ка­ко­го из приведённых зна­че­ний числа X ложно высказывание: НЕ (X < 6) ИЛИ (X < 5)?

1) 7

2) 6

3) 5

---

Задание 2. Для ка­ко­го из приведённых зна­че­ний числа X ис­тин­но высказывание: НЕ (X < 6) И (X < 7)?

1) 5

2) 6

3) 7

---

Задание 3. Для ка­ко­го из приведённых зна­че­ний числа X ис­тин­но высказывание: (X < 8) И НЕ (X < 7)?

1) 9

2) 8

3) 7

---

Задание 4. Для ка­ко­го из приведённых зна­че­ний числа X ис­тин­но высказывание: НЕ(X > 5) И (X > 4)?

1) 4

2) 5

3) 6

---

Задание 5. Для ка­ко­го из приведённых зна­че­ний числа X ис­тин­но высказывание: НЕ(X < 5) И (X < 6)?

1) 6

2) 5

3) 4

---

Задание 6. Для ка­ко­го из приведённых зна­че­ний числа X ис­тин­но высказывание: (X < 7) И НЕ (X < 6)?

1) 4

2) 5

3) 6

---

Задание 7. Для ка­ко­го из приведённых зна­че­ний числа X ложно высказывание: НЕ (X < 7) ИЛИ (X < 6)?

1) 4

2) 5

3) 6

---

Задание 8. Для ка­ко­го из приведённых чисел ис­тин­но высказывание: НЕ (число < 100) И НЕ (число чётное)?

1) 123

2) 106

3) 37

---

Задание 9. Для ка­ко­го из приведённых чисел ис­тин­но высказывание: (число < 100) И НЕ (число чётное)?

1) 156

2) 105

3) 23

---

Задание 10. Для ка­ко­го из приведённых чисел ис­тин­но высказывание: НЕ (число <50) И (число чётное)?

1) 24

2) 45

3) 74

---

Задание 11. Для ка­ко­го из приведённых чисел ис­тин­но высказывание: (число <75) И НЕ (число чётное)?

1) 46

2) 53

3) 80

---

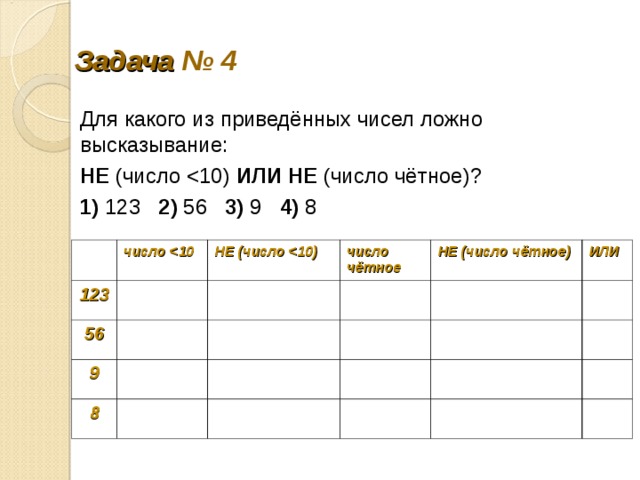
Задание 12. Для ка­ко­го из приведённых чисел ложно высказывание: НЕ (число <10) ИЛИ НЕ (число чётное)?

1) 123

2) 56

3) 9

---

Задание 13. Для ка­ко­го из приведённых чисел ложно высказывание: (число < 40) ИЛИ НЕ (число чётное)?

1) 123

2) 56

3) 9

---

Задание 14. Для ка­ко­го из приведённых чисел ложно высказывание: НЕ (число > 50) ИЛИ (число чётное)?

1) 123

2) 56

3) 9

---

Задание 15. Для ка­ко­го из приведённых зна­че­ний числа X ис­тин­но высказывание: НЕ (X < 3) И (X < 4)?

1) 5

2) 2

3) 3

---

Задание 16. Для ка­ко­го из приведённых зна­че­ний числа X ис­тин­но высказывание: (X < 5) И НЕ (X < 4)?

1) 5

2) 2

3) 3

---

Задание 17. Для какого из приведённых чисел истинно высказывание:

НЕ (Первая цифра чётная) И (Последняя цифра нечётная)?

1) 1234

2) 6843

3) 3561

---

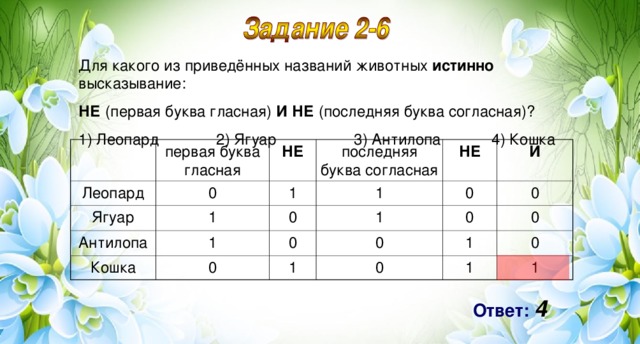
Задание 18. Для ка­ко­го из приведённых имён ис­тин­но высказывание:

НЕ (Первая буква гласная) И НЕ (Последняя буква согласная)?

1) Инна

2) Нелли

3) Иван

---

Задание 19. Для ка­ко­го из приведённых имён ис­тин­но высказывание:

НЕ (Первая буква гласная) И НЕ (Последняя буква согласная)?

1) Анна

2) Роман

3) Олег

---

Задание 20. Для ка­ко­го из приведённых имён ис­тин­но высказывание:

НЕ (Первая буква согласная) И НЕ (Последняя буква гласная)?

1) Ольга

2) Михаил

3) Валентина

4) Ян

Подготовка к ОГЭ: решение задачи 2 (логика)

1. Подготовка к ОГЭ: решение задачи 2 (логика)

Автор: Мочалова Марина Владимировна,
учитель информатики
ГБОУ лицей №144 Калининского р-на
г.Санкт-Петербург
Содержание
1. Теория
2. Разбор решений задач
3. Задачи для самостоятельного решения
4. Источники
Теория
Операции сравнения:
> строго больше
< строго меньше
>= больше или равно
<= меньше или равно
= равно
<> не равно
Логические операции:
— НЕ – логическое отрицание (инверсия)
— И – логическое умножение (конъюнкция,
одновременное выполнение условий)
— ИЛИ – логическое сложение (дизъюнкция,
выполнение хотя бы одного условия из нескольких)
Теория
Порядок выполнения действий:
— выражения в скобках
— НЕ
— И
— ИЛИ
— <, <=, >, >=, =, <>
Пример:
5
1
4
3
2
7
6
НЕ ((Х = 7) И НЕ (Y <>9)) ИЛИ (Z > 0)
Разбор решения задач
Задание 1. Для какого из приведенных чисел ложно высказывание:
НЕ (число > 50) ИЛИ (число четное)
1) 123 2) 56
3) 9
4) 8
Обозначим высказывания: А — число > 50, В — число четное. Перепишем
условие задачи, исходя из того, что высказывание должно быть ложным:
НЕ А ИЛИ В = 0.
Логическая сумма двух переменных равна 0 только в случае, если обе
переменные равны 0.
Получаем два равенства: НЕ А = 0, В=0. Рассмотрим каждое отдельно.
НЕ А = 0, следовательно, А = 1. Это означает, что искомое число > 50. Этому
условию удовлетворяют числа под номерами 1) и 2).
В=0. Это означает, что искомое число нечетное. По этому условию остается
число 123 под номером 1).
Ответ: 1
Разбор решения задач
Задание 2. Для какого из приведенных чисел истинно высказывание:
(число < 75) И НЕ (число четное)
1) 46
2) 53
3) 98 4) 99
Обозначим высказывания: А — число <75 и В — число четное. Перепишем у
словие задачи, исходя из того, что высказывание должно быть истинным:
А И НЕ В = 1.
Логическое произведение двух переменных равно 1 только в случае,
если обе переменные равны 1.
Получаем два равенства: А = 1, НЕ В=1. Рассмотрим каждое отдельно.
А = 1. Это означает, что искомое число меньше 75. Это числа под
номерами 1) и 2).
НЕ В =1 , т.е. В=0. Это означает, что искомое число нечетное. По этому
условию остается число 53 под номером 2).
Ответ: 2
Разбор решения задач
Задание 3. Для какого из приведенных значений числа Х истинно высказывание:
НЕ (Х > 5) И (Х > 4)
1) 4
2) 5
3) 6
4) 7
Способ 1 (с помощью алгебры логики).
Обозначим высказывания: А — Х > 5, В — Х > 4. Перепишем условие задачи, исходя
из того, что высказывание должно быть истинным: НЕ А И В = 1.
Логическое произведение двух переменных равно 1 только в случае, если обе
переменные равны 1.
Получаем два равенства: НЕ А = 1, В=1. Рассмотрим каждое отдельно.
НЕ А = 1, следовательно, А = 0. Это означает, что искомое число меньше или
равно 5. Это числа под номерами 1) и 2).
В=1. Это означает, что искомое Х больше 4. Этому условию удовлетворяет только
число 5 под номером 2).
Способ 2 (с помощью рассуждений).
Проанализируем условие задачи. Из него следует, что искомое число должно
быть одновременно строго больше 4 и при этом не более 5. Этому условию соответствует только число 5: оно строго больше 4 и при этом не превышает 5.
Ответ: 2
Разбор решения задач
Задание 4. Для какого из приведенных чисел истинно высказывание:
(число > 100) И НЕ (число нечетное)
1) 35
2) 4598
3) 54321
4) 24
Обозначим высказывания: А — число > 100 и В — число нечетное.
Перепишем условие задачи, исходя из того, что высказывание должно быть
истинным: А И НЕ В = 1.
Логическое произведение двух переменных равно 1 только в случае если обе
переменные равны 1.
Получаем два равенства: А = 1, НЕ В=1. Рассмотрим каждое отдельно.
А = 1. Это означает, что искомое число больше 100. Это числа под номерами
2) и 3).
НЕ В=1, т.е. В=0. Это означает, что искомое число четное. По этому условию
остается число 4598 под номером 2).
Ответ: 2.
Разбор решения задач
Задание 5. Для какого из приведенных значений числа Х ложно высказывание:
НЕ (Х > 2) ИЛИ ((Х < 4) И (Х > 1)).
1) 1
2) 2
3) 3
4) 4
Обозначим высказывания: А — Х > 2 , В — Х < 4, С Х > 1. Перепишем условие
задачи, исходя из того, что высказывание должно быть ложным:
НЕ А ИЛИ ( В И С) = 0.
Логическая сумма двух переменных равна 0 только в случае, если обе
переменные равны 0.
Получаем два равенства: НЕ А = 0, (В И С) =0. Рассмотрим каждое отдельно.
НЕ А = 0, следовательно, А = 1. Это означает, что искомое число больше 2. Это
числа под номерами 3) и 4).
(ВиС)=0. Это равенство распадается на два отдельных – либо В=0 либо С=0.
В=0 означает, что искомое число больше или равно 4. По этому условию остается
число 4 под номером 4).
С=0 означает, что Х должно быть меньше или равно 1, но это не удовлетворяет
предыдущим двум условиям, поэтому С не влияет на решение задачи (поскольку
значение С умножается на В=0).
Таким образом, решением является число 4 под номером 4)..
Ответ: 4
Разбор решения задач
Задание 6. Для какого из приведенных чисел истинно высказывание:
НЕ (число > 10000) И (число нечетное)
1) 54321
2) 45980
3) 125 4) 24
Способ 1 (метод рассуждений). Проанализируем условие задачи. Из него
следует, что число должно быть одновременно и нечетным и не более 10000.
Этому условию удовлетворяет только одно число 125, т.е. получаем ответ 3).
Способ 2 (с помощью алгебры логики). Обозначим высказывания:
А — число больше 10000 В — число нечетное. Перепишем условие задачи,
исходя из того, что высказывание должно быть истинным: НЕ А И В = 1.
Логическое произведение двух переменных равно 1 только в случае, если обе
переменные равны 1.
Получаем два равенства: НЕ А = 1, В=1. Рассмотрим каждое отдельно.
НЕ А = 1, т.е. А = 0. Это означает, что искомое число должно быть не больше
10000. Это числа под номерами 3) и 4).
В=1. Это означает, что искомое число нечетное. По этому условию остается
число 125 под номером 3).
Ответ: 3
Разбор решения задач
Задание 7. Для какого из приведенных чисел ложно высказывание:
НЕ (число < 10) ИЛИ НЕ(число четное)
1) 123 2) 56 3) 9
4) 8
Обозначим высказывания: А — число < 10 и В — число четное. Перепишем
условие задачи, исходя из того, что высказывание должно быть ложным:
НЕ А ИЛИ НЕ В = 0.
Логическая сумма двух переменных равна 0 только в случае если обе
переменные равны 0.
Получаем два равенства: НЕ А = 0, НЕ В=0. Рассмотрим каждое отдельно.
НЕ А = 0, тогда А = 1. Это означает, что искомое число меньше 10. Это числа
под номерами 3) и 4).
НЕ В=0 т.е. В=1. Это означает, что искомое число четное. По этому условию
остается число 8 под номером 4).
Ответ: 4
Разбор решения задач
Задание 8 . Для какого из приведенных значений числа Х ложно высказывание:
(число > 3) ИЛИ НЕ ((число < 4) И (число > 2))
1) 1
2) 2
3) 3
4) 4
Обозначим высказывания: А — число > 3, В — число < 4, С — число > 2.
Перепишем условие задачи, исходя из того, что высказывание должно быть
ложным:
А ИЛИ НЕ (В И С)= 0.
Логическая сумма двух переменных равна 0 только в случае, если обе
переменные равны 0.
Получаем два равенства: А = 0, НЕ (В И С)=0. Рассмотрим каждое отдельно.
А = 0. Это означает, что искомое число <= 3. Это числа под номерами 1) , 2) и 3).
НЕ (В И С) = 0 или (В И С) = 1. Это равенство распадается на два: В = 1 и С = 1.
В = 1 означает, что искомое число Х< 4. По этому условию остаются те же числа
под номерами 1), 2) и 3).
Условие С = 1 означает, что искомое число должно быть строго больше 2. Этому
условию удовлетворяет только одно число 3.
Ответ: 3.
Разбор решения задач
Задание 9. Для какого из приведенных значений числа Х ложно
высказывание: (НЕ (Х >= 6) И НЕ (Х = 5)) ИЛИ (Х <= 7).
1) 5
2) 6
3) 7
4) 8
Введем обозначения: А — Х >= 6, В — Х=5, С — Х >= 7. Перепишем условие
задачи, используя принятые нами обозначения и учитывая, что исходное
логическое выражение должно быть ложным:
(НЕ А И НЕ В) ИЛИ С= 0.
Логическая сумма равна 0 только в случае, если все слагаемые равны 0.
Получаем 2 уравнения:
(НЕ А И НЕ В)=0 и С=0.
Рассмотрим сначала второе равенство С=0. Оно означает, что искомое
число Х должно быть строго больше 7. Этому условию удовлетворяет только
одно число 8.
Сделаем проверку найденного решения по первому уравнению
(НЕ А И НЕ В)=0.
Логическое произведение двух переменных равно 0 в случае, если хотя бы
один из сомножителей равен 0. Найденное число 8 дает нам А =1 (А: Х >=6)
или НЕ А =0, поэтому второй сомножитель НЕ В =0 можно не рассматривать.
Ответ: 4.
Разбор решения задач
Задание 10. Для какого из приведенных значений числа Х истинно
высказывание: (Х > 4) И (Х < 7) И (Х < 6).
1) 5
2) 6
3) 3
4) 4
Введем обозначения: А — Х > 4, В — Х < 7, С — Х < 6.
Перепишем условие задачи, используя принятые обозначения и учитывая,
что исходное логическое выражение должно быть истинным: А и В и С = 1.
Логическое произведение нескольких переменных равно 1 в случае, если все
логические переменные равны 1. Получаем три равенства: А = 1, В = 1, С = 1.
Рассмотрим каждое из них отдельно.
А = 1. Это означает, что искомое число Х > 4. Этому условию удовлетворяют
числа 5 и 6.
В = 1. Это означает, что искомое число Х < 7. Этому условию удовлетворяют
все данные в ответе числа, поэтому необходимо также рассмотреть последне
е равенство.
С = 1. Это означает, что искомое число Х < 6. Этому условию удовлетворяет
только одно число 5 под номером 1).
Ответ: 1.
Разбор решения задач
Здание 11. Для какого из приведенных имен истинно высказывание
НЕ (1 буква согласная) И НЕ (последняя буква гласная)?
1) Андрейка 2) Иван 3) Михаил 4) Никита
Введем обозначения:
А — первая буква согласная, В — последняя буква гласная.
Перепишем исходное выражение, используя принятые нами обозначения и
учитывая, что оно должно быть истинным.
НЕ А И НЕ В = 1.
Логическое произведение равно 1 (истинно) только в том случае, если обе
переменные равны 1. Таким образом, исходное уравнение распадается на
два равенства и каждое решается отдельно.
НЕ А = 1. Это означает, что А = 0, т.е. первая буква искомого слова должна
быть гласной. Этому условию удовлетворяют имена под номерами 1) и 2).
НЕ В = 1, т.е. В = 0. Отсюда получаем что последняя буква имени должна
быть согласной. Этому условию удовлетворяет имя Иван под номером 2).
Ответ: 2.
Разбор решения задач
Задание 12.Для какого из приведенных имен истинно высказывание
НЕ (1 буква гласная) И (количество букв < 6).
1) Иван 2) Николай 3) Семен 4) Илья
Введем обозначения: А — первая буква гласная, В — количество букв меньше
6. Перепишем условие задачи, используя принятые обозначения и
учитывая, что оно должно быть истинным: НЕ А И В = 1.
Логическое произведение двух переменных истинно только в случае, если
обе переменные равны 1. Получаем 2 равенства, которые рассматриваем
отдельно каждое.
НЕ А = 1, или А = 0. Это означает, что первая буква в искомом имени
должна быть согласной. Этому условию удовлетворяют имена под
номерами 2) и 3).
В = 1, следовательно, в имени должно быть букв 5 и менее. Это имя Семен
под номером 3).
Ответ: 3.
Разбор решения задач
Задание 13. Для какого из приведенных имен истинно высказывание
НЕ (1 буква согласная) И НЕ (3 буква гласная).
1) Елена 2) Полина 3) Кристина 4) Анна
Введем обозначения: А — первая буква согласная, В — третья буква гласная. П
ерепишем условие согласно принятым нами обозначениям и учитывая,
что высказывание должно быть истинным:
НЕ А И НЕ В = 1.
Логическое произведение двух переменных истинно только в случае
истинности каждой переменной. Таким образом, решение задачи
распадается на решение двух равенств:
НЕ А = 1. Это значит, что А = 0, т.е. первая буква имени должна быть гласной.
Это имена под номерами 1) и 4).
НЕ В = 1. Это означает, что В = 0, т.е, третья буква имени должна быть
согласной. Это условие выполняется только в имени Анна под номером 4).
Ответ: 4.
Разбор решения задач
Задание 14. Для какой из приведенных последовательностей цветных бусин
истинно высказывание
(последняя бусина зеленая) ИЛИ (вторая бусина красная ) И (четвертая бусина зеленая).
1) ЗКЗСЖ 2) КСЗЖК 3) ККСЗК 4) ЗЗКЗС
Введем обозначения: А — последняя бусина зеленая, Б — вторая бусина красная, С — четвер
тая бусина зеленая.
Перепишем условие задачи, используя введенные обозначения и учитывая, что оно
должно быть истинным.
А ИЛИ В И С = 1
Расставим скобки согласно приоритету логических операций (логическое умножение –
операция И выполняется прежде логического сложения — операции ИЛИ). Получим
А ИЛИ (В И С) = 1.
Логическая сумма равна 1 в случае, если хотя бы одно из слагаемых равно 1. Получаем
два уравнения.
А = 1 означает, что последняя бусина должна быть зеленой. Но ни в одном варианте
ответа такой последовательности нет.
Второе равенство В И С = 1 требует одновременно истинности обоих высказываний.
В = 1 означает, что в ответе должна быть вторая бусина красная. Это условие выполняется
только в последовательности под номером 3). Но необходимо убедиться, что при этой
последовательности также и С = 1. Действительно, в этой последовательности четвертая
бусина зеленая, значит, С = 1.
Ответ: 3.
Разбор решения задач
Задание 15. Для какой из приведенных последовательностей цветных бусин
истинно высказывание
(первая бусина красная) и (вторая бусина синяя) и не (последняя бусина желтая).
1) КСЖЗЖ 2) КСЗЖЖ 3) КСКЖЗ 4) СКЗЖС
Введем обозначения: А — первая бусина красная, Б — вторая бусина синяя,
С — последняя бусина желтая.
Перепишем условие задачи, используя введенные обозначения и учитывая,
что оно должно быть истинным.
А И В И НЕ С = 1
Логическое произведение равно 1 в случае, если все сомножители равны 1.
Получаем три уравнения.
А = 1 означает, что первая бусина должна быть красной. Это варианты
ответов под номерами 1, 2, 3.
Второе равенство В = 1 означает, что вторая бусина синяя. Это те же
последовательности под номерами 1, 2, 3.
НЕ С = 1 означает, что С = 0, то есть в ответе последняя буква не должна быть
желтой. Это условие выполняется только в последовательности под номером
3).
Ответ: 3.
Разбор решения задач
Задание 16.Для какой из приведенных последовательностей цветных бусин
ложно высказывание
НЕ (последняя бусина зеленая) ИЛИ (первая бусина синяя ) ИЛИ (вторая бусина красная).
1) КСЖЗС 2) ССКЖЗ 3) ЖКЗСЗ 4) КСЗКЗ
Введем обозначения: А — последняя бусина зеленая, Б — первая бусина синяя,
С – вторая бусина красная.
Перепишем условие задачи, используя введенные обозначения и учитывая, что
оно должно быть ложным.
НЕ А ИЛИ В ИЛИ С = 0
Логическая сумма равна 0 только в случае, все слагаемые равны 0. Получаем три
уравнения.
НЕ А = 0 означает, что А = 1, то есть последняя бусина должна быть зеленой. Это
варианты ответов под номерами 2, 3, 4.
Второе равенство В = 0 требует, чтобы первая бусина не была синей. Этому
условию удовлетворяют ответы под номерами 3 и 4.
С = 0 означает, что в ответе второй бусиной не может быть красная. Это условие
выполняется только в последовательности под номером 4).
Ответ: 4.
Разбор решения задач
Задание 17. Для какого из приведенных чисел истинно высказывание
НЕ (первая цифра четная) И НЕ (сумма цифр четная).
1) 638 2) 442 3) 357 4) 123
Введем обозначения А — первая цифра четная, В — сумма цифр четная.
Перепишем условие задачи, используя принятые обозначения и
учитывая, высказывание должно быть истинным.
НЕ А И НЕ В = 1. Логическое произведение равно 1 (истинно) в том случае,
если оба сомножителя равны 1. Получаем два уравнения.
НЕ А = 1 или А = 0. Это означает, что в искомом числе первая цифра
нечетная. Этому условию удовлетворяют числа под номерами 3) и 4).
НЕ В = 1 или В = 0. Это означает, что в числе сумма цифр должна быть
нечетной. Этому условию удовлетворяет только число под номером 3).
Ответ: 3.
Задачи для самостоятельного решения
18. Для какого из приведенных имен истинно высказывание
НЕ (первая буква гласная) И (третья буква согласная).
1) Елена 2) Полина 3) Кристина 4) Анна
Ответ: 2.
19.Для какого из приведенных слов истинно высказывание
(первая буква гласная) И НЕ (последняя буква согласная).
1) слива 2) яблоко 3) банан 4) ананас
Ответ: 2.
20. Для какого из приведенных имен истинно высказывание
НЕ (первая буква согласная) И (количество букв меньше 5).
1) Никита 2) Иван 3) Семен 4) Игорь
Ответ: 2.
21. Для какого из приведенных слов истинно высказывание
(первая буква гласная) И НЕ (третья буква согласная).
1) Елена 2) Полина 3) Кристина 4) Анна
Ответ: 2.
Задачи для самостоятельного решения
22. Для какого из приведенных имен истинно высказывание
НЕ ((первая буква согласная) ИЛИ (последняя буква гласная)).
1) Максим 2) Марина 3) Ольга 4) Олег
Ответ: 4
23. Для какого из приведенных имен ложно высказывание
НЕ ((третья буква согласная) И (последняя буква гласная)).
1) Анна 2) Елена 3) Павел 4) Егор
Ответ: 1.
24. Для какого из приведенных имен истинно высказывание
НЕ ((первая буква гласная) ИЛИ НЕ (последняя буква согласная)).
1) Емеля 2) Иван 3) Михаил 4) Никита
Ответ: 3.
25. Для какого из приведенных значений числа Х ложно высказывание:
НЕ (Х < 6) ИЛИ ((Х < 5) И (Х >= 4)).
1) 7 2) 6 3) 5
4) 4
Ответ: 3.
Задачи для самостоятельного решения
26. Для какого из приведенных значений числа Х истинно
высказывание:
((Х >3) И НЕ (Х < 4)) ИЛИ (Х <1 ).
1) 1 2) 2 3) 3
4) 4
Ответ: 4.
27. Для какой из приведенных последовательностей цветных бусин
истинно высказывание
(вторая бусина желтая) И НЕ (четвертая бусина зеленая ) И НЕ (последняя
бусина красная).
1) СЗККЖК 2) ЖЖКСЗК 3) СЖСЗКЗ 4) КЖССКС
Ответ: 4.
28. Для какого из приведенных значений числа Х истинно высказывание:
(Х <3) И ((Х < 2) ИЛИ (Х > 2)).
1) 1 2) 2 3) 3
4) 4
Ответ: 1.
Задачи для самостоятельного решения
29. Для какой из приведенных последовательностей цветных бусин
истинно высказывание
(НЕ (первая бусина красная) И (третья бусина синяя )) ИЛИ (пятая
бусина зеленая).
1) КЗКЖСС 2) СККЖКЗ 3) ЖКЗСЗК 4) ЗСЖКЖС
Ответ: 3.
30. Для какого из приведенных значений числа Х истинно
высказывание:
(Х > 1) И (Х > 2) И (Х <> 3).
1) 1 2) 2 3) 3
4) 4
Ответ: 4
Источники
— открытый банк заданий ОГЭ ФИПИ
www.fipi.ru/content/otkrytyy-bankzadaniy-oge
— демоверсии ОГЭ по информатике
2017 г. и ранее
— сайт К. Полякова
http://kpolyakov.spb.ru

Что такое четные числа? Определение | Четные и нечетные числа

Четные числа — это числа, которые можно разделить на две равные группы или пары и которые точно делятся на 2. Например, 2, 4, 6, 8, 10 и т. д. — четные числа. Эти числа можно сгруппировать в равные пары. Однако эту группировку нельзя выполнить для таких чисел, как 5, 7, 9 или 11. Таким образом, 5, 7, 9 или 11 не являются четными числами. Давайте узнаем больше о четных числах, разнице между нечетными и четными числами, а также о некоторых примерах четных чисел на этой странице.

1.	Что такое четные числа?
2.	Нечетные и четные числа
3.	Свойства четных чисел
4.	Часто задаваемые вопросы о четных числах

Что такое четные числа?

Четное число — это число, кратное 2. Можно сказать, что любое число, которое полностью делится на 2, является четным числом. Это можно понять с помощью примера.

Предположим, у Джона 6 мячей. Если он попытается сгруппировать их, он может соединить все 6 шаров и сформировать 3 пары. Нет шаров, которые остались непарными. Следовательно, он может сделать вывод, что 6 — четное число. Теперь разделим 6 на 2. Получим частное 3, равное количеству образовавшихся пар. Получаем остаток как 0, что равно количеству шаров, которые нельзя спарить. Всякий раз, когда Джон пытается соединить четное количество мячей, он останется без мяча. Другими словами, всякий раз, когда четное число делится на 2, мы всегда получаем в остатке 0,9.0005

Нечетные и четные числа

Целые числа можно разделить на четные и нечетные. Нечетные числа — это те числа, которые не делятся полностью на 2. Тогда как четные числа полностью делятся на 2. Пройдемся по списку всех четных чисел от одной до двухсот. Обратите внимание на числа, указанные ниже. Сможете ли вы найти закономерность или связь между всеми четными числами от одного до двухсот?

Список четных чисел от 1 до 200

Список четных номеров (1-200)
2	4	6	8	10
12	14	16	18	20
22	24	26	28	30
32	34	36	38	40
42	44	46	48	50
52	54	56	58	60
62	64	66	68	70
72	74	76	78	80
82	84	86	88	90
92	94	96	98	100
102	104	106	108	110
112	114	116	118	120
122	124	126	128	130
132	134	136	138	140
142	144	146	148	150
152	154	156	158	160
162	164	166	168	170
172	174	176	178	180
182	184	186	188	190
192	194	196	198	200

Выполним сложение различных комбинаций четных и нечетных чисел и посмотрим на результаты.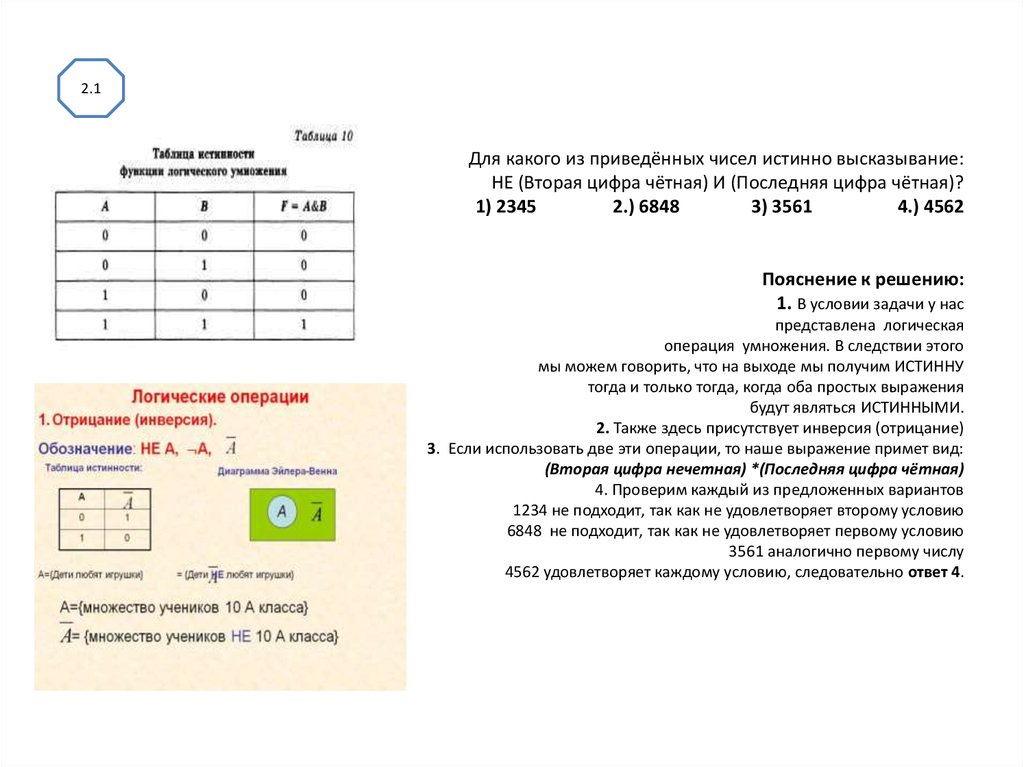 Мы увидим, как числа изменяются от нечетных к четным, когда нечетные и четные числа складываются друг с другом. Записывайте полученные результаты.

Номер 1	Номер 2	Число 1 + Число 2 = Сумма
4 [четный]	8 [четный]	4 + 8 = 12 [четное]
7 [Нечетный]	3 [Нечетный]	7 + 3 = 10 [четное]
1 [Нечетный]	6 [четный]	1 + 6 = 7 [Нечетное]
2 [четный]	9 [Нечетный]	2 + 9 = 11 [Нечетное]

Подведем итоги.

Последовательные четные числа

Последовательные числа могут быть перечислены как 2, 4, 6, 8, 10, 12, 14 и т. д. Последовательные числа — это те числа, которые непрерывно следуют друг за другом в порядке от наименьшего числа к наибольшему. Например, 1, 2, 3, 4 и т. д. — последовательные натуральные числа. Итак, когда нам нужно перечислить последовательные четные числа, мы можем перечислить все четные числа в порядке от наименьшего числа до наибольшего числа. Например, 2, 4, 6, 8, 10, 12, 14 и так далее — последовательные четные числа.

Четные натуральные числа

Четные натуральные числа могут быть указаны как 66, 24, 8, 100 и т. д. Четные числа — это те числа, которые делятся на 2, а натуральные числа — это счетные числа, начинающиеся с 1, 2, 3, 4, 5 и так далее. Итак, если мы выберем все четные числа из списка натуральных чисел, они будут называться четными натуральными числами.

Свойства четных чисел

Давайте посмотрим на различные свойства чисел, такие как сложение, умножение и вычитание, и на то, как ведет себя четное число в таких случаях:

Свойство сложения четных чисел

• Сумма двух четных чисел является четным числом. Например, 14 + 8 = 22 
.
• Сумма четного числа и нечетного числа является нечетным числом. Например, 8 + 9 = 17 
.
• Сумма двух нечетных чисел является четным числом. Например, 13 + 7 = 20 
.

Свойство вычитания четных чисел

• Разница между двумя четными числами является четным числом. Например, 42 — 8 = 34
• Разница между четным числом и нечетным числом является нечетным числом. Например, 22 — 7 = 15 
.
• Разница между двумя нечетными числами является четным числом. Например, 35 — 15 = 20 
.

Свойство умножения четных чисел

• Произведение двух четных чисел является четным числом. Например, 12 × 4 = 48 
.
• Произведение четного числа на нечетное число равно четному числу. Например, 8 × 5 = 40 
.

Четные простые числа

Существует только одно четное простое число, равное 2. Все остальные четные числа имеют делители, отличные от 1 и самого числа. Например, делители 4 равны 1, 2 и 4. Следовательно, существует только одно четное простое число, равное 2.

☛Статьи по теме

• Составные номера
• Нечетные числа
• Реальные числа
• Натуральные числа
• Целые числа
• Иррациональные числа
• Подсчет чисел
• Кардинальные числа
• Четные и нечетные числа
• Сумма четных чисел
• Четные числа от 1 до 100
• Четные числа от 1 до 1000
• Рабочие листы по четным и нечетным числам
• Рациональные числа

Cuemath — одна из ведущих мировых платформ для обучения математике, предлагающая онлайн-уроки по математике в режиме реального времени один на один для классов K-12. Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.

Часто задаваемые вопросы о четных числах

Что такое четные числа в математике?

Числа, которые полностью делятся на 2, называются четными числами . Эти числа при делении на 2 оставляют 0 в остатке. Например, 2, 4, 6, 8 и так далее — четные числа.

Какие четные числа от 1 до 100?

Список четных чисел от 1 до 100 выглядит следующим образом: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36 , 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70,72, 74, 76, 78, 80, 82, 84, 86 , 88, 90, 92, 94, 96, 98, 100.

Какое самое маленькое четное число?

2 — наименьшее четное число. Это также единственное четное простое число.

Все ли четные числа натуральные?

Да, все четные числа, которые полностью делятся на 2, тоже натуральные числа. Например, 14, 18, 22, 24 и т. д.

Что такое формула четных чисел?

Поскольку каждое четное число кратно 2, его формула задается как n = 2k, где ‘k’ — целое число. Если мы заменим «k» на любое число, мы получим четное число. Например, если «k» заменить на 3 в 2k, (2 × 3) = 6. Мы получим 6, которое является четным числом.

Является ли 0 четным или нечетным числом?

Любое число, которое можно разделить на два, чтобы получить еще одно целое число, считается четным. Ноль также является одним из них, потому что когда 0 делится на 2, он дает остаток 0, что означает, что 0 делится на 2. Следовательно, 0 — четное число.

Почему 4 четное число?

Поскольку 4 кратно 2 и может быть разделено на две равные группы, это четное число. Другими словами, это четное число, потому что оно полностью делится на 2.

В чем разница между нечетными и четными числами?

Четное число — это число, кратное 2. Например, тогда как нечетное число не кратно 2.

Что такое HCF двух последовательных четных чисел?

HCF двух последовательных четных чисел равен 2. Наибольший общий делитель (HCF) любых двух чисел является их наибольшим общим делителем. Например, 16 и 18 — два последовательных четных числа, и их HCF равен 2.

Как найти четное число?

Чтобы найти четное число, мы должны разделить данное число на 2. Если оно полностью делится на 2 без остатка, то это четное число. Если данное число не делится полностью на 2, то это нечетное число.

Какие четные числа меньше 10?

Четные числа меньше 10 могут быть записаны как 2, 4, 6 и 8. Эти числа полностью делятся на 2 без остатка.

Что такое четные составные числа?

Четные числа — это те числа, которые полностью делятся на 2. Например, 2, 4, 6, 8, 10 и т. д. — четные числа. Составные числа — это те числа, у которых делители больше 1 и само число. Например, 4, 6, 9, 15 и так далее. Мы знаем, что все четные числа, кроме 2, имеют делители больше 1 и самого числа. Интересно, что 2 — единственное четное число, которое считается простым числом. Следовательно, кроме 2, все четные числа являются составными числами. Например, 4, 6, 8, 10, 12, 14 и так далее — четные составные числа. Это также показывает, что наименьшее четное составное число равно 4.

Какое самое большое четырехзначное четное число?

Самое большое 4-значное четное число — 9998. Мы знаем, что самое большое 4-значное число — 9999, значит, первое четное число после этого — 9998.

Какова сумма двух последовательных четных чисел?

Сумма двух последовательных четных чисел всегда является четным числом. Например, 4 + 16 = 20 или 66 + 12 = 78 и так далее.

30 четное или нечетное?

Да, 30 — четное число, потому что оно делится на 2. Мы также можем проверить это, взглянув на последнюю цифру числа 30, которая равна нулю. Если последняя цифра числа 0, 2, 4, 6 или 8, это четное число.

Ис 90 четное число?

Да, 90 — четное число, поскольку оно делится на 2. Это также можно проверить, взглянув на последнюю цифру числа 90, которая равна 0. Если последняя цифра числа — 0, 2, 4, 6 или 8 это четное число.

16 четное или нечетное?

Да, 16 — четное число, поскольку оно полностью делится на 2. Это можно проверить, взглянув на последнюю цифру числа 16, которая равна 6. Если последняя цифра числа — 0, 2, 4, 6 или 8 это четное число.

Какое единственное четное простое число?

Единственным четным простым числом является 2. Поскольку 2 делится на 2, это четное число, а поскольку 2 имеет только 2 делителя, 1 и 2, оно также является простым числом. Поэтому, что интересно, 2 — единственное четное простое число.

Ноль — четное или нечетное число?

проверено Cite

Несмотря на то, что были приложены все усилия для соблюдения правил стиля цитирования, могут быть некоторые расхождения. Пожалуйста, обратитесь к соответствующему руководству по стилю или другим источникам, если у вас есть какие-либо вопросы.

Выберите стиль цитирования

MLAAPChicago Manual of Style

Написано

Джонатан Хогебак

Стажер редактора Британской энциклопедии.

Джонатан Хогебак

Факт проверен

Редакторы Британской энциклопедии

Редакторы Encyclopaedia Britannica курируют предметные области, в которых они обладают обширными знаниями, будь то многолетний опыт, полученный в результате работы над этим контентом, или в результате обучения для получения ученой степени. Они пишут новый контент, а также проверяют и редактируют контент, полученный от участников.

The Editors of Encyclopaedia Britannica

© koya979/Shutterstock.com

Математическая четность обычно является одним из первых правил, изучаемых на первых уроках арифметики, хотя вы можете не знать этого названия. Именно так мы делим все целые числа на две категории: четные числа и нечетные числа. Определить четность целого числа — числа, которое можно записать без остатка или дробной части — так же просто, как задать один вопрос: делится ли число на 2? Если да, то оно четное; если нет, то странно.

Итак, где именно 0 попадает в эти категории? Большинство людей сбивает с толку число 0, не зная, является ли оно целым числом, и не подозревая о его расположении в качестве числа, потому что технически оно означает пустое множество. По правилам четности ноль является четным или нечетным?

Как целое число, которое можно записать без остатка, 0 классифицируется как целое число.