Тест по физике Основы электродинамики 11 класс
Тест по физике Основы электродинамики. Магнитное поле 11 класс с ответами. Тест состоит из 2 вариантов. В каждом варианте по 6 заданий.
Вариант 1
A1. Индукция магнитного поля — это векторная физическая величина, равная отношению:
1) силы, действующей на элемент длины проводника, помещенный в данную точку поля, к произведению силы тока на длину элемента
2) силы тока, действующей на элемент длины проводника, помещенный в данную точку поля, к произведению силы на длину элемента
3) напряжения, действующего на элемент длины проводника, помещенный в данную точку поля, к произведению силы тока на длину элемента
4) напряжения, действующего на элемент длины проводника, помещенный в данную точку поля, к произведению работы тока на длину элемента
А2. При увеличении тока в контуре в 4 раза индукция магнитного поля:
1) увеличится в 4 раза
2) уменьшится в 4 раза
3) увеличится в 16 раз
4) не изменится
А3.
Три частицы влетели в однородное магнитное поле. На рисунке траектории их движения показаны штриховой линией.
Линии магнитной индукции направлены от наблюдателя. Отрицательный заряд имеет:
1) только частица 1
2) только частица 2
3) только частица 3
4) частицы 2 и 3
А4. Доказательством реальности существования магнитного поля может служить:
1) наличие источника поля
2) отклонение заряженной частицы, движущейся в поле
3) взаимодействие двух проводников с током
4) существование электромагнитных волн
В1. Горизонтальный проводник длиной l = 0,20 ми массой m = 0,01 кг, подвешенный на двух тонких нитях, находится в однородном вертикальном магнитном поле с индукцией В = 0,25 Тл. На какой угол α от вертикали отклонятся нити, если по проводнику пропустить ток
C1. Протон с энергией W = 1,0 МэВ влетел в однородное магнитное поле, перпендикулярное линиям индукции.
Какой должна быть минимальная протяженность поля l в направлении движения протона, чтобы направление его движения изменилось на противоположное? (Магнитная индукция поля В = 1 Тл.)
Вариант 2
A1. Индукция магнитного поля показывает, чему равна:
1) сила, действующая на элемент проводника с током единичной длины, если по нему идет ток единичной силы
2) сила, действующая на проводник с током, если по нему идет ток единичной силы
4) сила тока, действующая на проводник с током единичной длины
А2. На рисунке изображен проводник с током. Символ «+» означает, что ток в проводнике направлен от наблюдателя. Куда направлен вектор магнитной индукции поля в точке а?
1) только в направлении 1
2) только в направлении 2
3) в направлении 1 или 3
4) только в направлении 4
А3. В горизонтально расположенном проводнике длиной 50 см и массой 10 г сила тока равна 20 А.
1) 10-2 Тл
2) 10 Тл
3) 0,1 мТл
4) 100 Тл
А4. Для двух параллельных проводников, находящихся в вакууме, модуль силы взаимодействия между элементами токов, на которые можно разложить любые участки проводников, прямо пропорционален токам, протекающим по проводникам, длинам элементов и обратно пропорционален квадрату расстояния между ними — гласит закон:
1) Ампера
2) Фарадея
3) Ленца
4) Ньютона
В1. На горизонтальных рельсах, расстояние между которыми
C1.
Электрон, ускоренный разностью потенциалов U = 400 В, влетел в однородное магнитное поле с индукцией В = 1,5 мТл и описал дугу окружности. Найдите радиус этой окружности R.
Ответы на тест по физике Основы электродинамики. Магнитное поле 11 класс
Вариант 1
А1-1
А2-2
А3-1
А4-2
В1. 45°
С1. 14 см
Вариант 2
А1-1
А2-1
А3-1
А4-1
В1. 1,4 А
С1. 4,5 см
Версия формата PDF
Тест Основы электродинамики. Магнитное поле 11 класс
(180 Кб)
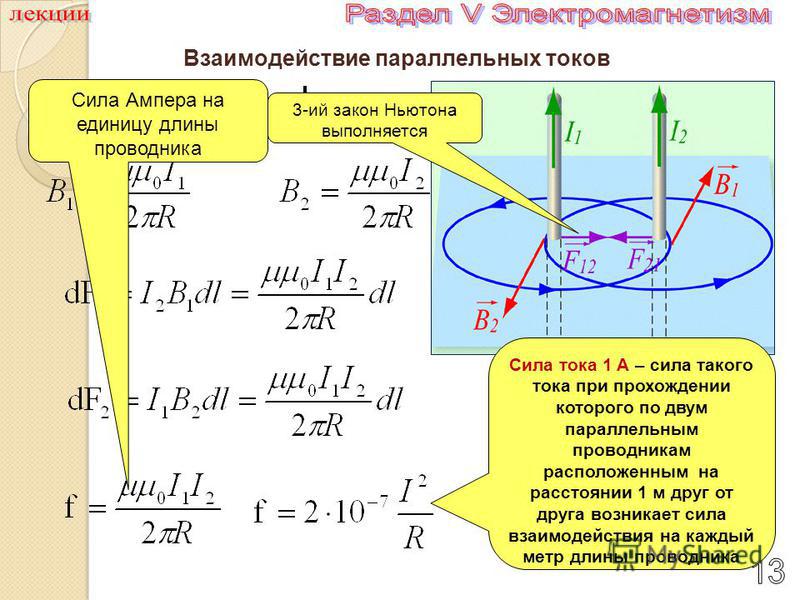
Взаимодействие параллельных токов. Сила Ампера. Взаимодействие параллельных проводников с током. Работа сил магнитного поля по перемещению витка с током Сила взаимодействия двух параллельных токов
Магнитное поле оказывает на рамку с током ориентирующее действие. Следовательно, вращающий момент, испытываемый рамкой, есть результат действия сил на отдельные ее элементы. Обобщая результаты исследования действия магнитного поля на различные проводники с током.
Ампер установил, что сила dF
Направление вектора dF может быть найдено, согласно (111.1), по общим правилам векторного произведения, откуда следуетправило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В , а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток.
Модуль силы Ампера (см. (111.1)) вычисляется по формуле
где a -угол между векторами d
Закон Ампера применяется для определения силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока I 1 и I 2 ; (направления токов указаны на рис. 167), расстояние между которыми равно R.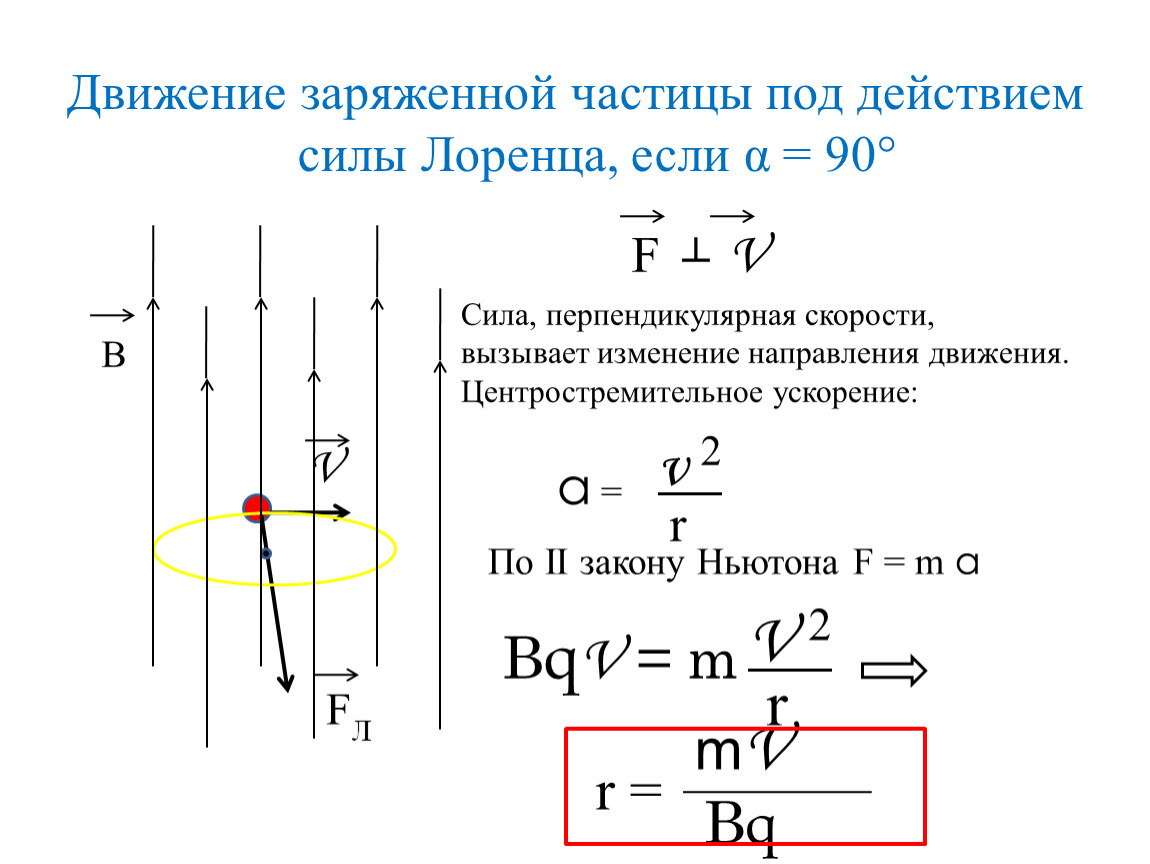
Каждый из проводников создает магнитное поле, которое действует по закону Ампера на другой проводник с током. Рассмотрим, с какой силой действует магнитное поле тока I 1 на элемент dl второго проводника с током I 2 . Ток I 1 создает вокруг себя магнитное поле, линии магнитной индукции которого представляют собой концентрические окружности. Направление вектора
Направление силы dF 1 , с которой поле B 1 действует на участок dl второго тока, определяется по правилу левой руки и указано на рисунке. Модуль силы, согласно (111.2), с учетом того, что угол a между элементами тока I 2 и вектором B 1 прямой, равен
подставляя значение для В 1 , получим Рассуждая аналогично, можно показать, что сапа dF 2 с которой магнитное поле тока I 2 действует на элемент dl первого проводника с током
Сравнение выражений (111.
3) и (111.4) показывает, что
т. е. два параллельных тока одинакового направления притягиваются друг к другу с силой
(111.5)
Если токи имеют противоположные направления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания, определяемая формулой (111.5).
Закон Био-Савара-Лапласа.
Электрическое поле действует как на неподвижные, так и на движущиеся в нем электрические заряды. Важнейшая особенность магнитного поля состоит в том, что оно действует
164) индукцию поля dB , записывается в виде где dМодуль вектора d
Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:
Расчет характеристик магнитного поля (В и Н ) по приведенным формулам в общем случае сложен.
Однако если распределение тока имеет определенную симметрию, то применение закона Био — Савара — Лапласа совместно с принципом суперпозиции позволяет просто рассчитать конкретные поля. Рассмотрим два примера.
1. Магнитное поле прямого тока — тока, текущего по тонкому прямому проводу бесконечной длины (рис. 165). В произвольной точке А, удаленной от оси проводника на расстояние R, векторы dB от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к вам»). Поэтому сложение векторов dB можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол a (угол между векторами dl и r ), выразив через него все остальные величины. Из рис. 165 следует, что
(радиус дуги CD вследствие малости dl равен r , и угол FDC по этой же причине можно считать прямым). Подставив эти выражения в (110.2), получим, что магнитная индукция, создаваемая одним элементом проводника, равна
(110.
4)
Так как угол a для всех элементов прямого тока изменяется в пределах от 0 до p, то, согласно (110.3) и (110.4),
Следовательно, магнитная индукция поля прямого тока
(110.5)
2. Магнитное поле в центре кругового проводника с током (рис. 166). Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитные поля одинакового направления — вдоль нормали от витка. Поэтому сложение векторов dB можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sina =1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, согласно (110.2),
Следовательно, магнитная индукция поля в центре кругового проводника с током
Сила взаимодействия параллельных токов. Закон Ампера
Если взять два проводника с электрическими токами, то они будут притягиваться друг к другу, если токи в них направлены одинаково и отталкиваться, если токи текут в противоположных направлениях.
{-7}Н$ на каждый метр длины.
Закон Ампера для проводника произвольной формы
Если проводник с током находится в магнитном поле, то на каждый носитель тока действует сила равная:
где $\overrightarrow{v}$ — скорость теплового движения зарядов, $\overrightarrow{u}$ — скорость упорядоченного их движения. От заряда, это действие передается проводнику, по которому заряд перемещается. Значит, на проводник с током, который находится в магнитном, поле действует сила.
Выберем элемент проводника с током длины $dl$. Найдем силу ($\overrightarrow{dF}$) с которой действует магнитное поле на выделенный элемент. Усредним выражение (2) по носителям тока, которые находятся в элементе:
где $\overrightarrow{B}$ — вектор магнитной индукции в точке размещения элемента $dl$. Если n — концентрация носителей тока в единице объема, S — площадь поперечного сечения провода в данном месте, тогда N — число движущихся зарядов в элементе $dl$, равное:
Умножим (3) на количество носителей тока, получим:
Зная, что:
где $\overrightarrow{j}$- вектор плотности тока, а $Sdl=dV$, можно записать:
Из (7) следует, что сила, действующая на единицу объема проводника равна, плотность силы ($f$):
Формулу (7) можно записать в виде:
где $\overrightarrow{j}Sd\overrightarrow{l}=Id\overrightarrow{l}.
$
Формула (9) закон Ампера для проводника произвольной формы. Модуль силы Ампера из (9) очевидно равен:
где $\alpha $ — угол между векторами $\overrightarrow{dl}$ и $\overrightarrow{B}$. Сила Ампера направлена перпендикулярно плоскости, в которой лежат векторы $\overrightarrow{dl}$ и $\overrightarrow{B}$. Силу, которая действует на провод конечной длины можно найти из (10) путем интегрирования по длине проводника:
Силы, которые действуют на проводники с токами, называют силами Ампера.
Направление силы Ампера определяется правилом левой руки (Левую руку надо расположить так, чтобы линии поля входили в ладонь, четыре пальца были направлены по току, тогда отогнутый на 900 большой палец укажет направление силы Ампера).
Пример 1
Задание: Прямой проводник массой m длиной l подвешен горизонтально на двух легких нитях в однородном магнитном поле, вектор индукции этого поля имеет горизонтальное направление перпендикулярное проводнику (рис.1). Найдите силу тока и его направление, который разорвет одну из нитей подвеса.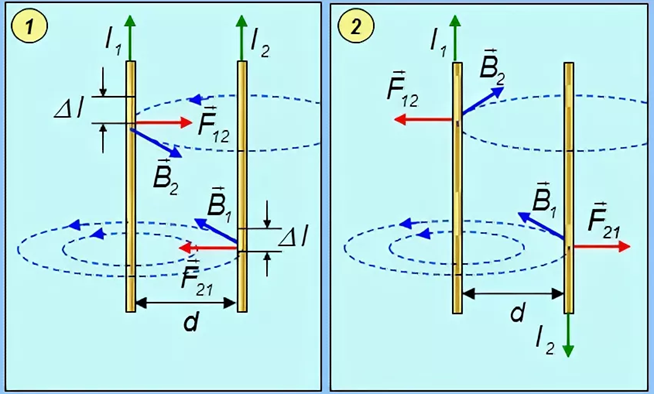
Индукция поля B. Каждая нить разорвется при нагрузке N.
Для решения задачи изобразим силы, которые действуют на проводник (рис.2). Будем считать проводник однородным, тогда можно считать, что точка приложения всех сил — середина проводника. Для того, чтобы сила Ампера была направлена вниз, ток должен течь в направлении из точки А в точку В (рис.2) (На рис.1 магнитное поле изображено, направленным на нас, перпендикулярно плоскости рисунка).
В таком случае уравнение равновесия сил, приложенных к проводнику с током запишем как:
\[\overrightarrow{mg}+\overrightarrow{F_A}+2\overrightarrow{N}=0\ \left(1.1\right),\]
где $\overrightarrow{mg}$ — сила тяжести, $\overrightarrow{F_A}$ — сила Ампера, $\overrightarrow{N}$ — реакция нити (их две).
Спроектируем (1.1) на ось X, получим:
Модуль силы Ампера для прямого конечного проводника с током равен:
где $\alpha =0$ — угол между векторами магнитной индукции и направлением течения тока.
Подставим (1.
3) в (1.2) выразим силу тока, получим:
Ответ: $I=\frac{2N-mg}{Bl}.$ Из точки А и точку В.
Пример 2
Задание: По проводнику в виде половины кольца радиуса R течет постоянный ток силы I. Проводник находится в однородном магнитном поле, индукция которого равна B, поле перпендикулярно плоскости, в которой лежит проводник. Найдите силу Ампера. Провода, которые подводят ток вне поля.
Пусть проводник находится в плоскости рисунка (рис.3), тогда линии поля перпендикулярны плоскости рисунка (от нас). Выделим на полукольце бесконечно малый элемент тока dl.
На элемент тока действует сила Ампера равная:
\\ \left(2.1\right).\]
Направление силы определяется по правилу левой руки. Выберем координатные оси (рис.3). Тогда элемент силы можно записать через его проекции (${dF}_x,{dF}_y$) как:
где $\overrightarrow{i}$ и $\overrightarrow{j}$ — единичные орты. Тогда силу, которая действует на проводник, найдем как интеграл по длине провода L:
\[\overrightarrow{F}=\int\limits_L{d\overrightarrow{F}=}\overrightarrow{i}\int\limits_L{dF_x}+\overrightarrow{j}\int\limits_L{{dF}_y}\left(2.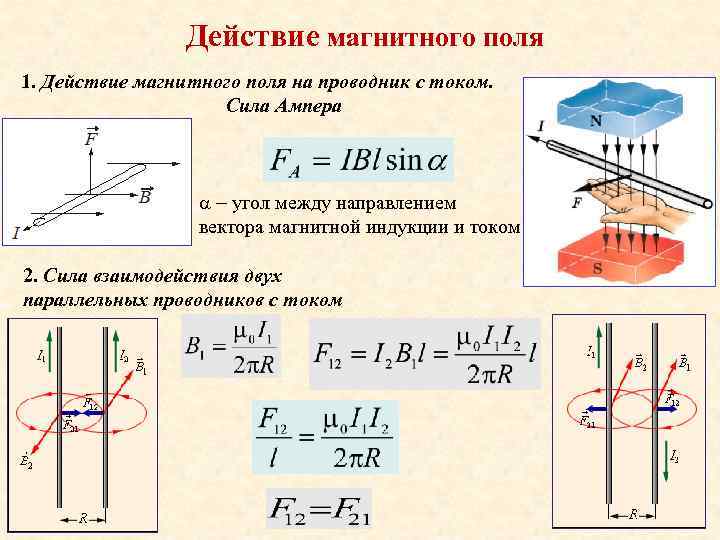
{\frac{\pi }{2}}_{-\frac{\pi }{2}}{cos\alpha d\alpha }=2IBR\overrightarrow{j}.\]
Ответ: $\overrightarrow{F}=2IBR\overrightarrow{j}.$
На
магнитную стрелку, расположенную вблизи
проводника с током, действуют силы,
которые стремятся повернуть стрелку.
Французский физик А. Ампер наблюдал
силовое взаимодействие двух проводников
с токами и установил закон взаимодействия
токов.
Магнитное
поле, в отличие от электрического,
оказывает силовое действие только на
движущиеся заряды (токи).
Характеристика,
для описания магнитного поля — вектор
магнитной индукции .
Вектор
магнитной индукции
определяет
силы, действующие на токи или движущиеся
заряды в магнитном поле. За положительное
направление вектора принимается
направление от южного полюса S к северному
полюсу N магнитной стрелки, свободно
устанавливающейся в магнитном поле.
Таким образом, исследуя магнитное поле,
создаваемое током или постоянным
магнитом, с помощью маленькой магнитной
стрелки, можно в каждой точке пространства
определить направление
вектора .
Взаимодействие
токов вызывается их магнитными полями:
магнитное поле одного тока действует
силой Ампера на другой ток и наоборот.
Как
показали опыты Ампера, сила,
действующая на участок проводника,
пропорциональна силе тока I, длине Δl
этого участка и синусу угла α между
направлениями тока и вектора магнитной
индукции: F ~ IΔl sin α
Эта сила называется силой Ампера . Она достигает максимального по модулю значения F max , когда проводник с током ориентирован перпендикулярно линиям магнитной индукции. Модуль вектора определяется следующим образом: модуль вектора магнитной индукции равен отношению максимального значения силы Ампера, действующей на прямой проводник с током, к силе тока I в проводнике и его длине Δl:
В общем случае сила Ампера выражается соотношением: F = IBΔl sin α
Это
соотношение принято называть законом
Ампера.
В
системе единиц СИ за единицу магнитной
индукции принята индукция такого
магнитного поля, в котором на каждый
метр длины проводника при силе тока 1 А
действует максимальная сила Ампера
1 Н.
Эта единица называется тесла (Тл).
Тесла – очень крупная единица. Магнитное поле Земли приблизительно равно 0,5·10 –4 Тл. Большой лабораторный электромагнит может создать поле не более 5 Тл. Сила Ампера направлена перпендикулярно вектору магнитной индукции и направлению тока, текущего по проводнику. Для определения направления силы Ампера обычно используют правило левой руки. Магнитное взаимодействие параллельных проводников с током используется в системе СИ для определения единицы силы тока – ампера: Ампер – сила неизменяющегося тока, который при прохождении по двум параллельным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1 м один от другого в вакууме, вызвал бы между этими проводниками силу магнитного взаимодействия, равную 2·10 –7 H на каждый метр длины. Формула, выражающая закон магнитного взаимодействия параллельных токов, имеет вид:
14. Закон Био-Савара-Лапласа. Вектор магнитной индукции. Теорема о циркуляции вектора магнитной индукции.
Закон Био Савара Лапласа определяет величину модуля вектора магнитной индукции в точке выбранной произвольно находящейся в магнитном поле. Поле при этом создано постоянным током на некотором участке.
Магнитное поле любого тока может быть вычислено как векторная сумма (суперпозиция) полей, создаваемых отдельными элементарными участками тока:
Элемент тока длины dl создает поле с магнитной индукцией: или в векторной форме:
Здесь I – ток; – вектор, совпадающий с элементарным участком тока и направленный в ту сторону, куда течет ток; – радиус-вектор, проведенный от элемента тока в точку, в которой мы определяем ; r – модуль радиус-вектора; k
Вектор магнитной индукции — это основная силовая характеристика магнитного поля (обозначается ). Вектор магнитной индукции направлен перпендикулярно плоскости, проходящей через и точку, в которой вычисляется поле.
Направление связано
с направлением « правилом
буравчика »: направление
вращения головки винта дает направление ,
поступательное движение винта
соответствует направлению тока в
элементе.
Таким образом, закон Био–Савара–Лапласа устанавливает величину и направление вектора в произвольной точке магнитного поля, созданного проводником с током I.
Модуль вектора определяется соотношением:
где α – угол между и ; k – коэффициент пропорциональности, зависящий от системы единиц.
В международной системе единиц СИ закон Био–Савара–Лапласа для вакуума можно записать так: где – магнитная постоянная.
Теорема о циркуляции вектора : циркуляция вектора магнитной индукции равна току, охваченному контуром, умноженному на магнитную постоянную. ,
Рассмотрим провод, находящийся с магнитном поле и по которому течет ток (рис.12.6).
На каждый носитель тока (электрон), действует сила Лоренца . Определим силу, действующей на элемент провода длины dl
Последнее выражение носит название закона Ампера .
Модуль силы Ампера вычисляется по формуле:
.
Сила Ампера направлена перпендикулярно плоскости, в которой лежат векторы dl и B.
Применим закон Ампера для вычисления силы взаимодействия двух находящихся в вакууме параллельных бесконечно длинных прямых токов (рис.12.7).
Расстояние между проводниками — b. Предположим, что проводник I 1 создает магнитное поле индукцией
По закону Ампера на проводник I 2 , со стороны магнитного поля, действует сила
, учитывая, что (sinα =1)
Следовательно, на единицу длины (dl =1) проводника I 2 , действует сила
.
Направление силы Ампера определяют по правилу левой руки: если ладонь левой руки расположить так, чтобы в нее входили линии магнитной индукции, а четыре вытянутых пальца расположить по направлению электрического тока в проводнике, то отставленный большой палец укажет направление силы, действующей на проводник со стороны поля.
12.4. Циркуляция вектора магнитной индукции (закон полного тока). Следствие.
Магнитное поле в отличие от электростатического — непотенциальное поле: циркуляция вектора В магнитной индукции поля вдоль замкнутого контура не равна нулю и зависит от выбора контура.
Такое поле в векторном анализе называют вихревым полем.
Рассмотрим в качестве примера магнитное поле замкнутого контура L произвольной формы, охватывающего бесконечно длинный прямолинейный проводник с током l , находящегося в вакууме (рис.12.8).
Линии магнитной индукции этого поля представляют собой окружности, плоскости которых перпендикулярны проводнику, а центры лежат на его оси (на рис. 12.8 эти линии изображены пунктиром). В точке А контура L вектор В магнитной индукции поля этого тока перпендикулярен радиусу-вектору .
Из рисунка видно, что
где — длина проекции вектора dl на направление вектора В . В то же время малый отрезок dl 1 касательной к окружности радиуса r можно заменить дугой окружности: , где dφ — центральный угол, под которым виден элемент dl контура L из центра окружности.
Тогда получаем, что циркуляция вектора индукции
Во всех точках линии вектор магнитной индукции равен
интегрируя вдоль всего замкнутого контура, и учитывая, что угол изменяется от нуля до 2π, найдем циркуляцию
Из формулы можно сделать следующие выводы:
1.
Магнитное поле прямолинейного тока – вихревое поле и не консервативно, так как в нем циркуляция вектора В вдоль линии магнитной индукции не равна нулю;
2. циркуляция вектора В магнитной индукции замкнутого контура, охватывающего поле прямолинейного тока в вакууме одинакова вдоль всех линий магнитной индукции и равна произведению магнитной постоянной на силу тока.
Если магнитное поле образовано несколькими проводниками с током, то циркуляция результирующего поля
Данное выражение называется теоремой о полном токе .
Отсюда нетрудно получить выражение для индукции магнитного поля каждого из прямолинейных проводников. Магнитное поле прямолинейного проводника с током должно обладать осевой симметрией и, следовательно, замкнутые линии магнитной индукции могут быть только концентрическими окружностями, располагающимися в плоскостях, перпендикулярных проводнику. Это означает, что векторы B1 и B2 магнитной индукции параллельных токов I 1 и I 2 лежат в плоскости, перпендикулярной обоим токам.
Поэтому при вычислении сил Ампера, действующих на проводники с током, в законе Ампера нужно положить sin α = 1. Из закона магнитного взаимодействия параллельных токов следует, что модуль индукции B магнитного поля прямолинейного проводника с током I на расстоянии R от него выражается соотношением
Для того, чтобы при магнитном взаимодействии параллельные токи притягивались, а антипараллельные отталкивались, линии магнитной индукции поля прямолинейного проводника должны быть направлены по часовой стрелке, если смотреть вдоль проводника по направлению тока. Для определения направления вектора B магнитного поля прямолинейного проводника также можно пользоваться правилом буравчика: направление вращения рукоятки буравчика совпадает с направлением вектора B если при вращении буравчик перемещается в направлении тока Магнитное взаимодействие параллельных проводников с током используется в Международной системе единиц (СИ) для определения единицы силы тока – ампера:
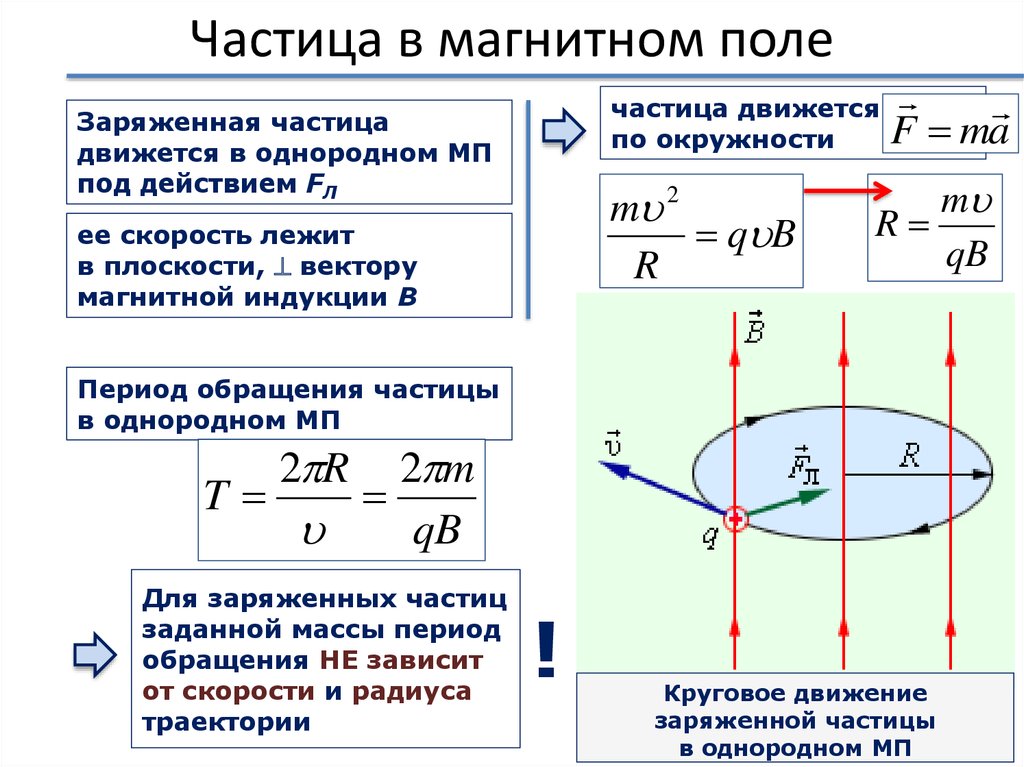
Вектор магнитной индукции — это основная силовая характеристика магнитного поля (обозначается В).
В магнитного поля (рисунок — 3.34). В таком случае сила Лоренца обеспечивает центростремительное ускорение a = v 2 /R и частица движется по окружности радиусом R в плоскости, перпендикулярной линиям индукции магнитного поля.под действием силы Лоренца: F n = qvB sinα, учитывая, что α = 90°, запишем уравнение движения такой частицы: т v 2 /R= qvB. Здесь m — масса частицы, R – радиус окружности по которой движется частица. Откуда можно найти отношение e/m — называют удельным зарядом, который показывает заряд единицы массы частицы.
с) Если заряженная частица влетает со скоростью v 0 в магнитное поле под любым углом α , то данное движение можно представить ее как сложное и разложить ее на две составляющие по. Траектория движения представляет собой винтовую линию, ось которой совпадает с направлением В . Направление, в котором закручивается траектория, зависит от знака заряда частицы. Если заряд положителен, траектория закручивается против часовой стрелки.
Траектория, по которой движется отрицательно заряженная частица, закручивается по часовой стрелке (предполагается, что мы смотрим на траекторию вдоль направления В ; частица при этом летит от нас.
Магнитная сила между двумя параллельными проводниками
Цели обучения
К концу этого раздела вы сможете:
- Описывать эффекты магнитной силы между двумя проводниками.
- Рассчитайте силу между двумя параллельными проводниками.
Можно ожидать, что между проводниками с током действуют значительные силы, поскольку обычные токи создают значительные магнитные поля, а эти поля воздействуют на обычные токи значительными силами. Но вы можете не ожидать, что сила между проводами используется для определяют ампер. Вы также можете удивиться, узнав, что эта сила как-то связана с тем, почему большие автоматические выключатели сгорают, когда они пытаются отключить большие токи.
Силу между двумя длинными прямыми и параллельными проводниками, разделенными расстоянием r , можно найти, применяя то, что мы разработали в предыдущих разделах.
На рис. 1 показаны провода, их токи, поля, которые они создают, и последующие силы, которые они воздействуют друг на друга. Рассмотрим поле, создаваемое проводом 1, и силу, действующую на провод 2 (назовем силу Ф 2 ). Поле, создаваемое I 1 на расстоянии r , принимается равным
[латекс]{B}_{1}=\frac{\mu_{0}{I}_{1}}{ 2\pi r}\\[/латекс].
Рис. 1. (a) Магнитное поле, создаваемое длинным прямым проводником, перпендикулярно параллельному проводнику, как показано RHR-2. (b) Вид сверху на два провода, показанных на (а), с одной линией магнитного поля, показанной для каждого провода. RHR-1 показывает, что сила между параллельными проводниками притягивается, когда токи имеют одинаковое направление. Подобный анализ показывает, что сила отталкивающая между токами в противоположных направлениях.
Это поле однородно вдоль провода 2 и перпендикулярно ему, поэтому сила F 2 , действующая на провод 2, определяется выражением [латекс]F=IlB\sin\theta\\[/latex] с [ латекс]\sin\theta =1\\[/латекс]:
[латекс]{F}_{2}={I}_{2}{\text{lB}}_{1}\\[/ латекс].
По третьему закону Ньютона силы на проводах равны по величине, поэтому мы просто пишем F для величины F 2 . (Обратите внимание, что F 1 = − F 2 .) Поскольку провода очень длинные, удобно мыслить в терминах F / l , силы на единицу длины. Подстановка выражения для B 1 в последнее уравнение и изменение порядка членов дает
[латекс]\frac{F}{l}=\frac{{\mu }_{0}{I}_{1} {I}_{2}}{2\mathrm{\pi r}}\text{.}\\[/latex]
F / l сила на единицу длины между двумя параллельными токами I 1 и I 2 разделены расстоянием r . Сила притяжения, если токи имеют одинаковое направление, и отталкивания, если они направлены в противоположные стороны. Эта сила ответственна за пинч-эффект в электрических дугах и плазме. Сила существует независимо от того, есть ли токи в проводах или нет.
В электрической дуге, где токи движутся параллельно друг другу, существует притяжение, которое сжимает токи в трубку меньшего размера. В больших автоматических выключателях, таких как те, которые используются в системах распределения электроэнергии по соседству, эффект защемления может концентрировать дугу между пластинами выключателя, пытаясь отключить большой ток, прожечь дыры и даже зажечь оборудование. Другой пример пинч-эффекта можно найти в солнечной плазме, где струи ионизированного материала, такие как солнечные вспышки, формируются под действием магнитных сил. 9{-7}\text{ Н/м}\\[/латекс].
Поскольку μ 0 равно точно 4π × 10 −7 Т ⋅ м/А по определению, а поскольку 1 Т = 1 Н/(А ⋅ м), сила на метр равна в точности 2 × 10 −7 Н/м. На этом основано рабочее определение ампера.
Ампер Официальное определение ампера: Один ампер тока через каждый из двух параллельных проводников бесконечной длины, разделенных на один метр в пустом пространстве, свободном от других магнитных полей, вызывает силу ровно 2 × 10 −7 Н/м на каждом проводнике.
Прямые провода бесконечной длины нецелесообразны, поэтому на практике баланс токов создается с помощью витков провода, разделенных несколькими сантиметрами. Сила измеряется для определения силы тока. Это также дает нам метод измерения кулона. Измеряем заряд, протекающий при токе в один ампер за одну секунду. То есть 1 Кл = 1 А ⋅ с. Как для ампера, так и для кулона метод измерения силы между проводниками является наиболее точным на практике.
Концептуальные вопросы
1. Сила притяжения или отталкивания между горячей и нейтральной линиями, подвешенными к опорам электропередач? Почему?
2. Если у вас есть три параллельных провода в одной плоскости, как на рис. 2, с токами в двух крайних, протекающих в противоположных направлениях, возможно ли, чтобы средний провод отталкивался от обоих? Привлекают обоих? Объяснять.
Рисунок 2. Три параллельных копланарных провода с токами в двух крайних в противоположных направлениях.
3. Предположим, что два длинных прямых провода идут перпендикулярно друг другу, не касаясь друг друга.
Оказывает ли одно действие силы на другое? Если да, то каково его направление? Оказывает ли один чистый крутящий момент на другой? Если да, то каково его направление? Обоснуйте свои ответы, используя правила правой руки.
4. Используйте правила правой руки, чтобы показать, что сила между двумя петлями на рисунке 3 притягивает, если токи имеют одинаковое направление, и отталкивает, если они направлены в противоположные стороны. Согласуется ли это с тем, что одинаковые полюса петель отталкиваются, а разные полюса петель притягиваются? Нарисуйте эскизы, чтобы обосновать свои ответы.
Рис. 3. Две петли проводов, по которым текут токи, могут оказывать друг на друга силы и крутящие моменты.
5. Если одна из петель на рисунке 3 слегка наклонена по отношению к другой, а их токи имеют одинаковое направление, каковы направления крутящих моментов, которые они оказывают друг на друга? Означает ли это, что полюса создаваемых ими магнитоподобных полей совпадут друг с другом, если петлям будет позволено вращаться?
6.
Линии электрического поля могут быть экранированы эффектом клетки Фарадея. Можем ли мы иметь магнитное экранирование? Можем ли мы иметь гравитационное экранирование?
Упражнения
1. (a) Горячий и нейтральный провода, подводящие постоянный ток к легкорельсовому пригородному поезду, имеют ток 800 А и разделены расстоянием 75,0 см. Какова величина и направление силы между 50,0 м этих проводов? (b) Обсудите практические последствия этой силы, если таковые имеются.
2. Усилие на метр между двумя проводами соединительного кабеля, используемого для запуска заглохшего автомобиля, составляет 0,225 Н/м. а) Какова сила тока в проводах, если расстояние между ними 2 см? б) Сила притягивает или отталкивает?
3. Отрезок провода длиной 2,50 м, питающий двигатель подводной лодки, несет ток 1000 А и испытывает отталкивающую силу 4,00 Н от параллельного провода на расстоянии 5,00 см. Каково направление и величина тока в другом проводе?
4. Провод, идущий к двигателю пригородного поезда с током 400 А, испытывает силу притяжения 4,00 × 10 −3 Н/м из-за параллельного провода, ведущего к фаре 5,00 А.
а) На каком расстоянии друг от друга расположены провода? б) Направлены ли течения в одном направлении?
5. Шнур прибора переменного тока имеет горячие и нейтральные провода, разделенные расстоянием 3,00 мм, и по нему проходит ток силой 5,00 А. а) Какова средняя сила на метр между проводами шнура? б) Какова максимальная сила на метр между проводами? в) Являются ли силы притягивающими или отталкивающими? (d) Нужны ли шнурам электроприборов какие-либо специальные конструктивные особенности для компенсации этих сил?
6. На рисунке 4 показан длинный прямой провод рядом с прямоугольной токовой петлей. Каковы направление и величина полной силы, действующей на петлю?
Рисунок 4.
7. Найдите направление и величину силы, действующей на каждый провод на рис. 5(а), путем сложения векторов.
Рисунок 5.
8. Найдите направление и величину силы, действующей на каждый провод на рис. 5(b), используя сложение векторов.
Избранные решения задач и упражнения
1.
(a) 8,53 Н, отталкивающая (b) Эта сила является отталкивающей, и поэтому никогда не существует риска, что два провода коснутся и произведут короткое замыкание.
3. 400 А в обратном направлении
5. (а) 1,67 × 10 -3 Н/м (б) 3,33 × 10 -3 Н/м (в) Отталкивающая (г) Нет, эти являются очень малыми силами
7. (a) Верхний провод: 2,65 × 10 -4 Н/м с, 10,9º влево от верха (b) Нижний левый провод: 3,61 × 10 -4 Н/м, 13,9 º вниз справа (c) Нижний правый провод: 3,46 × 10 −4 Н/м, 30,0º вниз слева
22,10: Магнитная сила между двумя параллельными проводниками
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2704
- OpenStax
- OpenStax
Цели обучения
К концу этого раздела вы сможете:
- Описывать эффекты магнитной силы между двумя проводниками.
- Рассчитайте силу между двумя параллельными проводниками.
Можно ожидать, что между проводниками с током действуют значительные силы, поскольку обычные токи создают значительные магнитные поля, а эти поля воздействуют на обычные токи значительными силами. Но вы можете не ожидать, что сила между проводами используется для определения ампера. Вы также можете удивиться, узнав, что эта сила как-то связана с тем, почему большие автоматические выключатели сгорают, когда они пытаются отключить большие токи.
Силу между двумя длинными прямыми и параллельными проводниками, разделенными расстоянием \(r\), можно найти, применяя то, что мы разработали в предыдущих разделах. На рисунке \(\PageIndex{1}\) показаны провода, их токи, поля, которые они создают, и последующие силы, которые они воздействуют друг на друга. Рассмотрим поле, создаваемое проводом 1, и силу, которую он оказывает на провод 2 (назовем силу \(F_{2}\)). Поле из-за \(I_{1}\) на расстоянии \(r\) равно
\[B_{1} = \frac{\mu_{0}I_{1}}{2\pi r}.
\label{22.11.1}\]
Это поле однородно вдоль провода 2 и перпендикулярно ему, поэтому сила \(F_{2}\), действующая на провод 2, определяется выражением \(F = IlB sin\theta\) с \(sin \theta = 1\): \[F_{2} = I_{2}lB_{1}.\label{22.11.2}\] По третьему закону Ньютона силы на проводах равны по величине, поэтому мы просто пишем \ (F\) для величины \(F_{2}\). (Обратите внимание, что \(F_{1} = -F_{2}\).) Поскольку провода очень длинные, удобно думать в терминах \(F/l\), сила на единицу длины. Подстановка выражения для \(B_{1}\) в последнее уравнение и перестановка членов дает
\[\frac{F}{l} = \frac{\mu_{0}I_{1}I_{2}}{2\pi r}.
\label{22.11.3}\]
\(F/l\) сила на единицу длины между двумя параллельными токами \(I_{1}\) и \(I_{2}\), разделенными расстоянием \(r\). Сила притяжения, если токи имеют одинаковое направление, и отталкивания, если они направлены в противоположные стороны.
Эта сила отвечает за пинч-эффект в электрических дугах и плазме. Сила существует независимо от того, есть ли токи в проводах или нет. В электрической дуге, где токи движутся параллельно друг другу, существует притяжение, которое сжимает токи в трубку меньшего размера. В больших автоматических выключателях, таких как те, которые используются в системах распределения электроэнергии по соседству, эффект защемления может концентрировать дугу между пластинами выключателя, пытаясь отключить большой ток, прожечь дыры и даже зажечь оборудование. Другой пример пинч-эффекта можно найти в солнечной плазме, где струи ионизированного материала, такие как солнечные вспышки, формируются под действием магнитных сил. 9{-7} Н/м\) на каждом проводнике.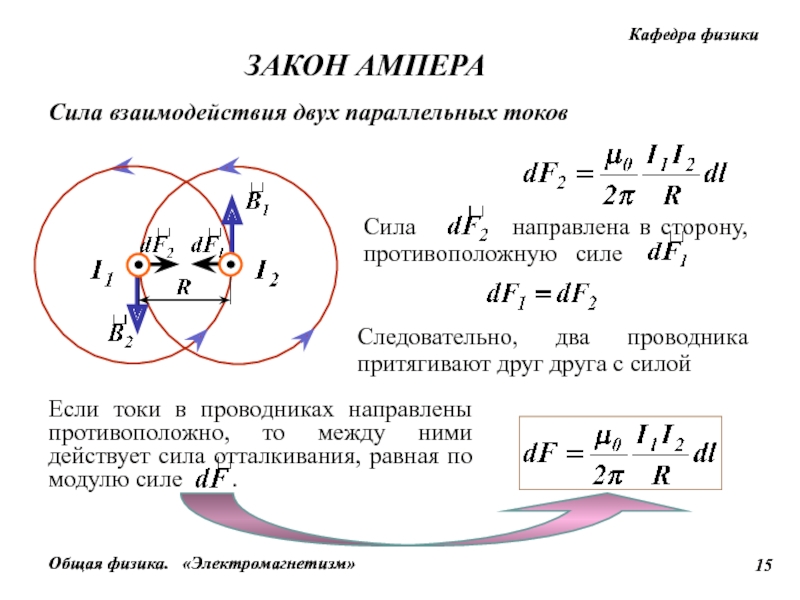
Прямые провода бесконечной длины непрактичны, поэтому на практике баланс токов строится с помощью витков провода, разделенных несколькими сантиметрами. Сила измеряется для определения силы тока. Это также дает нам метод измерения кулона. Измеряем заряд, протекающий при токе в один ампер за одну секунду. То есть \(1 C = 1 A \cdot s\). Как для ампера, так и для кулона метод измерения силы между проводниками является наиболее точным на практике.
- Сила между двумя параллельными токами \(I_{1}\) и \(I_{2}\), разделенными расстоянием \(r\), имеет величину на единицу длины, определяемую \[\frac{F} {l} = \frac{\mu_{0}I_{1}I_{2}}{2\pi r}.\]
- Сила притяжения, если токи имеют одинаковое направление, и отталкивания, если они направлены в противоположные стороны.
Эта страница под названием 22.10: Магнитная сила между двумя параллельными проводниками распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
- Метки
- Магнитная сила
- параллельные проводники
- источник@https://openstax.
Leave A Comment