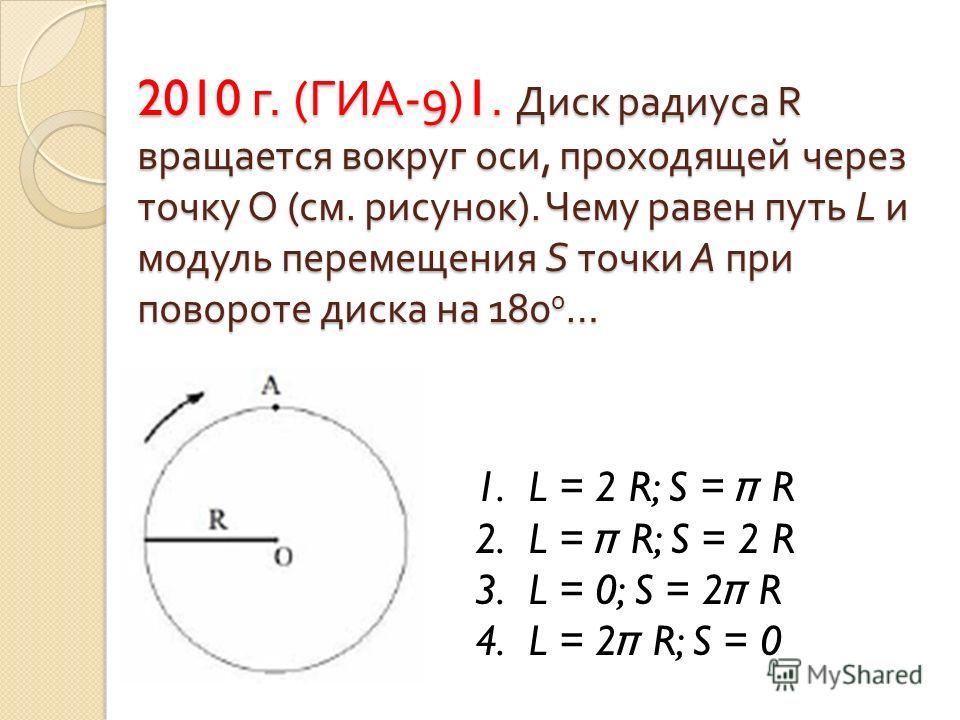
Ребят помогите по физике 9 класс. Диск радиусом R вращается вокруг оси, проходящей через
Определите давление машинного масла на дно сосуда, если высота его столба 2 см.
Найти период колебаний в контуре, емкость конденсатора в котором 10 ПФ, индуктивность катушки 5 мкГн.
ДЕФОРМАЦИЯ. СИЛА УПРУГости конспект
Плотность тела,плавающего на поверхности воды,в 3 раза меньше плотности этой жидкости. Чему равно отношение объёмов надводной и подводной частей тела? …
При подаче напряжения 4,5В на концы никелированного
Сопротивление металлического проводника с ростом температуры…___________. Объясните почему?______________________________________________________ ____
… _________________________________________________________________ [2]2.При прохождении тока через сверхпроводник наблюдаются такие действия, как…_________________________________________________________________ [1]3.В сильном магнитном поле сверхпроводящие свойства становятся …___________________ [1]4.
ТЕСТA1. Выталкивающая сила действует1) на тела со стороны твёрдых тел2) только на тела, находящиеся в жидкости3) только на тела, находящиеся в газе4)
… на тела, находящиеся в жидкости или газеА2. На рисунке показано тело, подвешенное к пружине. При опускании тела в сосуд с жидкостью растяжение пру¬жины1) увеличится2) уменьшится3) не изменится4) может как увеличиться, так и уменьшитьсяА3. Вес тела, полностью погружённого в воду1) меньше веса этого тела в воздухе2) равен весу этого тела в воздухе3) больше веса этого тела в воздухе4) может быть как больше, так и меньше веса тела в воздухеА4. Действующая на тело сила Архимеда зависит1) от плотности тела и объёма тела2) от плотности жидкости и объёма жидкости3) от плотности жидкости и объёма тела, погружён¬ного в жидкость4) от плотности тела и объёма жидкостиА5. Металлическую деталь объёмом 0,0003 м3 погрузили в керосин. Плотность керосина 800 кг/м3.
Работа #7. Измерение работы и мощности электрического тока. СРОЧНО!!!!!
1. Какая сила возникает при погружении тела в жидкость?
А. Сила тяжести Б. Сила Архимеда В. Вес тела
2. От чего зависит Архимедова сила?
А. От плотност
… и тела и плотности жидкости Б. От объема тела и плотности тела
В. От плотности жидкости и объема тела Г. От веса тела.
3. Архимедова сила вычисляется по формуле:
А. Fa = ρтVт g Б. Fa = ρжVт g В. Fa = ρжVж g Г. ) Fа= ρтVжg
4. В каких единицах измеряется выталкивающая сила ?
А. Н Б. кг В. Па Г. Н/кг
5. Переведите объем 40 см3 в м3
А. 0,4 м3 Б. 0,04 м3 В. 0,004 м3 Г. 0,00004 м3
6. Сплошные шары одинаковой массы — алюминиевый и железный уравновешены на
весах. Нарушится ли равновесие, если оба шара погрузить в воду?
А. Не нарушится, т.к. их массы одинаковы.
Б. Нарушится, т.к. объемы шаров разные. В. Затрудняюсь ответить.
7. Какая из приведённых ниже величин не нужна для расчёта выталкивающей силы,
действующей на тело, погруженное в жидкость?
А. Объём тела. Б. Плотность жидкости. В. Плотность тела. Г. Постоянная g.
8. Два шарика одинакового объема из дерева и железа опустили в воду.
Какая сила возникает при погружении тела в жидкость?
А. Сила тяжести Б. Сила Архимеда В. Вес тела
2. От чего зависит Архимедова сила?
А. От плотност
… и тела и плотности жидкости Б. От объема тела и плотности тела
В. От плотности жидкости и объема тела Г. От веса тела.
3. Архимедова сила вычисляется по формуле:
А. Fa = ρтVт g Б. Fa = ρжVт g В. Fa = ρжVж g Г. ) Fа= ρтVжg
4. В каких единицах измеряется выталкивающая сила ?
А. Н Б. кг В. Па Г. Н/кг
5. Переведите объем 40 см3 в м3
А. 0,4 м3 Б. 0,04 м3 В. 0,004 м3 Г. 0,00004 м3
6. Сплошные шары одинаковой массы — алюминиевый и железный уравновешены на
весах. Нарушится ли равновесие, если оба шара погрузить в воду?
А. Не нарушится, т.к. их массы одинаковы.
Б. Нарушится, т.к. объемы шаров разные. В. Затрудняюсь ответить.
7. Какая из приведённых ниже величин не нужна для расчёта выталкивающей силы,
действующей на тело, погруженное в жидкость?
А. Объём тела. Б. Плотность жидкости. В. Плотность тела. Г. Постоянная g.
8. Два шарика одинакового объема из дерева и железа опустили в воду.

Как называют прибор для измерения атмосферного давление
ось проходит через центр вокруг
ось проходит через центр вокруг
Задача 16868
Непроводящая сфера радиуса R = 50 мм, заряженная равномерно с поверхностной плотностью σ = 10,0 мкКл/м2, вращается с угловой скоростью ω = 70 рад/с вокруг оси, проходящей через ее центр. Найти магнитную индукцию в центре сферы.
Задача 40473
Медный шар радиуса R вращается с частотой n вокруг оси, проходящей через его центр. Момент силы М за время t увеличивает угловую скорость вращения шара вдвое, совершая работу А. Найти время t и работу A.
Задача 40476
Однородный диск массой 5 кг и радиусом 0,2 м вращается вокруг оси, проходящей через его центр. Зависимость угловой скорости вращения диска от времени задана уравнением ω = А + Вt, где В = 8 рад/с2. Найти величину касательной силы, приложенной к ободу диска. Трением пренебречь.
Задача 40509
Сплошной шар радиусом 10 см и массой 0,5 кг вращается вокруг оси, проходящей через его центр, с частотой 5 об/с. На шар подействовал постоянный вращающий момент, вследствие чего шар сделал 200 об за 15 с. Найти этот вращающий момент, а также нормальное ускорение точек на поверхности шара спустя 20 с от начала ускоренного вращения.
Задача 40553
Однородный диск радиусом R = 0,2 м и весом P = 5 H вращается вокруг оси, проходящей через его центр. Зависимость угловой скорости вращения диска от времени дается уравнением ω = А + Вt, где В = 8 рад/с2. Найти величину силы, приложенной по касательной к ободу диска. Трением пренебречь.
Найти величину силы, приложенной по касательной к ободу диска. Трением пренебречь.
Задача 14922
Медный шар радиусом R = 10 см вращается с частотой n = 2 с–1 вокруг оси, проходящей через его центр. Какую работу надо совершить, чтобы увеличить угловую скорость вращения шара вдвое?
Задача 25925
Диск весом в 1 кг и диаметром 60 см вращается вокруг оси, проходящей через центр перпендикулярно его плоскости, делая 20 об/с, какую работу надо совершить, чтобы остановить диск?
Задача 14631
Однородный диск радиусом R = 0,2 м и массой m = 5 кг вращается вокруг оси, проходящей через его центр перпендикулярно к его плоскости. Зависимость угловой скорости со вращения диска от времени t дается уравнением ω = А + Bt, где B = 8 рад/с2. Найти касательную силу F, приложенную к ободу диска. Трением пренебречь.
Задача 14647
Диск диаметром D = 60 см и массой m = 1 кг вращается вокруг оси, проходящей через центр перпендикулярно к его плоскости с частотой n = 20 об/с.
Задача 14652
Медный шар радиусом R = 10 см вращается с частотой n = 2 об/с вокруг оси, проходящей через его центр. Какую работу А надо совершить, чтобы увеличить угловую скорость ω вращения шара вдвое?
Задача 11159
Шар массой m = 10 кг и радиусом R = 20 см вращается вокруг оси, проходящей через его центр. Уравнение вращения шара имеет вид φ = A+Bt
Задача 26555
Сплошной шар радиусом 10 см и массой 1,5 кг вращается вокруг оси, проходящей через его центр, с частотой 5 об/с. На шар подействовал постоянный вращающий момент, вследствие чего шар сделал 200 оборотов за 15 с. Найти этот вращающий момент и нормальное ускорение точек на поверхности шара через 20 с от начала его ускоренного вращения.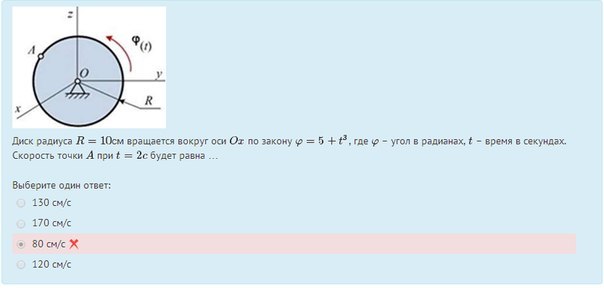
Задача 26692
Шар массой 10 кг и радиусом 20 см вращается вокруг оси, проходящей через его центр. Угол поворота изменяется во времени по закону φ = А + Вt2 + Сt3, где А = 5 рад; B = 4 рад/c2 ; C = -1 рад/c3. Определить величину момента сил, приложенных к шару в момент времени 2 с.
Задача 12452
Диск массой m = 2 кг и радиусом R = 10 см вращается вокруг оси, проходящей через его центр. Уравнение движения диска имеет вид φ = Ct3, где C = –1 рад/с3. Определить вращающий момент М в момент времени t = 2 с, если момент сил торможения постоянен и равен 12 Н·м.
Задача 12453
Маховик в виде диска радиуса R = 18 см и массой m = 12 кг свободно вращается вокруг оси, проходящей через его центр, с частотой ν = 6 с–1. При торможении маховик останавливается через t = 7 с. Определите тормозящий момент.
Задача 12454
Диск диаметром D = 60 см и массой m = 1 кг вращается вокруг оси, проходящей через центр перпендикулярно к его плоскости с частотой n = 20 об/с.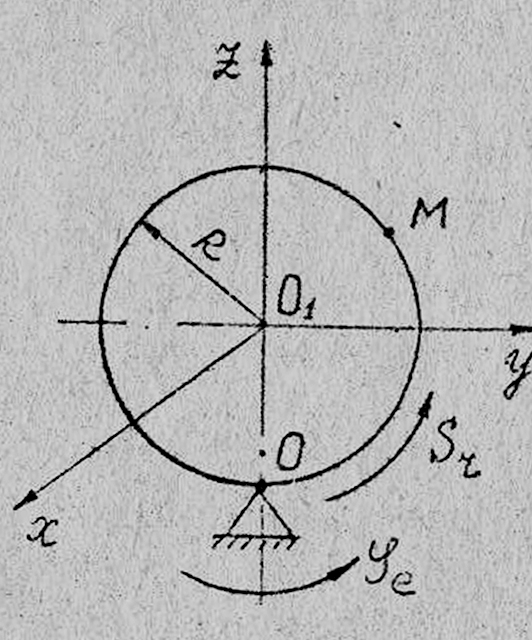 Какую работу А надо совершить, чтобы остановить диск?
Какую работу А надо совершить, чтобы остановить диск?
Задача 13828
Диск массой 2 кг и радиусом 0,1 м вращается вокруг оси, проходящей через его центр. Уравнение движения φ = 5 – 6t 2 + t3. Определить момент сил, действующих на диск, в момент времени 4 с. Определишь закон изменения момента сил.
Задача 13829
Шар массой 10 кг и радиусом 20 см вращается вокруг оси, проходящей через ее центр. Уравнение вращения шара имеет вид: φ = 2+4t2–t3. Найти закон изменения момента сил, действующих на шар. Определить момент сил в момент времени 2 с.
Задача 16064
Шар массой 10 кг и радиусом 20 см вращается вокруг оси, проходящей через его центр. Зависимость угла поворота шара от времени имеет вид: φ = Сt2, где С = 10 рад/с2. Определить момент сил, действующих на шар.
Задача 16591
Сплошной цилиндр массой 1 кг и радиусом 0,05 м вращается вокруг оси, проходящей через его центр. В точке, наиболее удаленной от оси вращения, на цилиндр действует сила, касательная к поверхности. Угол поворота цилиндра меняется по закону φ(t) = 2 + 2t + t2, рад. Вычислите величину силы, тормозящий момент силы, время равнозамедленного движения и кинетическую энергию в начале движения.
В точке, наиболее удаленной от оси вращения, на цилиндр действует сила, касательная к поверхности. Угол поворота цилиндра меняется по закону φ(t) = 2 + 2t + t2, рад. Вычислите величину силы, тормозящий момент силы, время равнозамедленного движения и кинетическую энергию в начале движения.
Задача 17490
Цилиндр массой 5 кг и радиусом 15 см вращается вокруг оси, проходящей через его центр. Уравнение вращения цилиндра имеет вид: φ(t) = 1+6t2–t3, рад. Найти закон изменения момента сил, действующих на цилиндр, их величину в момент времени 3 с. Вычислить момент инерции цилиндра, если ось вращения будет проходить по его поверхности.
Задача 17513
Диск массой 5 кг и радиусом 10 см вращается вокруг оси, проходящей через его центр. Уравнение вращения диска имеет вид φ = φ0 + 2t2 – t3, рад. Найти закон изменения момента сил, действующего на диск. Вычислите момент сил в момент времени 4 с. Вычислить момент инерции диска, если ось вращения будет проходить через половину радиуса.
Вычислить момент инерции диска, если ось вращения будет проходить через половину радиуса.
Задача 19142
Шар массой 2 кг и радиусом 10 см вращается вокруг оси, проходящей через его центр. Уравнение вращения шара имеет вид: φ(t) = φ0 + 4t2 – t3. Найти закон изменения момента сил, действующих на шар, величину их в момент времени 2 с. Вычислите момент инерции шара, если ось вращения будет проходить через половину радиуса.
Задача 20119
Шар массой 10 кг и радиусом 20 см совершает вращательное движение вокруг оси, проходящей через его центр. Уравнение движения имеет вид φ = 5 + 4t2 – t3 (рад). Вычислить момент сил и момент импульса шара при t = 2 с.
Задача 19854
Однородный шар радиуса r = 0,1 м и массы m = 2 кг может вращаться вокруг оси z, проходящей через его центр. На «экватор» шара намотана нить, за которую тянут так, что зависимость угла поворота шара от времени имеет вид φ(t) = Bt4, где B = 1 рад·с–4. Определить силу натяжения нити через две секунды после начала вращения шара, если со стороны оси на вращающийся шар действует постоянный тормозящий момент, величина которого |Mтр| = 10 Н·м.
Определить силу натяжения нити через две секунды после начала вращения шара, если со стороны оси на вращающийся шар действует постоянный тормозящий момент, величина которого |Mтр| = 10 Н·м.
Задача 19908
На рисунке дан график зависимости момента импульса шара, вращающегося вокруг оси, проходящей через его центр, от времени. 1) Построить график зависимости момента силы, действующей на шар, от времени. 2) Определить величину угловой скорости и углового ускорения шара при t = 2 с. Масса шара 1 кг, радиус шара 50 см.
Задача 20455
Сплошной диск массой 0,2 кг вращается вокруг оси, проходящей через его центр масс под действием момента сил 0,8·10–2 Н·м. Закон вращения имеет вид φ = 5–t+2t2. Определить радиус диска.
StudyPort.Ru — Вращательное движение твердых тел
Страница 1 из 3
3.1. Найти момент инерции J и момент импульса L земного шара относительно оси вращения.
Решение:
3.2. Два шара одинакового радиуса R = 5 см закреплены на концах невесомого стержня. Расстояние между шарами r = 0,5 м. Масса каждого шара m = 1 кг. Найти: а) момент инерции J1 системы относительно оси, проходящей через середину стержня перпендикулярно к нему; б) момент инерции J2 системы относительно той же оси, считая шары материальными точками, массы которых сосредоточены в их центрах; в) относительную ошибку б = (J1 — J2)/ J2, которую мы допускаем при вычислении момента инерции системы, заменяя величину J1 величиной J2.
Решение:
3.3. К ободу однородного диска радиусом R = 0,2 м прило касательная сила F = 98,1 Н. При вращении на диск действует момент сил трения Mтр=98,1 Н*м.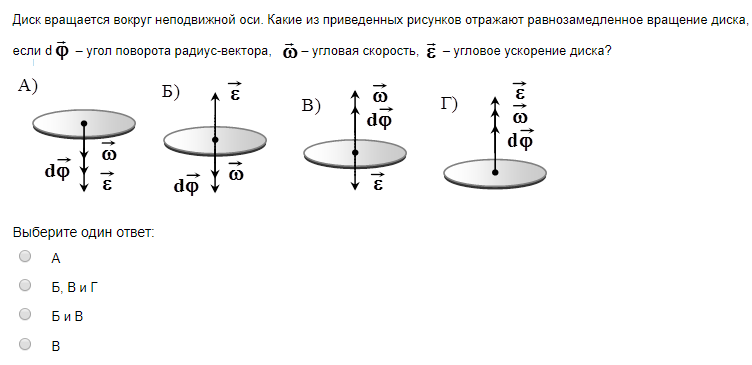 Найти массу m дисков, если известно, что диск вращается с угловым ускоре е = 100 рад/с2.
Найти массу m дисков, если известно, что диск вращается с угловым ускоре е = 100 рад/с2.
Решение:
3.4. Однородный стержень длиной l = 1 м и массой m = 0,5 кг вращается в вертикальной плоскости вокруг горизонтальной оси, проходящей через середину стержня. С каким угловым ускорением е вращается стержень, если на него действует момент сил М = 98,1 мН*м?
Решение:
3.5. Однородный диск радиусом R = 0,2 м и массой m = 0,5 кг вращается вокруг оси, проходящей через его центр перпендикулярно к его плоскости. Зависимость угловой скорости w вращения диска от времени t дается уравнением w = А + Bt, где В = 8 рад/с2. Найти касательную силу F, приложенную к ободу диска. Трением пренебречь.
Решение:
3.6. Маховик, момент инерции которого J = 63,6кгм2 враща с угловой скоростью w = 31,4 рад/с. Найти момент сил тор М, под действием которого маховик останавливается через время t = 20 с. Маховик считать однородным диском.
Найти момент сил тор М, под действием которого маховик останавливается через время t = 20 с. Маховик считать однородным диском.
Решение:
3.7. К ободу колеса радиусом 0,5м и массой m = 50 кг при касательная сила F = 98,1 Н. Найти угловое ускорение s колеса. Через какое время t после начала действия силы колесо будет иметь частоту вращения n = 100 об/с? Колесо считать однородным диском. Трением пренебречь.
Решение:
3.8. Маховик радиусом R = 0,2 м и массой m = 10 кг соединен с мотором при помощи приводного ремня. Сила натяжения ремня, идущего без скольжения, T = 14,7Н. Какую частоту вра n будет иметь маховик через время t = 10 с после начала движения? Маховик считать однородным диском. Трением пренебречь.
Решение:
3.9. Маховое колесо, момент инерции которого J = 245 кг л, вращается с частотой n = 20 об/с. Через время t = 1 мин после того, как на колесо перестал действовать момент сил М, оно остановилось. Найти момент сил трения и число оборотов N, которое сделало колесо до полной остановки после прекра действия сил. Колесо считать однородным диском.
Через время t = 1 мин после того, как на колесо перестал действовать момент сил М, оно остановилось. Найти момент сил трения и число оборотов N, которое сделало колесо до полной остановки после прекра действия сил. Колесо считать однородным диском.
Решение:
З.10. Две гири с массами m1 =2 кг и m2=1кг соединены нитью, перекинутой через блок массой m = 1 кг. Найти ускорение а, с которым движутся гири, и силы натяжения T1 и T2 нитей, к которым подвешены гири. Блок считать однородным диском. Трением пренебречь.
Решение:
3.11. На барабан массой m0=9кг намотан шнур, к концу которого привязан груз массой m = 2 кг. Найти ускорение а гру. Барабан считать однородным цилиндром. Трением прене.
Решение:
3.12. На барабан радиусом R = 0,5 м намотан шнур, к концу которого привязан груз массой m = 10 кг. Найти момент инерции J барабана, если известно, что груз опускается с ускорением а = 2,04 м/с2.
Найти момент инерции J барабана, если известно, что груз опускается с ускорением а = 2,04 м/с2.
Решение:
3.13. На барабан радиусом R = 20 см, момент инерции кото J = 0,1 кгм2, намотан шнур, к концу которого привязан груз массой m = 0,5 кг. До начала вращения барабана высота груза над полом hQ = 1 м. Через какое время t груз опустится до пола? Найти кинетическую энергию WK груза в момент удара о пол и силу натяжения нити T. Трением пренебречь.
Решение:
3.14. Две гири с разными массами соединены нитью, переки через блок, момент инерции которого J = 50 кгм2 и радиус R = 20 см. Момент сил трения вращающегося блока = 98,1 Нм. Найти разность сил натяжения нити T1 -T2по обе стороны блока, если известно, что блок вращается с угловым ускорением e = 2,36 рад/с2. Блок считать однородным диском.
Блок считать однородным диском.
Решение:
3.15. Блок массой m = 1 кг укреплен на конце стола ( см. рис. и задачу 2.31). Гири 1 и 2 одинаковой массы m1=m2=1кг соединены нитью, перекинутой через блок. Коэффициент трения гири 2 о стол к = 0,1 . Найти ускорение а, с которым движутся гири, и силы натяжения T1и T2нитей. Блок считать однород диском. Трением в блоке пренебречь.
Решение:
3.16. Диск массой m = 2 кг катится без скольжения по гори плоскости со скоростью v = 4 м/с. Найти кинети энергию Wk диска.
Решение:
3.17. Шар диаметром D = 6 см и массой m = 0,25 кг катится без скольжения по горизонтальной плоскости с частотой враще n = 4 об/с. Найти кинетическую энергию WK шара.
Решение:
3.18. Обруч и диск одинаковой массы m1 = m2 катятся без скольжения с одной и той же скоростью v. Кинетическая энер обруча WKl =4кгсм. Найти кинетическую энергию Wk2 диска.
Кинетическая энер обруча WKl =4кгсм. Найти кинетическую энергию Wk2 диска.
Решение:
3.19. Шар массой m = 1 кг катится без скольжения, ударяется о стенку и откатывается от нее. Скорость шара до удара о стенку v = 10 см/с, после удара u = 8 см/с. Найти количество теплоты Q, выделившееся при ударе шара о стенку.
Решение:
3.20. Найти относительную ошибку б, которая получится при вычислении кинетической энергии WK катящегося шара, если не учитывать вращения шара.
Решение:
Чертов — Страница 38
Раздел: Физика, ЧертовЧертов – 3.23. Вал массой m = 100 кг и радиусом R = 5 см вращался с частотой n = 8 с-1. К цилиндрической поверхности вала прижали тормозную колодку с силой F = 40 Н, под действием которой вал остановился через t = 10 с. Определить коэффициент трения f. Скачать решение: Скачать решение задачи
Определить коэффициент трения f. Скачать решение: Скачать решение задачи
Смотреть материал
Раздел: Физика, ЧертовЧертов – 3.22. На горизонтальную ось насажены маховик и легкий шкив радиусом R = 5 см. На шкив намотан шнур, к которому привязан груз массой m = 0,4 кг. Опускаясь равноускоренно, груз прошел путь s = 1,8 м за время t = 3 с. Определить момент инерции J маховика. Массу шкива считать пренебрежимо малой. Скачать […]
Смотреть материал
Раздел: Физика, ЧертовЧертов – 3.21. Тонкий однородный стержень длиной l = 50 см и массой m = 400 г вращается с угловым ускорением e = 3 рад/с2 около оси, проходящей перпендикулярно стержню через его середину. Определить вращающий момент М. Скачать решение: Скачать решение задачи
Смотреть материал
Раздел: Физика, ЧертовЧертов – 3. 20. Однородный диск радиусом R = 10 см может свободно вращаться вокруг горизонтальной оси, перпендикулярной плоскости диска и проходящей через точку О на нем (см.рис.ниже). Диск отклонили на угол a и отпустили. Определить для начального момента времени угловое e и тангенциальное аt ускорения точки В, находящейся на диске. Вычисления выполнить для следующих случаев: […]
20. Однородный диск радиусом R = 10 см может свободно вращаться вокруг горизонтальной оси, перпендикулярной плоскости диска и проходящей через точку О на нем (см.рис.ниже). Диск отклонили на угол a и отпустили. Определить для начального момента времени угловое e и тангенциальное аt ускорения точки В, находящейся на диске. Вычисления выполнить для следующих случаев: […]
Смотреть материал
Раздел: Физика, ЧертовЧертов – 3.19. Тонкий однородный стержень длиной l = 1 может свободно вращаться вокруг горизонтальной оси, проходящей через точку О на стержне (см. рис. ниже). Стержень отклонили от вертикали на угол a и отпустили. Определить для начального момента времени угловое e и тангенциальное аt ускорения точки В на стержне. Вычисления произвести для следующих случаев: 1) […]
Смотреть материал
Раздел: Физика, ЧертовЧертов – 3.18. Определить момент инерции J тонкой плоской пластины со сторонами а = 10 см и b = 20 см относительно оси, проходящей через центр масс пластины параллельно большей стороне. Масса пластины равномерно распределена по ее площади с поверхностной плотностью s = 1,2 кг/м2. Скачать решение: Скачать решение задачи
Масса пластины равномерно распределена по ее площади с поверхностной плотностью s = 1,2 кг/м2. Скачать решение: Скачать решение задачи
Смотреть материал
Раздел: Физика, ЧертовЧертов – 3.17. Найти момент инерции J плоской однородной прямоугольной пластины массой т = 800 г относительно оси, совпадающей с одной из ее сторон, если длина а другой стороны равна 40 см. Скачать решение: Скачать решение задачи
Смотреть материал
Раздел: Физика, ЧертовЧертов – 3.16. В однородном диске массой т = 1 кг и радиусом r = 30 см вырезано круглое отверстие диаметром d = 20 см, центр которого находится на расстоянии l = 15 см от оси диска (см. рис. ниже). Найти момент инерции J полученного тела относительно оси, проходящей перпендикулярно плоскости диска через его центр. […]
Смотреть материал
Раздел: Физика, ЧертовЧертов – 3.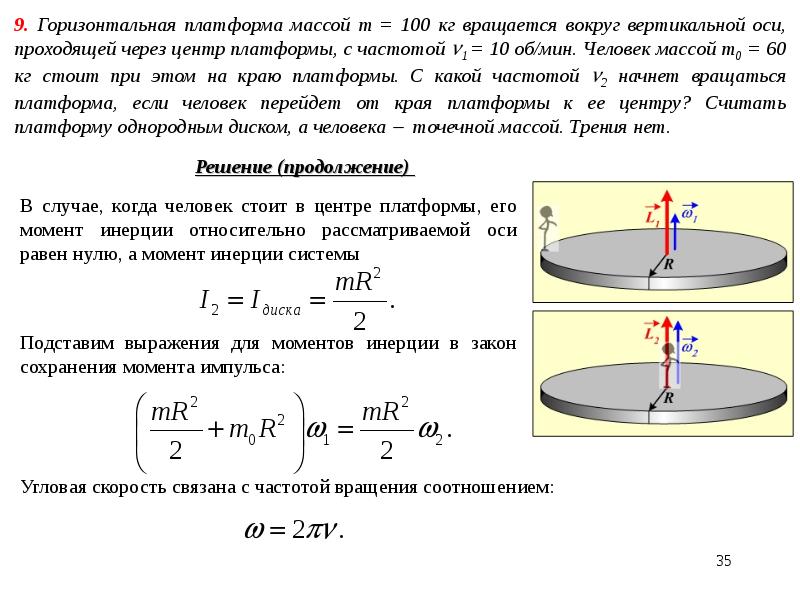 15. Диаметр диска d = 20 см, масса т = 800 г. Определить момент инерции J диска относительно оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. Скачать решение: Скачать решение задачи
15. Диаметр диска d = 20 см, масса т = 800 г. Определить момент инерции J диска относительно оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. Скачать решение: Скачать решение задачи
Смотреть материал
Раздел: Физика, ЧертовЧертов – 3.14. Определить момент инерции J кольца массой т = 50 г и радиусом R= 10 см относительно оси, касательной к кольцу. Скачать решение: Скачать решение задачи
Смотреть материал
popov — Стр 7
A B
AV
42 (Россия, 1999, 3 балла). В кривошипно-ползунном механизме, изображённом на рисунке, ОА = АВ = l, а шатун АВС представляет собой равносторонний треугольник. В заданном положении кривошип ОА имеет угловую скорость ω и угловое ускорение ε. Определить ускорение точки С шатуна относительно кривошипа и её ускорение Кориолиса.
| A | C | |
|
| ||
| ε | B | |
|
| ||
ω | ϕ |
| |
O | B | ||
|
43 (Россия, 2000, 4 балла). Определить скорость и ускорение точки В кулисного камня механизма в положении, определяемом углом ϕ, если длина кривошипа ОА = r, расстояние между осями вращения кривошипа и кулисы O1O = r и АВ = r/2. Угловая скорость кривошипа ω = const.
O1
A
B
ϕ ω
O
44 (Россия, 2000, 3 балла). Стержень ОА вращается в плоскости рисунка вокруг точки О с угловой скоростью ω и угловым ускорением ε, выталкивая диск радиуса R, движущийся в этой плоскости. Определить скорость и ускорение центра диска С в зависимости от угла наклона стержня ϕ.
Определить скорость и ускорение центра диска С в зависимости от угла наклона стержня ϕ.
A
ε
C
O ϕ
45 (Урал, Оренбург, 2000, 4 балла). Тяжёлый диск радиуса R скатывается на двух нерастяжимых нитях, намотанных на него и расположенных в его плоскости. Свободные концы нитей закреплены. Нити при движении диска постоянно натянуты. В некоторый момент угловая скорость диска равна ω, а угол между нитями α. Какова в этот момент скорость центра диска?
α
Rω
O
46 (СССР, 1986, 4 балла). Известны координаты двух точек А (1, –2, –3) и В (–1, 4, 5), скорости которых равны vA (5, 3, 2) и vB (–7, 3, –1). Могут ли точки А и В принадлежать одному твёрдому телу?
47. (СССР, 1989, 6 баллов). Квадратная пластинка АВСD со стороной 2l движется в своей плоскости. Ускорения её
вершин А, В, С равны, соответственно, aA = a, aB = a, aC = a 5 , а угловая скорость равна ω. Определить ускорение вершины D и угловое ускорение пластинки.
48 (Тамбов, ТГТУ, 1995, 7 баллов). Диск радиуса r катится по горизонтальной плоскости без скольжения. Скорость и ускорение центра О диска равны v0 и a0, соответственно. Найти ускорение такой точки М обода, для которой касательное и нормальное ускорения равны по модулю. Рассмотреть частный случай, для которого w2 = 2e.
Диск радиуса r катится по горизонтальной плоскости без скольжения. Скорость и ускорение центра О диска равны v0 и a0, соответственно. Найти ускорение такой точки М обода, для которой касательное и нормальное ускорения равны по модулю. Рассмотреть частный случай, для которого w2 = 2e.
49 (Тамбов, ТГТУ, 1995, 7 баллов). Квадрат ABCD совершает плоское движение, касаясь вершинами А и В двух прямых ON1 и ON2, при этом va = v = const, ÐN1ON2 = 120°. Для положения квадрата, когда ОА = а = ОВ, найти на стороне AD такую точку М, для которой ускорение относительно точки В будет направлено параллельно АВ. Вычислить величину и указать направление абсолютного ускорения точки М.
50 (Тульск. политехн. ин-т, 1987). Два диска 1 и 2, находясь во внешнем зацеплении, вращаются вокруг неподвижных осей О1 и О2. Стержни 3 и 4 шарнирно соединены между собой и в некоторых точках с дисками. Для произвольного положения механизма построением найти МЦС стержней 3 и 4.
5.4.КИНЕМАТИКА СЛОЖНОГО ДВИЖЕНИЯ
1(РСФСР, 1982, 3 балла). Стержень длины 2а вращается вокруг оси О по закону j = е2t рад. Из точки А к оси движется точка М. Каким образом должно изменяться во времени её расстояние АМ для того, чтобы абсолютное ускорение точки М всегда было направлено по стержню?
Стержень длины 2а вращается вокруг оси О по закону j = е2t рад. Из точки А к оси движется точка М. Каким образом должно изменяться во времени её расстояние АМ для того, чтобы абсолютное ускорение точки М всегда было направлено по стержню?
ϕ
2 (Л., 1988). Точка М движется по радиусу вращающего диска согласно закону ОМ = x0 + v0t. Определить закон вращения диска, если известно, что абсолютное ускорение точки M в любой момент времени направлено по радиусу; абсолютную скорость точки М в момент, когда x = 2×0.
ω
3 (Зап.-Сиб. зона, Новосибирск. ин-т. железнодорожн. трансп., 1990). По однородной балке (струне) АВ длины l,
изгибные колебания которой описываются уравнением y(x, t) = a cos(ωt) sin(πx/l), скользит кольцо М по закону АМ = s(t) = vt. Определить составляющие скорости и ускорения кольца при условии a << l.
4 (Брянск, 1986). По поверхности Земли в плоскости меридиана движется точка М с некоторой постоянной, относительной скоростью u. Угловая скорость вращения Земли ω, радиус R. При каком значении u ускорение точки будет постоянным по модулю. Найти также это ускорение.
Угловая скорость вращения Земли ω, радиус R. При каком значении u ускорение точки будет постоянным по модулю. Найти также это ускорение.
5 (Тамбовск. ин-т хим. машиностр., 1989). Колесо радиуса R катится без скольжения по горизонтальной плоскости, при этом центр колеса имеет постоянную скорость v. С колесом шарнирно связан стержень АВ длины l > 2R, второй конец которого скользит по той же плоскости. По стержню в направлении от А к В движется точка M с постоянной относительной скоростью vr = v. Определить абсолютную скорость и абсолютное ускорение точки M в положении, показанном на рисунке, когда шарнир В совпадает с наивысшей точкой колеса, а стержень наклонён к горизонтальной плоскости под углом 60°; МВ
= l/2.
6 (Тамбовск. ин-т хим. машиностр., 1989). Плоский механизм состоит из трёх зубчатых колес 1, 2, 3 одинакового радиуса R = 1 м. Колесо 1 неподвижно, колеса 2 и 3 приводятся в движение с помощью кривошипа ОА, вращающегося с угловой скоростью ω = 1 рад/с..doc_html_d43c9b5567afee6d.jpg) По ободу колеса 3 движется точка М с постоянной относительной скоростью vr = 2 м/с. Определить абсолютную скорость и абсолютное ускорение этой точки в момент времени, когда она совпадает с верхней точкой В колеса 3 (ω = const).
По ободу колеса 3 движется точка М с постоянной относительной скоростью vr = 2 м/с. Определить абсолютную скорость и абсолютное ускорение этой точки в момент времени, когда она совпадает с верхней точкой В колеса 3 (ω = const).
7 (Тольяттинск. политехн. ин-т, 1987). Диск 1 катится без скольжения по неподвижному диску 2 от начального положения 1 с постоянной угловой скоростью ω1 = 2ω. Ползун А движется вдоль диаметра ВD по закону s(t) = CA = r sin(ωt). Определить и показать абсолютные ускорения ползуна для положений 2 и 3 диска.
8 (Россия, 1993, 6 баллов). Диск радиусом R катится без скольжения в вертикальной плоскости. Через центр диска проходит тонкий канал, внутри которого из точки О в точку А в некоторые момент времени t1 начинает двигаться равноускоренно точка М. К моменту времени t2, когда канал впервые (после начала движения точки по каналу) занимает вертикальное положение, точка М проходит расстояние, равное 1,5R. Абсолютное ускорение точки М в этот момент времени направлено параллельно неподвижной плоскости, а скорость и ускорение центра С равны, соответственно: vC = U, aC = U2/R. Определить закон движения точки М по каналу и её абсолютное ускорение при t = t2, если начальная относительная скорость равна нулю, а значения t1 и t2 неизвестны.
Определить закон движения точки М по каналу и её абсолютное ускорение при t = t2, если начальная относительная скорость равна нулю, а значения t1 и t2 неизвестны.
9 (Россия, 1994, 4 балла). Точка М движется в плоскости xOy согласно уравнениям: x = t2, у = t2. Плоскость хОу вращается с угловой скоростью ω = е– t вокруг неподвижной оси, ей перпендикулярной и проходящей через начало координат. Определить абсолютное ускорение точки М в тот момент времени, когда оно впервые после начала движения направлено вдоль прямой, соединяющей точку М с началом координат.
10 (Тамбовск. ин-т хим. машиностр., 1992, 8 баллов).Стержень АВ = l движется в плоскости рисунка, касаясь своими концами двух неподвижных плоскостей, образующих между собой угол 120°. Скорость конца А постоянна и равна v. По стержню АВ движется точка М с некоторой относительной скоростью U. Найти значение U, если известно, что абсолютное ускорение точки М в положении, совпадающем с серединой С стержня, направлено вдоль АВ.
11 (Тамбовск. ин-т хим. машиностр., 1993, 8 баллов). Диск радиуса R катится по горизонтальной прямой без скольжения. Скорость центра O диска постоянна и равна v. По ободу диска в направлении, противоположном вращению диска, движется точка M с постоянной относительной скоростью U, равной по модулю v. Определить абсолютные скорость и ускорение точки М для положения её на диске, определяемом углом α, и вид траектории дальнейшего движения точки.
12 (Тамбов, ТГТУ, 1996, 8 баллов). Кривошип ОА длиной R вращается вокруг неподвижной точки О с угловой скоростью ω. Обруч с центром в точке С и радиуса R, шарнирно соединённый в точке А с кривошипом, скользит по неподвижной прямой ON. По обручу с постоянной скоростью U движется точка М в направлении против часовой стрелки.
Для положения данного механизма, движущегося в плоскости хОу, когда ÐAON = 30° и CM || ON, найти абсолютные скорость и ускорение точки М.
13 (СССР, 1988, 5 баллов). Прямая АB вращается в плоскости вокруг точки О с постоянной угловой скоростью w. Вдоль прямой движется точка М так, что её абсолютная скорость и ускорение взаимно перпендикулярны. Определить абсолютные скорость и ускорение точки М, если в начальный момент времени s0 = b, s&0 = 0. Найти их численные значения
Вдоль прямой движется точка М так, что её абсолютная скорость и ускорение взаимно перпендикулярны. Определить абсолютные скорость и ускорение точки М, если в начальный момент времени s0 = b, s&0 = 0. Найти их численные значения
при b = 2 см и w = 3 рад/с.
w
14 (СССР, 1989, 7 баллов). Два обруча радиуса r катятся без скольжения по направляющей в разные стороны. Скорости центров А и В обручей постоянны и равны, соответственно, v1 и v2. Определить ускорение кольца М, надетого на два обруча, в зависимости от угла j.
ϕ
15 (РСФСР, 1985, 7 баллов). Определить закон относительного движения ползуна х = = х(t) и закон вращения стержня j = j (t) при условии, что векторы скорости v и ускорения a ползуна во всё время движения составляют со стержнем углы 45° и 90°, соответственно. Начальные условия движения: t0 = 0, j0 = 0, j& 0 = w0, x = x0.
| 16 (Аз. ССР, 1984). Диск с прорезью для ползуна В равномерно вращается с угловой | |
| скоростью w1 = 1 с–1 по ходу часовой стрелки. | |
| направлении с угловой скоростью w0 =3 с–1 . Считая, что ОА = r = 0,1 м, АВ = 2r = 0,2 м, | |
ϕ | определить абсолютные скорость и ускорение центра ползуна В в тот момент, когда угол между | |
шатуном AB и кривошипом ОА равен 90°. |
| |
|
| |
| ω | ω |
17 (БССР, 1982). Движение центра тяжести снаряда задано уравнениями x = v0tcosa, y = v0tsina – gt2/2 (v0, a, g – const). Снаряд вращается вокруг своей оси, совпадающей с касательной к траектории, с постоянной угловой скоростью wr. Определить в наивысшем положении снаряда величины абсолютных ускорений тех точек его поверхности, кориолисово ускорение которых максимально, если диаметр снаряда равен 2R. Вращение Земли не учитывать.
18 (БССР, 1984). Стержни 1 и 2, расположенные в одной плоскости, вращаются вокруг центров O1 и О2 с равными по величине угловыми скоростями w. Стержни соединены между собой системой шарнирно скреплённых ползунов, один из которых скользит вдоль стержня 1, а второй – вдоль стержня 2. Определить скорость точки М для положения, указанного на рисунке, если O1O2 = l.
ω
ω
19 (БССР, 1984). Определить скорость и ускорение точки С плоского механизма в положении, указанном на рисунке, если известны скорости vA и vB, а ускорения точек А и В равны нулю.
20(БССР, 1986). Вдоль шатуна АВ кривошипно-ползунного механизма совершает колебания муфта M по закону СМ = s
=r sin(ωt). Кривошип ОА вращается вокруг горизонтальной оси О по закону ϕ = ωt. Определить модули абсолютной скорости и абсолютного ускорения муфты М при t = 0, если ОА = r, AC = CB = 2r.
ϕ
21 (Кирг. ССР, 1987). Кривошип ОА радиуса 2r вращается вокруг оси О с постоянной угловой скоростью ωe.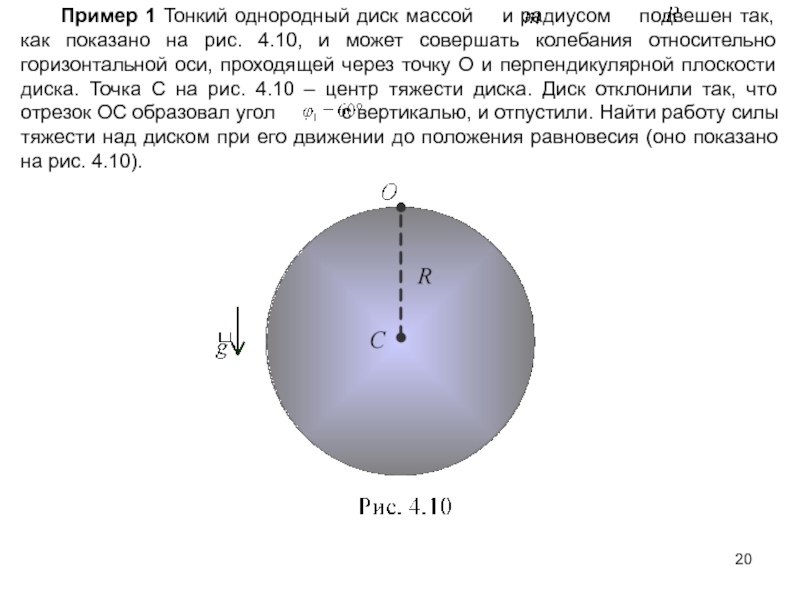 На пальце А свободно надето колесо радиуса r, вращающееся с угловой скоростью ωr против часовой стрелки. Определить величины и направления ускорений точек M и N колеса, находящихся на концах диаметра, совпадающего с осью кривошипа.
На пальце А свободно надето колесо радиуса r, вращающееся с угловой скоростью ωr против часовой стрелки. Определить величины и направления ускорений точек M и N колеса, находящихся на концах диаметра, совпадающего с осью кривошипа.
ω
ω
22 (Молд. ССР, 1987). По шатуну АВ нецентрального кривошипно-шатунного механизма движется точка М с постоянной по величине относительной скоростью u. Кривошип ОА вращается с угловой скоростью ω. Определить, при какой относительной скорости u абсолютная скорость точки М при её прохождении через середину шатуна АВ будет горизонтальна в положении механизма, указанном на рисунке; величину абсолютного ускорения точки M в тот же момент времени при условии, что ω = const, ОА = r, АВ = l, l = 2r.
ω
23 (Л., 1982). Окружность радиусом r вращается с постоянной угловой скоростью ω рад/с вокруг оси АВ. По окружности равномерно с относительной скоростью u м/с движется точка М. Определить, абсолютное ускорение точки M в том положении, где её относительная и переносная скорости равны по величине, т. е. ωr = u.
е. ωr = u.
ω
24 (Л., 1984). Определить постоянную относительную скорость ползуна D кривошипно-ползунного механизма в положении, указанном на рисунке, если известно, что абсолютное ускорение ползуна D в этот момент времени направлено вдоль шатуна АВ. Угловая скорость ω0 кривошипа постоянна.
ω
25 (Л., 1985). Диск вращается с постоянной угловой скоростью ω вокруг центральной оси, перпендикулярной плоскости диска. Из центра O движется в радиальном направлении точка М. Её начальная относительная скорость равна v0. Каково должно быть уравнение относительного движения точки ОМ = x = x(t) для того, чтобы её абсолютное ускорение всё время было равно ускорению Кориолиса.
ω
26 (Брянск. ин-т транспортн. машиностр., 1988). Прямолинейный стержень АВ длиной l = 1 м скользит своими концами вдоль осей координат, при этом vA = 2 м/с = const. Вдоль стержня в направлении от А к В движется точка М с постоянной относительной скоростью vr = 2 м/с. Определить абсолютное ускорение точки М в тот момент, когда она окажется равноудалённой от МЦС и МЦУ стержня АВ.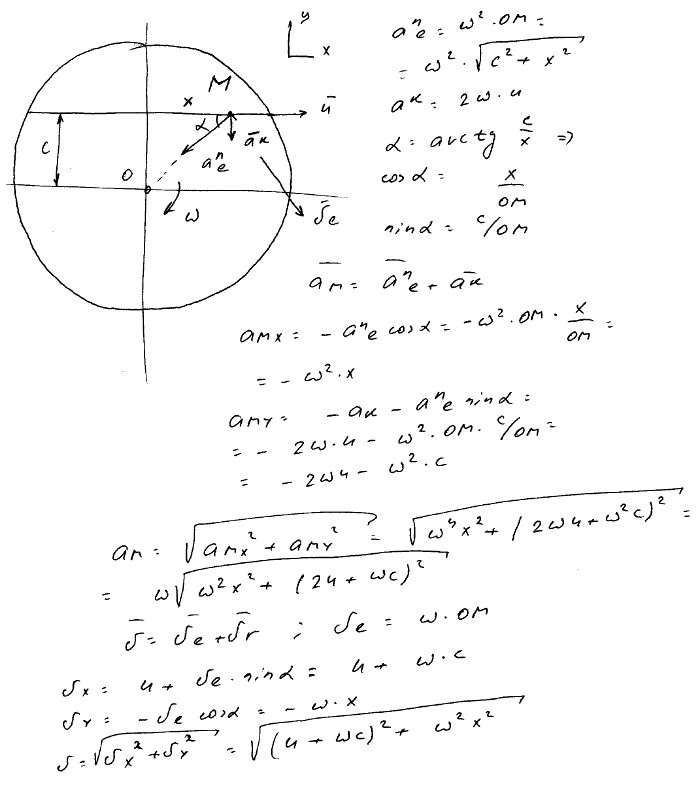 СО. Определить угловую скорость кулисы СD, если a Bкор = 1 см/с2, 0,8 < VBотн < 3 см/с.
СО. Определить угловую скорость кулисы СD, если a Bкор = 1 см/с2, 0,8 < VBотн < 3 см/с.
29 (Тамбовск. ин-т хим. машиностр., 1988). Ползуны А и В движутся по горизонтальной направляющей ЕN в разные стороны с постоянными скоростями vA = v и vB = 2v. Определить для данного положения механизма угловую скорость и угловое ускорение стержня СD, который может скользить в муфте M и поворачиваться вместе с ней вокруг неподвижной точки O; АС = СВ = l.
30 (Россия, 1995, 5 баллов). Кольцеобразный жёлоб радиусом r вращается с постоянной угловой скоростью w вокруг оси, перпендикулярной его плоскости и проходящей через точку О1, лежащую на оси жёлоба. Кривошип ОА, имеющий продольную прорезь, вращается в противоположном направлении с угловой скоростью 2w относительно желоба вокруг точки О, находящейся на одном диаметре с точкой О1 и жёстко связанной с жёлобом. Стержень (штифт) М, перпендикулярный плоскости кольца, скользит одновременно в жёлобе и прорези кривошипа. Пренебрегая толщиной кольца, определить величину ускорения штифта М как функцию угла поворота диаметра О1О (для углов, меньших p/4), если в начальный момент времени прямые О1О и ОА совпадали.
y
A
O1
M
ω
x O
31 (Россия, 1995, 5 баллов). Кривошипно-шатунный механизм состоит из кривошипа ОА, равной ему длины шатуна АВ и вдвое большего их шатуна ВС. Скорости точек А и С равны, постоянны и направлены в разные стороны. В положении,
указанном на чертеже, когда кривошип ОА расположен вертикально, а шатун АВ ему перпендикулярен, определить отношение угловых ускорений шатунов АВ и ВС.
A B
C
O VC
32 (Россия, 1999, 6 баллов). Полукруглый толкатель А радиуса R = 2 м движется ускоренно по горизонтальной плоскости
со скоростью v = 2 м/с и ускорением а = 2 м/с2. Навстречу ему, так же ускоренно с теми же скоростью и ускорением, движется ползун В. Ползун соединён шарнирно со стержнем ВС длиной 2R, который опирается на толкатель. Определить скорость и ускорение точки С в положении механизма, при котором стержень образует с горизонталью угол 45° .
C
A
B
33 (Урал, Оренбург, 2000, 5 баллов). Линейка АВ длиной l скользит своими концами по двум взаимно перпендикулярным направляющим Ох и Оу, вращающимся вокруг точки О с постоянной угловой скоростью ω. Закон изменения угла в относительном движении ϕ = ϕ0 + ωt. Для точки М, делящей АВ в отношении 1 : 3, определить траекторию и скорость в абсолютном движении. Рассмотреть два случая: 1) когда вращение происходит против хода часовой стрелки и 2) по ходу часовой стрелки.
Линейка АВ длиной l скользит своими концами по двум взаимно перпендикулярным направляющим Ох и Оу, вращающимся вокруг точки О с постоянной угловой скоростью ω. Закон изменения угла в относительном движении ϕ = ϕ0 + ωt. Для точки М, делящей АВ в отношении 1 : 3, определить траекторию и скорость в абсолютном движении. Рассмотреть два случая: 1) когда вращение происходит против хода часовой стрелки и 2) по ходу часовой стрелки.
| Y |
|
| A |
|
| ϕ |
|
O | B | x |
| ||
|
|
34 (Урал-Поволжье, Оренбург, 2001, 5 баллов). В шарнирном параллелограмме стержень ОА вращается в плоскости параллелограмма с постоянной угловой скоростью ω1, а стержень ОС – с постоянной угловой скоростью ω2 вокруг неподвижной точки О. По стержню АВ движется равномерно точка М со скоростью v. OA = а, ОС = b. Определить величину и направление абсолютной скорости и абсолютного ускорения точки М в зависимости от угла α и от расстояния АМ = х.
По стержню АВ движется равномерно точка М со скоростью v. OA = а, ОС = b. Определить величину и направление абсолютной скорости и абсолютного ускорения точки М в зависимости от угла α и от расстояния АМ = х.
C
35(Тамбовск. ин-т хим. машиностр., 1992, 8 баллов). Для изображённого на рисунке плоского механизма дано: vС = v
=const, ωОА = ω = = const; OA = OB = r, BC = 2r. Определить ωАВ, ωВС, εАВ, εВС.
36 (Тамбовск. ин-т хим. машиностр., 1993, 7 баллов). Изогнутый под прямым углом стержень MON вращается с угловой скоростью ω вокруг оси O. Стержень АВ длиной l на концах имеет шарнирно закреплённые ползуны, скользящие по сторонам прямого угла, при этом относительная скорость ползуна А равна v. Найти положение мгновенного центра скоростей С стержня АB и вычислить расстояние ОС.
37(Тамбовск. ин-т хим. машиностр., 1993, 8 баллов). Для данного положения механизма определить скорость точки
Ви угловые скорости звеньев АВ и ВС, если ω1 = ω2 = ω, OA = l, AB = a.
О
38 (Брянск. ин-т транспортн. машиностр., 1987). Диск радиуса R = 1 м катится без скольжения по прямолинейному рельсу, при этом в данный момент времени скорость его центра O равна v0 = 4 м/с и ускорение a0 = 2 м/с. В точке А шарнирно с диском скреплён прямолинейный стержень АВ, конец В которого перемещается вдоль того же рельса. По стержню АВ в направлении от В к А движется точка М. Найти расстояние AM, при котором в показанном на рисунке положении системы абсолютное ускорение точки М будет направлено вдоль стержня АВ.
39 (МВТУ, 1986). В кривошипно-шатунном механизме шатун выполнен в виде диска радиуса R = ОА = 0,2 м с центром на ползуне В. К ободу диска приварена трубка, в которой может перемещаться шарик (точка) М. Определить абсолютные скорость и ускорение шарика при t1 = 1 с после начала движения. Кривошип вращается по закону ϕ = (t2 + 2,14)/2 радиан, если вести отсчёт от вертикали, как это показано на рисунке, а шарик движется так, что расстояние от центра А изменяется согласно уравнению АМ = (π + t2/2 + t – 1,5)/5 м.
40 (Томск. политехн. ин-т, 1985). Пластина 1 движется по наклонной плоскости по закону s(t) = 0,1t2 + 0,4t (м). По пластине катится без скольжения каток 2 радиуса R = 0,2 (м), обмотанный нерастяжимой нитью. Конец А нити закреплён на плоскости. В момент времени t1 = 1 (с) механизм занимает положение, указанное на рисунке. Определить угловую скорость и угловое ускорение катка 2 в момент времени t1.
РЕШЕНИЕ ЗАДАЧ ДИНАМИКИ И СТАТИКИ
(Окончание. Начало см. «Наука и жизнь» № 4, 2001 г.)Продолжаем публиковать разбор конкурсных задач по физике, которые в последние годы предлагались поступающим на физический факультет МГУ.
Задача 3 (1998 г.). Космический корабль движется по круговой орбите вокруг Земли так, что все время находится на прямой, соединяющей Землю и Луну, на таком расстоянии, что действие их гравитационных сил на корабль уравновешено. Найти вес космонавта в корабле, если масса космонавта равна m, отношение масс Земли и Луны равно k, радиус орбиты Луны в n раз больше радиуса Земли, а ускорение свободного падения у поверхности Земли равно g.
Решение. Будем решать задачу, используя геоцентрическую систему отсчета, считая ее инерциальной, то есть не станем учитывать орбитального движения Земли. Одновременно пренебрежем влиянием всех остальных небесных тел на движение Луны и космического корабля. По условию задачи орбиту Луны следует считать круговой. Поэтому на основании второго закона Кеплера можно утверждать, что Луна по своей орбите движется равномерно. Следовательно, согласно законам кинематики, ее ускорение направлено к центру Земли и равно аn = ω Rл, где ω — угловая скорость, а Rл — радиус орбиты Луны. При сделанных предположениях можно утверждать, что ускорение Луны обусловлено действием на нее только гравитационных сил со стороны Земли (массой космического корабля можно пренебречь). Тогда, согласно закону всемирного тяготения и второму закону Ньютона, пренебрегая размерами Луны, получим
,
где G — гравитационная постоянная, а mл и mз — массы Луны и Земли соответственно.
Учитывая, что ускорение свободного падения на полюсе вблизи поверхности Земли
,
из написанных соотношений следует, что угловая скорость движения Луны, а следовательно, и космического корабля (так как он все время остается на прямой, соединяющей Землю и Луну) равна
.
Здесь учтено, что по условию задачи
.
По условию задачи космический корабль находится на таком расстоянии r от Земли, что гравитационные силы, действующие на него со стороны Земли и Луны, уравновешивают друг друга. Это, согласно закону всемирного тяготения, возможно только в том случае, если с учетом ранее сделанных предположений выполняется соотношение
.
Поскольку по условию задачи
,
то радиус орбиты корабля
.
Следовательно, центростремительное ускорение корабля определяется соотношением
.
Поскольку действия Земли и Луны на корабль скомпенсированы, а действием всех других небесных тел мы пренебрегаем и считаем геоцентрическую систему отсчета инерциальной, вычисленное ускорение может быть обеспечено только за счет работы двигателей самого корабля. Пренебрегая размерами корабля по сравнению с радиусом его орбиты, следует считать, что такое же ускорение относительно инерциальной системы отсчета имеет и космонавт. Поэтому на основании второго закона Ньютона получаем, что на космонавта корабль должен действовать с силой F=maкn . Следовательно, согласно третьему закону Ньютона, вес космонавта в системе отсчета, связанной с кораблем, равен
Пренебрегая размерами корабля по сравнению с радиусом его орбиты, следует считать, что такое же ускорение относительно инерциальной системы отсчета имеет и космонавт. Поэтому на основании второго закона Ньютона получаем, что на космонавта корабль должен действовать с силой F=maкn . Следовательно, согласно третьему закону Ньютона, вес космонавта в системе отсчета, связанной с кораблем, равен
.
Задача 4 (2000 г.). На горизонтальном диске на расстоянии R от его оси лежит маленькая шайба. Диск медленно раскручивают так, что его угловая скорость равномерно возрастает со временем. Через время τ после начала раскручивания шайба стала скользить по диску. Найти коэффициент трения шайбы о диск, если за время τ диск сделал n оборотов.
Решение. Поскольку диск первоначально покоился и его угловую скорость увеличивают с постоянным угловым ускорением ε, по аналогии с законами изменения проекции скорости и координаты точки при прямолинейном равнопеременном движении можно утверждать, что к моменту времени τ угловая скорость диска должна стать равной ω(τ)=ετ и диск должен повернуться на угол φ(τ) = ετ 2/2. За один оборот диск поворачивается на угол 2, по условию задачи он за время τ совершил n оборотов, поэтому из написанных выше выражений следует, что диск раскручивали с угловым ускорением ε=4ν/τ.
За один оборот диск поворачивается на угол 2, по условию задачи он за время τ совершил n оборотов, поэтому из написанных выше выражений следует, что диск раскручивали с угловым ускорением ε=4ν/τ.
По определению, длина дуги окружности радиуса R, заключенная между радиусами, образующими угол φ, равна Rφ. Следовательно, тангенциальная составляющая ускорения точки диска, находящейся на расстоянии R от оси вращения, равна αφ=εR. Вспоминая, что нормальная составляющая ускорения точки, движущейся с угловой скоростью со по дуге с радиусом кривизны R, равна
,
можно утверждать, что ускорение шайбы к моменту времени τ относительно лабораторной системы отсчета, в которой ось диска неподвижна, должно стать равным
.
Считая, как обычно, указанную систему отсчета инерциальной и пренебрегая действием воздуха на шайбу, можно утверждать, что ускорение шайбы обусловлено действием на нее только тангенциальной составляющей силы реакции диска (плоскость диска по условию задачи горизонтальна). Поэтому, согласно второму закону Ньютона, максимальное значение тангенциальной составляющей силы реакции диска — силы сухого трения — должно быть равно
Поэтому, согласно второму закону Ньютона, максимальное значение тангенциальной составляющей силы реакции диска — силы сухого трения — должно быть равно
.
Учитывая, что при выполнении сделанных ранее предположений шайба прижимается к диску только за счет действия на нее силы тяжести, нормальная составляющая силы реакции диска должна быть равна N=mg, где g — ускорение свободного падения. Поэтому, вспоминая закон Кулона—Амона для сил сухого трения, можно утверждать, что μ= Fτmax /N. Подставив в это выражение ранее полученные соотношения, определим искомый коэффициент трения шайбы о диск
.
Задача 5 (1997 г.). Из тонкого резинового шнура массой m жесткостью k изготовили кольцо радиусом r. Каким стал бы радиус кольца, если бы оно вращалось равномерно с угловой скоростью ω вокруг своей оси?
Решение. Из кинематики известно, что ускорение движущейся по криволинейной траектории точки в общем случае можно представить в виде суммы двух компонент: нормальной аn, направленной по радиусу кривизны траектории, и тангенциальной аτ, направленной по касательной к траектории в сторону возрастания траекторной координаты и характеризующей быстроту изменения проекции скорости на это направление. Требуется определить радиус кольца при заданной угловой скорости вращения, то есть когда все точки кольца движутся равномерно, аτ равно нулю. В условии задачи не указано, какие тела действуют на кольцо и как расположена его ось. Выбрав из всех возможных случаев простейший, будем считать, что ось кольца неподвижна относительно инерциальной системы отсчета, и так как вращение кольца происходит с постоянной скоростью, действие окружающих тел на любую из точек кольца скомпенсировано. Кольцо сделано из тонкого шнура, все точки которого находятся на одинаковом расстоянии от его оси и их ускорение равно αn=ω2R, где R — искомый радиус кольца.
Требуется определить радиус кольца при заданной угловой скорости вращения, то есть когда все точки кольца движутся равномерно, аτ равно нулю. В условии задачи не указано, какие тела действуют на кольцо и как расположена его ось. Выбрав из всех возможных случаев простейший, будем считать, что ось кольца неподвижна относительно инерциальной системы отсчета, и так как вращение кольца происходит с постоянной скоростью, действие окружающих тел на любую из точек кольца скомпенсировано. Кольцо сделано из тонкого шнура, все точки которого находятся на одинаковом расстоянии от его оси и их ускорение равно αn=ω2R, где R — искомый радиус кольца.
Это ускорение при сделанных предположениях могут обеспечить лишь силы натяжения, возникающие за счет упругой деформации шнура. На рис. 5 показаны участок вращающегося кольца, ограниченный радиусами R, образующими малый угол ∆α, и силы, действующие на него со стороны соседних участков. Поскольку эти силы направлены по касательным к оси кольца в соответствующих точках и тангенциальная составляющая ускорения точек кольца равна нулю, модули этих сил — сил натяжения — должны быть равны.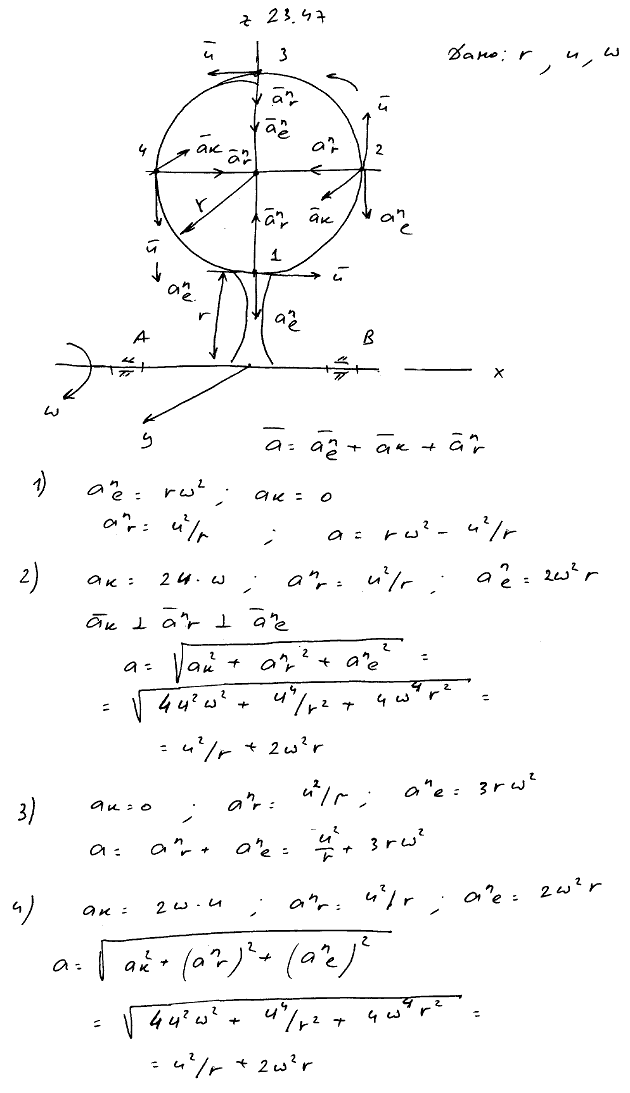 Считая, что при заданной угловой скорости применим закон Гука, величина силы натяжения
Считая, что при заданной угловой скорости применим закон Гука, величина силы натяжения
.
Силы натяжения, действующие на концы рассматриваемого участка, направлены перпендикулярно соответствующим радиусам, их результирующая равна и направлена к оси вращения. Поэтому на основании второго закона Ньютона можно утверждать, что
,
так как рассматриваемый участок кольца можно в силу малости угла ∆α принять за материальную точку массой
.
Из написанных уравнений следует, что при сделанных предположениях радиус кольца при заданной угловой скорости вращения должен быть равен
.
Из этого выражения видно, что при увеличении угловой скорости вращения до
радиус кольца должен неограниченно возрастать, то есть кольцо разорвется. В действительности разрушение кольца произойдет при несколько меньшей угловой скорости ωп, когда силы натяжения кольца достигнут величины Fmax, при которой нарушается закон Гука. Таким образом, если угловая скорость вращения кольца
Таким образом, если угловая скорость вращения кольца
,
то искомый радиус кольца равен
.
При попытке заставить кольцо вращаться с угловой скоростью ω>ωп кольцо должно разорваться.
Задача 6 (2000 г.). В узкую прямоугольную кювету налили воду и положили два гладких одинаковых цилиндра так, что их оси оказались горизонтальны и параллельны длинным стенкам кюветы. При этом цилиндры касались стенок кюветы только своими образующими, верхний цилиндр погрузился в воду наполовину, а нижний — касался ее поверхности своими верхними точками. Найти силы, действующие со стороны цилиндров на стенки кюветы, если объем каждого из них равен V=20 см3.
Решение. Будем решать задачу, полагая, что торцы цилиндров находятся на одинаковом расстоянии от параллельных им стенок кюветы, кювета с ее содержимым покоится относительно ЛСО и эту систему можно считать инерциальной. Верхний цилиндр погружен в воду наполовину, поэтому можно утверждать, что равнодействующая F1 сил гидростатического давления на верхний цилиндр должна быть равна -ρVg/2, где g~9,8 м/с2 — ускорение свободного падения, а ρ~1 г/см3 — плотность воды.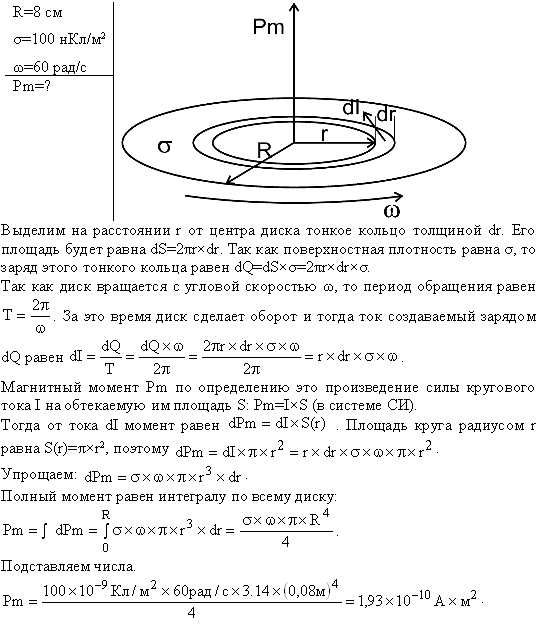 Действующая же со стороны воды на полностью погруженный нижний цилиндр сила будет в два раза больше и равна F2=-ρVg. Из соображений симметрии ясно, что линии действия сил F1 и F2 должны пересекать середины осей цилиндров под прямым углом. Поскольку по условию задачи цилиндры гладкие, силы их взаимодействия должны лежать в плоскости, проходящей через оси цилиндров, и быть перпендикулярными этим осям. Перпендикулярными осям цилиндров, но направленными горизонтально будут и силы реакции со стороны стенок кюветы, так как эти стенки вертикальны. Вспомнив, что при равновесии сумма моментов действующих на твердое тело сил должна быть равна нулю, можно утверждать, что равнодействующие сил тяжести, действующих на цилиндры, должны лежать в вертикальных плоскостях, проходящих через их оси. Более того, опираясь на сказанное, можно доказать, что при заданном расположении цилиндров и выполнении сделанных предположений равнодействующие всех рассмотренных сил должны лежать в вертикальной плоскости, проходящей через середины этих цилиндров.
Действующая же со стороны воды на полностью погруженный нижний цилиндр сила будет в два раза больше и равна F2=-ρVg. Из соображений симметрии ясно, что линии действия сил F1 и F2 должны пересекать середины осей цилиндров под прямым углом. Поскольку по условию задачи цилиндры гладкие, силы их взаимодействия должны лежать в плоскости, проходящей через оси цилиндров, и быть перпендикулярными этим осям. Перпендикулярными осям цилиндров, но направленными горизонтально будут и силы реакции со стороны стенок кюветы, так как эти стенки вертикальны. Вспомнив, что при равновесии сумма моментов действующих на твердое тело сил должна быть равна нулю, можно утверждать, что равнодействующие сил тяжести, действующих на цилиндры, должны лежать в вертикальных плоскостях, проходящих через их оси. Более того, опираясь на сказанное, можно доказать, что при заданном расположении цилиндров и выполнении сделанных предположений равнодействующие всех рассмотренных сил должны лежать в вертикальной плоскости, проходящей через середины этих цилиндров.
На рис. 6 показаны сечение кюветы вертикальной плоскостью, равнодействующие сил реакции стенок Fcl и Fc2, сил гидростатического давления F1 и F2, сил взаимодействия цилиндров N1 и N2 и сил тяжести. Буквами D и С обозначены точки приложения сил F1 и F2, а буквой m — масса цилиндра. Поскольку цилиндры находятся в равновесии, сумма всех сил, действующих на каждый из них, должна быть равна нулю и, следовательно, должны выполняться соотношения:
,
причем, согласно третьему закону Ньютона, N1=N2.
Решая полученную систему уравнений с учетом того, что F2 = 2F1 = ρgV, силы взаимодействия двух тел равны по величине и треугольник ABC является прямоугольным, а потому sin α = ВС/AC = 0,5, определим искомые силы действия цилиндров на стенки кюветы:
.
Задача 7 (2000 г.). Горизонтальная штанга длиной r, на конце которой закреплен
груз массой m, вращается на подшипнике с угловой скоростью ω вокруг вертикальной
стойки штатива высотой h (рис. 7). При какой угловой скорости основание штатива
— тонкий диск массой М и радиусом R (R >r — перестанет касаться всей плоскостью
горизонтальной поверхности стола? Массой штанги и стойки пренебречь. Считать,
что диск не скользит по столу, а размеры груза существенно меньше r.
7). При какой угловой скорости основание штатива
— тонкий диск массой М и радиусом R (R >r — перестанет касаться всей плоскостью
горизонтальной поверхности стола? Массой штанги и стойки пренебречь. Считать,
что диск не скользит по столу, а размеры груза существенно меньше r.
Решение. Все тела, указанные в условии, будем считать твердыми. Поскольку вращение груза по условию задачи происходит с неизменной угловой скоростью ω, то действием сил сопротивления движению штанги и груза следует пренебречь. Кроме того, как обычно, лабораторную систему отсчета, относительно которой штатив при достаточно малой угловой скорости вращения покоится, будем считать инерциальной. Тогда на основании второго закона Ньютона можно утверждать, что со стороны штанги на груз действует сила, горизонтальная составляющая которой обеспечивает грузу центростремительное ускорение —ω2r, а вертикальная составляющая уравновешивает действие на груз силы тяжести mg, где g — ускорение свободного падения.
Основываясь на сказанном и на третьем законе Ньютона, можно утверждать, что на штангу со стороны груза действует сила Fr, горизонтальная и вертикальная составляющие которой показаны на рис. 8. Кроме этих сил на штатив действуют еще сила тяжести и сила реакции стола. По условию задачи масса штанги со стойкой достаточно мала, а основанием штатива является тонкий однородный диск. Следовательно, равнодействующая всех действующих на штатив сил тяжести Mg приложена к центру диска, как и показано на рисунке. При критической скорости вращения со стороны стола на штатив может действовать лишь сила, точка приложения которой совпадает с точкой О на краю диска, лежащей в вертикальной плоскости, в которой располагаются оси стойки и штанги штатива в данный момент времени (см. рис. 8). При этом положение штатива становится неустойчивым. Однако, как и при меньших угловых скоростях вращения, сумма всех действующих на штатив сил и сумма моментов этих сил относительно произвольной оси должны быть равны нулю, так как штатив все еще остается неподвижным. Отсюда следует, что алгебраическая сумма моментов силы тяжести Mg и силы Fr относительно горизонтальной оси, проходящей через точку О перпендикулярно указанной вертикальной плоскости, должна быть равна нулю, то есть
Отсюда следует, что алгебраическая сумма моментов силы тяжести Mg и силы Fr относительно горизонтальной оси, проходящей через точку О перпендикулярно указанной вертикальной плоскости, должна быть равна нулю, то есть
,
поскольку плечо силы реакции стола относительно точки О равно нулю. Отметим, что из равенства нулю суммы всех действующих на штатив сил и моментов этих сил относительно указанной оси следует равенство нулю их моментов относительно любой параллельной ей оси. Так как линии действия всех приложенных к штативу сил лежат в указанной выше вертикальной плоскости, можно утверждать, что при выполнении последнего соотношения алгебраическая сумма моментов всех действующих на штатив сил относительно любой другой оси также будет равна нулю. Таким образом, искомая угловая скорость вращения груза, при которой основание штатива перестанет касаться всей плоскостью горизонтальной поверхности стола, равна
.
Boddeker Ch 10 Вращение вокруг фиксированной оси
Boddeker Ch 10 Вращение вокруг фиксированной оси шасси
10. 1 # 1
1 # 1
В течение определенного промежуток времени угловое положение распашной двери описывается θ = 2t 2 + 10t + 5, где θ в радианах, а t в секундах. Определите угловое положение, угловую скорость и угловое ускорение дверь (а) при t = 0,00 секунды, (б) при t = 3,00 секунды.
q = 5 + 10т + 2т 2 | w = dq / dt Вт = 10 + 4т | a = dw / dt а = 4 |
(а) t = 0 | ||
q = 5 рад | w = 10 рад / с | a = 4 рад / с 2 |
(б) t = 3 | ||
q = 53 рад | w = 22 рад / с | a = 4 рад / с 2 |
шасси
10. 2 # 2
2 # 2
Сверло для стоматолога начинается с отдыха. После 3,2 с постоянного углового ускорения он поворачивается как скорость 2,51 х 10 4 об. / мин. (а) Найдите угловое ускорение сверла. (b) Определите угол (в радианах), на который сверло вращается во время этот период. а = Dv / Dt а = Dw / Dt
(а) а = 2,51 x 10 4 об / мин (2 прад / об) (1 мин / 60 с) / 3,2 с a = 821 рад / с 2 | (б) q = а т 2 q = 4200 радиан |
шасси 10.2 # 8
Вращающееся колесо требуется 3,00 с, чтобы совершить 37,0 оборота. Его угловая скорость на конец интервала 3,00 с составляет 98,0 рад / с. Что такое постоянная угловая ускорение колеса?
а = (ω f ω 0 ) / t ω 0 = ω f — АТ | ИЛИ | ω пр. (ω f + ω 0 ) = (q f — q 0 ) / т (98 + ω 0 ) = 37 (2 π) / 3 ω 0 = 57 рад |
q — q 0 = при 2 + (ω f — а т) т q = ω f т — по телефону 2 37 (2π) = 98 (3) а3 2 а = 13.7 рад / с 2 | а = (ω f ω 0 ) / т а = (98 57) / 3 a = 13,7 рад / с 2 |
шасси 10.3 # 17
Диск 8 см в
Радиус вращается с постоянной скоростью 1200 об / мин вокруг своей центральной оси.
Определите (а) его угловую скорость, (б) тангенциальную скорость в точке на расстоянии 3 см от
его центр, (c) радиальное ускорение точки на ободе, и (d)
общее расстояние, на которое точка на ободе перемещается за 2 секунды.
(а) Вт = 1200 об / мин (2прад / об) (1 мин / 60 с) w = 126 рад / с | (б) v = w r v = 126рад / сек (0,03 м) v = 3,77 м / с | (в) а = v 2 / r = w 2 r 2 / r а = ш 2 г а = 1260 м / с 2 |
шасси 10.4 # 21
4 частицы связаны жесткими стержнями незначительной массы. Источник находится в центре. Если система вращается в плоскости x-y вокруг оси z со скоростью 6 рад / сек, вычисление (а) момент инерция системы относительно оси z (б) кинетическая энергия вращения системы | ||
r 1 = r 2 = r 3 = r 4 г = ((6/2) 2 + (4/2) 2 ) г = 13 метры (а) I = S j м j r j 2 I = (3 + 2 + 2 + 4) 13 I = 143 кг · м 2 | (б) К R = Iw 2 К R = 143 (6 рад / с) 2 К R = 2. | |
шасси 10.5 # 23
Три одинаковых стержни длиной L и массой m сварены перпендикулярно друг другу. Узел вращается вокруг оси, проходящей через конец одного стержня. и параллельно другому. Определите момент инерции этого структура. Ответ: 11 мл 2 /12 Подсказка: ср необходимо добавить инерцию для всех трех стержней Я = Я х + I y + I z |
Для I y вся масса расположена на L / 2 от точка поворота я y = м (L / 2) 2 я y = 1/4 мл 2 Для I z стержень по оси Z поворачивается вокруг конец (формула из диаграммы) я я = 1/3 мл 2 Для I x масса варьируется от L / 2 до L / √2 Правая половина (тоже можно сделать сразу все) я х = r 2 дм l = m / L и l = dm / dx я х = r 2 l dx, где r 2 = x 2 + (L / 2) 2 А x изменяется от 0 до L / 2 Работа на правый Я = Я х + I y + I z I = мл 2 /3 + мл 2 /4 + мл 2 /3 I = 11 мл 2 /12 | Правая половина x Я х = r 2 l dx где r 2 = x 2 + (L / 2) 2 I x = l (x 2 + (L / 2) 2 ) dx I x = l x 2 dx + l (L / 2) 2 dx (от x 0 до L / 2) I x = l / 3 x 3 + л / 4 л 2 x (от 0 до л / 2) I x = l / 3 (Л 3 /8) + л / 4 л 2 (л / 2) Я х = (м / л) (л 3 /24) + (м / л) (л 3 /8) Я х = мл 2 /24 + мл 2 /8 я х = мл 2 /6 (для правой половины) я х = mL 2 /3 для всего стержня по оси x |
шасси
10. Найди сеть крутящий момент на колесе вокруг оси через O, если a = 10 см и b = 25 см. | |
S t = t куб.см — t СС S t = 0,1 м * 12N 0,25 м * (9N + 10N) S t = -3,55 Нм |
шасси 10.7 # 35
Модель самолета массой 0,75 кг привязывается тросом так, что летит по кругу 30 м в радиус.Двигатель самолета обеспечивает полезную тягу 0,8 Н перпендикулярно к привязной провод. (a) Найдите крутящий момент, создаваемый чистой осью относительно центр круга. (b) Найдите угловое ускорение самолета, когда он находится в горизонтальном полете. (c) Найдите линейное ускорение самолета по касательной к его траектория полета.
(а) т = r x F т = 30 м * 0,8 Н т = 24 Нм | (б) т = Я 24 = (0. a = 0,0356 рад / с 2 | (c) a T = а * г а т = 0,0356 * 30 а т = 1,07 м / с 2 |
шасси 10.8 # 47 Это задача описывает экспериментальный метод определения момента инерции объекта неправильной формы, такого как полезная нагрузка для спутника.Счетчик груз массой m подвешен на шнуре, намотанном на катушку радиуса r, образующие часть поворотного стола, поддерживающего объект. Поворотный стол может вращаться без трения. | ||
Когда противовес выходит из состояния покоя и опускается на расстояние h, приобретение скорости v. Покажите, что момент инерции I вращающегося аппарата г. 2 (2gh / v 2 1). | К R + К = U грав Iw 2 + mv 2 = mgh Iw 2 = mgh — mv 2 I = 2 (mgh — mv 2 ) / w 2 I = (2 мг-ч — мв 2 ) / (об / об) 2 I = mr 2 (2gh — v 2 ) / v 2 I = г-н 2 (2 г / в 2 — 1) | |
шасси 10.9 # 52
Шар для боулинга масса M, радиус R и момент инерции 2/5 MR 2 . Если это начнется из состояния покоя, сколько работы нужно на нем сделать, чтобы он катился без скольжения с линейной скоростью v? Выразите работу в терминах М и v.
Работа = датских кроныРабота = К + К R Работа = Mv 2 + Iw 2 | Работа = Mv 2 + 2 / 5MR 2 (в / р) 2 Работа = Mv 2 + 2/10 Мв 2 Работа = 7/10 Мв 2 |
Однородный диск массы m и радиуса r может вращаться
Типы изображений кошачьей рвоты
Однородный круглый диск массы m = 24.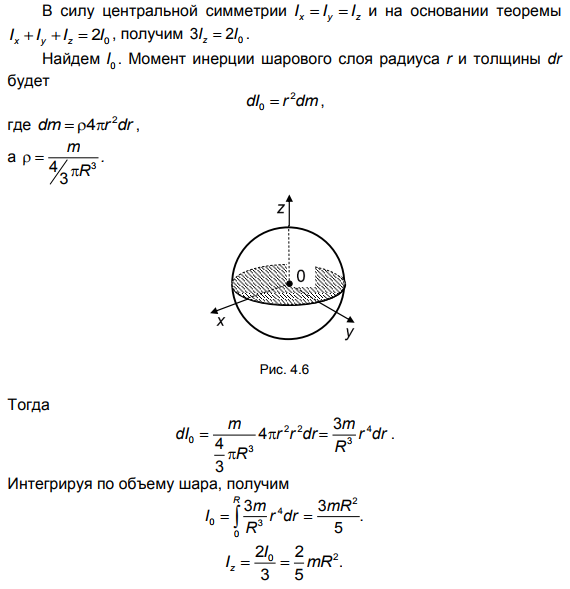 0 \\ mathrm {g} и радиусом r = 40.0 \\ mathrm {cm} свисает вертикально с неподвижного горизонтального шарнира без трения в точке на нем … Однородный круглый диск с массой m = 24,0 \\ mathrm {g} и радиус r = 40,0 \\ mathrm {cm} свисает вертикально с неподвижного горизонтального шарнира без трения в точке на нем… Однородный диск имеет радиус R и общую массу M. Плотность диска определяется по формуле. В момент инерции всего диска мы сначала посмотрим на небольшой участок диска (см. рисунок 5). Площадь кольца, расположенного на расстоянии r от центра и имеющего ширину dr, составляет
0 \\ mathrm {g} и радиусом r = 40.0 \\ mathrm {cm} свисает вертикально с неподвижного горизонтального шарнира без трения в точке на нем … Однородный круглый диск с массой m = 24,0 \\ mathrm {g} и радиус r = 40,0 \\ mathrm {cm} свисает вертикально с неподвижного горизонтального шарнира без трения в точке на нем… Однородный диск имеет радиус R и общую массу M. Плотность диска определяется по формуле. В момент инерции всего диска мы сначала посмотрим на небольшой участок диска (см. рисунок 5). Площадь кольца, расположенного на расстоянии r от центра и имеющего ширину dr, составляет
Ne tv gold apk download uptodown
ArXiv обсуждения для 583 организаций, включая Texas A&M High Energy Physics, UNAM-ICF astro, UBC, Немецкий центр космологического линзирования и ARI HPC group.AAO AIFA Clusters AIP Cosmology AIP, Потсдам AIfA AIfA-Cosmo AIfA-Galaxies AMNH AOB APC
Hisense q8 vs h8
Горизонтально ориентированный однородный диск массы M и радиуса R свободно вращается вокруг неподвижной вертикальной оси, проходящей через его центр. Диск имеет радиальную направляющую, по которой без трения может скользить небольшое тело массой m. Легкая нить, проходящая через полую ось диска, привязана к корпусу.
Диск имеет радиальную направляющую, по которой без трения может скользить небольшое тело массой m. Легкая нить, проходящая через полую ось диска, привязана к корпусу.
Детский комбинезон
27 апреля 2016 г. · Однородный диск массы M и радиуса R подвешен в вертикальной плоскости из точки на его периферии…. точка поворота к центру масс. Момент инерции диска … 25 апр, 2018 · 12. Два диска вращаются вокруг своих осей перпендикулярно дискам и проходят через центры дисков. Диск Dt имеет массу 2 кг, радиус 0,2 м и начальную угловую скорость 50 рад / с. Диск D2 имеет массу 4 кг, радиус 0,1 м и начальную угловую скорость 200 рад / с. Два диска соприкасаются лицом друг к другу, их оси… карусель.Первоначально таракан и диск вращаются вместе с угловой скоростью wo. Затем таракан проходит половину пути к центру диска. ПРИМЕЧАНИЕ. Дайте ответ в терминах указанных переменных.
Решения для домашних заданий
Ch 11, Rolling Motion
Домашнее задание: Ch21; 11, 14, 19, 30, 34, 54Вопросы 1, 2, 3, 4, 10, 12, 13, 15
| Hmwk, Ch 10 | Домашнее задание Задания | Дом PHY 1350 | Hmwk, Ch 12 |
Дополнительные задачи из четвертого издания Serway
(4ед) 11. * Сплошная сфера имеет радиус 0,200 м и массу 150 кг.
Сколько работы требуется, чтобы шар катился с угловой скоростью
50,0 рад / с на горизонтальной поверхности? Предположим, сфера начинается с состояния покоя.
и катится без скольжения.
* Сплошная сфера имеет радиус 0,200 м и массу 150 кг.
Сколько работы требуется, чтобы шар катился с угловой скоростью
50,0 рад / с на горизонтальной поверхности? Предположим, сфера начинается с состояния покоя.
и катится без скольжения.
(4ed) 11. * Проверьте уравнение 11.14 и покажите, что перекрестное произведение может быть записывается как
Задачи из текущего (5-го) издания Serway and Beichner.
11.11 Два вектора равны A = — 3 i + 4 j и B = 2 я + 3 д.
Найти (a) A x B
и (b) угол между A и B.
A x B = i (A y B z — A z B y ) + j (A z B x — A x B z ) + k (A x B y — A y В x )
A x B = i (4 0 — 0 3) + j (0 2 — (- 3) 0) + к ((-3) 3-4 2)
A x B = i (0) + j (0) + k (- 17) = — 17 к
Мы также можем записать это кросс-произведение как
| A x B | = A B sin
A = | A | = КОРЕНЬ [(- 3) 2 + (4) 2 + (0 ) 2 ] = КОРЕНЬ [9 + 16] =
A = SQRT [25] = 5
B = | B | = КОРЕНЬ [2 2 + 3 2 + 0 2 ] = SQRT [13]
| A x B | = 17
sin = | A x B | / (AB) = 17 / [(5) КОРЕНЬ (13)] = 17 / [(5) (3.
61)] = 0,943
= 70,56 o
11,14 Студент утверждает, что нашел вектор A такой, что ( 2 i — 3 j + 4 k) x A = 4 i + 3 j — k. Вы верите это требование? Объяснять.
Нам понадобится перекрестное произведение в форме уравнения 11.14,
D x E = (Dx i + Dy j + Dz k ) x (Ex i + Ey j + Ez k )
= i (Dy Ez — Dz Ey) + j (Dz Ex — Dx Ez) + k (Dx Ey — Dy Ez)
(я намеренно избегал записи A x B , так как этот вопрос уже есть выражение, включающее что-то вроде C x A , с вектором — это второй или последний вектор в выражение.Теперь мы можем продолжить и оценить (2 i — 3 j + 4 к ) х А ,
(2 i — 3 j + 4 k ) x A = (2 i — 3 j + 4 k ) x (Ax i + Ay j + Az k )
= i [(- 3) Az — 4 Ay] + j [4 Ax — 2 Az] + k [2 Ay — (- 3) Ax]
= 4 i + 3 j — k
Это дает три уравнения для трех компонентов вектора A ,
i [(- 3) Az — 4 Ay] + j [4 Ax — 2 Az] + k [ 2 Ay — (- 3) Ax] = 4 i + 3 j — k
— 3 Az — 4 Ay = 4
4 оси — 2 азимута = 3
2 Ay + 3 Ax = — 1
Теперь мы просто пробираемся через болото одновременных уравнений,
3 Az + 4 Ay = — 4
3 Az = — 4 Ay — 4
Az = (- 4 Ay — 4) / 3
4 оси — 2 азимута = 3
4 Ax — 2 [(- 4 Ay — 4) / 3] = 3
4 Ax + 8 Ay / 3 + 8/3 = 3
12 Ax + 8 Ay + 8 = 9
12 Ax + 8 Ay = 1
2 Ay + 3 Ax = — 1
Умножьте это последнее уравнение на 4
12 Ax + 8 Ay = — 4
Теперь вычтите это из 12 Ax + 8 Ay = 1
И у нас «проблемы» с этим результатом в
0 = 4
Что это значит? Есть , а не , решение для нашего набора из трех одновременные уравнения.
Значит вектора А не существует! Как это быть? Что это значит?
В общем, если мы напишем B x A = V , это приведет к вектор V расположен на перпендикулярно как B , так и A . В наш случай, который требует, чтобы вектор (4 i + 3 j — k ) был перпендикулярен на (2 i — 3 j + 4 k ). Так ли это? Давайте проверим это и посмотреть.Если бы эти два вектора были перпендикулярны, то их точек продукт должен исчезнуть .
Помните, что
A B = A B cos
и что
A B = Ax Bx + Ay By + Az Bz
(4 i + 3 j — k ) (2 i — 3 j + 4 k ) =
= 42 + 3 (- 3) + (- 1) 4 = 8 — 9 — 4 = — 5
, и это , а не ноль.
11,19 Легкий жесткий стержень длиной 1,00 м вращается в плоскости xy примерно шарнир через центр стержня. Две частицы массой 4,00 кг и 3,00 кг присоединены к его концам. Определить угловой момент системы относительно начала координат в то время скорость каждой частицы составляет 5,00 м / с.
L Tot = L стержень + L 1 + L 2
Нам говорят, что удочка — это «легкий» стержень, что является другим способом сказать его масса и момент инерции достаточно малы, ими можно пренебречь.Следовательно,
L Всего = L 1 + L 2
Угловой момент для «точечной частицы» равен
.L = m r v t
L 1 = (3,0 кг) (0,5 м) (5,0 м / с) = 7,5 кг · м 2 / с
L 2 = (4,0 кг) (0,5 м) (5,0 м / с) = 10,0 кг · м 2 / с
L Tot = L 1 + L 2 = 17.
5 кг · м 2 / с
11.30 Вращается однородный твердый диск массой 3,00 кг и радиусом 0,200 м. вокруг фиксированной оси, перпендикулярной его грани. Если угловая частота вращение составляет 6.00 рад / с, рассчитайте угловой момент диска, когда ось вращения
(а) проходит через его центр масс и
(b) проходит через точку на полпути между центром и ободом.
I CM = (1/2) M R 2
I CM = (1/2) (3,00 кг) (0,200 м) 2
I CM = 0,06 кг м 2
L = I = (0,06 кг · м 2 ) (6,0 1 / с)
L = 0,54 кг · м 2 / с
I = I CM + M d 2
I = (1/2) M R 2 + M (R / 2) 2
I = (1/2) M R 2 + (1/4) M R 2
I = (0.
06 + 0,03) кг м 2
I = 0,09 кг · м 2
L = I = (0,09 кг · м 2 ) (6,0 1 / с)
L = 0,72 кг · м 2 / с
11,34 Карусель спортивная радиусом R = 2,0 м имеет момент инерция I = 250 кг · м 2 и вращается со скоростью 10 об / мин. Ребенок 25 кг прыгает на край карусели. Какая новая угловая скорость карусель?
Lf = Li
Li = Ii i
Ii = 250 кг · м 2
i = 10 об / мин
Li = (250 кг · м 2 ) (10 об / мин) = 2 500 (кг · м 2 об. / мин)
Lf = Если f
If = I MgR + I ребенок
I ребенок = m r 2 = (25 кг) (2.0 м) 2 = 100 кг · м 2
Если = (250 + 100) кг м 2 = 350 кг м 2
f = Lf / If = Li / If = [2 500 кг м 2 об / мин] / [350 кг · м 2 ]
f = 7,14 об / мин
11,54 Снаряд массой m движется вправо со скоростью v o . Снаряд попадает в конец неподвижного стержня массой
M и длиной d, которая поворачивается вокруг оси без трения через ее центр.
Снаряд попадает в конец неподвижного стержня массой
M и длиной d, которая поворачивается вокруг оси без трения через ее центр.
(a) Найдите угловую скорость системы сразу после столкновения.
(b) Определите частичную потерю механической энергии из-за столкновения.
Перед столкновением неподвижный стержень имеет нулевой угловой момент и снаряд имеет угловой момент
L = м v r
L = m v o (d / 2)
L i = m v o d / 2
После столкновения стержень с прилипшим к нему снарядом вращается. с угловой скоростью.
L f = I
I = I стержень + I pjt
I стержень = (1/12) M d 2
I pjt = m (d / 2) 2 = (1/4) m d 2
I = (1/12) M d 2 + (1/4) m d 2 = [(1/12) M + (1/4) м] d 2
L f = [(1/12) M + (1/4) m] d 2 = m v o d / 2 = L i
= [m v o d / 2] / [(1/12) M + (1/4) м] d 2
= [m v o ] / [(1/24) M + (1/8) m] d
Концептуальные вопросы
Q11. 1 Можно ли рассчитать крутящий момент, действующий на
твердое тело без указания центра вращения? Независимо от крутящего момента
расположения центра вращения?
1 Можно ли рассчитать крутящий момент, действующий на
твердое тело без указания центра вращения? Независимо от крутящего момента
расположения центра вращения?
НЕТ! Легко сказать «найти крутящий момент, вызванный этими сил ». Но это бессмысленное утверждение. Что такое , всегда требуется — или имелось в виду или подразумевается — это «найти крутящий момент относительно такого-то и такого-то центр вращения, вызванный этими силами ». Иногда — потому что рисунка или каких-то ограничений, таких как петли на двери — мы не можем в частности, заявляет, что «в отношении такого-то центра вращения «, но эта информация требуется до утверждения имеет какое-то значение!
Q11.2 Является ли тройной продукт определением A (B x C) скалярная или векторная величина?
Объясните, почему операция (A Б) х С не имеет значения.
( B x C ) — вектор. Для удобства звоним
это вектор D . То есть D = ( B x C ). Теперь наше выражение
это A ( B x C ) = A D и что
это просто скалярное произведение или скалярное произведение, поэтому этот результат
скаляр.
Для удобства звоним
это вектор D . То есть D = ( B x C ). Теперь наше выражение
это A ( B x C ) = A D и что
это просто скалярное произведение или скалярное произведение, поэтому этот результат
скаляр.
Однако, поскольку ( A B ) является скаляром, выражение (A B) x C бессмысленно, потому что мы не определили (скалярный) x C , скаляр «скрещен» с вектором. Мы не определили операцию написано так со скаляром и «оператором перекрестного произведения» и вектор.
Q11.3 В некоторых гонках на мотоциклах гонщики проезжают мимо холмы, и мотоциклы на короткое время взлетают в воздух.Если мотоцикл гонщик держит дроссель открытым, покидая холм и поднимаясь в воздух, мотоцикл стремится носом вверх. Почему это происходит?
Очень интересное наблюдение!
Как только мотоцикл находится в воздухе, а дроссельная заслонка еще
откроется, заднее колесо будет разгоняться до . Это означает, что угловой момент заднего колеса увеличится на .
Это означает, что угловой момент заднего колеса увеличится на .
Мы можем представить это как вектор, указывающий на из экран,
Но, пока мотоцикл находится в воздухе, net angular импульс — всего углового момента всей «системы» — можно не изменить.Пока мотоцикл находится в воздухе, крутящие моменты отсутствуют. на нем, чтобы изменить его полный угловой момент. Итак, остальная часть «системы» должен изменить угловой момент в направлении против направления ,
«Остальная часть системы» — это всего лишь остальная часть мотоцикла. и всадник. Так что они должны «поднять нос»,
Q11.4 Если крутящий момент, действующий на частицу, примерно происхождение равно нулю, что вы можете сказать о его угловом моменте об этом происхождении?
Его угловой момент , постоянная . (не обязательно ноль — всего константа ).
(не обязательно ноль — всего константа ).
Q11.10 Ученый в отеле обратился за помощью к посыльному. носить таинственный чемодан. Когда неосведомленный коридорный завернул за угол неся чемодан, он вдруг по неизвестной причине отошел от него. В этот момент встревоженный коридорный уронил чемодан и убежал. Что как вы думаете, могло быть внутри чемодана?
Большой приводной маховик может дать такой эффект.Считать попытки переместить гироскоп и его реакцию, когда вы пытаетесь переместить его ось вращения.
Q11.12 Три объекта однородной плотности — твердая сфера,
цельный цилиндр и полый цилиндр — размещаются на вершине склона
как на Рисунке Q11.12. Если все они выходят из состояния покоя на одной высоте
и катитесь без скольжения, какой предмет первым достигает дна? Что достигает
это последний? Вы должны попробовать это дома и отметить, что результат не зависит от
массы и радиусы объектов.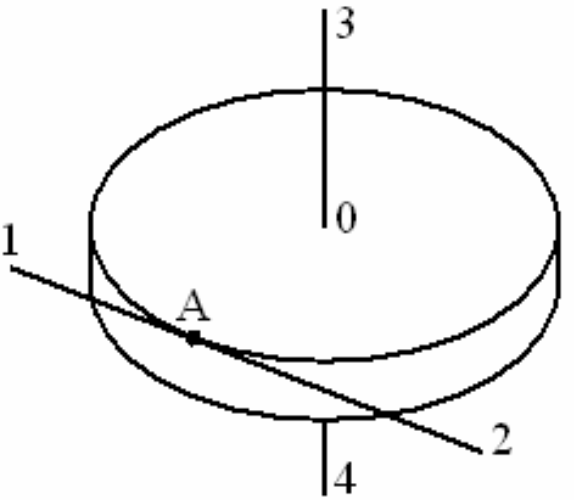
[[Рис. Q11.12]]
Тот, у которого наименьший момент инерции — или «вращательный масса »- легче всего повернуть, так что он первым доберется до дна. один с наименьшим моментом инерции — это твердая сфера . Следующий твердый цилиндр . Последний — полый цилиндр .
Q11.13 Мышь изначально находится в покое на горизонтальном поворотном столе установлен на вертикальной оси без трения.Если мышь начинает ходить периметр или окружность, что происходит с поворотным столом?
Без внешних крутящих моментов — потому что на трении меньше вертикальная ось — полный угловой момент сохранен. Это означает
полный угловой момент остается постоянным . Когда мышь начинает
Обходя по окружности, он получает угловой момент, поэтому поворотный стол должен
поверните на в противоположном направлении , чтобы получить угловой момент, чтобы противостоять этому.
Q11.15 Часто, когда высокий дайвер хочет выполнить сальто в воздухе она прижимает ноги к груди. Почему это заставляет ее вращаться Быстрее? Что ей делать, если она хочет выйти из сальто?
После того, как ныряльщик вылетел за борт, он не Ее угловой момент остается постоянным . Ее угловой момент является произведением ее момента инерции и ее угловой скорости .Когда она принимает позу «подворачивания», это делает ее момент инерции — ее «вращательная масса» — малая . Чтобы сохранить момент импульса постоянный угловая скорость увеличивается на .
Когда она выходит из положения «втягивания» и разгибается ее тело, это делает ее момент инерции большим и ее угловую скорость уменьшает , чтобы сохранить ее угловой момент постоянным .
Веселее наблюдать, как это выполняет высокий ныряльщик или фигура.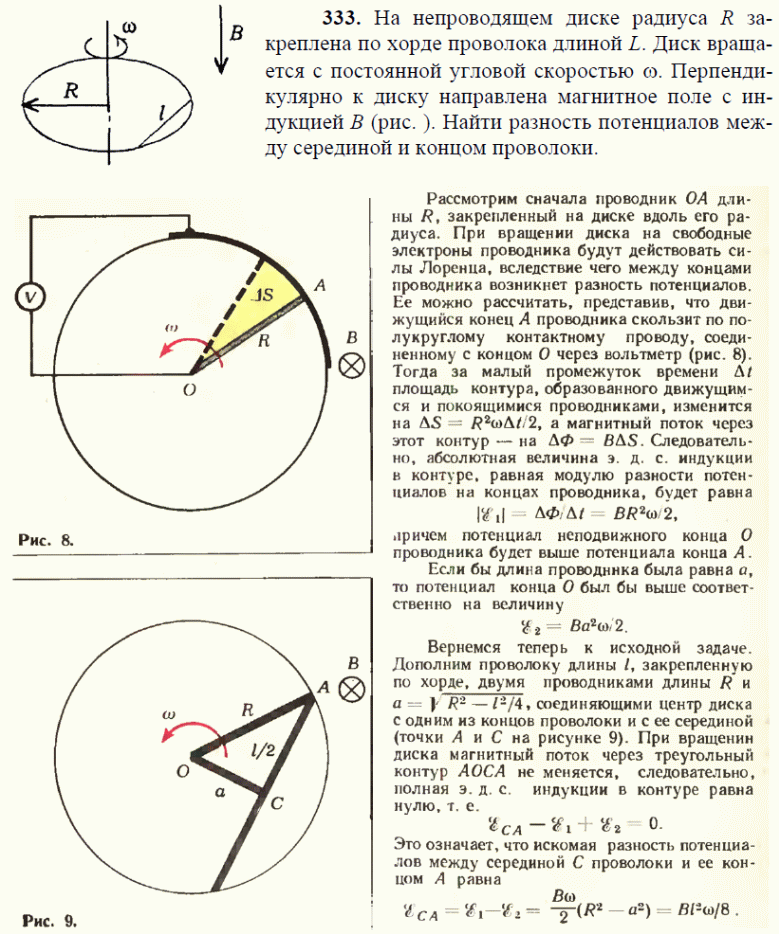 конькобежец.Но вы можете сами продемонстрировать те же идеи на вращающемся стуле.
с парочкой тяжелых книг в руках. Или мы также продемонстрировали
это в классе с хорошим поворотным столом и грузами,
конькобежец.Но вы можете сами продемонстрировать те же идеи на вращающемся стуле.
с парочкой тяжелых книг в руках. Или мы также продемонстрировали
это в классе с хорошим поворотным столом и грузами,
Решения дополнительных проблем от четвертого Serway выпуск
(4ed) 11.1 Твердая сфера имеет радиус 0,200 м и массу 150 кг. Сколько работы требуется, чтобы шар катился с угловой скоростью из 50.0 рад / с на горизонтальной поверхности? Предположим, сфера начинается с состояния покоя. и катится без скольжения.
Момент инерции твердого шара
I = (2/5) M R 2
Для нашей конкретной сферы это означает
I = (2/5) (150 кг) (0,200 м) 2
I = 2,4 кг м 2
Пока он катится, он имеет кинетическую энергию поступательного движения K tr и кинетическую энергию вращения K rot
K Tot = K tr + K rot = (1/2) m v 2 + (1/2) Я 2
v = r = (0.
200 м) (50 рад / с) = 10 м / с
K Tot = (1/2) m v 2 + (1/2) I 2
K Tot = (1/2) (150 кг) (10 м / с) 2 + (1/2) (2,4 кг м 2 ) (50 рад / с) 2
К Всего = 7 500 Дж + 3 000 Дж
К Всего = 10 500 Дж
Так как работа равна изменению кинетической энергии и начальной кинетической энергии. энергия равна нулю, так как эта сфера начинается из состояния покоя, это тоже работа сделано.
Вт = 10 500 Дж
(4ed) 11.2 Проверьте уравнение 11.14 и покажите, что перекрестное произведение может записывается как
Во-первых, вспомните, что значит расширить или оценить любой детерминант, Рассмотрим следующий определитель:Этот определитель может быть расширен или оценен путем создания чередующейся серии .с Cx, - Cy и Cz, каждый из которых умножается на кофактор оставшихся членов в определителе при удалении строки и столбца Cx, Cy и Cz.Обратите внимание на отрицательный знак - Cy; это важно.
Эти детерминанты два на два легко оценить. Просто помните, чтоЭто означаетииЭто означает, и это действительно уравнение 11.14.
| Hmwk, Ch 10 | Домашнее задание Задания | Дом PHY 1350 | Hmwk, Ch 12 |
(c) Дуг Дэвис, 2001; все права защищены
10.
 E: Введение в вращение с фиксированной осью (упражнения)
E: Введение в вращение с фиксированной осью (упражнения)Концептуальные вопросы
10.1 Вращательные переменные
- Часы на стене. Когда вы смотрите на это, каково направление вектора угловой скорости секундной стрелки?
- Какое значение имеет угловое ускорение секундной стрелки часов на стене?
- Взмах бейсбольной битой.Все ли точки летучей мыши имеют одинаковую угловую скорость? Та же тангенциальная скорость?
- Лезвия блендера на прилавке вращаются по часовой стрелке, если смотреть на него сверху. Если блендер установить на большую скорость, в каком направлении будет угловое ускорение лопастей?
10.2 Вращение с постоянным угловым ускорением
- Если твердое тело имеет постоянное угловое ускорение, какова функциональная форма угловой скорости с точки зрения временной переменной?
- Если твердое тело имеет постоянное угловое ускорение, какова функциональная форма углового положения?
- Если угловое ускорение твердого тела равно нулю, какова функциональная форма угловой скорости?
- Безмассовый трос с грузами, привязанными к обоим концам, вращается вокруг фиксированной оси через центр.
 Может ли полное ускорение троса / массы быть нулевым, если угловая скорость постоянна?
Может ли полное ускорение троса / массы быть нулевым, если угловая скорость постоянна?
10.3 Связь угловых и поступательных величин
- Объясните, почему центростремительное ускорение меняет направление скорости при круговом движении, но не его величину.
- При круговом движении тангенциальное ускорение может изменять величину скорости, но не ее направление. Поясните свой ответ.
- Предположим, что блюдо стоит на краю вращающейся пластины микроволновой печи.Испытывает ли она ненулевое тангенциальное ускорение, центростремительное ускорение или и то, и другое, когда: (а) пластина начинает вращаться быстрее? (б) Пластина вращается с постоянной угловой скоростью? (c) Пластина замедляется до полной остановки?
10,4 Момент инерции и кинетическая энергия вращения
- Что, если бы другая планета того же размера, что и Земля, была бы выведена на орбиту вокруг Солнца вместе с Землей. Будет ли момент инерции системы увеличиваться, уменьшаться или оставаться прежним?
- Сплошная сфера вращается вокруг своей оси с постоянной скоростью.
 {2}} {3} \).{2}} {4} \)) г.
{2}} {3} \).{2}} {4} \)) г. - Почему момент инерции обруча с массой M и радиусом R больше, чем момент инерции диска с такой же массой и радиусом?
10,6 Крутящий момент
- Какие три фактора влияют на крутящий момент, создаваемый силой относительно определенной точки поворота?
- Приведите пример, в котором малая сила вызывает большой крутящий момент. Приведите другой пример, в котором большая сила вызывает небольшой крутящий момент.
- При уменьшении массы гоночного велосипеда наибольшая выгода достигается за счет уменьшения массы шин и колесных дисков.Почему это позволяет гонщику развивать большее ускорение, чем такое же уменьшение массы рамы велосипеда?
- Может ли единичная сила создать нулевой крутящий момент?
- Может ли набор сил иметь нулевой чистый крутящий момент и отличную от нуля результирующую силу?
- Может ли набор сил иметь результирующую силу, равную нулю, и чистый крутящий момент, который не равен нулю?
- В выражении \ (\ vec {r} \ times \ vec {F} \) может ли \ (| \ vec {r} | \) когда-либо быть меньше плеча рычага? Может ли оно быть равно плечу рычага?
10.
 7 Второй закон Ньютона для вращения
7 Второй закон Ньютона для вращения- Если бы вы остановили вращающееся колесо с постоянной силой, где на колесе вы бы применили силу, чтобы вызвать максимальное отрицательное ускорение?
- Стержень повернут вокруг одного конца. К нему действуют две силы \ (\ vec {F} \) и \ (- \ vec {F} \). При каких обстоятельствах стержень не будет вращаться?
Проблемы
10.1 Вращательные переменные
- Вычислить угловую скорость Земли.
- Звезда легкой атлетики пробегает 400 м по круговой трассе длиной 400 м за 45 с. Какова его угловая скорость при постоянной скорости?
- Колесо вращается с постоянной скоростью 2,0 x 10 3 об / мин. а) Какова его угловая скорость в радианах в секунду? б) На какой угол он поворачивается за 10 с? Выразите решение в радианах и градусах.
- Частица движется на 3,0 м по окружности радиусом 1,5 м. а) На какой угол он вращается? (б) Если частица совершит это путешествие за 1.
 0 с при постоянной скорости, какова его угловая скорость? (c) Каково его ускорение?
0 с при постоянной скорости, какова его угловая скорость? (c) Каково его ускорение? - Компакт-диск вращается со скоростью 500 об / мин. Если диаметр диска составляет 120 мм, (а) какова тангенциальная скорость точки на краю диска? (б) В точке на полпути к центру диска?
- Необоснованные результаты . Пропеллер самолета вращается со скоростью 10 об / с, когда пилот выключает двигатель. Пропеллер снижает свою угловую скорость на постоянную 2.0 рад / с 2 на период времени 40 с. Какая скорость вращения воздушного винта за 40 с? Это разумная ситуация?
- Гироскоп замедляется с начальной скорости 32,0 рад / с до 0,700 рад / с 2 . Сколько времени нужно, чтобы отдохнуть?
- При взлете пропеллеры БПЛА (беспилотного летательного аппарата) увеличивают свою угловую скорость на 3,0 с из состояния покоя со скоростью \ (\ omega \) = (25,0 т) рад / с, где t измеряется в секундах. (а) Какова мгновенная угловая скорость гребных винтов при t = 2.
 0 с? б) Что такое угловое ускорение?
0 с? б) Что такое угловое ускорение? - Угловое положение стержня изменяется на 20.0t 2 радиан с момента времени t = 0. На стержне есть две борта, как показано на следующем рисунке, один на расстоянии 10 см от оси вращения, а другой — на расстоянии 20 см от оси вращения. ось вращения. (а) Какова мгновенная угловая скорость стержня при t = 5 с? б) Какое угловое ускорение стержня? (c) Каковы тангенциальные скорости шариков при t = 5 с? (d) Каковы тангенциальные ускорения бусинок при t = 5 с? (e) Каковы центростремительные ускорения шариков при t = 5 с?
10.2 Вращение с постоянным угловым ускорением
- Колесо имеет постоянное угловое ускорение 5,0 рад / с 2 . Начиная с покоя, получается 300 рад. а) Какова его конечная угловая скорость? б) Сколько времени проходит, пока он проходит через 300 радиан?
- За интервал времени 6,0 с маховик с постоянным угловым ускорением проходит 500 радиан, приобретая угловую скорость 100 рад / с.
 (а) Какая угловая скорость в начале 6.0 с? б) Какое угловое ускорение маховика?
(а) Какая угловая скорость в начале 6.0 с? б) Какое угловое ускорение маховика? - Угловая скорость вращающегося твердого тела увеличивается с 500 до 1500 об / мин за 120 с. а) Что такое угловое ускорение тела? б) На какой угол он поворачивается за эти 120 с?
- Маховик замедляется с 600 до 400 об / мин при 40 оборотах. а) Какое угловое ускорение маховика? б) Сколько времени проходит за 40 оборотов?
- Колесо 1.Радиус 0 м вращается с угловым ускорением 4,0 рад / с 2 . а) Если начальная угловая скорость колеса равна 2,0 рад / с, какова его угловая скорость через 10 с? б) На какой угол он поворачивается за 10 с? (c) Каковы тангенциальная скорость и ускорение точки на ободе колеса в конце 10-секундного интервала?
- Вертикальное колесо диаметром 50 см запускается из состояния покоя и вращается с постоянным угловым ускорением 5,0 рад / с 2 вокруг фиксированной оси через его центр против часовой стрелки.(а) Где находится точка, которая изначально находится внизу колеса при t = 10 с? (б) Каково линейное ускорение точки в данный момент?
- Круглый диск радиусом 10 см имеет постоянное угловое ускорение 1,0 рад / с 2 ; при t = 0 его угловая скорость составляет 2,0 рад / с.
 (а) Определите угловую скорость диска при t = 5,0 с. б) На какой угол он повернулся за это время? (c) Каково тангенциальное ускорение точки на диске при t = 5,0 с?
(а) Определите угловую скорость диска при t = 5,0 с. б) На какой угол он повернулся за это время? (c) Каково тангенциальное ускорение точки на диске при t = 5,0 с? - Угловая скорость vs.время для вентилятора на воздушной подушке показано ниже. а) На какой угол вращаются лопасти вентилятора в первые 8 секунд? (b) Проверьте результат, используя кинематические уравнения.
- У стержня длиной 20 см к концам прикреплены две бусины. Стержень с бусинами начинает вращаться из состояния покоя. Если тангенциальная скорость бусинок должна составлять 20 м / с за 7 с, какое угловое ускорение стержня позволяет достичь этого?
10.3 Связь угловых и поступательных величин
- Торнадо на пике — 60.0 м в диаметре и скорость ветра 500 км / ч. Какова его угловая скорость в оборотах в секунду?
- Мужчина стоит на карусели, вращающейся со скоростью 2,5 рад / с. Если коэффициент статического трения между обувью человека и каруселью равен \ (\ mu \) S = 0,5, как далеко от оси вращения он сможет стоять без скольжения?
- Ультрацентрифуга ускоряется от состояния покоя до 100 000 об / мин за 2,00 мин. (а) Какое среднее угловое ускорение в рад / с 2 ? (б) Каково тангенциальное ускорение точки 9.50 см от оси вращения? (c) Какое центростремительное ускорение в м / с 2 и кратное g этой точки при полных оборотах в минуту? (d) Каково общее расстояние, пройденное точкой в 9,5 см от оси вращения ультрацентрифуги?
- Ветряная турбина вращается против часовой стрелки со скоростью 0,5 об / с и замедляется до остановки за 10 с. Его лопасти имеют длину 20 м. а) Какое угловое ускорение турбины? (б) Каково центростремительное ускорение кончика лопастей при t = 0 с? (c) Какова величина и направление полного линейного ускорения кончика лопастей при t = 0 с?
- Что такое (а) угловая скорость и (б) линейная скорость точки на поверхности Земли на 30 ° северной широты.Примем радиус Земли 6309 км. (c) На какой широте ваша линейная скорость будет 10 м / с?
- Ребенок массой 30 кг сидит на краю карусели на расстоянии 3,0 м от оси вращения. Карусель разгоняется от состояния покоя до 0,4 об / с за 10 с. Если коэффициент статического трения между ребенком и поверхностью карусели равен 0,6, упадет ли ребенок раньше 5 с?
- Велосипедное колесо радиусом 0,3 м вращается из состояния покоя до 3 об / с за 5 с.Какова величина и направление вектора полного ускорения на краю колеса за 1,0 с?
- Угловая скорость маховика с радиусом 1,0 м изменяется согласно соотношению \ (\ omega \) (t) = 2,0t. Постройте график a c (t) и t (t) от t = 0 до 3,0 с для r = 1,0 м. Проанализируйте эти результаты, чтобы объяснить, когда c >> a t и когда c << a t для точки на маховике с радиусом 1,0 м.
10.4 Момент инерции и вращательная кинетическая энергия
- Система точечных частиц показана на следующем рисунке. Каждая частица имеет массу 0,3 кг, и все они лежат в одной плоскости. а) Каков момент инерции системы относительно данной оси? (б) Если система вращается со скоростью 5 об / с, какова ее кинетическая энергия вращения?
- (a) Рассчитайте кинетическую энергию вращения Земли вокруг своей оси. (б) Какова кинетическая энергия вращения Земли на ее орбите вокруг Солнца?
- Рассчитайте кинетическую энергию вращения колеса мотоцикла весом 12 кг, если его угловая скорость составляет 120 рад / с, а его внутренний радиус равен 0.280 м и внешний радиус 0,330 м.
- Питчер бейсбола бросает мяч движением, при котором предплечье вращается вокруг локтевого сустава, а также другие движения. Если линейная скорость мяча относительно локтевого сустава составляет 20,0 м / с на расстоянии 0,480 м от сустава, а момент инерции предплечья равен 0,500 кг-м 2 , какова кинетическая энергия вращения предплечье?
- Дайвер делает сальто во время ныряния, подвернув конечности.Если ее кинетическая энергия вращения составляет 100 Дж, а момент инерции в группировке составляет 9,0 кг • м 2 , какова ее частота вращения во время сальто?
- Самолет совершает посадку на высоте 300 метров, пропеллер падает. Самолет летит со скоростью 40,0 м / с по горизонтали. Пропеллер имеет скорость вращения 20 об / с, момент инерции 70,0 кг • м 2 и массу 200 кг. Пренебрегайте сопротивлением воздуха. а) С какой поступательной скоростью пропеллер ударяется о землю? (б) Какая скорость вращения пропеллера при ударе?
- Если сопротивление воздуха присутствует в предыдущей задаче и снижает кинетическую энергию вращения воздушного винта при ударе на 30%, какова скорость вращения воздушного винта при ударе?
- Нейтронная звезда массой 2 x 10 30 кг и радиусом 10 км вращается с периодом 0.02 секунды. Какова его кинетическая энергия вращения?
- Электрическая шлифовальная машина, состоящая из вращающегося диска массой 0,7 кг и радиусом 10 см, вращается со скоростью 15 об / с. При нанесении на грубую деревянную стену скорость вращения уменьшается на 20%. (а) Какова конечная кинетическая энергия вращения вращающегося диска? б) Насколько уменьшилась его кинетическая энергия вращения?
- Система состоит из диска массой 2,0 кг и радиусом 50 см, на котором установлен кольцевой цилиндр массой 1.0 кг с внутренним радиусом 20 см и внешним радиусом 30 см (см. Ниже). Система вращается вокруг оси через центр диска и кольцевой цилиндр со скоростью 10 об / с. а) Каков момент инерции системы? б) Какова его кинетическая энергия вращения?
10.5 Расчет моментов инерции
- Во время игры в футбольный мяч кикер вращает ногой вокруг тазобедренного сустава. Момент инерции опоры составляет 3,75 кг • м 2 , а кинетическая энергия вращения — 175 Дж.а) Какова угловая скорость ноги? (b) Какова скорость кончика ботинка игрока, если он находится на расстоянии 1,05 м от тазобедренного сустава?
- Каков момент инерции стержня массы m относительно оси, показанной ниже, с помощью теоремы о параллельности осей?
- Найдите момент инерции стержня в предыдущей задаче прямым интегрированием.
- Унифицированный стержень массой 1,0 кг и длиной 2,0 м может свободно вращаться вокруг одного конца (см. Следующий рисунок).Если стержень выходит из состояния покоя под углом 60 ° по отношению к горизонтали, какова скорость кончика стержня, когда он проходит горизонтальное положение?
- Маятник состоит из стержня массой 2 кг и длиной 1 м с твердой сферой на одном конце массой 0,3 кг и радиусом 20 см (см. Следующий рисунок). Если маятник выходит из состояния покоя под углом 30 °, какова угловая скорость в самой низкой точке?
- Твердая сфера радиусом 10 см может свободно вращаться вокруг оси.Сфере наносят резкий удар так, чтобы ее центр масс начинался из положения, показанного на следующем рисунке, со скоростью 15 см / с. Каков максимальный угол между диаметром и вертикалью?
- Рассчитайте момент инерции путем прямого интегрирования тонкого стержня массы M и длины L вокруг оси, проходящей через стержень в точке L / 3, как показано ниже. Проверьте свой ответ с помощью теоремы о параллельных осях.
10,6 Момент
- Два маховика с незначительной массой и разными радиусами скреплены вместе и вращаются вокруг общей оси (см. Ниже).Меньший маховик радиусом 30 см имеет шнур, на котором действует тяговое усилие 50 Н. Какое тяговое усилие необходимо приложить к шнуру, соединяющему больший маховик с радиусом 50 см, чтобы комбинация не вращалась?
- На автомобиле болты крепления головки блока цилиндров необходимо затягивать с моментом 62,0 Н · м. Если механик использует гаечный ключ длиной 20 см, какое перпендикулярное усилие он должен приложить к концу гаечного ключа, чтобы правильно затянуть болт?
- (a) При открытии двери вы нажимаете на нее перпендикулярно с силой 55.0 Н на расстоянии 0,850 м от петель. Какой крутящий момент вы прилагаете к петлям? б) Имеет ли значение, если вы нажимаете на ту же высоту, что и петли? Есть только одна пара петель.
- При затяжке болта вы нажимаете перпендикулярно гаечному ключу с усилием 165 Н на расстоянии 0,140 м от центра болта. Какой крутящий момент вы прилагаете в Ньютон-метрах (относительно центра болта)?
- Какая подвесная масса должна быть помещена на шнур, чтобы шкив не вращался (см. Следующий рисунок)? Масса на плоскости без трения равна 5.0 кг. Внутренний радиус шкива составляет 20 см, а внешний — 30 см.
- Простой маятник состоит из безмассового троса длиной 50 см, соединенного с осью, и небольшой массы в 1,0 кг, прикрепленной на другом конце. Каков крутящий момент вокруг оси поворота, когда маятник образует угол 40 ° по отношению к вертикали?
- Рассчитайте крутящий момент вокруг оси z, которая выходит за пределы страницы в начале координат на следующем рисунке, учитывая, что F 1 = 3 Н, F 2 = 2 Н, F 3 = 3 Н, F 4 = 1.8 Н.
- Качели длиной 10,0 м и равномерной массой 10,0 кг расположены под углом 30 ° по отношению к земле (см. Следующий рисунок). Ось находится на высоте 6,0 м. Какая величина силы должна быть приложена перпендикулярно качелям на поднятом конце, чтобы качели едва начали вращаться?
- Маятник состоит из стержня массой 1 кг и длиной 1 м, соединенного с осью с твердой сферой, прикрепленной на другом конце с массой 0.5 кг и радиус 30 см. Каков крутящий момент вокруг оси поворота, когда маятник находится под углом 30 ° по отношению к вертикали?
- Для подъема подъемного моста требуется крутящий момент 5,00 x 10 3 Н • м (см. Следующий рисунок). Какое напряжение необходимо для создания этого крутящего момента? Было бы легче поднять подъемный мост, если бы угол \ (\ theta \) был больше или меньше?
- Горизонтальная балка длиной 3 м и массой 2,0 кг имеет массу 1.0 кг и шириной 0,2 м на конце балки (см. Следующий рисунок). Каков крутящий момент системы относительно опоры у стены?
- Какая сила должна быть приложена к концу стержня вдоль оси x длиной 2,0 м, чтобы создать крутящий момент на стержне относительно начала координат 8,0 \ (\ hat {k} \) Н • м?
- Каков крутящий момент относительно источника силы (5.0 \ (\ hat {i} \) — 2.0 \ (\ hat {j} \) + 1.0 \ (\ hat {k} \)) N, если она приложена в точке, положение которой: \ (\ vec {r} \) = (−2.0 \ (\ hat {i} \) + 4.0 \ (\ hat {j} \)) м?
10,7 Второй закон Ньютона для вращения
- У вас есть точильный камень (диск) весом 90,0 кг, радиусом 0,340 м и вращающимся со скоростью 90,0 об / мин, и вы прижимаете к нему стальной топор с радиальной силой 20,0 Н. (a) Предполагая, что кинетический коэффициент трения между сталью и камнем составляет 0,20, рассчитайте угловое ускорение точильного камня. б) Сколько поворотов сделает камень, прежде чем остановится?
- Предположим, вы прикладываете силу 180 Н по касательной к 0.Радиус 280 м, точильный камень 75,0 кг (сплошной диск). а) Какой крутящий момент прилагается? (b) Какое угловое ускорение при пренебрежимо малом встречном трении? (c) Каково угловое ускорение, если противодействующая сила трения в 20,0 Н действует на 1,50 см от оси?
- Маховик (I = 50 кг • м 2 ), начиная с состояния покоя, приобретает угловую скорость 200,0 рад / с при постоянном крутящем моменте от двигателя в течение 5 с. а) Какое угловое ускорение маховика? б) Какова величина крутящего момента?
- К твердому телу, момент инерции которого равен 4, приложен постоянный крутящий момент.0 кг • м 2 вокруг оси вращения. Если колесо трогается с места и достигает угловой скорости 20,0 рад / с за 10,0 с, каков крутящий момент?
- К шлифовальному кругу прилагается крутящий момент 50,0 Н • м (I = 20,0 кг • м 2 ) в течение 20 с. (a) Если он начинается в состоянии покоя, какова угловая скорость шлифовального круга после снятия крутящего момента? (b) На какой угол движется колесо при приложении крутящего момента?
- Маховик (I = 100.0 кг • м 2 ), вращающийся со скоростью 500,0 об / мин, останавливается трением за 2,0 мин. Каков момент трения на маховике?
- Однородный круглошлифовальный круг массой 50,0 кг и диаметром 1,0 м приводится в движение электродвигателем. Трение в подшипниках незначительное. (а) Какой крутящий момент необходимо приложить к колесу, чтобы вывести его из состояния покоя до 120 об / мин за 20 оборотов? (b) Инструмент с коэффициентом кинетического трения с колесом 0,60 прижимают перпендикулярно колесу с силой 40.0 Н. Какой крутящий момент должен обеспечивать двигатель, чтобы колесо вращалось с постоянной угловой скоростью?
- Предположим, когда Земля была создана, она не вращалась. Однако после приложения равномерного крутящего момента через 6 дней он вращался со скоростью 1 об / день. а) Какое было угловое ускорение в течение 6 дней? б) Какой крутящий момент был приложен к Земле в этот период? (c) Какая сила, касающаяся Земли на ее экваторе, создаст этот крутящий момент?
- Шкив момента инерции 2.0 кг • м 2 устанавливается на стене, как показано на следующем рисунке. Легкие струны оборачиваются вокруг двух окружностей шкива, и к ним прикрепляются грузы. Что такое (а) угловое ускорение шкива и (б) линейное ускорение грузов? Примем следующие данные: r 1 = 50 см, r 2 = 20 см, m 1 = 1,0 кг, m 2 = 2,0 кг.
- Блок массой 3 кг скользит по наклонной плоскости под углом 45 ° с безмассовым тросом, прикрепленным к шкиву массой 1 кг и радиусом 0.5 м в верхней части склона (см. Следующий рисунок). Шкив можно представить как диск. Коэффициент кинетического трения по плоскости 0,4. Какое ускорение блока?
- Тележка, показанная ниже, перемещается по столешнице при падении блока. Какое ускорение тележки? Пренебрегая трением, примите следующие данные: m 1 = 2,0 кг, m 2 = 4,0 кг, I = 0,4 кг • m 2 , r = 20 см.
- Единый стержень массы и длины удерживается вертикально двумя струнами незначительной массы, как показано ниже.(а) Каково линейное ускорение свободного конца палки сразу после перерезания струны? б) середины палки?
- Тонкая палка массой 0,2 кг и длиной L = 0,5 м прикреплена к ободу металлического диска массой M = 2,0 кг и радиусом R = 0,3 м. Палочка может свободно вращаться вокруг горизонтальной оси через другой конец (см. Следующий рисунок). (a) Если комбинацию отпускают, когда клюшка находится в горизонтальном положении, какова скорость центра диска, когда клюшка вертикальна? б) Каково ускорение центра диска в момент отпускания ручки? (c) В момент прохождения палкой вертикали?
10.8 Работа и мощность для вращательного движения
- Ветряная турбина вращается со скоростью 20 об / мин. Если ее выходная мощность составляет 2,0 МВт, какой крутящий момент создается на турбине от ветра?
- Глиняный цилиндр радиусом 20 см на гончарном круге вращается с постоянной скоростью 10 об / с. Гончар прикладывает к глине усилие 10 Н. руками, при этом коэффициент трения между его руками и глиной равен 0,1. Какую мощность гончар должен передать кругу, чтобы он вращался с такой постоянной скоростью?
- Точильный камень цилиндрической формы имеет массу 10 кг и радиус 12 см.(a) Какова кинетическая энергия вращения точильного камня, когда он вращается со скоростью 1,5 x 10 3 об / мин? (b) После выключения двигателя точильного камня лезвие ножа прижимается к внешнему краю точильного камня с перпендикулярной силой 5,0 Н. Коэффициент кинетического трения между точильным камнем и лезвием равен 0,80. Используйте теорему о рабочей энергии, чтобы определить, сколько оборотов сделает точильный камень до остановки.
- Однородный диск массой 500 кг и радиусом 0.25 м установлен на подшипниках качения, поэтому он может свободно вращаться вокруг вертикальной оси через его центр (см. Следующий рисунок). Шнур оборачивается вокруг обода диска и натягивается с усилием в 10 Н. а) Сколько работы совершается силой в момент, когда диск совершил три оборота, начиная с состояния покоя? (b) Определите крутящий момент, создаваемый силой, а затем вычислите работу, совершаемую этим крутящим моментом в момент, когда диск совершил три оборота? (c) Какая угловая скорость в этот момент? (d) Какова мощность силы в этот момент?
- Пропеллер ускоряется из состояния покоя до угловой скорости 1000 об / мин в течение 6 секунд.0 секунд при постоянном крутящем моменте 2,0 x 10 3 Н • м. а) Каков момент инерции гребного винта? (b) Какая мощность подается на винт через 3,0 с после того, как он начинает вращаться?
- Сфера массой 1,0 кг и радиусом 0,5 м прикреплена к концу безмассового стержня длиной 3,0 м. Стержень вращается вокруг оси, которая находится на противоположном конце сферы (см. Ниже). Система вращается горизонтально вокруг оси с постоянной скоростью 400 об / мин. После вращения с этой угловой скоростью в вакууме возникает сопротивление воздуха, обеспечивающее силу 0.15 Н на сфере, противоположной направлению движения. Какую мощность обеспечивает сопротивление воздуха системе через 100,0 с после создания сопротивления воздуха?
- Единый стержень длиной L и массой M удерживается вертикально, одним концом опираясь на пол, как показано ниже. Когда стержень отпускается, он вращается вокруг своего нижнего конца, пока не упадет на пол. Если предположить, что нижний конец стержня не скользит, какова линейная скорость верхнего конца, когда он ударяется об пол?
- Спортсмен в тренажерном зале прилагает постоянную силу 50 Н к педалям велосипеда со скоростью 60 об / мин.Длина педальных рычагов 30 см. Какую мощность передает на велосипед спортсмен?
- Блок массой 2 кг на плоскости без трения, наклоненной под углом 40 °, имеет шнур, прикрепленный к шкиву массой 1 кг и радиусом 20 см (см. Следующий рисунок). (а) Каково ускорение блока по плоскости? б) Какую работу выполняет шнур на шкиве?
- Маленькие тела массой m 1 и m 2 прикреплены к противоположным концам тонкого жесткого стержня длиной L и массой M.Стержень установлен так, чтобы он мог свободно вращаться в горизонтальной плоскости вокруг вертикальной оси (см. Ниже). На каком расстоянии d от m 1 должна находиться ось вращения, чтобы потребовалось минимальное количество работы, чтобы установить стержень, вращающийся с угловой скоростью \ (\ omega \)?
Дополнительные проблемы
- Велосипедист едет так, что колеса велосипеда имеют скорость вращения 3,0 об / с. Если велосипедист тормозит так, что скорость вращения колес уменьшается на 0.3 об / с 2 , сколько времени нужно, чтобы велосипедист полностью остановился?
- Вычислить угловую скорость орбитального движения Земли вокруг Солнца.
- Поворотный столик фонографа, вращающийся со скоростью 33 \ (\ frac {1} {3} \) об / мин, замедляется и останавливается через 1,0 мин. (а) Какое угловое ускорение поворотного стола при условии, что оно постоянное? (б) Сколько оборотов делает поворотный стол при остановке?
- С помощью струны гироскоп из состояния покоя ускоряется до 32 рад / с за 0.40 с при постоянном угловом ускорении. а) Каково его угловое ускорение в рад / с 2 ? б) Сколько революций происходит в процессе?
- Предположим, на компакт-диск упал кусок пыли. Если скорость вращения компакт-диска составляет 500 об / мин, а пылинка находится на расстоянии 4,3 см от центра, каково общее расстояние, пройденное пылью за 3 минуты? (Игнорируйте ускорения из-за вращения компакт-диска.)
- Система точечных частиц вращается вокруг фиксированной оси со скоростью 4 об / с.Частицы зафиксированы друг относительно друга. Массы и расстояния до оси точечных частиц равны m 1 = 0,1 кг, r 1 = 0,2 м, m 2 = 0,05 кг, r 2 = 0,4 м, м 3 = 0,5 кг, r 3 = 0,01 м. а) Каков момент инерции системы? б) Какова кинетическая энергия вращения системы?
- Рассчитайте момент инерции фигуриста с учетом следующей информации. (а) Фигурист с весом 60,0 кг приблизительно представляет собой цилиндр с 0.110-метровый радиус. (b) Фигуриста с вытянутыми руками приблизительно соответствует цилиндру массой 52,5 кг, радиусом 0,110 м и двумя руками длиной 0,900 м, каждая по 3,75 кг, которые выходят прямо из цилиндра, как стержни, вращающиеся вокруг него. их концы.
- Палочка длиной 1,0 м и массой 6,0 кг может свободно вращаться вокруг горизонтальной оси через центр. К двум его концам прикреплены небольшие тела массой 4,0 и 2,0 кг (см. Следующий рисунок). Стик выходит из горизонтального положения.Какова угловая скорость палки, когда она движется по вертикали?
- Маятник состоит из стержня длиной 2 м и массой 3 кг, на одном конце которого прикреплен твердый шар массой 1 кг и радиусом 0,3 м. Ось вращения показана ниже. Какова угловая скорость маятника в самой низкой точке, если он выходит из состояния покоя под углом 30 °?
- Рассчитайте крутящий момент силы 40 Н вокруг оси, проходящей через O и перпендикулярной плоскости страницы, как показано ниже.
- Двое детей толкают противоположные стороны двери во время игры. Оба толкаются горизонтально и перпендикулярно двери. Один ребенок толкает с силой 17,5 Н на расстоянии 0,600 м от петель, а второй ребенок толкает на расстоянии 0,450 м. Какую силу должен приложить второй ребенок, чтобы дверь не двигалась? Предположим, трение незначительно.
- Сила 20 \ (\ hat {j} \) Н прилагается в \ (\ vec {r} \) = (4.0 \ (\ hat {i} \) — 2.0 \ (\ hat {j} \) ) м.Каков момент этой силы относительно начала координат? 119. Автомобильный двигатель может развивать крутящий момент 200 Н • м. Рассчитайте угловое ускорение, возникающее, если 95,0% этого крутящего момента приложено к ведущему валу, оси и задним колесам автомобиля, учитывая следующую информацию. Автомобиль подвешен так, чтобы колеса могли свободно вращаться. Каждое колесо действует как диск массой 15,0 кг с радиусом 0,180 м. Стенки каждой шины действуют как кольцевое кольцо весом 2,00 кг с внутренним радиусом 0,180 м и внешним радиусом 0.320 м. Протектор каждой шины действует как обруч весом 10,0 кг и радиусом 0,330 м. Ось массой 14,0 кг действует как штанга с радиусом 2,00 см. Приводной вал весом 30,0 кг действует как стержень с радиусом 3,20 см.
- Точильный камень массой 50 кг и радиусом 0,8 м поддерживает постоянную скорость вращения 4,0 об / с с помощью двигателя, в то время как нож прижимается к кромке с силой 5,0 Н. Коэффициент кинетического трения между точильным камнем и лезвие 0,8. Какая мощность обеспечивает двигатель для поддержания постоянной скорости вращения точильного камня?
Задачи
- Угловое ускорение вращающегося твердого тела определяется выражением \ (\ alpha \) = (2.0 — 3,0 т) рад / с 2 . Если тело начинает вращаться из состояния покоя при t = 0, а) какова угловая скорость? (б) Угловое положение? (c) На какой угол он поворачивается за 10 с? (d) Где находится вектор, перпендикулярный оси вращения, указывающий на 0 ° при t = 0 при t = 10 с?
- За последний век земной день увеличился на 0,002 с. Если это увеличение периода Земли постоянно, сколько времени потребуется Земле, чтобы прийти в состояние покоя?
- Диск с массой m, радиусом R и площадью A имеет поверхностную плотность \ (\ sigma = \ frac {mr} {AR} \) (см. Следующий рисунок).Каков момент инерции диска относительно оси, проходящей через центр?
- Зорч, заклятый враг Человека Вращения, решает замедлить вращение Земли до одного раза в 28,0 ч, приложив противодействующую силу на экваторе и параллельно ему. Вращение Человека не беспокоит сразу, потому что он знает, что Зорч может проявлять силу только 4,00 x 10 7 Н (немного больше, чем тяга ракеты Сатурн V). Как долго Зорч должен использовать эту силу, чтобы достичь своей цели? (Этот период дает Ротационному человеку время, чтобы посвятить его другим злодеям.)
- Шнур оборачивается вокруг обода сплошного цилиндра радиусом 0,25 м, и на показанный шнур действует постоянная сила в 40 Н, как показано на следующем рисунке. Цилиндр установлен на подшипниках качения, его момент инерции составляет 6,0 кг • м 2 . (a) Используйте теорему об энергии работы, чтобы рассчитать угловую скорость цилиндра после удаления 5,0 м шнура. (b) Если сила 40 Н заменяется грузом 40 Н, какова угловая скорость цилиндра после 5?0 м шнура размотались?
Авторы и авторство
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими участвующими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Физический маятник — угловой SHM
Физический маятник — это твердое тело, повернутое в точке O.При небольшом смещении он совершает угловое простое гармоническое движение в вертикальной плоскости с периодом времени \ begin {align} T = 2 \ pi \ sqrt {\ frac {I} {mgl}} \ nonumber \ end {align} где $ I $ — момент инерции относительно оси вращения, проходящей через точку подвеса O, а $ l $ — расстояние центра масс C от точки O.
Временной период физического маятника равен $ T = 2 \ pi \ sqrt {I / mgl} $.Восстанавливающий момент на физическом маятнике относительно точки O равен $ \ tau = mg l \ sin \ theta $.2} = — \ frac {mgl \ sin \ theta} {I} \ приблизительно- \ frac {mgl} {I} \ theta \ nonumber \ end {align} Это дифференциальное уравнение для угловой SHM. Ее решение с начальным условием $ \ theta = \ theta_0 $ и $ \ dot \ theta = 0 $ (маятник выпущен из начального угла $ \ theta_0 $) есть \ begin {align} \ тета = \ тета_0 \ соз (\ омега т) \ end {align} Физический маятник можно использовать для измерения ускорения свободного падения $ g $ (аналогично простому маятнику). Физический маятник также используется для измерения момента инерции тела.
Решенные задачи на физическом маятнике
Проблема из IIT JEE 2011
Металлический стержень длиной $ L $ и массой $ m $ поворачивается одним концом.Тонкий диск массы $ M $ и радиуса $ R (случай A) Диск не может вращаться вокруг своего центра, и ( Case B ) диск может свободно вращаться вокруг своего центра. Система стержень-диск выполняет СТМ в вертикальной плоскости после выхода из того же смещенного положения. Какое из следующих утверждений истинно?
- восстанавливающий крутящий момент в случае A = восстанавливающий крутящий момент в случае B.
- восстанавливающий крутящий момент при A $
- Угловая частота для случая A $> $ Угловая частота для случая B.
- Угловая частота корпуса A $
Решение: Рассмотрим движение центра масс C, находящегося на расстоянии $ r_C = \ frac {M + m / 2} {M + m} \, L $ от точки поворота O.
Вес системы диск-стержень, $ (M + m) g $, действует на C, создавая против часовой стрелки восстанавливающий крутящий момент вокруг O, \ begin {align} \ tau & = (M + m) gr_C \ sin \ theta \ nonumber \\ & = \ влево (M + m / 2 \ вправо) gL \ sin \ theta, \ nonumber \ end {align} где $ \ theta $ — угловое смещение. Поскольку силы остаются неизменными, восстанавливающие моменты равны в обоих случаях: , корпус A, и , корпус B, .2 \ вправо). \ end {align} Теперь рассмотрим только движение диска. Когда диск был выпущен, он находился в состоянии покоя с его угловой скоростью $ \ omega = 0 $ и моментом количества движения относительно его центра масс $ L = I_ \ text {cm} \ omega = 0 $. На диск нет внешнего крутящего момента относительно его центра масс, потому что диск может свободно вращаться и его вес проходит через центр масс. Таким образом, угловой момент диска относительно его центра масс сохраняется, т. Е. Угловой момент и угловая скорость диска всегда остаются равными нулю.Подставьте $ \ omega = 0 $ в уравнение выше, чтобы получить $ \ omega_B> \ omega_A $.Проблема найти точку приостановки, которая минимизирует период времени
Тонкий диск радиуса $ r $ и массы $ m $ подвешен как маятник в вертикальной плоскости из точки O, расположенной на расстоянии $ x $ над его центром. Он испытывает небольшие угловые колебания. При каком значении $ x $ амплитуда углового ускорения диска минимальна?
- $ r / \ sqrt {2} $
- $ r / \ sqrt {3} $
- руб.
- $ \ sqrt {3} r / 2 $
Решение: Рассмотрим момент времени, когда угловое смещение диска составляет $ \ theta $ (см. Рисунок).2} = 0, \ nonumber \ end {align} что дает $ x = r / \ sqrt {2} $. Предлагаем вам показать, что диск проходит SHM. Частота колебаний максимальна при $ x = r / \ sqrt {2} $.
Задача о центре удара и маятнике Катера
Твердое тело может вращаться вокруг фиксированной точки O, как показано на рисунке. Момент инерции тела относительно точки O равен $ I_0 $, а расстояние между O и центром масс C тела составляет $ d $. Сила $ F $ приложена к телу перпендикулярно линии, соединяющей O и центр масс, на расстоянии $ x $ от O.Найдите расстояние $ x $, на котором не будет реакции в точке O в направлении F. Пренебрегайте гравитацией.
- $ d $
- $ 2I_O / (мкр) $
- $ d / 2 $
- $ I_O / (мкр) $
Решение: Пусть сила реакции в точке поворота O равна нулю. Крутящий момент относительно неподвижной точки O равен $ \ tau_O = xF $ (против часовой стрелки). Используйте $ \ tau_O = I_O \ alpha $, чтобы получить угловое ускорение тела. \ begin {align} \ label {ahd: eqn: 1} \ альфа = xF / I_O.2 $, чтобы получить момент инерции тела относительно оси, проходящей через центр масс C. Удалите $ \ alpha $ из приведенных выше уравнений, чтобы получить $ x = I_O / (md) $.
Точка P называется центром удара тела. Если линия действия силы $ F $ перпендикулярна OC и проходит через P, то сила реакции в точке O равна нулю. Давайте посмотрим на некоторые реальные жизненные ситуации, в которых центр ударных играет важную роль.
В игре в крикет, если вы держите биту в точке O, а мяч попадает в центр удара P, вы чувствуете себя комфортно, потому что сила реакции в ваших руках равна нулю.Если мяч попадает в какую-то другую точку, чем вы чувствуете джхан-джхана-хат (жалящую боль) в ваших руках.
Другая ситуация — обратимый маятник Катера. Тело колеблется под действием силы тяжести, если его подвешивать за точку. Частота колебаний одинакова независимо от того, подвешиваете ли вы тело к точке O или к точке P.
Больше проблем с физическим маятником
Кольцо на вешалке
Физический маятник состоит из кольца радиуса $ R $ и массы $ m $.Кольцо поворачивается по периметру. Кольцо вытягивается так, что его центр масс составляет небольшой угол $ \ theta_0 $ от вертикали, и освобождается от покоя.
- Какая угловая частота колебаний?
- Какова угловая скорость кольца в нижней части его качания?
Подвесная измерительная ручка
Физический маятник состоит из измерителя, который поворачивается в небольшом отверстии, просверленном в стержне на расстоянии $ d $ от отметки 50 см.Период колебаний 2,5 с. Найдите $ d $.
Диск, прикрепленный к световому стержню
Физический маятник состоит из диска массой $ m = 1 $ кг и радиуса $ R = 5 $ см, закрепленного на конце безмассового стержня. Другой конец стержня поворачивается вокруг точки P на потолке. Расстояние от точки поворота до центра масс боба составляет $ l = 4 $ м. Первоначально боб выходит из состояния покоя под небольшим углом $ \ theta_0 $ по отношению к вертикали. Найдите период боба?
Вопросы о физическом маятнике
Вопрос 1: В эксперименте по измерению ускорения свободного падения в качестве физического маятника использовалась метровая палка массой $ m $ и длиной $ L $.В измерителе просверливается несколько небольших отверстий, чтобы подвешивать его в разных точках. Студент измерил период времени $ T $ для разных $ l $ (подвешивая измерительную ручку к разным отверстиям). Какое из следующих утверждений верно
Вопрос 2: Три физических маятника A, B и C масс $ m_0 $, $ 2m_0 $ и $ 3 m_0 $ соответственно имеют одинаковую форму и одинаковые размеры.

 Кривошип ОА равномерно вращается в обратном
Кривошип ОА равномерно вращается в обратном = Δq / Δ т
= Δq / Δ т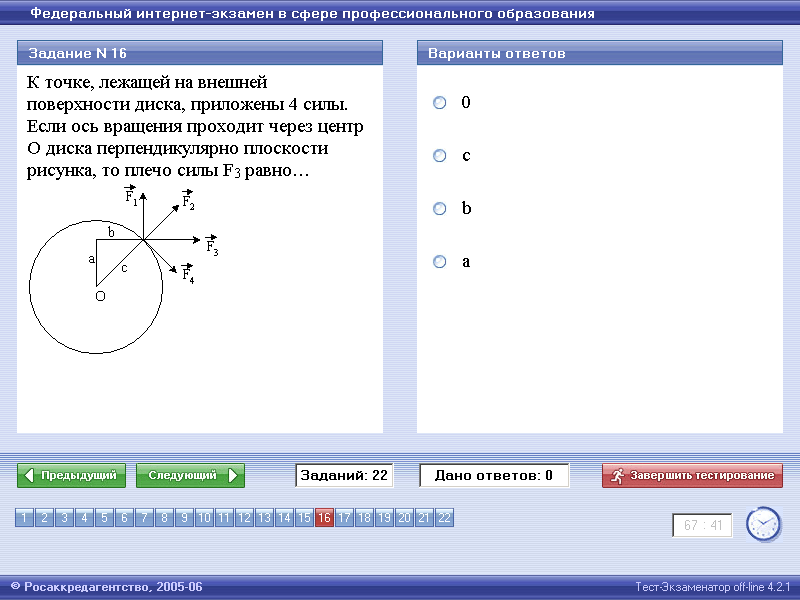 57 x 10 3 Дж
57 x 10 3 Дж 6 # 31
6 # 31 75
* 30 2 ) а
75
* 30 2 ) а
 61)] = 0,943
61)] = 0,943 Значит вектора А не существует! Как это
быть? Что это значит?
Значит вектора А не существует! Как это
быть? Что это значит?
 5 кг · м 2 / с
5 кг · м 2 / с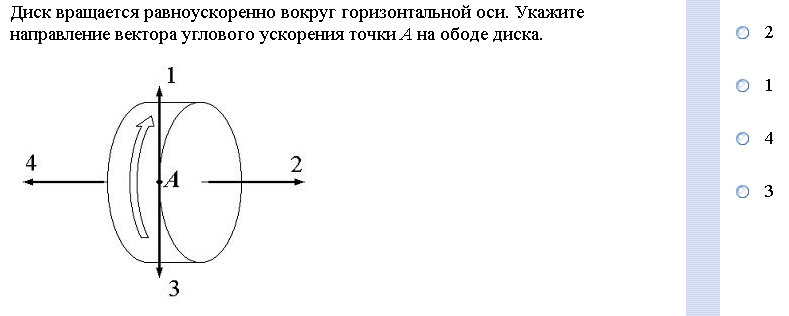 06 + 0,03) кг м 2
06 + 0,03) кг м 2  200 м) (50 рад / с) =
10 м / с
200 м) (50 рад / с) =
10 м / с с Cx, - Cy и Cz, каждый из которых умножается на кофактор оставшихся членов
в определителе при удалении строки и столбца Cx, Cy и Cz.Обратите внимание на отрицательный знак - Cy; это важно.
с Cx, - Cy и Cz, каждый из которых умножается на кофактор оставшихся членов
в определителе при удалении строки и столбца Cx, Cy и Cz.Обратите внимание на отрицательный знак - Cy; это важно.  Может ли полное ускорение троса / массы быть нулевым, если угловая скорость постоянна?
Может ли полное ускорение троса / массы быть нулевым, если угловая скорость постоянна?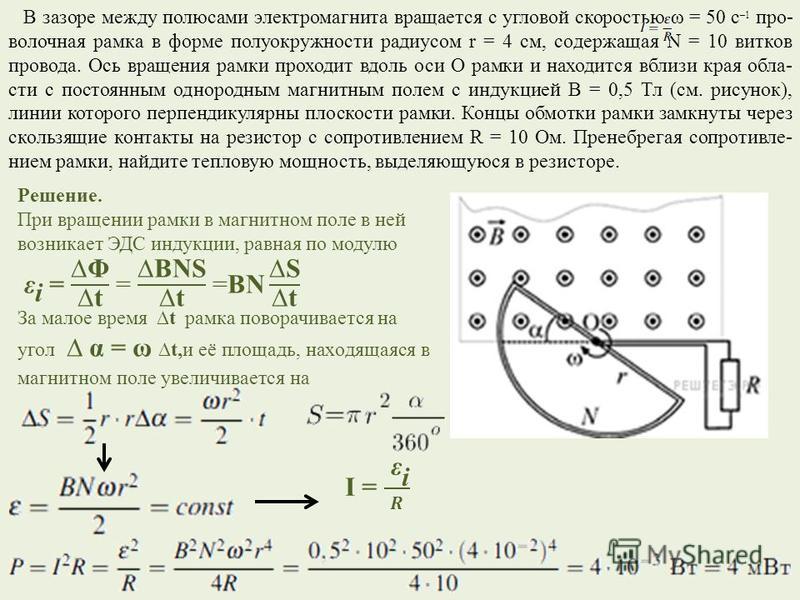 {2}} {3} \).{2}} {4} \))
{2}} {3} \).{2}} {4} \)) 0 с при постоянной скорости, какова его угловая скорость? (c) Каково его ускорение?
0 с при постоянной скорости, какова его угловая скорость? (c) Каково его ускорение? 0 с? б) Что такое угловое ускорение?
0 с? б) Что такое угловое ускорение? (а) Какая угловая скорость в начале 6.0 с? б) Какое угловое ускорение маховика?
(а) Какая угловая скорость в начале 6.0 с? б) Какое угловое ускорение маховика? (а) Определите угловую скорость диска при t = 5,0 с. б) На какой угол он повернулся за это время? (c) Каково тангенциальное ускорение точки на диске при t = 5,0 с?
(а) Определите угловую скорость диска при t = 5,0 с. б) На какой угол он повернулся за это время? (c) Каково тангенциальное ускорение точки на диске при t = 5,0 с?
Leave A Comment