Решутест. Продвинутый тренажёр тестов
Решутест. Продвинутый тренажёр тестов- Главная
- ЕГЭ
- Математика профильная
- Стереометрия
- Конус
Решил заданий
Не решил заданий
Осталось заданий
История решения
1293 — не приступал 9019 — не приступал 8568 — не приступал 1316 — не приступал 1275 — не приступал 5996 — не приступал 8804 — не приступалФормат ответа: цифра или несколько цифр, слово или несколько слов. Вопросы на соответствие «буква» — «цифра» должны записываться как несколько цифр. Между словами и цифрами не должно быть пробелов или других знаков.
Вопросы на соответствие «буква» — «цифра» должны записываться как несколько цифр. Между словами и цифрами не должно быть пробелов или других знаков.
Примеры ответов: 7 или здесьисейчас или 3514
Раскрыть Скрыть
№1Высота конуса равна 4, а диаметр основания — 6. Найдите образующую конуса.
Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания конуса.
№3Диаметр основания конуса равен 6, а длина образующей — 5. Найдите высоту конуса.
№4Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 30°. В ответе укажите $\frac{V}{\pi }$.
№5Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на π.
№6Объем конуса равен 16.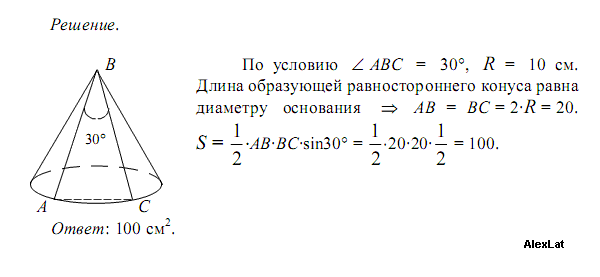
Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Так твой прогресс будет сохраняться.
РегистрацияМы отправили код на:
ИзменитьПолучить код повторно через 00:00
Я прочитал(-а) Политику конфиденциальности и согласен(-на) с правилами использования моих персональных данных
Ништяк!
Решено верно
Браво!
Решено верно
Крутяк!
Решено верно
Зачёт!
Решено верно
Чётко!
Решено верно
Бомбезно!
Решено верно
Огонь!
Решено верно
Юхууу!
Решено верно
Отпад!
Решено верно
Шикарно!
Решено верно
Блестяще!
Решено верно
Волшебно!
Решено верно
Практикум по решению стереометрических задач.
 Конус.Подготовка к ЕГЭ
Конус.Подготовка к ЕГЭПрактикум по решению
стереометрических задач
Конус
в заданиях ЕГЭ
Задача №1
Задача №2
Задача №3
Задача №4
Задача №5
Задача №6
Задача №7
Задача № 8
Задача № 9
Задача № 10
Задача № 11
Задача № 12
Задача № 13
Задача № 14
Задача № 22
Задача № 23
Задача № 24
Задача № 25
Задача № 26
Задача № 27
Задача № 28
Задача № 29
Задача № 30
Задача № 31
Задача № 15
Задача № 16
Задача № 17
Задача № 18
Задача № 19
Задача № 20
Задача № 21
- Задачи для самостоятельного решения
Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 3 и 9, а второго — 6 и 9. Во сколько раз площадь боковой поверхности второго конуса больше площади боковой поверхности первого?
Радиус основания и образующая первого конуса равны соответственно 3 и 9, а второго — 6 и 9. Во сколько раз площадь боковой поверхности второго конуса больше площади боковой поверхности первого?
Решение.
Т.к. площадь боковой поверхности конуса: S= π rl ,
значит S 1 = π ·3·9= 27 π , S 2 = π ·6·9= 54 π , тогда S 2 : S 1 = 54 π : 27 π = 2
Объём конуса равен 135. Через точку, делящую высоту конуса в отношении 1:2, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью.
решениеР
Решение: Отношение объемов конусов равно кубу их коэффициента подобия. Высоты конусов относятся как 1:3,поэтому их объемы относятся как 1:27. Следовательно, объем отсекаемого конуса равен 135 : 33 = 5.
Объём конуса равен 32. Через середину высоты конуса проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью .
Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью .
Решение.
Отношение объемов конусов равно кубу их коэффициента подобия k .
Так как высоты конусов относятся как 1:2, то k равно одной второй, а значит объем отсекаемого конуса будет равен
32 : 2 ³ = 4.
Объём конуса равен 50 π
Решение.
Найдём радиус основания конуса по формуле: V=1/3· π R²h .
Откуда R²=3V: π h = R²= 150 π : 6 π = 25 ,тогда R = 5
Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 3 раза?
Решение.
Объем конуса вычисляется по формуле V=1/3·Soc.·h .
Значит, если высоту увеличить в 3 раза, то и объём увеличится в 3 раза
Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 1,5 раза?
Решение.
Объем конуса вычисляется по формуле
V=1/3·Soc.·h = 1/3 · π R²·h .
Значит, если радиус основания увеличить в 1,5 раза, то и объём конуса увеличится в 2,25 раза
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза?
Решение.
Площадь боковой поверхности конуса вычисляется по формуле
S= π R·L, где L -образующая .
Значит если увеличить L в 3 раза , то площадь боковой поверхности конуса тоже увеличится
в 3 раза .
Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшится в 1,5 раза, а образующая останется прежней?
Решение.
Площадь боковой поверхности конуса вычисляется по формуле
S= π R·L . Значит, если радиус основания уменьшится в 1,5 раза, то площадь боковой поверхности конуса тоже уменьшится в 1,5 раза.
Высота конуса равна 4, а диаметр основания — 6. Найдите образующую конуса.
По теореме Пифагора
Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания конуса.
Решение.
По теореме Пифагора… .
Ответ: 6.
Диаметр основания конуса равен 6, а длина образующей — 5. Найдите высоту конуса.
По теореме Пифагора….
Ответ: 4.
В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём жидкости равен 70 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
Решение .
Меньший конус подобен большему с коэффициентом 0,5. Объемы подобных тел относятся как куб коэффициента подобия. Поэтому объем большего конуса в 8 раз больше объема меньшего конуса, он равен 560 мл. Следовательно, необходимо долить 560 − 70 = 490 мл жидкости.
В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём сосуда 1600 мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах .
Пусть х — высота налитой жидкости, у — радиус окружности в основании конуса. Тогда 2 х — высота сосуда, 2 у — радиус окружности в основании сосуда (так как поверхность жидкости отсекает от конического сосуда конус подобный данному).
Найдем отношения объёмов конусов
Таким образом, объём сосуда в 8 раз больше объёма налитой жидкости: 1600 : 8 = 200
Объём конуса равен 96π, а его высота равна 8. Найдите радиус основания конуса.
Решение .Найдём радиус основания конуса из формулы: V=1/3· π R²h
Откуда R²=3V: π h =
Даны два конуса. Радиус основания и образующая первого конуса равны, соответственно, 2 и 4, а второго — 6 и 8. Во сколько раз площадь боковой поверхности второго конуса больше площади боковой поверхности первого?
Во сколько раз площадь боковой поверхности второго конуса больше площади боковой поверхности первого?
1)Найдём площадь боковой поверхности первого конуса: S 1 = π ·R 1 ·L1 = π ·2·4=8 π
2) Найдём площадь боковой поверхности второго конуса: S 2 = π ·R 2 ·L 2 = π · 6 · 8 = 4 8 π
3) Найдём отношение площадей этих конусов:
S 2 : S 1 = 48 π : 8 π = 6
Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна 3√2. Найдите площадь боковой поверхности конуса.
1) Заметим, что конус и цилиндр имеют общую высоту и равные радиусы основания. Площадь боковой поверхности цилиндра равна S б. п. = 2 π R·h, но R=h следовательно S б.п. = 2 π R² и =3√2 = π R² =1,5√2
п. = 2 π R·h, но R=h следовательно S б.п. = 2 π R² и =3√2 = π R² =1,5√2
2) Площадь боковой поверхности конуса равна S= π R·L, Но L² = R²+h², но R=h = L² = 2 R² = L = R√2.
Значит S б.п. = π R·L = π R· R√2 = π R²·√ 2 =
= 1,5√2 ·√ 2 = 3
Диаметр основания конуса равен 12, а длина образующей — 10. Найдите площадь осевого сечения этого конуса.
Решение .
Осевым сечением конуса является равнобедренный треугольник, основание которого —это диаметр основания конуса, а высота совпадает с высотой конуса.
Но L² = R²+h² = h = √100-36=√64=8
Следовательно, площадь осевого сечения
равна 0,5 · 12 · 8 = 48 .
 «
«
Высота конуса равна 8, а длина образующей — 10. Найдите площадь осевого сечения этого конуса.
Решение .
Осевым сечением конуса является равнобедренный треугольник, основание которого — диаметр основания конуса, а высота совпадает с высотой конуса.
Но L² = R²+h² = R=√100-64=√36=6
Следовательно, диаметр осевого сечения конуса равен 12, а площадь осевого сечения равна 0,5 · 12 · 8 = 48.
Площадь основания конуса равна 18. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 3 и 6, считая от вершины. Найдите площадь сечения конуса этой плоскостью
Сечение плоскостью, параллельной основанию, представляет собой круг, радиус которого относится к радиусу основания конуса как 3 : 9. Площади подобных фигур относятся как квадрат коэффициента подобия, поэтому площадь сечения в 9 раз меньше площади основания. Тем самым, она равна 2.
Тем самым, она равна 2.
Площадь основания конуса равна 16π, высота — 6. Найдите площадь осевого сечения конуса.
Решение . Осевым сечением конуса является равнобедренный треугольник, высота которого совпадает с высотой конуса, а основание является диаметром основания конуса. Поэтому площадь осевого сечения равна половине произведения высоты конуса на диаметр его основания или произведению высоты конуса на радиус основания R . Поскольку по условию π R²=16 π , то радиус основания конуса равен 4, а тогда искомая площадь осевого сечения равна 24 .
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Радиус сферы равен 10√2. Найдите образующую конуса.
Решение .
Высота конуса перпендикулярна основанию и равна радиусу сферы. Тогда по теореме Пифагора получаем:
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса .
Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса .
Решение.
Формулу для объёма шара:
V=4/3 · π R³ ,
а формула объёма конуса:
V=1/3 · π R³.
Значит объём конуса в 4 раза меньше объёма шара.
Тогда объём конуса равен 28 : 4 = 7
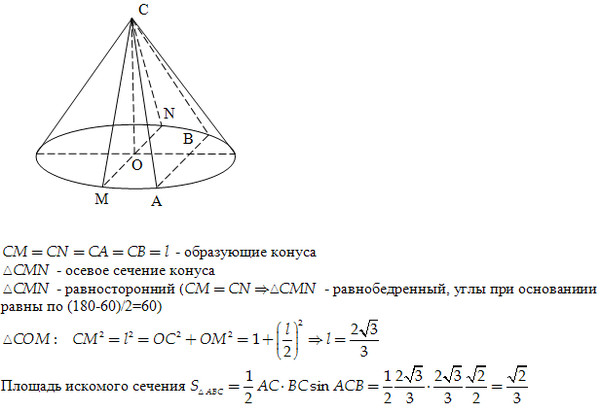
Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
Значит, в прямоугольном треугольнике, образованном высотой, образующей и радиусом основания конуса, катет, равный радиусу, вдвое меньше гипотенузы. Тогда он лежит напротив угла 30°. Следовательно, угол между образующей конуса и плоскостью основания равен 60°.
Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на π .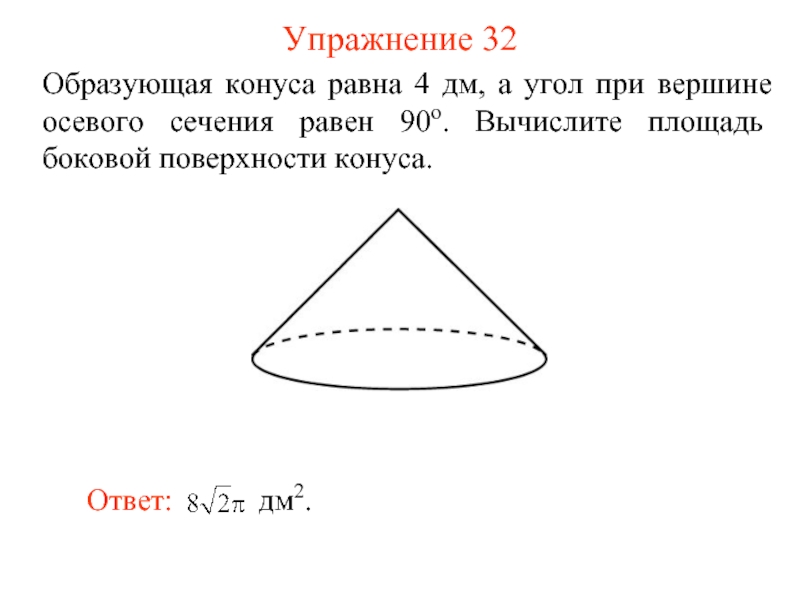
Решение.
Найдем образующую по теореме Пифагора:
L=√h²+R²=√16+9=√25=5
Площадь полной поверхности конуса
Длина окружности основания конуса равна 3, образующая равна 2. Найдите площадь боковой поверхности конуса.
Решение .
Площадь боковой поверхности конуса равна
Конус получается при вращении равнобедренного прямоугольного треугольника АВС вокруг катета, равного 6. Найдите его объем, деленный на π .
Решение .
Треугольник АВС – так же равнобедренный, т.к. углы при основании АВ равны 45 ° . Тогда радиус основания равен 6, и объем конуса, деленный на π :
Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на π.
Решение.
В треугольнике, образованном радиусом основания r , высотой h и образующей конуса l , углы при образующей равны, поэтому высота конуса равна радиусу его основания: h = r . Тогда объем конуса, деленный на вычисляется следующим образом:
Тогда объем конуса, деленный на вычисляется следующим образом:
Найдите объем конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 30 ° . В ответе укажите V/ π .
30 °
Высоту конуса найдем по свойству стороны прямоугольного треугольника, находящейся напротив угла в 30 °- она вдвое меньше гипотенузы, которой в данном случае является образующая конуса.
Радиус по теореме Пифагора: R=√2²-1=√3
Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на π .
Решение.
Радиус основания конуса r равен половине
диагонали квадрата ABCD :
r=√2/2·AB=2√2
Тогда объем конуса, деленный на π :
Найдите объем V части конуса, изображенной на рисунке. В ответе укажите V/ π .
В ответе укажите V/ π .
Решение .
Объем данной части конуса равен
Найдите объем V части конуса, изображенной на рисунке. В ответе укажите V/ π .
Решение.
Объем данной части конуса равен
Найдите объем V части конуса, изображенной на рисунке. В ответе укажите V/ π .
Решение.
Объем данной части конуса равен
Найдите объем V части конуса, изображенной на рисунке. В ответе укажите V/ π .
Решение .
Объем данной части конуса равен
Задачи
для самостоятельного решения
1) Объём конуса равен 27. Через точку, делящую высоту конуса в отношении 1:2, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью.
Через точку, делящую высоту конуса в отношении 1:2, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью.
Ответ:1
2) Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса. Ответ:2
3) Объем конуса равен 128. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса .
1) Объём конуса равен 9 π , а его высота равна 3 . Найдите радиус основания конуса.
Ответ:3
2) Объём конуса равен 25 π , а его высота равна 3 . Найдите радиус основания конуса.
Ответ:5
1) Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 18,5 раза?
2) Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 24 раза?
3) Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 10 раз?
1) Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 40 раз?
2) Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 22 раза?
3) Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 31 раз?
1) Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 36 раз?
2) Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 11 раз?
3) Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 1,5 раза?
1) Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшится в 8 раз, а образующая останется прежней?
2) Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшится в 36 раз, а образующая останется прежней?
3) Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшится в 21 раз, а образующая останется прежней?
1) Высота конуса равна 8, а диаметр основания — 30. Найдите образующую конуса.
Найдите образующую конуса.
Ответ: 17
2) Высота конуса равна 5, а диаметр основания — 24. Найдите образующую конуса.
Ответ: 13
3) Высота конуса равна 6, а диаметр основания — 16. Найдите образующую конуса.
Ответ: 10
1) Высота конуса равна 72, а длина образующей — 90. Найдите диаметр основания конуса.
Ответ:108
2) Высота конуса равна 21, а длина образующей — 75. Найдите диаметр основания конуса.
3) Высота конуса равна 57, а длина образующей — 95. Найдите диаметр основания конуса.
1) Диаметр основания конуса равен 108, а длина образующей — 90. Найдите высоту конуса.
Ответ: 72
2) Диаметр основания конуса равен 42, а длина образующей — 75. Найдите высоту конуса.
Ответ: 72
3) Диаметр основания конуса равен 24, а длина образующей — 13. Найдите высоту конуса.
Ответ: 5
1) В сосуде, имеющем форму конуса, уровень жидкости достигает 1/3 высоты. Объём жидкости равен 14 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
Объём жидкости равен 14 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
Ответ: 364
- В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём жидкости равен 40 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
- Ответ: 280
3) В сосуде, имеющем форму конуса, уровень жидкости достигает 1/4 высоты. Объём жидкости равен 6 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд? Ответ:
Площадь основания конуса равна 36π, высота —10. Найдите площадь осевого сечения конуса. Ответ:60
1) Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 116. Найдите объем конуса.
2) Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 160. Найдите объем конуса.
3) Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 132.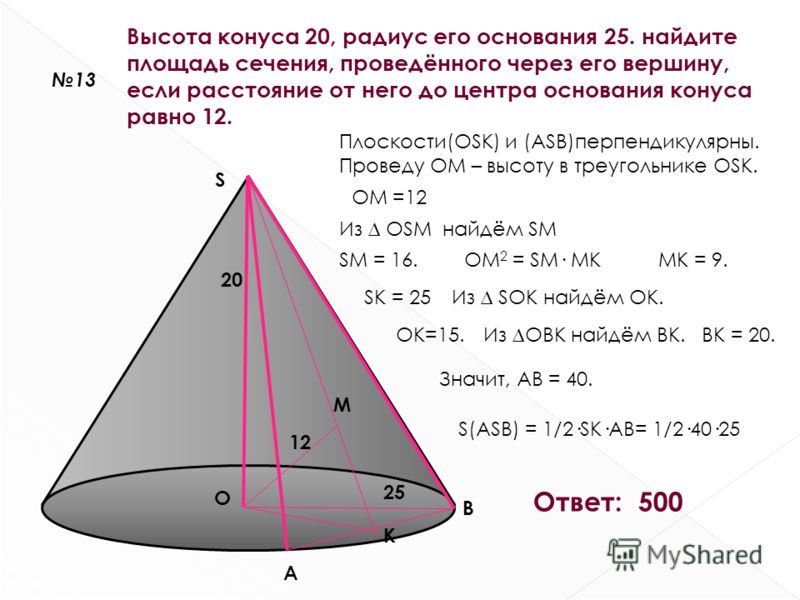 Найдите объем конуса.
Найдите объем конуса.
1) Радиус основания конуса равен 12 , высота равна 16 . Найдите площадь полной поверхности конуса, деленную на π .
2) Радиус основания конуса равен 28 , высота равна 21 . Найдите площадь полной поверхности конуса, деленную на π .
3) Радиус основания конуса равен 15 , высота равна 36 . Найдите площадь полной поверхности конуса, деленную на π .
1) Длина окружности основания конуса равна 6, образующая равна 2. Найдите площадь боковой поверхности конуса. Ответ: 6
2) Длина окружности основания конуса равна 5, образующая равна 8. Найдите площадь боковой поверхности конуса.
3) Длина окружности основания конуса равна 8, образующая равна 6. Найдите площадь боковой поверхности конуса .
1) Конус получается при вращении равнобедренного прямоугольного треугольника АВС вокруг катета, равного 15. Найдите его объем, деленный на π .
2) Конус получается при вращении равнобедренного прямоугольного треугольника АВС вокруг катета, равного 120. Найдите его объем, деленный на π .
Найдите его объем, деленный на π .
3) Конус получается при вращении равнобедренного прямоугольного треугольника АВС вокруг катета, равного 60. Найдите его объем, деленный на π .
1) Диаметр основания конуса равен 66, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на π.
2) Диаметр основания конуса равен 12, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на π.
3) Диаметр основания конуса равен 36, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на π.
1) Найдите объем конуса, образующая которого равна 44 и наклонена к плоскости основания под углом 30 ° . В ответе укажите V/ π .
Ответ: 10 648
2) Найдите объем конуса, образующая которого равна 51 и наклонена к плоскости основания под углом 30 ° .
В ответе укажите V/ π .
3) Найдите объем конуса, образующая которого равна 34 и наклонена к плоскости основания под углом 30 ° . В ответе укажите V/ π .
В ответе укажите V/ π .
1) Конус описан около правильной четырехугольной пирамиды со стороной основания 3 и высотой 13. Найдите его объем, деленный на π .
Ответ:19,5
2) Конус описан около правильной четырехугольной пирамиды со стороной основания 8 и высотой 12 . Найдите его объем, деленный на π .
3) Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 9 . Найдите его объем, деленный на π .
1) Найдите объем V части конуса, изображенной на рисунке. В ответе укажите V/ π .
Найдите объем V части конуса, изображенной на рисунке. В ответе укажите V/ π .
Найдите объем V части конуса, изображенной на рисунке. В ответе укажите V/ π .
Найдите объем V части конуса, изображенной на рисунке. В ответе укажите V/ π .
Математическая задача: Угол конуса
Диаметр основания конуса 1,5 м. Угол при центральной вершине осевого сечения равен 86°. Вычислите объем конуса.Правильный ответ:
V = 0,5 M 3Пошаговые пошаговые объяснения:
D = 1,5 м r = D/2 = 1,5/2 = 43 = 0,75 м S1 = πt r2 =3,1416⋅ 0,752≐1,7671 м2 A=86 ∘ tan A/2 = r/h h=r/tan(A/2)=0,75/tan(86/2)≐0,8043 м V=31 ⋅ S1 ⋅ h =31⋅ 1,7671⋅ 0,8043=0,5 м3
Нашли ошибку или неточность? Не стесняйтесь напишите нам . Спасибо!
Советы по использованию соответствующих онлайн-калькуляторов
Совет: конвертер единиц объема поможет вам преобразовать единицы объема.
См. также наш калькулятор прямоугольного треугольника.
См. также наш калькулятор тригонометрического треугольника.
Для решения этой словесной задачи по математике необходимо знать следующие знания:
- алгебра
- выражение переменной из формулы
- объемная геометрия
- конус
- планиметрия
- прямоугольный треугольник
- треугольник
- гониометрия и тригонометрия
- тангенс
Единицы физических величин:
- объем
- угол
Класс задачи:
- Практика для 14-летних
- Средняя школа
Мы рекомендуем вам посмотреть это обучающее видео по этой математической задаче: видео1
- Башня
Сколько м² медной пластины необходимо заменить на крышу башни конической формы диаметром 24 м, а угол при вершине осевого сечения равен 144°? - Сторона конуса
Рассчитайте объем и площадь конуса, высота которого равна 10 см, а осевое сечение конуса имеет угол 30 градусов между высотой и стороной конуса.
- Сфера
Точка пересечения плоскости и сферы представляет собой окружность радиусом 60 мм. Конус, основанием которого является этот круг, а вершиной — центр сферы, имеет высоту 34 мм. Вычислите площадь поверхности и объем шара. - Конус
Рассчитайте объем и площадь поверхности конуса с диаметром основания d=15 см и стороной конуса с основанием под углом 52°. - Сферический сегмент
Асферическое сечение, осевое сечение которого имеет угол j = 120° в центре сферы, является частью сферы радиусом r = 10 см. Рассчитать поверхность разреза. - Осевое сечение
Рассчитайте объем и поверхность конуса, осевое сечение которого представляет собой равносторонний треугольник со стороной a = 18 см. - Вычислить 71764
Угол при основании равнобедренного треугольника на 18° больше, чем угол при центральной вершине. Вычислите величину внутренних углов. - Рассчитать 70634
Осевое сечение цилиндра представляет собой прямоугольник с диагональю u = 20 см. Высота цилиндра в два раза больше диаметра основания. Вычислите объем баллона в литрах.
Высота цилиндра в два раза больше диаметра основания. Вычислите объем баллона в литрах. - Максимум объема
Оболочка конуса образована навивкой круглого сечения радиусом 1. При каком центральном угле данного кругового сечения объем получившегося конуса будет максимальным? - Осевое сечение конуса
Осевое сечение конуса представляет собой равнобедренный треугольник, в котором отношение диаметра конуса к стороне конуса составляет 2:3. Вычислите его объем, если знаете, что его площадь равна 314 см². - Осевой разрез
Осевой разрез конуса представляет собой равносторонний треугольник площадью 208 м². Вычислите объем конуса. - Осевой разрез
Осевой разрез цилиндра имеет диагональ 40 см. Размер раковины и поверхность основания находятся в соотношении 3:2. Вычислите объем и площадь поверхности этого цилиндра. - Равнобедренный 81130
Угол при вершине равнобедренного треугольника равен 78°. Основание 28,5см. Длина плеча? - Угол при вершине
В равнобедренном треугольнике угол при вершине на 30° больше, чем угол при основании. Насколько велики внутренние углы?
Насколько велики внутренние углы? - Центральный угол
Круг имеет диаметр 46 см. Какая длина дуги соответствует центральному углу 30°? - Вращающийся конус
Вращающийся конус имеет диаметр основания 18 дм и высоту 12 дм. Рассчитайте объем V. - Конус A2V
Поверхность конуса в плоскости представляет собой дугу окружности с центральным углом 126° и площадью 415 см². Вычислите объем конуса.
Перпендикулярность | Основы GD&T
Специальное примечание: Перпендикулярность в геометрических размерах и допусках может означать две совершенно разные вещи в зависимости от того, какой опорный элемент вызывается. Нормальная форма или Перпендикулярность поверхности — это допуск, который контролирует перпендикулярность между двумя 90° поверхностей, или элементов. Перпендикулярность поверхности контролируется двумя параллельными плоскостями, выступающими в качестве зоны допуска. Перпендикулярность оси — это допуск, определяющий, насколько перпендикулярной должна быть определенная ось к базе. Перпендикулярность оси контролируется цилиндром вокруг теоретически идеально параллельной оси. Обратите особое внимание, если в качестве ссылки используется отверстие или штифт, поскольку на этих элементах обычно указывается перпендикулярность оси.
Перпендикулярность оси — это допуск, определяющий, насколько перпендикулярной должна быть определенная ось к базе. Перпендикулярность оси контролируется цилиндром вокруг теоретически идеально параллельной оси. Обратите особое внимание, если в качестве ссылки используется отверстие или штифт, поскольку на этих элементах обычно указывается перпендикулярность оси.
Относительно нулевой точки : Да Применимо MMC или LMC: Да GD &T Выноска на чертеже: Перпендикулярность поверхности: Перпендикулярность оси: Описание: Поверхность:
Перпендикулярность — довольно распространенный символ, который требует, чтобы указанная поверхность или линия были перпендикулярны или .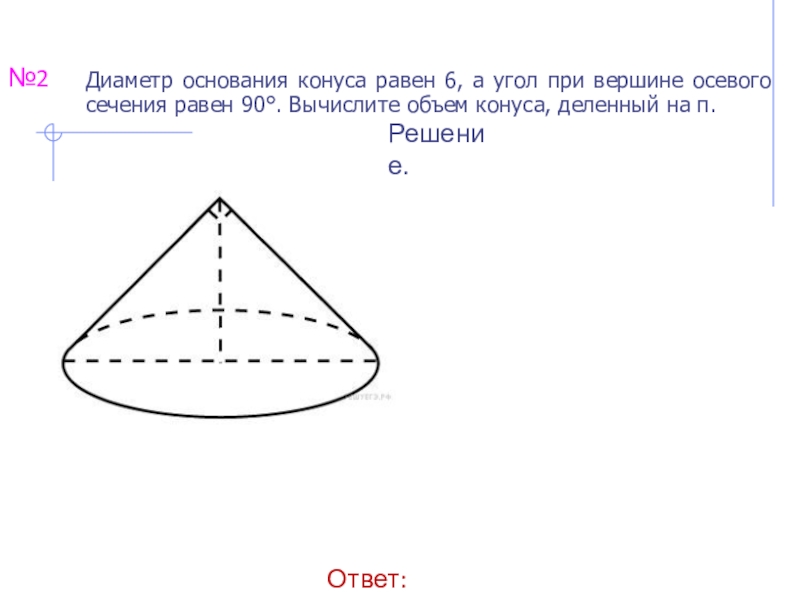 0° от базовой поверхности или линии. Перпендикулярность может относиться к 2D-линии, но чаще она описывает ориентацию одной плоскости поверхности, перпендикулярной другой базовой плоскости. Допуск условного обозначения перпендикулярности косвенно управляет углом 90° между деталями, контролируя положение, в котором должны лежать поверхности. См. зону допуска ниже для более подробной информации.
0° от базовой поверхности или линии. Перпендикулярность может относиться к 2D-линии, но чаще она описывает ориентацию одной плоскости поверхности, перпендикулярной другой базовой плоскости. Допуск условного обозначения перпендикулярности косвенно управляет углом 90° между деталями, контролируя положение, в котором должны лежать поверхности. См. зону допуска ниже для более подробной информации.
Примечание. Перпендикулярность не влияет на угол ссылочного элемента — допуск выражается в единицах расстояния. (мм/дюйм)
Ось: Управление осью также может быть вызвано для перпендикулярности и является одной из наиболее распространенных форм вызова осей. Когда на него ссылаются для круглого элемента, рамка управления элементом будет содержать символ диаметра (Ø). Перпендикулярность оси может быть применена к положительному элементу (штифт/выступ) или к отрицательному элементу (отверстию). Когда Перпендикулярность используется для осевого управления элементом, символ теперь задает цилиндрическую границу, где должна лежать ось указанного элемента. Эта цилиндрическая граница формируется путем взятия линии, которая перпендикулярна базовому элементу. Когда вызывается эта версия перпендикулярности, она должна использоваться с максимальным состоянием материала, чтобы облегчить измерение детали. См. пример 2 ниже, чтобы узнать, как измеряются эти конкретные детали.
Эта цилиндрическая граница формируется путем взятия линии, которая перпендикулярна базовому элементу. Когда вызывается эта версия перпендикулярности, она должна использоваться с максимальным состоянием материала, чтобы облегчить измерение детали. См. пример 2 ниже, чтобы узнать, как измеряются эти конкретные детали.
Две параллельные плоскости или линии, ориентированные перпендикулярно базовому элементу или поверхности. Плоскости удерживаются перпендикулярно к базе, но только для того, чтобы весь элемент попал в зону допуска.
Помните: Перпендикулярность не определяет напрямую угол поверхности, на которую ссылаются; он контролирует оболочку (например, плоскостность), где должна быть поверхность.
Ось:
Цилиндр, окружающий заданную теоретическую ось, которая перпендикулярна опорному элементу. Зона допуска — это диаметр этого символа, в котором должна лежать центральная ось измеряемого элемента.
Калибровка/Измерение: Поверхность:
Перпендикулярность измеряется с помощью штангенциркуля, аналогично плоскостности, однако штангенциркуль (или его часть) зафиксирован в 90°, чтобы измерить, насколько перпендикулярна поверхность. Вся поверхность должна быть измерена, если это плоский элемент.
Ось:
Чтобы гарантировать, что деталь или элемент аксиально перпендикулярны, максимальное состояние материала чаще всего вызывается для перпендикулярности оси, чтобы облегчить измерение с помощью калибра. Это позволяет проектировать его как для отрицательного (отверстие), так и для положительного (штифт) элемента и может учитывать дополнительный допуск.*
Размер датчика для внутреннего элемента (например, отверстия):
Калибр Ø (штифт) = Мин. Ø отверстия (MMC) – Допуск перпендикулярности
Размер калибра для внешнего элемента (например, штифта):
Калибр Ø (калибра) = Макс. Ø штифта (MMC) + Допуск перпендикулярности
Ø штифта (MMC) + Допуск перпендикулярности
См. Пример № 2 ниже для хорошего примера перпендикулярности оси с использованием MMC.
*Примечание к дополнительному допуску:
Когда для перпендикулярности используется функциональный калибр, любое отличие фактического размера элемента от максимального состояния материала будет дополнительным допуском. Цель обозначения максимального состояния материала состоит в том, чтобы гарантировать, что, когда деталь находится в наихудших допусках, ориентация 9Размер отверстия/штифта 0139 и всегда будет собираться вместе. Это означает, что если вы сделаете булавку меньше, вы получите больше бонусной терпимости для себя. Этот бонус можно добавить к допуску GD&T, что расширит допуск перпендикулярности.
Бонусный допуск = разница между MMC и фактическим состоянием (см. пример 2 ниже)
Еще не запутались? Не беспокойся! Дополнительные сведения см. в разделах «Максимальное состояние материала».
Перпендикулярность — это особая форма угловатости, равная 90°. Все символы ориентации (Угловатость, Параллельность и Перпендикулярность) вызывают конкретную оболочку элемента, связанную с базой.
Перпендикулярный символ также тесно связан с плоскостностью, когда базовая/измеренная поверхность является плоскостью поверхности. Когда вы вызываете Перпендикулярность, подразумевается плоскостность (вы измеряете изменение поверхности между двумя параллельными плоскостями = Плоскостность). Перпендикулярность всегда измеряется относительно базы, а плоскостность — нет.
Ось: Перпендикулярность тесно связана со всеми другими символами GD&T ориентации при вызове на оси. Зона допуска теперь относится к однородности и цилиндрической оболочке центральной оси. Перпендикулярность и параллелизм можно вызвать на отверстиях и цилиндрических штифтах, часто с добавлением MMC.
Когда две поверхности нуждаются в постоянном угле 90°, Перпендикулярность эффективна. Фланцевые подшипники и критические квадратные кромки обычно ссылаются на него. Перпендикулярность также обычно указывается на углах цилиндров, где плоское дно должно быть перпендикулярно изогнутым сторонам.
Ось:Перпендикулярность очень часто обозначается на центральной оси отверстия. Почти всегда ваше отверстие должно быть перпендикулярно поверхности, в которой оно просверлено. В этом случае она вызывается рядом с MMC, чтобы гарантировать, что, если в это отверстие необходимо вставить штифт или болт, деталь может войти во весь перпендикуляр и всегда будет входить. См. пример 2 для этого объяснения.
Перпендикулярность поверхности Пример: Край стопорного блока для рельса должен образовывать 90°, чтобы обеспечить надлежащий стыковочный контакт. Основание блока будет нашей базой, а грань, где стопорный блок соприкасается, будет нашей опорной поверхностью. Чтобы гарантировать, что эта грань всегда перпендикулярна и плоская, чтобы обеспечить хороший контакт, вам нужно будет строго контролировать как угол, так и размерную ширину детали.
Основание блока будет нашей базой, а грань, где стопорный блок соприкасается, будет нашей опорной поверхностью. Чтобы гарантировать, что эта грань всегда перпендикулярна и плоская, чтобы обеспечить хороший контакт, вам нужно будет строго контролировать как угол, так и размерную ширину детали.
Обеспечение перпендикулярных/плоских поверхностей без символа GD&T
С помощью перпендикулярности вы можете открыть размер ширины и очень точно контролировать угол грани, содержащей деталь. Ваша зона допуска остается прежней, но теперь вашу деталь легче контролировать и изготавливать.
Контроль перпендикулярности с помощью символа GD&T.
Перпендикулярность оси Пример с MMC: Если у вас есть важный элемент отверстия, который должен оставаться параллельным формируемой поверхности, можно вызвать перпендикулярность, чтобы гарантировать прямолинейность отверстия. В этом примере отверстие под болт должно оставаться перпендикулярным его поверхности.
Перпендикулярность на отверстии под ММС
Без выноски MMC вам нужно было бы контролировать только центральную ось отверстия и измерять ее, чтобы убедиться, что она находится под углом 90° к нижней поверхности. Однако, когда MMC вызывается на отпечатке, вы контролируете как размер, так и ориентацию отверстия. Теперь вы можете проверить оба допуска с помощью функционального калибра со следующими размерами:
Формула для функционального калибра перпендикулярности:
Калибр Ø (штифтовой калибр) = Мин. Ø отверстия – Допуск перпендикулярности
Калибр Ø = 90,9 – 0,2 = 9,7
Ø отверстия + Перпендикулярность отверстия > 9,7 (Ø штифта) в спецификации.
Из-за сноски Max Material Condition, если у вас есть отверстие больше, чем MMC 9,9, у вас будет дополнительный допуск, который можно добавить к вашей перпендикулярности. (Согласно печати Ø отверстия не может быть больше 10,1)
В приведенном ниже примере — отверстие находится в минимальном состоянии материала (наибольший размер отверстия) с отверстием в LMC, ваш бонусный допуск, который можно добавить к перпендикулярности, равен рассчитывается следующим образом:
Бонусный допуск = Фактический размер детали – Максимальное состояние материала часть находится в наибольшем диаметре.


 Высота цилиндра в два раза больше диаметра основания. Вычислите объем баллона в литрах.
Высота цилиндра в два раза больше диаметра основания. Вычислите объем баллона в литрах.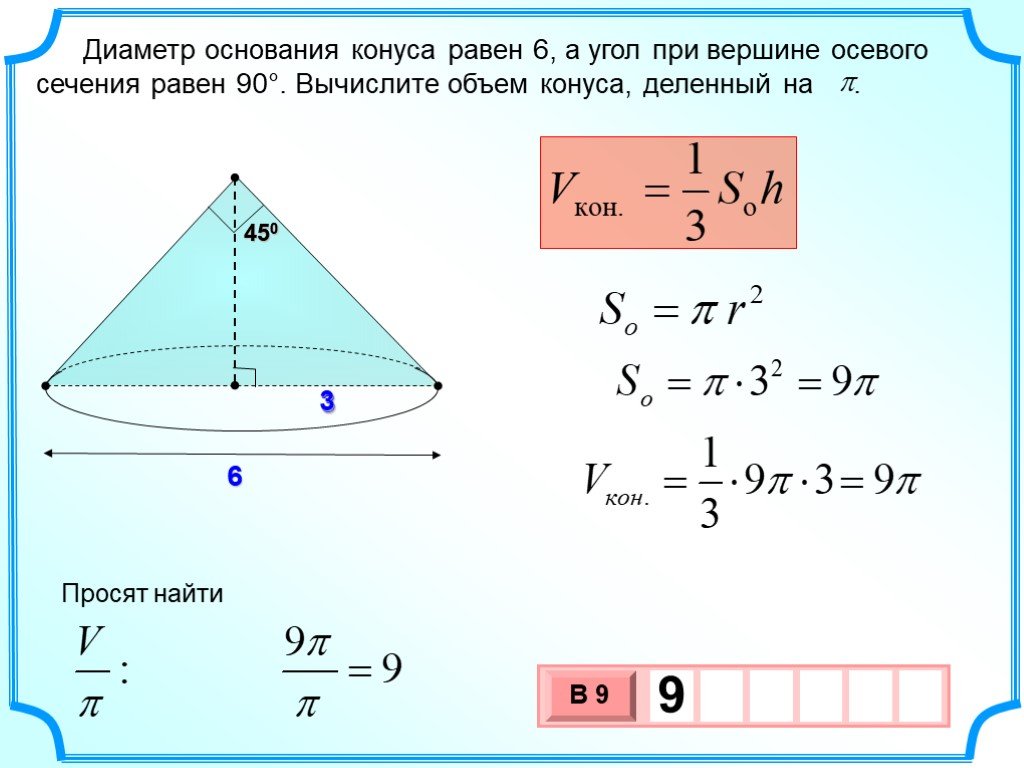 Насколько велики внутренние углы?
Насколько велики внутренние углы?
Leave A Comment