Диагонали ромба | Треугольники

Поскольку ромб является одним из видов параллелограмма, то диагонали ромба в точке пересечения делятся пополам.

Кроме этого, диагонали ромба обладают другими свойствами.

Теорема.

(Свойство диагоналей ромба)

Диагонали ромба пересекаются под прямым углом.

Диагонали ромба являются биссектрисами его углов.

 

Дано:

ABCD — ромб,

AC и BD — диагонали.

Доказать:

   

AC и BD — биссектрисы углов ромба.

Доказательство:

Рассмотрим треугольник ABC.

 

AB=BC (по определению ромба).

Следовательно, треугольник ABC — равнобедренный с основанием AC (по определению равнобедренного треугольника).

Так как диагонали ромба в точке пересечения делятся пополам, то AO=OC.

Значит, BO — медиана треугольника ABC (по определению медианы).

Следовательно, BO — высота и биссектриса треугольника ABC (по свойству равнобедренного треугольника).

То есть,

   

BD — биссектриса углов ABC (и ADC).

 

Из треугольника ABD аналогично доказывается, что AC — биссектриса углов BAD и BCD.

Что и требовалось доказать.

www.treugolniki.ru

Все формулы длины диагоналей ромба

Свойства ромба:

1. Ромб — частный случай параллелограмма

2. Противоположные стороны — параллельны

3. Все четыре стороны — равны

4. Диагонали пересекаются под прямым углом (90°)

5. Диагонали являются биссектрисами

 

a — сторона

ромба

D — большая диагональ

d — меньшая диагональ

α — острый угол

β — тупой угол

 

Формулы диагоналей через сторону и угол, ( D d):

 

 

Формулы диагоналей через сторону и половинный угол, (D d):

 

Формулы диагоналей через сторону и другую диагональ, (D d):

 

Формулы диагоналей через угол и другую диагональ, (D d):

 

Формулы диагоналей через площадь (D d):

 

Формулы площади ромба

Формула периметра ромба

Все формулы по геометрии

Подробности
Автор: Administrator

www-formula.ru

Диагонали ромба пересекаются под прямым углом

Добрый вечер!
Да, факт, что диагонали ромба пересекаются под прямым углом — известный всеми, но почему-то употреблять это данное в силе не каждый. Давайте же разбираться почему. Это происходит из-за того, что из виду выпускается то, что точкой пересечения диагонали делятся пополам.
Давайте рассмотрим какую-то любую задачу. К примере, нам дан ромб ABCD. AC и BD — это диагонали ромба, который равны 20 и 30 см соответственно. Нам нужно найти периметр данного ромба.
Первым делом вспоминаем, что диагонали пересекаются под прямым углом и делятся пополам. Из этого получаем, что у нас пересечением образовываются прямоугольные треугольники (их аж 4, но они будут во всём одинаковые). Точка О — точка пересечения диагоналей. Отрезок BO — это половина диагонали BD — 15 см, а ОС — это половина диагонали АС — 10 см. Так как рассматривается прямоугольный треугольник ВОС, то выходит, что нам известны катеты этого прямоугольного треугольника, гипотенуза которого — это и есть сторона ромба, которую мы можем найти, используя теорему Пифагора: 

   

 

   

 

   

 

   

 

   

 

   

  

   

Это мы с Вами нашли одну сторону. Теперь надо найти периметр этого ромба. А периметр — это сумма всех сторон. У ромба их всего 4, так к тому же они ещё и одинаковые. Поэтому периметр ромба мы будем находить по такой формуле: 

   

 

   

 

   

Ответ:  см

ru.solverbook.com

Свойства ромба | Треугольники

Свойства ромба — это свойства параллелограмма плюс собственные свойства.

Перечислим их.

Свойства ромба

1) Стороны ромба равны (по определению ромба).

2) Противолежащие углы ромба равны (по свойству параллелограмма).

3) Сумма углов, прилежащих к одной стороне ромба, равна 180º (по свойству параллелограмма).

4) Диагонали ромба пересекаются и точкой пересечения делятся пополам (по свойству параллелограмма).

5) Диагонали ромба взаимно перпендикулярны.

6) Диагонали ромба являются биссектрисами его углов.

7) Сумма квадратов диагоналей ромба равна сумме квадратов его сторон (по свойству параллелограмма).

8) Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба (по свойству параллелограмма).

9) Угол между высотами ромба, проведенными из вершины острого угла, равен тупому углу ромба.

 

Проиллюстрируем эти свойства для ромба ABCD:

 

1) AB=BC=CD=AD;

2) ∠A=∠C; ∠B=∠D;

3) ∠A+∠B=180º; ∠B+∠C=180º; ∠C+∠D=180º; ∠A+∠D=180º;

 

4) AC ∩ BD=O, AO=CO, BO=DO;

   

6) ∠ABO=∠CBO=∠ADO=∠CDO,

∠BAO=∠BCO=∠DAO=∠DCO;

   

 

 

 

8) ∠FBK=∠A;

 

 

 

 

 

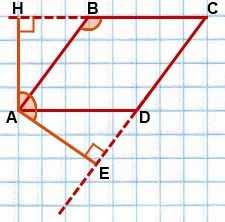
9) ∠HAE=∠ABC.

www.treugolniki.ru

Ромб. Свойства и признаки ромба

Категория: Справочные материалы

Елена Репина 2013-07-26 2015-04-11

Ромб – это параллелограмм, у которого все стороны равны.

Если у ромба – прямые углы, то он называется квадратом.

Свойства ромба


1. Поскольку ромб – это параллелограмм, то все свойства параллелограмма  верны для ромба.

Помимо этого:

2. Диагонали ромба перпендикулярны.

3. Диагонали ромба являются биссектрисами его углов.

4. Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4.

Признаки ромба

 

Чтобы параллелограмм   оказался ромбом, необходимо выполнение одного из следующих условий:

1. Все стороны параллелограмма равны между собой ().

2. Диагонали пересекаются под прямым углом ().

3. Диагонали параллелограмма являются биссектрисами его углов.

 

Площадь ромба

 

 

Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.

Автор: egeMax | комментария 3

egemaximum.ru

Найти углы ромба

Свойства ромба:

1.

Ромб — частный случай параллелограмма

2. Противоположные стороны — параллельны

3. Все четыре стороны — равны

4. Диагонали пересекаются под прямым углом (90°)

5. Диагонали являются биссектрисами

 

a — сторона ромба

D — большая диагональ

d — меньшая диагональ

α — острый угол

β — тупой угол

 

Формулы косинуса углов через диагональ и сторону:

 

 

Формулы синуса углов через диагонали :

 

Формулы синуса углов через площадь S и сторону :

 

Формулы тангенса половинных углов через диагонали

 

Формулы соотношения острого и тупого углов:

 

Для определения величины угла в градусах или радианах, используем функции arccos или arcsin или arctg

 

 

 

 

Формулы площади ромба

Формула периметра ромба

Все формулы по геометрии

Подробности
Автор: Administrator

www-formula.ru

Большая диагональ и острый угол ромба

Если известна большая диагональ и острый угол ромба, то, используя свойства ромба, можно найти остальные его элементы.

Большая диагональ ромба равна D, острый угол — α. Найти меньшую диагональ, стороны, периметр и площадь ромба, а также его высоту и радиус вписанной окружности.

Пусть AC — большая диагональ ромба ABCD, AC=D. ∠BAD=α.

Проведём вторую диагональ: AC ∩ BD=O.

Так как диагонали ромба являются биссектрисами его углов, пересекаются под прямым углом и в точке пересечения делятся пополам, то треугольник AOB — прямоугольный,

   

По определению тангенса, 

   

   

   

По определению косинуса,

   

   

Периметр ромба 

   

площадь — 

   

   

Опустим перпендикуляр OF из точки пересечения диагоналей к стороне AD. OF — радиус вписанной в ромб окружности. Из прямоугольного треугольника AOF

   

   

Высота ромба в два раза больше радиуса вписанной окружности, следовательно,

   

www.treugolniki.ru