Диагональ трапеции авсд делит ее на два прямоугольных равнобедренных: 2. Диагональ трапеции АВСD делит ее на 2 прямоугольных равнобедренных треугольника. Найдите среднюю линию трапеции,…

Свойства прямоугольной трапеции: диагоналей, углов, сторон, высоты

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Свойства прямоугольной трапеции

В данной публикации мы рассмотрим определение и основные свойства прямоугольной трапеции.

Напомним, трапеция называется прямоугольной, если углы при одной из ее боковых сторон прямые, т.е. равняются 90°.

• Свойство 1
• Свойство 2
• Свойство 3
• Свойство 4

Свойство 1

Два угла прямоугольной трапеции обязательно являются прямыми, принадлежат одной боковой стороне, а вершины данных углов – смежные.

Для рисунка выше:

• ∠BAD = ∠ABC = α = 90°
• ∠BAD и ∠ABC принадлежат боковой стороне AB
• Вершины A и B – смежные.

Свойство 2

Одна из боковых сторон прямоугольной трапеции перпендикулярна ее основаниям.

На рисунке выше: AB ⊥ AD и AB ⊥ BC.

Свойство 3

Высота прямоугольной трапеции (h) совпадает с меньшей боковой стороной (AB), перпендикулярной основаниям.

Свойство 4

Каждая из диагоналей прямоугольной трапеции делит ее на два треугольника, один из которых, также, является прямоугольным.

• Диагональ AC делит трапецию на треугольники ABC и ACD, причем ΔABC является прямоугольным с прямым углом в вершине B.
• Диагональ BD делит трапецию на ΔABD (прямоугольный) и ΔBCD.

Примечание: остальные свойства, которые применимы ко всем видам трапеций, приведены в нашей публикации – “Что такое трапеция: определение, виды, свойства”.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Найдите среднюю линию трапеции

В этой статье для вас сделана очередная подборка задач с трапецией. Условия так или иначе связаны с её средней линией. Типы заданий взяты из открытого банка типовых задач. Если есть желание, то можете освежить свои теоретические знания связанные с трапецией. На блоге уже рассмотрены задачи условия которых связаны с площадью трапеции, а также с углами. Кратко о средней линии:

Средняя линия трапеции соединяет середины боковых сторон. Она параллельна основаниям и равна их полусумме.

Перед решением задач давайте рассмотрим теоретический пример.

Дана трапеция ABCD. Диагональ АС пересекаясь со средней линией образует точку К, диагональ BD точку L. Доказать, что отрезок KL равен половине разности оснований.

Давайте сначала отметим тот факт, что средняя линия трапеции делит пополам любой отрезок концы которого лежат на её основаниях. Этот вывод напрашивается сам собой. Представьте отрезок соединяющий две точки оснований, он разобьёт данную трапецию на две других. Получится, что отрезок параллельный основаниям трапеции и проходящий через середину боковой стороны на другой боковой стороне пройдёт через её середину.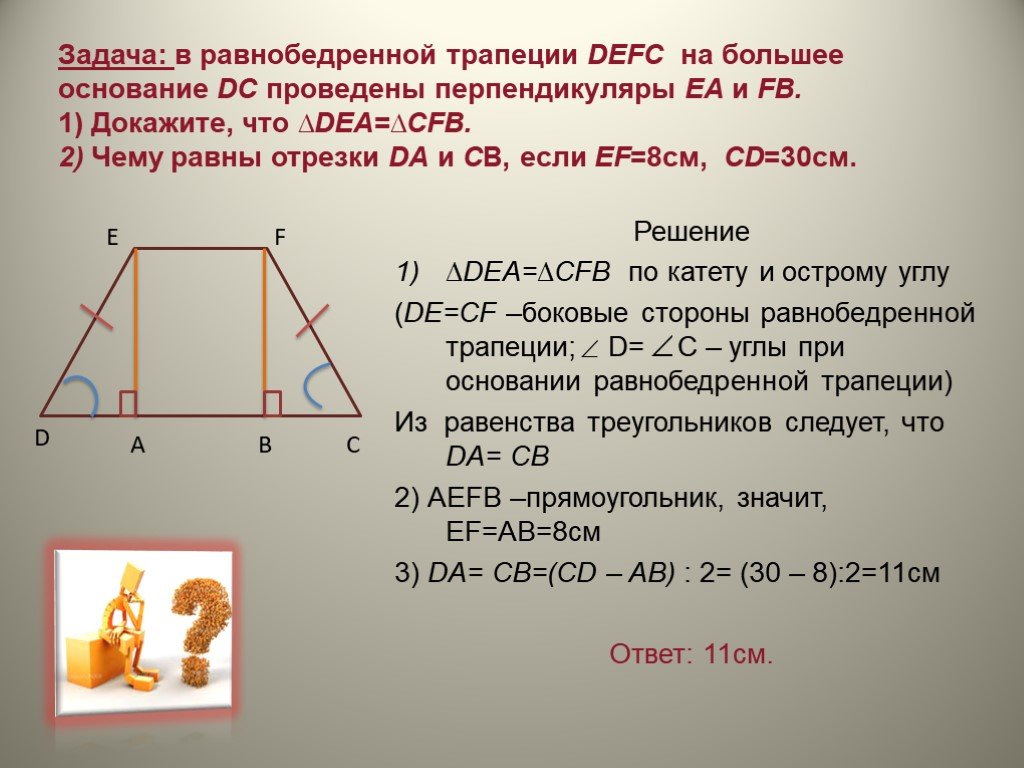

Так же это основывается на теореме Фалеса:

Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.

То есть в данном случае К середина АС и L середина BD. Следовательно EK есть средняя линия треугольника АВС, LF есть средняя линия треугольника DCB. По свойству средней линии треугольника:

Можем теперь выразить отрезок KL через основания:

Доказано!

Данный пример приведён не просто так. В задачах для самостоятельного решения имеется именно такая задача. Только в ней не сказано, что отрезок соединяющий середины диагоналей лежит на средней линии.  Рассмотрим задачи:

27819. Найдите среднюю линию трапеции, если ее основания равны 30 и 16.

Вычисляем по формуле:

Ответ: 23

27820. Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции.

Выразим большее основание:

Таким образом:

Ответ: 38

27836. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции.

Для того, чтобы найти среднюю линию необходимо знать основания. Основание АВ найти просто: 10+4=14. Найдём DC.

Построим второй перпендикуляр DF:

Отрезки AF, FE и EB будут равны соответственно 4, 6 и 4. Почему?

В равнобедренной трапеции перпендикуляры опущенные к большему основанию разбивают его на три отрезка. Два из них, являющиеся катетами отсекаемых прямоугольных треугольников, равны друг другу. Третий отрезок равен меньшему основанию, так как при построении указанных высот образуется прямоугольник, а в прямоугольнике противолежащие стороны равны. В данной задаче:

Таким образом DC=6. Вычисляем:

Ответ: 10

27839.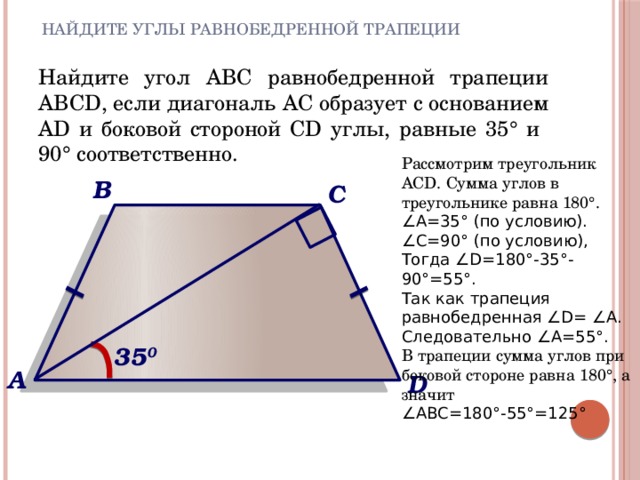 Основания трапеции относятся 2:3, а средняя линия равна 5. Найдите меньшее основание.

Введём коэффициент пропорциональности х. Тогда АВ=3х, DC=2х. Можем записать:

Следовательно меньшее основание равно 2∙2=4.

Ответ: 4

27840. Периметр равнобедренной трапеции равен 80, ее средняя линия равна боковой стороне. Найдите боковую сторону трапеции.

Исходя из условия можем записать:

Если обозначить среднюю линию через величину х, то получится:

Второе уравнение уже можно записать в виде:

Ответ: 20

27841. Средняя линия трапеции равна 7, а одно из ее оснований больше другого на 4. Найдите большее основание трапеции.

Обозначим меньшее основание (DC) как х, тогда большее (AB) будет равно х+4. Можем записать

Получили, что меньшее основание рано пяти, значит большее равно 9.

Ответ: 9

27842. Средняя линия трапеции равна 12. Одна из диагоналей делит ее на два отрезка, разность которых равна 2. Найдите большее основание трапеции.

Большее основание трапеции мы без труда найдём если вычислим отрезок ЕО. Он является средней линией в треугольнике ADB, и АВ=2∙ЕО.

Что имеем? Сказано что средняя линия равна 12 и разность отрезков ЕО и ОF равна 2. Можем записать два уравнения и решить систему:

Понятно, что в данном случае подобрать пару чисел можно без вычислений, это 5 и 7. Но, всё-таки, решим систему:

Значит ЕО=12–5=7. Таким образом, большее основание равно АВ=2∙ЕО=14.

Ответ: 14

27844. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.

Сразу отметим, что высота проведённая через точку пересечения диагоналей в равнобедренной трапеции лежит на оси симметрии и разбивает трапецию на две равные прямоугольные трапеции, то есть основания этой высотой делятся пополам.

Казалось бы, для вычисления средней линии мы должны найти основания. Тут небольшой тупик возникает… Как зная высоту, в данном случае, вычислить основания? А ни как! Таких трапеций с фиксированной высотой и диагоналями пересекающимися по углом 90 градусов можно построить множество.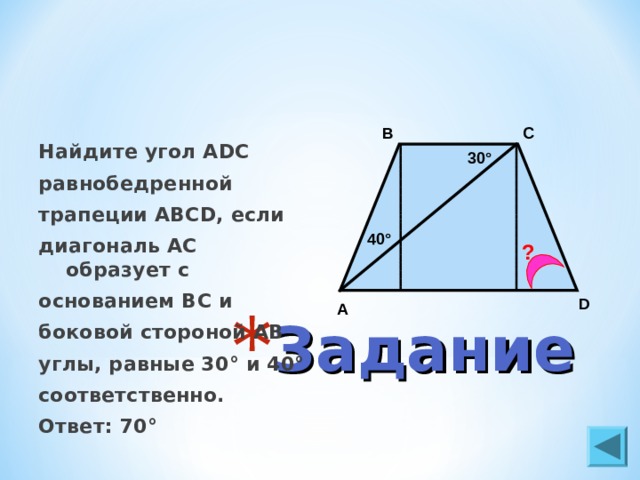 Как быть?

Посмотрите на формулу средней линии трапеции. Ведь нам необязательно знать сами основания, достаточно узнать их сумму (или полусумму). Это мы сделать можем.

Так как диагонали пересекаются под прямым углом, то высотой EF образуются равнобедренные прямоугольные треугольники:

При чём:

Из выше сказанного следует, что FO=DF=FC, а OE=AE=EB. Теперь запишем чему равна высота выраженная через отрезки DF и AE:

Таким образом, средняя линия равна 12.

*Вообще это задачка, как вы поняли, для устного счёта. Но, уверен, представленное подробное объяснение необходимо. А так… Если взглянуть на рисунок (при условии, что при построении соблюдён угол между диагоналями), сразу в глаза бросается равенство FO=DF=FC, а OE=AE=EB.

Ответ: 12

В составе прототипов имеется ещё типы заданий с трапециями. Построена она на листе в клетку и требуется найти среднюю линию, сторона клетки обычно равна 1, но может быть  другая величина.

27848. Найдите среднюю линию трапеции ABCD, если стороны квадратных клеток равны 1.

Всё просто, вычисляем основания по клеткам и используем формулу: (2+4)/2=3

Ответ: 3

Если же основания построены под углом к клеточной сетке, то есть два способа. Например!

28854.Найдите среднюю линию трапеции ABCD, если стороны квадратных клеток равны √2.

В данном случае видно, что средняя линия трапеции равна трём диагоналям клетки. Диагональ одной клетки по теореме Пифагора будет равна:

Значит средняя линия равна 2∙3=6.

Конечно, есть и другой путь решения.

Если допустить мысль, что основания трапеции могут лежать по отношению к сетке под углом не 45 градусов, а например 30, или другим, то вполне применим следующий метод (таких задач на ЕГЭ не предвидится):

Вычисляем основания используя теорему Пифагора, а далее используем формулу средней линии.

Основание AD при данных условиях это диагональ в прямоугольном треугольнике с катетами равными 4 сторонам клетки, вычисляем:

Основание BC это диагональ в прямоугольном треугольнике катетами равными  2 сторонам клетки, вычисляем:

Средняя линия будет равна  (8+4)/2=6.

*То есть при данном подходе, как бы ни была построена трапеция всегда можно вычислить основания.

Ответ: 6

27853. Найдите высоту трапеции ABCD, опущенную из вершины B, если стороны квадратных клеток равны √2.

Высота трапеции равна диагонали клетки. Вычисляем по теореме Пифагора:

Ответ: 2

27821. Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.

Посмотреть решение

27838.Периметр трапеции равен 50, а сумма непараллельных сторон равна 20. Найдите среднюю линию трапеции.

Посмотреть решение

27843. Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.

Посмотреть решение

На этом всё, успеха вам!

С уважением, Александр Крутицких.

P,S: Расскажите о сайте в социальных сетях.

Как найти длину диагонали трапеции

Все ресурсы по продвинутой геометрии

6 Диагностические тесты 57 практических тестов Вопрос дня Карточки Learn by Concept

Расширенная справка по геометрии » Плоская геометрия » Четырехугольники » Трапеции » Как найти длину диагонали трапеции

Какова длина диагоналей трапеции ? Предположим, что фигура представляет собой равнобедренную трапецию.

Возможные ответы:

Правильный ответ:

Пояснение:

Чтобы найти длину диагонали, нам нужно использовать теорему Пифагора. Следовательно, нам нужно начертить внутри трапеции следующий треугольник:

Мы знаем, что длина основания треугольника . Вычитая вершину трапеции из низа трапеции, получаем:

Разделив на два, имеем длину каждой дополнительной стороны по низу трапеции:

Складывая эти два значения вместе, мы получаем .

В формуле длины диагонали используется теорема Пифагора:

, где  – точка между  и , представляющая основание треугольника.

Подставив наши значения, получим:

Сообщить об ошибке

Найдите длину обеих диагоналей этого четырехугольника.

Возможные ответы:

Правильный ответ:

Объяснение:

Все длины с одной отметкой имеют длину 5, а все длины сторон с двумя отметками имеют длину 4.

Зная это, мы можем сложить длины сторон, чтобы найти, что одна диагональ является гипотенузой в этом прямоугольном треугольнике. :

Используя теорему Пифагора, получаем:

возьмем квадратный корень из каждой стороны

Точно так же можно найти другую диагональ этого прямоугольного треугольника:

Снова используя теорему Пифагора, получаем ответ

Сообщить об ошибке

Найдите длину диагоналей этой равнобедренной трапеции, при .

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти длину диагоналей, разделите верхнюю сторону на 3 части, как показано ниже:

Две конгруэнтные части плюс 8 дают в сумме 14. Таким образом, две конгруэнтные части в сумме дают 6. Каждая из них должна быть 3. Это означает, что вершина прямоугольного треугольника с диагональю в качестве гипотенузы должна быть равна 11, так как .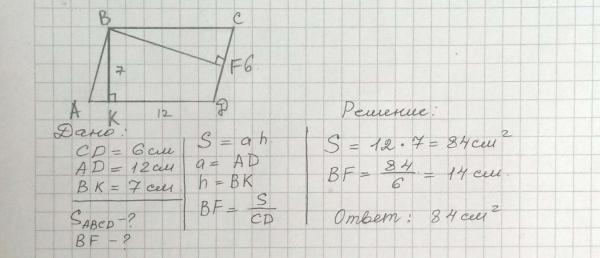

Мы можем найти диагональ, показанную на рисунке, с помощью теоремы Пифагора:

извлечь квадратный корень из обеих сторон

Сообщить об ошибке

Сообщить об ошибке нижеприведенный.

Возможные ответы:

Правильный ответ:

Пояснение:

Чтобы вычислить длину диагонали, мы сначала должны предположить, что высота перпендикулярна как вершине, так и основанию трапеции.

Зная это, мы можем провести диагональ, как показано ниже, и использовать теорему Пифагора, чтобы найти диагональ.

Теперь мы берем квадратный корень с обеих сторон:

Сообщите о ошибке

.

Возможные ответы:

Правильный ответ:

Объяснение:

1) Диагональ можно найти по теореме Пифагора.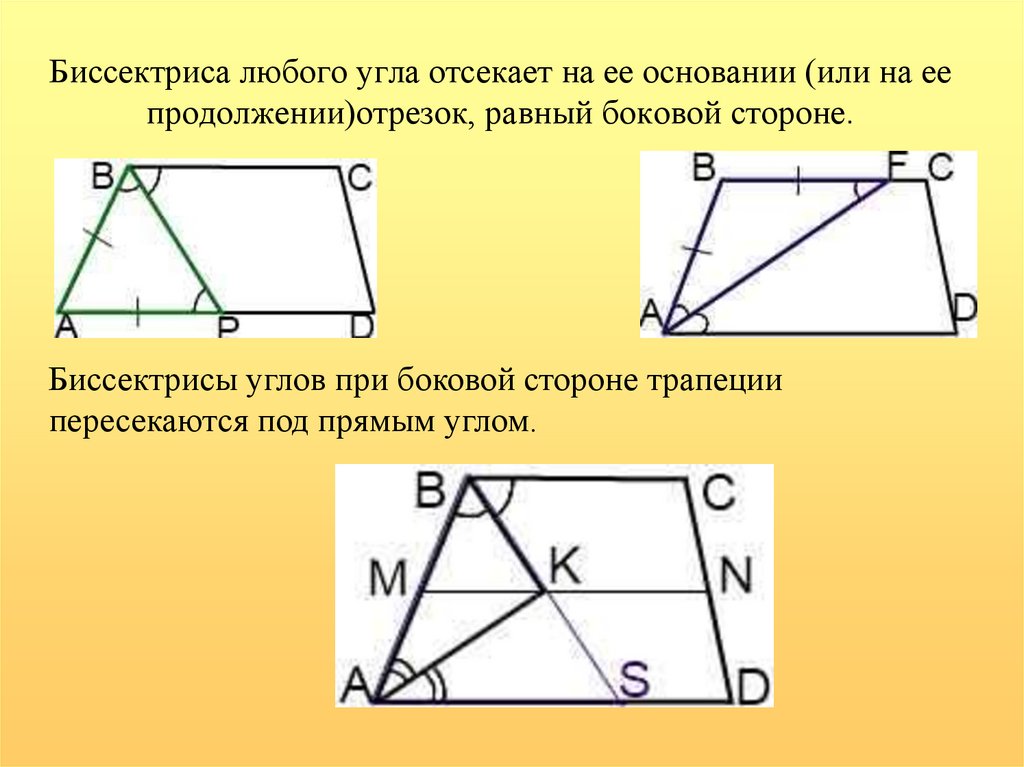

2) Длина основания ,  должна быть найдена, потому что  это длина основания .

3) .

4) Using the Pythagorean Theorem on  to find ,

5) Using the Pythagorean Theorem on  to find ,

 

Сообщить об ошибке

Рисунок выполнен НЕ в масштабе.

См. рисунок выше, на котором показана трапеция  с диагональю . До ближайшего целого числа укажите длину .

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы проиллюстрировать, как определить правильную длину, проведите перпендикулярный отрезок от  до , назвав точку пересечения .

 делит трапецию на прямоугольник  и прямоугольный треугольник  .

Противоположные стороны прямоугольника равны, значит .

. Два угла трапеции, лежащие на одном и том же катете, в частности, и  , являются дополнительными, поэтому

Итак, а

 является гипотенузой прямоугольного треугольника , поэтому по теореме Пифагора его длина может быть рассчитана как

Набор  и :

Сообщить об ошибке

Рисунок НЕ выполнен в масштабе.

См. рисунок выше, на котором показана трапеция  с диагональю . До ближайшего целого числа укажите длину .

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы проиллюстрировать, как определить правильную длину, проведите перпендикулярный отрезок от  до , назвав точку пересечения .

 делит трапецию на прямоугольник  и прямоугольный треугольник  .

Противоположные стороны прямоугольника равны, значит .

. Два угла трапеции, лежащие на одном и том же катете, в частности, и  , являются дополнительными, поэтому

Итак, и

 является гипотенузой прямоугольного треугольника , поэтому по теореме Пифагора его длина может быть рассчитана как

Установить и:

 

Сообщить об ошибке

Рис.

См. рисунок выше, на котором показана трапеция с диагональю . До ближайшего целого числа укажите длину .

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы проиллюстрировать, как определить правильную длину, проведите перпендикулярный отрезок от  до , назвав точку пересечения .

 делит трапецию на прямоугольник  и прямоугольный треугольник  .

Противоположные стороны прямоугольника равны, значит .

. Два угла трапеции вдоль одной и той же ноги- в частности, и- являются дополнительными, так что

к теореме 45-45-45

4. прямоугольного треугольника, поэтому по теореме Пифагора его длина может быть рассчитана равной

SET и:

Отчет о ошибке

Уведомление об авторских правах

Все передовые ресурсы геометрии

6 Диагностические тесты 57 практических тестов Вопрос дня Карточки Учитесь по понятиям

Площадь трапеции — формулы, примеры, решения

1. Трапеция — что это за фигура?
2. Особенности трапеции
3. Теорема: площадь трапеции
4. Вычисление площадей в прошлые времена
5. Вычисление площадей в современном мире
   1. Формула площади трапеции по основанию и высоте
   2. Формула площади трапеции в основании и на осевой линии
   3. Формула площади трапеции через радиус вписанной окружности и угол
   4. Формула площади трапеции через диагонали и угол между ними
6. Трапеция и созвездия
7. Трапеции в экспериментальной физике

Учащиеся должны выполнять разные домашние задания по геометрии. Однако больше всего трудностей возникает у учащихся средних классов, поскольку они изучали только математику и алгебру, и геометрию. Например, им нужно найти перпендикулярное расстояние, площадь поверхности или параллельные стороны трапеции. Сегодня мы поговорим именно о трапециях, нахождении площади и рассмотрении ее как одной из важнейших теорем.

Трапеция — что это за фигура?

Трапеция – это четырехугольник, имеющий две параллельные стороны и две непараллельные стороны. Параллельные стороны называются основаниями трапеции, а две другие — боковыми сторонами. Высота трапеции – это расстояние между прямыми, на которых лежат основания трапеции, любым общим перпендикуляром этих прямых. Средняя линия трапеции – это отрезок, соединяющий середины сторон.

Особенности трапеции

Если в трапецию вписана окружность, то сумма оснований всегда совпадает с суммой сторон: a + b = c + d, а средняя линия всегда равна полусумме сторон:

Равнобедренная трапеция — это трапеция, стороны которой равны AB = CD. Тогда диагонали AC = BD и углы при основании равны:

Из всех трапеций только около равнобедренной трапеции можно описать окружность, если сумма противоположных прямых углов равна 180°. В равнобедренной трапеции расстояние от вершины одного основания до проекции противоположной вершины, которая непосредственно связана с основанием, всегда совпадает с осевой линией.

Прямоугольная трапеция — это разновидность трапеции, угол основания которой равен 90°.

Теорема: площадь трапеции

Чтобы вычислить площадь произвольного многоугольника, мы делаем следующее: делим многоугольник на треугольники и находим площадь треугольника. Сумма площадей этих треугольников равна площади многоугольника. С помощью этой методики выводим формулу расчета площади запасной части трапеции. Условимся называть высотой трапеции перпендикуляр, проведенный из любой точки одного из оснований на прямую, содержащую другое основание. На рисунке ниже мы указали, что отрезок линии BH является высотой трапеции ABCD:

Исходя из этого, получаем теорему: «Площадь трапеции равна произведению полусуммы ее оснований на высоту». Используя формулу площади, мы можем доказать эту теорему.

Дана трапеция: ABCD, AD, BC — длины оснований, BH — высота.

Докажите: площадь этой трапеции ABCD будет равна S = ½ (AD + BC) · BH.

Доказательство: проведите диагональ BD. Он делит трапецию на два треугольника ABD и BCD. Это означает, что периметр трапеции ABCD будет равен сумме площадей этих треугольников.

В треугольнике ABD: AD — основание, BH — высота. В треугольнике BCD: BC является основанием.

Нарисуем высоту ДК. Площадь S треугольника ABD = 1/2 AD · BH; площадь S треугольника BCD = 1/2 BC · DK. Так как BH = DK, то площадь S треугольника BCD = 1/2 BC · BH. Таким образом, площадь S трапеции ABCD = 1/2 AD · BH + 1/2 BC · BH = 1/2 (AD + BC) · BH. Что требовалось доказать.

Вычисление площадей в прошлые времена

Еще 4-5 тысяч лет назад вавилоняне умели определять площадь трапеции в квадратных единицах. Древние египтяне 4000 лет назад использовали почти те же приемы, что и мы: сумму параллельных сторон делили пополам и умножали на высоту.

Определение площадей геометрических фигур — одна из древнейших практических задач. Люди не сразу нашли правильный подход к их решению. Один из самых простых и доступных способов вычисления площадей открыл Евклид. При расчете площадей он использовал простой прием, называемый методом разбиения.

Вычисление площадей в современном мире

Сегодня существует множество формул для вычисления длин сторон, вершин, параллельных оснований и площади трапеции. Мы рассмотрим самые основные из них. Приведенные ниже формулы просты в использовании, но если вам сложно их понять и вам нужна помощь с домашним заданием, вы всегда можете обратиться в нашу службу. Опытные авторы проконсультируют вас по всем заданиям, и вы значительно улучшите свою успеваемость.

Формула площади трапеции по основанию и высоте

Дана произвольная трапеция. Для нахождения его площади используем следующую формулу:

В этой формуле:

• а, b — основания трапеции;
• hh — высота трапеции.

Представим, что нам нужно найти площадь трапеции, у которой известны основания, численно равные 10 см и 8 см. Также известный рост, 6 см в длину.

Решение:

• а = 8;
• б = 10;
• ч = 6;

Сразу подставляем цифры в полученную формулу и вычисляем значение:

Ответ: 54 квадратных сантиметра.

Формула площади основания и средней линии трапеции

Следует отметить, что средняя линия трапеции равна половине суммы ее оснований. Таким образом, нахождение площади через центральную линию есть не что иное, как метод, аналогичный первому. Насколько:

В этой формуле:

• S = l ⋅ h;
• l — средняя линия трапеции;
• h — высота.

Предположим, нам нужно найти площадь трапеции, если известно, что средняя линия равна 5 см, а высота трапеции в два раза больше ее высоты.

Решение:

• л = 5;
• ч = 2 ⋅ л.

Найдите высоту трапеции:

h = 2 ⋅ 5 = 10

Площадь:

S = l ⋅ h = 5 ⋅ 10 = 50 см.кв.

Ответ: 50 квадратных сантиметров

Формула площади трапеции через радиус и угол вписанной окружности

Этот случай подходит только для равнобедренной трапеции: радиус вписанной окружности;

α — угол между основанием и стороной.

Предположим, нам дан радиус вписанной окружности в трапецию, равный 4 см. Угол α равен 90 градусов. Нам нужно найти площадь трапеции.

Решение:

• r = 4;
• α = 90.

По формуле:

Ответ: 64 квадратных сантиметра.

Формула площади трапеции через диагонали и угол между ними

Существует простая формула для нахождения площади трапеции через диагонали и угол между ними:

В этой формуле:

• d1, d2 — диагонали трапеций;
• α — угол между диагоналями.

Пусть две диагонали трапеции равны 20 см и 7 см. При пересечении они образуют угол 30 градусов. Нам нужно найти площадь трапеции.

Решение:

• d1 = 20;
• д2 = 7;
• α = 30°.

Площадь:

Ответ: 35 квадратных сантиметров.

Трапеция и созвездия

Трапеция встречается не только в домашнем задании по математике. Эту цифру можно найти при изучении созвездий. Выдающимся астеризмом весеннего неба является трапеция Льва, которую можно наблюдать по вечерам с февраля по май. Эта фигура расположена в зодиакальном созвездии Льва, образуя тело животного, и по форме напоминает трапецию.

Четыре яркие звезды созвездия α, β, γ и δ расположены на вершинах трапеции – тела льва. А голову льва образуют звезды, расположенные в виде серпа. Отсюда и название — трапеция Льва.

Трапеции в экспериментальной физике Посмотреть

Союз физики и математики предполагает непрерывное движение науки вперед. В физике ученые проводят опыты, суть которых становится полностью ясной только после математического анализа.