Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Решено
перед самой ареной цирка в.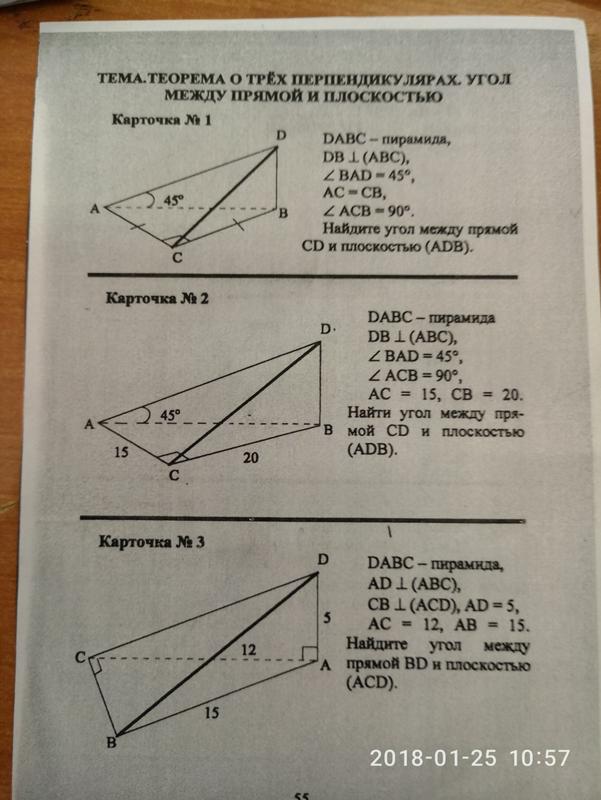 ..
..
решение
розвязати задачу
Пользуйтесь нашим приложением
Зачёт по геометрии в 8-м классе по теме «Четырёхугольники»
- Пономарёва Татьяна Александровна, учитель математики
Разделы: Математика
Цель: проверка уровня усвоения учебного материала по данной теме.
Теоретическая частьВопросы к зачёту
- Что такое параллелограмм?
- Что такое прямоугольник?
- Что такое ромб?
- Что такое квадрат? Перечислите свойства квадрата.
- Что такое трапеция? Какая трапеция называется равнобокой.

- Сформулируйте и докажите признак параллелограмма.
- Сформулируйте и докажите свойство противолежащих сторон и углов параллелограмма.
- Сформулируйте и докажите свойство диагоналей прямоугольника.
- Сформулируйте и докажите свойство диагоналей ромба.
- Сформулируйте и докажите свойство средней линии трапеции.
Задачи к зачёту
1 вариант
1. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол параллелограмма.
2. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD = 104°. Найдите угол между диагоналями параллелограмма.
Ответ дайте в градусах.
3. Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 15°. Ответ дайте в градусах.
4. Сумма двух углов равнобокой трапеции равна 150°. Найдите больший угол трапеции. Ответ дайте в градусах.
Сумма двух углов равнобокой трапеции равна 150°. Найдите больший угол трапеции. Ответ дайте в градусах.
5. Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
2 вариант
1. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма.
2. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD = 169°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
3. Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 33°. Ответ дайте в градусах.
4. Сумма двух углов равнобокой трапеции равна 196°. Найдите меньший угол трапеции. Ответ дайте в градусах.
5. Основания трапеции равны 3 и 14. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
3 вариант
1. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 50° и 85°. Найдите меньший угол параллелограмма.
2. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD = 111°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
3. Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 31°.Ответ дайте в градусах.
4. Сумма двух углов равнобокой трапеции равна 140°. Найдите больший угол трапеции. Ответ дайте в градусах.
5. Основания трапеции равны 8 и 17. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
4 вариант
1.
2. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD = 17°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
3. Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 13°. Ответ дайте в градусах.
4. Сумма двух углов равнобокой трапеции равна 220°. Найдите меньший угол трапеции. Ответ дайте в градусах.
5. Основания трапеции равны 12 и 15. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
5 вариант
1. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30°. Найдите больший угол параллелограмма.
2. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD = 63°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
3. Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 14°. Ответ дайте в градусах.
4. Сумма двух углов равнобокой трапеции равна 268°. Найдите меньший угол трапеции. Ответ дайте в градусах.
5. Основания трапеции равны 13 и 16. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Ответы к заданиям.
Как найти длину диагонали параллелограмма
Все математические ресурсы ACT
14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Learn by Concept
ACT Math Help » Геометрия » Плоская геометрия » Четырехугольники » Параллелограммы » Как найти длину диагонали параллелограмма
Если прямоугольный участок измеряется , какова длина диагонали участка в футах?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы ответить на этот вопрос, мы должны найти диагональ прямоугольника на . Поскольку прямоугольник состоит из прямых углов, диагональ прямоугольника образует прямоугольный треугольник с двумя сторонами.
Поскольку прямоугольник состоит из прямых углов, диагональ прямоугольника образует прямоугольный треугольник с двумя сторонами.
Поскольку диагональ образована прямоугольным треугольником, мы можем использовать теорему Пифагора, а именно:
и каждый из катетов треугольника представляет собой длину гипотенузы, которая в данном случае одинакова. как длина диагонали.
Затем мы можем подставить известные значения и найти
Теперь мы должны извлечь квадратный корень из каждой стороны, чтобы найти
Следовательно, диагональ прямоугольника равна .
Сообщить об ошибке
является параллелограммом. Найдите длину диагонали .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти длину диагонали, мы можем рассмотреть только треугольник и использовать закон косинусов, чтобы найти длину неизвестной стороны.
Закон косинусов:
Где – длина неизвестной стороны, и – длины известных сторон, и – угол между и .
Из задачи:
Сообщить об ошибке
является параллелограммом. Найдите длину диагонали .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти длину диагонали, мы можем рассмотреть только треугольник и использовать закон косинусов, чтобы найти длину неизвестной стороны.
Закон косинусов:
Где – длина неизвестной стороны, и – длины известных сторон, и – угол между и .
Из задачи:
Сообщить об ошибке
является параллелограммом. Найдите длину диагонали .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти длину диагонали, мы можем рассмотреть только треугольник и использовать закон косинусов, чтобы найти длину неизвестной стороны.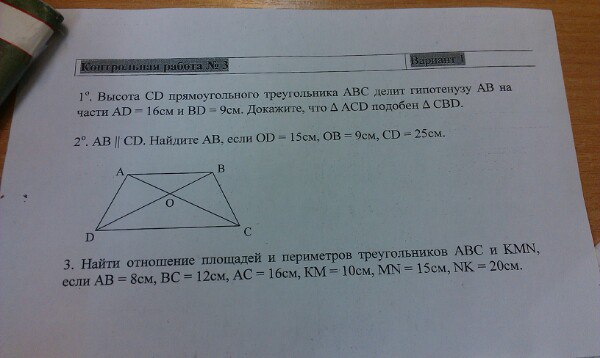
Закон косинусов:
Где – длина неизвестной стороны, и – длины известных сторон, и – угол между и .
Из задачи:
Сообщить об ошибке
является параллелограммом. Найдите длину диагонали .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти длину диагонали, мы можем рассмотреть только треугольник и использовать закон косинусов, чтобы найти длину неизвестной стороны.
Закон косинусов:
Где — длина неизвестной стороны, и — длины известных сторон, и — угол между и.
Из задачи:
Сообщить об ошибке
является параллелограммом. Найдите длину диагонали. .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти длину диагонали, мы можем рассмотреть только треугольник и использовать закон косинусов, чтобы найти длину неизвестной стороны.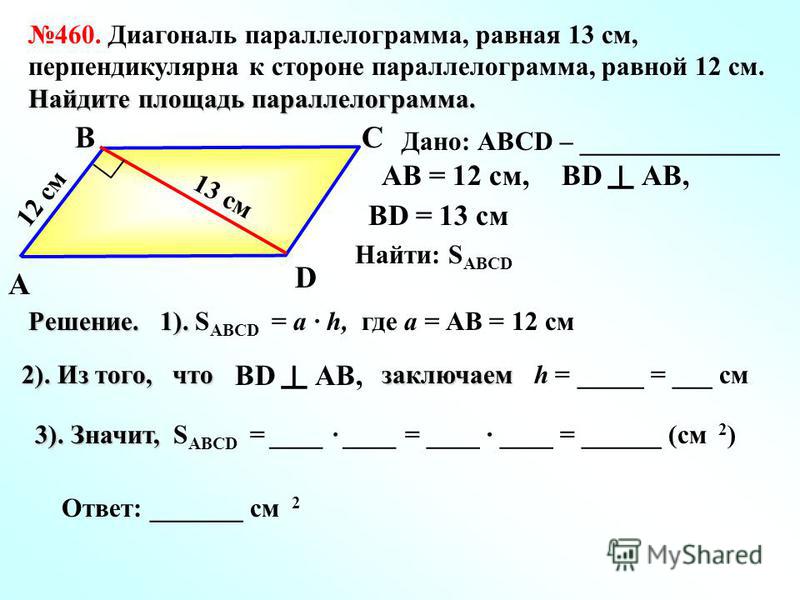
Закон косинусов:
Где – длина неизвестной стороны, и – длины известных сторон, и – угол между и .
Из задачи:
Сообщить об ошибке
является параллелограммом. Найдите длину диагонали .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти длину диагонали, мы можем рассмотреть только треугольник и использовать закон косинусов, чтобы найти длину неизвестной стороны.
Закон косинусов:
Где – длина неизвестной стороны, и – длины известных сторон, и – угол между и .
Из проблемы:
Сообщить об ошибке
Уведомление об авторских правах
Все ресурсы ACT Math
14 диагностических тестов 767 практических тестов Вопрос дня Карточки Learn by Concept
Математика, часть II Решения для 9-го класса по математике, глава 5
Математика, часть II Решения Решения для 9-го класса по математике, глава 5 Четырехугольники представлены здесь с простыми пошаговыми объяснениями. Эти решения для четырехугольников чрезвычайно популярны среди учащихся 9-го класса по математике. Решения для четырехугольников пригодятся для быстрого выполнения домашних заданий и подготовки к экзаменам. Все вопросы и ответы из сборника решений по математике, часть II, класс 9Математика Глава 5 предоставляется здесь для вас бесплатно. Вам также понравится безрекламный опыт решения Mathematics Part II Solutions Solutions от Meritnation. Все решения по математике, часть II Решения для класса 9 по математике подготовлены экспертами и на 100% точны.
Эти решения для четырехугольников чрезвычайно популярны среди учащихся 9-го класса по математике. Решения для четырехугольников пригодятся для быстрого выполнения домашних заданий и подготовки к экзаменам. Все вопросы и ответы из сборника решений по математике, часть II, класс 9Математика Глава 5 предоставляется здесь для вас бесплатно. Вам также понравится безрекламный опыт решения Mathematics Part II Solutions Solutions от Meritnation. Все решения по математике, часть II Решения для класса 9 по математике подготовлены экспертами и на 100% точны.
Страница № 62:
Вопрос 1:
Диагонали параллелограмма WXYZ пересекаются друг с другом в точке O. Если ∠XYZ = 135°, то какова мера ∠XWZ и ∠YZW ?
Если л (OY)= 5 см, то л (ВГ)= ?
Ответ:
В параллелограмме противоположные углы равны.
∠XYZ = ∠XWZ = 135°
Кроме того, WX || ZY
Итак, ∠YZW + ∠XWZ = 180° (Поскольку внутренние углы по одну сторону от секущей являются дополнительными)
⇒∠YZW+135°=180°⇒∠YZW=45°
)= 5
мы знаем, что диагонали параллелограмма делят друг друга пополам.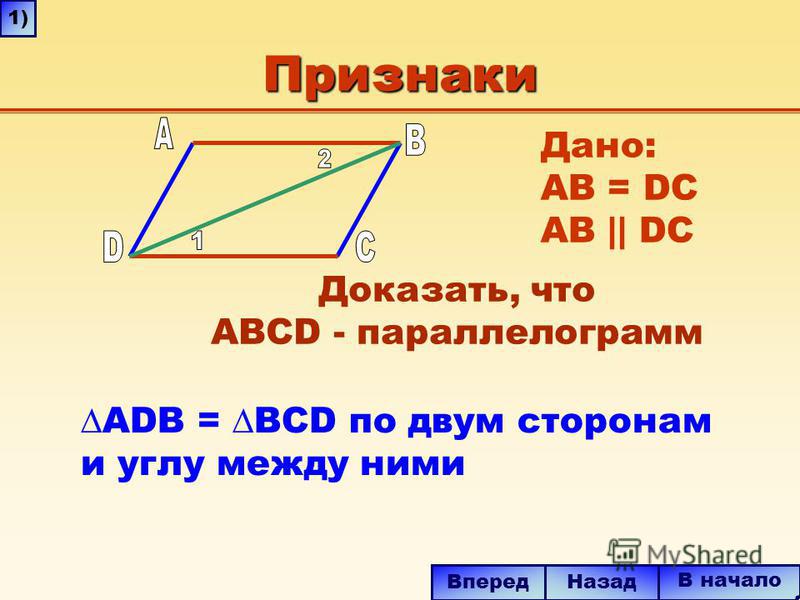
Итак, l (WY) = 2×OY=2×5=10 см
Страница № 62:
Вопрос 2:
В параллелограмме ABCD, если ∠A = 3x + 2°, ∠B = 2x — 32°, найдите значение x , а затем найдите меры ∠C и ∠D.
Ответ:
Внутренние углы по одну сторону от секущей являются дополнительными.
∠A +∠B = 180°
⇒3x + 12° + 2x — 32° = 180°
⇒5x-20=180°⇒5x=200⇒x=40° +12=132°
∠B=2x-32=2×40°-32=48°
Кроме того, противоположные углы параллелограмма равны.
∠A=∠C=132°∠B=∠D=48°
Страница № 62:
Вопрос 3:
Периметр параллелограмма равен 150 см. Одна его сторона больше другой на 25 см. Найдите длины всех сторон.
Ответ:
Периметр = 150 см
Пусть одна из сторон будет х .
Другая сторона = x+25
Периметр = сумма всех сторон
x+x+x+25+x+25=150⇒4x+50=150⇒4x=100⇒x=25
Таким образом, стороны равны 25 см. , 25 см, 50 см и 50 см
Страница № 62:
Вопрос 4:
Если отношение величин двух смежных углов параллелограмма равно 1 : 2, найдите величины всех углов параллелограмма.
Ответ:
Пусть два смежных угла равны x и 2x.
Внутренние углы по одну сторону от поперечной являются дополнительными.
Итак,
x+2x=180°⇒3x=180°⇒x=60°
Таким образом, смежные углы равны 60° и 120°.
Противоположные углы параллелограмма равны.
Итак, углы параллелограмма будут 60°, 120°, 60° и 120°.
Страница № 62:
Вопрос 5:
Диагонали параллелограмма пересекаются в точке O. Если AO = 5, BO = 12 и AB = 13, то покажите, что □ABCD является ромбом.
Ответ:
In △AOB,
AO = 5 см
OB = 12 см
AB = 13 см
5, 12 и 13 образуют пифагорову тройку.
Таким образом, △AOB — прямоугольный треугольник с прямым углом в точке O.
ABCD — параллелограмм.
Итак, диагонали делят друг друга пополам.
⇒AO = OC = 5 см
Также OB = OD = 12 см.
Таким образом, в параллелограмме ABCD диагонали делятся пополам под прямым углом.
Значит, ABCD — ромб.
Страница № 62:
Вопрос 6:
На данном рисунке □PQRS и □ABCR — два параллелограмма. Если ∠P = 110°, то найдите меры всех углов □ABCR.
Если ∠P = 110°, то найдите меры всех углов □ABCR.
Ответ:
В □PQRS,
∠P = 110°
Мы знаем, что противоположные углы параллелограмма равны.
Итак, ∠P = ∠R = 110°
В □ABCR
∠R =∠B = 110° (Противоположные углы параллелограмма равны)
Внутренние углы по одну сторону от поперечной являются дополнительными.
Итак,
∠R+∠A=180°⇒110°+∠A=180°⇒∠A=180°-110°⇒∠A=70°
И ∠A =∠C = 110°.
Страница № 62:
Вопрос 7:
На данном рисунке □ABCD является параллелограммом. Точка E лежит на луче AB так, что BE = AB, тогда докажите, что прямая ED делит отрезок BC пополам в точке F.
Ответ:
□ABCD — параллелограмм
Итак, AD || CB
⇒ AD || BF
Дано: AB = BE, значит, B — середина AE.
Согласно теореме, обратной теореме о средней точке,
F является серединой DE. Итак, DF = FE
В △EBF и △DCF,
DF = FE (доказано выше)
DC = BE (Чередующиеся внутренние углы параллельных прямых AE и CD)
Таким образом, △EBF ≅ △DCF (конгруэнтность SAS)
Следовательно, FB = FC (CPCT)
Следовательно, ED делит пополам сегмент BC в точке F.
Страница № 97:
0269
На данном рисунке □ABCD — параллелограмм, P и Q — середины сторон AB и DC соответственно, затем докажите, что □APCQ — параллелограмм.
Ответ:
□ABCD — параллелограмм,
AB ≅ CD и AB || CD
P и Q являются средними точками AB и CD соответственно.
Итак, AP ≅ CQ и AP || CQ
Таким образом, □APCQ также является параллелограммом.
Страница № 67:
Вопрос 2:
Используя тест на противоположные углы для параллелограмма, докажите, что каждый прямоугольник является параллелограммом.
Ответ:
Пусть ABCD — прямоугольник.
∠A = ∠B = ∠C = ∠D = 90°.
Чтобы любой четырехугольник был параллелограммом, пара противоположных углов должна быть конгруэнтна.
В прямоугольнике ABCD
∠A = ∠C = 90°
∠B = ∠D = 90°
Таким образом, прямоугольник ABCD является параллелограммом.
Страница № 67:
Вопрос 3:
На данном рисунке G – точка пересечения медиан ∆DEF. Возьмем точку H на луче DG такую, что D-G-H и DG = GH, затем докажем, что
Возьмем точку H на луче DG такую, что D-G-H и DG = GH, затем докажем, что
□GEHF — параллелограмм.
Ответ:
G — точка пересечения медиан ∆DEF.
Пусть точка, в которой медиана делит EF на две равные части, равна A.
Таким образом, EA = AF. …..(1)
мы знаем, что точка пересечения медиан делит каждую медиану в отношении 2 : 1.
Итак, пусть DG = 2 x и GA = x
Учитывая, что DG = GH
Итак, GA = AH = x
Таким образом, точка A делит EF и GH на две равные части.
Следовательно, □GEHF является параллелограммом, поскольку диагонали EF и GH делят друг друга пополам.
Страница № 67:
Вопрос 4:
Докажите, что четырехугольник, образованный пересечением биссектрис всех углов параллелограмма, является прямоугольником. параллелограмм.
⇒∠BAD+∠CDA=180° внутренние углы на одной стороне поперечной дополнительны⇒12∠BAD+12∠CDA=12×180°⇒∠SAD+∠SDA=90° . ….1
….1
∠SAD+∠SDA+∠ASD=180° Свойство суммы углов в △ASD⇒90°+∠ASD=180°⇒∠ASD=90°⇒ 9 ∠ Вертикально противоположные углы 90 273 Аналогично , ∠PQR=90°
⇒∠DAB+∠CBA=180° внутренние углы с одной и той же стороны поперечной дополнительны⇒12∠DAB+12∠CBA=12×180°⇒∠BAR+∠RBA = 9 ° RBA = В △ABR , ∠BAR+∠RBA+∠ARB=180°⇒90°+∠ARB=180°⇒∠ARB=90° Аналогично, ∠DPC=90°
Таким образом, PQRS представляет собой прямоугольник.
Страница № 67:
Вопрос 5:
Если на данном рисунке точки P, Q, R, S находятся на сторонах параллелограмма так, что AP = BQ = CR = DS, то докажите, что □PQRS является параллелограммом.
Ответ:
ABCD — параллелограмм
Значит, противоположные стороны равны и параллельны.
⇒AD≅BC и AB≅CD
Дано, AP = BQ = CR = DS
AD-SD=BC-BQ⇒AS=CQ …..1 (1))
AP = CR (Дано)
∠PAS=∠RCQ Противоположные углы параллелограмма равны Таким образом, △APS≅≅△RCQ SAS-конгруэнтность⇒SP=RQ жалеть.
Следовательно, PQRS — параллелограмм.
Страница № 69:
Вопрос 1:
Диагонали прямоугольника ABCD пересекаются в точке O. Если AC = 8 см, то найти BO, а если ∠CAD = 35°, то найти ∠ACB
Ответ:
03 Диагонали прямоугольника равны.Таким образом, AC = BD = 8 см
Кроме того, прямоугольник является параллелограммом, поэтому его диагонали делят друг друга пополам.
Таким образом, BO = OD = 4 см
Теперь, AD || CB
Итак, ∠CAD = ∠ACB = 35° (Поскольку внутренние углы равны)
Страница № 69:
Вопрос 2:
В ромбе PQRS, если PQ = 7,5, найдите QR. Если ∠QPS = 75°, найдите меру ∠PQR и ∠SRQ.
Ответ:
Все стороны ромба равны.
Итак, PQ = QR = 7,5 см
Ромб также является параллелограммом, поэтому
∠QPS = ∠SRQ = 75° (противоположные углы параллелограмма конгруэнтны)
Кроме того, ∠QPS + ∠PQR = 180° (внутренние углы по одну сторону от секущей являются дополнительными)
+ 180°⇒∠PQR=105°
Страница № 69:
Вопрос 3:
Диагонали квадрата IJKL пересекаются в точке M. Найдите меры ∠IMJ, ∠JIK и ∠LJK .
Найдите меры ∠IMJ, ∠JIK и ∠LJK .
Ответ:
Диагонали квадрата перпендикулярны друг другу.
Итак, ∠IMJ = 90°.
У квадрата все 4 угла прямые.
Кроме того, диагонали квадрата делят противоположные углы пополам.
Итак, ∠JIK = 12×90°=45°
Аналогично, ∠LJK = 12×90°=45°
Страница № 69:
Вопрос 4:
Диагонали ромба равны 20 см и 21 см. соответственно, то найти сторону ромба и его периметр.
Ответ:
Пусть ABCD — ромб.
AC = 20 см и BD = 21 см
Мы знаем, что диагонали ромба делятся пополам под прямым углом.
Итак, АО = ОС = 10 см
А ВО = ОД = 10,5 см
В △АОБ,
АО2+ОВ2=АВ2⇒102+10,52=АВ2⇒100+110,25=АВ2⇒АВ2=210,25⇒АВ=14,5 см
Таким образом, каждая сторона ромба = 14,5 см.
Периметр = AB + BC + CD + DA = 14,5 + 14,5 + 14,5 + 14,5 = 58 см.
Страница № 69:
Вопрос 5:
Укажите с указанием причин, являются ли следующие утверждения «верными» или «ложными».
(i) Каждый параллелограмм является ромбом.
(ii) Каждый ромб является прямоугольником.
(iii) Каждый прямоугольник является параллелограммом.
(iv) Каждый квадрат является прямоугольником.
(v) Каждый квадрат является ромбом.
(vi) Каждый параллелограмм является прямоугольником.
Ответ:
(i) Каждый параллелограмм является ромбом.
Неверно, каждый ромб является параллелограммом, но наоборот неверно.
(ii) Каждый ромб является прямоугольником.
Неверно, так как в прямоугольнике все углы прямые, а в ромбе то же самое неверно.
(iii) Каждый прямоугольник является параллелограммом.
Верно, что у всех прямоугольников противоположные пары сторон равны и параллельны, а диагонали делят друг друга пополам.
(iv) Каждый квадрат является прямоугольником.
Верно, так как все углы прямые, а диагонали конгруэнтны друг другу.
(v) Каждый квадрат является ромбом.
Верно, так как диагонали ромба являются перпендикулярными биссектрисами друг к другу, а также делят пополам пару противоположных углов.
(vi) Каждый параллелограмм является прямоугольником.
Неверно, так как в параллелограмме противоположные углы равны, но не прямые.
Страница № 71:
Вопрос 1:
В □IJKL, сторона IJ || сторона KL ∠I = 108° ∠K = 53°, тогда найдите меру ∠J и ∠L.
Ответ:
Дано: сторона IJ || сторона KL
Таким образом, внутренние углы по одну сторону от секущей будут дополнительными.
∠I + ∠L = 180º
⇒108° + ∠L = 180º
⇒∠L = 72º
Аналогично, ∠K + ∠J = 180º
⇒53° + ∠J = 180º
⇒∠J = 127º
Стр. CD , сторона ВС || сторона AD, сторона AB ≅ сторона DC. Если ∠A = 72°, то найдите меру ∠B и ∠D.
Ответ:
сторона BC || сторона AD
Внутренние углы на той же стороне поперечной являются дополнительными.
∠A + ∠B = 180º
⇒72° + ∠B = 180º
⇒∠B = 180º − 72°
⇒∠B = 108º
Конструкция: Draw BP || CD
Итак, до нашей эры || АД и БП || CD
⇒PBCD является параллелограммом
⇒CD ≅ BP
Теперь CD = BP и CD = AB
⇒BP = AB
⇒∠BAP=∠BPA=72°
BP || CD поэтому,
∠CDP=∠BPA=72° соответствующие углы равны
∠B = 108º
∠D = 72º (Рисунок 5. 32) сторона ВС || сторона AD и если сторона BA ≅ сторона CD, то докажите, что ∠ABC≅ ∠DCB.
32) сторона ВС || сторона AD и если сторона BA ≅ сторона CD, то докажите, что ∠ABC≅ ∠DCB.
Ответ:
Конструкция: Нарисовать линию CE || АБ
СЕ || AB (По конструкции)
AE || BC (Дай)
Итак, ABCE — параллелограмм.
Так как, AB || (соответствующие углы) (Дано)
Итак, CE ≅ CD
⇒ ∠CED = ∠CDE = ∠ x (равнобедренный треугольник) …..(2)
Из (1) и (2) имеем
∠BAE = ∠CDE = ∠ x ….. (3)
∠CEA = 180ºC – ∠ 0274 x
В параллелограмме противоположные углы равны. (4) ∆CED,
∠ECD+∠CED+∠EDC=180 °⇒∠ECD+x+x=180º⇒∠ECD=180º-2x
Теперь ∠DCB = ∠BCE + ∠ECD = x + 180º − 2 x = 180º − x
Таким образом, ∠ABC≅ ∠DCB
Страница № 73:
Вопрос 1:
На данном рисунке точки X, Y, Z являются серединами сторон AB, сторон BC и сторон AC ∆ABC соответственно. АВ = 5 см, АС = 9 см и ВС = 11 см. Найдите длину XY, YZ, XZ.
АВ = 5 см, АС = 9 см и ВС = 11 см. Найдите длину XY, YZ, XZ.
Ответ:
Учитывая, что X, Y и Z являются серединами сторон AB, BC и CA соответственно.
По теореме о средней точке,
XZ || BC и XZ = 12BC
BC = 11 см
⇒XZ = BC2=112=5,5 см
Аналогично,
XY=AC2=92=4,5 смYZ=AB2=52=2,5 см
Страница № 73:
Вопрос 2:
На данном рисунке □ PQRS и □ MNRL являются прямоугольниками. Если точка M является серединой стороны PR, то докажите, что
(i) SL = LR, (ii) LN = 12SQ.
Ответ:
(i) Учитывая, что M является серединой PR. …..(1)
∠PSR = ∠MLR = 90° (Поскольку □ PQRS и □MNRL являются прямоугольниками)
Таким образом, ЛМ || SP (соответствующие углы равны) …..(2)
Из (1) и (2) имеем
L — середина SR (обратная теорема о средней точке)
Таким образом, SL = LR
(ii)
∠RNM = ∠RQP = 90° (Поскольку □ PQRS и □MNRL являются прямоугольниками)
Таким образом, MN || PQ (соответствующие углы равны) . ….(4)
….(4)
Из (1) и (4) получаем
N является серединой RQ (Обратное из теоремы о средней точке)
Соедините LN и SQ
По теореме о средней точке,
LN || SQ и LN = 12SQ
Страница № 73:
Вопрос 3:
На данном рисунке ∆ ABC представляет собой равносторонний треугольник. Точки F,D и E являются серединами сторон AB, BC и AC соответственно. Покажите, что ∆FED — равносторонний треугольник.
Ответ:
∆ABC — равносторонний треугольник.
Итак, AB = BC = CA
⇒12AB=12BC=12CA⇒FB=BD=EC …..1
Точки F, D и E являются серединами сторон AB, сторон BC и сторон AC соответственно.
По теореме о средней точке
FE=12BC=BDDE=12AB=FBFD=12AC=EC
Из (1) имеем FB = BD = EC
Итак, FE = DE = FD
Таким образом, ∆FED равносторонний треугольник.
Страница № 73:
Вопрос 4:
На данном рисунке сегмент PD является медианой ∆ PQR. Точка T является средней точкой сегмента PD. Произведенный QT пересекает PR в точке M. Покажите, что PMPR= 13,9.0273 [Подсказка: DN || QM]
Точка T является средней точкой сегмента PD. Произведенный QT пересекает PR в точке M. Покажите, что PMPR= 13,9.0273 [Подсказка: DN || QM]
Ответ:
PD — это медиана QR.
Итак, D — середина QR.
DN рисуется параллельно QM.
Согласно теореме, обратной теореме о средней точке, N является серединой MR. …..(1)
Аналогично, T является серединой PD
Кроме того, DN || QM
Итак, согласно обратной теореме о средней точке,
M является серединой PN. …..(2)
Из (1) и (2) имеем
PM = MN = NR
⇒PMPR=PMPM+MN+NR=PMPM+PM+PM=13PM=13⇒PMPR=13
Отсюда доказано.
Страница № 73:
Вопрос 1:
Выберите правильный альтернативный ответ и заполните пропуски.
(i) Если все пары смежных сторон четырехугольника равны, то он называется ….
(A) прямоугольник (B) параллелограмм (C) трапеция, (D) ромб
( ii) Если диагональ квадрата равна 12 2 см, то периметр квадрата равен .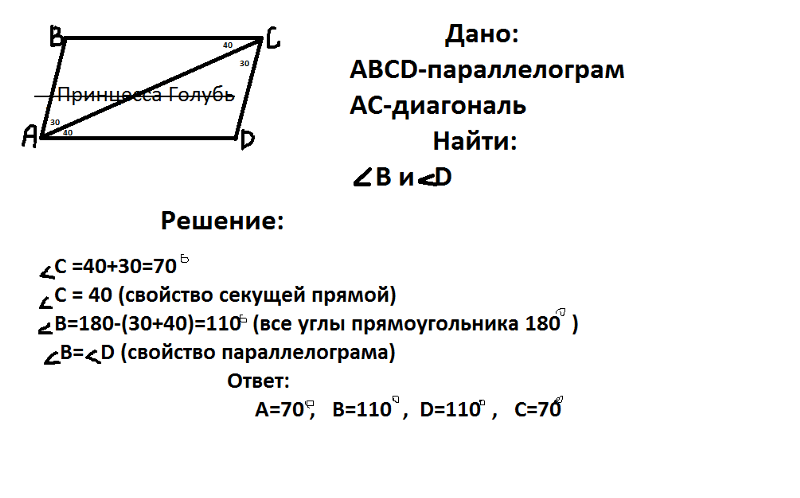 …..
…..
(A) 24 см (B) 24 2 см (C) 48 см (D) 48 2 см
(iii) Если противоположные углы ромба равны (2 x ) ° и (3 x — 40) ° тогда значение x равно …
(A) 100 ° (B) 80 ° (C) 160 ° 9083 3 ° 9083 3 ° 9083 3 ° 9083 3 ° 9086 30 40 5 (i) Если все пары смежных сторон четырехугольника равны, то это ромб. (ii) (iii) Ромб также является параллелограммом, поэтому , противоположные углы будут равны. Смежные стороны прямоугольника равны 7 см и 24 см. Найдите длину его диагонали. Если диагональ квадрата 13 см, то найдите его сторону. Соотношение двух смежных сторон параллелограмма равно 3 : 4, а его периметр равен 112 см. Найдите длину каждой его стороны. Пусть две стороны равны 3 х и 4 х . Диагонали PR и QS ромба PQRS равны 20 см и 48 см соответственно. Найдите длину стороны PQ. Диагонали прямоугольника PQRS пересекаются в точке M. Если ∠QMR = 50°, найдите меру ∠MPS. На соседнем рисунке Дано: seg AB || seg PQ , seg AB ≅seg PQ На данном рисунке □ABCD — трапеция. АБ || DC . Точки P и Q являются серединами отрезков AD и отрезков BC соответственно. На соседнем рисунке □ABCD — это трапеция AB || ОКРУГ КОЛУМБИЯ . Точки M и N являются серединами диагоналей AC и DB соответственно, тогда докажите, что MN || АБ. Ответ:
Следовательно, правильный ответ — вариант D.
Пусть диагональ AC = 122 см
, так как это квадрат, поэтому все углы равны 90°.
В △ABC мы применяем теорему Пифагора,
AB2+BC2=AC2⇒AB2+AB2=AC2 Итак, AB = BC = CD = AD = 12 см
Периметр квадрата ABCD = 4ABD = 4×12 см=48 см
Следовательно, правильный ответ — вариант C.
Таким образом, (2 x ) ° = (3 x — 40)°
⇒3x-2x=40°⇒x=40°
Следовательно, правильный ответ – вариант D.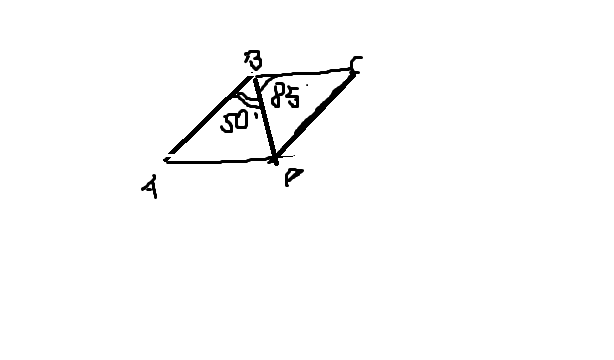
Номер страницы 74:
Вопрос 2:
Ответ:
В прямоугольнике все углы равны 90º.
О применении теоремы Пифагора в △ABD,
AB2+AD2=DB2⇒242+72=DB2⇒576+49=DB2⇒DB2=625⇒DB=25 см
Таким образом, длина диагонали равна 25 см. Страница № 74:
Вопрос 3:
Ответ:
Пусть PQRS будет квадратом.
Пусть диагональ SQ = 13 см
Все углы квадрата прямые.
В △SPQ, применяя теорему Пифагора,
SP2+PQ2=SQ2⇒SP2+SP2=SQ2 ∵Все стороны квадрата равны⇒2SP2=SQ2⇒2SP2=132⇒SP2=1692⇒SP=6,023 см. каждая сторона = 6,52 см. Страница № 74:
Вопрос 4:
Ответ:

В параллелограмме противоположные стороны равны.
Итак, стороны 3 x, 3 x, 4 x и 4 x
Периметр = 112 см
3x+3x+4x1x1x=112 14 ⇒x=8
Итак,
3x=3×8=24 см4x=4×8=32 см
Таким образом, стороны равны 24 см, 32 см, 24 см и 32 см. Страница № 74:
Вопрос 5:
Ответ:
Диагонали ромба делятся пополам под прямым углом.
PR = 20 см
⇒PO=12PR=12×20=10 см
Аналогично, QS = 48 см
⇒QO=12SQ=12×48=24 см PQ2⇒242+102=PQ2⇒PQ2=576+100⇒PQ2=676⇒PQ=26 см Страница № 74:
Вопрос 6:
Ответ:
В данном прямоугольнике PQRS
∠QMR = ∠PMS = 50° (противоположные углы равны)
(Диагонали прямоугольника равны)
Итак,
12SQ=12PR ⇒SM=PM
⇒∠MSP=∠MPS (Угол, противоположный равным сторонам, равен)
In △PMS,
∠PMS+∠MSP+∠MPS=180°⇒50°+2∠MPS=180°⇒2∠MPS=130°⇒∠MPS=65° :
если сегмент AB || сегмент PQ , сегмент AB ≅ сегмент PQ, сегмент AC || seg PR, seg AC ≅ seg PR, затем докажите, что seg BC || сегмент QR и сегмент BC ≅ сегмент QR.
Ответ:
Итак, ABQP является параллелограммом, так как пара противоположных сторон конгруэнтны и параллельны.
Таким образом, seg AP || сегмент BQ , сегмент AP ≅сегмент BQ …..(1)
Аналогично, сегмент AC || seg PR, seg AC ≅ seg PR
Итак, APRC — параллелограмм.
Таким образом, сегмент AP || seg CR, seg AP ≅ seg CR …..(2)
Из (1) и (2) имеем
seg BQ || seg CR
Кроме того, seg BQ ≅ seg CR
Таким образом, BQRC является параллелограммом, так как пара противоположных сторон конгруэнтны и параллельны.
Следовательно, сегмент BC || seg QR и seg BC≅seg QR, поскольку BQRC является параллелограммом. Страница № 74:
Вопрос 8:
Затем докажите, что PQ || AB и PQ = 12(AB + DC). Ответ:
Конструкция: Соединить PB и расширить его, чтобы встретить CD, произведенный в R.
Доказать: PQ || AB и PQ = 12( AB + DC)
Доказательство: в △ABP и △DRP,
∠APB=∠DPR Вертикально противоположные углы ∠PDA=∠PAB P – середина 9 н.э.0273 Таким образом, по соответствию ASA △ABP ≅ △DRP.
Согласно CPCT, PB = PR и AB = RD.
В △BRC
Q — середина BC (Дано)
P — середина BR (Поскольку PB = PR)
Итак, по теореме о средней точке, PQ || RC
⇒PQ || DC
Но АБ || DC (Дано)
Итак, PQ || АБ.
Кроме того, PQ = 12RC
PQ=12RD+DCPQ=12AB+DC ∵AB=RD Страница № 74:
Вопрос 9:
Ответ:
Строительство: Регистрация MN. Кроме того, присоедините DM и предъявите его AB в P.

 09.14
09.14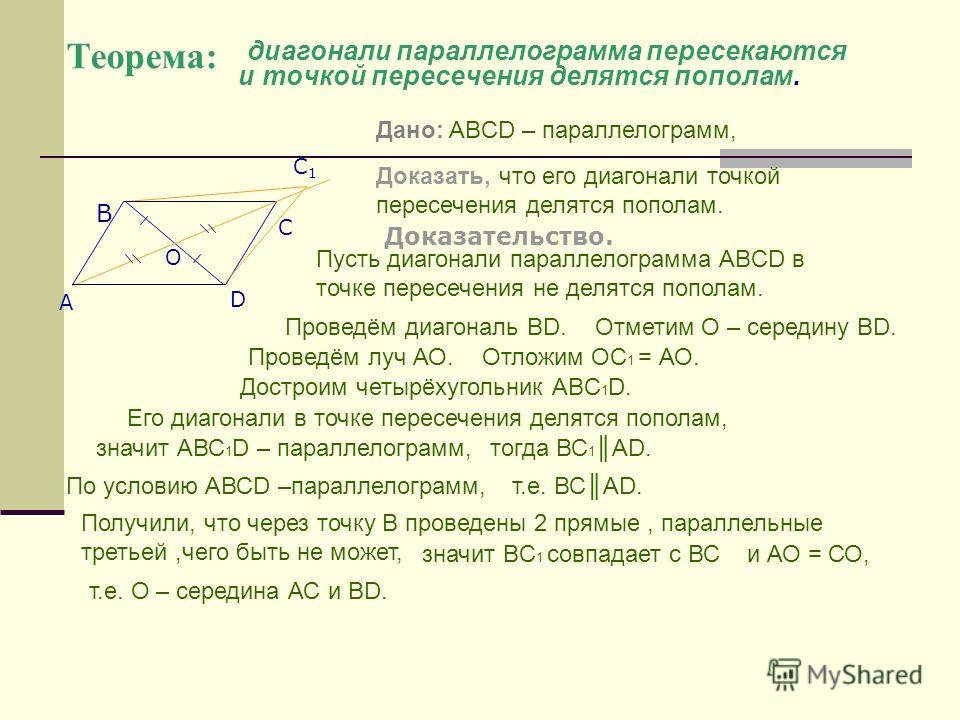
Leave A Comment