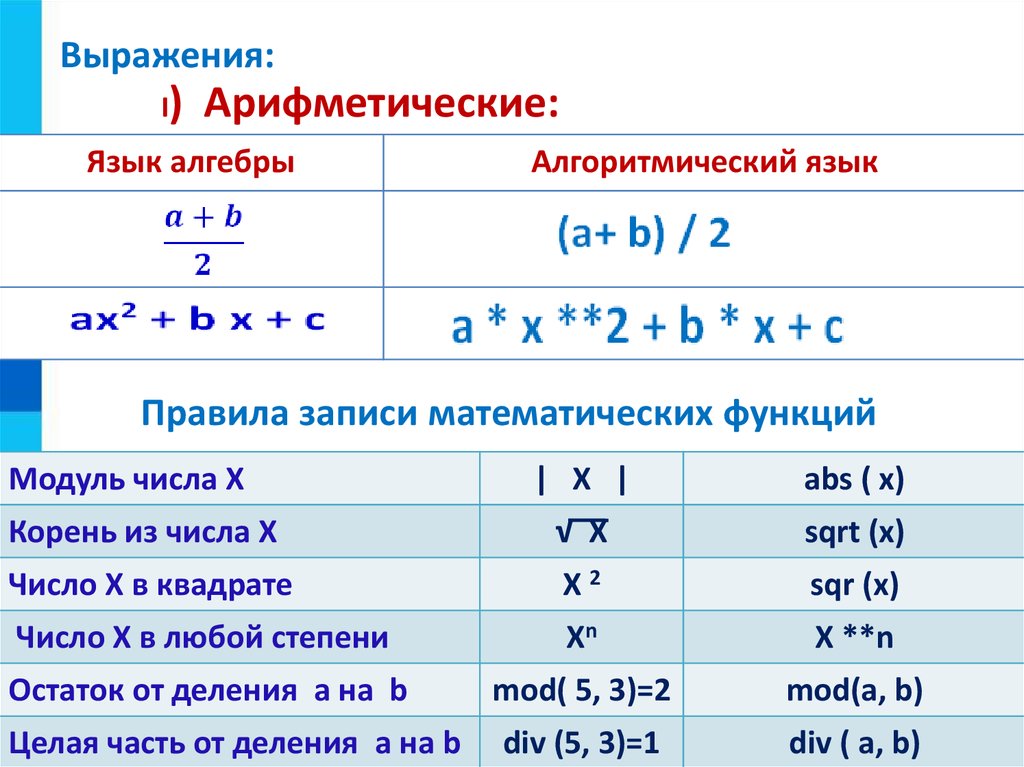
Скалярное произведение векторов. Формулы и определение
Поможем понять и полюбить математику
Начать учиться
325.5K
Числа можно сравнивать друг с другом, складывать, вычитать, умножать и делить. И так как скаляр не самое стандартное, но все таки число, с ним можно проделывать те же операции. Этот материал посвятим скалярному произведению векторов.
Основные определения
Система координат — это совокупность определений, позволяющих определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Мы уже рассказывали, как найти координаты точки.
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
Вектор с началом в точке A и концом в точке B принято обозначать как . Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: .
Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то есть число, которое не зависит от выбора системы координат.
При умножении вектора на вектор получается число. Если длины векторов , — это числа, косинус угла — число, то скалярное произведение этих векторов можно найти по формуле .
Чтобы разобраться в теме этой статьи, нам еще нужно узнать особенности угла между векторами.
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Угол между векторами
Угол между векторами может принимать значения от 0° до 180° градусов включительно. Аналитически это можно записать в виде двойного неравенства: либо .
Значок угла можно опустить и писать просто: .
Пусть даны два вектора .
Отложим их от некоторой точки О пространства: . . Тогда угол между векторами — это угол .
Угол между векторами может быть прямым, тупым, острым или равным нулю. Рассмотрим каждый случай:
1. Если векторы сонаправлены, то угол между ними равен 0°.
Так как косинус угла в 0° равен единице, то скалярное произведение сонаправленных векторов является произведением их длин. Если два вектора равны, то такое скалярное произведение называют скалярным квадратом.
2. Если угол между векторами равен 90°, то такие векторы перпендикулярны друг другу.
Если угол между векторами равен 90°, то такие векторы перпендикулярны друг другу.
Так как косинус прямого угла равен 0, то скалярное произведение перпендикулярных векторов равно 0.
3. Если векторы направлены в разные стороны, тогда угол между ними 180°.
Так как косинус угла в 180° равен -1, то скалярное произведение противоположно направленных векторов равно произведению их длин, взятому с обратным знаком.
Важно!
Так как косинус тупого угла отрицательный, то скалярное произведение векторов, которые образуют тупой угол, является тоже отрицательным.
Скалярное произведение векторов
Определение скалярного произведения можно сформулировать двумя способами:
Скалярное произведение двух векторов a и b дает в результате скалярную величину, которая равна сумме попарного произведения координат векторов a и b.
- Геометрическая интерпретация.
, где α — угол между векторами a и b
- Алгебраическая интерпретация.
Что важно запомнить про геометрическую интерпретацию скалярного произведения:
- Если угол между векторами острый и векторы ненулевые, то скалярное произведение положительно, так как cosα > 0.
- Если угол между векторами тупой и векторы ненулевые, то скалярное произведение отрицательно, так как cosα < 0.
- Если угол между векторами прямой, то скалярное произведение равно 0, так как cosα = 0.
Скалярное произведение в координатах
Вычисление скалярного произведения можно произвести через координаты векторов в заданной плоскости или в пространстве.
Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов и .
То есть для векторов , на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид:
А для векторов в трехмерном пространстве скалярное произведение в координатах находится так:
В n-мерном пространстве скалярное произведение векторов a = {a1; a2; … ; an} и b = {b1; b2; … ; bn} можно найти по формуле:
a * b = a1 * b1 + a2 * b2 + … + an * bn
Свойства скалярного произведения векторов
Скалярное произведение вектора самого на себя всегда больше или равно нулю.

Скалярное произведение вектора самого на себя равно квадрату его модуля:
Операция скалярного произведения коммуникативна, то есть соответствует переместительному закону:
Операция скалярного умножения дистрибутивна, то есть соответствует распределительному закону:
Сочетательный закон для скалярного произведения:
Если скалярное произведение двух ненулевых векторов равно нулю, то эти векторы ортогональны, то есть перпендикулярны друг другу:
Эти свойства очень легко обосновать, если отталкиваться от определения скалярного произведения в координатной форме и от свойств операций сложения и умножения действительных чисел.
Примеры вычислений скалярного произведения
Пример 1.
Вычислите скалярное произведение двух векторов →a и →b, если их длины равны 3 и 7 соответственно, а угол между ними равен 60 градусам.
Как решаем:
У нас есть все данные, чтобы вычислить скалярное произведение по определению:
Ответ: .
Пример 2.
Найти скалярное произведение векторов и , если .
Как решаем:
Используем формулу .
В данном случае:
Ответ: .
Пример 3.
Как найти скалярное произведение векторов и , если векторы и перпендикулярны и их длины равны 3 и 2 единицы соответственно.
По свойству дистрибутивности скалярного произведения имеем
Сочетательное свойство позволяет нам вынести коэффициенты за знак скалярного произведения:
В силу свойства коммутативности последнее выражение примет вид
Итак, после применения свойств скалярного произведения имеем
Осталось применить формулу для вычисления скалярного произведения через длины векторов и косинус угла между ними:
Ответ: .
Пример 4.
Как решаем:
Введем систему координат.
Если сделать выносной рисунок основания призмы, получим понятный плоскостной рисунок с помощью которого можно легко найти координаты всех интересующих точек.
Точка А имеет координаты (0;0;0). Точка С — (1;0;0). Точка В — (1/2;√3/2;0). Тогда точка В1 имеет координаты (1/2;√3/2;1), а точка С1 – (1;0;1).
Найдем координаты векторов и :
Найдем длины векторов и :
Найдем скалярное произведение векторов через их координаты и :
Найдем косинус угла между прямыми AB1 и BC1:
, ,
Ответ: 1/4.
Пример 5.
а) Проверить ортогональность векторов: и .
б) Выяснить, будут ли перпендикулярными отрезки KL и MN, если K(3;5), L(-2;0), M(8;-1), N(1;4).
Как решаем:
а) Выясним, будут ли ортогональны пространственные векторы. Вычислим их скалярное произведение: , следовательно .
б) Здесь речь идёт об обычных отрезках плоскости, а задача всё равно решается через векторы. Найдем их:
Вычислим их скалярное произведение: , значит, отрезки KL и MN не перпендикулярны.
Обратите внимание на два существенных момента:
- В данном случае нас не интересует конкретное значение скалярного произведения, важно, что оно не равно нулю.
- В окончательном выводе подразумевается, что если векторы не ортогональны, значит, соответствующие отрезки тоже не будут перпендикулярными.
 Геометрически это очевидно, поэтому можно сразу записывать вывод об отрезках, что они не перпендикулярны.
Геометрически это очевидно, поэтому можно сразу записывать вывод об отрезках, что они не перпендикулярны.
Ответ: а) , б) отрезки KL, MN не перпендикулярны.
Пример 6.
Даны три вершины треугольника A(-1; 0), B(3; 2), C(5; -4). Найти угол при вершине B — ∠ABC.
Как решаем:
По условию чертеж выполнять не требуется, но для удобства можно сделать:
Требуемый угол ∠ABC помечен красной дугой. Сразу вспоминаем школьное обозначение угла: ∠ABC — особое внимание на среднюю букву B — это и есть нужная нам вершина угла. Для краткости можно также записать просто ∠B.
Из чертежа видно, что угол ∠ABC треугольника совпадает с углом между векторами и , иными словами: .
Найдем векторы:
Вычислим скалярное произведение:
Вычислим длины векторов:
Найдем косинус угла:
Когда такие примеры не будут вызывать трудностей, можно начать записывать вычисления в одну строчку:
Полученное значение не является окончательным, поэтому нет особого смысла избавляться от иррациональности в знаменателе.
Найдём сам угол:
Если посмотреть на чертеж, то результат действительно похож на правду. Для проверки угол также можно измерить и транспортиром.
Ответ: ∠ABC = arccos(1/5√2) ≈1,43 рад. ≈ 82°
Важно не перепутать, что в задаче спрашивалось про угол треугольника, а не про угол между векторами. Поэтому указываем точный ответ: arccos(1/5√2) и приближенное значение угла: ≈1,43 рад. ≈ 82°, которое легко найти с помощью калькулятора.
А те, кому мало и хочется еще порешать, могут вычислить углы ∠A, ∠C, и убедиться в справедливости канонического равенства ∠A + ∠B + ∠C = 180°.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
101.8K
Сумма разрядных слагаемых
К следующей статье
473. 7K
7K
Построение графиков функций
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
371. На прямой даны три точки Л, Я и С, причём АВ = 83см, АС = 97см. Найдите длину отрезка ВС. Математика 5 класс Никольский С.М. – Рамблер/класс
371. На прямой даны три точки Л, Я и С, причём АВ = 83см, АС = 97см. Найдите длину отрезка ВС. Математика 5 класс Никольский С.М. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
371.
На прямой даны три точки Л, Я и С, причём АВ = 83см, АС = 97см. Найдите длину отрезка ВС. Сколько решений имеет задача?
ответы
ответ
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
3 класс
Репетитор
Химия
Алгебра
похожие вопросы 5
Значение выражения. ГДЗ Математика 6 класс Чесноков. Дидактические материалы по математике для 6 класса. Вар.1 Вопр.259
Кто выполнит? Найдите значение выражения:
(Подробнее…)
ГДЗМатематика6 классЧесноков А.С.
№ 149. ГДЗ Физика 10 класс Рымкевич. Какова масса тележки?
Помогите посчитать!
Под действием некоторой силы тележка, двигаясь из состояния покоя, прошла путь 40 см.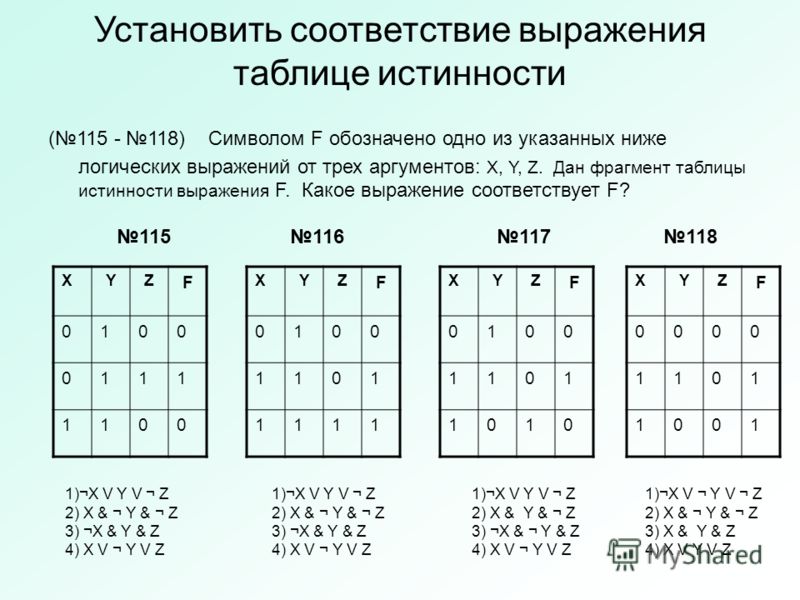 Когда на тележку (Подробнее…)
Когда на тележку (Подробнее…)
ГДЗФизика10 классРымкевич А.П.
Привет! Помогите определить вес мальчика. № 188. ГДЗ Физика 10 класс Рымкевич.
Определить вес мальчика массой 40 кг в положении А и В (рис. 51), если R1 = 20 м, v1= 10 м/с, R2 = 10 м, v2 = 5 м/с.
(Подробнее…)
ГДЗФизика10 классРымкевич А.П.
365. Постройте отрезки длиной 7 см, 11 см 4 мм, 14 см 6 мм. Никольский С.М. Математика 5 класс
365.
Постройте отрезки длиной 7 см, 11 см 4 мм, 14 см 6 мм.
ГДЗМатематика5 классНикольский С.М.
370. На прямой даны три точки Л, Я и С, причём АВ= 13см, АС = 4 см. Найдите длину отрезка ВС. 5 класс Математика Никольский С.М.
370.
На прямой даны три точки Л, Я и С, причём АВ= 13см, АС = 4 см. Найдите длину отрезка ВС. (Задача имеет два решения.)
ГДЗМатематика5 классНикольский С.М.
Эквивалентные выражения и примеры — Turito
Ювон говорит, что все три выражения эквивалентны.
- Найдите значение каждого выражения для n=1
- Найдите значение каждого выражения для n=2.
8n + 6, 2(4n + 3), 14n
Решение: Подставьте n=2, затем найдите значения данных выражений.
- Найдите значение каждого выражения для n=3.
8н + 6, 2(4н + 3), 14н
Решение: Подставьте n=2, затем найдите значения данных выражений.
- Критическое рассуждение
Согласны ли вы с Джувоном, что все три выражения эквивалентны? Объяснять.
Решение:
Нет, я не согласен с Ювоном.
8n+6 и 2(4n+3) эквивалентны.
Поскольку 2(4n+3) = 2x4n + 2×3 = 8n+6
Мы применили свойство распределения к сложению
a(b + c) = a(b) + a(c)
При подстановке одного и того же числа в два выражения, имеющие форму дистрибутивного свойства, всегда равны.
Аналогично, свойства операций
- Коммутативное свойство с добавлением и умножением
- Ассоциативное свойство с добавлением и умножением
- Распределительные свойства через добавление и выявление
OK, дайте эквивалентные выражения.
Эквивалентные выражения имеют одно и то же значение независимо от значения, которое заменяется на ту же переменную в выражениях.
Свойства операций
Коммутативное свойство
добавления A + B = B + A
Умножения A X B = B X A
Ассоциативная свойство
(A + B) + C = A A A A + ( b + c)
умножения (a x b) C = a × (b c)
Распределительное свойство
при сложении a(b + c) = a(b) + a(c)при вычитании a(b – c) = a(b) – a(c)
1:
Использовать свойства операций для записи эквивалентных выражений для 3(4x – 1) и 2x + 4?
Решение:
Case1
Используйте дистрибутив и ассоциативные свойства , чтобы написать выражение, эквивалентное 3(4x – 1).
3(4x – 1) = 3(4x) – 3(1) ……. Распределительное свойство
= (3.4) x – 3 ….. Ассоциативное свойство умножения
∴ 3(4x – 1) = 12x – 3
12x – 3 и 3(4x – 1) являются эквивалентными выражениями.
Случай 2:
Используйте распределительное свойство в обратном порядке, чтобы написать выражение, эквивалентное 2x + 4.
Найдите общий делитель обоих членов, который больше
- 2х + 4 =2(х) + 2(2) …………. Распределительное свойство
= 2(x+2) ……………2 – общий множитель
Итак, 2(x 2) эквивалентно 2x+4.
Попробуйте!
Напишите выражение, эквивалентное 3x – 27.
Решение:
Общий делитель 3 и 27 равен 3
3x – 2 0 0 3 (90 0 3 (x) – 3 (x) – =3(x– 9)
Итак, 3x – 27 эквивалентно 3(y – 9).
Пример 2
Какие из приведенных ниже выражений эквивалентны?
6x – 3 3x 3(2x – 1)
Решение:
3 (2x — 1) = 3 (2x) — 3 (1)
= 6x — 3
SO, 3 (2x — 1) и 6x — 3 — эквивалентные выражения
Шаг 2:
Свойства операции не могут определить эквивалентность выражений.
Либо 6x-3≠3x
3(2x-1) ≠3x
Таким образом, ни 6x-3, ни 3(2x-1) не эквивалентны 4x.
Пример 3:
Являются ли 6(n+3) – 4 и 6n + 14 эквивалентными выражениями?
Решение:
Шаг 1:
Используйте свойства операций для упрощения 6(n + 3) – 4.
6(n + 3) – 4 = 6(n) + 6(3) – 4 ……………. Используйте распределительное свойство
= 6n + 18 – 4
6(n + 3) – 4 = 6n+14
Обобщите, когда два выражения называют одно и то же число независимо от значения переменной, они эквивалентны.
Шаг 2:
Подставьте 3 вместо n , чтобы доказать эквивалентность выражений.
Случай 1:
6 (n + 3) — 4 = 6 (3) + 6 (3) — 4
= 18 + 18 — 4
6 (n + 3) — 4 = 32
Случай 2:
6n + 14 = (3) + 14
= 18+ 14
6n + 14 = 32
Итак, 6 (n + 3) — 4 и 6n + 14 — эквивалентные выражения.
Попробуй!
Являются ли 2(x – 3) + 1 и 2x + 6 эквивалентными выражениями? Используйте замену, чтобы оправдать свою работу.
Решение:
Использовать распределительное свойство:
2(x – 3) + 1 = 2x – 6 +1
0003
2 (x — 3) + 1 = 2x — 5
. Данное выражение составляет 2x + 6
, так что 2x — 6 ♠ 2x + 6.
Критика рассуждения
- Джейми говорит, что выражения 6x. — 2x + 4 и 4(x + 1) не эквивалентны, потому что в одном выражении есть вычитаемый член, а в другом нет. Вы согласны? Объяснять.
Решение:
Шаг 1:
6x – 2x + 4 = 4x + 4
Шаг 2:
4(x + 1) = 4x + 4
Нет, я не согласен, так как данные выражения эквивалентны.
- Два приведенных ниже выражения эквивалентны? Объяснять. 4(n + 3) – (3 + n) и 3n +9
Решение:
Шаг 1:
Использование распределительного свойства:
4(n + 3) – (3) = 4n + 12 – 3 – n
4(n + 3) – (3 + n) = 3n + 9
Итак, 4(n+3) – (3+n) = 3n+9
Мышление высшего порядка
3. Запишите выражение которое имеет только один термин и эквивалентно приведенному ниже выражению.
Запишите выражение которое имеет только один термин и эквивалентно приведенному ниже выражению.
(F.G 2 ) ÷ 5 — (G 2 . F)
Решение:
(F.G 2 ) ÷ 5 — (G 2 . F.G.G.G.G.G.G327 / (G 2 . 5
= ф.г 2 – 5 ф.г 2
= -4 f.g 2 / 5
Construct Arguments
- Команда колледжа Флориды по гольфу, состоящая из 14 человек, планирует торжественный банкет. Чтобы найти общую стоимость блюд, команда использует выражение 5 (g + 14), где g — количество гостей, пришедших на банкет. Член команды говорит, что эквивалентное выражение равно 5g + 14. Вы согласны? Объяснять.
Решение:
Я не согласен с членом команды,
Эквивалентная дробь для 5(g + 14)
5(g + 14) = 5(g) + 5(14)
= 5 g + 70
5g + 70 ≠ 5g + 14
Итак, утверждение члена команды неверно.
- Основной вопрос. Как определить и записать эквивалентные выражения?
- Структура использования. Какое свойство операций вы могли бы использовать, чтобы написать эквивалентное выражение для y + 3? Напишите эквивалентное выражение.
- Обобщение — Являются ли выражения z3 и 3z эквивалентными? Объяснять.
- Эквивалентны ли выражения 3(y + 1) и 3y +3 при y=1? у = 27 у = 3?
- Аргументы построения — эквивалентны ли выражения 3(y + 1) и 3y + 3 для любого значения y ?
- 6.Используйте свойства операций для завершения эквивалентных выражений.
и). 3(x-6) ii) 2x+10 iii) 8(2y + 2) iv) 5,7 +(3z +0,3)
- Напишите буквы выражений, эквивалентных данному выражению.
5(2x + 3)
а. 10x + 15 б. 5x + 15x c. 10x + 8
10x + 8
- Напишите алгебраическое выражение для площади прямоугольного ковра. Затем используйте свойства операций, чтобы написать эквивалентное выражение.
Ответы:
- возьмем следующие выражения:
2x + 18 и 2(x+ 9)
2(x+9) = 2x + 18
Таким образом, 2x + 18 и 2(x+9) эквивалентны выражениям.
Мы можем найти, что два выражения эквивалентны, записав их простейшие формы.
- По свойству коммутативности, a + b = b + a тогда,
y+3 = 3+y
- Данные выражения z3 и 3z не являются эквивалентными выражениями.
z3
≠ 3z
- Даны выражения 3(y + 1) и 3y +3
Если y = 1
, 3 (y+1) = 3 (1+1)
= 3 (2)
3 (y+1) = 6
3y+3 = 3 (1) + 3
3y + 3 = 3 + 3
3y + 3 = 6
Выражения 3 (y + 1) и 3y + 3 эквивалентны при замене y = 1
, если y = 27
Тогда,
3(y+1) = 3(27+1)
= 3(28)
3(y+1) = 84
3y+3 = 3(27) + 3
= 81 + 3
3y+3 = 84
Выражения 3(y+1) и 3y+3 эквивалентны при подстановке y=27.
Если y = 3
, то
3(y+1) = 3(3+1)
3)+3
= 9+3
3y+3 = 12
Выражения 3(y+1) и 3y+3 эквивалентны при подстановке y=3.
- Данные выражения 3(y+1) и 3y+3
, если y = 6
, 3 (y+1) = 3 (6+1)
= 3 (7)
= 21
3y+3 = 3 (6) +3
= 18 + 3
= 21
Итак, данные выражения эквивалентны.
- 3 (x — 6) = 3x — 18
- 2x + 10 = 10 + 2x
- 8 (y + 2) = 8y + 16
- 0005 5,7 + (3z + 0,3) = (5,7 + 3z) + 0,3
- Данное выражение равно 5(2x – 3)
5(2x – 3) = 10x – 15
вариант «a ”
- Дано, длина прямоугольного коврика = 2(x – 1)
ширина прямоугольного коврика = 5
Площадь прямоугольного коврика
= l × b кв. 1) × 5
1) × 5
= (2 × 5)(x – 1)……….. По коммутативному свойству умножения
= 10(x – 1) …………. По распределительному свойству вычитания.
∴ Площадь прямоугольного ковра = (10x – 10) квадратных единиц
Ключевое понятиеДва алгебраических выражения эквивалентны, если они имеют одинаковое значение, когда любое число заменяет переменную. Вы можете использовать свойства операций для записи эквивалентных выражений.
Свойства операций
- Переместительное свойство
сложения a + b = b + a
умножения a x b = b x a
- Ассоциативное свойство
сложения (a + b) + C = a + (b + c)
умножения (a x b) C = a × (b c)
- Распределительное свойство
сложения a(b) + c) = a(b) + a(c)
при вычитании a(b – c) = a(b) – a(c)
Ключевая концепция:
- Использование свойств операций для записи эквивалентных выражений .

- Использовать свойства идентификации эквивалентных выражений.
- Используйте подстановку для выравнивания эквивалентных выражений.
Концептуальная карта:
Вычисление алгебраических выражений,… Пошаговое решение математических задач
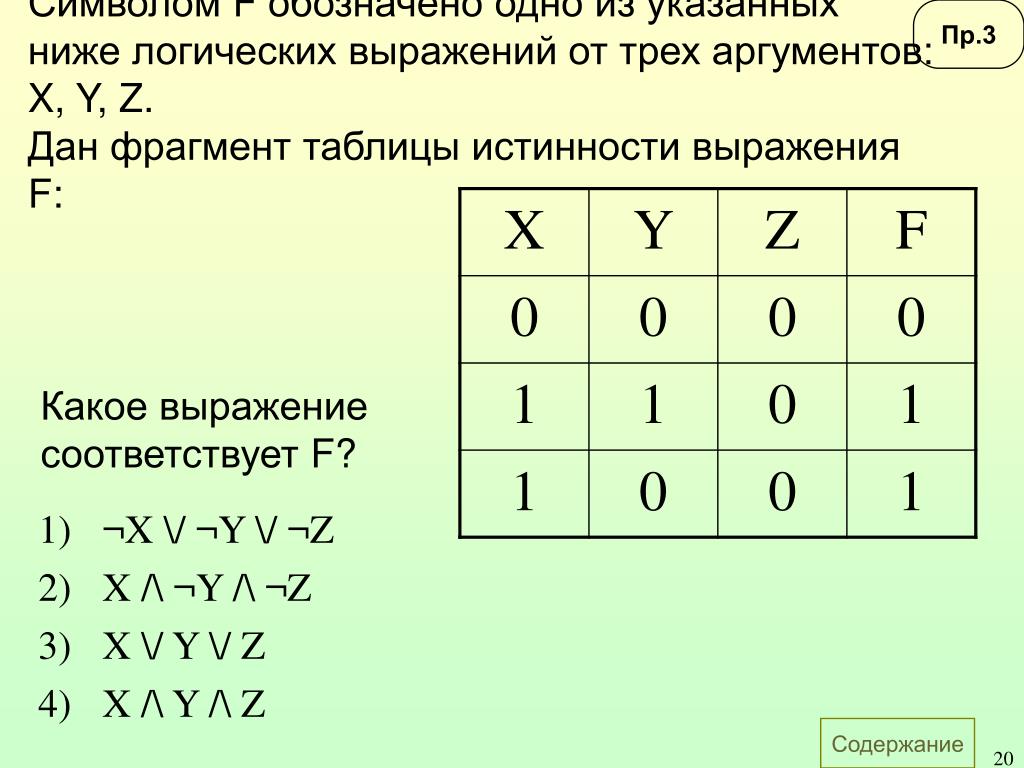
3.1 Вычисление алгебраических выражений
Тот же набор правил для целых чисел в порядке следования также используется с целыми числами. Правила изложены здесь для удобства использования
.
Правила порядка выполнения операций
1. Работайте с символами включения (скобки, квадратные или фигурные скобки), начиная с самой внутренней пары. 92 = 8 ÷ 4-9 показателей
= 2-9 деление
= -7 Вычитание
2. (7+8) ÷ 5*4-20
(7+8) ÷ 5*4-20 = 15 ÷ 5*4-20 скобков
= 3*4-20 Разделение
= 12-20 Умножение
= -8 Вычитание
3. 4*5- (6*2-3)+4 ÷ 2
4*5-(6*2-3)+4÷2=4*5-(9)+4÷2 скобки0003
= 13 вычитание и добавление
4. (-5-6)/11+3 (-5)
(-5-6)/11+3 (-5)
(-5-6)/11+3 (-5) =-11/11+3 (— 5) Дробная полоса является символом включения
= -1+(-15) Разделение и умножение
= -16 Дополнение
Практическая викторина

 Геометрически это очевидно, поэтому можно сразу записывать вывод об отрезках, что они не перпендикулярны.
Геометрически это очевидно, поэтому можно сразу записывать вывод об отрезках, что они не перпендикулярны.
 Одинаковые члены можно комбинировать, добавляя (или вычитая) коэффициенты.
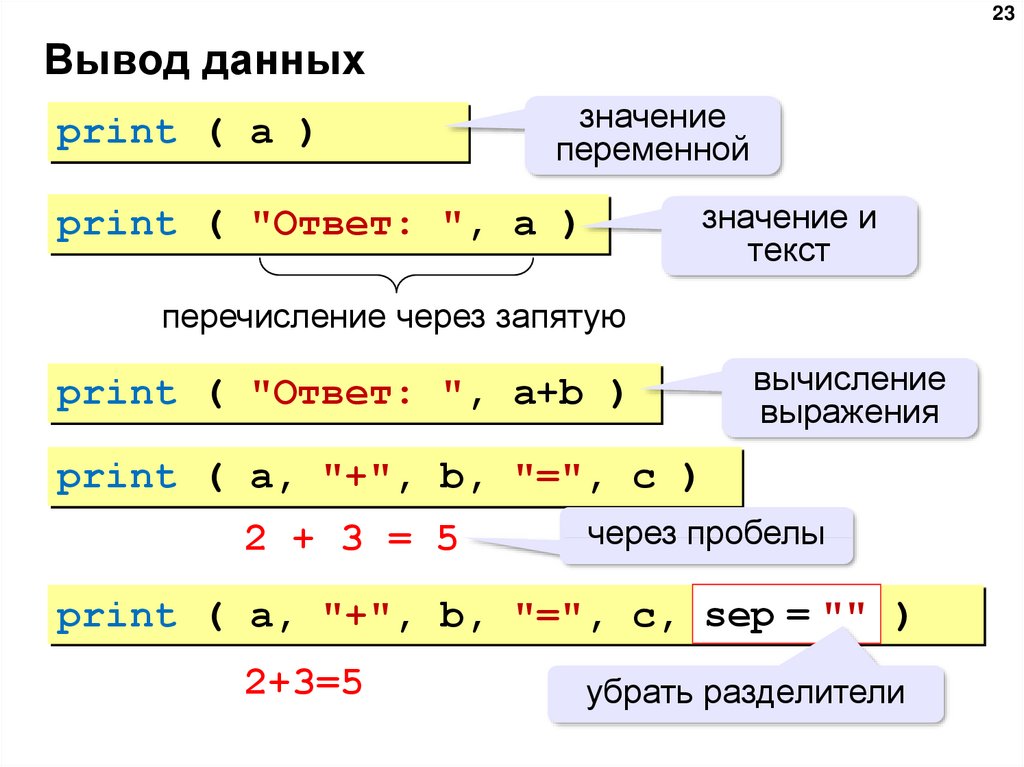
Одинаковые члены можно комбинировать, добавляя (или вычитая) коэффициенты. Итак, если задача сформулирована на английском языке, мы можем перевести фразы в алгебраические символы и приступить к решению задачи по правилам, разработанным для алгебры.
Итак, если задача сформулирована на английском языке, мы можем перевести фразы в алгебраические символы и приступить к решению задачи по правилам, разработанным для алгебры. произведение двух чисел x на y
произведение двух чисел x на y  7меньше числа
7меньше числа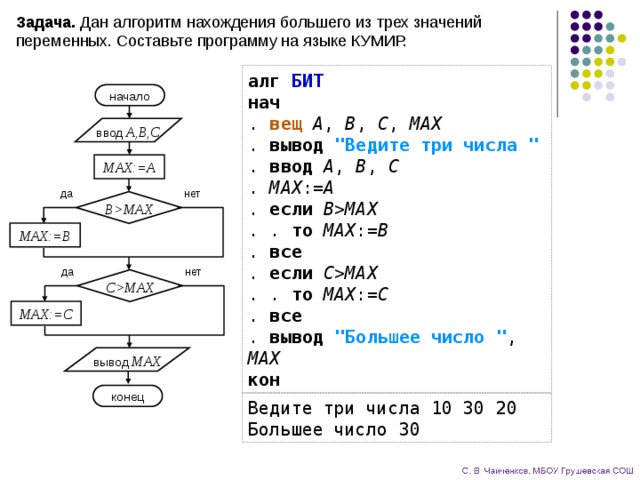
 (Это не включает упрощение выражений и комбинирование подобных терминов.)
(Это не включает упрощение выражений и комбинирование подобных терминов.)
 Верное утверждение будет получено, если нет ошибок.
Верное утверждение будет получено, если нет ошибок.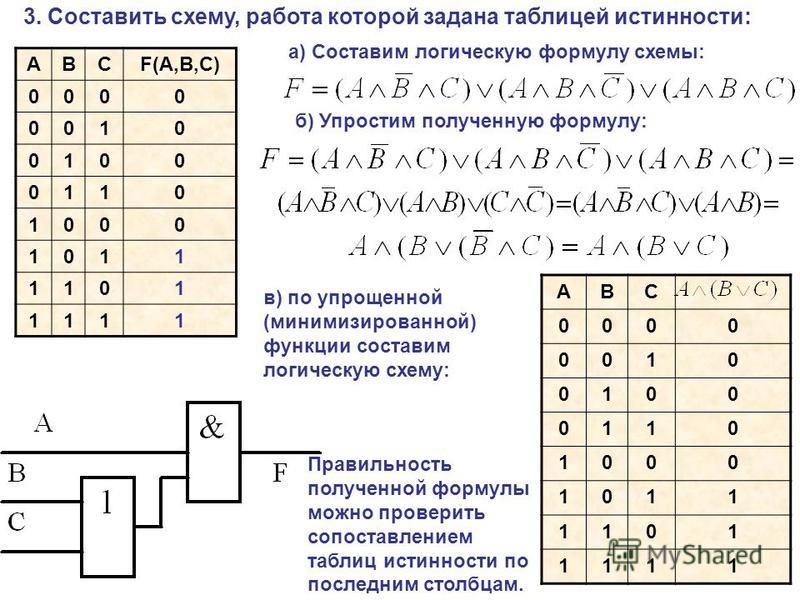 Какими будут показания в градусах Цельсия? Подстановка 212° вместо F дает
Какими будут показания в градусах Цельсия? Подстановка 212° вместо F дает Дана P=a+b+c Формула периметра треугольника
Дана P=a+b+c Формула периметра треугольника


Leave A Comment