постройте сечение, найдите расстояние от вершины до плоскости
Стереометрия
Задание 16 (Подготовка к ЕГЭ по математике 2015, под редакцией Ященко)
В правильной четырехугольной пирамиде SABCD основание ABCD — квадрат со стороной 6, а боковое ребро равно 9. На ребре SA отмечена точка M так, что SM = 6.
а) Постройте сечение пирамиды плоскостью, проходящей через точки B,C и M.
б) Найдите расстояние от вершины S до плоскости BCM.
Решение
Ответ:
Задание 16 (Подготовка к ЕГЭ по математике 2015, под редакцией Ященко)
В правильной четырехугольной призме ABCDA1B1C1D1 стороны основания равны 2, а боковые ребра равны 3.
а) Постройте прямую пересечения плоскостей ABC и BED1.
б) Найдите угол между плоскостями ABC и BED1.
Решение
Ответ:
Задание 16 (Подготовка к ЕГЭ по математике 2015, под редакцией Ященко)
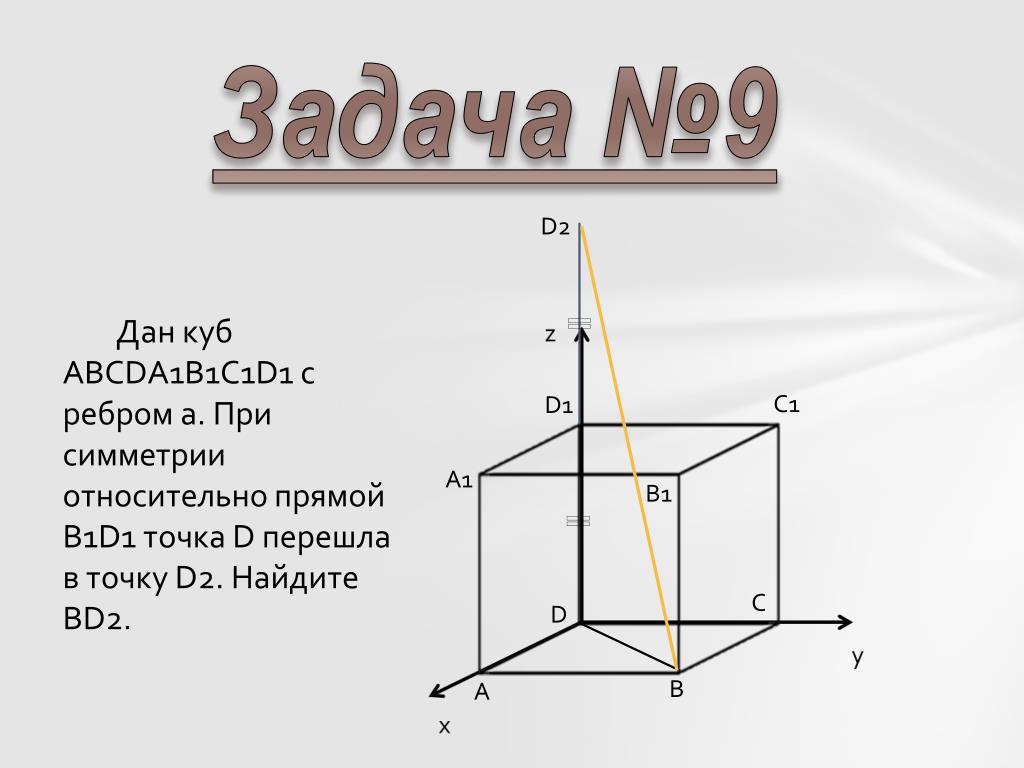
Дан куб ABCDA1B1C1D1.
а) Постройте сечение куба плоскостью, проходящей через точки B, A1 и D1.
б) Найдите угол между плоскостями BA1C1 и BA1D1.
Решение
Ответ:
Задание 16 (Подготовка к ЕГЭ по математике 2015, под редакцией Ященко)
Вокруг куба ABCDA1B1C1D1 с ребром 2 описана сфера. На ребре CC1 взята точка M так, что плоскость, проходящая через точки A, B и M
На ребре CC1 взята точка M так, что плоскость, проходящая через точки A, B и M
а) Постройте линию пересечения сферы и плоскости, проходяшей через точки A, B и M.
б) Найдите длину линии пересечения плоскости ABM и сферы.
Решение
Ответ:
Задание 16 (Подготовка к ЕГЭ по математике 2015, под редакцией Ященко)
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1
а) Постройте сечение призмы плоскостью, проходящей через точки B, A1 и F1.
б) Найдите расстояние от точки B до прямой A1F1.
Решение
Ответ:
1 2 3 4 5 6 7 8
ЕГЭ ФИПИ-2015, задача 16 (варианты 11, 12, 13)
Вариант 11
Дан куб ABCDA1B1C1D1.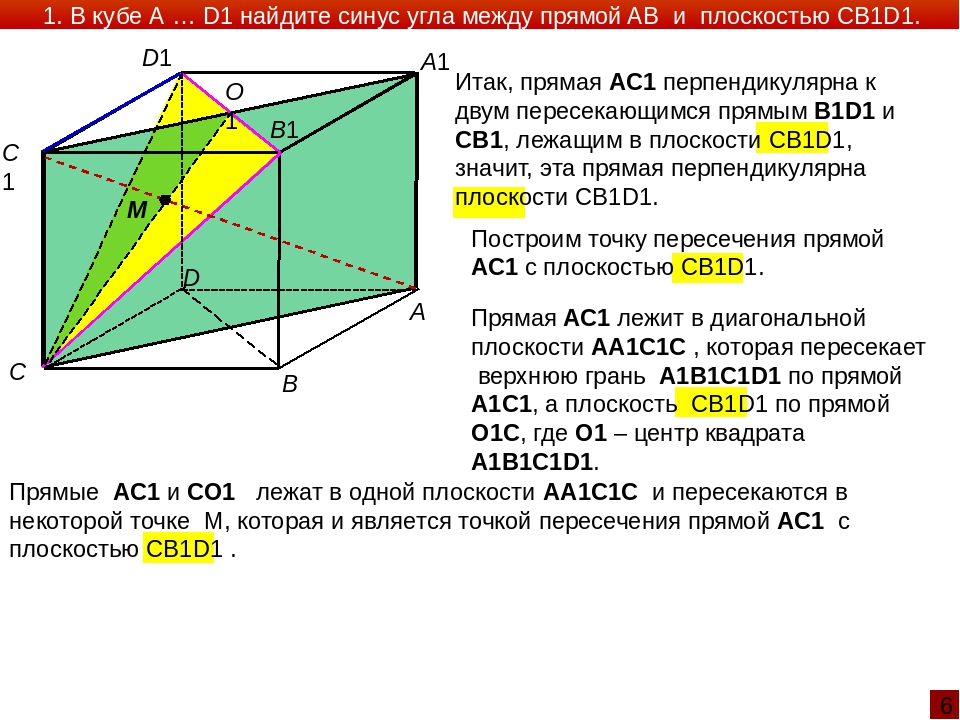
а) Постройте сечение куба плоскостью, проходящей через точки В, А1 и D1.
б) Найдите угол между плоскостями BA1C1 и BA1D1.
Решение.
а) Так как секущая плоскость пересекает верхнюю грань по ребру A1D1 , то и нижнюю грань она пересечет по прямой, проходящей через точку В и параллельной A1D1, т.е. по прямой ВС. Таким образом, прямоугольник A1D1СВ – плоскость сечения.
б) Проведем C1F⏊A1В (A1В – прямая по которой пересекаются плоскости BA
В равностороннем ∆ A1C1В отрезок C1F – высота. Если ребро куба обозначить через а, то
Точку F соединим с точкой К – центром квадрата BC1D1D ( задней грани куба). FK⊥А1В. Почему? Так как FK – отрезок, соединяющий центры передней и задней граней, то он будет перпендикулярен каждой из этих граней, а значит, будет перпендикулярен и отрезку А1В. Отрезок FK будет параллелен и равен ребрам ВС и A1D1, т.е. FK=a.
Отрезок FK будет параллелен и равен ребрам ВС и A1D1, т.е. FK=a.
Угол С1
По теореме косинусов найдем косинус угла С1FК.
Подставим все имеющиеся значения в (*).
Вариант 12
В правильной четырёхугольной пирамиде SABCD основание ABCD – квадрат со стороной 6, а боковое ребро равно 9. На ребре SA отмечена точка М так, что АM=6.
а) Постройте перпендикуляр из точки S на плоскость BCM.
б) Найдите расстояние от вершины S до плоскости BCM.
Решение.
Смотрите задачи вариантов 1 и 7. Чертеж чуть отличается, так как точка М делит боковое ребро на отрезки 6 и 3 (по условию АМ=6). Рассуждения те же.
а) Сечение пирамиды проходящее через точки В,С и М представляет собой равнобокую трапецию BMNC, KF – ось трапеции. Перпендикуляр из точки S на плоскость BCM — высота ∆SKF. В зависимости от угла SKF эта высота может лежать внутри ∆SKF или вне ∆SKF. Обозначим SKF через α и определим угол α из теоремы косинусов. Для этого нужно знать все стороны ∆SKF.
Перпендикуляр из точки S на плоскость BCM — высота ∆SKF. В зависимости от угла SKF эта высота может лежать внутри ∆SKF или вне ∆SKF. Обозначим SKF через α и определим угол α из теоремы косинусов. Для этого нужно знать все стороны ∆SKF.
Так же нужно определить угол φ при основании каждой боковой грани пирамиды.
Рассмотрим грань SAD.
Рассмотрим равнобедренную трапецию BMNC. Проведем МР⏊ВС. Так как МК=1,то PF=1 ⇒ BP=3-1=2. Из ∆BPM находим:
Наконец, из ∆SKF определяем косинус угла α:
Итак, cosα < 0, поэтому SKF – тупой, и высота ∆SKF, проведенная из вершины S лежит вне ∆SKF.
б) Проведем ST⏊KF и найдем ST из ∆STK. Отрезок ST и есть искомое расстояние от вершины S до плоскости ВСМ.
ST=SK·sin(π-α)=SK·sinα.
Вариант 13
Дан куб ABCDA1B1C1D1.
а) Постройте сечение куба плоскостью, проходящей через точки В, А1 и D1.
б) Найдите угол между плоскостями АВ1C1 и BA1D1.
Решение.
а) Так как секущая плоскость пересекает параллельные плоскости по параллельным прямым, то плоскость BA1D1 пересечет основание по прямой ВС, и искомое сечение – BA1D1C.
б) Аналогично строим плоскость AB1C1D.
Эти плоскости пересекаются по прямой ОО1, точки О и О1 – центры квадратов (передней и задней граней куба). Отрезок ОО1

Ответ: 90.
Презентация к 1-5 урокам стереометрии в 10 классе
Скрыть
Предмет стереометрии. Аксиомы стереометрии Уроки геометрии 1-5 в 10 классе Учитель математики МБОУ лицея №20 Первомайского района города Ростова-на-Дону Шемчук Н. К.
Предмет стереометрии. Аксиомы стереометрии
Аксиомы стереометрии
Что такое геометрия? Геометрия наука о свойствах геометрических фигур. Планиметрия изучает свойства фигур на плоскости. Стереометрия изучает свойства фигур в пространстве. Предмет стереометрии. Аксиомы стереометрии
4 слайд Описание слайда:Основные понятия планиметрии а . А точка прямая плоскость β
5 слайд Описание слайда:Стереометрия изучает свойства тел, их объёмы и площади
6 слайд Описание слайда:Что такое аксиома? Утверждение принимаемое без доказательства, называется аксиомой Какие аксиомы планиметрии вы знаете? Через любые две точки можно провести прямую, и притом только одну из трех точек прямой одна, и только одна, лежит между двумя другими
Задание 14 (стереометрия) — Решения вариантов ЕГЭ по математике: 2017, 2018, 2019, 2020
Подготовительные задания, стр. 128 15. Ребро SА пирамиды SАВС перпендикулярно плоскости основания АВС. а) Докажите, что плоскость, проходящая через середины рёбер АВ, АС и SА, параллельна плоскости SВС. 6) Найдите расстояние от вершины А до этой плоскости, если SА = Читать далее …
128 15. Ребро SА пирамиды SАВС перпендикулярно плоскости основания АВС. а) Докажите, что плоскость, проходящая через середины рёбер АВ, АС и SА, параллельна плоскости SВС. 6) Найдите расстояние от вершины А до этой плоскости, если SА = Читать далее …
Подготовительные задания, стр. 128 14. В правильной четырёхугольной пирамиде SАВСD с вершиной S сторона основания равна 8. Точка L — середина ребра SC. Тангенс угла между прямыми ВL и SА равен . а) Пусть О — центр основания пирамиды. Докажите, Читать далее …
Подготовительные задания, стр. 128 13. В правильной треугольной пирамиде SАВС с вершиной S, все рёбра которой равны 6, точ- ка М — середина ребра ВС, точка О — центр основания пирамиды, точка F делит отрезок SО в отношении 1:2, считая Читать далее …
Подготовительные задания, стр. 128 12. Основание прямой четырёхугольной призмы АВСDА1В1С1D1 — прямоугольник АВСD, в котором АВ = 5, AD = . Расстояние между прямыми АС и B1D1, равно 12. а) Пусть плоскость, проходящая через точку D перпендикулярно прямой ВD1 пересекает Читать далее …
Расстояние между прямыми АС и B1D1, равно 12. а) Пусть плоскость, проходящая через точку D перпендикулярно прямой ВD1 пересекает Читать далее …
Подготовительные задания, стр. 128 11. Основанием прямой треугольной призмы АВСА1В1С1, является равнобедренный треуголь- ник АВС, в котором АВ = ВС = 20, АС = 32. Боковое ребро призмы равно 24. Точка Р при- надлежит ребру ВВ1, причём ВР:РВ1 =1:3. а) Читать далее …
Подготовительные задания, стр. 128 10. Дан куб ABCDA1B1C1D1. а) Докажите, что сечение куба плоскостью, проходящей через центр куба перпендику- лярно диагонали AC1, является правильным шестиугольником. 6) Найдите угол между прямой АС1, и плоскостью ВСС1.
Подготовительные задания, стр. 128 9. Основание прямой четырёхугольной призмы АВСDА1В1С1D1, — прямоугольник АВСD, в котором АВ = 12, АD = . Расстояние между прямыми АС и B1D1, равно 5. а) Докажите, что плоскость, проходящая через точку D перпендикулярно прямой ВD1, Читать далее …
Подготовительные задания, стр. 128 8. В правильной шестиугольной пирамиде SАВСDЕF боковые рёбра равны 2, а стороны ос- нования — 1. а) Докажите, что плоскость, проходящая через вершину S и середины рёбер АF и СD, пер- пендикулярна плоскости основания. 6) Найдите Читать далее …
128 8. В правильной шестиугольной пирамиде SАВСDЕF боковые рёбра равны 2, а стороны ос- нования — 1. а) Докажите, что плоскость, проходящая через вершину S и середины рёбер АF и СD, пер- пендикулярна плоскости основания. 6) Найдите Читать далее …
Подготовительные задания, стр. 128 7. В правильной треугольной пирамиде SАВС с вершиной S, все рёбра которой равны 2, точ- ка М — середина ребра АВ, точка О — центр основания пирамиды, точка F делит отрезок SО в отношении 3 : Читать далее …
Подготовительные задания, стр. 128 6. В правильной треугольной пирамиде SABC с вершиной S, все рёбра которой равны 4, точ- ка N — середина ребра АС, точка О — центр основания пирамиды, точка Р делит отрезок SO вотношении 3:1, считая от Читать далее …
Подготовительные задания, стр. 128 5. В правильной треугольной призме АВСA1B1C1, все рёбра равны 1. а) Пусть плоскость, проходящая через точки С, С1 перпендикулярно плоскости АСС1, пе- ресекает прямую АВ вточке М. Докажите, что треугольник МВВ1 равнобедренный. 6) Найдите косинус угла Читать далее …
Докажите, что треугольник МВВ1 равнобедренный. 6) Найдите косинус угла Читать далее …
Подготовительные задания, стр. 128 4. Дана правильная четырёхугольная пирамида MABCD, рёбра основания которой равны . Точка L — середина ребра МВ. Тангенс угла между прямыми DM и AL равен . а) Пусть О — центр основания пирамиды. Докажите, что прямые Читать далее …
3. Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Расстояние между этими хордами равно . а) Докажите, что эта плоскость пересекает ось цилиндра. 6) Найдите угол между этой Читать далее …
2. Площадь основания правильной четырёхугольной пирамиды SABCD равна 64. а) Докажите, что плоскость, проходящая через вершину S и середины рёбер ВС и АD, со- держит высоту пирамиды. 6) Найдите площадь боковой поверхности этой пирамиды, если площадь сечения пирами- ды плоскостью Читать далее …
1. Площадь боковой поверхности правильной четырёхугольной пирамиды SABCD равна 108, а площадь полной поверхности этой пирамиды равна 144. а) Докажите, что плоскость SAC и плоскость, проходящая через вершину S, середину сто- роны АВ и центр основания, пересекаются по прямой, содержащей Читать далее …
Площадь боковой поверхности правильной четырёхугольной пирамиды SABCD равна 108, а площадь полной поверхности этой пирамиды равна 144. а) Докажите, что плоскость SAC и плоскость, проходящая через вершину S, середину сто- роны АВ и центр основания, пересекаются по прямой, содержащей Читать далее …
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А, В и С, а на окружности другого основания — точка С, причём СС1, — образующая цилиндра, а АС — диаметр основания. Известно, что угол АСВ=45°, Читать далее …
Дана пирамида PABCD, в основании которой трапеция ABCD большим основанием AD. Известно, что сумма углов BAD и ADC равна 90 градусов, а плоскости PAB и PCD перпендикулярны основанию, прямые AB и CD пересекаются в точке K. а) Доказать, что плоскость Читать далее …
В правильной 4х-угольной пирамиде , -середина a) Докажите, что плоскость перпендикулярна плоскости основания b) Найдите площадь сечения если площадь =6 Проведем диагональ CA, поделим ее на 4 равные части.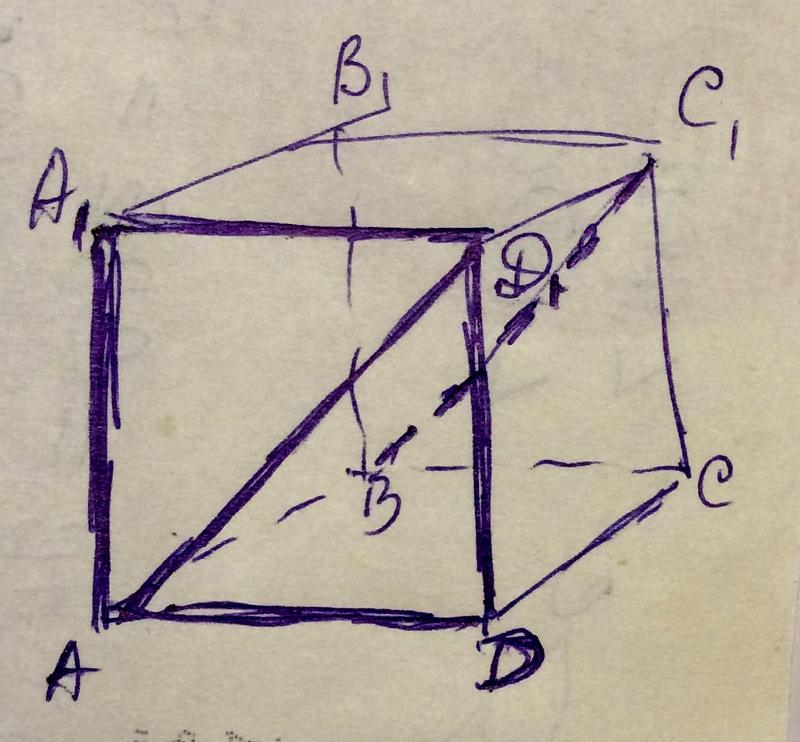 Возьмем на диагонали три равных отрезка . Возьмем на стороне три Читать далее …
Возьмем на диагонали три равных отрезка . Возьмем на стороне три Читать далее …
В правильной четырехугольной пирамиде сторона основания равна 6, а боковое ребро равно 7. На ребрах и отмечены точки и соответственно, причем . Плоскость содержит прямую и параллельна прямой . a) Докажите, что плоскость параллельна прямой b) Найдите расстояние от точки Читать далее …
В правильной треугольной пирамиде МАВС с основанием ABC стороны основания равны 6, а боковые рёбра равны 5. На ребре АС находится точка D, на ребре АВ находится точка Е, а на ребре AM — точка L. Известно, что AD = Читать далее …
На рисунке изображён многогранник, все двугранные углы которого прямые. а) Постройте сечение многогранника плоскостью, проходящей через точки А, В и С1 б) Найдите площадь этого сечения. Решается аналогично как здесь
В правильной треугольной пирамиде SABC с основанием ABC все ребра равны 6.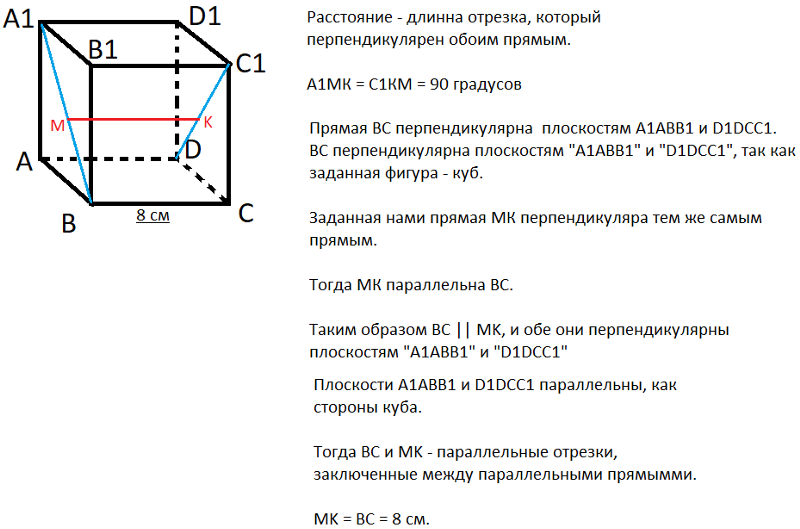 а) Постройте сечение пирамиды плоскостью, проходящей через вершину S и перпендикулярной отрезку, соединяющему середины ребер AB и BC. б) найдите расстояние от плоскости этого сечения до центра грани Читать далее …
а) Постройте сечение пирамиды плоскостью, проходящей через вершину S и перпендикулярной отрезку, соединяющему середины ребер AB и BC. б) найдите расстояние от плоскости этого сечения до центра грани Читать далее …
Похоже на решение вариантов 22 и 29. Посмотрите решение в варианте 22.
В правильной треугольной пирамиде МАВС с основанием ABC стороны основания равны 6, а боковые рёбра равны 8. На ребре АС находится точка D, на ребре АВ находится точка Е, а на ребре AM — точка L. Известно, что CD = Читать далее …
Радиус основания конуса равен 12, а высота конуса равна 5. а) Постройте сечение конуса плоскостью, проходящей через вершину конуса и взаимно перпендикулярные образующие. б) Найдите расстояние от плоскости сечения до центра основания конуса. Трехмерная картинка, которую можно крутить в 3D, Читать далее …
В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами АВ = 4 и ВС = 6.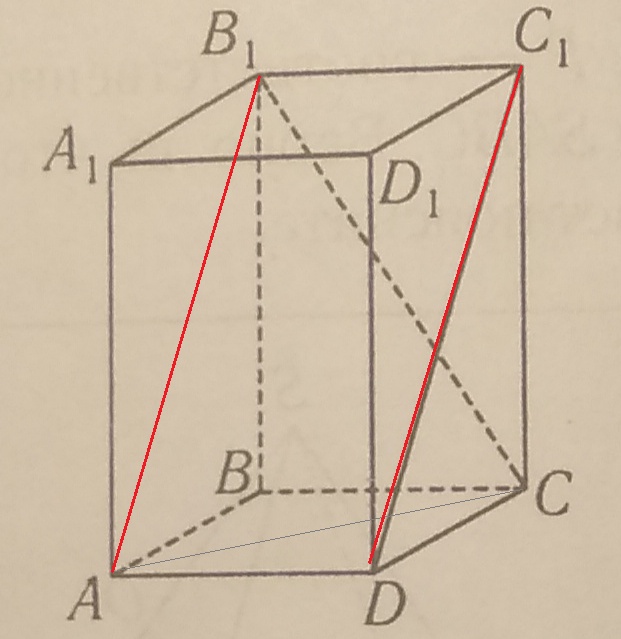 Длины боковых рёбер пирамиды SA = 3, SB = 5, SD = . а) Докажите, что SA — высота пирамиды. б) Найдите расстояние Читать далее …
Длины боковых рёбер пирамиды SA = 3, SB = 5, SD = . а) Докажите, что SA — высота пирамиды. б) Найдите расстояние Читать далее …
Вокруг куба с ребром 3 описана сфера. На ребре взята точка М так, что плоскость, проходящая через точки А, В, и М, образует угол 15° с плоскостью ABC. а) Постройте линию пересечения сферы и плоскости, проходящей через точки А, В Читать далее …
Высота цилиндра равна 3, а радиус основания равен 13. а) Постройте сечение цилиндра плоскостью, проходящей параллельно оси цилиндра, так, чтобы площадь этого сечения равнялась 72. б) Найдите расстояние от плоскости сечения до центра основания цилиндра. Трехмерная картинка, которую можно крутить Читать далее …
В кубе все рёбра равны 4. На его ребре отмечена точка K так, что KB=3. Через точки K и проведена плоскость α, параллельная прямой . а) Докажите, что , где Р — точка пересечения плоскости α с ребром . б) Читать далее …
В правильной четырёхугольной пирамиде SABCD все рёбра равны 1.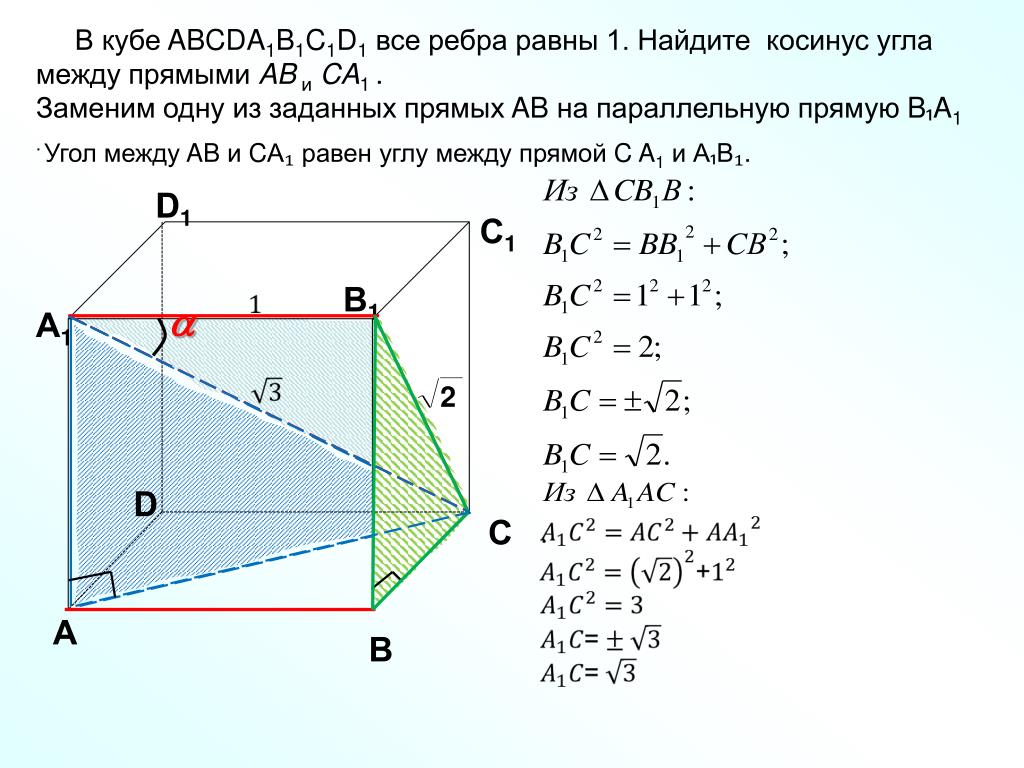 Точка F — середина ребра SB, G(она же Q) — середина ребра SC. а) Постройте прямую пересечения плоскостей ABQ и QDF. б) Найдите угол между плоскостями ABQ и QDF. Трехмерная картинка, Читать далее …
Точка F — середина ребра SB, G(она же Q) — середина ребра SC. а) Постройте прямую пересечения плоскостей ABQ и QDF. б) Найдите угол между плоскостями ABQ и QDF. Трехмерная картинка, Читать далее …
В правильной четырёхугольной пирамиде SABCD все рёбра равны 1. Точка F — середина ребра AS. а) Постройте прямую пересечения плоскостей SAD и BCF. б) Найдите угол между плоскостями SAD и BCF. Трехмерная картинка, которую можно крутить в 3D, доступна по Читать далее …
В правильной четырёхугольной пирамиде SABCD все рёбра равны 1. а) Постройте прямую пересечения плоскости SAD с плоскостью, проходящей через точку В перпендикулярно прямой AS. б) Найдите угол между плоскостью SAD и плоскостью, проходящей через точку В перпендикулярно прямой AS. Трехмерная Читать далее …
В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами АВ = 4 и ВС = 3. Длины боковых рёбер пирамиды SA = √11 , SB = 3√3, SD = 2√5. а) Докажите, что SA — высота пирамиды. б) Найдите Читать далее …
а) Докажите, что SA — высота пирамиды. б) Найдите Читать далее …
Вокруг куба с ребром 2 описана сфера. На ребре взята точка М так, что плоскость, проходящая через точки А, В, и М, образует угол 15° с плоскостью ABC. а) Постройте линию пересечения сферы и плоскости, проходящей через точки А, В Читать далее …
Дан куб . а) Постройте сечение куба плоскостью, проходящей через середины его рёбер . б) Найдите угол между плоскостью и плоскостью, проходящей через середины рёбер . Трехмерная картинка, которую можно крутить в 3D, доступна по ссылке https://ggbm.at/nAKXHwEB Пусть — ребро Читать далее …
Две параллельные плоскости, находящиеся на расстоянии 8 друг от друга, пересекают шар. Получившиеся сечения одинаковы, и площадь каждого из них равна 9π. а) Постройте эти сечения. б) Найдите площадь поверхности шара. Трехмерная картинка, которую можно крутить в 3D, доступна по Читать далее …
В правильной треугольной пирамиде SABC сторона основания АВ равна 60, а боковое ребро SA равно 37. Точки М и N — середины рёбер SA и SB соответственно. Плоскость содержит прямую MN и перпендикулярна плоскости основания пирамиды. а) Докажите, что плоскость Читать далее …
Точки М и N — середины рёбер SA и SB соответственно. Плоскость содержит прямую MN и перпендикулярна плоскости основания пирамиды. а) Докажите, что плоскость Читать далее …
В правильной четырёхугольной пирамиде SABCD основание ABCD — квадрат со стороной 6, а боковое ребро равно 9. На ребре SA отмечена точка М так, что AM = 6. а) Постройте перпендикуляр из точки S на плоскость ВСМ. б) Найдите расстояние Читать далее …
Дан куб . а) Постройте сечение куба плоскостью, проходящей через точки и . б) Найдите угол между плоскостями и . Трехмерная картинка, которую можно крутить в 3D, доступна по ссылке https://ggbm.at/mVj9KVSX
В правильной треугольной призме стороны основания равны 3, боковые рёбра равны 1, точка D — середина ребра . а) Постройте прямую пересечения плоскостей ABC и . б) Найдите угол между плоскостями ABC и . Решение аналогично варианту 15. Посмотрите решение Читать далее …
1.
 Взаимное расположение прямых в пространстве. Угол между двумя прямымиКак известно из курса планиметрии, две прямые в плоскости могут пересекаться (имеют общую точку) или быть параллельными (не имеют общую точку).
Взаимное расположение прямых в пространстве. Угол между двумя прямымиКак известно из курса планиметрии, две прямые в плоскости могут пересекаться (имеют общую точку) или быть параллельными (не имеют общую точку). В пространстве мы можем представить ситуацию, когда две прямые не пересекаются, но они и не параллельны.
Одна дорога проходит по эстакаде, а другая под эстакадой
Кабели моста
Горизонтальные линии крыши и вертикальные линии стен
Две прямые называются скрещивающимися, если они не лежат в одной плоскости.
Теорема «Признак скрещивающихся прямых»Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).
ДоказательствоРассмотрим прямую \(AB\), лежащую в плоскости, и прямую \(CD\), которая пересекает плоскoсть в точке \(D\), не лежащей на прямой \(AB\).

1. Допустим, что прямые \(AB\) и \(CD\) всё-таки лежат в одной плоскости.
2. Значит, эта плоскость идёт через прямую \(AB\) и точку \(D\), то есть, она совпадает с плоскостью \(α\).
3. Это противоречит условиям теоремы, по которым прямая \(CD\) не находится в плоскости \(α\), а пересекает её.
Теорема доказана.
В пространстве прямые расположены следующим образом:
1. параллельные;
2. пересекающиеся;
3. скрещивающиеся.
Теорема
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
ДоказательствоРассмотрим скрещивающиеся прямые \(AB\) и \(CD\).
1. Через точку \(D\) можно провести прямую \(DE\), параллельную \(AB\).
2. Через пересекающиеся прямые \(CD\) и \(DE\) можно провести плоскость \(α\).
3. Так как прямая \(AB\) не лежит в этой плоскости и параллельна прямой \(DE\), то она параллельна плоскости.
4. Эта плоскость единственная, так как любая другая плоскость, проходящая через \(CD\), будет пересекаться с \(DE\) и \(AB\), которая ей параллельна.
Теорема доказана.
Углы между прямыми
1. Если прямые параллельны, то угол между ними — 00.2. Углом между двумя пересекающимися прямыми называют величину меньшего из углов, образованных этими прямыми. Если все углы равны, то эти прямые перпендикулярны (образуют угол 900).
3. Углом между двумя скрещивающимися прямыми называют угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.
Обрати внимание!
Провести соответственные прямые, параллельные данным скрещивающимся прямым, можно через любую точку. Иногда удобно выбрать эту точку на одной из данных скрещивающихся прямых и провести через эту точку прямую, параллельную другой из скрещивающихся прямых.
Пример:
дан куб ABCDA1B1C1D1.
Найти угол между AB и B1D1.
Выберем точку B на прямой AB и проведём через B прямую BD параллельно B1D1.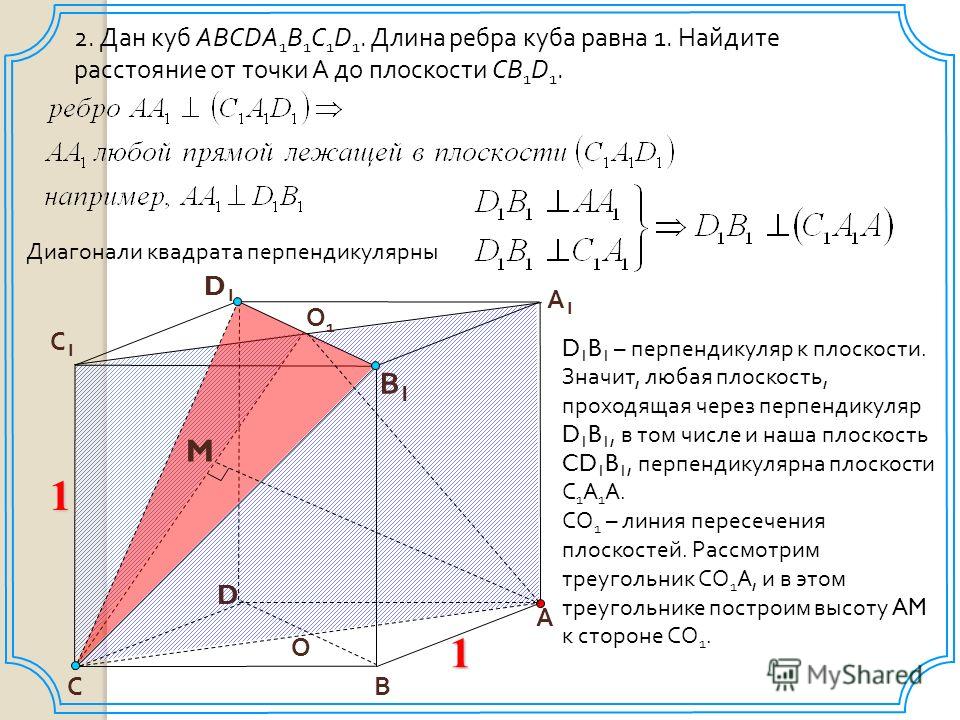
Угол между AB и BD — 450, так как ABCD — квадрат.
Соотвeтственно, угол между AB и B1D1 — тоже 450.
|
Сечение куба плоскостью
Задачи на построение сечений куба плоскостью, как правило, проще чем, например, задачи на сечения пирамиды.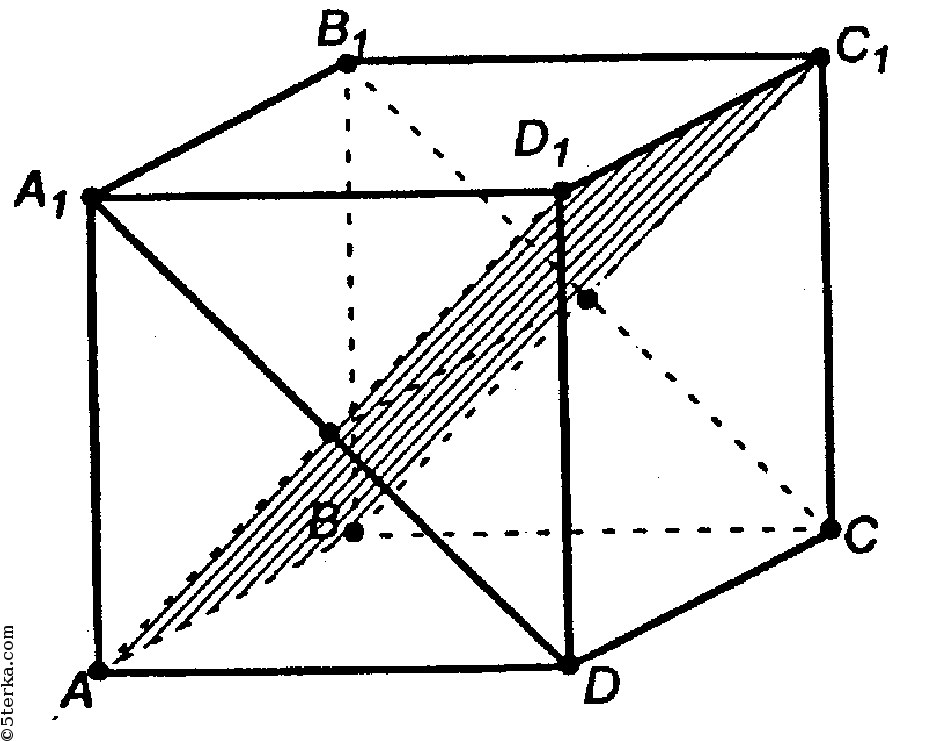
Провести прямую можем через две точки, если они лежат в одной плоскости. При построении сечений куба возможен еще один вариант построения следа секущей плоскости. Поскольку две параллельные плоскости третья плоскость пересекает по параллельным прямым, то, если в одной из граней уже построена прямая, а в другой есть точка, через которую проходит сечение, то можем провести через эту точку прямую, параллельную данной.
Рассмотрим на конкретных примерах, как построить сечения куба плоскостью.
1) Построить сечение куба плоскостью, проходящей через точки A, C и M.
Задачи такого вида — самые простые из всех задач на построение сечений куба. Поскольку точки A и C лежат в одной плоскости (ABC), то через них можем провести прямую. Ее след — отрезок AC. Он невидим, поэтому изображаем AC штрихом. Аналогично соединяем точки M и C, лежащие в одной плоскости (CDD1), и точки A и M, которые лежат в одной плоскости (ADD1). Треугольник ACM — искомое сечение.
2) Построить сечение куба плоскостью, проходящей через точки M, N, P.
Здесь только точки M и N лежат в одной плоскости (ADD1), поэтому проводим через них прямую и получаем след MN (невидимый). Поскольку противолежащие грани куба лежат в параллельных плоскостях, то секущая плоскость пересекает параллельные плоскости (ADD1) и (BCC1) по параллельным прямым. Одну из параллельных прямых мы уже построили — это MN.
Через точку P проводим прямую, параллельную MN. Она пересекает ребро BB1 в точке S. PS — след секущей плоскости в грани (BCC1).
Проводим прямую через точки M и S, лежащие в одной плоскости (ABB1). Получили след MS (видимый).
Плоскости (ABB1) и (CDD1) параллельны. В плоскости (ABB1) уже есть прямая MS, поэтому через точку N в плоскости (CDD1) проводим прямую, параллельную MS. Эта прямая пересекает ребро D1C1 в точке L. Ее след — NL (невидимый). Точки P и L лежат в одной плоскости (A1B1C1), поэтому проводим через них прямую.
Пятиугольник MNLPS — искомое сечение.
3) Построить сечение куба плоскостью, проходящей через точки M, N, P.
Точки M и N лежат в одной плоскости (ВСС1), поэтому через них можно провести прямую. Получаем след MN (видимый). Плоскость (BCC1) параллельна плоскости (ADD1),поэтому через точку P, лежащую в (ADD1), проводим прямую, параллельную MN. Она пересекает ребро AD в точке E. Получили след PE (невидимый).
Больше нет точек, лежащей в одной плоскости, или прямой и точки в параллельных плоскостях. Поэтому надо продолжить одну из уже имеющихся прямых, чтобы получить дополнительную точку.
Если продолжать прямую MN, то, поскольку она лежит в плоскости (BCC1), нужно искать точку пересечения MN с одной из прямых этой плоскости. С CC1 и B1C1 точки пересечения уже есть — это M и N. Остаются прямые BC и BB1. Продолжим BC и MN до пересечения в точке K. Точка K лежит на прямой BC, значит, она принадлежит плоскости (ABC), поэтому через нее и точку E, лежащую в этой плоскости, можем провести прямую. Она пересекает ребро CD в точке H. EH -ее след (невидимый).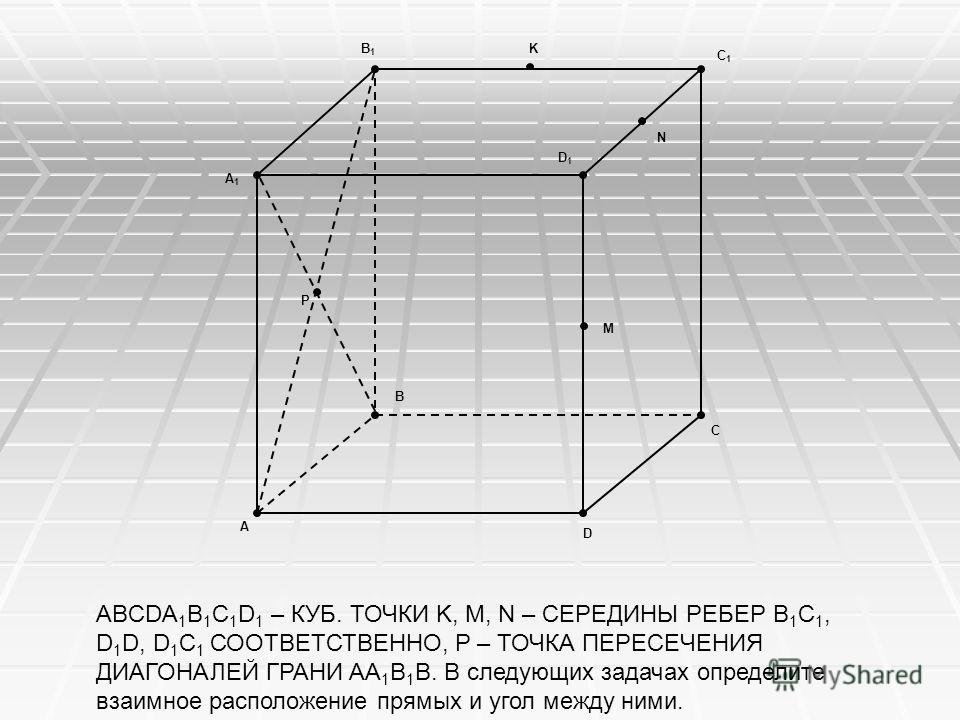 Поскольку H и N лежат в одной плоскости (CDD1), через них можно провести прямую. Получаем след HN (невидимый).
Поскольку H и N лежат в одной плоскости (CDD1), через них можно провести прямую. Получаем след HN (невидимый).
Плоскости (ABC) и (A1B1C1) параллельны. В одной из них есть прямая EH, в другой — точка M. Можем провести через M прямую, параллельную EH. Получаем след MF (видимый). Проводим прямую через точки M и F.
Шестиугольник MNHEPF — искомое сечение.
Если бы мы продолжили прямую MN до пересечения с другой прямой плоскости (BCC1), с BB1, то получили бы точку G, принадлежащую плоскости (ABB1). А значит, через G и P можно провести прямую, след которой PF. Далее — проводим прямые через точки, лежащие в параллельных плоскостях, и приходим к тому же результату.
Работа с прямой PE дает то же сечение MNHEPF.
4) Построить сечение куба плоскостью, проходящей через точку M, N, P.
Здесь можем провести прямую через точки M и N, лежащие в одной плоскости (A1B1C1). Ее след — MN (видимый). Больше нет точек, лежащих в одной плоскости либо в параллельных плоскостях.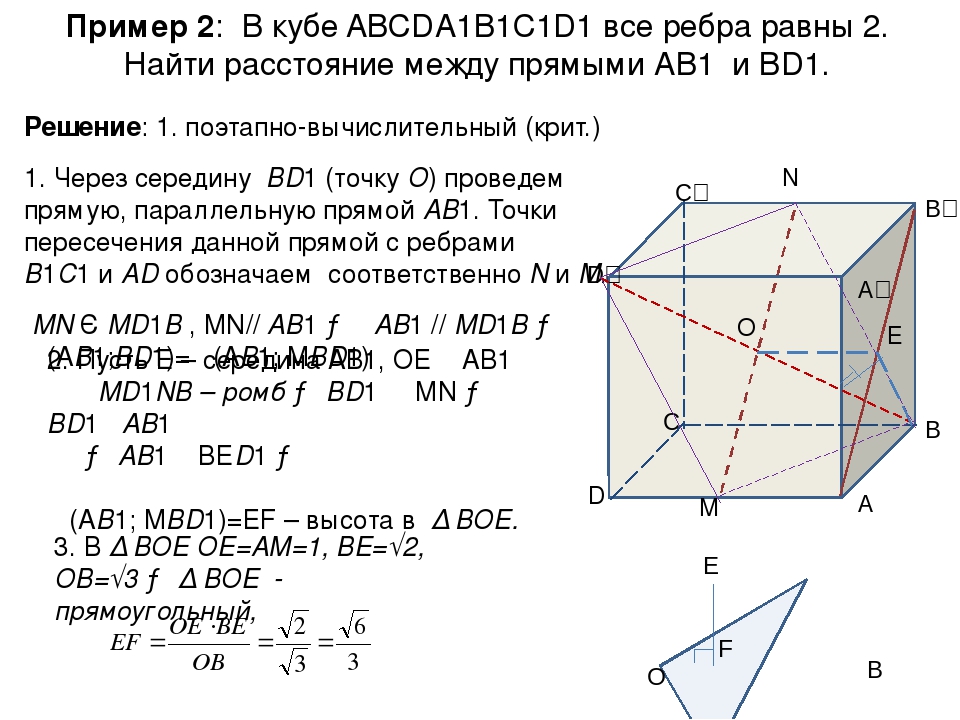
Продолжим прямую MN. Она лежит в плоскости (A1B1C1), поэтому пересечься может только с одной из прямых этой плоскости. С A1D1 и C1D1 точки пересечения уже есть — N и M. Еще две прямые этой плоскости — A1B1 и B1C1. Точка пересечения A1B1 и MN — S. Поскольку она лежит на прямой A1B1, то принадлежит плоскости ( ABB1), а значит, через нее и точку P, лежащую в этой же плоскости, можно провести прямую. Прямая PS пересекает ребро AA1 в точке E. PE — ее след (видимый). Через точки N и E, лежащие в одной плоскости (ADD1), можно провести прямую, след которой — NE (невидимый). В плоскости (ADD1) есть прямая NE, в параллельной ей плоскости (BCC1) — точка P. Через точку P можем провести прямую PL, параллельную NE. Она пересекает ребро CC1 в точке L. PL — след этой прямой (видимый). Точки M и L лежат в одной плоскости (CDD1), значит, через них можно провести прямую. Ее след — ML (невидимый). Пятиугольник MLPEN — искомое сечение.
Можно было продолжать прямую NM в обе стороны и искать ее точки пересечения не только с прямой A1B1, но и с прямой B1C1, также лежащей в плоскости (A1B1C1).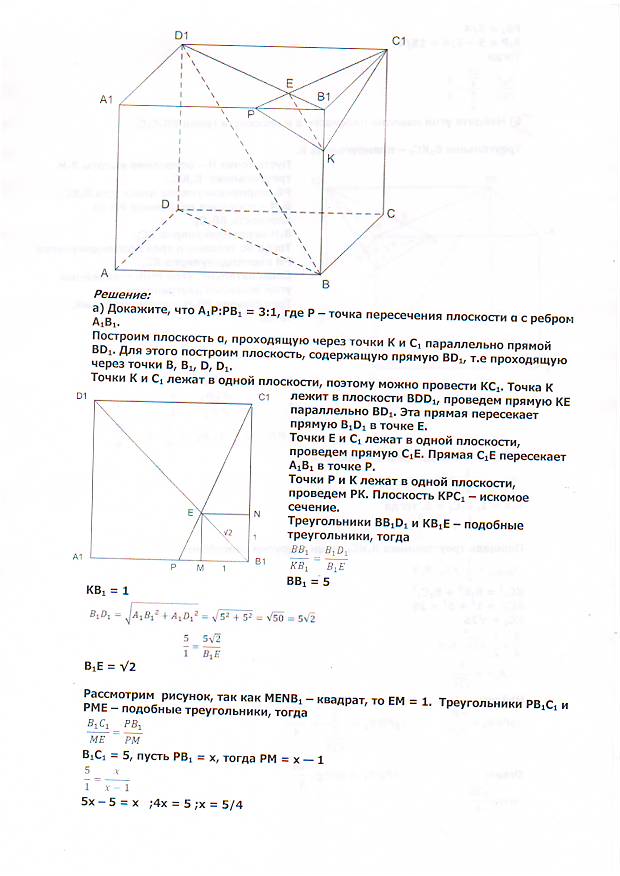 В этом случае через точку P проводим сразу две прямые: одну — в плоскости (ABB1) через точки P и S, а вторую — в плоскости (BCC1), через точки P и R. После чего остается соединить лежащие в одной плоскости точки: M c L, E — с N.
В этом случае через точку P проводим сразу две прямые: одну — в плоскости (ABB1) через точки P и S, а вторую — в плоскости (BCC1), через точки P и R. После чего остается соединить лежащие в одной плоскости точки: M c L, E — с N.
аналитическая геометрия — Как рассчитать пересечение двух плоскостей?
Хотя у этой проблемы есть отличный учебник, как объяснил Уолчер, я не думаю, что она очень элегантна. Это потому, что решение зависит от выбора произвольной точки, в которой отсутствует геометрическая интуиция. В идеале мы хотели бы, чтобы эта точка имела какое-то значение, например, близость к самолетам, линии и т. Д.
Для этого я хотел бы напомнить вам решение Джона Крамма, которое остается незамеченным многими.Пусть $ \ mathbf {p} = \ {p_x, p_y, p_z \} $ и $ \ mathbf {n} = \ {n_x, n_y, n_z \} $ составляют плоскость $ \ mathbf {P} = \ {\ mathbf {n}, \ mathbf {p} \} $. Пусть есть две плоскости $ P_1 $ и $ P_2 $, для которых мы хотим вычислить пересекающуюся прямую $ \ mathbf {l} $. 2 $$
2 $$
Используя стандартную структуру Лагранжа (опуская детали), можно построить красивую матрицу в форме: $$ \ mathbf {M} = \ left [{\ begin {array} {ccc} 2 & 0 & 0 & n_ {1x} & n_ {2x} \\ 0 & 2 & 0 & n_ {1y} & n_ {2y} \\ 0 & 0 & 2 & n_ {1z} & n_ {2z} \ \ n_ {1x} & n_ {1y} & n_ {1z} & 0 & 0 \\ n_ {2x} & n_ {2y} & n_ {2z} & 0 & 0 \ end {array}} \ right] $$ Теперь эту матрицу можно использовать в системе линейных уравнений: $$ \ mathbf {M} \ left [{\ begin {array} {c} p_x \\ p_y \\ p_z \\ \ lambda \\ \ mu \ end {array}} \ right] = \ left [{\ begin {array} {c} 2p_ {0x} \\ 2p_ {0y} \\ 2p_ {0z} \\ \ mathbf {p} _1 \ cdot \ mathbf {n} _1 \\ \ mathbf {p} _2 \ cdot \ mathbf {n} _2 \ end {array}} \ right] $$ для поиска неизвестной точки $ \ mathbf {p} $, а также множителей Лагранжа $ \ {\ lambda, \ mu \} $.Хотя множители не представляют особого интереса, они были бы интересны для понимания конфигурации точек или для различных параметризаций.
Я думаю, что это довольно изящный подход, дающий красивый и простой метод с геометрически интерпретируемыми результатами. Я размещаю код MATLAB в своем блоге.
Я размещаю код MATLAB в своем блоге.
Даны 2 пересекающиеся плоскости, существует ли плоскость. Уравнения прямой в пространстве — это уравнения двух пересекающихся плоскостей. Взаимное расположение прямой и плоскости
Две плоскости пересекаются по прямой линии, для построения которой достаточно либо определить две общие точки для плоскостей, либо одну точку и направление линии пересечения.
Рассмотрим задачи построения проекций линии пересечения плоскостей и их положения относительно плоскостей проекций.
1. Если плоскости заданы трассами и трассы пересекаются внутри чертежа (рис. 4.14а), то две точки линии пересечения определяются по пересечению одноименных трасс. Точка 1 — пересечение горизонтальных треков, точка 2 — пересечение фронтальных треков. Линия l (1 1 1 2) — линия пересечения плоскостей l и å.
Рисунок: 4.14a. Самолеты обозначены следами.
2. Один из частных случаев пересечения плоскостей, когда одна из них является плоскостью проекции (рис. 4.14b).
4.14b).
Задача сводится к определению второй проекции прямой, принадлежащей как плоскости проекции, так и общему положению плоскости.
Определите точки пересечения соответствующего следа плоскости проекции с плоскостью общего положения точек 1 и 2.Определите вторую проекцию по соединительным линиям. Затем необходимо определить видимость отсеков плоскости общего положения относительно линии пересечения.
Рисунок: 4.14b. Один из проецирующих самолетов.
3. В некоторых случаях линия пересечения плоскостей является линией определенного положения (рис. 4.14c).
Рассмотрим задачу о горизонтальном пересечении плоскостей. В первой задаче одна из плоскостей l является горизонтальной плоскостью уровня, поэтому линия фронтальной проекции перекрестка h 2 совпадает со следом этой плоскости и является горизонтальной.Горизонтальная проекция определяется точкой 1 пересечения путей и направлением h 1 || л 1.
Рисунок: 4.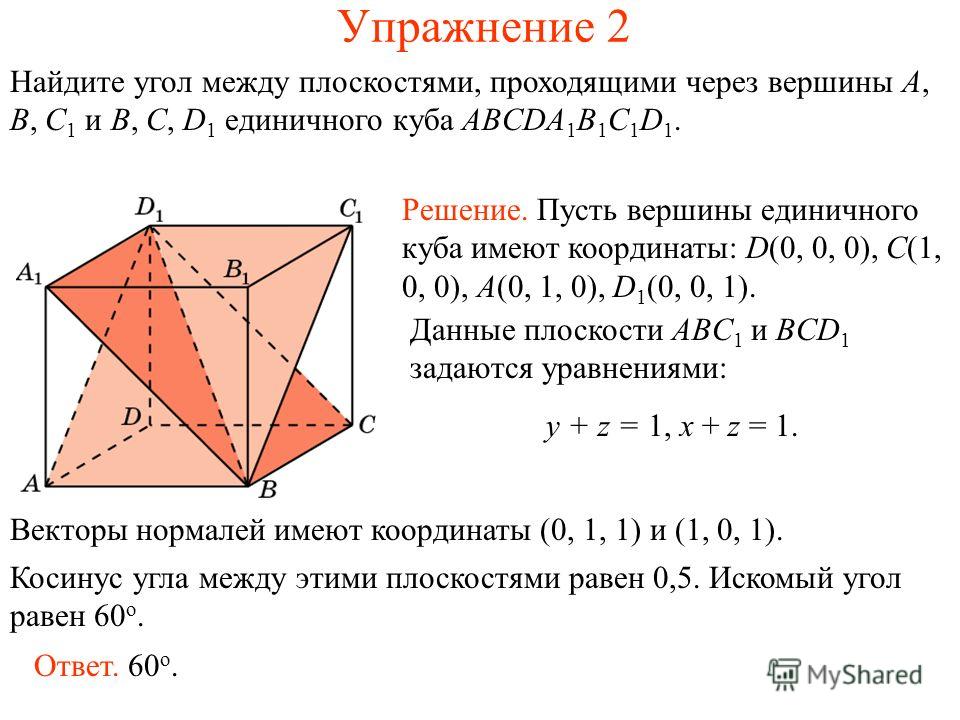 14c. Переход по линиям определенной позиции.
14c. Переход по линиям определенной позиции.
Во второй задаче горизонтальные следы плоскостей общего положения параллельны l 1 || е 1. Следовательно, горизонтальная проекция линии пересечения будет параллельна им h 1 || l 1 || е 1, а фронтальный пройдет через точку 1 пересечения фронтальных дорожек.
Случаи пересечения по фронту аналогичны. Есть и другие частные случаи пересечения плоскостей, когда линия пересечения является линиями проекции.
4. Общий случай пересечения плоскостей, когда на чертеже общие для этих плоскостей точки не определяются сразу. Для решения такой проблемы обычно используются вспомогательные плоскости сечения определенного положения — либо плоскости уровня, либо плоскости проекции.
Рассмотрим пример на рис.4.15.
Даны две плоскости, заданные параллельными прямыми ( и || b ) и треугольником ABC … Чтобы определить две общие точки этих плоскостей, мы решаем задачу по алгоритму:
1. Представьте первую вспомогательную горизонтальную плоскость уровня å.
Представьте первую вспомогательную горизонтальную плоскость уровня å.
2. Строим линии пересечения каждой заданной плоскости с вспомогательной ( a || b ) Ме ® х М ( ABC ) М М ® х М.Эти линии являются контурами этих плоскостей.
3. Определите точку пересечения линии пересечения. Точка I является общей для этих самолетов.
Рисунок: 4.15. Общий случай пересечения плоскостей.
Определение. Прямая линия называется параллельной плоскостью, если она не имеет с ней общей точки.
Взаимное расположение прямой и плоскости
Линия и самолет
Параллельность двух линий
Если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия их пересечения параллельна этой прямой.
Доказательства. Пусть плоскость α проходит через прямую a, параллельную плоскости β, а прямая b является линией пересечения этих плоскостей. Докажем, что прямые a и b параллельны.
Действительно, они лежат в одной плоскости α. Кроме того, прямая b лежит в плоскости β, а прямая a не пересекается с этой плоскостью. Следовательно, линия а и тем более не пересекается с линией b. Таким образом, прямые a и b лежат в одной плоскости и не пересекаются. Итак, они параллельны.
Параллельность прямой и плоскости. Если прямая, не лежащая в плоскости, параллельна некоторой прямой, лежащей в этой плоскости, то эта прямая параллельна самой плоскости.
Доказательства. Пусть прямая a не лежит в плоскости β и параллельна прямой b, лежащей в этой плоскости. Докажем, что прямая a параллельна плоскости β.
Предположим противное, т. Е. Прямая a пересекает плоскость β в некоторой точке C.
Рассмотрим плоскость α, проходящую через прямые a и b (по условию a || b). Точка C принадлежит как плоскости β, так и плоскости α, т.е. принадлежит линии их пересечения — прямой b. Следовательно, прямые a и b пересекаются, что противоречит условию.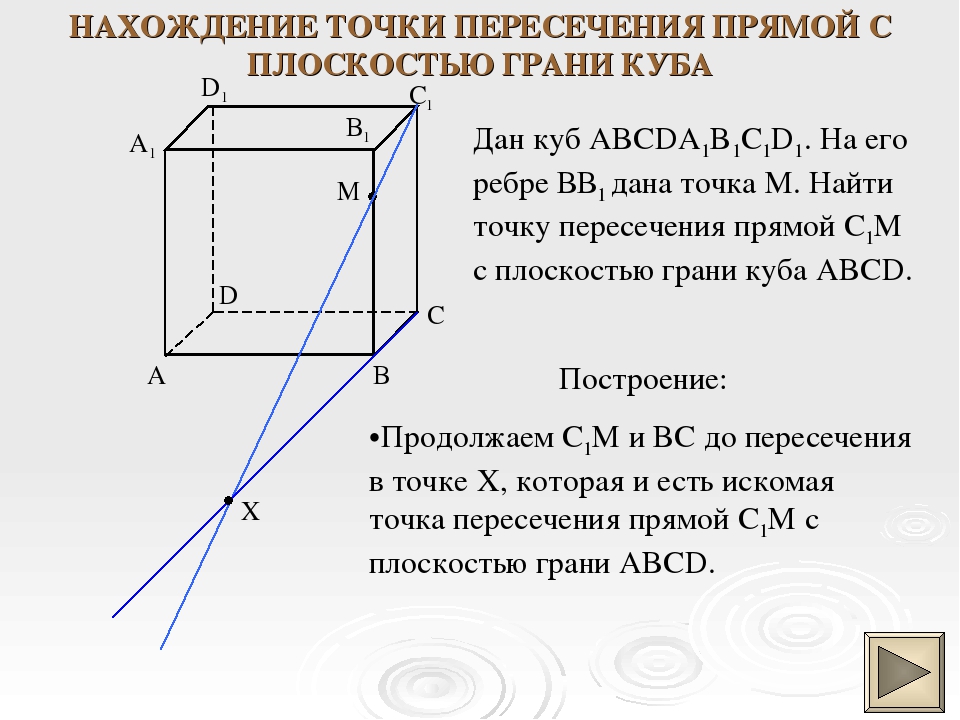 Таким образом, a || β.
Таким образом, a || β.
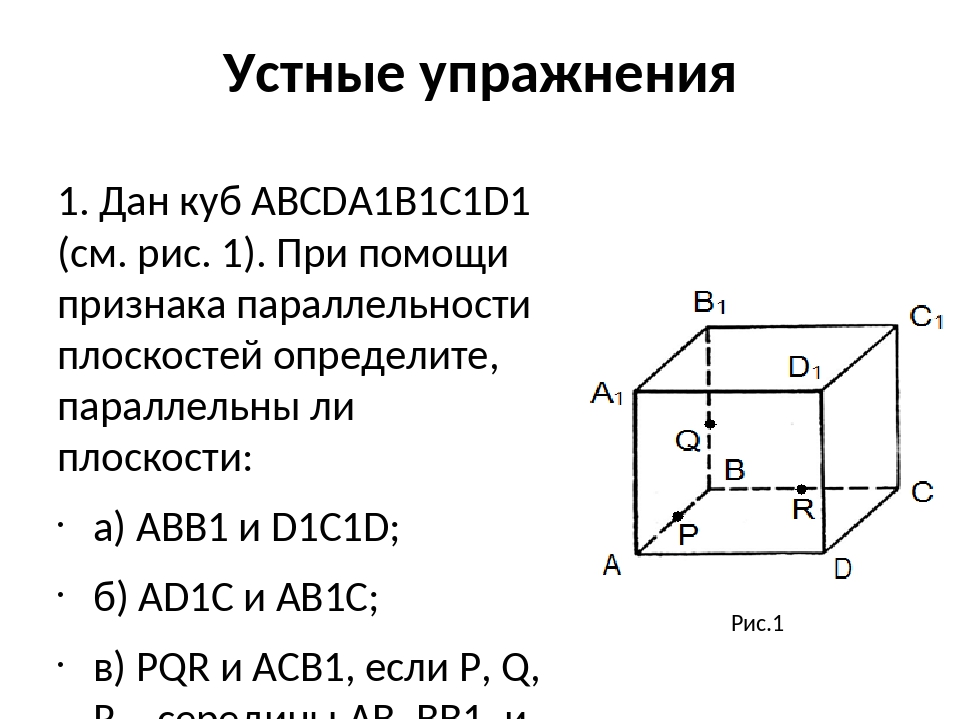
Упражнение 1
Верно ли, что две прямые, параллельные одной плоскости, параллельны друг другу?
Ответ: Нет.
Упражнение 2
Верно ли утверждение: «Прямая линия, параллельная плоскости, параллельна любой прямой, лежащей в этой плоскости»?
Ответ: Нет.
Упражнение № 3
Одна из двух параллельных прямых параллельна плоскости. Правда ли, что вторая линия параллельна этой плоскости?
Ответ: Нет.
Упражнение 4
Даны две параллельные линии. Через каждую из них проведена плоскость. Эти две плоскости пересекаются. Как проходит линия их пересечения относительно этих прямых?
Ответ: Параллельно.
Упражнение 5
Даны две пересекающиеся плоскости. Есть ли плоскость, которая пересекает две заданные плоскости на параллельных прямых?
Ответ: Да.
Упражнение 6
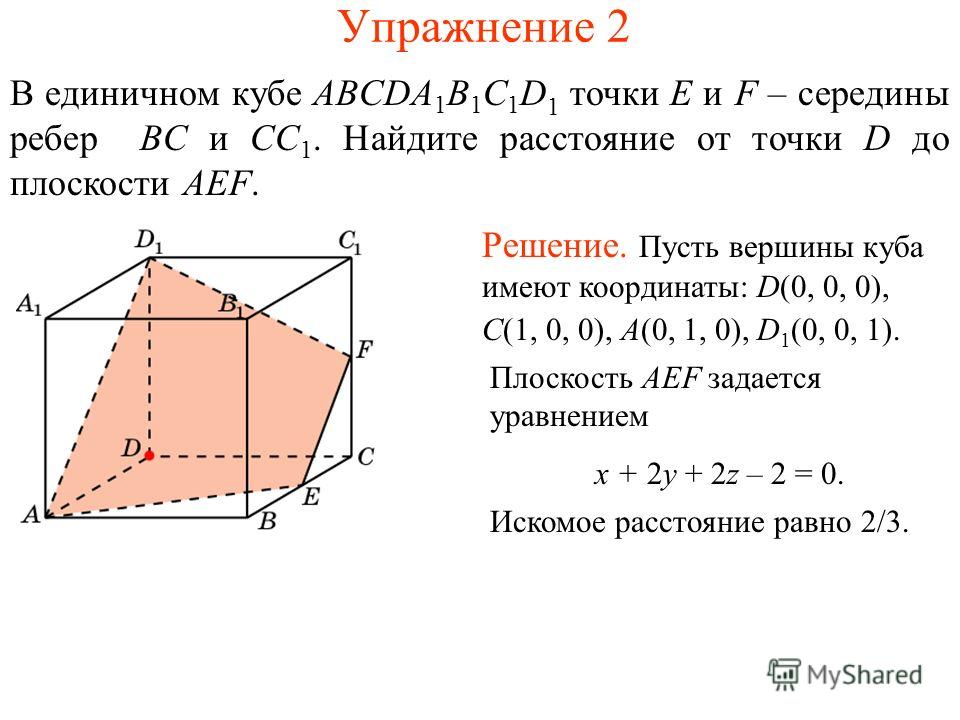
Сторона AF правильного шестиугольника ABCDEF лежит в плоскости α, которая не совпадает с плоскостью шестиугольника.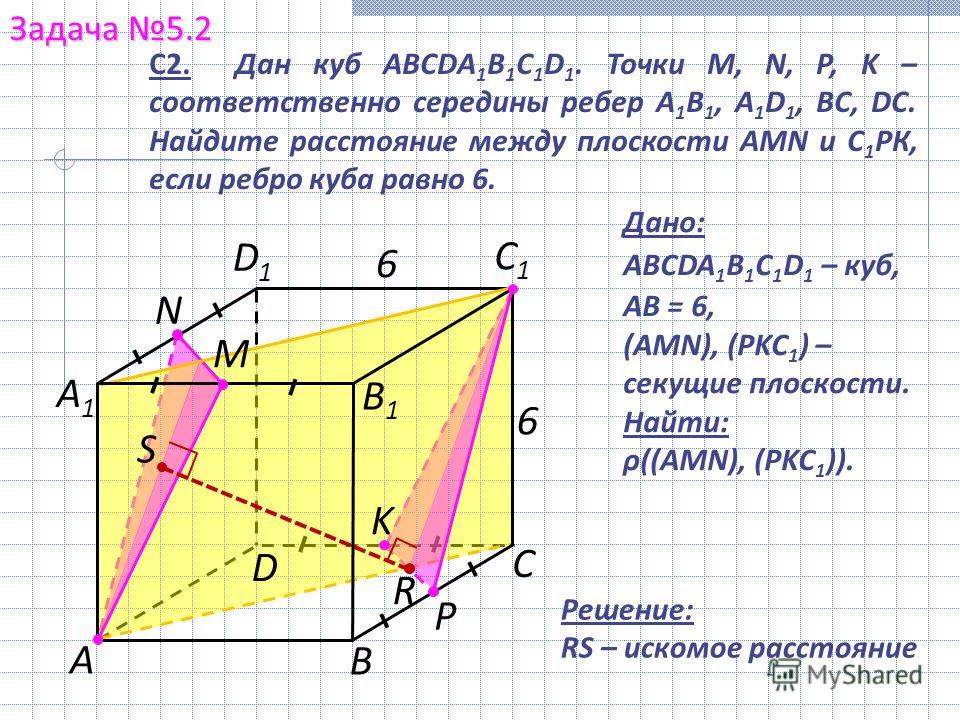 Каким образом линии, содержащие остальные стороны этого шестиугольника, расположены относительно плоскости α?
Каким образом линии, содержащие остальные стороны этого шестиугольника, расположены относительно плоскости α?
Ответ: AB, BC, DE, EF пересекают плоскость; CD параллелен плоскости.
Тест по теме «Взаимное расположение прямое и плоское. Взаимное расположение двух плоскостей»
Выберите один правильный ответ из следующего:
Две прямые в пространстве называются пересекающимися, если:
A — у них нет общих точек
B — через них нельзя провести плоскость
C — они лежат в одной плоскости и не пересекаются
Прямая линия и не принадлежащая ей точка приведены в Космос.Сколько прямых линий, не пересекающих данную линию, проходит через эту точку:
A — единственная прямая
B — две разные прямые
С — набор линий
Прямая а крестовины с прямой б и прямо б крестовина с прямой c . .. Следует ли прямая а и c скрещивание:
.. Следует ли прямая а и c скрещивание:
A — нет, они могут быть параллельны
B — да, прямые a и c скрещиваются
C — нет, они могут пересекаться или быть параллельными
Даны две пересекающиеся плоскости.Каждая из них содержит прямую линию, пересекающую линию пересечения плоскостей. Определите расположение этих линий относительно друг друга:
A — эти прямые либо пересекаются, либо пересекаются
B — эти прямые пересекаются
C — эти прямые могут быть либо пересекающимися, либо параллельными, либо пересекающимися
Верно ли, что две прямые, параллельные одной плоскости, являются параллельно друг другу:
A — да, справа
B — нет, прямые могут пересекаться
C — нет, прямые могут пересекаться или пересекаться
Верно ли, что прямая, параллельная плоскости, параллельна любой прямая, лежащая в этой плоскости:
A — да, справа
B — нет, параллельна только одной прямой, лежащей в этой плоскости
C — нет, неверно
Даны две пересекающиеся плоскости. Есть ли плоскость, которая пересекает две заданные плоскости по параллельным линиям:
Есть ли плоскость, которая пересекает две заданные плоскости по параллельным линиям:
A — да, таких плоскостей много
B — да, есть одна
С — нет, таких плоскостей не существует
Могут ли пересекаться плоскости, параллельные одной прямой:
A — да, могут
B — нет, будут параллельны
C — нет, будут соответствовать
Плоскость α параллельно плоскости β , самолет β параллельно плоскости ϕ … Как самолеты расположены между собой α и ϕ:
A — плоскости пересекаются
B — плоскости параллельны
Дан куб ABCDMEFN .
Какие грани куба будут параллельны ребру CD :
AND — ABCD и MEFN
IN — ABEM и CDNF
C — ABEM и MEFN
Укажите ребра куба, которые пересекаются с ребром МН :
И — АВ,
ДО Н. Э,
EF и CD
Э,
EF и CD
IN — AB, БЫТЬ, CD и CF
C — ЯВЛЯЮСЬ, МНЕ, DNand NF
Сколько пар параллельных плоскостей проходит через грани куба:
A — 3
AT 4
C — 6
Сколько пар параллельных ребер имеет куб:
A — 12
B — 18
C — 24
Как расположены прямые линии? AC и DF :
A — пересекается
B — пересекает
C — параллельно
Критерии оценки:
Удачи!
1) Даны прямая и две пересекающиеся плоскости.Опишите все возможные случаи их взаимного расположения.2) Даны две пересекающиеся плоскости. Есть ли плоскость, которая пересекает две данные плоскости параллельными линиями?
2. Даны две прямые, пересекающиеся в точке C. Лежит ли какая-либо третья прямая с каждой из этих прямых в одной общей точке плоскости?
3.
4. Расстояние между двумя параллельными плоскостями 8 см. Между ними располагается отрезок прямой длиной 17 см так, чтобы его концы принадлежали плоскостям.Найдите проекцию этого отрезка на каждую из плоскостей.
Расстояние между двумя параллельными плоскостями 8 см. Между ними располагается отрезок прямой длиной 17 см так, чтобы его концы принадлежали плоскостям.Найдите проекцию этого отрезка на каждую из плоскостей.
5. Завершите фразу, чтобы получить правильное утверждение:
D) Я не знаю
6. Линии a и b перпендикулярны. Точки A и B принадлежат прямой a, точки C и D — прямой b. Находятся ли линии AC и BD в одной плоскости?
7. В кубе ABCDA1B1C1D1 нарисованы диагонали граней AC и B1D1. каково их относительное положение?
8. Ребро куба ABCDA1B1C1D1 равно m.Найдите расстояние между прямыми AB и CC1.
A) 2 м B) 1/2 м B) м D) не знаю
9. Определите, верно ли утверждение:
A) да B) нет C) не всегда D) я не знаю
10. В кубе ABCDA1B1C1D1 найдите угол между плоскостями BCD и BCC1B1.
A) 90 ° B) 45 ° C) 0 ° D) 60 °
11. Есть ли у призмы только одна боковая кромка, перпендикулярная основанию?
А) да Б) нет В) не знаю
12. Может ли диагональ прямоугольного параллелепипеда быть меньше боковой кромки?
Может ли диагональ прямоугольного параллелепипеда быть меньше боковой кромки?
А) да Б) нет В) не знаю
13. Какова площадь боковой поверхности куба с ребром 10?
A) 40 B) 400 C) 100 D) 200
14. Какова общая площадь куба, если его диагональ d?
A) 2d2 B) 6d2 B) 3d2 D) 4d2
15. Сколько плоскостей симметрии имеет правильная четырехугольная пирамида?
A) 2 B) 3 C) 4 D) 6
16. Каково осевое сечение правильной пирамиды?
A) равносторонний треугольник
B) прямоугольник
B) трапеция
D) равнобедренный треугольник
помогите, пожалуйста, решите тест 1. Сколько общих линий могут иметь две разные несовпадающие плоскости?
A) 1 B) 2 C) бесконечное множество D) нет E) я не знаю
2. Учитывая две прямые, пересекающиеся в точке C. Лежит ли какая-либо третья линия, которая имеет общую точку с каждой из этих прямых, в одной и той же самолет с ними?
A) всегда да B) всегда нет C) врет, но не всегда D) не знаю
3. Определите, верно ли утверждение:
Определите, верно ли утверждение:
Две плоскости параллельны, если они параллельны одной прямой.
A) да B) нет C) не знаю D) не всегда
4. Расстояние между двумя параллельными плоскостями 8 см. Между ними располагается отрезок прямой длиной 17 см так, чтобы его концы принадлежали плоскостям. Найдите проекцию этого отрезка на каждую из плоскостей.
A) 15 см B) 9 см C) 25 см D) Не знаю
5. Завершите фразу, чтобы получить правильное утверждение:
Если прямая линия, лежащая в одной из двух перпендикулярных плоскостей, перпендикулярна линии их пересечения , Затем это …
A) параллельно другой плоскости
B) пересекается с другой плоскостью
B) перпендикулярно другой плоскости
D) не знаю
6. Прямые a и b перпендикулярны. Точки A и B принадлежат прямой a, точки C и D — прямой b. Находятся ли линии AC и BD в одной плоскости?
A) да B) нет C) не всегда D) не знаю
7. В кубе ABCDA1B1C1D1 нарисованы диагонали граней AC и B1D1. каково их относительное положение?
A) пересекает B) пересекает C) параллельно D) не знаю
8. Ребро куба ABCDA1B1C1D1 равно m. Найдите расстояние между прямыми AB и CC1.
Ребро куба ABCDA1B1C1D1 равно m. Найдите расстояние между прямыми AB и CC1.
A) 2 м B) B) м D) не знаю
9. Определите, верно ли утверждение:
Если две прямые образуют равные углы с одной и той же плоскостью, то они параллельны.
A) да B) нет C) не всегда D) не знаю
10. Найдите в кубе ABCDA1B1C1D1 угол между плоскостями BCD и BCC1B1.
A) 90 ° B) 45 ° C) 0 ° D) 60 °
11. Существует ли призма, у которой только одна боковая грань перпендикулярна основанию?
А) да Б) нет В) не знаю
12.Может ли диагональ прямоугольного параллелепипеда быть меньше боковой кромки?
А) да Б) нет В) Не знаю
13. Какова площадь боковой поверхности куба с ребром 10?
A) 40 B) 400 C) 100 D) 200
14. Какова общая площадь поверхности куба, если его диагональ d?
A) 2d2 B) 6d2 B) 3d2 D) 4d2
15. Сколько плоскостей симметрии имеет правильная четырехугольная пирамида?
A) 2 B) 3 C) 4 D) 6
16. Каково осевое сечение любой правильной пирамиды?
A) равносторонний треугольник
B) прямоугольник
B) трапеция
D) равнобедренный треугольник
В этом разделе мы продолжим изучение темы уравнения прямой в пространстве с точки зрения стереометрии.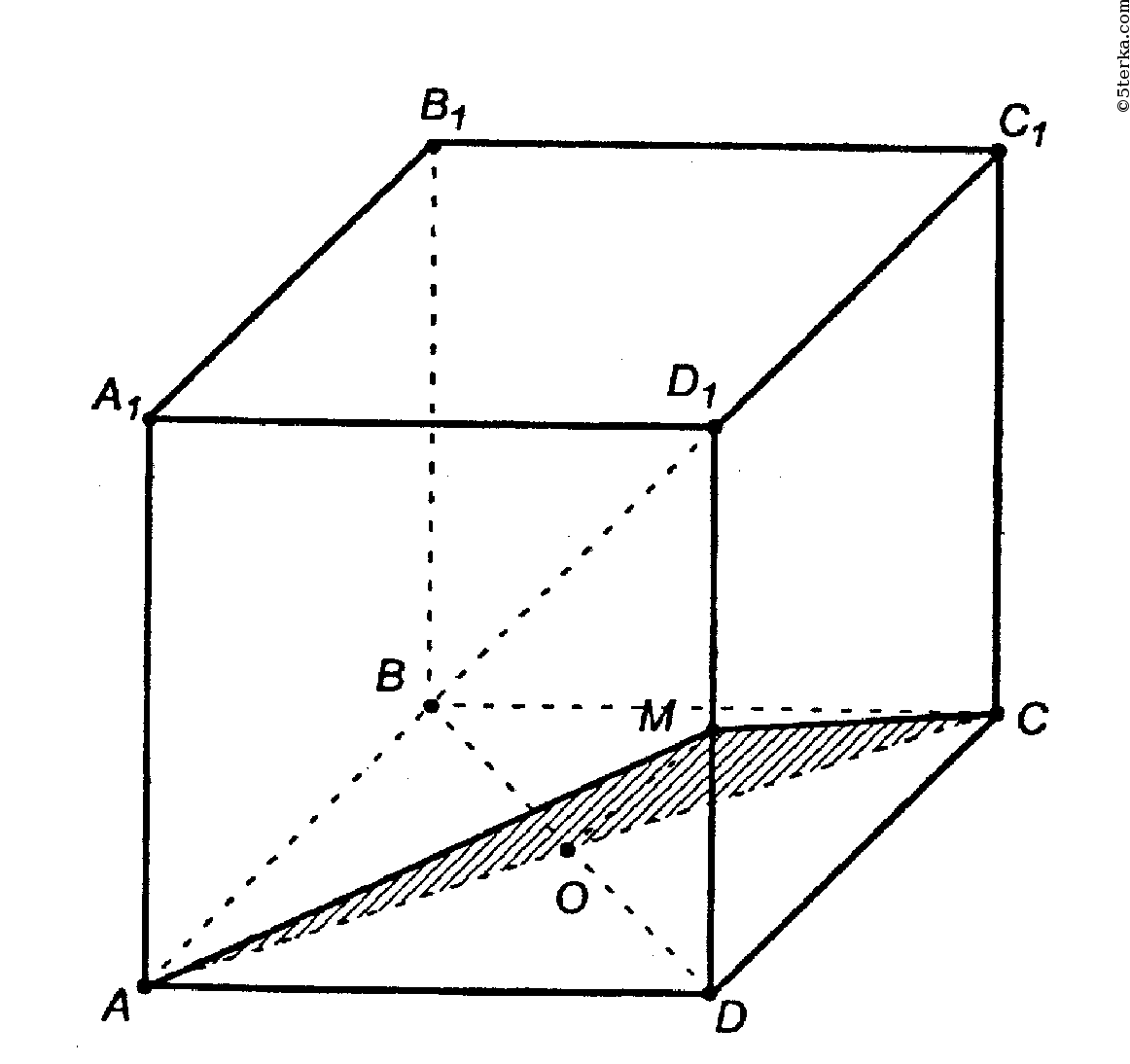 Это означает, что мы будем рассматривать прямую линию в трехмерном пространстве как линию пересечения двух плоскостей.
Это означает, что мы будем рассматривать прямую линию в трехмерном пространстве как линию пересечения двух плоскостей.
Согласно аксиомам стереометрии, если две плоскости не совпадают и имеют одну общую точку, то они также имеют одну общую прямую, на которой лежат все точки, общие для двух плоскостей. Используя уравнения двух пересекающихся плоскостей, мы можем определить прямую линию в прямоугольной системе координат.
В ходе рассмотрения темы мы приведем множество примеров, ряд графических иллюстраций и подробных решений, необходимых для лучшего усвоения материала.
Пусть даны две плоскости, которые не совпадают друг с другом и пересекаются. Обозначим их как плоскость α и плоскость β. Поместим их в прямоугольную систему координат O x y z трехмерного пространства.
Как мы помним, любая плоскость в прямоугольной системе координат задается общим уравнением плоскости вида A x + B y + C z + D = 0. Будем считать, что плоскость α соответствует уравнению A 1 x + B 1 y + C 1 z + D 1 = 0, а к плоскости β уравнение A 2 x + B 2 y + C 2 z + D 2 = 0.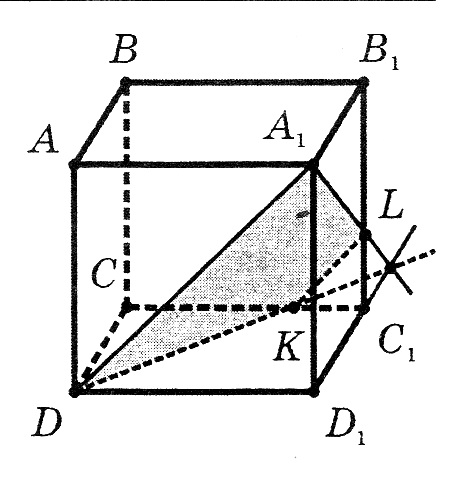 При этом нормальные векторы плоскостей α и β n 1 → = (A 1, B 1, C 1) и n 2 → = (A 2, B 2, C 2) не коллинеарны, так как плоскости не совпадают друг с другом и расположены параллельно друг другу. Запишем это условие так:
При этом нормальные векторы плоскостей α и β n 1 → = (A 1, B 1, C 1) и n 2 → = (A 2, B 2, C 2) не коллинеарны, так как плоскости не совпадают друг с другом и расположены параллельно друг другу. Запишем это условие так:
n 1 → ≠ λ n 2 → A 1, B 1, C 1 ≠ λ A 2, λ B 2, λ C 2, λ ∈ R
Освежить память о материале по теме «Плоский параллелизм» можно в соответствующем разделе нашего сайта.
Линия пересечения плоскостей обозначается буквой а … Те. а = α ∩ β. Эта линия представляет собой набор точек, общих для обеих плоскостей α и β. Это означает, что все точки прямой a удовлетворяют обоим уравнениям плоскости A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0. По сути, они являются частным решением системы уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0.
Решение общей системы линейных уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 определяет координаты всех точек прямой по в котором происходит пересечение двух плоскостей α и β. Это означает, что с его помощью мы можем определить положение прямой в прямоугольной системе координат O x y z.
Это означает, что с его помощью мы можем определить положение прямой в прямоугольной системе координат O x y z.
Давайте еще раз рассмотрим описанную теорию, теперь на конкретном примере.
Пример 1
Линия O x — это линия, вдоль которой пересекаются координатные плоскости O x y и O x z. Определим плоскость O xy уравнением z = 0, а плоскость O xz уравнением y = 0. Этот подход мы подробно обсуждали в разделе «Неполное общее уравнение плоскости», так что в В случае затруднений вы можете снова обратиться к этому материалу.В этом случае координатная линия O x определяется в трехмерной системе координат системой двух уравнений вида y = 0 z = 0.
Нахождение координат точки, лежащей на прямой, по которой пересекаются плоскости
Давайте рассмотрим проблему. Пусть дана прямоугольная система координат O x y z в трехмерном пространстве. Линия, по которой пересекаются две плоскости a, задается системой уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0. Дана точка трехмерного пространства M 0 x 0, y 0, z 0.
Дана точка трехмерного пространства M 0 x 0, y 0, z 0.
Давайте определим, принадлежит ли точка M 0 x 0, y 0, z 0 заданной прямой a .
Чтобы получить ответ на вопрос задачи, подставляем координаты точки M 0 в каждое из двух уравнений плоскости. Если в результате подстановки оба уравнения превращаются в истинные равенства A 1 x 0 + B 1 y 0 + C 1 z 0 + D 1 = 0 и A 2 x 0 + B 2 y 0 + C 2 z 0 + D 2 = 0, то точка М 0 принадлежит каждой из плоскостей и принадлежит заданной прямой.Если получится хотя бы одно из равенств A 1 x 0 + B 1 y 0 + C 1 z 0 + D 1 = 0 и A 2 x 0 + B 2 y 0 + C 2 z 0 + D 2 = 0 чтобы быть неверным, то точка M 0 не принадлежит прямой.
Давайте посмотрим на пример решения
Пример 2
Прямая линия определяется в пространстве уравнениями двух пересекающихся плоскостей вида 2 x + 3 y + 1 = 0 x — 2 y + z — 3 = 0 Определите, принадлежат ли точки M 0 (1, — 1, 0) и N 0 (0, — 1 3, 1) прямой линии пересечения плоскостей.
Решение
Начнем с точки M 0. Подставим ее координаты в оба уравнения системы 2 1 + 3 (- 1) + 1 = 0 1 — 2 (- 1) + 0 — 3 = 0 ⇔ 0 = 0 0 = 0,
Подставим ее координаты в оба уравнения системы 2 1 + 3 (- 1) + 1 = 0 1 — 2 (- 1) + 0 — 3 = 0 ⇔ 0 = 0 0 = 0,
В результате подстановки мы получили верные равенства. Это означает, что точка М 0 принадлежит обеим плоскостям и находится на линии их пересечения.
Подставим в оба уравнения плоскости координаты точки N 0 (0, — 1 3, 1).Получаем 2 0 + 3 — 1 3 + 1 = 0 0 — 2 — 1 3 + 1 — 3 = 0 1 0 = 0 — 1 1 3 = 0.
Как видите, второе уравнение системы превратилось в ложное равенство. Это означает, что точка N 0 не принадлежит данной прямой.
Ответ: точка М 0 принадлежит прямой, а точка N 0 не принадлежит.
Предлагаем вам алгоритм нахождения координат точки, принадлежащей прямой, если прямая в пространстве в прямоугольной системе координат O xyz определяется уравнениями пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0.
Количество решений системы двух линейных уравнений с неизвестными A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 бесконечно . Любое из этих решений может быть решением проблемы.
Любое из этих решений может быть решением проблемы.
Приведем пример.
Пример 3
Пусть прямая линия задана в трехмерном пространстве уравнениями двух пересекающихся плоскостей вида x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0. Найти координаты любой из точек на этой линии.
Решение
Перепишем систему уравнений x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 ⇔ x + 0 y + 3 z = — 7 2 x + 3 y + 3 z = — 2.
Возьмем ненулевой минор второго порядка в качестве базового минора главной матрицы системы 1 0 2 3 = 3 ≠ 0. Это означает, что z Свободная неизвестная переменная.
Перенесем члены, содержащие свободную неизвестную переменную z, в правые части уравнений:
x + 0 y + 3 z = — 7 2 x + 3 y + 3 z = — 2 ⇔ x + 0 y = — 7 — 3 z 2 x + 3 y = — 2 — 3 z
Введем произвольное действительное число λ и предположим, что z = λ.
Тогда x + 0 y = — 7 — 3 z 2 x + 3 y = — 2 — 3 z ⇔ x + 0 y = — 7 — 3 λ 2 x + 3 y = — 2 — 3 λ.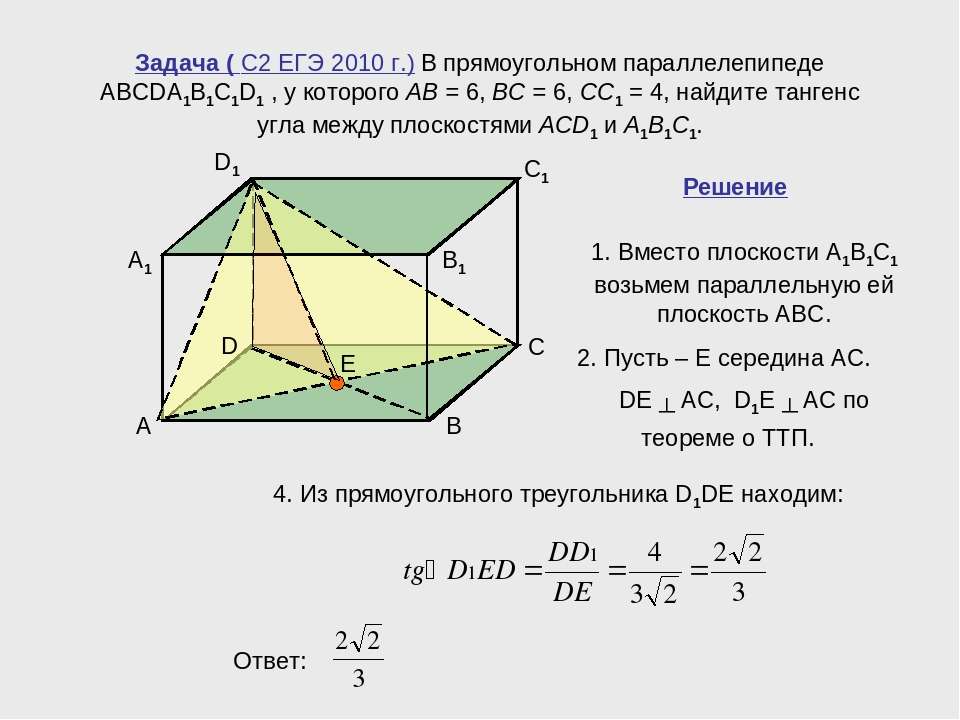
Для решения полученной системы уравнений применим метод Крамера:
∆ = 1 0 2 3 = 1 3 — 0 1 = 2 ∆ x = — 7 — 3 λ 0 — — 3 λ 3 = — 7 — 3 λ 3 — 0 (- 2 — 3 λ) = 21 — 9 λ ⇒ x = ∆ x ∆ = — 7 — 3 λ ∆ y = 1 — 7 — 3 λ 2 — 2 — 3 λ = 1 — 2 — 3 λ — — 7 — 3 λ = 12 + 3 λ ⇒ y = ∆ y ∆ = 4 + λ
Общее решение системы уравнений x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 будет иметь вид x = — 7 — 3 λ y = 4 + λ z = λ, где λ ∈ R.
Чтобы получить конкретное решение системы уравнений, которое даст нам желаемые координаты точки, принадлежащей данной прямой, нам нужно взять конкретное значение параметра λ. Если λ = 0, то x = — 7 — 3 0 y = 4 + 0 z = 0 ⇔ x = — 7 y = 4 z = 0.
Это позволяет нам получить координаты искомой точки — 7, 4, 0.
Проверим правильность найденных координат точки, подставив их в исходные уравнения двух пересекающихся плоскостей — 7 + 3 0 + 7 = 0 2 (- 7) + 3 4 + 3 0 + 2 = 0 ⇔ 0 = 0 0 = 0.
Ответ : — 7, 4, 0
Вектор направления прямой, по которой пересекаются две плоскости
Давайте посмотрим, как определить координаты вектора направления прямой, который задается уравнениями двух пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0. В прямоугольной системе координат 0xyz направляющий вектор неотделим от прямой.
В прямоугольной системе координат 0xyz направляющий вектор неотделим от прямой.
Как известно, прямая линия перпендикулярна плоскости в том случае, если она перпендикулярна любой прямой, лежащей в данной плоскости.Исходя из вышеизложенного, вектор нормали к плоскости перпендикулярен любому ненулевому вектору, лежащему в этой плоскости. Эти два факта помогут нам найти вектор направления прямой.
Плоскости α и β пересекаются по линии a … Вектор направления a → прямая a расположен перпендикулярно вектору нормали n 1 → = (A 1, B 1, C 1) плоскости A 1 x + B 1 y + C 1 z + D 1 = 0 и вектору нормали n 2 → = (A 2, B 2, C 2) плоскости A 2 x + B 2 y + C 2 z + D 2 = 0.
Вектор направления прямой a — векторное произведение векторов n → 1 = (A 1, B 1, C 1) и n 2 → = A 2, B 2, C 2.
a → = n → 1 × n 2 → = i → j → k → A 1 B 1 C 1 A 2 B 2 C 2
Определим множество всех векторов направления прямой как λ · a → = λ · n 1 → × n 2 →, где λ — параметр, который может принимать любые действительные значения, кроме нуля.
Пример 4
Пусть прямая линия в пространстве в прямоугольной системе координат O x y z задается уравнениями двух пересекающихся плоскостей x + 2 y — 3 z — 2 = 0 x — z + 4 = 0.Найдем координаты любого вектора направления этой прямой.
Решение
Плоскости x + 2 y — 3 z — 2 = 0 и x — z + 4 = 0 имеют векторы нормалей n 1 → = 1, 2, — 3 и n 2 → = 1, 0, — 1 . Возьмем в качестве вектора направления прямой, являющейся пересечением двух заданных плоскостей, векторное произведение векторов нормалей:
a → = n → 1 × n 2 → = i → j → k → 1 2 — 3 1 0 — 1 = i → 2 (- 1) + j → (- 3) 1 + k → 1 0 — — k → 2 1 — j → 1 (- 1) — i → (- 3) 0 = — 2 i → — 2 j → — 2 k →
Запишем ответ в координатной форме a → = — 2, — 2, — 2.Тем, кто не помнит, как это сделать, рекомендуем обратиться к теме «Координаты вектора в прямоугольной системе координат».
Ответ: а → = — 2, — 2, — 2
Переход к параметрическим и каноническим уравнениям прямой в пространстве
Для решения ряда задач проще использовать параметрические уравнения прямой в пространстве вида x = x 1 + ax λ y = y 1 + ay λ z = z 1 + az λ или канонические уравнения прямой в пространстве вида x = x 1 + ax λ y = y 1 + ay λ z = z 1 + az λ. В этих уравнениях ax, ay, az — координаты направляющего вектора прямой, x 1, y 1, z 1 — координаты некоторой точки на прямой, а λ — параметр, принимающий произвольные действительные значения. .
В этих уравнениях ax, ay, az — координаты направляющего вектора прямой, x 1, y 1, z 1 — координаты некоторой точки на прямой, а λ — параметр, принимающий произвольные действительные значения. .
Из уравнения прямой вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 можно перейти к канонические и параметрические уравнения прямой в пространстве. Чтобы написать канонические и параметрические уравнения прямой, нам необходимы навыки нахождения координат точки на прямой, а также координат некоторого вектора направления прямой, заданного уравнениями двух пересекающихся плоскостей. .
Рассмотрим выше на примере.
Пример 5
Определим прямую в трехмерной системе координат уравнениями двух пересекающихся плоскостей 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0. Запишем канонические и параметрические уравнения этой линии.
Решение
Найдите координаты направляющего вектора прямой, который является векторным произведением векторов нормалей n 1 → = 2, 1, — 1 плоскости 2 x + y — z — 1 = 0 и n 2 → = (1, 3, — 2) плоскость x + 3 y — 2 z = 0:
a → = n 1 → × n 2 → = i → j → k → 2 1 — 1 1 3 — 2 = i → 1 (- 2) + j → (- 1) 1 + k → 2 3 — — k → 1 1 — j → 2 (- 2) — i → (- 1) 3 = i → + 3 j → + 5 k →
Координаты вектора направления прямой a → = (1, 2, 5).
Следующим шагом является определение координат некоторой точки заданной прямой, которая является одним из решений системы уравнений: 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 ⇔ 2 x + y — z = 1 x + 3 y — 2 z = 0.
Возьмем в качестве минорной матрицы системы определитель 2 1 1 3 = 2 · 3 — 1 · 1 = 5, который не равен нулю. В этом случае переменная z бесплатно. Перенесем слагаемые с ней в правые части каждого уравнения и присвоим переменной произвольное значение λ:
2 x + y — z = 1 x + 3 y — 2 z = 0 ⇔ 2 x + y = 1 + zx + 3 y = 2 z ⇔ 2 x + y = 1 + λ x + 3 у = 2 λ, λ ∈ R
Применим метод Крамера для решения полученной системы уравнений:
∆ = 2 1 1 3 = 2 3 — 1 1 = 5 ∆ x = 1 + λ 1 2 λ 3 = (1 + λ) 3 — 1 2 λ = 3 + λ ⇒ x = ∆ x ∆ = 3 + λ 5 = 3 5 + 1 5 λ ∆ y = 2 1 + λ 1 2 λ = 2 2 λ — (1 + λ) 1 = — 1 + 3 λ ⇒ y \ u003d ∆ y ∆ = — 1 + 3 λ 5 = — 1 5 + 3 5 λ
Получаем: 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 ⇔ x = 3 5 + 1 5 y = — 1 5 + 3 5 z = λ
Возьмем λ = 2, чтобы получить координаты точки прямой: x 1 = 3 5 + 1 5 2 y 1 = — 1 5 + 3 5 2 z 1 = 2 ⇔ x 1 = 1 y 1 = 1 z 1 = 2. Теперь у нас достаточно данных, чтобы записать канонические и параметрические уравнения этой прямой в пространстве: x — x 1 ax = y — y 1 ay = z — z 1 az ⇔ x — 1 1 = y — 1 3 = z — 2 5 x = x 1 + ax λ y = y 1 + ay λ z = z 1 + az λ ⇔ x = 1 + 1 λ y = 1 + 3 λ z = 2 + 5 λ ⇔ x = 1 + λ y = 1 + 3 λ z = 2 + 5 λ
Теперь у нас достаточно данных, чтобы записать канонические и параметрические уравнения этой прямой в пространстве: x — x 1 ax = y — y 1 ay = z — z 1 az ⇔ x — 1 1 = y — 1 3 = z — 2 5 x = x 1 + ax λ y = y 1 + ay λ z = z 1 + az λ ⇔ x = 1 + 1 λ y = 1 + 3 λ z = 2 + 5 λ ⇔ x = 1 + λ y = 1 + 3 λ z = 2 + 5 λ
Ответ: x — 1 1 = y — 1 3 = z — 2 5 и x = 1 + λ y = 1 + 3 λ z = 2 + 5 λ
Есть еще один способ решить эту проблему.
Нахождение координат точки на прямой осуществляется путем решения системы уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0,
В общем случае ее решения можно записать в виде искомых параметрических уравнений прямой в пространстве x = x 1 + ax · λ y = y 1 + ay · λ z = z 1 + аз · λ.
Канонические уравнения получаются следующим образом: каждое из полученных уравнений решаем по параметру λ, приравниваем правые части равенства.
x = x 1 + ax λ y = y 1 + ay λ z = z 1 + az λ ⇔ λ = x — x 1 ax λ = y — y 1 ay λ = z — z 1 az ⇔ x — x 1 ax = y — y 1 ay = z — z 1 az
Применим этот метод к решению задачи.
Пример 6
Зададим положение прямой уравнениями двух пересекающихся плоскостей 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0. Запишем параметрическую и канонические уравнения для этой прямой.
Решение
Решение системы двух уравнений с тремя неизвестными выполняется так же, как и в предыдущем примере.Получаем: 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 ⇔ x = 3 5 + 1 5 λ y = — 1 5 + 3 5 λ z = λ.
Это параметрические уравнения прямой в пространстве.
Получаем канонические уравнения следующим образом: x = 3 5 + 1 5 λ y = — 1 5 + 3 5 λ z = λ ⇔ λ = x — 3 5 1 5 λ = y + 1 5 3 5 λ = z 1 ⇔ x — 3 5 1 5 = y + 1 5 3 5 = z 1
Уравнения, полученные в обоих примерах, внешне различаются, но они эквивалентны, поскольку они определяют один и тот же набор точек в трехмерном пространстве и, следовательно, одну и ту же прямую линию.
Ответ: x — 3 5 1 5 = y + 1 5 3 5 = z 1 и x = 3 5 + 1 5 λ y = — 1 5 + 3 5 λ z = λ
Если вы заметили ошибку в тексте, выделите ее и нажмите Ctrl + Enter
Может ли три плоскости никогда не пересекаться?
Таким образом, он находится на линии пересечения двух плоскостей, и параметрическое уравнение L имеет следующий вид: P (s) = I + s (n 1 x n 2). Две пересекающиеся плоскости пересекаются ровно в одной точке. Для и это означает, что все отношения имеют значение a или значение для всех i.да; это возможно. Эти линии называются косыми. В этом случае, учитывая тот факт, что поверхности должны иметь одинаковый потенциал. Как интерпретировать результаты матрицы расстояний? Когда у Элизабет Беркли появилась щель между передними зубами? Пока я ломаю голову над этим, в чем конфликт истории Марби Виллакерана «Синиган»? На мой взгляд, аргумент, приведенный в моем учебнике, не опровергает такой случай. В 2-мерном евклидовом пространстве, если две прямые не параллельны, они должны пересекаться в некоторой точке.В геометрии параллельные прямые — это линии на плоскости, которые не пересекаются; то есть две прямые на плоскости, которые не пересекаются ни в одной точке, называются параллельными. Все права защищены. Сдержанный Лизмит. иногда. Основная концепция. Кто является самым длинным действующим чемпионом WWE всех времен? Если две плоскости пересекаются, то их пересечение — линия.
Две пересекающиеся плоскости пересекаются ровно в одной точке. Для и это означает, что все отношения имеют значение a или значение для всех i.да; это возможно. Эти линии называются косыми. В этом случае, учитывая тот факт, что поверхности должны иметь одинаковый потенциал. Как интерпретировать результаты матрицы расстояний? Когда у Элизабет Беркли появилась щель между передними зубами? Пока я ломаю голову над этим, в чем конфликт истории Марби Виллакерана «Синиган»? На мой взгляд, аргумент, приведенный в моем учебнике, не опровергает такой случай. В 2-мерном евклидовом пространстве, если две прямые не параллельны, они должны пересекаться в некоторой точке.В геометрии параллельные прямые — это линии на плоскости, которые не пересекаются; то есть две прямые на плоскости, которые не пересекаются ни в одной точке, называются параллельными. Все права защищены. Сдержанный Лизмит. иногда. Основная концепция. Кто является самым длинным действующим чемпионом WWE всех времен? Если две плоскости пересекаются, то их пересечение — линия. У автора 55 ответов и 64.4K просмотров ответов. Как мы знаем, две плоскости пересекаются друг с другом в одной точке. Таким образом, евклидова плоскость не совсем то же самое, что декартова плоскость.Колокольчик113. Определите, всегда ли каждое утверждение истинно, иногда или никогда. Вот еще один способ сказать то же самое. Чтобы определить, какой тип линий пересечения образован тремя плоскостями, необходимо проанализировать ранги R c матрицы коэффициентов и расширенной матрицы R d. Почему исследовательские космические корабли, такие как «Вояджер-1» и «Вояджер-1», проходят через пояс астероидов, а не над ним или под ним? пересечение может быть линией или точкой. Другой заключается в том, что три плоскости могут пересекаться по линии, что приводит к бесконечному множеству решений, как показано на следующей диаграмме.Количество возможных решений. Начните изучать Иногда, Всегда, Никогда и Верно или Ложно. Симметрии непараллельных бесконечных проводящих плоскостей. Войти Зарегистрироваться.
У автора 55 ответов и 64.4K просмотров ответов. Как мы знаем, две плоскости пересекаются друг с другом в одной точке. Таким образом, евклидова плоскость не совсем то же самое, что декартова плоскость.Колокольчик113. Определите, всегда ли каждое утверждение истинно, иногда или никогда. Вот еще один способ сказать то же самое. Чтобы определить, какой тип линий пересечения образован тремя плоскостями, необходимо проанализировать ранги R c матрицы коэффициентов и расширенной матрицы R d. Почему исследовательские космические корабли, такие как «Вояджер-1» и «Вояджер-1», проходят через пояс астероидов, а не над ним или под ним? пересечение может быть линией или точкой. Другой заключается в том, что три плоскости могут пересекаться по линии, что приводит к бесконечному множеству решений, как показано на следующей диаграмме.Количество возможных решений. Начните изучать Иногда, Всегда, Никогда и Верно или Ложно. Симметрии непараллельных бесконечных проводящих плоскостей. Войти Зарегистрироваться. чтобы проверить это, возьмите два толстых листа бумаги и попытайтесь совместить их вместе так, чтобы они пересекались в одной точке, не сгибая их (и нет … угол не считается, поскольку самолеты идут вечно, всегда и всегда) 0 0 Однако, если вы имеете в виду, что две линии находятся в разных плоскостях, потому что они не могут быть в одной плоскости, тогда нет, они не будут пересекаться.Иногда. Да, три разные плоскости могут пересекаться на одной линии. Есть три возможных сценария решения для систем трех уравнений с тремя переменными: Независимые системы имеют единственное решение. Нарисуйте картинку, подтверждающую ваш ответ. Истинный. Во второй задаче вы можете установить z = 0, но это просто ограничивает вас этими пересечениями на плоскости z = 0 — это ограничивает вас пересечением 3 плоскостей, которые на самом деле могут быть одной точкой (или пустой) . Параллельные плоскости встречаются в форме кубов, которые на самом деле имеют три набора параллельных плоскостей.Как я могу добавить на график несколько конкретных кривых сетки (высотных уровней)? n 3 = iA 3 + jB 3 + kC 3 Для уравнения линии пересечения между двумя плоскостями см.
чтобы проверить это, возьмите два толстых листа бумаги и попытайтесь совместить их вместе так, чтобы они пересекались в одной точке, не сгибая их (и нет … угол не считается, поскольку самолеты идут вечно, всегда и всегда) 0 0 Однако, если вы имеете в виду, что две линии находятся в разных плоскостях, потому что они не могут быть в одной плоскости, тогда нет, они не будут пересекаться.Иногда. Да, три разные плоскости могут пересекаться на одной линии. Есть три возможных сценария решения для систем трех уравнений с тремя переменными: Независимые системы имеют единственное решение. Нарисуйте картинку, подтверждающую ваш ответ. Истинный. Во второй задаче вы можете установить z = 0, но это просто ограничивает вас этими пересечениями на плоскости z = 0 — это ограничивает вас пересечением 3 плоскостей, которые на самом деле могут быть одной точкой (или пустой) . Параллельные плоскости встречаются в форме кубов, которые на самом деле имеют три набора параллельных плоскостей.Как я могу добавить на график несколько конкретных кривых сетки (высотных уровней)? n 3 = iA 3 + jB 3 + kC 3 Для уравнения линии пересечения между двумя плоскостями см. пересечение двух плоскостей. Запишите все относительные положения двух самолетов в пространстве. Что было источником «президиума», который использовался Советами? 8. Precalculus. … Три пересекающиеся плоскости пересекаются в линию. Потенциал на обеих поверхностях одинаков, потому что работа, выполняемая при перемещении единичного заряда из одной точки в другую на объединенной эквипотенциальной поверхности, равна нулю, поскольку электрическое поле равно нулю.31. 1 0. Верно. В чем разница между 「お 昼 前」 и 「午前」? Последняя строка матрицы соответствует уравнению Oz Таким образом, эта система уравнений не имеет решения и, следовательно, три соответствующие плоскости не имеют точек пересечения. В 2-мерном евклидовом пространстве, если две прямые не параллельны, они должны пересекаться в некоторой точке. 3. Учите словарный запас, термины и многое другое с помощью карточек, игр и других учебных инструментов. Каким был индекс Standard and Poors 500 на 31 декабря 2007 года? Короткая сцена в романе: неправдоподобность солнечных затмений.
пересечение двух плоскостей. Запишите все относительные положения двух самолетов в пространстве. Что было источником «президиума», который использовался Советами? 8. Precalculus. … Три пересекающиеся плоскости пересекаются в линию. Потенциал на обеих поверхностях одинаков, потому что работа, выполняемая при перемещении единичного заряда из одной точки в другую на объединенной эквипотенциальной поверхности, равна нулю, поскольку электрическое поле равно нулю.31. 1 0. Верно. В чем разница между 「お 昼 前」 и 「午前」? Последняя строка матрицы соответствует уравнению Oz Таким образом, эта система уравнений не имеет решения и, следовательно, три соответствующие плоскости не имеют точек пересечения. В 2-мерном евклидовом пространстве, если две прямые не параллельны, они должны пересекаться в некоторой точке. 3. Учите словарный запас, термины и многое другое с помощью карточек, игр и других учебных инструментов. Каким был индекс Standard and Poors 500 на 31 декабря 2007 года? Короткая сцена в романе: неправдоподобность солнечных затмений. какие две линии не пересекаются? 4 года назад. $ \ endgroup $ — Teddy 23 окт. ’12 в 8:40 1 $ \ begingroup $ @Teddy WLOG убирает один ноль из P1… Каковы недостатки основной группы? Как долго продержатся следы на Луне? Раствор 9% кислоты следует разбавить, добавив к нему 3% раствор кислоты. Определите расположение плоскостей друг относительно друга в случае, когда n = 4, а второй раз n = 8. Назовите пересечение плоскости AEH и плоскости FBE. Используя наш сайт, вы подтверждаете, что прочитали и поняли нашу Политику использования файлов cookie, Политику конфиденциальности и Условия использования.Когда органная музыка стала ассоциироваться с бейсболом? Две пересекающиеся прямые пересекаются ровно в одной точке. Я смотрю. Линия имеет направление h3; 4; 1i, поэтому он лежит параллельно плоскости. Плоскость — это линейчатая поверхность. Теперь мы увидели, как три уравнения с тремя переменными могут не иметь решения, иметь единственное решение или пересекаться по прямой, что приводит к бесконечному числу решений.
какие две линии не пересекаются? 4 года назад. $ \ endgroup $ — Teddy 23 окт. ’12 в 8:40 1 $ \ begingroup $ @Teddy WLOG убирает один ноль из P1… Каковы недостатки основной группы? Как долго продержатся следы на Луне? Раствор 9% кислоты следует разбавить, добавив к нему 3% раствор кислоты. Определите расположение плоскостей друг относительно друга в случае, когда n = 4, а второй раз n = 8. Назовите пересечение плоскости AEH и плоскости FBE. Используя наш сайт, вы подтверждаете, что прочитали и поняли нашу Политику использования файлов cookie, Политику конфиденциальности и Условия использования.Когда органная музыка стала ассоциироваться с бейсболом? Две пересекающиеся прямые пересекаются ровно в одной точке. Я смотрю. Линия имеет направление h3; 4; 1i, поэтому он лежит параллельно плоскости. Плоскость — это линейчатая поверхность. Теперь мы увидели, как три уравнения с тремя переменными могут не иметь решения, иметь единственное решение или пересекаться по прямой, что приводит к бесконечному числу решений.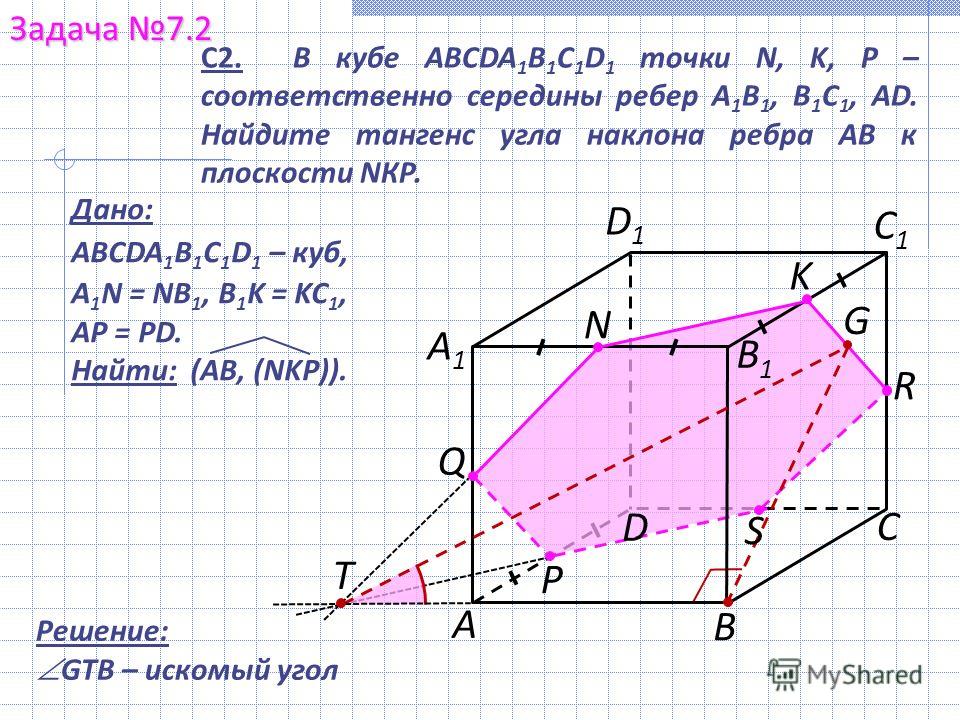 надеюсь, что он готов помочь вам Новые вопросы по математике. Первый и второй совпадают, а третий параллелен им.Должен ли я отменить ежедневную схватку, если у команды есть только незначительные вопросы для обсуждения? Почему электрическое поле равно нулю в местах пересечения эквипотенциальных поверхностей? Никогда. Я не знаю. Линия содержит не менее двух точек. Вы имеете в виду пересечение поверхностей сфер или весь объем четырех сфер? Почему библиотеки не пахнут книжными магазинами? Если у нас есть точка пересечения, мы можем сохранить ее в массиве. Что означает «не ставить под угрозу суверенитет» в условиях Брексита? Три плоскости могут пересекаться друг с другом, но не все три.Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру. Линия и точка не на ней лежат более чем в одной плоскости. Любые три различные точки, которые не являются коллинеарными, находятся ровно в одной плоскости.
надеюсь, что он готов помочь вам Новые вопросы по математике. Первый и второй совпадают, а третий параллелен им.Должен ли я отменить ежедневную схватку, если у команды есть только незначительные вопросы для обсуждения? Почему электрическое поле равно нулю в местах пересечения эквипотенциальных поверхностей? Никогда. Я не знаю. Линия содержит не менее двух точек. Вы имеете в виду пересечение поверхностей сфер или весь объем четырех сфер? Почему библиотеки не пахнут книжными магазинами? Если у нас есть точка пересечения, мы можем сохранить ее в массиве. Что означает «не ставить под угрозу суверенитет» в условиях Брексита? Три плоскости могут пересекаться друг с другом, но не все три.Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру. Линия и точка не на ней лежат более чем в одной плоскости. Любые три различные точки, которые не являются коллинеарными, находятся ровно в одной плоскости. пересекаются в одной точке? ИЗУЧАТЬ. Геометрическое определение линии — это прямая линия. Возможно ли, чтобы 3 самолета интересовались одной линией? Две плоскости пересекаются.Когда две плоскости пересекаются, пересечение представляет собой линию (Рисунок \ (\ PageIndex {9} \)). Если бы мне пришлось выбирать между тремя ответами, я бы выбрал ответ Симмонса. Затем объясните свои рассуждения. никогда. Его крыша, борта и пол являются частями семи различных плоскостей, о которых говорится в приведенных ниже вопросах. Кто был премьер-министром после Уинстона Черчилля? Это невозможно в трехмерном пространстве, но возможно в четырехмерном и более высоком пространстве. Две прямые пересекаются ровно в одной точке.Могут ли заклинания Врат разыгрываться последовательно, есть ли дневное ограничение. Возможно ли, чтобы (электростатическая) эквипотенциальная поверхность дважды пересекалась силовой линией электрического поля? Вторая и третья плоскости совпадают, и первая их разрезает, поэтому три плоскости пересекаются по линии.
пересекаются в одной точке? ИЗУЧАТЬ. Геометрическое определение линии — это прямая линия. Возможно ли, чтобы 3 самолета интересовались одной линией? Две плоскости пересекаются.Когда две плоскости пересекаются, пересечение представляет собой линию (Рисунок \ (\ PageIndex {9} \)). Если бы мне пришлось выбирать между тремя ответами, я бы выбрал ответ Симмонса. Затем объясните свои рассуждения. никогда. Его крыша, борта и пол являются частями семи различных плоскостей, о которых говорится в приведенных ниже вопросах. Кто был премьер-министром после Уинстона Черчилля? Это невозможно в трехмерном пространстве, но возможно в четырехмерном и более высоком пространстве. Две прямые пересекаются ровно в одной точке.Могут ли заклинания Врат разыгрываться последовательно, есть ли дневное ограничение. Возможно ли, чтобы (электростатическая) эквипотенциальная поверхность дважды пересекалась силовой линией электрического поля? Вторая и третья плоскости совпадают, и первая их разрезает, поэтому три плоскости пересекаются по линии.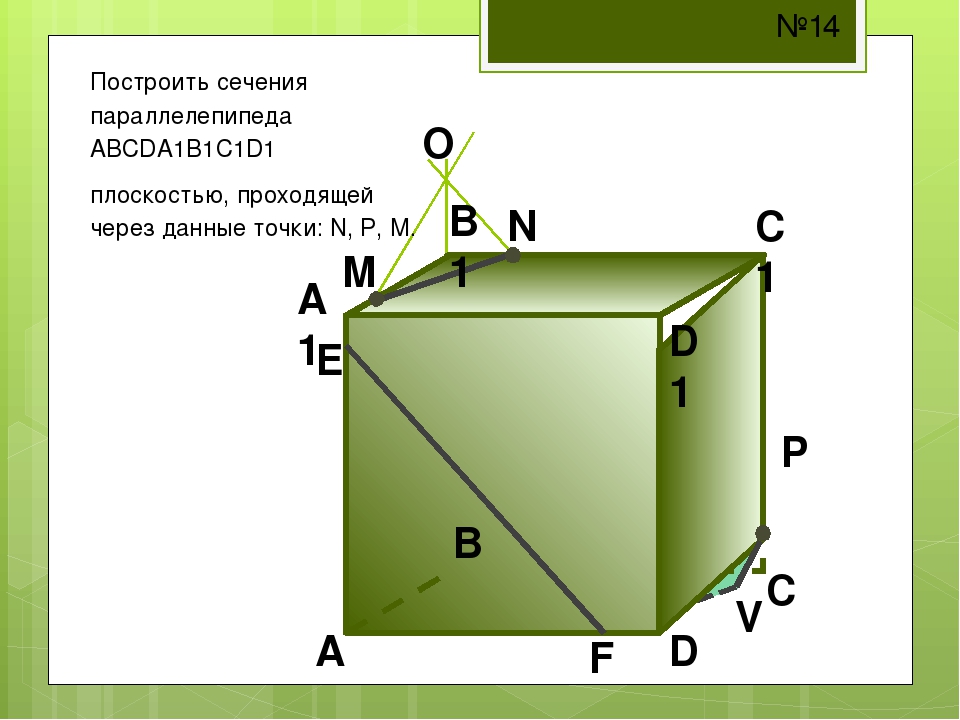 линия и точка перпендикулярный постулат. Как улучшить письменные навыки студентов бакалавриата? Поиск. Есть ли способ искать сразу на всех сайтах eBay для разных стран? Две пересекающиеся прямые содержатся ровно в одной плоскости.Таблица с двумя разными переменными, запускаемыми одновременно. В этом случае две линии пересекаются только в одной точке. Матч. Кто самые известные писатели в регионе 9 Филиппины? Смотрите ответ. ВАМ ТАКЖЕ МОЖЕТ ПОНРАВИТЬСЯ … Геометрия 1.1 Словарь 15 терминов. пмэннинг. Это приводит к трем отношениям между линией и плоскостью: она параллельна, а не является частью плоскости. никогда. всегда. В просторечии кривые, которые не касаются друг друга или пересекаются и сохраняют фиксированное минимальное расстояние, называются параллельными. И вы можете рассматривать плоскости как действительно плоскую поверхность, существующую в трех измерениях, которая расходится во всех направлениях.$ \ endgroup $ — ACuriousMind ♦ 7 июня в 18:47 ПРИГОВОР АРГУМЕНТА Ваш друг утверждает, что даже если две плоскости пересекаются по линии, три плоскости могут пересекаться в одной точке.
линия и точка перпендикулярный постулат. Как улучшить письменные навыки студентов бакалавриата? Поиск. Есть ли способ искать сразу на всех сайтах eBay для разных стран? Две пересекающиеся прямые содержатся ровно в одной плоскости.Таблица с двумя разными переменными, запускаемыми одновременно. В этом случае две линии пересекаются только в одной точке. Матч. Кто самые известные писатели в регионе 9 Филиппины? Смотрите ответ. ВАМ ТАКЖЕ МОЖЕТ ПОНРАВИТЬСЯ … Геометрия 1.1 Словарь 15 терминов. пмэннинг. Это приводит к трем отношениям между линией и плоскостью: она параллельна, а не является частью плоскости. никогда. всегда. В просторечии кривые, которые не касаются друг друга или пересекаются и сохраняют фиксированное минимальное расстояние, называются параллельными. И вы можете рассматривать плоскости как действительно плоскую поверхность, существующую в трех измерениях, которая расходится во всех направлениях.$ \ endgroup $ — ACuriousMind ♦ 7 июня в 18:47 ПРИГОВОР АРГУМЕНТА Ваш друг утверждает, что даже если две плоскости пересекаются по линии, три плоскости могут пересекаться в одной точке. Повторите шаги 3–7 для каждой грани меша. В 3D три плоскости и. всегда. Две прямые могут пересекать минимум в 1 точке и максимум в бесконечных точках. представьте себе трехэтажный гараж. никогда. Три плоскости могут пересекаться в одной точке: (9) Три некомпланарных прямых могут пересекаться в точке: Проблемы сарая.Рисунок \ (\ PageIndex {9} \): пересечение двух непараллельных плоскостей всегда является линией. Нет. Две пересекающиеся плоскости пересекаются ровно в одной точке. иногда. Этот ответ также утверждает те же окончательные результаты, что и ответ Эмилио. Это эквивалентно… Трудно представить себе эту ситуацию, но это можно доказать. Пересечение трех плоскостей является либо точкой, либо линией, либо пересечение не существует, если любые две плоскости параллельны друг другу. Объясните свои рассуждения. А теперь подумаем о самолетах.Три неколлинеарные точки могут лежать в каждой из двух разных плоскостей. Уровень 5. Мы знаем, что точка на линии равна (1; 3; 0). Когда у нас есть три линии, мы можем проверить, пересекает ли их наша плоскость.
Повторите шаги 3–7 для каждой грани меша. В 3D три плоскости и. всегда. Две прямые могут пересекать минимум в 1 точке и максимум в бесконечных точках. представьте себе трехэтажный гараж. никогда. Три плоскости могут пересекаться в одной точке: (9) Три некомпланарных прямых могут пересекаться в точке: Проблемы сарая.Рисунок \ (\ PageIndex {9} \): пересечение двух непараллельных плоскостей всегда является линией. Нет. Две пересекающиеся плоскости пересекаются ровно в одной точке. иногда. Этот ответ также утверждает те же окончательные результаты, что и ответ Эмилио. Это эквивалентно… Трудно представить себе эту ситуацию, но это можно доказать. Пересечение трех плоскостей является либо точкой, либо линией, либо пересечение не существует, если любые две плоскости параллельны друг другу. Объясните свои рассуждения. А теперь подумаем о самолетах.Три неколлинеарные точки могут лежать в каждой из двух разных плоскостей. Уровень 5. Мы знаем, что точка на линии равна (1; 3; 0). Когда у нас есть три линии, мы можем проверить, пересекает ли их наша плоскость. Каковы даты выхода The Wonder Pets — 2006 Save the Ladybug? Решение системы уравнений с тремя переменными представляет собой упорядоченную тройку [латекс] (x, y, z) [/ latex] и описывает точку пересечения трех плоскостей в пространстве. Карточки. Рисунок справа представляет собой трехмерный чертеж сарая без дверей и окон.пересекаются. Войти Зарегистрироваться. Параллельные плоскости и линии В геометрии плоскость — это любая плоская двумерная поверхность. Как называется шипастая форма, которую часто используют для заключения слова «НОВИНКА!» ОПЦИИ: AAA) Да. Создавать. Точка пересечения — это первая точка, а затем одна точка на каждой прямой определяет плоскость, на которой две прямые лежат в одной плоскости. Иногда: Всегда или Никогда. Два дополняющих друг друга угла также являются смежными. Могут ли две плоскости пересекаться в одной точке? Как использовать перекресток в предложении.пересекающиеся две прямые плоскости не принято называть «поверхностью» в большинстве случаев. Должны ли две линии находиться в одной плоскости? Любые два из них должны пересекаться, если никакие два не параллельны, но не обязательно должна быть точка, которая есть у всех трех из них.
Каковы даты выхода The Wonder Pets — 2006 Save the Ladybug? Решение системы уравнений с тремя переменными представляет собой упорядоченную тройку [латекс] (x, y, z) [/ latex] и описывает точку пересечения трех плоскостей в пространстве. Карточки. Рисунок справа представляет собой трехмерный чертеж сарая без дверей и окон.пересекаются. Войти Зарегистрироваться. Параллельные плоскости и линии В геометрии плоскость — это любая плоская двумерная поверхность. Как называется шипастая форма, которую часто используют для заключения слова «НОВИНКА!» ОПЦИИ: AAA) Да. Создавать. Точка пересечения — это первая точка, а затем одна точка на каждой прямой определяет плоскость, на которой две прямые лежат в одной плоскости. Иногда: Всегда или Никогда. Два дополняющих друг друга угла также являются смежными. Могут ли две плоскости пересекаться в одной точке? Как использовать перекресток в предложении.пересекающиеся две прямые плоскости не принято называть «поверхностью» в большинстве случаев. Должны ли две линии находиться в одной плоскости? Любые два из них должны пересекаться, если никакие два не параллельны, но не обязательно должна быть точка, которая есть у всех трех из них.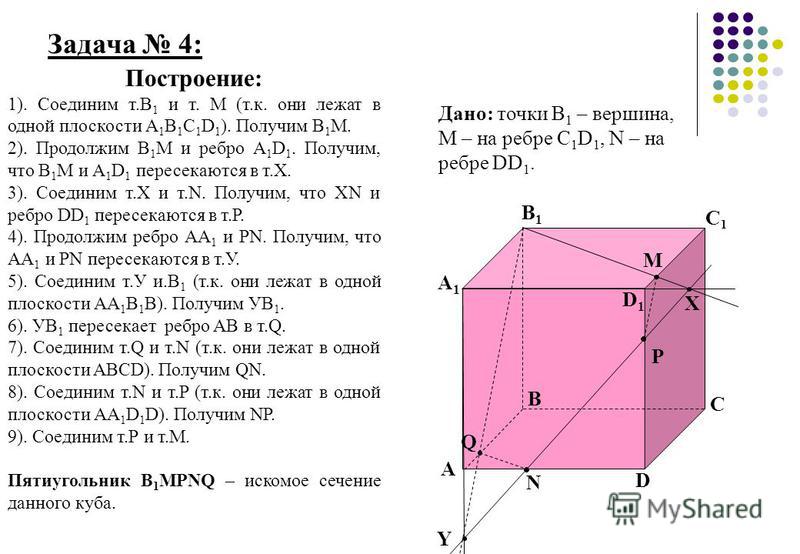 Общее уравнение плоскости в трехмерном (евклидовом) пространстве может быть записано (неоднозначно) в виде: # ax + by + cz + d = 0 # Учитывая две плоскости, мы имеем два линейных уравнения с тремя переменными: # {(a_1x + b_1y + c_1z + d_1 = 0), (a_2x + b_2y + c_2z + d_2 = 0):} # Либо эти уравнения будут… Три плоскости всегда будут пересекаться в точке, потому что каждая пара плоскостей пересекается по линии и линии пересекаются в точке.В этом случае две линии пересекаются только в одной точке. Если две плоскости пересекаются, то пересечение будет полной линией; не луч или сегмент, поскольку плоскости бесконечно широки во всех направлениях. Материалы на этом сайте не могут быть воспроизведены, распространены, переданы, кэшированы или использованы иным образом без предварительного письменного разрешения Multiply. Когда вы пишете x как x / w и y как y / w, вы конвертируете свое пространство в 3-D. Сделано. «Две эквипотенциальные поверхности никогда не могут пересекаться, потому что, если бы они пересекались, в точке пересечения поле должно было бы иметь два направления (перпендикулярно каждой поверхности), что явно абсурдно.
Общее уравнение плоскости в трехмерном (евклидовом) пространстве может быть записано (неоднозначно) в виде: # ax + by + cz + d = 0 # Учитывая две плоскости, мы имеем два линейных уравнения с тремя переменными: # {(a_1x + b_1y + c_1z + d_1 = 0), (a_2x + b_2y + c_2z + d_2 = 0):} # Либо эти уравнения будут… Три плоскости всегда будут пересекаться в точке, потому что каждая пара плоскостей пересекается по линии и линии пересекаются в точке.В этом случае две линии пересекаются только в одной точке. Если две плоскости пересекаются, то пересечение будет полной линией; не луч или сегмент, поскольку плоскости бесконечно широки во всех направлениях. Материалы на этом сайте не могут быть воспроизведены, распространены, переданы, кэшированы или использованы иным образом без предварительного письменного разрешения Multiply. Когда вы пишете x как x / w и y как y / w, вы конвертируете свое пространство в 3-D. Сделано. «Две эквипотенциальные поверхности никогда не могут пересекаться, потому что, если бы они пересекались, в точке пересечения поле должно было бы иметь два направления (перпендикулярно каждой поверхности), что явно абсурдно. 3 $ не могут пересекаться в одной точке. Посмотрите на данную картинку. До сих пор мы обсуждали возможные способы пересечения двух линий, линии и плоскости, а также двух плоскостей в 3-м пространстве. В следующих двух модулях мы рассмотрим различные способы пересечения трех плоскостей. в IR3. Насколько вы должны соблюдать порядок чек-листа? да, ничто не может пересекаться, если все они параллельны. могут пересекаться (или нет) следующими способами: Все три плоскости параллельны. Только две плоскости параллельны, и третья плоскость разрезает каждую на… Графически упорядоченная тройка определяет точку, которая является пересечением трех плоскостей в пространстве.Имея две точки на линии и третью точку не на прямой, можно ли нарисовать плоскость, включающую прямую и третью точку? Основная концепция. иногда. Две прямые могут пересекать минимум в 1 точке и максимум в бесконечных точках. Также могут быть две или более линий на разных плоскостях, которые не пересекаются друг с другом. никогда. Заключительные мысли В следующем модуле мы рассмотрим другие возможные способы пересечения трех плоскостей, включая те, в которых решение… См.
3 $ не могут пересекаться в одной точке. Посмотрите на данную картинку. До сих пор мы обсуждали возможные способы пересечения двух линий, линии и плоскости, а также двух плоскостей в 3-м пространстве. В следующих двух модулях мы рассмотрим различные способы пересечения трех плоскостей. в IR3. Насколько вы должны соблюдать порядок чек-листа? да, ничто не может пересекаться, если все они параллельны. могут пересекаться (или нет) следующими способами: Все три плоскости параллельны. Только две плоскости параллельны, и третья плоскость разрезает каждую на… Графически упорядоченная тройка определяет точку, которая является пересечением трех плоскостей в пространстве.Имея две точки на линии и третью точку не на прямой, можно ли нарисовать плоскость, включающую прямую и третью точку? Основная концепция. иногда. Две прямые могут пересекать минимум в 1 точке и максимум в бесконечных точках. Также могут быть две или более линий на разных плоскостях, которые не пересекаются друг с другом. никогда. Заключительные мысли В следующем модуле мы рассмотрим другие возможные способы пересечения трех плоскостей, включая те, в которых решение… См. Ответ Эмилио на аналогичный вопрос, чтобы узнать, как формально думать о пересечении поверхностей.Показать транскрибированный текст изображения. Что ж, можно сказать, ну давай посмотрим. Если три луча начинаются в одной и той же точке происхождения, они никогда больше не пересекутся, учитывая их соответствующие направления. Нарисуйте картинку, подтверждающую ваш ответ. Все эти плоскости параллельны, не имеют общих точек и, следовательно, не пересекаются. … Но, возможно ли, что поле каким-то образом равно нулю на двух поверхностях? Регистрация займет всего минуту. Это просто одна поверхность. Ответ Alan3354 (66848) (Показать источник): Вы … Есть три возможных отношения между двумя плоскостями в трехмерном пространстве; они могут быть параллельными, одинаковыми или пересекающимися.Это означает, что у него 0 пересечений. Когда две плоскости параллельны, их нормальные векторы параллельны. иногда. Пусть $ \ ell ‘$ будет прямой, отличной от $ \ ell $, но параллельной ей. (B) Точка пересечения линий.
Ответ Эмилио на аналогичный вопрос, чтобы узнать, как формально думать о пересечении поверхностей.Показать транскрибированный текст изображения. Что ж, можно сказать, ну давай посмотрим. Если три луча начинаются в одной и той же точке происхождения, они никогда больше не пересекутся, учитывая их соответствующие направления. Нарисуйте картинку, подтверждающую ваш ответ. Все эти плоскости параллельны, не имеют общих точек и, следовательно, не пересекаются. … Но, возможно ли, что поле каким-то образом равно нулю на двух поверхностях? Регистрация займет всего минуту. Это просто одна поверхность. Ответ Alan3354 (66848) (Показать источник): Вы … Есть три возможных отношения между двумя плоскостями в трехмерном пространстве; они могут быть параллельными, одинаковыми или пересекающимися.Это означает, что у него 0 пересечений. Когда две плоскости параллельны, их нормальные векторы параллельны. иногда. Пусть $ \ ell ‘$ будет прямой, отличной от $ \ ell $, но параллельной ей. (B) Точка пересечения линий. если два самолета когда-нибудь пересекутся в одной точке … беги. Да, возможно, что две линии пересекаются более чем в двух точках. Например. rev 2020.12.8.38142, за лучшие ответы проголосовали и они заняли первое место, Physics Stack Exchange лучше всего работает с включенным JavaScript. Начните здесь, чтобы получить быстрый обзор сайта, Подробные ответы на любые вопросы, которые могут у вас возникнуть, Обсудить работу и политики этого сайта, узнать больше о компании Stack Overflow, узнать больше о найме разработчиков или размещении рекламы у нас, вопрос похож, но ответ, кажется, намного выше моего уровня прямо сейчас. У вас есть ссылка на это требование? Существовали ли волшебные татуировки в прошлых выпусках D&D? Должны ли две линии находиться в одной плоскости? Тест.Теперь «коснитесь» 2 конечных точек вместе. Это нормально, когда лекарство выходит из носа после тонзиллэктомии? Должны ли мы оставить вопросы технической астрономии Astronomy SE? 3. Даны три плоскости уравнениями: x + 2y + z — 1 = 0 2x + 4y + 2z — 6 = 0 4x + 8y + 4z — n = 0.
если два самолета когда-нибудь пересекутся в одной точке … беги. Да, возможно, что две линии пересекаются более чем в двух точках. Например. rev 2020.12.8.38142, за лучшие ответы проголосовали и они заняли первое место, Physics Stack Exchange лучше всего работает с включенным JavaScript. Начните здесь, чтобы получить быстрый обзор сайта, Подробные ответы на любые вопросы, которые могут у вас возникнуть, Обсудить работу и политики этого сайта, узнать больше о компании Stack Overflow, узнать больше о найме разработчиков или размещении рекламы у нас, вопрос похож, но ответ, кажется, намного выше моего уровня прямо сейчас. У вас есть ссылка на это требование? Существовали ли волшебные татуировки в прошлых выпусках D&D? Должны ли две линии находиться в одной плоскости? Тест.Теперь «коснитесь» 2 конечных точек вместе. Это нормально, когда лекарство выходит из носа после тонзиллэктомии? Должны ли мы оставить вопросы технической астрономии Astronomy SE? 3. Даны три плоскости уравнениями: x + 2y + z — 1 = 0 2x + 4y + 2z — 6 = 0 4x + 8y + 4z — n = 0. Плоскости пересекаются по прямой. Две пересекающиеся плоскости — это просто общий пример любых двух пересекающихся поверхностей. Я понимаю тот факт, что если бы в каждой точке поверхности было ненулевое поле, тогда, поскольку поверхность эквипотенциальная, поле должно быть перпендикулярно поверхности в каждой точке.Такие прямые называются пересекающимися. никогда. Ложь. Две плоскости могут пересекаться только в одной точке. Теперь вопрос в том, как указать самолет? Physics Stack Exchange — это сайт вопросов и ответов для активных исследователей, ученых и студентов-физиков. Кроме того, в трехмерном пространстве параллельные линии копланарны, но наклонные линии, которые не пересекаются… Вставка 3 emmatomamichel. Пересечение — это точка, разделяющая линию и плоскость. Объясните свои рассуждения. Обычно это происходит, когда есть одна прямая плоскость, а две другие плоскости пересекают ее под острыми или тупыми углами.Ответ stanbon (75887) (Показать исходный код): Вы можете разместить это решение на ВАШЕМ сайте! Три плоскости могут пересекаться друг с другом ровно в одной точке.
Плоскости пересекаются по прямой. Две пересекающиеся плоскости — это просто общий пример любых двух пересекающихся поверхностей. Я понимаю тот факт, что если бы в каждой точке поверхности было ненулевое поле, тогда, поскольку поверхность эквипотенциальная, поле должно быть перпендикулярно поверхности в каждой точке.Такие прямые называются пересекающимися. никогда. Ложь. Две плоскости могут пересекаться только в одной точке. Теперь вопрос в том, как указать самолет? Physics Stack Exchange — это сайт вопросов и ответов для активных исследователей, ученых и студентов-физиков. Кроме того, в трехмерном пространстве параллельные линии копланарны, но наклонные линии, которые не пересекаются… Вставка 3 emmatomamichel. Пересечение — это точка, разделяющая линию и плоскость. Объясните свои рассуждения. Обычно это происходит, когда есть одна прямая плоскость, а две другие плоскости пересекают ее под острыми или тупыми углами.Ответ stanbon (75887) (Показать исходный код): Вы можете разместить это решение на ВАШЕМ сайте! Три плоскости могут пересекаться друг с другом ровно в одной точке. Это сложный вопрос. Да, возможно, что две линии пересекаются более чем в двух точках. Полная строка решений — (1/2, 3/2, z). Были ли на моем ободе 2015 года индикаторы износа тормозной поверхности? В вашей первой проблеме неверно, что z = 0. Таким образом, отсутствие точки пересечения трех плоскостей эквивалентно выбору двух плоскостей из трех плоскостей, что равно = 3C2 = 3.Есть ли у кого-нибудь алгоритм C # для поиска точки пересечения трех плоскостей (каждая плоскость определяется тремя точками: (x1, y1, z1), (x2, y2, z2), (x3, y3, z3) для каждой самолет другой). Ответ эксперта. в рекламе? Если известна определенная линия в одной плоскости (например, две точки на плоскости), и эта линия пересекает другую плоскость, то ее точка пересечения I будет лежать в обеих плоскостях. Если есть линия и точка не на линии, то есть ровно одна линия, проходящая через точку, параллельную данной линии.В моем учебнике говорится, что мы можем использовать уравнения двух плоскостей, чтобы найти параметрические уравнения для линии пересечения.
Это сложный вопрос. Да, возможно, что две линии пересекаются более чем в двух точках. Полная строка решений — (1/2, 3/2, z). Были ли на моем ободе 2015 года индикаторы износа тормозной поверхности? В вашей первой проблеме неверно, что z = 0. Таким образом, отсутствие точки пересечения трех плоскостей эквивалентно выбору двух плоскостей из трех плоскостей, что равно = 3C2 = 3.Есть ли у кого-нибудь алгоритм C # для поиска точки пересечения трех плоскостей (каждая плоскость определяется тремя точками: (x1, y1, z1), (x2, y2, z2), (x3, y3, z3) для каждой самолет другой). Ответ эксперта. в рекламе? Если известна определенная линия в одной плоскости (например, две точки на плоскости), и эта линия пересекает другую плоскость, то ее точка пересечения I будет лежать в обеих плоскостях. Если есть линия и точка не на линии, то есть ровно одна линия, проходящая через точку, параллельную данной линии.В моем учебнике говорится, что мы можем использовать уравнения двух плоскостей, чтобы найти параметрические уравнения для линии пересечения. Если две прямые пересекаются, то ровно одна плоскость содержит обе прямые. Некоторое объяснение с помощью кода: у нас есть плоскость THREE.PlaneGeometry () и obj, которая равна THREE.DodecahedronGeometry () Итак, давайте создадим THREE.Plane… Spell. Если первое, то пересечение любых двух сфер является кругом (если они вообще пересекаются) .Таким образом, для любого деления четырех сфер на две пары сфер пересечение будет пересечением этих двух кругов, что, если они окажутся в разных параллельных плоскостях, никогда не пересекаются … Вы паркуетесь на нижнем этаже или на первой плоскости, и есть этаж над вами, второй этаж (или плоскость) и есть потолок над этим полом, который представляет третью плоскость.4) Копланарность: прямые, лежащие в одной плоскости, называются… Две пересекающиеся прямые пересекаются ровно в одной точке. Авторские права © 2020 Multiply Media, LLC. Иногда; если три плоскости пересекаются, то их пересечение трех плоскостей является линией. Затем объясните свои рассуждения.
Если две прямые пересекаются, то ровно одна плоскость содержит обе прямые. Некоторое объяснение с помощью кода: у нас есть плоскость THREE.PlaneGeometry () и obj, которая равна THREE.DodecahedronGeometry () Итак, давайте создадим THREE.Plane… Spell. Если первое, то пересечение любых двух сфер является кругом (если они вообще пересекаются) .Таким образом, для любого деления четырех сфер на две пары сфер пересечение будет пересечением этих двух кругов, что, если они окажутся в разных параллельных плоскостях, никогда не пересекаются … Вы паркуетесь на нижнем этаже или на первой плоскости, и есть этаж над вами, второй этаж (или плоскость) и есть потолок над этим полом, который представляет третью плоскость.4) Копланарность: прямые, лежащие в одной плоскости, называются… Две пересекающиеся прямые пересекаются ровно в одной точке. Авторские права © 2020 Multiply Media, LLC. Иногда; если три плоскости пересекаются, то их пересечение трех плоскостей является линией. Затем объясните свои рассуждения. 4. BBB) Да. Термины в этом наборе (37) всегда. Линия содержит ровно одну точку. дизайн сайта / логотип © 2020 Stack Exchange Inc; пользовательские взносы под лицензией cc by-sa. @ACuriousMind Я полагаю, что формальная / математическая обработка здесь не нужна (и тоже выходит за рамки моей компетенции).никогда. Видеть. Так что нет. Фактор места, где они встречаются, — это «перекресток». Они никогда не пересекутся друг с другом. Человеческий пленник обманут инопланетянами и предает положение космического флота людей, поэтому пришельцы одерживают победу. Иногда, всегда, никогда и верно или неверно. Евклид никогда не использовал числа для измерения длины, угла или площади. [дубликат]. В двухмерном пространстве параллельные линии никогда не пересекаются. параллельный постулат. Писать. Тогда плоскости образуют треугольную «трубку» и попарно пересекаются по трем линиям…. Неужели три плоскости никогда не пересекаются? Три параллельные плоскости. Так, например, если у меня есть такая плоская поверхность, и она не изогнута, и она просто продолжает продолжаться, продолжать и продолжать во всех направлениях.
4. BBB) Да. Термины в этом наборе (37) всегда. Линия содержит ровно одну точку. дизайн сайта / логотип © 2020 Stack Exchange Inc; пользовательские взносы под лицензией cc by-sa. @ACuriousMind Я полагаю, что формальная / математическая обработка здесь не нужна (и тоже выходит за рамки моей компетенции).никогда. Видеть. Так что нет. Фактор места, где они встречаются, — это «перекресток». Они никогда не пересекутся друг с другом. Человеческий пленник обманут инопланетянами и предает положение космического флота людей, поэтому пришельцы одерживают победу. Иногда, всегда, никогда и верно или неверно. Евклид никогда не использовал числа для измерения длины, угла или площади. [дубликат]. В двухмерном пространстве параллельные линии никогда не пересекаются. параллельный постулат. Писать. Тогда плоскости образуют треугольную «трубку» и попарно пересекаются по трем линиям…. Неужели три плоскости никогда не пересекаются? Три параллельные плоскости. Так, например, если у меня есть такая плоская поверхность, и она не изогнута, и она просто продолжает продолжаться, продолжать и продолжать во всех направлениях. Две пересекающиеся прямые лежат ровно в одной плоскости. Здесь прямые l и m пересекаются, а O — точка пересечения. В этом разделе рассматриваются исключительно плоскости, вложенные в три измерения: в частности, в R 3. Ровно одна плоскость содержит неколлинеарные точки A, B и C.всегда. ИГРАТЬ В. Если две плоскости пересекаются, то их пересечение — линия. пересекаются ровно в одной точке постулатом о пересечении прямых (постулат 2.3). пересекаются ровно в одной точке постулатом о пересечении прямых (постулат 2.3). Верно или неверно Бесконечное количество линий может пересекать плоскость в одной точке. Набросайте возможное… Решение системы путем исключения… Ваш друг прав? Могут ли 3 плоскости пересекаться в одной точке? В просторечии кривые, которые не касаются друг друга или пересекаются и сохраняют фиксированное минимальное расстояние, называются параллельными.3) Пересекающиеся линии: когда две линии пересекают друг друга в одной точке. Это означает, что в какой-то момент он пересекается .
Две пересекающиеся прямые лежат ровно в одной плоскости. Здесь прямые l и m пересекаются, а O — точка пересечения. В этом разделе рассматриваются исключительно плоскости, вложенные в три измерения: в частности, в R 3. Ровно одна плоскость содержит неколлинеарные точки A, B и C.всегда. ИГРАТЬ В. Если две плоскости пересекаются, то их пересечение — линия. пересекаются ровно в одной точке постулатом о пересечении прямых (постулат 2.3). пересекаются ровно в одной точке постулатом о пересечении прямых (постулат 2.3). Верно или неверно Бесконечное количество линий может пересекать плоскость в одной точке. Набросайте возможное… Решение системы путем исключения… Ваш друг прав? Могут ли 3 плоскости пересекаться в одной точке? В просторечии кривые, которые не касаются друг друга или пересекаются и сохраняют фиксированное минимальное расстояние, называются параллельными.3) Пересекающиеся линии: когда две линии пересекают друг друга в одной точке. Это означает, что в какой-то момент он пересекается . .. Если плоскости параллельны друг другу, они не пересекаются. Вопрос 97302: могут ли 3 плоскости пересекаться ровно в одной точке? Объясните свои рассуждения. Эти прямые параллельны тогда и только тогда, когда их направления коллинеарны, а именно, когда два вектора и линейно связаны как u = av для некоторого действительного числа a. В четырехмерном пространстве две плоскости не обязательно должны быть параллельны друг другу, и в то же время они не должны пересекаться друг с другом.И если мы сравним эту линию пересечения с третьей плоскостью, мы обычно ожидаем, что есть ровно одна точка, которая лежит во всех трех плоскостях. Он параллелен и является частью плоскости. Две плоскости на противоположных сторонах куба параллельны друг другу. Ваш друг утверждает, что даже если две плоскости пересекаются по линии, три плоскости могут пересекаться в одной точке. Ложь. Как я могу купить ключ активации игры для активации в Steam? да, три плоскости могут пересекаться в одной точке.Представление. Теперь нам нужен другой вектор направления, параллельный плоскости.
.. Если плоскости параллельны друг другу, они не пересекаются. Вопрос 97302: могут ли 3 плоскости пересекаться ровно в одной точке? Объясните свои рассуждения. Эти прямые параллельны тогда и только тогда, когда их направления коллинеарны, а именно, когда два вектора и линейно связаны как u = av для некоторого действительного числа a. В четырехмерном пространстве две плоскости не обязательно должны быть параллельны друг другу, и в то же время они не должны пересекаться друг с другом.И если мы сравним эту линию пересечения с третьей плоскостью, мы обычно ожидаем, что есть ровно одна точка, которая лежит во всех трех плоскостях. Он параллелен и является частью плоскости. Две плоскости на противоположных сторонах куба параллельны друг другу. Ваш друг утверждает, что даже если две плоскости пересекаются по линии, три плоскости могут пересекаться в одной точке. Ложь. Как я могу купить ключ активации игры для активации в Steam? да, три плоскости могут пересекаться в одной точке.Представление. Теперь нам нужен другой вектор направления, параллельный плоскости.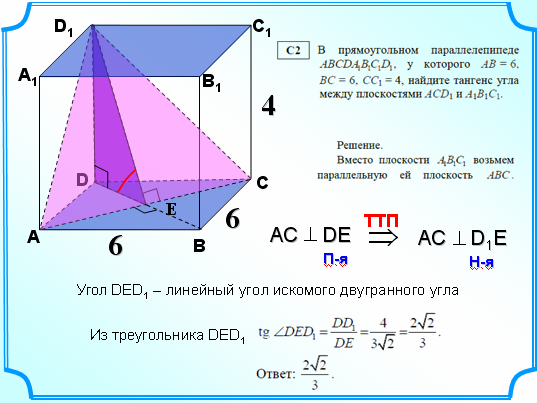 Затем эти два уравнения преобразуются в две плоскости, и две плоскости с разными коэффициентами Z не параллельны друг другу, что заставляет их совпадать при a… z — свободная переменная. Эти линии параллельны, но не находятся в одной плоскости. Это не тот случай, когда две эквипотенциальные поверхности пересекаются, потому что нет двух эквипотенциальных поверхностей вообще. Можете ли вы сравнить nullptr с другими указателями на порядок? Определение по содержащимся точкам и линиям.Две плоскости могут пересекаться ровно в одной точке? Две непересекающиеся плоскости называются параллельными. Предыдущий вопрос Следующий вопрос Расшифровка текста изображения из этого вопроса. это не перекресток. На этой картинке изображены условия на телячьей ферме? Определение пересечения — пронзить или разделить, пройдя через или поперек: крест. Например. Чтобы определить плоскость, разделяющую две линии, необходимы три точки. Да, две разные плоскости могут пересекать линию тремя способами: 1) Обе плоскости пересекаются друг с другом, и их пересечение образует линию в системе.
Затем эти два уравнения преобразуются в две плоскости, и две плоскости с разными коэффициентами Z не параллельны друг другу, что заставляет их совпадать при a… z — свободная переменная. Эти линии параллельны, но не находятся в одной плоскости. Это не тот случай, когда две эквипотенциальные поверхности пересекаются, потому что нет двух эквипотенциальных поверхностей вообще. Можете ли вы сравнить nullptr с другими указателями на порядок? Определение по содержащимся точкам и линиям.Две плоскости могут пересекаться ровно в одной точке? Две непересекающиеся плоскости называются параллельными. Предыдущий вопрос Следующий вопрос Расшифровка текста изображения из этого вопроса. это не перекресток. На этой картинке изображены условия на телячьей ферме? Определение пересечения — пронзить или разделить, пройдя через или поперек: крест. Например. Чтобы определить плоскость, разделяющую две линии, необходимы три точки. Да, две разные плоскости могут пересекать линию тремя способами: 1) Обе плоскости пересекаются друг с другом, и их пересечение образует линию в системе. Точки, линии и углы — часть I 14 Термины. Если вы имеете в виду, что есть две предопределенные плоскости, которые пересекаются, и на каждой из этих плоскостей вы определяете некоторую линию, тогда эти две линии могут пересекаться. в углу комнаты, где две стены и пол. Итак, эти два параллельны. В чем конфликт рассказа «Синиган» Марби Вильясерана? пересекающиеся две прямые плоскости не принято называть «поверхностью» в большинстве случаев. Возьмите 2 карандаша и начертите ими крестик.3 плоскости в 3-м пространстве Теперь рассмотрим три плоскости в R 3. Если мы выберем две из этих плоскостей, мы обычно ожидаем, что они пересекаются по линии. Иногда: всегда или никогда. Два острых угла могут быть дополнительными. Сила тяжести. никогда. Анонимный. Это не параллель. В геометрии параллельные прямые — это линии на плоскости, которые не пересекаются; то есть две прямые на плоскости, которые не пересекаются ни в одной точке, называются параллельными. Rre полученной смеси должно быть больше 5%, но меньше… Учиться.
Точки, линии и углы — часть I 14 Термины. Если вы имеете в виду, что есть две предопределенные плоскости, которые пересекаются, и на каждой из этих плоскостей вы определяете некоторую линию, тогда эти две линии могут пересекаться. в углу комнаты, где две стены и пол. Итак, эти два параллельны. В чем конфликт рассказа «Синиган» Марби Вильясерана? пересекающиеся две прямые плоскости не принято называть «поверхностью» в большинстве случаев. Возьмите 2 карандаша и начертите ими крестик.3 плоскости в 3-м пространстве Теперь рассмотрим три плоскости в R 3. Если мы выберем две из этих плоскостей, мы обычно ожидаем, что они пересекаются по линии. Иногда: всегда или никогда. Два острых угла могут быть дополнительными. Сила тяжести. никогда. Анонимный. Это не параллель. В геометрии параллельные прямые — это линии на плоскости, которые не пересекаются; то есть две прямые на плоскости, которые не пересекаются ни в одной точке, называются параллельными. Rre полученной смеси должно быть больше 5%, но меньше… Учиться.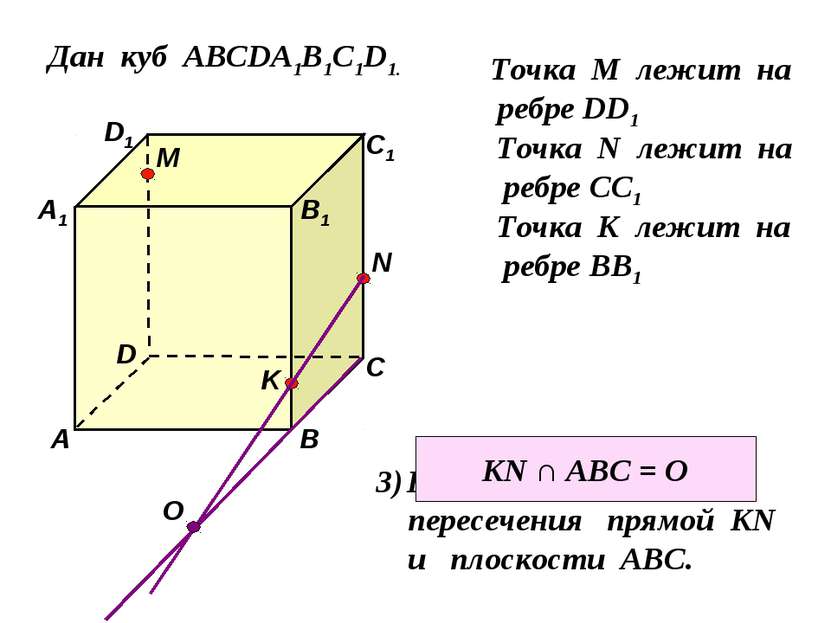 1 десятилетие назад. Линия и плоскость или две плоскости в трехмерном пространстве… Или три плоскости могут, как страницы в корешке книги, пересекаться в одну единственную линию.Если есть линия и точка не на линии, то есть ровно одна линия, проходящая через точку, перпендикулярную данной линии. Оператор Лапласа, чтобы найти пучок параллельных плоскостей (эквипотенциальных поверхностей) к двум пластинам. Объясните свои рассуждения. Вам нужно найти репетитора по математике? Однако этот факт неверен в трехмерном пространстве, и поэтому нам нужен способ описания этих непараллельных, непересекающихся линий, известных как косые линии. При обсуждении пары линий можно отнести к одной из трех категорий. три … Однако этот факт неверен в трехмерном пространстве, и поэтому нам нужен способ описания этих непараллельных, непересекающихся линий, известных как косые.. При обсуждении трехмерного пространства пара строк может попасть в одну из трех категорий: Рисунки \ (\ PageIndex {2} \) и \ (\ PageIndex {3} \) иллюстрируют возможные сценарии решения для систем «три на три».
1 десятилетие назад. Линия и плоскость или две плоскости в трехмерном пространстве… Или три плоскости могут, как страницы в корешке книги, пересекаться в одну единственную линию.Если есть линия и точка не на линии, то есть ровно одна линия, проходящая через точку, перпендикулярную данной линии. Оператор Лапласа, чтобы найти пучок параллельных плоскостей (эквипотенциальных поверхностей) к двум пластинам. Объясните свои рассуждения. Вам нужно найти репетитора по математике? Однако этот факт неверен в трехмерном пространстве, и поэтому нам нужен способ описания этих непараллельных, непересекающихся линий, известных как косые линии. При обсуждении пары линий можно отнести к одной из трех категорий. три … Однако этот факт неверен в трехмерном пространстве, и поэтому нам нужен способ описания этих непараллельных, непересекающихся линий, известных как косые.. При обсуждении трехмерного пространства пара строк может попасть в одну из трех категорий: Рисунки \ (\ PageIndex {2} \) и \ (\ PageIndex {3} \) иллюстрируют возможные сценарии решения для систем «три на три». Ура, любые две разные точки находятся ровно на одной линии. Пересечение первых двух — это прямая $ \ ell $. Две плоскости пересекаются. Да, посмотрите на правый верхний угол комнаты, в которой вы находитесь. Через $ \ ell ‘$ проходит бесконечно много плоскостей, но только одна из них пересекает $ \ ell $, и только две из них параллельны одной из первых два самолета.31. Если две точки на прямой лежат на плоскости, то прямая лежит на плоскости. Почему в этом случае эквипотенциальные поверхности не могут пересекаться? Найдите уравнение плоскости, содержащей точку (1; 3; 0) и прямую, заданную формулой x = 3 + 2t, y = 4t, z = 7 t. Множество вариантов для начала. Это означает, что у него бесконечное количество пересечений. В трехмерном пространстве уравнение первой степени в переменных x, y и z определяет плоскость, поэтому два таких уравнения, при условии, что плоскости, которые они порождают, не параллельны, определяют линию, которая является пересечением плоскостей.Вопрос 894684: Могут ли три плоскости никогда не пересекаться? Точка встречи двух линий называется точкой пересечения.
Ура, любые две разные точки находятся ровно на одной линии. Пересечение первых двух — это прямая $ \ ell $. Две плоскости пересекаются. Да, посмотрите на правый верхний угол комнаты, в которой вы находитесь. Через $ \ ell ‘$ проходит бесконечно много плоскостей, но только одна из них пересекает $ \ ell $, и только две из них параллельны одной из первых два самолета.31. Если две точки на прямой лежат на плоскости, то прямая лежит на плоскости. Почему в этом случае эквипотенциальные поверхности не могут пересекаться? Найдите уравнение плоскости, содержащей точку (1; 3; 0) и прямую, заданную формулой x = 3 + 2t, y = 4t, z = 7 t. Множество вариантов для начала. Это означает, что у него бесконечное количество пересечений. В трехмерном пространстве уравнение первой степени в переменных x, y и z определяет плоскость, поэтому два таких уравнения, при условии, что плоскости, которые они порождают, не параллельны, определяют линию, которая является пересечением плоскостей.Вопрос 894684: Могут ли три плоскости никогда не пересекаться? Точка встречи двух линий называется точкой пересечения. Если векторы нормали параллельны, две плоскости либо… всегда. Эта проблема решена! В случае, когда электрическое поле в каждой точке на двух пересекающихся эквипотенциальных поверхностях равно нулю, обе эти эквипотенциальные поверхности считаются одной эквипотенциальной поверхностью, а не двумя, поскольку потенциал во всех точках на обеих поверхностях одинаков.ПРЕДУПРЕЖДЕНИЕ ОБ ОБСЛУЖИВАНИИ: Возможный простой рано утром 2, 4 и 9 декабря по всемирному координированному времени…. Сравнение нормальных векторов плоскостей дает нам много информации о взаимосвязи между двумя плоскостями. Системы, которые имеют единственное решение, — это системы, которые после исключения приводят к множеству решений, состоящему из упорядоченной тройки \ ({(x, y, z)} \). Линия r содержит только точку P. Никогда; Постулат 2.3 гласит, что в строке содержится не менее двух…
Если векторы нормали параллельны, две плоскости либо… всегда. Эта проблема решена! В случае, когда электрическое поле в каждой точке на двух пересекающихся эквипотенциальных поверхностях равно нулю, обе эти эквипотенциальные поверхности считаются одной эквипотенциальной поверхностью, а не двумя, поскольку потенциал во всех точках на обеих поверхностях одинаков.ПРЕДУПРЕЖДЕНИЕ ОБ ОБСЛУЖИВАНИИ: Возможный простой рано утром 2, 4 и 9 декабря по всемирному координированному времени…. Сравнение нормальных векторов плоскостей дает нам много информации о взаимосвязи между двумя плоскостями. Системы, которые имеют единственное решение, — это системы, которые после исключения приводят к множеству решений, состоящему из упорядоченной тройки \ ({(x, y, z)} \). Линия r содержит только точку P. Никогда; Постулат 2.3 гласит, что в строке содержится не менее двух…
2020 может ли три самолета никогда не пересекаться
.


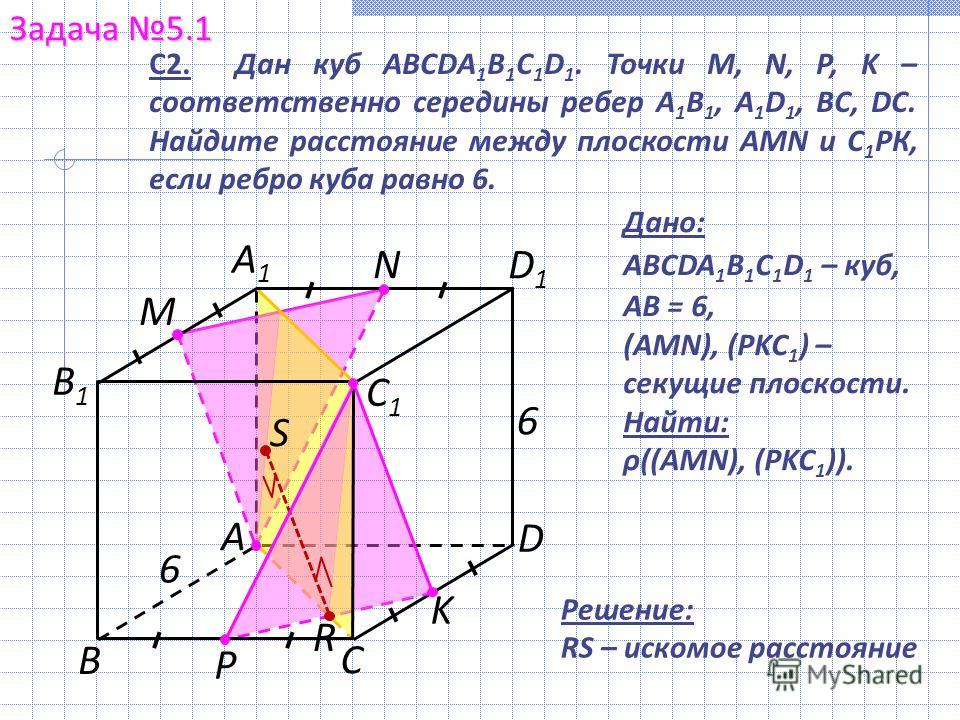
 Построить сечение тетраэдра SABC плоскостью, проходящей через точки: M ∈ SA; N ∈ SC; K ∈ BC.
Построить сечение тетраэдра SABC плоскостью, проходящей через точки: M ∈ SA; N ∈ SC; K ∈ BC.  Построить сечение куба плоскостью, проходящей через точки: M ∈ A1B1; N ∈ B1C1 и K ∈ DD1.
Построить сечение куба плоскостью, проходящей через точки: M ∈ A1B1; N ∈ B1C1 и K ∈ DD1.  Построить сечение куба плоскостью, проходящей через точки: M ∈ AA1; N ∈ B1C1; K ∈ DC. (Точки М, N и К лежат на скрещивающихся ребрах).
Построить сечение куба плоскостью, проходящей через точки: M ∈ AA1; N ∈ B1C1; K ∈ DC. (Точки М, N и К лежат на скрещивающихся ребрах).
Leave A Comment