геометрия — Как доказать, что две прямые в кубе перпендикулярны, без использования векторов
спросил
Изменено 2 года, 9 месяцев назад
Просмотрено 3к раз
$\begingroup$
Дано: Куб $ABCDA_1B_1C_1D_1$
Докажите, что $BD$ перпендикулярно $AC_1$
Я понятия не имею, как это доказать. Также я не умею использовать векторы (мы их в школе не изучали). Я могу использовать все теоремы из стереометрии (думаю, другое название для этого — объемная геометрия, но в основном мы имеем дело с трехмерными фигурами (нахождение их объема, площади, углов между разными сторонами и т. д.), плоскостями и линиями в пространстве)
- геометрия
- 3d
$\endgroup$
$\begingroup$
Пусть $M$ — середина $BD$, а $O$ — середина $AC_1$. Тогда $OM$ перпендикулярно $DB$, а $AC$ перпендикулярно $DB$. Отсюда следует, что $DB$ перпендикулярна двум различным прямым в плоскости $A\vee C\vee C_1$, а значит, и всем прямым в этой плоскости, в частности, $A\vee C_1$.
Тогда $OM$ перпендикулярно $DB$, а $AC$ перпендикулярно $DB$. Отсюда следует, что $DB$ перпендикулярна двум различным прямым в плоскости $A\vee C\vee C_1$, а значит, и всем прямым в этой плоскости, в частности, $A\vee C_1$.
$\endgroup$
$\begingroup$
Перпендикулярно означает, что если вы переведете $BD$ так, чтобы он начинался с $A$, результирующие линии будут перпендикулярны. Поэтому переместите $ABCD$ влево, чтобы получить квадрат в той же плоскости, скажем, $A’ADD’.$ Обратите внимание, что $C_1 D’ = \sqrt{5}, AC_1 = \sqrt{3},$ и $ AD’ = \sqrt{2},$, так что это прямоугольный треугольник.
$\endgroup$
$\begingroup$
Без расчета. Просто используйте аксиомы.
- $AC$ перпендикулярно $BD$.
- $A’C’$ перпендикулярно $B’D’$.
Существует аксиома, говорящая, что
Одна плоскость проходит через две параллельные прямые.
- Плоскость $ACC’A’$ перпендикулярна $BDD’B’$.
Другие аксиомы:
Если прямая $L$ перпендикулярна плоскости, то каждая прямая плоскости перпендикулярна $L$.
$\endgroup$
$\begingroup$
Пока мы отвечаем на старые вопросы…
Пусть $B’$ и $D’$ — соответствующие середины $\overline{BB_1}$ и $\overline{DD_1}$, так что $ \overline{B’D’}\parallel\overline{BD}$. И $\overline{B’D’}$, и $\overline{AC_1}$ содержат центр куба, что делает $\square AB’C_1D’$ плоским четырехугольником; стороны этого четырехугольника явно равны, что делает его ромбом, поэтому его диагонали, $\overline{AC_1}$ и $\overline{B’C’}$, перпендикулярны. $\квадрат$
$\endgroup$
12.5 Линии и плоскости
Линии и плоскости, пожалуй, самые простые из кривых и поверхностей в
трехмерное пространство.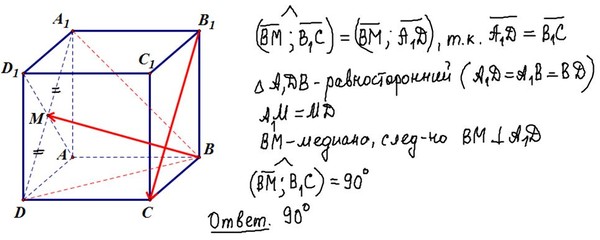 Они также окажутся важными, поскольку мы стремимся
понимать более сложные кривые и поверхности.
Они также окажутся важными, поскольку мы стремимся
понимать более сложные кривые и поверхности.
Уравнение линии в двух измерениях: $ax+by=c$; это разумно ожидать, что линия в трех измерениях задается $ax + by +cz = d$; разумно, но неправильно — оказывается, что это уравнение плоскости.
У плоскости нет очевидного «направления», как у линии. можно связать плоскость с направлением очень полезным способом, однако: есть ровно два направления, перпендикулярные самолет. Любой вектор с одним из этих двух направлений называется
Предположим, две точки $\ds (v_1,v_2,v_3)$ и $\ds (w_1,w_2,w_3)$ лежат в плоскости;
тогда вектор $\ds\langle w_1-v_1,w_2-v_2,w_3-v_3\rangle$ параллелен
к самолету; в частности, если этот вектор положить хвостом в
$\ds (v_1,v_2,v_3)$, то его головка находится в точке $\ds (w_1,w_2,w_3)$ и лежит в
самолет.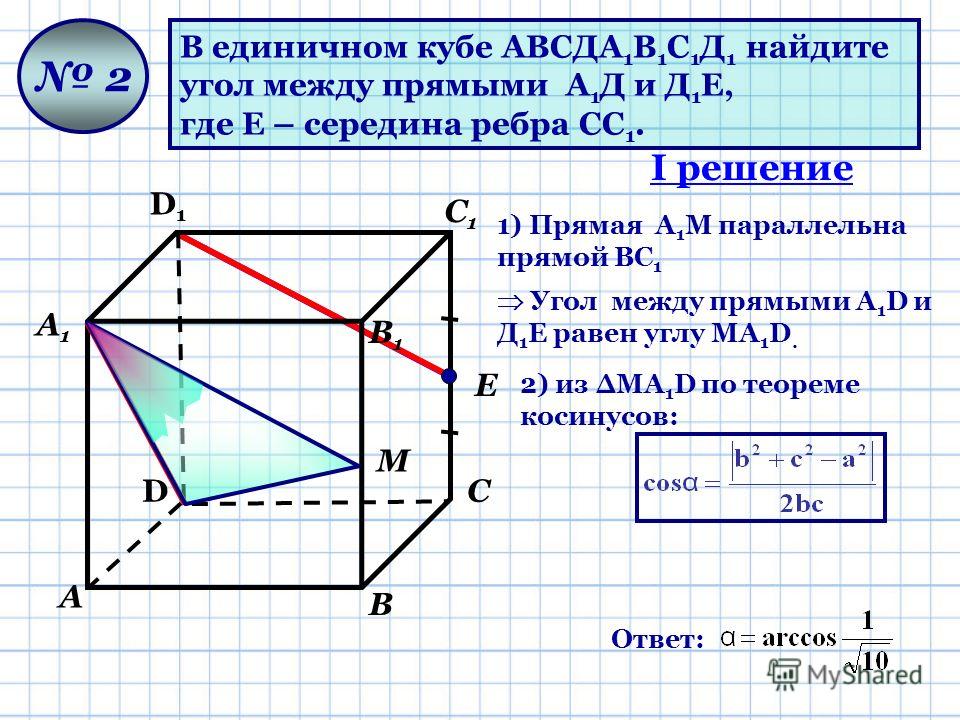 В результате любой вектор, перпендикулярный плоскости,
перпендикулярно $\ds \langle w_1-v_1,w_2-v_2,w_3-v_3\rangle$. На самом деле, это
Легко видеть, что плоскость состоит из
В результате любой вектор, перпендикулярный плоскости,
перпендикулярно $\ds \langle w_1-v_1,w_2-v_2,w_3-v_3\rangle$. На самом деле, это
Легко видеть, что плоскость состоит из 
Рисунок 12.5.1. Плоскость, определяемая векторами, перпендикулярными нормали.
Таким образом, для вектора $\langle a,b,c\rangle$ мы знаем, что все плоскости перпендикулярные этому вектору, имеют вид $ax+by+cz=d$, и любая поверхность этой формы является плоскостью, перпендикулярной $\langle a,b,c\rangle$.
Пример 12.5.1 Найдите уравнение для плоскости, перпендикулярной $\langle 1,2,3\rangle$ и содержащий точку $(5,0,7)$.
Используя приведенный выше вывод,
плоскость равна $1x+2y+3z=1\cdot5+2\cdot0+3\cdot7=26$. Поочередно, мы
знаем, что плоскость равна $x+2y+3z=d$, и чтобы найти $d$, можно подставить
известную точку на плоскости, чтобы получить $5+2\cdot0+3\cdot7=d$, поэтому $d=26$. Мы могли бы также записать это просто как $(x-5)+2(y)+3(z-7)=0$, что для
много целей прекрасное представление; всегда можно умножить
чтобы получить $x+2y+3z=26$.
$\квадрат$
Мы могли бы также записать это просто как $(x-5)+2(y)+3(z-7)=0$, что для
много целей прекрасное представление; всегда можно умножить
чтобы получить $x+2y+3z=26$.
$\квадрат$
Пример 12.5.2 Найдите вектор нормали к плоскости $2x-3y+z=15$.
Одним из примеров является $\langle 2, -3,1\rangle$. Любой вектор, параллельный или антипараллельно с этим также работает, например $-2\langle 2, -3,1\rangle=\langle -4,6,-2\rangle$ также нормальна к плоскости. $\квадрат$
Нам часто нужно будет найти уравнение для плоскости при заданных информация о самолете. Хотя иногда может быть немного более короткие пути к желаемому результату, это всегда возможно, и обычно целесообразно использовать данную информацию, чтобы найти нормаль к плоскость и точку на плоскости, а затем найти уравнение в виде выше.
Пример 12.5.3. Плоскости $x-z=1$ и $y+2z=3$ пересекаются по прямой. Найди третья плоскость, содержащая эту прямую и перпендикулярная плоскости $x+y-2z=1$.
Во-первых, заметим, что две плоскости перпендикулярны тогда и только тогда, когда их
нормальные векторы перпендикулярны. Таким образом, мы ищем вектор $\langle
a,b,c\rangle$, то есть
перпендикулярно $\langle 1,1,-2\rangle$. Кроме того, поскольку
желаемая плоскость должна содержать определенную линию, $\langle
a,b,c\rangle$ должны быть перпендикулярны любому вектору, параллельному этому
линия. Так как $\langle
a,b,c\rangle$ должны быть перпендикулярны двум векторам, мы можем найти это по
вычисление перекрестного произведения двух. Итак, нам нужен вектор, параллельный
к линии пересечения данных плоскостей. Для этого достаточно
знать две точки на прямой. Чтобы найти две точки на этой прямой,
необходимо найти две точки, находящиеся одновременно на двух плоскостях,
$x-z=1$ и $y+2z=3$. Любая точка на обеих плоскостях будет удовлетворять
$x-z=1$ и $y+2z=3$. Легко найти значения для $x$ и $z$
удовлетворяющие первому, такие как $x=1, z=0$ и $x=2, z=1$. Затем
мы можем найти соответствующие значения для $y$, используя второе уравнение,
а именно $y=3$ и $y=1$, поэтому
$(1,3,0)$ и $(2,1,1)$ находятся на прямой
пересечения, потому что оба находятся в обеих плоскостях.
Таким образом, мы ищем вектор $\langle
a,b,c\rangle$, то есть
перпендикулярно $\langle 1,1,-2\rangle$. Кроме того, поскольку
желаемая плоскость должна содержать определенную линию, $\langle
a,b,c\rangle$ должны быть перпендикулярны любому вектору, параллельному этому
линия. Так как $\langle
a,b,c\rangle$ должны быть перпендикулярны двум векторам, мы можем найти это по
вычисление перекрестного произведения двух. Итак, нам нужен вектор, параллельный
к линии пересечения данных плоскостей. Для этого достаточно
знать две точки на прямой. Чтобы найти две точки на этой прямой,
необходимо найти две точки, находящиеся одновременно на двух плоскостях,
$x-z=1$ и $y+2z=3$. Любая точка на обеих плоскостях будет удовлетворять
$x-z=1$ и $y+2z=3$. Легко найти значения для $x$ и $z$
удовлетворяющие первому, такие как $x=1, z=0$ и $x=2, z=1$. Затем
мы можем найти соответствующие значения для $y$, используя второе уравнение,
а именно $y=3$ и $y=1$, поэтому
$(1,3,0)$ и $(2,1,1)$ находятся на прямой
пересечения, потому что оба находятся в обеих плоскостях.
Теперь мы знаем, что $\langle 1,1,1\rangle$ нормальна к искомой плоскости. и $(2,1,1)$ — точка на плоскости. Поэтому уравнение плоскость равна $x+y+z=4$. В качестве быстрой проверки, поскольку $(1,3,0)$ также находится на линия, она должна быть в самолете; поскольку $1+3+0=4$, мы видим, что это действительно дело.
Обратите внимание, что если бы мы использовали $\langle -3,-3,-3\rangle$ в качестве нормали, мы открыли бы уравнение $-3x-3y-3z=-12$, то мы вполне могли бы заметили, что мы можем разделить обе части на $-3$, чтобы получить эквивалент $x+y+z=4$. $\квадрат$
Итак, теперь мы понимаем уравнения плоскостей; давайте обратимся к
линии. К сожалению, это оказывается весьма неудобным
представить типичную линию одним уравнением; нам нужно подойти
линии по-другому.
К сожалению, это оказывается весьма неудобным
представить типичную линию одним уравнением; нам нужно подойти
линии по-другому.
В отличие от плоскости, линия в трех измерениях имеет очевидную направление, а именно направление любого параллельного ему вектора. Фактически линия может быть определена и однозначно идентифицирована путем предоставления одной точки на прямой и вектор, параллельный прямой (в одном из двух возможных направления). То есть линия состоит именно из тех точек, которые мы можем достичь, начав с точки и пройдя некоторое расстояние в направление вектора. Давайте посмотрим, как мы можем перевести это на более математический язык.
Предположим, что прямая содержит точку $\ds (v_1,v_2,v_3)$ и параллельна
к вектору $\langle a,b,c\rangle$; мы называем $\langle a,b,c\rangle$ a вектор направления для линии.
Если мы поместим вектор $\ds
\langle v_1,v_2,v_3\rangle$ с хвостом в начале координат и головой
в $\ds (v_1,v_2,v_3)$, и если мы поместим вектор $\langle
a,b,c\rangle$ хвостом в $\ds (v_1,v_2,v_3)$, то голова
$\langle a,b,c\rangle$ находится в точке на прямой. Мы можем добраться до любых указать на линии, выполнив то же самое, за исключением использования
$t\langle a,b,c\rangle$ вместо $\langle a,b,c\rangle$, где $t$
некоторое действительное число. Из-за того, как работает сложение векторов,
точка в начале вектора $t\langle a,b,c\rangle$ — это точка
в начале вектора $\ds\langle v_1,v_2,v_3\rangle+t\langle
a,b,c\rangle$, а именно $\ds (v_1+ta,v_2+tb,v_3+tc)$; видеть
рисунок 12.5.2.
Мы можем добраться до любых указать на линии, выполнив то же самое, за исключением использования
$t\langle a,b,c\rangle$ вместо $\langle a,b,c\rangle$, где $t$
некоторое действительное число. Из-за того, как работает сложение векторов,
точка в начале вектора $t\langle a,b,c\rangle$ — это точка
в начале вектора $\ds\langle v_1,v_2,v_3\rangle+t\langle
a,b,c\rangle$, а именно $\ds (v_1+ta,v_2+tb,v_3+tc)$; видеть
рисунок 12.5.2.
Рисунок 12.5.2. Векторная форма линии.
Другими словами, когда $t$ проходит через все возможные действительные значения,
вектор $\ds \langle v_1,v_2,v_3\rangle+t\langle a,b,c\rangle$ указывает на
каждая точка на линии, когда ее конец находится в начале координат. Другой
общий способ записать это как набор параметрические уравнения :
$$ x= v_1+ta\qquad y=v_2+tb \qquad z=v_3+tc.$$
Иногда полезно использовать эту форму линии даже в двух случаях.
размеры; векторная форма прямой на плоскости $x$-$y$ есть
$\ds \langle v_1,v_2\rangle+t\langle a,b\rangle$, что совпадает с
$\ds \langle v_1,v_2,0\rangle+t\langle a,b,0\rangle$.
Пример 12.5.4. Найдите векторное выражение для линии, проходящей через $(6,1,-3)$ и $(2,4,5)$. Чтобы получить вектор, параллельный прямой, мы вычитаем $\langle 6,1,-3\rangle-\langle2,4,5\rangle=\langle 4,-3,-8\rangle$. Линия тогда задается как $\langle 2,4,5\rangle+t\langle 4,-3,-8\rangle$; там конечно, много других возможностей, таких как $\langle 6,1,-3\rangle+t\langle 4,-3,-8\rangle$. $\квадрат$
Пример 12.5.5 Определить, совпадают ли прямые $\langle 1,1,1\rangle+t\langle 1,2,-1\rangle$ и $\langle 3,2,1\rangle+t\langle -1,-5,3\rangle$ параллельны, пересекаются или ни один.
В двух измерениях две линии либо пересекаются, либо параллельны; в
В трех измерениях линии, которые не пересекаются, могут быть не параллельны.
В этом случае, поскольку векторы направления линий не
параллельны или антипараллельны, мы знаем, что прямые не параллельны.
Если они пересекаются, то должно быть два значения $a$ и $b$, так что
$\langle 1,1,1\rangle+a\langle 1,2,-1\rangle=
\langle 3,2,1\rangle+b\langle -1,-5,3\rangle$, то есть
$$\выравнивание{
1+а&=3-б\кр
1+2а&=2-5б\кр
1-а&=1+3б\кр
}$$
Это дает три уравнения с двумя неизвестными, поэтому может быть, а может и не быть.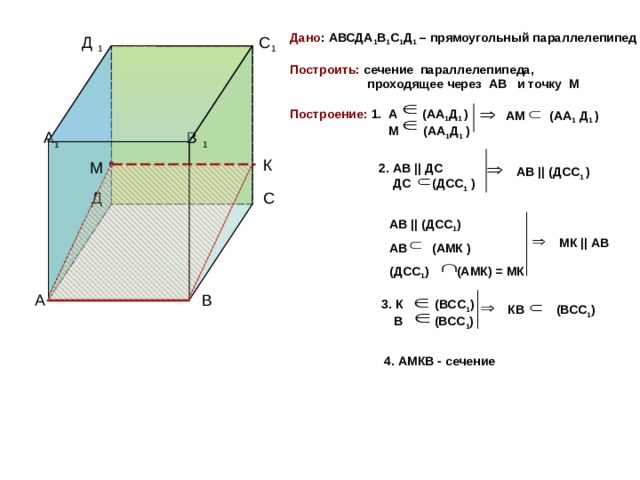 решение в общем. В этом случае легко обнаружить, что $a=3$
и $b=-1$ удовлетворяет всем трем уравнениям, поэтому прямые пересекаются в
точка $(4,7,-2)$.
$\квадрат$
решение в общем. В этом случае легко обнаружить, что $a=3$
и $b=-1$ удовлетворяет всем трем уравнениям, поэтому прямые пересекаются в
точка $(4,7,-2)$.
$\квадрат$
Пример 12.5.6. Найти расстояние от точки $(1,2,3)$ до плоскости $2x-y+3z=5$. Расстояние от точки $P$ до плоскости является кратчайшим расстояние от $P$ до любой точки плоскости; это расстояние, измеряемое от $P$ перпендикулярно плоскости; видеть рисунок 12.5.3. Это расстояние является абсолютным значением скалярной проекции $\ds \overrightarrow{\распорка QP}$ на вектор нормали $\bf n$, где $Q$ — любая точка плоскости. Легко найти точку на плоскости, скажем, $(1,0,1)$. Таким образом, расстояние равно $$ {\ overrightarrow {\ распорка QP} \ cdot {\ bf n} \ over | {\ bf n} |} = {\ langle 0,2,2 \ rangle \ cdot \ langle 2, -1,3 \ rangle \ over | \ langle 2, — 1,3 \ rangle |} = {4\over\sqrt{14}}. $$ $\квадрат$
Рисунок 12.5.3. Расстояние от точки до плоскости.
Пример 12.5.7. Найти расстояние от точки $(-1,2,1)$ до прямой
$\langle 1,1,1\rangle + t\langle 2,3,-1\rangle$. Мы снова хотим расстояния
измеряется перпендикулярно линии, как показано на
рисунок 12.5.4. Желаемое расстояние равно
$$
|\overrightarrow{\ распорка QP}|\sin\theta=
{|\overrightarrow{\strut QP}\times{\bf A}|\over|{\bf A}|},
$$
где $\bf A$ — любой вектор, параллельный прямой. Из уравнения
линии, мы можем использовать $Q=(1,1,1)$ и ${\bf A}=\langle 2,3,-1\rangle$, поэтому
расстояние
$$
{|\langle -2,1,0\rangle\times\langle2,3,-1\rangle|\over\sqrt{14}}=
{|\langle-1,-2,-8\rangle|\over\sqrt{14}}={\sqrt{69}\over\sqrt{14}}.
$$
$\квадрат$
Мы снова хотим расстояния
измеряется перпендикулярно линии, как показано на
рисунок 12.5.4. Желаемое расстояние равно
$$
|\overrightarrow{\ распорка QP}|\sin\theta=
{|\overrightarrow{\strut QP}\times{\bf A}|\over|{\bf A}|},
$$
где $\bf A$ — любой вектор, параллельный прямой. Из уравнения
линии, мы можем использовать $Q=(1,1,1)$ и ${\bf A}=\langle 2,3,-1\rangle$, поэтому
расстояние
$$
{|\langle -2,1,0\rangle\times\langle2,3,-1\rangle|\over\sqrt{14}}=
{|\langle-1,-2,-8\rangle|\over\sqrt{14}}={\sqrt{69}\over\sqrt{14}}.
$$
$\квадрат$
Рисунок 12.5.4. Расстояние от точки до прямой.
Вы можете использовать Sage для вычисления расстояний до линий и плоскостей, так как это просто включает векторную арифметику, которую мы уже видели. Конечно, вы также можете использовать Sage для выполнения некоторых вычислений, связанных с нахождение уравнений плоскостей и прямых.
Пример 12.5.1 Найдите уравнение плоскости, содержащее $(6,2,1)$ и
перпендикулярно $\langle 1,1,1\rangle$.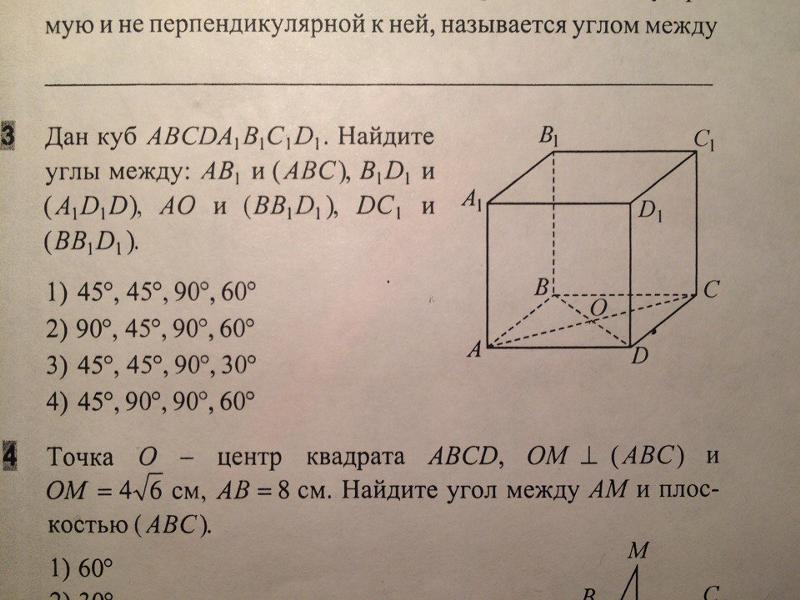 (отвечать)
(отвечать)
Пример 12.5.2 Найдите уравнение плоскости, содержащее $(-1,2,-3)$ и перпендикулярно $\langle 4,5,-1\rangle$. (отвечать)
Пример 12.5.3 Найдите уравнение плоскости, содержащее $(1,2,-3)$, $(0,1,-2)$ и $(1,2,-2)$. (отвечать)
Пример 12.5.4 Найдите уравнение плоскости, содержащее $(1,0,0)$, $(4,2,0)$ и $(3,2,1)$. (отвечать)
Пример 12.5.5 Найдите уравнение плоскости, содержащее $(1,0,0)$ и строка $\langle 1,0,2\rangle + t\langle 3,2,1\rangle$. (отвечать)
Пример 12.5.6 Найдите уравнение плоскости, содержащей прямую пересечение $x+y+z=1$ и $x-y+2z=2$ и перпендикулярно плоскость $2x+3y-z=4$. (отвечать)
Пример 12.5.7 Найдите уравнение плоскости, содержащей прямую пересечение $x+2y-z=3$ и $3x-y+4z=7$ и перпендикулярно плоскость $6x-y+3z=16$. (отвечать)
Пример 12.5.8 Найдите уравнение плоскости, содержащей прямую
пересечение $x+3y-z=6$ и $2x+2y-3z=8$ и перпендикулярно
плоскость $3x+y-z=11$. (отвечать)
(отвечать)
Пример 12.5.9 Найдите уравнение прямой через $(1,0,3)$ и $(1,2,4)$. (отвечать)
Пример 12.5.10 Найдите уравнение прямой через $(1,0,3)$ и перпендикулярно плоскости $x+2y-z=1$. (отвечать)
Пример 12.5.11 Найдите уравнение прямой, проходящей через начало координат и перпендикулярно плоскости $x+y-z=2$. (отвечать)
Пример 12.5.12 Найдите $a$ и $c$ так, чтобы $(a,1,c)$ лежало на прямой, проходящей через $(0,2,3)$ и $(2,7,5)$. (отвечать)
Пример 12.5.13 Объясните, как найти решение в пример 12.5.5.
Пример 12.5.14 Определить, являются ли строки $\langle 1,3,-1\rangle+t\langle 1,1,0\rangle$ и $\langle 0,0,0\rangle+t\langle 1,4,5\rangle$ параллельны, пересекаются или ни то, ни другое. (отвечать)
Пример 12.5.15 Определить, являются ли строки $\langle 1,0,2\rangle+t\langle
-1,-1,2\rangle$ и $\langle 4,4,2\rangle+t\langle 2,2,-4\rangle$
параллельны, пересекаются или ни то, ни другое. (отвечать)
(отвечать)
Пример 12.5.16 Определить, являются ли строки $\langle 1,2,-1\rangle+t\langle 1,2,3\rangle$ и $\langle 1,0,1\rangle+t\langle 2/3,2,4/3\rangle$ параллельны, пересекаются или ни то, ни другое. (отвечать)
Пример 12.5.17 Определить, являются ли строки $\langle 1,1,2\rangle+t\langle 1,2,-3\rangle$ и $\langle 2,3,-1\rangle+t\langle 2,4,-6\rangle$ параллельны, пересекаются или ни то, ни другое. (отвечать)
Пример 12.5.18 Найдите единичный вектор нормали к каждой из координатных плоскостей.
Пример 12.5.19 Покажите, что $\langle 2,1,3 \rangle + t \langle 1,1,2 \rangle$ и $\langle 3, 2, 5 \rangle + s \langle 2, 2, 4 \rangle$ одинаковы линия.
Пример 12.5.20 Дайте краткое описание каждого из следующих процессов:
а. Даны две различные точки, найти прямую, которая проходит через них.
б. Даны три точки (не все на одной прямой), найдите плоскость что проходит через них. Зачем нужна оговорка, что не все точки лежат на одной прямой?
в.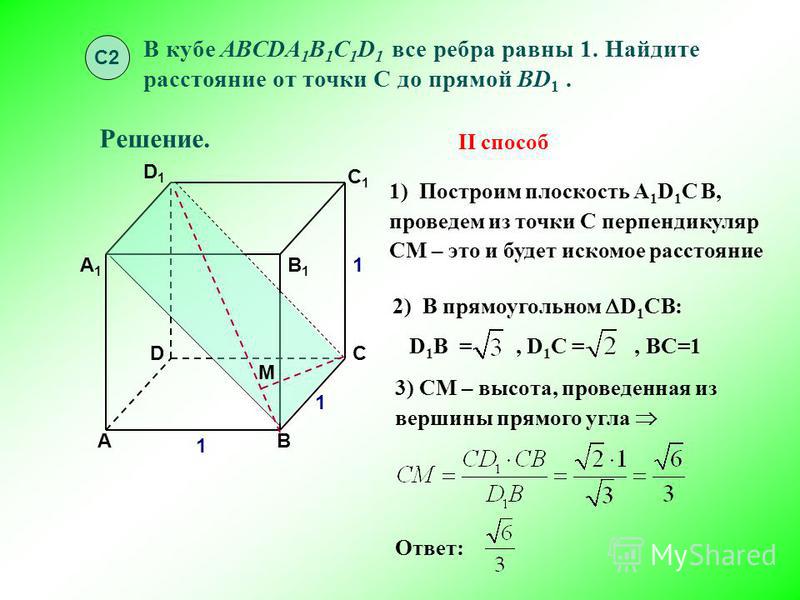 Даны прямая и точка, не лежащие на этой прямой, найти плоскость, на которой
содержит их обоих.
Даны прямая и точка, не лежащие на этой прямой, найти плоскость, на которой
содержит их обоих.
д. Даны плоскость и точка, не лежащие на плоскости, найти прямую, перпендикулярен плоскости, проходящей через данную точку.
Пример 12.5.21 Найдите расстояние от $(2,2,2)$ до $x+y+z=-1$. (отвечать)
Пример 12.5.22 Найдите расстояние от $(2,-1,-1)$ до $2x-3y+z=2$. (отвечать)
Пример 12.5.23 Найдите расстояние от $(2,-1,1)$ до $\langle 2,2,0\rangle+t\langle 1,2,3\rangle$. (отвечать)
Пример 12.5.24 Найдите расстояние от $(1,0,1)$ до $\langle 3,2,1\rangle+t\langle 2,-1,-2\rangle$. (отвечать)
Пример 12.5.25 Найдите расстояние между линиями $\langle 5,3,1\rangle+t\langle 2,4,3\rangle$ и $\langle 6,1,0\rangle+t\langle 3,5,7\rangle$. (отвечать)
Пример 12.5.26 Найдите расстояние между линиями
$\langle 2,1,3\rangle+t\langle -1,2,-3\rangle$ и
$\langle 1,-3,4\rangle+t\langle 4,-4,1\rangle$.

Leave A Comment