Список учебных материалов, доступных онлайн в данной категории:  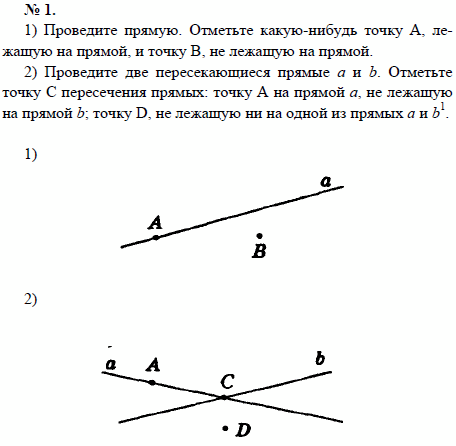 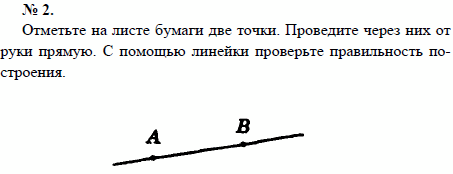   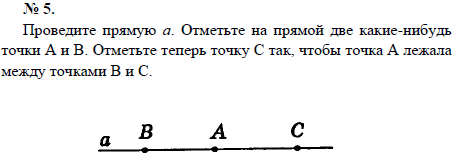 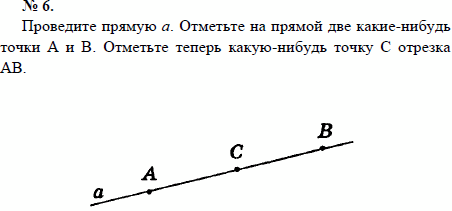 1459. 1459.        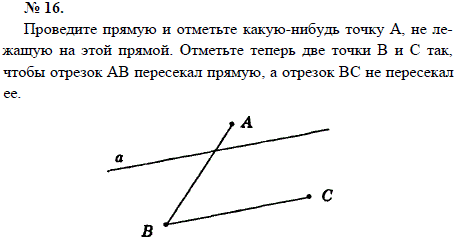 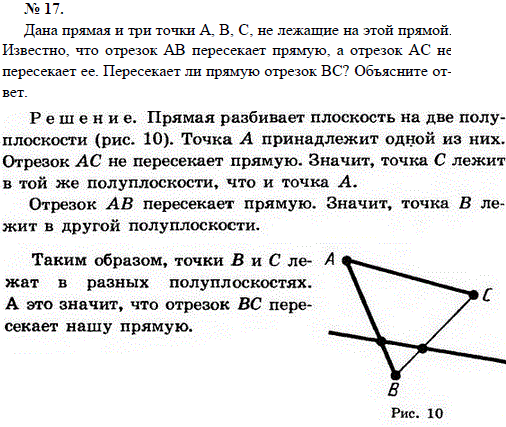 1469. Даны прямая и четыре точки А, В, С и D, не лежащие на этой прямой. Пересекает ли прямую отрезок AD, если: 1) отрезки АВ, ВС и CD пересекают прямую; 2) отрезки АС и ВС пересекают прямую, а отрезок BD не пересекает; 3) отрезки АВ и CD пересекают прямую, а отрезок ВС не пересекает; 4) отрезки АВ и CD не пересекают прямую, а отрезок ВС пересекает; 5) отрезки АВ, ВС, CD не пересекают прямую; 6) отрезки АС, ВС и BD пересекают прямую? Объясните ответ (решение) 1469. Даны прямая и четыре точки А, В, С и D, не лежащие на этой прямой. Пересекает ли прямую отрезок AD, если: 1) отрезки АВ, ВС и CD пересекают прямую; 2) отрезки АС и ВС пересекают прямую, а отрезок BD не пересекает; 3) отрезки АВ и CD пересекают прямую, а отрезок ВС не пересекает; 4) отрезки АВ и CD не пересекают прямую, а отрезок ВС пересекает; 5) отрезки АВ, ВС, CD не пересекают прямую; 6) отрезки АС, ВС и BD пересекают прямую? Объясните ответ (решение) 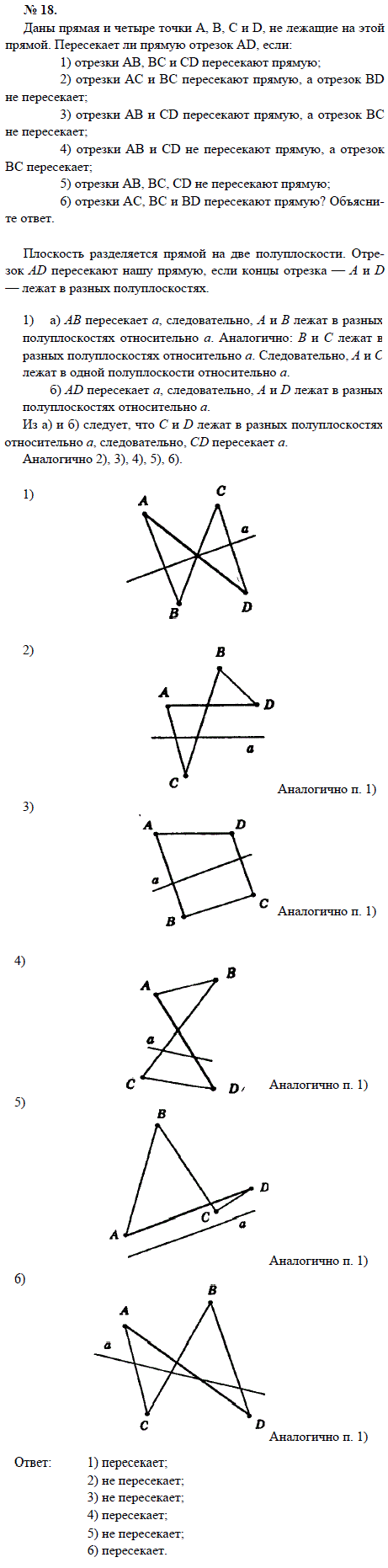 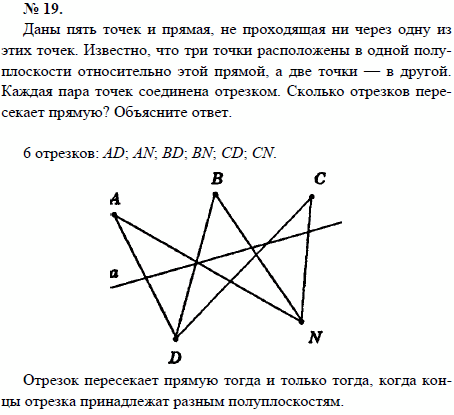  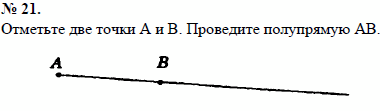   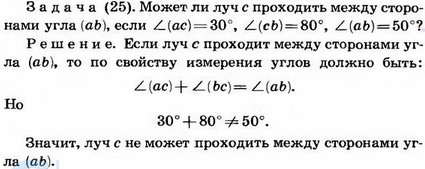    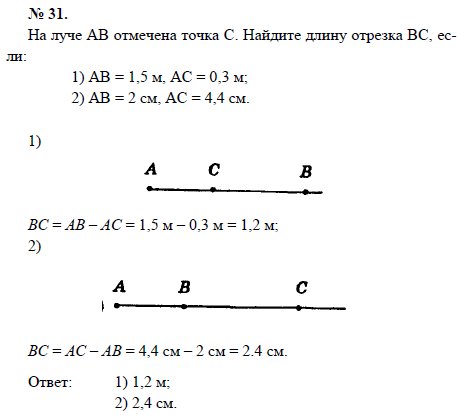 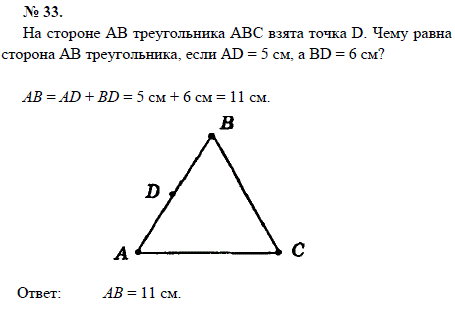 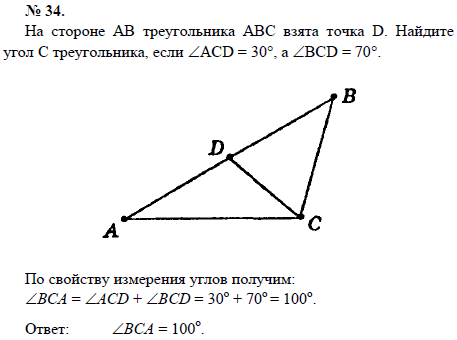     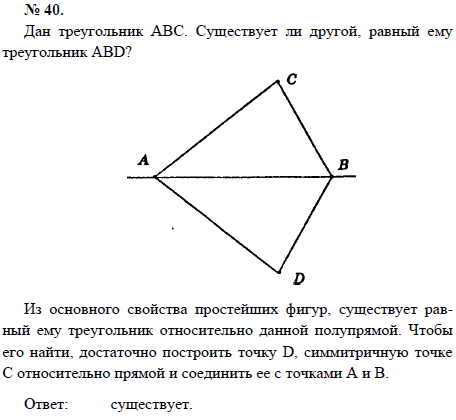   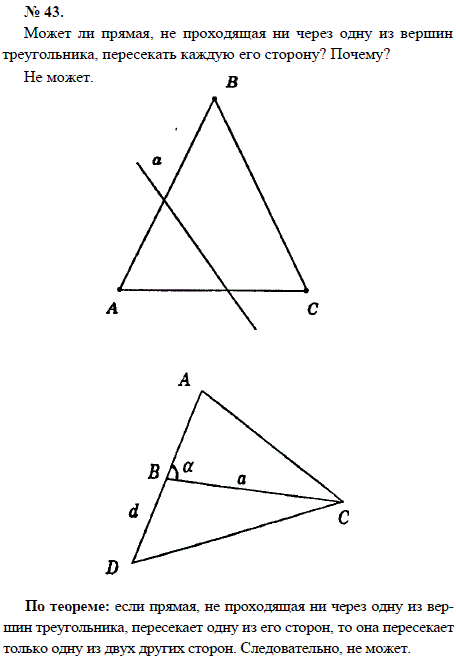 1490. Даны четыре различные точки А, В, С и D. Известно, что точки А, В, С лежат на одной прямой и точки В, С, D также лежат на одной прямой. Докажите, что все четыре точки А, В, С, D лежат на одной прямой (решение) 1490. Даны четыре различные точки А, В, С и D. Известно, что точки А, В, С лежат на одной прямой и точки В, С, D также лежат на одной прямой. Докажите, что все четыре точки А, В, С, D лежат на одной прямой (решение)            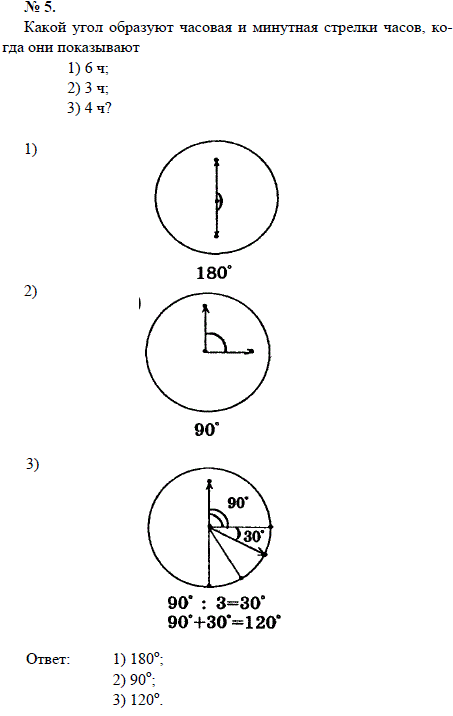  |
Вступление
Это вторая часть моей статьи посвящена вычислительной геометрии. Думаю, эта статья будет интереснее предыдущей, поскольку задачки будут чуть сложнее.
Задача №1
Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.
Решение
Понятно, что если прямая задана своим уравнением ax + by + c = 0, то тут и решать нечего. Достаточно подставить координаты точки в уравнение прямой и проверить чему оно равно. Если больше нуля, то точка находится в верхней полуплоскости, если равна нулю, то точка находится на прямой и если меньше нуля, то точка находится в нижней полуплоскости. Интереснее случай, когда прямая задана, задана координатами двух точек назовем их P
Задача №2
Определить принадлежит ли точка лучу.
Решение
Давайте вспомним, что такое луч: луч — это прямая, ограниченная точкой с одной стороны, а с другой стороны бесконечная. То есть луч задается некоторой начальной точкой и любой точкой лежащей на нем. Пусть точка P1(x1, y1) — начало луча, а P2(x2, y2) — любая точка принадлежащая лучу. Понятно, что если точка принадлежит лучу, то она принадлежит и прямой проходящей через эти точки, но не наоборот. Поэтому принадлежность прямой является необходимым, но не достаточным условием для принадлежности лучу. Поэтому от проверки косового произведения нам никуда не деться. Для достаточного условия нужно вычислить еще и скалярное произведение тех же векторов. Если оно меньше нуля, то точка не принадлежит лучу, если же оно не отрицательно, то точка лежит на луче. Почему так? Давайте посмотрим на рисунок.
Итак, для того чтобы точка M(x, y) лежала на луче с начальной точкой P1(x1, y1), где P2(x2, y2) лежит на луче необходимо и достаточно выполнения двух условий:
1. [P1P2, P1M] = 0 – косое произведение (точка лежит на прямой)
2. (P1P2, P1M) ≥ 0 – скалярное произведение (точка лежит на луче)
Задача №3
Определить принадлежит ли точка отрезку.
Пусть точки P1(x1, y1), P2(x2, y2) концы заданного отрезка. Опять-таки необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через P1, P2. Далее нам нужно определить лежит ли точка между точками P1 и P2, для этого нам на помощь приходит скалярное произведение векторов только на этот раз других: (MP1, MP2). Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка. Почему так? Посмотрим на рисунок.
Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P1(x1, y1), P2(x2, y2) необходимо и достаточно выполнения условий:
1. [P1P2, P1M] = 0 – косое произведение (точка лежит на прямой)
2. (MP1,MP2) ≤ 0 – скалярное произведение (точка лежит между P1 и P2)
Задача №4
Взаимное расположение двух точек относительно прямой.
Решение
В этой задаче необходимо определить по одну или по разные стороны относительно прямой находятся две точки.
Если точки находятся по разные стороны относительно прямой, то косые произведения имеют разные знаки, а значит их произведение отрицательно. Если же точки лежат по одну сторону относительно прямой, то знаки косых произведений совпадают, значит, их произведение положительно.
Итак:
1. [P1P2, P1M1] * [P1P2, P1M2] < 0 – точки лежат по разные стороны.
2. [P1P2, P1M1] * [P1P2, P1M2] > 0 – точки лежат по одну сторону.
3. [P1P2, P1M1] * [P1P2, P1M2] = 0 – одна (или две) из точек лежит на прямой.
Кстати, задача об определении наличия точки пересечения у прямой и отрезка решается точно также. Точнее, это и есть эта же задача: отрезок и прямая пересекаются, когда концы отрезка находятся по разные стороны относительно прямой или когда концы отрезка лежат на прямой, то есть необходимо потребовать [P1P2, P1M1] * [P1P2, P1M2] ≤ 0.
Задача №5
Определить пересекаются ли две прямые.
Решение
Будем считать, что прямые не совпадают. Понятно, что прямые не пересекаются, только если они параллельны. Поэтому, найдя условие параллельности, мы можем, определить пересекаются ли прямые.
Допустим прямые заданы своими уравнениями a1x + b1y + c1 = 0 и a2x + b2y + c2 = 0. Тогда условие параллельности прямых заключается в том, что a1b2 — a2b1 = 0.
Если же прямые заданы точками P1(x1, y1), P2(x2, y2), M1(x3, y3), M2(x4, y4), то условие их параллельности заключается в проверки косого произведения векторов P1P2 и M1M2: если оно равно нулю, то прямые параллельны.
В общем, то когда прямые заданы своими уравнениями мы тоже проверяем косое произведение векторов (-b1, a1), (-b2, a2) которые называются направляющими векторами.
Задача №6
Определить пересекаются ли два отрезка.
Решение
Вот эта задача мне, действительно, нравится. Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:
Итак, нам нужно проверить, чтобы концы каждого из отрезков лежали по разные стороны относительного концов другого отрезка. Пользуемся косым произведением векторов. Посмотрите на первый рисунок: [P1P2, P1M2] > 0, [P1P2, P1M1] < 0 => [P1P2, P1M2] * [P1P2, P1M1] < 0. Аналогично
[M1M2, M1P1] * [M1M2, M1P2] < 0. Вы наверно думаете, почему не меньше либо равно. А потому, что возможен следующий случай, при котором векторное произведение как раз и равно нулю, но отрезки не пересекаются:
Поэтому нам необходимо сделать еще одну проверку, а именно: принадлежит ли хотя бы один конец каждого отрезка другому (принадлежность точки отрезку). Эту задачу мы уже решали.
Итак, для того чтобы отрезки имели общие точки необходимо и достаточно:
1. Концы отрезков лежат по разные стороны относительно другого отрезка.
2. Хотя бы один из концов одного отрезка принадлежит другому отрезку.
Задача №7
Расстояние от точки до прямой.
Решение
Пусть прямая задана двумя точками P1(x1, y1) и P2(x2, y2).
В предыдущей статье мы говорили о том, что геометрически косое произведение — это ориентированная площадь параллелограмма, поэтому SP1P2M = 0,5*[P1P2, P1M]. С другой стороны каждому школьнику известна формула для нахождения площади треугольника: половина основание на высоту.
SP1P2M = 0,5*h*P1P2.
Приравнивая эти площади, находим
По модулю взяли потому, что первая площадь ориентированная.
Если же прямая задана уравнением ax + by + c = 0, то уравнение прямой проходящей через точку M перпендикулярной заданной прямой есть: a(y — y0) – b(x — x0) = 0. Теперь спокойно можно решить систему из полученных уравнений, найти их точку пересечения и вычислить расстояние от исходной точки до найденной: оно будет ровно ρ = (ax0 + by0 + c)/√(a2 + b2).
Задача №8
Расстояние от точки до луча.
Решение
Эта задача отличается от предыдущей тем, что в этом случае может получиться, так что перпендикуляр из точки не падает на луч, а падает на его продолжение.
В случае, когда перпендикуляр не падает на луч необходимо найти расстояние от точки до начала луча – это и будет ответом на задачу.
Как же определить падает ли перпендикуляр на луч или нет? Если перпендикуляр не падает на луч, то угол MP1P2 – тупой иначе острый (прямой). Поэтому по знаку скалярного произведения векторов мы можем определить попадает ли перпендикуляр на луч или нет:
1. (P1M, P1P2) < 0 перпендикуляр не попадает на луч
2. (P1M, P1P2) ≥ 0 перпендикуляр попадает на луч
Задача №9
Расстояние от точки до отрезка.
Решение
Рассуждаем аналогично предыдущей задаче. Если перпендикуляр не падает на отрезок, то ответом будет минимальное из расстояний от данной точки до концов отрезка.
Чтобы определить попадает ли перпендикуляр на отрезок нужно по аналогии с предыдущей задачей использовать скалярное произведение векторов. Если перпендикуляр не падает на отрезок, то либо угол MP1P2 либо угол MP2P1 будут тупыми. Поэтому по знаку скалярных произведений мы можем определить попадает ли перпендикуляр на отрезок или нет:
Если (P1M, P1P2) < 0 или (P2M, P2P1) < 0 то перпендикуляр не падает на отрезок.
Задача №10
Определить количество точек прямой и окружности.
Решение
Прямая и окружность может иметь нуль, одну или две точки пересечения. Давайте посмотрим на рисунки:
Здесь из рисунков и так все понятно. Мы имеем две точки пересечения, если расстояние от центра окружности до прямой меньше радиуса окружности. Одну точку касания, если расстояние от центра до прямой равно радиусу. И наконец, ни одной точки пересечения, если расстояние от центра окружности до прямой больше радиуса окружности. Поскольку задача нахождения расстояние от точки до прямой была уже нами решена, то и эта задача тоже решена.
Задача №11
Взаимное расположение двух окружностей.
Решение
Возможные случаи расположения окружностей: пересекаются, касаются, не пересекаются.
Рассмотрим случай, когда окружности пересекаются, и найдем площадь их пересечения. Эту задачу я очень люблю, так как потратил на ее решение изрядное количество времени (было это давно — на первом курсе).
Вспомним теперь, что такое сектор и сегмент.
Пересечение кругов состоит из двух сегментов O1AB и O2AB.
Казалось бы необходимо сложить площади этих сегментов и все. Однако, все не так просто. Необходимо еще определить всегда ли эти формулы верны. Оказывается, нет!
Рассмотрим случай, когда центр второго круга O2 совпадает с точкой C. В этом случае d2 = 0 и за значение α примем α = π. В этом случае имеем полукруг с площадью 1/2 πR22.
Теперь рассмотрим случай, когда центр второго круга O2 находится между точками O1 и C. В этом случае получим отрицательное значение величины d2. Использование отрицательного значения d2 приводит к отрицательному значению α. В этом случае необходимо для правильного ответа прибавить к α 2π.
Заключение
Ну вот и все. Мы рассмотрели не все, но наиболее часто встречаемые задачи вычислительной геометрии касающиеся взаимного расположения объектов.Надеюсь, Вам понравилось.
Раздел «Прямые и плоскости в пространстве» занимает важное место в стереометрии. Тест дает возможность определить уровень усвоения материала и быстро выявить пробелы в знаниях, создает условия для мотивации, повышения интереса к предмету, способствует развитию и совершенствованию самостоятельной деятельности учащихся и устраняет перегрузку домашнего задания.
Тест по
теме «Прямые и плоскости в пространстве»
ВАРИАНТ 1
1) Прямую, перпендикулярную любой прямой в плоскости, называют…
а)
наклонной к плоскости; б) перпендикуляром к плоскости; в)
секущей; г) лучом. (1 балл)
2)
Наклонной к плоскости называют прямую, пересекающую плоскость и …
а) не пересекающую перпендикуляр;
б) лежащую в ней;
в) не имеющую с ней общих точек;
г) не
перпендикулярную ей. (1 балл)
3) Параллельными называют плоскости,…
а) не имеющие общих прямых;
б) у которых одна общая точка;
в) у которых две общих точки;
г) не
имеющие ни одной общей точки. (1 балл)
4)
Прямая, проходящая через основания перпендикуляра и наклонной, называется …
а) секущей;
б) параллельной плоскости;
в) проекцией наклонной на плоскость;
г)
перпендикуляром к плоскости. (1 балл)
5) Наклонная перпендикулярна прямой в плоскости, если …
а) перпендикуляр пересекается с проекцией наклонной на плоскость;
б) проекция наклонной параллельна этой прямой;
в) проекция наклонной перпендикулярна этой прямой;
г)
прямая совпадает с проекцией наклонной. (1 балл)
6)
Если из точки вне плоскости провести к ней перпендикуляр и наклонные, то …
а) перпендикуляр длиннее наклонной;
б) наклонная длиннее перпендикуляра;
в) проекция наклонной короче перпендикуляра;
г)
наклонная и ее проекция равны. (1 балл)
7) Прямая параллельна плоскости, если они…
а) пересекают прямую в одной и той же точке;
б) перпендикулярны одной и той же прямой;
в) удалены от данной точки на равные расстояния;
г)
пересекают плоскость в одной точке. (1 балл)
8) Углом между наклонной и плоскостью называют…
а) угол между наклонной и перпендикуляром;
б) угол между проекцией и перпендикуляром;
в) угол между наклонной и ее проекцией;
г)
угол между наклонной и прямой в плоскости. (1 балл)
9)
Через … проходит единственная плоскость,
а) две точки; б) три параллельные прямые;
в) три попарно пересекающиеся прямые;
г) четыре
точки. (1 балл)
10)
Прямая пересекает плоскость, если прямая и плоскость . . .
а) не имеют ни одной общей точки;
б) имеют две общие точки;
в) имеют только одну общую точку;
г) имеют
три общих точки. (1 балл)
11) Если прямая пересекает плоскость квадрата в точке пересечения диагоналей и перпендикулярна двум смежным его сторонам, то она . . .
а) параллельна двум другим сторонам квадрата;
б) перпендикулярна диагоналям квадрата;
в) параллельна диагоналям квадрата;
г)
образует с плоскостью квадрата угол в 30 градусов. (2 балла)
12) Если две параллельные плоскости пересечь третьей, то . . .
а) линии пересечения равны;
б) линии пересечения параллельны;
в) линии пересечения перпендикулярны;
г)
плоскости совпадают. (1 балл)
13) Если две параллельные плоскости пересечь двумя параллельными прямыми, то …
а) прямые пересекаются в точке;
б) плоскости пересекаются по прямой, параллельной одной из прямых;
в) отрезки, заключенные между плоскостями равны;
г)
плоскости перпендикулярны одной из прямых. (1 балл)
14) Если наклонная длиной 16 см образует с плоскостью угол в 60°, то ее проекция на плоскость равна…
а)
32 см; б) 8
см; в) 8
cm; г) 256 см2. (2 балла)
15) Наклонные АВ и АС образуют с плоскостью углы в 30° и 45° соответственно. Тогда . . .
а) проекция наклонной АВ длиннее проекции наклонной АС на плоскость;
б) наклонная АВ короче наклонной АС;
в) наклонная АВ длиннее наклонной АС;
г)
проекции наклонных равны. (1 балл)
16) Если в прямоугольном треугольнике катет в два раза меньше гипотенузы, то …
а) прилежащий катету угол равен 30 градусам;
б) прилежащий катету угол равен 60 градусам;
в) прилежащий катету угол равен 90 градусам;
г)
противолежащий угол равен 60 градусам. (2 балла)
17) Перпендикуляром к-плоскости называют прямую, . . .
а) пересекающую плоскость;
б) перпендикулярную некоторой прямой в плоскости;
в) перпендикулярную любой прямой в плоскости;
г)
лежащую в параллельной плоскости. (1 балл)
18) Та из наклонных больше, у которой . . .
а) проекция равна перпендикуляру;
б) проекция больше;
в) проекция меньше;
г)
проекция больше перпендикуляра. (1 балл)
19) Планиметрия — это измерения . . .
а)
углов; б)
отрезков; в) на
плоскости; г) в пространстве. (1 балл)
20) Угол между наклонной и плоскостью . . .
а) меньше
90 градусов; б) больше 90
градусов; в) равен 60
градусам; г) тупой. (1 балл)
21) Проекцией наклонной на плоскость называют прямую, . . .
а) перпендикулярную плоскости;
б) пересекающую наклонную под углом 30 градусов;
в) проходящую через точки наклонной и перпендикуляра;
г)
проходящую через основания наклонной и перпендикуляра. (1 балл)
22) Если две точки прямой принадлежат плоскости, то прямая …
а) называется проекцией точки на плоскость; б) лежит в плоскости;
в)
пересекает плоскость под прямым
углом; г) называется перпендикуляром
к плоскости. (1 балл)
23) Прямые, имеющие одну общую точку называют . . .
а)
скрещивающимися; б) пересекающимися; в) параллельными; г) совпадающими. (1 балл)
24) Две плоскости параллельны, если они . . .
а) перпендикулярны одной и той же прямой;
б) параллельны одной и той же прямой;
в) пересекаются в одной точке;
г)
пересекают одну и ту же прямую. (1 балл)
25) Если две прямые параллельны третьей, то они..
а) перпендикулярны друг другу;
б) параллельны между собой;
в)
совпадают; г) пересекаются. (1 балл)
26) Расстояние между двумя параллельными плоскостями равно 10 см, а отрезок, заключенный между плоскостями равен 12 см. Тогда проекция отрезка на одну из плоскостей равна…
a) см;
б)44см; в) см; г) 2см. (2 балла)
27) Две наклонные, длиной 10 см образуют между собой угол в 60 градусов. Расстояние между их проекциями на плоскость равно…
а) 10 см;
б) 5см; в) см;
г) 20см. (2 балла)
28) Две плоскости совпадают, если они имеют . . .
а) две общих точки; б) три общих точки; в) одну общую прямую; г) одну общую точку. (2 балла)
Ответы:
1-б, 2-г, 3-г, 4-в, 5-в, 6-б, 7-б, 8-в, 9-в, 10-в, 11-б, 12-б, 13-в, 14-б, 15-а,в,
16-б, 17-в, 18-б, 19-в, 20-а, 21-г, 22-б, 23-б, 24-а, 25-б, 26-а, 27-а, 28-б.
Критерии оценок:
более 30 баллов — «5»
от 20 до 29 — «4»
от 14 до 19 баллов — «3»
Теорема о прямой и параллельной ей плоскости
Анна Малкова
Ей не повезло.
В школьных учебниках ее и теоремой-то редко называют. Говорят, что это «лемма». Или «следствие». Или «задача». Как будто это что-то необязательное и незначительное. А на самом деле это важнейшая теорема о прямой и параллельной ей плоскости.
Даже если в школе ее доказывают — не говорят, зачем она нужна. Доказали — и забыли.
Но при этом в стереометрии — и особенно в задачах ЕГЭ по математике — есть множество ситуаций, когда без этой важнейшей теоремы не обойтись.
Встречайте:
Теорема о прямой и параллельной ей плоскости:
Пусть прямая m параллельна плоскости . Если плоскость проходит через прямую m и пересекает плоскость по прямой c, то c параллельна m.

Для чего нам эта теорема? Например, для того, чтобы построить сечение пирамиды плоскостью, параллельной плоскости основания.
1. Постройте сечение тетраэдра плоскостью, проходящей через точки M, N, K. Точка N лежит на ребре

Покажем, что плоскость сечения пересекает плоскость основания пирамиды по прямой NT, параллельной MK.
Прямая MK параллельна AB, лежащей в плоскости основания ABC. Значит,
Плоскость сечения проходит прямую MK, параллельную плоскости ABC. По теореме о прямой и параллельной ей плоскости, линия пересечения плоскости сечения и плоскости AВC параллельна прямой MK. Трапеция MKNT — искомое сечение.
Таких задач, где в сечении пирамиды получается трапеция (или параллелограмм), в вариантах Профильного ЕГЭ очень много.
2. В правильной четырехугольной пирамиде PABCD, все ребра которой равны 8, точка K — середина бокового ребра AP.
а) Постройте сечение пирамиды плоскостью, проходящей через точку K и параллельной прямым PB и BC.
б) Найдите площадь сечения.

Пусть точка M — середина AB. Тогда как средняя линия
Пусть точка N — середина PD. Поскольку KN — средняя линия и тогда
Построим сечение пирамиды плоскостью KMN. Пусть плоскости KMN и ABC пересекаются по прямой МE. Покажем, что
По теореме о прямой и параллельной ей плоскости,
Это значит, что Прямая ME содержит точку О, являющуюся проекцией вершины P на плоскость ABC. Трапеция KNEM — искомое сечение.
б) Найдём площадь сечения.

где — высота трапеции KNEM.
Пусть H — середина KN,
тогда
Есть еще одна теорема — такая же полезная, как и теорема о прямой и параллельной ей плоскости. Вот она:
Теорема. Пусть плоскости и пересекаются по прямой р. Плоскость параллельна прямой р. Тогда она пересекает плоскости и по прямым, параллельным .

Как ее назвать? Согласитесь, сложно придумать короткое название. Для себя (не для оформления на экзамене!) можно запомнить эту картинку как «домик» или «книжечку». Главное — запомнить формулировку и увидеть, как теорема применяется в решении задач.
Уравнение прямой
Линия — это бесконечная линия, которая образует кратчайший путь между двумя точками.
Уравнение прямой на плоскости
Общая форма линейного уравнения
Любое уравнение прямой на плоскости можно записать в общем виде
A x + B y + C = 0
, где A и B не равны нулю.

Форма перехвата наклона линейного уравнения
Общее уравнение прямой, когда B ≠ 0, может быть приведено к следующей форме
y = k x + b
, где k — это наклон линии , а b — это y-пересечение . Наклон линии равен тангенсу угла между этой линией и положительным направлением оси X. Y-координата — это место, где линия пересекает ось Y.
k = tg φ
Уравнение прямой, проходящей через две разные точки на плоскости
Если линия проходит через две точки A (x 1 , y 1 ) и B (x 2 , y 2 ), так что x 1 x 2 и y 1 ≠ y 2 , то уравнение линии можно найти с помощью следующей формулы
| х — х 1 | = | г — г 1 |
| x 2 — x 1 | y 2 — y 1 |
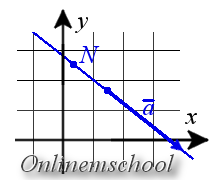
Параметрические уравнения прямой на плоскости
Параметрическое уравнение линии можно записать как
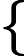 | х = 1 т + х 0 |
| y = m t + y 0 |
, где N (x 0 , y 0 ) — это координаты точки, лежащей на прямой, a = {l, m} — координаты вектора направления линии.
Каноническое уравнение прямой на плоскости
Если вам известны координаты точки A (x 0 , y 0 ) Если вам известны координаты точки n = {l; m}, тогда уравнение прямой можно записать в канонической форме, используя следующую формулу
Пример 1. Найти уравнение прямой, проходящей через две точки A (1, 7) и B (2, 3).
Решение. Используем формулу для уравнения прямой, проходящей через две точки
x — 12 — 1 = y — 73 — 7
Из этого уравнения мы выражаем y через x
x — 11 = y — 7-4
Найдите форму пересечения уклона линейного уравнения.
Умножьте уравнения на -4.
у — 7 = -4 (х — 1)
у = -4х + 11
Найти параметрические уравнения этой линии
Мы используем MN в качестве вектора направления линии.
MN = {2 — 1; 3 — 7} = {1; -4}
Используем координаты точки М в параметрических уравнениях прямой
x = t + 1y = -4t + 7
Пример 2. Найти уравнение прямой, проходящей через две точки M (1, 3) и N (2, 3).Решение. Нельзя использовать Уравнение прямой, проходящей через две разные точки, так как M y — N y = 0.
Найдите параметрические уравнения этой линии. Мы используем MN в качестве вектора направления линии.
MN = {2 — 1; 3 — 3} = {1; 0}
Используем координаты точки М в параметрических уравнениях прямой
x = t + 1y = 3
Уравнение прямой в пространстве
Уравнение прямой, проходящей через две разные точки в пространстве
Если линия проходит через две точки A (x 1 , y 1 , z 1 ) и B (x 2 , y 2 , z 2 ), так что x 1 X 2 , y 1 , y 2 и z 1 , z 2 , тогда уравнение для линии можно найти с помощью следующей формулы
| х — х 1 | = | г — г 1 | = | z — z 1 |
| x 2 — x 1 | y 2 — y 1 | z 2 — z 1 |
Параметрические уравнения прямой в пространстве
Параметрическое уравнение линии можно записать как
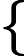 | х = 1 т + х 0 |
| y = m t + y 0 | |
| z = n t + z 0 |
где (x 0 , y 0 , z 0 ) — координаты точки, лежащей на прямой, {l; м; n} — координаты вектора направления линии.
Каноническое уравнение прямой в пространстве
Если вам известны координаты точки A (x 0 , y 0 , z 0 ), лежащей на прямой, и вектора направления линии n = {l; м; n}, тогда уравнение прямой можно записать в канонической форме, используя следующую формулу.
| х — х 0 | = | г — г 0 | = | z — z 0 |
| л | м | n |
Прямая как пересечение двух плоскостей
Если прямая является пересечением двух плоскостей, то уравнение прямой можно найти как решение следующей системы уравнений
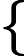 | A 1 x + B 1 y + C 1 z + D 1 = 0 |
| A 2 x + B 2 y + C 2 z + D 2 = 0 |
при условии, что не было равенства
| A 1 | = | B 1 | = | C 1 | |
| A 2 | B 2 | C 2 |
Задача: Уравнение вертикальной линии, проходящей через точку (4, -3).
Решение: x = 4
Чтобы понять , почему , прочитайте следующее пошаговое решение
1. Прочитайте , поймите ситуацию, определите и извлеките важной информации.
- Есть бесконечные линии, проходящие через точку (4, -3).
- Имеется , только одна прямая линия — ось Y , проходящая через точку (4, -3). Эта линия горизонтальна , параллельна оси x, и все ее точки имеют одинаковую букву «у» (-3) . Эта линия пересекает ось Y в точке пересечения Y.
- Имеется , только одна прямая линия — ось x проходит через точку (4, -3), параллельна к оси y, причем все ее точки имеют одинаковую «x» (4) .Он пересекает ось х в точке пересечения х.
2. Переведите каждого из ключевых слов в задаче в соответствующие им математических символов .
Каждая точка линии идентифицируется ее координатами (x, y). Все точки этой вертикальной линии, проходящей через (4, -3), имеют одинаковую координату х «4». x = 4.
3. Установить и решить уравнение:
x = 4 Уравнение вертикальной линии, проходящей через (4, -3).Это верно только тогда, когда значение координаты x равно «4», для любого значения «y» .
4. Проверьте свой ответ.
- Наклон (м) вертикальной линии не определен. Вертикальные линии не имеют наклона (это не существует в определенных понятиях)!
м = ВХОД / РАБОТА;
RISE = любой;
RUN = 0, потому что при переходе из точки (4, -3) в другую точку на вертикальной линии x = 0 , так как мы не движемся горизонтально (только вертикально)!
(м) = подъем / бег; м = ВЗЛЕТ / 0 ; наклон неопределенный
Итак, наша линия, представленная x = 4 — это вертикальная линия!
- Уравнение вертикальной линии является частным случаем уравнения стандартной формы, где
A = 0, B = 1, C = 4
0y + x = 4;
x = 4 Представляет стандартное уравнение формы запрошенной вертикальной линии.Независимо от того, что является значением y, значение x всегда является постоянным значением «4», «x» не изменяется: изменяя «y», мы перемещаемся вертикально к оси x.
5. Неформат :
- Вертикальные линии не могут быть написаны в форме пересекающегося наклона (наклон не определен, и y-пересечения нет).
- x-точка пересечения нашей вертикальной линии равна (4,0).
- График нашей вертикальной линии x = 4: нанесите заданную точку (4, -3) и точку пересечения x (4,0) и проведите линию через точки (4, -3) и (4,0).
- В двумерной геометрии вертикальные линии не имеют y-пересечения.
- Математически , единственная вертикальная линия , имеющая бесконечные точки пересечения y , равна x = 0 , поскольку ее точки совпадают с точками оси y. График линии — это ось y, и каждое действительное число для y можно рассматривать как точку пересечения y.
- В трехмерной геометрии вертикальная линия имеет только один y-перехват ! Он не обязательно должен быть перпендикулярен оси X или параллелен оси Y.
- Математически две параллельные линии пересекаются на бесконечности! Найдите точку пересечения y. Подумайте немного (?)
Если прямая линия проходит через две точки (x 1 , y 1 ) и (x 2 , y 2 ), то формула для нахождения наклона линии равна
м. = (Y 2 — y 1 ) / (x 2 — x 1 )
Давайте рассмотрим несколько примеров, чтобы понять, как найти наклон прямой, проходящей через две точки.
Пример 1:
Найти наклон прямой, проходящей через точки (3, — 2) и (-1, 4).
Решение:
Формула для нахождения наклона линии, проходящей через две точки, равна
m = (y 2 — y 1 ) / (x 2 — x 1 )
Заменитель (x 1 , y 1 ) = (3, -2) и (x 2 , y 2 ) = (-1, 4).
м = [4 — (-2)] / (-1 — 3)
= (4 + 2) / (-4)
= 6 / (-4)
= -3/2
Таким образом, наклон данной линии равен -3/2.
Пример 2:
Найти наклон прямой, проходящей через точки (5, — 2) и (4, -1).
Решение:
Формула для нахождения наклона линии, проходящей через две точки, равна
m = (y 2 — y 1 ) / (x 2 — x 1 )
Заменитель (x 1 , y 1 ) = (5, -2) и (x 2 , y 2 ) = (4, -1).
м = [-1 — (-2)] / (4 — 5)
= (-1 + 2) / (-1)
= 1 / (-1)
= -1
т. , наклон данной линии -1.
Пример 3:
Найти наклон прямой, проходящей через точки (-2, — 1) и (4, 0).
Решение:
Формула для нахождения наклона линии, проходящей через две точки, равна
m = (y 2 — y 1 ) / (x 2 — x 1 )
Заменитель (x 1 , y 1 ) = (-2, -1) и (x 2 , y 2 ) = (4, 0).
м = (0 — 1) / [4 — (-2)]
= -1 / (4 + 2)
= -1/6
Таким образом, наклон данной линии равен -1 / 6.
Пример 4:
Найти наклон прямой, проходящей через точки (1, 2) и (-4, 5).
Решение:
Формула для нахождения наклона линии, проходящей через две точки, равна
m = (y 2 — y 1 ) / (x 2 — x 1 )
Заменитель (x 1 , y 1 ) = (1, 2) и (x 2 , y 2 ) = (-4, 5).
м = (5 — 2) / (-4 — 1)
= 3 / (-5)
= -3/5
Таким образом, наклон данной линии равен -3/5.
Помимо материалов, приведенных выше, если вам нужны какие-либо другие материалы по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
Вы также можете посетить следующие веб-страницы по различным материалам по математике.
ПРОБЛЕМЫ СЛОВА
Словесные задачи HCF и LCM
Словесные задачи по простым уравнениям
Словесные задачи по линейным уравнениям
Словесные задачи по квадратным уравнениям
Алгебральные задачи
Проблемы со словами в поездах
Проблемы со словами в области и по периметру
Проблемы со словами при прямом и обратном изменении
Проблемы со словами в цене за единицу
Проблемы со словами в размере единицы
Слово задачи по сравнению курсов
Преобразование словарных задач в обычных единицах
Преобразование словарных задач в метрических единицах
Задачи со словами по простым интересам
Задачи со сложными интересами в словах
Задачи со словами о типах ngles
словесные задачи о дополнительных и дополнительных углах
двузначные задачи о словах
трехзначные задачи о словах
процентные задачи о словах
задачи о прибылях и убытках
слова разметки и уценки задачи
Десятичные слова задачи
Проблемы со словами на дробях
Проблемы со словами на смешанных дробях
Проблемы со словами в одношаговом уравнении
Проблемы со словами в линейных неравенствах
Слово с коэффициентами и пропорциями задачи
Задачи со временем и работой
Задачи со словами на множествах и диаграммах Венна
Задачи со словами в возрасте
Задачи со словами теоремы Пифагора
Процент числа слова про oblems
Задачи на слово на постоянной скорости
Задачи на слово на средней скорости
Задачи на слово на сумму углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Ярлыки на прибыль и убытки
Процентные ярлыки
Ярлыки временного стола
Сокращения времени, скорости и расстояния
Сокращения отношений и пропорций
Область и диапазон рациональных функций
Область действия и диапазон рациональных функции с отверстиями
Графическое представление рациональных функций
Отображение рациональных функций с отверстиями
Преобразование повторяющихся десятичных дробей в дроби
Десятичное представление рациональных чисел
Поиск квадратного корня с помощью длинных ди зрение
л.Метод CM для решения задач времени и работы
Перевод словесных задач в алгебраические выражения
Остаток при делении 2 степени 256 на 17
Остаток при делении 17 степени 23 на 16
Сумма всех трехзначных чисел, кратных 6
Сумма всех трехзначных чисел, кратных 7
Сумма всех трехзначных чисел, кратных 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
Обучение не для оценки, это процесс для понимания концепции.
Мы твердо верим, что глубокое понимание концепции имеет значение. Наша конечная цель всегда состоит в том, чтобы студенты глубже поняли концепцию.
Наши студенты всегда выставляют оценки только благодаря пониманию концепции.
Мы являемся экспертами в SCAT (математика и английский), SAT (математический английский), ACT (математика и английский), SAT Level 1 & 2 (предметные тесты), исчисление, предварительное исчисление и многое другое.
Для онлайн-классов, пожалуйста, свяжитесь:
WhatsApp: + 91-
37004Skype ID: rams_tpt
,Видеоурок
по нахождению уравнения для линии Из 2 точек
Перехват склона против формы склона точки
Есть несколько разных способов найти уравнение прямой из 2 точек.
Первая половина этой страницы будет посвящена написанию уравнения в форме перехвата наклона, как в примере 1 ниже.
Однако, если вам удобно использовать форму линии с наклоном точки, перейдите ко второй части этой страницы, потому что написать уравнение из 2 точек проще с формой с наклоном точки.
Пример
Уравнение из 2-х точек с использованием формы перехвата наклона
Найти уравнение прямой через точки (3,7) и (5,11)
Шаг 1 Шаг 2 Шаг 3Замените любую точку в уравнении. Вы можете использовать (3,7) или (5,11)
Шаг 4 Шаг 5Подставим b, -1, в уравнение из шага 2
Используйте наш калькулятор
Вы можете использовать калькулятор ниже, чтобы найти уравнение прямой из любых двух точек.Просто введите числа в поля ниже и калькулятор (у которого здесь есть своя страница) автоматически вычислит уравнение линии в наклоне точки и формах пересечения наклона
Ответ:
$ $
(попробуйте этот калькулятор «уравнение из 2 баллов» на своей странице здесь.)
Очистить
точек переключения
Поделитесь этой точной проблемой! (Эта ссылка покажет ту же работу, которую вы можете увидеть на этой странице)
Практические проблемы
Задача 1
Найти уравнение прямой через следующие 2 точки: (4,5) и (8,7)
Покажи ответ Шаг 1 Ответ Шаг 3Замените любую точку в уравнении.Вы можете использовать (4,5) или (8,7)
Ответ ,
Leave A Comment