Через точку пересечения диагоналей параллелограмма авсд: Через точку пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны AD и ВС в точках Е и F соответственно. Найдите стороны

П3. Признаки параллелограмма | Сайт учителя математики Косыхиной Н.В.

Репетитор по математике
Косыхина Наталья Владимировна

1 2 3 4 &raquo

Параграф 3. Задача 1
Заполните пропуски. 1) Если в четырёхугольнике каждые две противолежащие стороны равны, то этот четырёхугольник — параллелограмм. 2) Если в четырёхугольнике

Параграф 3. Задача 10
Диагонали параллелограмма ABCD пересекаются в точке О. Точки М, N, К и Р — середины отрезков АО, ВО, СО и

Параграф 3. Задача 11
На сторонах параллелограмма ABCD отметили точки M, E, F и K так, чмо AM = AK = CE = CF.

Параграф 3. Задача 12
Точки M и K — середины сторон BC и AD параллелограмма ABCD. Докажите, что четырехугольник MNKP — параллелограмм. Дано: ABCD

Параграф 3. Задача 13
Дано: AM = CK, BO = OD, MO = OK. Доказать: ABCD — параллелограмм. Доказательство. Рассмотрим четырехугольник BMKD. MK и

Параграф 3. Задача 14
Дано: ABCD — параллелограмм, BE -биссектриса ∠ABC, DF- биссектриса ∠ADC Доказать: Прямая FE проходит через точку пересечения диагоналей параллелограмма ABCD.

Параграф 3. Задача 15
На сторонах параллелограмма ABCD отметили точки F, M, K и E так, что AF= CK, AE = CM. Докажите, что

Параграф 3. Задача 16.
На сторонах параллелограмма ABCD отметили точки N, M, K и R так, что ∠BAK = ∠DCM, BN = DR. Докажите,

Признаки параллелограмма.
Теорема 1. Доказательство
Докажите теорему: Если в четырёхугольнике каждые две противолежащие стороны равны, то этот четырёхугольник — параллелограмм. Доказательство. На рисунке изображён четырёхугольник

Признаки параллелограмма. Теорема 2. Доказательство

Докажите теорему: Если в четырёхугольнике две противолежащие стороны равны и параллельны, то этот четырёхугольник — параллелограмм. Доказательство. На рисунке изображён

Признаки параллелограмма. Теорема 3. Доказательство
Докажите теорему: Если в четырёхугольнике диагонали точкой пересечения делятся пополам, то этот четырёхугольник — параллелограмм. Доказательство. На рисунке изображён четырёхугольник

Параграф 3. Задача 5
Отметьте знаком два из данных равенств, выполнения которых достаточно для доказательства, что четырёхугольник ABCD — параллелограмм. AB = CD АВ

1 2 3 4 &raquo
2018-2023

Точка — пересечение — диагональ — параллелограмм
Cтраница 1
Точка пересечения диагоналей параллелограмма является центром симметрии параллелограмма.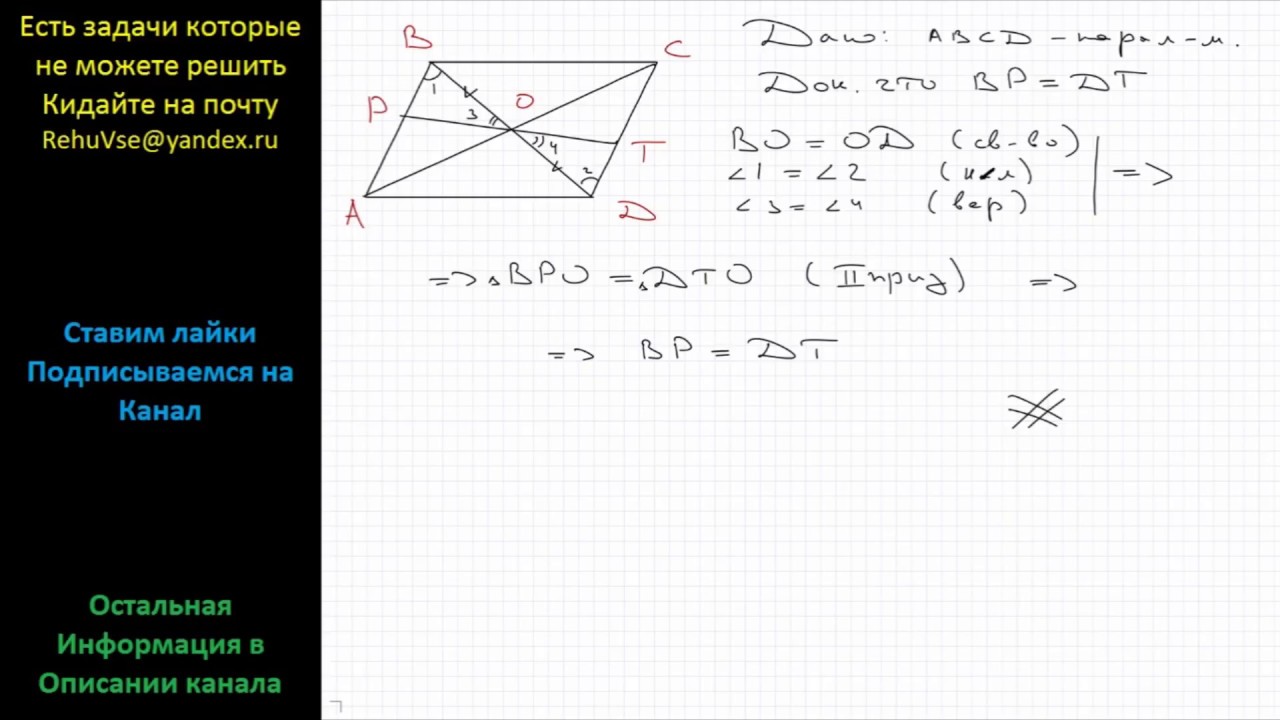 Отсюда, в частности, следует, что диагонали делятся точкой пересечения пополам. [1]
Через точку пересечения диагоналей параллелограмма проведена прямая. Доказать, что отрезок ее между параллельными сторонами делится в этой точке пополам. [2]
Через точку пересечения диагоналей параллелограмма проведена прямая. Докажите, что отрезок этой прямой, заключенной между параллельными сторонами, делится этой точкой пополам. [3]

Докажите, что точка пересечения диагоналей параллелограмма является его центром симметрии. [4]
Пусть О — точка пересечения диагоналей параллелограмма ABCD, тогда О А — ОС, OB — OD и поэтому вершины А и С ( и также В и D) симметричны относительно точки О. [5]
Найти геометрическое место точек пересечения диагоналей параллелограммов, вписанных в данный четырехугольник так, что стороны этих параллелограммов параллельны диагоналям четырехугольника.
[6]
Центр тяжести S находится в точке пересечения диагоналей параллелограмма. [7]
Основание высоты правильной четырехугольной пирамиды ( рис. 259 6) находим как точку пересечения диагоналей параллелограмма, изображающего основание этой пирамиды — квадрат ABCD. Аналогично находится на рисунке правильной шестиугольной пирамиды ( рис. 259, в) основание ее высоты. [8]
Основание высоты правильной четырехугольной пирамиды ( рис. 259, б) находим как точку пересечения диагоналей параллелограмма, изображающего основание этой пирамиды — квадрат ABCD. Аналогично находится на рисунке правильной шестиугольной пирамиды ( рис. 259, в) основание ее высоты. [9]

Основание высоты правильной четырехугольной пирамиды ( рис. 242, б) находим как точку пересечения диагоналей параллелограмма, изображающего основание этой пирамиды-квадрат ABCD. Аналогично находится на рисунке правильной шестиугольной пирамиды ( рис. 242, в) основание ее высоты. [10]
Основание высоты правильной четырехугольной пирамиды ( рис. 242, б) находим как точку пересечения диагоналей параллелограмма, изображающего основание этой пирамиды — квадрат ABCD. Аналогично находится на рисунке правильной шестиугольной пирамиды ( рис. 242, в) основание ее высоты. [11]

Основание высоты правильной четырехугольной пирамиды ( рис. 259, б) находим как точку пересечения диагоналей параллелограмма, изображающего основание этой пирамиды — квадрат ABCD. Аналогично находится на рисунке правильной шестиугольной пирамиды ( рис., 259, в) основание ее высоты. [12]
Выразить через а и Ь векторы MA, MB, MC и MD, где М есть точка пересечения диагоналей параллелограмма. [13]
Точка С должна иметь координаты ( х1 хг у Уг) — Решение. Пусть О — точка пересечения диагоналей параллелограмма A BCD, тогда она является серединой диагоналей.
[14]
MC ЛЮ, где М есть точка пересечения диагоналей параллелограмма. [15]
Страницы: 1 2
Диагонали параллелограмма ABCD пересекаются в точке O. Через O проведена прямая a, пересекающая AD в точке P и BC в точке Q. Покажите, что PQ делит параллелограмм на две части равной площади.
Вопрос
Обновлено:26/04/2023
NCERT EXEMPLAR-Площади параллелограммов и треугольников-Площади параллелограммов и треугольников
20 видео
РЕКЛАМА
লিখিত জবাব
Решение
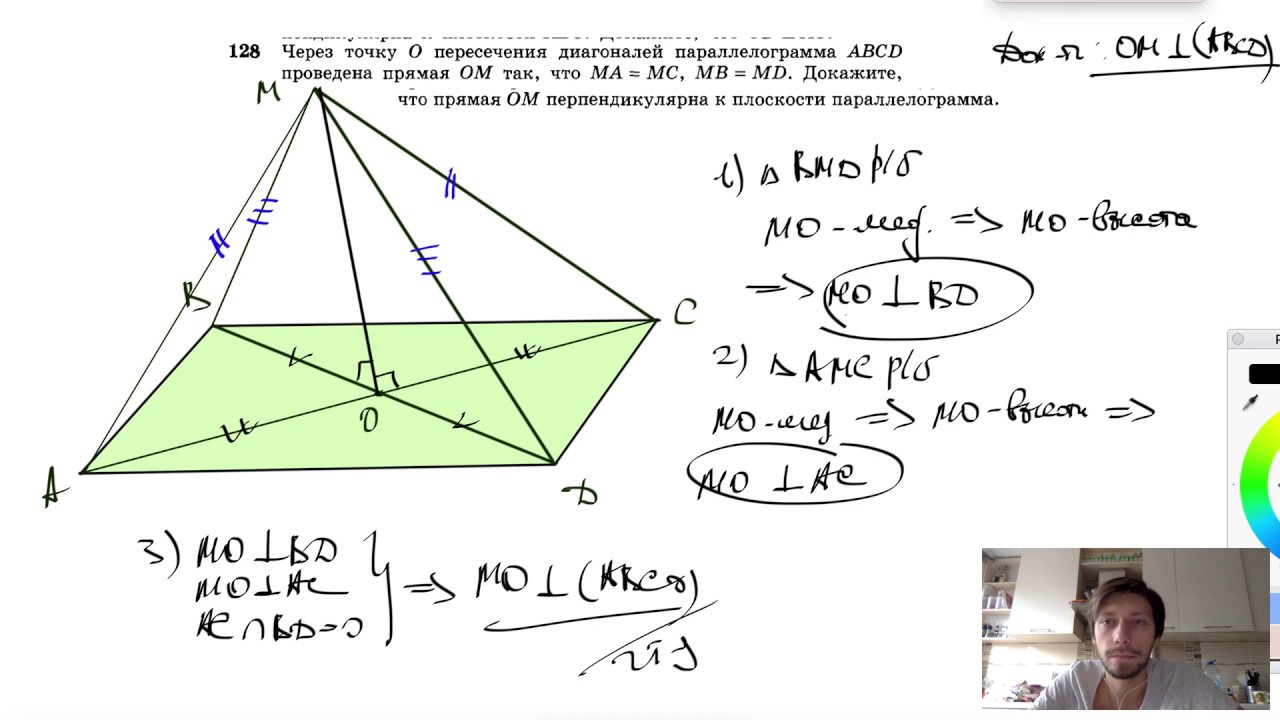
Дано В параллелограмме ABCD диагонали пересекаются в точке O и проводят прямую PQ, пересекающую AD и BC.
Чтобы доказать, что PQ делит параллелограмм ABCD на две части равной площади.
т. е. ar(ABQP)=ar(CDPQ)

Доказательство Мы знаем, что диагонали параллелограмма делят друг друга пополам.
∴ OA=OC и OB=OD …(i)
In ΔAOB и ΔCOD,
OA=OC
OB=OD [из уравнения (i)]
и ∠AOB=∠COD [вертикально противоположные углы]
∴ ΔAOB≅ΔCOD [по правилу конгруэнтности SAS]
Тогда ar(ΔAOB)=ar(ΔCOD) . ..(ii)
[так как конгруэнтные фигуры имеют одинаковую площадь]
Теперь в ΔAOP и ΔCOQ
∠PAO=∠OCQ [альтернативные внутренние углы]
OA=OC [из уравнения. (i)]
и ∠AOP=∠COQ [вертикально противоположные углы]
∴ ΔAOP≅ΔCOQ [по правилу конгруэнтности ASA]
∴ ar(ΔAOP)=ar(ΔCOQ) …(iii)
[так как конгруэнтные фигуры имеют одинаковую площадь]
Аналогично, ar(ΔPOD)=ar(ΔBOQ) …(iv)
Теперь ar(ABQP)=ar(ΔCOQ)+ar(ΔCOD)+ar(ΔPOD)
=ar(ΔAOP)+ar(ΔAOB)+ar(ΔBOQ) [из ур. (ii), (iii) и (iv)]
⇒ ar(ABQP)=ar(CDPQ) Таким образом, доказано.
Пошаговое решение от экспертов, которое поможет вам избавиться от сомнений и получить отличные оценки на экзаменах.
Ab Padhai каро бина объявления ке
Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!
সংশ্লিষ্ট ভিডিও
Диагонали параллелограмма ABCD пересекаются в О.А. линия через О пересекает АВ в Х и округ Колумбия у Ю.

Докажите, что ОХ=ОУ.
Диагонали параллелограмма ABCD пересекаются в точке О. Через О , время пересекает AD в П и до нашей эры в Q . Покажите, что PQ делит параллелограмм на две части равной площади.
15 O — точка пересечения диагоналей AC и BD трапеции ABCD с AB || ОКРУГ КОЛУМБИЯ. Через O проведен отрезок PQ, параллельный AB, пересекающему AD в P и BC в Q. Убедитесь, что PO=QO ,
диагонали параллелограмма ABCD пересекаются в точке О. Через О, линия нарисовано, чтобы пересечь AD в П и до нашей эры в К. Покажите, что PQ делит параллелограмм на две части равной площади.

1414826
P и Q — точки на противоположных сторонах AD и BC параллелограмма ABCD, такие, что PQ проходит через точку пересечения O его диагоналей AC и BD. Покажите, что PQ делится пополам в точке O.
26522190
O — точка пересечения диагоналей AC и BD трапеции ABCD с AB||DC. Через O проведен отрезок PQ параллельно AB, пересекающему AD в P и BC в Q, докажите, что PO=QO.
26861959
यदि चतुर्भुज ABCD के विकर्ण AC तथा BD बिं दु O पर प्रतिच्छेद करते है , तथा चतुर्भुज को चार ब राबर क्षेत्रफल वाले त्रिभुजों में विभाजित करत े हो, तो सिद्ध कीजिये कि चतुर्भुज ABCD एक समान्तर चत ुर्भुज है।
105884826
समांतर चतुर्भुज ABCD के विकर्ण बिंदु О पर प्रतिच्छेद करते है। O से एक रेखा खींची गई है जो AD तथा BC को क्रमशः P तथा Q प र प्रतिच्छेदित करती है। सिद्ध कीजिए कि रेखाखण्ड PQ समांतर चतुर्भुज को द ो बराबर क्षेत्रफल वाले भागों में विभाजित करती है ।
105884868
समांतर चतुर्भुज ABCD के विकर्ण O पर प् रतिच्छेद करते है | O से एक रेखा खींची जाती है तो AD से P पर तथा BC से Q पर मि लती है |साबित करें की PQ समांतर चतुर्भुज ABCD को बराबर क्षेत्रफल वाले दो भागों में बांटता है|
109837278
В параллелограмме ABCD середины сторон BC и AD равны Q и P соответственно. Докажите, что если диагонали параллелограмма ABCD пересекаются в точке O, то POQ будет прямой.
480152314
Текст Решение
P и Q — точки на противоположных сторонах AD и BC параллелограмма ABCD такие, что PQ проходит через точку пересечения O его диагоналей AC и BD. Покажите, что PQ делится пополам в точке O.
642505469
Диагонали параллелограмма ABCD пересекаются в точке O. Через O проведена прямая a, пересекающая AD в точке P и BC в точке Q. Покажите, что PQ делит параллелограмм на две части равной площади.
642505499
O — точка пересечения диагоналей AC и BD трапеции ABCD с AB||DC. Через O проведен отрезок PQ параллельно AB, пересекающему AD в P и BC в Q, докажите, что PO=QO.
642505956
Диагонали параллелограмма ABCD пересекаются в точке О. Через О , время пересекает AD в П и до нашей эры в Q . Покажите, что PQ делит параллелограмм на две части равной площади.
642565227
диагонали параллелограмма ABCD пересекаются в точке О. Через О, линия нарисовано, чтобы пересечь AD в П и до нашей эры в К. Покажите, что PQ делит параллелограмм на две части равной площади.
642572582
Ответ: Диагонали параллелограмма ABCD…
Задача 1E: Примечание. Упражнения, отмеченные звездочкой, носят более сложный характер. a Как показано, должен… Задача 2E: a Как показано, должен ли RSTV быть параллелограммом? b При показанных размерах необходимо ли, чтобы RS=8? Задача 3E: Предположим, что на чертеже WY и XZ делят друг друга пополам. Какой тип четырехугольника WXYZ? Задача 4E: Предположим, что на чертеже ZX является серединным перпендикуляром к WY. Какой тип четырехугольника… Задача 5E: Плотник раскладывает доски длиной 8 футов, 8 футов, 4 фута и 4 фута, ставя их встык. a Если… Задача 6E: Плотник соединяет четыре доски длиной 6 футов, 6 футов, 4 фута и 4 фута в указанном порядке, чтобы сформировать… Задача 7E: В параллелограмме ABCD не показано, AB=8, mB=110 и ВС=5. Какая диагональ имеет большую длину? Задача 8E: В четырехугольнике WXYZ показаны меры выбранных углов. a Какой тип четырехугольника… Задача 9E: В ABC M и N являются серединами AC и BC соответственно. Если AB=12,36, какой длины MN? Задача 10E: В ABC M и N являются серединами AC и BC соответственно. Если MN=7,65, какова длина AB? Задача 11E. В упражнениях с 11 по 14 предположим, что X, Y и Z являются серединами сторон RST. Если RS=12, ST=14,… Задача 12E: В упражнениях с 11 по 14 предположим, что X, Y и Z являются серединами сторон RST. Если XY=6, YZ=8 и… Задача 13EЗадача 14E: В упражнениях с 11 по 14 предположим, что X, Y и Z являются серединами сторон RST. Если периметр… Задача 15E Задача 16E Задача 17E: Для компактности опускающиеся колеса носилок или каталки складываются под него, как показано на рисунке. В… Задача 18E: Для компактности выпадающие ножки гладильной доски складываются под доску. Выдвижной механизм… Задача 19E: В упражнениях с 19 по 24 завершите каждое доказательство. Дано: 12 и 34. Докажите: MNPQ — воздушный змей. ДОКАЗАТЕЛЬСТВА Утверждений… Задача 20E. В упражнениях с 19 по 24 завершите каждое доказательство. Дано: Четырехугольник ABCD с серединами E, F, G и H… Задача 21E: В упражнениях 19–24 завершите каждое доказательство. Дано: M-Q-T и P-Q-R такие, что MNPQ и QRST являются s… Задача 22E: В упражнении 19-24 завершите каждое доказательство. Дано: WXYZ с диагоналями WY и XZ WMXYMZ Докажите: Задача 23E: В упражнении 19–24 завершите каждое доказательство. Дано: Воздушный змей HJKL с диагональю HK Докажите: HK делит LHJ пополам Задача 24E: В упражнении 19to24, завершите каждое доказательство. Дано: MNPQ, где T — середина MN, а S — середина… Задача 25E Задача 26E: В упражнениях с 25 по 28 напишите формальное доказательство каждой теоремы или следствия. Если диагонали a… Задача 27E Задача 28E Задача 29E: В упражнениях 29-31, M и Na являются серединами сторон RS и RT стороны RST, соответственно…. Задача 30E: В упражнениях 29-31, M и Na являются серединами сторон RS и RT от RST соответственно. Дано:… Задача 31E: В упражнениях с 29 по 31 M и Na являются серединами сторон RS и RT стороны RST соответственно. Дано:… Задача 32E Задача 33E: В упражнениях с 32 по 35 рассмотрим воздушный змей ABCD с ABAD и BCDC. Для воздушного змея ABCD mC=m-30, а mA=mB-50…. Задача 34E: В упражнениях с 32 по 35 рассмотрим воздушный змей ABCD с ABAD и BCDC.