Через любые две точки можно провести прямую, и притом только одну.
Р ассмотрим теперь две прямые. Если они имеют общую точку, то говорят, что эти прямые пересекаются. На рисунке 6 прямые а и b пересекаются в точке О, а прямые р и q не
Рис. 6 пересекаются. Две прямые не могут иметь двух и более общих точек. В самом деле, если бы две прямые имели две общие точки, то каждая из прямых проходила бы через эти точки. Но через две точки проходит только одна прямая. Таким образом, можно сделать вывод:
Две прямые либо имеют только одну общую точку, либо не имеют общих точек.
Прямую, на которой отмечены две точки, например А и В, иногда обозначают двумя буквами: АВ или ВА. Для краткости вместо слов «точка А лежит на прямой а» используют запись А а, а вместо слов «точка В не лежит на прямой а» — запись В

3. Провешивание прямой на местности
П риложим к листу бумаги линейку, отметим точки А и В и какую-нибудь точку С, лежащую между А и В (рис. 8, а). Затем передвинем линейку вправо так, чтобы ее левый конец оказался около точки С, и отметим точку D около правого конца линейки (рис. 8, б). Точки А, В, С и D лежат на одной прямой. Если мы проведем теперь отрезок АВ, а затем отрезок BD, то получим отрезок AD, более длинный, чем линейка.
Аналогичный прием используется для «проведения» длинных отрезков прямых на местности. Этот прием заключается в следующем. Сначала отмечают какие-нибудь точки
 Следующую веху ставят
так, чтобы ее закрывали вехи, стоящие в
точках В
и С, и
т. д.
Следующую веху ставят
так, чтобы ее закрывали вехи, стоящие в
точках В
и С, и
т. д.О писанный прием называется провешиванием прямой (от слова «веха»). Он широко используется на практике, например при рубке лесных просек, при прокладывании трассы шоссейной или железной дороги, линий высоковольтных передач и т. д.
Н а рисунке 7, а выделена часть прямой, ограниченная двумя точками. Такая часть прямой называется отрезком.
Итак, отрезок – это часть прямой, ограниченная двумя точками. Точки, ограничивающие отрезок, называются его концами. На рисунке 7, б изображен отрезок с концами А и В. Такой отрезок обозначается АВ или ВА. Отрезок АВ содержит точки А и В и все точки прямой АВ, лежащие между А и В.
5. Луч
П роведем прямую
 11). Эта точка
разделяет прямую на две части, каждая
из которых называется лучом,
исходящим из точки О (на
рисунке 11 один из лучей выделен цветной
линией). Точка О называется началом каждого
из лучей. Обычно
луч обозначают либо малой латинской
буквой (например, луч h на
рисунке 12, а), либо двумя большими
латинскими буквами, первая из которых
обозначает начало луча, а вторая —
какую-нибудь точку на луче (например,
луч ОА на
рисунке 12, б).
11). Эта точка
разделяет прямую на две части, каждая
из которых называется лучом,
исходящим из точки О (на
рисунке 11 один из лучей выделен цветной
линией). Точка О называется началом каждого
из лучей. Обычно
луч обозначают либо малой латинской
буквой (например, луч h на
рисунке 12, а), либо двумя большими
латинскими буквами, первая из которых
обозначает начало луча, а вторая —
какую-нибудь точку на луче (например,
луч ОА на
рисунке 12, б).6. Угол
Н апомним, что угол
Обозначение угла: 1) АОВ
2) hk !!!!!!!!!!!!!!!
у
гол называется развернутым, если
обе его стороны лежат на одной прямой. Можно сказать, что каждая сторона
развернутого угла является продолжением
другой стороны. На рисунке 14 изображен развернутый
угол с вершиной
Можно сказать, что каждая сторона
развернутого угла является продолжением
другой стороны. На рисунке 14 изображен развернутый
угол с вершиной
Л юбой угол разделяет плоскость на две части. Если угол неразвернутый, то одна из частей называется внутренней, а другая — внешней областью этого угла (рис. 15, а).
На рисунке 15, б изображен неразвернутый угол. Точки А, В, С лежат внутри этого угла (т. е. во внутренней области угла), точки D и Е — на сторонах угла, а точки Р и Q — вне угла (т. е. во внешней области угла).
Если угол развернутый, то любую из двух частей, на которые он разделяет плоскость, можно считать внутренней областью угла.
Фигуру, состоящую из угла и его внутренней области, также называют углом.
Е
сли
луч исходит из вершины неразвернутого
угла и проходит внутри угла, то он делит
этот угол на два угла.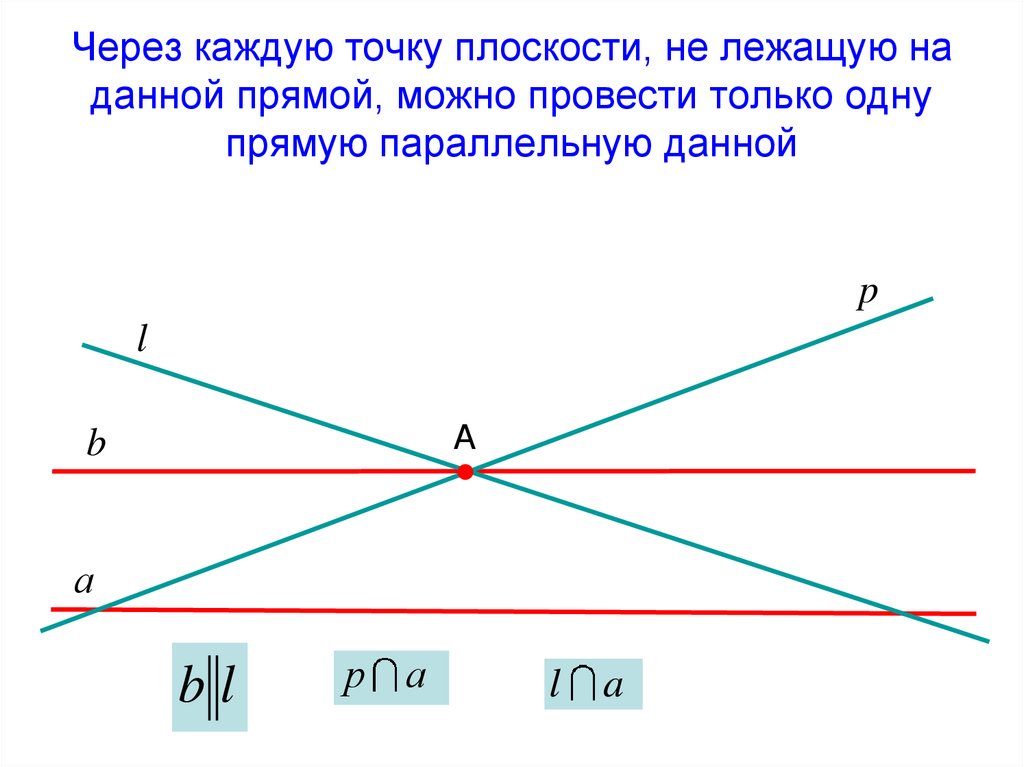
На рисунке 16, а луч ОС делит угол АОВ на два угла: АОС и СОВ. Если угол АОВ развернутый, то любой луч ОС, не совпадающий с лучами ОА и ОБ, делит этот угол на два угла: АОС и СОВ (рис. 16, б).
Геометрия Аксиомы стереометрии
Материалы к уроку
Конспект урока
|
Аксиомы стереометрии
Аксиома – это утверждение не требующее доказательства.
Аксиомы стереометрии – утверждения о свойствах геометрических тел, принимаемые в качестве исходных положений, на основе которых доказываются все теоремы и вообще строится вся геометрия.
|
|
|
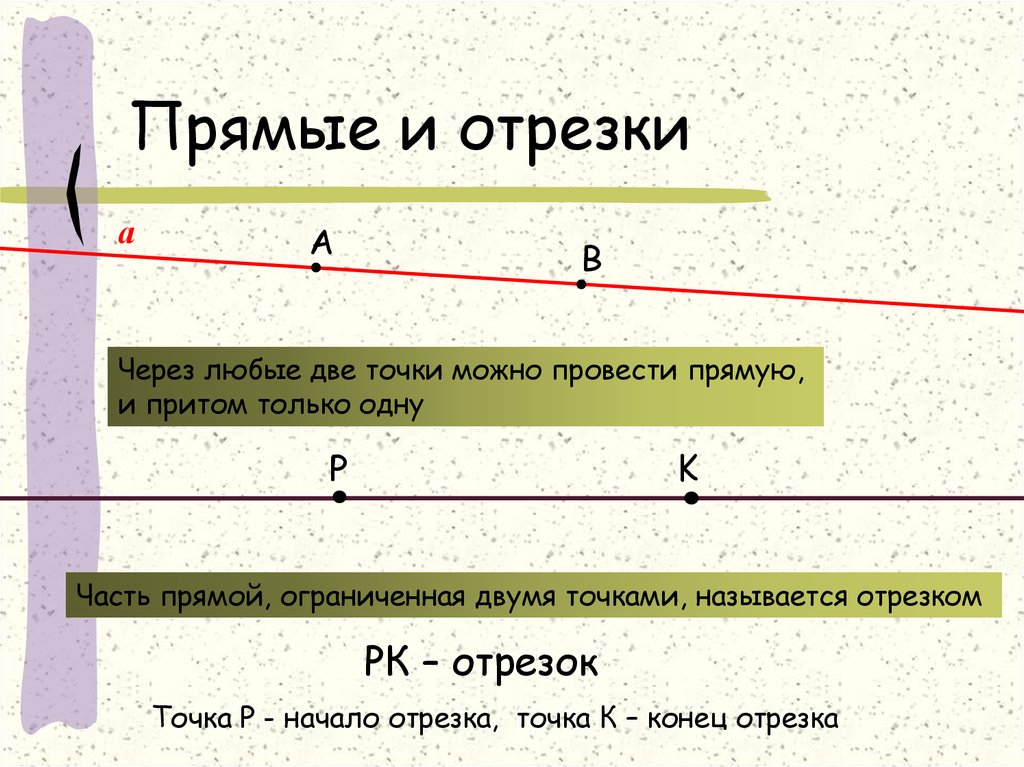
Аксиома А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. Аксиома А1 состоит из двух частей. Первая часть утверждает, что через три точки проходит плоскость, т.е. существует хотя бы одна плоскость.
А вторая часть аксиомы говорит, что такая плоскость только одна.
На экране изображены три точки A, B и C.
Если C не принадлежит прямой AB, то существует плоскость α, проходящая через эти три точки, причем, только одна.
Символ читается как существует.
По этой аксиоме, три точки, не лежащие на одной прямой, однозначно определяют плоскость.
Поэтому плоскости иногда обозначают тремя большими буквами, используя любые три точки плоскости, не лежащие на одной прямой.
У нас на экране плоскость обозначена как α.
|
Аксиома 1 (существование плоскости)
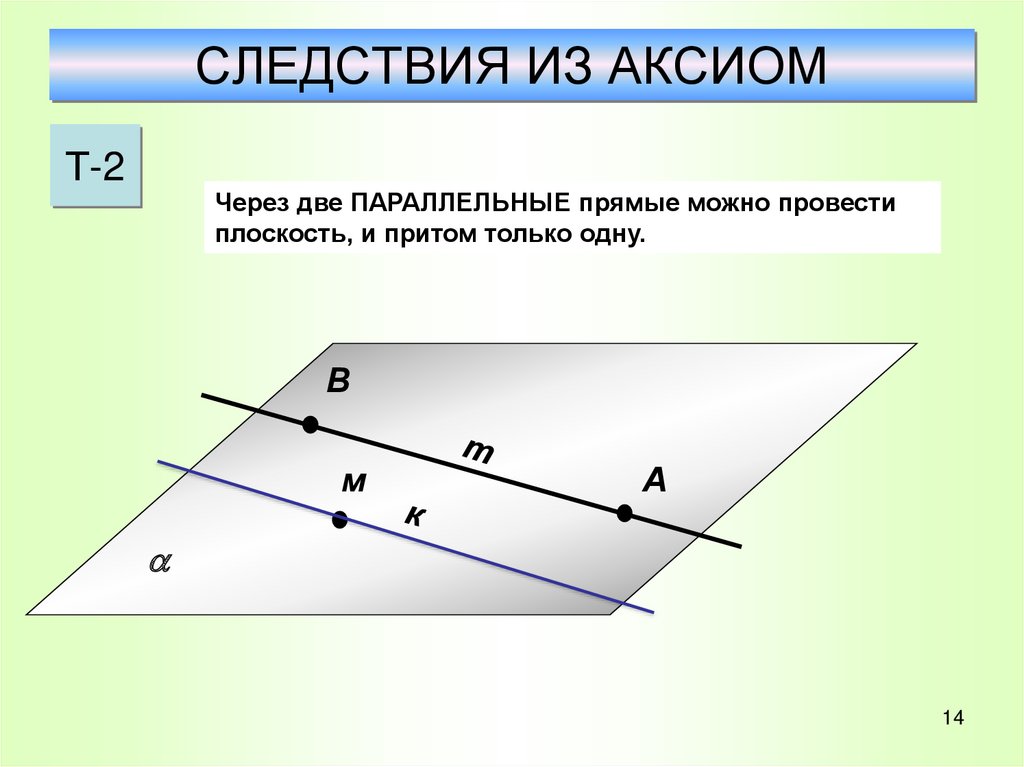
Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
|
|
Аксиома А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
В этом случае говорят, что прямая лежит в плоскости или плоскость проходит через прямую.
На экране вы видите две точки A и B.
Если точки A и B принадлежат плоскости , то прямая AB лежит в плоскости α, плоскость проходит через прямую AB.
Эта аксиома устанавливает взаимосвязь между прямой и плоскостью, то есть тот факт, что плоскость действительно плоская и прямая ее не «протыкает», а целиком содержится в ней.
Из аксиомы A2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются.
|
Аксиома А2 Если две точки прямой лежат в плоскости, то все точки этой прямой лежат в этой плоскости. В этом случае говорят, что прямая лежит в плоскости или плоскость проходит через прямую.
|
|
Аксиома А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. В этом случае говорят, что плоскости пересекаются по прямой, проходящей через эту точку..
На экране мы видим, плоскости имеют общую точку M. Если точка M – общая для плоскостей , то они пересекаются по прямой a, проходящей через точку M.
Эта аксиома очень важная. Она утверждает, что две плоскости не могут пересекаться по одной единственной точке.
|
Аксиома A3 Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. Говорят, что плоскости пересекаются по прямой, проходящей через эту точку.
|
|
Справедливость фактов планиметрии Мы с вами познакомились с тремя аксиомами стереометрии.
Возникает вопрос: «Можем ли мы пользоваться теми фактами, которые справедливы на плоскости: теорема Пифагора, формулы площади треугольников, параллелограмма? Или все эти формулы, теоремы для нас уже не имеют значения?»
Оказывается можем. В планиметрии мы имели дело с одной плоскостью, на которой располагались все рассматриваемые нами фигуры. В стереометрии много плоскостей.
И в каждой из плоскостей, справедливы все факты планиметрии. В любой из плоскостей выполняется теорема Пифагора для прямоугольного треугольника, верны формулы длины окружности, верны формулы для площади.
Все что мы изучали, мы теперь можем применять смело в каждой из рассматриваемых плоскостей.
|
Аксиомы стереометрии не противоречат аксиомам планиметрии. В стереометрии принимаются все факты планиметрии для каждой плоскости.
|
|
Переходим к решению задач Задача 1. По рисунку назовите: А) плоскости, в которых лежат прямые PE, MK, DB, AB, EC; Б) точки пересечения прямой DK с плоскостью ABC, прямой CE с плоскостью ADB.
Решение. а) Так как точки P и E принадлежат плоскости ADB, то прямая PE лежит в плоскости ADB (аксиома А2). Аналогично MK лежит в плоскости BCD.
Так как точки B и D лежат одновременно в двух плоскостях ABD и BCD, то прямая BD лежит в двух плоскостях ABD и BCD. Аналогично AB лежит в двух плоскостях ABD и ABC.
Точки E и C лежат одновременно в двух плоскостях ABC и CDE, значит прямая CE лежит в двух плоскостях ABC и CD.
б) Заметим, что точка C принадлежит прямой DK и плоскости ABC, следовательно, прямая DK пересекается с плоскостью ABD в точке E. Аналогично, CE пересекается с плоскостью ABD в точке E.
|
Задача 1. По рисунку назовите: а) плоскости, в которых лежат прямые PE, MK, DB, AB, EC; б) точки пересечения прямой DK с плоскостью ABC, прямой CE с плоскостью ADB.
|
|
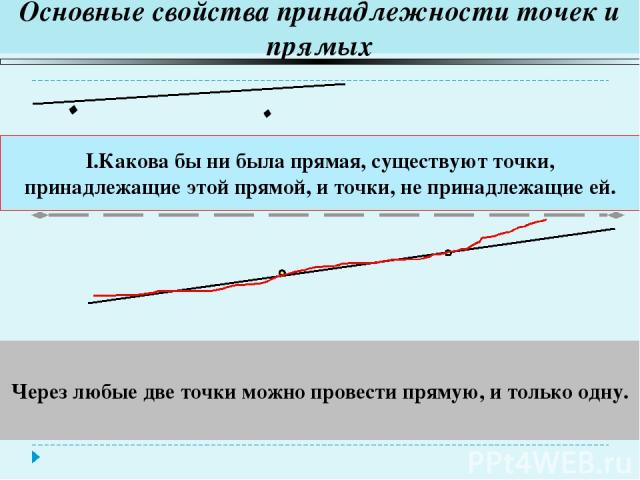
Задача 2. Точки A, B, C и D не лежат в одной плоскости. Могут ли какие-то три из них лежать на одной прямой?
Дано: A, B, C, D – не лежат в одной плоскости Найти: Могут ли 3 из них лежать на одной прямой? Решение. Пусть точки A, B, C лежат на прямой m, а точка D не лежит на этой прямой. Тогда по аксиоме А1 существует плоскость , проходящая через точки A, C и D. Две точки A и С прямой m принадлежат в плоскости , значит и точка B этой прямой принадлежит этой плоскости.
Получается, что в одной плоскости лежат все четыре точки, что противоречит условию задачи.
Ответ: Точки A, B, C и D не могут лежать на одной прямой.
|
Задача 2. Точки A, B, C и D не лежат в одной плоскости. Могут ли какие-то три из них лежать на одной прямой?
Дано: A, B, C, D – не лежат в одной плоскости Найти: Могут ли 3 из них лежать на одной прямой? Получили противоречие, по условию задачи точки не лежат в одной плоскости. Предположение неверно, никакие три точки не лежат на одной прямой. Ответ: Нет |
|
Задача 3. Докажите, что через три данные точки, лежащие на одной прямой, проходит плоскость.
Дано: Точки A, B, C принадлежат прямой m Доказать: Существует плоскость, проходящая через A, B, C Найти :Количество плоскостей Решение. Возьмем произвольную точку D, не лежащую на прямой m.
Через три точки A, C и D можно провести плоскость α (аксиома A1). Так как две точки A и C прямой m принадлежат плоскости α, то и точка B прямой m принадлежит этой плоскости. Все три точки принадлежат плоскости. Значит плоскость α – искомая плоскость. Так как мы взяли произвольную точку D, то таких плоскостей бесконечное множество. Ответ: Через три данные точки, лежащие на одной прямой, может проходить бесконечное множество плоскостей.
|
Задача 3. Докажите, что через три данные точки , лежащие на одной прямой, проходит плоскость. Сколько существует таких плоскостей?
Дано:
Доказать: Найти: Количество плоскостей
Решение. Пусть .
(аксиома A1).
(аксиома A2).
Плоскость α – искомая плоскость.
Т. к D – произвольная точка, то таких плоскостей бесконечное множество. Ответ: бесконечное множество.
|
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитораОставить заявку на подбор
Q2Напишите, сколько линий можно провести через i заданную точку ii две заданные фиксированные точки iii три кол.
 ..
..Перейти к
- Упражнение 23 (А)
- Упражнение 23(Б)
- Повторное упражнение
- Система счисления (закрепление чувства числа)
- Оценка
- Числа в Индии и международной системе (со сравнением)
- Место Значение
- Натуральные числа и целые числа (включая шаблоны)
- Отрицательные числа и целые числа
- Номер строки
- HCF и LCM
- Игра с числами
- Наборы
- Соотношение
- Доля (включая словесные задачи)
- Унитарный метод
- Фракции
- Десятичные дроби
- Процент (Процент)
- Представление о скорости, расстоянии и времени
- Основные понятия (алгебра)
- Основные операции (связанные с алгебраическими выражениями)
- Замена (включая использование скобок в качестве группирующих символов)
- Обрамление алгебраических выражений (включая вычисление)
- Простые (линейные) уравнения (включая текстовые задачи)
- Основные понятия (геометрия)
- Углы (с их типами)
- Свойства углов и линий (включая параллельные линии)
- Треугольники (включая типы, свойства и конструкцию)
- четырехугольник
- Полигоны
- Круг
- Повторное упражнение по симметрии (включая построения по симметрии)
- Распознавание твердых тел
- Периметр и площадь плоских фигур
- Обработка данных (включая пиктограмму и гистограмму)
- Среднее и медиана
Главная >
Селина Солюшнс
Класс 6
Математика
>
Глава 23. Основные понятия (геометрия)
>
Упражнение 23 (А)
>
Вопрос 2
Основные понятия (геометрия)
>
Упражнение 23 (А)
>
Вопрос 2
Вопрос 2 Упражнение 23(A)
В2) Напишите, сколько прямых можно провести через:
(i) данная точка?
(ii) две фиксированные точки?
(iii) три точки на одной прямой?
(iv) три точки, не лежащие на одной прямой?
Ответ:
Решение:
(i) Через заданную точку можно провести бесконечную прямую.
(ii) Через две заданные точки можно провести только одну прямую.
(iii) Через три точки, лежащие на одной прямой, можно провести только одну прямую.
(iv) Никакая линия не может быть проведена через три точки, не лежащие на одной прямой.
Стенограмма видео
Привет Добро пожаловать в обучение Лидо
сегодня мы увидим вопрос
то есть написать
сколько линий можно провести через
Этих четырех утверждений сколько
линии можно рисовать
от заданной точки, если взять точку
здесь
В любой момент вы берете эту точку
извини
взять любую точку
или здесь одна точка, если взять любую точку
сколько линий можно нарисовать
ты можешь рисовать вот так ты можешь рисовать вот так
этот
можно и так нарисовать
вы можете нарисовать новое аниме, как это
если вы можете рисовать бесконечные точки в
конечный
бесконечные точки для этого также мы можем
рисовать любые точки
Любой угол, который мы можем сохранить, и мы можем
рисовать любые линии так бесконечные точки
для первого ответ
бесконечный
Мы пойдем со вторым случаем
Второй случай
это первое, это второе
две заданные неподвижные точки, если вам даны две
точки крепления присваиваются заданным фиксированным
точки
сколько линий ты можешь нарисовать ты можешь нарисовать
только одна строка бросает его
ты не можешь так рисовать, если рисуешь
вот так и уйдет
тебе это не нравится ты можешь только рисовать
одна линия
хорошо, ты можешь нарисовать только одну линию, я
буду спасать хорошо
двухпиксельные точки, где вы рисуете одну линию
хорошо, так что только одна строка возможна только
можно в одну строку
одна строка, затем идет третий случай. Третий случай
три коллинеарных точки три колониальных
точка коллинеарна значит лежит на
та же линия
эти три колониальные точки сколько
линии можно рисовать только одну
линия через это
Хорошо, это тоже одна строка
если взять другой случай четвертый
три неколлинеарные точки берем три
Неколониальные точки
одна точка здесь, одна точка здесь, одна
ты можешь нарисовать
количество линий, проходящих через
той же точки нет, мы не можем нарисовать
Линия не будет такой прямо
скрипка будет вот такой
линия будет только прямой
так что нет
точки можно рисовать, линии нельзя
привлечено к этому
Ответы — бесконечные строки, одна строка, одна
линия
и ни строчки надеюсь ты это понимаешь
видео
если у вас есть какие-либо сомнения, вы можете отбросить их.
раздел комментариев и спасибо за
просмотр этого дал
Третий случай
три коллинеарных точки три колониальных
точка коллинеарна значит лежит на
та же линия
эти три колониальные точки сколько
линии можно рисовать только одну
линия через это
Хорошо, это тоже одна строка
если взять другой случай четвертый
три неколлинеарные точки берем три
Неколониальные точки
одна точка здесь, одна точка здесь, одна
ты можешь нарисовать
количество линий, проходящих через
той же точки нет, мы не можем нарисовать
Линия не будет такой прямо
скрипка будет вот такой
линия будет только прямой
так что нет
точки можно рисовать, линии нельзя
привлечено к этому
Ответы — бесконечные строки, одна строка, одна
линия
и ни строчки надеюсь ты это понимаешь
видео
если у вас есть какие-либо сомнения, вы можете отбросить их.
раздел комментариев и спасибо за
просмотр этого дал
Связанные вопросы
Q1) Укажите, верно или неверно, если неверно, исправьте утверждение. (i) Точка имеет ширину, но не длину. (ii) Ра…
Q3) Заштрихованная область на данном рисунке показывает плоскость: (a) Имя: (i) три коллинеарных точки. (ii) th…
(ii) th…
Q4) Исправьте утверждение, если оно неверно: (i) Луч можно бесконечно продолжать в любую сторону. (ii) …
Q5) Укажите верно или неверно, если неверно, укажите правильное утверждение: (i) В строке имеется счетное число точек…
Q6) Укажите, кажутся ли следующие пары прямых или лучей параллельными или пересекающимися. (i) (ii…
Q7) Приведите два примера из вашего окружения для каждого из следующего: (i) точки (ii) отрезки линии…
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно? 100003
Оценка
Числа в Индии и международной системе (с сравнением)
Значение места
Натуральные числа и целые числа (включая шаблоны)
Отрицательные числа и целые числа
Line
HCF и LCM
.
Множества
Отношение
Пропорция (включая словесные задачи)
Унитарный метод
Дроби
Десятичные дроби
Проценты (проценты)
Представление о скорости, расстоянии и времени
Основные понятия (алгебра)
Основные операции (относящиеся к алгебраическим выражениям)
Подстановка (включая использование скобок в качестве группирующих символов)
Обрамление алгебраических выражений (включая простые 900 вычисления) (Линейные) Уравнения (включая текстовые задачи)
Основные понятия (геометрия)
Углы (с их типами)
Свойства углов и прямых (включая параллельные прямые)
Треугольники (включая типы, свойства и строительство)
Кваровнопочечные
Полигоны
Круг
Упражнение по симметрии (включая конструкции на симметрии)
Распознавание твердых веществ
Периметр и область плоскости
. (включая пиктограмму и гистограмму)
Среднее и медиана
Курсы
Быстрые ссылки
Условия и политика
Условия и политика
2022 © Quality Tutorials Pvt Ltd Все права защищены
Сколько линий можно провести через две различные заданные точки.
 ..
..Перейти к
- Базовая геометрическая концепция. Упражнение 10.
- Зная наши цифры
- Целые числа
- Целые числа
- Игра с числами
- Наборы
- Фракции
- Десятичные
- Соотношение и пропорция
- Алгебра
- Основная геометрическая концепция
- Понимание симметричных форм
- Симметрия
- Практическая геометрия
- Измерение
- Обработка данных
Главная >
ML Aggarwal Solutions
Класс 6
Математика
>
Глава 10. Основные геометрические понятия
>
Базовая геометрическая концепция. Упражнение 10.
>
Вопрос 1
Основные геометрические понятия
>
Базовая геометрическая концепция. Упражнение 10.
>
Вопрос 1
Вопрос 1 Основные геометрические понятия Упражнение 10
Сколько прямых можно провести через две различные заданные точки?
Ответ:
Линия — это набор точек, которые неограниченно простираются в двух направлениях. У него есть только одно измерение — длина. Коллинеарные точки — это точки, лежащие на одной прямой.
Через две различные заданные точки можно провести только одну прямую.
Связанные вопросы
Сколько прямых можно провести через три точки, лежащие на одной прямой?
Отметьте в тетради три неколлинеарные точки А, В и С. Проведите прямые через эти точки, беря…
Используйте рисунок, чтобы назвать: (i) Пять точек (ii) Прямая линия (iii) Четыре луча (iv) Пять отрезков прямой
Используйте рисунок, чтобы назвать: (i) Прямую, содержащую точку E.


 Эту же плоскость можно обозначить как ABC
Эту же плоскость можно обозначить как ABC



 Значит предположение неверно, никакие три точки не лежат на одной прямой.
Значит предположение неверно, никакие три точки не лежат на одной прямой. Сколько существует таких плоскостей?
Сколько существует таких плоскостей?
Leave A Comment