ЭДС индукции. Примеры решения задач по физике. 10-11 класс
- Подробности
- Просмотров: 1114
Задачи по физике — это просто!
Не забываем, что решать задачи надо всегда в системе СИ!
А теперь к задачам!
Элементарные задачи из курса школьной физики на вычисление ЭДС индукции.
Задача 1
За время 5 мс в соленоиде, содержащем 500 витков провода, магнитный поток равномерно убывает от 7 мВб до 3 мВб.
Найдите ЭДС индукции в соленоиде.
Задача 2
Какой магнитный поток пронизывает каждый виток катушки, имеющей 1000 витков, если при равномерном исчезновении магнитного поля в течение 0,1 с в катушке индуцируется ЭДС равная 10 В ?
Задача 3
Виток проводника площадью 2 см2 расположен перпендикулярно вектору магнитной индукции.
Задача 4
В однородном
магнитном поле перпендикулярно к направлению вектора индукции , модуль которого 0,1 Тл, движется провод длиной 2 метра со скоростью 5 м/с, перпендикулярной проводнику.
Какая ЭДС индуцируется в этом проводнике?
Задача 5
Перпендикулярно вектору магнитной индукции перемещается проводник длиной 1,8 метра со скоростью 6 м/c. ЭДС индукции равна 1,44 В.
Найти магнитную индукцию магнитного поля.
Задача 6
Самолет имеет размах крыльев 15 метров. Горизонтальная скорость полета равна720 км/час.
Определить разность потенциалов, возникающих между концами крыльев. Вертикальная составляющая магнитной индукции (перпендикулярно поверхности Земли) равна 50 мкТл.
Задача 7
Магнитный поток через контур проводника сопротивлением 0,03 Ом за 2 секунды изменился на 0,012 Вб.
Найдите силу тока в проводнике если изменение потока происходило равномерно.
Задача 8
В однородном магнитном поле находится плоский виток площадью 10 см2, расположенный перпендикулярно вектору магнитной индукции.
Задача 9
Сопротивление замкнутого контура равно 0,5 Ом. При перемещении кольца в магнитном поле магнитный поток через кольцо изменился на 5×10-3 Вб.
Какой за это время прошел заряд через поперечное сечение проводника?
Магнитный поток и ЭДС индукции
Продолжаем решать задачи на магнитный поток и ЭДС индукции. Здесь уже будет потяжелее: придется и производную, и первообразную находить. Но задачи интересные, и даже геометрические знания пригодились, а именно, формула площади треугольника.
Задача  см
см , находится в однородном магнитном поле, индукция которого
, находится в однородном магнитном поле, индукция которого  Тл. Площадь контура за время
Тл. Площадь контура за время  c равномерно уменьшается до
c равномерно уменьшается до  см
см (плоскость контура при этом остается перпендикулярной магнитному полю). Определите силу тока (в мкА), протекающего по контуру в течение времени
(плоскость контура при этом остается перпендикулярной магнитному полю). Определите силу тока (в мкА), протекающего по контуру в течение времени  , если сопротивление контура
, если сопротивление контура  Ом.
Ом.
![Rendered by QuickLaTeX.com \[E=-\frac{\Delta \Phi}{\Delta t }\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-f54a0b8c1e483b4fa911275c90fb00f2_l3.png)
Поток уменьшился с  до
до  , его изменение
, его изменение  . Следовательно,
. Следовательно,
![Rendered by QuickLaTeX.com \[E =-\frac{ B(S_2-S_1)}{\Delta t }\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-88f22344a30da563ef0bb94d7abb48dd_l3.png)
Ток равен
![Rendered by QuickLaTeX.com \[I=\frac{E}{R}=\frac{ B(S_1-S_2)}{R\Delta t } =\frac{ 10^{-2} (10-2)\cdot10^{-4}}{1\cdot0,5}=16\cdot10^{-6}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-dac238668f64a1f0faaa3f6b69f88bc1_l3.png)
Ответ: 16 мкА
Задача 2. Медное кольцо радиусом  см из проволоки диаметром
см из проволоки диаметром  мм расположено в однородном магнитном поле, изменяющемся со скоростью
мм расположено в однородном магнитном поле, изменяющемся со скоростью  Тл/с. Плоскость кольца перпендикулярна силовым линиям магнитного поля. Определите силу индукционного тока, возникающего в кольце. Удельное сопротивление меди равно
Тл/с. Плоскость кольца перпендикулярна силовым линиям магнитного поля. Определите силу индукционного тока, возникающего в кольце. Удельное сопротивление меди равно  Ом
Ом м.
м.
Сопротивление кольца равно
![Rendered by QuickLaTeX.com \[R=\frac{\rho l}{S}=\frac{\rho \cdot2 \pi R}{\frac{\pi d^2}{4}}=\frac{8\rho R}{d^2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-daf76cbfc1cb2eaebca06b57f6aceef7_l3.png)
Ток в кольце будет равен
![Rendered by QuickLaTeX.com \[I=\frac{E}{R}=\frac{ \Delta \Phi}{R\Delta t } =\frac{\Delta B}{\Delta t}\cdot\frac{S}{R}=\frac{\Delta B}{\Delta t}\cdot \frac{\pi R^2 d^2}{8\rho}=0,2\cdot\frac{ \pi \cdot(0,15)^2\cdot(10^{-3})^2}{8\cdot1,7\cdot 10^{-8}}=0,693\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-3ab24d08ea36cc0583328f7d1675307a_l3.png)
Ответ: 0,693 А
Задача 3. При изменении силы тока в замкнутом контуре индуктивностью  Гн ЭДС самоиндукции изменялась согласно графику (см. рис.). Чему равна величина изменения тока в интервале времени 1-4 с?
Гн ЭДС самоиндукции изменялась согласно графику (см. рис.). Чему равна величина изменения тока в интервале времени 1-4 с?

К задаче 3
Так как
![Rendered by QuickLaTeX.com \[E=-L\frac{dI}{dt}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-75ff9d3d49a5001c7a8adbefc95bc7f4_l3.png)
То, чтобы найти ток, нужно найти интеграл. То есть – определить площадь под графиком с первой по 4 секунду. Площадь будет равна сумме площадей трапеции и прямоугольника: 3+8.
![Rendered by QuickLaTeX.com \[I=\int\limits_{1}^{4} \frac{E}{L}\, dt=\frac{11\cdot10^{-3}}{0,1}=0,11\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-08abc089a051c118c304ecdc0eed57d0_l3.png)
Ответ: 0,11 А
Задача 4. В однородном магнитном поле с индукцией В = 0,2 Тл начинает двигаться металлический стержень длиной  см перпендикулярно вектору магнитной индукции. Координата стержня изменяется по закону
см перпендикулярно вектору магнитной индукции. Координата стержня изменяется по закону  . Какая разность потенциалов возникает между концами стержня через 5 с?
. Какая разность потенциалов возникает между концами стержня через 5 с?
Скорость стержня к указанному моменту времени будет равна:
![Rendered by QuickLaTeX.com \[\upsilon=\frac{dx}{dt}=-3+4t=17\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-91517c625439a97b5c65d4cb64790471_l3.png)
Следовательно, ЭДС:
![Rendered by QuickLaTeX.com \[E=Bl\upsilon=0,2\cdot0,2\cdot17=0,68\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2435df5c221e2cfd5160b6c595f47366_l3.png)
Ответ: 0,68 В.
Задача 5. Проводящий квадратный контур со стороной  см, помещенный в однородное магнитное поле с индукцией В = 0,5 Тл, вектор которой перпендикулярен плоскости контура, складывают пополам (см. рис.). Какой заряд протечет по контуру, если сопротивление единицы длины контура равно
см, помещенный в однородное магнитное поле с индукцией В = 0,5 Тл, вектор которой перпендикулярен плоскости контура, складывают пополам (см. рис.). Какой заряд протечет по контуру, если сопротивление единицы длины контура равно  Ом/м?
Ом/м?

К задаче 5
Площадь контура, складывая его, уменьшают до нуля. Поэтому изменение потока равно  . Следовательно,
. Следовательно,
![Rendered by QuickLaTeX.com \[\frac{dq}{dt}\cdot R=\frac{d \Phi}{dt}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-554b057de677b5c01217106c7b6f6367_l3.png)
Откуда
![Rendered by QuickLaTeX.com \[dq=\frac{ d \Phi }{R}=\frac{\Delta \Phi }{R}=\frac{BS}{R}=\frac{Bl^2}{4lr}=\frac{0,5\cdot0,1}{4\cdot0,1}=0,125\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-020bdfab184fd77ab9852cc92e199a39_l3.png)
Ответ: 0,125 Кл.
Задача 6. Напряжение на зажимах рамки, начинающей вращаться в однородном магнитном поле, изменяется с течением времени согласно графику на рисунке. Чему приблизительно равна величина магнитного потока, пересекающего рамку в момент времени  с?
с?

К задаче 7
Напряжение на зажимах, или ЭДС, есть производная потока, поэтому поток – первообразная ЭДС. ЭДС, судя по графику, можно записать так:
![Rendered by QuickLaTeX.com \[E=U=-U_m \cos(\omega t)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-3f636afc7bc128c037f1e4f7383a9285_l3.png)
Период равен 4 с, тогда  . Амплитуда ЭДС равна 40 мВ, следовательно,
. Амплитуда ЭДС равна 40 мВ, следовательно,
![Rendered by QuickLaTeX.com \[E=-0,04 \cos(\frac{\pi t}{2})\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-f9c30d895fbac13ca7b01544ec48d95a_l3.png)
Определяем первообразную, то есть берем интеграл:
![Rendered by QuickLaTeX.com \[\Phi=\int\limits_{~}^{~} (-0,04 \cos(\frac{\pi t}{2}))\, dx=-0,04\frac{2}{\pi}\sin (\frac{\pi t}{2})\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a6a2178adab11739ed5a2655b95b8c76_l3.png)
Подставим нужное время:
![Rendered by QuickLaTeX.com \[\Phi=-0,04\frac{2}{\pi}\sin (\frac{\pi \cdot2,5}{2}))=-0,04\frac{2}{\pi}\cdot \left(-\frac{\sqrt{2}}{2}\right)=17,8\cdot10^{-3}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a06df7d5c65fc9a900589d58301f6f52_l3.png)
Ответ: 18 мВб.
Задача 7. Плоская проволочная рамка находится в магнитном поле, его плоскость перпендикулярна линиям индукции. При равномерном уменьшении магнитного поля до нуля за время  с в рамке возник постоянный ток
с в рамке возник постоянный ток  А. Какой ток
А. Какой ток  потечет по рамке при ее повороте в этом поле с постоянной угловой скоростью на угол
потечет по рамке при ее повороте в этом поле с постоянной угловой скоростью на угол  за время
за время  с вокруг оси, перпендикулярной вектору В и лежащей в плоскости рамки?
с вокруг оси, перпендикулярной вектору В и лежащей в плоскости рамки?
И в том, и в другом случае меняется поток через рамку. Но индукция поля остается неизменной, ее–то и надо найти:
![Rendered by QuickLaTeX.com \[I_1=\frac{\Delta \Phi_1}{Rt_1}=\frac{\Delta B S}{Rt_1}=\frac{B S}{Rt_1}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2ae8094cd6622c15ae6e2a5837f4b206_l3.png)
Откуда
![Rendered by QuickLaTeX.com \[B=\frac{ I_1Rt_1 }{S}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8aa3a2a508667bca47efe1bfce06497c_l3.png)
Если рамку повернуть, то изменится площадь, пронизываемая потоком:
![Rendered by QuickLaTeX.com \[S_2=S\cos{\alpha}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ebf1413314e66e4af12d86c08b8653ef_l3.png)
Тогда
![Rendered by QuickLaTeX.com \[I_2=\frac{\Delta \Phi_2}{Rt_2}=\frac{\Delta S B }{Rt_2}=\frac{B S\cos{\alpha}}{Rt_2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-cdb182a56f8ca6761d0829258dcb435f_l3.png)
Подставим индукцию, найденную ранее:
![Rendered by QuickLaTeX.com \[I_2=\frac{ S\cos{\alpha}}{Rt_2}\cdot \frac{ I_1Rt_1 }{S}=\frac{I_1t_1\cos{\alpha}}{t_2}=\frac{0,024\cdot2\cdot0,5}{4}=0,006\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b0537e12550adac28ec0e200ce92f6e2_l3.png)
Ответ: 6 мА.
Задача 8. Квадратная рамка со стороной  см помещена в однородное магнитное поле с индукцией
см помещена в однородное магнитное поле с индукцией  мТл так, что линии индукции перпендикулярны плоскости рамки (см. рис.). Сопротивление рамки 1 Ом. Какое количество тепла выделится в рамке за 10 с, если ее выдвигать из области, в которой создано поле со скоростью 1 см/с, перпендикулярной линиям индукции? Поле сосредоточено в некоторой четко ограниченной области.
мТл так, что линии индукции перпендикулярны плоскости рамки (см. рис.). Сопротивление рамки 1 Ом. Какое количество тепла выделится в рамке за 10 с, если ее выдвигать из области, в которой создано поле со скоростью 1 см/с, перпендикулярной линиям индукции? Поле сосредоточено в некоторой четко ограниченной области.

К задаче 8
Площадь рамки, помещенная в поле, будет изменяться. Поэтому поток меняется и в рамке наводится ЭДС.
![Rendered by QuickLaTeX.com \[E=Bl\upsilon\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-5b64c9507b07a80fcad547d3f78067ff_l3.png)
Ток будет равен:
![Rendered by QuickLaTeX.com \[I=\frac{E}{R}=\frac{ Bl\upsilon }{R}=\frac{0,1\cdot0,02\cdot 0,01}{1}=2\cdot10^{-5}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ab01e6f626c74af4d6d7abd68464a158_l3.png)
При протекании такого тока выделится количество теплоты
![Rendered by QuickLaTeX.com \[Q=I^2Rt=(2\cdot10^{-5})^2\cdot 1\cdot 10=8\cdot10^{-10}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-71c0819c65e812564bd710f1516af3f4_l3.png)
Ответ: 0,8 нДж
Задача 9. Квадратная рамка помещена в однородное магнитное поле. Нормаль к плоскости рамки составляет с направлением магнитного поля угол  . Сторона рамки
. Сторона рамки  см. Известно, что среднее значение ЭДС индукции, возникающей в рамке при выключении поля в течение времени
см. Известно, что среднее значение ЭДС индукции, возникающей в рамке при выключении поля в течение времени  с, равно 50 мВ. С какой силой подействовало бы это магнитное поле на протон, влетевший в него со скоростью
с, равно 50 мВ. С какой силой подействовало бы это магнитное поле на протон, влетевший в него со скоростью  м/с перпендикулярно вектору
м/с перпендикулярно вектору  ?
?
 . Следовательно,
. Следовательно,
![Rendered by QuickLaTeX.com \[E=\frac{\Delta\Phi}{\Delta t}=\frac{BS_r}{\Delta t }\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8b0f846e0a81f9a59ed558f9f638c3b9_l3.png)
Пронизываемая потоком площадь рамки равна
![Rendered by QuickLaTeX.com \[S_r=S\cos{\alpha}=L^2\cos{\alpha}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8bbca4d2f2e744f3b99235db2a2bcd24_l3.png)
Тогда
![Rendered by QuickLaTeX.com \[E=\frac{BL^2\cos{\alpha}}{\Delta t }\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-1b4459348dd0efeb29ee05f8606e3a76_l3.png)
Найдем из этого выражения индукцию поля:
![Rendered by QuickLaTeX.com \[B=\frac{E\Delta t }{ L^2\cos{\alpha}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a92eae5023a908373ce80270eb40b7c2_l3.png)
Сила Лоренца равна
![Rendered by QuickLaTeX.com \[F=B q \upsilon=\frac{E\Delta t q \upsilon }{ L^2\cos{\alpha}}=\frac{50\cdot10^{-3}\cdot0,01\cdot1,6\cdot10^{-19}\cdot10^4}{ (0,1)^2\cdot0,5}=1,6\cdot10^{-16}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-df4cc0e10f14aa4a4abb4f3fa1da690f_l3.png)
Ответ:  Н.
Н.
Задача 10. Рамка сопротивлением 15 Ом, имеющая форму равностороннего треугольника, помещена в однородное магнитное поле с индукцией  Тл. Плоскость рамки составляет с направлением вектора
Тл. Плоскость рамки составляет с направлением вектора  угол
угол  . Определите длину стороны рамки
. Определите длину стороны рамки  , если при равномерном уменьшении индукции В до нуля в течение
, если при равномерном уменьшении индукции В до нуля в течение  с в проводнике рамки выделяется количество тепла 0,5 мДж.
с в проводнике рамки выделяется количество тепла 0,5 мДж.
По закону Джоуля-Ленца
![Rendered by QuickLaTeX.com \[Q=I^2Rt\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-edea0d3a0e8be89363e774d449ad944d_l3.png)
Откуда
![Rendered by QuickLaTeX.com \[I=\sqrt{\frac{Q}{Rt}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-563efd2de4a6f5727d782c2666ac7fe3_l3.png)
По закону Ома  ,
,
![Rendered by QuickLaTeX.com \[E=\sqrt{\frac{QR}{t}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-e3407b6c3bafac6ca6517939de27846d_l3.png)
Площадь рамки равна  , площадь, пронизываемая потоком, равна
, площадь, пронизываемая потоком, равна
![Rendered by QuickLaTeX.com \[S_B=\frac{1}{2}a^2 \sin^2{\alpha}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-85be45b81a4d3b39878916cce3a8adf5_l3.png)
Тогда
![Rendered by QuickLaTeX.com \[E=\frac{BS}{t}=\frac{B}{2t}a^2 \sin^2{\alpha}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-4a8507d872fcbb56c080ba22df7c7aab_l3.png)
Откуда
![Rendered by QuickLaTeX.com \[a^2=\frac{2Et}{B\sin^2{\alpha}}=\frac{2\sqrt{QRt}}{B\sin^2{\alpha}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2f5f800fc77ac271b7a9c046a990023f_l3.png)
![Rendered by QuickLaTeX.com \[a=\frac{1}{\sin{\alpha}}\sqrt{\frac{2\sqrt{QRt}}{B}}=\frac{2}{\sqrt{3}}\sqrt{\frac{2\cdot\sqrt{0,5\cdot10^{-3}\cdot15\cdot0,03}}{0,04}}=1\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-72557b558c833fdcdc7ec4c1c13372a2_l3.png)
Ответ:  м.
м.
ЭДС индукции в движущихся проводниках
ЭДС – это аббревиатура трех слов: электродвижущая сила. ЭДС индукции () появляется в проводящем теле, которое находится в переменном магнитном поле. Если проводящим телом является, например, замкнутый контур, то в нем течет электрический ток, который называют током индукции.
Закон Фарадея для электромагнитной индукции
Основным законом, который используют при расчетах, связанных с электромагнитной индукцией является закон Фарадея. Он говорит о том, что электродвижущая сила электромагнитной индукции в контуре равна по величине и противоположна по знаку скорости изменения магнитного потока () сквозь поверхность, которую ограничивает рассматриваемый контур:
Закон Фарадея (1) записан для системы СИ. Надо учитывать, что из конца вектора нормали к контуру обход контура должен проходить против часовой стрелки. Если изменение потока происходит равномерно, то ЭДС индукции находят как:
Магнитный поток, который охватывает проводящий контур, может изменяться в связи с разными причинами. Это может быть и изменяющееся во времени магнитное поле и деформация самого контура, и перемещение контура в поле. Полная производная от магнитного потока по времени учитывает действие всех причин.
ЭДС индукции в движущемся проводнике
Допустим, что проводящий контур перемещается в постоянном магнитном поле. ЭДС индукции возникает во всех частях контура, которые пересекают силовые линии магнитного поля. При этом, результирующая ЭДС, появляющаяся в контуре будет равна алгебраической сумме ЭДС каждого участка. Возникновение ЭДС в рассматриваемом случае объясняют тем, что на любой свободный заряд, который движется вместе с проводником в магнитном поле, будет действовать сила Лоренца. При воздействии сил Лоренца заряды движутся и образуют в замкнутом проводнике ток индукции.
Рассмотри случай, когда в однородном магнитном поле находится прямоугольная проводящая рамка (рис.1). Одна сторона рамки может двигаться. Длина этой стороны равна l. Это и будет наш движущийся проводник. Определим, как можно вычислить ЭДС индукции, в нашем проводнике, если он перемещается со скоростью v. Величина индукции магнитного поля равна B. Плоскость рамки перпендикулярна вектору магнитной индукции. Выполняется условие .
ЭДС индукции в рассматриваемом нами контуре будет равна ЭДС, которая возникает только в подвижной его части. В стационарных частях контура в постоянном магнитном поле индукции нет.
Для нахождения ЭДС индукции в рамке воспользуемся основным законом (1). Но для начала определимся с магнитным потоком. По определению поток магнитной индукции равен:
где , так как по условию плоскость рамки перпендикулярна направлению вектора индукции поля, следовательно, нормаль к рамке и вектор индукции параллельны. Площадь, которую ограничивает рамка, выразим следующим образом:
где – расстояние, на которое перемещается движущийся проводник. Подставим выражение (2), с учетом (3) в закон Фарадея, получим:
где v – скорость движения подвижной стороны рамки по оси X.
Если угол между направлением вектора магнитной индукции () и вектором скорости движения проводника () составляет угол , то модуль ЭДС в проводнике можно вычислить при помощи формулы:
Примеры решения задач
Электромагнитная индукция – FIZI4KA

Явление электромагнитной индукции
Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
Опыты Фарадея
- На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
- Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
- Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.


Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.
Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Объяснения возникновения индукционного тока
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.
Свойства вихревого электрического поля:
- источник – переменное магнитное поле;
- обнаруживается по действию на заряд;
- не является потенциальным;
- линии поля замкнутые.
Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.
Магнитный поток
Магнитным потоком через площадь \( S \) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции \( B \), площади поверхности \( S \), пронизываемой данным потоком, и косинуса угла \( \alpha \) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):


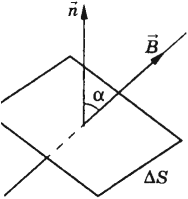

Обозначение – \( \Phi \), единица измерения в СИ – вебер (Вб).
Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м2, расположенную перпендикулярно вектору магнитной индукции:


Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла \( \alpha \) магнитный поток может быть положительным (\( \alpha \) < 90°) или отрицательным (\( \alpha \) > 90°). Если \( \alpha \) = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Закон электромагнитной индукции Фарадея
Закон электромагнитной индукции (закон Фарадея):
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:
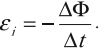
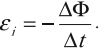
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из \( N \) витков, то ЭДС индукции:
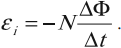
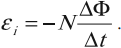
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением \( R \):
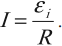
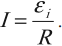
При движении проводника длиной \( l \) со скоростью \( v \) в постоянном однородном магнитном поле с индукцией \( \vec{B} \) ЭДС электромагнитной индукции равна:
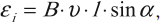
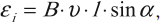
где \( \alpha \) – угол между векторами \( \vec{B} \) и \( \vec{v} \).
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
- вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Правило Ленца
Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Алгоритм решения задач с использованием правила Ленца:
- определить направление линий магнитной индукции внешнего магнитного поля;
- выяснить, как изменяется магнитный поток;
- определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
- по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.
Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
Самоиндукция
Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.
При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.
В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.
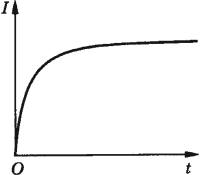

Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.
При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.
Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.
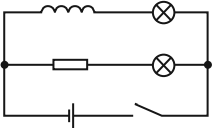

Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.
При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.
ЭДС самоиндукции \( \varepsilon_{is} \), возникающая в катушке с индуктивностью \( L \), по закону электромагнитной индукции равна:
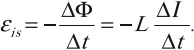
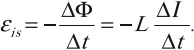
ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.
Индуктивность
Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток \( \Phi \) через контур из этого проводника пропорционален модулю индукции \( \vec{B} \) магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.
Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:
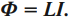
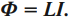
Индуктивность – коэффициент пропорциональности \( L \) между силой тока \( I \) в контуре и магнитным потоком \( \Phi \), создаваемым этим током:
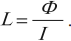
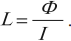
Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.
Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:
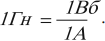
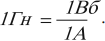
Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.
Энергия магнитного поля
При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.
Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:
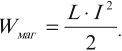
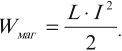
Основные формулы раздела «Электромагнитная индукция»


Алгоритм решения задач по теме «Электромагнитная индукция»:
1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.
2. Записать формулу:
- закона электромагнитной индукции;
- ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.
3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.
4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).
5. Решить полученную систему уравнений относительно искомой величины.
6. Решение проверить.
Электромагнитная индукция
3.7 (73.33%) 3 votesЭлектродвижущая сила индукции
Электрические токи порождают вокруг себя магнитные поля. Данная связь дала толчок к многочисленным попыткам создать электрический ток в контуре при помощи магнитного поля.
Данную задачу решил М. Фарадей в 1831 году. Ученый открыл явление электромагнитной индукции.
Электромагнитная индукция
Явление электромагнитной индукции заключается в том, что в замкнутом проводящем контуре, если изменяется поток магнитной индукции, который рассматриваемый контур охватывает, появляется электрический ток. Возникающий электрический ток называют током индукции.
Анализируя свои множественные эксперименты, М. Фарадей пришел к выводу о том, что:
- Индукционный ток появляется всегда при изменении магнитного потока, который охватывает проводящий контур. Так, если в однородном магнитном поле проводящий замкнутый контур повернуть, то в момент разворота в нем будет течь ток индукции. В этом случае индукция магнитного поля постоянна около проводящего контура, переменным является только поток магнитной индукции, который изменяется за счет изменения площади контура.
- Величина тока индукции не связана со способом изменения магнитного потока. Она определена только скоростью его изменения. Сила тока индукции тем больше, чем больше скорость перемещения магнита, или быстрота изменения силы тока, или скорость перемещения катушек.
Готовые работы на аналогичную тему
Электромагнитная индукция подтверждает связь между электрическими и магнитными явлениями.
Закон Фарадея
Анализируя данные своих экспериментов, М. Фарадей предложил количественный закон, описывающий электромагнитную индукцию. Ученый доказал, что каждый раз при изменении потока магнитной индукции, который сцеплен с проводящим контуром, в проводнике появляется ток индукции. Наличие индукционного тока означает то, что в цепи присутствует электродвижущая сила (ЭДС), которую в данном случае называют электродвижущей силой электромагнитной индукции ($Ɛ_i$).
Величина тока индукции, а значит, и величина $Ɛ_i$ зависит от скорости изменения магнитного потока:
$\left|Ɛ_{i} \right|=\frac{dФ}{dt}\left( 1 \right)$.
где $Ф$ — поток магнитной индукции.
Определимся со знаком ЭДС индукции. Знак потока магнитной индукции связан с выбором положительной нормали к рассматриваемому проводящему контуру. А направление силы тока и направление нормали связывает правило правого буравчика (винта). Получается, что фиксируя направление нормали, мы устанавливаем знак магнитного потока, направление тока и $Ɛ_i$ в контуре.
Сформулируем закон электромагнитной индукции Фарадея в окончательном виде:
Определение 1
Не зависимо от причины изменения магнитного потока, который охватывает замкнутый проводящий контур, электродвижущая сила индукции, появляющаяся в этом контуре равна:
$Ɛ_{i}=-\frac{dФ}{dt}\left( 2 \right)$.
где под $\frac{dФ}{dt}$ понимают полную скорость изменения потока магнитной индукции, охватываемого проводником.
Минус в формуле (2) указывает на то, что:
- При росте потока магнитной индукции (скорость изменения магнитного потока больше нуля) ($\frac{dФ}{dt}>0)$, ЭДС индукции меньше нуля ($Ɛ_i
- При уменьшении потока магнитной индукции (скорость изменения магнитного потока меньше нуля), ЭДС индукции больше нуля ($Ɛ_i>0$). Что значит, направление потока и направление поля тока индукции совпадают.
Замечание 1
Знак минус в формуле (2) – это математическое отображение правила Ленца, которое используют для того, чтобы найти направление тока индукции.
Закон Фарадея справедлив при:
- произвольных перемещениях замкнутого проводящего контура;
- при любых его деформациях;
- изменениях магнитного поля.
ЭДС индукции измеряется с Международной системе единиц (СИ) в вольтах (В).
$\left[ Ɛ_{i} \right]=\left[ \frac{dФ}{dt} \right]=\frac{Вб}{с}$=В.
Значение закона Фарадея
Закон Фарадея выражает новое физическое явление, в котором переменное магнитное поле порождает электрическое поле. Отсюда делается вывод о том, что электрическое поле может порождаться не только электрическими зарядами, но и изменяющимся магнитным полем.
Электромагнитная индукция – это всеобщий фундаментальный закон природы, реализующий связь между электрическими и магнитными полями.
Природа электродвижущей силы индукции
Если проводник перемещается в магнитном поле, то на свободные электроны его вещества действуют силы Лоренца. Эти электроны под воздействием названной силы приходят в движение относительно проводника, что означает: в проводнике появляется ток.
Рисунок 1. Проводники. Автор24 — интернет-биржа студенческих работ
Рассмотрим прямой участок $DG$ проводника на рис.1. Этот участок перемещается со скоростью $\vec v$ по проводникам $CK$ и $AL$, как по направляющим. При этом контур $AGDCA$ постоянно замкнут. Вектор индукции внешнего магнитного поля нормален плоскости рассматриваемого контура. Магнитное поле будем считать однородным. На заряды, которые перемещаются вместе с проводником, действует сила Лоренца, равная:
$\vec{F}_{L}=q\left( \vec{v}\times \vec{B} \right)\left( 3 \right)$.
где$ \vec{B}$– индукция внешнего магнитного поля. Под воздействием силы Лоренца свободные электроны проводника приходят в движение и образуют электрический ток. Направление этого тока принимают за положительный обход контура, положительная нормаль ($\vec n$) к площади контура указана на рис.1.
Наличие силы Лоренца эквивалентно тому, что в проводнике на заряды действует электрическое поле напряженность которого равна:
$\vec{E}=\frac{\vec{F}_{L}}{q}=\vec{v}\times \vec{B}\left( 4 \right)$.
Поэтому ЭДС индукции между точками 1 и 2 проводника найдем как:
$\left( Ɛ_{i} \right)_{21}=\int\limits_1^2 \vec{E} d\vec{l}=\int\limits_1^2\left( \vec{v}\times \vec{B} \right) d\vec{l}\left( 5 \right)$.
В случае, который мы рассматриваем на рис.1 точки 1 и 2 соответствуют точкам $D$ и $G$:
$\left( Ɛ_{i} \right)_{DG}=\int\limits_G^D {vBdl=vBl\, \left( 6 \right).} $
На не движущихся участках замкнутого контура, который мы рассматриваем, ЭДС не возникает. Следовательно, ЭДС контура равна ЭДС подвижного проводника $DG$, перемещающейся в магнитном поле.
$Ɛ_{i}=\int\limits_{AGDCA} {\vec{E}d\vec{l}=vBl\, \left( 7 \right).} $
Скорость перемещения проводника выразим как:
$v=\frac{dx}{dt}\left( 8 \right)$.
где $x$ — координата контактов проводника в точках $D$ и $G$ направляющими проводниками:
$Ɛ_{i}=Bl\frac{dx}{dt}\left( 9 \right)$.
Учитывая, что:
$Ф=-xlB$ (10),
где $Ф$ — поток магнитной индукции через поверхность, которую ограничивает контур $AGDCA$. Знак минус указывает на то, что направления векторов $\vec B$ и $ d\vec S$ противоположны,
окончательно имеем:
$Ɛ_{i}=-\frac{dФ}{dt}\left( 11 \right)$.
Выражение (11) мы получили, рассматривая движение части проводника. При перемещении нескольких участков проводника, ЭДС индукции находят как алгебраическую сумму ЭДС индукции, появляющихся на каждом участке.
ГБОУ ЦО №170
Колпинского района
Санкт-Петербурга
Итоговая контрольная работа
по физике
11 класс
Учитель Максимова Зоя Николаевна
2019
Пояснительная записка
Итоговая контрольная работа за курс физики 11 класса
Базовый уровень
Контрольная работа предполагает проверку знаний учащихся по всем темам курса физики11 класса на базовом уровне.
В работу включены задания по темам:
Тема курса физики 11 класса№№ заданий
Магнитное поле
1-3
Электромагнитная индукция.
4-6
Колебания и волны
7-9
Оптика
10-12
Излучения и спектры.
13-15
Физика атома и атомного ядра.
16-18
Выполнение контрольной работы рассчитано на два урока
Количество вариантов-2
Критерии оценивания:
«5»- 30б
«4» 24-29б
«3» 18-23 б
«2»- менее 18 б
Вариант№1
Длина активной части проводника 20 см. Угол между направлением тока и индукцией магнитного поля равен 900. С какой силой магнитное поле с индукцией 50мТл действует на проводник, если сила тока в нем 10 А?
Определите индуктивность катушки, которую при силе тока 6 А пронизывает магнитный поток 120мВб.
Установить соответствие:
А. Магнитный поток 1. Тл
Б. Магнитная индукция 2. Дж
В. Индуктивность 3. Гн
4. Вб
4. Один раз металлическое кольцо падает на стоящий вертикально полосовой магнит так, что надевается на него, второй раз так, что пролетает мимо него. Плоскость кольца в обоих случаях горизонтальна. Ток в кольце
| возникает в обоих случаях | ||
| 2) | не возникает ни в одном из случаев |
| 3) | возникает только в первом случае |
| 4) | возникает только во втором случае |
5. Найдите ЭДС индукции в контуре, если за 0,01с магнитный поток увеличился на 400 мВб.
6. Электромагнитная индукция – это:
1) явление, характеризующее действие магнитного поля на движущийся
заряд;
2) явление возникновения в замкнутом контуре электрического тока при
изменении магнитного потока;
3)явление, характеризующее действие магнитного поля на проводник с
током.
7. Математический маятник совершает свободные гармонические колебания. Какую величину можно определить, если известны длина l и период колебаний T маятника?
8. На рисунке показан график зависимости силы тока в металлическом проводнике от времени. Определите частоту колебаний тока.
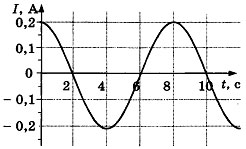
1) 8 Гц
2) 0,125 Гц
3) 6 Гц
4) 4 Гц
9. Расстояние между ближайшими гребнями волн 10м. Какова частота ударов волн о корпус, если скорость волн 3 м/с ?
10. Луч света падает на плоское зеркало. Угол отражения равен 24°. Угол между падающим лучом и зеркалом….
11. Если предмет находится от собирающей линзы на расстоянии больше двойного фокусного расстояния, то его изображение будет…
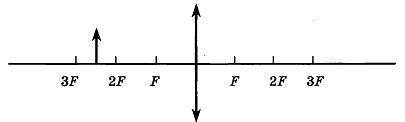
12. Какое оптическое явление объясняет радужную окраску мыльных пузырей?
1) Дисперсия 2) Дифракция 3) Интерференция 4) Поляризация
13. Непрерывные (сплошные) спектры дают тела, находящиеся
А. только в твердом состоянии при очень больших температурах;
Б. в газообразном молекулярном состоянии, в котором молекулы не связаны или слабо связаны
друг с другом;
В. в газообразном атомарном состоянии, в котором атомы практически не взаимодействуют
друг с другом;
Г. в твердом или жидком состоянии, а также сильно сжатые газы
14. Какое из перечисленных ниже электромагнитных излучений имеет наибольшую частоту?
А. Радиоволны.
Б. Инфракрасное излучение.
В. Видимое излучение.
Г. Ультрафиолетовое излучение.
Д. Рентгеновское излучение.
15. Какое из приведённых ниже выражений определяет понятие дисперсия?
А. Наложение когерентных волн.
Б. Разложение света в спектр при преломлении.
В. Преобразование естественного света в плоскополяризованный.
Г. Огибание волной препятствий.
Д. Частичное отражение света на разделе двух сред.
16. Написать недостающие обозначения в следующей ядерной реакции:
? +1H 1 = 12Mg24 + 2He4
17. Атом натрия 11Na23 содержит
11 протонов, 23 нейтрона и 34 электрона
2)
23 протона, 11 нейтронов и 11 электронов
3)
12 протонов, 11 нейтронов и 12 электронов
4)
11 протонов, 12 нейтронов и 11 электронов
18. Определите, какие из реакций называют термоядерными
А. Реакции деления легких ядер
Б. Реакции деления тяжелых ядер
В. Реакции синтеза между легкими ядрами
Г. Реакции синтеза между тяжелыми ядрами
Вариант№2
По катушке протекает ток, создающий магнитное поле энергией 5 Дж. Магнитный поток через катушку 10 Вб. Найти силу тока
Определите силу тока, проходящего по прямолинейному проводнику, перпендикулярному однородному магнитному полю, если на активную часть проводника длиной 10 см действует сила в 50 Н при магнитной индукции 20 Тл.
Установить соответствие:
А.Магнитная индукция 1. Гн
Б. Индуктивность 2. Тл
В. Магнитный поток 3. А
4. Вб
4. Один раз полосовой магнит падает сквозь неподвижное металлическое кольцо южным полюсом вниз, второй раз северным полюсом вниз. Ток в кольце| возникает в обоих случаях | ||
| 2) | не возникает ни в одном из случаев |
| 3) | возникает только в первом случае |
| 4) | возникает только во втором случае |
5. Чему равно изменение магнитного потока в контуре за 0,04с, если при этом возникла ЭДС индукции 8В?
6. Индукционный ток возникает в любом замкнутом проводящем контуре,
если:
1) Контур находится в однородном магнитном поле;
2) Контур движется поступательно в однородном магнитном поле;
3) Изменяется магнитный поток, пронизывающий контур.
7. Как изменится период малых колебаний математического маятника, если его длину увеличить в 4 раза?
увеличится в 4 раза 2) увеличится в 2 раза 3) уменьшится в 4 раза4) уменьшится в 2 раза8. На рисунке показан график зависимости силы тока в металлическом проводнике от времени. Определите амплитуду колебаний тока
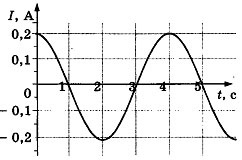
1) 0,4 А 2) 0,2 А 3) 0,25 А 4) 4 А
9. Динамик подключен к выходу звукового генератора. Частота колебаний 170 Гц. Определите длину звуковой волны в воздухе, зная, что скорость звуковой волны в воздухе 340 м/с.
10. Луч света падает на плоское зеркало. Угол отражения равен 12°. Угол между падающим лучом и зеркалом…
11. Расстояние от предмета до экрана, где получается четкое изображение предмета, 4 м. Изображения в 3 раза больше самого предмета. Найдите фокусное расстояние линзы.
12. Какое явление доказывает, что свет — это поперечная волна?
1) Дисперсия 2) Дифракция 3) Интерференция 4) Поляризация
13. Вещество в газообразном атомарном состоянии дает:
А. непрерывный спектр излучения Б. линейчатый спектр излучения
В. полосатый спектр излучения Г. сплошной спектр поглощения
Д.полосатый спектр поглощения
14. Спектральный анализ позволяет определить:
А. химический состав вещества; Б. скорость движения тела; В. объем тела;
Г. массу тела; Д. температуру тела; Е. давление воздуха.
15. Генератор ВЧ работает на частоте 150 МГц. Длина волны электромагнитного излучения равна…
16. Какое из трех типов излучений ( α-, β- или γ-излучение) обладает наибольшей проникающей способностью?
α -излучение
2)
β -излучение
3)
γ -излучение
4)
все примерно в одинаковой степени
17. Опыты Э. Резерфорда по рассеянию α-частиц показали, что
А. почти вся масса атома сосредоточена в ядре.
Б. ядро имеет положительный заряд.
Какое(-ие) из утверждений правильно(-ы)?
2)
только Б
3)
и А, и Б
4)
ни А, ни Б
18. Атом магния 12Mg24 содержит…
протонов-… ; нейтронов-….; электронов-…
Ответы :
Вариант №1 | Вариант №2 | ||
0,1Н | 1А | 3б | |
0,02 Гн(20мГн) | 25А | 3б | |
214 | 214 | 2б | |
3 | 1 | 1б | |
40В | 0,32 Вб | 2б | |
3 | 1б | ||
2 | 2 | 2б | |
0,125 Гц | 0,2А | 1б | |
0,3Гц | 2м | 2б | |
66ᵒ | 78ᵒ | 2б | |
Уменьшенным, обратным и действительным | 0,75м | 3б | |
1 | 4 | 1б | |
Г | Б | 1б | |
Д | А | 1б | |
Б | 2м | 2б | |
13Al | 3 | 1б | |
4 | 3 | 1б | |
В | 12; 12; !2 | 1б |
ЭДС индукции в движущихся проводниках формула
ЭДС индукции и сила Лоренца
Появление электродвижущей силы (ЭДС) в телах, перемещающихся в магнитном поле легко объяснить, если вспомнить о существовании силы Лоренца. Пусть стержень движется в однородном магнитном поле с индукцией рис.1. Пусть направление скорости движения стержня () и перпендикулярны друг другу.
Между точками 1 и 2 стержня индуцируется ЭДС, которая направлена от точки 1 к точке 2. Движение стержня – это перемещение положительных и отрицательных зарядов, которые входят в состав молекул этого тела. Заряды вместе с телом перемещаются в сторону движения стержня. Магнитное поле оказывает воздействие на заряды при помощи силы Лоренца, пытаясь переместить положительные заряды в сторону точки 2, а отрицательные заряды к противоположному концу стержня. Так, действие силы Лоренца порождает ЭДС индукции.
Если в магнитном поле движется металлический стержень, то положительные ионы, находясь в узлах кристаллической решетки, не могут двигаться вдоль стержня. При этом подвижные электроны скапливаются в избытке на конце стержня около точки 1. Противоположный конец стержня будет испытывать недостаток электронов. Появившееся напряжение определяет собой ЭДС индукции.
В том случае, если движущийся стержень сделан из диэлектрика, разделение зарядов при воздействии силы Лоренца, приводит к его поляризации.
ЭДС индукции будет равна нулю, если проводник перемещается параллельно направлению вектора (то есть угол между и равен нулю).
ЭДС индукции в прямом проводнике, движущемся в магнитном поле
Получим формулу для вычисления ЭДС индукции, которая возникает в прямолинейном проводнике, имеющем длину l, движущемся параллельно самому себе в магнитном поле (рис.2). Пусть v – мгновенная скорость проводника, тогда за время он опишет площадь равную:
При этом проводник пересечет все линии магнитной индукции, которые проходят через площадку . Получим, что изменение магнитного потока () сквозь контур в который входит перемещающийся проводник:
где – составляющая магнитной индукции, перпендикулярная к площадке . Подставим выражение для (2) в основной закон электромагнитной индукции:
получим:
При этом направление тока индукции определено законом Ленца. То есть индукционный ток имеет такое направление, что механическая сила, которая действует на проводник, замедляет перемещение проводника.
ЭДС индукции в плоском витке, вращающемся в магнитном поле
Если плоский виток вращается в однородном магнитном поле, угловая скорость его вращения равна , ось вращения находится в плоскости витка и , тогда ЭДС индукции можно найти как:
где S – площадь, которую ограничивает виток; – поток самоиндукции витка; – угловая скорость; () – угол поворота контура. Необходимо заметить, что выражение (5) справедливо, тогда, когда ось вращения составляет прямой угол с направлением вектора внешнего поля .
Если вращающаяся рамка имеет N витков и ее самоиндукцией можно пренебречь, то:
Примеры решения задач
Страница не найдена | MIT
Перейти к содержанию ↓- образование
- Исследовательская работа
- новаторство
- Прием + помощь
- Студенческая жизнь
- Новости
- Alumni
- О MIT
- Больше ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Alumni
- О MIT
Попробуйте поискать что-нибудь еще! Что вы ищете? Посмотреть больше результатов
Предложения или отзывы?
,ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯНа рисунке 32.1 показан стержень из проводящего материала, перемещаемый с скорость v в однородном магнитном поле B. Магнитная сила, действующая на свободную электрон в стержне будет направлен вверх и имеет величину, равную
(32.1)
Рисунок 32.1. Движущийся проводник в магнитном поле. В результате действия магнитной силы электроны начнут накапливаться в верхней части стержня. Распределение заряда стержня будет поэтому меняются, и в верхней части стержня будет избыток электронов (отрицательный заряд), а в нижней части стержня будет дефицит электронов (положительный заряд). Это распределение заряда создаст электрическое поле в жезл Напряженность этого электрического поля будет увеличиваться до электростатическая сила, создаваемая этим полем, равна по величине магнитная сила.В этот момент восходящий поток электронов прекратится и(32.2)
или
(32.3)
Индуцированное электрическое поле будет генерировать разность потенциалов, дельта В между концами стержня, равного
(32.4)
где L — длина стержня. Если концы стержня связаны с Схема, обеспечивающая обратный путь для накопленного заряда, стержень будет Источник ЭДС.Поскольку ЭДС связана с движением стержня через Магнитное поле называется , , ЭДС движения, , . Уравнение (32.4) показывает, что величина эдс пропорциональна скорости v. на рисунке 32.1 мы видим, что vL — это площадь, пройденная стержнем за второй. Величина BvL — это магнитный поток, проходящий через стержень за второй. Таким образом
(32,5)
Хотя эта формула была получена для особого случая, показанного на рисунке 32.1, это действует в общем. Держит стержни и проволоки произвольной формы, движущиеся через произвольные магнитные поля.
Уравнение (32.5) связывает индуцированную ЭДС со скоростью, с которой изменения магнитного потока. В системе, показанной на рисунке 32.1, поток изменения из-за движения стержня. Прилагаемый магнитный поток также может быть изменяется, если изменяется сила приложенного магнитного поля. В обоих случаях Результатом будет индуцированная ЭДС.Связь между индуцированной ЭДС и изменение магнитного потока известно как закон индукции Фарадея:
«Индуцированная ЭДС вдоль движущейся или изменяющейся математической траектории в константе или изменение магнитного поля равно скорости, с которой магнитный поток проникает через тропинка. «
Если мы рассмотрим замкнутый путь, закон Фарадея можно сформулировать следующим образом:
«Индуцированная ЭДС вокруг замкнутого математического пути в магнитном поле равна к скорости изменения магнитного потока, перехваченного областью в пределах дорожка «
или
(32.6)
Знак минус в уравнении (32.6) указывает, насколько полярность наведенной ЭДС связано со знаком потока и скоростью изменения потока. Знак поток устанавливается по правому правилу:
«Согните пальцы правой руки в том направлении, в котором мы находимся расчет ЭДС вокруг пути; магнитный поток будет положительным, если линии магнитного поля указывают в направлении большого пальца, а отрицательные в противном случае. «
Пример: проблема 32.13
Металлический стержень длиной L и массой m свободно скользит без трения, на двух параллельных металлических дорожках. Треки соединены на одном конце так, чтобы они и стержень образуют замкнутый контур (см. рисунок 32.2). Стержень имеет сопротивление R, и треки имеют незначительное сопротивление. Равномерное магнитное поле перпендикулярно плоскости этой цепи. Магнитное поле увеличивается с постоянной скоростью дБ / дт. Первоначально магнитное поле имеет напряженность B 0 , и стержень находится в состоянии покоя на расстоянии х 0 от соединенный конец рельсов.Выразите ускорение стержня в этом мгновенный с точки зрения заданных количеств.
Рисунок 32.2. Задача 32.13.Магнитный поток [Phi], окруженный стержнем и дорожками в момент времени t = 0 с, равен дается
(32,7)
Магнитное поле увеличивается с постоянной скоростью, и, следовательно, магнитный поток в замкнутом пространстве также увеличивается:
(32,8)
Закон индукции Фарадея теперь можно использовать для определения индуцированной ЭДС:
(32.9)
В результате наведенной ЭДС ток будет протекать через стержень с величина равна
(32.10)
Направление тока вдоль провода и, следовательно, перпендикулярно магнитное поле. Сила, приложенная магнитным полем к стержню, равна дается
(32.11)
(см. главу 31). Объединяя уравнения (32.10) и (32.11), получаем для силы на провод
(32.12)
Следовательно, ускорение стержня в момент времени t = 0 с равно
. (32.13)
Пример: проблема 32.12
а) Длинный соленоид имеет 300 витков провода на метр и имеет радиус 3,0 см Если ток в проводе увеличивается со скоростью 50 А / с, при чем скорость увеличивается сила магнитного поля в соленоиде?
б) Соленоид окружен катушкой со 120 витками.Радиус этого Катушка 6,0 см. Какая индуцированная ЭДС будет генерироваться в этой катушке, пока ток в соленоиде увеличивается?
а) Магнитное поле в соленоиде обсуждалось в главе 31. Если соленоид имеет n витков на метр, и если I — ток через каждую катушку, чем поле внутри соленоида равно
(32.14)
Следовательно,
(32.15)
В этой задаче n = 300 витков / метр и dI / dt = 50 А / с.Изменение в магнитное поле при этом равно
(32.16)
Это уравнение показывает, что магнитное поле увеличивается со скоростью 0,019 T / S.
б) Поскольку магнитное поле в соленоиде меняется, магнитный поток окруженный катушкой тоже изменится. Флюс, окруженный одиночная обмотка этой катушки
(32.17)
где r в = 3.0 см — это радиус соленоида. Здесь мы имеем Предполагается, что сила магнитного поля вне соленоида равна нулю. Общий поток, окруженный внешними катушками, равен
(32.18)
Скорость изменения магнитного потока за счет этого изменения магнитного поля составляет дается
(32.19)
В результате изменения тока в соленоиде будет индуцирована ЭДС во внешней катушке, со значением, равным
(32.20)
Если концы катушки соединены, ток будет течь через проводник. Направление тока в катушке можно определить с помощью закон Ленца , который гласит, что
«индуцированные ЭДС всегда имеют такую полярность, чтобы противостоять изменение, которое порождает их «Давайте применим закон Ленца к проблеме 32.12. Направление магнитного поля может быть определен с использованием правила правой руки и направлен вправо.Если ток в соленоиде увеличивает поток, также увеличивается. Электрический ток во внешней катушке будет течь в таком направлении, чтобы противостоять этому изменению. Это означает, что ток в этой катушке будет течь против часовой стрелки ( поле, создаваемое индуцированным током, направлено противоположно полю генерируется большим соленоидом).
Стержень, движущийся в магнитном поле, будет иметь индуцированную ЭДС в результате магнитная сила, действующая на свободные электроны.Индуцированная ЭДС будет пропорциональна линейной скорости v стержня. Если мы посмотрим на стержень с В системе отсчета, в которой стержень находится в состоянии покоя, магнитная сила будет равна нулю. Тем не менее, все еще должна быть индуцированная ЭДС. Так как этой эдс не может быть генерируется магнитным полем, это должно быть из-за электрического поля, которое существует в движущейся системе отсчета. Величина этого электрического поля должно быть таким, чтобы создавалась та же индуцированная эдс, что и в система отсчета, в которой движется стержень.Это требует, чтобы
(32.21)
Электрическое поле E ‘, которое существует в системе отсчета движущегося стержня, называется индуцированного электрического поля . ЭДС генерируется между Концы стержня равны
(32.22)
что эквивалентно уравнению (32.4). Если индуцированное электрическое поле находится в положении зависимый, то мы должны заменить уравнение (32.22) с интегральным выражением
(32.23)
где интеграл распространяется от одного конца стержня к другому концу стержень.
Разница между наведенным электрическим полем и электрическим полем генерируется распределением статического заряда в том, что в первом случае поле не является консервативным и интеграл по пути по замкнутому пути равен
(32.24)
который не равен нулю, если магнитный поток зависит от времени.
Изменяющийся ток в проводнике (например, в катушке) вызывает изменение магнитного поля. поле.Это зависящее от времени магнитное поле может вызвать ток в секунду проводник, если он находится в этом поле. ЭДС, индуцированная в эту секунду проводник, [эпсилон] 2 , будет зависеть от магнитного потока через него проводник:
(32.25)
Поток [Phi] B1 зависит от напряженности магнитного поля генерируется проводником 1 и, следовательно, пропорционально току Я 1 через этот проводник:
(32.26)
Здесь постоянная L 21 зависит от размера двух катушек, от их расстояние разноса и количество витков в каждой катушке. Постоянная L 21 называется взаимной индуктивностью двух катушек. Используя эту константу, уравнение (32.25) можно переписать как
(32.27)
Единицей индуктивности является Генри (H), и из уравнения (32.27) мы заключаем, что
(32.28)
Когда магнитное поле, создаваемое катушкой, изменяется (из-за изменения ток) магнитный поток, окруженный катушкой, также изменится. Это изменение в потоке будет вызывать ЭДС в катушке, а так как ЭДС вызвана изменением ток через катушку он называется самоиндуцированной ЭДС. ЭДС самоиндукции равна
(32.29)
В уравнении (32.29) L называется самоиндуктивности катушки.Самоиндуцированная ЭДС будет действовать в таком направлении, чтобы противостоять изменениям в ток.
Пример: проблема 32.32
Длинный соленоид радиуса R имеет n витков на единицу длины. Циркуляр Катушка провода радиуса R ‘с n’ витками окружает соленоид. Что взаимная индукция? Имеет ли значение катушка провода?
Предполагается, что поле внутри соленоида бесконечно длинное соленоид и имеет прочность, равную
(32.30)
Поток, окруженный внешней катушкой, равен
(32.31)
Индуцированная ЭДС во внешней катушке равна
(32.32)
Таким образом, взаимная индуктивность L 12 равна
. (32,33)
Если постоянный ток протекает через индуктор, не зависящий от времени магнитный поле создано.Если источник тока внезапно отключается, изменение в замкнутом магнитном потоке будет генерировать ЭДС самоиндукции, которая будет пытаться чтобы сохранить ток в первоначальном направлении. Электрическая энергия доставленный самоиндуцированной ЭДС первоначально был сохранен в индуктивности в форма магнитной энергии. Количество магнитной энергии, накопленной в магнитном поле может быть определено путем расчета полной мощности, передаваемой мощностью источник для создания магнитного поля.Предположим, что после батареи подключенный к индуктору ток увеличивается со скоростью dI / dt. ЭДС самоиндукции, созданная этим зависящим от времени током, равна
(32.34)
Ток должен доставлять дополнительную мощность, чтобы преодолеть эту самоиндуцированную ЭДС. требуемая мощность будет зависеть от времени и равна
(32,35)
Работа, проделанная током, сохраняется в индукторе в виде магнитной энергии. Изменение dU магнитной энергии индуктора при этом равно
(32.36)
Общая энергия, запасенная в магнитном поле индуктора при токе достигает своего конечного значения, можно получить интегрированием уравнения (32.36) между I = 0 и я = I f .
(32,37)
Для соленоида длины l самоиндукция равна
(32.38)
Магнитная энергия, накопленная в соленоиде, равна
(32.39)
где V — объем соленоида. Магнитная энергия может быть выражена в условия B и V:
(32.40)
где B = u 0 n I — магнитное поле в соленоиде. Общая Магнитная энергия индуктора теперь может быть выражена через плотность магнитной энергии u, которая определяется как
(32.41)
Магнитная энергия, запасенная в магнитном поле, равна плотности энергии время объем. Хотя мы вывели формулу для магнитной энергии плотность для частного случая очень длинного соленоида, его вывод действителен для любого произвольного магнитного поля.
Пример: проблема 32.46
Тороид квадратного сечения имеет внутренний радиус R 1 и внешний радиус R 2 .Тороид имеет N витков провода, несущего текущий я; предположим, что N очень большое.
а) Найти плотность магнитной энергии как функцию радиуса.
б) Интегрируя плотность энергии, найдите полную магнитную энергию, запасенную в соленоид.
в) Выведите самоиндуктивность из формулы U = L . I 2 /2.
а) Применим закон Ампера, используя сферическую амперовую петлю с радиусом r
(32.42)
Ток, заключенный в амперную петлю, равен
. (32,43)
Используя закон Ампера, мы можем определить магнитное поле B:
(32.44)
Плотность магнитной энергии при этом равна
(32.45)
б) Предположим, что высота тороида равна h. Посмотрите на кусочек тороид, показанный на рисунке 32.3.
Рисунок 32.3. Поперечное сечение тороида задачи 32.46. Объем dV этого среза равен(32,46)
Магнитная энергия, запасенная в этом сегменте, равна
(32.47)
Общая магнитная энергия, запасенная в тороиде, может быть получена путем интегрирования уравнение (32,47) относительно r между r = R 1 и r = R 2 :
(32.48)
в) Магнитная энергия, запасенная в индуктивности индуктивности L, равна 0.5 л Я 2 . Сравнивая это с уравнением (32.48), мы заключаем, что само индуктивность L тороида равна
(32,49)
Цепь RL состоит из резистора и индуктора, расположенных последовательно с батарея (см. рисунок 32.4). Применяя второе правило Кричхоффа к этому Для одноконтурной схемы получаем следующее дифференциальное уравнение
(32.50)
Рисунок 32.4. Схема RL. Это дифференциальное уравнение имеет решение(32,51)
Это решение действительно, если батарея подключена при t = 0. Уравнение (32.51) показывает, что ток при t = 0 с равен 0 и неуклонно растет, чтобы достичь конечное значение e / R при t = [бесконечность]. Постоянная времени цепи RL L / R. Если ток достиг стабильного значения и батарея внезапно отсоединенный, проводник может генерировать ток через резистор, который будет постепенно затухать как функция времени.Если начальный ток равен [эпсилон] / R, ток в момент времени t будет равен
(32,52)
Пример: проблема 32.54
То, что джоулево тепло рассеивается током в уравнении (32,52) в резистор во временном интервале между t = 0 и t = [бесконечность]? Сравнить с начальная магнитная энергия в индукторе.
Ток через резистор дается в уравнении (32.51).Мощность рассеивается по этому ток в резисторе равен
(32,53)
Полная энергия, рассеиваемая этим током в резисторе между t = 0 и t = [бесконечность] равно
(32,54)
Магнитная энергия, запасенная в индукторе, равна
(32,55)
и мы заключаем, что вся магнитная энергия, накопленная в индукторе, рассеивается как джоулева жара в резисторе.
Присылайте комментарии, вопросы и / или предложения по электронной почте [email protected] и / или посетите домашнюю страницу Фрэнка Вольфса. ,
Индуктивность
- Изучив этот раздел, вы сможете описать:
- • Единица индуктивности.
- • Факторы, влияющие на индуктивность.
- • Напряжение и e.m.f.
- • Самоиндукция.
- • Назад по.м.ф. и его последствия.
Индуктивность
Ток, генерируемый в проводнике изменяющимся магнитным полем, пропорционален скорости изменения магнитного поля.Этот эффект называется ИНДУКТИВНОСТЬЮ и обозначается символом L. Он измеряется в единицах, называемых Генри (H), названных в честь американского физика Джозефа Генри (1797-1878). Один генри — это величина индуктивности, необходимая для создания эдс 1 вольт в проводнике, когда ток в проводнике изменяется со скоростью 1 Ампер в секунду. Генри является довольно большой единицей для использования в электронике, с милли-генри (мГн) и микро-генри (мкГн), более распространенными. Эти единицы описывают одну тысячную и одну миллионную часть Генри соответственно.
Хотя Генри дается символ (заглавная буква) H — имя Генри, применительно к единице индуктивности используется строчная буква h. Генри во множественном числе могут быть генри или генри; Американский национальный институт стандартов и технологий рекомендует использовать в американских публикациях генри.
Факторы, влияющие на индуктивность.
Количество индуктивности в индуктивности зависит от:
- а. Количество витков провода в индуктивности.
- б.Материал ядра.
- гр. Форма и размер ядра.
- д. Форма, размер и расположение проволоки, из которой состоят катушки.
Поскольку индуктивность (в Генри) зависит от очень многих переменных величин, довольно трудно точно рассчитать; многочисленные формулы были разработаны для учета различных конструктивных особенностей. Кроме того, эти формулы часто должны использовать специальные константы и таблицы данных преобразования для работы с необходимой степенью точности.Использование компьютерных программ и автоматизированного проектирования несколько облегчило ситуацию. Однако внешние эффекты, вызванные другими компонентами и проводкой рядом с индуктором, также могут влиять на его значение индуктивности после его сборки в цепи, поэтому, когда требуется точное значение индуктивности, одним из подходов является расчет приблизительного значения и расчет индуктор, так что он регулируется.
Типичная формула для аппроксимации значения индуктивности индуктора приведена ниже.Эта конкретная версия предназначена для расчета индуктивности «соленоида, намотанного одним слоем витков бесконечно тонкой ленты, а не проволоки, и с витками, равномерно и близко расположенными».
Рис. 3.2.1 Миниатюрный переменный индуктор.
Где:
- L — индуктивность по Генри.
- d — диаметр катушки в метрах.
- n — число витков в катушке.
- l — длина катушки в метрах.
Для катушек, не соответствующих точно приведенным выше техническим требованиям, должны быть включены дополнительные факторы. На рис. 3.2.1 показан один из способов получения достаточно точной индуктивности, используемой в некоторых ВЧ и РЧ цепях. Миниатюрный индуктор намотан на пластиковую форму, в которую ввинчен ферритовый сердечник (железная пыль), чтобы обеспечить сердечник, дающий нужную индуктивность.
Напряжение и э.м.ф.
Напряжение , наведенное в проводник, называется e.m.f. (электродвижущая сила), потому что его источником является изменение магнитного поля вокруг и снаружи проводника. Любое внешнее напряжение (в том числе напряжение, создаваемое внешней батареей или источником питания) называется e.m.f., в то время как напряжение (разность потенциалов или внутреннее напряжение) на внутреннем компоненте в цепи называется напряжением.
Назад по э.ф.
Обратный e.m.f. (также называемый счетчиком e.m.f.) представляет собой ЭДС, создаваемую через индуктор изменяющимся магнитным потоком вокруг проводника, вызванным изменением тока в индуктивности.Его значение можно рассчитать по формуле:
Где:
- E — это индуцированная спина e.m.f. в вольтах
- L — индуктивность катушки в генри.
- ΔI — изменение тока в амперах.
- Δt — время, необходимое для изменения тока в секундах.
Примечания:
Δ (греч. D — дельта) обозначает разницу или изменение свойства.
Таким образом, формула описывает обратную ЭДС как зависящую от индуктивности (в Генри), умноженной на скорость изменения тока (в амперах в секунду).
Знак минус перед L указывает, что полярность индуцированной обратной эдс будет изменена по сравнению с изменяющимся напряжением на проводнике, которое первоначально вызывало изменяющийся ток и, следовательно, изменяющееся магнитное поле.
Помните, что при работе с практическими значениями в милли- или микрогенри все значения, используемые в формуле, должны быть преобразованы в стандартные значения ампер и секунд Генри, как описано в нашей брошюре «Советы по математике».
Пример
Поскольку значение обратной ЭДС зависит от скорости изменения тока, оно будет наибольшим, когда произойдет самое быстрое изменение.Например, скорость изменения чрезвычайно высока всякий раз, когда ток через индуктор отключается; тогда изменение может быть от максимума до нуля всего за несколько миллисекунд.
Представьте, что индуктор 200 мГн, подключенный к источнику питания 9 В, пропускает ток 2 А. Когда ток отключается, он падает до нуля через 10 мсек, что будет генерировать обратная эдс на катушке?
E = 200 мГн x 2A / 10 мс
или
E = 200 x 10 -3 x 2/10 x 10 -3
= 40 вольт
Таким образом, обратная ЭДС, генерируемая при выключении, более чем в 4 раза превышает напряжение питания!
Эти импульсы высокого напряжения, возникающие при отключении индуктивного элемента, такого как двигатель или катушка реле, могут привести к повреждению выходного транзистора или интегральной схемы, переключающей устройство.Поэтому существенная защита обеспечивается включением диода в выходной каскад, как показано на рис. 3.2.2 и 3.2.3
Защита от ЭМП
Рис. 3.2.2 Задняя часть Диод защиты.
Защитный диод на рис. 3.2.2, подключенный через индуктор, обычно имеет обратное смещение, так как напряжение на его катоде, подключенном к шине питания + V, будет более положительным, чем его анод на коллекторе транзистора. Однако при выключении большой скачок напряжения противоположной полярности появляется на катушке индуктивности из-за коллапсирующего магнитного поля.Во время этого скачка напряжения коллектор транзистора может иметь более высокий потенциал, чем источник питания, за исключением того, что если это произойдет, диод станет смещенным в прямом направлении и предотвратит повышение напряжения коллектора выше, чем шина питания.
Рис. 3.2.3 Защитные диоды в ULN2803.
На Рис. 3.2.3 показан популярный И.С. (ULN2803) для переключения индуктивных нагрузок. Выходы восьми инвертирующих усилителей каждый защищен диодом, общие катоды которого подключены к положительной шине питания + V на выводе 10.
Самоиндукция
То, как работает самоиндукция, зависит от двух взаимосвязанных действий, происходящих одновременно, и от каждого из этих действий в зависимости от другого.
Акция 1.
Любой проводник, в котором меняется ток, будет создавать вокруг себя изменяющееся магнитное поле.
Акция 2.
Любой проводник в ИЗМЕНЯЕМОМ магнитном поле будет иметь измененную ЭДС, индуцированную в него.Значение этой индуцированной ЭДС и величина индуцированного тока, который она производит в проводнике, будет зависеть от скорости изменения магнитного поля; чем быстрее изменяется поток поля, тем больше будет индуцированный э.м.ф. и его последующее течение.
Эффект индуктора, индуцирующего ЭДС в себя, называется самоиндукцией (но часто упоминается просто как Индукция). Когда индуктор индуцирует эдс в отдельный соседний индуктор, это называется взаимной индукцией и является свойством, используемым трансформаторами.
Изменяющееся магнитное поле, создаваемое вокруг проводника изменяющимся током в проводнике, вызывает изменение ЭДС на этом проводнике. Эта изменяющаяся ЭДС, в свою очередь, создает переменный ток, протекающий в направлении, противоположном исходному току. Следовательно, изменения в этом токе противодействуют изменениям в исходном токе.
Следовательно, действие действия 2 заключается в ограничении изменений, происходящих из-за действия 1. Если исходный ток увеличивается, индуцированный ток замедлит скорость увеличения.Точно так же, если исходный ток уменьшается, индуцированный ток замедлит скорость снижения. Общий результат этого заключается в уменьшении амплитуды переменного тока через индуктор, а также в уменьшении амплитуды переменного напряжения на индуктивности.
Поскольку сила магнитного поля, создаваемого исходным током, зависит от скорости (скорости) изменения тока, индуктор уменьшает поток переменного тока (AC) больше на высоких частотах, чем на низких.Этот ограничивающий эффект, создаваемый индуцированной ЭДС, будет больше на более высоких частотах, потому что на высоких частотах ток и, следовательно, поток изменяется быстрее. Название, данное этому эффекту, — Индуктивная реактивность.
Индуктивное сопротивление.
Reactance создает противодействие потоку переменного тока. Как и сопротивление, оно измеряется в омах, но поскольку сопротивление имеет одинаковое значение на любой частоте, а сопротивление переменному току в индуктивности изменяется в зависимости от частоты, его нельзя назвать сопротивлением.Вместо этого он называется Reactance (X). Конденсаторы также обладают свойством реактивного сопротивления, но они реагируют на частоту по-другому, поэтому существует два типа реактивного сопротивления; Индукторы имеют индуктивное сопротивление (X L ), а конденсаторы имеют емкостное сопротивление (X C ).
,Наука
- Анатомия и физиология
- астрономия
- астрофизика
- Биология
- Химия
- наука о планете Земля

Leave A Comment