ЧАРУЮЩИЕ ТАЙНЫ ЖИДКОСТИ | Наука и жизнь
Существует поразительная возможность овладеть предметом математически,
не понимая существа дела.
А. Эйнштейн
Эксперимент остается навсегда.
П. Л. Капица
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
‹
›
Открыть в полном размере
Тысячи лет люди наблюдают вечно изменчивое течение воды и пытаются разгадать ее тайну. Первоклассные физики и математики ломали и продолжают ломать головы, стараясь понять природу и прихотливое поведение потока воды. Но вступив в XXI век, мы с сожалением должны констатировать, что с конца XIX столетия — времени наивысшего расцвета науки о движении сплошных сред (гидродинамики в случае жидкости и аэродинамики в случае газа) — мы очень мало продвинулись в понимании природы этого вечно меняющегося течения.
ПОСТОЯНСТВО ПОТОКА МАССЫ ЖИДКОСТИ
Его еще называют законом неразрывности, законом непрерывности, уравнением сплошности жидкости или законом сохранения вещества в гидродинамике. По существу, этот закон был открыт Б. Кастелли в 1628 году. Он установил, что скорость течения жидкости в трубах обратно пропорциональна площади их поперечного сечения. Другими словами, чем уже сечение канала, тем с большей скоростью движется в нем жидкость.
ВЯЗКОСТЬ ЖИДКОСТИ
И. Ньютон (конец XVII века) экспериментально установил, что любой жидкости свойственна вязкость, то есть внутреннее трение. Вязкость приводит к возникновению сил трения между движущимися с различными скоростями слоями жидкости, а также между жидкостью и омываемым ею телом.
Им же было установлено, что сила трения пропорциональна коэффициенту вязкости жидкости и градиенту (перепаду) скорости потока в направлении, перпендикулярном его движению. Жидкости, подчиняющиеся этому закону, называют ньютоновскими в отличие от неньютоновских жидкостей, у которых зависимость между силой вязкого трения и скоростью жидкости имеет более сложный характер.
В силу вязкого трения скорость жидкости на поверхности омываемого ею тела всегда равна нулю. Это совсем не очевидно, но тем не менее подтверждается во множестве экспериментов.
Опыт. Убедимся, что скорость газа на поверхности обдуваемого им тела равна нулю.
Возьмем вентилятор и припудрим его лопасти пылью. Включим вентилятор в сеть и через несколько минут выключим. Пыль на лопастях как была, так и осталась, хотя вентилятор вращался с довольно большой скоростью и она должна была бы слететь.
Омывая лопасти вентилятора с большой скоростью, поток воздуха на их поверхности имеет нулевую скорость, то есть неподвижен.
Поэтому пыль на них и остается. По этой же причине с гладкой поверхности стола легко можно сдуть крошки, а пыль приходится вытирать.
#1# ИЗМЕНЕНИЕ ДАВЛЕНИЯ ЖИДКОСТИ В ЗАВИСИМОСТИ ОТ СКОРОСТИ ЕЕ ДВИЖЕНИЯ.
Д. Бернулли в своей книге «Гидродинамика» (1738) получил для идеальной жидкости, не обладающей вязкостью, математическую формулировку закона сохранения энергии в жидкости, который носит теперь название уравнения Бернулли. Оно связывает давление в потоке жидкости с ее скоростью и утверждает, что давление жидкости при ее движении меньше там, где сечение потока
#13#
Это уравнение играет фундаментальную роль в гидродинамике, несмотря на то, что оно, строго говоря, справедливо только для идеальной, то есть не имеющей вязкости, жидкости.
#2#
Опыт 1. Убедимся, что чем выше скорость воздуха, тем меньше давление в нем.
Зажжем свечу и через тонкую трубочку, например для коктейля, сильно дунем в нее так, чтобы струйка воздуха прошла примерно на расстоянии 2 см от пламени. Пламя свечи отклонится по направлению к трубочке, хотя на первый взгляд кажется, что воздух должен если и не задуть его, то по крайней мере отклонить в противоположную сторону.
Почему? Согласно уравнению Бернулли, чем выше скорость потока, тем меньше давление в нем. Воздух выходит из трубочки с большой скоростью, так что давление в струе воздуха меньше, чем в окружающем свечу неподвижном воздухе. Перепад давления при этом направлен в сторону выходящего из трубочки воздуха, что и отклоняет к ней пламя свечи.
#4#
Принцип работы пульверизатора: атмосферное давление выжимает жидкость в струю воздуха, где давление ниже.
На этом принципе работают пульверизаторы, струйные насосы и автомобильные карбюраторы: жидкость втягивается в поток воздуха, давление в котором ниже атмосферного.
Опыт 2. Возьмем лист писчей бумаги за верхние края, поднесем его к стене и удержим на расстоянии примерно 3-5 см от стены. Подуем в промежуток между стеной и листом. Вместо того, чтобы отклониться от стенки, лист прижимается к ней за счет силы, которую может создавать только возникший перепад давления, направленный к стене. Значит, давление в струе воздуха между листом и стеной меньше, чем в неподвижном воздухе снаружи. Чем сильнее дуть в промежуток, тем плотнее будет прижиматься листок к стене.
#5#
Уравнение Бернулли объясняет также классический опыт с трубой переменного сечения. В силу закона неразрывности для сохранения потока массы жидкости в суженной части трубы ее скорость должна быть выше, чем в широкой. Следовательно, давление выше там, где труба шире, и ниже там, где она уже.
На этом принципе работает устройство для измерения скорости или расхода жидкости — трубка Вентури.
Падение внутреннего давления в потоке — хорошо проверенный экспериментальный факт, тем не менее он, вообще говоря, парадоксален. Действительно, интуитивно ясно, что жидкость, «протискиваясь» из широкой части трубы в узкую, «сжимается», а это должно привести к росту давления в ней. Такому поведению жидкости в настоящее время нет объяснения даже на молекулярном уровне, по крайней мере, автор его нигде не обнаружил.
#6# СОПРОТИВЛЕНИЕ, ИСПЫТЫВАЕМОЕ ТЕЛОМ ПРИ ДВИЖЕНИИ В ЖИДКОСТИ
Существование сопротивления среды было обнаружено еще Леонардо да Винчи в XV столетии. Мысль, что сопротивление жидкости движению тела пропорционально скорости тела, впервые высказал английский ученый Дж. Уиллис. Ньютон во втором издании своей знаменитой книги «Математические начала натуральной философии» установил, что сопротивление состоит из двух членов, одного — пропорционального квадрату скорости и другого — пропорционального скорости.
Необходимо отметить, что сопротивление жидкости движущемуся в нем телу в значительной мере обусловливается именно наличием вязкости. В идеальной жидкости, в которой вязкость отсутствует, сопротивление вообще не возникает.
Опыт 1. Посмотрим, как возникает сопротивление движущегося в жидкости тела. Хотя в опыте тело неподвижно, а движется воздух, результата это не меняет. Какая разница, что движется — тело в воздухе или воздух относительно неподвижного тела?
#7#
Возьмем свечу и коробок спичек. Зажжем свечу, поставим перед ней на расстоянии примерно 3 см коробок и сильно дунем на него.
Пламя свечи отклоняется к коробку. Это означает, что позади коробка давление стало меньше, чем позади свечи, и разность давлений направлена по движению потока воздуха. Следовательно, тело при движении в воздухе или жидкости испытывает торможение.
Поток воздуха набегает на переднюю поверхность коробка, огибает его по краям и не смыкается позади, а отрывается от препятствия. Поскольку давление воздуха меньше там, где его скорость выше, давление по краям коробка меньше, чем позади него, где воздух неподвижен. Позади коробка возникает разность давлений, направленная от центра к его краям. В результате воздух за коробком устремляется к его краям, образуя завихрения, что и приводит к уменьшению давления.
Сопротивление зависит от скорости движения тела в жидкости, свойств жидкости, формы тела и его размеров. Важную роль в создании сопротивления играет форма задней стороны движущегося тела. Позади плоского тела возникает пониженное давление, поэтому сопротивление можно уменьшить, предотвратив срыв потока.
Для этого телу придают обтекаемую форму. Поток плавно огибает тело и смыкается непосредственно за ним, не создавая области пониженного давления.
Опыт 2. Чтобы продемонстрировать различный характер обтекания, а следовательно, и сопротивле ния тел различной формы, возьмем шар, например мяч для пинг-понга или тенниса, приклеим к нему бумажный конус и поставим за ним горящую свечу.
#8#
Повернем тело шариком к себе и подуем на него. Пламя отклонится от тела. Теперь повернем тело к себе острым концом и снова подуем. Пламя отклоняется к телу. Этот опыт показывает, что форма задней поверхности тела определяет направление перепада давления позади нее, а следовательно , и сопротивление тела в потоке воздуха.
В первом опыте пламя отклоняется от тела; это означает, что перепад давления направлен по потоку. Струя воздуха плавно обтекает тело, смыкается за ним и далее движется обычной струей, которая отклоняет пламя свечи назад и может даже задуть его.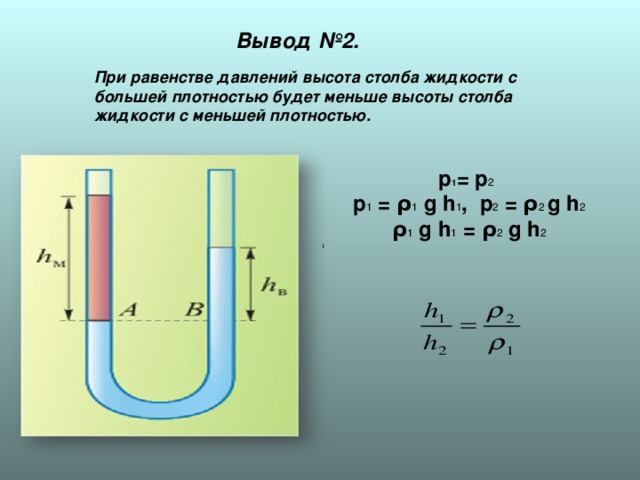
Во втором опыте пламя отклоняется к телу — как и в эксперименте с коробком, позади тела создается разрежение, перепад давления направлен против потока. Следовательно, в первом опыте сопротивление тела меньше, чем во втором.
ПАДЕНИЕ ДАВЛЕНИЯ В ВЯЗКОЙ ЖИДКОСТИ ПРИ ЕЕ ДВИЖЕНИИ В ТРУБЕ ПОСТОЯННОГО СЕЧЕНИЯ
Опыт показывает, что давление в жидкости, текущей по трубе постоянного сечения, падает вдоль трубы по течению: чем дальше от начала трубы, тем оно ниже. Чем уже труба, тем сильнее падает давление. Это объясняется наличием вязкой силы трения между потоком жидкости и стенками трубы.
Опыт. Возьмем резиновую или пластиковую трубку постоянного сечения и такого диаметра, чтобы ее можно было насадить на носик водопроводного крана. Сделаем в трубке два отверстия и откроем воду. Из отверстий начнут бить фонтанчики, причем высота ближнего к крану фонтанчика будет заметно выше, чем расположенного дальше по потоку. Это показывает, что давление воды в ближайшем к крану отверстии выше, чем в дальнем: оно падает вдоль трубы в направлении потока.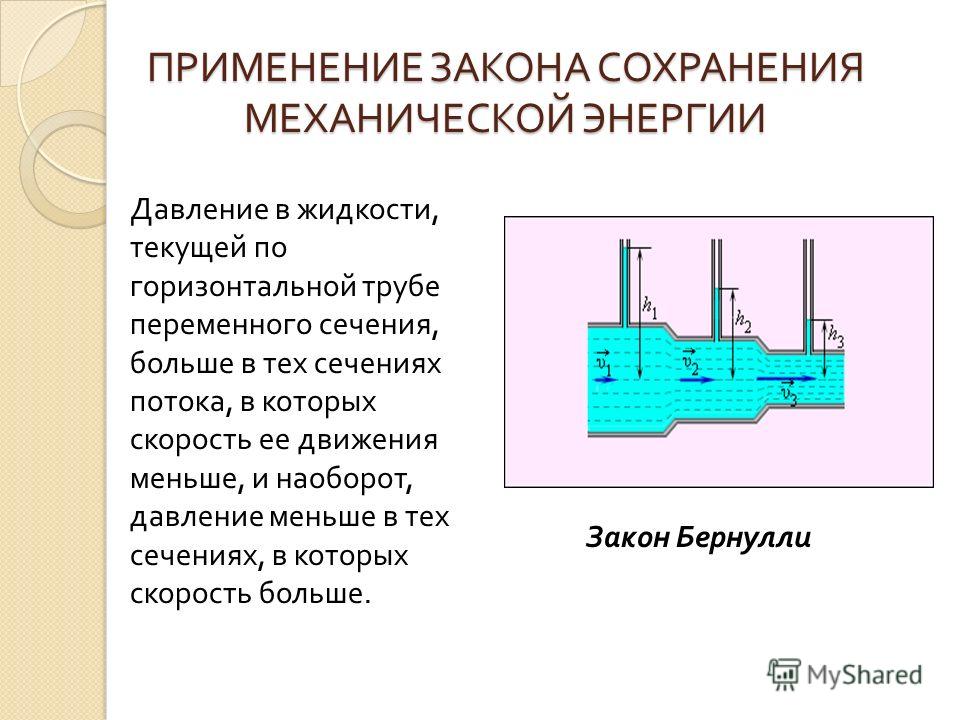
#9#
Объяснение этого явления на молекулярном уровне автору не известно. Поэтому приведем классическое объяснение. Выделим в жидкости маленький объем, ограниченный стенками трубки и двумя сечениями слева и справа. Так как жидкость течет по трубке равномерно, то разность давлений слева и справа от выделенного объема должна быть уравновешена силами трения между жидкостью и стенками трубки. Следовательно, давление справа, в направлении потока жидкости, будет меньше давления слева. Отсюда заключаем, что давление жидкости уменьшается в направлении течения воды.
На первый взгляд приведенное объяснение удовлетворительно. Однако возникают вопросы, ответа на которые пока нет.
1. Согласно уравнению Бернулли, уменьшение давления в жидкости при ее движении вдоль трубы должно означать, что скорость ее, наоборот, должна расти вдоль потока, то есть течение жидкости должно ускоряться. Но этого не может быть в силу закона неразрывности.
2. Силы трения между стенками трубы и жидкостью должны в принципе тормозить ее. Если это так, то при торможении скорость жидкости вдоль канала должна падать, что в свою очередь приведет к росту давления в ней по потоку. Однако внешнее давление, прокачивающее жидкость по трубе, компенсирует силы трения, заставляя жидкость течь равномерно с одинаковой по всему каналу скоростью. А раз так, то и давление жидкости вдоль канала должно быть везде одинаковым.
Итак, налицо экспериментальный факт, который легко проверить, однако объяснение его остается открытым.
ЭФФЕКТ МАГНУСА
Речь идет о возникновении силы, перпендикулярной потоку жидкости при обтекании ею вращающегося тела. Этот эффект был обнаружен и объяснен Г. Г. Магнусом (около середины XIX столетия) при изучении полета вращающихся артиллерийских снарядов и их отклонения от цели. Эффект Магнуса состоит в следующем. При вращении летящего тела близлежащие слои жидкости (воздуха) увлекаются им и также получают вращение вокруг тела, то есть начинают циркулировать вокруг него.
Встречный поток рассекается телом на две части. Одна часть направлена в ту же сторону, что и циркулирующий вокруг тела поток; при этом происходит сложение скоростей набегающего и циркулирующего потоков, значит, давление в этой части потока уменьшается. Другая часть потока направлена в сторону, противоположную циркуляции, и здесь результирующая скорость потока падает, что приводит к увеличению давления. Разность давлений с обеих сторон вращающегося тела и создает силу, которая перпендикулярна к направлению встречного, набегающего потока жидкости (воздуха).
#10#
Опыт. Склеим из листа плотной бумаги цилиндр. Из доски, положенной одним краем на стопку книг, сделаем на столе наклонную плоскость и положим на нее цилиндр. Скатившись, он вроде бы должен дальше двигаться по параболе и упасть дальше от края. Однако вопреки ожидаемому траектория его движения загибается в другую сторону, и цилиндр залетает под стол. Все дело в том, что он не просто падает, а еще и вращается, создавая вокруг себя циркуляцию воздуха.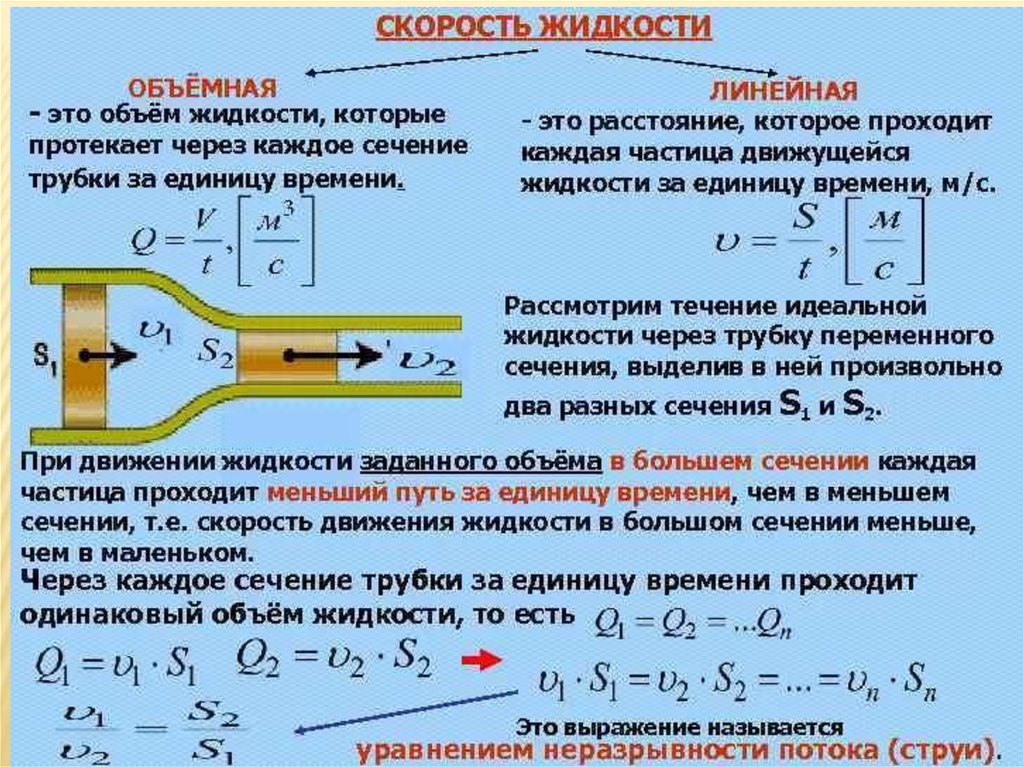
Возникает избыточное давление, направленное в сторону, противоположную поступательному движению цилиндра.
#11#
Эффект Магнуса позволяет игрокам в пинг-понг и теннис отбивать «крученые» мячи, а футболистам — посылать «сухой лист», ударяя мяч по краю.
ЛАМИНАРНЫЙ И ТУРБУЛЕНТНЫЙ ПОТОКИ
Опыт обнаруживает две совершенно разные картины движения жидкости. При низких скоростях наблюдается спокойное, слоистое течение, которое называется ламинарным. При больших скоростях течение становится хаотическим, частицы и отдельные области жидкости движутся беспорядочно, закручиваясь в вихри; такое течение называется турбулентным. Переход от ламинарного течения к турбулентному и обратно осуществляется при определенной скорости жидкости и зависит также от вязкости и плотности жидкости и характерного размера обтекаемого жидкостью тела. До сих пор не ясно, возникают ли вихри с самого начала и имеют просто очень малые размеры, не видимые нами, или вихри возникают начиная с некоторой скорости движения жидкости.
Опыт. Посмотрим, как происходит переход ламинарного потока в турбулентный. Откроем кран и пустим воду сначала тоненькой струйкой, а потом все сильнее и сильнее (конечно, так, чтобы не затопить соседей). Тоненькая струйка движется плавно и спокойно. По мере того, как увеличивается напор воды, скорость струи растет, и, начиная с некоторого момента, вода в ней начинает закручиваться — возникают вихри. Появляясь сначала только в ограниченной области струи, с ростом напора вихри в конце концов охватывают все течение — оно становится турбулентным.
#12# Струя воды падает в поле тяжести, испытывая ускорение. Как только скорость течения возрастает настолько, что число Рейнольдса превышает критическое значение, ламинарное течение (вверху) переходит в турбулентное. Для данного течения Re»2300.
Оценить скорость течения жидкости или газа, при которой возникает турбулентность, можно при помощи так называемого числа Рейнольдса Re = ρvl/μ, где ρ — плотность жидкости или газа, μ — их вязкость (вязкость воздуха, например, 18,5.
10-6 Па.с; воды — 8,2.10-2 Па.с), v — скорость потока, l — характерный линейный размер (диаметр трубы, длина обтекаемого тела и пр.). Для каждого вида течений существует такая критическая величина Reкр, что при Re<Reкр возможно только ламинарное течение, а при Re>Reкр оно может стать турбулентым. Если измерить скорость течения воды из крана или вдоль желоба, то, исходя из приведенных значений, можно самим определить, при каком значении Reкр в потоке начинает развиваться турбулентность. Оно должно быть порядка 2000.
Физика. 8 класс
Физика. 8 класс
ОглавлениеГлава 1. Общие сведения о движении§ 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ. МАТЕРИАЛЬНАЯ ТОЧКА § 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА) В ПРОСТРАНСТВЕ § 3. ПЕРЕМЕЩЕНИЕ § 4. ПОНЯТИЕ О ВЕКТОРАХ. ВЕКТОР ПЕРЕМЕЩЕНИЯ. КООРДИНАТЫ ТЕЛА § 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ § 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ § 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР § 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ § 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ § 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ § 11.  ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ (ПРОДОЛЖЕНИЕ)§ 12. ЕДИНИЦЫ ИЗМЕРЕНИЙ ДЛИНЫ И ВРЕМЕНИ Глава 2. Прямолинейное неравномерное движение § 13. СРЕДНЯЯ СКОРОСТЬ § 14. МГНОВЕННАЯ СКОРОСТЬ § 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ § 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ § 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ § 18. СРЕДНЯЯ СКОРОСТЬ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ И СКОРОСТЬЮ § 19. ИЗМЕРЕНИЕ УСКОРЕНИЯ § 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ § 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ Глава 3. Криволинейное движение § 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ § 23. УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ § 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ § 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ § 26. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА § 27. ОБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА Динамика Глава 4. Законы движения § 28. ТЕЛА И ИХ ОКРУЖЕНИЕ. ПЕРВЫЙ ЗАКОН НЬЮТОНА § 29.  ПОЧЕМУ ВОЗНИКАЮТ УСКОРЕНИЯ§ 30. ВЗАИМОДЕЙСТВИЕ TEЛ. УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ § 31. ИНЕРТНОСТЬ ТЕЛ § 32. МАССА ТЕЛ § 33. МАССА ЛУНЫ § 34. СИЛА § 35. ВТОРОЙ ЗАКОН НЬЮТОНА § 36. ВТОРОЙ ЗАКОН НЬЮТОНА (продолжение) § 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР § 38. ТРЕТИЙ ЗАКОН НЬЮТОНА § 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА Глава 5. Силы природы § 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ § 41. СИЛА УПРУГОСТИ § 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ § 43. ПОСТОЯННАЯ ВСЕМИРНОГО ТЯГОТЕНИЯ § 44. СИЛА ТЯЖЕСТИ § 45. ВЕС ТЕЛ § 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ § 47. МАССА ЗЕМЛИ § 48. СИЛА ТРЕНИЯ. ТРЕНИЕ ПОКОЯ § 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ § 50. СИЛА СОПРОТИВЛЕНИЯ, ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА В ЖИДКОСТИ ИЛИ В ГАЗЕ Глава 6. Применение законов движения § 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ УПРУГОСТИ § 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ ТЯЖЕСТИ § 53. ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ § 54.  НЕВЕСОМОСТЬ§ 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ § 56. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ГОРИЗОНТАЛЬНО § 57. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ § 58. ДВИЖЕНИЕ ПЛАНЕТ § 59. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ ТРЕНИЯ § 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ § 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ ИЛИ В ЖИДКОСТИ § 62. НАКЛОН ТЕЛ ПРИ ДВИЖЕНИИ НА ПОВОРОТАХ § 63. ПРИ КАКИХ УСЛОВИЯХ ТЕЛА ДВИЖУТСЯ ПОСТУПАТЕЛЬНО? ЦЕНТР МАСС И ЦЕНТР ТЯЖЕСТИ § 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА Равновесие тел Глава 7. Элементы статики § 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ § 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ § 67. ПРАВИЛО МОМЕНТОВ § 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ § 69. РАВНОВЕСИЕ ТЕЛ НА ОПОРАХ Законы сохранения в механике Глава 8. Закон сохранения импульса § 70. СИЛА И ИМПУЛЬС § 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА § 72. 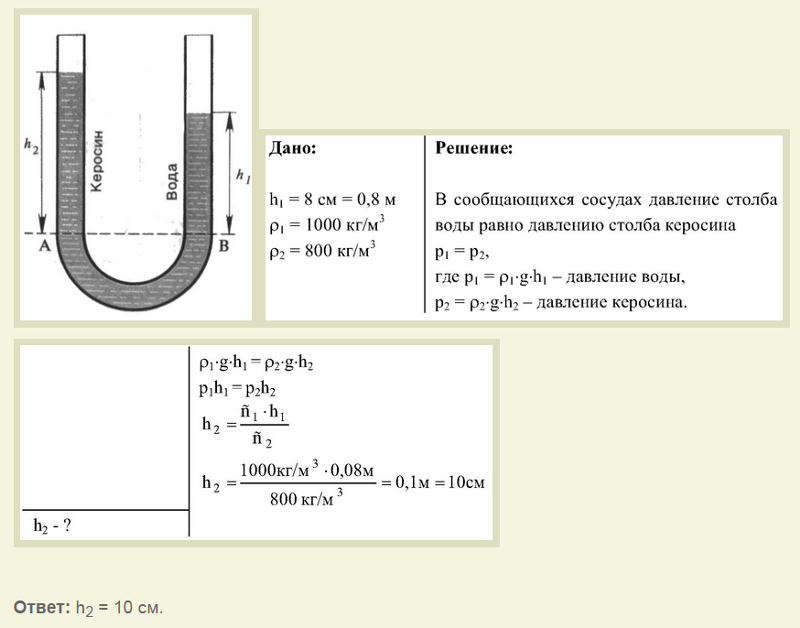 РЕАКТИВНОЕ ДВИЖЕНИЕГлава 9. Механическая работа и мощность § 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ КАК ПРОИЗВЕДЕНИЕ § 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ § 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ, РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ § 77. РАБОТА СИЛЫ ТЯЖЕСТИ § 78. РАБОТА СИЛЫ УПРУГОСТИ § 79. РАБОТА СИЛЫ ТРЕНИЯ § 80. МОЩНОСТЬ Глава 10. Закон сохранения энергии § 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ § 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ § 84. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГО ДЕФОРМИРОВАННОГО ТЕЛА § 85. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ТЕЛА, НАХОДЯЩЕГОСЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ § 36. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ § 87. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ § 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И СИЛА ТРЕНИЯ § 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ И ИСПОЛЬЗОВАНИЕ МАШИН § 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ § 91. СТОЛКНОВЕНИЕ ТЕЛ § 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ЗАКОН БЕРНУЛЛИ § 93. О ЗНАЧЕНИИ ЗАКОНОВ СОХРАНЕНИЯ Заключение Лабораторные работы 1.  Определение ускорения тела при равноускоренном движении2. Определение коэффициента трения скольжения 3. Изучение движения тела по параболе 4. Выяснение условия равновесия рычага 5. Определение центра тяжести плоской пластины Ответы к упражнениям |
— М.: Просвещение, 1973. — 256 с.
Более высокое давление в шинах НЕ значит быстрее – Rene Herse Cycles
Это было одной из первых вещей, которую вы усвоили как велосипедист: если вы хотите ехать быстро, убедитесь, что ваши шины накачаны до максимального давления. Чем сильнее накачаны ваши шины, тем быстрее они катятся.
Теперь мы знаем, что это , а не правда. Осознание того, что давление в шинах не влияет на производительность, является ключом к революции, которая охватила мир велоспорта в последние годы. Без этих новых знаний вседорожные велосипеды и их гибкие широкие шины не имели бы никакого смысла. Вот как это работает.
Ярлык: Если вы просто хотите узнать, насколько накачивать шины, наш калькулятор давления в шинах позволит вам оптимизировать давление в шинах для достижения наименьшего сопротивления качению.
Сопротивление шин определяется двумя факторами:
Гистерезисные потери: При каждом повороте колес шины изгибаются. Вы можете видеть это на фотографии выше: обе шины сплющены в местах соприкосновения с дорогой. Сгибание шин требует энергии — представьте, что вы сжимаете теннисный мяч. Энергия на велосипеде может поступать только из одного источника: выходной мощности гонщика. Уменьшите потери энергии при сгибании, и вы будете двигаться быстрее.
Самый простой способ уменьшить эту потерю энергии: больше накачивайте шины, и они будут меньше прогибаться . Меньшая гибкость означает, что меньше энергии преобразуется в тепло, поскольку каркас шины деформируется под весом велосипеда и водителя.
Вы также можете уменьшить потери, облегчив изгиб каркаса шины . Мягкую оболочку легче согнуть, чем жесткую, поэтому она поглощает меньше энергии при одинаковом сгибании. Представьте, что вы сжимаете зефир вместо теннисного мячика.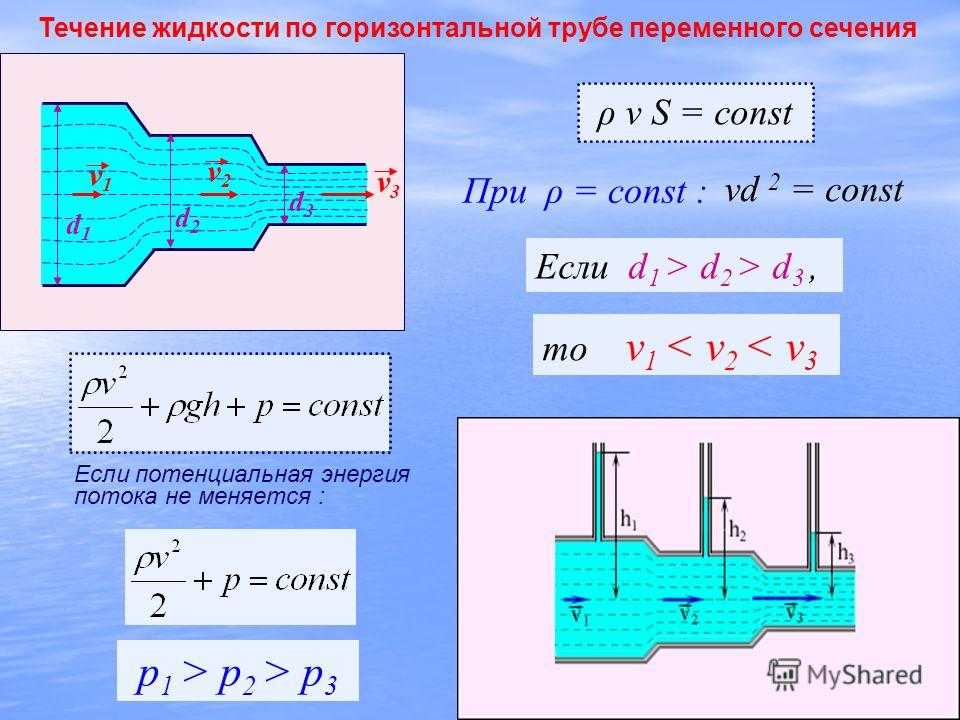
Итак, нам нужна эластичная шина, выдерживающая высокое давление. Это означает, что мы должны сделать его узким. Почему широкая шина не может быть эластичной, а может работать при высоком давлении?
Давление – это сила, приходящаяся на площадь поверхности. Например, PSI означает фунтов на квадратный дюйм . Чем больше окружность шины (больше дюймов), тем больше на нее будет действовать сила (больше фунтов). Представьте кожух в виде цепи, на каждом звене которой стоит слон. Если цепь состоит из десяти звеньев, она должна выдержать вес десяти слонов. Сделайте цепь в два раза длиннее, и на ней будут стоять двадцать слонов. Цепь должна быть вдвое прочнее. Или вы должны уменьшить вес каждого слона. Возвращаясь к шинам, это означает, что более широкой шине либо нужен более прочный (читай: более жесткий) каркас, либо вам нужно снизить давление.
Резюме: Лучший способ уменьшить гистерезисные потери — использовать гибкие шины, сделать их узкими и сильно накачать.
С более широкими шинами у вас может быть либо гибкий каркас, либо высокое давление, но не то и другое одновременно. В любом случае, более широкие шины будут иметь больше гистерезисных потерь. Если вы посмотрите только на гистерезисные потери, «широкие высокопроизводительные шины» покажется оксюмороном.
Это было общепринятым мнением, когда мы начали смотреть на характеристики шин еще в 2006 году. Это не неверно, но упускает из виду второй фактор, который также влияет на скорость вращения велосипеда, а давление в шинах работает противоположным образом.
Потери в подвеске: Когда велосипед вибрирует, теряется энергия. Большая часть этой энергии поглощается телом всадника, когда мягкие ткани трутся друг о друга. Десятилетия назад армия США изучала сиденья танков и обнаружила, что дискомфорт, который мы испытываем от вибраций, вызван трением между мягкими тканями нашего тела. Это трение потребляет энергию, которая превращается в тепло. (Потрите руки друг о друга, чтобы увидеть, как трение создает тепло.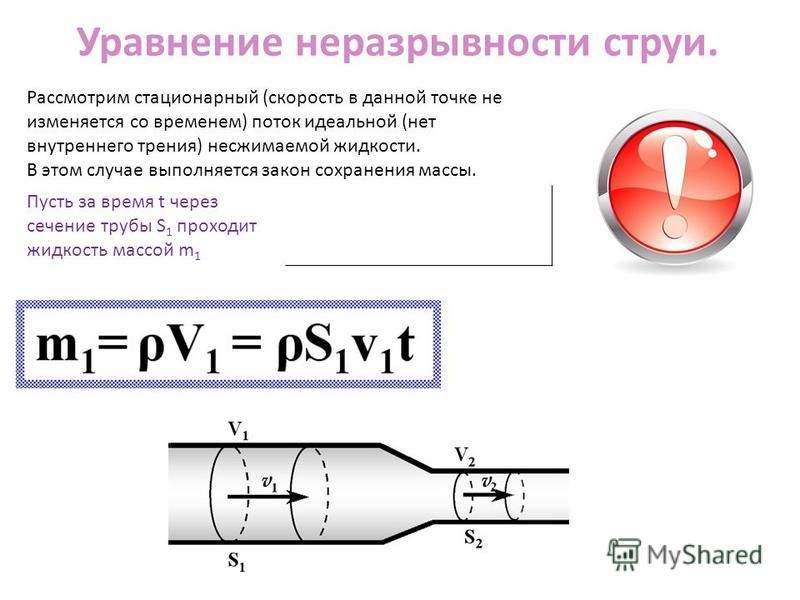
) Чем неприятнее вибрации, тем больше энергии теряется.
Горные байкеры давно знают, что подпрыгивание замедляет скорость вашего велосипеда. Самый быстрый горный велосипед тот, который лучше всего поглощает удары. Шоссейные велосипедисты привыкли думать, что нам нужно «перетерпеть» , чтобы ехать быстро. Мы терпели дискомфорт от узких шин высокого давления, потому что думали, что они катятся быстрее. Мы думали, что дорожное покрытие слишком гладкое, чтобы потери подвески имели значение.
В Bicycle Quarterly мы начали тестировать характеристики шин на реальных дорогах в 2006 году. Сначала мы также предполагали, что более высокое давление катит быстрее. Однако, как велосипедисты на длинные дистанции, мы подозревали, что существует точка убывающей отдачи. Мы думали так: в короткой гонке мы можем терпеть всевозможные неудобства, если это сделает нас быстрее. Но мы можем терпеть дискомфорт только до тех пор, пока он не повлияет на нашу выходную мощность.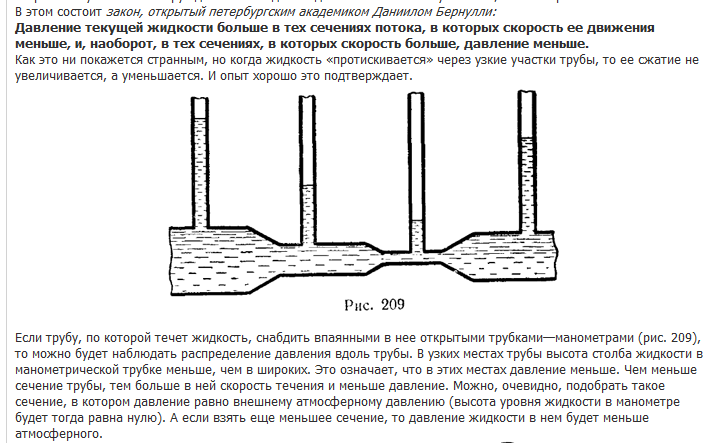
В поездке до 1200 км (750 миль) из Париж-Брест-Париж , мы могли бы потерять 5% в сопротивлении качению, если мы выиграем 20% в комфорте. Что мы хотели знать: где находится эта точка убывающей отдачи?
В то время сопротивление шин испытывали на стальных барабанах, которые измеряли только гистерезисные потери. На стальных барабанах, несомненно, более высокое давление дает лучшие результаты, как показывают все шины в таблице выше. Возьмите Vittoria Rubino Pro (второй снизу): при давлении 60 фунтов на квадратный дюйм требуется на 40% больше энергии, чем при 120 фунтов на квадратный дюйм. Я упоминаю эту шину, потому что позже вы увидите, как она работает в реальных условиях.
Барабанные испытания также показывают, что высокое давление важнее эластичности каркаса: в приведенной выше таблице самая медленная шина при 120 фунтах на кв. дюйм имеет меньшее сопротивление (13,4 Вт), чем вторая по скорости шина при 60 фунтах на кв. дюйм (13,9 Вт). Вот почему производители шин изготавливали свои широкие шины с жестким каркасом, чтобы они могли выдерживать высокое давление.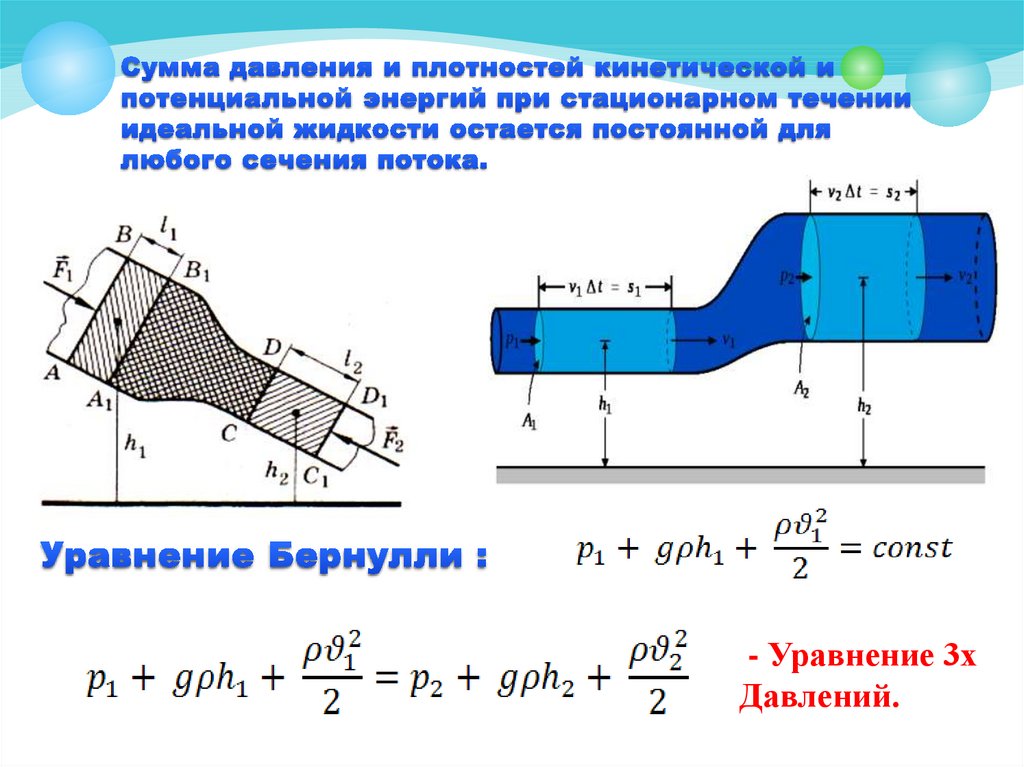
Широкая, эластичная шина, рассчитанная на низкое давление, скажем, 60 фунтов на квадратный дюйм, будет плохо работать на стальном барабане. Вот почему их не существовало — кому захочется делать медленную «высокопроизводительную» шину? Все это имело смысл, если вы тестировали свои шины на стальных барабанах.
Каково же было наше удивление, когда мы обнаружили, что в реальном мире — на реальных дорогах — шины ведут себя совершенно иначе. Мы протестировали множество шин двумя разными методами (прокат и измеритель мощности) и всегда находили одно и то же: более высокое давление не делает шины быстрее.
Мы также обнаружили, что преимущества мягких оболочек намного больше, чем предполагают испытания в стальных барабанах. Почему? Потому что потери в подвеске значительны даже на очень ровных дорогах. И более низкое давление, и гибкий корпус уменьшают вибрации мотоцикла и, следовательно, потери в подвеске. Но вы не можете измерить потери в подвеске, если у вас нет гонщика на байке.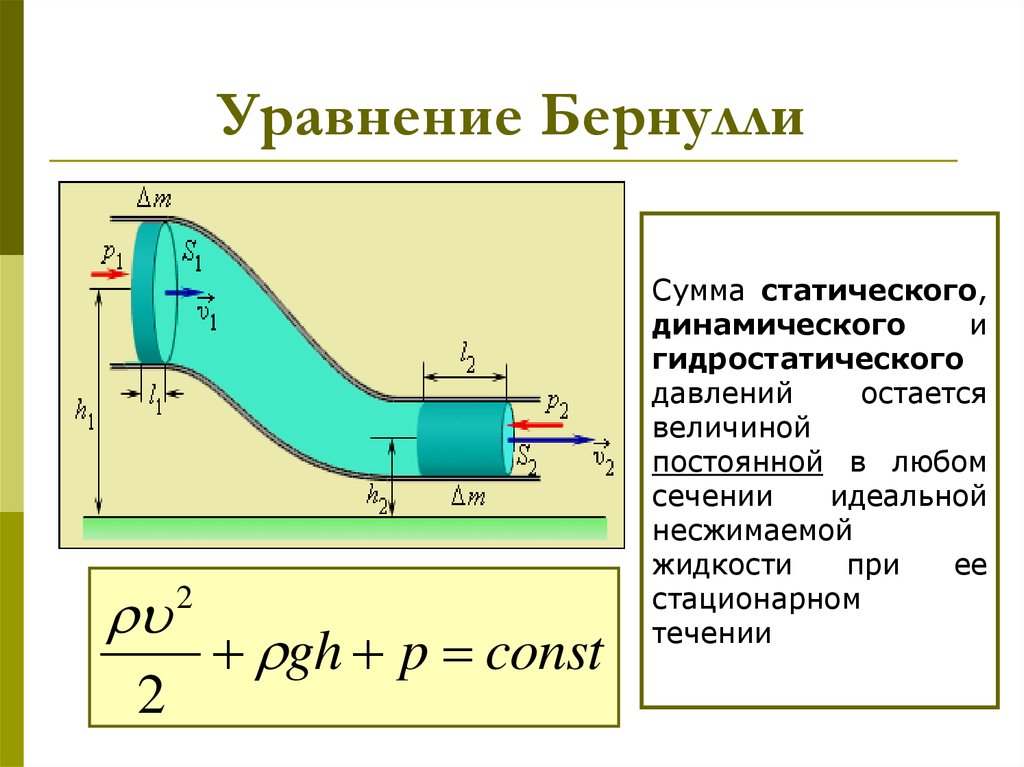
Вот почему более ранние исследования (и многие последующие) не дали значимых результатов…
Выше приведены реальные дорожные результаты для трех шин Vittoria 700C x 25 мм, включая Rubino Pro. Мы тестировали на совершенно новом ультрагладком асфальте. Для Rubino нет разницы в скорости между 80 и 110 psi. Это ясно для всех трех шин, которые вы здесь видите: более высокое давление не делает их быстрее. (Обратите внимание, что мощность указана для всего велосипеда и водителя, а не только для одной шины. Вот почему измерения мощности намного выше, чем при испытаниях на барабане.)
Происходит следующее: по мере увеличения давления в шине шина меньше изгибается, и гистерезисные потери снижаются. Однако шина также сильнее вибрирует, и увеличиваются потери в подвеске. Они примерно компенсируют друг друга, поэтому в приведенной выше таблице нет четкой тенденции.
Прежде чем мы продолжим, важно отметить, что мы убедились, что эти результаты являются статистически значимыми.
Это означает, что мы видим реальные различия в производительности, а не просто «шум» в данных. (Наш анализ данных выполнен Марком Ванде Кампом, у которого есть докторская степень по статистике.)
График показывает еще несколько вещей: слишком много: истерезисные потери огромны. Экстремальность — это полностью спущенная шина — очень медленная. В какой-то момент в шине достаточно воздуха, чтобы избежать чрезмерного изгиба. Выше этой «точки излома» гистерезисные потери и потери при подвеске начинают уравновешивать друг друга.
Точка разрыва немного выше (87 фунтов на квадратный дюйм).Резюме: На реальных дорогах, даже на гладких, более высокое давление не приводит к ускорению движения.
Мы протестировали множество шин — выше из наших первых испытаний в 2006 году, когда измерялось время скатывания на тщательно выбранном испытательном холме — и мы всегда находили одно и то же: выше точки разрыва повышение давления в шинах не делает ты быстрее.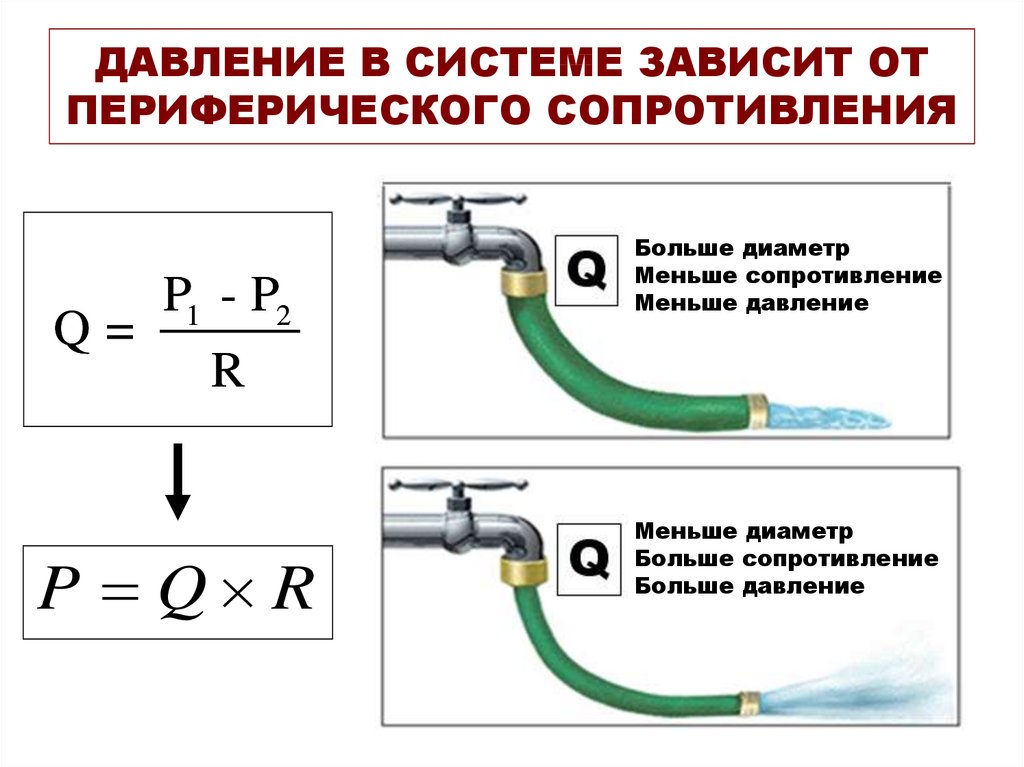
Точка разрыва выше у более жестких шин. Для трубчатых элементов точка разрыва ниже испытанных нами значений давления.
Хотел бы я, чтобы мы провели это тестирование, когда я еще участвовал в гонках. В то время я запускал 21,5-миллиметровые Clement Criterium при грохочущем давлении 130 фунтов на квадратный дюйм. Я был бы быстрее — намного быстрее — на 28-миллиметровом Campione Del Mondos при гораздо более низком давлении.
Что, если мы добьемся очень высокого давления в шинах? Мы прогнали 25-миллиметровую шину до 200 фунтов на квадратный дюйм, и она не стала быстрее. (Не пытайтесь повторить это дома, эксплуатация этих шин при таком давлении небезопасна!)
Приведенные выше результаты были получены на ультрагладком асфальте (Vittoria) и относительно неровном, но не ухабистом асфальте (другие). Влияет ли дорожное покрытие на предел прочности шины?
Чтобы испытать экстремальность, мы протестировали различные шины на дорожных полосах, которые хорошо заменяют булыжники.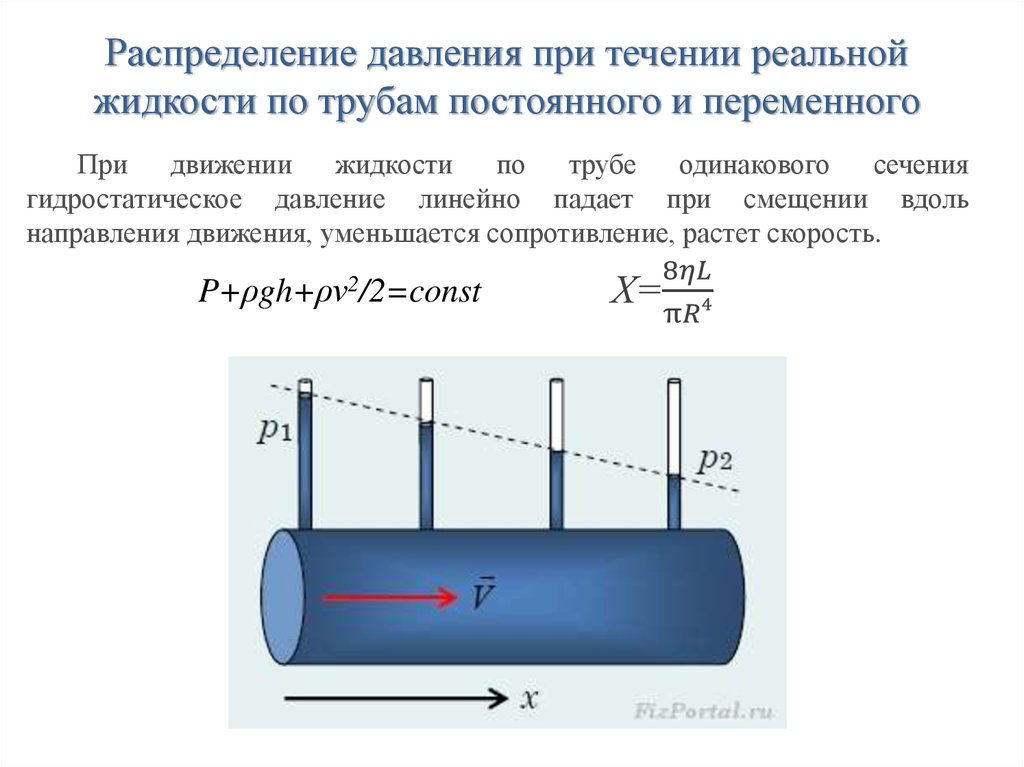
(В отличие от настоящих булыжников, вибрационные полосы очень регулярны, поэтому мы можем получить воспроизводимые результаты.) Мы также протестировали каждую шину на гладком асфальте рядом с вибрирующими полосами.
На гладком асфальте (слева) шины Compass/Rene Herse диаметром 26 мм катятся так же быстро при давлении 75 фунтов на квадратный дюйм, как и при давлении 95 фунтов на квадратный дюйм. Это подтверждает то, что мы обнаружили раньше: даже на ровных дорогах давление в шинах не имеет значения.
На отбойниках (справа) более высокое давление было медленнее: 26-миллиметровые шины Compass/Rene Herse использовали на на 20% больше энергии при 95 фунтах на квадратный дюйм, чем при 75 фунтах на квадратный дюйм.
Резюме: На действительно шероховатых поверхностях более высокое давление катится медленнее. Более широкие шины катятся быстрее по неровным поверхностям, потому что они могут выдерживать более низкое давление.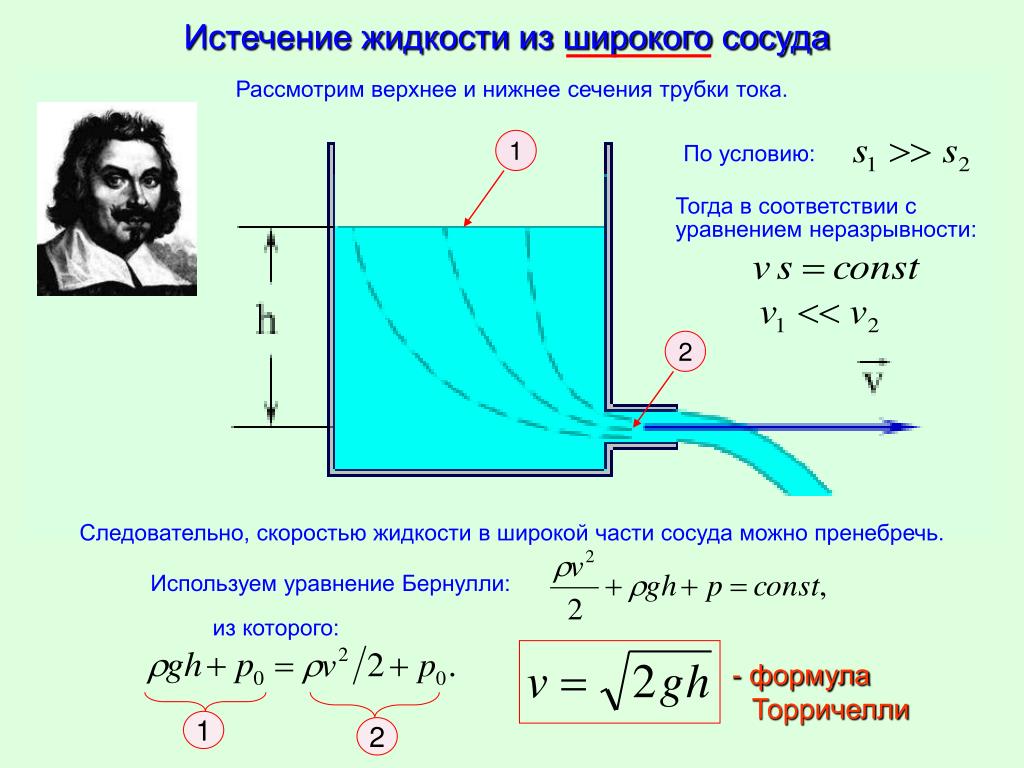
Итак, теперь мы знаем, что более высокое давление не делает ваш велосипед быстрее — будь то на сверхгладком асфальте, на неровных поверхностях, таких как булыжники, или где-то между ними. Для гибких шин точка разрыва — даже на гладких поверхностях — близка к точке, когда шина становится непригодной для езды, потому что боковины разрушаются при резком прохождении поворотов. На неровных поверхностях трудно достичь точки разрыва — шина сжимается до того, как ее характеристики ухудшаются.
Заключение: Если вы хотите ехать быстро, вам нужны эластичные шины. Вот и все. Накачивание их сильнее не сделает вас быстрее. На неровных поверхностях это на самом деле делает вас медленнее.
Когда мы увидели эти результаты, мы поняли, что это может произвести революцию в велосипедах: если бы нам не нужно было высокое давление, чтобы двигаться быстро, мы могли бы делать широкие шины с гибким каркасом, эксплуатировать их при низком давлении и при этом катиться так же быстро.
как мы делали на узких «гоночных» шинах. С этими широкими гибкими шинами мы могли бы ездить по дорогам и тропам, которые не доставят особого удовольствия на традиционном гоночном велосипеде с узкими шинами.
Мы придумали новое поколение велосипедов — гоночные велосипеды со сверхширокими гибкими шинами — и назвали их Allroad Bikes (пока без дефиса). Это было давно, в 2006 году.
Тогда мы решили воплотить этот новый тип велосипеда из мечты в реальность. Первым шагом было изготовление шин, необходимых для этих вседорожных велосипедов. Сначала мы работали с другими производителями, но для того, чтобы получить именно те шины, которые нам нужны, мы представили собственные шины действительно большой ширины (см. выше). Велосипедной индустрии потребовалось некоторое время, чтобы присоединиться к нам, но теперь наши идеи общеприняты: вседорожные и гравийные велосипеды являются наиболее важным сегментом рынка высокопроизводительных велосипедов.
Вседорожные велосипеды — это больше, чем преходящее увлечение, потому что они, наконец, исправляют один из недостатков традиционных спортивных велосипедов: необходимость менять комфорт на скорость.
Теперь мы знаем, что дискомфорт не только неприятен, он на самом деле замедляет вас. Проще говоря:
Комфорт = Скорость
Езда на велосипеде стала намного веселее на вседорожных велосипедах, которые сочетают в себе удовольствие от езды на спортивном велосипеде с комфортом и способностью преодолевать любые препятствия благодаря широким шинам. Это велосипеды будущего, и они здесь, чтобы остаться.
Калькулятор давления в шинах:
• Наш калькулятор давления в шинах помогает оптимизировать давление в шинах для достижения наименьшего сопротивления качению.
Почему более высокое давление в шинах кажется быстрее, но на самом деле замедляет вас
Ощущение скорости.
Восприятие вибрации и скорости
Вибрация и езда на велосипеде
Давление в шинах и импеданс
Подключение скорости и вибрации
Что мы можем сделать как велосипедисты
Когда я учился в университете, у меня была Kia Sephia 2001 года выпуска, подвеска которой была хуже выставочного зала.
Во время поездки в Долину Смерти я задался вопросом, каково это — разогнаться до 100 миль в час, и разогнался до 105 миль в час. Было ощущение, что мы летим, но вибрация нервировала, и я боялся за свою жизнь!
Вскоре после этого случая я одолжил у друга новую Acura TL для поездки. Я взглянул на спидометр и увидел, что двигаюсь со скоростью около 100 миль в час в зоне 75 миль в час. Это случалось больше раз, чем я признаю здесь, но в то время я не мог понять, почему я могу вести разговор с комфортом, разгоняясь до 100 миль в час в одной машине, в то время как чувствую, что умру в другой.
Есть несколько факторов, влияющих на восприятие скорости, но я хочу сосредоточиться на вибрации.
В моей старой машине вибрация давала ощущение скорости и неминуемой гибели, чего не было в новой машине. Вибрация имитирует ощущение скорости. При движении с той же скоростью просто добавление вибрации к системе заставит вас чувствовать себя быстрее.
С тех пор я езжу в настроенных гоночных автомобилях со скоростью более 200 миль в час в полном комфорте.
Однако, когда настройка отключена, все становится очень быстро.
В автомобилях используются амортизаторы для поглощения вибрации. В горных велосипедах и гравийных велосипедах используются большие шины с более низким давлением, а иногда и амортизаторы, которые помогают поглощать вибрацию. В этих дисциплинах общеизвестно, что более низкое давление в шинах создает лучшее сцепление с дорогой, снижает вибрацию и повышает скорость.
Однако в шоссейном велоспорте мы слышим о важности «чувства скорости», которое обычно возникает из-за чрезмерно накачанных шин, вызывающих вибрацию. Вибрация вызывает отскок или движение вверх и вниз, что влияет на ваше сцепление с поверхностью, по которой вы едете. На асфальте небольшая вибрация влияет на сцепление, но все же позволяет проходить повороты, тогда как при езде по грязи с перекачанными шинами движение вверх и вниз может привести к скольжению.
Если учесть мой опыт вождения двух разных автомобилей, мы поняли, что добавление вибрации будет ощущаться быстрее.
И хотя более высокое давление в шинах может «чувствовать себя быстрее», мы знаем, что это неправда.
Ранее мы писали о давлении в шинах и пределе импеданса. Вот краткий обзор:
Величина сопротивления качению влияет на вашу скорость. В лаборатории при увеличении давления в шинах сопротивление качению уменьшается. (Отлично!) Однако на асфальте сопротивление качению уменьшается до точки, а затем резко возрастает, что делает вас медленнее. (О.) Точка, в которой сопротивление качению перестает уменьшаться и начинает увеличиваться, называется точкой разрыва импеданса. Подробнее о сопротивлении качению и импедансе читайте в этой статье.
Как только достигается предельная точка импеданса, ваши шины начинают подпрыгивать вверх и вниз на небольших неровностях тротуара, что увеличивает вибрацию велосипеда. Вы чувствуете себя быстрее, но на самом деле ваше сопротивление качению подскочило, и вы теряете скорость. Видите, куда мы идем с этим?
Изучив человеческое восприятие скорости, я наткнулся на исследование, проведенное в Италии, в котором проверялось человеческое восприятие гладкости дорожного покрытия на разных скоростях.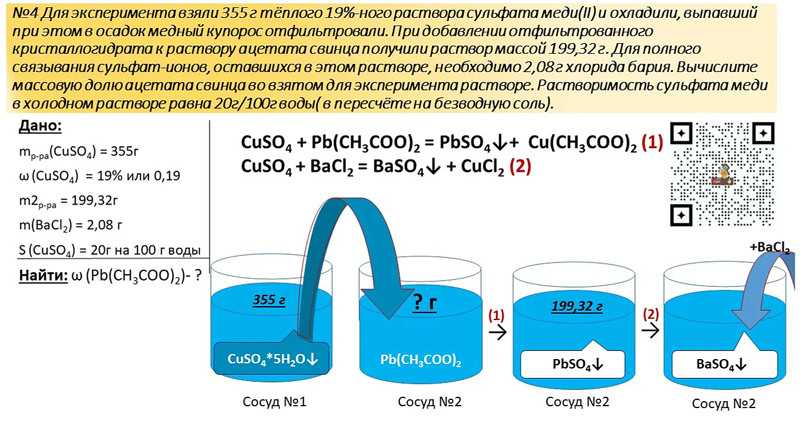
Вот что они нашли:
Для одной и той же дороги (с одинаковой гладкостью) люди сообщали, что качество дорожного покрытия тем хуже, чем быстрее они едут. На приведенном ниже графике показано количество людей, которые сообщили, что дорога была в очень хорошем, хорошем, посредственном или плохом состоянии на скоростях 60 км/ч, 70 км/ч, 80 км/ч и 90 км/ч.
В ходе исследования они измерили вертикальное движение, чтобы определить вибрацию, ощущаемую участниками, и определили, что вибрация в автомобиле увеличивается с увеличением скорости.
В недавней статье FLO мы обсуждали наши выводы о том, как скорость влияет на точку излома импеданса. Чем быстрее вы идете, тем раньше вы достигнете точки останова импеданса. Это означает, что если вы достигнете точки останова импеданса на скорости 20 миль в час и продолжите крутить педали до 30 миль в час, вы преодолеете точку останова импеданса и резко увеличите сопротивление качению. Как только вы преодолеете точку разрыва импеданса, ватты, которые вы вкладываете в педали, больше не просто двигают вас вперед, но также двигают вас вверх и вниз (вибрация), создавая неэффективность.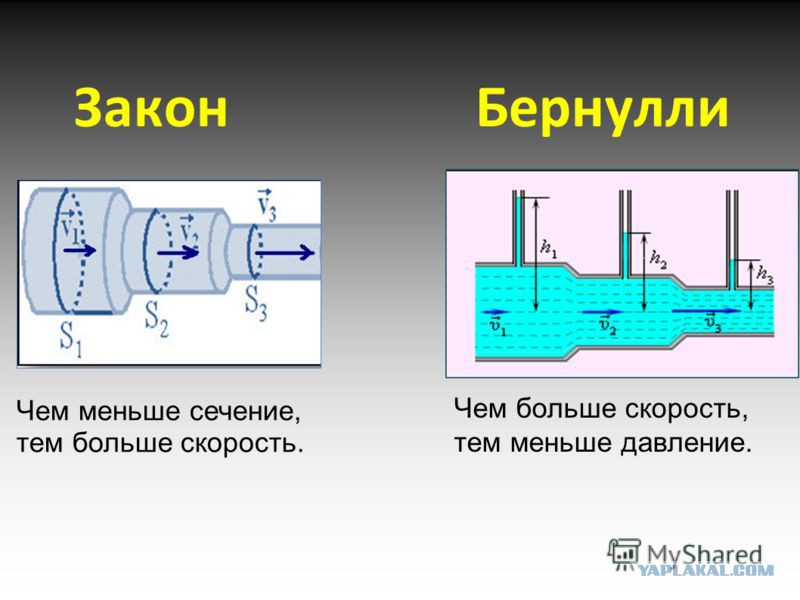
Наша работа и это исследование доказывают, что с увеличением скорости увеличивается и вибрация. Чтобы достичь наибольшей эффективности и двигаться быстрее, цель состоит в том, чтобы уменьшить вибрацию, даже если вы чувствуете себя быстрее.
Когда мы едем на шоссейном велосипеде, мы должны отказаться от нашего менталитета «чувствовать себя быстрее». Причина, по которой это кажется быстрым, заключается в том, что вы испытываете вибрацию. Эта вибрация бесполезна по нескольким причинам:
1. Как велосипедист, мы хотим, чтобы мощность, вложенная в педали, двигала нас вперед, а не вверх и вниз. Вибрация создает движение вверх и вниз, что тратит впустую ватты, которые мы вкладываем в педали.
2. Наше сцепление с дорогой уменьшается, так как подпрыгивания создают небольшие промежутки времени, когда наш контакт с дорогой уменьшается. Когда вы устраняете подпрыгивание, шина остается в контакте с дорожным покрытием и улучшает сцепление с дорогой.
3.
Leave A Comment