Что такое средняя и мгновенная скорость, среднее и мгновенное ускорение, тангенсальное и нормальное ускорение?

Средняя скорость – это физическая величина, равная отношению вектора перемещения точки к промежутку времени &#916;t, за который произошло это перемещение. Направление вектора средней скорости совпадает с направлением вектора перемещения . Средняя скорость определяется по формуле: Формула средней скорости Мгновенная скорость, то есть скорость в данный момент времени – это физическая величина, равная пределу, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени &#916;t: <a rel=»nofollow» href=»http://av-physics.narod.ru/mechanics/speed.htm» target=»_blank»>http://av-physics.narod.ru/mechanics/speed.htm</a> Среднее ускорение вычисляется как разность конечной и начальной скоростей, которая делится на разность конечного и начального времени: _ a = (V1 — V0)/(t1 — t0) Среднее ускорение отличается от фактического (мгновенного) ускорения в данный момент времени. Например, при резком нажатии педали тормоза автомобиль получает большое ускорение в первый момент времени. Если же водитель затем отпустит педаль тормоза, то ускорение уменьшится. <a rel=»nofollow» href=»http://www.prosto-o-slognom.ru/fizika/04.html» target=»_blank»>http://www.prosto-o-slognom.ru/fizika/04.html</a> Тангенциа&#769;льное ускоре&#769;ние — компонента ускорения, направленная по касательной к траектории движения. Совпадает с направлением вектора скорости при ускоренном движении и противоположно направлено при замедленном. Характеризует изменение модуля скорости. Центростремительное или Нормальное ускорение \mathbf a_n — возникает (не равно нулю) всегда при движении точки по окружности (конечного радиуса) (также обозначается иногда \mathbf w_\tau, \mathbf u_\tau итд) . Является составляющей вектора ускорения a, перпендикулярной вектору мгновенной скорости. Вектор нормального ускорения всегда направлен к центру окружности, а модуль равен: |\vec a| = \omega ^2 r = {v^2 \over r}

touch.otvet.mail.ru

Ускорение | Физика для всех

Ускорение – это величина, которая характеризует быстроту изменения скорости.

Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).

Среднее ускорение

Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:

 

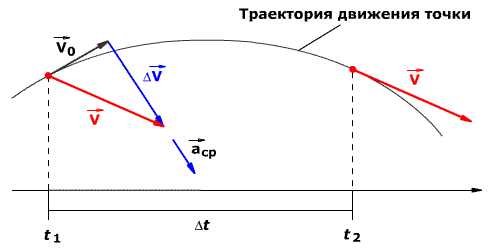Рис. 1.8. Среднее ускорение.В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть

Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки, при котором за одну секунду скорость этой точки увеличивается на 1 м/с. Иными словами, ускорение определяет, насколько изменяется скорость тела за одну секунду. Например, если ускорение равно 5 м/с2, то это означает, что скорость тела каждую секунду увеличивается на 5 м/с.

Мгновенное ускорение

Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:

При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть

v2 > v1

а направление вектора ускорения совпадает с вектором скорости 

Если скорость тела по модулю уменьшается, то есть

v2 < v1

то направление вектора ускорения противоположно направлению вектора скорости  Иначе говоря, в данном случае происходит замедление движения, при этом ускорение будет отрицательным (а < 0). На рис. 1.9 показано направление векторов ускорения при прямолинейном движении тела для случая ускорения и замедления.

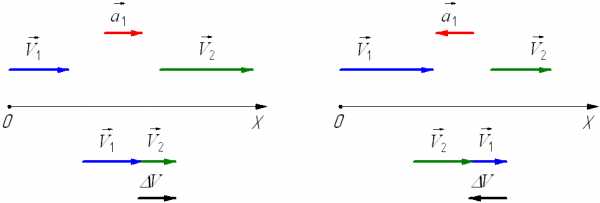
Рис. 1.9. Мгновенное ускорение.

При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).

Тангенциальное ускорение

Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.

Рис. 1.10. Тангенциальное ускорение.

Направление вектора тангенциального ускорения  (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.

Нормальное ускорение

Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой Вектор нормального ускорения направлен по радиусу кривизны траектории.

Полное ускорение

Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:

(согласно теореме Пифагора для прямоугольно прямоугольника).

Направление полного ускорения также определяется правилом сложения векторов:

av-mag.ru

Kvant. Скорость ускорение — PhysBook

Соколов Е. Скорость и ускорение //Квант. — 2011. — № 1. — С. 34

По специальной договоренности с редколлегией и редакцией журнала «Квант»

Для описания состояния движущегося тела в данный момент времени в кинематике вводятся понятия вектора скорости \(~\vec{\upsilon}\) и вектора ускорения \(~\vec{a}\) . А когда есть два вектора, то естественно поставить вопрос об их взаимном расположении. Например, такой: может ли угол между скоростью и ускорением быть равным 37° ?

Вопрос непростой, и в нашем классе его обсуждение превратилось в оживленную дискуссию.

Первым у нас всегда спешит с ответом Саша.


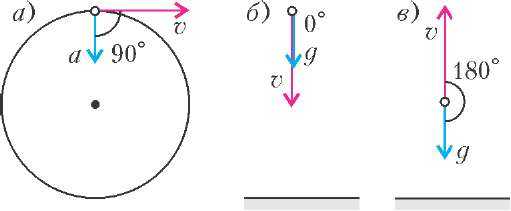
— Конечно, нет, такого быть не может! А вот угол 90° между скоростью и ускорением может быть (рис.1,а). Мы уже встречались с тем, что когда тело движется по окружности с постоянной по модулю скоростью, то у него есть ускорение. Это ускорение всегда направлено перпендикулярно скорости, т.е. к центру окружности, поэтому ему дали специальное название — центростремительное ускорение.


— И не только 90°, — поправила его Яна. — Помните, мы говорили, что при свободном падении ускорение тела всегда направлено вниз (рис.1,б). Поэтому угол между скоростью и ускорением может быть равен 0°.


— А ведь свободное падение это не только движение вниз, — вмешалась Маша. — Свободным падением можно называть любое движение тела под действием только силы тяжести, например в отсутствие сопротивления воздуха. Поэтому даже когда мяч летит вверх, его ускорение, согласно нашему правилу, по-прежнему направлено вниз (рис.1,е). Угол между скоростью и ускорением в этом случае равен 180°.


— Вот мы и ответили на ваш вопрос: угол между скоростью и ускорением может принимать три значения, — подытожил разговор Иван.


— Ну что же, вы нашли три возможных угла. Можете отдохнуть и полюбоваться еще одной знакомой вам картинкой (рис.2). Скажу честно — это намек. На рисунке 2 изображена траектория тела, брошенного под углом к горизонту. Такую ситуацию мы не раз обсуждали и говорили, что скорость тела в каждой точке направлена по касательной к траектории, а ускорение все время направлено вниз. Ведь куда бы ни летело тело, оно всегда свободно падает. Нарисуем для нескольких точек траектории векторы скорости и ускорения (рис.3). В верхнее точке А скорость направлена горизонтально, а ускорение направлено вниз. В этой точке угол между скоростью и ускорением равен 90° . Для точки В соответствующий угол острый, а для точки С — тупой. И понятно, что величины этих углов могут быть любыми.

Итак, вот итог наших размышлений: угол между скоростью и ускорением может быть любым.

Это хорошо, что мы нашли правильный ответ, но, к сожалению, жизнь наша от этого только усложнилась. Ведь если бы существовало только три угла, то достаточно было бы выбрать один вариант из трех. Но теперь мы знаем, что ускорение может быть направлено куда угодно, и вариантов стало бесконечно много. Как же быть? Как в задачах правильно рисовать, куда направлено ускорение тела? Сейчас разберемся. Но прежде сделаем общее замечание.

В процессе эволюции человек приобрел способность «видеть» скорость и траекторию. Так, мы хорошо представляем себе, куда полетит брошенный нами снежок, и легко сможем увернуться от летящего в нас снежка. Поэтому вопросы, связанные со скоростью и траекторией, обычно не вызывают сложностей. Но мы не имеем возможности «видеть» ускорение. Вот почему просто так, по наитию, не стоит пытаться его рисовать. Определить, как направлено ускорение в каждом случае, мы можем только с помощью рассуждений, применяя специальные правила. О двух таких правилах мы уже знаем: при равномерном движении тела по окружности ускорение следует направлять к центру окружности (доказывается в кинематике), а при свободном падении — вертикально вниз (доказывается в динамике).


— А есть общее правило для любого движения?


— Да, есть. И его под силу вывести любому первокурснику. Но вы еще не первокурсники, а я очень не люблю рассказывать что-то без доказательств. Давайте поступим так: превратим наше обсуждение в тест на обучаемость. Я честно, хотя и без доказательств, расскажу вам все, что нужно для построения ускорения, и даже открою вам некоторые секреты, а потом вы попытаетесь построить ускорение в десяти простых случаях.


— Согласны. Только разве сложно, зная правила, получить ответ?


— Вот это мы как раз и проверим на опыте. А пока слушайте и задавайте вопросы.

Найти направление ускорения помогают два понятия: нормальная составляющая ускорения и тангенциальная составляющая ускорения. Общее правило заключается в том, что сначала строится каждая из этих составляющих (это несложно сделать), а уже по ним — само ускорение, как показано на рисунке 4.

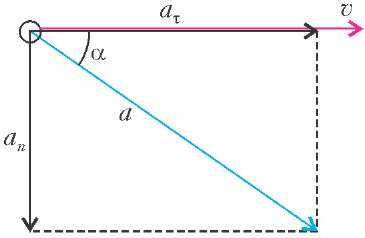
Нормальная составляющая ускорения — это составляющая, перпендикулярная скорости. Величину нормальной составляющей ускорения всегда можно найти по уже знакомой нам формуле

\(~a_n = \dfrac{\upsilon^2}{R}. \)

Эта составляющая перпендикулярна скорости и направлена по радиусу R к центру кривизны траектории. Нормальная составляющая ускорения (второе, уже знакомое нам название этой составляющей — центростремительное ускорение) характеризует быстроту изменения направления скорости.

Тангенциальная, или касательная, составляющая ускорения — это составляющая, направленная параллельно скорости. Она характеризует быстроту изменения скорости по величине и определяется по формуле

\(~a_\tau = \dfrac{\Delta \upsilon}{\Delta t}\)

Направлять тангенциальную составляющую следует либо по направлению скорости, либо против — в зависимости от того, увеличивается скорость или уменьшается.

Определив обе эти составляющие, мы можем с помощью рисунка 4 восстановить само ускорение (иногда говорят «полное ускорение»). При необходимости модуль ускорения и угол между скоростью и ускорением можно вычислить с помощью теоремы Пифагора и понятия арктангенса:

\(~a = \sqrt{a_n^2 + a_\tau^2}, \ \ \ \alpha = \arctan{ \dfrac{a_n}{a_\tau} }. \)

Ну как, понятно?


— Да, вроде все ясно. Сначала рисуем нормальную составляющую ускорения перпендикулярно скорости в направлении к центру кривизны — так же, как мы рисовали центростремительное ускорение. Потом строим вторую составляющую — вдоль или против скорости. И после этого по рисунку 4 находим само ускорение.


— Все правильно. Но прежде чем переходить к тесту, я хочу обратить ваше внимание на очень важные частные случаи. Выполните, пожалуйста, такое упражнение: а) укажите два случая движения тела, в которых нормальная составляющая ускорения обращается в ноль; б) укажите два случая движения тела, в которых тангенциальная составляющая ускорения обращается в ноль. Лучше будет, если вы сами ответите на эти вопросы, но ничего страшного не произойдет, если вы просто прочтете следующие два абзаца.

а) Нормальная составляющая ускорения обращается в ноль тогда, когда обращается в ноль выражение \(~a_n = \dfrac{\upsilon^2}{R}\) . А это может произойти в двух случаях. Первый случай видят все: нормальная составляющая обращается в ноль, если скорость обращается в ноль. Поэтому нормальная составляющая ускорения всегда равна нулю в точках остановки тела.

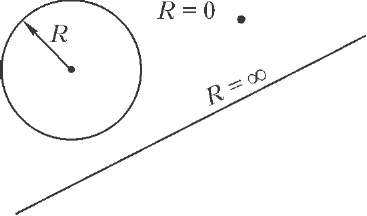
Второй случай увидит лишь тот, кто знает, что общего у прямой, окружности и точки. Оказывается, и точка, и прямая есть частные случаи окружности (рис. 5). Точка — это окружность с радиусом, равным нулю, а прямая — это окружность с радиусом, равным бесконечности. Не верите? Попробуйте нарисовать на компьютере окружность очень большого радиуса. Она практически не будет отличаться от прямой линии. Итак, второй случай, когда нормальная составляющая обращается в ноль, — это случай, когда R = ∞ , т.е. когда тело движется по прямой. При прямолинейном движении нормальной составляющей ускорения нет.

б) Тангенциальная составляющая ускорения обращается в ноль тогда, когда обращается в ноль выражение \(a_\tau = \dfrac{\Delta \upsilon }{\Delta t} = \upsilon ‘ (t)\) А это тоже может произойти в двух случаях. Первый случай — это равномерное движение, когда модуль скорости вообще не изменяется. Второй случай — это моменты времени, когда модуль скорости достигает максимума или минимума и производная от модуля скорости по времени становится равной нулю.

Наш рассказ о кинематическом методе построения ускорения закончен. Теперь попробуйте выполнить приведенный ниже тест. В нем собраны, пожалуй, все возможные случаи построения ускорения. Отметим, что этот тест не так прост, как кажется.

Тест. Для каждого из десяти положений тела, изображенных на рисунке 6, определите, как направлено его ускорение.

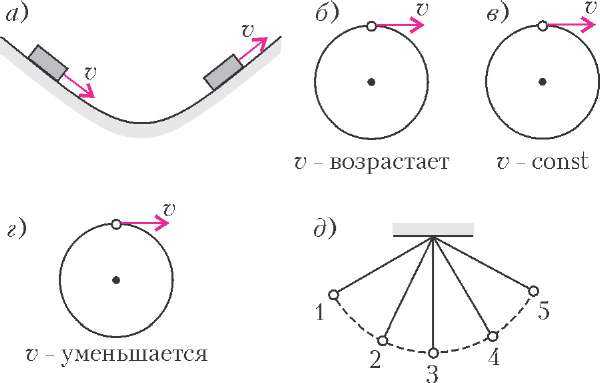
а) Санки скатываются с горки, а затем заезжают на горку.

б )Тело движется по окружности с возрастающей скоростью.

в) Тело движется по окружности с постоянной скоростью.

г) Тело движется по окружности с уменьшающейся скоростью.

д) Математический маятник совершает колебания. Точки 1 и 5 — крайние точки, 2 и 4 — промежуточные, 3 — самая нижняя точка.

В заключение — одно полезное замечание. Наш разговор о направлении ускорения мы вели на языке кинематики. Однако говорить об этом можно и на языке динамики. Иногда (но не всегда) динамические рассуждения могут оказаться проще кинематических. Например, с помощью динамики очень легко ответить на исходный вопрос об угле 37° . Динамика учит, что ускорение порождается силой.

Согласно второму закону Ньютона, \(~\vec{ a } = \dfrac{ \vec{F} }{ m }\) , т.е. куда направлена сила, туда направлено и ускорение. Силу мы можем прикладывать в любом направлении по нашему желанию, поэтому и ускорение, создаваемое этой силой, может иметь любое направление.

Ответы

а) В каждом из двух случаев ускорение совпадает с тангенциальной составляющей ускорения (рис.7, а).

б) Тело движется по окружности, значит, у тела есть нормальная составляющая ускорения, которая направлена к центру окружности. Кроме этого, по условию задачи скорость тела возрастает, следовательно, есть и тангенциальная составляющая ускорения, которая направлена вдоль скорости. Полное ускорение \(\vec{а}\) изображено на рисунке 7, б.

в) См. рис.7, в

г) См. рис.7, г.

д) Прежде всего отметим, что траектория движения математического маятника — это окружность (рис.7, д). Поэтому, там, где скорость тела не равна нулю, есть нормальная составляющая ускорения.

Крайние точки 1 и 5 — это точки поворота. Скорость в этих точках обращается в ноль, поэтому нормальная составляющая ускорения в обеих точках равна нулю. А есть ли в этих точках тангенциальная составляющая? Вот здесь, бывает, ошибаются даже самые сильные школьники. Правильный ответ — да, тангенциальное ускорение в точках остановки есть. Проще всего применить к этим точкам второй метод рассуждений — динамический. В точках 1 и 5 на тело действуют две силы: сила тяжести и сила натяжения нити. Касательная составляющая силы тяжести и создает тангенциальное ускорение.

www.physbook.ru