Ответов пока нет | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Физика | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
ПРОВЕРОЧНАЯ РАБОТА «ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ» (10 КЛАСС, УГЛУБЛЕННЫЙ УРОВЕНЬ)
Вариант 1
1.
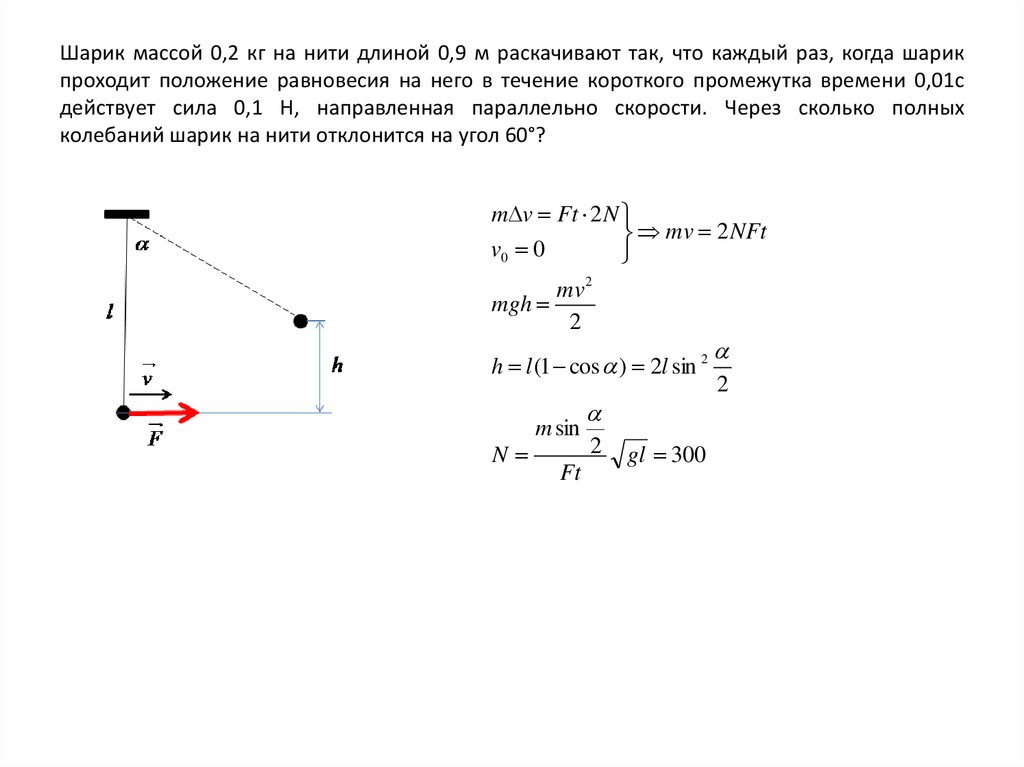На
наклонной плоскости находится брусок массой 4 кг, для которого составили
таблицу зависимости модуля силы трения Fтр от угла наклона плоскости
к горизонту α с погрешностью не более 0,01 Н. Основываясь на данных,
приведенных в таблице, и используя закон сухого трения определите коэффициент
трения скольжения и определите, при каких углах наклона брусок покоится.
α, рад | 0 | 0,05 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 |
Fтр, Н | 0 | 2,0 | 4,0 | 7,72 | 7,52 | 7,26 | 6,5 | 6,02 | 5,5 | 4,9 | 4,26 |
2.
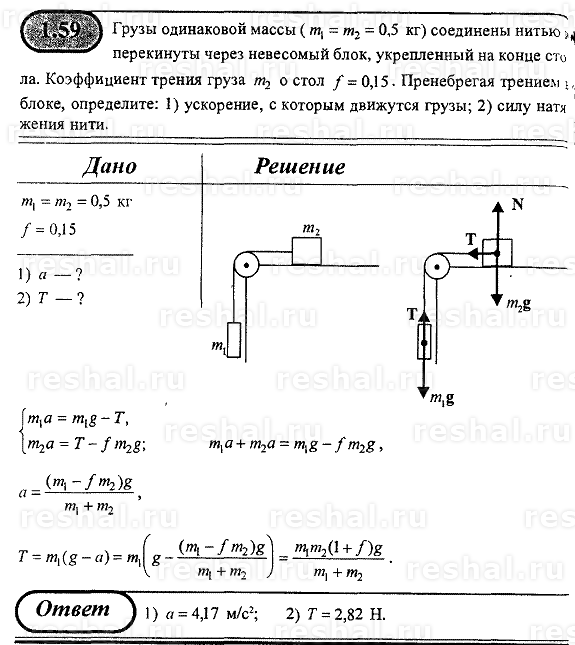Груз массой 4
кг подвешен к укреплённому в лифте динамометру. Лифт начинает подниматься с
постоянным ускорением 1 м/с2. Чему равно установившееся показание
динамометра?
3. С вершины наклонной плоскости из состояния покоя скользит с ускорением лёгкая коробочка, в которой находится груз массой
Для каждой величины определите соответствующий характер изменения:
А) время движения 1) увеличится
Б) ускорение 2) уменьшится
В) модуль работы силы трения 3) не изменится
4. На шероховатой наклонной плоскости покоится деревянный брусок. Угол наклона плоскости увеличили, но брусок относительно плоскости остался в покое. Как изменились при этом сила нормального давления бруска на плоскость и коэффициент трения бруска о плоскость?
Для каждой величины определите соответствующий характер изменения:
А) сила трения 1) увеличилась
Б) коэффициент трения 2) уменьшилась
3) не изменилась
5.
Маленькая шайба массы т, способная перемещаться
вдоль гладкого стержня, находится на поверхности горизонтального диска,
равномерно вращающегося с угловой скоростью ω
Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ ФОРМУЛЫ
А) модуль ускорения шайбы, находящейся на расстоянии R от оси вращения 1) ω22 R+μg
Б) кинетическая энергия шайбы, находящейся на расстоянии r от оси вращения 2) +μg
3) μmg(R-r)
4)
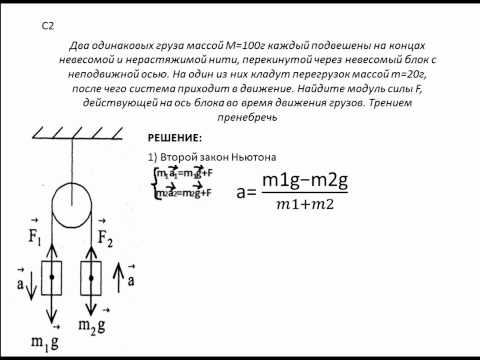
6.
Два груза подвешены на достаточно длинной невесомой нерастяжимой
нити, перекинутой через идеальный блок (см. рисунок). Грузы удерживали
неподвижно, а затем осторожно отпустили, после чего они начали двигаться
равноускоренно. Опустившись на 2 м, левый груз приобрёл скорость
4 м/с. Определите силу натяжения нити, если масса правого груза т =
1 кг. Трением пренебречь.
7. После удара шайба начала скользить вверх по шероховатой наклонной плоскости с начальной скоростью υ0 и после остановки соскользнула обратно. Выберите из предложенного перечня все верные утверждения, которые соответствуют результатам проведенным экспериментальным наблюдениям.
1) Время движения шайбы вверх равно времени движения шайбы вниз;
2) Модуль максимальной скорости шайбы при движении вниз меньше υ0;
3) При движении вверх и вниз работа силы трения шайбы о плоскость одинакова;
4) Изменение потенциальной энергии шайбы при движении до верхней точки равно кинетической энергии шайбы сразу после удара;
5) модуль
ускорения шайбы при движении вверх меньше, чем модуль ускорения при движении
вниз.
Вариант 2
1. На наклонной плоскости находится брусок массой 5 кг, для которого составили таблицу зависимости модуля силы трения Fтр от угла наклона плоскости к горизонту α с погрешностью не более 0,01 Н. Основываясь на данных, приведенных в таблице, и используя закон сухого трения определите коэффициент трения скольжения и определите, при каких углах наклона брусок движется.
α, рад | 0 | 0,05 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 |
Fтр, Н | 0 | 2,0 | 4,0 | 7,72 | 7,52 | 7,26 | 6,92 | 6,5 | 6,02 | 5,5 | 4,9 | 4,26 |
2.
Груз массой 4 кг подвешен к
укреплённому в лифте динамометру. Лифт начинает спускаться с верхнего этажа с
постоянным ускорением. Показания динамометра при этом равны 36 Н. Чему равно и
куда направлено ускорение лифта?
3. С вершины наклонной плоскости из состояния покоя скользит с ускорением лёгкая коробочка, в которой находится груз массой m (см. рисунок). Как изменятся время движения, ускорение и модуль работы силы трения, если с той же наклонной плоскости будет скользить та же коробочка с грузом массой m/2 ?
Для каждой величины определите соответствующий характер изменения:
А) время движения 1) увеличится
Б) ускорение 2) уменьшится
В) модуль работы силы трения 3) не изменится
4. На шероховатой
наклонной плоскости покоится деревянный брусок. Угол наклона плоскости
уменьшили, но брусок относительно плоскости остался в покое.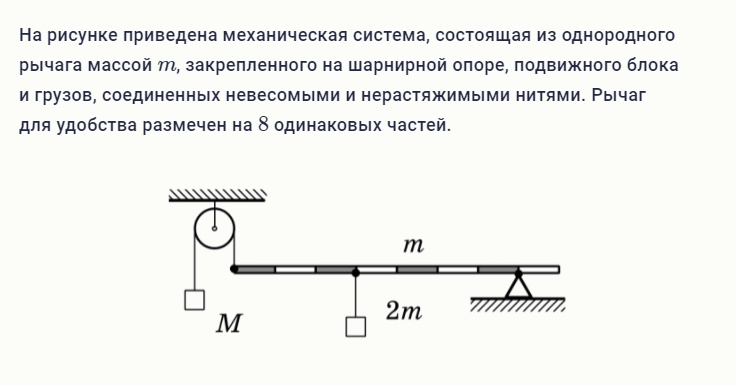
Как изменились при
этом сила нормального давления бруска на плоскость и коэффициент трения бруска
о плоскость?
Для каждой величины определите соответствующий характер изменения:
А) сила трения 1) увеличилась
Б) коэффициент трения 2) уменьшилась
3) не изменилась
5. Брусок массой m соскальзывает из состояния покоя по наклонной плоскости высотой h и длиной S. Коэффициент трения между бруском и плоскостью μ. Установите соответствие между физическими величинами и формулами.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ ФОРМУЛЫ
А) сила трения, действующая на брусок 1)
Б) время движения бруска 2) )
3)
4)
6.
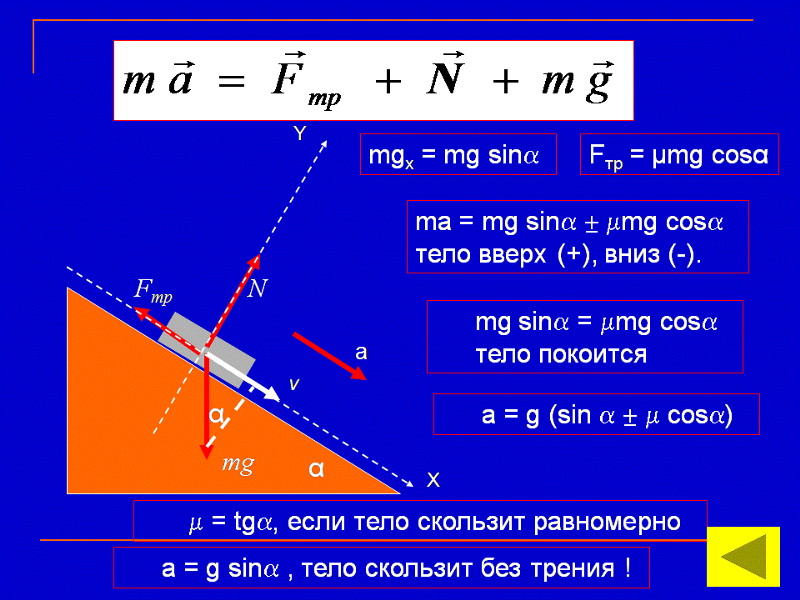Брусок массой М = 300 г соединён с грузом массой т
= 200 г невесомой и нерастяжимой нитью, перекинутой через невесомый
идеальный блок (см. рис.). Брусок скользит без трения по неподвижной наклонной
плоскости, составляющей угол 30° с горизонтом. Чему равно ускорение груза т?
7. Брусок массой 0,5 кг покоится на шероховатой горизонтальной плоскости. На него начинают действовать горизонтальной силой F, модуль которой изменяется с течением времени так, как показано на рисунке. Коэффициент трения бруска о плоскость равен 0,2.
Выберите из предложенного перечня все утверждения, которые соответствуют результатам проведённого опыта.
1) В промежутке от 1 с до 2 с брусок двигался с ускорением.
2) В промежутке от 0 с до 2 с сила трения, действующая на брусок, не менялась.
3) Кинетическая энергия бруска в промежутке от 0 до 6 с всё время возрастала.
4) В момент времени 5 с
ускорение бруска равно 2 м/с2.
5) В промежутке от 2 с до 3 с импульс бруска увеличился на 2 кг м/с.
Вариант 3
1. На наклонной плоскости находится брусок массой 7 кг, для которого составили таблицу зависимости модуля силы трения Fтр от угла наклона плоскости к горизонту α с погрешностью не более 0,01 Н. Основываясь на данных, приведенных в таблице, и используя закон сухого трения определите коэффициент трения скольжения и определите, при каких углах наклона брусок покоится.
α, рад | 0 | 0,05 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 |
Fтр, Н | 0 | 2,0 | 4,0 | 7,72 | 7,52 | 7,26 | 6,92 | 6,5 | 6,02 | 5,5 | 4,9 | 4,26 |
2.
Груз подвешен на пружине
жёсткостью 100 Н/м к потолку лифта. Лифт равноускоренно опускается вниз на
расстояние 5 м в течение 2 с. Какова масса груза, если удлинение пружины при
установившемся движении груза равно 1,5 см?
3. С вершины наклонной плоскости из состояния покоя скользит с ускорением лёгкая коробочка, в которой находится груз массой m (см. рисунок). Как изменятся время движения, ускорение и модуль работы силы трения, если с той же наклонной плоскости будет скользить та же коробочка с грузом массой m?
Для каждой величины определите соответствующий характер изменения:
А) время движения 1) увеличится
Б) ускорение 2) уменьшится
В) модуль работы силы трения 3) не изменится
4. В первой серии опытов
брусок с грузом перемещали при помощи нити равномерно и прямолинейно вверх по
наклонной плоскости. Во второй серии опытов точно так же перемещали этот
брусок, но сняв с него груз.
Как изменились при переходе от первой серии опытов
ко второй модуль работы силы трения при перемещении бруска на одинаковые
расстояния и коэффициент трения между бруском и плоскостью?
Для каждой величины определите соответствующий характер её изменения:
А) модуль работы силы трения 1) увеличилась
Б) коэффициент трения 2) уменьшилась
3) не изменилась
5. Маленькая шайба массы т, способная перемещаться вдоль
гладкого стержня, находится на поверхности горизонтального диска, равномерно
вращающегося с угловой скоростью ω1 на расстоянии r от оси О, с которой шайба
соединена лёгкой недеформированной пружинкой жёсткости k (см.
рисунок). Коэффициент трения между шайбой и диском μ. Как только угловая
скорость начинает медленно и плавно возрастать, шайба начинает смещаться.
При
угловой скорости ω2 расстояние до оси стало R, при
этом диск стал вновь вращаться равномерно.
Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ ФОРМУЛЫ
А) модуль скорости шайбы, находящейся на расстоянии R от оси вращения 1) ω22R
Б) модуль равнодействующей сил, действующих на шайбу на расстоянии R 2) ω2 R
3) k(R-r)+μmg
4) k(R-r)
6.
Груз массой 1 кг, находящийся на столе, связан
лёгкой нерастяжимой нитью, переброшенной через идеальный блок, с другим грузом.
На первый груз действует горизонтальная постоянная сила F, равная
по модулю 10 Н (см. рисунок). Второй груз движется из состояния покоя с
ускорением 2 м/с2, направленным вверх. Коэффициент трения скольжения
первого груза по поверхности стола равен 0,2. Чему равна масса второго груза?
7. После удара шайба начала скользить вверх по шероховатой наклонной плоскости с начальной скоростью υ0 и после остановки соскользнула обратно. Выберите из предложенного перечня все верные утверждения, которые соответствуют результатам проведенным экспериментальным наблюдениям.
1) Время движения шайбы вверх больше времени движения шайбы вниз;
2) Модуль максимальной скорости шайбы при движении вниз меньше υ0;
3) При движении вверх и вниз работа силы трения шайбы о плоскость одинакова;
4) Изменение потенциальной энергии шайбы при движении до верхней точки равно кинетической энергии шайбы сразу после удара;
5) модуль
ускорения шайбы при движении вверх больше, чем модуль ускорения при движении
вниз.
Вариант 4
1. На наклонной плоскости находится брусок массой 10 кг, для которого составили таблицу зависимости модуля силы трения Fтр от угла наклона плоскости к горизонту α с погрешностью не более 0,01 Н. Основываясь на данных, приведенных в таблице, и используя закон сухого трения определите коэффициент трения скольжения и определите, при каких углах наклона брусок движется.
α, рад | 0 | 0,05 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 |
Fтр, Н | 0 | 2,0 | 4,0 | 7,72 | 7,52 | 7,26 | 6,92 | 6,5 | 6,02 | 5,5 | 4,9 | 4,26 |
2.
Груз массой 0,4 кг подвешен на пружине жёсткостью 100 Н/м к потолку
лифта, Лифт равноускоренно поднимается вверх на расстояние 5 м в течение 2 с.
Каково удлинение пружины при установившемся движении груза?
3. С вершины наклонной плоскости из состояния покоя скользит с ускорением лёгкая коробочка, в которой находится груз массой m (см. рисунок). Как изменятся время движения, ускорение и модуль работы силы трения, если с той же наклонной плоскости будет скользить та же коробочка с грузом массой 3m?
Для каждой величины определите соответствующий характер изменения:
А) ускорение 1) увеличится
Б) время движения 2) уменьшится
В) модуль работы силы трения 3) не изменится
4. В первой серии опытов брусок с грузом перемещали при помощи нити
равномерно и прямолинейно вверх по наклонной плоскости. Во второй серии опытов
точно так же перемещали этот брусок, закрепив на нём ещё один груз.
Как изменились при переходе от первой серии опытов ко второй сила натяжения нити и коэффициент трения между бруском и плоскостью?
Для каждой величины определите соответствующий характер её изменения:
А) сила натяжения нити 1) увеличилась
Б) коэффициент трения 2) уменьшилась
3) не изменилась
5. Брусок массой m соскальзывает из состояния покоя по наклонной плоскости высотой h и длиной S. Коэффициент трения между бруском и плоскостью μ. Установите соответствие между физическими величинами и формулами.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ ФОРМУЛЫ
А) ускорение бруска 1)
Б) скорость бруска в конце наклонной плоскости 2) 3)
3) )
4)
6.
Два груза, связанные
нерастяжимой и невесомой нитью, движутся по гладкой горизонтальной поверхности
под действием постоянной горизонтальной силы F, приложенной к
грузу М1 (см. рисунок). Нить обрывается
при значении силы натяжения нити 4 Н, при этом модуль силы F равен
10 Н. Чему равна масса первого груза М1, если
масса второго М2 =2 кг?
7. Брусок массой 0,5 кг покоится на шероховатой горизонтальной плоскости. На него начинают действовать горизонтальной силой F, модуль которой изменяется с течением времени так, как показано на рисунке. Коэффициент трения бруска о плоскость равен 0,2.
Выберите из предложенного перечня два утверждения, которые соответствуют результатам проведённого опыта.
1) В промежутке от 1 с до 2 с брусок покоился.
2) В момент времени 1,5
с сила трения, действующая на брусок, равна 1,5 Н.
3) Кинетическая энергия бруска в момент времени 1 с равна 0.
4) В момент времени 5 с ускорение бруска равно 2 м/с2.
5) В промежутке от 2 с до 4 с импульс бруска увеличился на 1 кг м/с.
5.4 Масса и вес | University Physics Volume 1
Цели обучения
К концу раздела вы сможете:
- Объяснять разницу между массой и весом
- Объясните, почему падающие объекты на Земле никогда не находятся в состоянии свободного падения
- Опишите понятие невесомости
Масса и вес часто используются как синонимы в повседневном разговоре. Например, наши медицинские записи часто показывают наш вес в килограммах, но никогда в правильных единицах измерения — ньютонах. Однако в физике есть важное различие. Вес — это притяжение Земли к объекту. Это зависит от удаленности от центра Земли. В отличие от веса, масса не зависит от местоположения. Масса объекта одинакова на Земле, на орбите или на поверхности Луны.
9{2}. [/latex]
Хотя почти во всем мире в качестве единицы силы используется ньютон, в США наиболее привычной единицей силы является фунт (фунт), где 1 Н = 0,225 фунта. lb человек весит 1000 Н.
Вес и гравитационная сила
Когда объект падает, он ускоряется по направлению к центру Земли. Второй закон Ньютона гласит, что результирующая сила, действующая на объект, отвечает за его ускорение. Если сопротивлением воздуха можно пренебречь, результирующая сила, действующая на падающий объект, представляет собой гравитационную силу, обычно называемую ее вес [латекс] \overset{\to }{w} [/латекс], или его сила тяжести, действующая на объект массой м . Вес можно обозначить как вектор, потому что он имеет направление; вниз — это, по определению, направление силы тяжести, и, следовательно, вес — это направленная вниз сила. Величина веса обозначается как w . Галилей сыграл важную роль в том, чтобы показать, что в отсутствие сопротивления воздуха все тела падают с одинаковым ускорением g .
Используя результат Галилея и второй закон Ньютона, мы можем вывести уравнение для веса.
Рассмотрим объект массой м , падающий на Землю. На него действует только нисходящая сила тяжести, которая представляет собой вес [латекс] \overset{\to }{w} [/латекс]. Второй закон Ньютона гласит, что величина чистой внешней силы, действующей на объект, равна [латекс] {\ overset {\ to {F}} _ {\ text {net}} = m \ overset {\ to }{a}. [/latex] Мы знаем, что ускорение объекта под действием силы тяжести равно [латекс] \overset{\to }{g}, [/latex] или [латекс] \overset{\to }{a}=\overset{ \к {г} [/латекс]. Подставив их во второй закон Ньютона, мы получим следующие уравнения. 9{2})=9,80\,\текст{N}. [/latex]
Когда чистая внешняя сила, действующая на объект, представляет собой его вес, мы говорим, что это свободное падение , то есть единственная сила, действующая на объект, — это гравитация. Однако когда объекты на Земле падают вниз, они никогда не находятся в состоянии свободного падения, потому что на объект всегда действует некоторая направленная вверх сила сопротивления воздуха.
{2} [/латекс]. Таким образом, масса 1,0 кг имеет вес 90,8 с. ш. на Земле и всего около 1,7 с. ш. на Луне.
Самое широкое определение веса в этом смысле состоит в том, что вес объекта — это гравитационная сила, действующая на него со стороны ближайшего крупного тела, такого как Земля, Луна или Солнце. Это наиболее распространенное и полезное определение веса в физике. Однако оно резко отличается от определения веса, используемого НАСА и популярными средствами массовой информации в связи с космическими путешествиями и исследованиями. Когда они говорят о «невесомости» и «микрогравитации», они имеют в виду явление, которое в физике называется «свободным падением». Мы используем предыдущее определение веса, силы [латекс] \overset{\to }{w} [/латекс] из-за гравитации, действующей на объект массой м , и мы тщательно различаем свободное падение и фактическую невесомость.
Имейте в виду, что вес и масса — разные физические величины, хотя и тесно связанные между собой. Масса — это внутреннее свойство объекта: это количество материи.
Количество или количество материи объекта определяется количеством содержащихся в нем атомов и молекул различных типов. Поскольку эти числа не меняются, в ньютоновской физике масса не меняется; следовательно, его реакция на приложенную силу не меняется. Напротив, вес — это гравитационная сила, действующая на объект, поэтому он зависит от гравитации. Например, человек ближе к центру Земли, на небольшой высоте, такой как Новый Орлеан, весит немного больше, чем человек, который находится на большей высоте в Денвере, даже если они могут иметь одинаковую массу.
Заманчиво приравнять массу к весу, потому что большинство наших примеров происходят на Земле, где вес объекта лишь немного зависит от местоположения объекта. Кроме того, трудно сосчитать и идентифицировать все атомы и молекулы в объекте, поэтому масса редко определяется таким образом. Если мы рассмотрим ситуации, в которых [латекс] \overset{\to }{g} [/latex] является константой на Земле, мы увидим, что вес [латекс] \overset{\to }{w} [/latex] непосредственно пропорциональна массе m , так как [латекс] \overset{\to }{w}=m\overset{\to }{g}, [/latex], то есть чем массивнее объект, тем больше он весит.
{2} [/латекс], объект весит 8,4 Н. Однако масса объекта по-прежнему составляет 5,0 кг. на Луне. 9{2}? [/latex]
Стратегия
Нам дан вес камня, который мы используем для нахождения чистой силы, действующей на камень. Однако нам также необходимо знать его массу, чтобы применить второй закон Ньютона, поэтому мы должны применить уравнение для веса, [латекс] w = мг [/латекс], чтобы определить массу.
Решение
Никакие силы не действуют в горизонтальном направлении, поэтому мы можем сосредоточиться на вертикальных силах, как показано на следующей диаграмме свободного тела. Мы обозначаем ускорение в сторону; технически это не часть диаграммы свободного тела, но помогает напомнить нам, что объект ускоряется вверх (поэтому результирующая сила направлена вверх). 9{2})\hfill \\ \hfill F-180\,\text{N}& =\hfill & 27\,\text{N}\hfill \\ \hfill F& =\hfill & 207\,\text{ N}=210\,\text{N до двух значащих цифр}\hfill \end{array} [/latex]
Значение
Чтобы применить второй закон Ньютона в качестве основного уравнения при решении задачи, иногда приходится полагаться на другие уравнения, например, на вес или одно из кинематических уравнений, чтобы завершить решение.
Проверьте свои знания
Для (Пример) найдите ускорение, когда сила, приложенная фермером, равна 230,0 Н.
Показать решение
Сможете ли вы избежать поля с валунами и благополучно приземлиться прямо перед тем, как закончится топливо, как это сделал Нил Армстронг в 1969 году? Эта версия классической видеоигры точно имитирует реальное движение лунного посадочного модуля с правильной массой, тягой, расходом топлива и лунной гравитацией. Настоящим лунным посадочным модулем трудно управлять.
Используйте эту интерактивную симуляцию, чтобы перемещать Солнце, Землю, Луну и космическую станцию, чтобы увидеть влияние их гравитационных сил и орбитальных траекторий. Визуализируйте размеры и расстояния между различными небесными телами и отключите гравитацию, чтобы увидеть, что было бы без нее. 9{2} [/латекс]. В этой задаче силы действуют на сиденье и ремень безопасности.
Тело массой 2,00 кг толкают вертикально вверх под действием вертикальной силы 25,0 Н.
Каково его ускорение?
Показать решение
Автомобиль массой 12 500 Н трогается с места и разгоняется до 83,0 км/ч за 5,00 с. Сила трения равна 1350 Н. Найти приложенную силу двигателя.
Предполагается, что тело массой 10,0 кг находится в гравитационном поле Земли с [латексом] g=9{2}, [/latex] какова величина его приложенной силы?
Бейсболист выполняет трюк для телевизионной рекламы. Он поймает бейсбольный мяч (массой 145 г), брошенный с высоты 60,0 м над перчаткой. Его перчатка останавливает мяч за 0,0100 с. С какой силой его перчатка действует на мяч?
Показать решение
Когда Луна находится прямо над головой на закате, сила воздействия Земли на Луну, [латекс] {F}_{\text{EM}} [/латекс], по существу составляет [латекс] 9{22}\,\text{kg}, [/latex] определяют величину ускорения Луны.
Torque — AP Physics 1
All AP Physics 1 Ресурсы
7 Диагностические тесты 170 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
AP Physics 1 Справка » Ньютоновская механика » Круговое, вращательное и гармоническое движение » Круговое и вращательное движение » Крутящий момент
Болт, соединяющий основную и заднюю раму горного велосипеда, требует крутящего момента для затяжки.
Если вы можете приложить усилие к ключу в любом заданном направлении, какова минимальная длина ключа, которая приведет к необходимому крутящему моменту?
Возможные ответы:
Правильный ответ:
Объяснение:
Минимальная длина ключа предполагает, что максимальная сила приложена под углом . Следовательно, мы можем использовать упрощенное выражение для крутящего момента:
Здесь это длина ключа.
Переставляя длину и подставляя наши значения, получаем:
Сообщить об ошибке
Однородный стержень длиной 50 см и массой 0,2 кг помещен на точку опоры на расстоянии 40 см от левого конца стержня. . На каком расстоянии от левого конца стержня нужно подвесить груз массой 0,6 кг, чтобы уравновесить стержень?
Возможные ответы:
50см
45см
42см
48см
Штанга не может быть сбалансирована с этой массой
Правильный ответ:
45см
Объяснение:
Крутящие моменты против часовой стрелки и по часовой стрелке относительно точки поворота должны быть равными, чтобы стержень мог балансировать.
Принимая точку опоры за точку поворота, крутящий момент против часовой стрелки возникает из-за веса стержня, гравитационной силы, действующей вниз в центре стержня. Если мы используем точку опоры в качестве точки отсчета, то центр стержня находится на расстоянии 15 см от точки отсчета.
Установите равным крутящему моменту по часовой стрелке из-за дополнительной массы на расстоянии r справа от оси вращения.
.
Решение для r дает r = 0,05 м справа от оси, то есть 40 + 5 см от левого конца стержня.
Сообщить об ошибке
Груз массой 2 кг подвешен на веревке, которая наматывается на закрепленный на потолке блок без трения с массой 0,01 кг и радиусом 0,25 м. Другой конец веревки прикреплен к невесомой подвесной платформе, на которую можно поместить груз массой 0,5 кг. В то время как система изначально находится в равновесии, веревка позже перерезается над весом, а платформа впоследствии поднимается, потянув за веревку.
Каков крутящий момент на шкиве, когда система неподвижна?
Возможные ответы:
10N*M
19.
6n*M
0n*M
9.8n*M
Правильный ответ:
0n*M
Объяснение:
Чистый крутящий момент на шкиве равен нулю. Помните, что если предположить, что сила действует перпендикулярно радиусу. Поскольку в этой задаче шкив симметричен (это означает, что r одинаково) и натяжение всей веревки одинаково (это означает, что F одинаково), мы знаем, что крутящий момент против часовой стрелки компенсирует крутящий момент по часовой стрелке, таким образом, сеть крутящий момент равен нулю.
На изображении ниже T 1 (из-за платформы с 4 грузами по 0,5 кг) = T 2 (масса 2 кг).
Сообщить об ошибке
Два ученика балансируют на 10-метровых качелях. Качели сконструированы таким образом, что каждая сторона качелей имеет длину 5 м. Студент слева весит 60 кг и стоит в трех метрах от центра. Студент справа весит 45 кг. Качели параллельны земле.
Предположим, что доска, на которой качаются качели, не имеет массы.
На каком расстоянии от центра должен находиться ученик справа, если он хочет, чтобы качели оставались параллельными земле?
Возможные ответы:
Правильный ответ:
Объяснение:
Крутящий момент определяется уравнением . Поскольку оба студента будут прилагать направленную вниз силу, перпендикулярную длине качелей, . В нашем случае сила — это сила тяжести, указанная ниже, и расстояние от центра качелей.
Поскольку крутящий момент должен быть равен нулю, чтобы качели оставались параллельными (не двигались), более легкий ученик справа должен сделать свой крутящий момент справа равным крутящему моменту ученика слева. Мы можем определить требуемое расстояние, установив их крутящие моменты равными друг другу.
Сообщить об ошибке
Два ученика балансируют на 10-метровых качелях.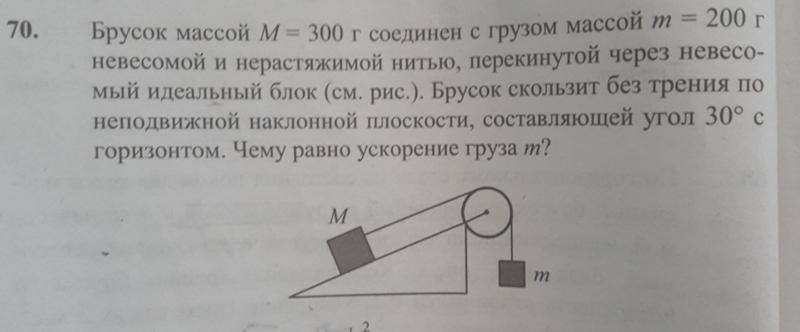
Качели сконструированы таким образом, что каждая сторона качелей имеет длину 5 м. Студент слева весит 60 кг и стоит в трех метрах от центра. Студент справа весит 45 кг. Качели параллельны земле. Предположим, что доска, на которой качаются качели, не имеет массы.
Представьте, что два студента сидят на качелях так, что крутящий момент равен . Какое из следующих изменений изменит крутящий момент качелей?
Возможные ответы:
Оба ученика перемещаются к центру на один метр.
Более тяжелый ученик продвинулся вперед на 1 м, а более легкий — на 1,33 м.
Еще один ученик стоит прямо в центре качелей.
Еще два ученика садятся на качели, каждый весом 45 кг. Они оба сидят на противоположных концах качелей, в пяти метрах от центра.
Правильный ответ:
Оба ученика перемещаются к центру на один метр.
Объяснение:
Крутящий момент в данном случае зависит как от силы, прилагаемой учениками, так и от их расстояния от точки вращения.
В результате оба ученика, продвинувшись вперед на один метр, вызовут ненулевой крутящий момент на качелях. Это связано с тем, что соотношение силы и расстояния более тяжелого ученика приведет к меньшему крутящему моменту на его стороне, чем у более легкого ученика.
Сообщить об ошибке
Трехметровая балка незначительного веса находится в равновесии с точкой опоры, расположенной на расстоянии 1 м от ее левого конца. Если к его правому концу приложить силу 50 Н, то какую силу нужно будет приложить к левому концу?
Возможные ответы:
Правильный ответ:
Пояснение:
Это пример вращательного равновесия с участием крутящего момента. Формула для крутящего момента: , где — угол, который вектор силы составляет с объектом, находящимся в равновесии, и — расстояние от точки опоры до точки вектора силы.
Для достижения равновесия наши крутящие моменты должны быть равны.
Поскольку силы приложены перпендикулярно балке, становится равным 1. Расстояние от точки опоры до левого конца равно 1 м, а расстояние до правого конца равно 2 м.
Поскольку сила 50 Н в два раза дальше от точки опоры, чем сила, которая должна быть приложена к левой стороне, она должна быть вдвое меньше, чем сила слева. Сила слева может быть равна 100 Н.
Сообщить об ошибке
Одна сторона качелей несет груз в четырех метрах от точки опоры и груз в двух метрах от точки опоры. Чтобы уравновесить качели, какую массу нужно поместить в девяти метрах от точки опоры на стороне, противоположной первым двум массам?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы качели были сбалансированы, система должна находиться в равновесии вращения.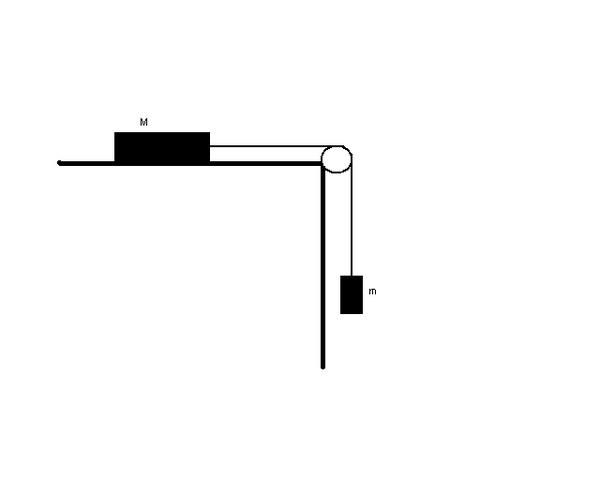
Чтобы это произошло, крутящий момент должен быть одинаковым с обеих сторон.
Общий крутящий момент должен быть одинаковым с обеих сторон, чтобы чистый крутящий момент был равен нулю.
Подставьте формулу для крутящего момента в это уравнение.
Теперь мы можем использовать данные значения для определения недостающей массы.
Ускорение силы тяжести исключается из каждого члена.
Сообщить об ошибке
Две массы висят под безмассовой измерительной рейкой. Масса 1 расположена на отметке 10 см при весе 15 кг, а масса 2 расположена на отметке 60 см при весе 30 кг. В какой точке между двумя массами должна быть прикреплена нить, чтобы уравновесить систему?
Возможные ответы:
Правильный ответ:
Пояснение:
Эта задача касается крутящего момента и равновесия.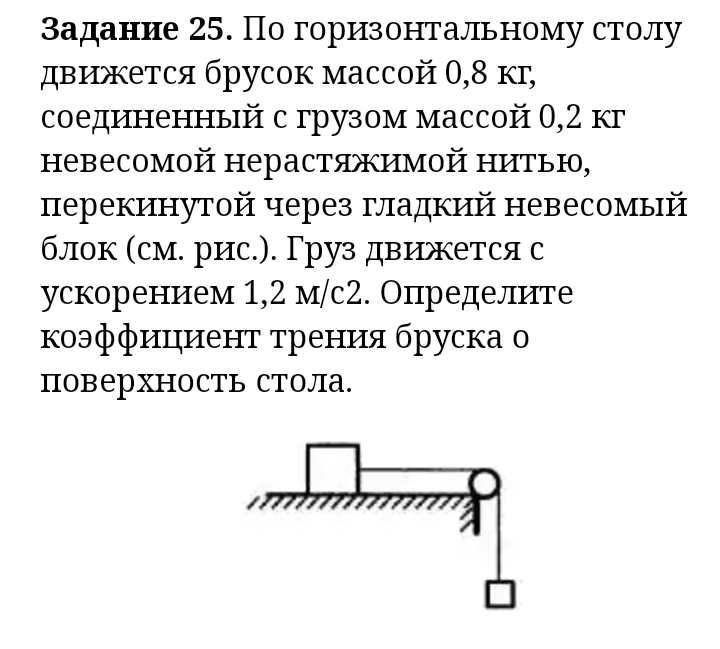
Отметив, что струна находится между двумя массами, мы можем использовать уравнение крутящего момента . Мы можем использовать уравнение, чтобы найти крутящий момент. Поскольку сила перпендикулярна расстоянию, мы можем использовать уравнение (синус 90 o равен 1). Сила, присутствующая в этой ситуации, — это гравитация, поэтому F=mg, и, используя переменную x в качестве позиции для строки, мы можем найти r.
x=43, таким образом, нить находится на отметке 43см.
Сообщить об ошибке
Аттракцион в музее науки помогает учащимся узнать о силе крутящего момента. Есть длинная металлическая балка с одной точкой поворота. На одном конце перекладины висит полноценный седан, а на другом конце веревка, за которую студенты могут тянуть вниз, поднимая автомобиль над землей.
Балка имеет длину 40 метров, а точка поворота находится на расстоянии 5 метров от одного конца. На коротком конце балки висит автомобиль массой 500 кг. Пренебрегая массой балки, какова минимальная масса студента, который может повиснуть на веревке и начать поднимать автомобиль с земли?
Возможные ответы:
Дополнительная информация необходима для ответа
Правильный ответ:
Объяснение:
Мы пытаемся найти, какую силу нужно приложить к веревке, чтобы получить нулевой крутящий момент на балке.
Leave A Comment