{\circ}$

Свойства биссектрис

  1. Теорема (Свойство биссектрисы). Биссектриса внутреннего угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон (рис. 2):

    $$\frac{x}{y} = \frac{a}{b}$$

  2. Биссектрисы внутренних углов треугольника пересекаются в одной точке, называемой инцентром, в центре вписанной в этот треугольник окружности.
  3. Биссектрисы одного внутреннего и двух внешних углов треугольника пересекаются в одной точке. Эта точка является центром одной из трех вневписанных окружностей этого треугольника.
  4. Основания биссектрис двух внутренних и одного внешнего углов треугольника лежат на одной прямой, если биссектриса внешнего угла не параллельна противоположной стороне треугольника.
  5. Если биссектрисы внешних углов треугольника не параллельны противоположным сторонам, то их основания лежат на одной прямой.

  6. Теорема Штейнера-Лемуса

    . Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный.

    Якоб Штейнер (1796 — 1863) — швейцарский математик, основатель синтетической геометрии кривых линий и поверхностей 2-го и высших порядков. Даниель Христиан Лудольф Лемус (1780 — 1863) — французский математик.

  7. Построение треугольника по трем заданным биссектрисам с помощью циркуля и линейки невозможно, причём даже при наличии трисектора.
  8. В равнобедренном треугольнике биссектриса угла, противоположного основанию, является медианой и высотой.

  9. Расстояния от сторон угла до любой точки биссектрисы одинаковы.

    Если задан треугольник со сторонами $a$, $b$ и $c$, то длина биссектрисы, проведенной к стороне $c$, вычисляется по формуле:

    $$l_{c}=\frac{\sqrt{a b(a+b+c)(a+b-c)}}{a+b}$$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. В треугольнике $ABC$ проведена биссектриса $AD$. Найти периметр треугольника, если $AC=4$, $DC=2$ и $BD=3$.

Решение. Сделаем чертеж (рис. 3).

По теореме про свойство биссектрисы имеем:

$$\frac{B D}{D C}=\frac{A B}{A C} \Rightarrow \frac{3}{2}=\frac{A B}{4} \Rightarrow A B=\frac{3 \cdot 4}{2}=6$$

А тогда периметр треугольника, как сумма всех сторон, равен:

$$P_{\Delta A B C}=6+3+2+4=15$$

Ответ. $P_{\Delta A B C}=15$

Читать дальше: что такое вершина угла.

Биссектриса углов треугольника

См. также биссектриса угла.

Биссектриса треугольника – отрезок биссектрисы угла, соединяющий вершину этого угла с точкой на противолежащей стороне.

У биссектрис угла треугольника есть масса свойств, которые описываются через свойства треугольника. Это поможет в решении задач.

Свойства биссектрис треугольника

  • Биссектриса треугольника, проведенная из данной вершины, тождественна биссектрисе соответствующего угла. Биссектриса угла треугольника, выходящая из его вершины, делит этот угол треугольника пополам 

  • Все три биссектрисы треугольника пересекаются в одной точке

    , которая расположена всегда в плоскости треугольника и является центром вписанной окружности. Примечание. Имеются ввиду биссектрисы внутренних углов треугольника.

  • Каждая биссектриса треугольника делится точкой пересечения биссектрис в отношении суммы прилежащих сторон к противолежащей, считая от вершины

  • Биссектриса  любого внутреннего угла треугольника делит противоположную сторону на части, пропорциональные сторонам треугольника
  • Биссектрисы одного внутреннего и двух внешних углов треугольника пересекаются в одной точке. Эта точка — центр одной из трёх вневписанных окружностей этого треугольника.
  • Угол между биссектрисами двух смежных углов (между внутренними и внешними биссектрисами углов треугольника при одной вершине) равен 90 градусам

Свойства биссектрис равнобедренного треугольника


  • У равнобедренного треугольника медиана, биссектриса и высота, проведенные к основанию треугольника, совпадают

  • Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса), и третья биссектриса одновременно является медианой и высотой того угла, из которого она выходит.

  • В равнобедренном треугольнике две биссектрисы равны, а третья биссектриса является его медианой и высотой


  • Одна и только одна биссектриса внешнего угла неравностороннего треугольника может быть параллельна противоположной стороне — основанию, если треугольник равнобедренный

Свойства биссектрис равностороннего треугольника

Формулы нахождения биссектрисы угла



a, b, c — стороны треугольника, при этом биссектриса проведена из угла, находящегося между сторонами a, b
α,β,γ — углы треугольника, противолежащие сторонам a,b,c соответственно
p — полупериметр треугольника (половина суммы всех его сторон)

ca, cb — отрезки, на которые биссектрисой, проведенной из угла c разбита сторона c

lc — длина биссектрисы, проведенной к стороне c из угла γ.

Длина биссектрис треугольника может быть выражена через равенство с квадратом суммы всех его сторон.


Формулы нахождения расстояния от угла до точки пересечения биссектрис



где

lco — длина отрезка, лежащего на биссектрисе от вершины угла до центра пересечения биссектрис

r — радиус окружности, вписанной в треугольник
R — радиус описанной окружности
a, b, c — стороны треугольника, при этом биссектриса проведена из угла, находящегося между сторонами a, b
γ — угол треугольника, противолежащий стороне c 
p — полупериметр треугольника (половина суммы всех его сторон) 

Примеры решения задач

Примечание. В данном уроке изложены задачи по геометрии о биссектрисе. Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме.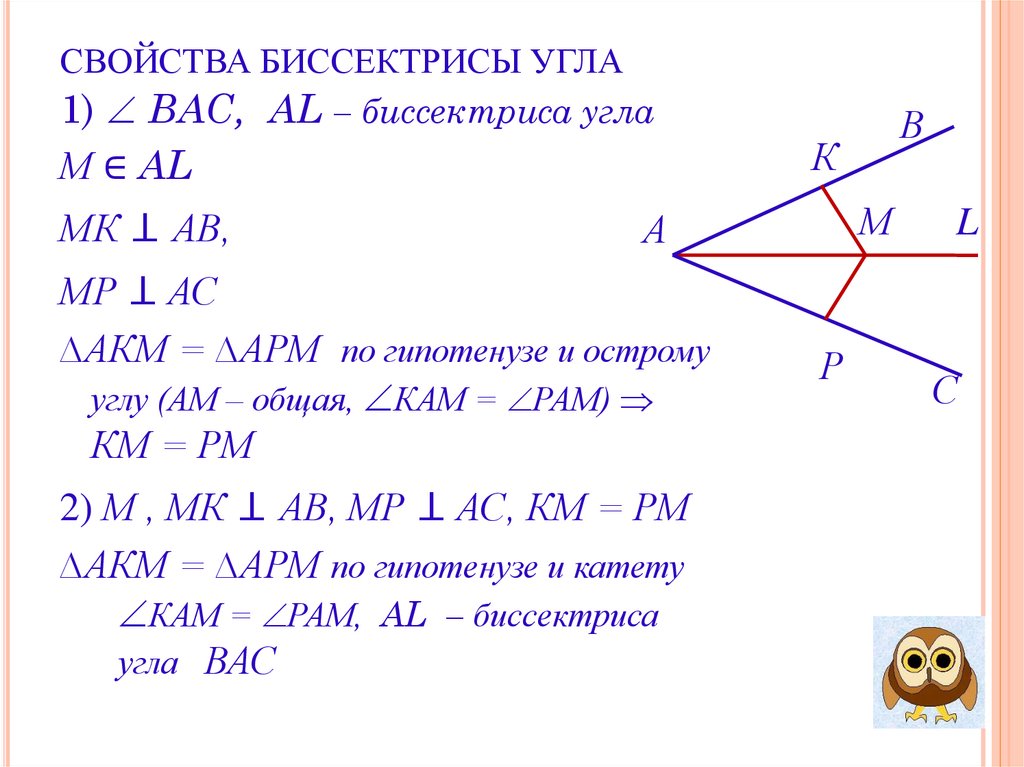

Почти наверняка курс будет дополнен.


Задача.

Луч AD является биссектрисой угла A. На сторонах угла A отмечены точки B,C так что угол ADC равен углу ADB. Доказать, что AB=AC.

Решение.
Рассмотрим треугольники ADB и ADC. Сторона AD у них общая, углы DAC и DAB равны, так как биссектриса AD делит угол А пополам, а углы ADC и ADB равны по условию задачи. Таким образом, треугольники ADB и ADC равны по стороне и двум углам.

Следовательно AB = AC.

0  

 Биссектриса угла | Описание курса | Биссектриса внешнего угла 

   

Теорема

о биссектрисе угла

Горячая математика

Предупреждение: это имя используется по-разному в разных учебниках. В некоторых учебниках это относится к теореме, которая утверждает, что любая точка биссектрисы угла равноудалена от двух сторон угла.

То, что большинство учебников называют теоремой биссектрисы угла, звучит так:

Ан биссектриса угла в треугольнике делит противоположную сторону на два отрезка, которые находятся в той же пропорции, что и две другие стороны треугольника.

На рисунке выше п л ¯ делит пополам ∠ р п Вопрос , так р л л Вопрос «=» п р п Вопрос .

Ан биссектриса угла угла треугольника делит противоположную сторону на два отрезка, пропорциональных двум другим сторонам треугольника.

По теореме о биссектрисе угла

Б Д Д С «=» А Б А С

Доказательство:

Рисовать Б Е ↔ ∥ А Д ↔ .

Продлевать С А ¯ встречаться Б Е ↔ в точку Е .

По теореме о боковых делителях

С Д Д Б «=» С А А Е ———(1)

Углы ∠ 4 и ∠ 1 соответствующие углы.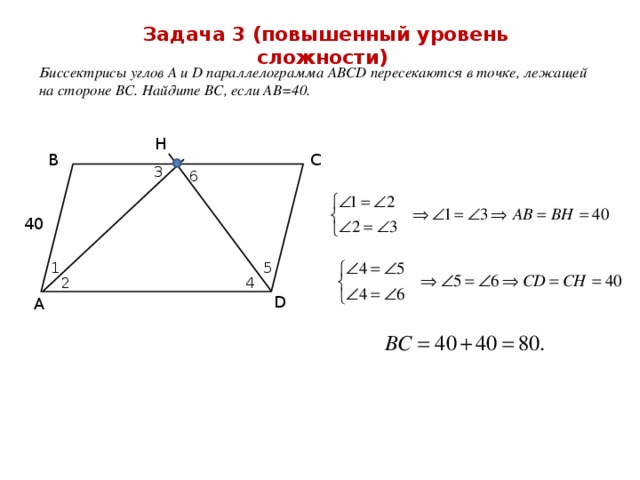

Так, ∠ 4 ≅ ∠ 1

С А Д ¯ это биссектриса угла ∠ С А Б , ∠ 1 ≅ ∠ 2 .

Посредством Теорема об альтернативном внутреннем угле , ∠ 2 ≅ ∠ 3 .

Следовательно, по свойству транзитивности ∠ 4 ≅ ∠ 3 .

Так как углы ∠ 3 и ∠ 4 являются конгруэнтный , треугольник Δ А Б Е является равнобедренный треугольник с А Е «=» А Б .

Замена А Е к А Б в уравнении (1),

С Д Д Б «=» С А А Б

Пример:

Найдите значение Икс .

По теореме треугольник-угол-биссектриса

А Б Б С «=» А Д Д С .

Заменять.

5 12 «=» 3,5 Икс

Крест умножить.

5 Икс «=» 42

Разделите обе части на 5 .

5 Икс 5 «=» 42 5 Икс «=» 8.4

Значение Икс является 8.4 .

Угол бисектор Теорема (определение, примеры и видео)

Написано

Malcolm McKinsey

Проверясь по факту

Paul Mazzola

Угла Bisector Bisector Bisector Bisector.

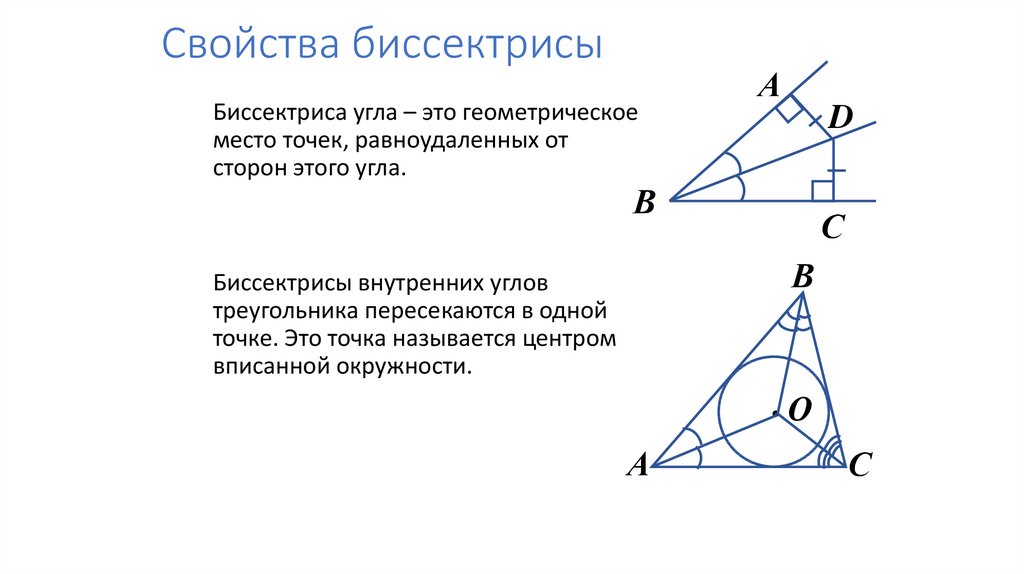 помогает найти неизвестные длины сторон треугольников, поскольку биссектриса делит сторону, противоположную этому углу, на два отрезка, которые пропорциональны двум другим сторонам треугольника.

Определение биссектрисы угла

Как построить биссектрису угла

Начертите △ABC  на листе бумаги. Внутренние углы A, B, C имеют противоположные стороны a, b, c .

Получите линейный объект и поместите одну конечную точку в ∠A . Позвольте другому концу пересекать сторону аа. Разделите ∠A на два равных угла. Вы  разделили пополам   ∠A .

Линейный объект представляет собой биссектрису угла . Когда он пересек сторону аа, противоположную ∠A , он разделил △ABC на два меньших треугольника и разделил сторону аа на две части.

Биссектриса угла Теорема

Замените ваш объект нарисованным отрезком или лучом. Там, где биссектриса угла пересекает сторону аа, обозначьте точку D . Биссектриса угла теперь является отрезком AD и образует два меньших треугольника: △ACD и △ABD . Сторона aa теперь состоит из двух отрезков: CD и DB .

Теорема о биссектрисе угла

Одна из версий теоремы о биссектрисе угла: биссектриса угла треугольника делит противоположную сторону внутреннего угла на два отрезка, которые пропорциональны двум другим сторонам треугольника.

Биссектриса угла AD делит сторону aa на два отрезка: CD и DB . CD и DB относятся к сторонам b ( CA ) и c ( BA ) в той же пропорции, что и CA и BA связаны друг с другом. △ACD  и  △ABD , созданные биссектрисой угла, также пропорциональны.

Теорема о биссектрисе угла. Пример треугольника

Соотношения и пропорции

Соотношения сравнивают значения. Вы можете установить отношения между сторонами CA и BA и отрезками CD и DB .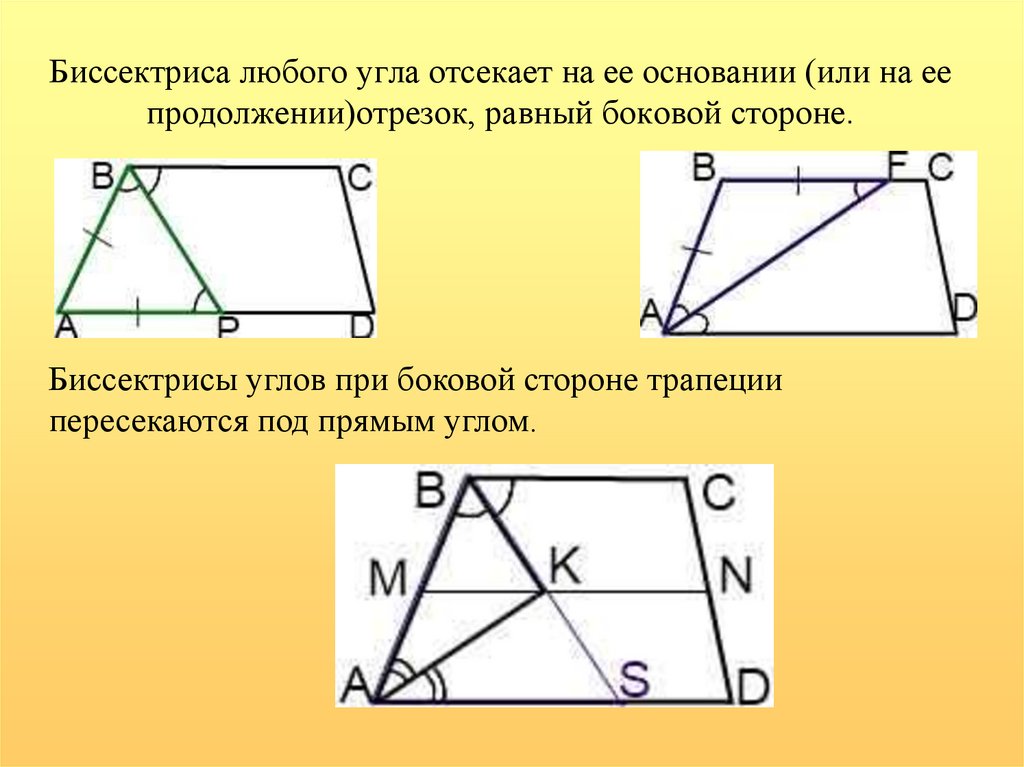 Пропорции  сравнить пропорции; вы можете узнать, равны ли два отношения.

Для △ABC  с биссектрисой угла AD , сторонами CA  и BA , а также стороной aa, разделенной на CD и DB , мы можем сравнить их отрезки и отношения между сторонами и линиями: между ними можно установить отношения и отношения между сторонами и отрезками.

Отрезок CD (от биссектрисы угла AD ) имеет такое же отношение к отрезку DB , как сторона треугольника CA относится к стороне BA .

Будьте внимательны, чтобы правильно установить коэффициенты. CD  – меньший из двух отрезков, поэтому он является числителем нашего отношения. DB  – это более длинный сегмент линии. Таким образом, CD относится к DB , поскольку более короткая сторона треугольника CA относится к более длинной стороне треугольника BA .

Появляются и другие коэффициенты. Сравните отрезки стороны, разделенной на биссектрису угла, с остальными сторонами:

Отношения и пропорции биссектрисы угла

Отношения двух сторон нового, меньшего  △CDA  та же связь, что и две стороны нового, меньшего  △DBA .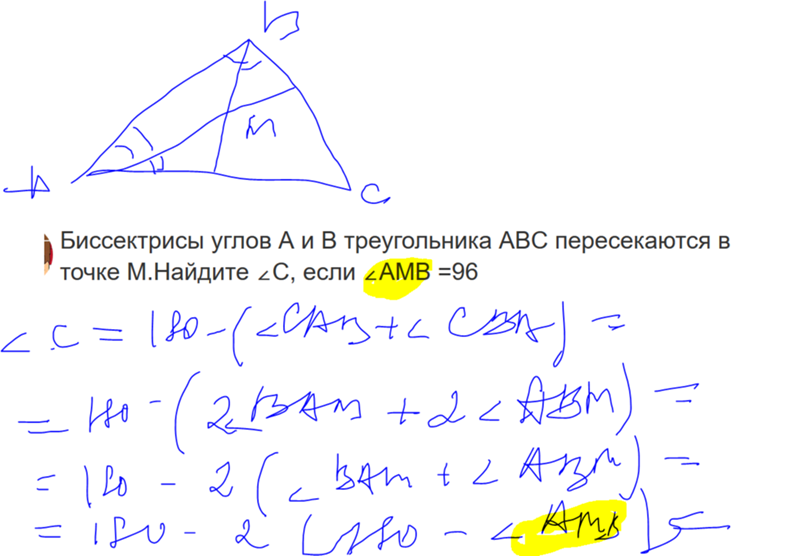 Они в одинаковых пропорциях.

Примеры биссектрисы угла

Откуда вы знаете, что отрезок, выходящий из внутреннего угла, является биссектрисой угла? Проверьте соотношения.

Предположим, нам говорят, что отрезок AD делит сторону а на CD и DB , длины 10 см и 30 см . Нам также говорят, что сторона CA  это 30 см и сбоку BA  это 90 см . Посмотрите, пропорциональны ли отношения друг другу:

Теорема о биссектрисе угла Примеры

Мы видим, что 1030\frac{10}{30}3010 – это то же отношение, что и 3090\frac{30}{90}9030​, поэтому  AD является биссектрисой угла.

Биссектриса угла треугольника

Использование теоремы о биссектрисе угла для нахождения неизвестной стороны

сторона c . Биссектриса угла делит сторону a на CD и DB (общая длина стороны a , CB ).

Предположим, что эти длины:

Вспомним наши соотношения и подставим значения:

Теорема о биссектрисе угла — Решение длины стороны frac{500}{10}10500​) , мы получаем BA=50 метровBA=50 метровBA=50 метров.