Задание 26 ОГЭ по математике. Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=9 и MB=12.

© 2007 — 2023 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.

Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.


Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.

Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.

Фотографии предоставлены

Главная → Видеоуроки →  ОГЭ (ГИА) по математике. Задача 26.

Описание видеоурока:

Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=9 и MB=12. Касательная к описанной окружности треугольника ABC, проходящая через точку С, пересекает прямую AB в точке D. Найдите CD.

Валерий Волков 3 21.07.2018

Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями!

Новости образования

ЕГЭ по математике

Профильный уровень

Задание 1     Задание 2

Задание 3     Задание 4

Задание 5     Задание 6

Задание 7     Задание 8

Задание 9     Задание 10

Задание 11     Задание 12

Задание 13     Задание 14

Задание 15     Задание 16

Задание 17     Задание 18

Задание 19     Задание 20

Задание 21

ГИА по математике

Задача 1     Задача 2

Задача 3     Задача 4

Задача 5     Задача 6

Задача 7     Задача 8

Задача 9     Задача 10

Задача 11     Задача 12

Задача 13     Задача 14

Задача 15     Задача 16

Задача 17     Задача 18

Задача 19     Задача 20

Задача 21     Задача 22

Задача 23     Задача 24

Задача 25     Задача 26

Демонстрационные варианты ОГЭ по математике

Математика. 5 класс.

Натуральные числа

Обыкновенные дроби

Десятичные дроби

Проценты

Математика. 6 класс.

Делимость чисел

Сложение и вычитание дробей с разными знаменателями

Умножение и деление обыкновенных дробей

Отношения и пропорции

Положительные и отрицательные числа

Измерение величин

Математика. 7 класс.

Преобразование выражений

Многочлены

Формулы сокращенного умножения

Математика. 8 класс.

Модуль числа. Уравнения и неравенства.

Квадратные уравнения

Квадратные неравенства

Уравнения с параметром

Задачи с параметром

Математика. 9 класс.

Функции и их свойства

Прогрессии

Векторы

Комбинаторика, статистика и теория вероятностей

Математика. 10 — 11 класс.

Числовые функции

Тригонометрические функции

Тригонометрические уравнения

Преобразование тригонометрических выражений

Производная

Степенные функции

Показательная функция

Логарифмические функции

Первообразная и интеграл

Уравнения и неравенства

Комбинаторика

Создаёте видеоуроки?

Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала.

Актуально

Физкультминутки для школьников и дошкольников

Подготовка к ЕГЭ Подготовка к ОГЭ

Задание №26 ОГЭ по математике с решением

Разбор типовых вариантов заданий №26 ОГЭ по математике

Первый вариант задания

Биссектриса СМ треугольника ABC делит сторону АВ на отрезки AM = 5 и MB =10. Касательная к описанной окружности треугольника ABC, проходящая через точку С, пересекает прямую АВ в точке D. Найдите CD.

Алгоритм решения:
  1. Делаем чертеж.
  2. Определяем равенство угла между касательной и хордой и угла АВС.
  3. Определяем соотношение отрезков из свойства биссектрисы угла треугольника и найдем АВ.
  4. Показываем, что треугольники DAC и DCB подобны.
  5. Составляем соотношения сторон подобных треугольников.
  6. Составляем систему равенств.
  7. Решаем систему.
  8. Записываем ответ.
Решение:

1. Выполняем чертеж данной задачи:

2. Рассматриваем АСD. В нем:

Согласно свойству углов окружности, касательной и секущей, угол, который образован этими линиями, равен половине градусной меры дуги, заключенной между сторонами этого угла. ∠DСА равен половине градусной меры дуги АС, заключенной между его сторонами СD и СА.
Но вписанный ∠СВА опирается на ту же дугу АС и по свойству вписанного угла равен половине меры этой дуги. Следовательно, ∠ СВА=∠ АСD.
3. Согласно свойству биссектрисы угла треугольника, она делит АВ на отрезки АМ и МВ, пропорциональные сторонам АС и ВС.  Таким образом,

4. Рассмотрим DAC и DCB. У них:

∠ DCA = ∠ DBC по доказанному выше,

∠ D – общий.

Следовательно, DAC DCB по двум углам.

5. Из определения и свойств подобных треугольников имеем:

6. Составим систему равенств:

7. Решим систему:

Ответ: 10.

Второй вариант задания

Биссектриса СМ треугольника ABC делит сторону АВ на отрезки AM = 9 и MB = 12. Касательная к описанной окружности треугольника ABC, проходящая через точку С, пересекает прямую АВ в точке D. Найдите CD.

Алгоритм решения:
  1. Сделаем чертеж.
  2. Определим равенство углов CDB и АВС.
  3. Определим соотношение отрезков, воспользовавшись свойством биссектрисы угла треугольника, и определим длину АВ.
  4. Покажем, что треугольники DAC и DCB подобны.
  5. Составим соотношения сторон подобных треугольников.
  6. Составим систему равенств.
  7. Решим систему.
  8. Запишем ответ.
Решение:

1. Делаем чертеж.

2. Рассмотрим АСD. В нем, согласно свойству углов окружности, касательной и секущей,
угол, который образован этими линиями, равен половине градусной меры дуги, заключенной между сторонами этого угла.
⇒∠DСА равен половине градусной меры дуги АС, заключенной между его сторонами СD и СА.
Но вписанный ∠СВА опирается на ту же дугу АС и по свойству вписанного угла равен половине меры этой дуги. Следовательно, ∠ СВА=∠ АСD.
3. Согласно свойству биссектрисы угла треугольника, согласно которому она делит АВ на отрезки АМ и МВ, пропорциональные сторонам АС и ВС. Таким образом,

4. Рассмотрим DAC и DCB. У них:

∠ DCA = ∠ DBC по доказанному выше,

∠ D – общий.

Значит, DAC DCB по двум углам.

5. Из определения и свойств подобных треугольников имеем:

6. Составим систему равенств:

7. Решим систему:

Отсюда

Так как AD = DB-21, имеем:

Таким образом, искомая длина CD=36.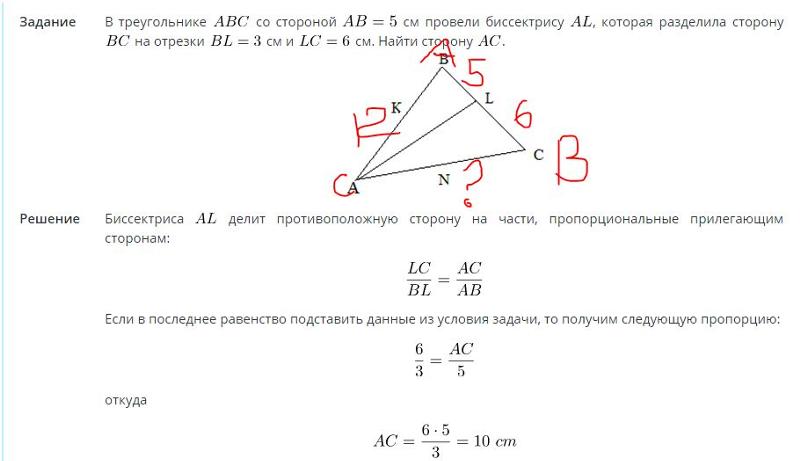

Ответ: 36.

Четвертый вариант задания

Точки М и N лежат на стороне АС треугольника ABC на расстояниях соответственно 9 и 11 от вершины А. Найдите радиус окружности, проходящей через точки М и N и касающейся луча АВ, если cos ∠BAC = √11 / 6

Алгоритм решения:
  1. Сделаем чертеж.
  2. Установим подобие треугольников AFM и ANF.
  3. Определим сторону FM.
  4. Определим ∠FNA.
  5. Найдем .
  6. Составим теорему синусов и найдем радиус окружности.
  7. Запишем ответ.
Решение:

1. Рассмотрим треугольники AFM и ANF. У них:

Угол A является общим, а

 по доказанному выше.

Следовательно, треугольник AFM подобен треугольнику ANF по двум углам. Отсюда вытекает:

3. В треугольнике AFM сторона AF=3, сторона AM=9. Воспользуемся теоремой косинусов для определения FM:

Полученное значение означает, что AFM является равнобедренным. У него основание AF.

4. По свойству равнобедренного треугольника ∠FAM=∠AFM.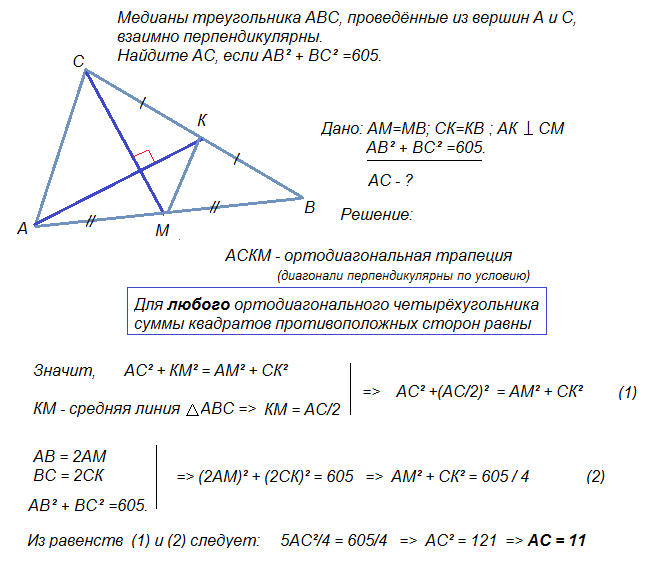 Отсюда

5. Найдем

Значит,

6. Из FMN по теореме синусов:

где R – радиус описанной окружности.

Отсюда получим значение радиуса окружности:

Ответ: 5,4.

Демонстрационный вариант ОГЭ 2019

Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC . Найдите радиус окружности, вписанной в треугольник ABC .

Решение:

Пусть O — центр данной окружности, а Q — центр окружности, вписанной в треугольник ABC .

Точка касания M окружностей делит AC пополам по условию.

Лучи AQ и AO — биссектрисы смежных углов, так как касательные к окружностям равноудалены от центра. Так как  AQ и AO — биссектрисы смежных углов, то угол OAQ прямой — смежные углы в сумме дают 180°, значит сумма их биссектрис:

180°/2 = 90°.

Далее рассмотрим прямоугольный треугольник OAQ.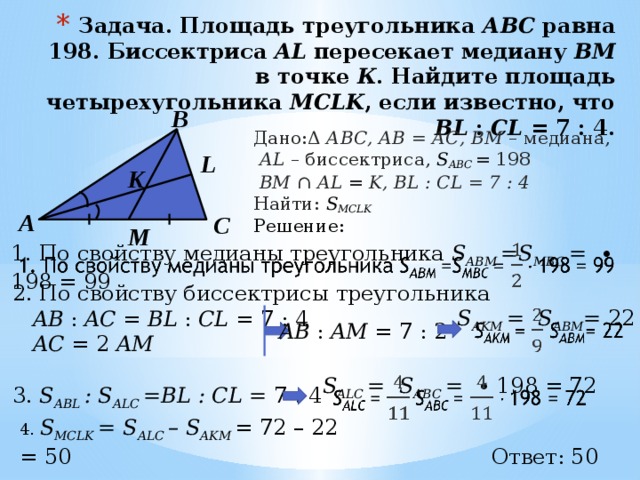 По свойству высоты в прямоугольном треугольнике, получаем:

AM² = MQ•MO

Отсюда:

QM = AM² / MO

QM = 6² / 8 = 4,5

Ответ: 4,5

Математическая сцена — Треугольники — Урок 2

Математическая сцена — Треугольники — Урок 2

2008 Расмус Эф и Джанн Сак

Треугольники

Урок 2   Некоторые важные характеристики

Прямая линия, пересекающая окружность только один раз (касается окружности) называется касательной к окружности. Угол между радиусом и касательной  в точке пересечения всегда равен 90.

Прямая, которая делит угол на две равные части, называется углом биссектриса. Все точки биссектрисы угла равноудалены от плеч или сторон угла, который делится пополам. Окружность, нарисованная так, что стороны угла касаются окружности, ее центр лежит на биссектрисе угла.

На диаграмме выше линия от V до O биссектриса угла V. Отрезки VA и VB имеют одинаковую длину и перпендикулярны AO и BO соответственно.

Пример 1

В на диаграмме ниже угол V = 40, а отрезки VA и VB равны 40 см. Найдите угол AOB, обозначенный x, и радиус круга.

VAOB — четырехугольник, поэтому сумма углы 360. Мы знаем три из углы и, следовательно, может вычислить четвертый.

   х = 360 – 90 – 40 − 90 = 140

Если проводим биссектрису угла VO получаем прямоугольный треугольник с углами 20, 90 и 70. С помощью тригонометрии получаем:

загар 20 = х / 40

                 x = 40×tan 20 ≈ 14,6 см

Биссектриса делит сторона треугольника, противоположная углу в том же отношении, что и прямая отрезки, примыкающие к углу.

Биссектриса угла A делит сторону a в отношении c/b. Если мы назовем эти части x и y, тогда справедливо следующее правило:

           

Пример 2

Треугольник ABC имеет следующие размеры:

   a = 30 см, b = 40 см og c = 20 см.

Биссектриса угла А делит сторону а на две части. Вычислите длину этих частей. Мы используем те же обозначения, что и в правиле выше.

Сторона а делится на части длины 10 см и 30 − 10 = 20 см .

Каждый треугольник имеет одну точку который равноудален от всех трех сторон треугольника. Это точка в которого пересекаются биссектрисы всех углов треугольника. С использованием эту точку как центр, мы можем нарисовать круг, который касается всех трех сторон треугольник. Это называется вписанным окружность треугольника.

Из диаграммы выше видно, что угол биссектрисы AO, BO и CO делят треугольник на три меньших треугольника, каждый из которых которая имеет высоту r. Их площади равны ×a×r, ×b×r и ×с×r. Общая площадь, то есть площадь треугольника ABC, следовательно:

 Область F = ×a×r + ×b×r + ×c×r = ×r(a + б + в)

Окружность круг, назовем его u, это a + b + c , который означает, что мы можем записать формулу площади треугольника как:

           

Есть вторая точка, которая может быть внутри или вне треугольника, то есть на равном расстоянии от всех углов треугольника. В этой точке пересекаются все три перпендикулярные биссектрисы треугольника. Это связано с тем, что точки биссектрисы равноудалены от углов , образующих конечные точки сторон, которые они делят пополам.

Эта точка образует центр окружности, которую можно провести через все углы треугольника. Его называют ограниченным окружность треугольника.

На приведенной выше диаграмме показан треугольник ABC с описанной окружностью. Два прямоугольных треугольника имеют нарисовано на схеме. Треугольник ACE образован проведением высоты h из угол С к стороне с. Треугольник BCD находится путем проведения диаметра окружности из С через центр О в точка D на окружности. Треугольники ACE и BCD подобны они оба прямоугольные треугольники и угол A = угол D . (оба охватывают дугу CB) Следовательно, имеют место следующие соотношения:

Ввод этого значения для h в формулу площади F  треугольник, F = ×c×h  мы получить следующий результат:

Мы также можем использовать далее:

Что приводит к правилу:

Если мы найдем h и положим значение h = b×sin A в формулу для площади F = ×c×h получаем правило площади треугольника:

Пример 3

Треугольник со сторонами 17 см, 17 см и 16 см.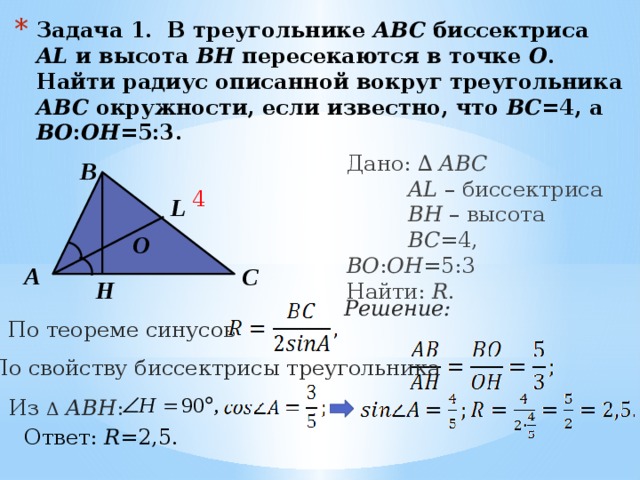

а) Найдите площадь треугольника.

Использование Правило Пифагора для нахождения высоты h.

  ч 2 + 8 2 = 17 2

ч 2 = 289 — 64 = 225

            высота = 15 см

Сейчас мы можем вычислить площадь F.

   Ф = ×16×15 = 120 см 2  

б) Найдите радиус вписанной круг.

Периметр треугольника  u = 17 + 17 + 16 = 50 см.

Площадь F = 120 = ×r×50

r =120×2/50 = 14,8 см

в) Найдите радиус описанный круг.

    Площадь F = 120 = 17×17×16/4R

        480R = 17×17×16

            R = 17×17×16 / 480 = 289 / 30 ≈ 9,6 см

г) Найдите углы треугольника.

Следовательно, B ≈ 62 и C ≈ 180 − 2×62 ≈ 56 .

Медиана треугольника — это отрезок, проведенный от угла до середины противоположной стороны. Медианы треугольника все пересекаются в одной точке. Эта точка делит каждую медиану в соотношении 1: 2.

На приведенной выше диаграмме M 1 , M 2 и M 3 являются средними точками. сторон треугольника. Медианы пересекаются в точке Т, которая делит M 1 C на части x и 2x.

Медианы делят треугольник на шесть меньших треугольники, пронумерованные на схеме 1-6. Эти все треугольники имеют одинаковую площадь. Таким образом, точка Т является центром тяжести треугольник. Если бы треугольник был сделан из материала и вырезан, то мы могли бы уравновесить его на булавке или гвозде, помещенном в точку Т.

В равнобедренном треугольнике центры вписанной и

описанных окружностей находятся в одной точке.

Медианы треугольника пересекаются в одной точке.

Высоты треугольника также пересекаются в одной точке.

Пример 4

Длина медианы треугольника 24 см. Вычислите длину отрезков, на которые его делят другие медианы.

Мы называем один сегмент x, тогда другой 2x.

    х + 2х = 24

          3x = 24

            х = 8

Медиана разделена на части длиной 8 см и 16 см

Пример 5

Треугольник ABC нарисован в координатах система.
А = (-4, -4), В = (12, 0) и С = (4, 16). Найдите координаты точка пересечения медиан.

Начнем с поиска середина стороны BC

Теперь находим уравнение медианы, проходящей через A. Это линия, проходящая через A = (−4, −4) и (8, 8).

   градиент k = (8 + 4)/(8 + 4) = 1

Используя уравнение прямой в виде:

   г = к(х — х 1 ) + у 1

получаем y = 1 (х — 8) + 8

   г = х

Далее делаем то же самое для медиана через точку B. Сначала мы находим середину AC.

Уравнение медиана через B теперь найдена. Это линия, проходящая через B= (12, 0) и (0, 6).

Градиент к = (0 — 6) / (12 — 0) = —

 Следовательно  y = −(x − 0) + 6

   у = −x + 6

Решение двух уравнений y = x и y = −x + 6 получаем:

   х = −х + 6

   х + х = 6

       1x = 6

            x = 4 и, следовательно, y = 4.

Медианы пересекаются в точке (4, 4) .

Правило Цеваса:

Это правило названо в честь итальянского математик Джованни Чева, 90 010

Если мы нарисуем любые три линии в треугольнике что все проходят через одну точку, скажем, P и угол треугольника. Назовите точки пересечения сторон AB, AC и BC, X, Y и Z соответственно.

Тогда правило такое:

           

Это правило, конечно, выполняется для медиан, высот и любых других линий, которые идут от одного угла треугольника к противоположные стороны и пересекаются в одной точке.

Пример 6

На диаграмме ниже найдите длину линии отрезки, на которые Z делит BC.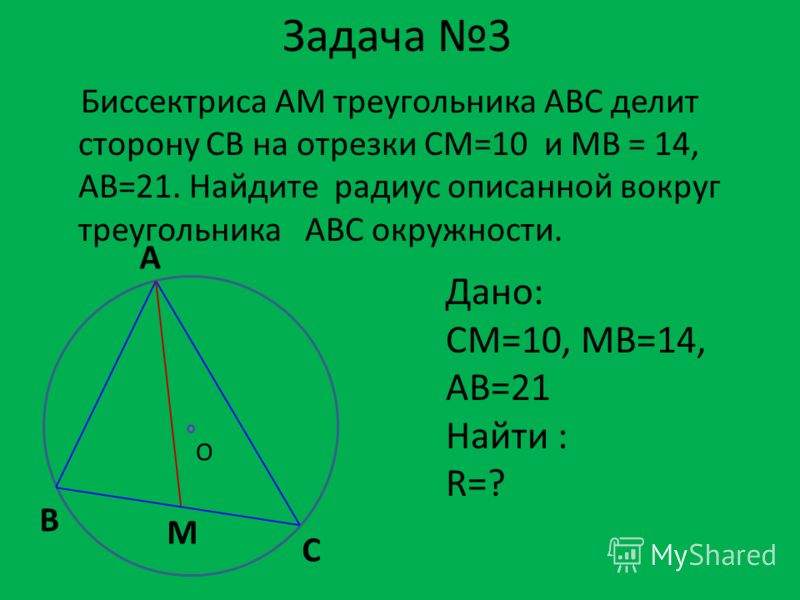

Если x = BZ, то ZC = 17 − x. Используя правило, мы получить:

Therfore Z разделяет сторону до н.э. на отрезки длины 5,5 см и 11,5 см .

Попробуйте пройти викторину 2 по треугольникам. Не забудьте использовать контрольный список, чтобы следить за своей работой.

Урок На какие отрезки биссектриса угла делит сторону треугольника

Этот Урок (На какие отрезки биссектриса угла делит сторону треугольника) создан by ikleyn(48143)   : Посмотреть исходный код, Показать
Об иклейн :

Теорема
В треугольнике биссектриса делит сторону, к которой она проведена, на два отрезка, пропорциональных отношению двух других сторон треугольника. Доказывать.


Доказательство
Имеем треугольник ABC ( рис. 1 ) с вершинами                          
A , B и C 903 01 . 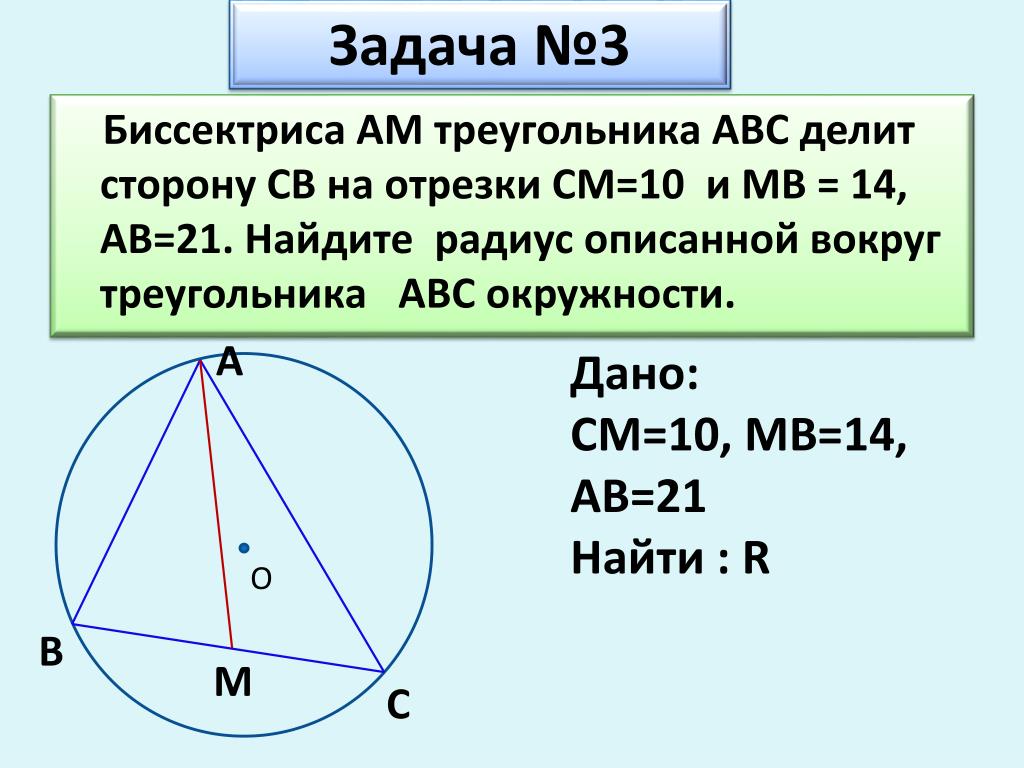Стороны треугольника BC и AC имеют длину
и и b соответственно, как показано на рисунке 1 .
Биссектриса угла CD угла C делит сторону AB
на отрезки AD и BD длиной y и x 9 0301 соответственно.
Теорема утверждает, что .

Мы будем использовать Закон синусов . Это было установлено в
уроках Закон синусов и Закон синусов — Геометрическое
Доказательство, которые находятся в рамках темы Треугольники раздела
Геометрия на этом сайте.



     Рисунок 1 . К теореме 1                       


   Рисунок 2 . К доказательству теоремы

Итак, проведем перпендикуляры DE и DF из точки D к сторонам AC и BC треугольника до точек пересечения E и F соответственно ( рисунок 2 ).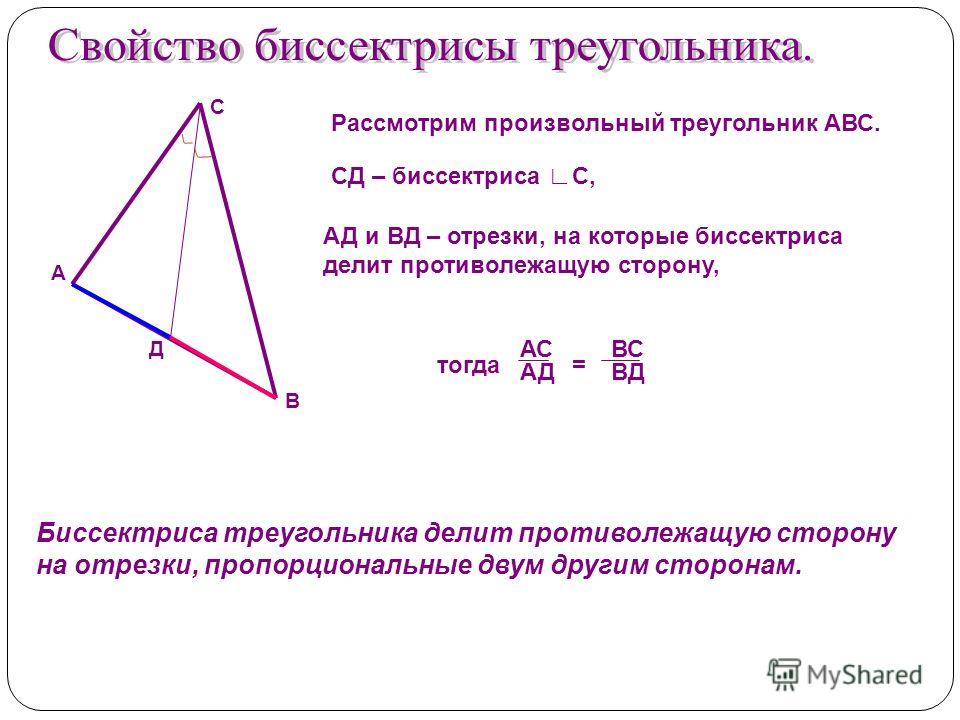
Так как CD — биссектриса угла, то точка D равноудалена от сторон AC и BC угла ACB (см. урок Свойства биссектрисы угла в теме Треугольники раздела Геометрия на этом сайте). Следовательно, перпендикуляры DE и DF имеют одинаковую длину. Если обозначить эту длину как z , то ( рис. 2 )

, .

Теперь применим Закон синусов для треугольника ABC в виде

и подставьте выражения из и выше. После отмены и преобразований вы получите

,

именно то, что нужно продемонстрировать. Доказательство завершено.

Ниже приведены примеры, показывающие, как применять проверенные Теорема .

Проблема 1
Длина сторон треугольника 4 см, 5 см и 6 см.
Найдите длины отрезков, биссектриса которого пересекает сторону 5 см.

Раствор
Пусть и — длина отрезков, биссектриса которого пересекает сторону 5 см.
Тогда у вас есть система двух уравнений для и :

Последнее уравнение основано на теореме выше.

Чтобы решить систему, выразите из второго уравнения

и подставьте его в первое уравнение. Вы получаете

,
,
,

и далее

.

Ответить . Отрезки, которые пересекает биссектриса угла со стороной 5 см, имеют длину 2 см и 3 см.

Проблема 2
Периметр треугольника 60 см. (60 = 4*(4 + 5 +6) = 16 + 20 + 24)
Биссектриса делит одну сторону треугольника на отрезки по 8 и 12 см.
Найдите две другие стороны треугольника.

Раствор
Позвольте и быть длиной двух других сторон треугольника.
Длина первой стороны треугольника 8 см + 12 см = 20 см.
Следовательно, суммарная длина двух других сторон треугольника равна 60 см — 20 см = 40 см.
Следовательно, у вас есть система двух уравнений и :

Последнее уравнение основано на теореме выше.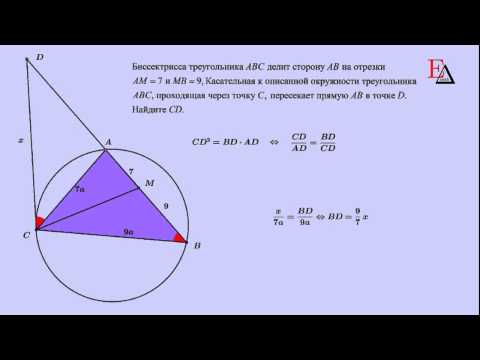

Чтобы решить систему, выразите из второго уравнения

и подставьте его в первое уравнение. Вы получаете

,
,
,

и далее

.

Ответить . Две другие стороны треугольника равны 16 см и 24 см.


Приложение
Доказав теорему , мы можем легко вывести формулы            
, выражающие длины отрезков, к которым относится биссектриса угла
разрезает сторону треугольника.

Действительно, пусть и — длина отрезков биссектрисы угла
, проведенной между сторонами треугольника и разрезающей сторону .
Тогда у вас есть система двух уравнений для и :

Рисунок 1 . К Приложению

Последнее уравнение основано на приведенной выше теореме .

Чтобы решить систему, выразите из второго уравнения

и подставьте его в первое уравнение.