Арифметическая прогрессия an задана условиями а1 48 аn 1 аn 17: a1 =48, an + 1 =an −17. Найдите сумму первых семи её членов

Арифметическая прогрессия задана » задачи

прогрессия »

Арифметическая прогрессия задана уравнением an=2n-4. Найдите сумму ее членов с 10 по 15.

Решение: $$ a_n=2n-4\\a_1=2*1-4=2-4=-2\\a_2=2*2-4=4-4=0\\d=a_2-a_1=0-(-2)=2\\\\a_9=a_1+8d\\a_9=-2+8*2=-2+16=14\\S_9=(a_1+a_9):2*9\\S_9=(-2+14):2*9=12:2*9=6*9=54\\\\a_{15}=a_1+14d\\a_{15}=-2+14*2=-2+28=26\\S_{15}=(a_1+a_{15}):2*15\\S_{15}=(-2+26):2*15=24:2*15=12*15=180\\\\S_{10-15}=S_{15}-S_9=180-54=26 $$
А1=2*1-4=-2
а2=2*2-4=0
S=2a1+d(n-1)/2*n
S10=2*(-2)+2*(10-1)/2*10=70
S11=2*(-2)+2*(11-1)/2*11=88
S12=2*(-2)+2*(12-1)/2*12=108
S13=2*(-2)+2*(13-1)/2*13=130
S14=2*(-2)+2*(14-1)/2*14=154
S15=2*(-2)+2*(15-1)/2*15=180
Арифметическая прогрессия задана первыми двумя членами: a1=100, a2=97. Укажите наименьшее значение n, при котором an<0.

Решение: здесь разность прогрессии равна -3,
$$ a_{1}+(n-1)d =0 $$
$$ a_{n} $$ меньше 0,
найдём $$ a_{1}+(n-1)d = 0 $$
100 +(n-1)(-3) =0
n-1=-100/-3
n=1+ 33 +1/3
n= 34 1/3
пр n= 34 а=100+(34-1)*(-3)=1
при n= 35 а=1-3=-2
Ответ: наименьшее значение n, при котором an<0 n=35.
$$ a_1=100;a_2=97;\\\\d=a_2-a_1=97-100=-3;\\\\a_n=a_1+(n-1)*d;\\\\a_n=100+(n-1)*(-3)=100-3n+3=103-3n;\\\\a_n<0;\\\\103-3n<0;\\\\103<3n;\\\\3n>103;\\\>\frac{103}{3}=34\frac{1}{3};\\\=35; $$
ответ: 35
проверка
$$ a_{34}=103-3*34=103-102=1>0;\\\\a_{35}=103-3*35=103-105=-2<0 $$
Задание 7 (137305)

Арифметическая прогрессия задана условиями а1=6, аn+1=an+6 Какое из данных чисел является членом этой прогрессии
1.80
2. 56
3.48
4.32

Решение: $$ a_1=6;a_{n+1}=a_n+6 $$
разность арифметичесской прогрессии равна
$$ d=a_{n+1}-a_n=(a_n+6)-a_n=a_n+6-a_n=6 $$
$$ d=6 $$
формула общего члена арифметической прогрессии
$$ a_n=a_1+(n-1)*d $$
номер n-го члена прогрессии $$ n=\frac{a_n-a_1}{d}+1 $$
проверяем 1.
$$ a_n=80; $$
$$ n=\frac{80-6}{6}+1 $$ — не натуральное число -не подходит
проверяем 2.
$$ a_n=56 $$
$$ n=\frac{56-6}{6}+1 $$ — не натуральное число — не подходит
проверяем 3.
$$ a_n=48 $$
$$ n=\frac{48-6}{6}+1=8 $$ — натуральное число — подходит
48 — является 8-м членом данной прогресси
проверям 4.
$$ a_n=32 $$
$$ n=\frac{32-6}{6}+1 $$ — не натуральное число — не подходит
ответ: 3. (48 — 8-й член прогрессии)
2. В арифметической прогрессии (an) a10=30; a30=90. Найти d

3. Арифметическая прогрессия задана условием: a1 =-5,5; an+1= an+0,5. Найдите двадцать четвёртый член этой прогрессии.
Решение: Используем свойство арифметической прогрессии an=ak+(n-k)*d (1)
2) отсюда d=(an-ak)/(n-k)=(90-30)/(30-10)=60/20=3
ответ: d=3
3) Из выражения an+1=an+0.5 следует по определению прогрессии d=0.5
тогда подставим в (1): a24=a1+(24-1)*d=-5.5+23*0.5=6
Ответ: a24=6
2) a10=30 a10 = a1 + 9d a1 + 9d = 30
a30 = 90 a30 = a1 + 29d a1 +29d=90 вычтем из 2 уравнения 1-е. получим 20d = 60⇒d = 3
3) an+1 = an + 0,5 эту запись надо понять так: чтобы найти последующий член, надо к предыдущему прибавить 0,5.
То есть 0,5 — это разность прогрессии. (d = 0,5)
a24 = a1 + 23d = -5,5 + 23·0,5 = — 5,5 + 11,5 = 6
1. в арифм. прогрессии найдите а1, если d=3 а6=17

2. Найдите сумму последовательности нечётных натуральных числ с 35 по 70 включительно.
3. Найдите сумму последовательных чётных натуральных чисел не превосходящих 155.
Решение: 1.
a6=a1+d*(6-1)
a1+3*5=17
a1+15=17
a1=2
2.
a1=35
d=2
последнее нечетное число будет 69, найдем его номер:
69=a1+d(n-1)
69=35+2n-2
2n=36
n=18
Сумма: (35+69)/2 * 18=104/2 * 18=52*18=936
3.
a1=2
d=2
последнее четное число будет 154, найдем его номер:
154=a1+d*(n-1)
154=2+2*(n-1)
154=2+2*n-2
154=2*n
n=77
Сумма: (2+154)/2 * 77=78*77=6006

Урок -зачёт по теме : Арифмитическая прогрессия» | Методическая разработка по алгебре (9 класс) на тему:

Муниципальное общеобразовательное учреждение Лицей Усть-Кутского муниципального образования

Урок-зачет в 9 классе

по маршрутным листам по теме

АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ

Усть-Кут

2015

Урок-зачет в 9 классе

по маршрутным листам

Тема урока: «Арифметическая прогрессия»

Цели урока:

Образовательные и развивающие:

1. Обобщение и систематизация теоретического материала по данной теме

2.Развивать умения и навыки применять формулы прогрессии при решении задач.

3.Формировать и развивать умения и навыки: поиск способов решения, используя алгоритмы решения, самопроверки по образцу, взаимопроверки;

4.Отрабатывать навыки самооценивания знаний и умений, выбора задания, соответствующего уровню знаний учащегося.

Воспитательные: 1.Вырабатывать внимание, самостоятельность при работе на уроке;

2.Способствовать формированию активности, максимальной работоспособности, чувства ответственности.

Структура урока:

1. Вводно-мотивационная часть.

1.1. Организационный момент.

1.2. Устная работа.

2. Основная часть урока.

2.1. Проверка теоретических знаний по теме,

2. 2 Применения их при решении практических заданий (устно).

2.3. Решение письменных заданий.

( чередование индивидуальной и парной форм работы с последующей самопроверкой и самооценкой заданий).

3. Рефлексивно-оценочная часть урока.

3.1. Обсуждение результатов индивидуальной и парной работы.

3.2. Информация о домашнем задании.

3.3. Подведение итогов урока.

МАРШРУТНЫЙ ЛИСТ

обучения, взаимоконтроля, самоконтроля по теме:

Арифметическая прогрессия

Ученика(цы) 9Б класса ___________________________

Дата______________________________

1. Знание теории и практические устные задания.

№	Вопросы	Максимальный балл	Полученный балл
1.	. Запишите рекуррентную формулу для арифметической прогресси.	1
2.	При каком условии прогрессия является возрастающей, при каком — убывающей?	1
3.	Запишите формулу n члена арифметической прогрессии.	1
4.	Запишите формулы суммы n членов арифметической прогрессии	1
5.	Запишите характеристическое свойство арифметической прогрессии.	1
6.	1; 3; 5; 7; 9; : Верно ли, что это арифметическая прогрессия?	1
7.	1; 4; 9; 16; 25; : Верно ли, что это арифметическая прогрессия?	1
8.	1; 3; 5; 7; 11; 13; 17; : Верно ли, что арифметическая прогрессия?	1
9.	1; 2; 3; 4; 5; : Верно ли, что эта арифметическая прогрессия является возрастающей?	1
10.	Записать первый член арифметической прогрессии 6, 8, 10,:	1
11.	Записать разность арифметической прогрессии 25, 21, 17,:	1
12.	Записать второй член прогрессии а1=2; d=5.	1
13.	Найти первый член арифметической прогрессии, заданной формулой an=3 — 4n.
	ИТОГО:	13

Письменные задания (базовый уровень)

№ задания	Проверяемые умения и навыки	Ответ	Максимальный балл	Экспертная оценка
	Пусть (вn) — арифметическая прогрессия:
1.	в1=11, d=3. Найдите в11.		1
2.	в1=137, d= -7. Найдите S10		1
3.	в13= — 27, в15= — 13. Найдите в14.		1
4.	в43= — 208, d= — 7. Найдите в1.		1
5.	в1=28, в15= — 21. Найдите d.		1
	ИТОГО:		5

Задания на «4».

1.Найти разность арифметической прогрессии:

а1 = 12, а5 = 40 (2б)

2.Найти первый член арифметической прогрессии:

а7 = 9, d = 40 (2б)

3.Число 29 является членом арифметической прогрессии 9, 11, 13,: Найдите номер этого члена. (2б)

4.Найти девятнадцатый член арифметической прогрессии.

а13 = 10, а20 = 38 (2б)

Задания на «5».

1.Найти аn, если а1 = 40, n = 20, S20 = 40 арифметической прогрессии. (3б)

2.В арифметической прогрессии 59, 55, 51,: Найти сумму всех её членов. (2б)

3.Составьте формулу n — го члена арифметической прогрессии.

а3 = 12, а10 = 40 (2б)

4.Найти сумму первых тридцати членов арифметической прогрессии (аn), заданной формулой n — го члена аn = — 2n + 8 (3б)

26 баллов и более – «5»

21 – 26 баллов – «4»

16 — 20 баллов – «3»

Менее 15 баллов – «2»

Домашняя работа

1 вариант нечетные номера

2 вариант четные

Задачи из ОГЭ.

1.Дана арифметическая прогрессия (an), разность которой равна −5,3, a1=−7,7.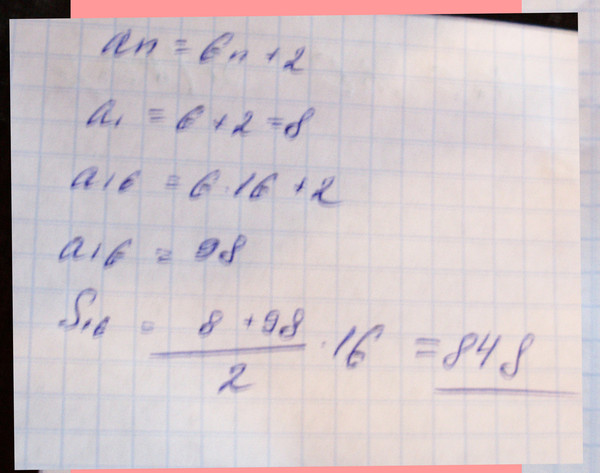 Найдите a7. 2.Дана арифметическая прогрессия (an), разность которой равна 5,5, a1=−6,9. Найдите a6. 3.Дана арифметическая прогрессия (an), разность которой равна 5,1, a1=−0,2. Найдите сумму первых семи ее членов.

4. Дана арифметическая прогрессия (an), разность которой равна 5, a1=−4,8. Найдите сумму первых 15 ее членов.

5.Арифметическая прогрессия задана условием an=−11,9+7,8n. Найдите a11. 6.Арифметическая прогрессия задана условиями c1=−3, cn+1=cn−1. Найдите c5. 7.Арифметическая прогрессия задана условиями c1=3, cn+1=cn−2. Найдите c7.

8.Дана арифметическая прогрессия 11; 18; 25; … . Какое число стоит в этой последовательности на 6-м месте?

9.Дана арифметическая прогрессия 7; 12; 17; … . Какое число стоит в этой последовательности на 7-м месте?

10.Дана арифметическая прогрессия 10; 5; 0; … . Какое число стоит в этой последовательности на 61-м месте?

11.Арифметическая прогрессия задана условиями a1=−9, an+1=an−16. Найдите сумму первых 17 ее членов.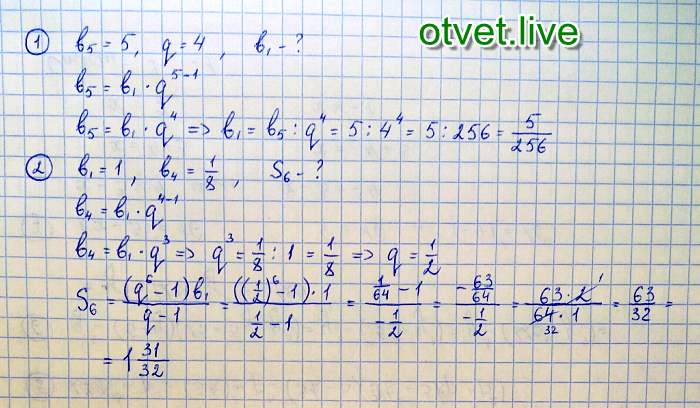

12. Дана арифметическая прогрессия 35; 32; 29; … . Найдите первый отрицательный член этой прогрессии.

13.В первом ряду кинозала 40 мест, а в каждом следующем на 2 больше, чем в предыдущем. Сколько мест в ряду с номером n?

14. В первом ряду кинозала 30 мест, а в каждом следующем на 1 больше, чем в предыдущем. Сколько мест в ряду с номером n?

15.Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 8 квадратов больше, чем в предыдущей. Сколько квадратов в 16-й строке?

16.Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 4 квадратов больше, чем в предыдущей. Сколько квадратов в 12-й строке?

17. В арифметической прогрессии (an) a1=0,6, a6=−2,4. Найдите разность арифметической прогрессии.

18.В арифметической прогрессии (an) a1=−24, a13=96. Найдите разность арифметической прогрессии.

19.Дана арифметическая прогрессия −1,5;0,5;2,5;…. Найдите сумму первых десяти ее членов. 20.Арифметическая прогрессия (an) задана условием an=−1,5−1,5n. Найдите сумму первых шести членов прогрессии.

21.Арифметическая прогрессия задана условием an=100−15n. Найдите сумму первых пяти членов прогрессии.

22. Арифметическая прогрессия an задана условием an=10−2,9n. Найдите сумму первых десяти членов прогрессии.

Источник: http://www.itmathrepetitor.ru/zadachi-dlya-ogeh-arifmeticheskaya-progre/

Ответы к домашней работе:

-39,5
20,6 16.48
105,7 17.- 0,6
453 18. 10
73,9 19. 75
-7 20. – 40,5
-9 21. 275
46 22. -59,5
37
-290
-2329
-1
38+2n
29+n
122

n-й член арифметической прогрессии

Горячая математика

Учитывая арифметическая последовательность с первым сроком а 1 и общая разница г , н й (или общий) термин дан кем-то а н «=» а 1 + ( н − 1 ) г .

Пример 1:

Найди 27 й член арифметической прогрессии 5 , 8 , 11 , 54 , … .

а 1 «=» 5 , г «=» 8 − 5 «=» 3

Так,

а 27 «=» 5 + ( 27 − 1 ) ( 3 ) «=» 83

Пример 2:

Найди 40 й термин для арифметической прогрессии, в которой
а 8 «=» 60 и а 12 «=» 48 .

Заменять 60 для а 8 и 48 для а 12 в формуле
а н «=» а 1 + ( н − 1 ) г получить система линейных уравнений с точки зрения а 1 и г .

а 8 «=» а 1 + ( 8 − 1 ) г → 60 «=» а 1 + 7 г а 12 «=» а 1 + ( 12 − 1 ) г → 48 «=» а 1 + 11 г

Вычесть второе уравнение из первого уравнения и решить для г .

12 «=» − 4 г − 3 «=» г

Затем 60 «=» а 1 + 7 ( − 3 ) . Решить для а .
60 «=» а 1 − 21 81 «=» а 1

Теперь используйте формулу, чтобы найти а 40 .

а 40 «=» 81 + 39 ( − 3 ) «=» 81 − 117 «=» − 36 .

Смотрите также: сигма-обозначение ряда и н й член геометрической прогрессии

9.

2: Арифметические последовательности и ряды

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 6248

Аноним
LibreTexts

Цели обучения

Определите общую разность арифметической последовательности.
Найдите формулу общего члена арифметической прогрессии.
Вычислить $n$-ю частичную сумму арифметической прогрессии.

Арифметические последовательности

Арифметика последовательность ¹² или арифметика

прогрессия ¹³ , представляет собой последовательность чисел, где каждое последующее число является суммой предыдущего числа и некоторой константы \(d\ ).

$a_{n}=a_{n-1}+d \quad\color{Cerulean}{Арифметика\:последовательность}$

И поскольку $a_{n}-a_{n-1}= d$, константа $d$ называется общим разным ¹⁴ . Например, последовательность положительных нечетных целых чисел представляет собой арифметическую последовательность

$1,3,5,7,9, \ldots$

Здесь $a_{1} = 1$ и разность между любыми два последовательных члена равны $2$. Мы можем построить общий термин $a_{n}=a_{n-1}+2$, где

$a_{1}=1$
$а_{2}=а_{1}+2=1+2=3$
$а_{3}=а_{2}+2=3+2=5$
$а_{4 }=a_{3}+2=5+2=7$
$a_{5}=a_{4}+2=7+2=9$
$\vdots$

В общем, учитывая первый член $a_{1}$ арифметической прогрессии и его общую разность $d$, мы можем написать следующее:

$\begin{array}{l}{a_{2}= a_{1}+d} \\ {a_{3}=a_{2}+d=\left(a_{1}+d\right)+d=a_{1}+2 d} \\ {a_{ 4}=a_{3}+d=\влево(a_{1}+2 d\вправо)+d=a_{1}+3 d} \\ {a_{5}=a_{4}+d=\ влево(a_{1}+3d\вправо)+d=a_{1}+4d} \\ {\quad\:\:\vdots}\end{массив}$ 9{th}\) член: $7, 10, 13, 16, 19, …$

Решение

Начните с нахождения общего различия,

$d=10-7=3$

Обратите внимание, что разница между любыми двумя последовательными терминами равна $3$. {th}\).

Решение

Начните с нахождения общей разности $d$. В этом случае нам дан первый и седьмой член:

$\begin{array}{l}{a_{n}=a_{1}+(n-1) d\quad \color{Cerulean} { Используйте \: n=7.}} \\ {a_{7}=a_{1}+(7-1) d} \\ {a_{7}=a_{1}+6 d}\end{массив} $

Подставьте $a_{1} = −8$ и $a_{7} = 10$ в приведенное выше уравнение, а затем найдите общую разность $d$.

$\begin{align} 10 &=-8+6 d \\ 18 &=6 d \\ 3 &=d \end{align}$

Затем, используя первый член $a_{1} = −8$ и общую разность $d = 3$, найдите уравнение для $n$-го члена последовательности.

$\begin{выровнено} a_{n} &=-8+(n-1) \cdot 3 \\ &=-8+3 n-3 \\ &=-11+3 n \end{выровнено }$

С $a_{n} = 3n − 11$, где $n$ — натуральное число, найдите недостающие члены.

$ \left. \begin{выровнено} a_{1}&=3(1)-11=3-11=-8\\ a_{2} &=3(2)-11=6-11= -5 \\ a_{3} &=3(3)-11=9-11=-2 \\ a_{4} &=3(4)-11=12-11=1 \\ a_{5} & =3(5)-11=15-11=4 \\ a_{6} &=3(6)-11=18-11=7 \\ a_{7}&=3(7)-11=21- 111=10 \end{выровнено} \right\} \color{Cerulean}{арифметика\:среднее}$

Ответ :

$-5,-2,1,4,7$

В некоторых случаях первый член арифметической последовательности не может быть задан.

Пример $\PageIndex{4}$:

Найдите общий член арифметической последовательности, где $a_{3} = −1$ и $a_{10} = 48$.

Решение

Для определения формулы общего члена нам нужны $a_{1}$ и $d$. Линейная система с этими переменными может быть сформирована с использованием данной информации и $a_{n}=a_{1}+(n-1) d$:

$\left\{\begin{array}{c}{a_{3}=a_{1}+(3-1) d} \\ {a_{10}=a_{1}+(10- 1) d}\end{array}\right.\Rightarrow \left\{\begin{array}{l}{-1=a_{1}+2 d \quad\color{Cerulean}{Use \:a_{ 3}=-1.}} \\ {48=a_{1}+9 d\quad\:\color{Cerulean}{Использование\: a_{10}=48.}}\end{массив}\right. $

Исключите $a_{1}$, умножив первое уравнение на $−1$ и прибавив результат ко второму уравнению.

$\left\{\begin{array}{l}{-1=a_{1}+2 d} \\ {48=a_{1}+9 d}\end{array}\right. \ quad \ stackrel {\ color {Cerulean} {x (-1)}} {\ Longrightarrow} \ color {black} {+} \ left \ {\ begin {array} {l} {1 = -a_ {1} — 2д} \\ {48=а_{1}+9d} \end{массив}\right. \\ $

$\begin{align} 49 &=7 d \\ 7 &=d \end{aligned}$

Подставьте $d = 7$ в $−1 = a_{1 } + 2d$, чтобы найти $a_{1}$.

$-1=a_{1}+2(7)$
$-1=a_{1}+14$
$-15=a_{1}$

Далее используйте первый член $a_{1} = −15$ и общую разность $d = 7$, чтобы найти формулу для общего члена.

$\begin{align} a_{n} &=a_{1}+(n-1) d \\ &=-15+(n-1) \cdot 7 \\ &=-15+7 n -7 \\ &=-22+7 n \end{выровнено}$ 9{й}\) терм: $\frac{3}{2}, 2, \frac{5}{2}, 3, \frac{7}{2}, \dots$

Ответ

$a_{n}=\frac{1}{2} n+1; a_{100}=51$

www.youtube.com/v/_ovjvVKtKpQ

Арифметический ряд

Арифметический ряд ряд ¹⁶ представляет собой сумму членов арифметической последовательности. Например, сумма первых $5$ членов последовательности, определяемой $a_{n} = 2n − 1$, выглядит следующим образом: 9{5}(2 n-1) \\ &=[2(\color{Cerulean}{1}\color{black}{)}-1]+[2(\color{Cerulean}{2}\color{ черный} {)}-1]+[2(\color{Cerulean}{3}\color{black}{)}-1]+[2(\color{Cerulean}{4}\color{black}{) }-1]+[2(\color{Cerulean}{5}\color{black}{)}-1] \\ &=1+3+5+7+9 \\ &=25 \end{выровнено} \)

Добавление $5$ положительных нечетных целых чисел, как мы сделали выше, управляемо. Однако рассмотрите возможность добавления первых $100$ положительных нечетных целых чисел. Это было бы очень утомительно. Поэтому далее мы разрабатываем формулу, которую можно использовать для вычисления суммы первых $n$ членов, обозначаемых $S_{n}$, любой арифметической последовательности. В общем

$S_{n}=a_{1}+\влево(a_{1}+d\вправо)+\влево(a_{1}+2 d\вправо)+\ldots+a_{n}$

Записав этот ряд в обратном порядке, мы имеем

$S_{n}=a_{n}+\left(a_{n}-d\right)+\left(a_{n}-2 d\right) +\ldots+a_{1}$

И складывая эти два уравнения вместе, члены, включающие $d$, добавляют к нулю, и мы получаем $n$ множителей $a_{1} + a_{n }$:

$2 S_{n}=\left(a_{1}+a_{n}\right)+\left(a_{1}+a_{n}\right)+\ldots+\left (a_{n}+a_{1}\right)$
$2 S_{n}=n\left(a_{1}+a_{n}\right)$

Деление обеих частей на $2$ приводит нас к формуле для $n$-й частичной суммы арифметических последовательностей ¹⁷ :

$S_{n}=\frac{n \left(a_{1}+a_{n}\right)}{2}$

Используйте эту формулу для вычисления суммы первых $100$ членов последовательности, определяемой $a_{n} = 2п — 1$. Здесь $a_{1} = 1$ и $a_{100} = 199$.

$\begin{align} S_{100} &=\frac{100\left(a_{1}+a_{100}\right)}{2} \\ &=\frac{100(1+199) )}{2} \\ &=10 000 \end{выровнено}$

Пример $\PageIndex{5}$:

Найти сумму первых $50$ членов данной последовательности: $4,9,14,19,24, \dots$

Решение

Определите, есть ли общее различие между данными терминами.

$d=9-4=5$

Обратите внимание, что разница между любыми двумя последовательными членами равна $5$. Последовательность действительно является арифметической прогрессией, и мы можем написать

$\begin{aligned} a_{n} &=a_{1}+(n-1) d \\ &=4+(n-1) \cdot 5 \\ &=4+5 n-5 \\ &=5 n-1 \end{выровнено}$ 9{th}\) частичная сумма.

$\begin{align} S_{n} &=\frac{n\left(a_{1}+a_{n}\right)}{2} \\ S_{35} &=\frac{35 \cdot\left(a_{1}+a_{35}\right)}{2} \\ &=\frac{35[6+(-130)]}{2} \\ &=\frac{35( -124)}{2} \\ &=-2,170 \end{align}$

Ответ :

$-2,170$

Пример $\PageIndex{7}$:

первый ряд сидений в открытом амфитеатре содержит $26$ мест, второй ряд содержит $28$ мест, третий ряд содержит $30$ мест и так далее. Если есть $18$ рядов, какова общая вместимость театра?

Рисунок $\PageIndex{1}$: Римский театр

Решение

Начните с поиска формулы, которая определяет количество мест в любом ряду. Здесь количество мест в каждом ряду образует последовательность:

$26,28,30, \точки$

Обратите внимание, что разница между любыми двумя последовательными членами равна $2$. Последовательность представляет собой арифметическую прогрессию, где $a_{1} = 26$ и $d = 2$.

$\begin{align} a_{n} &=a_{1}+(n-1) d \\ &=26+(n-1) \cdot 2 \\ &=26+2 n-2 \\ &=2 n+24 \end{выровнено}$ 9{th}\) частичная сумма следующим образом:

$\begin{aligned} S_{n} &=\frac{n\left(a_{1}+a_{n}\right)}{2} \\ S_{18} &=\frac{18 \cdot\left(a_{1}+a_{18}\right)}{2} \\ &=\frac{18(26+60)}{2} \\ &=9(86) \\ &=774 \end{aligned}$

Ответ :

Всего $774$ мест.

Упражнение $\PageIndex{2}$

Найдите сумму первых $60$ членов данной последовательности: $5, 0, −5, −10, −15, …$

Ответ

$S_{60}=-8,550$

www. youtube.com/v/baYq2a_kBKo

Ключевые выводы

Арифметическая последовательность — это последовательность, в которой разность $d$ между последовательными членами постоянна.
Общий член арифметической последовательности может быть записан через его первый член $a_{1}$, общую разность $d$ и индекс $n$ следующим образом: $a_{n} = а_{1} + (п — 1) d$.
Арифметический ряд — это сумма членов арифметической прогрессии.
$n$-я частичная сумма арифметической последовательности может быть вычислена с использованием первого и последнего членов следующим образом: $S_{n}=\frac{n\left(a_{1}+a_{n}\ справа)}{2}$.

Упражнение $\PageIndex{3}$

Запишите первые $5$ членов арифметической последовательности, зная ее первый член и общую разность. Найдите формулу для его общего члена.

$а_{1}=5; г=3$
$а_{1}=12; г=2$
$a_{1}=15; d=-5$
$а_{1}=7; г=-4$
$a_{1}=\frac{1}{2}; d=1$
$a_{1}=\frac{2}{3}; d=\frac{1}{3}$
$a_{1}=1; d=-\frac{1}{2}$
$a_{1}=-\frac{5}{4}; d=\frac{1}{4}$
$а_{1}=1,8; d=0,6$
$а_{1}=-4,3; г=2,1$

Ответить

1. $5,8,11,14,17 ; а_{п}=3 п+2$

3. $15,10,5,0,-5 ; а_{п}=20-5 п$

5. $\frac{1}{2}, \frac{3}{2}, \frac{5}{2}, \frac{7}{2}, \frac{9{й}$ срок.

$3, 9, 15, 21, 27,…$
$3, 8, 13, 18, 23,…$
$−3, −7, −11, −15, −19,…$
$-6, -14, -22, -30, -38,…$
$-5, -10, -15, -20, -25,…$
$2, 4, 6, 8, 10,…$
$\frac{1}{2}, \frac{5}{2}, \frac{9}{2}, \frac{13}{2}, \frac{17}{2}, \ldots $
$-\frac{1}{3}, \frac{2}{3}, \frac{5}{3}, \frac{8}{3}, \frac{11}{3}, \ ldots$
$\frac{1}{3}, 0,-\frac{1}{3},-\frac{2}{3},-1, \ldots$ 9{th}\) член последовательности, состоящей из любого другого положительного четного целого числа: $2, 6, 10, 14,…$
Каким числом является член $355$ в арифметической последовательности $−15, −5, 5, 15, 25,…$?
Под каким номером находится член $−172$ в арифметической последовательности $4, −4, −12, −20, −28,…$?
Для заданной арифметической последовательности, определяемой рекуррентным соотношением $a_{n}=a_{n-1}+5 $, где $a_{1} = 2$ и $n > 1$, найдите уравнение что дает общий термин в терминах $a_{1}$ и общую разность $d$.
Для заданной арифметической последовательности, определяемой рекуррентным соотношением $a_{n}=a_{n-1}-9$, где $a_{1} = 4$ и $n > 1$, найдите уравнение что дает общий термин в терминах $a_{1}$ и общую разность $d$.

Ответить

1. $a_{n}=6 n-3 ; a_{100}=597$

3. $a_{n}=1-4 n ; a_{100}=-399$

5. $a_{n}=-5 n ; a_{100}=-500$

7. $a_{n}=2 n-\frac{3}{2} ; a_{100}=\frac{397}{2}$

9. $a_{n}=\frac{2}{3}-\frac{1}{3} n; a_{100}=-\frac{98}{3}$

11. $a_{n}=1,2 n-0,4 ; a_{100}=119,6$

13. $99$

15. $157$

17. $38$

19. $a_{n}=5 n-3$

Упражнение $\PageIndex{5}$

Учитывая члены арифметической последовательности, найдите формулу для общего члена.

$a_{1}=6$ и $a_{7}=42$
$a_{1}=-\frac{1}{2}$ и $a_{12}=-6$
$a_{1}=-19$ и $a_{26}=56$
$a_{1}=-9$ и $a_{31}=141$
$a_{1}=\frac{1}{6}$ и $a_{10}=\frac{37}{6}$
$a_{1}=\frac{5}{4}$ и $a_{11}=\frac{65}{4}$
$a_{3}=6$ и $a_{26}=-40$
$a_{3}=16$ и $a_{15}=76$
$a_{4}=-8$ и $a_{23}=30$
$a_{5}=-7$ и $a_{37}=-135$
$a_{4}=-\frac{23}{10}$ и $a_{21}=-\frac{25}{2}$
$a_{3}=\frac{1}{8}$ и $a_{12}=-\frac{11}{2}$
$a_{5}=13,2$ и $a_{26}=61,5$
$a_{4}=-1,2$ и $a_{13}=12,3$

Ответить

1. $a_{n}=6 n$

3. $a_{n}=3 n-22$

5. $a_{n}=\frac{2}{3} n-\frac{1}{2}$

7. $a_{n}=12-2 n$

9. $a_{n}=2 n-16$

11. $a_{n}=\frac{1}{10}-\frac{3}{5} n$

13. $a_{n}=2,3 n+1,7$

Упражнение $\PageIndex{6}$

Найдите все средние арифметические между заданными терминами.

$a_{1}=-3$ и $a_{6}=17$
$a_{1}=5$ и $a_{5}=-7$
$a_{2}=4$ и $a_{8}=7$
$a_{5}=\frac{1}{2}$ и $a_{9}=-\frac{7}{2}$
$a_{5}=15$ и $a_{7}=21$
$a_{6}=4$ и $a_{11}=-1$

Ответить

1. $1, 5, 9, 13$

3. $\frac{9}{2}, 5, \frac{11}{2}, 6, \frac{13}{2}$

5. $18$

Упражнение $\PageIndex{7}$

Рассчитайте указанную сумму по формуле для общего члена.

$a_{n}=3 n+5 ; S_{100}$
$a_{n}=5 n-11 ; S_{100}$
$a_{n}=\frac{1}{2}-n, S_{70}$
$a_{n}=1-\frac{3}{2} n; S_{120}$
$a_{n}=\frac{1}{2} n-\frac{3}{4}; S_{20}$
$a_{n}=n-\frac{3}{5}; S_{150}$
$a_{n}=45-5n; S_{65}$
$a_{n}=2 n-48 ; S_{95}$
$a_{n}=4,4-1,6n; S_{75}$
$a_{n}=6,5 n-3,3 ; S_{67}$

Ответить

1. $15 650$

3. $−2450$

5. $90$

7. $−7800$

9. $−4 230$ 9{175}(-0,2 н-1,6)\)

Найдите сумму первых $200$ натуральных чисел.

Найдите сумму первых $400$ натуральных чисел.

Ответить

1. $38 640$

3. $124 750$

5. $−18 550$

7. $−765$

9. $10 578$

11. $20,100$

Упражнение $\PageIndex{9}$

Общий термин для последовательности положительных нечетных целых чисел определяется выражением $a_{n} = 2n − 1$, а общий термин для последовательности положительных четных целых чисел определяется выражением $a_{n} = 2n$. Найдите следующее.

Сумма первых $50$ положительных нечетных целых чисел.
Сумма первых $200$ положительных нечетных чисел.
Сумма первых $50$ положительных четных чисел.
Сумма первых $200$ положительных четных чисел.
Сумма первых $k$ положительных нечетных чисел.
Сумма первых $k$ положительных четных чисел.
Первый ряд сидений в маленьком театре состоит из $8$ мест. После этого в каждом ряду на $3$ больше мест, чем в предыдущем ряду. Если есть $12$ рядов, сколько всего мест в театре?
Первый ряд сидений в открытом амфитеатре содержит $42$ мест, второй ряд содержит $44$ мест, третий ряд содержит $46$ мест и так далее. Если есть $22$ рядов, какова общая вместимость театра?
Если треугольная стопка кирпичей имеет $37$ кирпичей в нижнем ряду, $34$ кирпичей во втором ряду и так далее с одним кирпичом сверху. Сколько кирпичей в стопке?
В каждом последующем ряду треугольной стопки кирпичей на один кирпич меньше, пока сверху не останется только один кирпич. Сколько рядов будет в стопке, если всего кирпичей $210$?
Контракт о зарплате на $10$ лет предлагает $65 000$) в первый год с увеличением на $\(3 200$ каждый последующий год. Определите общую сумму обязательств по заработной плате за $10$ летний период.
Башня с часами бьет в колокол столько раз, сколько указано в часах. В час дня он бьет один раз, в два часа он бьет два раза и так далее. Сколько раз в день бьет колокол на башне с часами?

Ответить

9{2}\)

7. $294$ мест

9. $247$ кирпич

11. $$794 000$

Упражнение $\PageIndex{10}$

Является ли последовательность Фибоначчи арифметической последовательностью? Объяснять.
Используйте формулу для $n$-й частичной суммы арифметической последовательности $S_{n}=\frac{n\left(a_{1}+a_{n}\right)}{2}$ и формула для общего члена $a_{n}=a_{1}+(n-1) d$ для получения новой формулы для n-й частичной суммы $S_{n}=\frac{n}{ 2}\влево[2 a_{1}+(n-1) d\вправо]$. В каких случаях эта формула будет полезна? Объясните на примере собственного изготовления. 9{35}(3 n+4)=1659\).
Известная история связана с плохим поведением Карла Фридриха Гаусса в школе. В качестве наказания учитель дал ему задание сложить первые $100$ целых чисел. Легенда гласит, что молодой Гаусс ответил правильно в течение нескольких секунд. Каков ответ и как, по-вашему, ему удалось так быстро найти сумму?

Ответить

1. Ответ может отличаться

3. Ответ может отличаться

Сноски

¹² Последовательность чисел, в которой каждое последующее число является суммой предыдущего числа и некоторой константы $d$.

¹³ Используется при обращении к арифметической последовательности.

¹⁴ Константа $d$, полученная вычитанием любых двух последовательных членов арифметической последовательности; $a_{n}-a_{n-1}=d$.

¹⁵ Члены между заданными членами арифметической последовательности.

Арифметическая прогрессия задана » задачи

Арифметическая прогрессия задана уравнением an=2n-4. Найдите сумму ее членов с 10 по 15.

Арифметическая прогрессия задана первыми двумя членами: a1=100, a2=97. Укажите наименьшее значение n, при котором an<0.

Задание 7 (137305)

2. В арифметической прогрессии (an) a10=30; a30=90. Найти d

1. в арифм. прогрессии найдите а1, если d=3 а6=17

Урок -зачёт по теме : Арифмитическая прогрессия» | Методическая разработка по алгебре (9 класс) на тему:

n-й член арифметической прогрессии