Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
12.17
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Алла на 6 лет моложе Веры.
Сейчас папа в 11 раз старше Аллы и на 24 года старше Веры. Через сколько лет папа будет в 3 раза старше Веры?
Решено
На доске написано натурвльное число b. Про него сказали три утверждения 1. Это число четное, 2. Это число меньше 102, 3. Уравнение х2 + 20х +b=0 имеет хотя бы 1 корень. Какое наибольшее число
На экзамене 20 билетов, Андрей не выучил 1 из них. Найдите вероятность того, что ему попадется выученный билет
Решено
Сколько дров надо сжечь в топке паровой машины с КПД=33 %, чтобы получить воду при 14 °С из снега массой 104 кг, взятого при температуре−11 °С.
Билеты в кино стоят 4…
Пользуйтесь нашим приложением
Арксинус. Решение простейших уравнений с синусом. Часть 2
Арксинусом числа \(a\) (\(a∈[-1;1]\)) называют число \(x∈[-\frac{π}{2};\frac{π}{2}]\) синус которого равен \(a\) т.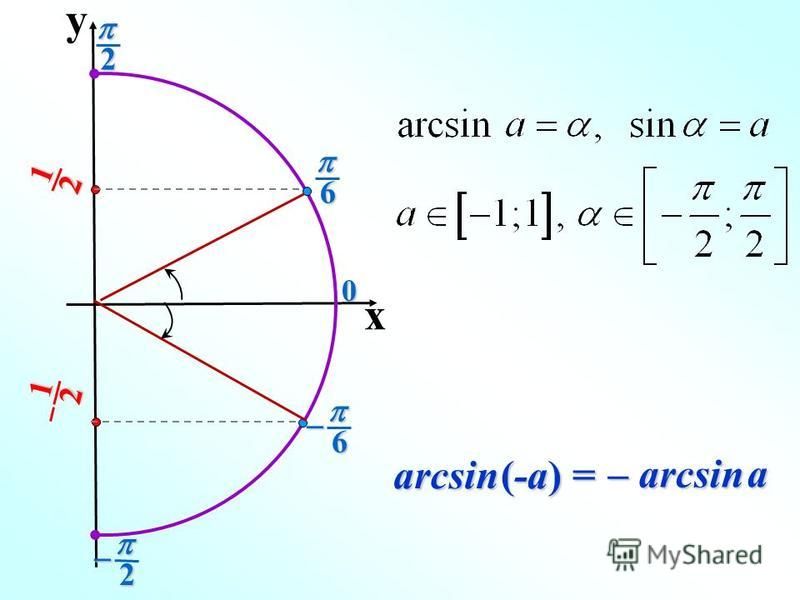
е.
\(\arcsin a=x\) \(<=>\) \(\sin x=a\)
Примеры:
\(\arcsin{\frac{\sqrt{2}}{2}}=\frac{π}{4}\) потому что \(\sin \frac{π}{4}=\frac{\sqrt{2}}{2}\) и \(\frac{π}{4}∈[-\frac{π}{2}; \frac{π}{2}]\)
\(\arcsin 1=\frac{π}{2}\) потому что \(\sin\frac{π}{2}=1\) и \(\frac{π}{2}∈[-\frac{π}{2};\frac{π}{2}]\)
\(\arcsin 0=0\) потому что \(\sin 0=0\) и \(0∈[-\frac{π}{2};\frac{π}{2}] \)
\(\arcsin\sqrt{3}\) – не определен, потому что \(\sqrt{3}>1\)
Проще говоря, арксинус обратен синусу.
На круге это выглядит так:
Как вычислить арксинус?
Чтобы вычислить арксинус — нужно ответить на вопрос: синус какого числа (лежащего в пределах от \(-\frac{π}{2}\) до \(\frac{π}{2}\) ) равен аргументу арксинуса?
Например, вычислите значение арксинуса:
а) \(\arcsin(-\frac{1}{2})\)
б) \(\arcsin(\frac{\sqrt{3}}{2})\)
в) \(\arcsin(-1)\)
а) Синус какого числа равен \(-\frac{1}{2}\)? Или в более точной формулировке можно спросить так: если \(\sin x=-\frac{1}{2}\), то чему равен \(x\)? Причем, обратите внимание, нам нужно такое значение, которое лежит между \(-\frac{π}{2}\) и \(\frac{π}{2}\).
Ответ очевиден:
\(\arcsin(-\frac{1}{2})=-\frac{π}{6}\)
б) Синус какого числа равен \(\frac{\sqrt{3}}{2}\)? Кто-то вспоминает тригонометрический круг, кто-то таблицу, но в любом случае ответ \(\frac{π}{3}\).
\(\arcsin(-\frac{\sqrt{3}}{2})=-\frac{π}{3}\)
в) Синус от чего равен \(-1\)?
Иначе говоря, \(\sin x=-1\), \(x=\) ?
\(\arcsin(-1)=-\frac{π}{2}\)
Тригонометрический круг со всеми стандартными арксинусами:
Зачем нужен арксинус? Решение уравнения \(\sin x=a\)
Чтобы понять зачем придумали арксинус, давайте решим уравнение: \(\sin x=\frac{1}{2}\).
Это не вызывает затруднений:
\( \left[ \begin{gathered}x=\frac{π}{6}+2πn, n∈Z\\ x=\frac{5π}{6}+2πl, l∈Z\end{gathered}\right.\)
Внимание! Если вдруг затруднения всё же были, то почитайте здесь о решении простейших уравнений с синусом.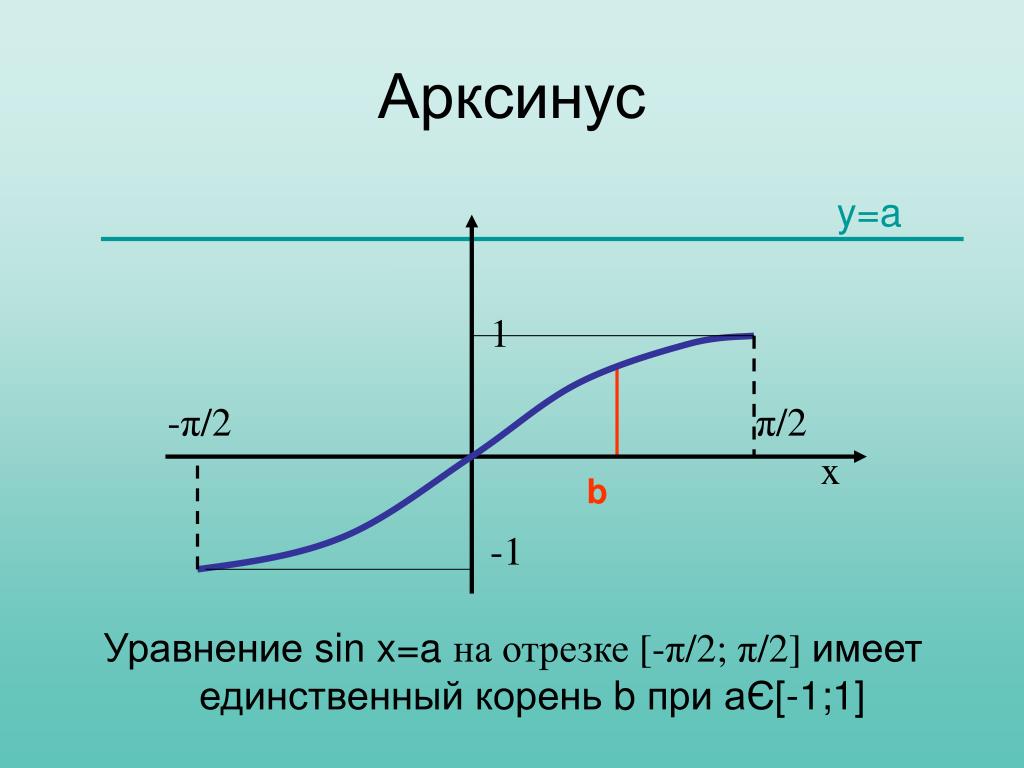
А теперь решите уравнение: \(\sin x=\frac{1}{3}\).
Что тут будет ответом? Не \(\frac{π}{6}\), не \(\frac{π}{4}\), даже не \(\frac{π}{7}\) — вообще никакие привычные числа не подходят, однако при этом очевидно, что решения есть. Но как их записать?
Вот тут-то на помощь и приходит арксинус! Значение правой точки равно \(\arcsin\frac{1}{3}\), потому что известно, что синус равен \(\frac{1}{3}\). Длина дуги от \(0\) до правой точки тогда тоже будет равна \(\arcsin\frac{1}{3}\). Тогда чему равно значение второй точки? С учетом того, что правая точка находится на расстоянии равному \(\arcsin\frac{1}{3}\) от \(π\), то её значение составляет \(π- \arcsin\frac{1}{3}\).
Ок, значение этих двух точек нашли. Теперь запишем полный ответ: \( \left[ \begin{gathered}x=\arcsin \frac{1}{3}+2πn, n∈Z\\ x=π-\arcsin \frac{1}{3}+2πl, l∈Z\end{gathered}\right.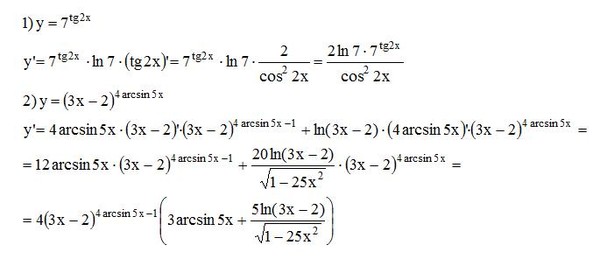
\) Без арксинусов решить уравнение \(\sin x=\frac{1}{3}\) не получилось бы. Как и уравнение \(\sin x=0,125\), \(\sin x=-\frac{1}{9}\), \(\sin x=\frac{1}{\sqrt{3}}\) и многие другие. Фактически без арксинуса мы можем решать только \(9\) простейших уравнений с синусом:
С арксинусом – бесконечное количество.
Пример. Решите тригонометрическое уравнение: \(\sin x=\frac{1}{\sqrt{3}}\).
Решение:
Ответ: \( \left[ \begin{gathered}x=\arcsin \frac{1}{\sqrt{3}}+2πn, n∈Z\\ x=π-\arcsin \frac{1}{\sqrt{3}}+2πl, l∈Z\end{gathered}\right.\)
Пример. Решите тригонометрическое уравнение: \(\sin x=\frac{1}{\sqrt{2}}\).
Решение:
Кто поторопился написать ответ \( \left[ \begin{gathered}x=\arcsin \frac{1}{\sqrt{2}}+2πn, n∈Z\\ x=π-\arcsin \frac{1}{\sqrt{2}}+2πl, l∈Z\end{gathered}\right.\), тот на ЕГЭ потеряет 2 балла.
Дело в том, что в отличии от прошлых примеров \(\arcsin \frac{1}{\sqrt{2}}\) — вычислимое значение, но чтобы это стало очевидно нужно избавиться от иррациональности в знаменателе аргумента. Для этого умножим и числитель и знаменатель дробь на корень из двух \(\frac{1}{\sqrt{2}} = \frac{1 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}}= \frac{\sqrt{2}}{2}\). Таким образом, получаем:
\(\arcsin \frac{1}{\sqrt{2}} = \arcsin \frac{\sqrt{2}}{2}=\frac{π}{4}\)
Значит в ответе вместо арксинусов нужно написать \(\frac{π}{4}\).
Ответ: \( \left[ \begin{gathered}x=\frac{π}{4}+2πn, n∈Z\\ x=\frac{3π}{4}+2πl, l∈Z\end{gathered}\right.\)
Пример. Решите тригонометрическое уравнение: \(\sin x=\frac{7}{6}\).
Решение:
И вновь тот, кто поторопился написать \( \left[ \begin{gathered}x= \arcsin \frac{7}{6}+2πn, n∈Z\\ x=π- \arcsin\frac{7}{6}+2πl, l∈Z\end{gathered}\right.
\) на ЕГЭ потеряет \(2\) балла. Что не так? – спросите вы. Ведь точно не табличное значение, почему нельзя написать \(\arcsin\frac{7}{6}\)? Пролистайте до самого верха, туда, где было определение арксинуса. Там написана маленькая, но очень важная деталь – аргумент арксинуса должен быть меньше или равен \(1\) и больше или равен \(-1\). Ведь синус не может выходить за эти пределы! И если решить уравнение с помощью круга, а не бездумно пользоваться готовыми формулами, то станет очевидно, что у такого уравнения решений нет.
Ответ: решений нет.
Думаю, вы уловили закономерность.
Если \(\sin x\) равен не табличному значению между \(1\) и \(-1\), то решения будут выглядеть как: \( \left[ \begin{gathered}x= \arcsin a +2πn, n∈Z\\ x=π- \arcsin a +2πl, l∈Z\end{gathered}\right.\)
Арксинус отрицательного числа
Прежде чем научиться решать тригонометрические уравнения с отрицательным синусом советую запомнить формулу:
\(\arcsin({-a})=-\arcsin a\)
Если хотите понять логику этой формулы, внимательно рассмотрите картинку ниже:
Примеры:
\(\arcsin(-0,7)=-\arcsin 0,7\)
\(\arcsin(-\frac{\sqrt{3}}{2})=-\arcsin\frac{\sqrt{3}}{2}=-\frac{π}{6}\)
\(\arcsin(-\frac{\sqrt{7}}{2}) \neq -\arcsin\frac{\sqrt{7}}{2}\)
Удивил последний пример? Почему в нем формула не работает? Потому что запись \(\arcsin(-\frac{\sqrt{7}}{2})\) в принципе неверна, ведь \(-\frac{\sqrt{7}}{2}<-1\), а значит арксинус от \(-\frac{\sqrt{7}}{2}\) взять нельзя – он не вычислим, не существует, точно также как \(\sqrt{-5}\) или \(\frac{3}{0}\).
Пример. Решите тригонометрическое уравнение: \(\sin x=-\frac{1}{\sqrt{3}}\).
Решение:
Можно воспользоваться готовой формулой и написать:
\( \left[ \begin{gathered}x=\arcsin (-\frac{1}{\sqrt{3}})+2πn, n∈Z\\ x=π-\arcsin (-\frac{1}{\sqrt{3}})+2πl, l∈Z\end{gathered}\right.\)
\( \left[ \begin{gathered}x=-\arcsin (\frac{1}{\sqrt{3}})+2πn, n∈Z\\ x=π+\arcsin (\frac{1}{\sqrt{3}})+2πl, l∈Z\end{gathered}\right.\)
Но я фанатка круга, поэтому:
Ответ: \( \left[ \begin{gathered}x=-\arcsin \frac{1}{\sqrt{3}}+2πn, n∈Z\\ x=π+\arcsin \frac{1}{\sqrt{3}}+2πl, l∈Z\end{gathered}\right.\)
На всякий случай, уточню, что при решении уравнений написанное синим писать не обязательно – это скорее пояснения, как надо рассуждать.
Смотрите также:
Синус
Тригонометрические уравнения
3-8
исчисление — более простая форма $\sin{(\frac{1}{2}\arcsin{x})}$
Задавать вопрос
спросил
Изменено 5 лет, 9 месяцев назад
Просмотрено 374 раза
$\begingroup$
Мне было интересно, как вычислить $$\sin{(\frac{1}{2}\arcsin{x})}, \quad|x|\le1,$$
Я имею в виду, как избавиться от функции синуса и обратного синуса и получить
$$\frac{-\sqrt{1 — x}}{2} + \frac {\sqrt{1 + x}}{2},$$ — это ответ, который дает Wolfram Alpha.
Leave A Comment