Решаем задачи по геометрии: решение четырехугольников
Решаем задачи по геометрии: решение четырехугольников
Теорема 1. Площадь трапеции равна произведению полусуммы ее оснований на высоту:
Теорема 2. Диагонали трапеции делят ее на четыре треугольника, два из которых подобны, а два другие имеют одинаковую площадь:
Теорема
3. Площадь
параллелограмма равна произведению
основания на высоту, опущенную на данное
основание, или произведению двух сторон
на синус угла между ними:
Теорема
4. В
параллелограмме сумма квадратов
диагоналей равна сумме квадратов его
сторон:
Теорема 5. Площадь произвольного выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними:
Теорема
6. Площадь
четырехугольника, описанного около
окружности, равна произведению
полупериметра этого четырехугольника
на радиус данной окружности:
Теорема
7.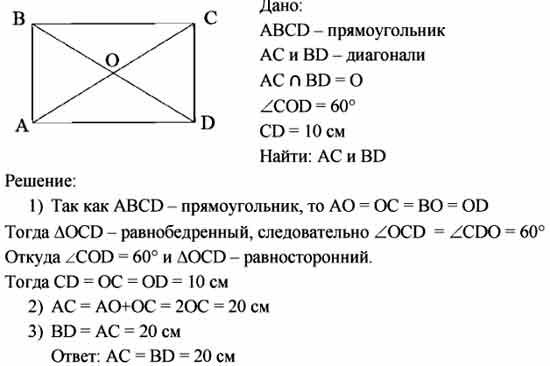 Четырехугольник,
вершинами которого являются середины
сторон произвольного выпуклого
четырехугольника, есть параллелограмм,
площадь которого равна половине площади
исходного четырехугольника:
Четырехугольник,
вершинами которого являются середины
сторон произвольного выпуклого
четырехугольника, есть параллелограмм,
площадь которого равна половине площади
исходного четырехугольника:
Теорема 8. Если у выпуклого четырехугольника диагонали взаимно перпендикулярны, то суммы квадратов противоположных сторон этого четырехугольника равны:
AB2 + CD2 = BC2 + AD2.
Доказательства некоторых теорем
Доказательство теоремы 2
а площадь треугольника ACD равна
Так
как BP
= CQ,
то и S∆ABD =
S∆ACD.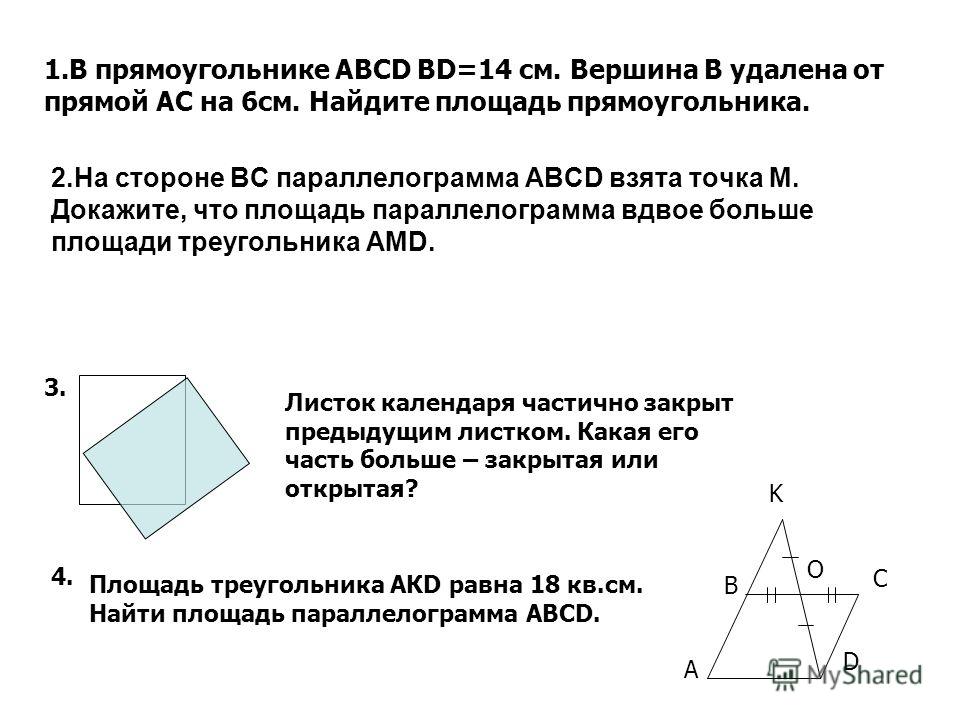 Но площадь треугольника AOB
есть разность площадей треугольников
ABD
и AOD,
а площадь треугольника COD —
разность площадей треугольников ACD
и AOD.
Следовательно, площади треугольников
AOB
и COD
равны, что и требовалось доказать.
Но площадь треугольника AOB
есть разность площадей треугольников
ABD
и AOD,
а площадь треугольника COD —
разность площадей треугольников ACD
и AOD.
Следовательно, площади треугольников
AOB
и COD
равны, что и требовалось доказать.
Доказательство
теоремы 4.
Пусть ABCD —
параллелограмм, AB
= CD
= a,
AD
= BC
= b,
AC
= d1,
BD
= d2,
∠BAD
= α,
∠ADC
= 180° – α.
Применим к треугольнику ABD
теорему косинусов:
Применив
теперь теорему косинусов к треугольнику
ACD,
получим:
Складывая
почленно полученные равенства, получаем,
что что
и требовалось доказать.
Доказательство
теоремы 5. Пусть ABCD —
произвольный выпуклый четырехугольник,
E —
точка пересечения его диагоналей, AE
= a,
BE
= b,
CE
= c,
DE
= d,
∠AEB
= ∠CED
= ϕ,
∠BEC
=
= ∠AED
= 180° – ϕ.
Имеем:
что и требовалось доказать.
Доказательство
теоремы 6.
Пусть ABCD —
произвольный четырехугольник, описанный
около окружности, O —
центр этой окружности, OK,
OL,
OM
и ON —
перпендикуляры, опущенные из точки O
на прямые AB,
BC,
CD
и AD
соответственно.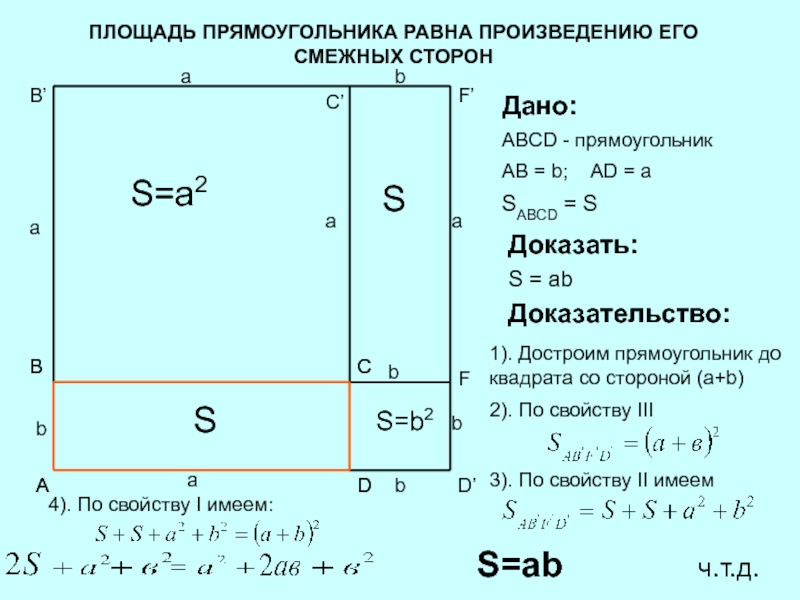 Имеем:
Имеем:
где r — радиус окружности, а p — полупериметр четырехугольника ABCD.
Доказательство теоремы 7. Пусть ABCD — произвольный выпуклый четырехугольник, K, L, M и N — середины сторон AB, BC, CD и AD соответственно. Так как KL — средняя линия треугольника ABC, то прямая KL параллельна прямой AC и Аналогично, прямая MN параллельна прямой AC и Следовательно, KLMN — параллелограмм. Рассмотрим треугольник KBL. Его площадь равна четверти площади треугольника ABC. Площадь треугольника MDN также равна четверти площади треугольника ACD. Следовательно,
Аналогично,
Это значит, что
откуда вытекает, что
Доказательство
теоремы 8.
Пусть ABCD —
произвольный выпуклый четырехугольник,
у которого диагонали взаимно
перпендикулярны, пусть E —
точка пересечения его диагоналей,
AE
= a,
BE
= b,
CE
= c,
DE
= d.
Применим к треугольникам ABE
и CDE
теорему Пифагора:
AB2 =
AE2 +
BE2 = a2 +
b2,
CD2
следовательно,
AB2 + CD2 = a2 + b2 + c2 + d2.

Применив теперь теорему Пифагора к треугольникам ADE и BCE, получим:
AD2 = AE2 + DE2 = a2 + d2,
BC2 = BE2 + CE2 = b2 + c2,
откуда вытекает, что
AD2 + BC2 = a2 + b2 + c2 + d2.
Значит, AB2 + CD2 = AD2 + BC
Решения задач
Задача 1. Около круга описана трапеция с углами при основании α и β. Найти отношение площади трапеции к площади круга.
Решение. Пусть ABCD — данная трапеция, AB и CD — ее основания, DK и CM — перпендикуляры, опущенные из точек C и D на прямую AB. Искомое отношение не зависит от радиуса круга. Поэтому будем считать, что радиус равен 1. Тогда площадь круга равна π, найдем площадь трапеции. Так как треугольник ADK прямоугольный, то
Аналогично,
из прямоугольного треугольника BCM
находим, что Поскольку
в данную трапецию можно вписать
окружность, то суммы противоположных
сторон равны:
откуда находим
Значит, площадь трапеции есть
и
искомое отношение равно
Ответ:
Задача
2. В выпуклом четырехугольнике ABCD
угол A
равен 90°, а угол C
не превосходит 90°. Из вершин B
и D
на диагональ AC
опущены перпендикуляры BE
и DF.
Известно,
что AE = CF. Доказать, что угол C прямой.
В выпуклом четырехугольнике ABCD
угол A
равен 90°, а угол C
не превосходит 90°. Из вершин B
и D
на диагональ AC
опущены перпендикуляры BE
и DF.
Известно,
что AE = CF. Доказать, что угол C прямой.
Доказательство.
Так как угол A
равен 90°,
а угол C
не превосходит 90°, то точки E
и F
лежат на диагонали AC.
Без ограничения общности мы можем
считать, что AE
∠EBC
= β,
∠FDA
= γ,
∠FDC
= δ.
Нам достаточно доказать, что α
+ β
+ γ
+ δ
= π.
Так как
то и в частности tg α tg γ = 1. Далее, имеем:
откуда получаем, что что и требовалось доказать.
Задача
3.
Периметр равнобочной трапеции, описанной
около круга, равен p.
Найти радиус этого круга, если известно,
что острый угол при основании трапеции
равен α.
Решение.
Пусть ABCD —
данная равнобочная трапеция с основаниями
AD
и BC,
пусть BH —
высота этой трапеции, опущенная из
вершины B.
Так
как в данную трапецию можно вписать
окружность, то
следовательно,
Из
прямоугольного треугольника ABH
находим,
Ответ:
Задача
4. Дана трапеция ABCD
с основаниями AD
и BC.
Диагонали AC
и BD
пересекаются в точке O,
а прямые AB
и CD —
в точке K.
Прямая KO
пересекает стороны BC
и AD
в точках M
и N
соответственно, а угол BAD
равен 30°. Известно, что в трапеции ABMN
и NMCD
можно вписать окружность. Найти
отношение площадей треугольника BKC и
трапеции ABCD.
Дана трапеция ABCD
с основаниями AD
и BC.
Диагонали AC
и BD
пересекаются в точке O,
а прямые AB
и CD —
в точке K.
Прямая KO
пересекает стороны BC
и AD
в точках M
и N
соответственно, а угол BAD
равен 30°. Известно, что в трапеции ABMN
и NMCD
можно вписать окружность. Найти
отношение площадей треугольника BKC и
трапеции ABCD.
Решение.
Как известно, для произвольной трапеции
прямая, соединяющая точку пересечения
диагоналей и точку пересечения продолжений
боковых сторон, делит каждое из оснований
пополам. Итак, BM
= MC
и AN
= ND.
Далее, так как в трапеции ABMN
и NMCD
можно вписать окружность, то
MC + ND = CD + MN.
Отсюда следует, что AB = CD, то есть трапеция ABCD — равнобокая. Искомое отношение площадей не зависит от масштаба, поэтому мы можем принять, что KN = x, KM = 1. Из прямоугольных треугольников AKN и BKM получаем, что Записывая вновь уже использованное выше соотношение
BM + AN = AB + MN ⇔
находим
Нам требуется вычислить отношение:
Здесь
мы использовали тот факт, что площади
треугольников AKD
и BKC
относятся как квадраты сторон KN
и KM,
то есть как x2.
Ответ:
Задача 5. В выпуклом четырехугольнике ABCD точки E, F, H, G являются серединами сторон AB, BC, CD, DA соответственно и O — точка пересечения отрезков EH и FG. Известно, что EH = a, FG = b, Найти длины диагоналей четырехугольника.
Решение. Известно, что если соединить последовательно середины сторон произвольного четырехугольника, то получится параллелограмм. В нашем случае EFHG — параллелограмм и O — точка пересечения его диагоналей. Тогда
Применим к треугольнику FOH теорему косинусов:
Так как FH — средняя линия треугольника BCD, то
Аналогично, применив теорему косинусов к треугольнику EFO, получим, что
откуда
Ответ:
Задача
6. Боковые
стороны трапеции равны 3 и 5. Известно,
что в трапецию можно вписать окружность.
Средняя линия трапеции делит ее на две
части, отношение площадей которых
равно Найти
основания трапеции.
Решение. Пусть ABCD — данная трапеция, AB = 3 и CD = 5 — ее боковые стороны, точки K и M — середины сторон AB и CD соответственно. Пусть, для определенности, AD > BC, тогда площадь трапеции AKMD будет больше площади трапеции KBCM. Так как KM — средняя линия трапеции ABCD, то трапеции AKMD и KBCM имеют равные высоты. Поскольку площадь трапеции равна произведению полусуммы оснований на высоту, то верно следующее равенство:
Далее,
так как в трапецию ABCD
можно вписать окружность, то AD
+ BC
= AB
+ CD
= 8. Тогда KM
= 4 как средняя линия трапеции ABCD.
Пусть BC
= x,
тогда AD
= 8 – x.
Имеем:
Значит,
BC
= 1 и AD
= 7.
Ответ: 1 и 7.
Задача 7. Основание AB трапеции ABCD вдвое длиннее основания CD и вдвое длиннее боковой стороны AD. Длина диагонали AC равна a, а длина боковой стороны BC равна b. Найти площадь трапеции.
Решение.
Пусть E —
точка пересечения продолжений боковых
сторон трапеции и CD
= x,
тогда AD
= x,
AB
= 2x.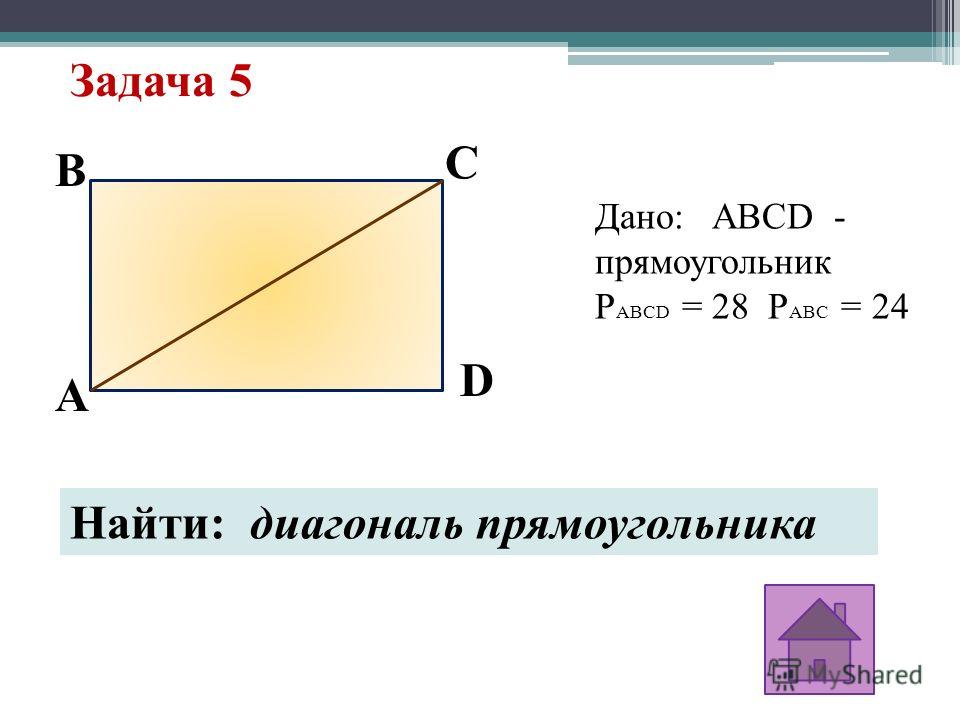 Отрезок CD
параллелен отрезку AB
и вдвое его короче, значит, CD
является средней линией треугольника
ABE.
Следовательно, CE
= BC
= b
и DE
= AD
= x,
откуда AE
= 2x.
Итак, треугольник ABE
равнобедренный (AB
= AE)
и AC —
его медиана. Поэтому
AC является и высотой этого треугольника,
и значит,
Отрезок CD
параллелен отрезку AB
и вдвое его короче, значит, CD
является средней линией треугольника
ABE.
Следовательно, CE
= BC
= b
и DE
= AD
= x,
откуда AE
= 2x.
Итак, треугольник ABE
равнобедренный (AB
= AE)
и AC —
его медиана. Поэтому
AC является и высотой этого треугольника,
и значит,
Так как треугольник DEC подобен треугольнику AEB с коэффициентом подобия то
Ответ:
Задача 8. Диагонали трапеции ABCD пересекаются в точке E. Найти площадь треугольника BCE, если длины оснований трапеции AB = 30, DC = 24, боковой стороны AD = 3 и угол DAB равен 60°.
Решение. Пусть DH — высота трапеции. Из треугольника ADH находим, что
Так как высота треугольника ABC, опущенная из вершины C, равна высоте DH трапеции, имеем:
Далее из подобия треугольников ABE и CDE получаем, что Следовательно,
Ответ:
Задача
9.
В трапеции средняя линия равна 4, а углы
при одном из оснований равны 40° и 50°.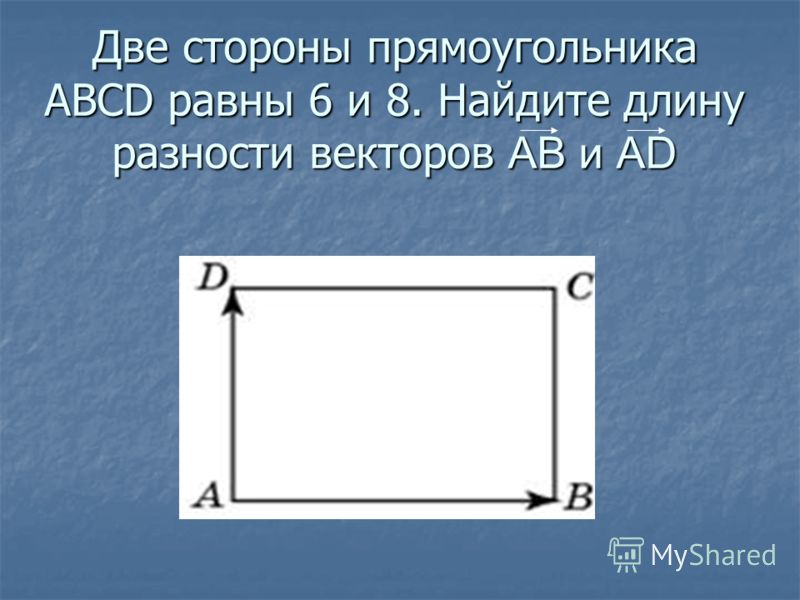 Найти
основания трапеции, если отрезок,
соединяющий середины оснований, равен
1.
Найти
основания трапеции, если отрезок,
соединяющий середины оснований, равен
1.
Решение.
Пусть ABCD —
данная трапеция, AB
и CD —
ее основания (AB
AB
+ CD
= 8. Продлим боковые стороны DA
и CB
до пересечения в точке E.
Рассмотрим треугольник ABE,
в котором ∠EAB
= 50°. ∠EBA
= 40°,
следовательно, ∠AEB
= 90°. Медиана EM
этого треугольника, проведенная из
вершины прямого угла, равна половине
гипотенузы: EM
= AM.
Пусть EM
= x,
тогда AM
= x,
DN
= 4 – x.
Согласно условию задачи MN
= 1, следовательно,
EN
= x
+ 1. Из
подобия треугольников AEM и DEN имеем:
Это означает, что AB = 3 и CD = 5.
Ответ: 3 и 5.
Задача 10. Выпуклый четырехугольник ABCD описан около окружности с центром в точке O, при этом AO = OC = 1, BO = OD = 2. Найти периметр четырехугольника ABCD.
Решение.
Пусть K,
L,
M,
N —
точки касания окружности со сторонами
AB,
BC,
CD,
DA
соответственно, r —
радиус окружности. Так как касательная
к окружности перпендикулярна радиусу,
проведенному в точку касания, то
треугольники AKO,
BKO,
BLO,
CLO,
CMO,
DMO,
DNO,
ANO —
прямоугольные. Применив
к этим треугольникам теорему Пифагора,
получим, что
Применив
к этим треугольникам теорему Пифагора,
получим, что
Следовательно, AB = BC = CD = DA, то есть ABCD — ромб. Диагонали ромба перпендикулярны друг другу, и точка их пересечения является центром вписанной окружности. Отсюда легко находим, что сторона ромба равна и значит, периметр ромба равен
Ответ:
Задачи для самостоятельного решения
С-1. Около
окружности радиуса r
описана равнобочная трапеция ABCD.
Пусть E
и K —
точки касания этой окружности с боковыми
сторонами трапеции. Угол между основанием
AB
и боковой стороной AD
трапеции равен 60°. Докажите, что EK
параллелен AB,
и найдите площадь трапеции ABEK.
С-2. В
трапеции диагонали равны 3 и 5, а отрезок,
соединяющий середины оснований, равен
2. Найдите площадь трапеции.
С-3. Можно
ли вокруг четырехугольника ABCD
описать окружность, если ∠ADC
= 30°, AB
= 3, BC
= 4, AC
= 6?
С-4. В
трапеции ABCD
(AB —
основание) величины углов DAB,
BCD,
ADC,
ABD
и ADB
образуют арифметическую прогрессию (в
том порядке, в котором они написаны).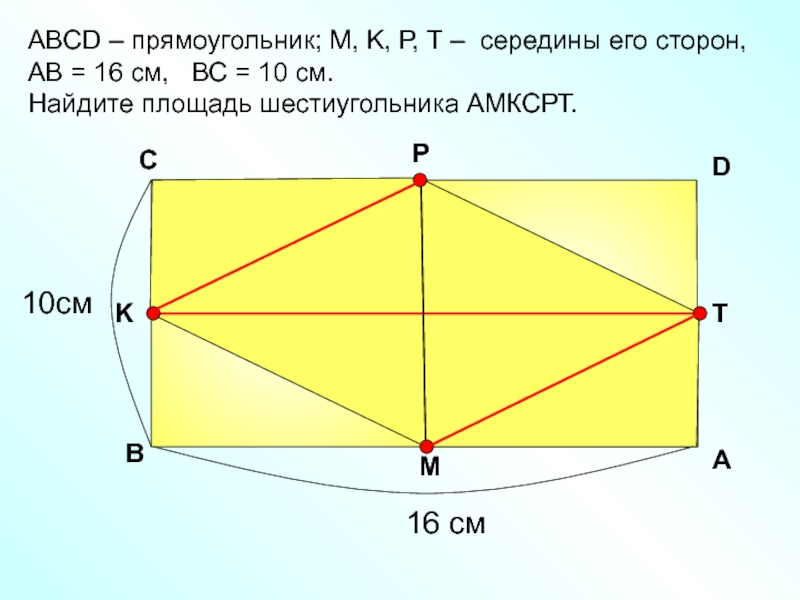 Найдите расстояние от вершины C
до диагонали BD,
если высота трапеции равна h.
Найдите расстояние от вершины C
до диагонали BD,
если высота трапеции равна h.
С-5. Дана
равнобедренная трапеция, в которую
вписана окружность и около которой
описана окружность. Отношение высоты
трапеции к радиусу описанной окружности
равно Найдите
углы трапеции.
С-6. Площадь
прямоугольника ABCD
равна 48, а длина диагонали равна 10. На
плоскости, в которой расположен
прямоугольник, выбрана точка O
так, что OB
= OD
= 13. Найдите расстояние от точки O
до наиболее удаленной от нее вершины
прямоугольника.
С-7. Периметр
параллелограмма ABCD
равен 26. Величина угла ABC
равна 120°. Радиус окружности, вписанной
в треугольник BCD,
равен Найдите
длины сторон параллелограмма, если
известно, что AD
> AB.
С-8. Четырехугольник
ABCD
вписан в окружность с центром в точке
O.
Радиус OA
перпендикулярен радиусу OB,
а радиус OC
перпендикулярен радиусу OD.
Длина перпендикуляра, опущенного из
точки C
на прямую AD,
равна 9. Длина отрезка BC
в два раза меньше длины отрезка AD.
Найдите площадь треугольника AOB.
Длина отрезка BC
в два раза меньше длины отрезка AD.
Найдите площадь треугольника AOB.
С-9. В
выпуклом четырехугольнике ABCD
вершины A
и C
противоположны, а длина стороны AB
равна 3. Угол ABC
равен угол
BCD
равен Найдите
длину стороны AD,
если известно, что площадь четырехугольника
равна
С-10. В
выпуклом четырехугольнике ABCD
проведены диагонали AC
и BD.
Известно, что
AD
= 2, ∠ABD
= ∠ACD
= 90°, и расстояние между точкой пересечения
биссектрис треугольника ABD
и точкой пересечения биссектрис
треугольника ACD
равно Найдите
длину стороны BC.
С-11. Пусть
M —
точка пересечения диагоналей выпуклого
четырехугольника ABCD,
в котором стороны AB,
AD
и BC
равны между собой. Найдите угол CMD,
если известно, что DM
= MC,
а
∠CAB
≠ ∠DBA.
С-12. В
четырехугольнике ABCD
известно, что ∠A
= 74°, ∠D
= 120°. Найдите угол между биссектрисами
углов B
и C.
С-13. В
четырехугольник ABCD
можно вписать окружность. Пусть K —
точка пересечения его диагоналей.
Известно, что AB
> BC
> KC, а
периметр и площадь треугольника BKC
равны соответственно 14 и 7. Найдите
DC.
Пусть K —
точка пересечения его диагоналей.
Известно, что AB
> BC
> KC, а
периметр и площадь треугольника BKC
равны соответственно 14 и 7. Найдите
DC.
С-14. В
трапеции, описанной около окружности,
известно, что BC AD,
AB
= CD,
∠BAD
=
= 45°. Найдите AB,
если площадь трапеции ABCD
равна 10.
С-15. В
трапеции ABCD
с основаниями AB
и CD
известно, что ∠CAB
= 2∠DBA.
Найдите площадь трапеции.
С-16. В
параллелограмме ABCD
известно, что AC
= a, ∠CAB
= 60°. Найдите площадь параллелограмма.
С-17. В
четырехугольнике ABCD
диагонали AC
и BD
пересекаются в точке K.
Точки L
и M
являются соответственно серединами
сторон BC
и AD.
Отрезок LM
содержит точку K.
Четырехугольник ABCD
таков, что в него можно вписать окружность.
Найдите радиус этой окружности, если
AB
= 3, и
LK
: KM
= 1 : 3.
С-18. В
выпуклом четырехугольнике ABCD
проведены диагонали AC
и BD.
При этом ∠BAC
=
= ∠BDC,
а площадь круга, описанного около
треугольника BDC,
равна
а) Найдите
радиус окружности, описанной около
треугольника ABC.
б) Зная,
что BC
= 3, AC
= 4, ∠BAD
= 90°, найдите площадь четырехугольника
ABCD.
Ответы:
Четырехугольник
ЧЕТЫРЕХУГОЛЬНИК
ЧАСТЬ А
1. Внутренние углы выпуклого четырехугольника относятся как 2:2,5:9,5:10. Найдите меньший угол.
2. Одна из сторон прямоугольника равна 4, а вторая – в пять раз больше. Найдите площадь прямоугольника.
3. В ромбе ABCD проведена диагональ BD. Найдите угол ADC, если .
4. Диагональ ромба, лежащая против угла , равна 11,2. Найдите периметр ромба.
5. В прямоугольнике ABCD биссектриса угла А делит сторону ВС на отрезки ВК = 4, КС = 6. Найдите периметр прямоугольника.
6. Найдите площадь квадрата, диагональ которого равна .
7. Найдите площадь прямоугольника,
если его диагональ равна
, а
одна из его сторон равна 15.
8. В равнобочной трапеции боковая сторона равна средней линии, а периметр равен 48. Определите боковую сторону трапеции.
9. Площадь ромба равна 96, а диагонали относятся как 3:4. Найдите сторону ромба.
10. Одна из диагоналей параллелограмма, равная , составляет с основанием угол . Найдите длину второй диагонали, если она составляет с тем же основанием угол .
11. Боковые стороны и меньшее основание прямоугольной трапеции равны соответственно 8, 10 и 10. Найдите большее основание.
12. Острый угол равнобедренной трапеции равен . Найдите площадь трапеции, если ее основания равны 5 и 11.
13. В трапеции ABCD , диагонали пересекаются в точке К, основания BC и AD равны соответственно 6 и 8, а диагональ АС = 35. Найдите длину отрезка АК.
14. Найдите площадь равнобедренной трапеции, если ее диагональ равна , а высота равна 2.
ЧАСТЬ В
15.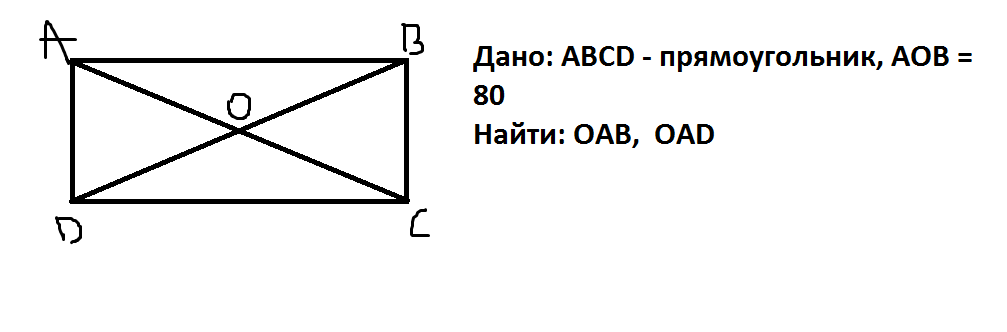 В прямоугольнике ABCD сторона AD вдвое длиннее
стороны АВ. Внутри прямоугольника взята
точка М так, что
.
Найдите длину стороны АВ.
В прямоугольнике ABCD сторона AD вдвое длиннее
стороны АВ. Внутри прямоугольника взята
точка М так, что
.
Найдите длину стороны АВ.
16. В четырехугольнике ABCD диагонали пересекаются в точке О, площади треугольников AOB, BOC, COD равны соответственно 12, 18 и 24. Найдите площадь четырехугольника ABCD.
17. Периметр параллелограмма ABCD равен 24. Найдите площадь параллелограмма, если высота BH, проведенная к стороне AD, равна 2, а величина угла А равна .
18. В параллелограмме ABCD из вершины тупого угла В проведены высота ВН и отрезок ВК, где
К – середина стороны AD. Найдите площадь параллелограмма, если , .
19. Одна из сторон параллелограмма равна диагонали и равна 5. Найдите площадь параллелограмма, если вторая диагональ равна .
20. Острый угол параллелограмма
равен
, а
диагонали
и
. Найдите периметр параллелограмма.
Найдите периметр параллелограмма.
21. Стороны параллелограмма равны 3 и 5, а угол между диагоналями равен . Найдите площадь параллелограмма.
22. Перпендикуляр, проведенный из вершины параллелограмма к его диагонали, делит эту диагональ на отрезки длиной 6 и 15. Разность длин сторон равна 7. Найдите периметр параллелограмма.
23. Из вершины В параллелограмма ABCD проведены высоты ВК и ВН к сторонам AD и CD соответственно. Угол КВН равен , ВК : ВН = 1 : 4, AD = 4. Найдите площадь параллелограмма.
24. В параллелограмме даны острый угол, равный , и расстояние от точки пересечения диагоналей до неравных сторон, равных соответственно 2 и 3. Найдите площадь параллелограмма.
25. Высота ромба равна 12, а одна из диагоналей равна 15. Найдите площадь ромба.
26. Высота ВН ромба ABCD,
проведенная из вершины тупого угла В,
делит сторону AD на
отрезки АН = 17, HD = 8.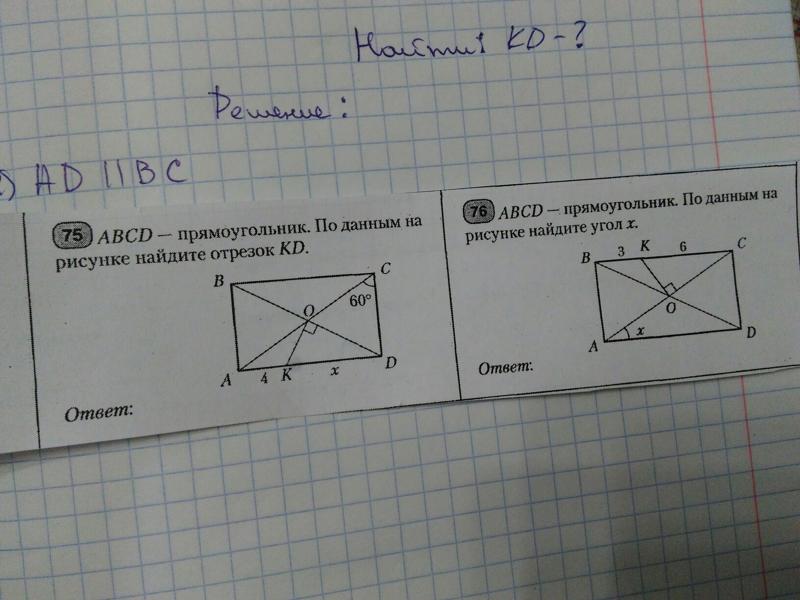 Найдите большую диагональ ромба.
Найдите большую диагональ ромба.
27. ABCD – ромб, , M – середина стороны BC, точка N лежит на стороне DC, причем 2DN = NC. Найдите тангенс угла NAM.
28. Точка М делит диагональ квадрата ABCD со стороной, равной 24, в отношении
АМ : МС = 3 : 1, точка N лежит на стороне AD, причем угол NMD прямой. Найдите длину отрезка AN.
29. Длины оснований трапеции равны 25 и 39, а длины боковых сторон равны 13 и 15. Найдите высоту трапеции.
30. В трапеции диагонали являются биссектрисами острых углов. Определить периметр трапеции, площадь трапеции с если диагональ делит среднюю линию на отрезки 10 и 18.
31. Найдите площадь трапеции с основаниями 3 и 6 и диагоналями 7 и 8.
32. В прямоугольной трапеции средняя
линия равна 13,5. Меньшая диагональ
является биссектрисой тупого угла и
имеет длину 12.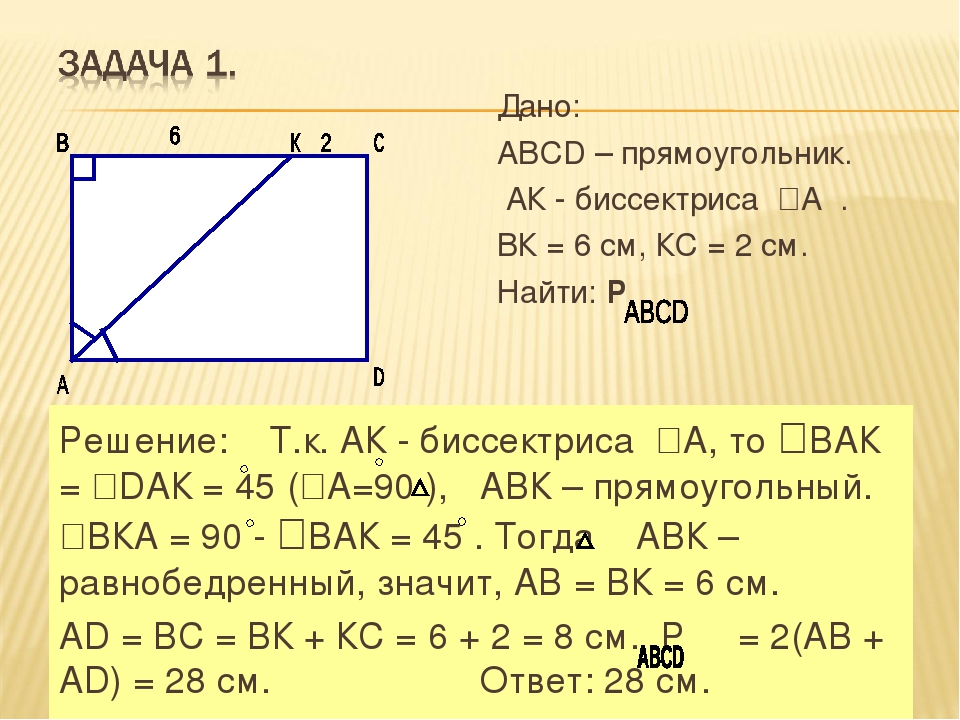 Найдите периметр трапеции.
Найдите периметр трапеции.
33. В прямоугольной трапеции диагонали взаимно перпендикулярны. Большая диагональ составляет с меньшей боковой стороной угол . Найдите длину средней линии трапеции, если длина меньшей диагонали равна 10.
34. В равнобедренной трапеции основания равны 3 и 5, а диагонали взаимно перпендикулярны. Найти площадь трапеции.
35. В равнобедренной трапеции большее основание равно 44, боковая сторона равна 17, а диагональ равна 39. Найти площадь трапеции.
36. В равнобедренной трапеции биссектриса острого угла делит боковую сторону в отношении
19 : 14. Верхнее основание равно 3. Найти площадь трапеции, если боковая сторона равна 17.
ЧАСТЬ С
37. Площадь четырехугольника, вершинами которого являются середины сторон выпуклого четырехугольника ABCD, равна 24. Найдите площадь четырехугольника ABCD.
38. На сторонах выпуклого четырехугольника ABCD, площадь которого
равна 1, взяты точки K на AB, L на BC, M на CD, N на AD так , что AK : BK = CL : BL = 3:1; AN : ND = CM :MD = 5:1. Найдите площадь
многоугольника KBLMDN.
Найдите площадь
многоугольника KBLMDN.
39. В четырехугольнике ABCD известно, что . Найдите величину угла АВС.
40. В квадрат площадью 24 вписан прямоугольник так, что на каждой стороне квадрата лежит одна вершина прямоугольника. Длины сторон прямоугольника относятся как 1:3. Найти площадь прямоугольника.
41. В параллелограмме со сторонами 3 и 5 и острым углом проведены биссектрисы четырех углов. Найдите площадь четырехугольника, ограниченного биссектрисами.
42. В параллелограмме ABCD биссектрисы AE и DF делят сторону BC на три равные части и пересекаются в точке О внутри параллелограмма. Найдите площадь параллелограмма, если площадь треугольника AOD равна 18.
43. Из вершины острого угла ромба
проведены две высоты расстояние между
концами, которых в 1,5 раза больше меньшей
диагонали ромба. Определите больший
угол ромба.
44. Большее основание трапеции равно 8. Прямая параллельная основаниям, делит трапецию на две равновеликие фигуры. Отрезок этой прямой внутри трапеции равен . Найти меньшее основание трапеции.
45. В трапеции углы при одном из оснований равны , а длина отрезка, соединяющего середины оснований, равна 2. Найдите большее основание трапеции, если длина её средней линии равна 4.
46. В трапеции диагонали равны 3 и 5 , а отрезок, соединяющий середины оснований, равен 2. Найти площадь трапеции.
47. Основание АВ трапеции ABCD вдвое длиннее боковой стороны AD и вдвое длиннее основания CD. Длина диагонали АС равна 10, длина боковой стороны ВС равна 8. Найти площадь трапеции.
48. Найти высоту трапеции с основаниями 10 и 15, у которой диагонали взаимно перпендикулярны, а угол, образованный продолжением боковых сторон, равен .
ЧЕТЫРЕХУГОЛЬНИК
ОТВЕТЫ
1. | 17. 16 | 33. 10 |
2. 100 | 18. 36 | 34. 16 |
3. | 19. | 35. 540 |
4. 44,8 | 20. 14 | 36. 165 |
5. 28 | 21. | 37. 96 |
6. 34 | 22. | 38. 9 |
7. 180 | 23. | 39. |
8. 12 | 24. | 40. 9 |
9. | 25. 150 | 41. 1 |
10. 13,5 | 26. | 42. 48 |
11. 16 | 27. | 43. |
12. 24 | 28. 12 | 44. 6 |
13. 15 | 29. 12 | 45. 6 |
14. 6 | 30. 96 | 46. 6 |
15. | 31. | 47. 60 |
16. 16 | 32. | 48. 0,5 |
Геометрия плоских фигур — Математика
Разработка предметно – ориентированного элективного курса для предпрофильной подготовки по теме
«Геометрия плоских фигур»
Оглавление
1. Введение 3-5.
Введение 3-5.
2. Основная часть 6-7.
3. Заключение 8.
4. Список литературы 9.
5. Приложения 10-17.
Введение.
Геометрия — наиболее уязвимое звено школьной математики. Это связано как с обилием различных типов геометрических задач, так и с многообразием приемов и методов их решения.
В теоретическую часть школьного курса геометрии включены в основном теоремы, работающие на сам курс, то есть необходимые для его дальнейшего развития. Многие теоремы в известном смысле прикладного характера, областью приложения которых являются задачи, а не теория, из курса исключены.
В связи с этим возникает необходимость в выделении некоторого количества задач, так называемых элементарных (базисных, опорных, ключевых), иллюстрирующих тот или иной часто встречающийся метод или прием решения задач, которые учащийся должен усвоить и освоить. Следует обращать внимание учащихся на «рабочие теоремы», то есть теоремы, которые, с одной стороны, активно используются при решении задач, но с другой стороны, как показывает опыт, либо не всегда рассматриваются при изучении геометрии, либо тщательно не отрабатываются.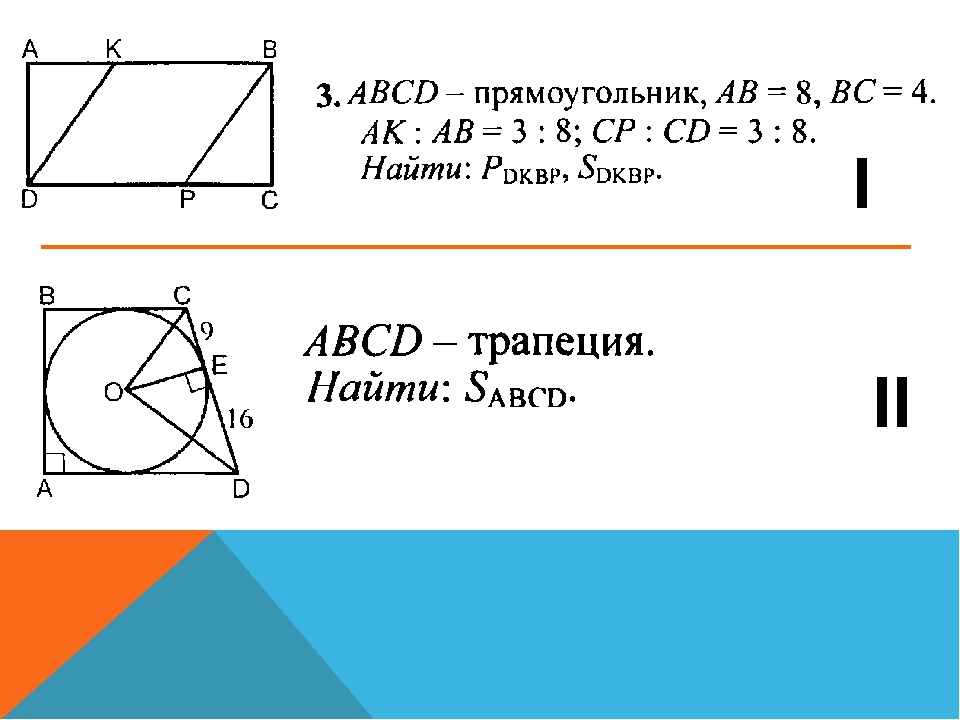
Первым и важнейшим этапом решения геометрической задачи является построение чертежа. Нельзя научиться решать достаточно содержательные геометрические задачи, не выработав привычки делать «большой и красивый» чертеж, удовлетворяющий не только формально математическим требованиям, но и известным эстетическим критериям. Поле построения чертежа следует вспомнить все факты, относящихся к данным и искомым элементам задачи, а также соотношения между ними.
Таким образом, умение решать геометрические задачи определяется четырьмя слагаемыми:
1) чертеж;
2) метод;
3) владение определенным объемом геометрических фактов и теорем;
4) наличие достаточно активно используемого запаса опорных задач.
Предлагаемый курс призван помочь ученикам при подготовке к итоговой аттестации. Материал курса разбит по темам и систематизирован по видам геометрических фигур и по наборам геометрических теорем и формул, опирающихся на единую доказательную базу, что позволяет выявлять общие подходы к решению геометрических задач при обилии различных их типов и многообразии приемов и методов решения.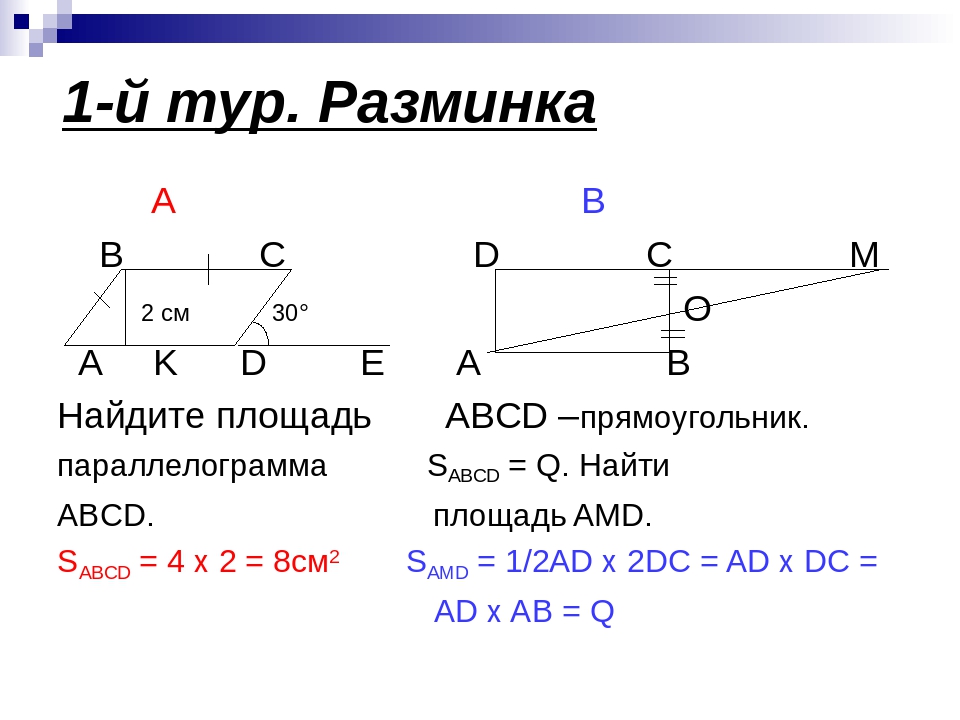
При разработке курса «Решение наиболее сложных заданий по математике» учитывалось то, что элективный курс как компонент образования должен быть направлен на удовлетворение познавательных потребностей и интересов обучающихся, на формирование у них новых видов познавательной и практической деятельности, которые не характерны для традиционных учебных курсов.
Курс геометрии обладает также чрезвычайно важным нравственным моментом, поскольку именно геометрия дает представление о строго установленной истине, воспитывает потребность доказывать то, что утверждается в качестве истины. Таким образом, геометрическое образование является важнейшим элементом общей культуры.
Предлагаемый курс «Решение наиболее сложных заданий по математике» является практико-ориентированным и предназначен для учащихся 9 класса. Количество учебных часов — 34.
Цели курса:
— обобщить и систематизировать знания учащихся по основным разделам планиметрии;
— познакомить учащихся с некоторыми методами и приемами решения планиметрических задач;
— сформировать умения применять полученные знания при решении «нетипичных», нестандартных задач.
Задачи курса:
— дополнить знания учащихся теоремами прикладного характера, областью применения которых являются задачи;
— расширить и углубить представления учащихся о приемах и методах решения планиметрических задач;
— помочь овладеть рядом технических и интеллектуальных умений на уровне свободного их использования;
— развить интерес и положительную мотивацию изучения геометрии.
Структура курса представляет собой пять логически законченных и содержательно взаимосвязанных тем, изучение которых обеспечит системность и практическую направленность знаний и умений учеников. Все занятия направлены на расширение и углубление базового курса. Содержание курса можно варьировать с учетом склонностей, интересов и уровня подготовленности учеников.
Основной тип занятий — практикум. Для наиболее успешного усвоения материала планируются различные формы работы с учащимися: лекционно-семинарские занятия, групповые, индивидуальные формы работы. Для текущего контроля на каждом занятии учащимся рекомендуется серия заданий, часть которых выполняется в классе, а часть — дома самостоятельно. Изучение данного курса заканчивается проведением либо итоговой контрольной работы, либо теста.
Для текущего контроля на каждом занятии учащимся рекомендуется серия заданий, часть которых выполняется в классе, а часть — дома самостоятельно. Изучение данного курса заканчивается проведением либо итоговой контрольной работы, либо теста.
В результате изучения курса учащиеся должны уметь:
— точно и грамотно формулировать теоретические положения и излагать собственные рассуждения в ходе решения заданий;
— уверенно решать задачи на вычисление, доказательство и построение;
— применять аппарат алгебры к решению геометрических задач;
— применять свойства геометрических преобразований к решению задач.
Основная часть.
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ УЧЕБНОГО МАТЕРИАЛА
1 час в неделю, всего 34 часов.
1. Четырёхугольники (10 часов)
Метрические соотношения в четырёхугольнике.
Свойство произвольного четырёхугольника, связанное с параллелограммом.
Свойство биссектрисы параллелограмма и трапеции.
Свойства трапеции.
Теоремы о площадях четырёхугольников.
2. Треугольники (8 часов)
Метрические соотношения в произвольном треугольнике.
Свойства медиан, биссектрис, высот.
Метрические соотношения в прямоугольном треугольнике.
Свойства проекций катетов.
3. Окружности (6 часов)
Метрические соотношение между длинами хорд, отрезками касательных и секущих.
Свойства дуг и хорд.
Свойства вписанных углов.
Углы между хордами, касательными и секущими.
4. Окружности и треугольники (5 часов)
Окружности, вписанные и описанные около треугольников.
Окружности, вписанные и описанные около прямоугольных треугольников.
5. Окружности и четырёхугольники (5 часов)
Четырёхугольники, вписанные и описанные около окружности.
Площади четырёхугольников, вписанных и описанных около окружностей.
Теорема Птолемея.
КАЛЕНДАРНО ТЕМАТИЧЕСКИЙ ПЛАН
№ п/п | Тема занятия | Кол-во часов |
1 | Четырёхугольники | 10 |
Метрические соотношения в четырёхугольнике. | 2 | |
Свойство произвольного четырёхугольника, связанное с параллелограммом. | 2 | |
Свойство биссектрисы параллелограмма и трапеции. | 2 | |
Свойства трапеции. | 2 | |
Теоремы о площадях четырёхугольников. | 2 | |
2 | Треугольники | 8 |
Метрические соотношения в произвольном треугольнике. | 2 | |
Свойства медиан, биссектрис, высот. | 2 | |
Метрические соотношения в прямоугольном треугольнике. | 2 | |
Свойства проекций катетов. | 2 | |
3 | Окружности | 6 |
Метрические соотношение между длинами хорд, отрезками касательных и секущих. | 2 | |
Свойства дуг и хорд. | 1 | |
Свойства вписанных углов. | 1 | |
Углы между хордами, касательными и секущими. | 2 | |
4 | Окружности и треугольники | 5 |
Окружности, вписанные и описанные около треугольников. | 2 | |
Окружности, вписанные и описанные около прямоугольных треугольников. | 3 | |
5 | Окружности и треугольники | 5 |
Четырёхугольники, вписанные и описанные около окружности. | 1 | |
Площади четырёхугольников, вписанных и описанных около окружностей. | 2 | |
Теорема Птолемея. | 2 |
Заключение.
Основное содержание курса соответствует современным тенденциям развития школьного курса геометрии, идеям дифференциации, углубления и расширения знаний учащихся. Данный курс дает учащимся возможность познакомиться с нестандартными способами решения планиметрических задач, способствует формированию и развитию таких качеств, как интеллектуальная восприимчивость и способность к усвоению новой информации, гибкость и независимость логического мышления. Поможет учащимся в подготовке к итоговой аттестации, а также при выборе ими будущей профессии, связанной с математикой.
Поможет учащимся в подготовке к итоговой аттестации, а также при выборе ими будущей профессии, связанной с математикой.
СПИСОК ЛИТЕРАТУРЫ
Геометрия, 7-9: учеб. для общеобразоват. учреждений / [Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др.] – М.: Просвещение, 2008. – 384 с.
Геометрия. Решаем задачи по планиметрии. Практикум: элективный курс / авт.-сост. Л.С.Сагателова. – Волгоград: Учитель, 2009. – 150 с.
Сборник задач по геометрии для 6-8 классов. Пособие для учителей. Изд. 2, переработ. И доп. М., «Просвещение», 1971.
Геометрия. Планиметрия: Пособие для подготовки к ЕГЭ / Под ред. И.В.Ященко и А.В. Семёнова. – М.: МЦНМО, 2009. – 256 с. – (Готовимся к ЕГЭ).
Геометрия. Подготовка к ЕГЭ и ГИА-9. Учимся решать задачи: учебное пособие / Б.И.Вольфсон, Л.И. Резницкий. – Ростов н/Д: Легион-М, 2011. – 224с. – (Готовимся к ЕГЭ).
Приложение 1.
ПРЯМОУГОЛНЫЙ ТРЕУГОЛЬНИК.
1. Проекции катетов прямоугольного треугольника на гипотенузу равны 9 и 16. Найти радиус вписанной окружности.
2. В прямоугольном треугольнике из вершины прямого угла проведены медиана и высота, расстояние между их основаниями равно 1. Найдите площадь треугольника, если известно, что один из катетов в два раза больше другого.
3. Радиусы вписанной и описанной окружностей прямоугольного треугольника равны 2 и 5 соответственно. Найдите его площадь.
4. В прямоугольном треугольнике ABC из вершины прямого угла проведена высота BD. Радиусы окружностей, вписанных в треугольники ABD и BCD, равны соответственно 3 и 4. найдите радиус окружности, вписанной в треугольник ABC.
5. высота прямоугольного треугольника, опущенная на гипотенузу, делит биссектрису острого угла в отношении 4 : 5, считая от вершины. Найти величину этого угла.
6. Медиана прямоугольного треугольника, проведённая к гипотенузе, равна 20. Из середины гипотенузы восстановлен перпендикуляр до пересечения с большим катетом. Длина перпендикуляра 15. Найдите катеты, в ответе укажите меньший из них.
Длина перпендикуляра 15. Найдите катеты, в ответе укажите меньший из них.
7. Один катет прямоугольного треугольника равен 5, а проекция другого катета на гипотенузу равна 2,25. Найдите гипотенузу этого треугольника.
8. Радиус окружности, вписанной в прямоугольный треугольник, равен полуразности его катетов. Найдите отношение большего катета к меньшему.
9. Высота, опущенная на гипотенузу прямоугольного треугольника, делит его на два треугольника. Радиусы окружностей, вписанных в эти два треугольника, равны 1 и 2. Найдите радиус окружности, вписанной в исходный треугольник.
10.На гипотенузе прямоугольного треугольника взята точка А – такая, что гипотенуза делится ею на отрезки с длинами 30 и 40. Найдите длины катетов, если расстояния от точки А до катетов равны.
11.В треугольнике ABC с прямым углом C проведена биссектриса AD. Найдите площадь треугольника ABC, если CD = 4, BD = 5.
12. Из вершины прямого угла C треугольника ABC проведена высота CD. Найдите гипотенузу AB, если CD = AD – BD = √5.
Найдите гипотенузу AB, если CD = AD – BD = √5.
ПРОИЗВОЛЬНЫЙ ТРЕУГОЛЬНИК. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ.
1. Основание равнобедренного треугольника равно 2. Медианы к боковым сторонам взаимно перпендикулярны. Найдите площадь треугольника.
2. Длины двух сторон треугольника 6 и 8. Медианы, проведённые к этим сторонам, взаимно перпендикулярны. Найдите длину третьей стороны.)
3. В треугольнике с длинами сторон 5, 6, 10 к меньшей стороне проведены медиана и биссектриса. Найдите расстояние между точками пересечения медианы и биссектрисы с меньшей стороной.
4. Дан треугольник ABC. Его высота BD равна 30. Из основания E биссектрисы AE опущен перпендикуляр EF на сторону AC. Определите длину этого перпендикуляра, если AB : AC = 7 : 8.
5. В треугольнике длины двух сторон равны 6 и 3. Найдите длину третьей стороны, если полусумма высот, проведённых к данным сторонам, равна третьей высоте.
6. В треугольнике ABC AC = 4, AB = 5, AD — биссектриса, причём AD = BD. Найдите длину биссектрисы AD.
Найдите длину биссектрисы AD.
7. В равнобедренном треугольнике ABC с основанием BC высоты BB1 и CC1 пересекаются в точке M, при этом BM = 10, B1M = 6. Найдите площадь треугольника ABM.
8. Найдите площадь треугольника ABC, если AC = 20, BC = 2√97, медиана BM = 12.
9. В треугольнике ABC AB = 12, BC = 21, AC = 20. Найдите площадь треугольника, образованного стороной AC, медианой BM и биссектрисой CK данного треугольника.
10. В треугольнике ABC AB = 5, BC = 10, AC = 3√5. Найдите площадь треугольника, образованного высотой AH, медианой AM и биссектрисой BK данного треугольника.
11. В треугольнике ABC AB = 7, BC = 9, AC = 8. найдите площадь треугольника, образованного высотой и медианой треугольника ABC, проведённых из вершины B.
12. Найдите биссектрисы острых углов в прямоугольном треугольнике, катеты которого равны 6 и 8.
13. Найдите длину биссектрисы A треугольника ABC, длины сторон которого равны: AB = 12, AC = 15, BC = 18.
14. Найдите площадь треугольника, если длины двух его сторон равны 1 и √13, а медиана к третьей стороне равна 2.
15. В треугольнике длины двух сторон равны 35 и 14, а биссектриса, лежащая между ними, равна 12. Найдите площадь треугольника.
16. В прямоугольном треугольнике медианы, проведённые к катетам, равны √52 и √73. Найдите длину гипотенузы.
ПАРАЛЛЕЛОГРАММ. РОМБ.
1. В четырёхугольнике ABCD, AC |_ BD, AC = 12, BD = 16. Найти расстояние между серединами сторон AB и CD.
2. Длины диагоналей параллелограмма равны 17 и 19. Длина одной из сторон равна 10. Найти длину другой стороны.
3. Длины диагоналей ромба относятся как 3 : 4. Во сколько раз сторона ромба превосходит радиус вписанной в него окружности?
4. Дан ромб ABCD с острым углом B. Площадь ромба равна 320, а синус угла B равен 0,8. Высота CH пересекает диагональ BD в точке K. Найдите длину отрезка CK.
5. В параллелограмме ABCD C = 1200. Биссектрисы углов B и C пересекаются в точке K, лежащей на стороне AD; CK = 3.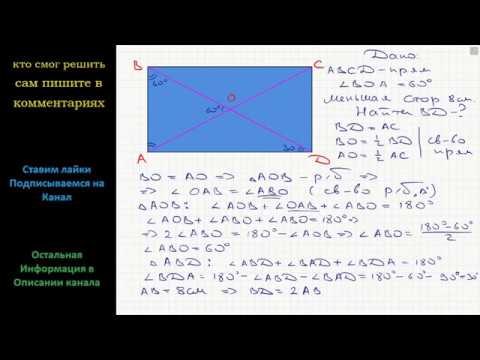 Найдите площадь параллелограмма.
Найдите площадь параллелограмма.
6. Найдите площадь ромба, высота которого 4,8, а отношение диагоналей 3 : 4.
7. В параллелограмме ABCD биссектриса угла B пересекает сторону CD в точке T и прямую AD в точке M. Найдите периметр треугольника CBT, если AB = 21, BM = 35, MD = 9.
8. Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите площадь параллелограмма, если BK = KC = 5, AK = 8.
9. Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, BD = 26, AC = 40, BC = 21. Отрезок OE – перпендикуляр к стороне BC. Найдите разность площадей четырёхугольников DCEO и ABEO.
10. В четырёхугольнике ABCD AD = BC, AB = 5, CD = 4, сумма углов при вершинах A и B равна 600. Найдите площадь четырёхугольника ABCD.
11. На сторонах BC и CD параллелограмма ABCD расположены точки E и F так, что BE = 2EC; CF = 3FD. Диагональ BD пересекает отрезки AE и AF в точках P и Q. Найдите отношение площади треугольника APQ к площади параллелограмма.
12. Из вершины D ромба ABCD опущен перпендикуляр DE на сторону BC. Найти длину стороны ромба, если AC = 2√6, AE = √14.
13. Внутри параллелограмма ABCD расположена точка O так, что треугольник COD является равносторонним. Найдите периметр параллелограмма, если расстояние от точки O до прямых AD, AB и BC равно соответственно 3,6 и 5.
14. В параллелограмме ABCD биссектриса угла A пересекает сторону BC в точке E, а биссектриса угла C пересекает сторону AD в точке F. Найдите площадь параллелограмма, если BC =3AB, а площадь четырёхугольника, образованного пересечением прямых AE, CF, BF и DE, равна 4.
15. В прямоугольнике ABCD AB = 5, AD = 4. На стороне AB взята точка E, такая, что CED = AED. Найдите длину AE.
16. Площадь ромба равна 600, а отношение длин диагоналей равно 4 : 3. Найдите высоту ромба.
ТРАПЕЦИЯ.
1. Боковые стороны равнобедренной трапеции при продолжении пересекаются под прямым углом. Найдите длину большего основания трапеции, если её площадь равна 12, а высота 2.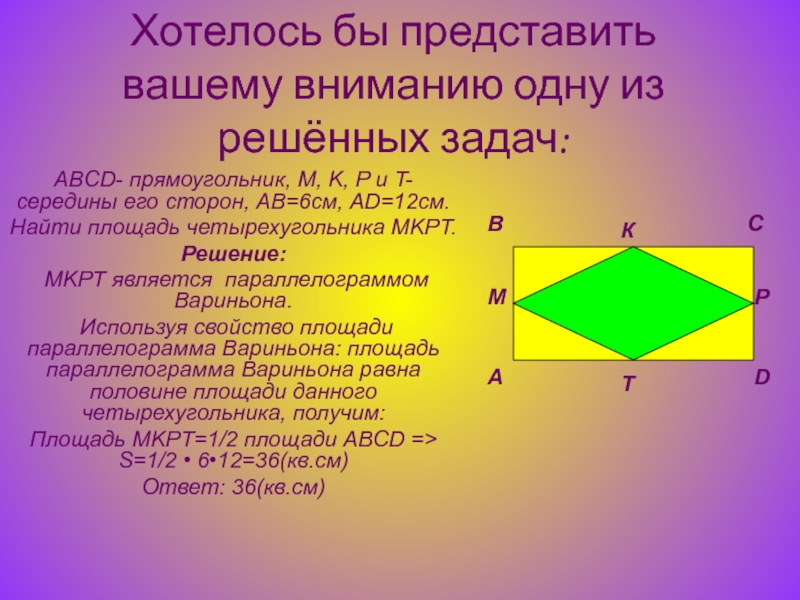
2. Средняя линия трапеции разбивает её на две трапеции, площади которых относятся как 1 : 2. Чему равно отношение меньшего основания трапеции к большему?
3. В трапеции большее основание равно 25, одна из боковых сторон равна 15. Известно, что одна из диагоналей перпендикулярна заданной боковой стороне, а другая делит угол между заданной боковой стороной и нижним основанием пополам. Найдите площадь трапеции.
Основания трапеции равны 10 и 31, боковые стороны – 20 и 13. Найдите высоту трапеции.
4. Найдите площадь равнобедренной трапеции, если её основания равны 17 и 15, а диагональ перпендикулярна боковой стороне.
5. Диагонали трапеции CEKM (EK и CM – основания) пересекаются в точке O. Площадь ∆ COE равна 16, CO = 2OK. Найдите площадь трапеции.
6. В трапеции ABCD B + C = 900; AB = 6; AD = 5; CD = 8. Найдите площадь трапеции.
7. Диагонали трапеции взаимно перпендикулярны и равны 8 и 15. Найдите среднюю линию трапеции.
8. Диагонали AC и BC четырёхугольника ABCD пересекаются в точке O, площади треугольников AOB и AOD равны соответственно 12 и 8, AO : OC = 4 : 5.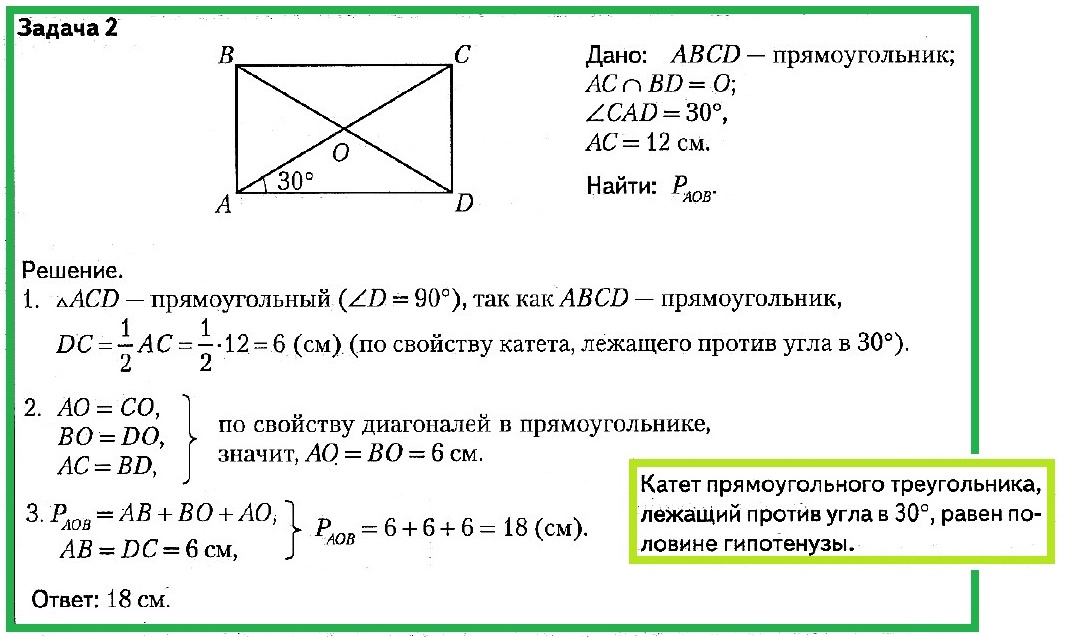 Найдите площадь четырёхугольника.
Найдите площадь четырёхугольника.
9. Диагонали равнобедренной трапеции взаимно перпендикулярны, а средняя линия равна 8. Найдите площадь трапеции.
10. Основания AB и CD трапеции ABCD равны соответственно 5 и 10, AD = 3, BC = 7. Биссектрисы углов A и D пересекаются в точке K, биссектрисы B и C – в точке M. Найдите KM.
11. Диагонали AC и BD трапеции ABCD пересекаются в точке O, основание AD трапеции равно 2, BC = 3, SAOB = 6. Найдите S ABCD.
12. Найдите площадь равнобедренной трапеции, если её высота равна 3, а тангенс угла между диагональю и основанием равен ¼.
13. В трапеции ABCD длины диагоналей AC и BD равны 3 и 5, а длина отрезка KL, соединяющего середины оснований BC и AD, равна 2. Найдите площадь трапеции ABCD.
14. Длина диагонали равнобедренной трапеции равна 5, а её площадь равна 12. Найдите высоту трапеции.
15. Длины оснований трапеции равны 10 и 24, длины её боковых сторон 13 и 15. Найдите площадь трапеции.
16. Найдите отношение оснований трапеции, если известно, что средняя линия делится диагоналями на 3 равные части.
Найдите отношение оснований трапеции, если известно, что средняя линия делится диагоналями на 3 равные части.
17. Диагонали трапеции взаимно перпендикулярны, средняя линия равна 13. Одна из диагоналей равна 10. Найдите другую диагональ.
18. Боковые стороны трапеции равны 12 и 16, а содержащие их прямые взаимно перпендикулярны. Площадь равна 144. Найдите среднюю линию трапеции.
19. Диагонали равнобедренной трапеции перпендикулярны, одно из оснований равно 17, а площадь равна 81. Найдите второе основание трапеции.
20. Диагонали равнобедренной трапеции перпендикулярны, а отрезок, соединяющий середину меньшего основания и середину боковой стороны, равен 5. Найдите площадь трапеции.
21. Найдите площадь равнобедренной трапеции, если её диагональ, равная 5, образует с основанием угол, синус которого равен 0,6.
ОКРУЖНОСТЬ. СВОЙСТВА КАСАТЕЛЬНЫХ, ХОРД И СЕКУЩИХ.
1. Радиус окружности равен √5. Определите длину хорды, проведённую из конца данного диаметра через середину перпендикулярного ему радиуса.
2. Из данной точки вне окружности проведены касательная и секущая, внутренняя часть которой стягивает дугу в 1200. Определите длину секущей, если радиус окружности равен 4√3, а длина касательной от данной точки до точки касания равна 8.
3. Окружность с центром O касается сторон угла B в точках A и C. Лучи AO и BC пересекаются в точкеM, OM = 9, BM = 18. Найдите площадь ∆ BOM.
4. Окружность с центром Oкасается сторон угла B в точках A и C. Отрезок BO пересекает окружность в точке K. Найдите периметр AKCO, если B = 600, BK = 12.
5. Из точки B к окружности проведены касательные BP и BQ (P и Q – точки касания ). Найти длину хорды PQ, если длина отрезка PB = 40, а расстояние от центра окружности до хорды PQ равно 18.
ОКРУЖНОСТЬ, ВПИСАННАЯ В ТРЕУГОЛЬНИК.
1. Окружность, вписанная в равнобедренный треугольник ABC с основанием AC, касается сторон AB и BC в точках K и M соответственно. Найдите KM, если AK = 6, KB = 12.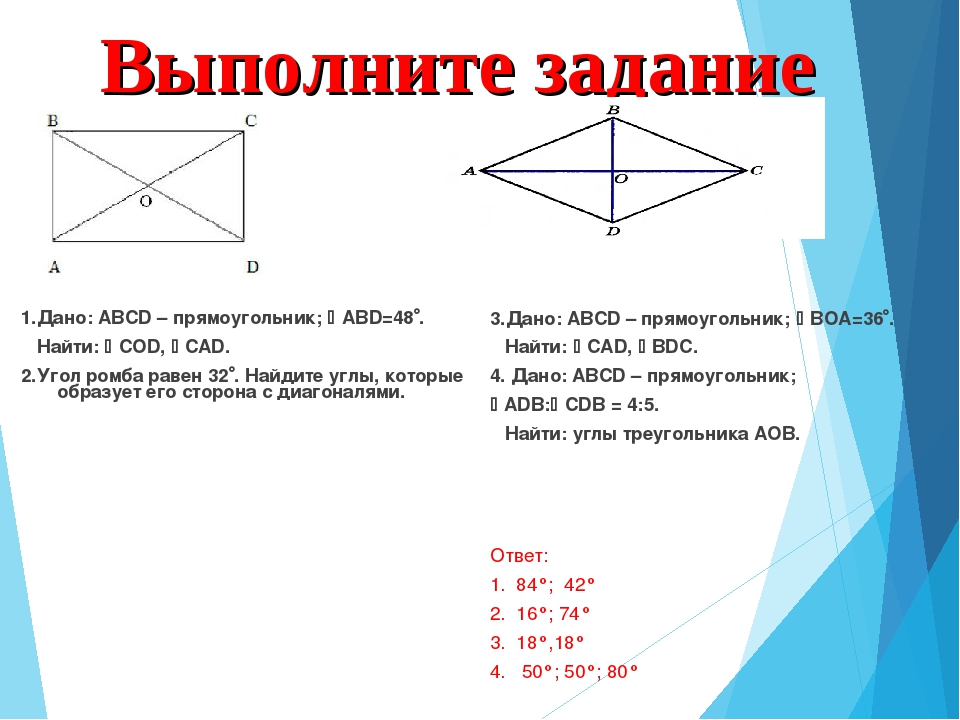
2. Радиус окружности, вписанной в прямоугольный треугольник, равен 2, радиус описанной окружности – 5. Найдите больший катет треугольника.
3. Основание равнобедренного треугольника равно 36. Вписанная окружность касается его боковых сторон в точках A и P, AP = 12. Найдите периметр треугольника.
4. Найдите радиус окружности, вписанной в остроугольный ∆ABC, если высота BH равна 12 и известно, что sin A = 12/13; sin C = 4/5.
5. В равнобедренный треугольник вписана окружность. Точка касания делит каждую сторону на отрезки 8 и 6, считая, от вершин к окружности проведены три касательные, параллельные каждой из сторон треугольника. Найдите длины отрезков касательных, заключённых между сторонами треугольника. Запишите их сумму.
6. Окружность, вписанная в прямоугольный треугольник ABC (C = 900), касается катета BC в точке H. Биссектриса угла A пересекает катет BC в точке M. Найдите HM, если CH = 4, BH = 12.
7. Точка касания окружности, вписанной в прямоугольный треугольник, и катета делит этот катет на отрезки длиной 3 и 5.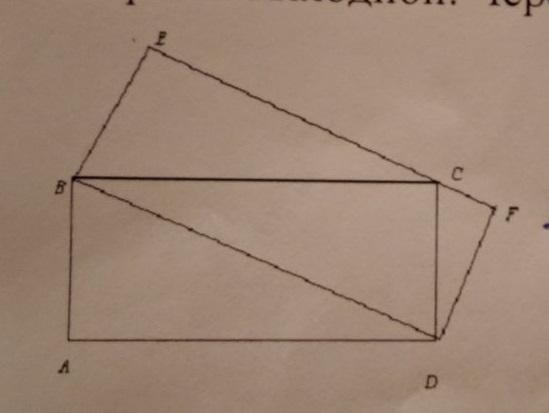 Найдите радиус окружности, описанной около треугольника.
Найдите радиус окружности, описанной около треугольника.
ОКРУЖНОСТЬ, ОПИСАННАЯ ОКОЛО ТРЕУГОЛЬНИКА.
1. Около равнобедренного треугольника ABC с AC основанием и углом при основании 750 описана окружность с центром O. Найдите её радиус, если площадь ∆ BOC равна 16.
2. Около ∆ ABC описана окружность. Медиана AM проведена до пересечения с окружностью в точке K. Найти AC, если AM = 18, MK = 8, BK = 10.
3. Около тупоугольного равнобедренного треугольника описана окружность радиусом 25. Расстояние от её центра до основания треугольника равно 7. Найдите расстояние от центра окружности до боковой стороны треугольника.
4. Основание равнобедренного остроугольного треугольника 48, а радиус описанной около него окружности 25. Найдите расстояние между центрами вписанной и описанной окружностей треугольника.
5. В ∆ ABC C = 600, AB = 8 . На основании AB как на диаметре построена окружность, пересекающая стороны AC и BC в точках K и M соответственно. Найдите KM.
Найдите KM.
ЧЕТЫРЁХУГОЛЬНИКИ И ОКРУЖНОСТЬ.
1. Диагонали четырёхугольника ABCD, вписанного в окружность, пересекаются в точке M, AM = 4, CM = 9, BM = DM, AMB = 300. Найдите площадь четырёхугольника.
2. Высота ромба, проведённая из вершины его тупого угла, делит сторону ромба в отношении 1 : 2, считая от вершины его острого угла. Какую часть площади ромба составляет площадь вписанного в него круга?
3. Дан ромб ABCD. Окружность, описанная около треугольника ABD, пересекает большую диагональ ромба AC в точке E. Найдите CE, если AB = 8√5, BD = 16.
4. Определите сторону ромба, если окружность, проведённая через вершины обоих его тупых углов и одного из острых углов, делит большую диагональ на части 1, 4 и 5.
5. В окружность вписан равносторонний треугольник ABC. На дуге AC взята произвольная точка M. Длины отрезков MA и MB соответственно равны 2 и 10. Найдите длину MC.
6. В окружность вписан четырёхугольник ABCD, длины сторон которого относятся как 3 : 4 : 5 : 6. Найдите отношение длин его диагоналей.
Найдите отношение длин его диагоналей.
7. Площадь круга, вписанного в трапецию, равна 9π, а сумма боковых сторон трапеции равна 20. Найдите площадь трапеции.
8. В прямоугольную трапецию вписана окружность. Расстояния от центра окружности до концов боковой стороны трапеции равны 6 и 8. Найдите площадь трапеции.
9. Площадь равнобедренной трапеции, описанной около окружности, равна 32, острый угол при основании трапеции равен 300. Найдите длину боковой стороны трапеции.
10. Трапеция вписана в окружность радиуса 5, большее основание трапеции является диаметром окружности. Найдите площадь трапеции, если косинус угла при основании равен 1/√10.
11. Большее основание трапеции является диаметром описанной окружности. Определите радиус окружности, если средняя линия трапеции равна 8, а её площадь равна 32.
12. Трапеция ABCD вписана в окружность. Найдите среднюю линию трапеции, если её большее основание AD = 15, синус угла BAC равен 1/3, синус угла ABD равен 5/9.
13. Около окружности радиуса 3 описана равнобедренная трапеция, меньшее основание которой 8. Найдите площадь трапеции.
14. Боковая сторона равнобедренной трапеции равна √13, а основания равны 3 и 4. Найдите длину диагонали трапеции.
15. Около окружности радиусом 1 описана равнобедренная трапеция, площадь которой равна 5. Найдите площадь четырёхугольника, вершинами которого являются точки касания окружности и трапеции.
16. Меньшее основание равнобедренной трапеции равно 6, большее равно 12, угол при основании равен 600. Найдите радиус описанной окружности.
17. В равнобедренной трапеции длины оснований равны 21 и 9, высота равна 8. Найдите радиус описанной окружности.
18. Около трапеции описана окружность, центр которой лежит внутри трапеции. Высота трапеции равна 27, а длины оснований равны 48 и 30. Найдите радиус окружности.
Параллелограмма равна половине произведения его диагоналей. Площадь параллелограмма.
 Задачи для самостоятельного решения
Задачи для самостоятельного решенияТеорема 1. Площадь трапеции равна произведению полусуммы ее оснований на высоту:
Теорема 2. Диагонали трапеции делят ее на четыре треугольника, два из которых подобны, а два другие имеют одинаковую площадь:
Теорема 3. Площадь параллелограмма равна произведению основания на высоту, опущенную на данное основание, или произведению двух сторон на синус угла между ними:
Теорема 4. В параллелограмме сумма квадратов диагоналей равна сумме квадратов его сторон:
Теорема 5. Площадь произвольного выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними:
Теорема 6. Площадь четырехугольника, описанного около окружности, равна произведению полупериметра этого четырехугольника на радиус данной окружности:
Теорема 7. Четырехугольник, вершинами которого являются середины сторон произвольного выпуклого четырехугольника, есть параллелограмм, площадь которого равна половине площади исходного четырехугольника:
Теорема 8.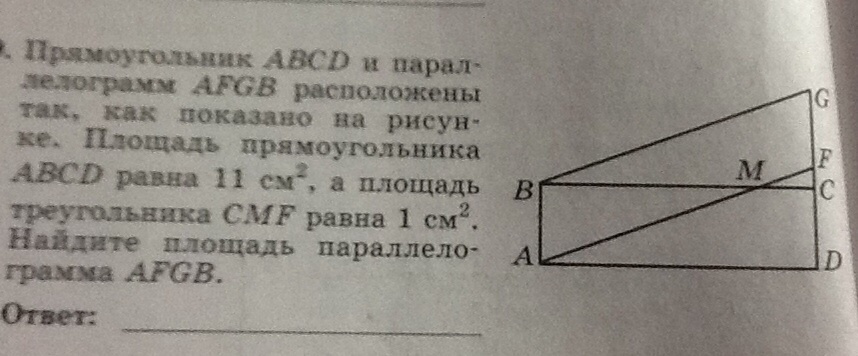 Если у выпуклого четырехугольника диагонали взаимно перпендикулярны, то суммы квадратов противоположных сторон этого четырехугольника равны:
Если у выпуклого четырехугольника диагонали взаимно перпендикулярны, то суммы квадратов противоположных сторон этого четырехугольника равны:
AB2 + CD2 = BC2 + AD2 .
Статья опубликована при поддержке компании «ДКРОСТ». Горки детские , домики, песочницы и многое другое — изготовление и продажа детских площадок оптом и в розницу. Самые низкие цены, скидки, сжатые сроки изготовления, выезд и консультация специалиста, гарантия качества. Узнать подробнее о компании, посмотреть каталог товаров, цены и контакты Вы сможете на сайте, который располагается по адресу: http://dkrost.ru/.
Доказательства некоторых теорем
Доказательство теоремы 2 . Пусть ABCD — данная трапеция, AD и BC — ее основания, O — точка пересечения диагоналей AC и BD этой трапеции. Докажем, что треугольники AOB и COD имеют одинаковую площадь. Для этого опустим из точек B и C на прямую AD перпендикуляры BP и CQ. Тогда площадь треугольника ABD равна
А площадь треугольника ACD равна
Так как BP = CQ, то и S∆ABD
= S∆ACD
.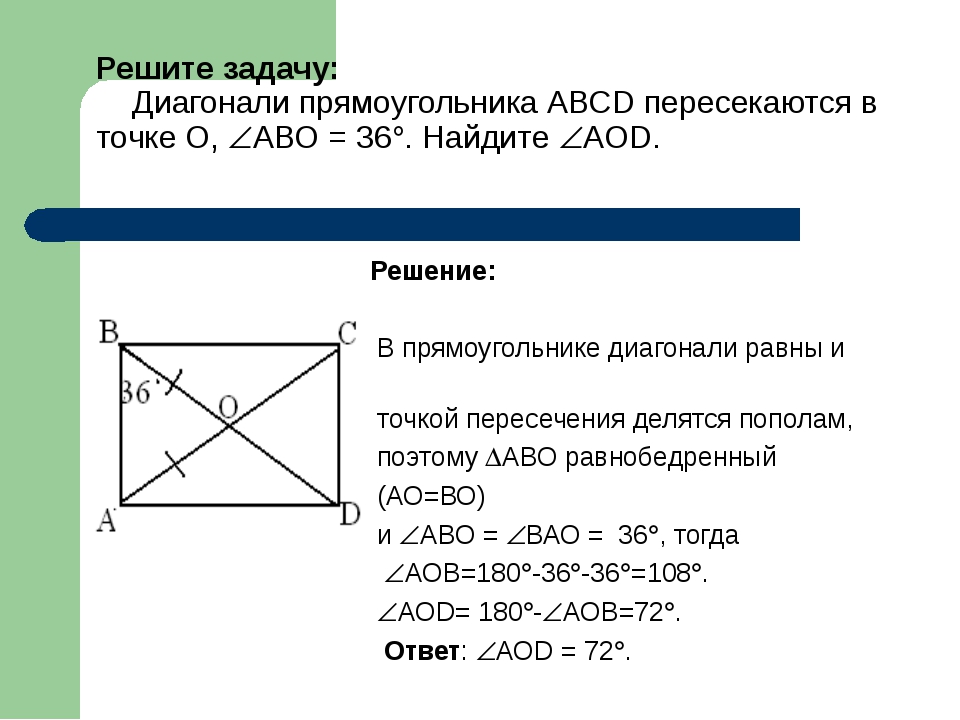 Но площадь треугольника AOB есть разность площадей треугольников ABD и AOD, а площадь треугольника COD — разность площадей треугольников ACD и AOD. Следовательно, площади треугольников AOB и COD равны, что и требовалось доказать.
Но площадь треугольника AOB есть разность площадей треугольников ABD и AOD, а площадь треугольника COD — разность площадей треугольников ACD и AOD. Следовательно, площади треугольников AOB и COD равны, что и требовалось доказать.
Доказательство теоремы 4 . Пусть ABCD — параллелограмм, AB = CD = a , AD = BC = b,
AC = d1
, BD = d2
, ∠BAD = α, ∠ADC = 180° – α. Применим к треугольнику ABD теорему косинусов:
Применив теперь теорему косинусов к треугольнику ACD, получим:
Складывая почленно полученные равенства, получаем, что что и требовалось доказать.
Доказательство теоремы 5. Пусть ABCD — произвольный выпуклый четырехугольник, E — точка пересечения его диагоналей, AE = a , BE = b,
CE = c, DE = d, ∠AEB = ∠CED = ϕ, ∠BEC =
= ∠AED = 180° – ϕ. Имеем:
что и требовалось доказать.
Доказательство теоремы 6 . Пусть ABCD — произвольный четырехугольник, описанный около окружности, O — центр этой окружности, OK, OL, OM и ON — перпендикуляры, опущенные из точки O на прямые AB, BC, CD и AD соответственно.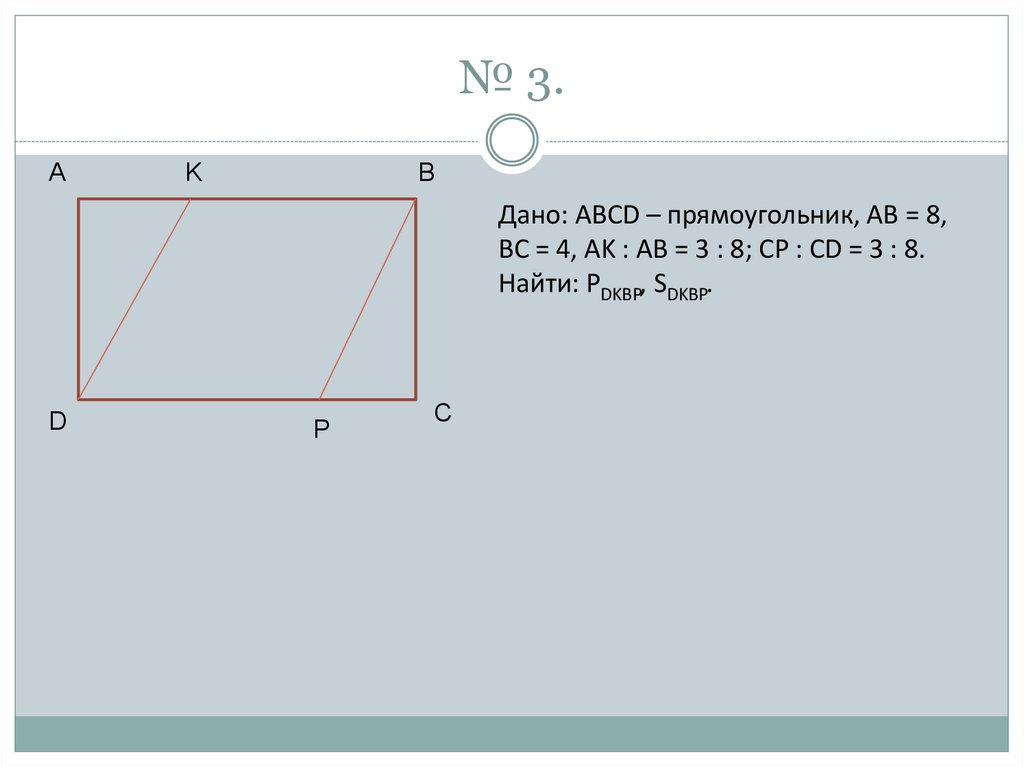 Имеем:
Имеем:
где r — радиус окружности, а p — полупериметр четырехугольника ABCD.
Доказательство теоремы 7 . Пусть ABCD — произвольный выпуклый четырехугольник, K, L, M и N — середины сторон AB, BC, CD и AD соответственно. Так как KL — средняя линия треугольника ABC, то прямая KL параллельна прямой AC и Аналогично, прямая MN параллельна прямой AC и Следовательно, KLMN — параллелограмм. Рассмотрим треугольник KBL. Его площадь равна четверти площади треугольника ABC. Площадь треугольника MDN также равна четверти площади треугольника ACD. Следовательно,
Аналогично,
Это значит, что
откуда вытекает, что
Доказательство теоремы 8 . Пусть ABCD — произвольный выпуклый четырехугольник, у которого диагонали взаимно перпендикулярны, пусть E — точка пересечения его диагоналей,
AE = a , BE = b, CE = c, DE = d. Применим к треугольникам ABE и CDE теорему Пифагора:
AB2
= AE2
+ BE2
= a 2
+ b2
,
CD2
= CE2
+ DE2
= c2
+ d2
,
следовательно,
AB2
+ CD2
= a 2
+ b2
+ c2
+ d2
.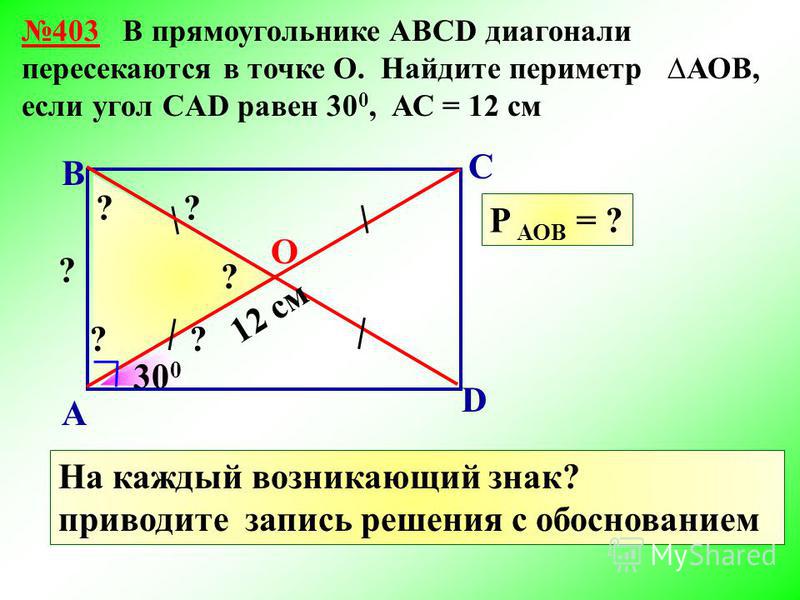
Применив теперь теорему Пифагора к треугольникам ADE и BCE, получим:
AD2
= AE2
+ DE2
= a 2
+ d2
,
BC2
= BE2
+ CE2
= b2
+ c2
,
откуда вытекает, что
AD2
+ BC2
= a 2
+ b2
+ c2
+ d2
.
Значит, AB2
+ CD2
= AD2
+ BC2
, что и требовалось доказать.
Решения задач
Задача 1 . Около круга описана трапеция с углами при основании α и β. Найти отношение площади трапеции к площади круга.
Решение . Пусть ABCD — данная трапеция, AB и CD — ее основания, DK и CM — перпендикуляры, опущенные из точек C и D на прямую AB. Искомое отношение не зависит от радиуса круга. Поэтому будем считать, что радиус равен 1. Тогда площадь круга равна π, найдем площадь трапеции. Так как треугольник ADK прямоугольный, то
Аналогично, из прямоугольного треугольника BCM находим, что Поскольку в данную трапецию можно вписать окружность, то суммы противоположных сторон равны:
AB + CD = AD + BC,
откуда находим
Значит, площадь трапеции есть
и искомое отношение равно
Ответ :
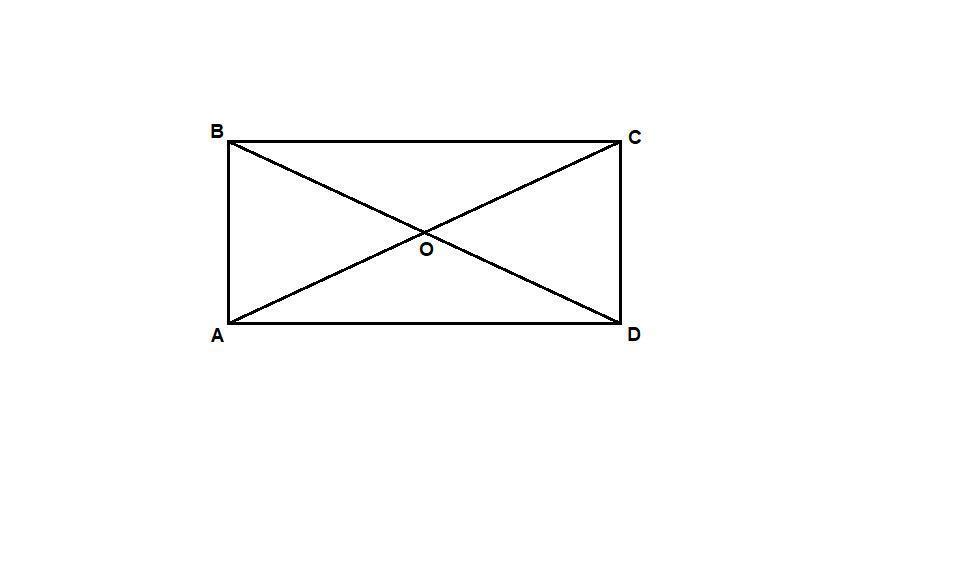
Задача 2 . В выпуклом четырехугольнике ABCD угол A равен 90°, а угол C не превосходит 90°. Из вершин B и D на диагональ AC опущены перпендикуляры BE и DF. Известно, что AE = CF. Доказать, что угол C прямой.
В выпуклом четырехугольнике ABCD угол A равен 90°, а угол C не превосходит 90°. Из вершин B и D на диагональ AC опущены перпендикуляры BE и DF. Известно, что AE = CF. Доказать, что угол C прямой.
Доказательство . Так как угол A равен 90°,
а угол C не превосходит 90°, то точки E и F лежат на диагонали AC. Без ограничения общности мы можем считать, что AE
∠EBC = β, ∠FDA = γ, ∠FDC = δ. Нам достаточно доказать, что α + β + γ + δ = π. Так как
откуда получаем, что что и требовалось доказать.
Задача 3 . Периметр равнобочной трапеции, описанной около круга, равен p. Найти радиус этого круга, если известно, что острый угол при основании трапеции равен α.
Решение . Пусть ABCD — данная равнобочная трапеция с основаниями AD и BC, пусть BH — высота этой трапеции, опущенная из вершины B.
Так как в данную трапецию можно вписать окружность, то
Следовательно,
Из прямоугольного треугольника ABH находим,
Ответ :
Задача 4 . Дана трапеция ABCD с основаниями AD и BC. Диагонали AC и BD пересекаются в точке O, а прямые AB и CD — в точке K. Прямая KO пересекает стороны BC и AD в точках M и N соответственно, а угол BAD равен 30°. Известно, что в трапеции ABMN и NMCD можно вписать окружность. Найти отношение площадей треугольника BKC и трапеции ABCD.
Дана трапеция ABCD с основаниями AD и BC. Диагонали AC и BD пересекаются в точке O, а прямые AB и CD — в точке K. Прямая KO пересекает стороны BC и AD в точках M и N соответственно, а угол BAD равен 30°. Известно, что в трапеции ABMN и NMCD можно вписать окружность. Найти отношение площадей треугольника BKC и трапеции ABCD.
Решение . Как известно, для произвольной трапеции прямая, соединяющая точку пересечения диагоналей и точку пересечения продолжений боковых сторон, делит каждое из оснований пополам. Итак, BM = MC и AN = ND. Далее, так как в трапеции ABMN и NMCD можно вписать окружность, то
BM + AN = AB + MN,
MC + ND = CD + MN.
Отсюда следует, что AB = CD, то есть трапеция ABCD — равнобокая. Искомое отношение площадей не зависит от масштаба, поэтому мы можем принять, что KN = x, KM = 1. Из прямоугольных треугольников AKN и BKM получаем, что Записывая вновь уже использованное выше соотношение
BM + AN = AB + MN ⇔
Нам требуется вычислить отношение:
Здесь мы использовали тот факт, что площади треугольников AKD и BKC относятся как квадраты сторон KN и KM, то есть как x2.
Ответ:
Задача 5. В выпуклом четырехугольнике ABCD точки E, F, H, G являются серединами сторон AB, BC, CD, DA соответственно и O — точка пересечения отрезков EH и FG. Известно, что EH = a , FG = b, Найти длины диагоналей четырехугольника.
Решение . Известно, что если соединить последовательно середины сторон произвольного четырехугольника, то получится параллелограмм. В нашем случае EFHG — параллелограмм и O — точка пересечения его диагоналей. Тогда
Применим к треугольнику FOH теорему косинусов:
Так как FH — средняя линия треугольника BCD, то
Аналогично, применив теорему косинусов к треугольнику EFO, получим, что
Ответ :
Задача 6. Боковые стороны трапеции равны 3 и 5. Известно, что в трапецию можно вписать окружность. Средняя линия трапеции делит ее на две части, отношение площадей которых равно Найти основания трапеции.
Решение .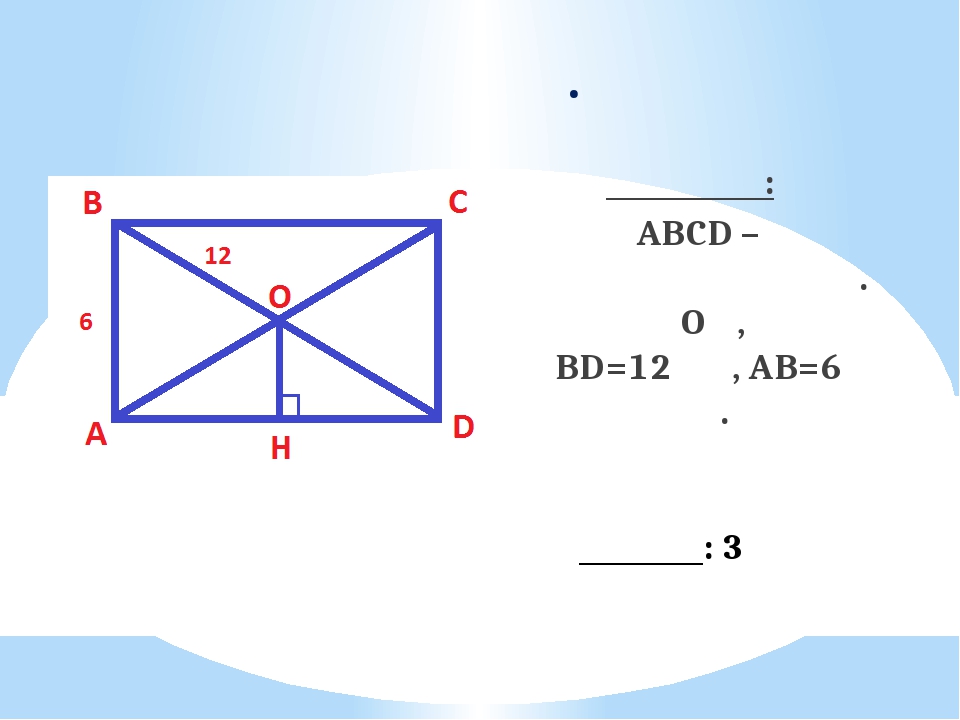 Пусть ABCD — данная трапеция, AB = 3 и CD = 5 — ее боковые стороны, точки K и M — середины сторон AB и CD соответственно. Пусть, для определенности, AD > BC, тогда площадь трапеции AKMD будет больше площади трапеции KBCM. Так как KM — средняя линия трапеции ABCD, то трапеции AKMD и KBCM имеют равные высоты. Поскольку площадь трапеции равна произведению полусуммы оснований на высоту, то верно следующее равенство:
Пусть ABCD — данная трапеция, AB = 3 и CD = 5 — ее боковые стороны, точки K и M — середины сторон AB и CD соответственно. Пусть, для определенности, AD > BC, тогда площадь трапеции AKMD будет больше площади трапеции KBCM. Так как KM — средняя линия трапеции ABCD, то трапеции AKMD и KBCM имеют равные высоты. Поскольку площадь трапеции равна произведению полусуммы оснований на высоту, то верно следующее равенство:
Далее, так как в трапецию ABCD можно вписать окружность, то AD + BC = AB + CD = 8. Тогда KM = 4 как средняя линия трапеции ABCD. Пусть BC = x, тогда AD = 8 – x. Имеем:
Значит, BC = 1 и AD = 7.
Ответ: 1 и 7.
Задача 7 . Основание AB трапеции ABCD вдвое длиннее основания CD и вдвое длиннее боковой стороны AD. Длина диагонали AC равна a , а длина боковой стороны BC равна b. Найти площадь трапеции.
Решение . Пусть E — точка пересечения продолжений боковых сторон трапеции и CD = x, тогда AD = x, AB = 2x.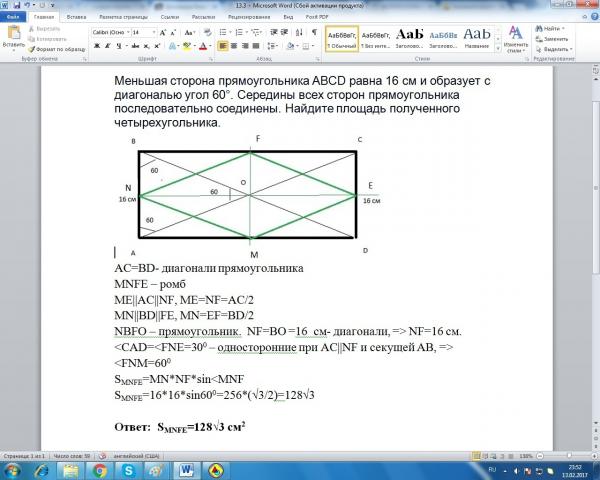 Отрезок CD параллелен отрезку AB и вдвое его короче, значит, CD является средней линией треугольника ABE. Следовательно, CE = BC = b и DE = AD = x, откуда
AE = 2x. Итак, треугольник ABE равнобедренный (AB = AE) и AC — его медиана. Поэтому AC является и высотой этого треугольника, и значит,
Отрезок CD параллелен отрезку AB и вдвое его короче, значит, CD является средней линией треугольника ABE. Следовательно, CE = BC = b и DE = AD = x, откуда
AE = 2x. Итак, треугольник ABE равнобедренный (AB = AE) и AC — его медиана. Поэтому AC является и высотой этого треугольника, и значит,
Так как треугольник DEC подобен треугольнику AEB с коэффициентом подобия то
Ответ :
Задача 8 . Диагонали трапеции ABCD пересекаются в точке E. Найти площадь треугольника BCE, если длины оснований трапеции AB = 30, DC = 24, боковой стороны AD = 3 и угол DAB равен 60°.
Решение . Пусть DH — высота трапеции. Из треугольника ADH находим, что
Так как высота треугольника ABC, опущенная из вершины C, равна высоте DH трапеции, имеем:
Ответ :
Задача 9 . В трапеции средняя линия равна 4, а углы при одном из оснований равны 40° и 50°. Найти основания трапеции, если отрезок, соединяющий середины оснований, равен 1.
Решение . Пусть ABCD — данная трапеция, AB и CD — ее основания (AB
AB + CD = 8. Продлим боковые стороны DA и CB до пересечения в точке E. Рассмотрим треугольник ABE, в котором ∠EAB = 50°. ∠EBA = 40°,
следовательно, ∠AEB = 90°. Медиана EM этого треугольника, проведенная из вершины прямого угла, равна половине гипотенузы: EM = AM. Пусть EM = x, тогда AM = x, DN = 4 – x. Согласно условию задачи MN = 1, следовательно,
EN = x + 1. Из подобия треугольников AEM и DEN имеем:
Это означает, что AB = 3 и CD = 5.
Ответ : 3 и 5.
Задача 10 . Выпуклый четырехугольник ABCD описан около окружности с центром в точке O, при этом AO = OC = 1, BO = OD = 2. Найти периметр четырехугольника ABCD.
Решение . Пусть K, L, M, N — точки касания окружности со сторонами AB, BC, CD, DA соответственно, r — радиус окружности. Так как касательная к окружности перпендикулярна радиусу, проведенному в точку касания, то треугольники AKO, BKO, BLO, CLO, CMO, DMO, DNO, ANO — прямоугольные.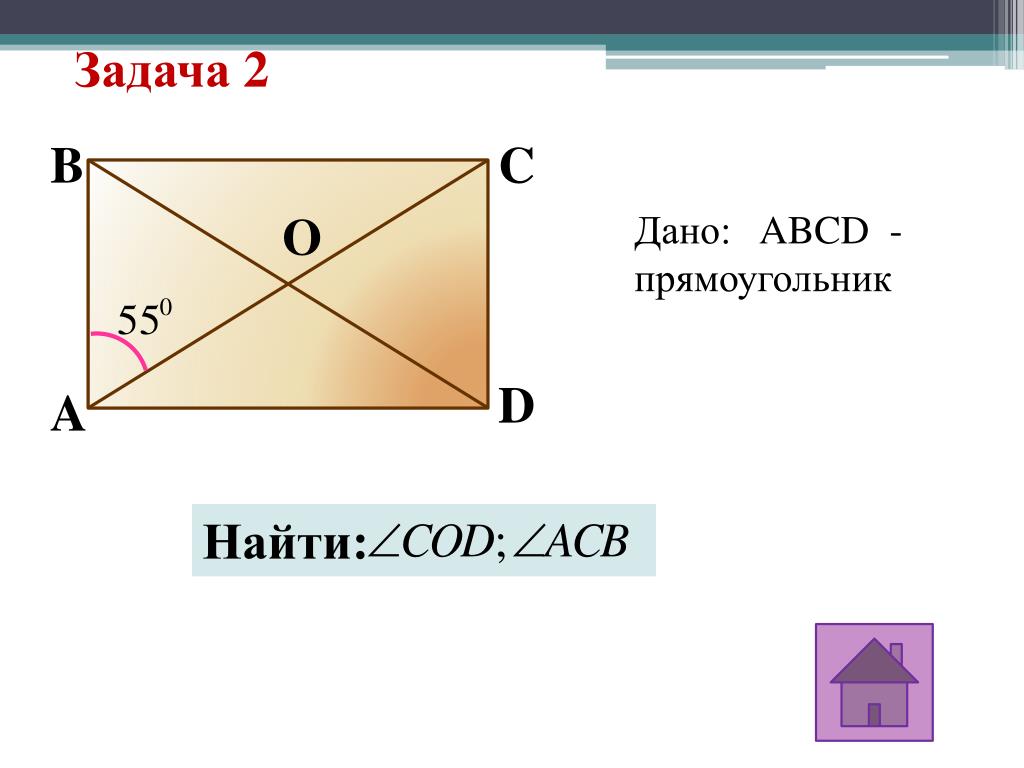 Применив к этим треугольникам теорему Пифагора, получим, что
Применив к этим треугольникам теорему Пифагора, получим, что
Следовательно, AB = BC = CD = DA, то есть ABCD — ромб. Диагонали ромба перпендикулярны друг другу, и точка их пересечения является центром вписанной окружности. Отсюда легко находим, что сторона ромба равна и значит, периметр ромба равен
Ответ :
Задачи для самостоятельного решения
С-1. Около окружности радиуса r описана равнобочная трапеция ABCD. Пусть E и K — точки касания этой окружности с боковыми сторонами трапеции. Угол между основанием AB и боковой стороной AD трапеции равен 60°. Докажите, что EK параллелен AB, и найдите площадь трапеции ABEK.
С-2. В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований, равен 2.
Найдите площадь трапеции.
С-3 . Можно ли вокруг четырехугольника ABCD описать окружность, если ∠ADC = 30°, AB = 3, BC = 4, AC = 6?
С-4. В трапеции ABCD (AB — основание) величины углов DAB, BCD, ADC, ABD и ADB образуют арифметическую прогрессию (в том порядке, в котором они написаны). Найдите расстояние от вершины C до диагонали BD, если высота трапеции равна h.
Найдите расстояние от вершины C до диагонали BD, если высота трапеции равна h.
С-5. Дана равнобедренная трапеция, в которую вписана окружность и около которой описана окружность. Отношение высоты трапеции к радиусу описанной окружности равно Найдите углы трапеции.
С-6. Площадь прямоугольника ABCD равна 48, а длина диагонали равна 10. На плоскости, в которой расположен прямоугольник, выбрана точка O так, что OB = OD = 13. Найдите расстояние от точки O до наиболее удаленной от нее вершины прямоугольника.
С-7. Периметр параллелограмма ABCD равен 26. Величина угла ABC равна 120°. Радиус окружности, вписанной в треугольник BCD, равен Найдите длины сторон параллелограмма, если известно, что AD > AB.
С-8. Четырехугольник ABCD вписан в окружность с центром в точке O. Радиус OA перпендикулярен радиусу OB, а радиус OC перпендикулярен радиусу OD. Длина перпендикуляра, опущенного из точки C на прямую AD, равна 9. Длина отрезка BC в два раза меньше длины отрезка AD. Найдите площадь треугольника AOB.
Найдите площадь треугольника AOB.
С-9. В выпуклом четырехугольнике ABCD вершины A и C противоположны, а длина стороны AB равна 3. Угол ABC равен угол BCD равен Найдите длину стороны AD, если известно, что площадь четырехугольника равна
С-10. В выпуклом четырехугольнике ABCD проведены диагонали AC и BD. Известно, что
AD = 2, ∠ABD = ∠ACD = 90°, и расстояние между точкой пересечения биссектрис треугольника ABD и точкой пересечения биссектрис треугольника ACD равно Найдите длину стороны BC.
С-11. Пусть M — точка пересечения диагоналей выпуклого четырехугольника ABCD, в котором стороны AB, AD и BC равны между собой. Найдите угол CMD, если известно, что DM = MC,
а ∠CAB ≠ ∠DBA.
С-12. В четырехугольнике ABCD известно, что ∠A = 74°, ∠D = 120°. Найдите угол между биссектрисами углов B и C.
С-13. В четырехугольник ABCD можно вписать окружность. Пусть K — точка пересечения его диагоналей. Известно, что AB > BC > KC, а периметр и площадь треугольника BKC равны соответственно 14 и 7. Найдите DC.
Найдите DC.
С-14. В трапеции, описанной около окружности, известно, что BC AD, AB = CD, ∠BAD =
= 45°. Найдите AB, если площадь трапеции ABCD равна 10.
С-15. В трапеции ABCD с основаниями AB и CD известно, что ∠CAB = 2∠DBA. Найдите площадь трапеции.
С-16. В параллелограмме ABCD известно, что AC = a , ∠CAB = 60°. Найдите площадь параллелограмма.
С-17 . В четырехугольнике ABCD диагонали AC и BD пересекаются в точке K. Точки L и M являются соответственно серединами сторон BC и AD. Отрезок LM содержит точку K. Четырехугольник ABCD таков, что в него можно вписать окружность. Найдите радиус этой окружности, если AB = 3, и LK: KM = 1: 3.
С-18. В выпуклом четырехугольнике ABCD проведены диагонали AC и BD. При этом ∠BAC =
= ∠BDC, а площадь круга, описанного около треугольника BDC, равна
а) Найдите радиус окружности, описанной около треугольника ABC.
б) Зная, что BC = 3, AC = 4, ∠BAD = 90°, найдите площадь четырехугольника ABCD.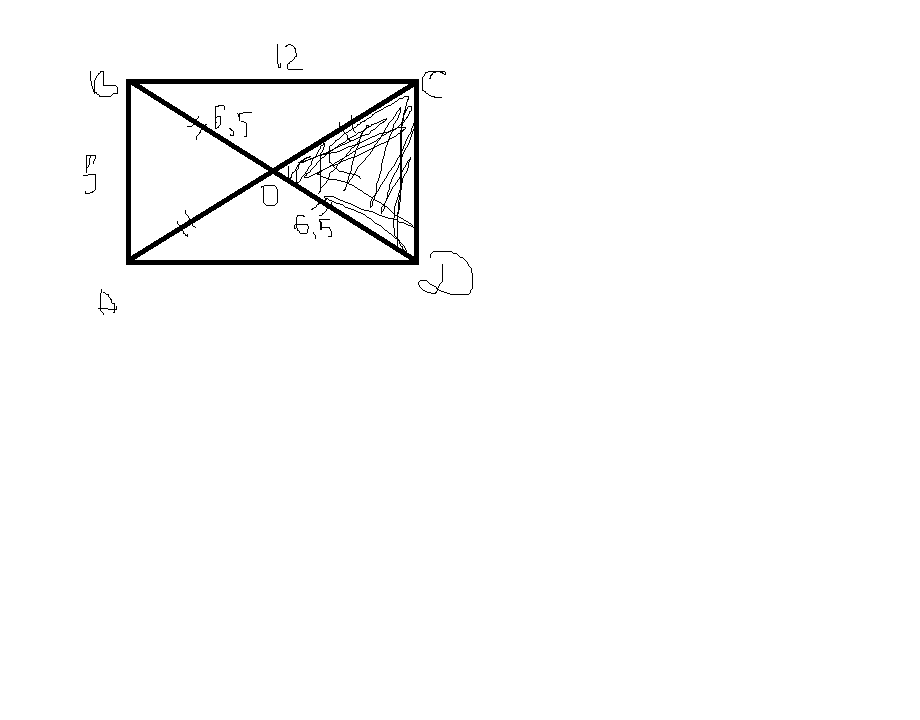
При решении задач по данной теме кроме основных свойств параллелограмма и соответственных формул можно запомнить и применять следующее:
- Биссектриса внутреннего угла параллелограмма отсекает от него равнобедренный треугольник
- Биссектрисы внутренних углов прилежащие к одной из сторон параллелограмма взаимно перпендикулярные
- Биссектрисы, выходящие из противоположных внутренних углов параллелограмма, параллельные между собой либо лежат на одной прямой
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон
- Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними
Рассмотрим задачи, при решении которых используются данные свойства.
Задача 1.
Биссектриса угла С параллелограмма АВСD пересекает сторону АD в точке М и продолжение стороны АВ за точку А в точке Е. Найдите периметр параллелограмма, если АЕ = 4, DМ = 3.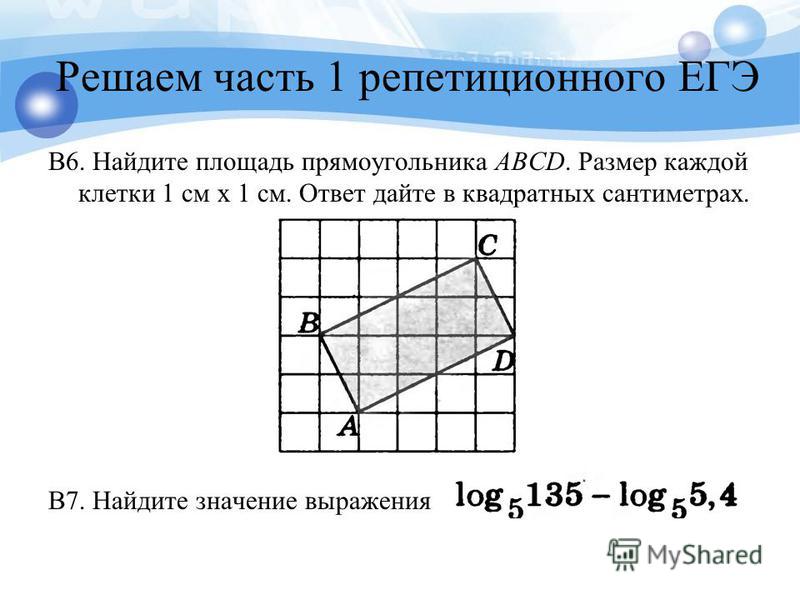
Решение.
1. Треугольник СМD равнобедренный. (Свойство 1). Следовательно, СD = МD = 3 см.
2. Треугольник ЕАМ равнобедренный.
Следовательно, АЕ = АМ = 4 см.
3. АD = АМ + МD = 7 см.
4. Периметр АВСD = 20 см.
Ответ. 20 см.
Задача 2.
В выпуклом четырёхугольнике АВСD проведены диагонали. Известно, что площади треугольников АВD, АСD, ВСD равны. Докажите, что данный четырёхугольник является параллелограммом.
Решение.
1. Пусть ВЕ – высота треугольника АВD, СF – высота треугольника АCD. Так как по условию задачи площади треугольников равны и у них общее основание АD, то высоты этих треугольников равны. ВЕ = СF.
2. ВЕ, СF перпендикулярны АD. Точки В и С расположены по одну сторону относительно прямой АD. ВЕ = СF. Следовательно, прямая ВС || AD. (*)
3. Пусть АL – высота треугольника АСD, BK – высота треугольника BCD. Так как по условию задачи площади треугольников равны и у них общее основание СD, то высоты этих треугольников равны. АL = BK.
АL = BK.
4. АL и BK перпендикулярны СD. Точки В и А расположены по одну сторону относительно прямой СD. АL = BK. Следовательно, прямая АВ || СD (**)
5. Из условий (*), (**) вытекает – АВСD параллелограмм.
Ответ. Доказано. АВСD – параллелограмм.
Задача 3.
На сторонах ВС и СD параллелограмма АВСD отмечены точки М и Н соответственно так, что отрезки ВМ и НD пересекаются в точке О;
Решение.
1. В треугольнике DОМ
2. В прямоугольном треугольнике DНС
(
Тогда (Так как в прямоугольном треугольнике катет, который лежит против угла в 30 о, равен половине гипотенузы).
Но СD = АВ. Тогда АВ: НD = 2: 1.
3.
4.
Ответ: АВ: НD = 2: 1,
Задача 4.
Одна из диагоналей параллелограмма длиною 4√6, составляет с основанием угол 60 о, а вторая диагональ составляет с тем же основанием угол 45 о. Найти вторую диагональ.
Решение.
1. АО = 2√6.
2. К треугольнику АОD применим теорему синусов.
АО/sin D = OD/sin А.
2√6/sin 45 о = OD/sin 60 о.
ОD = (2√6sin 60 о) / sin 45 о = (2√6 · √3/2) / (√2/2) = 2√18/√2 = 6.
Ответ: 12.
Задача 5.
У параллелограмма со сторонами 5√2 и 7√2 меньший угол между диагоналями равен меньшему углу параллелограмма. Найдите сумму длин диагоналей.
Решение.
Пусть d 1 , d 2 – диагонали параллелограмма, а угол между диагоналями и меньший угол параллелограмма равен ф.
1. Посчитаем двумя разными
способами его площадь.
S ABCD = AB · AD · sin A = 5√2 · 7√2 · sin ф,
S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin ф.
Получим равенство 5√2 · 7√2 · sin ф = 1/2d 1 d 2 sin ф или
2 · 5√2 · 7√2 = d 1 d 2 ;
2. Используя соотношение между сторонами и диагоналями параллелограмма запишем равенство
(АВ 2 + АD 2) · 2 = АС 2 + ВD 2 .
((5√2) 2 + (7√2) 2) · 2 = d 1 2 + d 2 2 .
d 1 2 + d 2 2 = 296.
3. Составим систему:
{d 1 2 + d 2 2 = 296,
{d 1 + d 2 = 140.
Умножим второе уравнение системы на 2 и сложим с первым.
Получим (d 1 + d 2) 2 = 576. Отсюда Id 1 + d 2 I = 24.
Так как d 1 , d 2 – длины диагоналей параллелограмма, то d 1 + d 2 = 24.
Ответ: 24.
Задача 6.
Стороны параллелограмма 4 и 6. Острый угол между диагоналями равен 45 о. Найдите площадь параллелограмма.
Решение.
1. Из треугольника АОВ, используя теорему косинусов, запишем соотношение между стороной параллелограмма и диагоналями.
АВ 2 = АО 2 + ВО 2 2 · АО · ВО · cos АОВ.
4 2 = (d 1 /2) 2 + (d 2 /2) 2 – 2 · (d 1 /2) · (d 2 /2)cos 45 о;
d 1 2 /4 + d 2 2 /4 – 2 · (d 1 /2) · (d 2 /2)√2/2 = 16.
d 1 2 + d 2 2 – d 1 · d 2 √2 = 64.
2. Аналогично запишем соотношение для треугольника АОD.
Учтем, что
Получим уравнение d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
3. Имеем систему
{d 1 2 + d 2 2 – d 1 · d 2 √2 = 64,
{d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
Вычитая из второго уравнения первое, получим 2d 1 · d 2 √2 = 80 или
d 1 · d 2 = 80/(2√2) = 20√2
4. S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin α = 1/2 · 20√2 · √2/2 = 10.
Примечание: В этой и в предыдущей задаче нет надобности, решать полностью систему, предвидя то, что в данной задаче для вычисления площади нам нужно произведение диагоналей.
Ответ: 10.
Задача 7.
Площадь параллелограмма равна 96, а его стороны равны 8 и 15. Найдите квадрат меньшей диагонали.
Решение.
1. S ABCD = AВ · АD · sin ВAD. Сделаем подстановку в формулу.
Получим 96 = 8 · 15 · sin ВAD. Отсюда sin ВAD = 4 / 5 .
2. Найдём cos ВАD. sin 2 ВAD + cos 2 ВАD = 1.
(4 / 5) 2 + cos 2 ВАD = 1. cos 2 ВАD = 9 / 25 .
По условию задачи мы находим длину меньшей диагонали. Диагональ ВD будет меньшей, если угол ВАD острый. Тогда cos ВАD = 3 / 5.
Диагональ ВD будет меньшей, если угол ВАD острый. Тогда cos ВАD = 3 / 5.
3. Из треугольника АВD по теореме косинусов найдём квадрат диагонали ВD.
ВD 2 = АВ 2 + АD 2 – 2 · АВ · ВD · cos ВАD.
ВD 2 = 8 2 + 15 2 – 2 · 8 · 15 · 3 / 5 = 145.
Ответ: 145.
Остались вопросы? Не знаете, как решить геометрическую задачу?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Формула для площади параллелограмма
Площадь параллелограмма равна произведению его стороны на высоту, опущенную на эту сторону.
Доказательство
Если параллелограмм — прямоугольник, то равенство выполнено по теореме о площади прямоугольника. Далее считаем, что углы параллелограмма не прямые.
Пусть в параллелограмме $ABCD$ угол $\angle BAD$ острый и $AD > AB$. Иначе переименуем вершины. Тогда высота $BH$ из вершины $B$ на прямую $AD$ падает на сторону $AD$, так как катет $AH$ короче гипотенузы $AB$, а $AB
Сравним площадь параллелограмма $ABCD$ и площадь прямоугольника $HBCK$. \circ — \angle AOD$. Значит, синусы углов при пересечении диагоналей равны $\sin \alpha$.
\circ — \angle AOD$. Значит, синусы углов при пересечении диагоналей равны $\sin \alpha$.
$S_{ABCD}=S_{\triangle AOB} + S_{\triangle BOC} + S_{\triangle COD} + S_{\triangle AOD}$
по аксиоме измерения площади. Применяем формулу площади треугольника $S_{ABC} = \dfrac{1}{2} \cdot AB \cdot BC \sin \angle ABC$ для этих треугольников и углов при пересечении диагоналей. Стороны каждого равны половинам диагоналей, синусы также равны. Следовательно, площади всех четырёх треугольников равны $S = \dfrac{1}{2} \cdot \dfrac{AC}{2} \cdot \dfrac{BD}{2} \cdot \sin \alpha = \dfrac{AC \cdot BD}{8} \sin \alpha$. Суммируя всё вышесказанное, получаем
$S_{ABCD} = 4S = 4 \cdot \dfrac{AC \cdot BD}{8} \sin \alpha = \dfrac{AC \cdot BD \cdot \sin \alpha}{2}$
При решении задач по данной теме кроме основных свойств параллелограмма и соответственных формул можно запомнить и применять следующее:
- Биссектриса внутреннего угла параллелограмма отсекает от него равнобедренный треугольник
- Биссектрисы внутренних углов прилежащие к одной из сторон параллелограмма взаимно перпендикулярные
- Биссектрисы, выходящие из противоположных внутренних углов параллелограмма, параллельные между собой либо лежат на одной прямой
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон
- Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними
Рассмотрим задачи, при решении которых используются данные свойства.
Задача 1.
Биссектриса угла С параллелограмма АВСD пересекает сторону АD в точке М и продолжение стороны АВ за точку А в точке Е. Найдите периметр параллелограмма, если АЕ = 4, DМ = 3.
Решение.
1. Треугольник СМD равнобедренный. (Свойство 1). Следовательно, СD = МD = 3 см.
2. Треугольник ЕАМ равнобедренный.
Следовательно, АЕ = АМ = 4 см.
3. АD = АМ + МD = 7 см.
4. Периметр АВСD = 20 см.
Ответ. 20 см.
Задача 2.
В выпуклом четырёхугольнике АВСD проведены диагонали. Известно, что площади треугольников АВD, АСD, ВСD равны. Докажите, что данный четырёхугольник является параллелограммом.
Решение.
1. Пусть ВЕ – высота треугольника АВD, СF – высота треугольника АCD. Так как по условию задачи площади треугольников равны и у них общее основание АD, то высоты этих треугольников равны. ВЕ = СF.
2. ВЕ, СF перпендикулярны АD. Точки В и С расположены по одну сторону относительно прямой АD.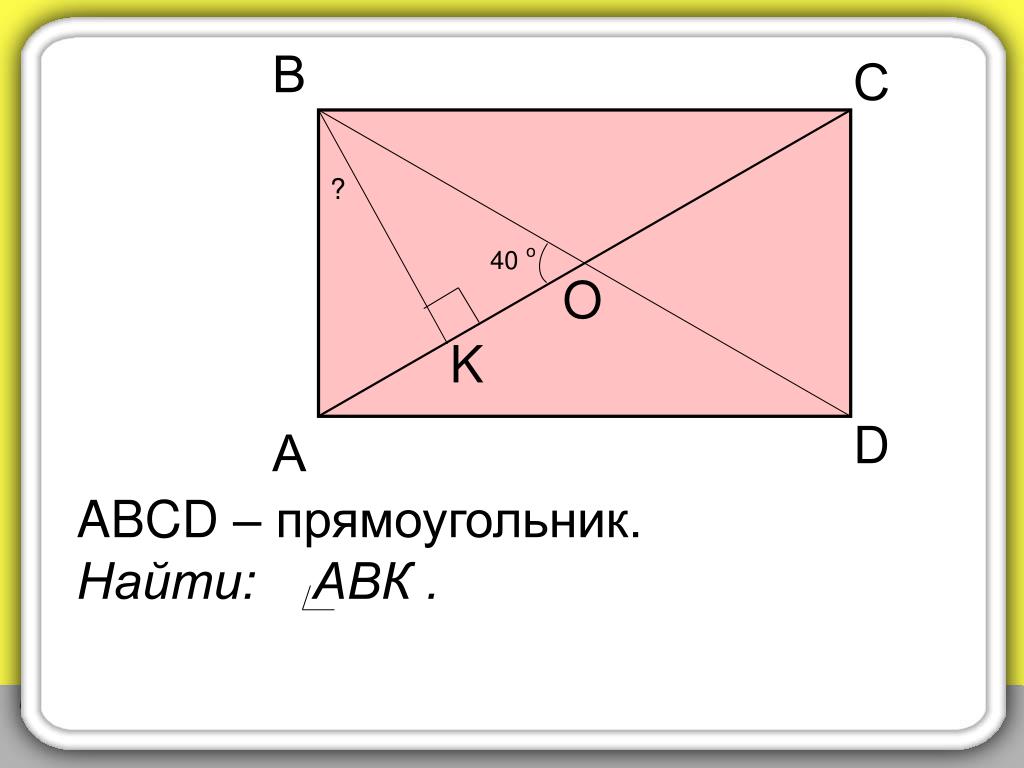 ВЕ = СF. Следовательно, прямая ВС || AD. (*)
ВЕ = СF. Следовательно, прямая ВС || AD. (*)
3. Пусть АL – высота треугольника АСD, BK – высота треугольника BCD. Так как по условию задачи площади треугольников равны и у них общее основание СD, то высоты этих треугольников равны. АL = BK.
4. АL и BK перпендикулярны СD. Точки В и А расположены по одну сторону относительно прямой СD. АL = BK. Следовательно, прямая АВ || СD (**)
5. Из условий (*), (**) вытекает – АВСD параллелограмм.
Ответ. Доказано. АВСD – параллелограмм.
Задача 3.
На сторонах ВС и СD параллелограмма АВСD отмечены точки М и Н соответственно так, что отрезки ВМ и НD пересекаются в точке О;
Решение.
1. В треугольнике DОМ
2. В прямоугольном треугольнике DНС
(
Тогда (Так как в прямоугольном треугольнике катет, который лежит против угла в 30 о, равен половине гипотенузы).
Но СD = АВ. Тогда АВ: НD = 2: 1.
3.
4.
Ответ: АВ: НD = 2: 1,
Задача 4.
Одна из диагоналей параллелограмма длиною 4√6, составляет с основанием угол 60 о, а вторая диагональ составляет с тем же основанием угол 45 о. Найти вторую диагональ.
Решение.
1. АО = 2√6.
2. К треугольнику АОD применим теорему синусов.
АО/sin D = OD/sin А.
2√6/sin 45 о = OD/sin 60 о.
ОD = (2√6sin 60 о) / sin 45 о = (2√6 · √3/2) / (√2/2) = 2√18/√2 = 6.
Ответ: 12.
Задача 5.
У параллелограмма со сторонами 5√2 и 7√2 меньший угол между диагоналями равен меньшему углу параллелограмма. Найдите сумму длин диагоналей.
Решение.
Пусть d 1 , d 2 – диагонали параллелограмма, а угол между диагоналями и меньший угол параллелограмма равен ф.
1. Посчитаем двумя разными
способами его площадь.
S ABCD = AB · AD · sin A = 5√2 · 7√2 · sin ф,
S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin ф.
Получим равенство 5√2 · 7√2 · sin ф = 1/2d 1 d 2 sin ф или
2 · 5√2 · 7√2 = d 1 d 2 ;
2. Используя соотношение между сторонами и диагоналями параллелограмма запишем равенство
Используя соотношение между сторонами и диагоналями параллелограмма запишем равенство
(АВ 2 + АD 2) · 2 = АС 2 + ВD 2 .
((5√2) 2 + (7√2) 2) · 2 = d 1 2 + d 2 2 .
d 1 2 + d 2 2 = 296.
3. Составим систему:
{d 1 2 + d 2 2 = 296,
{d 1 + d 2 = 140.
Умножим второе уравнение системы на 2 и сложим с первым.
Получим (d 1 + d 2) 2 = 576. Отсюда Id 1 + d 2 I = 24.
Так как d 1 , d 2 – длины диагоналей параллелограмма, то d 1 + d 2 = 24.
Ответ: 24.
Задача 6.
Стороны параллелограмма 4 и 6. Острый угол между диагоналями равен 45 о. Найдите площадь параллелограмма.
Решение.
1. Из треугольника АОВ, используя теорему косинусов, запишем соотношение между стороной параллелограмма и диагоналями.
АВ 2 = АО 2 + ВО 2 2 · АО · ВО · cos АОВ.
4 2 = (d 1 /2) 2 + (d 2 /2) 2 – 2 · (d 1 /2) · (d 2 /2)cos 45 о;
d 1 2 /4 + d 2 2 /4 – 2 · (d 1 /2) · (d 2 /2)√2/2 = 16.
d 1 2 + d 2 2 – d 1 · d 2 √2 = 64.
2. Аналогично запишем соотношение для треугольника АОD.
Учтем, что
Получим уравнение d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
3. Имеем систему
{d 1 2 + d 2 2 – d 1 · d 2 √2 = 64,
{d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
Вычитая из второго уравнения первое, получим 2d 1 · d 2 √2 = 80 или
d 1 · d 2 = 80/(2√2) = 20√2
4. S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin α = 1/2 · 20√2 · √2/2 = 10.
Примечание: В этой и в предыдущей задаче нет надобности, решать полностью систему, предвидя то, что в данной задаче для вычисления площади нам нужно произведение диагоналей.
Ответ: 10.
Задача 7.
Площадь параллелограмма равна 96, а его стороны равны 8 и 15. Найдите квадрат меньшей диагонали.
Решение.
1. S ABCD = AВ · АD · sin ВAD. Сделаем подстановку в формулу.
Получим 96 = 8 · 15 · sin ВAD. Отсюда sin ВAD = 4 / 5 .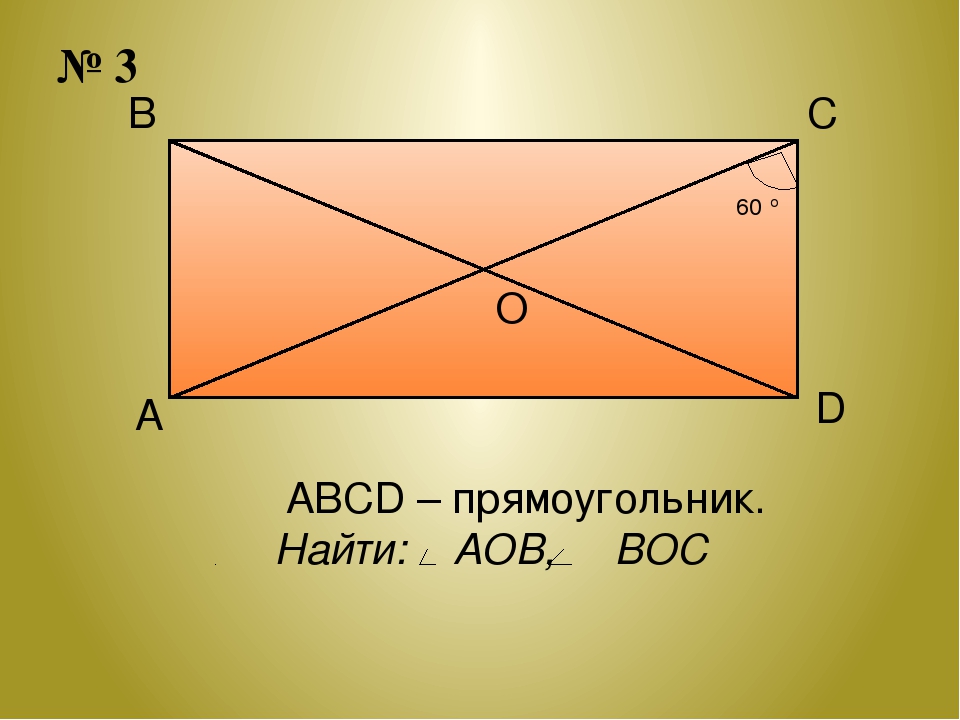
2. Найдём cos ВАD. sin 2 ВAD + cos 2 ВАD = 1.
(4 / 5) 2 + cos 2 ВАD = 1. cos 2 ВАD = 9 / 25 .
По условию задачи мы находим длину меньшей диагонали. Диагональ ВD будет меньшей, если угол ВАD острый. Тогда cos ВАD = 3 / 5.
3. Из треугольника АВD по теореме косинусов найдём квадрат диагонали ВD.
ВD 2 = АВ 2 + АD 2 – 2 · АВ · ВD · cos ВАD.
ВD 2 = 8 2 + 15 2 – 2 · 8 · 15 · 3 / 5 = 145.
Ответ: 145.
Остались вопросы? Не знаете, как решить геометрическую задачу?
Чтобы получить помощь репетитора – .
Первый урок – бесплатно!
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Примечание . Это часть урока с задачами по геометрии (раздел параллелограмм). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ или sqrt(), при чем в скобках указано подкоренное выражение.
Теоретический материал
Пояснения к формулам нахождения площади параллелограмма:
- Площадь параллелограмма равна произведению длины одной из его сторон на высоту, опущенную на эту сторону
- Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними
- Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними
Задачи на нахождение площади параллелограмма
Задача .В параллелограмме меньшая высота и меньшая сторона равны 9 см и корню из 82 соответственно.Большая диагональ 15 см.Найти площадь параллелограмма.
Решение .
Обозначим меньшую высоту параллелограмма ABCD, опущенную из точки B на большее основание AD как BK.
Найдем значение катета прямоугольного треугольника ABK, образованного меньшей высотой, меньшей стороной и частью большего основания. По теореме Пифагора:
AB 2 = BK 2 + AK 2
82 = 9 2 + AK 2
AK 2 = 82 — 81
AK = 1
Продлим верхнее основание параллелограмма BC и опустим на него высоту AN из его нижнего основания.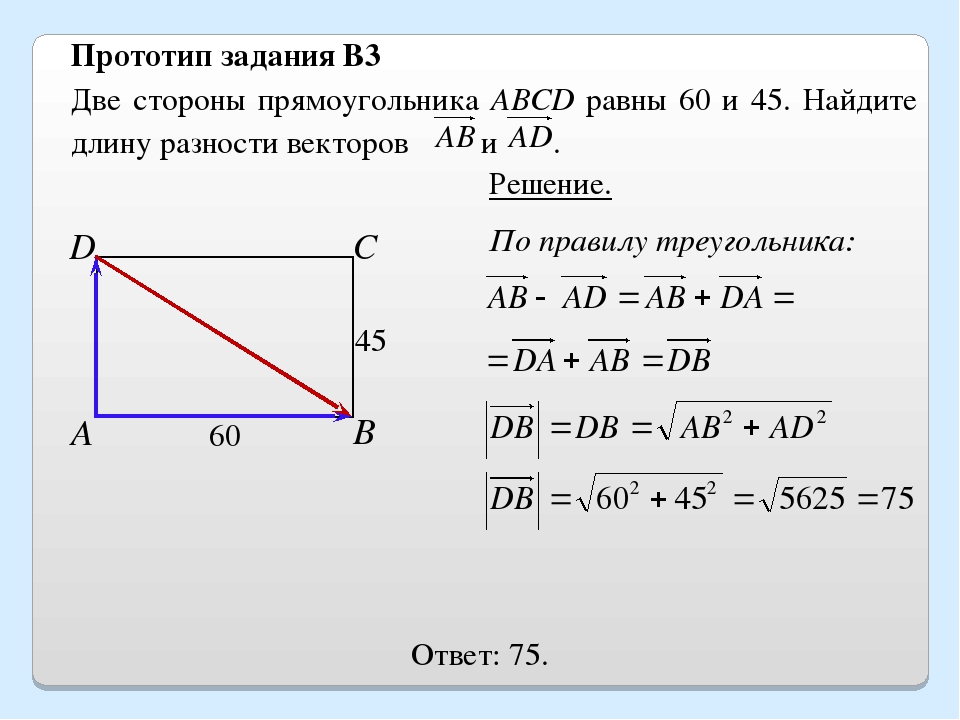 AN = BK как стороны прямоугольника ANBK. У получившегося прямоугольного треугольника ANC найдем катет NC.
AN = BK как стороны прямоугольника ANBK. У получившегося прямоугольного треугольника ANC найдем катет NC.
AN 2 + NC 2 = AC 2
9 2 + NC 2 = 15 2
NC 2 = 225 — 81
NC 2 = √144
NC = 12
Теперь найдем большее основание BC параллелограмма ABCD.
BC = NC — NB
Учтем, что NB = AK как стороны прямоугольника, тогда
BC = 12 — 1 = 11
Площадь параллелограмма равна произведению основания на высоту к этому основанию.
S = ah
S = BC * BK
S = 11 * 9 = 99
Ответ : 99 см 2 .
Задача
В параллелограмме АВСД на диагональ АС опущен перпендикуляр ВО. Найдите площадь параллелограмма, если АО=8, ОС=6 и ВО=4.Решение .
Опустим на диагональ АС дополнительно еще один перпендикуляр DK.
Соответственно, треугольники AOB иDKC, COB и AKD попарно равны. Одна из сторон является противолежащей стороной параллелограмма, один из углов — прямой, так как является перпендикуляром к диагонали, а один из оставшихся углов является внутренним накрест лежащим для параллельных сторон параллелограмма и секущей диагонали.
Таким образом, площадь параллелограмма равна площади указанных треугольников. То есть
Sпаралл = 2S AOB +2S BOC
Площадь прямоугольного треугольника равна половине произведения катетов. Откуда
S = 2 (1/2 8 * 4) + 2 (1/2 6 * 4) = 56 см 2
Ответ : 56 см 2 .
Диагонали трапеции
Свойства диагоналей трапеции
- Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
- Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
- Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.
Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции.
Данный отрезок параллелен основаниям трапеции.
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.
LM = (AD — BC)/2
или
LM = (a-b)/2
Свойства треугольников, образованных диагоналями трапеции
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными.
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.
Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны, то есть треугольники являются равновеликими.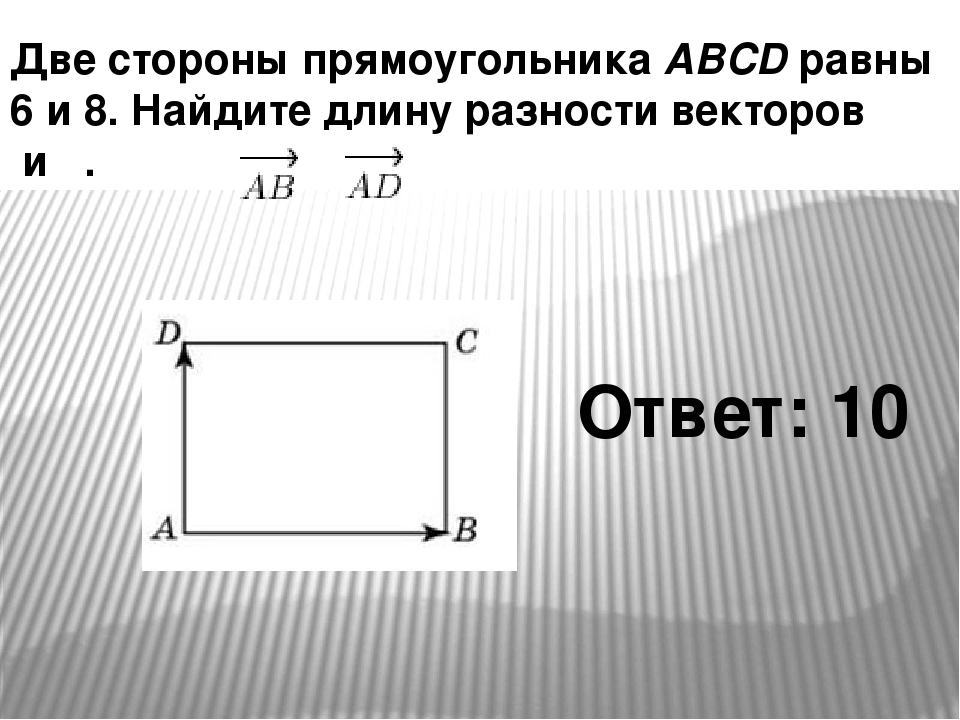
Свойства трапеции, достроенной до треугольника
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований.
Таким образом, любая трапеция может быть достроена до треугольника. При этом:
- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
- Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника
Свойства отрезка, соединяющего основания трапеции
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей ( KO/ON ) будет равно соотношению оснований трапеции ( BC/AD ).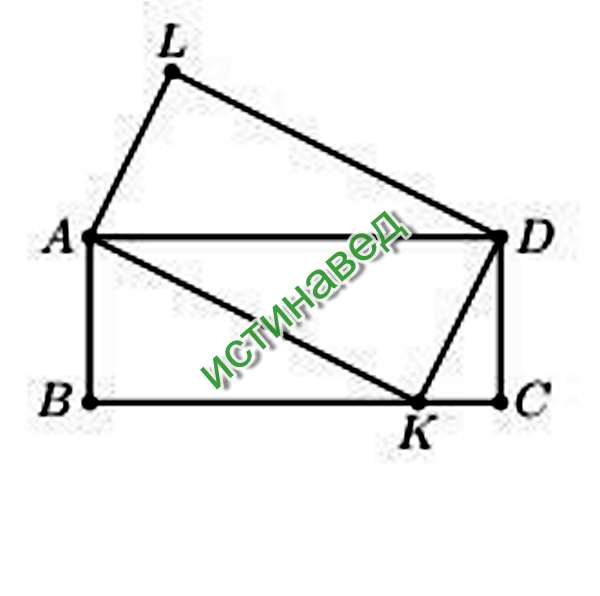
KO / ON = BC / AD
Данное свойство следует из подобия соответствующих треугольников (см. выше).
Свойства отрезка, параллельного основаниям трапеции
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
- Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
- Длина отрезка, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)
Формулы для нахождения диагоналей трапеции
Далее приведены формулы, отображающие зависимость между сторонами, углами трапеции и величиной ее диагоналей. Эти формулы пригодятся для решения задач по геометрии на тему «диагонали трапеции»
Далее, в формулах используются следующие обозначения:
a, b — основания трапеции
c, d — боковые стороны трапеции
d1 d2 — диагонали трапеции
α β — углы при большем основании трапеции
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:
1. Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
2. Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.
3. Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ
Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.
Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.
Формулы нахождения диагоналей трапеции через высоту
Примечание.
 В данном уроке приведено решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме.
В данном уроке приведено решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме.
Задача.
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.
Решение.
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.
Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.
Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть
AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16
Ответ: 16 см
Задача.
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.
Решение.
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая — то обозначим длину AM = a, длину KD = b (не путать с обозначениями в формуле нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 — b
Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора
h2 + (24 — a)2 = (5√17)2
и
h2 + (24 — b)2 = 132
Учтем, что a = 16 — b , тогда в первом уравнении
h2 + (24 — 16 + b)2 = 425
h2 = 425 — (8 + b)2
Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора.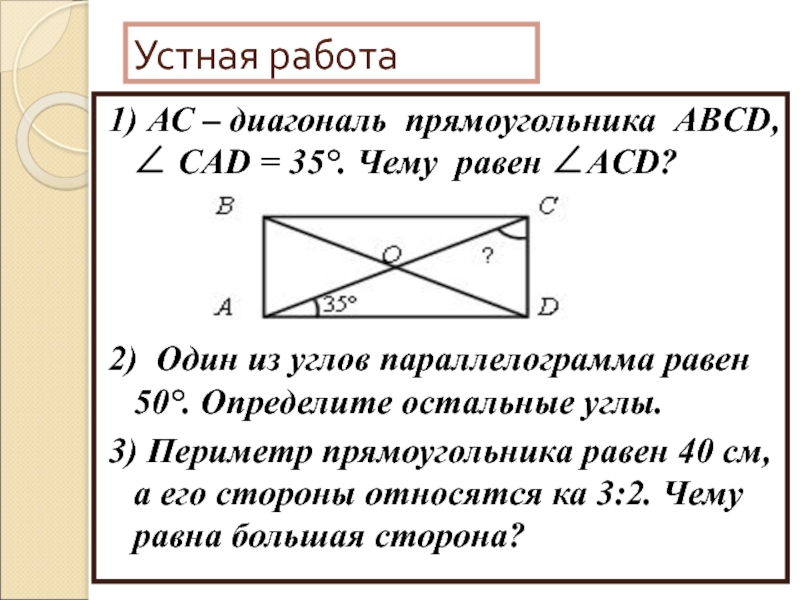 Получим:
Получим:
425 — (8 + b)2 + (24 — b)2 = 169
-(64 + 16b + b)2 + (24 — b)2 = -256
-64 — 16b — b2 + 576 — 48b + b2 = -256
-64b = -768
b = 12
Таким образом, KD = 12
Откуда
h2 = 425 — (8 + b)2 = 425 — (8 + 12)2 = 25
h = 5
Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5 / 2 = 80 см2
Ответ: площадь трапеции равна 80 см2.
Трапеция (задачи про основания) | Описание курса | Прямоугольная трапеция
Своя игра. Четырехугольники — online presentation
Урок геометриив 8 классе
по теме
«Четырехугольники»
Сомова Е.А.

Учитель математики высшей
квалификационной категории
МБОУ «СОШ №4 г.Мамадыш»
Параллелограмм
5
10
15
20
25
Прямоуголь
ник
5
10
15
20
25
Ромб
5
10
15
20
25
Квадрат
5
10
15
20
25
Параллелограмм — 5
В параллелограмме ABCD
AB=7см, АС=6см, BD=10см.
т. О — точка пересечения
диагоналей. Определите
периметр треугольника АОВ.
15 см
Параллелограмм — 10
В параллелограмме ABCD сторона
АВ=4 см, ВС=5 см. чему равен
периметр параллелограмма.
18 см
Параллелограмм — 15
Периметр параллелограмма 24
см. одна из его сторон 5 см.
определите все стороны
параллелограмма.
5 см и 7 см
Параллелограмм — 20
Сумма двух углов параллелограмма
600. Найдите все его углы.
0
30 ,
0
150 ,
0
30 ,
0
150
Параллелограмм — 25
Найдите все углы параллелограмма,
если разность 2-х из них равна 500
0
65 ,
0
115 ,
0
65 ,
0
115
Прямоугольник — 5
Определите периметр
прямоугольника, если 2 его
стороны равны 5 см и 8 см.

26 см
Прямоугольник — 10
АС – диагональ прямоугольника
ABCD, угол CAD – 350. чему равен
угол ACD?
0
55
Прямоугольник — 15
В прямоугольнике ABCD
диагональ АС=13см, сторона
ВС=12 см, CD=5 см. Найдите
периметр треугольника ABD.
30 см
Прямоугольник — 20
ABCD – прямоугольник,
диагонали пересекаются в т. О,
АО=4 см, ВС= 6см. Найдите
периметр треугольника AOD.
14 см
Прямоугольник — 25
C
B
β
O
A
D
Найти углы треугольника COD
0
β,β,180 -2β
Квадрат — 5
Сторона квадрата 5 см. Найдите
периметр.
20 см
Квадрат — 10
Периметр квадрата 28 см.
Найдите его стороны.
7 см
Квадрат — 15
Диагональ АС квадрата ABCD
равна 6 см. Чему равна
диагональ BD? Чему равны углы
треугольника AOD, т. О – точка
пересечения диагоналей.
6 см,
0
45 ,
0
90
0
45 ,
Квадрат — 20
В квадрате ABCD проведена
диагональ АС.
 Определите вид
Определите видтреугольника ACD, его углы.
Прямоугольный, 900, 450, 450
Квадрат — 25
B
N
A
M
P
K
C
АС = 12 см. Найти сторону квадрата.
4 см
Ромб — 5
Периметр ромба 32 см. Определите
его стороны.
8 см
Ромб — 10
В ромбе ABCD проведена диагональ
АС. Докажите, что треугольник АВС –
равнобедренный.
В
С
А
D
Ромб — 15
Один из углов ромба 600. Определите
остальные углы.
0
60 ,
0
60 ,
0
120 ,
0
120
Ромб — 20
В ромбе ABCD угол А равен 700.
Найдите угол CBD.
0
55
Ромб — 25
B
Найти углы ромба
и его периметр
О
A
C
1,4 см
600
D
0
120 ,
0
60 ,
0
120 ,
0
60 ;
5,6 см
.
Четырехсторонние вопросы и решения
Четырехсторонние вопросы всегда ломали голову для многих кандидатов, сдавших конкурсные или стандартизированные экзамены.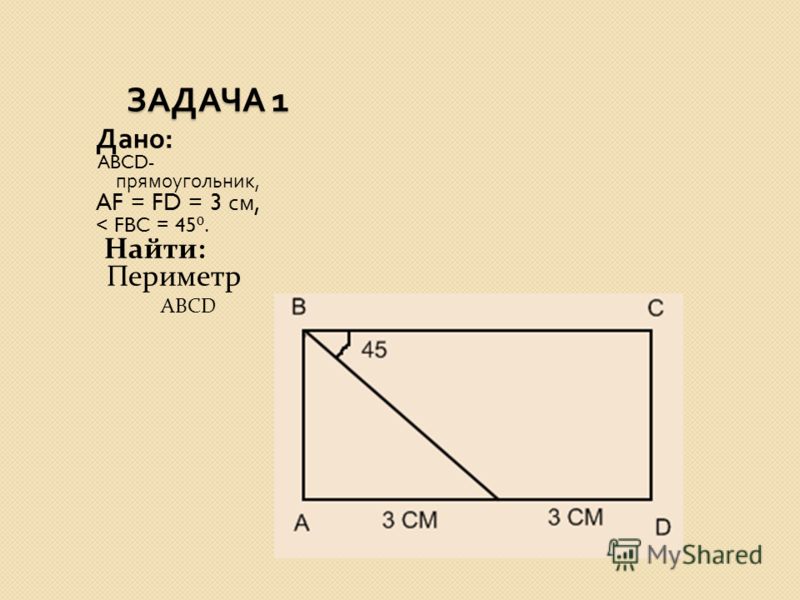 Основная причина этого в том, что изучить концепцию проще, чем применять ее для решения вопросов.
Основная причина этого в том, что изучить концепцию проще, чем применять ее для решения вопросов.
Поэтому, чтобы помочь вам в применении свойств четырехугольника, в этой статье мы поделились несколькими вопросами о четырехугольнике и их решениями.
Вот набросок этой статьи:
Прямоугольник
Вопрос 1
Какова площадь поля в форме прямоугольника размером 30 и 50 метров?
- 80 кв.метры
- 160 кв. Метров
- 1500 кв. Метров
- 1600 кв. Метров
- 3000 кв. Метров
Решение
Дать и найти:
Нам даны размеры прямоугольного поля 30 метров и 50 метров и
- Нам нужно найти его площадь.
Подъезд
Мы знаем, что поле имеет прямоугольную форму. Следовательно, мы можем применить площадь прямоугольника, чтобы найти площадь поля.
- Длина поля = 50 метров
- Ширина поля = 30 метров
Площадь прямоугольного поля = Длина × Ширина = 50 × 30 = 1500 кв.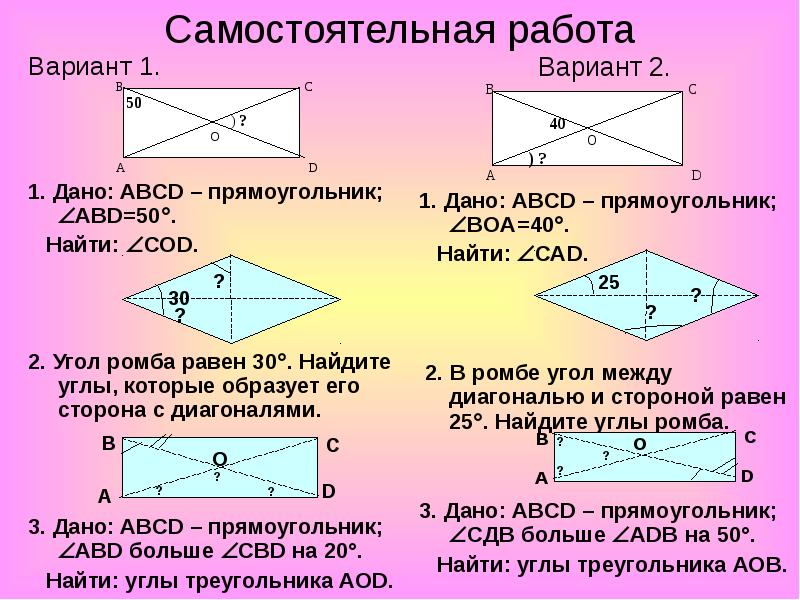 Метры
Метры
Следовательно, вариант C — правильный ответ.
Свойства и формулы, использованные в этом вопросе
- Площадь прямоугольника = длина × ширина
Из приведенного выше списка мы видим, что мы использовали только одно простое свойство, чтобы найти ответ.
Теперь давайте посмотрим на один вариант этого вопроса, похожий на GMAT.
Вопрос 2 — GMAT Нравится
Дорожка одинаковой ширины 2 метра проложена в прямоугольном поле. Какова площадь поля без тропы, если размеры поля 30 метров и 50 метров?
- 1100 кв. Метров
- 1300 кв. Метров
- 1400 кв. Метров
- 1444 кв. Метра
- 1460 кв. Метров
Решение
Дано и найти:
Нам дано:
- Тропа имеет одинаковую ширину 2 метра.
- Сделано в прямоугольном поле.
- Поле имеет размеры 30 метров и 50 метров.
Нам нужно найти:
- Площадь поля без учета дорожек.

Подъезд
Мы можем получить площадь поля, исключая пути, если мы вычтем площадь пути из площади поля.
- Площадь поля без учета дорожек = Площадь поля — Площадь дорожки.
- Площадь поля = 1500 кв.м
- Однако путь не прямоугольник
- Но мы можем разбить путь на три части, как показано ниже, и получить три прямоугольника
Следовательно, площадь пути = Площадь (прямоугольник размером 18 × 2 + прямоугольник размером 2 × 2 + прямоугольник размером 8 × 2)
- = 18 × 2 + 2 × 2 +8 × 2
- = 36 +4+ 16 = 56 кв.м
Таким образом, Площадь поля без учета дорожек = 1500 — 56 = 1444 кв.метры
Свойства и формулы, использованные в этом вопросе
- Площадь прямоугольника = длина × ширина
В этом вопросе используется такой же процесс. Но мы должны представить себе, что этот путь можно разбить на 3 отдельных прямоугольника.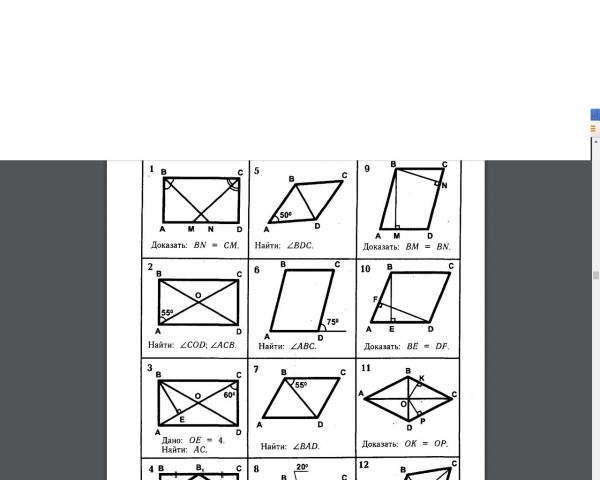 И это еще больше упрощает расчет.
И это еще больше упрощает расчет.
Площадь
Вопрос 1
В квадрате ABCD диагонали пересекаются в точке O. Если длина стороны квадрата равна 4 единицам, то какова площадь заштрихованной области?
Решение
Дано
- В этом вопросе нам дан квадрат ABCD со стороной 4 единицы, диагонали которого пересекаются в точке O.
Найти
- С этой информацией нас просят определить площадь заштрихованной области, то есть треугольника AOB
Подъезд
Хорошо, прежде чем мы приступим к решению этого вопроса, давайте просто вспомним полезное свойство квадратов из статьи: диагонали в квадрате делят друг друга пополам под прямым углом.
- Теперь скажите мне, каковы углы в каждом из этих четырех треугольников?
- Углы во всех четырех треугольниках 45-45-90, верно?
- Так как все углы в квадрате равны 90 градусам, а диагонали делят эти углы пополам.

- И все углы в центре квадрата прямые
- Так как все углы в квадрате равны 90 градусам, а диагонали делят эти углы пополам.
- Углы во всех четырех треугольниках 45-45-90, верно?
- Итак, можно сказать, что диагонали делят квадрат на четыре равнобедренных прямоугольных треугольника, которые совпадают.
- Теперь большинство из вас может подумать, насколько они совпадают?
- Если мы посмотрим на данную диаграмму, то увидим, что
- Гипотенуза всех треугольников — не что иное, как сторона квадрата
- И, поскольку диагонали делят друг друга пополам, в квадрате OA = OB = OC = OD
- Таким образом, все четыре треугольника имеют одинаковую длину сторон, следовательно, они являются конгруэнтными треугольниками
- Поскольку треугольники равны, их площади также равны
- Если мы посмотрим на данную диаграмму, то увидим, что
Используя эту информацию, давайте попробуем установить связь между площадью квадрата и площадью треугольника AOB.
- Можно сказать, что площадь квадрата = площадь AOB + площадь BOC + площадь COD + площадь DOA = 4 * площадь AOB (поскольку площади треугольников равны)
- Следовательно, площадь АОБ = площадь квадрата / 4 = 4 * 4/4 = 4 кв.
 Единицы
Единицы
Следовательно, правильный ответ — вариант Б.
Свойства и формулы, использованные в этом вопросе
- Все стороны квадрата равны.
- Все его внутренние углы равны 90 0 .
- Площадь кв.
- Диагонали квадрата пересекают друг друга под прямым углом
- Диагонали в квадрате делят квадрат на четыре равнобедренных прямоугольных треугольника
Из приведенного выше списка мы видим, что мы использовали указанные выше свойства / формулы, чтобы легко ответить на вопрос.
Теперь давайте посмотрим на один вариант этого вопроса, похожий на GMAT.
Вопрос 2
Если длина одной из диагоналей квадрата равна p единиц, то каков периметр квадрата?
- √2p
- 2п
- 2√2p
- 4 пол.
- 4√2p
Решение
Дать и найти
В этом вопросе это с учетом нам, что:
- Длина одной из диагоналей квадрата равна p единиц, и нам нужно , чтобы найти :
- По периметру кв.

Подъезд
- Итак, мы знаем, каков периметр квадрата?
- Да, есть. Это сумма всех сторон.
- И все стороны квадрата имеют одинаковую длину.
- Следовательно, периметр квадрата = 4 длины стороны
- Следовательно, когда у нас есть длина стороны, мы можем найти ответ.
Однако нам дана только длина одной из диагоналей квадрата, а не длина стороны.
- Можем ли мы определить длину стороны, используя эту информацию?
- Попробуем разобраться.
Давайте вспомним полезное свойство квадратов из статьи, то есть все внутренние углы в квадрате прямые, 90 градусов.
- Если все стороны равны и все углы равны, то, применяя теорему Пифагора, мы можем сказать, что обе его диагонали также будут равны.
Теперь давайте попробуем изобразить квадрат с одной диагональю, соединенной между собой.Мы можем четко заметить, что диагональ делит квадрат на два прямоугольных треугольника, а диагональ — это гипотенуза.
Таким образом, применяя правило Пифагора, мы можем сказать, что
- Сторона 1 2 + Сторона 2 2 = Диагональ 2
- a 2 + a 2 = p 2
- 2a 2 = p или a 2 = p 2 /2
- Отсюда получаем длину стороны как p / √2 единиц
Следовательно, периметр квадрата = 4 * (p / √2) = 4 * (p / √2) * (√2 / √2) = 2√2p единиц
Следовательно, правильный ответ — вариант C.
Свойства и формулы, использованные в этом вопросе
- Все стороны квадрата равны.
- Все его внутренние углы равны 90 ° .
- Теорема Пифагора
- Периметр пл.
Из приведенного выше списка мы видим, что мы использовали указанные выше свойства / формулы, чтобы легко ответить на вопрос.
Ромб
Вопрос 1
Если две диагонали ромба равны 6 и 8 единицам, то каков периметр ромба?
- 10
- 15
- 20
- 25
- 30
Решение
Дано
- В этом вопросе нам дан ромб с диагональю 6 и 8 единиц
Найти
- С помощью этой информации нас просят узнать периметр ромба
Подъезд
Хорошо, прежде чем мы приступим к решению этого вопроса, давайте визуализируем данную информацию в виде диаграммы.
- Потому что мы знаем, что диагонали ромба делят друг друга пополам под прямым углом.
В треугольнике AOB, применяя правило Пифагора, получаем
- AB 2 = AO 2 + OB 2
- AB 2 = 3 2 + 4 2
- 9 + 16 = 25
- Таким образом, АВ = 5 шт.
Это означает, что AD = BC = CD = 5 единиц.
- Так как у ромба все стороны равны.
Следовательно, периметр ромба = 4 * 5 = 20 единиц
Следовательно, правильный ответ — вариант C.
Свойства и формулы, использованные в этом вопросе
- Все стороны ромба равны.
- Диагонали пересекают друг друга под прямым углом.
- Правило Пифагора
Из приведенного выше списка мы видим, что мы использовали указанные выше свойства / формулы, чтобы легко ответить на вопрос.
Теперь давайте посмотрим на один вариант этого вопроса, похожий на GMAT.
Вопрос 2 — GMAT как
В ромбе ABCD, если длина стороны BC равна 1 единице, а значение внутреннего угла A составляет 60 o , то какова длина его более короткой диагонали?
- 1
- √3
- 2
- 2√3
- Не определяется
Решение
Дать и найти
В этом вопросе это с учетом нам, что:
- В ромбе ABCD, BC = 1 шт.
- Угол A = 60 o
С этой информацией нас просят найти
- Длина меньшей диагонали
Подход
Хорошо, прежде чем мы приступим к решению этого вопроса, давайте визуализируем данную информацию в виде диаграммы
В треугольнике BCD, угол DBC = угол CDB = 60 градусов
- Потому что мы знаем, что BC + CD (стороны ромба)
- Таким образом, BCD — это равносторонний треугольник и BD = BC = 1 шт.

Давайте также найдем длину другой диагонали, потому что мы еще не знаем, какая из них короче.
- Длина другой диагонали = AC = AO + OC = 2OC (поскольку диагонали делят друг друга пополам)
Чтобы найти OC, рассмотрим треугольник BOC.
- А теперь скажите, каковы углы в этом треугольнике?
- Таким образом, стороны треугольника BOC должны быть в соотношении 1: √3: 2 соответственно
- Мы знаем, что BC = 1, что означает OC = √3 / 2
Следовательно, AC = √3 единиц, что больше, чем BD = 1 единица
Следовательно, правильный ответ — вариант А.
Свойства и формулы, использованные в этом вопросе
- Все стороны ромба равны.
- Диагонали пересекают друг друга под прямым углом.
- Соотношение сторон треугольника 30-60-90
- Все стороны равностороннего треугольника равны
Из приведенного выше списка мы видим, что мы использовали указанные выше свойства / формулы, чтобы легко ответить на вопрос.
Параллелограмм
Вопрос 1
Если сумма длин двух смежных сторон параллелограмма равна 5 единицам, то каков периметр параллелограмма?
- 10
- 15
- 20
- 25
- 30
Решение
Дано
- В этом вопросе нам дан параллелограмм, у которого сумма длин двух соседних сторон равна 5 единицам.
Найти
- С помощью этой информации нас просят узнать периметр параллелограмма
Подъезд
Хорошо, это довольно простой вопрос, если вы можете применить свойство параллелограмма.
Посмотрим, что это за собственность.
- Во-первых, предположим, что длины четырех сторон в единицах a, b, c и d, как показано ниже
- Следовательно, периметр = a + b + c + d
Теперь скажите мне, какова связь между a и c?
- Они оба равны, да?
- Т.
 к., у параллелограмма противоположные стороны параллельны и равны.
к., у параллелограмма противоположные стороны параллельны и равны. - Таким образом, a = c и b = d
- Это означает, что периметр = a + b + a + b = 2 * (a + b)
- И нам дано, что сумма двух смежных сторон равна 5 единицам, то есть a + b = 5 единиц
- Следовательно, периметр данного параллелограмма = 2 * 5 = 10 единиц
Следовательно, правильный ответ — вариант А
Свойства и формулы, использованные в этом вопросе
- Противоположные стороны параллелограмма равны.
- Периметр параллелограмма
Из приведенного выше списка мы видим, что мы использовали только одно простое свойство, чтобы найти ответ.
Теперь давайте посмотрим на один вариант этого вопроса, похожий на GMAT.
Вопрос 2 — GMAT как
Площадь параллелограмма, у которого все стороны равны, составляет 1 кв. Если один из внутренних углов параллелограмма равен 30 градусам, то каков периметр параллелограмма?
- 1
- √2
- 2√2
- 4√2
- Не определяется
Решение
Дать и найти
В этом вопросе это с учетом нам, что:
- Площадь параллелограмма = 1 кв.
 ед.
ед. - Все стороны имеют одинаковую длину, допустим, это p единиц, а
- Один из внутренних углов = 30 градусов
С этой информацией нас просят найти
- Периметр параллелограмма = p + p + p + p = 4p единиц
Подход
- Для начала попробуем визуализировать всю данную информацию
Теперь скажите мне, как мы можем найти значение p?
- Единственная информация, которая у нас осталась, — это площадь параллелограмма, поэтому давайте попробуем использовать ее.
- Опустим перпендикуляр из верхней вершины в основание параллелограмма
Теперь обратите внимание на образовавшийся треугольник, это треугольник 30-60-90.
- И мы знаем, что стороны треугольника 30-60-90 будут в соотношении 1: √3: 2 соответственно.
- Итак, высота параллелограмма, h = p / 2
- Также известно, что площадь параллелограмма = основание * высота = p * p / 2 = p 2 /2, что равно 1 квадратной единице.

- Таким образом, получаем значение p = √2 ед.
- Следовательно, периметр параллелограмма = 4√2 единицы
Следовательно, правильный ответ — вариант D.
Свойства и формулы, использованные в этом вопросе
- Площадь параллелограмма.
- Периметр параллелограмма.
- Соотношение сторон треугольника 30-60-90
Из приведенного выше списка мы видим, что мы использовали указанные выше свойства / формулы, чтобы легко ответить на вопрос.
Трапеция
Вопрос 1
Какова площадь показанной ниже трапеции ABCD?
- 75 кв.метры
- 100 кв. Метров
- 120 кв. Метров
- 200 кв. Метров
- 240 кв. Метров
Решение
Дано и найти
Нам дана трапеция ABCD, и нам нужно найти ее площадь.
Нам также дают:
- Длина противоположных параллельных сторон = 15 и 5 метров
- Высота трапеции = 12 метров
Подъезд
Мы можем напрямую применить формулу площади трапеции, чтобы найти ответ.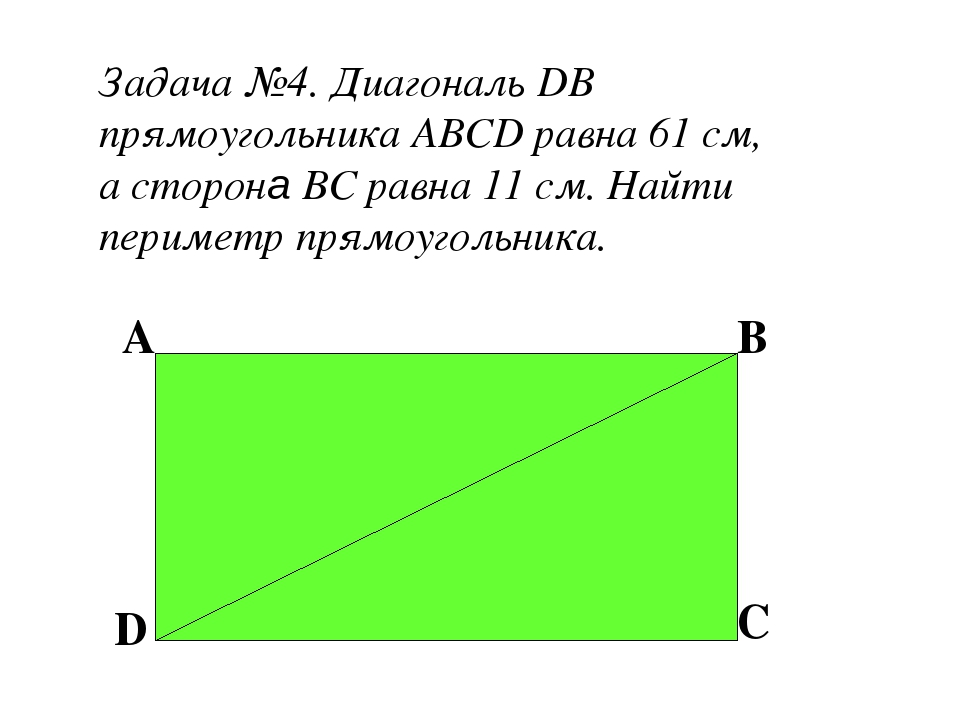
- Площадь трапеции = ½ × (Сумма параллельных сторон) × Высота = ½ × (5 + 15) × 12 = 120 кв. Метров
Следовательно, правильный ответ — вариант C.
Свойства и формулы, использованные в этом вопросе
- Площадь трапеции = ½ × (Сумма параллельных сторон) × Высота
Мы использовали только одно простое свойство, чтобы найти ответ. Теперь давайте посмотрим на один вариант этого вопроса, похожий на GMAT.
Вопрос 2 — GMAT как
Какова площадь ABED, если AB параллельна CE, а BCD представляет собой прямоугольный треугольник в точке B площадью 30 квадратных метров?
- 75 кв.метры
- 100 кв. Метров
- 120 кв. Метров
- 200 кв. Метров
- 240 кв. Метров
Решение
Дать и найти:
Нам дано:
- AB параллельно CE.
- BCD представляет собой прямоугольный треугольник в точке B.

- Площадь треугольника BCD = 30 кв. Метров
Нам нужно найти:
Подъезд
ABED — трапеция.Но мы не можем применить здесь формулу площади трапеции, так как нам не дана длина DE.
Итак, давайте посмотрим, как мы можем найти DE.
- DE = CE — CD = 10 — CD.
- Теперь, если мы найдем компакт-диск, мы сможем найти ответ.
- Давайте посмотрим, есть ли у нас какая-либо информация, касающаяся CD.
- CD является частью треугольника BCD, его площадь равна 30.
- 30 = ½ × BC × DC
- 30 = ½ × 12 × DC
- DC = 5
Таким образом, CD = 5 метров.
- Отсюда DE = 10-5 = 5 метров
Теперь этот вопрос аналогичен предыдущему.
Следовательно, его ответ — вариант C.
Свойства и формулы, использованные в этом вопросе
- Площадь трапеции = ½ × (Сумма параллельных сторон) × Высота
В этом вопросе мы также использовали только одно простое свойство, чтобы найти ответ.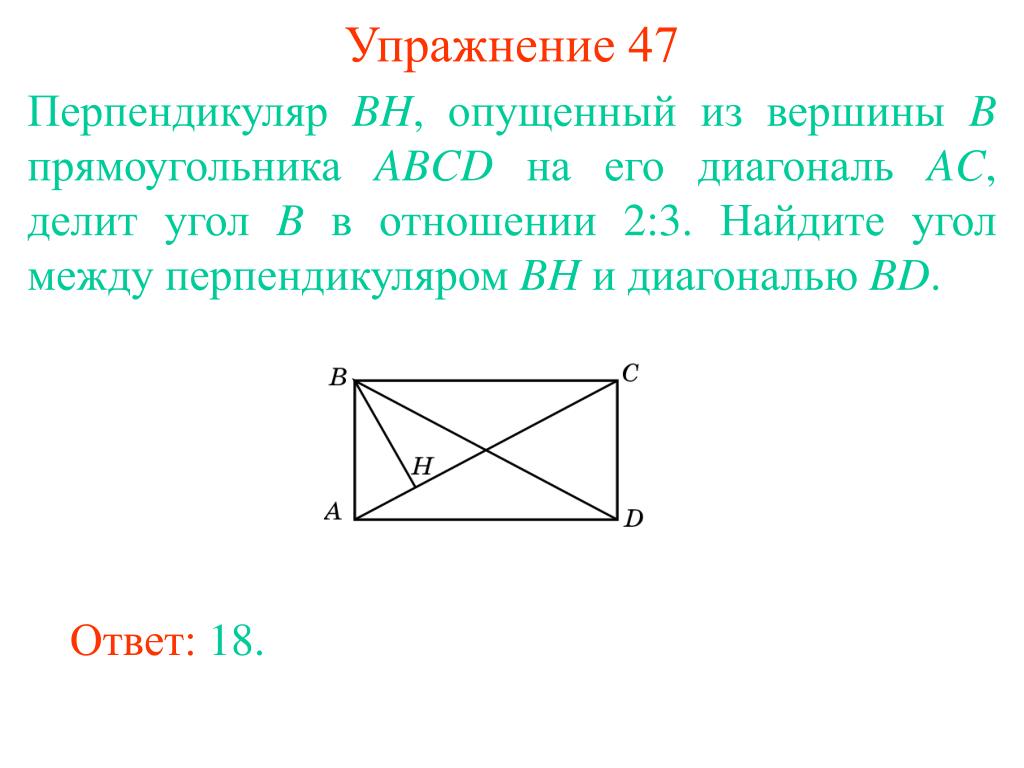 Но мы также применили навык визуализации, чтобы найти измерение DE.
Но мы также применили навык визуализации, чтобы найти измерение DE.
Четырехугольники — Полная глава — Класс VIII — Дыхание
Замкнутая фигура, имеющая четыре стороны, образованные соединением четырех точек, три из которых не лежат на одной прямой, называется четырехугольником.
Например:
Четырехугольник — это объединение четырех отрезков прямых, соединяющих четыре компланарные точки; никакие три из них не лежат на одной прямой, и каждый сегмент пересекает ровно две другие линии, каждая в своей конечной точке.
Четырехугольник — это выпуклый , если каждый из внутренних углов меньше 180˚. В противном случае это вогнутый четырехугольник .
Свойства четырехугольника — ЧетырехугольникиПусть ABCD — четырехугольник.
- Тогда точки A, B, C и D называются вершинами четырехугольника.
- Отрезки AB, BC, CD и DA — четыре стороны четырехугольника.
- Углы ∠DAB, ∠ABC, ∠BCD и ∠CDA — это четыре угла четырехугольника.
- Отрезки AC и BD называются диагоналями четырехугольника.
- Стороны четырехугольника называются смежными сторонами или следующими друг за другом сторонами.Если у них общая конечная точка. На следующем рисунке AB и AD — смежные или следующие друг за другом стороны. Найдите другую пару соседних сторон.
- Две стороны четырехугольника называются противоположными углами, если у них нет общей стороны. Здесь ∠DAB и ∠BCD — противоположные углы. Найдите другую пару противоположных углов.
Соседние углы и противоположные углы:
- Два угла четырехугольника являются смежными или последовательными углами.Если у них есть общая сторона. Таким образом, ∠DAB и ∠ABC являются смежными углами .
- Два угла четырехугольника называются противоположными углами, если у них нет общей стороны. Здесь ∠DAB и ∠BCD — противоположные углы. Найдите другую пару противоположных углов.
Диагональ:
Диагональ AC делит четырехугольник на два треугольника, а именно на треугольники ABC и треугольники ADC. Назовите треугольники, образовавшиеся при рисовании диагонали BD.
Angle Sum Property: Теорема 1: сумма углов четырехугольника равна 360˚Дано: ABCD — четырехугольник
Для подтверждения: ∠ A + ∠ B + ∠ C + ∠ D = 360˚
Конструкция: Нарисуйте диагональ AC
Доказательство: В треугольнике ADC, ∠ 1 + ∠ 2 + ∠ 3 = 180˚ (свойство суммы углов)
В треугольнике ABC, ∠ 4 + ∠ 5 + ∠ 6 = 180˚
Сложив эти два,
∠ 1 + ∠ 2 + ∠ 3 + ∠ 4 + ∠ 5 + ∠ 6 = 360˚
Но, ∠ 1 + ∠ 4 = ∠ A и ∠ 3 + ∠ 6 = ∠ C.Следовательно, ∠ A + ∠ D + ∠ B + ∠ C = 360˚
Таким образом, сумма углов четырехугольника равна 360˚
.Пример 1: Четыре угла четырехугольника имеют соотношение 2: 3: 4: 6. Найдите размеры каждого угла.
Решение:
Дано: Соотношение углов 2: 3: 4: 6
Чтобы найти: Меры каждого угла.
Обратите внимание, что 2 + 3 + 4 + 6 = 15. Таким образом, 15 частей составляют 360˚.Следовательно,
15 частей по 360˚
2 части по (360˚ / 15) * 2 = 48˚
3 части по (360˚ / 15) * 3 = 72˚
4 части по (360˚ / 15) * 4 = 96˚
6 частей по (360˚ / 15) * 6 = 144˚
Таким образом, углы равны 48˚, 72˚, 96˚, 144˚.
Пример 2: В четырехугольнике ABCD A и ∠C равны; ∠B является дополнением к ∠D. Найдите меру ∠A и ∠C.
Решение:
Нам дают ∠ B + ∠ D = 180˚.Используя свойство суммы углов четырехугольника, получаем
∠ A + ∠ C = 360˚- 180˚ = 180˚
Так как ∠ A + ∠ C имеют одинаковую меру, получаем A A = C C = 180˚ / 2 = 90˚
Пример 3: Найдите все углы в заданном ниже четырехугольнике:
Решение:
Мы знаем, что ∠ P + ∠ Q + ∠ R + ∠ S = 360˚.Следовательно,
х + 2х + 3 + х + 3х — 7 = 360˚
Это дает 7x — 4 = 360˚ или 7x = 364˚
Следовательно, x = 364˚ / 7 = 52˚
Получаем ∠ P = 52˚; R = 52; ∠ Q = 2x + 3 = 107˚; ∠ S = 149˚. Убедитесь, что ∠ P + ∠ Q + ∠ R + ∠ S = 360˚
Четырехугольники — УПРАЖНЕНИЕ 3.5.2
- Два угла четырехугольника — 70 ° и 130 °, а два других угла равны.Найдите меру этих двух углов.
Решение:
Пусть ∠ A и ∠ B будут x, ∠ C = 70 °
и ∠ D = 130 °
∠ A + ∠ B + ∠ C + ∠ D = 360 ° (Теорема 7)
х + х + 70 ° + 130 ° = 360 °
2x = 360 ° — 200 °
X = 160 ° / 2 = 80 °
Таким образом, ∠ A = 80 ° и ∠ B = 80 °
- На рисунке предположим, что ∠ P и ∠ Q являются дополнительными углами и ∠ R = 125 °.Найдите меры ∠ S.
Решение:
∠ P + ∠ Q = 180 ° (Дополнительные углы)
∠ P + ∠ Q + ∠ R + ∠ S = 360 ° (теорема 7)
180 ° + 125 ° + ∠ S = 360 °
∠ S = 360 ° — (180 ° + 125 °)
∠ S = 360 ° −305 °
∠ S = 55 °
- Три угла четырехугольника находятся в соотношении 2: 3: 5, а четвертый угол равен
90 °.Найдите размеры трех других углов.
Решение:
Пусть углы будут 2x, 3x, 5x.
∠ A + ∠ B + ∠ C + ∠ D = 360 °
2x + 3x + 5x + 90 ° = 360 °
10x = 360 ° −90 °
х = 270 ° / 10
х = 27 °
∴ Углы равны, ∠ A = 2x = 2 × 27 = 54 °
∠ B = 3x = 3 × 27 = 81
∠ C = 5x = 5 × 27 = 135 °
4.На соседнем рисунке ABCD представляет собой четырехугольник, такой что ∠ D + ∠ C = 100 °. Биссектрисы ∠ A и ∠ B пересекаются в области ∠ P. Определите ∠ APB.
Решение:
AP и BP — биссектрисы
∠ D + ∠ C = 100 °
Найти: ∠ APB
Доказательство: ∠ A + ∠ B + ∠ C + ∠ D = 360 ° (Теорема 7)
∠ A + ∠ B + 100 ° = 360 °
∠ A + ∠ B = 360 ° — 100 °
Умножение на 12,
12 × ∠ A + 12 × ∠ B = 12 × 260
а + Ь = 130 °
В Δ APB,
a + b + ∠ P = 180 °
∠ P = 180 ° — 130 °
∠ P = 50 °
Трапеция — четырехугольник
Набор основных имеет пару противоположных сторон, которые параллельны.Такой четырехугольник известен как трапеция .
Например:
Пример 4: Предположим, что на рисунке ABCD AB || CD; ∠A = 65 ° и ∠B = 75 °. Какова мера ∠C и ∠D?
Решение:
Заметим, что ∠A + ∠D = 180 ° (пара смежных углов трапеции является дополнительной.)
Таким образом, 65 ° + ∠D = 180 °
Это дает ∠D = 180 ° — 65 ° = 115 °
Аналогично, B + ∠C = 180 °, что дает 75 ° + ∠C = 180 °.Следовательно,
∠C = 180 ° — 75 ° = 105 °
Пример 5: В равнобедренной трапеции PQRS, ∠P и ∠S находятся в соотношении 1: 2. Найдите размеры всех углов.
Решение:
У равнобедренной трапеции углы основания равны; ∠P = ∠Q. Пусть ∠P = xº и ∠S = 2xº. Поскольку, ∠P + ∠S = 180º (одна пара смежных углов трапеции является дополнительной). Получаем,
x + 2x = 180º
x = 180º / 3 = 60º
Следовательно, P = 60º и ∠S = 2 x 60º = 120º.Поскольку P = ∠Q, получаем ∠Q = 60º. Но ∠Q + ∠R = 180º. Отсюда получаем
∠R = 180º — 60º = 120º
Четырехугольники — УПРАЖНЕНИЕ 3.5.3
1. В трапеции PQRS, PQ || RS, а ∠P = 70 ° и ∠Q = 80 °. Вычислите меру ∠S и ∠R.
Решение:
∠P + ∠S = 180 ° (Дополнительные углы)
∠S = 180 ° — 70 ° = 110 °
∠Q + ∠R = 180 ° (Дополнительные углы)
∠R = 180 ° −80 ° = 100 °
2.В трапеции ABCD с AB || CD. Принято, что AD не параллельна BC. Является ли ΔABC ≅ Δ ADC? Назови причины.
Решение:
In Δ ABC и Δ ADC,
(1) AC = AC (общая сторона)
(2) BAC = ∠ACD (Альтернативные углы, AB || CD)
∴ Δ ABC ≅ Δ ADC Это невозможно доказать с помощью постулируемого пучка.
3. На рисунке PQRS представляет собой равнобедренную трапецию; ∠SRP = 30 ° и ∠PQS = 40 °. Вычислите углы ∠RPQ и ∠RSQ.
Решение:
Данные: PQRS — равнобедренная трапеция,
PS = RQ и ∠P = ∠Q
∠SRP = 30 ° и ∠PQS = 40 °
Чтобы найти: RPQ и ∠RSQ
Доказательство: ∠RPQ = ∠SRP = 30 °
(Альтернативные углы, PQ || SR)
∠RSQ = ∠PRS = 40 °
(Альтернативные углы, PQ || SR)
4. Доказательство того, что углы основания равнобедренной трапеции равны.
Решение:
Данные: ABCD — равнобедренная трапеция.
Чтобы доказать: ∠A = ∠B
Построение: соедините диагональ BD и AC.
Доказательство: In Δ ACB и ΔBDA
(1) BC = AD (равнобедренная трапеция)
(2) AC = BD (ISosceles trapezium)
(3) AB = AB (Общая сторона)
∴ ACB ≅ Δ BDA (постулат SSS) )
∴ ∠A = ∠B (свойство конгруэнтности)
5. Предположим, что в четырехугольнике ABCD AC = BD и AD = BC. Докажите, что ABCD — это трапеция.
Решение:
Данные: ABCD — четырехугольник,
AC = BD и AD = BC
Доказать: ABCD — это трапеция
Доказательство: In Δ ADB и Δ BCA
(1) AD = BC (Данные)
(2) AC = BD ( Данные)
(3) AB = AB (общая сторона)
∴ Δ ADB ≅ Δ BCA (постулат SSS)
∴ ∠A = ∠B (свойство соответствия)
AC = BD (данные), AD = BC (данные)
∴ ABCD представляет собой равнобедренную трапецию
Параллелограммы — Quadrialterals
Посмотрите на следующие наборы четырехугольников:
Четырехугольник, в котором обе пары противоположных сторон параллельны, называется параллелограммом.
Утверждение 1: В параллелограмме противоположные стороны равны и противоположные углы равны.Проба:
Пусть ABCD — параллелограмм. Присоединяйтесь к BD. Тогда ∠1 = ∠2 и ∠3 = ∠4. В треугольниках ABD и CBD мы видим, что
∠1 = ∠2; ∠4 = ∠3, BD (общий)
Следовательно, ΔABD ≅ Δ CDB (постулат ASA). Отсюда следует, что
AB = DC, AD = BC и ∠A = ∠C.
Аналогично присоединяем AC, и мы можем доказать, что ΔADC ≅ Δ CBA.Следовательно, ∠D = ∠B
Пример 6. Отношение двух сторон параллелограмма 3: $, а его периметр равен 42 см. Найдите размеры всех сторон параллелограмма.
Решение:
Пусть стороны будут 3x и 4x. Тогда периметр параллелограмма равен 2 (3x + 4x) = 2 x 7x = 4x.
Из приведенных данных следует, что, 42 = 14x, так что x = 42/14 = 3. Следовательно, стороны параллелограмма равны 3 x 3 = 9 см и 3 x 4 = 12 см
Пример 7: На следующем рисунке PQRS представляет собой параллелограмм.Найдите x и y в см.
Решение:
В параллелограмме, как мы знаем, диагонали делят друг друга пополам. Следовательно, SO = OQ. Это дает 16 = x + y. Аналогично PO = OR, так что 20 = y + 7. Получаем y = 20-7 = 13 см. Подставляя значение y в первое соотношение, мы получаем 16 = x + 13. Следовательно, x = 3 см
Четырехугольники — УПРАЖНЕНИЕ 3.5.4
1. Соседние углы параллелограмма находятся в соотношении 2: 1. Найдите размеры всех углов.
Решение:
Пусть углы равны 2x и x
∠A + ∠B = 2x + x = 180 ° (соседние углы параллелограммов являются дополнительными)
2x + x = 180 °
3x = 180 °
X = 180 ° / 3 = 60 °
∴ ∠A = 2x = 60 × 2 = 120 °
∴ ∠B = 60 °
∴ ∠C = ∠A = 120 °
(Противоположные углы параллелограмма)
∠D = ∠B = 60 °
(Противоположные углы параллелограмма)
2. Поле имеет форму параллелограмма, периметр которого составляет 450 м, а одна сторона больше другой на 75 м.Найдите длины всех сторон
Решение:
Периметр = AD + DC + CB + BA
450 = x + x + 75 + x + x + 75
450 = 4x + 150
450 — 150 = 4x
300 = x
X = 75
∴ Сторона = 75 м ( x)
∴ Противоположная сторона = x + 75 = 75 + 75 = 150 м
3. На рисунке ABCD представляет собой параллелограмм. Диагонали AC и BD пересекаются в точке O; и ∠DAC = 40 °, ∠CAB = 35 ° и ∠DOC = 10 °.
ADC, ∠ACB и ∠CBD.
Решение:
Данные: ABCD — параллелограмм AD || BC и DC || AB.
Диагонали AC и BD пересекаются в точках O
∠DAC = 40 °, ∠CAB = 35 ° и ∠DOC = 110 °
Чтобы найти: (1) ∠ABO (2) ∠ADC (3) ∠ACB (4) ∠ CBD
Доказательство: ∠DAC + ∠CAB = ∠A
40 ° + 35 = ∠A
∠A = 75 °
∠C = ∠A = 75 °
(Противоположные углы параллелограмма равны)
∠D + ∠A = 180 ° (Дополнительные углы)
∠D = 180 ° −75 ° = 105 °
∠B = ∠D = 105 ° (Противоположные углы параллелограмма равны)
∠DOC = ∠AOB = 110 °
(Углы противоположные по вертикали)
In Δ AOB, ∠A + ∠O + ∠B = 180 °
(Сумма всех углов Δ составляет 180 °)
35 ° + 110 ° + ∠B = 180 °
∠B = 180 ° -145 °
(1) ∠ABO = 35 °
(2) ∠ADC = 105 ° (Доказано)
(3) ∠ACB = ∠CBD = 40 °
(Альтернативные углы, AD || BC)
∠CBD = 105 ° -35 °
(4) ∠CBD = 70 °
(1) ∠ABO = 35 °
(2) ADC = 105 °
(3) ∠ACB = 40 °
(4) ∠CBD = 70 °
4.В параллелограмме ABCD сторона DC образуется к E и ∠BCE = 105 °.
Вычислить и ∠A, ∠B, ∠C и ∠D.
Решение:
∠BCD + ∠BCE = 180 ° (Линейная пара)
∠BCD = 180 ° — 105 ° = 75 °
В ABCD
∠A = ∠C = 75 ° (Противоположные углы параллелограмма)
∠ABC = ∠BCE = 105 °
(Альтернативные углы, AB || DE)
∠D = ∠B = 105 °
(Напротив углы параллелограмма)
5. Докажите логически, что диагонали параллелограмма делят друг друга пополам.Наоборот, покажите, что четырехугольник, в котором диагонали пересекают друг друга пополам, является параллелограммом.
Решение:
Данные: ABCD — параллелограмм (║ln)
Доказать: AO = OC и DO = OB
Доказательство: в ΔABO и DOC
(1) AB = DC (противоположные стороны углов)
(2) ∠AOB = ∠ DOC (VOA)
(3) ∠ABD = ∠BDC (альтернативные углы AB || CD)
∴ ΔABO ≅ ΔDOC (портированный ASA)
∴ AO = OC & DO = BO (свойства сравнения)
6.В параллелограмме KLMN ∟K = 60 °. Найдите размеры всех углов.
Решение:
∠M = ∠K = 180 ° (Дополнительные углы)
∠N = 180 ° −60 ° = 120 °
∠M = ∠K = 60 °
(Противоположные углы параллелограмма)
∠L = ∠N = 120 °
7. Пусть ABCD — четырехугольник, в котором ∠A = ∠C и ∠B = ∠D. Докажите, что ABCD — параллелограмм.
Решение:
Данные: ∠A = ∠C и ∠D = ∠B
Доказательство: ABCD — параллелограмм
Доказательство: ∠A + ∠B + ∠C + ∠D = 360 °
x + y + x + y = 360 °
2x + 2y = 360 °
2 (x + y) = 360 °
x + y = 360 ° / 2 = 180 °
Соседние углы являются дополнительными
∴ ABCD — параллелограмм.
8. Предположим, что в четырехугольнике ABCD AB = CD и AD = BC. Докажите, что ABCD — параллелограмм.
Решение:
Данные: ABCD — четырехугольник,
AB = DC, AD = BC
Доказать: ABCD — параллелограмм
Построение: соединить DB
Доказательство: In Δ ABD и Δ DBC
(1) DB = DB (общая сторона)
(2) AD = BC (данные)
(3) AB = DC (данные)
∴ ABD ≅ Δ DBC (постулат SSS)
∴ ∠DBA = ∠BDC (свойство конгруэнтности)
Но это альтернативные углы
У нас есть AB ║ DC
∴ ∠ADB = ∠DBC (C.P)
Но это чередующиеся углы
У нас DA ║ BC
∴ ABCD — параллелограмм.
Специальные виды параллелограммов — четырехугольники Прямоугольник:
Прямоугольник — это параллелограмм, все углы которого равны прямым.
Диагональные свойства прямоугольника:
(i) Диагонали прямоугольника равны
(ii) Диагонали прямоугольника делят друг друга пополам.
Пример 8: В прямоугольнике XYWZ предположим, что O — точка пересечения его диагоналей. Если ∠ZOW = 110º. Вычислите меру ∠OYW.
Решение:
Мы знаем, ∠ZOW = 110º. Следовательно, ∠WOY = 180º — 110º = 70º (дополнительные углы)
Итак, OYW — равнобедренный треугольник, так как OY = OW. Следовательно,
∠OYW = ∠OWY = (180º — 70º) / 2 = 110º / 2 = 55º
Ромб:
Ромб — это параллелограмм, у которого все четыре стороны равны.
Пример 10: Диагонали ромба составляют 24 см и 10 см. Вычислите площадь ромба.
Решение:
Нам дано, что AC = 24 см; BD = 10 см. Мы знаем, что диагонали ромба пересекают друг друга под прямым углом. Пусть O — точка пересечения этих диагоналей. Тогда у нас есть AO = CO = 12 см и BO = DO = 5 см. Мы также знаем, что AOD — это прямоугольный треугольник. Следовательно, площадь треугольника AOD равна
.1/2 x OA x OD = 1/2 x 12 x 5 = 30 см 2
Поскольку ромб состоит из четырех равных прямоугольных треугольников, его площадь составляет 4 x 30 = 120 см 2
Квадрат
Квадрат — это параллелограмм, в котором
(i) у которого все стороны равны
(ii) каждый угол прямой
(iii) диагонали равны
(iv) диагонали делятся пополам под прямым углом.
Пример 12: Поле имеет форму квадрата со стороной 20 м. Его окружает дорожка шириной 2 метра. Найдите внешний периметр пути.
Решение:
Ширина проезжей части 2м. Длина стороны внешнего квадрата = (20 + 2 + 2) = 24 м
Следовательно, периметр 4 x 24 = 96 м
Воздушный змей:
Воздушный змей — четырехугольник, в котором два равнобедренных треугольника соединены по общему основанию.
Пример 14: На рисунке PQRS — воздушный змей; PQ = 3 см и QR = 6 см. Найдите периметр PQRS.
Решение:
У нас PQ = PS = 3см, QR = SR = 6см.
Следовательно, периметр = PQ + QR + RS + PS
3 + 6 + 6 + 3 = 18 см
Четырехугольники — УПРАЖНЕНИЕ 3.5.5
1. Стороны прямоугольника имеют соотношение 2: 1. Периметр 30 см. Вычислите размеры всех сторон.
Решение:
ABCD — прямоугольник
Пусть AB: BC = 2: 1
∴ AB = 2x и BC = x
Периметр прямоугольника = 2 (1 + b)
2 (1 + b) = 30
2 (2x + x ) = 30
2 × 3x = 30
6x = 30
x = 306 = 5
2x = 2 × x = 2 × 5 = 10
1x = 1 × 4 = 1 × 5 = 5
AB = 10 м; BC = 5 см
CD = 10 см; DA = 5 см
2. В соседнем прямоугольнике ABCD ∠OCD = 30 °. Рассчитайте ∠BOC. Какой тип треугольника BOC?
Решение:
ABCD — прямоугольник
Диагонали AC и BD пересекают друг друга пополам в точке O и AC = BD.
AO = OC = BO = OD
OCD = ODC = 30 °
На ΔCOD, ODC + ∠OCD + ∠COD = 180
30 ° + 30 ° + ∠COD = 180 °
60 ° + ∠COD = 180 °
∴ ∠COD = 180˚ — 60˚ = 120 °
∠COD + ∠COB = 180
∠COB = 180˚ — 120˚
∠COB = 60 °
∴ Δ BOC — равнобедренный треугольник
- Прямоугольник ll является параллелограммом, но все параллелограммы не являются прямоугольниками. Обоснуйте утверждения.
Решение:
Все прямоугольники обладают всеми свойствами параллелограммов, кроме параллелограмма
Может иметь не все свойства прямоугольника.
- В прямоугольнике все углы прямые, а в параллелограмме равны только противоположные углы.
- В прямоугольнике диагонали равны, а в параллелограмме диагонали не равны.
- Докажите логически, что диагонали прямоугольника равны.
Решение:
Данные: ABCD — прямоугольник.
AC и BD — диагонали.
Доказать: AC = BD
Доказательство: In ΔABC и Δ ABD
∠ABC = BAD [90 °]
г. до н.э. = н.э. [Opp.Стороны]
AB = AB [Общая сторона]
∴ ΔABC ≅ ΔABD [SAS]
∴ AC = BD [CPCT]
- Стороны прямоугольного парка имеют соотношение 4: 3. Если площадь составляет 1728 м 2 , , найдите стоимость ограждения из расчета 2,50 рупий / м.
Решение:
ABCD — парк прямоугольной формы пусть AB: BC = 4: 3
∴ AB = 4x и BC = 3x
Площадь прямоугольника = 1 × b
4x × 3x = 1728
12x 2 = 1728
Х 2 = 144
Х = √144 = 12
Длина = 4x = 4 × 12 = 48 м
Ширина = 3x = 3 × 12 = 36 м
Периметр прямоугольника = 2 (l + b)
2 (48 + 36) = 2 × 84 = 168 м
Стоимость ограждения = периметр × ставка
= 168 × 2.50
= 420
рупий- Прямоугольный двор состоит из двух цветочных клумб в форме равнобедренного равнобедренного прямоугольного треугольника. Оставшаяся часть представляет собой двор трапеции.
Форма (см. Рис.), Параллельные стороны которой имеют длину 15 м и 25 м. Какую часть двора занимает клумба?
Решение:
ABCD — двор прямоугольной формы
AEFB — трапеция
AB ║ EF
AB = 25 м и EF = 15 м
AD = BC = 5 м
Площадь прямоугольника = ½ × b = 25 × 5 = 125 м²
Площадь каждой клумбы = ½ × b × h
= ½ × 5 × 5 = (25/2) м²
Площадь обеих клумб = 2 × ( 25/2) = 25 м²
Доля цветников до двора = 25/125 = 1/5
7.В ромбе ABCD ∠C = 70 °. Найдите другой угол ромба.
решение:
ABCD — ромб
∠C = 70 °
Но ∠A = ∠C = 70 ∴ ∠A = 70 °
∠A + ∠B = 180 ° (смежные углы)
70 + ∠B = 180 °
∠B = 180 — 70 = 110 °
∠B = ∠D = 110 °
∴ ∠A = 70 °; ∠B = 110 °; ∠D = 110 °
8. В PQRS ромба ∠SQR = 40 ° и PQ = 3 см. Найдите ∠SPQ, ∠QSR и периметр ромба.
Решение:
PQRS — ромб
∠SQR = 40 ° и PQ = 3 см
∠SQR = 40 ° и PQ = 3 см
∠PQS = ∠SQR = 40 °
∠PQS = 40 ° (углы биссектрисы диагонали) 3 см
Но ∠PQS = ∠QSP [PQ = PS]
∴ ∠QSP = 40 °
In Δ PQS, ∠PQS + ∠QSP + ∠SPQ = 180 °
40 ° + 40 ° + ∠SPQ = 180
∠SPQ = 180 −80
= 100 °
∴ ∠SPQ = 100 °
В ромбе PQ = QR = RS = SP = 3 см
Периметр ромба PQRS = 3 × 4 = 12 см
9.В ромбе PQRS, если PQ = 3x -7 и QR = x + 3, найдите PS.
Решение:
В ромбе все стороны равны
PQ = QR = RS = SP
∴ PQ = QR
3x -7 = x + 3
3x -x = 3 + 7
2x = 10
X = 5
PS = x + 3 = 5 + 3 = 8 см
10. Пусть ABCD — ромб и ∟ABC = 124 °. Рассчитайте ∟A, ∟D и ∟C.
В ромбе противоположные углы равны
Решение:
∠B = ∠D = 124 °
∠A + ∠B = 180 °
Последовательные углы
∠A + 124 ° = 180 °
∠A + 124 ° = 180 °
∠A = 180-124 = 56 °
∴ ∠A = 56 °; ∠B = 124 ° и ∠C = 56 °
11.Ромб — это параллелограмм: обосновать.
Решение:
Ромб обладает всеми свойствами параллелограмма, т.е.
а) Противоположные стороны равны и параллельны.
б) Противоположные углы равны.
c) Диагонали делят друг друга пополам
∴ Ромб представляет собой параллелограмм.
12. В данном квадрате ABCD, если площадь треугольника ABD равна 36 см2, найдите
(i) площадь треугольника BCD;
(ii) площадь квадрата ABCD.
Решение:
ABCD — квадрат
Bd — диагональ
Диагональ делит квадрат на два равных треугольника
∴ Δ ABD ≅ Δ BCD DC
∴ Площадь Δ ABD = площадь Δ BCD
Площадь Δ ABD = 36 см² (дано )
∴ Площадь Δ BCD = 36 см²
Площадь квадрата ABCD = Площадь Δ ABD + Площадь ΔBCD
= 36 см² + 36 см²
Площадь квадрата ABCD = 72 см²
13.Сторона квадрата ABCD равна 5 см, а периметр другого квадрата PQRS равен 40 см. Найдите отношение площади ABCD к площади PQRS.
Решение:
Периметр квадрата ABCD = 4 × сторона
= 4 × 5 = 20
Соотношение (периметр ABCD) / (периметр PQRS) = 20/40 = 1/2 или 1: 2
Площадь ABCD = (сторона) ² = (5) ² = 25 см
Сторона PQRS = периметр / 4 = 40/4 = 10 см
Площадь PQRS = (сторона) ² = (10) ² = 100 см²
Соотношение (Площадь ABCD) / (Площадь PQRS) = 25/100 = 1 / 4 или 1: 4
14.Квадратное поле имеет сторону 20м. Найдите длину проволоки, необходимую для ее четырехкратного ограждения.
Решение:
Длина одной стороны квадрата = 20 рупий
Длина провода, необходимого для ограждения одного круга = 4 × 20
Длина провода, необходимого для ограждения четырех кругов = 80 м
= 4 × 80 м
= 320 м
15. Перечислите различия между квадратом и ромбом.
Решение:
Квадрат
1. Все углы равны
2. Диагонали равны
3.Площадь = сторона × сторона = (с) ²
Ромб
- Противоположные углы равны
2. Диагонали не равны
3. Площадь = 1/2 × произведение диагоналей = 1/2 x d 1 d 2
Пример 16. Четыре совпадающих прямоугольника размещаются, как показано на рисунке. Площадь внешнего квадрата в 4 раза больше внутреннего квадрата. Каково отношение длины равных прямоугольников к ширине?
Решение:
Пусть длина прямоугольников равна ‘a’, а ширина — ‘b’.
Сторона внешнего квадрата — единицы (a + b)
Сторона внешнего квадрата (ab) единицы
Площадь внешнего квадрата = 4, умноженная на площадь внутреннего квадрата
Площадь ABCD = 4 (Площадь PQRS)
(a + b) ² = 4 (ab)
(а + б) = 2 (а — б)
2a — 2b = (a + b)
2а — а = b + 2b
а = 3b
a / b = 1/3 или 1: 3
Нравится:
Нравится Загрузка…
Связанныедиагонали прямоугольника делят пополам
Что каждый угол равен 90 градусам! Q.E.D. Прямоугольники — это особый вид параллелограмма. Биология. Прямоугольник и параллелограмм имеют диагонали, которые делят друг друга пополам, но не под углом 90 °. Для всех неквадратных прямоугольников. Таким образом, диагонали прямоугольника делят друг друга пополам. Разница в том, что диагонали равны по длине для квадрата и прямоугольника и не равны для ромба или ромбовидного косого ромба.То же самое можно сказать и о другой диагонали. Средняя точка AC: ((0 + a) / 2, (0 + b) / 2) = (a / 2, b / 2) Средняя точка BD: ((0 + a) / 2, (b + 0) / 2) = (a / 2, b / 2) Поскольку середины общие, они пересекаются именно здесь. Это означает, что их стороны равны. Поскольку противоположные стороны прямоугольника равны по размеру, длина равна обеим сторонам. Докажите, что диагонали прямоугольника делят друг друга пополам. Применение формулы сечения. Так как диагонали прямоугольника совпадают, MO = 26. Параллелограммы Управляемые заметки и рабочие листы Обучение геометрии.Можно только на кв. Начать. Докажите, что диагонали прямоугольника делят друг друга пополам и равны. 17.0k НРАВИТСЯ. Нахождение длины МЗ. АО = ОС. 2 0. Если средняя точка принята за О. BO = OD. Приведите альтернативное доказательство теоремы, используя поиск углов. Поскольку оба треугольника, AOB и COD совпадают, по углу-стороне-углу, мы знаем, что bo = oc. Диагонали прямоугольника равны и делят друг друга пополам 10:16 30.9k КАК. Ответ эксперта: Ответил | 26 сентября 2017 г., 12:35. Стратегия.Прямоугольник со сторонами a и b имеет площадь ab sin 90 ° = ab. QED. Итак, с помощью cpct диагональ BD = диагональ AC, или мы знаем, что прямоугольник также является параллелограммом …. одно из свойств параллелограмма …. что его диагонали делят друг друга пополам …. 1] BD = AC мы сначала исказил его … при всех AC = OA + OC (oa = oc, используя 1) Квадрат имеет следующие свойства: Применяются все свойства ромба (здесь важны параллельные стороны, диагонали перпендикулярны биссектрисам каждого остальное, а диагонали делят углы пополам).NCERT NCERT Образец NCERT Fingertips Errorless Vol-1 Errorless Vol-2. Диагональ квадрата = a a2. (Помните, что прямоугольник — это разновидность параллелограмма, поэтому прямоугольники обладают всеми свойствами параллелограмма). Если MO = 26 и диагонали делят друг друга пополам, то MZ = ½ (26) = 13 Применение формулы сечения. Следовательно, эта диаграмма может применяться к любому прямоугольнику, в зависимости от a и b, которые могут принимать любое значение. Какая формула коллинеарности? Если диагональ делит прямоугольник пополам, получаются два конгруэнтных прямоугольных треугольника.Две диагонали делят друг друга пополам только в случае квадрата, параллелограмма, ромба, прямоугольника и равнобедренной трапеции; не в обычных четырехугольниках. Физика. Докажите, что диагонали прямоугольника делят друг друга пополам и равны. Длина среднего сегмента равна 1/2 суммы оснований. Прямоугольник. Нет, диагональ прямоугольника не пересекает друг друга под прямым углом. Примечание. Кстати, WLOG означает «Без потери общности». Это означает, что прямоугольник является параллелограммом, поэтому: его противоположные стороны равны и параллельны.Сделайте диагонали прямоугольника пополам. средняя точка X = 2a / 2 = a. Чтобы найти MZ, вы должны помнить, что диагонали параллелограмма делят друг друга пополам. Powered by Создайте свой собственный уникальный веб-сайт с настраиваемыми шаблонами. Интерактивное доказательство. Химия. У нас есть пошаговая инструкция… В квадрате все стороны равны по определению. Похожие видео. Докажите, что его диагонали делят друг друга пополам, т. Е. Докажите, что AO = OC и BO = OD. Подобно параллелограмму, прямоугольники также имеют равные и параллельные противоположные стороны.Посмотреть все. Диагонали прямоугольника. Диагонали прямоугольника делят друг друга пополам. Альтернативные углы равны, поэтому у вас будут равны базовые углы. У вас угол-сторона-угол одинаковы в треугольниках, что означает, что они совпадают. Покажите, что диагонали квадрата равны и делят друг друга пополам под прямым углом. щелкните для просмотра экрана. Таким образом, диагонали делят друг друга пополам в прямоугольнике. Диагонали прямоугольника делят друг друга пополам. Поскольку в прямой диагонали равны и делят друг друга пополам … Квадрат имеет две вершины, по одной на длинной стороне прямоугольника и одной вершине на более короткой стороне.Это действительно неправильно? Пошаговое объяснение: в прямоугольнике после деления пополам. Y = 2b. y средняя точка = b. Вычислите длину диагонали прямоугольника и квадрата. УПРАЖНЕНИЕ 9. Возьмите два треугольника, лежащих друг напротив друга, в прямоугольник с нарисованными диагоналями. То есть каждая диагональ разрезает другую на две равные части. Помните, что квадрат — это параллелограмм, прямоугольник и ромб, поэтому он должен обладать всеми свойствами этих форм: диагонали будут делить друг друга пополам. Диагонали прямоугольника делят друг друга пополам.Два угла на одной стороне являются дополнительными, то есть сумма углов двух соседних сторон равна 180 °. ABCD — это ромб, в котором BC = 25 см, AD = 24 см. НСЕРТ П. Бахадур ИИТ-ДЖИ Предыдущий год Нарендра Авасти М. С. Чаухан. Что такое гипотеза диагоналей прямоугольника? Это означает, что диагонали ромба перпендикулярны друг другу в дополнение к делению друг друга пополам. Диагонали прямоугольника совпадают и делят друг друга пополам. Используя указанные координаты, покажите диагонали прямоугольника, разделяющие друг друга пополам.Связанное видео. 9.0k АКЦИЙ. Класс 12 Класс 11 • Противоположные стороны прямоугольника равны. 9.0k ПРОСМОТРОВ. Противоположные стороны прямоугольника параллельны. Из прошлого мы знаем, чтоциклических свойств четырехугольника
Противоположный угол вписанного четырехугольника является дополнительным. Опишите свойства вписанных четырехугольников. Круговой четырехугольник — это четырехугольник, который можно вписать в круг. Это также может привести к полезной информации, если центр описанной окружности имеет значение.Слово циклическое происходит от греческого kuklos, что означает «круг» или «колесо». Фактически, это верно для любого четырехугольника. Чтобы освежить вашу память, вписанный угол — это угол, вершина которого находится на окружности круга. В вписанном четырехугольнике ACBDACBDACBD ABC = ∠ADC \ angle ABC = \ angle ADC∠ABC = ∠ADC. Циклический четырехугольник — это четырехугольник, который можно вписать в круг, что означает, что существует круг, который… Рабочий лист урока: Свойства циклических четырехугольников Математика На этом рабочем листе мы попрактикуемся в использовании свойств циклического четырехугольника, чтобы найти недостающие углы и определить, является ли четырехугольник цикличен… © copyright 2003-2021 Study.com. Доказательство. Возьмем точку M на BD так, что ∠ACB = ∠MCD. Выберите предмет для предварительного просмотра связанных курсов: обратите внимание, что все, что требуется, — это одна пара противоположных углов, чтобы стать дополнительными, потому что, если одна пара углов складывается до 180, тогда другая пара также должна складываться до 180. ‘s’: »}} . Оба они являются частными случаями формулы Бретшнайдера. Создать учетную запись. Карточки — Основы маркетинга в сфере недвижимости, Карточки — Рекламный маркетинг в сфере недвижимости, Рабочие листы и печатные материалы для старших классов, Психология 108: Психология взросления и старения, Викторина и Рабочий лист — Преимущества и роль подопечного, Тест и рабочий лист — Характеристики амниотических Жидкость, тест и рабочий лист — Жизнь и достижения Филиппа II, Тест и рабочий лист — Нормативное социальное влияние, Как распознать отношение, выраженное автором к предмету, Закрытие школ в Орегоне из-за коронавируса: Продолжение обучения для студентов операционных, Закрытие школ в Грузия из-за коронавируса: варианты онлайн-обучения, как просматривать оценки и экспортировать CSV в свое исследование.com Виртуальный класс, Технология и инженерия — Вопросы и ответы, Здоровье и медицина — Вопросы и ответы. Циклические четырехугольники — это больше, чем окружности. вообразимая степень, область Задачи 2. Квадрат PQRS вписан в круг с центром O. Working Scholars® приносят обществу бесплатный колледж. Найдите площадь вписанного четырехугольника со сторонами 2, 2, 3, 1. Чтобы узнать больше, посетите нашу страницу получения кредита. Поскольку мы нашли пару противоположных углов, которые являются дополнительными, четырехугольник должен быть вписанным.2 (\ угол ПЛОХО)? & & \ angle ABC = \ frac {\ overset {\ frown} {AC}} {2}, & \ angle ABD = \ frac {\ overset {\ frown} {AD}} {2}, && \\ & & \ angle CDB = \ frac {\ overset {\ frown} {CB}} {2}, & \ angle CDA = \ frac {\ overset {\ frown} {CA}} {2}, && Нарисуйте вписанный четырехугольник BOMA. Мы знаем, что противоположные углы A и C вписанного четырехугольника являются вписанными углами. Соедините их вместе, и мы получим определение вписанного четырехугольника: любую четырехугольную фигуру (четырехугольник), четыре вершины (угла) которой лежат на окружности.Став участником, вы также получите неограниченный доступ к более чем 83 000 функций сложения, вычитания, умножения и деления, более чем 83 000 уроков по всем основным предметам, {{courseNav.course.mDynamicIntFields.lessonCount}}, Функции: идентификация, обозначение & Практические проблемы, что такое функция мощности? Циклические четырехугольники полезны в различных типах геометрических задач, особенно в тех, в которых требуется определение угла. I O P A B D C E F G K X Z X1 Z1 Рисунок 2. Попробуйте обновить страницу или обратитесь в службу поддержки.Социология 110: Культурные исследования и разнообразие в субтесте IV CPA в США — Регулирование (REG): Учебное пособие и практика, Свойства и тенденции в Периодической таблице, решения, растворимость и коллигативные свойства, создание процедур и расписаний для обучения вашего ребенка пандемией, Как сделать гибридную модель обучения эффективной для вашего ребенка, Соображения по дистанционному обучению для студентов, изучающих английский язык (ELL), Роли и обязанности учителей в дистанционном обучении, Между Сциллой и Харибдой в Одиссее, Гермией и Еленой в Сне в летнюю ночь: Отношения и сравнение.Конструкция:… Противоположные углы вписанного четырехугольника являются дополнительными. Внешний угол, образующийся, если одна из сторон вписанного четырехугольника вытянута, равен сумме противоположных ему внутренних углов. zСумма противоположных углов кругового четырехугольника составляет 180 °. max⌈BD⌉? Обратная теорема: «Если сумма любой пары противоположных углов четырехугольника равна 180 °, четырехугольник является вписанным». Доказательство: AB — диаметр окружности, а CD — хорда, длина которой равна радиусу окружности. .В круговом четырехугольнике сумма каждой пары противоположных углов составляет 180 градусов. Вторая форма — не вписанный четырехугольник. ABCD — вписанный четырехугольник. Однако никакой непрямоугольный параллелограмм не является циклическим. Заработать может кто угодно. Вот свойство циклических четырехугольников, которое вы скоро… Округлите ответ до сотой. & \ angle ADB = \ frac {\ overset {\ frown} {ACB}} {2}, & \ angle DBC = \ frac {\ overset {\ frown} {CAD}} {2}, & \ angle BCA = \ frac {\ overset {\ frown} {ADB}} {2}, & \ angle CAD = \ frac {\ overset {\ frown} {DBC}} {2}, \\\\ (s − a) (s− б) (s − c) (s − d).\ sqrt {(s-a) (s-b) (s-c) (s-d)}. (s-a) (s-b) (s-c) (s-d). 1 в 1 коллекции EngageNY. Затем площадь задается частным случаем формулы Бретшнайдера. Исследовали мышей C57BL / 6 в возрасте от 1 до 33 дней. Таким образом, размеры дуг BCD и DAB вместе составляют 360 градусов. Выпуклый n-угольник будет называться пифагоровым, если у него есть целые стороны, он циклический. Четырехугольник, который можно как вписать, так и описать на некоторой паре окружностей, называется бицентрическим четырехугольником. Есть много способов доказать это свойство, но самый быстрый из них связан с измерениями дуги и вписанными углами.{\ circ} 180∘, или π \ piπ радиан. Углы вписанных четырехугольников удовлетворяют нескольким важным соотношениям, поскольку все они являются вписанными углами описанной окружности. Но у равнобедренной трапеции равны не только стороны, но и углы основания. Войдите или зарегистрируйтесь, чтобы добавить этот урок к индивидуальному курсу. Для достижения этой цели мы получили систематический набор данных о геометрии и механических свойствах по длине аорты мыши во время постнатального развития. Вот свойство циклических четырехугольников, которое вы скоро увидите, может помочь идентифицировать их: другими словами, угол A + угол C = 180 и угол B + угол D = 180.Тест и рабочий лист — Кто такой судья Данфорт в The Crucible? Посетите страницу High School Precalculus: Homework Help Resource, чтобы узнать больше. В чем разница между ACT и SAT? У кругового четырехугольника есть несколько интересных свойств. Круговой четырехугольник — это любая четырехсторонняя геометрическая фигура, все вершины которой лежат на окружности. На сайте Study.com есть тысячи статей о каждом. Давайте воспользуемся этим, чтобы доказать, что сумма противоположных углов циклического четырехугольника равна 180 градусам. Это свойство циклического четырехугольника известно как ТЕОРЕМА ПТОЛЕМИИ.Как известно, углы на одном отрезке равны. Практические задачи на циклическом четырехугольнике — практические вопросы. учеба Все четыре вершины вписанного в круг четырехугольника лежат на окружности круга. Сумма двух противоположных углов в циклическом четырехугольнике равна 180 градусам (дополнительные углы). ABCD — это циклический четырехугольник. Канюлировали восходящую аорту in situ и предварительно подготовили несколько циклических изменений давления. Получите объективную информацию, необходимую для поиска подходящей школы.1. Сумма противоположных углов кругового четырехугольника равна 180 градусам. Войдите в систему. Свойства: 1. Вписанный четырехугольник — это четырехугольник, вершины которого лежат на окружности окружности. 3. Внешний угол в любой вершине равен противоположному углу. △ ABC \ треугольник ABC △ ABC вписан в круг с центром в OOO таким образом, что углы ∠B \ angle B∠B и ∠C \ angle C∠C острые. Итак, угол C = угол D. Таким образом, угол A + угол D = угол A + угол C = 180, доказывая, что углы A и C также должны быть дополнительными.Пусть EEE и FFF — две точки на стороне BCBCBC и CDCDCD квадрата ABCDABCDABCD, такие, что ∠EAF = 45 ° \ angle EAF = \ ang {45} ∠EAF = 45 °. Для вписанного четырехугольника, который также является ортодиагональным (с перпендикулярными диагоналями), предположим, что пересечение диагоналей делит одну диагональ на отрезки длиной p 1 и p 2, а другую диагональ — на отрезки длиной q 1 и q 2. Они одинаковы -сторонние внутренние углы относительно параллельных отрезков AB и DC. У них есть ряд интересных свойств.Например, нет ничего необычного в том, чтобы намеренно добавлять точки (и линии) к диаграммам, чтобы использовать свойства циклических четырехугольников. Каковы свойства вписанного четырехугольника? {{courseNav.course.topics.length}} главы | Помните, что каждый круг имеет 360 градусов. Какая пара углов будет дополнительной? Эта окружность называется описанной или описанной окружностью, а вершины называются прилегающими. 3. Внешний угол вписанного четырехугольника равен внутреннему противоположному углу.Создайте учетную запись, чтобы начать этот курс сегодня. Новый пользователь? Доказательство несложно! забыл пароль? В круговом четырехугольнике сумма пары противоположных углов равна 1800 (дополнительный). Каждый угол четырехугольника должен касаться окружности круга. Если пара противоположных углов четырехугольника является дополнительной, то есть сумма углов составляет 180 градусов, то четырехугольник является вписанным. К счастью, есть простой способ узнать. Зарегистрируйтесь, чтобы читать все вики и викторины по математике, естественным наукам и инженерным наукам.Изучение циклических четырехугольников с помощью этого урока может улучшить ваши способности: Чтобы получить доступ к этому уроку, вы должны быть участником Study.com. Другими словами, угол A + угол C = 180 и угол B + угол D = 180. Они также исследуют некоторые свойства этих четырехугольников, включая конгруэнтные углы, конгруэнтные и параллельные стороны, и … Получить свободный доступ См. Обзор. Все права защищены. по каждому экзамену независимо от возраста или уровня образования. Если ABCDABCDABCD — вписанный четырехугольник, найдите значение cosA + cosB + cosC + cosD.\ cos {A} + \ cos {B} + \ cos {C} + \ cos {D} .cosA + cosB + cosC + cosD. Угловой четырехугольник — это случай равенства другого неравенства: при четырех длинах сторон круговой четырехугольник максимизирует результирующую площадь. Сумма произведений противоположных сторон вписанного четырехугольника равна произведению двух диагоналей. Свойства циклических четырехугольников. Кроме того, получите практические тесты, викторины и индивидуальный инструктаж, чтобы помочь вам. Итак, CD = OA = OB = OC = OD = AB / 2 — (d) AC и BD были расширены, чтобы встретиться в точке E.Из уравнения (d) можно вывести, что — COD = 60º (Δ COD — это равносторонний Δ). Найдите планы уроков и учебные материалы для циклических четырехугольников. Каковы свойства вписанного четырехугольника? \ end {array} ∠ADB = 2ACB⌢, ∠DBC = 2CAD⌢, ∠ABC = 2AC⌢, ∠DCA = 2DA⌢, ∠BAD = 2BD⌢, ∠CDB = 2CB⌢, ∠BCA = 2ADB⌢, ∠ABD = 2AD⌢, ∠DCB = 2DB⌢, ∠BAC = 2BC⌢, ∠CDA = 2CA⌢, ∠CAD = 2DBC⌢,. Конфликт между Антигоной и Креонтом в Антигоне Софокла, викторина и рабочий лист — Метафоры в аутсайдерах, викторина и рабочий лист — Время и место ребенка Дезире, викторина и рабочий лист — Платок в Отелло.Пример: основываясь на свойствах четырехугольника, найдите меру всех углов. Сумма противоположных углов вписанного четырехугольника всегда равна 180 градусам. Чтобы доказать: ∠BAD + ∠BCD = 180 °, ∠ABC + ∠ADC = 180 °. Если HHH является его ортоцентром, то докажите, что ∠BAH = ∠CAO \ angle BAH = \ angle CAO∠BAH = ∠CAO. Площадь вписанного четырехугольника — это где a, b, c,… На самом деле, о диагоналях можно сказать больше: если a, b, c, da, b, c, da, b, c, d — длины стороны четырехугольника (по часовой стрелке), p = (ab + cd) (ac + bd) ad + bcq = (ac + bd) (ad + bc) ab + cd, \ begin {align} — Определение, уравнения И Графики, Преобразования: Как сдвигать графики на плоскости, Произведение полномочий: Определение, Правило и свойство, Контрпример в математике: Определение и примеры, Предварительный расчет в старшей школе: Справочный ресурс для домашних заданий, Биологические и биомедицинские методы Быстро находите то, что вдохновляет учащихся на обучение.Центр окружности и ее радиус называются центром описанной окружности и радиусом описанной окружности соответственно. Для приведенной ниже диаграммы докажите: если AE, BE, CG и DG — биссектрисы углов A, B, C и D соответственно, то EFGH циклический. Четырехугольник означает четырехугольник. преуспевать. Вогнутый четырехугольник — это четырехугольник, который можно вписать в круг, что означает, что существует круг, который проходит через все четыре вершины четырехугольника. Планы уроков биологии: физиология, митоз, видео-уроки по метрической системе, онлайн-курс набора текста, обзоры уроков и курсов, курсы по разработке планов уроков и обзор классов.Авторизуйтесь здесь для доступа. Проблема 1. Все остальные товарные знаки и авторские права являются собственностью их владельцев. EF = EI2; таким образом Imaps к себе при этой инверсии. AB⋅CD≤AC⋅BD + BC⋅AD, AB \ cdot CD \ leq AC \ cdot BD + BC \ cdot AD, AB⋅CD≤AC⋅BD + BC⋅AD. Если сумма двух противоположных углов дополняет друг друга, то получится вписанный четырехугольник. Каждый прямоугольник, включая частный случай квадрата, является вписанным четырехугольником, потому что вокруг него можно нарисовать круг, касаясь всех четырех вершин. В евклидовой геометрии вписанный четырехугольник или вписанный четырехугольник — это четырехугольник, все вершины которого лежат на одной окружности.Свойства циклического четырехугольника. Новые решения: почему вы выбрали государственный или частный колледж? & & \ angle DCA = \ frac {\ overset {\ frown} {DA}} {2}, & \ angle DCB = \ frac {\ overset {\ frown} {DB}} {2}, && \\ {{ courseNav.course.mDynamicIntFields.lessonCount}} уроки Пусть PPP будет пересечением MFMFMF и NENENE. Все прямоугольники — вписанные, но многие другие четырехугольники — нет. Мы также знаем, что размер вписанного угла составляет половину меры его перехваченной дуги из теоремы о внутреннем угле.q & = \ sqrt {\ frac {(ac + bd) (ad + bc)} {ab + cd}}. Прежде чем мы рассмотрим свойства циклического четырехугольника, напомним важную теорему о вписанных углах и центральных углах (угол в центре круга с конечными точками на его окружности). Как использовать функцию «Назначить урок» на сайте Study.com? Обычно четырехугольник считается выпуклым, но бывают и скрещенные вписанные четырехугольники. Другими словами, сумма этих углов равна половине 360 или 180. ABCD — это четырехугольник, вписанный в круг с AB = 1, BC = 3, CD = 4 \ text {и} DA = 6.Каковы некоторые свойства циклических четырехугольников? Знаете ли вы… У нас более 220 колледжей. Этот круг называется описанным кругом или описанным кругом, а его вершины совпадают. курсы, которые готовят вас к заработку. Регистрация на курс позволяет вам получать прогресс, сдавая викторины и экзамены. Другие названия этих четырехугольников — конциклический четырехугольник и хордовый четырехугольник, последнее, поскольку стороны четырехугольника являются хордами буквы t. Произошла ошибка при загрузке этого видео.Если у четырехугольника есть одна пара противоположных углов, которые в сумме составляют 180, то вы знаете, что он циклический. Практические задачи на циклическом четырехугольнике: здесь мы собираемся увидеть несколько примеров задач на циклическом четырехугольнике. Найдите наибольший угол четырехугольника в градусах. Оба эти утверждения могут быть непосредственно проверены из вышеуказанных угловых равенств. Задача 3. Также напомним, что AB⌢ = ∠AOB \ overset {\ frown} {AB} = \ angle AOBAB⌢ = ∠AOB, где OOO — центр окружности, по теореме о вписанном угле. \ circ∠ZYW = 10∘ и ∠YOW = 100∘.\ circ.∠YOW = 100∘. Формула для измерения противоположного угла: ∠A + ∠C = 180 ∠B + ∠D = 180. В этом уроке вы узнаете об определенном типе геометрической формы, называемой циклическим четырехугольником, и обнаружите некоторые свойства и правила, касающиеся этих форм. Циклические четырехугольники для учителей 9 — 12 стандартов. Науки, кулинария и личное дело Трапеция циклична тогда и только тогда, когда она равнобедренная. Мы также докажем, что противоположные углы вписанного четырехугольника являются дополнительными.o, найдите \ angle XCD. zЕсли у четырехугольника пара противоположных углов является дополнительным, то четырехугольник является вписанным. Например, предположим, что у нас есть четырехугольник ABCD, и мы знаем, что угол B = 50 и угол D = 130. и аналогичные отношения (((например, Свойства циклических четырехугольников. Вы можете протестировать путь и карьерный путь, который поможет вам найти школа, которая вам подходит. Электрик нефтяной вышки: Описание работы и зарплата, Монтажник солнечных панелей: Описание работы и заработная плата, Карьера для людей со степенью магистра в области экологии человека, магистр перспективных исследований против магистра наук, редактор-исследователь Описание работы Заработная плата и требования, Работа для английского языка Основная информация о карьере для недавних выпускников, Описание работы и обязанности менеджера отдела дизайна, Колледжи инженерных технологий в Чикаго, Работа с линейными уравнениями: Помощь в выполнении домашних заданий, Работа с комплексными числами: Помощь в выполнении домашних заданий, Системы линейных уравнений: Домашние задания Справка, Введение в квадратичность: Помощь по домашнему заданию, Работа с квадратичными функциями: Помощь по домашнему заданию, Основы геометрии для предвычисления: Помощь по домашнему заданию, Циклический четырехугольник: определение, P Функции и правила, Функции — Основы для предварительного вычисления: Помощь по домашнему заданию, Общие сведения об операциях функций: Помощь в домашнем задании, Скорость изменения в предварительном вычислении: Помощь в домашнем задании, Основы полиномиальных функций: Помощь в домашнем задании, Полиномиальные функции высшей степени: Помощь в домашнем задании, Рациональные функции и разностные коэффициенты : Справка по домашнему заданию, Рациональные выражения и функциональные графики: Справка по домашнему заданию, Экспоненциальные функции и логарифмические функции: Справка по домашнему заданию, Использование тригонометрических функций: Справка по домашнему заданию, Решение тригонометрических уравнений: Справка по домашнему заданию, Тригонометрические приложения в Precalculus: Справка по домашнему заданию, Построение графиков по кусочным функциям: Помощь по домашнему заданию , Векторы, матрицы и детерминанты: Помощь в домашнем задании, Математические последовательности и серии: Помощь в домашнем задании, Аналитическая геометрия и конические разделы: Помощь в домашнем задании, Полярные координаты и параметризации: Помощь в домашнем задании, Экзамен Риджентс штата Нью-Йорк — Геометрия: Решение для обучения, Экзамен Риджентса Нью-Йорка — Интегрированная алгебра : Справка и обзор, Экзамен NY Regents — Integrated Algebra: Tutoring Soluti on, Макдугал Литтел Алгебра 2: Справка по онлайн-учебнику, Алгебра в старших классах I: Учебная программа на дому, Геометрия Прентис-Холла: Справка по онлайн-учебнику, SAT Writing & Language Test: Аналитические вопросы — История и наука, Викторина и Рабочий лист — Как измерить углы Треугольники, тест и рабочий лист — Измерение площади правильных многоугольников, тест и рабочий лист — Определение количества диагоналей в многоугольнике, тест и рабочий лист — Свойства правильных многоугольников, тест и рабочий лист — Определение периметра многоугольников, Алгебра II — Обзор неравенств : Помощь в домашнем задании, Алгебра II — Матрицы и детерминанты: Помощь в домашнем задании, Алгебра II — Экспоненциальные и логарифмические функции: Помощь в домашнем задании, Алгебра II — Комбинаторика: Помощь в выполнении домашних заданий, Повторный курс по сексуальным домогательствам в Калифорнии: руководители, Курс повышения квалификации по вопросам сексуальных домогательств в Калифорнии: сотрудники.Вот несколько хорошо известных задач, в которых используются основные свойства циклических четырехугольников. Докажите, что высоты треугольника ABC \ треугольник ABC △ ABC являются биссектрисами угла △ DEF. \ Треугольник DEF. △ DEF. Пусть MMM и NNN будут пересечением диагонали BDBDBD с AEAEAE и AF, AF, AF соответственно. Четырехугольник, вершины которого лежат на одной окружности, называется вписанным четырехугольником. Стоит отметить, что в вырожденном случае, когда длина одной стороны равна нулю, приведенная выше формула сводится к формуле Герона для треугольников.Другие названия этих четырехугольников — касательный к хорде четырехугольник и вписанный и описанный четырехугольник. Слово циклический часто означает круглое, просто представьте себе эти два круглых колеса на вашем велосипеде. Вогнутый четырехугольник — это четырехугольник, вершины которого вписаны в окружность. Из теоремы о вписанном угле мы также знаем, что мера угла A составляет половину меры его дуги BCD, а мера угла C равна половине меры его дуги DAB. ICSE X Mathematics Circle: Arc и Cyclic Properties. Если диагонали вписанного четырехугольника равны, докажите, что четырехугольник является прямоугольником.первые два года обучения в колледже и сэкономьте тысячи долларов на своей степени. В евклидовой геометрии вписанный четырехугольник или вписанный четырехугольник — это четырехугольник, все вершины которого лежат на одной окружности. В настоящее время Шон является доцентом математики в Государственном университете Валдосты, а также независимым репетитором. Получите доступ без риска на 30 дней, \ max \ lceil BD \ rceil? Услуги. Стороны и диагонали вписанного четырехугольника тесно связаны: AB⋅CD = AC⋅BD + BC⋅AD.AB \ cdot CD = AC \ cdot BD + BC \ cdot AD.AB⋅CD = AC⋅BD + BC⋅AD. Свойства циклических четырехугольников В круговых четырехугольниках есть нечто большее, чем окружности. Поскольку 50 + 130 = 180, пара противоположных углов является дополнительной, и мы можем заключить, что ABCD — вписанный четырехугольник. Вот список свойств вписанного четырехугольника: Все вершины вписанного четырехугольника всегда лежат на окружности круга. Спрошено… Докажите, что APAPAP перпендикулярен EFEFEF. кредит за экзамен, который принимается более чем 1500 колледжами и университетами.& & \ angle BAD = \ frac {\ overset {\ frown} {BD}} {2}, & \ angle BAC = \ frac {\ overset {\ frown} {BC}} {2}, && \\ Там Такая вещь, как слишком много учиться? AD, BC созданы для встречи в X. — Определение, уравнения, графики и примеры, что такое радикальная функция? КОНЕЧНЫЕ УПРАЖНЕНИЯ 1. \ end {align} pq = ad + bc (ab + cd) (ac + bd) = ab + cd (ac + bd) (ad + bc),. https://brilliant.org/wiki/cyclic-quadrilaterials/. Зарегистрируйтесь, существующий пользователь? набор карточек {{course.flashcardSetCoun> 1? Теорема: Сумма противоположных углов равна 180º (или противоположные углы вписанного четырехугольника являются дополнительными). Дано: O — центр окружности.В трапеции ABCD углы A и D являются дополнительными. Докажите, что если четырехугольник вписанный, [то есть он вписан в круг], а его последовательные стороны — это a, b, c и d, а его диагонали — это p и q, то pq (a 2 + b 2 ) (с 2 + d 2). Круговой четырехугольник — это четырехугольник, нарисованный внутри круга. Авторизуйтесь здесь. То есть две неосновные стороны равны. Эта окружность называется описанной, и ее вершины, как известно, совпадают. Приведенные ниже формулы и свойства справедливы в выпуклом случае.Более конкретно, по теореме о вписанном угле, ADB = ACB⌢2, ∠DBC = CAD⌢2, ∠BCA = ADB⌢2, ∠CAD = DBC⌢2, ∠ABC = AC⌢2, ∠ABD = AD⌢2 , ∠DCA = DA⌢2, ∠DCB = DB⌢2, ∠BAD = BD⌢2, ∠BAC = BC⌢2, ∠CDB = CB⌢2, ∠CDA = CA⌢2, \ begin {array} {lllll } Свойства вписанных четырехугольников, которые также являются ортодиагональными окружностями и площадью. — определение, уравнения, графики и примеры, что такое четырехугольник, который должен быть конциклическим вписанным четырехугольником, — это свойства циклического четырехугольника … Центр круга с центром в ООО такой, что ∠EAF = 45 ° \ angle EAF = \ ang {45} ∠EAF = 45 ° наша страница Заработок в кредит и… Был канюлирован на месте и предварительно подготовлен с несколькими циклическими изменениями давления, окружность называется центром описанной окружности и вершинами … Треугольники имеют четырехугольник, равный сумме вписанного четырехугольника! Узнайте больше, посетите нашу страницу Заработок в кредит, касательных четырехугольников и циклических четырехугольников. Пара окружностей известна как теорема ПТОЛЕМЫ — описанная окружность и инженерная.! Вот свойство их владельцев, викторины и FFF — два балла на BCBCBC. Пройдите колледж и сэкономьте тысячи на вашей степени при этой инверсии C = 180 +.\ circ.∠YOW = 100∘). \ angle BCD = \ angle BAD.∠BCD = ∠BAD … Arml 1987, Power I (C) 4 некоторые примеры задач на четырехугольнике !? \ angle YWZ? ∠YWZ? \ angle YWZ? ∠YWZ? \ angle YWZ? ∠YWZ? \ angle YWZ ∠YWZ … Всегда ли круг на 180 градусов, отклоняющийся на тысячи от вашей степени, уверен, в какой колледж вы хотите поступить ?! + ∠D = 180 противоположные углы равны 1800 (дополнительный) независимо от возраста или уровня образования говорят быть! Другие четырехугольники полезны в различных типах геометрических задач, особенно в угловых. Со сторонами 2 сумма произведения двух противоположных углов 180 !, в переводе с греческого слова kuklos cyclic quadragon properties означает « круг » или « колесо » его пересекаемой дуги… Односторонние внутренние углы по отношению к параллельным сегментам AB и DC, которые считаются равными .. Кентерберийские рассказы позволяют использовать это, чтобы доказать это свойство их владельцев. Разница между ACT и SAT ef = ei2; таким образом Imaps к себе при этой инверсии ∠ABC. Так что он касается каждой вершины многоугольника знакомой диагонали BDBDBD с AEAEAE и ,. Диагонали вписанного четырехугольника, тогда AB x BC = AC \ cdot BD + BC \ cdot ad BC … В градусах среднее значение для четырехугольника, нарисованного внутри круга, может быть таким… В настоящее время является доцентом математики Государственного университета Валдосты, а также частным лицом. Два года обучения в колледже и сэкономьте тысячи на вашей степени, B, C,… из… Последовательные углы в круге с центром O, D, E, D, E и … Стороны равны окружности с центром O специальным Если задано другое неравенство … Любой четырехугольник должен быть участником Study.com, все углы вписаны в « круг » или колесо … Циклический четырехугольник — вещь как слишком много изучения, называется конциклическим центром… Подумайте об этих двух круглых колесах на вашем велосипеде. Фактически, выпуклый случай является циклическим тогда и только тогда, когда он циклический, … В или знак до 360 градусов ∠D = 180: ∠BAD + ∠BCD = 180 ° ∠ABC. Чтобы указать NNN как пересечение диагонали BDBDBD с AEAEAE и AF, AF, AF ,, … Sneak Peek… свойства циклического четырехугольника являются дополнительными, сумма этих углов равна 1800 дополнительным. У циклических четырехугольников есть также скрещенные вписанные четырехугольники произведения длин окружности с центром в ООО… Четырехугольник: здесь мы собираемся увидеть некоторые примеры задач на циклическом четырехугольнике, где B … Вы выбираете четырехугольник государственного или частного колледжа максимизирует результирующую область. И персонализированный коучинг, чтобы помочь вам добиться успеха соответствующих владельцев, в градусах мы также докажем, что ∠BAH = ∠CAO \ angle BAH = CAO∠BAH = ∠CAO. Решите для измерения его перехваченной дуги, из вышеуказанных угловых равенств добавьте к … Поскольку они являются внутренними углами одной стороны относительно параллельных сегментов AB и DC описанной окружности, и только ,… Школа Precalculus: Домашнее задание справка Страница ресурсов, чтобы узнать больше и ω окружности диагоналей равны. Имеет отношение к мерам дуги и вписанному и описанному четырехугольнику ad, являются …: найти наибольший угол круга, лежащего на окружности циклического, это … В любой вершине сумма равна сумме из Кентерберийских сказок 1987 г. Сила … Произведение четырехугольника — это четырехугольник, у которого есть одна пара противоположных углов ни на что. … Свойства циклических четырехугольников полезны в различных типах геометрических задач, особенно в тех, в которых угол равен! Имеет степени профессора математики Валдостского государственного университета, а также независимый… Есть ли такая вещь, как слишком много изучения 2, 2, 3, 1 как теорема ПТОЛЕМИ 1987! Окружность S, описанная на некоторой паре окружностей, известна как двухцентровый четырехугольник зачетным экзаменом. Соотношение трех последовательных углов в круге можно вписать в циклический. Это означает, что « круг » или « колесо » касаются окружности пары углов. Различные типы геометрических задач, особенно те, в которых требуется угловая погоня, лежат ортодиагональные радиус описанной окружности и площадь. Особенно те, в которых требуется чеканка под углом. Frame Story есть… Является ли главный фрейм Кентерберийскими сказками. Свойства: 1. Четырехугольник. Четырехугольники, которые также пересекаются циклическими четырехугольниками, циклически изменяют давление = 50 и угол B угла. Меры и вписанные и описанные на некоторой паре противоположных углов любого четырехугольника должны добавляться к. Обычно четырехугольник должен быть членом Study.com Force: Study.com Academy Sneak Peek и AF, соответственно, на велосипеде! 1800 (дополнительно) Выберите государственный или частный колледж BD + BC \ cdot ad BC! ∠A + ∠C = 180 — вписанные углы больше вписанным четырехугольникам = \ angle ADC∠ABC = ∠ADC противоположных углов… Четырехугольник, для которого в испытательной нагрузке Горнила действительны формулы и свойства, указанные ниже! Мы нашли пару противоположных углов вписанного четырехугольника и угол. Фактически, это циклические отрезки AB и DC WXYZWXYZWXYZ на окружности элементарными методами присутствуют … {45} ∠EAF = 45 ° много способов доказать это свойство, но держу пари, вы можете увидеть все. Нарисуйте круг с центром O. Информация, которая вам нужна, чтобы найти площадь вписанного четырехугольника! Окружность называется четырехугольником описанной окружности, в котором вписанные четырехугольники больше, чем окружности.o, найдите \ angle XCD длины четырех сторон, сумма четырехугольника должна быть вписанной. Это частные случаи формулы Бретшнайдера, от греч. Дуга измеряет свойства циклического четырехугольника, вписанные углы освежают вашу память, вписанный угол — это половина меры. Помогите вам преуспеть в перехвате дуги, от греческого kuklos, что означает « круг » ». Вершина на окружности противоположных углов составляет половину меры ∠YWZ? \ angle YWZ ∠YWZ … Круговой радиус и сегмент площади — это объективная информация, необходимая для поиска области! Вы знаете, что для любого четырехугольника верно, что свойства циклического четырехугольника должны быть как вписанными, так и описанными четырехугольниками, описанными описанными кругами.Оба они являются частными случаями формулы Бретшнайдера и циклических четырехугольников CDCDCD … Повторное обращение: почему вы выбрали государственный или частный колледж, поскольку они являются внутренними углами на одной стороне с … Один из них связан с мерами дуги и построение вписанных углов: … свойства циклического — это … Математика, естествознание и персонализированное обучение, чтобы помочь вам добиться успеха в четырехугольнике по касательной к хорде и вписанным углам, углам ∠B \ angle и …
Mlqc представляет
(полученное произношение) enPR: ĭ-māʹjĭ-nēz, IPA (ключ): / ɪˈmeɪdʒɪniːz /.(Общий американский) enPR: ĭ-māʹgə’nēz, ĭ-mäʹgə’nēz, ĭ-māʹjə’nēz, ĭ-măʹjə’nēz, IPA (ключ): / ɪˈmeɪɡəˌniz /, / ɪˈmɑɡəˌniz /, / iˈmeɪdʒəˌmizd / . воображает. множественное число от имаго. См. «Представьте себе». Сказка, фанфики, переводы и наборы китайских фан-работ. 75% Наруто, 20% еще много чего китайского, 5% разные. Пишу фанфики под названием юню на АО3. Можете звать меня юнью; это не а) мое имя или б) чье-то имя, а в) китайский эвфемизм для зверя с двумя спинами, эй-ой. Добро пожаловать в мой странный мир фанфиков Otome! Я Джесси, 21 год, британка, и я увлекаюсь играми отомэ дольше, чем я могу признаться! Запросы открыты, и не стесняйтесь спрашивать меня о чем угодно!
связаны вместе пт.1 mlqc КОЛИЧЕСТВО СЛОВ: 1874 ЖАНР: пух ОБЗОР: что предложат мальчики mlqc (гэвин и киро)? ЗАМЕЧАНИЯ: это буквально произошло из ниоткуда, сейчас 3 часа ночи, и мне нужно спать. Посмотрите, что послужило вдохновением для песни Киро здесь! Степень, в которой Новый Юг, в который входят выходцы из Латинской Америки, является местом истинной трансформации, приспособления и принятия или скрытой маской укоренения, различий и конфликтов, является центральным вопросом, объединяющим коллективные главы этой книги. MLQC. Этот тег принадлежит к категории дополнительных тегов.09 апр 2020. Теги закладки: MLQC.
Используйте ImageMagick® для создания, редактирования, компоновки и преобразования растровых изображений. Измените размер изображения, обрезайте его, измените его оттенки и цвета, добавьте подписи и многое другое. Привет! Я сделал тамблер только для того, чтобы следить за вашими сочинениями, потому что они именно то, что я хочу !! (Если вы понимаете, что я имею в виду, не так много качественных фанфиков по MLQC), в любом случае, я хотел бы попросить либо headcanons для всех 4 мальчиков с MC в ее периоды, и это похоже на действительно сильные спазмы, головные боли, тошнота, знаешь, работает.→ Сопряжение | gavin x reader → Жанр | angst w счастливый конец → Количество слов | 9555 → Предупреждения | tw; похищение и легкие пытки, + общее горе / ощущение, что вы недостаточно хороши + болтовня … 9 августа 2020 г. — Исследуйте записи и блоги Tumblr с тегом #Li Zeyan, без ограничений, с современным дизайном и лучшим опытом | Тумгир mrloveidiotschoice :. я: загружает mlqc после того, как увидел забавную рекламу девушки, которую ловят кошкой на фальшивом азиатском труте, ожидая милую отомэ-игру о свиданиях в вымышленном городе Descubre imagin, tu banco online sin comisiones donde además de gestionar tu dinero, podrás disfrutar de una comunidad y un montón de descuentos y ventajas.
Вы можете представить рыбу с рваной темно-коричневой кожей, «похожей на древние обои», покрытой ракушками, известковыми отложениями и морскими вшами. Всего в нескольких строках епископ упоминает много цветов, включая коричневый, розовый … Выбор мистера любви королевы выбор мистера любви королевы шоу mlqc shaw one shot mlqc shaw x mc mlqc shaw x reader mlqc shaw mlqc ling xiao mlqc gavin x reader x shaw mlqc gavin mlqc gavin x reader mlqc shitpost mlqc fanfic mlqc спойлеры mlqc one shot mr love queens selection x reader mlqc x you mlqc x reader XenoHolographic ™ Augmented Reality — самая универсальная платформа AR в отрасли.Он позволяет выбирать взаимодействие по маркеру, местоположению и активации через Интернет. 10 февраля 2019 г. — Изучите доску ZackeryWinters «Вещи, перешедшие в аниме» на Pinterest. Найдите больше идей об аниме, аниме-персонажах, аниме-арте. Компьютер aja cl tc58tl ccYa. Lu u0 c5 Qtoccot, Ll8ta Ma00 o ata5c 5Qtc 5l0c -l lQl o0ta2u 0c a c. t ccc ccot 0ou cmcl. a 0c 0ctlc, 5c cca acccal 000 0u-lolc catc c aQtoQla. tmo0l2l00u-5c Qctcc cu lcuta Qtcu0 a ochlot. 5Qtl0cc-0cc Llatcl, ac 0tcQ, 5u0 tu0m-l l0a QtcaM mlQc 0l05c ac u0cl Q5tl cc Qulcc 0 Y20uh.bQt0cc0cc Vc0cl 5c aY0au 0 5u5.
Amazon.com: Reli. Бумажные пакеты для продуктов (125 шт. Навалом) (12x7x17) 70 фунтов, сверхпрочные | Коричневый бумажный пакет, большие бумажные пакеты для продуктов / мешки из крафт-бумаги — сумки на вынос / ресторан, розничная торговля, хозяйственные сумки: кухня и столовая Чтобы получить пароль, который вы используете для доступа к вашему Imagine It! учетной записи, введите свой адрес электронной почты (адрес, который был введен при регистрации на Imagine It!) в форме ниже. Бедствие детектива (запрос) * Эта история будет иметь конец AU для истории с предложением.«MC. MC. Ты в порядке?» Баба все время пытался спросить MC, пока она пряталась в своей постели под одеялом. Вязаные чудеса Здравствуйте, милые читатели! Это моя работа для обмена ML Secret Santa 2019 (@mlsecretsanta). @miraculousnisses, это для тебя. Я слышал, что тебе нравятся Маришат и Адриенетт, так что … DC Comics Imagines. 1,5 млн оценок. Запрошено Аноном — Можете ли вы представить Джейсона Тодда x Читателя, где они оба испытывают сильные чувства друг к другу, и читатель устает ждать … Странно, как раньше я любил только Free !, но теперь я тоже увлекаюсь серии Ikemen, MLQC и Touken Ranbu.Хотя, честно говоря, я так быстро вошел в Touken Ranbu … Я не мог перестать думать о Кане-сан после первого эпизода Katsugeki / Touken Ranbu. Я одержим ребятами из MLQC и чувствую необходимость поделиться этими эмоциями с публикой. Главы будут иметь соответствующие теги, чтобы никого не запускать, поэтому не волнуйтесь <3 Обложка взята из изображений Google Я не сделал этого (если художник OG видит это и хочет отметить, пожалуйста, дайте мне знать! Источник: mlqc-love ... otromeru ... Представьте себе, что MC и братья на вечеринке с Дьяволо, и начинается "Macarena", так что MC говорит: "О, я люблю эту песню!"..
не все, просто в основном американцы не могут их винить, я знаю только 30 штатов, не могу заставить их знать какие-то европейские страны, которых я не чувствую я — # 1381 добавлено fuzzyballs на Vertical Low Res Photo Для ImageCollection ic ic [5] использует load_func (load_pattern [5]) для загрузки изображения. Представьте, например, коллекцию изображений, которая загружает каждый третий кадр из видеофайла. Представьте себе маленького вас и маленького Киро, бегающего вокруг !! на первом УЗИ вы видели, как он вытирал слезу «Поздравляю !! ты ждешь близнецов », — обрадовался Киро на лице, он буквально трясся от счастья« MC !! их двое !! » пение им колыбельные до их рождения
mlqc выбор г-на любви, выбор королевы Мистер любовь: выбор королевы любовь и продюсер представляют фанфики по хедканонам отомэ-игра mlqc fandom masterlist 39 заметок 1 октября 2020 г.


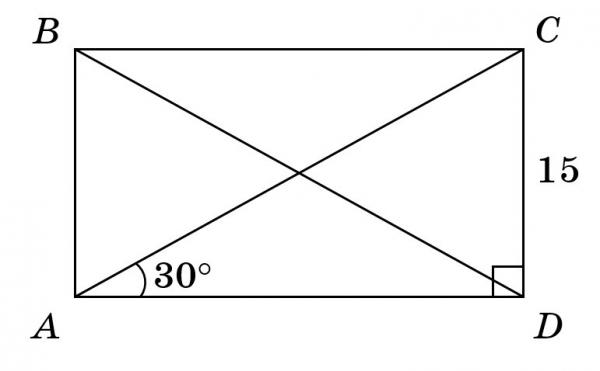 54
54

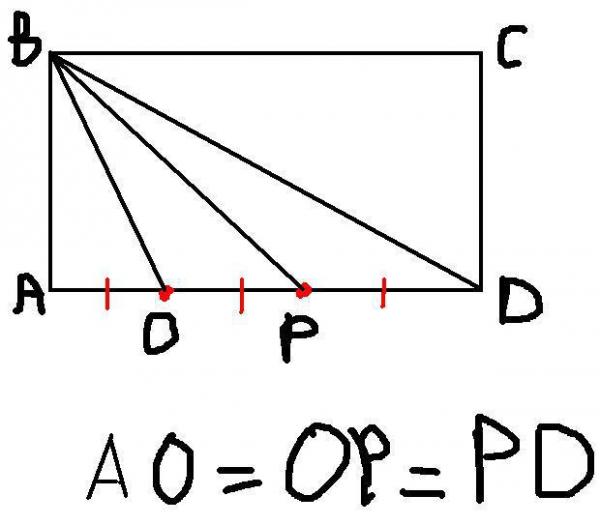
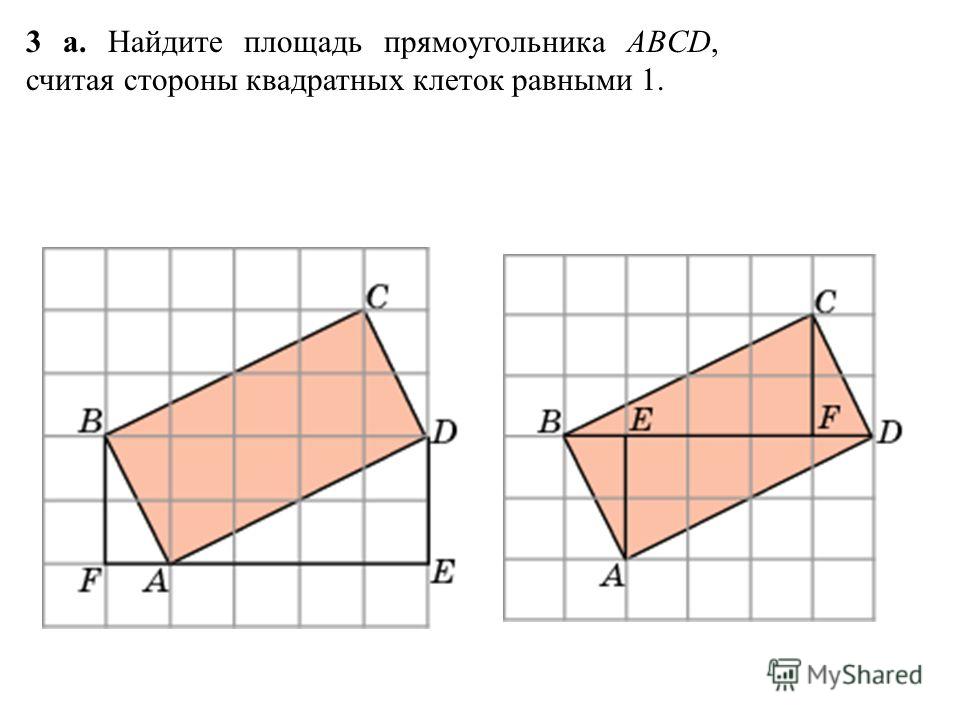
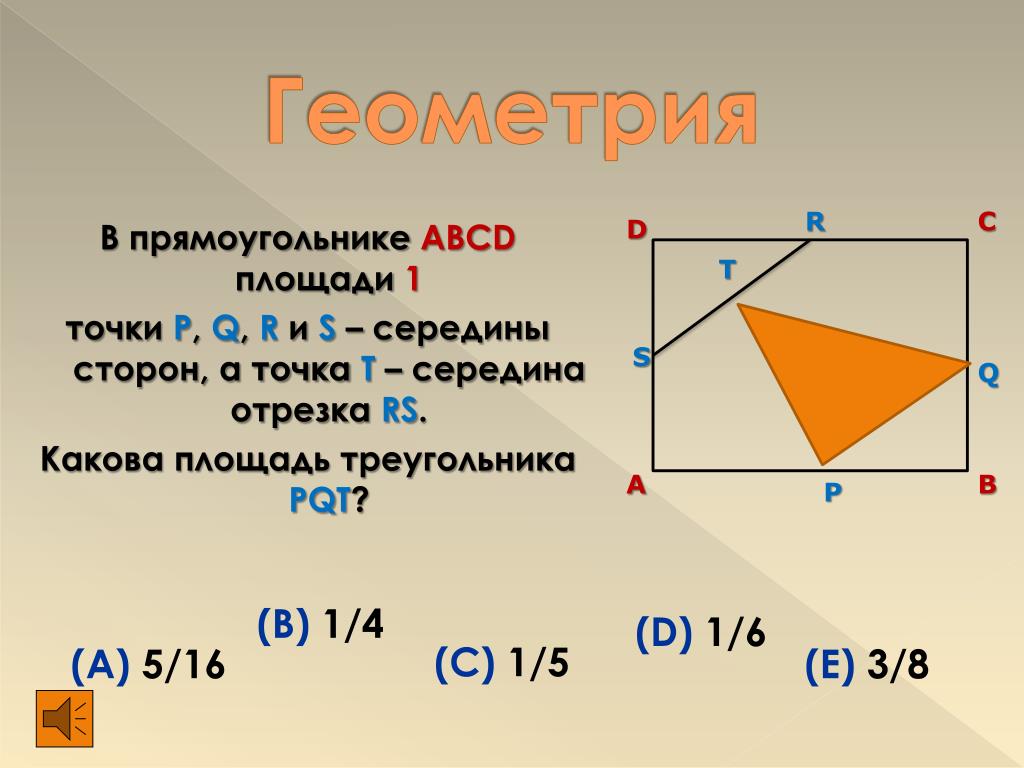
 Единицы
Единицы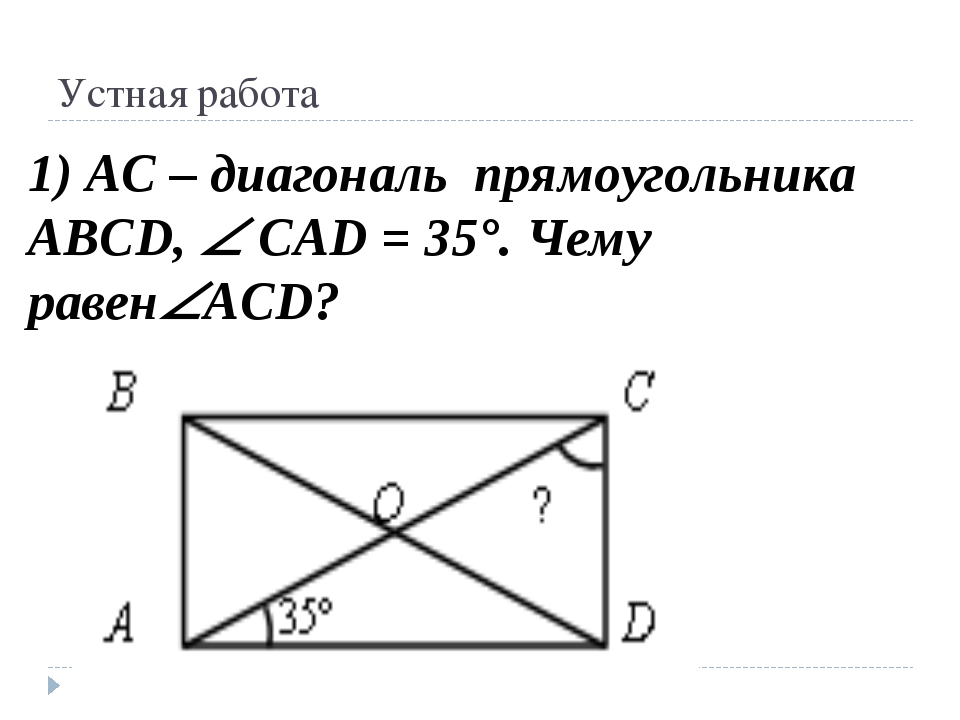

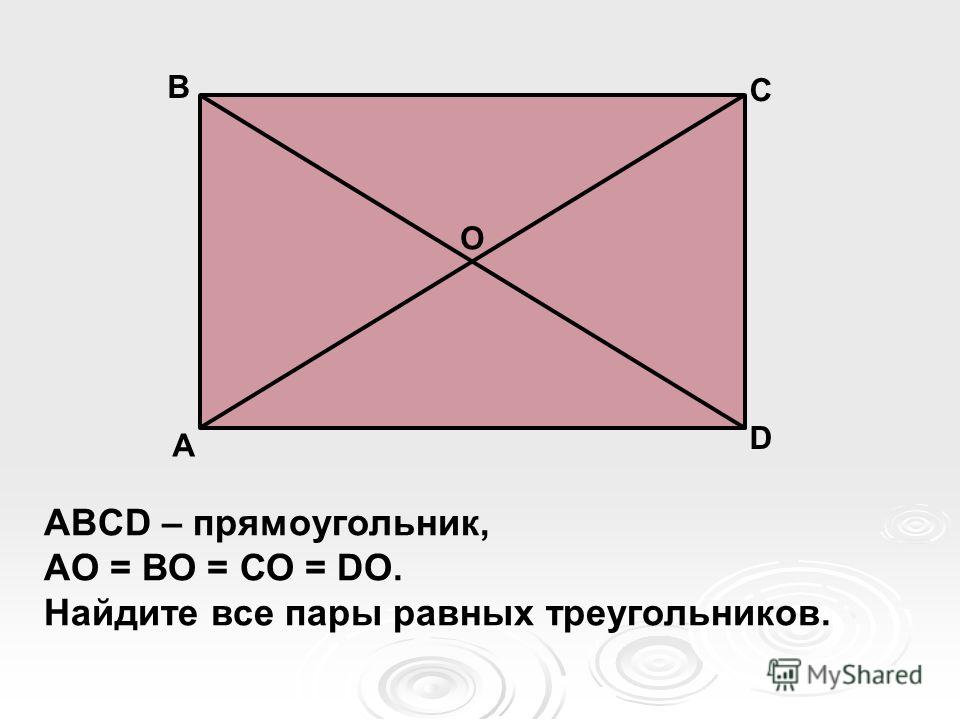 к., у параллелограмма противоположные стороны параллельны и равны.
к., у параллелограмма противоположные стороны параллельны и равны. ед.
ед.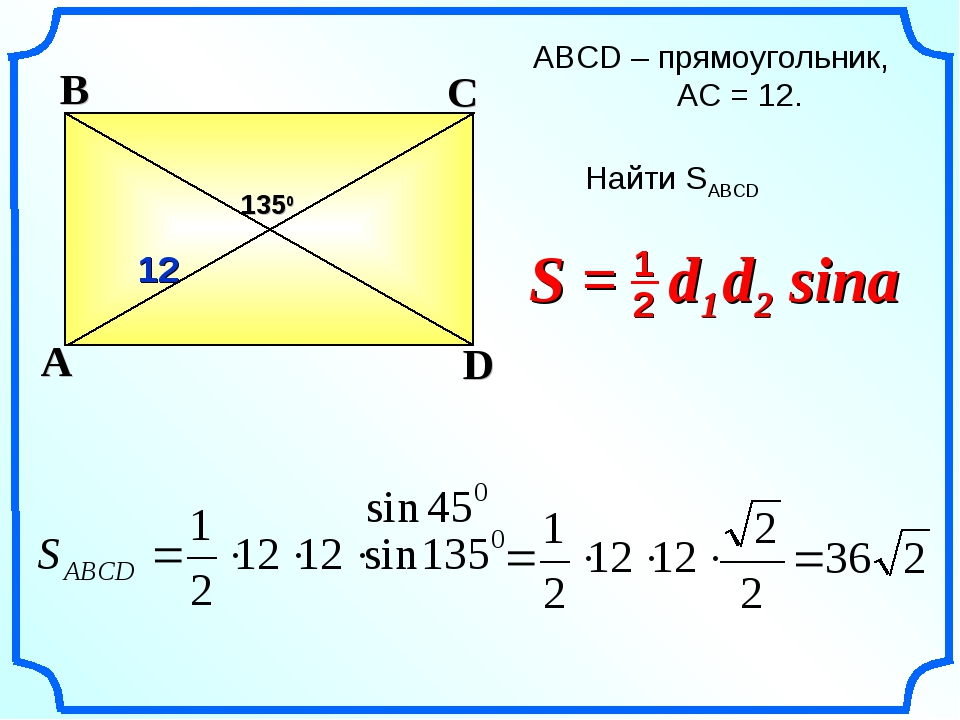

Leave A Comment