— 2. .

Практическая работа № 2. Равенство множеств. 

Подмножество. Надмножество

Вопросы к работе

  1. Какие множества называют равными?

  2. Когда два конечных множества будут равными?

  3. Когда множество А называется подмножеством множества В? Как множество В в этом случае называется по отношению к множеству А?

  4. Какие подмножества множества А называются тривиальными?

  5. Что такое “длина множества”?

  6. Сколько подмножеств можно создать для множества длины n?

Образцы решения заданий

Пример 1. Пусть А – множество двузначных натуральных чисел, В – множество четных двузначных чисел. Верно ли, что В есть подмножество множества А? 

Ответ: Каждое четное двузначное число содержится в множестве А. Следовательно, В  А.

Пример 2. Пусть А = {1; 2; 3}, В = {x | x  N , х < 4}. Верно ли, что  А = В.

Ответ. Множество В состоит из натуральных чисел, меньших 4. Каждый элемент из А входит в В. Следовательно,  А  В. Но натуральных чисел, меньших 4, кроме чисел 1,2,3, нет. Следовательно, каждый элемент из В входит в А. Значит, В  А. По определению, А = В.

Пример. 3. Дано множество А четных натуральных чисел и множество В натуральных чисел, кратных 4. В каком отношении включения находятся множества А и В? Ответ проиллюстрировать диаграммой Эйлера-Венна. 

Решение. Каждое натуральное число, кратное 4, является четным числом. Значит, B  А. Но не каждое четное число обязано делится на 4. Например, 6 не делится 4, т.е. А  В. Имеем диаграмму:  

  

                                     

1. Найдите все подмножества множества А = {1; 2;  3; 4}.

2. Установите, в каком отношении включения находятся множества А и В. Ответ проиллюстрируйте с помощью диаграммы Эйлера-Венна:

а)  А – множество натуральных четных чисел,

     В – множество натуральных чисел, кратных 7;

б)  А – множество натуральных четных чисел,

     В – множество натуральных нечетных чисел.

3. Дано множество А = {72; 56; 513; 117; 324}. Составьте подмножества множества А, состоящие из чисел, которые:

а) делятся на 4;

б) делятся на 9;

в) делятся на 5;

г) делятся на 10.

4. Установите, в каком отношении включения находятся множества решений неравенств от одного неизвестного x:

а) х  <  12  и  х  < 10;

б) х  <  12  и   x  > 15;

 в) x  <  12  и  x  > 10;        

 г)  x  < 12 и  –3x  >  – 36.

5. Изобразите с помощью диаграмм Эйлера-Венна отношение включения между множествами А и В, если:

а) А – множество натуральных четных чисел,

    В – множество натуральных чисел, кратных 3;

б) А – множество квадратов,

    В – множество прямоугольников;

в) А – множество квадратов,

    В – множество прямоугольных треугольников;

г) А – множество квадратов,

    В – множество прямоугольников с равными сторонами.

6. Приведите примеры множеств X,Y,Z,  чтобы отношение включения между ними были такими, как на диаграммах  а), б), с).

                     

                                       Индивидуальноее задание

  1. Даны пары множеств А и В. Укажите отношение включения между ними.

1)  А – множество городов северного полушария,

В – множество городов, находящихся в Азии;

2)  А – множество городов Российской Федерации,

В – Москва, Новосибирск, Владивосток, Мурманск, Грозный, Сочи, Барнаул.      

3)  А – множество городов Франции,

     В – множество городов Европы;

4)  А – множество рек Татарстана,

     В – множество рек Поволжья;

5)  А – множество озер Смоленщины,

     В – множество водоемов Смоленской области;

6)  А – множество административных центров Мордовии,

      В – множество городов Поволжья.  

7)   А – множество рек Сибири,

       В – множество рек СНГ;

8)   А – множество озер Канады,

       В – множество озер Северного полушария;

9)   А – множество городов Африки,

      В – множество населенных пунктов Южного полушария;

10)  А – множество городов Японии,

       В – множество городов Северного полушария;

  1. Среди следующих пар множеств найдите пары равных множеств:
  1. X = {3; 5; 7; 9},

Y – множество нечетных натуральных чисел, больших 2, но меньших 10;

  1. X = {4; 6; 8},

Y – множество четных натуральных чисел, больших 1, но меньших 9;

3)  X –  множество плоских четырехугольников,

Y – множество плоских фигур, ограниченных замкнутой ломаной из  четырех отрезков;

4)  X –   множество двузначных чисел, кратных 9,

Y – множество двузначных чисел, сумма цифр которых равна 9;

5)  X – множество сумм двух нечетных натуральных чисел,

Y – множество четных натуральных чисел;

6)   X –  множество точек плоскости, равноудаленных от точек М и К,

Y – множество точек прямой, проходящей через середину отрезка МК  перпендикулярно этому отрезку;

7) X – множество точек, лежащих на окружности с центром C и радиусом  5,

Y – множество точек, расстояние которых от точки  C равно 5;

8) X – множество точек, лежащих внутри круга, ограниченных   окружностью с центром C и радиуса 5,

Y – множество точек, расстояние которых от точки C меньше, чем 5;

9)   X – множество точек, лежащих вне круга, ограниченного окружностью с центром C и радиуса 5,

Y – множество точек, расстояние которых от точки C больше, чем 5;

10)  X – множество натуральных чисел, кратных 10,

Y – множество натуральных чисел, кратных 2 и 5 одновременно.

Задания для самоконтроля

1. Верно ли, что

а) {1; 2}  {{1; 2; 3}; {1; 3}; 1; 2};

б) {1; 2}  {{1; 2; 3}; {1; 3}; 1; 2};

в) {1; 3}  {{1; 2; 3}; {1; 3}; 1; 2};

г) {1; 3}  {{1; 2; 3}; {1; 3}; 1; 2}?

2. Равны ли следующие множества:

а) A = {2; 4; 6}, B = {6; 4; 2};

б) A = {1; 2; 3}, B = {I; II; III};

в) A = {{1; 2}, {2; 3}}, B = {2; 3; 1};

г) A = {, , , }, B = {12, 22, 32, 42}, где A  N, B  N.

3. Существуют ли такое множество, которое имеет 80 подмножеств?

4. Изобразите диаграмму Эйлера-Венна взаимодействия множеств N, Z, Q, R.

5. В чем ошибочность следующих формулировок:

а) Если элементы множества А принадлежат другому множеству В, то множество А включается в множество В;

б)  Если два множества содержат одни и те же элементы, то они равны.

Как исправить эти формулировки?

Решение задачи Характеристическое свойство множеств. Диаграммы Эйлера. Декартово произведение. Комбинаторные задачи. на Викиматик

1. Укажите характеристическое свойство элемента множеств: а) \(\left\{1,\ 4,\ 9,\ 16,\ 25,\ \dots \right\}\), б) \(\left\{21,\ 22,\ 23,\ 24,\ 25,\ 26\right\}\), в) \(\left\{10,\ 20,\ 30,\ 40,\ 50,\ 60,\ 70,\ 80,\ 90\right\}\).

2. Приведите примеры трех подмножеств множества параллелограммов. Изобразите соотношения между ними при помощи кругов Эйлера.

3. Изобразите на координатной прямой множества:

\(A=\left\{x:x\in {\rm N}{\rm ,}{\rm \ }x<11\right\},\ B=\left\{x:x\in {\rm R}{\rm ,}{\rm \ }x\le 3\right\},\ C=\left\{x:x\in {\rm R}{\rm ,}{\rm \ }{\rm -}6\le x\le 4,3\right\}\). Найдите \(B\cup C,\ A\cap B,\ B\backslash C\).

4. Изобразите при помощи кругов Эйлера отношения между множествами А, С и D, если:

а) А — множество нечетных чисел, С — множество четных чисел. D множество чисел, кратных 5;

б) А — множество натуральных чисел. С — множество четных чисел. D множество четных чисел, кратных 7;

в) А — множество чисел, кратных 4, С — множество четных чисел, D множество чисел, кратных 2.

В каждом множестве возьмите по 3 числа и укажите их расположение на диаграмме.

5. Даны множества \(A=\left\{2,\ 4,\ 6\right\},\ B=\left\{a,\ b,\ c\right\}\). Перечислите элементы множеств \(A\times B,\ B\times A\). Верно ли, что \(A\times B=B\times A\).

6. Изобразите на координатной плоскости декартово произведение \(A\times B\), если а) \(A=\left\{-3,\ -4,\ -5,\ -6,\ -7\right\}\), \(B=\left\{3,\ 4,\ 5,\ 6\right\}\), б) \(A=\left[-2;4\right]\), \(B=\left[-2;9\right]\), в) \(A=\left(4;\ \infty \right)\), \(B=\left[1;8\right]\).

7. 150 школьников третьих классов в зимние каникулы ходили в цирк, театр и на каток. В цирке были 68 человек, в театре 50, на кате 100. 25 школьников были и в цирке, и в театре, и катались на катке. В цирке и театре были 30 человек, 40 человек ходили в цирк и на каток, а 32 человека были в театре и катались на катке. Сколько школьников не ходили ни в театр, ни в цирк, ни на каток? На сколько школьников, ходивших только на каток, больше тех, кто ходил только в цирк?

8. Имеете 5 видов карандашей и 7 видов блокнотов. Сколькими способами можно составить подарочный набор, состоящий из карандаша и блокнота?

9. Сколькими способами могут быть присуждены первая, вторая и третья премии трем конкурсантам, если число соревнующихся равно 18?

10. Сколько можно составить пятизначных чисел, не кратных 5, из цифр 5,6,7,8,9, если любую из них можно использовать один раз?

11. В случайном эксперименте монету бросают три раза. Какова вероятность того, что герб выпадет ровно 2 раза?

12. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле 0,8. Найдите вероятность того, что биатлонист попал в мишень четыре раза и один промахнулся.

60, 61. Задачи на нахождение общих элементов множеств

Это надо знать
Объединением двух множеств является множество, каждый элемент которого является элементом какого-либо из исходных множеств.

Пример:

Задано множество всех делителей числа 16 и множество всех делителей числа 30. Укажите для этих множеств все их элементы (объединение множеств.

Решение:
Пусть А — множество всех делителей числа 16.
А={1, 2, 4, 8, 16}.
Пусть В — множество всех делителей числа 30.
В={1, 2, 3, 5, 6, 10, 15, 30}.

Найдем объединение множеств:
запишем числа, которые есть в  множестве А, и из множества В допишем те числа, которых нет в множестве А:    А ∪ B = {1, 2, 3, 4, 5, 6, 8, 10, 15, 16, 30}.

 Пересечением множеств называется множество, состоящее из всех общих элементов исходных множеств.

Пример:
Задано множество всех делителей числа 16 и множество всех делителей числа 30. Укажите для этих множеств их общие элементы (пересечение множеств).

Решение:
Пусть А — множество всех делителей числа 16.
А={1, 2, 4, 8, 16}.
Пусть В — множество всех делителей числа 30.
В={1, 2, 3, 5, 6, 10, 15, 30}.

Найдем пересечение множеств:
запишем числа, которые принадлежат и множеству А, и множеству В одновременно:  А ⋂ B = {1, 2}.

Упражнения для решения 1. Задано множество двузначных кратных числа 18 и множество двузначных кратных числа 24. Укажите для этих множеств:
       а) их общие элементы; б) все их элементы.

2. Найдите множества всех делителей чисел:
1) 20 и 30;    2) 50 и 125;     3) 60 и 90;      4) 18 и 45.
Укажите для этих множеств: а) их общие элементы; б) все их элементы.

3. Найдите множества всех делителей чисел 24, 30, 45. Укажите для этих множеств: а) их общие элементы; б) все их элементы.

4. Найдите множество всех двузначных кратных числу 15 и множество всех двузначных кратных числу 12. Укажите для этих множеств: а) их общие элементы; б) все их элементы.

5. Найдите множество всех двузначных кратных числу 20 и множество всех двузначных кратных числу 40. Укажите для этих множеств: а) их общие элементы; б) все их элементы.

6. Пусть A — это множество натуральных чисел, делящихся на 2, а В — множество натуральных чисел, делящихся на 4. Какой вывод можно сделать относительно данных множеств?

7. Найдите множество всех двузначных чисел, кратных числу 16, и множество всех двузначных чисел, кратных числу 24. Укажите для этих множеств: а) их общие элементы; б) все их элементы.

8. Числа 4373 и 826 разделили на одно и то же натуральное число и получили в остатках 8 и 7 соответственно. На какое число делили?
Домашнее задание  К уроку 60 (на 27.11)

1.Найдите множества всех делителей чисел 40, 60. Укажите для этих множеств:
а) их общие элементы; б) все их элементы.

2. Найдите множество всех двузначных чисел, кратных числу 16, и множество всех двузначных чисел, кратных числу 24. Укажите для этих множеств: а) их общие элементы; б) все их элементы.

3.  12 моих одноклассников любят читать детективы, 18 — фантастику, трое с удовольствием читают и то, и другое, а один вообще ничего не читает. Сколько учеников в нашем классе?

К уроку 61 (на 30.11)

1. Пусть A — это множество натуральных чисел, делящихся на 5, а В — множество натуральных чисел, делящихся на 2. Какой вывод можно сделать относительно пересечения этих множеств?

2. Найдите множества всех делителей чисел 36, 30, 48. Укажите для этих множеств: а) их общие элементы; б) все их элементы.

3. Числа 1049 и 1865 разделили на одно и то же натуральное число и получили в остатках 5 и 9 соответственно. На какое число делили?

Дискретная математика — тест 7

Главная / Алгоритмы и дискретные структуры / Дискретная математика / Тест 7 Упражнение 1:
Номер 1
Какие из множеств замкнуты относительно сложения?

Ответ:

&nbsp(1) множество натуральных чисел &nbsp

&nbsp(2) множество нечетных чисел &nbsp

&nbsp(3) множество квадратных корней из натуральных чисел &nbsp

&nbsp(4) множество натуральных чисел, кратных 3 &nbsp


Номер 2
Какие из множеств замкнуты относительно умножения?

Ответ:

&nbsp(1) множество натуральных чисел &nbsp

&nbsp(2) множество нечетных чисел &nbsp

&nbsp(3) множество положительных чисел &nbsp

&nbsp(4) множество отрицательных чисел &nbsp


Номер 3
Какие из множеств замкнуты относительно сложения?

Ответ:

&nbsp(1) множество положительных чисел &nbsp

&nbsp(2) множество отрицательных чисел &nbsp

&nbsp(3) множество целых степеней двойки &nbsp

&nbsp(4) множество четных чисел &nbsp


Упражнение 2:
Номер 1
Какие из операций ассоциативны?

Ответ:

&nbsp(1) вычитание чисел &nbsp

&nbsp(2) сложение чисел &nbsp

&nbsp(3) разность множеств &nbsp


Номер 2
Какие из операций ассоциативны?

Ответ:

&nbsp(1) умножение чисел &nbsp

&nbsp(2) объединение множеств &nbsp

&nbsp(3) деление чисел &nbsp


Номер 3
Какие из операций ассоциативны?

Ответ:

&nbsp(1) возведение в степень &nbsp

&nbsp(2) пересечение множеств &nbsp

&nbsp(3) объединение множеств &nbsp


Упражнение 3:
Номер 1
Какие из операций коммутативны?

Ответ:

&nbsp(1) вычитание чисел &nbsp

&nbsp(2) умножение чисел &nbsp

&nbsp(3) пересечение множеств &nbsp


Номер 2
Какие из операций коммутативны?

Ответ:

&nbsp(1) сложение чисел &nbsp

&nbsp(2) пересечение множеств &nbsp

&nbsp(3) разность множеств &nbsp


Номер 3
Какие из операций коммутативны?

Ответ:

&nbsp(1) деление чисел &nbsp

&nbsp(2) возведение в степень &nbsp

&nbsp(3) объединение множеств &nbsp


Упражнение 4:
Номер 1
Какие из операций над множествами ассоциативны?

Ответ:

&nbsp(1) объединение &nbsp

&nbsp(2) пересечение &nbsp

&nbsp(3) разность &nbsp


Номер 2
Какие из операций над множествами коммутативны?

Ответ:

&nbsp(1) объединение &nbsp

&nbsp(2) пересечение &nbsp

&nbsp(3) разность &nbsp


Номер 3
Отметьте дистрибутивны слева множества:

Ответ:

&nbsp(1) объединение относительно пересечения &nbsp

&nbsp(2) пересечение относительно разности &nbsp

&nbsp(3) разность относительно объединения &nbsp


Упражнение 5:
Номер 1
Отметьте подмножества, которые в алгебре целых чисел со сложением 
		образуют подалгебру:

Ответ:

&nbsp(1) множество чисел, кратных 5 &nbsp

&nbsp(2) множество [0,1] &nbsp

&nbsp(3) множество натуральных чисел &nbsp


Номер 2
Отметьте подмножества, которые в алгебре целых чисел с умножением 
		образуют подалгебру:

Ответ:

&nbsp(1) множество чисел, кратных 3 &nbsp

&nbsp(2) множество [0,1] &nbsp

&nbsp(3) множество отрицательных чисел &nbsp


Номер 3
Отметьте подмножества, которые в алгебре действительных чисел с умножением 
		образуют подалгебру:

Ответ:

&nbsp(1) множество целых степеней двойки &nbsp

&nbsp(2) множество {0,1,2} &nbsp

&nbsp(3) множество натуральных чисел &nbsp


Упражнение 6:
Номер 1
Какие из множеств с указанной операцией над элементами образуют полугруппу?

Ответ:

&nbsp(1) четные числа с операцией сложения &nbsp

&nbsp(2) целые числа с операцией вычитания &nbsp

&nbsp(3) рациональные числа с операцией умножения &nbsp

&nbsp(4) множество {-1,1} с операцией умножения &nbsp


Номер 2
Какие из множеств с указанной операцией над элементами образуют полугруппу?

Ответ:

&nbsp(1) неотрицательные целые числа с операцией сложения &nbsp

&nbsp(2) нечетные числа с операцией сложения &nbsp

&nbsp(3) положительные рациональные числа с операцией умножения &nbsp

&nbsp(4) нечетные числа с операцией умножения &nbsp


Номер 3
Какие из множеств с указанной операцией над элементами образуют полугруппу?

Ответ:

&nbsp(1) целые числа, кратные 7, с операцией сложения &nbsp

&nbsp(2) положительные рациональные числа с операцией деления &nbsp

&nbsp(3) степени двойки с целыми показателями с операцией умножения &nbsp

&nbsp(4) целые числа с операцией сложения &nbsp


Упражнение 7:
Номер 1
Какие из множеств с операцией сложения образуют группу?

Ответ:

&nbsp(1) целые числа, кратные 3 &nbsp

&nbsp(2) множество {-1,1} &nbsp

&nbsp(3) неотрицательные целые числа &nbsp

&nbsp(4) целые числа &nbsp


Номер 2
Какие из множеств с операцией сложения образуют группу?

Ответ:

&nbsp(1) нечетные числа &nbsp

&nbsp(2) рациональные числа &nbsp

&nbsp(3) множество [-1,1] &nbsp

&nbsp(4) целые числа, имеющие остаток от деления на 4, равный 3 &nbsp


Номер 3
Какие из множеств с операцией сложения образуют группу?

Ответ:

&nbsp(1) неотрицательные рациональные числа &nbsp

&nbsp(2) целые степени двойки &nbsp

&nbsp(3) целые числа, кратные 4 &nbsp

&nbsp(4) множество {0} (состоящее только из нуля) &nbsp


Упражнение 8:
Номер 1
Какие из множеств с указанной операцией над элементами образуют группу?

Ответ:

&nbsp(1) множество {-1,1} с операцией умножения &nbsp

&nbsp(2) рациональные числа с операцией умножения &nbsp

&nbsp(3) неотрицательные целые числа с операцией сложения &nbsp

&nbsp(4) четные числа с операцией сложения &nbsp


Номер 2
Какие из множеств с указанной операцией над элементами образуют группу?

Ответ:

&nbsp(1) степени двойки с целыми показателями с операцией умножения &nbsp

&nbsp(2) рациональные числа с операцией сложения &nbsp

&nbsp(3) положительные рациональные числа с операцией деления &nbsp

&nbsp(4) нечетные числа с операцией сложения &nbsp


Номер 3
Какие из множеств с указанной операцией над элементами образуют группу?

Ответ:

&nbsp(1) целые числа с операцией вычитания &nbsp

&nbsp(2) целые числа, кратные 3, с операцией сложения &nbsp

&nbsp(3) рациональные числа, отличные от нуля, с операцией умножения &nbsp

&nbsp(4) нечетные числа с операцией умножения &nbsp


Упражнение 9:
Номер 1
Чему равен единичный элемент в группе целых чисел со сложением?

Ответ:

&nbsp(1) его не существует &nbsp

&nbsp(2) 0 &nbsp

&nbsp(3) 1 &nbsp


Номер 2
Чему равен единичный элемент в группе целых степеней двойки с умножением?

Ответ:

&nbsp(1) его не существует &nbsp

&nbsp(2) 1 &nbsp

&nbsp(3) 2 &nbsp


Номер 3
Чему равен единичный элемент в группе {-1,1} с умножением?

Ответ:

&nbsp(1) его не существует &nbsp

&nbsp(2) 1 &nbsp

&nbsp(3) -1 &nbsp


Упражнение 10:
Номер 1
Какой элемент является образующей в группе целых чисел со сложением?

Ответ:

&nbsp(1) такого элемента не существует &nbsp

&nbsp(2) 0 &nbsp

&nbsp(3) 1 &nbsp


Номер 2
Какой элемент является образующей в группе целых степеней двойки с умножением?

Ответ:

&nbsp(1) такого элемента не существует &nbsp

&nbsp(2) 1 &nbsp

&nbsp(3) 2 &nbsp


Номер 3
Какой элемент является образующей в группе {-1,1} с умножением?

Ответ:

&nbsp(1) такого элемента не существует &nbsp

&nbsp(2) 1 &nbsp

&nbsp(3) -1 &nbsp


Упражнение 11:
Номер 1
Чему равна наименьшая верхняя грань для {c,e}?

Ответ:

&nbsp(1) a &nbsp

&nbsp(2) c &nbsp

&nbsp(3) b &nbsp


Номер 2
Чему равна наименьшая верхняя грань для {c,g}?

Ответ:

&nbsp(1) a &nbsp

&nbsp(2) c &nbsp

&nbsp(3) d &nbsp


Номер 3
Чему равна наименьшая верхняя грань для {b,f}?

Ответ:

&nbsp(1) a &nbsp

&nbsp(2) b &nbsp

&nbsp(3) d &nbsp


Упражнение 12:
Номер 1
Чему равна наибольшая нижняя грань для {b,d}?

Ответ:

&nbsp(1) e &nbsp

&nbsp(2) f &nbsp

&nbsp(3) g &nbsp


Номер 2
Чему равна наибольшая нижняя грань для {e,g}?

Ответ:

&nbsp(1) c &nbsp

&nbsp(2) f &nbsp

&nbsp(3) h &nbsp


Номер 3
Чему равна наибольшая нижняя грань для {c,f}?

Ответ:

&nbsp(1) e &nbsp

&nbsp(2) g &nbsp

&nbsp(3) h &nbsp


Множества.

Операции над множествами. Задачи на множество.

Множества. Операции над множествами

«Множество есть многое, мыслимое нами как единое»

основатель теории множеств

Георг Кантор

Понятия теории множеств

Понятие множества является одним из наиболее общих и наиболее важных математических понятий. Оно было введено в математику немецким ученым Георгом Кантором (1845-1918).Следуя Кантору, понятие «множество» можно определить так:

  • Множество- совокупность объектов, обладающих определенным свойством, объединенных в единое целое.

Множество – совокупность объектов, объединенных по какому – нибудь признаку.

Множества обозначают большими буквами латинского алфавита: А, В, С, D и т. д.

Объекты, составляющие множество, называются элементами множества.

множество

элемент

Трапеция, параллелограмм, ромб, квадрат, прямоугольник

Шар, прямоугольный параллелепипед, призма, пирамида, октаэдр

Натуральные числа

1, 4, 9, 16, 25, 36, 49, 64, 81, 100 ..

0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Двузначные четные числа

Множество четырехугольников

Пространственные тела

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11…

Квадраты чисел

Цифры десятичной системы счисления

10, 12, 14, 16 … 96, 98

множество прямых углов равностороннего треугольника

множество точек пересечения двух параллельных прямых

Пустое множество- множество, не содержащее ни одного элемента.

Обозначения некоторых числовых множеств:

N – множество натуральных чисел;

Z – множество целых чисел;

Q – множество рациональных чисел;

I — множество иррациональных чисел;

R – множество действительных чисел.

ВИДЫ МНОЖЕСТВ

А = {2; 3; 5; 7; 11; 13};

{х | 5

Конечные множества

ВИДЫ МНОЖЕСТВ

{1; 4; 9; 16; 25; …};

{10; 20; 30; 40; 50; …};

Бесконечные множества

Среди перечисленных ниже множеств укажите конечные и бесконечные множества:

а) множество чисел, кратных 13;

б) множество делителей числа 15;

в) множество деревьев в лесу;

г) множество натуральных чисел;

д) множество рек Ростовской области;

е) множество корней уравнения х + 3 = 11;

ж) множество решений неравенства х + 1

Отношения между множествами

ОБЪЕДИНЕНИЕ МНОЖЕСТВ

ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ

Разность множеств

Обозначение: A\ B

Результатом разности являются все элементы множества A без элементов множества B.

Симметрическая разность

Обозначение: A B

Результатом симметрической разности являются все элементы множества A и B без их пересечения .

Даны множества:

А = {2; 3; 8},

В = {2; 3; 8; 11},

С = {5; 11}.

Найдите: 1) АUВ; 2) АUС; 3) СUВ; 4) A\ B ;

5) A B .

Даны множества:

А = { a , b , c , d },

B = { c , d , e , f },

C = { c , e , g , k }.

Найдите: (АUВ)UС ; A\ B ; A B ; ( A\ B )UС.

Даны множества:

А – множество всех натуральных чисел, кратных 10,

В = {1; 2; 3;…, 41}.

Найдите А∩В.

Решение задачи

с помощью кругов Эйлера

K

Леона́рд Э́йлер  — швейцарский, немецкий и российский математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук.

k

В классе 30 человек, каждый из которых поёт или танцует. Известно, что поют 17 человек, а танцевать умеют 19 человек. Сколько человек поёт и танцует одновременно?

Всего 30

6

13

11

поют 17

танцуют 19

17+19=36, всего 30

36-30=6

Решение

Пусть А — это множество учеников, умеющих петь. Количество элементов в нём по условию равно n = 17. Пусть В — множество учеников, умеющих танцевать. Количество элементов в нём — m = 18. Множество совпадает со всем классом, т.к. каждый ученик в классе поёт или танцует. — это множество тех учеников класса, которые поют и танцуют одновременно. Пусть их количество равно k .

Согласно формуле доказанной выше

n + m- k = 17+ 19- k = 30 k = 6.

Ответ: 6 учеников в классе поют и танцуют одновременно.

Каждый учащийся в классе изучает английский или французский язык. Английский язык изучают 25 учащихся, французский — 27 учащихся, а два языка — 18 учащихся. Сколько учащихся в классе?

18

Немецкий 27

Английский 25

Только немецкий

27 – 18 = 9

Только английский

25 – 18 = 7

7

9

7 + 9 + 18 = 34

Ответ: в классе 34 ученика

Расположите 4 элемента в двух множествах так, чтобы в каждом из них было по 3 элемента.

Множества А и В содержат соответственно 5 и 6 элементов, а множество А ∩ В – 2 элемента. Сколько элементов в множестве А U В?

Объединение содержит 9 элементов

На школьной спартакиаде каждый из 25 учеников 9 –го

класса выполнил норматив или по бегу, или по прыжкам в высоту. Оба норматива выполнили 7 человек, а 11 учеников выполнили норматив по бегу, но не выполнили норматив по прыжкам в высоту. Сколько учеников выполнили норматив: а) по бегу; б) по прыжкам в высоту; в) по прыжкам при условии, что не выполнен норматив по бегу?

7

11

7

Из 52 школьников 23 собирают значки, 35 собирают марки, а 16 – и значки, и марки. Остальные не увлекаются коллекционированием. Сколько школьников не увлекаются коллекционированием?

Каждый из учеников 9-го класса в зимние каникулы ровно два раза был в театре, посмотрев спектакли А, В или С. При этом спектакли А, В, С видели соответственно 25, 12 и 23 ученика. Сколько учеников в классе?

Помощь с практическим заданием по математике и информатике, ЭИОС (edu.pglu.ru)

 
Задание 1
 

  1. Задайте множество (любым способом), которое содержит:

только 1 элемент;
только 2 элемента;
только 3 элемента;
только 7 элементов;
только 10 элементов;
только 12 элементов.
 

  1. Записать множество А, состоящее из всех гласных букв в слове «ЭЛЕКТРИЧЕСТВО».

 

  1. Записать множество всех правильных дробей со знаменателем 7.

 

 

  1. Среди перечисленных ниже множеств укажите конечные и бесконечные множества:

а) множество чисел, кратных 13;
б) множество делителей числа 15;
в) множество деревьев в лесу;
г) множество натуральных чисел;
д) множество рек Ростовской области;
е) множество корней уравнения х + 3 = 11;
ж) множество решений неравенства х + 1 < 3.

Конечные множестваБесконечные множества

 
 

  1. Какое из двух данных множеств В и С является подмножеством множества К, если В={-1; 3; 4}, C={0; 3; 4; 5), K={0; 2; 3; 4; 5; 6} ?

 

  1. Пользуясь схемой Эйлера-Венна поставьте в соответствие записи номер рисунка
      1

А                                 В
 
 
 
 
 
 
 
 

 2                 А                        В
 
 
 
 
 
 
 
 		 3А
 
 
 
 
 
 
 

 

 
 
 

  1. Расположи 9 элементов в трех множествах так,

чтобы в одном из них было 2 элемента, в другом 5 элементов,

а в третьем – 7 элементов.
 
 

  1. Даны множества:

А – множество всех натуральных чисел, кратных 10,

В = {1; 2; 3;…, 41}.
Найдите  А∩В.

  1. Даны множества: A = {1, 2, 8}, B = {0, 1, 3, 4}, U ={0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. Найти множества: A ∪ B, A ∩ B, A \ B.
  2. Даны множества:

А = {a, b, c, d},

B = {c, d, e, f},

C = {c, e, g, k}.
Найдите: (АUВ)UС.
Задайте множество (любым способом) которое содержит:
Только один элемент: А={3}
Только два элемента: D={1,a}
Только три элемента: B={1,5,b}
Только семь элементов: C={1,2,3,4,5,6,7}
Только десять элементов: A={x| xϵN 1≤x≤10}
Только двенадцать элементов: A={x| xϵZ ,-14≤x≤10 и x –четное}
Записать множество А, состоящее из всех гласных букв в слове “ЭЛЕКТРИЧЕСТВО”
А={э,е,и,о}
Записать множество всех правильных дробей со знаменателем 7.
А={1/7, 2/7, 3/7, 4/7, 5/7, 6/7}
Среди перечисленных ниже множеств укажите бесконечные и конечные множества:
а) множество чисел, кратных 13. Бесконечное множество.
б) множество делителей числа 15. Конечное множество (количество элементов множества можно сосчитать (1,-1,3,-3,5,-5,15,-15}
в) Множество деревьев в лесу. Бесконечное множество.
г) Множество натуральных чисел. Бесконечно.
д) Множество рек Ростовской области. Конечное множество.
е) Множество корней уравнения. Конечно.
ж) Множество решений неравенства x+1<3
(решение x<2). Бесконечно.
Какое из двух данных множеств В и С является подмножеством множества К, если В={-1,3,4}, C={0,3,4,5}, K={0,2,3,4,5,6}
Множество С является подмножеством множества К, так как все элементы множества С принадлежат множеству К. c={0,3,4,5}∁{0,2,3,4,5,6}=K.
Пользуясь схемой Эйлера Венна поставьте в соответствие записи номер рисунка
1
А В
2
АВ
3
А
АВ АВ ВА
2 1 3
Расположи 9 элементов в трех множествах так, чтобы в одном из них было 2 элемента, в другом 5 элементов, а в третьем- 7 элементов
Пусть даны элементы {1,a,b,c,7,8,9,d,k}, тогда
A={1,a}, B={a,b,c,8,9}, C={a,b,c,d,k,7,8}
А- множество всех натуральных чисел, кратных 10, В={1,2,3,…,41}
Найти A∩B
A∩B={10,20,30,40}
Даны множества : A={1,2,8}, B={0,1,3,4}, U={0,1,2,3,4,5,6,7,8,9}.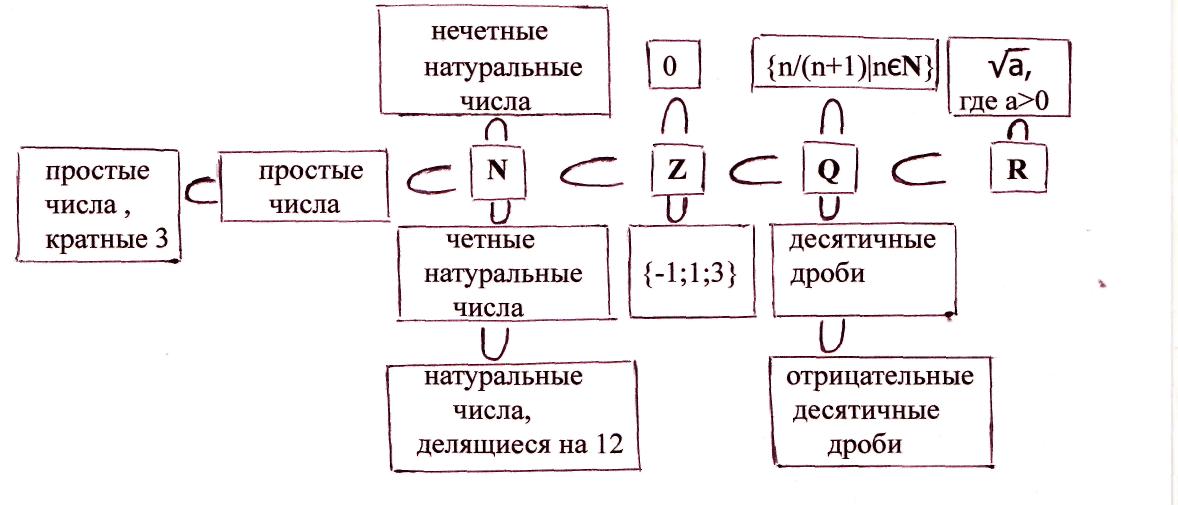 Найти множества: A∪B,A∩B,A\B
A∪B={0,1,2,3,4,8}
A∩B={1}
A\B={2,8}
Даны множества:
A={a,b,c,d}
B={c,d,e,f}
C={c,e,g,k}
Найти (A∪B)∪C
(A∪B)∪C={a,b,c,d,e,f,g,k}

Практическое занятие 1.2. Операции над множествами.

Вопросы и задания для подготовки к занятию:

1. Дайте определœения понятиям ʼʼобъединœение множествʼʼ, ʼʼпересечение множествʼʼ. Дайте этим операциям графическую иллюстрацию с помощью кругов Эйлера.

2. Сформулируйте свойства операций объединœение и пересечение множеств. Проиллюстрируйте их с помощью кругов Эйлера.

3. Дайте определœения понятиям ʼʼразность множествʼʼ, ʼʼдополнение множестваʼʼ. Дайте этим операциям графическую иллюстрацию с помощью кругов Эйлера.

4. Сформулируйте свойства разности множеств.

5. Известно, что . Следует ли из этого, что:

°

°

°

6. Найдите пересечение, объединœение, разность

° [1; 5] и [3; 7];

° А=;

° ;

° и;

° ; Ø..

7. Известно, что . Следует ли из этого, что:

°

°

8. Найдите разность числового отрезка [1; 5] и числового отрезка [3; 7].

9. Сформулируйте условия, при которых истинны следующие высказывания:

° ;

° .

Задания для самостоятельной работы

1. Перечислите элементы, принадлежащие пересечению множества букв в слове ʼʼматематикаʼʼ и множества букв в слове ʼʼграмматикаʼʼ. Из каких элементов состоит объединœение данных множеств?

2. Р – множество натуральных делителœей числа 18, Н – множество натуральны делителœей числа 24. укажите характеристическое свойство элементов пересечения множеств Р и Н и перечислите его элементы.

3. Найдите пересечение и объединœение множеств К и М, в случае если К – множество двузначных чисел, М – множество нечетных чисел. Верно ли, что: а) 21; б); в) ; г) .

4. Найти объединœение и пересечение множеств А и В, в случае если и .

5. Три множества Р, Н, М изображены тремя прямоугольниками (рис. 1). Отметьте штриховкой области, изображающие множество Х: а) МН; б) РН; в) (РН) (НМ).

Рис. 1.

6. В – множество правильных многоугольников, Т – множество прямоугольников. Из каких фигур состоит объединœение и пересечение множеств В и Т. Нарисуйте по две фигуры из каждого множества.

7. Даны множества: А ={а, b, с, d, е}, В ={с, d, f, k}, С = {b, с, d, f, m}. Перечислите элементы множеств К=(АÈВ)ÇС и Р =А È ВÇ С. Содержится ли элемент m в множестве К, а элемент f в множестве Р?

8. А – множество чисел, кратных 2, В – множество чисел, кратных 3, С – множество чисел, кратных 5. Укажите характеристическое свойство элементов множества (АВ) С и (АВ) С.

9. Найдите объединœение и пересечение множеств и дайте графическую иллюстрацию при помощи диаграмм Эйлера — Венна, если:

а) А = {5, 6, 7, 8, 9, 10}, В = {8, 9, 10, 11};

б) А= {х ÷ х = 5п, п ÎN}, В= {х ÷ х = 2п, п ÎN};

г) А={х ÷ х = 2п, п ÎN}, В= {х ÷ х = 2п, п ÎN}.

10. Изобразите на числовой прямой и запишите при помощи неравенства объединœение и пересечение множеств Р и Q:

а) Р = , Q=;

б) Р = , Q = ;

в) Р =, Q =

11. Множество А состоит из натуральных чисел от 2 до 10, множество В – из натуральных чисел от 5 до20. Перечислите элементы множеств А \ В и В \ А.

12. Р – множество двузначных чисел, М – множество четных натуральных чисел. изобразите данные множества при помощи кругов Эйлера, отметьте штриховкой разность множеств Р и М и укажите характеристическое свойство элементов, принадлежащей этой разности. Верно ли, что Р \ М содержит числа 21; 17?

13. Дано множество . Запишите два подмножества множества Х и дополнение этих подмножеств до множества Х.

14. Сформулируйте характеристическое свойство элементов дополнения множества Р до множества треугольников, если: а) Р – множество остроугольных треугольников; б) Р – множество равносторонних треугольников.

15. Найдите дополнение множества У до множества Х, если:

a) Х – множество точек прямой АВ;

b) множество точек отрезка АВ;

c) Х – множество точек квадрата͵ У – множество точек круга, вписанного в данный квадрат.

16. Найдите дополнение:

d) множества четных натуральных чисел до множества N;

e) множества отрицательных чисел до множества Z;

f) множества целых чисел до множества Q.

2. Отметьте на координатной прямой множество А и укажите характеристическое свойство элементов его дополнения до множества R, если: а) ; б) ; в).

3. Множества А, В и С таковы, что Ø. Изобразите их при помощи кругов Эйлера и отметьте штриховкой области, представляющие множества (А \ В) С, А \ ВС, А(В \ С), АВ \ С. Для каждого случая сделайте отдельный чертеж.

4. А – множество прямоугольников, В – множество правильных многоугольников, С – множество треугольников. постройте круги Эйлера для данных множеств и отметьте штриховкой области, изображающие множества: а) АВС; б) ВС; в) (АВ)’С.

5. Постройте три круга, изображающие три попарно пересекающихся множества А, В и С, и выделите штриховкой области, представляющие множества:

а) АÈВ\С, б) А\СÈВ\С; в) А\(ВÈС).

Практическое занятие 1.3. Разбиение множества на классы. Декартово произведение множеств.

Вопросы и задания для подготовки к занятию:

1. Дайте определœение понятиям ʼʼразбиение множества на классыʼʼ; ʼʼдекартово произведение множествʼʼ.

2. Какими свойствами обладает и не обладает операция ʼʼдекартово произведения множествʼʼ?

3. Найдите В ´ С и С ´ В если

a. В = {1, 2, 3} C = {10, 20, 30};

b. В = {а, о, и} C = {м, т, к};

c. В = {красивая, добрая, вежливая} C = {Маша, Наташа};

d. В = {0, 00, 000} C = {1, 11, 111};

4. Для каждого из множеств, приведенных в предыдущем задании, составьте таблицу, в ячейках которой будут расположены элементы соответствующего декартова произведения.

5. Элементы какого декартова произведения множеств задания 3 бывают отмечены в декартовой системе координат? Выполните соответствующие построения.

6. Из множества Р = {1, 2, 3, 4, 5, 6, 7, 8, 9} выделили подмножества А, В и С. В каком случае произошло разбиение множества Р на классы:

a. А ={1, 3, 5}, В = {2, 4, 6, 8}, С = {7, 9};

b. А = {5}, В = {3, 4, 8, 9}, С = {1, 6};

c. А = {1, 3, 5}, В = {2, 4, 6, 8}, С = {5, 7, 9};

d. А = {1, 3}, В = {4, 6, 8}, С = {5, 6, 9}.

7. Запишите всœе двузначные числа, цифры десятков которых принадлежат множеству А ={4, 5, 6}, а цифры единиц – множеству В={3, 7}.

Задания для самостоятельной работы

1. Множество А состоит из 3, 4, 5, 6, 7, 8, 9; множество В – его подмножество, состоящее из чисел, которые делятся на 3; множество С – подмножество, состоящее из чисел, которые при делœении на 3 дают в остатке 1; множество Е – подмножество. Состоящее из чисел, которые при делœении на 3 дают в остатке 2. Можно ли утверждать, что множество А разбивается в данном случае на попарно непересекающиеся подмножества В, С и Е?

2. Проверьте, выполняются ли условия классификации, если: а) множество углов разбили на острые, тупые и прямые; б) множество звуков русского языка – на гласные и согласные.

3. Из множества Т треугольников выделили два подмножества: Х — подмножество прямоугольных треугольников и У – подмножество равнобедренных треугольников. Постройте для данных множеств круги Эйлера; установите, на сколько непересекающихся областей разбился круг, изображающий множество Т, и всœе множества, изображенные этими областями, задайте описанием характеристического свойства. При помощи скольких свойств произведено разбиение множества треугольников на классы?

4. Изобразите при помощи кругов Эйлера множество натуральных чисел и его подмножества: четных чисел и чисел, кратных 7. Можно ли утверждать, что множество N разбито:

a. на два класса: четных чисел и чисел, кратных 7;

b. на 4 класса: четных чисел, кратных 7; нечетных чисел, некратных 7; четных чисел, некратных 7; нечетных чисел, кратных 7?

5. Изобразите на координатной плоскости элементы декартова произведения множеств Х и У, если:

a. и ;

b. и ;

c. и У=R;

d. Х=R и .

6. Фигуры, приведенные на рисунке, являются результатом изображения накоординатной плоскости декартова произведения множеств Х и У. Укажите для каждой фигуры эти множества.

7.

8.

9.

10.

11.

12.

7. На координатной плоскости постройте прямую, проходящую через точку Р (-2, 3) и параллельную оси ОХ. Установите, декартово произведение каких двух множеств изображается на координатной плоскости в виде этой прямой.

8. Найдите декартовы произведения множеств и изобразите их элементы на координатной плоскости:

a. А = {х÷ хÎ R, х > 0}; В = {у÷ у Î R, у < 0}

b. А = {х÷ хÎ R, х = 2}; В={у÷ у Î R , у > 0}

c. А = {х÷ хÎ R, -1 < х < 1}; В={у÷ у Î R, 0 < у < 1}.

Правил делимости — 7 — Made Easy

Зеркало, зеркало на стене, кто из них самый умный? Злая ведьма, Белоснежка, или ее 7 друзей Оставайтесь с нами, чтобы увидеть, чем закончится эта история Ведьма думает, что это потрясающе сделать зелье, которое также обладает снотворным действием. С Белоснежкой в ​​стране грез, злая ведьма может раскрыть свой план. Есть только один глюк, заминка для ведьмы Чтобы избежать билета в один конец в рай, Белоснежка опирается на правила делимости для числа 7 .

Пытаясь обмануть Белоснежку, ведьма предлагает ей корзину, наполненную 15 восхитительно выглядящими яблоками. Белоснежка не знает, что яблоки пропитаны снотворным, но, тем не менее, отвергает их. Почему? Потому что она не может равномерно разделить 15 яблок между 7 гномами и не выбирает фаворитов. Ведьма не унывает. Так что на следующий же день она возвращается. На этот раз у нее есть тележка, полная яблок. Ведьма сомневается, что Белоснежка может быстро вычислить такое большое частное и просто решит принять тележку и ее ядовитое содержимое.Ведьма с гордостью заявляет, что у нее 543 яблока, больше, чем гномы и Белоснежка могут съесть. И снова Белоснежка отказывается, потому что она не может разделить яблок поровну на группы по 7 штук. Как она это определила так быстро?

Делимость на 7

Белоснежка владеет правилом делимости для числа 7 , поэтому ей не нужно всегда полагаться на деление в столбик. Чтобы проверить, делится ли число без остатка на на 7: Возьмите последнюю цифру числа, удвойте Затем вычтите из оставшейся части числа. Если полученное число равно , делится на 7 без остатка, то же самое и исходное число.Давайте попробуем трюк с количеством яблок в тележке, 543. Последняя цифра — 3, , удвоить , чтобы получилось 6, вычитает из 6 из оставшихся цифр . 54 минус 6 равно 48. 48 не делится на 7 без остатка, поэтому 543 не делится на 7 без остатка.

Давайте проверим, на всякий случай. 7 переходит в 54 семь раз. Вычтем 49 из 54, уменьшим 3, 7 превратится в 53 семь раз, вычтем 49 из 53, в результате останется 4. Итак, мы были правы! 543 не делится на 7 без остатка!

Снова обрушился.Что делать злой ведьме? Белоснежка просто перехитрила ее?

Злая ведьма не сдается. Она собирает все яблоки в королевстве, а точнее 2478, и доставляет их Белоснежке. Посмотрим. Хорошо. последняя цифра — 8. Удвоить , и мы получим 16. Вычтем 16 из 247. Разница составляет 231. Это все еще большое число, поэтому мы просто делаем те же шаги снова. Удвойте последнюю цифру , что равно 2, а 23 минус 2 равно 21. 21 равно , делимому на 7 без остатка, поэтому огромная кучка яблок должна делиться на без остатка на 7 ! 7 трижды превращается в 24, вычитаем 21 из 24, уменьшаем 7, 7 превращается в 37 пять раз.

Вычитание из 37 дает 2, а 7 дает 28 ровно 4 раза. Что ты знаешь? Белоснежка была права! 2478 делится на 7 без остатка!

Пока мы были заняты расчетами, 77 пирожков готовы и ждут. Подготовлено Белоснежкой с любовью и заботой, ее пироги известны повсюду и повсюду.И потому что она такая милая, она предлагает ведьме пирог, который невозможно победить.

функций — Целые числа, делящиеся на 5, но не делящиеся на 7, являются счетно бесконечными

Рассмотрим карту $ f: \ mathbb {N} \ backslash 7 \ mathbb {N} \ to \ mathbb {N} $, заданную как $ f (n) = n- \ left \ lfloor \ frac {n} {7} \ right \ rfloor $. Тогда, если $ f (n) = f (m) $ с $ n \ geq m $, имеем $$ mn = \ left \ lfloor \ frac {m} {7} \ right \ rfloor — \ left \ lfloor \ frac {n} {7} \ right \ rfloor \ geq \ left \ lfloor \ frac {mn} {7 } \ right \ rfloor \ подразумевает nm \ leq \ left \ lceil \ frac {nm} {7} \ right \ rceil $$ Но это может быть правдой, только если $ n = m $ или $ n = m + 1 $.Но если $ n = m + 1 $, то $ f (m) = f (m + 1) $, и поэтому $ \ left \ lfloor \ frac {m + 1} {7} \ right \ rfloor = \ left \ lfloor \ frac {m} {7} \ right \ rfloor + 1 \ подразумевает 7 | (m + 1) $, поэтому $ m + 1 $ не входит в область определения $ f $, что означает инъективность $ f $.

Далее, если $ n \ in \ mathbb {N} $, то $$ f \ left (n + \ left \ lfloor \ frac {n} {6} \ right \ rfloor \ right) = n + \ left \ lfloor \ frac {n} {6} \ right \ rfloor — \ left \ lfloor \ frac {1} {7} \ left (n + \ left \ lfloor \ frac {n} {6} \ right \ rfloor \ right) \ right \ rfloor = n + \ left \ lfloor \ frac {n} {6} \ right \ rfloor — \ left \ lfloor \ frac {1} {7} \ left \ lfloor \ frac {7n} {6} \ right \ rfloor \ right \ rfloor = n + \ left \ lfloor \ frac {n} { 6} \ right \ rfloor — \ left \ lfloor \ frac {n} {6} \ right \ rfloor = n $$

Принимая во внимание наши предыдущие вычисления, показывают, что если $ 7 | (n + \ left \ lfloor \ frac {n} {6} \ right \ rfloor) $, тогда также $ f (n + \ left \ lfloor \ frac {n} {6} \ right \ rfloor — 1) = n $ , это показывает, что $ f $ сюръективен. {-1}: \ mathbb {N} \ to 5 \ mathbb {N} \ backslash 7 \ mathbb {N} $ — это биекция натуральных чисел на кратные $ 5 $, взаимно простые с $ 7 $. В качестве альтернативы обратная карта, идущая в другом направлении: $ n \ mapsto f \ left (\ frac {n} {5} \ right) = \ frac {n} {5} — \ left \ lfloor \ frac {n} {35 } \ right \ rfloor $.

Это явно создает желаемую биекцию по желанию, но имейте в виду, что это не самый эффективный способ продемонстрировать, что $ 5 \ mathbb {N} \ backslash 7 \ mathbb {N} $ счётно бесконечен, и часто это кейс.В самом деле, даже для этого относительно простого набора, для которого интуитивно очевидно, что оно счетно бесконечно, явное построение карт уже раздражает. Более эффективный подход — это подход Д.Б. — показать, что он содержит одно счетно бесконечное множество (степени 5 $) и содержится в другом (сами натуральные числа).

Понимание преподавателями Preservice о JSTOR

Abstract

Это исследование способствует растущему количеству исследований, посвященных содержанию знаний учителей по математике.Исследуемая область — элементарная теория чисел. Наше основное внимание было уделено концепции делимости и ее связи с делением, умножением, простыми и составными числами, факторизацией, правилами делимости и разложением на простые числа. Мы использовали теоретическую основу, ориентированную на конструктивизм, для анализа и интерпретации данных, полученных в ходе клинических интервью с учителями preservice. Ответы участников на вопросы и задания указывали на повсеместную предрасположенность к процедурным привязанностям, даже когда была очевидна некоторая степень концептуального понимания.Результаты этого исследования дают предварительный обзор когнитивных структур в элементарной теории чисел.

Информация о журнале

JRME, официальный журнал Национального совета учителей математики (NCTM), является ведущим исследовательским журналом в области математического образования и посвящен интересам учителей и исследователей на всех уровнях — от дошкольного до колледжа.

Информация об издателе

Национальный совет учителей математики — это общественный голос в области математического образования, обеспечивающий видение, руководство и профессиональное развитие для поддержки учителей в обеспечении высочайшего качества обучения математике для всех учащихся.NCTM, насчитывающая около 90 000 членов и 250 аффилированных лиц, является крупнейшей в мире организацией, занимающейся улучшением математического образования в классах от дошкольного до 12-го класса. «Принципы и стандарты школьной математики» Совета являются руководящими указаниями по обеспечению высокого качества математического образования и призывают всех учащихся заниматься более сложной математикой. NCTM нацелен на постоянный диалог и конструктивное обсуждение со всеми заинтересованными сторонами того, что лучше всего для студентов нашей страны.

Если натуральное число делится на 7, то оно также должно делиться на 21

  • 4. Докажите, что n2 + 3n делится на 2 для всех натуральных чисел n 21.

    4. Докажите, что n2 + 3n делится на 2 для всех натуральных чисел n 21.

  • Найдите наименьшее число, делящееся на каждое натуральное число, меньшее или равное 10

    Найдите наименьшее число, делящееся на каждое натуральное число, меньшее или равное 10.

  • Определите, является ли утверждение истинным или ложным.

    Определите, истинно это утверждение или нет. Объясните или покажите, почему: если натуральное число делится на 7, то оно также должно делиться на 21.

  • Какое наименьшее число нужно добавить к 1056, чтобы получить число, точно делимое на 23

    Какое наименьшее число нужно добавить к 1056, чтобы получить число, точно делимое на 23?

  • какое наименьшее число нужно вычесть из 13601, чтобы получить число, в точности делимое на 87

    какое наименьшее число нужно вычесть из 13601, чтобы получить число, в точности делимое на 87?

  • Найдите число, которое делится на 17, 3 и 9, но не делится на 7, 18, 5, 16 и 14.

    Найдите число, которое делится на 17, 3 и 9, но не делится на 7, 18, 5, 16 и 14.(1) -1 = 4, что делится на четыре, поэтому …

  • * эти вопросы связаны с Matlab Число 24 точно делится на восемь чисел (т.е. 1, 2, 3, 4, 6, 8, 12 и 24). Число 273 также точно делится на восемь чисел (i ….

    * эти вопросы относятся к Matlab Число 24 точно делится на восемь чисел (например, 1, 2, 3, 4, 6, 8, 12 и 24). Число 273 также точно делится на восемь чисел (т. Е. 1, 3, 7, 13, 21, 39, 91 и 273). Есть 10 чисел в диапазоне 1: 100, которые точно делятся на восемь чисел (т.е. 24, 30, 40, 42, 54, 56, 66, 70, 78 и 88). Сколько чисел в диапазоне n-1: 20000 …

  • Какие из следующих условий необходимы, а какие условия достаточны для натуральное число…

    Какие из следующих условий необходимы, а какие условия достаточны для натуральное число n делится на 6. Натуральные числа равны N = {0,1,2, …}

  • Сколько 6-значных чисел можно образовать, если образовавшееся число должно быть делимым…

    Сколько 6-значных чисел можно образовать, если образовавшееся число должно делится на 5 или 2, И это число не может начинаться с 0, бывший. 0538 … нельзя? Какие возможны договоренности? ¿Cuántos números de 6 dígitos se pueden formar si el número formado debe ser divisible ya sea 5 o 2, Y este número no puede comenzar con un 0, e.x. 0538 … нет разрешения? ¿Куалес сын лос Возможные arreglos?

    • Делимость

    на 7 и ее доказательство

    Это шестой пост в серии правил делимости.В этом посте мы обсуждаем делимость на 7.

    Простые шаги необходимы, чтобы проверить, делится ли число на 7. Сначала умножьте крайнюю правую цифру (единицу) на 2, а затем вычтите произведение из оставшихся цифр. Если разница делится на 7, то число делится на 7.

    Пример 1: Делится ли 623 на 7?

    3 x 2 = 6
    62 — 6 = 56
    56 делится на 7, поэтому 623 делится на 7.

    Если после процесса, описанного выше, число все еще велико, и трудно узнать, делится ли оно на 7, шаги можно повторить.Мы берем разницу в качестве нового числа, мы умножаем крайнюю правую цифру на 2, а затем вычитаем из оставшихся цифр.

    Пример 2 : Делится ли 3423 на 7?

    3 x 2 = 6
    342 — 6 = 336

    Мы повторяем процесс для 336. Умножаем 6 на 2, а затем вычитаем из 33.

    6 x 2 = 12
    33 — 12 = 21
    21 делится на 7, поэтому 3423 делится на 7.

    Обратите внимание, что если число все еще велико, этот процесс можно повторять снова и снова, пока не удастся определить, делятся ли оставшиеся цифры на 7.

    Delving Deeper (для любителей приключений)

    Следующая часть предназначена для студентов, которые имеют базовые знания о доказательствах. В частности, мы будем доказывать утверждение тогда и только тогда, когда . A тогда и только тогда, когда B требует доказать, что A подразумевает B и B подразумевает A .

    Позвольте быть числом, которое мы хотим разделить на 7. Позвольте быть цифрой единицы и быть оставшейся частью цифры.Тогда N = 10 a + b .

    Пояснение: Все целые числа N можно выразить как произведение 10 и числа, добавленного к его цифре единиц. Например, 983 = 10 (98) + 3, 5896 = 10 (598) + 6 и так далее.

    Мы присваиваем следующие операторы A и B .

    A : a — 2 b делится на 7.
    B : N делится на 7.

    Как мы уже упоминали выше, мы должны показать, что (1) A подразумевает B и (2) B подразумевает A . Это означает, что мы должны показать, что если делится на, то делится на. Оператор — это шаг, на котором мы умножаем цифру единицы на 2, а затем вычитаем из оставшихся цифр.

    Для (1) мы должны показать, что A подразумевает B . То есть мы должны показать, что если делится на, то делится на.

    Доказательство

    Если делится на, то мы можем найти такое натуральное число, что (Вы понимаете, почему?).

    Умножаем обе стороны на, получаем. Сложив с двух сторон, у нас есть. Сейчас же, . Обратите внимание, что левая часть нашего уравнения равна, а правая часть может быть разделена на. Следовательно, делится на. Это доказывает наше первое утверждение о том, что If делится на, делится на. #

    Для (2) мы должны показать, что B подразумевает A .То есть мы должны показать, что если делится на 7, делится на.

    Доказательство

    Если делится на, то делится на. Это означает, что мы можем найти такое натуральное число, что. У нас есть вычитание с обеих сторон. Это означает, что . Факторинг, имеем

    Теперь, поскольку не делится на, делится на. Это доказывает второе утверждение: если делится на, то делится на #

    Из вышесказанного мы показали, что A подразумевает B и B подразумевает A .Мы показали, что процесс, который мы проделали выше, будет справедливым для всех случаев.

    3.3: Факторизация натуральных чисел на простые множители

    Цели обучения

    • уметь определять множители целого числа
    • уметь различать простые и составные числа
    • ознакомьтесь с основами арифметики
    • сможет найти разложение целого числа на простые множители

    Факторы

    Из наблюдений, сделанных в процессе умножения, мы увидели, что

    \ ((\ text {factor}) \ cdot (\ text {factor}) = \ text {product} \)

    Факторы, Произведение
    Два умножаемых числа — это факторов , а результат умножения — произведение . Теперь, используя наши знания о делении, мы можем видеть, что первое число является множителем второго числа, если первое число делится на второе число целое число раз (без остатка).

    Одно число как множитель Еще
    Первое число — это множитель второго числа, если первое число делится на второе число целое число раз (без остатка).

    Мы показываем это на следующих примерах:

    Пример \ (\ PageIndex {1} \)

    3 — это коэффициент 27, поскольку \ (27 \ div 3 = 9 \) или \ (3 \ cdot 9 = 27 \).

    Пример \ (\ PageIndex {2} \)

    7 — это коэффициент 56, поскольку \ (56 \ div 7 = 8 \) или \ (7 \ cdot 8 = 56 \).

    Пример \ (\ PageIndex {3} \)

    4 равно , а не , коэффициенту 10, поскольку \ (10 ​​\ div 4 = \ text {2R2} \). (Есть остаток.) ​​

    Определение множителей целого числа

    Мы можем использовать тесты на делимость из [ссылка] , чтобы определить всех делителей целого числа.

    Образец набора A

    Найдите все множители 24.

    Решение

    \ (\ begin {array} {lll} {\ text {Попробуйте 1:}} & {24 \ div 1 = 24} & {\ text {1 и 24 являются множителями}} \\ {\ text {Попробуйте 2: }} & {\ text {24 четное число, поэтому 24 делится на 2.}} & {} \\ {} & {24 \ div 2 = 12} & {\ text {2 и 12 являются множителями}} \\ {\ text {Попробуйте 3:}} & {2 + 4 = 6 \ text {и 6 делится на 3, поэтому 24 делится на 3.}} & {} \\ {} & {24 \ div 3 = 8 } & {\ text {3 и 8 — множители}} \\ {\ text {Попробуйте 4:}} & {24 \ div 4 = 6} & {\ text {4 и 6 — множители}} \\ {\ text {Попробуйте 5:}} & {24 \ div 5 = \ text {4R4}} & {\ text {5 не является фактором}} \ end {array} \)

    Следующее число, которое нужно попробовать, — 6, но у нас уже есть 6 — фактор.Как только мы обнаружим фактор, который мы уже обнаружили, мы можем остановиться.

    Все целые числовые множители числа 24 равны 1, 2, 3, 4, 6, 8, 12 и 24.

    Практический набор A

    Найдите все множители каждого из следующих чисел.

    6

    Ответ

    1, 2, 3, 6

    Практический набор A

    12

    Ответ

    1, 2, 3, 4, 6, 12

    Практический набор A

    18

    Ответ

    1, 2, 3, 6, 9, 18

    Практический набор A

    5

    Ответ

    1, 5

    Практический набор A

    10

    Ответ

    1, 2, 5, 10

    Практический набор A

    33

    Ответ

    1, 3, 11, 33

    Практический набор A

    19

    Ответ

    1, 19

    Простые и составные числа

    Обратите внимание, что единственными множителями 7 являются сами 1 и 7, а единственными множителями 3 являются сами 1 и 3.Однако у числа 8 есть множители 1, 2, 4 и 8, а у числа 10 есть множители 1, 2, 5 и 10. Таким образом, мы можем видеть, что целое число может иметь только двух множителей ( само и 1) и еще одно целое число может иметь несколько множителей .

    Мы можем использовать это наблюдение, чтобы сделать полезную классификацию целых чисел: простых и составных чисел.

    Определение: простое число

    Целое число (больше единицы), единственными делителями которого являются он сам и 1, называется простым числом .

    Число 1 — это Не простое число
    Первые семь простых чисел — это 2, 3, 5, 7, 11, 13 и 17. Обратите внимание, что целое число 1 — это , а не , которое считается простым. число, а целое число 2 — это первое простое число , а — только четное простое число .

    Определение: составное число

    Целое число, состоящее из факторов, отличных от него самого и единицы, называется составным числом . Составные числа не являются простыми числами.

    Некоторые составные числа: 4, 6, 8, 9, 10, 12 и 15.

    Образец набора B

    Определите, какие целые числа простые, а какие составные.

    39. Поскольку 3 делится на 39, число 39 составное: \ (39 \ div 3 = 13 \)

    Образец набора B

    47. Несколько попыток деления убедят нас, что 47 делится только на 1 и 47. Следовательно, 47 простое.

    Практический набор B

    Определите, какие из следующих целых чисел являются простыми, а какие — составными.

    3

    Ответ

    премьер

    Практический набор B

    16

    Ответ

    композит

    Практический набор B

    21

    Ответ

    композит

    Практический набор B

    35

    Ответ

    композит

    Практический набор B

    47

    Ответ

    премьер

    Практический набор B

    29

    Ответ

    премьер

    Практический набор B

    101

    Ответ

    премьер

    Практический набор B

    51

    Ответ

    композит

    Основные принципы арифметики

    Простые числа очень полезны при изучении математики.Мы увидим, как они используются, в следующих разделах. Теперь сформулируем основной принцип арифметики.

    Фундаментальный принцип арифметики
    За исключением порядка множителей, каждое натуральное число, кроме 1, может быть разложено на множители одним и только одним способом как произведение простых чисел.

    Определение: простое факторизация

    Когда число разложено на множители так, что все его множители являются простыми числами. факторизация называется простой факторизацией числа.

    Техника разложения на простые множители проиллюстрирована в следующих трех примерах.

    \ (10 ​​= 5 \ cdot 2 \). И 2, и 5 — простые числа. Следовательно, \ (2 \ cdot 5 \) — разложение на простые множители 10.
    11. Число 11 — простое число. Факторизация на простые множители применяется только к составным числам. Таким образом, 11 не имеет разложения на простые множители .
    \ (60 = 2 \ cdot 30 \). Число 30 не простое: \ (30 = 2 \ cdot 15 \).

    \ (60 = 2 \ cdot 2 \ cdot 15 \)

    Число 15 не простое: \ (15 = 3 \ умножить на 5 \)

    \ (60 = 2 \ CDOT 2 \ CDOT 3 \ CDOT 5 \)

    Мы будем использовать экспоненты.2 \ cdot 3 \ cdot 5 \) — разложение на простые множители 60.

    Факторизация натурального числа на простые множители

    Следующий метод позволяет найти разложение натурального числа на простые множители.

    Метод определения простого факторизации натурального числа

    1. Разделите число несколько раз на наименьшее простое число, которое разделит его целое число раз (без остатка).
    2. Когда простое число, используемое на шаге 1, больше не делится на данное число без остатка, повторите процесс деления со следующим по величине простым числом, которое делит данное число.
    3. Продолжайте этот процесс, пока частное не станет меньше делителя.
    4. Разложение данного числа на простые множители дает произведение всех этих простых делителей. Если число не имеет простых делителей, это простое число.

    Возможно, мы сможем использовать некоторые из тестов на делимость, которые мы изучили в [ссылка] , чтобы найти простые числа, которые делят данное число.

    Образец набора C

    Найдите разложение 60 на простые множители.

    Решение

    Поскольку последняя цифра 60 равна 0, что является четным, 60 делится на 2. Мы будем многократно делить на 2, пока не перестанем. Разделим следующим образом:

    \ (\ begin {array} {l} {\ text {30 снова делится на 2}} \\ {\ text {15 не делится на 2, но делится на 3, следующее простое число}} \\ {\ text {5 не делится на 3, но делится на 5, следующее простое число.}} \ end {array} \)

    Частное 1, наконец, меньше делителя 5, а факторизация 60 на простые множители является произведением этих простых делителей.2 \ CDOT 3 \ CDOT 5 \)

    Образец набора C

    Найдите разложение 441 на простые множители.

    Решение

    441 не делится на 2, так как его последняя цифра не делится на 2.

    441 делится на 3, поскольку \ (4 + 4 + 1 = 9 \) и 9 делится на 3.

    \ (\ begin {array} {l} {\ text {147 делится на} 3 (1 + 4 + 7 = 12).} \\ {\ text {49 не делится на 3 и не делится на 5. Он делится на 7.}} \ end {array} \)

    Частное 1, наконец, меньше делителя 7, а разложение 441 на простые множители является произведением этих простых делителей.2 \)

    Образец набора C

    Найдите разложение 31 на простые множители.

    Решение

    \ (\ begin {array} {ll} {\ text {31 не делится на 2}} & {\ text {Его последняя цифра нечетная}} \\ {} & {31 \ div 2 = \ text { 15R1}} \\ {} & {\ text {Частное 15 больше делителя 3. Продолжить.}} \\ {\ text {31 не делится на 3}} & {\ text {Цифры } 3 + 1 = 4, \ text {и 4 не делится на 3.}} \\ {} & {31 \ div 3 = \ text {10R1}} \\ {} & {\ text {Частное, 10 , больше делителя 3.Продолжить.}} \\ {\ text {31 не делится на 5}} & {\ text {Последняя цифра 31 не равна 0 или 5.}} \\ {} & {31 \ div 5 = \ text { 6R1}} \\ {} & {\ text {Частное 6 больше делителя 5. Продолжить.}} \\ {\ text {31 не делится на 7.}} & {\ text {Divide на 7.}} \\ {} & {31 \ div 7 = \ text {4R1}} \\ {} & {\ text {Частное, 4 меньше делителя, 7.}} \\ {} & {\ text {Мы можем остановить процесс и сделать вывод, что 31 — простое число.}} \ end {array} \)

    Число 31 — простое число

    Практический набор C

    Найдите разложение каждого целого числа на простые множители.2 \ cdot 11 \)

    Практический набор C

    17

    Ответ

    17 простое

    Практический набор C

    61

    Ответ

    61 простое

    Упражнения

    Для следующих проблем определите недостающий фактор (факторы).

    Упражнение \ (\ PageIndex {1} \)

    \ (14 = 7 \ cdot \)

    Ответ

    2

    Упражнение \ (\ PageIndex {2} \)

    \ (20 = 4 \ cdot \)

    Упражнение \ (\ PageIndex {3} \)

    \ (36 = 9 \ cdot \)

    Ответ

    4

    Упражнение \ (\ PageIndex {4} \)

    \ (42 = 21 \ cdot \)

    Упражнение \ (\ PageIndex {5} \)

    \ (44 = 4 \ cdot \)

    Ответ

    11

    Упражнение \ (\ PageIndex {6} \)

    \ (38 = 2 \ cdot \)

    Упражнение \ (\ PageIndex {7} \)

    \ (18 = 3 \ cdot \).

    Ответ

    \ (3 \ cdot 2 \)

    Упражнение \ (\ PageIndex {8} \)

    \ (28 = 2 \ cdot \).

    Упражнение \ (\ PageIndex {9} \)

    \ (300 = 2 \ cdot 5 \ cdot \).

    Ответ

    \ (2 \ CDOT 3 \ CDOT 5 \)

    Упражнение \ (\ PageIndex {10} \)

    \ (840 = 2 \ cdot \).

    Для следующих задач найдите все множители каждого из чисел.

    Упражнение \ (\ PageIndex {11} \)

    16

    Ответ

    1, 2, 4, 8, 16

    Упражнение \ (\ PageIndex {12} \)

    22

    Упражнение \ (\ PageIndex {13} \)

    56

    Ответ

    1, 2, 4, 7, 8, 14, 28, 56

    Упражнение \ (\ PageIndex {14} \)

    105

    Упражнение \ (\ PageIndex {15} \)

    220

    Ответ

    1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110, 220

    Упражнение \ (\ PageIndex {16} \)

    15

    Упражнение \ (\ PageIndex {17} \)

    32

    Ответ

    1, 2, 4, 8, 16, 32

    Упражнение \ (\ PageIndex {18} \)

    80

    Упражнение \ (\ PageIndex {19} \)

    142

    Ответ

    1, 2, 71, 142

    Упражнение \ (\ PageIndex {20} \)

    218

    Для следующих задач определите, какие из целых чисел являются простыми, а какие составными.

    Упражнение \ (\ PageIndex {21} \)

    23

    Ответ

    премьер

    Упражнение \ (\ PageIndex {22} \)

    25

    Упражнение \ (\ PageIndex {23} \)

    27

    Ответ

    композит

    Упражнение \ (\ PageIndex {24} \)

    2

    Упражнение \ (\ PageIndex {25} \)

    3

    Ответ

    премьер

    Упражнение \ (\ PageIndex {26} \)

    5

    Упражнение \ (\ PageIndex {27} \)

    7

    Ответ

    премьер

    Упражнение \ (\ PageIndex {28} \)

    9

    Упражнение \ (\ PageIndex {29} \)

    11

    Ответ

    премьер

    Упражнение \ (\ PageIndex {30} \)

    34

    Упражнение \ (\ PageIndex {31} \)

    55

    Ответ

    составной (\ (5 \ cdot 11 \))

    Упражнение \ (\ PageIndex {32} \)

    63

    Упражнение \ (\ PageIndex {33} \)

    1,044

    Ответ

    композит

    Упражнение \ (\ PageIndex {34} \)

    924

    Упражнение \ (\ PageIndex {35} \)

    339

    Ответ

    композит

    Упражнение \ (\ PageIndex {36} \)

    103

    Упражнение \ (\ PageIndex {37} \)

    209

    Ответ

    составной \ ((11 \ cdot 19) \)

    Упражнение \ (\ PageIndex {38} \)

    667

    Упражнение \ (\ PageIndex {39} \)

    4,575

    Ответ

    композит

    Упражнение \ (\ PageIndex {40} \)

    119

    Для следующих задач найдите разложение каждого целого числа на простые множители.2 \)

    Упражнение \ (\ PageIndex {50} \)

    148,225

    Упражнения на обзор

    Упражнение \ (\ PageIndex {51} \)

    Округлите 26 584 до ближайшей десятки.

    Ответ

    26 580

    Упражнение \ (\ PageIndex {52} \)

    Насколько 106 больше 79?

    Упражнение \ (\ PageIndex {53} \)

    Верно или нет? Ноль, деленный на любое ненулевое целое число, равен нулю.2 \ div 3 \).

    Ответ

    14

    Правила делимости (тесты)

    Легко проверить, можно ли точно разделить одно число на другое

    делится на

    «Делится на» означает «при делении одного числа на другое получается целое число»

    Примеры:

    14 — это , делимое на 7, потому что 14 ÷ 7 = 2 ровно

    15 — это , а не , делимое на 7, потому что 15 ÷ 7 = 2 1 7 (результат , а не целое число)

    0 — это , делимое на 7, потому что 0 ÷ 7 = 0 ровно (0 — целое число)

    «Может быть разделено на» и «может быть разделено на» означает одно и то же.

    Правила делимости

    Эти правила позволяют проверить, делится ли одно число на другое, без необходимости выполнять слишком много вычислений!

    Пример: делится ли 723 на 3?

    Можно попробовать разделить 723 на 3

    Или используйте правило «3»: 7 + 2 + 3 = 12 и 12 ÷ 3 = 4 точно Да

    Примечание. Ноль делится на любого числа (кроме самого себя), поэтому мы получаем «да» на все эти тесты.

    1

    Любое целое число (не дробное) делится на 1


    2

    Последняя цифра четная (0,2,4,6,8)

    12 8 Есть

    12 9 №

    3

    Сумма цифр делится на 3

    381 (3 + 8 + 1 = 12 и 12 ÷ 3 = 4) Да

    217 (2 + 1 + 7 = 10 и 10 ÷ 3 = 3 1 / 3 ) №

    Это правило можно повторить при необходимости:

    99996 (9 + 9 + 9 + 9 + 6 = 42, затем 4 + 2 = 6) Да

    4

    Последние 2 цифры делятся на 4

    13 12 равно (12 ÷ 4 = 3) Да

    70 19 не равно (19 ÷ 4 = 4 3 / 4 ) Нет

    Быстрая проверка (полезная для небольших чисел) состоит в том, чтобы вдвое уменьшить число вдвое, и результатом будет целое число.

    12/2 = 6, 6/2 = 3, 3 — целое число. Есть

    30/2 = 15, 15/2 = 7,5, что не является целым числом. №

    5

    Последняя цифра 0 или 5

    17 5 Есть

    80 9 №

    6

    Четно и делится на 3 (проходит как правило 2, так и правило 3 выше)

    114 (четно, и 1 + 1 + 4 = 6 и 6 ÷ 3 = 2) Да

    308 (четно, но 3 + 0 + 8 = 11 и 11 ÷ 3 = 3 2 / 3 ) №

    7

    Удвойте последнюю цифру и вычтите ее из числа, образованного другими цифрами.Результат должен делиться на 7. (Мы можем снова применить это правило к этому ответу)

    672 (Двойное 2 равно 4, 67−4 = 63 и 63 ÷ 7 = 9) Да

    105 (Двойная 5 равна 10, 10−10 = 0, а 0 делится на 7) Да

    905 (Двойное 5 равно 10, 90-10 = 80 и 80 ÷ 7 = 11 3 / 7 ) №

    8

    Последние три цифры делятся на 8

    109 816 (816 ÷ 8 = 102) Есть

    216 302 (302 ÷ 8 = 37 3 / 4 ) №

    Быстрая проверка — это трижды уменьшить вдвое, и результат все равно будет целым числом:

    816/2 = 408, 408/2 = 204, 204/2 = 102 Да

    302/2 = 151, 151/2 = 75.5 №

    9

    Сумма цифр делится на 9

    (Примечание: это правило может быть повторено при необходимости)

    1629 (1 + 6 + 2 + 9 = 18, и снова 1 + 8 = 9) Да

    2013 (2 + 0 + 1 + 3 = 6) №

    10

    Число заканчивается на 0

    22 0 Есть

    22 1 №

    11

    Сложить и вычесть цифры поочередно (добавить цифру, вычесть следующую цифру, добавить следующую цифру и т. Д.).Затем проверьте, делится ли этот ответ на 11.

    1 3 6 4 (+ 1−3 + 6−4 = 0 ) Да

    9 1 3 (+ 9−1 + 3 = 11 ) Есть

    3 7 2 9 (+ 3−7 + 2−9 = −11 ) Да

    9 8 7 (+ 9-8 + 7 = 8 ) №

    12

    Число делится на 3 и 4 (он проходит как правило 3, так и правило 4 выше)

    648
    ( По 3? 6 + 4 + 8 = 18 и 18 ÷ 3 = 6 Да)
    (По 4? 48 ÷ 4 = 12 Да)
    Оба пройдены, поэтому Да

    524
    ( По 3? 5 + 2 + 4 = 11, 11 ÷ 3 = 3 2 / 3 Нет)
    (Нет необходимости проверять по 4) Нет

    Есть еще много всего! Существуют не только тесты на делимость для больших чисел, но и другие тесты для чисел, которые мы показали.