A 2 b 2 как решить: Формулы сокращенного умножения с примерами

Формулы сокращенного умножения с примерами

Формулами сокращенного умножения (ФСУ) называют несколько наиболее часто встречающихся в практике случаев умножения многочленов.

ФСУ используются при упрощении алгебраических выражений (в том числе в работе с алгебраическими дробями), решении уравнений и неравенств, при разложении на множители и т.д. Ниже мы рассмотрим наиболее популярные формулы и разберем как они получаются.

Квадрат суммы

Пусть у нас возводиться в квадрат сумма двух одночленов, вот так: \((a+b)^2\). Возведение в квадрат – это умножение числа или выражения само на себя, то есть, \((a+b)^2=(a+b)(a+b)\). Теперь мы можем просто раскрыть скобки, перемножив их как делали это здесь, и привести подобные слагаемые. Получаем:

А если мы опустим промежуточные вычисления и запишем только начальное и конечное выражения, получим окончательную формулу:

Квадрат суммы: \((a+b)^2=a^2+2ab+b^2\)

Большинство учеников учат ее наизусть. А вы теперь знаете, как эту формулу вывести, и если вдруг забудете – всегда можете это сделать.
Хорошо, но как ей пользоваться и зачем эта формула нужна? Квадрат суммы позволяет быстро писать результат возведения суммы двух слагаемых в квадрат. Давайте посмотрим на примере.

Пример. Раскрыть скобки: \((x+5)^2\)
Решение:

Обратите внимание, насколько быстрее и меньшими усилиями получен результат во втором случае. А когда вы эту и другие формулы освоите до автоматизма – будет еще быстрее: вы сможете просто сразу же писать ответ. Поэтому они и называются формулы СОКРАЩЕННОГО умножения. Так что, знать их и научиться применять – точно стоит.

На всякий случай отметим, что в качестве \(a\) и \(b\) могут быть любые выражения – принцип остается тем же. Например:

Если вы вдруг не поняли какие-то преобразования в двух последних примерах – повторите свойства степеней и тему приведения одночлена к стандартному виду.

Пример. Преобразуйте выражение \((1+5x)^2-12x-1 \) в многочлен стандартного вида.

Решение:

\((1+5x)^2-12x-1= \)		Раскроем скобки, воспользовавшись формулой квадрата суммы…
\(=1+10x+25x^2-12x-1=\)		…и приведем подобные слагаемые.
\(=25x^2-2x\)		Готово.

Ответ: \(25x^2-2x\).

Важно! Необходимо научиться пользоваться формулами не только в «прямом», но и в «обратном» направлении.

Пример. Вычислите значение выражения \((368)^2+2·368·132+(132)^2\) без калькулятора.

Решение:

\((368)^2+2·368·132+(132)^2=\)		Мда… возводить в квадрат трехзначные числа, перемножить их же, а потом все это складывать – удовольствие ниже среднего. Давайте искать другой путь: обратите внимание, что данное нам числовое выражение очень похоже на правую часть формулы. Применим ее в обратную сторону: \(a^2+2ab+b^2=(a+b)^2\)
\(=(368+132)^2=\)		Вот теперь вычислять гораздо приятнее!
\(=(500)^2=250 000.\)		Готово.

Ответ: \(250 000\).

Квадрат разности

Выше мы нашли формулу для суммы одночленов. Давайте теперь найдем формулу для разности, то есть, для \((a-b)^2\):

В более краткой записи имеем:

Квадрат разности: \((a-b)^2=a^2-2ab+b^2\)

Применяется она также, как и предыдущая.

Пример. Упростите выражение \((2a-3)^2-4(a^2-a)\) и найдите его значение при \(a=\frac{17}{8}\).

Решение:

\((2a-3)^2-4(a^2-a)=\)		Если сразу подставить дробь в выражение – придется возводить ее в квадрат и вообще делать объемные вычисления. Попробуем сначала упростить выражение, воспользовавшись формулой выше и раскрыв скобки.
\(=4a^2-12a+9-4a^2+4a=\)		Теперь приведем подобные слагаемые.
\(=-8a+9=\)		Вот теперь подставляем и наслаждаемся простотой вычислений.
\(=-8·\frac{17}{8}+9=-17+9=8\)		Пишем ответ.

Ответ: \(8\).

Разность квадратов

Итак, мы разобрались с ситуациями произведения двух скобок с плюсом в них и двух скобок с минусом. Остался случай произведения одинаковых скобок с разными знаками. Смотрим, что получится:

Получили формулу:

Разность квадратов \(a^2-b^2=(a+b)(a-b)\)

Эта формула одна из наиболее часто применяемых при разложении на множители и работе с алгебраическими дробями. 

Пример. Сократите дробь \(\frac{x^2-9}{x-3}\).

Решение:

\(\frac{x^2-9}{x-3}\)\(=\)		Да, я знаю, что рука так и тянется сократить иксы и девятку с тройкой – однако так делать ни в коем случае нельзя, ведь и в числителе, и в знаменателе стоит минус! Попробуем воспользоваться формулой.
\(=\) \(\frac{x^2-3^2}{x-3}\)\(=\)\(\frac{(x+3)(x-3)}{x-3}\)\(=\)		Вот теперь все плюсы и минусы попрятались в скобки, и значит без проблем можем сокращать одинаковые скобки.
\(=x+3\)		Готов ответ.

Ответ: \(x+3\).

Пример.Разложите на множители \(25x^4-m^{10} t^6\).
Решение:

\(25x^4-m^{10} t^6\)		Воспользуемся формулами степеней: \((a^n )^m=a^{nm}\) и \(a^n b^n=(ab)^n\).
\(=(5x^2 )^2-(m^5 t^3 )^2=\)		Ну, а теперь пользуемся формулой \(a^2-b^2=(a+b)(a-b)\), где \(a=5x^2\) и \(b=m^5 t^3\).
\(=(5x^2-m^5 t^3 )(5x^2+m^5 t^3 )\)		Готов ответ.

Это три основные формулы, знать которые нужно обязательно! Есть еще формулы с кубами (см. выше), их тоже желательно помнить либо уметь быстро вывести. Отметим также, что в практике часто встречаются сразу несколько таких формул в одной задаче – это нормально. Просто приучайтесь замечать формулы и аккуратно применяйте их, и все будет хорошо.

Пример (повышенной сложности!).Сократите дробь \(\frac{x^2-4xy-9+4y^2}{x-2y+3}\) .
Решение:

\(\frac{x^2-4xy-9+4y^2}{x-2y+3}\)\(=\)		На первый взгляд тут тихий ужас и сделать с ним ничего нельзя (вариант «лечь и помереть» всерьез не рассматриваем). Однако давайте попробуем поменять два последних слагаемых числителя местами и добавим скобки (просто для наглядности).
\(\frac{(x^2-4xy+4y^2)-9}{x-2y+3}\)\(=\)		Теперь немного преобразуем слагаемые в скобке: \(4xy\) запишем как \(2·x·2y\), а \(4y^2\) как \((2y)^2\).
\(\frac{(x^2-4xy+(2y)^2)-9}{x-2y+3}\)\(=\)		Теперь приглядимся – и заметим, что в скобке у нас получилась формула квадрата разности, у которой \(a=x\), \(b=2y\). Сворачиваем по ней к виду скобки в квадрате. И одновременно представляем девятку как \(3\) в квадрате.
\(\frac{(x-2y)^2-3^2}{x-2y+3}\)\(=\)		Еще раз внимательно смотрим на числитель… думаем… думаем… и замечаем формулу разности квадратов, у которой \(a=(x-2y)\), \(b=3\). Раскладываем по ней к произведению двух скобок.
\(\frac{(x-2y-3)(x-2y+3)}{x-2y+3}\)\(=\)		И вот теперь сокращаем вторую скобку числителя и весь знаменатель.
\(x-2y-3\)		Готов ответ.

Скачать статью

Формулы сокращенного умножения

Формулы сокращенного умножения.

Цели:

— Изучение формул сокращенного умножения: квадрата суммы и квадрата разности двух выражений; разности квадратов двух выражений; куба суммы и куба разности двух выражений; суммы и разности кубов двух выражений.

— Применение формул сокращенного умножения при решении примеров.

Для упрощения выражений, разложения многочленов на множители, приведения многочленов к стандартному виду используются формулы сокращенного умножения. Формулы сокращенного умножения нужно знать наизусть.

Пусть а, b   R. Тогда:

1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

(a + b)² = a² + 2ab + b²

2. Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

(a — b)² = a² — 2ab + b²

3. Разность квадратов двух выражений равна произведению разности этих выражений и их суммы.

a² — b² = (a -b) (a+b)

4. Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

(a + b)³ = a³ + 3a²b + 3ab² + b³

5. Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

(a — b)³ = a³ — 3a²b + 3ab² — b³

6. Сумма кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений.

a³ + b³ = (a + b) (a² — ab + b²)

7. Разность кубов двух выражений равна произведению разности первого и второго выражения на неполный квадрат суммы этих выражений.

a³ — b³ = (a — b) (a² + ab + b²)

Применение формул сокращенного умножения при решении примеров.

Пример 1.

Вычислить

а) (40+1)²

б) 98²

Решение:

а) Используя формулу квадрата суммы двух выражений, имеем

(40+1)² = 40² + 2 · 40 · 1 + 1² = 1600 + 80 + 1 = 1681

б) Используя формулу квадрата разности двух выражений, получим

98² = (100 – 2)² = 100²

— 2 · 100 · 2 + 2² = 10000 – 400 + 4 = 9604

Пример 2.

Вычислить

Решение

Используя формулу разности квадратов двух выражений, получим

Пример 3.

Упростить выражение

(х — у)² + (х + у)²

Решение

Воспользуемся формулами квадрата суммы и квадрата разности двух выражений

(х — у)² + (х + у)² = х² — 2ху + у² + х² + 2ху + у² = 2х² + 2у²

 

Формулы сокращенного умножения в одной таблице:

(a + b)² = a² + 2ab + b²
(a — b)² = a² — 2ab + b²
a² — b² = (a — b) (a+b)
(a + b)³ = a³ + 3a²b + 3ab² + b³
(a — b)³ = a³ — 3a²b + 3ab² — b³
a³ + b³ = (a + b) (a² — ab + b²)
a³ — b³ = (a — b) (a² + ab + b²)

Формулы сокращенного умножения / Блог :: Бингоскул

Содержание:

• Таблица формул сокращенного умножения
• Примеры использования
• Формулы для квадратов
• Формулы для кубов
• Формулы для четвертой степени

Таблица формул сокращенного умножения

Примеры использования формул

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

(a+b)² = a²+2ab+b²

Пример: (x + 3y)² = x² + 2 ·x·3y + (3y)² = x² + 6xy + 9y²

---

 

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

(a-b)² = a²-2ab+b²

Пример: (4x –y)² = (4x)²-2·4x·y + y² = 16x² — 8xy + y²

---

Разность квадратов двух выражений равна произведению разности самих выражений на их сумму.

a²–b² = (a–b)(a+b)

Пример: 9x² – 16y² = (3x)² – (4y)² = (3x – 4y)(3x + 4y)

---

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

(a+b)³ = a³+3a²b+3ab²+b³

Пример: (x + 2y)³ = x³ + 3·x²·2y + 3·x·(2y)² + (2n)³ = x³ + 6x²y + 12xy² + 8y³

---

Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

(a-b)³ = a³— 3a²b+3ab²

-b³

Пример: (2x – y)³ = (2x)³-3·(2x)²·y + 3·2x·y² – y³ = 8x³ – 12x²y + 6xy² – y³

---

Сумма кубов двух выражений равна произведению суммы самих выражений на неполный квадрат их разности.

a³+b³ = (a+b)(a²–ab+b²)

Пример: 125 + 8y³ = 5³ + (2y)³ = (5 + 2y)(5² — 5·2y + (2y)²) = (5 + 2y)(25 – 10y + 4y²)

---

Разность кубов двух выражений равна произведению разности самих выражений на неполный квадрат их суммы.

a³— b

3 = (a-b)(a²+ab+b²)

Пример: 64x³ – 8 = (4x)³ – 2³ = (4x – 2)((4x)² + 4x·2 + 2²) = (4x – 2)(16x² + 8x + 4)

---

Формулы для квадратов

• (a \pm b)^2= a^2 \pm 2ab + b^2
• a^2 — b^2 = (a + b)(a — b)
• (a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc

 

Формулы для кубов

• (a \pm b)^3= a^3 \pm 3a^2b +3ab^2 \pm b^3
• a^3 — b^3 = (a \pm b)(a^2\mp ab+b^2)
• (a+b+c)^3=a^3+b^3+c^3+3a^2b+3a^2c+3ab^2+3ac^2+3b^2c+3bc^2+6abc

Формулы для четвертой степени

• (a \pm b)^4= a^4 \pm 4a^3b +6a^2b^2\pm 4ab^3+b^4
• a^4 — b^4 = (a-b)(a+b)(a^2 +b^2) (выводится из a^2 — b^2)

 

---

В заданиях ЕГЭ по математике применяются формулы сокращенного умножения.

Решай с ответами задание 5 по математике база ЕГЭ

Смотри также: Основные формулы по математике

Формулы сокращенного умножения

Для того что бы упростить алгебраические многочлены, существуют формулы сокращенного умножения. Их не так уж и много и они легко запоминаются, а запомнить их нужно. Обозначения которые используются в формулах, могут принимать любой вид (число или многочлен).

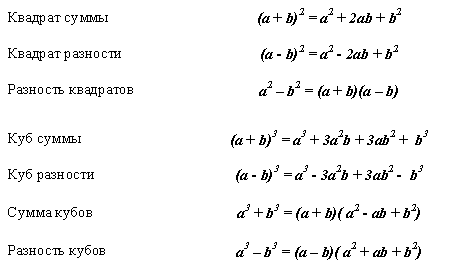
Первая формула сокращенного умножения называется разность квадратов. Она заключается в том что из квадрата одного числа отнимается квадрат второго числа равен величине разности данных чисел, а также их произведению.

а² — b² = (а — b)(a + b)

Разберем для наглядности:

22² — 4² = (22-4)(22+4)=18 * 26 = 468
9а² — 4b²c² = (3a — 2bc)(3a + 2bc)

Вторая формула о сумме квадратов. Звучит она как, сумма двух величин в квадрате равняется квадрату первой величины к ней прибавляется двойное произведение первой величины умноженное на вторую, к ним прибавляется квадрат второй величины.

(а + b)² = a² +2ab + b²

Благодаря данной формуле, становится намного проще вычислять квадрат от большого числа, без использования вычислительной техники.

Так к примеру: квадрат от 112 будет равен
1) В начале разберем 112 на числа квадраты которых нам знакомы
112 = 100 + 12
2) Вписываем полученное в скобки возведенные в квадрат
112² = (100+12)²
3) Применяя формулу, получаем:
112² = (100+12)² = 100² + 2 * 100 * 12 + 122 = 10000 + 2400+ 144 = 12544

Третья формула это квадрат разности. Которая гласит о том, что две вычитаемые друг друга величины в квадрате равняются, тому что, от первой величины в квадрате отнимаем двойное произведение первой величины умноженное на вторую, прибавляя к ним квадрат второй величины.

(а +b)² = а² — 2аb + b²

где (а — b)² равняется (b — а)². В доказательство чему, (а-b)² = а²-2аb+b² = b²-2аb + а² = (b-а)²

Четвертая формула сокращенного умножения называется куб суммы. Которая звучит как: две слагаемые величины в кубе равны кубу 1 величины прибавляется тройное произведение 1 величины в квадрате умноженное на 2-ую величину, к ним прибавляется тройное произведение 1 величины умноженной на квадрат 2 величины, плюс вторая величина в кубе.

(а+b)³ = а³ + 3а²b + 3аb² + b³

Пятая, как вы уже поняли называется куб разности. Которая находит разности между величинами, как от первого обозначения в кубе отнимаем тройное произведение первого обозначения в квадрате умноженное на второе, к ним прибавляется тройное произведение первого обозначения умноженной на квадрат второго обозначения, минус второе обозначение в кубе.

(а-b)³ = а³ — 3а²b + 3аb² — b³

Шестая называется — сумма кубов. Сумма кубов равняется произведению двух слагаемых величин, умноженных на неполный квадрат разности, так как в середине нет удвоенного значения.

а³ + b³ = (а+b)(а²-аb+b²)

По другому можно сказать сумму кубов можно назвать произведение в двух скобках.

Седьмая и заключительная, называется разность кубов (ее легко перепутать с формулой куба разности, но это разные вещи). Разность кубов равняется произведению от разности двух величин, умноженных на неполный квадрат суммы, так как в середине нет удвоенного значения.

а³ — b³ = (а-b)(а²+аb+b²)

И так формул сокращенного умножения всего 7, они похожи друг на друга и легко запоминаются, единственно важно не путаться в знаках. Они так же рассчитаны на то, что их можно использовать в обратном порядке и в учебниках собрано довольно много таких заданий. Будьте внимательны и все у вас получится.

Если у вас появились вопросы по формулам, обязательно пишите их в комментариях. Будем рады ответить вам!

Если Вы находитесь в декретном отпуске, но хотите зарабатывать деньги. Просто перейдите по ссылке Интернет бизнес с Орифлейм. Там все очень подробно написано и показано. Будет интересно!

---

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

---

7.3.1. Примеры для закрепления формул сокращенного умножения

1)    Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

       (a+b)² = a²+2ab+b² 

  a) (x + 2y)² = x² + 2 ·x·2y + (2y)² = x² + 4xy + 4y²

б) (2k + 3n)² = (2k)² + 2·2k·3n + (3n)² = 4k² + 12kn + 9n²

2)    Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

        (a-b)² = a²-2ab+b²

 а)   (2a – c)² = (2a)²-2·2a·c + c² = 4a² – 4ac + c²

б)   (3a – 5b)² = (3a)²-2·3a·5b + (5b)² = 9a² – 30ab + 25b²

3)    Разность квадратов двух выражений равна произведению разности самих выражений на их сумму.

         a²–b² = (a–b)(a+b)

a)      9x² – 16y² = (3x)² – (4y)² = (3x – 4y)(3x + 4y)

б)  (6k – 5n)( 6k + 5n) = (6k)² – (5n)² = 36k² – 25n²

4)  Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

        (a+b)³ = a³+3a²b+3ab²+b³

a)  (m + 2n)³ = m³ + 3·m²·2n + 3·m·(2n)² + (2n)³ = m³ + 6m²n + 12mn² + 8n³

б)  (3x + 2y)³ = (3x)³ + 3·(3x)²·2y + 3·3x·(2y)² + (2y)³ = 27x³ + 54x²y + 36xy² + 8y³

5)  Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

(a-b)³ = a³-3a²b+3ab²-b³

а)  (2x – y)³ = (2x)³-3·(2x)²·y + 3·2x·y² – y³ = 8x³ – 12x²y + 6xy² – y³

б)  (x – 3n)³ = x³-3·x²·3n + 3·x·(3n)² – (3n)³ = x³ – 9x²n + 27xn² – 27n³

6)  Сумма кубов двух выражений равна произведению суммы самих выражений на неполный квадрат их разности.

a³+b³ = (a+b)(a²–ab+b²)

a)      125 + 8x³ = 5³ + (2x)³ = (5 + 2x)(5² — 5·2x + (2x)²) = (5 + 2x)(25 – 10x + 4x²)

б)  (1 + 3m)(1 – 3m + 9m²) = 1³ + (3m)³ = 1 + 27m³

7)  Разность кубов двух выражений равна произведению разности самих выражений на неполный квадрат их суммы.

 a³-b³ = (a-b)(a²+ab+b²)

а) 64с³ – 8 = (4с)³ – 2³ = (4с – 2)((4с)² + 4с·2 + 2²) = (4с – 2)(16с² + 8с + 4)

б) (3a – 5b)(9a² + 15ab + 25b²) = (3a)³ – (5b)³ = 27a³ – 125b³

Дорогие друзья! Карта сайта поможет вам выбрать нужную тему.

Mathway | Популярные задачи

Mathway | Популярные задачи

Популярные задачи

Элементарная математика Основы алгебры Алгебра Тригонометрия Основы мат. анализа Математический анализ Конечная математика Линейная алгебра Химия

Для функционирования Mathway необходим javascript и современный браузер.

Этот веб-сайт использует cookie файлы, чтобы сделать использование нашего ресурса максимально удобным для вас.

Убедитесь, что ваш пароль содержит не менее 8 символов и как минимум один из следующих символов:

• число
• буква
• специальный символ: @$#!%*?&

Калькулятор онлайн — Упрощение многочлена (умножение многочленов) (с подробным решением)

С помощью данной математической программы вы можете упростить многочлен.
В процессе работы программа:
— умножает многочлены
— суммирует одночлены (приводит подобные)
— раскрывает скобки
— возводит многочлен в степень

Программа упрощения многочленов не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы вы могли проконтролировать свои знания по математике и/или алгебре.

Данная программа может быть полезна учащимся общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Примеры подробного решения >>

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.

Сообщение отправлено. Спасибо.

Произведение одночлена и многочлена. Понятие многочлена

Среди различных выражений, которые рассматриваются в алгебре, важное место занимают суммы одночленов. Приведем примеры таких выражений:
\( 5a^4 — 2a^3 + 0,3a^2 — 4,6a + 8 \)
\( xy^3 — 5x^2y + 9x^3 — 7y^2 + 6x + 5y — 2 \)

Сумму одночленов называют многочленом. Слагаемые в многочлене называют членами многочлена. Одночлены также относят к многочленам, считая одночлен многочленом, состоящим из одного члена.

Например, многочлен
\( 8b^5 — 2b \cdot 7b^4 + 3b^2 — 8b + 0,25b \cdot (-12)b + 16 \)
можно упростить.

Представим все слагаемые в виде одночленов стандартного вида:
\( 8b^5 — 2b \cdot 7b^4 + 3b^2 — 8b + 0,25b \cdot (-12)b + 16 = \)
\( = 8b^5 — 14b^5 + 3b^2 -8b -3b^2 + 16 \)

Приведем в полученном многочлене подобные члены:
\( 8b^5 -14b^5 +3b^2 -8b -3b^2 + 16 = -6b^5 -8b + 16 \)
Получился многочлен, все члены которого являются одночленами стандартного вида, причем среди них нет подобных. Такие многочлены называют многочленами стандартного вида.

За степень многочлена стандартного вида принимают наибольшую из степеней его членов. Так, двучлен \( 12a^2b — 7b \) имеет третью степень, а трехчлен \( 2b^2 -7b + 6 \) — вторую.

Обычно члены многочленов стандартного вида, содержащих одну переменную, располагают в порядке убывания показателей ее степени. Например:
\( 5x — 18x^3 + 1 + x^5 = x^5 — 18x^3 + 5x + 1 \)

Сумму нескольких многочленов можно преобразовать (упростить) в многочлен стандартного вида.

Иногда члены многочлена нужно разбить на группы, заключая каждую группу в скобки. Поскольку заключение в скобки — это преобразование, обратное раскрытию скобок, то легко сформулировать правила раскрытия скобок:

Если перед скобками ставится знак «+», то члены, заключаемые в скобки, записываются с теми же знаками.

Если перед скобками ставится знак «-», то члены, заключаемые в скобки, записываются с противоположными знаками.

Преобразование (упрощение) произведения одночлена и многочлена

С помощью распределительного свойства умножения можно преобразовать (упростить) в многочлен произведение одночлена и многочлена. Например:
\( 9a^2b(7a^2 — 5ab — 4b^2) = \)
\( = 9a^2b \cdot 7a^2 + 9a^2b \cdot (-5ab) + 9a^2b \cdot (-4b^2) = \)
\( = 63a^4b — 45a^3b^2 — 36a^2b^3 \)

Произведение одночлена и многочлена тождественно равно сумме произведений этого одночлена и каждого из членов многочлена.

Этот результат обычно формулируют в виде правила.

Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый из членов многочлена.

Мы уже неоднократно использовали это правило для умножения на сумму.

Произведение многочленов. Преобразование (упрощение) произведения двух многочленов

Вообще, произведение двух многочленов тождественно равно сумме произведении каждого члена одного многочлена и каждого члена другого.

Обычно пользуются следующим правилом.

Чтобы умножить многочлен на многочлен, надо каждый член одного многочлена умножить на каждый член другого и сложить полученные произведения.

Формулы сокращенного умножения. Квадраты суммы, разности и разность квадратов

С некоторыми выражениями в алгебраических преобразованиях приходится иметь дело чаще, чем с другими. Пожалуй, наиболее часто встречаются выражения \( (a + b)^2, \; (a — b)^2 \) и \( a^2 — b^2 \), т. е. квадрат суммы, квадрат разности и разность квадратов. Вы заметили, что названия указанных выражений как бы не закончены, так, например, \( (a + b)^2 \) — это, конечно, не просто квадрат суммы, а квадрат суммы а и b. Однако квадрат суммы а и b встречается не так уж часто, как правило, вместо букв а и b в нем оказываются различные, иногда довольно сложные выражения.

Выражения \( (a + b)^2, \; (a — b)^2 \) нетрудно преобразовать (упростить) в многочлены стандартного вида, собственно, вы уже встречались с таким заданием при умножении многочленов:
\( (a + b)^2 = (a + b)(a + b) = a^2 + ab + ba + b^2 = \)
\( = a^2 + 2ab + b^2 \)

Полученные тождества полезно запомнить и применять без промежуточных выкладок. Помогают этому краткие словесные формулировки.

\( (a + b)^2 = a^2 + b^2 + 2ab \) — квадрат суммы равен сумме квадратов и удвоенного произведения.

\( (a — b)^2 = a^2 + b^2 — 2ab \) — квадрат разности равен сумме квадратов без удвоенного произведения.

\( a^2 — b^2 = (a — b)(a + b) \) — разность квадратов равна произведению разности на сумму.

Эти три тождества позволяют в преобразованиях заменять свои левые части правыми и обратно — правые части левыми. Самое трудное при этом — увидеть соответствующие выражения и понять, чем в них заменены переменные а и b. Рассмотрим несколько примеров использования формул сокращенного умножения.

math — Как решить линейное одновременное уравнение с двумя переменными? Java

Переполнение стека

1. Около
2. Товары
3. Для команд

1. Переполнение стека Общественные вопросы и ответы
2. Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
3. работы Программирование и связанные с ним технические возможности карьерного роста
4. Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
5. реклама Обратитесь к разработчикам и технологам со всего мира

.

Обозначения движения кубика Рубика Пояснение

Чтобы передать определенный поворот или последовательность поворотов вокруг куба посредством письма, существуют определенные согласованные ключевые буквы, которые точно определяют, какой ход следует сделать: Есть 6 разных букв для поворота кубика Рубика, каждая для 6 граней кубика Рубика, которые должны быть повернуты:

• F (спереди): грань, обращенная к решателю.
• B (оборотная сторона): задняя грань.
• R (справа): правая грань.
• L (слева): левая грань.
• У (вверху): верхняя грань.
• D (вниз): лицевая сторона, противоположная верхней грани.

Буква означает поворот на один оборот, (90 °), по часовой стрелке , соответствующая грань.

Буква с последующим знаком апострофа (‘) (известная как «штрих») означает поворот соответствующей грани на один оборот (90 °), против часовой стрелки .

Буква, за которой следует « 2 », означает поворот соответствующей грани на 2 оборота ( на 180 ° ).Направление поворота здесь не имеет значения. (Однако иногда такие обозначения R2 ‘действительно появляются — в основном по причинам спидкуба, чтобы предложить быстрый и плавный способ выполнения алгоритма)

U
R
F
D
л
B
U ‘
R ‘
F ‘
D ‘
L ‘
B ‘
U2
R2
F2
D2
L2
B2

Эти обозначения всегда будут заглавными буквами. Причина в том, что маленькие буквы имеют разные значения:

Двухслойные витки

Маленькая буква означает поворот лица вместе с соответствующим средним слоем, что делает его поворотом в два слоя.Причина выполнения таких движений заключается в том, что это может уменьшить потребность во вращении куба (например: l равно для выполнения только R и x ‘- это знак вращения куба, объяснение впереди). Также принято использовать заглавную букву + w вместо маленькой буквы (например: Rw; она идентична r). За маленькими буквами может следовать штрих (‘) или 2, как за обычными поворотами, и означает то же самое.
u
руб.
f
г
л
б
u ‘
г ‘
f ‘
d ‘
л ‘
б ‘

Обороты среднего слоя

В кубике Рубика есть 3 различных возможных поворота среднего уровня, представленных буквами (только заглавные).В распространенных алгоритмах используется только один из трех, а два других используются редко. Еще вот обозначения:

• M (средний): средний слой параллельно лицевым сторонам R&L.
• E (экватор): средний слой, параллельный граням U и D.
• S (сбоку): средний слой параллельно граням F и B.

За витками среднего слоя может стоять штрих (‘) или 2, как и за обычными витками. Обороты среднего слоя всегда пишутся заглавными буквами.

млн
M ‘
E
E ‘
S
S ‘

Вращение куба

Это не настоящие повороты, и они предназначены для управления вращением всего куба. Иногда вращение куба позволяет выполнить гораздо более удобные повороты, например, повернуть грань R вместо грани B. Есть 3 возможные оси для вращения куба: оси X, Y и Z. Прямо как в математике. Эти же буквы используются для этих вращений. Лучший способ запомнить вращения — это просто подумать о трехмерном графике функции:

• x : вращение куба по оси X.(Лица справа и слева остались нетронутыми)
• y : вращение куба по оси Y. (Лица U&D остаются нетронутыми)
• z : вращение куба по оси Z. (Лица F и B остаются нетронутыми)

Вращения куба обычно записываются маленькими буквами, но это не имеет значения, и их можно было бы записать заглавными буквами — то же значение.

За вращением куба может стоять штрих (‘), означающий поворот куба на четверть оборота (90 °) по соответствующей оси против часовой стрелки, или за которым следует 2, что означает поворот куба на 180 ° вокруг оси.

х
х ‘
г
г ‘
г
z ‘

Совет: Если у вас возникли трудности с поиском правильного направления CW / C-CW грани (например, грани B или D), временно поверните куб, чтобы грань превратилась в грань F. лицом, чтобы определить направление CW / CCW. Просто представьте часы на циферблате и подумайте, куда пойдет стрелка)

Последовательность поворотов в ряду представлена ​​последовательностью букв и называется алгоритмом .

.