Конспект «Алгебра 7 класс. Все формулы и определения»
Алгебра 7 класс. Все формулы и определения.
Краткий курс алгебры за 7 класс.
«Алгебра 7 класс. Все формулы и определения» — это краткий курс алгебры за 7 класс. Цитаты взяты из учебника для общеобразовательных учреждений (авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под ред. С.А. Теляковского) — М.: Просвещение, 2013.
Выражения и их преобразования
☑ 1. Степенью числа а с натуральным показателем n, большим 1, называют произведение n множителей, каждый из которых равен а: Степенью числа а с показателем 1 называют само число а: а1 = а.
Степенью числа а с показателем 1 называют само число а: а1 = а.
Степень числа а ≠ 0 с показателем 0 равна 1: а0
☑ 2. Свойства степеней с натуральными показателями:
аm • аn = аm+n
При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.
аm : аn = аm-n, где а ≠ 0, m ≥ n
(аm)n = аmn
При возведении степени в степень основание оставляют прежним, а показатели перемножают.
(ab)n = аnbn
При возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают.
☑ 3. Одночленами называют произведения чисел, переменных и их степеней, а также сами числа, переменные и их степени. Например, 5а2х, –3а2b3, 4, х, у5 — одночлены.
Степенью одночлена
☑ 4. Многочленом называют сумму одночленов. Например, 3х5 – 4х2 + 1, 7a3b – ab2 + ab + 6—многочлены. Одночлены считают многочленами, состоящими из одного члена.
Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов. Например, степень многочлена 5х3у + 3х2у5 + ху равна степени одночлена
Степенью произвольного многочлена называют степень тождественно равного ему многочлена стандартного вида.
☑ 5. При сложении многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключённого в скобки. Например,
(3аb + 5с2) + (ab – с2) = 3ab + 5с2 + ab – с2 = 4аb + 4с2
При вычитании многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключённого в скобки. Например,
(6x2 – у) – (2x2 – 8у) = 6х2 – у – 2х2 + 8у = 4х2 + 7у
Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить. Например,
а2 (3аb – b3 + 1) = 3а3b – а2b3 + а2
Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить. Например,
(5х – 1)(3х + 2) = 15x2 – Зx + 10x – 2 = 15x2 + 7x – 2
☑ 6. Формулы сокращённого умножения:
(а + b)2 = а2 + 2аb + b2
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.
(а – b)2 = а2 – 2аb + b2
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.
(а + b)3 = а3 + 3а2b + 3ab2 + b3
Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(а – b)3 = а3 – 3а2b + Заb2 – b3
Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
(а – b)(а + b) = а2 – b2
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.
а3 + b3 = (а + b)(a2 – аb + b2)
Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.
а3 – b3 = (а – b)(a2 + ab + b2)
Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.
☑ 7. Разложением многочлена на множители называют представление многочлена в виде произведения многочленов.
Для разложения многочленов на множители применяют вынесение общего множителя за скобки, группировку, формулы сокращённого умножения. Например, многочлен 5х3 – х2у можно разложить на множители, вынеся за скобки х2:
5х3 – х2у = х
Многочлен 3х – 3у – ах + ау можно разложить на множители, используя способ группировки:
3х – 3у – ах + ау = (3x – 3у) – (ах – ау) = 3(х – у) – а (х – у) = (х – у)(3 – а).
Многочлен а4 – 25x2 можно разложить на множители, используя формулу разности квадратов двух выражений:
а4 – 25x2 = (а2)2 – (5x)2 = (а2 – 5x)(а2 + 5x).
Иногда многочлен удаётся разложить на множители, применив последовательно несколько способов.
Уравнения
☑ 8. Корнем уравнения с одной переменной называют значение переменной, при котором уравнение обращается в верное равенство. Например, число 8 — корень уравнения 3x +1 = 5х – 15, так как верно равенство
Решить уравнение с одной переменной — значит найти все его корни или доказать, что корней нет.
☑ 9. Уравнения с одной переменной, имеющие одни и те же корни, называют равносильными. Например, уравнения x2 = 25 и (х + 5)(х – 5) = 0 равносильны. Каждое из них имеет два корня: –5 и 5. Уравнения, не имеющие корней, также считают равносильными.
При решении уравнений с одной переменной используются следующие свойства:
- если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному;
- если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
☑ 10. Линейным уравнением с одной переменной называют уравнение вида ах = b, где х — переменная, а и b — числа.
Если а ≠ 0, то уравнение ах = b имеет единственный корень b/a.
Например, уравнение 7х = 2 имеет корень
Если а = 0 и b ≠ 0, то уравнение ах = b не имеет корней. Например, уравнение 0 • х = 7 не имеет корней.
Если а = 0 и b = 0, то корнем уравнения ах = b является любое число.
☑ 11. Решением уравнения с двумя переменными называют пару значений переменных, обращающую это уравнение в верное равенство. Например, пара чисел х = -1, у = 4 — решение уравнения 5х + 3у = 7.
Уравнения с двумя переменными, имеющие одни и те же решения, называют
В уравнении с двумя переменными можно переносить слагаемые из одной части в другую, изменяя их знаки, и обе части уравнения можно умножать или делить на одно и то же число, не равное нулю. При этом получаются уравнения, равносильные исходному.
☑ 12. Линейным уравнением с двумя переменными называют уравнение вида ах + by = с, где х и у — переменные, а, b и с — числа.
☑ 13. Графиком уравнения с двумя переменными называют множество точек координатной плоскости, координаты которых являются решениями этого уравнения.
Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.
☑ 14. Решением системы уравнений с двумя переменными называют пару значений переменных, обращающую каждое уравнение системы в верное равенство. Например, пара чисел х = 7, у = –1 — решение системы так как является верным каждое из равенств 7 + (–1) = 6 и 2 • 7 – (–1) = 15.
так как является верным каждое из равенств 7 + (–1) = 6 и 2 • 7 – (–1) = 15.
Решить систему уравнений — значит найти все её решения или доказать, что решений нет.
Системы уравнений с двумя переменными, имеющие одни и те же решения, называют равносильными. Системы, не имеющие решений, также считают равносильными.
☑ 15. Для решения систем линейных уравнений с двумя переменными используются графический способ, способ подстановки, способ сложения.
При графическом способе строят графики линейных уравнений (прямые) и анализируют их расположение:
- если прямые совпадают, то система имеет бесконечно много решений, причём координаты любой точки прямой являются решением системы;
- если прямые параллельны, то система не имеет решений; если прямые пересекаются, то система имеет единственное решение, причём координаты точки пересечения прямых являются решением системы.
При решении системы двух линейных уравнений с двумя переменными способом подстановки поступают следующим образом:
- выражают из какого–либо уравнения системы одну переменную через другую;
- подставляют в другое уравнение системы вместо этой переменной полученное выражение;
- решают получившееся уравнение с одной переменной; подставляют значение найденной переменной в одно из уравнений и находят соответствующее значение другой переменной.
При решении системы двух линейных уравнений с двумя переменными способом сложения поступают следующим образом:
- умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали в уравнениях противоположными числами;
- складывают почленно левые и правые части уравнений системы; решают получившееся уравнение с одной переменной; подставляют значение найденной переменной в одно из уравнений и находят соответствующее значение другой переменной.
Функции
☑ 16. Функциональная зависимость, или функция, — это такая зависимость между двумя переменными, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной.
Независимую переменную иначе называют аргументом, а о зависимой переменной говорят, что она является функцией этого аргумента. Все значения, которые принимает независимая переменная, образуют область определения функции.
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
☑ 17. Линейной функцией называют функцию, которую можно задать формулой вида у = kx + b, где х — независимая переменная, k и b — числа.
Графиком линейной функции у = kx + b является прямая. Число k называют угловым коэффициентом прямой, являющейся графиком функции у = kx + b.
Если k ≠ 0, то график функции у = kx + b пересекает ось х; если k = 0 и b ≠ 0, то прямая — график функции у = kx + b, параллельна оси х; если k = 0 и b = 0, то график функции совпадает с осью х.
Графики двух линейных функций пересекаются, если их угловые коэффициенты различны, и параллельны, если их угловые коэффициенты одинаковы.
Линейную функцию, задаваемую формулой у = kx при k ≠ 0, называют прямой пропорциональностью.
График прямой пропорциональности есть прямая, проходящая через начало координат. При k > 0 график расположен в первой и третьей координатных четвертях, а при k < 0 — во второй и четвёртой координатных четвертях.
☑ 18. График функции у = х2 — парабола. Этот график проходит через начало координат и расположен в первой и второй координатных четвертях. Он симметричен относительно оси у.
График функции у = х3 проходит через начало координат и расположен в первой и третьей координатных четвертях. Он симметричен относительно начала координат.
Статистические характеристики
☑ Средним арифметическим ряда чисел называют частное от деления суммы этих чисел на число слагаемых.
Модой ряда чисел называют число, которое встречается в данном ряду чаще других. Ряд чисел может иметь более одной моды или не иметь моды совсем.
Медианой упорядоченного ряда чисел с нечётным числом членов называют число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом членов называют среднее арифметическое двух чисел, записанных посередине.
Например, медиана ряда чисел 17, 21, 27, 29, 32, 37, 41 равна 29, а медиана ряда чисел 28, 43, 54, 56, 58, 62 равна 55.
Медианой произвольного ряда чисел называют медиану соответствующего упорядоченного ряда.
Размахом ряда чисел называют разность между наибольшим и наименьшим из этих чисел.
Вы смотрели Конспект «Алгебра 7 класс. Все формулы и определения» — краткий курс алгебры за 7 класс. Цитаты взяты из учебника для общеобразовательных учреждений (авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под ред. С.А. Теляковского). Выберите дальнейшие действия:
Основные правила математики. 7 класс алгебра – Сайт учителя математики Косыхиной Н.В.
Основные правила математики. 7 класс алгебра
Содержание
Уравнения. Равносильные уравнения. Свойства
Корень уравнения
- Корнем уравнения называют значение переменной, при котором уравнение обращается в верное числовое равенство.
- Решить уравнение означает найти все его корни или убедиться, что их вообще нет. Также можно сказать, что решить уравнение — это значит найти множество его корней.
Равносильные уравнения
Два уравнения называют равносильными, если они имеют одно и тоже множество корней.
Свойства уравнений
- Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получим уравнение, равносильное данному.
- Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, равносильное данному.
- Если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, равносильное данному
Линейное уравнение
Уравнение вида  , где
, где  — переменная,
— переменная,  и
и  некоторые числа, называют линейным уравнением с одной переменной.
некоторые числа, называют линейным уравнением с одной переменной.
Одночлены и многочлены
Одночлены
- Выражения, являющиеся произведениями чисел, переменных и их степеней, называют одночленами.
- Одночлен, содержащий только один отличный от нуля числовой множитель, стоящий на первом месте, а все остальные множители которого — степени с разными основаниями, называют одночленом стандартного вида. К одночленам стандартного вида также относят числа, отличные от нуля, переменные и их степени.
- Числовой множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена.
- Одночлены, имеющие одинаковые буквенные части, называют подобными. Степенью одночлена называют сумму показателей степеней всех переменных, входящих в него. Степень одночлена, являющегося числом, отличным от нуля, считают равной нулю.
- Нуль-одночлен степени не имеет.
Многочлены
- Выражение, являющееся суммой нескольких одночленов, называют многочленом.
- Одночлены, из которых состоит многочлен, называют членами многочлена.
- Одночлен является частным случаем многочлена. Считают, что такой многочлен состоит из одного члена.
Умножение одночлена на многочлен
Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый член многочлена и полученные произведения сложить.
Умножение многочлена на многочлен
Чтобы умножить многочлен на многочлен, можно каждый член одного многочлена умножить на каждый член другого и полученные произведения сложить.
Формулы сокращенного умножения
Разность квадратов двух выражений
Разность квадратов двух выражений равна произведению разности этих выражений и их суммы:
Произведение разности и суммы двух выражений
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений:
Квадрат суммы и квадрат разности двух выражений
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения:
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражении:
Преобразование многочлена в квадрат суммы или разности двух выражений
Формулы
позволяют «свернуть» трёхчлен в квадрат двучлена.
Трёхчлен, который можно представить в виде квадрата двучлена, называют полным квадратом.
Сумма и разность кубов двух выражений
Многочлен  называют неполным квадратом разности.
называют неполным квадратом разности.
Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности:
Многочлен  называют неполным квадратом суммы.
называют неполным квадратом суммы.
Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы:
Степень. Свойства степени с целым показателем
Свойства степени с целым показателем
Для любого  и любых целых
и любых целых  выполняются равенства:
выполняются равенства:
Для любых  ,
,  и любого целого
и любого целого  выполняются равенства:
выполняются равенства:
Функция. Область определения и область значений функции
Функция
Правило, с помощью которого по каждому значению независимой переменной можно найти единственное значение зависимой переменной, называют функцией, а соответствующую зависимость одной пeременной от другой — функциональной.
Обычно независимую переменную обозначают  , зависимую обозначают
, зависимую обозначают  , функцию(правило) –
, функцию(правило) –  .
.
Независимую переменную  называют аргументом функции. Значение зависимой переменной
называют аргументом функции. Значение зависимой переменной  называют значением функции.
называют значением функции.
Тогда функциональную зависимость обозначают  .
.
Значения, которые принимает аргумент, образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют область значений функции.
Способы задания функции
Описательный, табличный, с помощью формулы, графический.
График функции
Графиком функции называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
Линейная функция, её график и свойства
Системы линейных уравнений с двумя переменными
Уравнение с двумя переменными
Пару значений переменных, обращающую уравнение с двумя переменными в верное равенство, называют решением уравнения с двумя переменными.
Решить уравнение с двумя переменными – значит найти все его решения или показать, что оно не имеет решений.
Графиком уравнения с двумя переменными называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, координаты которых (пары чисел) являются решениями данного уравнения.
Если некоторая фигура является графиком уравнения, то выполняются два условия:
- все решения уравнения являются координатами точек, принадлежащих графику;
- координаты любой точки, принадлежащей графику, — это пара чисел, являющаяся решением данного уравнения.
Графический метод решения системы двух линейных уравнений с двумя переменными
Графический метод решения системы уравнений заключается в следующем:
- построить в одной координатной плоскости графики уравнений, входящих в систему;
- найти координаты всех точек пересечения построенных графиков;
- полученные пары чисел и будут искомыми решениями.
Если графиками уравнений, входящих в систему линейных уравнении, являются прямые, то количество решений этой системы зависит от взаимного расположения двух прямых на плоскости:
- если прямые пересекаются, то система имеет единственное решение.
- если прямые совпадают, то система имеет бесконечно много решении.
- если прямые параллельны, то система решений не имеет.
Решение системы двух линейных уравнений с двумя переменными методом подстановки
Чтобы решить систему линейных уравнений методом подстановки, следует:
- выразить из любого уравнения системы одну переменную через другую;
- подставить в уравнение системы вместо этой переменной выражение, полученное на первом шаге;
- решить уравнение с одной переменной, полученное на втором шаге;
- подставить найденное значение переменной в выражение, полученное на первом шаге;
- вычислить значение второй переменной;
- записать ответ.
Решение систем линейных уравнений методом сложения
Чтобы решить систему линейных уравнений методом сложения, следует:
- подобрать такие множители для уравнений, чтобы после преобразований коэффициенты при одной из переменной стали противоположными числами
- сложить почленно левые и правые части уравнений, полученных на первом шаге
- решить уравнение с одной переменной, полученной на втором шаге
- подставить найденное на третьем шаге значение переменной в любое из уравнений исходной системы;
- вычислить значение второй переменной;
- записать ответ.
Данная информация взята из УМК А.Г.Мерзляк, В.Б.Полонский, М.С. Якир
Формулы по математике 7 класс
Алгебраические выражения. 7кл.А.01
Числовое выражение – запись, состоящая из чисел, соединённых, знаками действий.
1,2 · ( — 3) — 9 ÷ 0,5 — числовое выражение.
Алгебраическое выражение – выражение, состоящее из чисел и букв, соединённых знаками действий.
2 ( m + n ) ; 3a + 2ab – 1 — aлгебраическое выражение.
Числовое значение алгебраического выражения – число, полученное в результате вычислений после замены в этом выражении букв числами.
3a + 2ab -1
Если a=2 , b= 3, тогда 3 · 2 + 2 · 2 · 3 – 1 =17
Если a=-1 , b= 5, тогда 3 ·(-1) + 2· (-1)· 5 – 1 = -14.
Алгебраическая сумма – запись, состоящая из нескольких алгебраических выражений, соединённых знаками « + » и « — ».
Правила раскрытия скобок
Если к алгебраическому выражению прибавляется алгебраическая сумма, заключённая в скобки, то скобки можно опустить, сохранив знак каждого слагаемого этой алгебраической суммы.
14 + ( 7 — 23 + 21 ) = 14 + 7 – 23 + 21
a +( b – c – d ) = a + b – c – d
Если из алгебраического выражения вычитается алгебраическая сумма, заключённая в скобки, то скобки можно опустить, изменив знак каждого слагаемого этой алгебраической суммы на противоположный.
14 – (7 — 23 + 21 ) = 14 – 7 + 23 – 21
a — ( b – c – d ) = a — b + c +d
Уравнение с одним неизвестным 7 кл.А.02
Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением.
Выражение, стоящее слева от знака равенства, называется левой частью уравнения, а выражение, стоящее справа от знака равенства, называется правой частью уравнения.
Каждое слагаемое левой или правой части уравнения называется членом уравнения.
Корнем уравнения называется то значение неизвестного, при котором это уравнение обращается в верное равенство.
Уравнение может иметь бесконечно много корней.
Уравнение может и не иметь корней.
9 х -23 = 5х- 11
9х-5х=23-11
4х=12│÷4
х=3 Ответ.х=3
Любой член уравнения можно перенести из одно части в другую, изменив его знак на противоположный.
Обе части уравнения можно умножить или разделить на одно ито же число, не равное нулю.
Алгоритм решения уравнения:
Переносят члены, содержащие неизвестное, в левую часть, а члены, не содержащие неизвестного, в правую часть.
Приводят подобные слагаемые.
Делят обе части уравнения на коэффициент при неизвестном, если он не равен нулю.
Алгоритм решения задач с помощью уравнения:
Свойства степеней 7 кл. А.03
Степенью числа а с натуральным показателем n , большим 1, называется произведение n множителей, каждый из которых равен а :
=а·а·а·а·…·а
n раз
а – основание степени, n-показатель степени
При умножении степеней с одинаковыми основаниями основание остаётся прежним, а показатели складываются.
При делении степеней с одинаковыми основаниями основание остаётся прежним, а показатели вычитаются.
При возведении степени в степень основание остаётся прежним, а показатели степеней перемножаются.
)m=
При возведении в степень произведения в эту степень возводится каждый множитель.
При возведении в степень дроби в эту степень возводится числитель и знаменатель.
, где b
Одночлены и многочлены 7 кл. А.04
Произведение числовых и буквенных множителей называют одночленом.
abc, (-4)a3ab, 2,5xу – одночлены.
Одночлены, которые содержат только один числовой множитель, стоящий на первом месте, и степени с различными буквенными основаниями, называют одночленами стандартного вида.
3,5 abc, -5ху3 — одночленами стандартного вида.
Многочленом называется алгебраическая сумма нескольких одночленов.
Приведением подобных слагаемых называют упрощение многочлена, при котором алгебраическая сумма подобных одночленов заменяется одним одночленом.
Результаты действий с одночленами и многочленами
Действие
Результат
Одночлен
Одночлен
Многочлен
Одночлен
·
Одночлен
Одночлен
Одночлен
Многочлен
Многочлен
Одночлен
·
Многочлен
Многочлен
Многочлен
Многочлен
Многочлен
Многочлен
·
Многочлен
Многочлен
Разложение многочленов на множители 7 кл. А.05
Если все члены многочлена содержат общий множитель, то этот множитель можно вынести за скобки.
Чтобы разложить многочлен на множители вынесением общего множителя за скобки, нужно:
Чтобы разложить многочлен на множители способом группировки, нужно:
Объединить члены многочлена в такие группы, которые имеют общий множитель в виде многочлена.
Вынести этот общий множитель за скобки
Формулы сокращённого умножения
( a – b )(a + b ) = a2 – b2
(a + b )2 = a2 + 2ab + b2
(a — b )2 = a2 — 2ab + b2
( a + b)3=a3 + 3 a2 b + 3 a b2 + b3
( a — b)3=a3 — 3 a2 b + 3 a b2 — b3
a3 + b3 = ( a + b )(a2 – ab + b2 )
a3 — b3 = ( a — b )(a2 + ab + b2 )
Алгебраические дроби 7 кл.А.06
Выражение называют алгебраической дробью.
Чтобы сократить алгебраическую дробь, нужно числитель и знаменатель разделить на их общий множитель.
Для приведения алгебраических дробей к общему знаменателю нужно:
Найти общий знаменатель данных дробей.
Для каждой дроби найти дополнительный множитель .
Умножить числитель каждой дроби на её дополнительный множитель.
Записать каждую дробь с найденным числителем и общим знаменателем.
Для сложения и вычитания алгебраических дробей с разными знаменателями нужно:
Найти общий знаменатель дробей.
Привести дроби к общему знаменателю.
Сложить или вычесть полученные дроби.
Упростить результат, если возможно.
Умножение и деление алгебраических дробей выполняется по тем же правилам, что и умножение, и деление обыкновенных дробей:
Линейная функция и её график 7 кл.А.07
у
ось ОХ – ось абсцисс Прямоуголь-
0 х ось ОУ – ось ординат ная система
О – начало координат координат
О1 –единичный отрезок
Линейной функцией называется функция вида у = kx + b, где k и b – заданные числа.
Графиком линейной функции у = kx + b является прямая.
Для построения графика функции у = kx + b достаточно построить две точки этого графика.
у = 2 х + 3 у = 2 х
у
у = 2 х + 3
у = 2 х
х
График функции у = kx + b получается сдвигом графика функции у = kx на b единиц вдоль оси ординат.
Графиками функций у = kx и у = kx + b являются параллельные прямые.
Системы двух уравнений 7кл.А.08
с двумя неизвестными
х + у = 10
х – у = 4 — система двух уравнений с двумя неизвестными
Решением системы двух уравнений с двумя неизвестными называют такую пару чисел х и у , которые при подстановке в эту систему обращают каждое её уравнение в верное равенство.
Решить систему уравнений — это значит найти все её решения или установить , что их нет.
Чтобы решить систему двух уравнений с двумя неизвестными способом подстановки, нужно:
из одного уравнения системы ( всё равно из какой) выразить одно неизвестное через другое, например у через х.
полученное выражение подставить в другое уравнение системы, получится одно уравнение с одним неизвестным х.
решить это уравнение, найти значение х.
подставив найденное значение х в выражение для у, найти значение у.
Чтобы решить систему двух уравнений с двумя неизвестными способом алгебраического сложения, нужно:
уравнять модули коэффициентов при одном из неизвестных.
Складывая и вычитая полученные уравнения, найти одно неизвестное.
Подставляя найденное значение в одно из уравнений исходной системы, найти второе неизвестное.
Чтобы решить систему двух уравнений с двумя неизвестными графическим способом, нужно:
Построить графики каждого из уравнений системы.
Найти координаты точки пересечения построенных прямых (если они пересекаются)
На плоскости возможны три случая взаимного расположения двух прямых- графиков уравнений системы.
Прямые пересекаются ,т .е. имеют одну общую точку. Система уравнений имеет единственное решение.
Прямые параллельны, т.е.не имеют общих точек. Система уравнений не имеет решений.
Прямые совпадают. Система уравнений имеет бесконечно много решений.
Алгебра
7 класс
Алгебраические выражения.
Уравнения с одним неизвестным.
Свойства степеней.
Одночлены и многочлены.
Разложение многочленов на множители.
Алгебраические дроби.
Линейная функция и её график.
Системы двух уравнений с двумя неизвестными.
Конспект «Алгебра 7 класс. Все формулы и определения»
Алгебра 7 класс. Все формулы и определения.
Краткий курс алгебры за 7 класс.
«Алгебра 7 класс. Все формулы и определения» — это краткий курс алгебры за 7 класс. Цитаты взяты из учебника для общеобразовательных учреждений (авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под ред. С.А. Теляковского) — М.: Просвещение, 2013.
Выражения и их преобразования
☑ 1. Степенью числа а с натуральным показателем n, большим 1, называют произведение n множителей, каждый из которых равен а: Степенью числа а с показателем 1 называют само число а: а1 = а.
Степенью числа а с показателем 1 называют само число а: а1 = а.
Степень числа а ≠ 0 с показателем 0 равна 1: а0 = 1.
☑ 2. Свойства степеней с натуральными показателями:
аm • аn = аm+n
При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.
аm : аn = аm-n, где а ≠ 0, m ≥ n
(аm)n = аmn
При возведении степени в степень основание оставляют прежним, а показатели перемножают.
(ab)n = аnbn
При возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают.
☑ 3. Одночленами называют произведения чисел, переменных и их степеней, а также сами числа, переменные и их степени. Например, 5а2х, –3а2b3, 4, х, у5 — одночлены.
Степенью одночлена называют сумму показателей степеней всех переменных, входящих в одночлен. Например, степень одночлена –8а2b4 равна 6.
☑ 4. Многочленом называют сумму одночленов. Например, 3х5 – 4х2 + 1, 7a3b – ab2 + ab + 6—многочлены. Одночлены считают многочленами, состоящими из одного члена.
Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов. Например, степень многочлена 5х3у + 3х2у5 + ху равна степени одночлена 3х2у5, т. е. равна 7.
Степенью произвольного многочлена называют степень тождественно равного ему многочлена стандартного вида.
☑ 5. При сложении многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключённого в скобки. Например,
(3аb + 5с2) + (ab – с2) = 3ab + 5с2 + ab – с2 = 4аb + 4с2
При вычитании многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключённого в скобки. Например,
(6x2 – у) – (2x2 – 8у) = 6х2 – у – 2х2 + 8у = 4х2 + 7у
Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить. Например,
а2 (3аb – b3 + 1) = 3а3b – а2b3 + а2
Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить. Например,
(5х – 1)(3х + 2) = 15x2 – Зx + 10x – 2 = 15x2 + 7x – 2
☑ 6. Формулы сокращённого умножения:
(а + b)2 = а2 + 2аb + b2
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.
(а – b)2 = а2 – 2аb + b2
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.
(а + b)3 = а3 + 3а2b + 3ab2 + b3
Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(а – b)3 = а3 – 3а2b + Заb2 – b3
Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
(а – b)(а + b) = а2 – b2
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.
а3 + b3 = (а + b)(a2 – аb + b2)
Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.
а3 – b3 = (а – b)(a2 + ab + b2)
Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.
☑ 7. Разложением многочлена на множители называют представление многочлена в виде произведения многочленов.
Для разложения многочленов на множители применяют вынесение общего множителя за скобки, группировку, формулы сокращённого умножения. Например, многочлен 5х3 – х2у можно разложить на множители, вынеся за скобки х2 : 5х3 – х2у = х2 (5х – у). Многочлен 3х – 3у – ах + ау можно разложить на множители, используя способ группировки:
3х – 3у – ах + ау = (3x – 3у) – (ах – ау) = 3(х – у) – а (х – у) = (х – у)(3 – а).
Многочлен а4 – 25x2 можно разложить на множители, используя формулу разности квадратов двух выражений:
а4 – 25x2 = (а2)2 – (5x)2 = (а2 – 5x)(а2 + 5x).
Иногда многочлен удаётся разложить на множители, применив последовательно несколько способов.
Уравнения
☑ 8. Корнем уравнения с одной переменной называют значение переменной, при котором уравнение обращается в верное равенство. Например, число 8 — корень уравнения 3x +1 = 5х – 15, так как верно равенство 3•8 + 1= 5•8 – 15.
Решить уравнение с одной переменной — значит найти все его корни или доказать, что корней нет.
☑ 9. Уравнения с одной переменной, имеющие одни и те же корни, называют равносильными. Например, уравнения x2 = 25 и (х + 5)(х – 5) = 0 равносильны. Каждое из них имеет два корня: –5 и 5. Уравнения, не имеющие корней, также считают равносильными.
При решении уравнений с одной переменной используются следующие свойства:
- если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному;
- если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
☑ 10. Линейным уравнением с одной переменной называют уравнение вида ах = b, где х — переменная, а и b — числа.
Если а ≠ 0, то уравнение ах = b имеет единственный корень b/a.
Например, уравнение 7х = 2 имеет корень 2/7.
Если а = 0 и b ≠ 0, то уравнение ах = b не имеет корней. Например, уравнение 0 • х = 7 не имеет корней.
Если а = 0 и b = 0, то корнем уравнения ах = b является любое число.
☑ 11. Решением уравнения с двумя переменными называют пару значений переменных, обращающую это уравнение в верное равенство. Например, пара чисел х = -1, у = 4 — решение уравнения 5х + 3у = 7.
Уравнения с двумя переменными, имеющие одни и те же решения, называют равносильными. Уравнения с двумя переменными, не имеющие решений, также считают равносильными.
В уравнении с двумя переменными можно переносить слагаемые из одной части в другую, изменяя их знаки, и обе части уравнения можно умножать или делить на одно и то же число, не равное нулю. При этом получаются уравнения, равносильные исходному.
☑ 12. Линейным уравнением с двумя переменными называют уравнение вида ах + by = с, где х и у — переменные, а, b и с — числа.
☑ 13. Графиком уравнения с двумя переменными называют множество точек координатной плоскости, координаты которых являются решениями этого уравнения.
Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.
☑ 14. Решением системы уравнений с двумя переменными называют пару значений переменных, обращающую каждое уравнение системы в верное равенство. Например, пара чисел х = 7, у = –1 — решение системы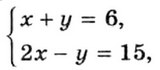 так как является верным каждое из равенств 7 + (–1) = 6 и 2 • 7 – (–1) = 15.
так как является верным каждое из равенств 7 + (–1) = 6 и 2 • 7 – (–1) = 15.
Решить систему уравнений — значит найти все её решения или доказать, что решений нет.
Системы уравнений с двумя переменными, имеющие одни и те же решения, называют равносильными. Системы, не имеющие решений, также считают равносильными.
☑ 15. Для решения систем линейных уравнений с двумя переменными используются графический способ, способ подстановки, способ сложения.
При графическом способе строят графики линейных уравнений (прямые) и анализируют их расположение:
- если прямые совпадают, то система имеет бесконечно много решений, причём координаты любой точки прямой являются решением системы;
- если прямые параллельны, то система не имеет решений; если прямые пересекаются, то система имеет единственное решение, причём координаты точки пересечения прямых являются решением системы.
При решении системы двух линейных уравнений с двумя переменными способом подстановки поступают следующим образом:
- выражают из какого–либо уравнения системы одну переменную через другую;
- подставляют в другое уравнение системы вместо этой переменной полученное выражение;
- решают получившееся уравнение с одной переменной; подставляют значение найденной переменной в одно из уравнений и находят соответствующее значение другой переменной.
При решении системы двух линейных уравнений с двумя переменными способом сложения поступают следующим образом:
- умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали в уравнениях противоположными числами;
- складывают почленно левые и правые части уравнений системы; решают получившееся уравнение с одной переменной; подставляют значение найденной переменной в одно из уравнений и находят соответствующее значение другой переменной.
Функции
☑ 16. Функциональная зависимость, или функция, — это такая зависимость между двумя переменными, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной.
Независимую переменную иначе называют аргументом, а о зависимой переменной говорят, что она является функцией этого аргумента. Все значения, которые принимает независимая переменная, образуют область определения функции.
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
☑ 17. Линейной функцией называют функцию, которую можно задать формулой вида у = kx + b, где х — независимая переменная, k и b — числа.
Графиком линейной функции у = kx + b является прямая. Число k называют угловым коэффициентом прямой, являющейся графиком функции у = kx + b.
Если k ≠ 0, то график функции у = kx + b пересекает ось х; если k = 0 и b ≠ 0, то прямая — график функции у = kx + b, параллельна оси х; если k = 0 и b = 0, то график функции совпадает с осью х.
Графики двух линейных функций пересекаются, если их угловые коэффициенты различны, и параллельны, если их угловые коэффициенты одинаковы.
Линейную функцию, задаваемую формулой у = kx при k ≠ 0, называют прямой пропорциональностью.
График прямой пропорциональности есть прямая, проходящая через начало координат. При k > 0 график расположен в первой и третьей координатных четвертях, а при k < 0 — во второй и четвёртой координатных четвертях.
☑ 18. График функции у = х2 — парабола. Этот график проходит через начало координат и расположен в первой и второй координатных четвертях. Он симметричен относительно оси у.
График функции у = х3 проходит через начало координат и расположен в первой и третьей координатных четвертях. Он симметричен относительно начала координат.
Статистические характеристики
☑ Средним арифметическим ряда чисел называют частное от деления суммы этих чисел на число слагаемых.
Модой ряда чисел называют число, которое встречается в данном ряду чаще других. Ряд чисел может иметь более одной моды или не иметь моды совсем.
Медианой упорядоченного ряда чисел с нечётным числом членов называют число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом членов называют среднее арифметическое двух чисел, записанных посередине.
Например, медиана ряда чисел 17, 21, 27, 29, 32, 37, 41 равна 29, а медиана ряда чисел 28, 43, 54, 56, 58, 62 равна 55.
Медианой произвольного ряда чисел называют медиану соответствующего упорядоченного ряда.
Размахом ряда чисел называют разность между наибольшим и наименьшим из этих чисел.
Вы смотрели Конспект «Алгебра 7 класс. Все формулы и определения» — краткий курс алгебры за 7 класс. Цитаты взяты из учебника для общеобразовательных учреждений (авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под ред. С.А. Теляковского). Выберите дальнейшие действия:
Все главные формулы по математике — Математика — Теория, тесты, формулы и задачи
Оглавление:
Формулы сокращенного умножения
К оглавлению…
Квадрат суммы:
Квадрат разности:
Разность квадратов:
Разность кубов:
Сумма кубов:
Куб суммы:
Куб разности:
Последние две формулы также часто удобно использовать в виде:
Квадратное уравнение и формула разложения квадратного трехчлена на множители
К оглавлению…
Пусть квадратное уравнение имеет вид:
Тогда дискриминант находят по формуле:
Если D > 0, то квадратное уравнение имеет два корня, которые находят по формуле:
Если D = 0, то квадратное уравнение имеет один корень (его кратность: 2), который ищется по формуле:
Если D < 0, то квадратное уравнение не имеет корней. В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:
Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой:
Только в случае если квадратное уравнение имеет два корня (т.е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:
Произведение корней квадратного уравнения может быть вычислено по формуле:
Парабола
График параболы задается квадратичной функцией:
При этом координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины:
Игрек вершины параболы:
Свойства степеней и корней
К оглавлению…
Основные свойства степеней:
Последнее свойство выполняется только при n > 0. Ноль можно возводить только в положительную степень.
Основные свойства математических корней:
Для арифметических корней:
Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при a больше либо равном нолю. Для корня нечетной степени выполняется также следующее равенство:
Для корня четной степени имеется следующее свойство:
Формулы с логарифмами
К оглавлению…
Определение логарифма:
Определение логарифма можно записать и другим способом:
Свойства логарифмов:
Логарифм произведения:
Логарифм дроби:
Вынесение степени за знак логарифма:
Другие полезные свойства логарифмов:
Арифметическая прогрессия
К оглавлению…
Формулы n-го члена арифметической прогрессии:
Соотношение между тремя соседними членами арифметической прогрессии:
Формула суммы арифметической прогрессии:
Свойство арифметической прогрессии:
Геометрическая прогрессия
К оглавлению…
Формулы n-го члена геометрической прогрессии:
Соотношение между тремя соседними членами геометрической прогрессии:
Формула суммы геометрической прогрессии:
Формула суммы бесконечно убывающей геометрической прогрессии:
Свойство геометрической прогрессии:
Тригонометрия
К оглавлению…
Пусть имеется прямоугольный треугольник:
Тогда, определение синуса:
Определение косинуса:
Определение тангенса:
Определение котангенса:
Основное тригонометрическое тождество:
Простейшие следствия из основного тригонометрического тождества:
Формулы двойного угла
Синус двойного угла:
Косинус двойного угла:
Тангенс двойного угла:
Котангенс двойного угла:
Тригонометрические формулы сложения
Синус суммы:
Синус разности:
Косинус суммы:
Косинус разности:
Тангенс суммы:
Тангенс разности:
Котангенс суммы:
Котангенс разности:
Тригонометрические формулы преобразования суммы в произведение
Сумма синусов:
Разность синусов:
Сумма косинусов:
Разность косинусов:
Сумма тангенсов:
Разность тангенсов:
Сумма котангенсов:
Разность котангенсов:
Тригонометрические формулы преобразования произведения в сумму
Произведение синусов:
Произведение синуса и косинуса:
Произведение косинусов:
Формулы понижения степени
Формула понижения степени для синуса:
Формула понижения степени для косинуса:
Формула понижения степени для тангенса:
Формула понижения степени для котангенса:
Формулы половинного угла
Формула половинного угла для тангенса:
Формула половинного угла для котангенса:
Тригонометрические формулы приведения
Формулы приведения задаются в виде таблицы:
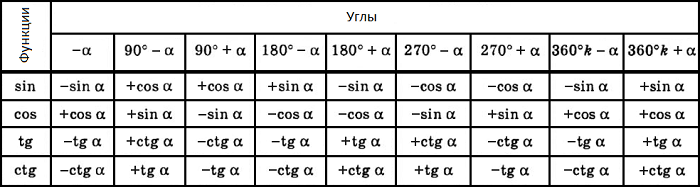
Тригонометрическая окружность
По тригонометрической окружности легко определять табличные значения тригонометрических функций:
Тригонометрические уравнения
К оглавлению…
Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:
Для остальных тригонометрических функций запись однозначна. Для косинуса:
Для тангенса:
Для котангенса:
Решение тригонометрических уравнений в некоторых частных случаях:
Геометрия на плоскости (планиметрия)
К оглавлению…
Пусть имеется произвольный треугольник:
Тогда, сумма углов треугольника:
Площадь треугольника через две стороны и угол между ними:
Площадь треугольника через сторону и высоту опущенную на неё:
Полупериметр треугольника находится по следующей формуле:
Формула Герона для площади треугольника:
Площадь треугольника через радиус описанной окружности:
Формула медианы:
Свойство биссектрисы:
Формулы биссектрисы:
Основное свойство высот треугольника:
Формула высоты:
Еще одно полезное свойство высот треугольника:
Теорема косинусов:
Теорема синусов:
Радиус окружности, вписанной в правильный треугольник:
Радиус окружности, описанной около правильного треугольника:
Площадь правильного треугольника:
Теорема Пифагора для прямоугольного треугольника (c — гипотенуза, a и b — катеты):
Радиус окружности, вписанной в прямоугольный треугольник:
Радиус окружности, описанной вокруг прямоугольного треугольника:
Площадь прямоугольного треугольника (h — высота опущенная на гипотенузу):
Свойства высоты, опущенной на гипотенузу прямоугольного треугольника:
Длина средней линии трапеции:
Площадь трапеции:
Площадь параллелограмма через сторону и высоту опущенную на неё:
Площадь параллелограмма через две стороны и угол между ними:
Площадь квадрата через длину его стороны:
Площадь квадрата через длину его диагонали:
Площадь ромба (первая формула — через две диагонали, вторая — через длину стороны и угол между сторонами):
Площадь прямоугольника через две смежные стороны:
Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними:
Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т.е. в том числе для любых треугольников):

Свойство касательных:
Свойство хорды:
Теорема о пропорциональных отрезках хорд:
Теорема о касательной и секущей:
Теорема о двух секущих:
Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу):
Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой):
Свойство центральных углов и хорд:
Свойство центральных углов и секущих:
Условие, при выполнении которого возможно вписать окружность в четырёхугольник:
Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:
Сумма углов n-угольника:
Центральный угол правильного n-угольника:
Площадь правильного n-угольника:
Длина окружности:
Длина дуги окружности:
Площадь круга:
Площадь сектора:
Площадь кольца:
Площадь кругового сегмента:
Геометрия в пространстве (стереометрия)
К оглавлению…
Главная диагональ куба:
Объем куба:
Объём прямоугольного параллелепипеда:
Главная диагональ прямоугольного параллелепипеда (эту формулу также можно назвать: «трёхмерная Теорема Пифагора»):
Объём призмы:
Площадь боковой поверхности прямой призмы (P – периметр основания, l – боковое ребро, в данном случае равное высоте h):
Объём кругового цилиндра:
Площадь боковой поверхности прямого кругового цилиндра:
Объём пирамиды:
Площадь боковой поверхности правильной пирамиды (P – периметр основания, l – апофема, т.е. высота боковой грани):
Объем кругового конуса:
Площадь боковой поверхности прямого кругового конуса:
Длина образующей прямого кругового конуса:
Объём шара:
Площадь поверхности шара (или, другими словами, площадь сферы):
Координаты
К оглавлению…
Длина отрезка на координатной оси:
Длина отрезка на координатной плоскости:
Длина отрезка в трёхмерной системе координат:
Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы):
Таблица умножения
К оглавлению…
Таблица квадратов двухзначных чисел
К оглавлению…
Расширенная PDF версия документа «Все главные формулы по школьной математике»:
К оглавлению…
Правила по алгебре 7 класс
— это выражение, состоящее из чисел.
— это выражение, состоящее из чисел и переменных (букв)
Уравнение вида где переменная, некоторые числа, называют линейным уравнением с одной переменной.
Математическая модель – составленное по данному условию уравнение.
Алгоритм – последовательность действий.
Выражения, соответственные значения которых равны при любых значениях, входящих в них переменных, называют тождественно равными.
Равенство, верное при любых значениях входящих в него переменных, называют тождеством.
Степень числа а с показателем 1 называют само это число.
При возведении отрицательного числа в степень с чётным показателем получаем положительное число. При возведении отрицательного числа в степень с нечётным показателем получаем отрицательного числа.
Свойства степени:
Одночлен – произведение чисел, переменных и их степеней.
Коэффициент одночлена – числовой множитель одночлена, записанного в стандартном виде.
Подобные одночлены – одночлены, имеющие одинаковую буквенную часть.
Многочлены – выражения, состоящие из суммы нескольких одночленов.
Многочлен стандартного вида – многочлен, состоящий из одночленов стандартного вида.
Степень многочлена стандартного вида – наибольшая степень из степени одночлена, из которых составлен многочлен.
Нуль – многочлен – число нуль, также многочлены, тождественно равные нулю.
Тождественно равные выражения – выражения, соответственные значения которых равны при любых значениях входящих в них переменных.
Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить.
Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого и полученные произведения сложить.
Разложение многочлена на множители: представление многочлена в виде произведения нескольких многочленов.
Формулы сокращенного умножения
Полный квадрат – трехчлен, который можно представить в виде квадрата двучлена.
P=4a, где а – независимая переменная(может принимать любые значения), Р – зависимая(изменятся в зависимости от а)
Функция – правило, с помощью которого по каждому значению независимой переменной можно найти единственное значение зависимой переменной.
Функциональная зависимость – зависимость одной переменной от другой.
Аргумент — независимая переменная.
Область определения – все значения, которые принимает аргумент.
Значение функции – значение зависимой переменной.
Заданная функция – функция, где указаны её область определения и правило, с помощью которого можно по каждому значению независимой переменной найти значение зависимой переменной.
Область значений функций – все значения, которые принимает зависимая переменная.
Способы задание функции: 1. Описательный, 2. С помощью формул, 3. Табличный.
Все точки координатной плоскости, которые можно отметить, действуя таким способом, образуют график функции.
График функции f – геометрическая фигура, состоящая из всех тех, и только тех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции f.
Линейная функция – функция, которую можно задать формулой Её график – прямая.
Линейная функция, которая задается формулой называют прямой пропорциональностью.
Случай, когда значение функции будет оставаться неизменным при любых значениях аргумента.
Равенство, содержащее две переменные называется уравнением с двумя переменными.
Пару значений, обращающую уравнение в верное равенство называют решением уравнения с двумя переменными.
Решить уравнение с двумя переменными – значит найти все его решения или показать, что оно не имеет решений.
График уравнения с двумя переменными – геометрическая фигура, состоящая из всех тех, и только тех точек координатной плоскости, координаты которых (пары чисел) являются решением данного уравнения.
Линейное уравнение с двумя переменными называют уравнение вида
Случай, когда графиком уравнения является прямая.
Решить систему уравнений – значит найти все её решения или показать, что оно не имеет решений.
Суть графического метода: 1) построить на одной координатной плоскости графики уравнений, входящих в систему, 2) найти координаты всех точек пересечения графиков, 3) полученные пары чисел будут искомыми рениями.
Суть метода подстановки: 1) выразить из любого уравнения системы одну переменную через другую, 2) подставить в другое уравнение системы, вместо этой переменной, 3) решить уравнение с одной переменной, 4) подставить найденное значение переменной в выражение, получено на первом шаге, 5) вычислить значение другой переменной.
Суть метода сложения: 1) подобрав «выгодные» множители, преобразовать одно или оба уравнения системы так, чтобы коэффициентом при одной из переменных стали противоположными числами, 2) сложить почленно левые и правые части уравнений, 3) решить уравнение с одной переменной, 4)подставить найденное на третьем шаге значение переменной в любое из уравнений исходной системы, 5) вычислить значение другой переменной.
Алгебра, 7 класс: уроки, тесты, задания
Информация о разделе
Математический язык. Математическая модель
-
Числовые и алгебраические выражения
-
Что такое математический язык
-
Что такое математическая модель
-
Линейное уравнение с одной переменной
-
Координатная прямая
Линейная функция
-
Координатная плоскость
-
Линейное уравнение с двумя переменными и его график
-
Линейная функция y = kx + m и её график
-
Линейная функция y = kx
-
Взаимное расположение графиков линейных функций
Системы двух линейных уравнений с двумя переменными
-
Основные понятия
-
Метод подстановки
-
Метод алгебраического сложения
-
Системы двух линейных уравнений с двумя неизвестными как математические модели реальных ситуаций
Степень с натуральным показателем и её свойства
-
Что такое степень с натуральным показателем
-
Таблица основных степеней
-
Свойства степени с натуральным показателем
-
Умножение и деление степеней с одинаковым показателем
-
Степень с нулевым показателем
Одночлены. Арифметические операции над одночленами
-
Понятие одночлена. Стандартный вид одночлена
-
Сложение и вычитание одночленов
-
Умножение одночленов. Возведение одночлена в натуральную степень
-
Деление одночлена на одночлен
Многочлены. Арифметические операции над многочленами
-
Основные понятия
-
Сложение и вычитание многочленов
-
Умножение многочлена на одночлен
-
Умножение многочлена на многочлен
-
Формулы сокращённого умножения
-
Деление многочлена на одночлен
Разложение многочлена на множители
-
Что такое разложение на множители
-
Вынесение общего множителя за скобки
-
Способ группировки
-
Разложение многочлена на множители с помощью формул сокращённого умножения
-
Разложение многочлена на множители с помощью комбинации различных приёмов
-
Сокращение алгебраических дробей
-
Тождества
Квадратичная функция y = x²
-
Квадратичная функция и её график
-
Графическое решение уравнений
-
Что означает в математике запись у = f(x)
вопросов и задач по алгебре для 7 класса
- Home
- Математика и предварительные вычисления
- Математические задачи
- Вопросы и задачи по алгебре
- Графики функций, уравнений и алгебры
- Бесплатные рабочие листы по математике для загрузки
- Аналитические учебные пособия и математические уравнения
- в Интернете
- Учебные пособия по математике
- Калькуляторы и решатели
- графики
- Бесплатные миллиметры
- Математическое программное обеспечение
- Прикладная математика
- Приложения математики in Physics and Engineering
- Antennas
- Exercises de Mathematiques Utilisant les Applets
- Calculus
- Calculus Tutorials and Problems
- Calculus Questions with Answers
- Free Calculus Worksheets Worksheets
Free Calculus Worksheets Worksheets to Download - Геометрия
- Учебники и задачи по геометрии
- Онлайн-калькуляторы и решатели геометрии
- Бесплатные рабочие листы по геометрии для загрузки
- Тригонометрия
- Учебники по тригонометрии и задачи для самопроверки
- Бесплатные ответы на вопросы
- Скачать
- Больше
- Статистика
- Элементарная статистика и вероятностные учебники и задачи
- Страницы математики на французском языке
- Сайт
- Abo ut автор
- Скачать
- Электронная почта
- Начальная математика
- Математика средней школы
- Математика средней школы
- Бесплатная практика для тестов SAT, ACT и Compass Math
- Статистика
- Home
- Математика и предварительные вычисления
- Математические задачи
- Вопросы и задачи по алгебре
- Графики функций, уравнений и алгебры
- Бесплатные рабочие листы по математике для загрузки
- Аналитические учебные пособия и математические уравнения
- в Интернете
- Учебные пособия по математике
- Калькуляторы и решатели
- графики
- Бесплатные миллиметры
- Математическое программное обеспечение
- Прикладная математика
- Приложения математики in Physics and Engineering
- Antennas
- Exercises de Mathematiques Utilisant les Applets
- Calculus
Математика Мамонт 7 класс Программа предалгебры
Math Mammoth Grade 7 Grade Complete Curriculum — это полная программа предварительной алгебры для 7 класса. Он полностью готовит студентов к программе алгебры 1.

227 страниц
201 страница уроков

292 страницы
258 страниц уроков
7-A содержимое и образцы
7-B содержимое и образцы
Руководство пользователя, класс 7
CCS Alignment / Contents
FAQ
Errata
Цены и заказ
Вы можете приобрести Math Mammoth Grade 7 для загрузки, на компакт-диске или в виде уже распечатанных книг.
Цифровая версия
7 класс: 39,50 $
(два рабочих текста, ключи ответов, тесты, совокупные обзоры, средство создания рабочих листов, Soft-Pak)
Только часть 7-A:
$ 19,75 (загрузить)
(Все для первой половины 7 класса по математике; включает Софт-Пак)
Только часть 7-B:
19,75 $ (загрузить)
(Все для второй половины 7 класса по математике; включает Софт-Пак)
Вы будете покупать загружаемые материалы у моего авторизованного реселлера Comecero, LLC.
CD
Полная оценка 7: 44,50 $
(два рабочих текста, ключи ответов, тесты, совокупные обзоры, средство создания рабочих листов, Soft-Pak)
Печатные копии
Ресурсный центр Rainbow продает тексты с идеальным переплетом либо с полноцветными, либо с внутренними страницами в оттенках серого:
Математика Мамонт 7 класс (ч / б)
Математика Мамонт 7 класс (цвет)
Lulu продает версии учебников для учащихся, а также книги с тестами и обзорами в переплетенных спиралью (катушками) версиях.
Рабочий текст 7-A $ 18,75
Рабочий текст 7-B $ 21,60
Тесты и совокупные обзоры $ 11,95
Ключи ответов $ 16,95 (точная привязка)
Другой вариант — приобрести только рабочих текстов учащихся в виде печатных книг и получить цифровую версию вспомогательных материалов : ключи ответов, тесты, совокупные обзоры, средство создания рабочих листов и программное обеспечение Soft-Pak. Используйте эту ссылку, чтобы добавить вспомогательные материалы в корзину (8,95 долларов США).
План урока
Вы можете приобрести план уроков по математике Mammoth Grade 7, чтобы использовать его в онлайн-планировщике Homeschool Planet .Выучить больше.
Рабочая тетрадь по обзору навыков
Эта рабочая тетрадь является дополнительной и предоставляет дополнительные практические занятия по темам учебной программы. Я рекомендую вам приобретать его только в том случае, если вы уверены, что ученику действительно нужна дополнительная практика. Выучить больше.
В основе учебной программы лежат два студенческих рабочих текста (A и B), каждый из которых охватывает примерно полгода работы по математике. Эти рабочие тексты содержат все инструкции и упражнения из одной книги, что упрощает подготовку к уроку.Рабочие тексты написаны непосредственно ученику, и, таким образом, они позволяют многим ученикам учиться самостоятельно и учиться прямо из книг.
Вы также получите отдельные ключи ответов, тесты по главам, дополнительные сводные обзоры (я рекомендую вам использовать хотя бы некоторые из них) и универсальное средство для создания рабочих листов (требуется доступ в Интернет) для тех случаев, когда вашему ребенку нужно немного больше практики ,
Характеристики
- Math Mammoth фокусируется на концептуальном понимании .В нем объясняется «ПОЧЕМУ», чтобы ваши дети могли понять математику, а не просто научиться «КАК» это делать.
- Концепции часто объясняются с помощью визуальных моделей , за которыми следуют упражнения с использованием этих моделей. Эти визуальные модели могут заменить для многих детей манипуляторы; однако при желании очень легко добавить к урокам соответствующие манипуляторы.
- Учебная программа ориентирована на овладение . Это означает, что он довольно долго концентрируется на теме, углубляясь в ее различные аспекты.Это способствует концептуальному пониманию, в отличие от спиральных учебных программ, которые часто имеют тенденцию слишком много прыгать от темы к теме.
- Math Mammoth Grade 7 — это в некотором смысле гибридная программа. Его можно использовать как традиционную программу предварительной алгебры или как математическую программу 7-го класса, которая соответствует стандартам Common Core и превосходит их. Если вы используете его в основном для предварительной алгебры, вы можете пропустить последнюю главу учебной программы (статистика). В противном случае вы можете пропустить главу о теореме Пифагора.
- Это требует очень небольшой подготовки учителя .

- Учебная программа не имеет отдельного руководства для учителя и не написана по сценарию. Во введении к каждой главе есть некоторые примечания для учителя относительно материала главы. Все инструкции написаны непосредственно для учащегося в рабочем тексте, а также существуют сопроводительные видеоролики, где вы можете увидеть, как Мария сама преподает материал.
- После введения каждой главы вы найдете список интернет-ссылок и ресурсов (игры, викторины, анимации и т. Д.), Которые можно использовать для развлечения, иллюстраций и дальнейшей практики.
Пожалуйста, прочтите FAQ для получения дополнительной информации.
Дополнительные возможности для цифровой версии (скачать / CD)
Файлы PDF включены для аннотации. Это означает, что при желании ваш ученик может заполнить их на компьютере, используя пишущую машинку и инструменты рисования в Acrobat Reader версии 9 или выше, или на планшетном устройстве, используя любое приложение PDF с возможностью аннотации. (Узнать больше.)
БОНУС! Если вы купите загружаемую версию или версию на компакт-диске, вы также получите программы Soft-Pak полностью БЕСПЛАТНО .6 программ Soft-Pak (4 математических, 1 языковая, 1 составитель списков) предлагают как экранные, так и печатные задания в формате с низким содержанием графики и высоким содержанием. Подробнее читайте и смотрите скриншоты.
Обзор тем
Основные направления обучения в Math Mammoth Grade 7:
- Введение в основы алгебры
- целые числа и их операции
- решение одношаговых уравнений, в том числе с отрицательными числами
- операций с отрицательными рациональными числами
- Решение линейных уравнений и написание уравнений для текстовых задач
- построение графиков линейных уравнений и введение в понятие уклона
- соотношения, ставки, пропорции и проценты Геометрия
- : угловые отношения, конструкции компаса и линейки, задачи рисования, Pi, площадь и окружность круга, поперечные сечения, образованные при резке твердых тел, площадь поверхности и объем
- теорема Пифагора (необязательно)
- вероятность
- статистика
См. Также оглавление 7-A и 7-B (в файлах примеров), которое позволит вам увидеть затронутые темы более подробно.
« … какой глоток свежего математического воздуха. От меня требуется минимальная подготовка, и моя дочь может самостоятельно выполнять учебную программу с небольшими инструкциями от меня. »
Дополнения
План урока
Мы предлагаем план уроков по математике Mammoth Grade 7 для онлайн-планировщика Homeschool Planet . Он доступен в двух версиях: обычный и план PLUS, который также включает PDF-файл плана. Выучить больше.
Введение
Math Mammoth Рабочие тексты 7-A и классов 7-B составляют полную учебную программу по математике для изучения математики седьмого класса.Это курс предварительной алгебры , и студенты могут продолжить обучение по программе алгебры 1 после его изучения.
Учебная программа соответствует Общим основным стандартам (CCS) для 7 класса, но также превосходит их в нескольких местах. Например, мы изучаем линейные уравнения более глубоко, чем требуется в CCS 7 класса, а учебная программа включает теорему Пифагора, которая в CCS относится к 8 классу. Вы можете получить доступ к документу с подробной информацией о выравнивании по этой ссылке или в загрузке версия этой учебной программы.
Мы начинаем с введения в основную алгебру , которое во многих смыслах представляет собой обзор тех же тем из 6-го класса. В первой главе рассматривается порядок операций, концепции выражения и уравнения, а также свойство распределения. Учащиеся узнают о коммутативных и ассоциативных свойствах сложения и умножения, а также упрощают выражения, не содержащие отрицательных чисел.
В главе 2 мы подробно изучаем целых чисел и их операции .Кое-что из этого, опять же, из 6-го класса, а что-то новое. Четыре операции над целыми числами объясняются с помощью двух наглядных моделей: числовой линии и счетчиков, которые, надеюсь, обеспечивают интуитивное понимание процессов. Студенты должны уметь складывать, вычитать, умножать и делить целые числа, когда они учатся решать уравнения в главе 3. В конце главы студенты также узнают об отрицательных дробях.
Урок о расстоянии содержит формулу, которая может показаться учителю незнакомой.Вы можете найти расстояние между двумя целыми числами, взяв абсолютное значение их разности. В символах расстояние между a и b равно | a — b | , Однако идея формулы проста, и большинство людей инстинктивно используют ее, не зная о формуле. Например, как далеко друг от друга 14 и 92? Чтобы решить эту проблему мысленно, мы находим их различие, но воспринимаем это различие в положительном смысле. Другими словами, мы не вычисляем 14 — 92 = −78 и заявляем, что расстояние отрицательно — 78 единиц, но вместо этого мы говорим, что расстояние составляет 78 единиц, потому что расстояние всегда положительно.Об этом позаботится абсолютное значение: оно превращает любую отрицательную величину в положительную.
В следующей главе (глава 3) студенты изучают простых одношаговых уравнений . Они уже знают основы решения таких уравнений с 6-го класса, но на этот раз мы используем в них отрицательные числа.
Глава 4 называется «Рациональные числа», которые представляют собой просто дроби и определенные десятичные дроби, поэтому учащийся уже хорошо с ними знаком. Цель главы — научить складывать, вычитать, умножать и делить как положительные, так и отрицательные дроби и десятичные дроби .Мы также решаем простые уравнения, включающие дроби и десятичные дроби, и узнаем о научных обозначениях и сложных дробях.
Последняя глава части 7-A посвящена линейным уравнениям. Студент учится решать различных типов линейных уравнений и практикует , используя их в простых словесных задачах . Мы изучаем линейные неравенства, но не так глубоко, как линейные уравнения. Наконец, студент составляет графики линейных уравнений и знакомится с концепцией наклона , который представляет собой крутизну линии.Студент продолжит изучение этих тем с более подробной информацией в курсе алгебры 1.
Часть B начинается с изучения соотношений и пропорций (глава 6). Студенты изучают расценки, пропорции, пропорциональные отношения и построение графиков, масштабирование геометрических фигур, планов этажей и карт.
Следующая глава дает подробные уроки о концепции процента. Студенты учатся решать самые разные задачи, связанные с процентами, включая процент изменения, проценты сравнения и простой процент проблемы.
Геометрия — это наше внимание в главе 8. Учащиеся рисуют геометрические фигуры с помощью транспортира и линейки, а также изучить некоторые основные геометрические конструкции. Другие темы этой главы — различные соотношения углов , площади и периметр круга , преобразование единиц площади и объема, площади поверхности, объема и поперечных сечений когда твердые тела нарезаются плоскостью.
Глава 9 посвящена квадратным корням, теореме Пифагора и ее приложениям.При необходимости вы можете опустить всю главу (например, из-за нехватки времени), поскольку теорема Пифагора также включена в любую математическую программу 8-го класса, которая следует за Common Core, а также в математические курсы средней школы.
Глава 10 представляет собой введение в вероятность . Помимо изучения основной идеи вероятности как отношения благоприятных событий ко всем возможным событиям, студенты сравнивают экспериментальные вероятности с теоретическими. вероятностное моделирование и даже разработать некоторые из них самостоятельно.
Наконец, в главе 11 учебная программа охватывает статистические концепции. Основными областями исследования являются случайная выборка и обучение сравнению двух популяций с использованием некоторых основных статистических показателей и графиков.
Пожалуйста, прочтите FAQ для получения дополнительной информации.
Отзывов / Отзывов о программе 7 класса
Math Mammoth · Доступная программа домашнего обучения для 7-х классов Grace, Grow & Edify blog
Math Mammoth Light Blue Series Уровень 7: обзор группы проверки TOS на Grace-Filled Homeschooling blog
Math Mammoth Light Blue Series Обзор 7-го класса — Фелисия Моллохан в блоге Homeschool4Life .
Обзор учебной программы предалгебры по математике Mammoth, автор Дэвид Чендлер из журнала «Математика без границ».
Я просто хотел выразить вам недовольство. Большое спасибо за ваш учебный план.Я только что накрыл 7-й класс распределительной собственности.
ДА!!!! Мне нравится, как вы это представили, и то, как проблемы приводят к пониманию. Мои ученики были в восторге от решения этих проблем. Для них это было похоже на забавную головоломку. Это большая жемчужина !!!!
Прекрасный.
деб б. 🙂
сентября 2015
Тара Дилан
июнь 2015
Алгебра: правила в скобках
8
Пояснение:
В данном выражении есть две круглые скобки: одна внутри другой. В этом случае мы сначала решаем внутренние скобки, а затем объединяем результат с другими терминами, чтобы оценить внешние скобки.
(2 + 4 * (5-2)) + (2 * (-3))
= (2 + 4 * 3) + (2 * (-3))- = (2 + 12) + (2 * (- 3))
- = 14+ (2 * (- 3))
- = 14 + (- (2 * 3)), поскольку a.(-b) = -ab
- = 14+ (-6)
- 14-6, поскольку a + (-b) = a-b
- = 8
30 математических формул для SAT, которые необходимо знать
Коэффициенты, проценты и статистика
13. Простые проценты
\ (A = Prt \)
Этот показатель появляется реже, чем сложные проценты на SAT, но он все равно появляется, поэтому о нем стоит знать. \ (P \) представляет основную сумму, \ (r \) — процентную ставку, выраженную в десятичной дроби, а \ (t \) — время, обычно в годах.
14.{Нт} \)
Хорошая новость в том, что \ (P \), \ (r \) и \ (t \) означают то же самое в этом уравнении, что и в простом интересе. \ (N \) представляет, сколько раз начисляются проценты в течение \ (1 \: t \). Например, если проценты начисляются ежеквартально в течение года, тогда \ (n = 4 \).
15. Среднее / Среднее
В математике слова «среднее» и «среднее» — это одно и то же: число, которое вы получаете, когда берете сумму набора и делите ее на количество значений в наборе.Вы также можете думать об этом как о сумме, деленной на количество. Вы должны знать, как рассчитать среднее значение и интерпретировать его. Убедитесь, что понимаете разницу между средним и медианным значением.
16. Случайная выборка
Технически это не формула, но многие из задач, связанных со статистикой в SAT, больше сосредоточены на интерпретации концепций в контексте, а не на выполнении математических операций. Случайная выборка — это случайный выбор участников для исследования из вашей популяции.Это гарантирует, что ваше исследование репрезентативно для населения.
17. Случайное присвоение
Случайное назначение — это случайное назначение участникам исследования лечения или испытания. Это снижает систематическую ошибку в вашем исследовании и означает, что вы можете приписать причинно-следственную связь лечению. На тесте SAT вас часто спрашивают, что снизит систематическую ошибку или насколько вы можете обобщить результаты для остальной части населения. В этих случаях вам необходимо определить случайную выборку и случайное распределение.
18. Стандартное отклонение
Вам не нужно рассчитывать стандартное отклонение для SAT, но вы будете протестированы по нему концептуально, как при случайной выборке и случайном назначении. Стандартное отклонение — это мера разброса в наборе данных. Более высокое стандартное отклонение означает больший спред, а меньшее стандартное отклонение означает меньший спред. Вам нужно знать, как изменения в наборе данных могут повлиять на стандартное отклонение, сделав его больше или меньше.2 \)
Обычно возникает один вопрос, связанный с уравнением круга. В этом уравнении \ ((h, k) \) — координата центра окружности, а \ (r \) — радиус окружности.
21. Коэффициент синусоиды
Некоторые учащиеся нервничают, когда слышат, что триггер находится в тесте SAT, но чаще всего это проявляется в виде триггерных соотношений. Помните, что для заданного угла в прямоугольном треугольнике значение синуса — это длина противоположной стороны, деленная на длину гипотенузы, или противоположной стороны / гипотенузы.
22. Косинусное отношение
Как и в случае с синусом, помните, что такое косинусное отношение: длина смежной стороны, деленная на длину гипотенузы, или смежная / гипотенуза.
23. Коэффициент касания
И последнее, но не менее важное: отношение касательных — это длина противоположной стороны, деленная на длину соседней стороны или противоположной / смежной стороны. Некоторые учащиеся находят мнемонический SOH CAH TOA полезным для запоминания тригонометрических соотношений.2 \)
Теорема Пифагора применяется к прямоугольным треугольникам и позволяет вам найти длину одной из сторон при любой другой длине стороны. \ (a \) и \ (b \) — катеты треугольника, а \ (c \) — гипотенуза.
26. Внутренний угол правильного многоугольника
\ (\ frac {(n-2) 180} {n} \)
SAT, вероятно, будет включать один вопрос с правильным многоугольником, который не является треугольником или квадратом. Правильные многоугольники обладают уникальными и согласованными свойствами в зависимости от количества сторон, и знание этих свойств может помочь вам решить эти проблемы.Это уравнение говорит вам, какой градус каждого угла основан на количестве сторон \ (n \).
27. 3-4-5 треугольник
SAT предоставляет вам два специальных прямоугольных треугольника, с которыми вы, возможно, уже знакомы на своем справочном листе, — треугольники 30-60-90 и 45-45-90. Однако 3-4-5 — это особый прямоугольный треугольник со сторонами, которые представляют собой простые целые числа. Этот треугольник часто включается в задачи SAT, особенно в части без калькулятора, так что будьте начеку! Это может избавить вас от необходимости использовать теорему Пифагора.
28. 5-12-13 треугольник
Другой особый прямоугольный треугольник со сторонами целых чисел, треугольник 5-12-13 менее известен и встречается реже, чем 3-4-5. Тем не менее, это помогает быстро решить оставшиеся стороны без теоремы Пифагора, поэтому проверяйте эти числа или их кратные в задачах треугольника.
29. Длина дуги по окружности
\ (длина \: of \: arc = \ frac {central \: angle} {360} \ pi d \)
Хотя вопросы о геометрии не составляют большую часть SAT, вы все равно можете найти вопрос о дугах или секторах в круге.2 \)
Подобно дуге, сектор — это область между двумя радиусами, отходящими от круга, вроде как кусок пирога. Опять же, умножьте меру в градусах на долю \ (360 \) и умножьте ее на уравнение для площади круга, чтобы найти площадь сектора.
Завершение
Перед тем, как вы отправитесь, мы собираемся предложить вам бонусный совет: вы можете запомнить идеальные квадраты и идеальные кубики. Это может помочь вам с квадратными уравнениями, которые часто включают квадраты, а кубы часто используются при решении задач с показателями.Их запоминание сократит потребность в математических вычислениях с помощью бумаги для заметок или калькулятора.
Лучший способ запоминать формулы — это попрактиковаться в их использовании. В отличие от теста по математике в старшей школе, где вы знаете, какие темы будут охвачены, SAT просто представит вам вопрос — вам решать, какие формулы применяются. Когда вы попрактикуетесь в использовании формул для решения различных задач, вы сможете быстро определить, какую формулу использовать.
Готовитесь к SAT? Загрузите наше бесплатное руководство с нашими 8 лучшими советами по освоению SAT.
Хотите знать, как ваш результат SAT влияет на ваши шансы зачисления в школы вашей мечты? Наша бесплатная система Chancing Engine не только поможет вам предсказать ваши шансы, но и расскажет, как вы конкурируете с другими кандидатами и какие аспекты вашего профиля нужно улучшить. Зарегистрируйтесь на бесплатную учетную запись CollegeVine сегодня , чтобы получить доступ к нашему движку Chancing Engine и ускорить реализацию стратегии обучения в колледже!
Ознакомьтесь с некоторыми другими нашими статьями по подготовке к математике:
,

Leave A Comment