64 корней из 6

Вы искали 64 корней из 6? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и корень 6 из 64, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «64 корней из 6».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как 64 корней из 6,корень 6 из 64,корень 6 из степени 64,корень из 64 в степени 6. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и 64 корней из 6. Просто введите задачу в окошко и нажмите «решить» здесь (например, корень 6 из степени 64).

Где можно решить любую задачу по математике, а так же 64 корней из 6 Онлайн?

Решить задачу 64 корней из 6 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Корень 6 степени из 64=2 нужно сравнить числа

Механический одометр (счётчик пройденного пути) для велосипеда — это прибор, крепится на руле и соединён тросиком с редуктором, установлевным на оси в … ереднего колеса При движении велосипеда спицы колеса врашают редуктор, это врашенне по передаётся счетчику, который показывает пройденное расстояние в километрах У Димы был Велосипед с колёсами диаметром 24 дюйма из одометром который был настроен по данным диаметр колеса когда Дима вырос ему купили дорожный велосипед с колёсами диаметром 28 зима переставила Одометр со своего старого велосипеда на новый но не настроил его под диаметр колеса нового велосипеда Воскресенье Дима поехал кататься на велосипеде в парк когда он вернулся Одометр показал пройдённое расстояние 13,2км Какое расстояние на самом деле проехал Дима

Решите уравнение 1)8,1-(3,1-y)=1 2)9,4+(8,6-x)=0,4 3)0,6(x+7)-0,5(x-3)=6,8 4)0,3(x-2)-0,2(x+4)=0,6 5)-7(0,3x-8)+3(0,4x+5)=8 6)0,87x-0,9x+1,3x=-15,24

Упростите выражение и подчеркните коэффициенты 1)12a•8b•(-15c)= 2)-3,8m•(-1,6)•(-3,5n)= 3)1,2•(-0,6a)•4c•64= 4)0,2x•(-5,7y)•5z= 5)7,54c•(-10b)•2a= 6 … )-3,15a•2b•(-3c)=

Раскройте скобки и найдите значение выражения. 1)17,24+(5,89-9,14)= 2)36,34-(6,45-63,66)= 3)-1,8+(3/5-7,2)= 4)-27,9+(-32,1+18,7)= 5)-1,8+(-3,5-19,03)= … 6)-3,84-(12,16+63,9)=

Выполните сложение чисел с разными знаками. 1)-64+79= 2)49+(-52)= 3)-3,563+0,739= 4)2,7+(-1,207)= 5)654,08+(-781,13)= 6)-2/7+5/42= 7)3/14+(-11/21)= 8) … -4/9+1= 9)-11/20+9/16= 10)5/6+(-8/9)=

Решите задания по математике

Выполните сложение отрицательных чисел. 1)-56+(44)= 2)-384,56+(-126,34)= 3)-13,356+(-8,93)= 4)-4/9+(-3/5)= 5)-11/25+(-13/5)= 6)-7/24+(-5/12)= 7)-9/14+ … (-13/21)= 8)-11/20+(-9/16)=

РЕШИТЕ СРОЧНО, ДОБАВЬТЕ НОМЕР ТЕЛЕФОНА, ЕСЛИ ТЫ ИЗ РФ, КИНУ 100 КИВИ.НУЖНО ПОЛНОЕ РЕШЕНИЕ С ОТВЕТАМИ

Срочноооо даю 35 баллов умоляю срочноооо

допомодітьАльпініст Богдан Упертий спочатку піднімався на вершину з базового табору X протягом двох годин зі сталою швидкістю 2 км/ год а потім не роб … лячи зупинки на вершині спускається з нею до базового табору Y протягом 3 годин зі сталою швидкістю 3 км/год знайдіть середню швидкість Уперто протягом усієї його подорожі​

Арифметический корень / math5school.

ru

 

Арифметический корень

Свойства корней

Значения некоторых корней n-й степени

Таблица квадратных корней натуральных чисел от 1 до 99

Таблица кубических корней натуральных чисел от 1 до 99

 

Арифметический корень

Арифметическим корнем  n-й степени из неотрицательного числа a называется неотрицательное число b,  n-я степень которого равна a.

Записывается так: 

 

Эта запись означает, что bn = a, где b и a – неотрицательные числа.

Число n называется показателем степени корня, число а – подкоренным выражением, b – значением арифметического корня n-й степени. Операция нахождения значения корня называется извлечением корня.

Корней чётной степени из отрицательных чисел не существует.

Корнем нечётной степени из отрицательного числа а называется такое отрицательное число

b, которое при его возведении в эту нечётную степень равно числу а.

Для корней нечётной степени справедливо равенство:

 

 

Свойства корней

Для положительных а и b, натуральных n и k (n ≥ 2, k ≥ 2), целого m выполняются следующие соотношения.

Кроме того, для любого числа а верно:

 

Значения некоторых корней

n-й степени
 3√8 = 2  4√16 = 2  5√32 = 2  6√64 = 2  7√128 = 2  8√256 = 2  9
√512 = 2		  10√1024 = 2
 3√27 = 3  4√81 = 3  5√243 = 3  6√729 = 3  7√2187 = 3  8√6561 = 3  9√19683 = 3  10√59049 = 3
 3√64 = 4  4√256 = 4  5√1024 = 4  6√4096 = 4  7√16384 = 4  8√65536 = 4  9√262144 = 4  10√1048576 = 4
 
3√125 = 5		  4√625 = 5  5√3125 = 5  6√15625 = 5  7√78125 = 5  8√390625 = 5  9√1953125 = 5  10√9765625 = 5
 3√216 = 6  4√1296 = 6  5√7776 = 6  6√46656 = 6  7√279936 = 6  8√1679616 = 6  9√10077696 = 6  10√60466176 = 6
 3√343 = 7  4√2401 = 7  5
√16807 = 7		  6√117649 = 7  7√823543 = 7  8√5764801 = 7  9√40353607 = 7  10√282475249 = 7

 

      Смотрите также:

Таблицы чисел

Алгебраические тождества

Степени

Логарифмы 

Графики элементарных функций

Построение графиков функций геометрическими методами

Тригонометрия

Таблицы значений тригонометрических функций

Треугольники

Четырёхугольники

Многоугольники

Окружность 

Площади геометрических фигур

Прямые и плоскости

Многогранники 

Тела вращения 

 

Урок 26.

контрольно-обобщающий урок по теме «квадратные корни» — Алгебра — 8 класс

Тема: Контрольно-обобщающий урок по теме «Квадратные корни»

Содержание модуля (краткое изложение модуля):

Квадратным корнем числа а называют такое число b, квадрат которого равен а, т.е. b2 = a.
82 = 64, (–8)2 = 64
числа 8 и –8 являются квадратными корнями из числа 64.
Арифметическим квадратным корнем из числа а называют такое число b, квадрат которого равен а, при этом b ≥ 0.
82 = 64, 8 ≥ 0, поэтому число 8 является арифметическим квадратным корнем из числа 64.
(–8)2 = 64, 8<0, поэтому число –8 не является арифметическим квадратным корнем

из числа 64.
Для любого а ≥ 0 верно равенство: (√a)2 = a.
Для любого а верно равенство: √(a2) = |a|.
Функция y = √x и её график


Точка М (a, b) принадлежит графику функции y = √x тогда и только тогда, когда b = √a, т.е. выполняются условия a ≥ 0 и а2 = b.
Свойства арифметического квадратного корня
  1. Если а ≥ 0 и b ≥ 0, то √ab=√a • √b

  2. Если a ≥ 0 и b>0, то √(a/b)=√a/√b

  3. Если a ≥ 0 и
    n     – натуральное число, то √(a2n)=|an|

Вынесение множителя за знак корня
а) √147 = √49 • 3 = √72 • √3 = 7√3 – вынесен множитель 7 за знак корня.
б) √a5 = √a4 • a = |a2|√a = a2√a
(так как a2 ≥ 0 для любого числа a, то |a2| = a2
в) √a7 = √a6 • a = √(a3)2 • a = |a3|√a
(если знак числа а неизвестен, раскрыть модуль невозможно)
За знак корня выносится модуль числа.
Внесение множителя под знак корня
а) 6√b = √62 • b = √36b – внесён множитель 6 под знак корня.
б) -6√b = -1 • 6√b = -√62 • b = -√36b
в) a√b.
Рассмотрим два случая:
если a ≥ 0, то a√b = |a|√b = √a2b
если aa√b = -|a|√b = -√a2b
Под знак корня вносится модуль числа, знак числа остаётся перед знаком корня.

Алгебра. 8 класс: учеб. для общеобразоват. организаций / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. – 6-е изд. – М.: Просвещение, 2017.


Таблица квадратных корней | Алгебра

В таблице приведены квадратные корни натуральных чисел от 1 до 100.

√1 = 1
√4 = 2
√9 = 3
√16 = 4
√25 = 5
√36 = 6
√49 = 7
√64 = 8
√81 = 9
√100 = 10 		√121 = 11
√144 = 12
√169 = 13
√196 = 14
√225 = 15
√256 = 16
√289 = 17
√324 = 18
√361 = 19
√400 = 20 		√441 = 21
√484 = 22
√529 = 23
√576 = 24
√625 = 25
√676 = 26
√729 = 27
√784 = 28
√841 = 29
√900 = 30 		√961 = 31
√1024 = 32
√1089 = 33
√1156 = 34
√1225 = 35
√1296 = 36
√1369 = 37
√1444 = 38
√1521 = 39
√1600 = 40
√1681 = 41
√1764 = 42
√1849 = 43
√1936 = 44
√2025 = 45
√2116 = 46
√2209 = 47
√2304 = 48
√2401 = 49
√2500 = 50 		√2601 = 51
√2704 = 52
√2809 = 53
√2916 = 54
√3025 = 55
√3136 = 56
√3249 = 57
√3364 = 58
√3481 = 59
√3600 = 60 		√3721 = 61
√3844 = 62
√3969 = 63
√4096 = 64
√4225 = 65
√4356 = 66
√4489 = 67
√4624 = 68
√4761 = 69
√4900 = 70 		√5041 = 71
√5184 = 72
√5329 = 73
√5476 = 74
√5625 = 75
√5776 = 76
√5929 = 77
√6084 = 78
√6241 = 79
√6400 = 80
√6561 = 81
√6724 = 82
√6889 = 83
√7056 = 84
√7225 = 85
√7396 = 86
√7569 = 87
√7744 = 88
√7921 = 89
√8100 = 90 		√8281 = 91
√8464 = 92
√8649 = 93
√8836 =  94
√9025 = 95
√9216 = 96
√9409 = 97
√9604 = 98
√9801 = 99
√10000 = 100

Степени — квадрат и куб, корни — квадратный и кубический и обратные величины чисел от 1 до 100.

Таблица степеней от 1 до 100. Таблица корней от 1 до 1000000

Степени — квадрат и куб, корни — квадратный и кубический и обратные величины чисел от 1 до 100. Таблица степеней от 1 до 100. Таблица корней от 1 до 1000000.

1

1

1,00000

1

1,0000

3,1623

1,0000

2,1544

4,6416

8

4

0,50000

2

1,4142

4,4721

1,2599

2,7144

5,8480

27

9

0,33333

3

1,7321

5,4772

1,4422

3,1072

6,6943

64

16

0,25000

4

2,0000

6,3246

1,5874

3,4200

7,3681

125

25

0,20000

5

2,2361

7,0711

1,7100

3,6840

7,9370

216

36

0,16667

6

2,4495

7,7460

1,8171

3,9149

8,4343

343

49

0,14286

7

2,6458

8,3666

1,9129

4,1213

8,8790

512

64

0,12500

8

2,8284

8,9443

2,0000

4,3089

9,2832

729

81

0,11111

9

3,0000

9,4868

2,0801

4,4814

9,6549

1000

100

0,10000

10

3,1623

10,0000

2,1544

4,6416

10,0000

1331

121

0,09091

11

3,3166

10,4881

2,2240

4,7914

10,3228

1728

144

0,08333

12

3,4641

10,9545

2,2894

4,9324

10,6266

2197

169

0,07692

13

3,6056

11,4018

2,3513

5,0658

10,9139

2744

196

0,07143

14

3,7417

11,8322

2,4101

5,1925

11,1869

3375

225

0,06667

15

3,8730

12,2474

2,4662

5,3133

11,4471

4096

256

0,06250

16

4,0000

12,6491

2,5198

5,4288

11,6961

4913

289

0,05882

17

4,1231

13,0384

2,5713

5,5397

11,9348

5832

324

0,05556

18

4,2426

13,4164

2,6207

5,6462

12,1644

6859

361

0,05263

19

4,3589

13,7840

2,6684

5,7489

12,3856

8000

400

0,05000

20

4,4721

14,1421

2,7144

5,8480

12,5992

9261

441

0,04762

21

4,5826

14,4914

2,7589

5,9439

12,8058

10648

484

0,04545

22

4,6904

14,8324

2,8020

6,0368

13,0059

12167

529

0,04348

23

4,7958

15,1658

2,8439

6,1269

13,2001

13824

576

0,04167

24

4,8990

15,4919

2,8845

6,2145

13,3887

15625

625

0,04000

25

5,0000

15,8114

2,9240

6,2996

13,5721

17576

676

0,03846

26

5,0990

16,1245

2,9625

6,3825

13,7507

19683

729

0,03704

27

5,1962

16,4317

3,0000

6,4633

13,9248

21952

784

0,03571

28

5,2915

16,7332

3,0366

6,5421

14,0946

24389

841

0,03448

29

5,3852

17,0294

3,0723

6,6191

14,2604

27000

900

0,03333

30

5,4772

17,3205

3,1072

6,6943

14,4225

29791

961

0,03226

31

5,5678

17,6068

3,1414

6,7679

14,5810

32768

1024

0,03125

32

5,6569

17,8885

3,1748

6,8399

14,7361

35937

1089

0,03030

33

5,7446

18,1659

3,2075

6,9104

14,8881

39304

1156

0,02941

34

5,8310

18,4391

3,2396

6,9795

15,0369

42875

1225

0,02857

35

5,9161

18,7083

3,2711

7,0473

15,1829

46656

1296

0,02778

36

6,0000

18,9737

3,3019

7,1138

15,3262

50653

1369

0,02703

37

6,0828

19,2354

3,3322

7,1791

15,4668

54872

1444

0,02632

38

6,1644

19,4936

3,3620

7,2432

15,6049

59319

1521

0,02564

39

6,2450

19,7484

3,3912

7,3061

15,7406

64000

1600

0,02500

40

6,3246

20,0000

3,4200

7,3681

15,8740

68921

1681

0,02439

41

6,4031

20,2485

3,4482

7,4290

16,0052

74088

1764

0,02381

42

6,4807

20,4939

3,4760

7,4889

16,1343

79507

1849

0,02326

43

6,5574

20,7364

3,5034

7,5478

16,2613

85184

1936

0,02273

44

6,6332

20,9762

3,5303

7,6059

16,3864

91125

2025

0,02222

45

6,7082

21,2132

3,5569

7,6631

16,5096

97336

2116

0,02174

46

6,7823

21,4476

3,5830

7,7194

16,6310

103823

2209

0,02128

47

6,8557

21,6795

3,6088

7,7750

16,7507

110592

2304

0,02083

48

6,9282

21,9089

3,6342

7,8297

16,8687

117649

2401

0,02041

49

7,0000

22,1359

3,6593

7,8837

16,9850

125000

2500

0,02000

50

7,0711

22,3607

3,6840

7,9370

17,0998

132651

2601

0,01961

51

7,1414

22,5832

3,7084

7,9896

17,2130

140608

2704

0,01923

52

7,2111

22,8035

3,7325

8,0415

17,3248

148877

2809

0,01887

53

7,2801

23,0217

3,7563

8,0927

17,4351

157464

2916

0,01852

54

7,3485

23,2379

3,7798

8,1433

17,5441

166375

3025

0,01818

55

7,4162

23,4521

3,8030

8,1932

17,6517

175616

3136

0,01786

56

7,4833

23,6643

3,8259

8,2426

17,7581

185193

3249

0,01754

57

7,5498

23,8747

3,8485

8,2913

17,8632

195112

3364

0,01724

58

7,6158

24,0832

3,8709

8,3396

17,9670

205379

3481

0,01695

59

7,6811

24,2899

3,8930

8,3872

18,0697

216000

3600

0,01667

60

7,7460

24,4949

3,9149

8,4343

18,1712

226981

3721

0,01639

61

7,8102

24,6982

3,9365

8,4809

18,2716

238328

3844

0,01613

62

7,8740

24,8998

3,9579

8,5270

18,3709

250047

3969

0,01587

63

7,9373

25,0998

3,9791

8,5726

18,4691

262144

4096

0,01563

64

8,0000

25,2982

4,0000

8,6177

18,5664

274625

4225

0,01538

65

8,0623

25,4951

4,0207

8,6624

18,6626

287496

4356

0,01515

66

8,1240

25,6905

4,0412

8,7066

18,7578

300763

4489

0,01493

67

8,1854

25,8844

4,0615

8,7503

18,8520

314432

4624

0,01471

68

8,2462

26,0768

4,0817

8,7937

18,9454

328509

4761

0,01449

69

8,3066

26,2679

4,1016

8,8366

19,0378

343000

4900

0,01429

70

8,3666

26,4575

4,1213

8,8790

19,1293

357911

5041

0,01408

71

8,4261

26,6458

4,1408

8,9211

19,2200

373248

5184

0,01389

72

8,4853

26,8328

4,1602

8,9628

19,3098

389017

5329

0,01370

73

8,5440

27,0185

4,1793

9,0041

19,3988

405224

5476

0,01351

74

8,6023

27,2029

4,1983

9,0450

19,4870

421875

5625

0,01333

75

8,6603

27,3861

4,2172

9,0856

19,5743

438976

5776

0,01316

76

8,7178

27,5681

4,2358

9,1258

19,6610

456533

5929

0,01299

77

8,7750

27,7489

4,2543

9,1657

19,7468

474552

6084

0,01282

78

8,8318

27,9285

4,2727

9,2052

19,8319

493039

6241

0,01266

79

8,8882

28,1069

4,2908

9,2443

19,9163

512000

6400

0,01250

80

8,9443

28,2843

4,3089

9,2832

20,0000

531441

6561

0,01235

81

9,0000

28,4605

4,3267

9,3217

20,0830

551368

6724

0,01220

82

9,0554

28,6356

4,3445

9,3599

20,1653

571787

6889

0,01205

83

9,1104

28,8097

4,3621

9,3978

20,2469

592704

7056

0,01190

84

9,1652

28,9828

4,3795

9,4354

20,3279

614125

7225

0,01176

85

9,2195

29,1548

4,3968

9,4727

20,4083

636056

7396

0,01163

86

9,2736

29,3258

4,4140

9,5097

20,4880

658503

7569

0,01149

87

9,3274

29,4958

4,4310

9,5464

20,5671

681472

7744

0,01136

88

9,3808

29,6648

4,4480

9,5828

20,6456

704969

7921

0,01124

89

9,4340

29,8329

4,4647

9,6190

20,7235

729000

8100

0,01111

90

9,4868

30,0000

4,4814

9,6549

20,8008

753571

8281

0,01099

91

9,5394

30,1662

4,4979

9,6905

20,8776

778688

8464

0,01087

92

9,5917

30,3315

4,5144

9,7259

20,9538

804357

8649

0,01075

93

9,6437

30,4959

4,5307

9,7610

21,0294

830584

8836

0,01064

94

9,6954

30,6594

4,5468

9,7959

21,1045

857375

9025

0,01053

95

9,7468

30,8221

4,5629

9,8305

21,1791

884736

9216

0,01042

96

9,7980

30,9839

4,5789

9,8648

21,2532

912673

9409

0,01031

97

9,8489

31,1448

4,5947

9,8990

21,3267

941192

9604

0,01020

98

9,8995

31,3050

4,6104

9,9329

21,3997

970299

9801

0,01010

99

9,9499

31,4643

4,6261

9,9666

21,4723

1000000

10000

0,01000

100

10,0000

31,6228

4,6416

10,0000

21,5443

Извлечение квадратного корня в столбик на бумаге

  1. Главная
  2. Алгебра
  3. Степени и корни
  4. Извлечение квадратного корня в столбик на бумаге

Сегодня калькуляторы доступны повсеместно, и операцию извлечения корня так и подмывает выполнить на каком-нибудь устройстве.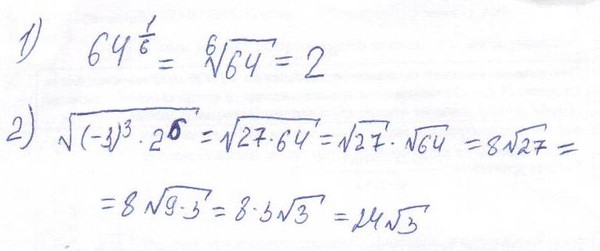 Но вычисляя корень на бумаге ученики используют и повторяют весь устный и письменный счёт, квадраты чисел, таблицу умножения. Рекомендуем учителю или родителю возводить в квадрат трёхзначные числа, и ученику раз в неделю или месяц вычислять корни. В конце каждого примера ученика ждёт автоматическая подсказка: если выше допущена хоть одна ошибка, то корень не будет извлекаться нацело. А если в остатке получился ноль, значит строгая дисциплина при вычислении корня была соблюдена полностью. Чтобы вы могли запомнить не только пример, а сам метод, который иллюстрируется примерами — мы разобрали целых три примера.

Извлечение квадратного корня из целых чисел. Пример 1.

Чтобы извлечь квадратный корень из целого числа мы будем циклично предпринимать одну и ту же последовательность действий: Подбери, Занеси, Вычти, Снеси, Удвой, Припиши. Сокращённо ПЗВ СУП — для запоминания: ПоЗоВи {гостей есть} СУП.

Пример 1: 763876. Число разделяем на грани (по два разряда) от запятой: 763876. В числе три грани — значит в корне будет три разряда. Сначала старшая грань 76.

Подбираем наибольшее число от 1 до 9 такое, чтоб его квадрат был меньше, чем 76. Это число 8 (т.к. 8 × 8 = 64, а 9 × 9 = уже 81, то есть > 76). Заносим 8 в ответ — это старший разряд ответа (сотни). Вычитаем 64 из 76 — остаётся 12. Сносим к 12-ти следующую грань — 38. Получается 1238. Удваиваем то что в ответе — восьмёрку. Получается 16 — запишем 16 слева от 1238. Приписываем к 16 справа коробочку для ещё одного разряда.

Снова

Подбираем наибольшее число от 1 до 9 такое, чтоб 16# × # было не больше, чем 1238. Это число 7 (т.к. 166 × 6 = 996 < 1238, 167 × 7 = 1169 < 1238, а 168 × 8 = 1344, то есть уже > 1238). Заносим 7 в ответ — это следующий разряд ответа (десятки). Вычитаем 167 × 7 из 1238 — остаётся 69. Сносим к 69-ти следующую грань — 76. Получается 6976. Удваиваем то, что в ответе — 87. Получается 174 — запишем 174 слева от 6976. Приписываем к 174 справа коробочку для ещё одного разряда.

Снова

Подбираем наибольшее число от 1 до 9 такое, чтоб 174# × # было не больше, чем 6976. Это число 4 (т.к. 1743 × 3 = 5229, 1744 × 4 = 6976, а 1745 × 5 = 8725, то есть уже > 6976). Заносим четвёрку в ответ — это будет разряд единиц. Вычитаем 1744 × 4 из 6976 — остаётся ноль.

Значит, квадратный корень из данного числа 763876 — число 874.

Пример 2: 79524.

Число разделяем на грани (по два разряда) от запятой: 079524. В числе три грани — значит, в корне будет три разряда. Старшую грань дополнили ноликом (и стало 07). Вот сначала направляем внимание на старшую грань 07.

Подбираем наибольшее число от 1 до 9 такое, чтоб его квадрат был меньше, чем 7. Это число 2 (т.к. 1 × 1 = 1 < 7, 2 × 2 = 4 < 7, а 3 × 3 = 9, а это уже > 7). Заносим 2 в ответ — это старший разряд ответа (сотни). Вычитаем 4 из 07 — остаётся 3. Сносим к 3 следующую грань — 95. Получается 395. Удваиваем то, что в ответе — двойку. Получается 4. Запишем 4 слева от 395. Припишем к 4 справа коробочку для ещё одного разряда.

Подбираем наибольшее число от 1 до 9 такое, чтоб 4# × # было не больше, чем 395. Это число 8 (т.к. 47 × 7 = 329 < 395, 48 × 8 = 384 < 395, а 49 × 9 = 441, то есть уже > 395) Заносим 8 в ответ — это будет разряд десятков. Вычитаем (48 × 8 = ) 384 из 395 — остаётся 11. Сносим к 11 следующую грань — 24. Получается 1124. Удваиваем то, что в ответе — 28. Получается 56. Запишем 56 слева от 1124. Приписываем к 56 справа коробочку для ещё одного разряда.

Подбираем наибольшее число от 1 до 9 такое, чтоб 56# × # было не больше, чем 1124. Это число 2 (т.к. 561 × 1 = 561 < 1124, 562 × 2 = 1124, 563 × 3 = 1689 > 1124). Заносим 2 в ответ — это будут единицы ответа. Вычитаем 562 × 2 из 1124 — остаётся 0. Значит квадратный корень из данного числа 79524 — это число 282.

Пример 3: 487204.

Число разделяем на грани (по два разряда) от запятой: 48’72’04. В числе три грани, значит в корне будет три разряда.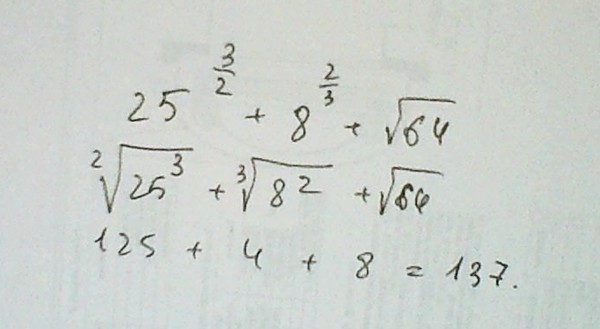 Сначала старшая грань 48.

Подбираем наибольшее число от 1 до 9 такое, чтоб его квадрат был не больше 48. Это число 6 (т.к. 6 × 6 = 36, а 7 × 7 = 49). Заносим 6 в ответ. Это разряд сотен. Вычитаем 36 из 48 — остаётся 12. Сносим к 12 следующую грань — 72. Получается 1272. Удваиваем то, что в ответе — 6. Получается 12. Припишем 12 слева от 1272. Приписываем к 12 коробочку для ещё одного разряда.

Подбираем наибольшее число от 1 до 9 такое, чтоб 12# × # было не больше, чем 1272. Это число 9, т.к. 129 × 9 = 1161 < 1272. Заносим 9 в ответ — это разряд десятков. Вычитаем (129 × 9 = )1161 из 1272 — остаётся 111. Сносим к 111 следующую грань — 04. Получается 11104. Удваиваем то, что в ответе — 69. Получается 138. Приписываем 138 слева от 11104. Приписываем к 111 справа коробочку для следующего разряда.

Подбираем наибольшее число от 1 до 9 такое, чтоб 138# × # было не больше, чем 11104. Это число 8 (т.к. 1388 × 8=11104, а 1389 × 9 = 12501 > 11104) Заносим 8 в ответ — это разряд единиц. Вычитаем 1388 × 8 = 11104 из 11104 — остаётся 0. Значит квадратный корень из данного числа 487204 — это число 698.

Онлайн калькулятор шестого корня — впечатляющий калькулятор шестого корня

Онлайн калькулятор шестого корня:

Воспользуйтесь нашим онлайн калькулятором шестого корня.

  • Корень шестой степени из 2 составляет ± 1,122.
  • Корень шестой степени из 64 составляет ± 2.
  • Корень шестой степени из 85 составляет ± 2,096.
  • Корень шестой степени из 125 составляет ± 2,236.
  • Корень шестой из 216 составляет ± 2,449.
  • Корень шестой степени из 256 составляет ± 2,519.
  • Корень шестой степени из 729 равен ± 3.
  • Корень шестой степени из 4096 составляет ± 3,999.

Формула калькулятора шестого корня:

a 6 = x., 6 √x = a

Формула шестого корня

Определение шестого корня:

Определение шестого корня :

В математике шестой корень числа x равен число r , которое при возведении в степень 6 дает x:

r 6 = x.

Как вычислить корень шестой степени

Что такое корень шестой степени 64?

Шестой корень из 64 имеет ровно один действительный корень шестой степени и два дополнительных комплексных корня шестой степени.

Шестой корень из 64 — это число, которое умножается само на себя 6 раз и дает 64.

Деление 64 на 2 дает 32, что равно:

64 = 2 X 32
= 2 X (16 X 2 )
= 2 X 2 X (8 X 2)
= 2 X 2 X 2 X (4 X 2)
= 2 X 2 X 2 X 2 X 2 X 2.

Шестой корень из 64 равен 2.

Что такое корень шестой из 729?

Шестой корень из 729 имеет ровно один действительный корень шестой степени и два дополнительных комплексных корня шестой степени.

Корень шестой степени из 729 — это число, которое умножается само на себя 6 раз и дает 729.Складывая цифры 729, мы получаем 7 + 2 + 9 = 18, это среднее кратно 9, это говорит нам, что 729 кратно 9.

Деление 729 на 9 дает 81, что равно:

729 = 9 X 81 = 9 X 9 X 9, что дает нам:

729 = 3 X 3 X 3 X 3 X 3 X 3.

Шестой корень из 729 равен 3.

Что такое корень шестой степени из 4096?

Шестой корень из 4096 имеет ровно один действительный корень шестой степени и два дополнительных комплексных корня шестой степени.

Корень шестой степени из 4096 — это число, которое умножается само на себя 6 раз, и получается 4096.

Разделив 4096 на 4, мы получим 1024, что равно:

4096 = 4 X 1024

= 4 X (4 X 256).

= 4 X 4 X (4 X 64).

= 4 X 4 X 4 X (4 X 16).

= 4 X 4 X 4 X 4 X 4 X 4.

Шестой корень 4096 равен 4, что является совершенным корнем шестой степени.

Идеальный шестой корень

117129 117129 Шестой корень 7
X 6 √x
Шестой корень из 1 1
Шестой корень из 64 2 Шестой корень из 64 2 3
Шестой корень из 4096 4
Шестой корень из 15 625 5
Шестой корень из 46 656 6 6
Шестой корень из 262144 8
Шестой корень из 531441 9
Шестой корень из 1 000 000 10
90 561
корень шестой 11
Корень шестой степени из 2 985 984 12
Список совершенных корней шестой степени.

Таблица шестого корня от 1 до 50:

Шестой корень 32 1,8171 90 90
x 6 √x x 6 √x
Шестой корень 1,0000 Шестой корень из 26 1,7212
Шестой корень из 2 1,1225 Шестой корень из 27 1,7321
Шестой корень из 3 1 , 2009 Шестой корень из 28 1,7426
Шестой корень из 4 1,2599 Шестой корень из 29 1,7528
Шестой корень из 5 1,3077 Шестой корень из 30 1,7627
Шестой корень из 6 1,3480 Шестой корень из 31 1,7724
Шестой корень из 7 1,3831 1,7818
Корень шестой из 8 1,4142 Корень шестой из 33 1,7910
Корень шестой из 9 1,4422 Корень шестой из 34 1, 7999
Шестой корень из 10 1,4678 Шестой корень из 35 1,8086
Шестой корень из 11 1,4913 Шестой корень из 36
Шестой корень из 12 1,5131 Шестой корень из 37 1,8254
Шестой корень из 13 1,5334 Шестой корень из 38 1,8336
Шестой корень из 14 1,5525 Шестой корень из 39 1,8415
Шестой корень из 15 1,5704 Шестой корень из 40 1,8493
Шестой корень 16 1,5874 Шестой корень из 41 1,8569
Корень шестой из 17 1,6035 Корень шестой из 42 1,8644
Корень шестой из 18 1,6189 Шестой корень из 43 1,8717
Шестой корень из 19 1,6335 Шестой корень из 44 1,8789
Шестой корень из 20 1,6475 Шестой корень 45 1,8860
Шестой корень из 21 1,6610 Шестой корень из 46 1,8929
Шестой корень из 22 1,6739 Шестой корень из 47 1 , 8997
Шестой корень из 23 1,6864 Шестой корень из 48 1,9064
Шестой корень из 24 1,6984 Шестой корень из 49 1,9129 1,9129
Корень шестой степени 25 1,7100 Шестой корень из 50 1,9194
Таблица шестого корня от 1 до 50:

Таблица шестого корня от 51 до 100:

52129 Шестой корень 9020 54 Шестой корень 1,944161 Шестой корень из 5829 корень из 67 71 Шестой корень из 100
x 6 √x x 6 √x
Шестой корень из 51 1,925728 Шестой корень из 76 2,058112
1,931971 Шестой корень из 77 2,062601
Шестой корень из 53 1,938114 Шестой корень из 78 2,067041
Шестой корень из 79 2,071434
Шестой корень из 55 1,950116 Шестой корень из 80 2,075782
Шестой корень 56 955981 Шестой корень из 81 2,080084
Шестой корень из 57 1,96176 Шестой корень из 82 2,084342
1,96720454 9012 корень из 83 2,088557
корень шестой из 59 1,973068 корень шестой из 84 2,09273
корень шестой из 60 1,978602 85 2,096862
Шестой корень 61 1,984061 Шестой корень 86 2,100953
Шестой корень 62 1,989445 2,105005
Шестой корень из 63 1,994757 Шестой корень из 88 2,109019
Шестой корень из 64 2 Шестой корень из 89 2,112299204
Шестой корень из 65 2,005175 Шестой корень из 90 2,116933
Шестой корень из 66 2,010284 Шестой корень из 91 2,120835
2,015328 Корень шестой из 92 2,124702
Корень шестой из 68 2,020311 Корень шестой из 93 2,128534
69 2,025232 Шестой корень из 94 2,132331
Шестой корень из 70 2,030095 Шестой корень из 95 2,136095
2,0349 Шестой корень 96 2,139826
Шестой корень 72 2,039649 Шестой корень 97 2,143525
Шестой корень 73 2 9012 , 044343 Шестой корень из 98 2,147193
Шестой корень из 74 2,048984 Шестой корень из 99 2,150829
Шестой корень из 75 2,053573 2,154435
Таблица корня шестой степени от 51 до 100:

Подробнее Калькулятор корня

Ссылка

: n Корень -й степени из Википедии

Нахождение квадратного и квадратного корня числа

Что такое квадратный корень?

Чтобы объяснить квадратные корни, давайте сделаем шаг назад и вспомним, что означает возведение числа в квадрат. Возвести в квадрат — это возвести число во вторую степень. Квадратные корни противоположны этому, и на самом деле это операция, обратная возведению в квадрат. Чтобы извлечь квадратный корень, нужно найти два одинаковых делителя числа.

Как найти квадратный корень из числа

Для чисел, которые представляют собой полные квадраты, вы можете найти целые числа в качестве ответов. Однако для чисел, которые не являются точными квадратами, вам придется использовать метод, включающий оценку (или вы можете использовать таблицу квадратных и квадратных корней).

Нахождение квадратного корня из полного квадратного числа

Давайте сначала рассмотрим этот вопрос здесь:

корень 64

Что такое квадратный корень из 64? Если у вас есть калькулятор, вы всегда можете просто набрать его и получить ответ. Но знаете ли вы, как найти квадратный корень из числа без калькулятора?

Теперь, если вы помните свои точные квадраты чисел, корень из 64 равен восьми. Восемь умножить на восемь даст вам 64. Но допустим, вы не можете свободно вспоминать идеальные числа.Как бы мы сделали это с нуля?

Во-первых, вам нужно найти все простые множители 64. Итак, давайте продолжим и сделаем это:

простые множители корня 64

Представьте, что вопрос теперь принимает вид 2x2x2x2x2x2 — здесь 2 умножается на 6 раз. Итак, мы только что определили, что 64 — это всего лишь квадратный корень из шести двоек, умноженных вместе.

радикальный знак

Прежде чем мы продолжим, мы должны помнить, что знак корня на самом деле означает «квадратный корень». Символ квадратного корня действительно должен быть записан здесь с крошечными двумя:

квадратный корень

Так как это квадратный корень, вы можете выбрать пару одинаковых чисел для работы и извлечь их из-под корня.В этом случае мы вынимаем 2 из первой пары двоек, еще 2 из второй пары и еще 2 из последней пары. Должно получиться примерно так:

вынимать пары

Теперь, если вы умножите 2 друг на друга, что вы получите? Вы обнаружите, что получите 8, что в точности соответствует тому, что вы запомнили бы, если бы знали свои идеальные квадраты. Однако это правильный способ найти квадратный корень из числа без запоминания.

Поиск квадратного корня из чисел, не являющихся точными квадратами

Основной метод нахождения квадратного корня из числа, не являющегося полным квадратом, выглядит следующим образом:

  1. Оценка: выберите число, которое при возведении в квадрат близко, но меньше квадратного корня из числа, которое вы пытаетесь найти.

  2. Разделить: разделите число, для которого вы находите квадратный корень, на число, которое вы выбрали на шаге 1

  3. Среднее: возьмите среднее значение числа, полученного на шаге 2, и квадратный корень

    4. .

  4. Повторить: повторяйте шаги 2 и 3, пока число не станет для вас достаточно точным

Теперь вы научились находить квадратный корень для чисел, которые одновременно являются и не являются точными квадратами. Продолжайте наши уроки, чтобы узнать, как работать с примерами различных радикальных чисел.

Калькулятор кубического корня | Определение

Как вычислить кубический корень в своей голове?

Как вы думаете, можно ли решить простые задачи с кубическими корнями без онлайн-калькулятора или даже карандаша или бумаги? Если вы думаете, что это невозможно или не можете сделать это, воспользуйтесь этим методом, это очень просто. Однако работает только для идеальных кубов . Забудьте обо всех правилах из учебников по арифметике и рассмотрите на мгновение следующий метод, описанный Робертом Келли.

Прежде всего, необходимо запомнить кубики чисел от 1 до 10 и последнюю цифру их кубиков. Он представлен в таблице ниже.

Номер 1 2 3 4 5 6 7 8 9 10
Куб 1 8 27 64 126 216 343 512 729 1000
Последняя цифра 1 8 7 4 5 6 3 2 9 0

Если у вас есть число, которое вы хотите найти кубический корень, сначала посмотрите на тысячи (пропустите последние три цифры).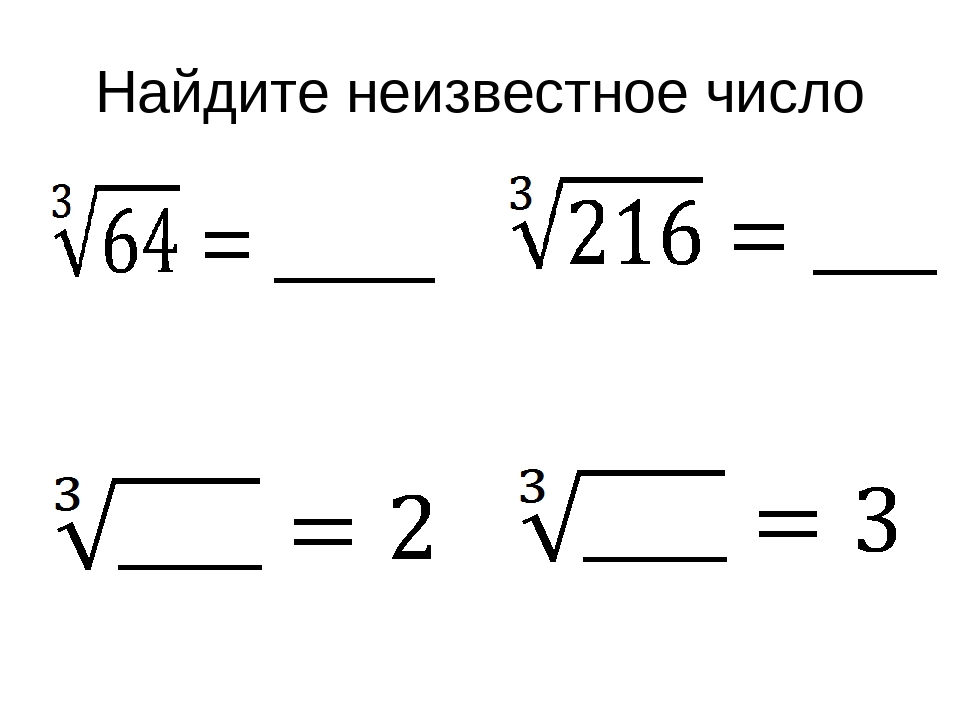 Например, для числа 185 193 тысячи равны 185. Куб из 5 равен 125, а из 6 — 216. Следовательно, очевидно, что число, которое вы ищете, находится между 50 и 60. Следующий шаг — игнорировать все остальные цифры, кроме последней цифры. Мы видим, что это 3, так что проверьте свою память или в нашей таблице. Вы обнаружите, что число, которое вы ищете, — 7. Итак, ответ: 57 ! Легкий?

Давайте возьмем еще один пример и сделаем это шаг за шагом!

  1. Подумайте о числе, которое вы хотите узнать как кубический корень.Возьмем 17576 .
  2. Пропустить три последние цифры.
  3. Найдите два ближайших известных вам кубических корня. Кубический корень из 8 равен 2, а кубический корень из 27 равен 3. Таким образом, ваше число находится между 20 и 30.
  4. Посмотрите на последнюю цифру. Последняя цифра 17576 — 6.
  5. Проверьте свою память (или по нашей таблице) — последняя цифра 6 соответствует цифре 6. Это последняя цифра вашего числа.
  6. Объедините два: 26 . Это кубический корень из 17576!

Напоминаем, что этот алгоритм работает только для идеальных кубиков! А вероятность того, что случайное число является идеальным кубом, увы, очень мала.У вас есть только 0,0091% шанс найти человека между 1 000 и 1 000 000. Если вы не уверены в своем числе, просто забудьте об этом правиле и воспользуйтесь нашим калькулятором кубического корня 🙂

Что такое квадратный корень из 64?

Иногда на простой вопрос, например, каков квадратный корень из 64, есть ответ, который может запутать некоторых. В этом случае развеем пару мифов.

Основная цель этого руководства — узнать кое-что о квадратных корнях и радикалах, чтобы вы могли без колебаний отвечать на вопросы об этом.2 \), и поскольку квадратное число не может быть отрицательным, \ (x \) может быть только неотрицательным (если мы хотим найти его квадратный корень). 3 = x \ ).п = х \).

Подробнее о вычислении квадратного корня

Мы сделали упор на том, что функция квадратного корня \ (\ sqrt x \) должна принимать неотрицательный аргумент \ (x \), если мы хотим вычислить квадратный корень.

Мы немного обманули, потому что мы не написали полное предложение: функция квадратного корня \ (\ sqrt x \) должна принимать неотрицательный аргумент \ (x \), если мы хотим иметь возможность вычислить квадратный корень в НАСТОЯЩЕЙ ЛИНИИ.

НО, если \ (x

Основная единица комплексного квадратного корня — квадратный корень из -1. Что такое \ (\ sqrt {-1} \) ???

Введите комплексные числа: существует комплексное число, называемое \ (i \), так что

\ [\ sqrt {-1} = я \]

С этого момента свойства квадратного корня работают одинаково. Например:

\ [\ sqrt {-4} = \ sqrt {4} \ sqrt {-1} = 2 \ sqrt {-1} = 2i \]

Если у вас есть какие-либо предложения или вы хотите сообщить о неисправном решателе / ​​калькуляторе, пожалуйста, не стесняйтесь по телефону , свяжитесь с нами .

Квадраты и квадратные корни — разница и примеры

Что такое квадрат числа?

В математике квадрат числа — это результат умножения числа на само себя. Слово квадрат обычно эквивалентно возведению числа в степень 2 и обозначается верхним индексом 2.

Например, квадрат 4 записывается как 4 2 , что дает 16 в качестве ответа. В данном случае 16 — это квадрат числа 4.

Ниже приведен список квадратов первых двенадцати чисел:

1 x 1 = 1 7 x 7 = 49
2 x 2 = 4 8 x 8 = 64
3 x 3 = 9 9 x 9 = 81
4 x 4 = 16 10 x 10 = 100
5 x 5 = 25 11 x 11 = 121
6 x 6 = 36 12 x 12 = 144

Возведение отрицательных чисел в квадрат

Квадрат отрицательного числа является положительным числом.Например, -3 x -3 станет 9, однако — 3 x 3 = -9, это потому, что -3 — это число, отличное от 3.

Что такое квадратный корень числа?

Квадратный корень — это операция, обратная возведению числа в квадрат. Другими словами, квадратный корень — это операция, которая отменяет показатель степени 2. Квадратный корень из числа x таков, что число y является квадратом x, упрощенно записывается как y 2 = x.

Например, 5 и — 5 являются квадратными корнями из 25, потому что:

5 x 5 = 25 и -5 x -5 = 25.

Квадратный корень числа x обозначается знаком корня √x или x 1/2 . Например, квадратный корень из 16 представлен как: √16 = 4. Число, квадратный корень которого вычисляется, называется подкоренным выражением. В этом выражении √16 = 4, число 16 — подкоренное выражение.

Свойства

  • Полное квадратное число имеет точный квадратный корень.
  • Четное совершенное число имеет четный квадратный корень.
  • Нечетное совершенное число имеет нечетный квадратный корень.
  • Квадратный корень отрицательного числа не определен.
  • Квадратные корни имеют только числа, оканчивающиеся четным числом нулей.

Нахождение квадратного корня чисел

  • Повторное вычитание :
    Этот метод включает в себя успешное и многократное вычитание нечетных чисел, таких как 1, 3, 5 и 7, из числа до достижения нуля. Квадрат числа равен числу или частоте вычитания числа.Предположим, нам нужно вычислить квадрат идеального числа, такого как 16, количество выполненных вычитаний равно 4, и поэтому квадратный корень из 16 равен 4.
  • Простое факторизация :
    В этом методе идеальное квадратное число факторизуется путем последовательного деления. Простые множители группируются в пары, и вычисляется произведение каждого числа. Следовательно, произведение представляет собой квадратный корень из числа. Чтобы найти квадрат совершенного числа, такого как: 144, выполняется как:
  1. 144 = 2 × 2 × 2 × 2 × 3 × 3.
  2. Соедините простые множители.
  3. Выбор одного числа из каждой пары.
  4. 2 × 2 × 3 = 12.
  5. Таким образом, √144 = 12.
  • Метод деления:
    Метод деления является подходящей техникой вычисления квадрата большого числа.

    Это следующие шаги:
  1. Полоса помещается над каждой парой цифр, начиная с правой стороны.
  2. Разделите число на левом конце на число, квадрат которого меньше или эквивалентен числам под левым концом.
  3. Возьмите это число в качестве делителя и частного. Аналогичным образом возьмите крайнее левое число в качестве делимого.
  4. Разделите, чтобы получить результат.
  5. Потяните вниз следующее число с полосой справа от остатка.
  6. Умножьте делитель на 2.
  7. Справа от этого нового делителя найдите подходящий делимый. Этот процесс повторяется до тех пор, пока мы не получим в качестве остатка ноль. Следовательно, квадрат числа равен частному.

Практические вопросы

1.Запишите значение

(a) √81

(b) √1

(c) √121

(d) √0

2. Найдите квадратные числа из следующего списка чисел: 2 6 11 14 16 18 24 25.

3. Запишите значение (a) 3² (b) 6 в квадрате c) 8² (d) 9 в квадрате (e) 12²

4. Я думаю о двух числах. Оба числа представляют собой квадратные числа больше 1. Если сумма этих чисел равна 100. Какие два числа?

5. Перечислите все квадратные числа от 0 до 100.

Ответы на практические вопросы

1. (a) √81 = 9, (b) √1 = 1 (c) √121 = 11 (d) √0 = 0

2 . Квадратные числа: 16 и 25

3. (a) 3² = 9 (b) 6 в квадрате = 36 c) 8 = 64² (d) 9 в квадрате = 81 (e) 12² = 144

4. 36 и 64 — квадратные числа

5. 1, 4, 9, 16, 25, 36, 49, 64 и 81

Предыдущий урок | Главная страница | Следующий урок

Решите нелинейные уравнения x ^ 2 = -64 Tiger Algebra Solver

Переставьте:

Переставьте уравнение, вычтя то, что находится справа от знака равенства, из обеих частей уравнения:

x ^ 2- (-64) = 0

Пошаговое решение:

Шаг 1:

Калькулятор полиномиальных корней:

1. 1 Найдите корни (нули): F (x) = x 2 +64
Калькулятор полиномиальных корней — это набор методов, направленных на поиск значений x, для которых F (x) = 0

Тест рациональных корней является одним из вышеупомянутые инструменты. Он может найти только рациональные корни, то есть числа x, которые можно выразить как частное двух целых чисел

Теорема рационального корня утверждает, что если полином обнуляется для рационального числа P / Q, то P является множителем конечной константы и Q является множителем ведущего коэффициента

В этом случае ведущий коэффициент равен 1, а конечная константа — 64.

Фактор (ы):

ведущего коэффициента: 1
конечной константы: 1, 2, 4, 8, 16, 32, 64

Давайте проверим ….

2,00 16.0012 Рациональные корни найдены в конце шага 1:
 x  2  + 64 = 0

Шаг 2:

 Решение уравнения с одной переменной:
 2.1 Решите: x  2  +64 = 0
 Вычтем 64 из обеих частей уравнения: 
 x  2  = -64 
 
 Когда две вещи равны, их квадратные корни равны. Извлекая квадратный корень из двух частей уравнения, мы получаем: 
 x = ± √ -64
 В математике i называется мнимой единицей. Это удовлетворяет i  2  = -1. Оба i и -i являются квадратными корнями из -1
 Соответственно, √ -64 = 
 √ -1 • 64 = 
 √ -1 • √ 64 = 
 i • √ 64
 Можно ли упростить √ 64?
 Да! Разложение на простые множители 64 равно 
 2 • 2 • 2 • 2 • 2 • 2 
 Чтобы можно было удалить что-то из-под корня, должно быть 2 экземпляра этого (потому что мы берем квадрат i.е. второй корень).
 √ 64 = √ 2 • 2 • 2 • 2 • 2 • 2 = 2 • 2 • 2 • √ 1 = 
 ± 8 • √ 1 = 
 ± 8
 Уравнение не имеет реальных решений. У него есть 2 воображаемых или сложных решения.
 x = 0,0000 + 8,0000 i 
 x = 0,0000 — 8,0000 i 
 Были найдены два решения:
  1.  x = 0,0000 — 8,0000 i 
  2.  x = 0,0000 + 8,0000 i 
 Решение уравнений с квадратными корнями
 Есть много вопросов GRE, связанных с уравнениями с квадратными корнями. Давайте поищем простые способы их решения.
 Возьмите пример из банка практических вопросов Economist GRE Tutor:
  (√512) × (√2048) =? 
  A) 32 
 B) 64 
 C) 512 
 D) 996 
 E) 1024 
 Если у вас есть два разных значения внутри знаков квадратного корня, попробуйте найти общий множитель. Проще всего было бы, если бы 512 было на самом деле множителем 2048.
 Конечно, когда вы это проверите, это так! Получается, что 512 x 4 = 2048
 Таким образом, выражение можно переписать как:
 (√512) × (√2048) 
 → (√512) × (√ (512 × 4)) 
 → (√512 ) × (√ (512) × (√4) 
 → 512 x 2 
 → 1024
 Вариант ответа E правильный.
 Напомним, что возведение квадратного корня из числа в квадрат дает это число:
 √n × √n = n
 Следовательно, обратите внимание, что (√512) × (√512) просто становится 512, без необходимости выполнять следующие действия. расчет:
 (√512) × (√512) = (√262,144) = (√512)
 Это было бы так много дополнительной работы, если бы нужно было взять квадрат 512!
 Также стоит запомнить, что происходит, когда 2 повышается до определенных степеней.
 Например, 2  1  = 2
 2  2  = 4 
 2  3  = 8 
 2  4  = 16 
 2  5  = 32 
 2  6  = 64 
 2  7  = 128 
 2  8  = 256
 Если вы запомните так далеко, вы быстро поймете, что, например, 2  9  = 512, 2  10  = 1024 и 2  11  = 2048 год.Это может быть полезно в таких вопросах, как приведенный выше.
 Давайте перейдем к другому вопросу, связанному с квадратным корнем:
  Если  m = √x  и  m  — целое число, то  x  НЕ МОЖЕТ быть каким из следующего: 
  A) 25 + 39 
 B) (0,3) (30) 
 C) 147/3 
 D) √25 
 E) 0 
 Варианты ответов выглядят сложными, поэтому сначала давайте упростим и преобразуем их в целые числа, если это возможно:
 A) 64 
 B) 9 
 C) 49 
 D) 5 
 E) 0
 Вопрос говорит нам, что √x — это m, которое является целым числом.
 Related Posts
Leave A Comment
P Q P / Q F (P / Q) Делитель
-1 65.00
-2 1-2,00 68,00
80,00
-8 1 -8.00 128.00
-16 1 -16.00 320.00
-32,00 1088,00
-64 1 -64.00 4160.00
1 1 1.00 65.00
68,00
4 1 4. 00 80,00
8 1 8,00 128,00
320.00
32 1 32.00 1088.00
64 1 64.00 4160.00
4160.00 Рациональные корни