Используя формулу Эйлера, найдём корни для p
$$i \sin{\left (4 p \right )} + \cos{\left (4 p \right )} = 1$$
значит
$$\cos{\left (4 p \right )} = 1$$
и
$$\sin{\left (4 p \right )} = 0$$
тогда
$$p = \frac{\pi N}{2}$$
где N=0,1,2,3,…
Перебирая значения N и подставив p в формулу для z
Значит, решением будет для z:
$$z_{1} = — \sqrt[4]{17}$$
$$z_{2} = \sqrt[4]{17}$$
$$z_{3} = — \sqrt[4]{17} i$$
$$z_{4} = \sqrt[4]{17} i$$
делаем обратную замену
$$z = x — 16$$
$$x = z + 16$$
Тогда, окончательный ответ:
$$x_{1} = — \sqrt[4]{17} + 16$$
$$x_{2} = \sqrt[4]{17} + 16$$
$$x_{3} = 16 — \sqrt[4]{17} i$$
$$x_{4} = 16 + \sqrt[4]{17} i$$
Почему число в степени 0 равно 1?
☰
Существует правило, что любое число, кроме нуля, возведенное в нулевую степень, будет равно единице:
20 = 1; 1.50 = 1; 10000
Однако почему это так?
Когда число возводится в степень с натуральным показателем, то имеется в виду, что оно умножается само на себя столько раз, каков показатель степени:
43 = 4 × 4 × 4; 26 = 2 × 2 × 2 × 2 × 2 × 2
Когда же показатель степени равен 1, то при возведении имеется всего лишь один множитель (если тут вообще можно говорить о множителях), и поэтому результат возведения равен основанию степени:
181 = 18; (–3.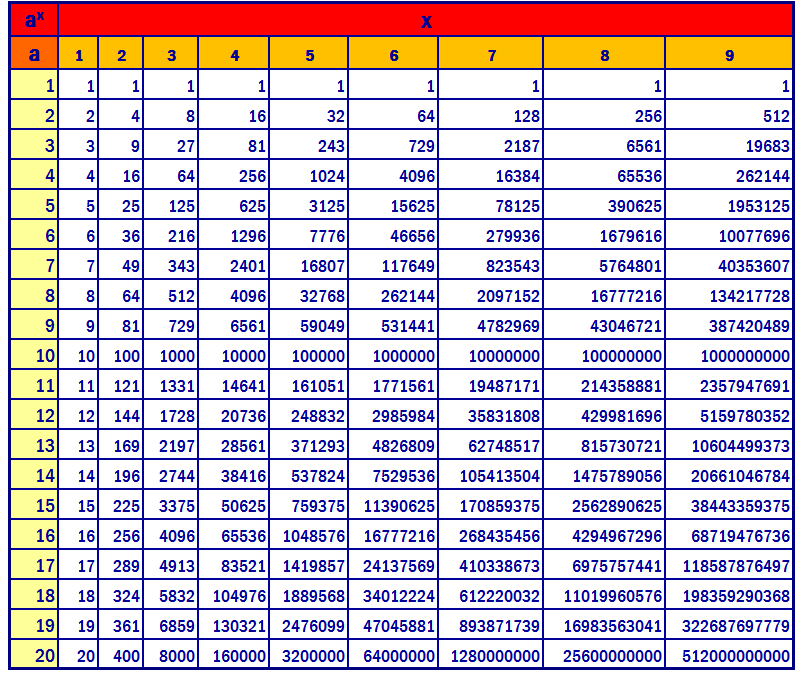 4)1 = –3.4
4)1 = –3.4
Но как в таком случае быть с нулевым показателем? Что на что умножается?
Попробуем пойти иным путем. Известно, что если у двух степеней одинаковые основания, но разные показатели, то основание можно оставить тем же самым, а показатели либо сложить друг с другом (если степени перемножаются), либо вычесть показатель делителя из показателя делимого (если степени делятся):
32 × 31 = 32+1 = 33 = 3 × 3 × 3 = 27
45 ÷ 43 = 45–3 = 42 = 4 × 4 = 16
А теперь рассмотрим такой пример:
82 ÷ 82 = 82–2 = 80 = ?
Что если мы не будем пользоваться свойством степеней с одинаковым основанием и произведем вычисления по порядку их следования:
82 ÷ 82 = 64 ÷ 64 = 1
Вот мы и получили заветную единицу. Таким образом нулевой показатель степени как бы говорит о том, что число не умножается само на себя, а делится само на себя.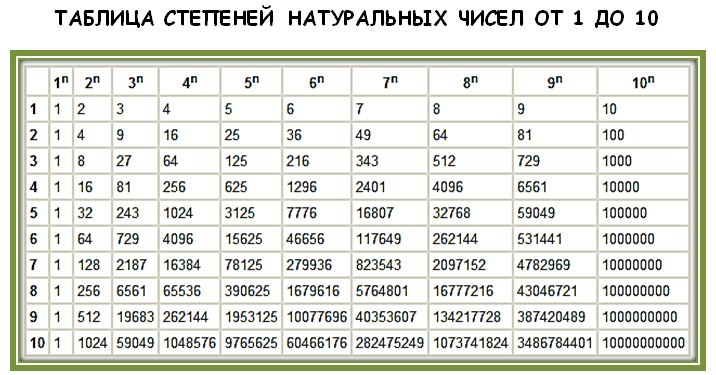
И отсюда становится понятно, почему выражение 00 не имеет смысла. Ведь нельзя делить на 0.
Можно рассуждать по-другому. Если имеется, например, умножение степеней 52 × 50 = 52+0 = 52, то отсюда следует, что 52 было умножено на 1. Следовательно, 5
Степень с натуральным показателем
Предварительные навыкиЧто такое степень?
Степенью называют произведение из нескольких одинаковых множителей. Например:
2 × 2 × 2
Значение данного выражения равно 8
2 × 2 × 2 = 8
Левую часть этого равенства можно сделать короче – сначала записать повторяющийся множитель и указать над ним сколько раз он повторяется. Повторяющийся множитель в данном случае это 2. Повторяется он три раза. Поэтому над двойкой записываем тройку:
23 = 8
Это выражение читается так: «два в третьей степени равно восемь» или «третья степень числа 2 равна 8».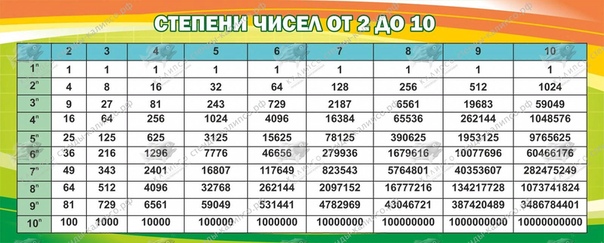
Короткую форму записи перемножения одинаковых множителей используют чаще. Поэтому надо помнить, что если над каким-то числом надписано другое число, то это есть перемножение нескольких одинаковых множителей.
Например, если дано выражение 53, то следует иметь ввиду, что это выражение равносильно записи 5 × 5 × 5.
Число, которое повторяется называют основанием степени. В выражении 53 основанием степени является число 5.
А число, которое надписано над числом 5 называют показателем степени. В выражении 53 показателем степени является число 3. Показатель степени показывает сколько раз повторяется основание степени. В нашем случае основание 5 повторяется три раза
Саму операцию перемножения одинаковых множителей называют возведением в степень.
Например, если нужно найти произведение из четырёх одинаковых множителей, каждый из которых равен 2, то говорят, что число 2 возводится в четвёртую степень:
Видим, что число 2 в четвёртой степени есть число 16.
Отметим, что в данном уроке мы рассматриваем степени с натуральным показателем. Это вид степени, показателем которой является натуральное число. Напомним, что натуральными называют целые числа, которые больше нуля. Например, 1, 2, 3 и так далее.
Вообще, определение степени с натуральным показателем выглядит следующим образом:
Степень числа a с натуральным показателем n — это выражение вида an, которое равно произведению n множителей, каждый из которых равен a
Примеры:
Следует быть внимательным при возведении числа в степень. Часто по невнимательности человек умножает основание степени на показатель.
Например, число 5 во второй степени есть произведение двух множителей каждый из которых равен 5. Это произведение равно 25
Теперь представим, что мы по невнимательности умножили основание 5 на показатель 2
Получилась ошибка, поскольку число 5 во второй степени не равно 10.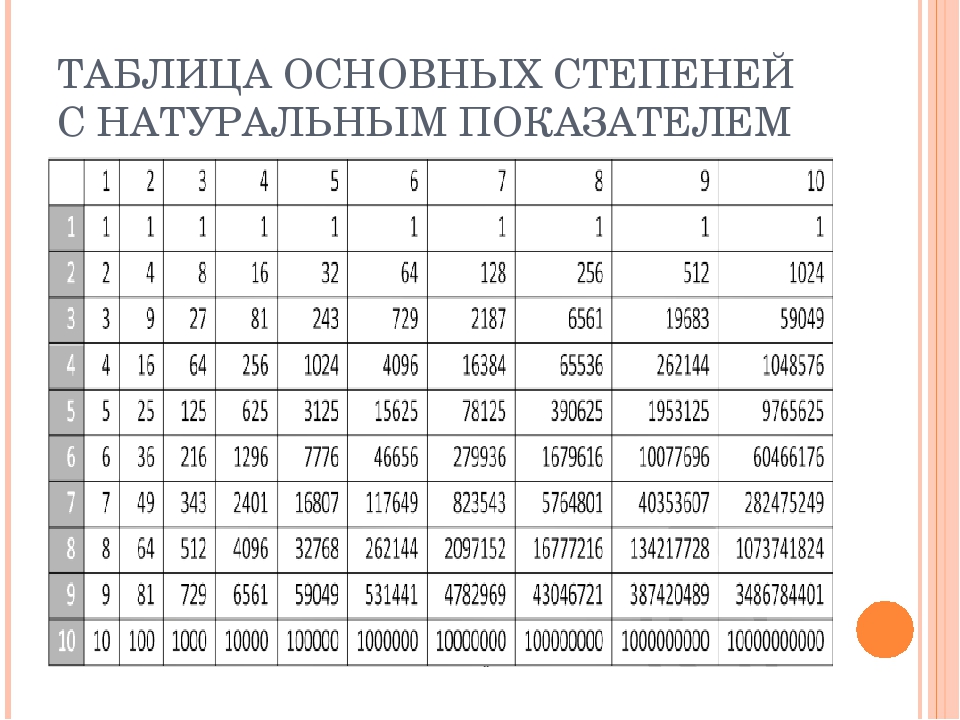
Дополнительно следует упомянуть, что степень числа с показателем 1, есть само это число:
Например, число 5 в первой степени есть само число 5
Соответственно, если у числа отсутствует показатель, то надо считать, что показатель равен единице.
Например, числа 1, 2, 3 даны без показателя, поэтому их показатели будут равны единице. Каждое из этих чисел можно записать с показателем 1
А если возвести 0 в какую-нибудь степень, то получится 0. Действительно, сколько бы раз ничего не умножалось на само себя получится ничего. Примеры:
А выражение 00 не имеет смысла. Но в некоторых разделах математики, в частности анализе и теории множеств, выражение 00 может иметь смысл.
Для тренировки решим несколько примеров на возведение чисел в степени.
Пример 1. Возвести число 3 во вторую степень.
Число 3 во второй степени это произведение двух множителей, каждый из которых равен 3
32 = 3 × 3 = 9
Пример 2.
Число 2 в четвертой степени это произведение четырёх множителей, каждый из которых равен 2
24 =2 × 2 × 2 × 2 = 16
Пример 3. Возвести число 2 в третью степень.
Число 2 в третьей степени это произведение трёх множителей, каждый из которых равен 2
23 =2 × 2 × 2 = 8
Возведение в степень числа 10
Чтобы возвести в степень число 10, достаточно дописать после единицы количество нулей, равное показателю степени.
Например, возведем число 10 во вторую степень. Сначала запишем само число 10 и в качестве показателя укажем число 2
102
Теперь ставим знак равенства, записываем единицу и после этой единицы записываем два нуля, поскольку количество нулей должно быть равно показателю степени
102 = 100
Значит, число 10 во второй степени это число 100. Связано это с тем, что число 10 во второй степени это произведение двух множителей, каждый из которых равен 10
102 = 10 × 10 = 100
Пример 2. Возведём число 10 в третью степень.
Возведём число 10 в третью степень.
В данном случае после единицы будут стоять три нуля:
103 = 1000
Пример 3. Возведем число 10 в четвёртую степень.
В данном случае после единицы будут стоять четыре нуля:
104 = 10000
Пример 4. Возведем число 10 в первую степень.
В данном случае после единицы будет стоять один нуль:
101 = 10
Представление чисел 10, 100, 1000 в виде степени с основанием 10
Чтобы представить числа 10, 100, 1000 и 10000 в виде степени с основанием 10, нужно записать основание 10, и в качестве показателя указать число, равное количеству нулей исходного числа.
Представим число 10 в виде степени с основанием 10. Видим, что в нём один нуль. Значит, число 10 в виде степени с основанием 10 будет представлено как 101
10 = 101
Пример 2. Представим число 100 в виде степени основанием 10.
100 = 102
Пример 3. Представим число 1 000 в виде степени с основанием 10.
1 000 = 103
Пример 4. Представим число 10 000 в виде степени с основанием 10.
10 000 = 104
Возведение в степень отрицательного числа
При возведении в степень отрицательного числа, его обязательно нужно заключить в скобки.
Например, возведём отрицательное число −2 во вторую степень. Число −2 во второй степени это произведение двух множителей, каждый из которых равен (−2)
(−2)2 = (−2) × (−2) = 4
Если бы мы не заключили в скобки число −2, то получилось бы что мы вычисляем выражение −22, которое не равно 4. Выражение −2² будет равно −4. Чтобы понять почему, коснёмся некоторых моментов.
Когда мы ставим перед положительным числом минус, мы тем самым выполняем операцию взятия противоположного значения.
Допустим, дано число 2, и нужно найти его противоположное число. Мы знаем, что противоположное числу 2 это число −2. Иными словами, чтобы найти противоположное число для 2, достаточно поставить минус перед этим числом. Вставка минуса перед числом уже считается в математике полноценной операцией. Эту операцию, как было указано выше, называют операцией взятия противоположного значения.
В случае с выражением −22 происходит две операции: операция взятия противоположного значения и возведение в степень. Возведение в степень является более приоритетной операцией, чем взятие противоположного значения.
Поэтому выражение −22 вычисляется в два этапа. Сначала выполняется операция возведения в степень. В данном случае во вторую степень было возведено положительное число 2
Затем выполнилось взятие противоположного значения. Это противоположное значение было найдено для значения 4. А противоположное значение для 4 это −4
−22 = −4
Скобки же имеют самый высокий приоритет выполнения. Поэтому в случае вычисления выражения (−2)2 сначала выполняется взятие противоположного значения, а затем во вторую степень возводится отрицательное число −2. В результате получается положительный ответ 4, поскольку произведение отрицательных чисел есть положительное число.
Поэтому в случае вычисления выражения (−2)2 сначала выполняется взятие противоположного значения, а затем во вторую степень возводится отрицательное число −2. В результате получается положительный ответ 4, поскольку произведение отрицательных чисел есть положительное число.
Пример 2. Возвести число −2 в третью степень.
Число −2 в третьей степени это произведение трёх множителей, каждый из которых равен (−2)
(−2)3 = (−2) × (−2) × (−2) = −8
Пример 3. Возвести число −2 в четвёртую степень.
Число −2 в четвёртой степени это произведение четырёх множителей, каждый из которых равен (−2)
(−2)4 = (−2) × (−2) × (−2) × (−2) = 16
Легко заметить, что при возведении в степень отрицательного числа может получиться либо положительный ответ либо отрицательный. Знак ответа зависит от показателя исходной степени.
Если показатель степени чётный, то ответ будет положительным. Если показатель степени нечётный, ответ будет отрицательным.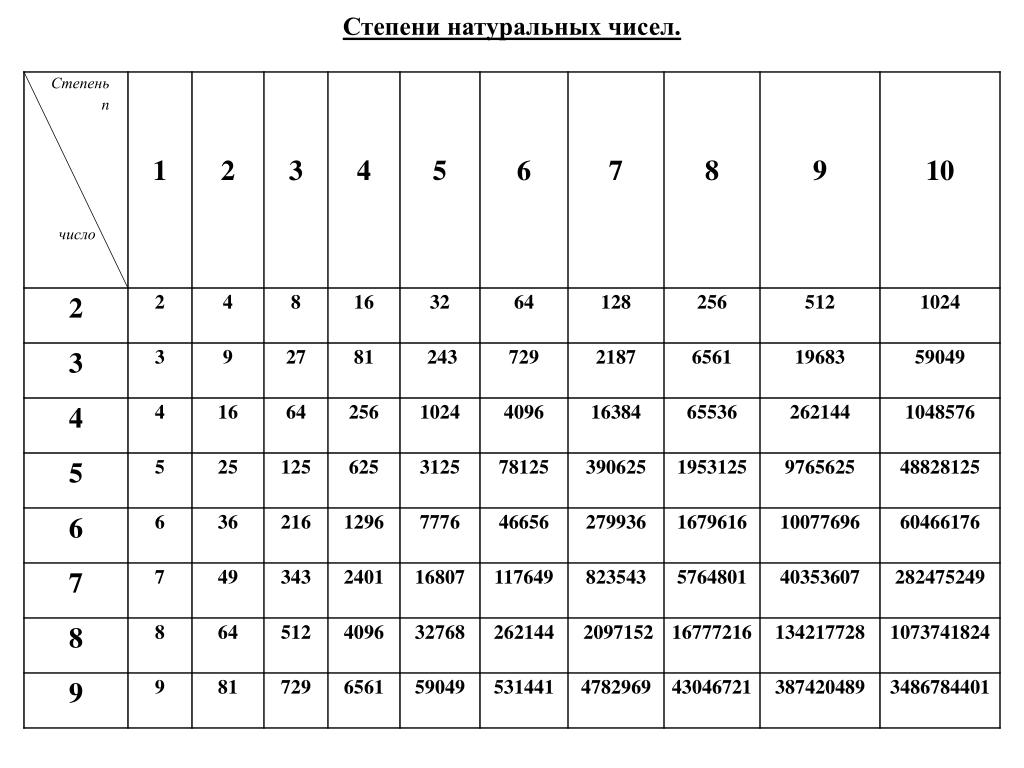 Покажем это на примере числа −3
Покажем это на примере числа −3
В первом и в третьем случае показатель был нечётным числом, поэтому ответ стал отрицательным.
Во втором и в четвёртом случае показатель был чётным числом, поэтому ответ стал положительным.
Пример 7. Возвести число −5 в третью степень.
Число −5 в третьей степени это произведение трёх множителей каждый из которых равен −5. Показатель 3 является нечётным числом, поэтому мы заранее можем сказать, что ответ будет отрицательным:
(−5)3 = (−5) × (−5) × (−5) = −125
Пример 8. Возвести число −4 в четвёртую степень.
Число −4 в четвёртой степени это произведение четырёх множителей, каждый из которых равен −4. При этом показатель 4 является чётным, поэтому мы заранее можем сказать, что ответ будет положительным:
(−4)4 = (−4) × (−4) × (−4) × (−4) = 256
Нахождение значений выражений
При нахождении значений выражений, не содержащих скобки, возведение в степень будет выполняться в первую очередь, далее умножение и деление в порядке их следования, а затем сложение и вычитание в порядке их следования.
Пример 1. Найти значение выражения 2 + 52
Сначала выполняется возведение в степень. В данном случае во вторую степень возводится число 5 — получается 25. Затем этот результат складывается с числом 2
2 + 52 = 2 + 25 = 27
Пример 10. Найти значение выражения −62 × (−12)
Сначала выполняется возведение в степень. Заметим, что число −6 не взято в скобки, поэтому во вторую степень будет возведено число 6, затем перед результатом будет поставлен минус:
−62 × (−12) = −36 × (−12)
Завершаем пример, умножив −36 на (−12)
−62 × (−12) = −36 × (−12) = 432
Пример 11. Найти значение выражения −3 × 22
Сначала выполняется возведение в степень. Затем полученный результат перемножается с числом −3
−3 × 22 = −3 × 4 = −12
Если выражение содержит скобки, то сначала нужно выполнить действия в этих скобках, далее возведение в степень, затем умножение и деление, а затем сложение и вычитание.
Пример 12. Найти значение выражения (32 + 1 × 3) − 15 + 5
Сначала выполняем действия в скобках. Внутри скобок применяем ранее изученные правила, а именно сначала возводим во вторую степень число 3, затем выполняем умножение 1 × 3, затем складываем результаты возведения в степень числа 3 и умножения 1 × 3. Далее выполняется вычитание и сложение в порядке их следования. Расставим такой порядок выполнения действия над исходным выражением:
(32 + 1 × 3) − 15 + 5 = 12 − 15 + 5 = 2
Пример 13. Найти значение выражения 2 × 53 + 5 × 23
Сначала возведем числа в степени, затем выполним умножение и сложим полученные результаты:
2 × 53 + 5 × 23 = 2 × 125 + 5 × 8 = 250 + 40 = 290
Тождественные преобразования степеней
Над степенями можно выполнять различные тождественные преобразования, тем самым упрощая их.
Допустим, потребовалось вычислить выражение (23)2. В данном примере два в третьей степени возводится во вторую степень. Иными словами, степень возводится в другую степень.
В данном примере два в третьей степени возводится во вторую степень. Иными словами, степень возводится в другую степень.
(23)2это произведение двух степеней, каждая из которых равна 23
При этом каждая из этих степеней является произведением трёх множителей, каждый из которых равен 2
Получили произведение 2 × 2 × 2 × 2 × 2 × 2, которое равно 64. Значит значение выражения (23)2 или равно 64
Этот пример можно значительно упростить. Для этого показатели выражения (23)2 можно перемножить и записать это произведение над основанием 2
Получили 26. Два в шестой степени это произведение шести множителей, каждый из которых равен 2. Это произведение равно 64
Данное свойство работает по причине того, что 23 это произведение 2 × 2 × 2, которое в свою очередь повторяется два раза. Тогда получается, что основание 2 повторяется шесть раз. Отсюда можно записать, что 2 × 2 × 2 × 2 × 2 × 2 это 26
Отсюда можно записать, что 2 × 2 × 2 × 2 × 2 × 2 это 26
Вообще, для любого основания a с показателями m и n, выполняется следующее равенство:
(an)m = an × m
Это тождественное преобразование называют возведением степени в степень. Его можно прочитать так: «При возведении степени в степень основание оставляют без изменений, а показатели перемножают».
После перемножения показателей, получится другая степень, значение которой можно найти.
Пример 2. Найти значение выражения (32)2
В данном примере основанием является 3, а числа 2 и 2 являются показателями. Воспользуемся правилом возведения степени в степень. Основание оставим без изменений, а показатели перемножим:
Получили 34. А число 3 в четвёртой степени есть 81
Рассмотрим остальные преобразования.
Умножение степеней
Чтобы перемножить степени, нужно по отдельности вычислить каждую степень, и полученные результаты перемножить.
Например, умножим 22 на 33.
22 это число 4, а 33 это число 27. Перемножаем числа 4 и 27, получаем 108
22 × 33 = 4 × 27 = 108
В этом примере основания степеней были разными. В случае, если основания будут одинаковыми, то можно записать одно основание, а в качестве показателя записать сумму показателей исходных степеней.
Например, умножим 22 на 23
В данном примере основания у степеней одинаковые. В этом случае можно записать одно основание 2 и в качестве показателя записать сумму показателей степеней 22 и 23. Иными словами, основание оставить без изменений, а показатели исходных степеней сложить. Выглядеть это будет так:
Получили 25. Число 2 в пятой степени есть 32
Данное свойство работает по причине того, что 22 это произведение 2 × 2, а 23 это произведение 2 × 2 × 2. Тогда получается произведение из пяти одинаковых множителей, каждый из которых равен 2. Это произведение представимо в виде 25
Это произведение представимо в виде 25
Вообще, для любого a и показателей m и n выполняется следующее равенство:
Это тождественное преобразование носит название основного свойства степени. Его можно прочитать так: «При перемножении степеней с одинаковыми основаниями, основание оставляют без изменений, а показатели складывают».
Отметим, что данное преобразование можно применять при любом количестве степеней. Главное, чтобы основание было одинаковым.
Например, найдем значение выражения 21 × 22 × 23. Основание 2 оставим без изменений, а показатели сложим:
В некоторых задачах достаточным бывает выполнить соответствующее преобразование, не вычисляя итоговую степень. Это конечно же очень удобно, поскольку вычислять большие степени не так-то просто.
Пример 1. Представить в виде степени выражение 58 × 25
В данной задаче нужно сделать так, чтобы вместо выражения 58 × 25 получилась одна степень.
Число 25 можно представить в виде 52. Тогда получим следующее выражение:
В этом выражении можно применить основное свойство степени — основание 5 оставить без изменений, а показатели 8 и 2 сложить:
Задачу можно считать решённой, поскольку мы представили выражение 58 × 25 в виде одной степени, а именно в виде степени 510.
Запишем решение покороче:
Пример 2. Представить в виде степени выражение 29 × 32
Число 32 можно представить в виде 25. Тогда получим выражение 29 × 25. Далее можно применить основание свойство степени — основание 2 оставить без изменений, а показатели 9 и 5 сложить. В результате получится следующее решение:
Пример 3. Вычислите произведение 3 × 3, используя основное свойство степени.
Все хорошо знают, что три умножить на три равно девять, но задача требует в ходе решения воспользоваться основным свойством степени. Как это сделать?
Как это сделать?
Вспоминаем, что если число дано без показателя, то показатель нужно считать равным единице. Стало быть сомножители 3 и 3 можно записать в виде 31 и 31
31 × 31
Теперь воспользуемся основным свойством степени. Основание 3 оставляем без изменений, а показатели 1 и 1 складываем:
31 × 31 = 32
Далее вычисляем значение выражения. Число 3 во второй степени равно числу 9
31 × 31 = 32 = 9
Пример 4. Вычислите произведение 2 × 2 × 32 × 33, используя основное свойство степени.
Произведение 2 × 2 заменим на 21 × 21, затем на 21 + 1, а затем на 22. Произведение 32 × 33 заменим на 32 + 3, а затем на 35
Далее вычисляем значение каждой степени и находим произведение:
Пример 5. Выполнить умножение x × x
Выполнить умножение x × x
Это два одинаковых буквенных сомножителя с показателями 1. Для наглядности запишем эти показатели. Далее основание x оставим без изменений, а показатели сложим:
Находясь у доски, не следует записывать перемножение степеней с одинаковыми основаниями так подробно, как это сделано здесь. Такие вычисления нужно выполнять в уме. Подробная запись скорее всего будет раздражать учителя и он снизит за это оценку. Здесь же подробная запись дана, чтобы материал был максимально доступным для понимания.
Решение данного примера желательно записать так:
Пример 6. Выполнить умножение x2 × x
Показатель второго сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
Пример 7. Выполнить умножение y3y2y
Показатель третьего сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
Пример 8. Выполнить умножение aa3a2a5
Показатель первого сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
Пример 9. Представить степень 38 в виде произведения степеней с одинаковыми основаниями.
В данной задаче нужно составить произведение степеней, основания которых будут равны 3, и сумма показателей которых будет равна 8. Можно использовать любые показатели. Представим степень 38 в виде произведения степеней 35 и 33
В данном примере мы опять же опирались на основное свойство степени. Ведь выражение 35 × 33 можно записать как 35 + 3, откуда 38.
Конечно можно было представить степень 38 в виде произведения других степеней. Например, в виде 37 × 31, поскольку это произведение тоже равно 38
Например, в виде 37 × 31, поскольку это произведение тоже равно 38
Представление степени в виде произведения степеней с одинаковыми основаниями это по большей части творческая работа. Поэтому не нужно бояться экспериментировать.
Пример 10. Представить степень x12 в виде различных произведений степеней с основаниями x.
Воспользуемся основным свойство степени. Представим x12 в виде произведений с основаниями x, и сумма показателей которых равна 12
Конструкции с суммами показателей были записаны для наглядности. Чаще всего их можно пропустить. Тогда получится компактное решение:
Возведение в степень произведения
Чтобы возвести в степень произведение, нужно возвести в указанную степень каждый множитель этого произведения и перемножить полученные результаты.
Например, возведём во вторую степень произведение 2 × 3. Возьмём в скобки данное произведение и в качестве показателя укажем 2
Возьмём в скобки данное произведение и в качестве показателя укажем 2
Теперь возведём во вторую степень каждый множитель произведения 2 × 3 и перемножим полученные результаты:
Принцип работы данного правила основан на определении степени, которое было дано в самом начале.
Возвести произведение 2 × 3 во вторую степень означает повторить данное произведение два раза. А если повторить его два раза, то можно получить следующее:
2 × 3 × 2 × 3
От перестановки мест сомножителей произведение не меняется. Это позволяет сгруппировать одинаковые множители:
2 × 2 × 3 × 3
Повторяющиеся множители можно заменить на короткие записи — основания с показателями. Произведение 2 × 2 можно заменить на 22, а произведение 3 × 3 можно заменить на 32. Тогда выражение 2 × 2 × 3 × 3 обращается в выражение 22 × 32.
Пусть ab исходное произведение. Чтобы возвести данное произведение в степень n, нужно по отдельности возвести множители a и b в указанную степень n
Данное свойство справедливо для любого количества множителей. Следующие выражения также справедливы:
Следующие выражения также справедливы:
Пример 2. Найти значение выражения (2 × 3 × 4)2
В данном примере нужно возвести во вторую степень произведение 2 × 3 × 4. Чтобы сделать это, нужно возвести во вторую степень каждый множитель этого произведения и перемножить полученные результаты:
Пример 3. Возвести в третью степень произведение a × b × c
Заключим в скобки данное произведение, и в качестве показателя укажем число 3
Далее возводим в третью степень каждый множитель данного произведения:
Пример 4. Возвести в третью степень произведение 3xyz
Заключим в скобки данное произведение, и в качестве показателя укажем 3
(3xyz)3
Возведём в третью степень каждый множитель данного произведения:
(3xyz)3 = 33x3y3z3
Число 3 в третьей степени равно числу 27. Остальное оставим без изменений:
Остальное оставим без изменений:
(3xyz)3 = 33x3y3z3 = 27x3y3z3
В некоторых примерах умножение степеней с одинаковыми показателями можно заменять на произведение оснований с одним показателем.
Например, вычислим значение выражения 52 × 32. Возведем каждое число во вторую степень и перемножим полученные результаты:
52 × 32 = 25 × 9 = 225
Но можно не вычислять по отдельности каждую степень. Вместо этого, данное произведение степеней можно заменить на произведение с одним показателем (5 × 3)2. Далее вычислить значение в скобках и возвести полученный результат во вторую степень:
52 × 32 = (5 × 3)2 = (15)2 = 225
В данном случае опять же было использовано правило возведения в степень произведения. Ведь, если (a × b)n = an × bn, то an × bn = (a × b)n.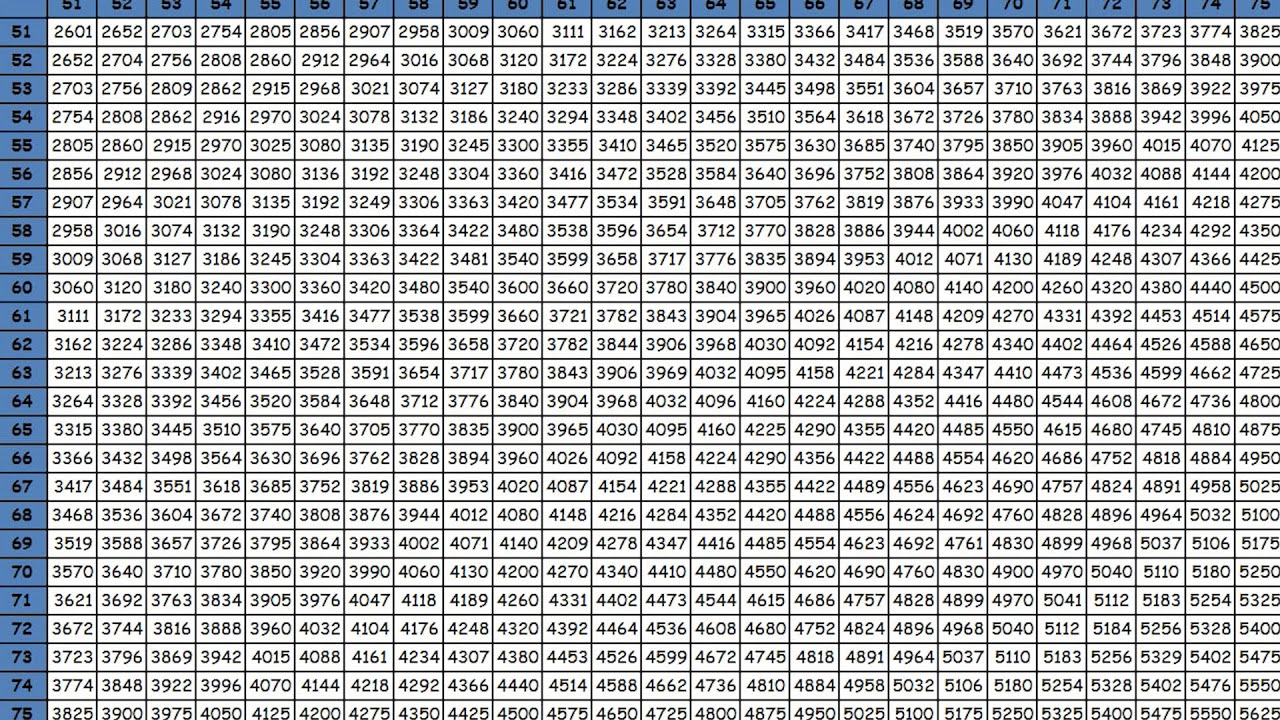 То есть левая и правая часть равенства поменялись местами.
То есть левая и правая часть равенства поменялись местами.
Возведение степени в степень
Это преобразование мы рассматривали в качестве примера, когда пытались понять суть тождественных преобразований степеней.
При возведении степени в степень основание оставляют без изменений, а показатели перемножают:
(an)m = an × m
К примеру, выражение (23)2 является возведением степени в степень — два в третьей степени возводится во вторую степень. Чтобы найти значение этого выражения, основание можно оставить без изменений, а показатели перемножить:
(23)2 = 23 × 2 = 26
Далее вычислить степень 26, которая равна 64
(23)2 = 23 × 2 = 26 = 64
Данное правило основано на предыдущих правилах: возведении в степень произведения и основного свойства степени.
Вернёмся к выражению (23)2. Выражение в скобках 23 представляет собой произведение из трёх одинаковых множителей, каждый из которых равен 2. Тогда в выражении (23)2 степень, находящуюся внутри скобок можно заменить на произведение 2 × 2 × 2.
Выражение в скобках 23 представляет собой произведение из трёх одинаковых множителей, каждый из которых равен 2. Тогда в выражении (23)2 степень, находящуюся внутри скобок можно заменить на произведение 2 × 2 × 2.
(2 × 2 × 2)2
А это есть возведение в степень произведения, которое мы изучили ранее. Напомним, что для возведения в степень произведения, нужно возвести в указанную степень каждый множитель данного произведения и полученные результаты перемножить:
(2 × 2 × 2)2 = 22 × 22 × 22
Теперь имеем дело с основным свойством степени. Основание оставляем без изменений, а показатели складываем:
(2 × 2 × 2)2 = 22 × 22 × 22 = 22 + 2 + 2 = 26
Как и раньше получили 26. Значение этой степени равно 64
(2 × 2 × 2)2 = 22 × 22 × 22 = 22 + 2 + 2 = 26 = 64
В степень также может возводиться произведение, сомножители которого тоже являются степенями.
Например, найдём значение выражения (22 × 32)3. Здесь показатели каждого множителя нужно умножить на общий показатель 3. Далее найти значение каждой степени и вычислить произведение:
(22 × 32)3 = 22×3 × 32×3 = 26 × 36 = 64 × 729 = 46656
Примерно тоже самое происходит при возведении в степени произведения. Мы говорили, что при возведении в степень произведения, в указанную степень возводится каждый множитель этого произведения.
Например, чтобы возвести произведение 2 × 4 в третью степень, нужно записать следующее выражение:
Но ранее было сказано, что если число дано без показателя, то показатель надо считать равным единице. Получается, что множители произведения 2 × 4 изначально имеют показатели равные 1. Значит в третью степень возводилось выражение 21 × 41. А это есть возведение степени в степень.
Перепишем решение с помощью правила возведения степени в степень. У нас должен получиться тот же результат:
У нас должен получиться тот же результат:
Пример 2. Найти значение выражения (33)2
Основание оставляем без изменений, а показатели перемножаем:
Получили 36. Число 3 в шестой степени есть число 729
Пример 3. Выполнить возведение в степень в выражении (xy)³
Возведём в третью степень каждый множитель произведения:
Пример 4. Выполнить возведение в степень в выражении (abc)⁵
Возведём в пятую степень каждый множитель произведения:
Пример 5. Выполнить возведение в степень в выражении (−2ax)3
Возведём в третью степень каждый множитель произведения:
Поскольку в третью степень возводилось отрицательное число −2, оно было взято в скобки.
Далее нужно вычислить то, что вычисляется. В данном случае можно вычислить (−2)3 — получится −8. Буквенная часть останется без изменений:
Буквенная часть останется без изменений:
Пример 6. Выполнить возведение в степень в выражении (10xy)2
Пример 7. Выполнить возведение в степень в выражении (−5x)3
Пример 8. Выполнить возведение в степень в выражении (−3y)4
Пример 9. Выполнить возведение в степень в выражении (−2abx)⁴
Пример 10. Упростите выражение x5 × (x2)3
Степень x5 пока оставим без изменений, а в выражении (x2)3 выполним возведение степени в степени:
x5 × (x2)3 = x5 × x2 × 3 = x5 × x6
Теперь выполним умножение x5× x6. Для этого воспользуемся основным свойством степени — основание x оставим без изменений, а показатели сложим:
Для этого воспользуемся основным свойством степени — основание x оставим без изменений, а показатели сложим:
x5 × (x2)3 = x5 × x2× 3 = x5 × x6 = x5 + 6 = x11
Пример 9. Найти значение выражения 43 × 22, используя основное свойство степени.
Основное свойство степени можно использовать в случае, если основания исходных степеней одинаковы. В данном примере основания разные, поэтому для начала исходное выражение нужно немного видоизменить, а именно сделать так, чтобы основания степеней стали одинаковыми.
Посмотрим внимательно на степень 43. Основание у этой степени есть число 4, которое можно представить в виде 22. Тогда исходное выражение примет вид (22)3 × 22. Выполнив возведение степени в степень в выражении (22)3, мы получим 26. Тогда исходное выражение примет вид 26 × 22, вычислить которое можно, используя основное свойство степени.
Тогда исходное выражение примет вид 26 × 22, вычислить которое можно, используя основное свойство степени.
Запишем решение данного примера:
Деление степеней
Чтобы выполнить деление степеней, нужно найти значение каждой степени, затем выполнить деление обыкновенных чисел.
Например, разделим 43 на 22.
Вычислим 43, получим 64. Вычислим 22, получим 4. Теперь разделим 64 на 4, получим 16
Если при делении степеней основания окажутся одинаковыми, то основание можно оставить без изменений, а из показателя степени делимого вычесть показатель степени делителя.
Например, найдем значение выражения 23 : 22
Основание 2 оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Значит, значение выражения 23 : 22 равно 2.
Данное свойство основано на умножении степеней с одинаковыми основаниями, или как мы привыкли говорить на основном свойстве степени.
Вернемся к предыдущему примеру 23 : 22. Здесь делимое это 23, а делитель 22.
Разделить одно число на другое означает найти такое число, которое при умножении на делитель даст в результате делимое.
В нашем случае, разделить 23 на 22 означает найти такую степень, которая при умножении на делитель 22 даст в результате 23. А какую степень можно умножить на 22, чтобы получить 23 ? Очевидно, что только степень 21. Из основного свойства степени имеем:
Убедиться, что значение выражения 23 : 22 равно 21 можно непосредственно вычислив само выражение 23 : 22. Для этого сначала найдём значение степени 23, получим 8. Затем найдём значение степени 22, получим 4. Разделим 8 на 4, получим 2 или 21, поскольку 2 = 21.
23 : 22 = 8 : 4 = 2
Таким образом, при делении степеней с одинаковыми основаниями выполняется следующее равенство:
Может случиться и так, что одинаковыми могут оказаться не только основания, но и показатели. В этом случае в ответе получится единица.
В этом случае в ответе получится единица.
Например, найдём значение выражения 22 : 22. Вычислим значение каждой степени и выполним деление получившихся чисел:
При решении примера 22 : 22 также можно применить правило деления степеней с одинаковыми основаниями. В результате получается число в нулевой степени, поскольку разность показателей степеней 22 и 22 равна нулю:
В математике принято считать, что любое число в нулевой степени есть единица:
Почему число 2 в нулевой степени равно единице мы выяснили выше. Если вычислить 22 : 22 обычным методом, не используя правило деления степеней, получится единица.
Пример 2. Найти значение выражения 412 : 410
Воспользуемся правилом деления степеней. Основание 4 оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
412 : 410 = 412 − 10 = 42 = 16
Пример 3.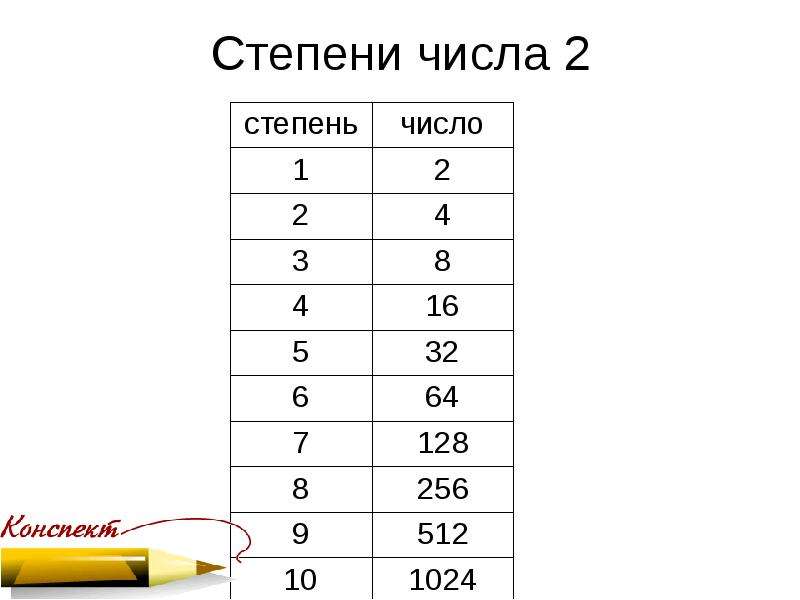 Представить частное x3 : x в виде степени с основанием x
Представить частное x3 : x в виде степени с основанием x
Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя. Показатель делителя равен единице. Для наглядности запишем его:
Пример 4. Представить частное x3 : x2 в виде степени с основанием x
Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Деление степеней можно записывать в виде дроби. Так, предыдущий пример можно записать следующим образом:
Числитель и знаменатель дроби разрешается записывать в развёрнутом виде, а именно в виде произведений одинаковых множителей. Степень x3 можно записать как x × x × x, а степень x2 как x × x. Тогда конструкцию x3 − 2 можно будет пропустить и воспользоваться сокращением дроби. В числителе и в знаменателе можно будет сократить по два множителя x. В результате останется один множитель x
Тогда конструкцию x3 − 2 можно будет пропустить и воспользоваться сокращением дроби. В числителе и в знаменателе можно будет сократить по два множителя x. В результате останется один множитель x
Или ещё короче:
Также, полезно уметь быстро сокращать дроби, состоящие из степеней. Например, дробь можно сократить на x2. Чтобы сократить дробь на x2 нужно числитель и знаменатель дроби разделить на x2
Деление степеней подробно можно не расписывать. Приведённое сокращение можно выполнить короче:
Или ещё короче:
Пример 5. Выполнить деление x12 : x3
Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Запишем решение при помощи сокращения дроби. Деление степеней x12 : x3 запишем в виде . Далее сократим данную дробь на x3.
Деление степеней x12 : x3 запишем в виде . Далее сократим данную дробь на x3.
Пример 6. Найти значение выражения
В числителе выполним умножение степеней с одинаковыми основаниями:
Теперь применяем правило деления степеней с одинаковыми основаниями. Основание 7 оставляем без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Завершаем пример, вычислив степень 72
Пример 7. Найти значение выражения
Выполним в числителе возведение степени в степень. Сделать это нужно с выражением (23)4
Теперь выполним в числителе умножение степеней с одинаковыми основаниями:
Теперь применяем правило деления степеней с одинаковыми основаниями:
Значит, значение выражения равно 16
В некоторых примерах можно сокращать одинаковые множители в ходе решения. Это позволяет упростить выражение и само вычисление в целом.
Это позволяет упростить выражение и само вычисление в целом.
Например, найдём значение выражения . Степень 43 запишем в виде возведения степени в степень (22)3. Тогда получим следующее выражение:
В числителе выполним возведение степени в степень. Сделать это нужно с выражением (22)3
В числителе и в знаменателе получившегося выражения содержится степень 26, которую можно сократить на 26
Видим, что в результате осталась единственная степень 32, значение которой равно 9.
Пример 8. Найти значение выражения
В знаменателе содержится произведение степеней с одинаковыми показателями. Согласно правилу возведения в степень произведения, конструкцию 75 × 45 можно представить в виде степени с одним показателем (7 × 4)5. Далее перемножим выражение в скобках, получим 285. В результате исходное выражение примет следующий вид:
Теперь можно применить правило деления степеней:
Значит, значение выражения равно 28. Запишем решение полностью:
Запишем решение полностью:
Возведение в степень обыкновенных дробей
Чтобы возвести в степень обыкновенную дробь, нужно возвести в указанную степень числитель и знаменатель этой дроби.
Например, возведём обыкновенную дробь во вторую степень. Возьмём в скобки данную дробь и в качестве показателя укажем 2
Если не брать в скобки всю дробь, то это равносильно возведению в степень только числителя данной дроби. Иными словами, если мы хотим возвести во вторую степень дробь , мы не должны записывать это как .
Итак, чтобы вычислить значение выражения , нужно возвести во вторую степень числитель и знаменатель данной дроби:
Получили дробь в числителе и в знаменателе которой содержатся степени. Вычислим каждую степень по отдельности
Значит обыкновенная дробь во второй степени равна дроби .
Приведённое правило работает следующим образом. Дробь во второй степень это произведение двух дробей, каждая из которых равна
Мы помним, что для перемножения дробей необходимо перемножить их числители и знаменатели:
А поскольку в числителе и в знаменателе происходит перемножение одинаковых множителей, то выражения 2 × 2 и 3 × 3 можно заменить на 22 и 32 соответственно:
Откуда и получится ответ .
Вообще, для любого a и b ≠ 0 выполняется следующее равенство:
Это тождественное преобразование называют возведением в степень обыкновенной дроби.
Пример 2. Возвести дробь в третью степень
Заключим данную дробь в скобки и в качестве показателя укажем число 3. Далее возведём числитель и знаменатель данной дроби в третью степень и вычислим получившуюся дробь:
Отрицательная дробь возводится в степень таким же образом, но перед вычислениями надо определиться какой знак будет иметь ответ. Если показатель четный, то ответ будет положительным. Если показатель нечетный, то ответ будет отрицательным.
Например, возведём дробь во вторую степень:
Показатель является чётным числом. Значит ответ будет положительным. Далее применяем правило возведения в степень дроби и вычисляем получившуюся дробь:
Ответ положителен по причине того, что выражение представляет собой произведение двух сомножителей, каждый из которых равен дроби
А произведение отрицательных чисел (в том числе и рациональных) есть положительное число:
Если возводить дробь в третью степень, то ответ будет отрицательным, поскольку в данном случае показатель будет нечётным числом. Правило возведения в степень остаётся тем же, но перед выполнением этого возведения, нужно будет поставить минус:
Правило возведения в степень остаётся тем же, но перед выполнением этого возведения, нужно будет поставить минус:
Здесь ответ отрицателем по причине того, что выражение представляет собой произведение трёх множителей, каждый из которых равен дроби
Сначала перемножили и , получили , но затем умножив на мы получим отрицательный ответ
Пример 3. Найти значение выражения
Выполним возведение в степень обыкновенной дроби:
Далее вычислим значение получившегося выражения:
Возведение в степень десятичных дробей
При возведении в степень десятичной дроби её необходимо заключить в скобки. Например, возведём во вторую степень десятичную дробь 1,5
Допускается переводить десятичную дробь в обыкновенную и возводить в степень эту обыкновенную дробь. Решим предыдущий пример, переведя десятичную дробь в обыкновенную:
Пример 2. Найти значение степени (−1,5)3
Показатель степени является нечётным числом. Значит ответ будет отрицательным
Значит ответ будет отрицательным
Пример 3. Найти значение степени (−2,4)2
Показатель степени является чётным числом. Значит ответ будет положительным:
Задания для самостоятельного решения
Задание 1. Найдите значение выражения:
Решение:
Задание 2. Найдите значение выражения:
Решение:
Задание 3. Найдите значение выражения:
Решение:
Задание 4. Найдите значение выражения:
Решение:
Задание 5. Найдите значение выражения:
Решение:
Задание 6. Найдите значение выражения:
Решение:
Задание 7. Представьте в виде степени произведение:
Решение:
Задание 8. Представьте в виде степени произведение:
Решение:
Задание 9. Представьте в виде степени произведение:
Решение:
Задание 10. Представьте в виде степени произведение:
Решение:
Задание 11. Представьте в виде степени произведение:
Представьте в виде степени произведение:
Решение:
Задание 12. Представьте в виде степени произведение:
Решение:
Задание 13. Представьте в виде степени частное:
Решение:
Задание 14. Представьте в виде степени частное:
Решение:
Задание 15. Представьте в виде степени частное:
Решение:
Задание 16. Представьте в виде степени частное:
Решение:
Задание 17. Представьте в виде степени частное:
Решение:
Задание 18. Представьте в виде степени частное и найдите значение получившейся степени при x = 3 и n = 2Решение:
Задание 19. Представьте в виде степени частное:
Решение:
Задание 20. Сократите дробь на c¹Решение:
Задание 21. Представьте в виде степени следующее произведение:
Решение:
Задание 22. Представьте в виде степени следующее произведение:
Решение:
Задание 23. Представьте в виде степени следующее произведение:
Представьте в виде степени следующее произведение:
Решение:
Задание 24. Представьте в виде степени следующее произведение:
Решение:
Задание 25. Представьте в виде степени следующее произведение:
Решение:
Задание 26. Представьте следующую степень в виде произведения степеней:
Решение:
Задание 27. Представьте следующую степень в виде произведения степеней:
Решение:
Задание 28. Представьте следующую степень в виде произведения степеней:
Решение:
Задание 29. Пользуясь тождественными преобразованиями степеней, найдите значение следующего выражения:
Решение:
Задание 30. Пользуясь тождественными преобразованиями степеней, найдите значение следующего выражения:
Решение:
Задание 31. Пользуясь тождественными преобразованиями степеней, найдите значение следующего выражения:
Решение:
Задание 32. Представьте в виде степени следующее выражение:
Решение:
Задание 33. Представьте в виде степени следующее выражение:
Представьте в виде степени следующее выражение:
Решение:
Задание 34. Представьте в виде степени следующее выражение:
Решение:
Задание 35. Представьте в виде степени следующее выражение:
Решение:
Задание 36. Представьте в виде степени следующее выражение:
Решение:
Задание 37. Представьте в виде степени следующее выражение:
Решение:
Задание 38. Найдите значение следующего выражения:
Решение:
Задание 39. Найдите значение следующего выражения:
Решение:
Задание 40. Найдите значение следующего выражения:
Решение:
Задание 41. Найдите значение следующего выражения:
Решение:
Задание 42. Найдите значение следующего выражения:
Решение:
Задание 43. Найдите значение следующего выражения:
Решение:
Задание 44. Найдите значение следующего выражения:
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Возведение в степень и извлечение корня из числа онлайн.

Корень из числа
Корень нечётной степени из положительного числа
В результате вычисления корня нечётной степени из положительного числа будет положительное число: .
Пример Вычислим корни нечётной степени из 8, 27, 125, 243
Корни 3 степени также называют кубическими корнями.
В результате вычисления корней 5-ой степени из положительных чисел, получили также положительные числа.
Корень нечётной степени из отрицательного числа
В результате вычисления корня нечётной степени из отрицательного числа будет отрицательное число: .
Пример Найдем корни 3 и 5 степеней из отрицательных чисел.
Корень четной степени из положительного числа
Корень чётной степени из положительного числа имеет два значения, положительное и отрицательное: .
Пример Вычислим корни 2 и 4 степени.
Корень 2-й степени называют квадратный корнем.
Корень четной степени из отрицательного числа
Корень четной степени из отрицательного числа не существует для вещественных чисел.
Корень любой степени из нуля
Числа в степени -1, 0, 1
Число в -1 степени
Число 3 в -1 степени можно представить в виде дроби . Обратная операция также верна ,
любую дробь можно представить как число в -1 степени, для этого нужно поменять числить и знаменатель местами.
Обратная операция также верна ,
любую дробь можно представить как число в -1 степени, для этого нужно поменять числить и знаменатель местами.
Число является обратным числом 5, т.е. их произведение равно единице , такое равенство выполнено для любого числа
Пример Представить дробь в степени -1
Число в 1 степени
Число в первой степени является самим числом a1=a
Число в 0 степени
Любое число в степени ноль равно единице a0=1
Возведение в степень: правила, примеры, дробная степень
Мы разобрались, что вообще из себя представляет степень числа. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Все определения будут проиллюстрированы примерами.
Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Все определения будут проиллюстрированы примерами.
Понятие возведения в степень
Начнем с формулирования базовых определений.
Определение 1Возведение в степень — это вычисление значения степени некоторого числа.
То есть слова «вычисление значение степени» и «возведение в степень» означают одно и то же. Так, если в задаче стоит «Возведите число 0,5 в пятую степень», это следует понимать как «вычислите значение степени (0,5)5.
Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.
Как возвести число в натуральную степень
Вспомним, что такое степень числа с натуральным показателем. Для степени с основанием a и показателем n это будет произведение n-ного числа множителей, каждый из которых равен a. Это можно записать так:
Это можно записать так:
Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.
Пример 1Условие: возведите -2 в степень 4.
Решение
Используя определение выше, запишем: (−2)4=(−2)·(−2)·(−2)·(−2). Далее нам нужно просто выполнить указанные действия и получить 16.
Возьмем пример посложнее.
Пример 2Вычислите значение 3272
Решение
Данную запись можно переписать в виде 327·327. Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии.
Выполним эти действия и получим ответ: 327·327=237·237=52949=103949
Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.
Разберем пример.
Выполните возведение в квадрат числа π.
Решение
Для начала округлим его до сотых. Тогда π2≈(3,14)2=9,8596. Если же π≈3.14159, то мы получим более точный результат: π2≈(3,14159)2=9,8695877281.
Отметим, что необходимость высчитывать степени иррациональных чисел на практике возникает сравнительно редко. Мы можем тогда записать ответ в виде самой степени (ln 6)3 или преобразовать, если это возможно: 57=1255.
Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:
a1=a
Это понятно из записи .
От основания степени это не зависит.
Пример 4Так, (−9)1=−9, а 73, возведенное в первую степень, останется равно 73.
Как возвести число в целую степень
Для удобства разберем отдельно три случая: если показатель степени — целое положительное число, если это ноль и если это целое отрицательное число.
В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими степенями, мы уже рассказали выше.
Теперь посмотрим, как правильно возводить в нулевую степень. При основании, которое отличается от нуля, это вычисление всегда дает на выходе 1. Ранее мы уже поясняли, что 0-я степень a может быть определена для любого действительного числа, не равного 0, и a0=1.
Пример 5Примеры:
50=1, (-2,56)0=1230=1
00- не определен.
У нас остался только случай степени с целым отрицательным показателем. Мы уже разбирали, что такие степени можно записать в виде дроби 1az, где а — любое число, а z — целый отрицательный показатель. Мы видим, что знаменатель этой дроби есть не что иное, как обыкновенная степень с целым положительным показателем, а ее вычислять мы уже научились. Приведем примеры задач.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Пример 6Возведите 2 в степень -3.
Решение
Используя определение выше, запишем: 2-3=123
Подсчитаем знаменатель этой дроби и получим 8: 23=2·2·2=8.
Тогда ответ таков: 2-3=123=18
Пример 7Возведите 1,43 в степень -2.
Решение
Переформулируем: 1,43-2=1(1,43)2
Вычисляем квадрат в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом:
В итоге у нас вышло (1,43)-2=1(1,43)2=12,0449. Этот результат нам осталось записать в виде обыкновенной дроби, для чего необходимо умножить ее на 10 тысяч (см. материал о преобразовании дробей).
Ответ: (1,43)-2=1000020449
Отдельный случай — возведение числа в минус первую степень. Значение такой степени равно числу, обратному исходному значению основания: a-1=1a1=1a.
Пример 8Пример: 3−1=1/3
913-1=13964-1=164 .
Как возвести число в дробную степень
Для выполнения такой операции нам потребуется вспомнить базовое определение степени с дробным показателем: amn=amnпри любом положительном a, целом m и натуральном n.
Таким образом, вычисление дробной степени нужно выполнять в два действия: возведение в целую степень и нахождение корня n-ной степени.
У нас есть равенство amn=amn, которое, учитывая свойства корней, обычно применяется для решения задач в виде amn=anm. Это значит, что если мы возводим число a в дробную степень m/n, то сначала мы извлекаем корень n-ной степени из а, потом возводим результат в степень с целым показателем m.
Проиллюстрируем на примере.
Пример 9Вычислите 8-23.
Решение
Способ 1. Согласно основному определению, мы можем представить это в виде: 8-23=8-23
Теперь подсчитаем степень под корнем и извлечем корень третьей степени из результата: 8-23=1643=133643=133433=14
Способ 2. Преобразуем основное равенство: 8-23=8-23=83-2
После этого извлечем корень 83-2=233-2=2-2 и результат возведем в квадрат: 2-2=122=14
Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.
Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.
Пример 10Возведите 44,89 в степень 2,5.
Решение
Преобразуем значение показателя в обыкновенную дробь: 44,892,5=44,8952.
А теперь выполняем по порядку все действия, указанные выше: 44,8952=44,895=44,895=44891005=44891005=6721025=67105==1350125107100000=13 501,25107
Ответ: 13 501,25107.
Если в числителе и знаменателе дробного показателя степени стоят большие числа, то вычисление таких степеней с рациональными показателями — довольно сложная работа. Для нее обычно требуется вычислительная техника.
Отдельно остановимся на степени с нулевым основанием и дробным показателем. Выражению вида 0mn можно придать такой смысл: если mn>0, то 0mn=0mn=0; если mn<0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0712=0, 0325=0, 00,024=0, а в целую отрицательную — значения не имеет: 0-43.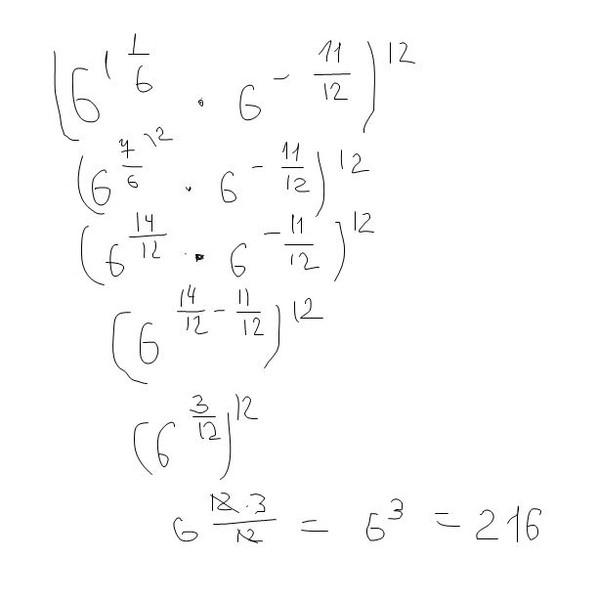
Как возвести число в иррациональную степень
Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.
Если нам нужно вычислить значение степени a с иррациональным показателем a, то мы берем десятичное приближение показателя и считаем по нему. Результат и будет приближенным ответом. Чем точнее взятое десятичное приближение, тем точнее ответ. Покажем на примере:
Пример 11Вычислите приближенное значение 2 в степени 1,174367….
Решение
Ограничимся десятичным приближением an=1,17. Проведем вычисления с использованием этого числа: 21,17≈2,250116. Если же взять, к примеру, приближение an=1,1743, то ответ будет чуть точнее: 21,174367. ..≈21,1743≈2,256833.
..≈21,1743≈2,256833.
ПОСЛЕДНЯЯ ЦИФРА СТЕПЕНИ
ПОСЛЕДНЯЯ ЦИФРА СТЕПЕНИ
Старцев Д.В. 11МБОУ СОШ № 77
Кулагина О.А. 11МБОУ СОШ № 77
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
«Математику уже затем учить следует,
что она ум в порядок приводит»
М. В. Ломоносов
Эти слова раскрывают сущность предмета математика, так как именно она, прежде всего, учит нас мыслить, рассуждать, анализировать, делать выводы, умозаключения и подводить итоги. Математика является одним из основных школьных предметов, потому, что все перечисленные качества необходимы не только математику, но и представителю любой другой науки. Развитием этих качеств занимается, прежде всего, математика. Существуют специальные задачи, которые направлены на формирование названных умений. Готовясь к различным математическим конкурсам, мы столкнулись с таким заданием « Какой будет последняя цифра числа ?» На первый взгляд эта задача может показаться достаточно сложной и я принялся за вычисления…
Развитием этих качеств занимается, прежде всего, математика. Существуют специальные задачи, которые направлены на формирование названных умений. Готовясь к различным математическим конкурсам, мы столкнулись с таким заданием « Какой будет последняя цифра числа ?» На первый взгляд эта задача может показаться достаточно сложной и я принялся за вычисления…
В ходе решения этой задачи возникла идея исследовать, а какой будет последняя цифра любого натурального числа в любой степени, есть ли какая-нибудь закономерность в том, как меняется последняя цифра степени натурального числа?
Цели работы
Составить опорную таблицу «Последние цифры степени», найти закономерности в них, научится вычислять последние цифры степеней.
Актуальность темы исследования обусловлена насущной необходимостью поиска быстрых алгоритмов решения практически важных задач, отработки навыков устного счета.
2. Последняя цифра степени
Выясним есть ли какая-нибудь закономерность в том, как меняется последняя цифра числа , где N , n – натуральные числа, с изменением показателя n. Для этого составим таблицу:
|
N n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
2 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
1024 |
2048 |
4096 |
8192 |
|
3 |
3 |
9 |
27 |
81 |
243 |
729 |
2187 |
6561 |
19683 |
59049 |
177147 |
531441 |
1594323 |
|
4 |
4 |
16 |
64 |
256 |
1024 |
4096 |
16384 |
65536 |
262144 |
1048576 |
4194304 |
16777216 |
67108864 |
|
5 |
5 |
25 |
125 |
625 |
3125 |
15625 |
78125 |
390625 |
1953125 |
9765625 |
48828125 |
244140625 |
1220703125 |
|
6 |
6 |
36 |
216 |
1296 |
7776 |
46656 |
279936 |
1679616 |
10077696 |
60466176 |
362797056 |
2176782336 |
13060694016 |
|
7 |
7 |
49 |
343 |
2401 |
16807 |
117649 |
823543 |
5764801 |
40353607 |
282475249 |
1977326743 |
13841287201 |
96889010407 |
|
8 |
8 |
64 |
512 |
4096 |
32768 |
262144 |
2097152 |
16777216 |
134217728 |
1073741824 |
8589934592 |
68719476736 |
549755813888 |
|
9 |
9 |
81 |
729 |
6561 |
59049 |
531441 |
4782969 |
43046721 |
387420489 |
3486784401 |
31381059609 |
282429536481 |
|
|
10 |
10 |
100 |
1000 |
10000 |
100000 |
1000000 |
10000000 |
100000000 |
1000000000 |
10000000000 |
100000000000 |
1000000000000 |
|
|
11 |
11 |
121 |
1331 |
14641 |
161051 |
1771561 |
19487171 |
214358881 |
2357947691 |
25937424601 |
285311670611 |
||
|
12 |
12 |
144 |
1728 |
20736 |
248832 |
2985984 |
35831808 |
429981696 |
5159780352 |
61917364224 |
743008370688 |
||
|
13 |
13 |
169 |
2197 |
28561 |
371293 |
4826809 |
62748517 |
815730721 |
10604499373 |
137858491849 |
Для наглядности составим таблицу, где будут записаны цифры, которыми оканчиваются записи натуральных чисел:
|
N n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
2 |
2 |
4 |
8 |
6 |
2 |
4 |
8 |
6 |
2 |
4 |
|
3 |
3 |
9 |
7 |
1 |
3 |
9 |
7 |
1 |
3 |
9 |
|
4 |
4 |
6 |
4 |
6 |
4 |
6 |
4 |
6 |
4 |
6 |
|
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
|
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
|
7 |
7 |
9 |
3 |
1 |
7 |
9 |
3 |
1 |
7 |
9 |
|
8 |
8 |
4 |
2 |
6 |
8 |
4 |
2 |
6 |
8 |
4 |
|
9 |
9 |
1 |
9 |
1 |
9 |
1 |
9 |
1 |
9 |
1 |
|
10 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
11 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
12 |
2 |
4 |
8 |
6 |
2 |
4 |
8 |
6 |
2 |
4 |
|
13 |
3 |
9 |
7 |
1 |
3 |
9 |
7 |
1 |
3 |
9 |
|
14 |
4 |
6 |
4 |
6 |
4 |
6 |
4 |
6 |
4 |
6 |
Заполняя столбики получаем такой результат: пятая и девятая и т. д. степень числа оканчивается той же цифрой, что и первая степень числа; шестая, десятая, четырнадцатая степень и т. д степень оканчивается той же цифрой, что и вторая степень числа; седьмая степень числа будет оканчиваться той же цифрой, что и третья степень числа.
д. степень числа оканчивается той же цифрой, что и первая степень числа; шестая, десятая, четырнадцатая степень и т. д степень оканчивается той же цифрой, что и вторая степень числа; седьмая степень числа будет оканчиваться той же цифрой, что и третья степень числа.
3. Закономерности возведения в степень
Результаты в таблице повторяются через каждые четыре столбца.
Про числа 1 и 10 писать не будем, т.к. результат всегда будет 1 или 0 соответственно.
Любая степень чисел 5 и 6 оканчивается соответственно на 5 и на 6.
Последние цифры степеней чисел 4 и 9 повторяются через каждые два шага, при возведении в четную степень последняя цифра не меняется, будет соответственно 4 или 9, при возведении в нечетную степень изменится на 6 или 1 соответственно.
Квадрат любого натурального числа может оканчиваться на 0, 1,4, 5, 6 и 9,
Куб натурального числа может оканчиваться любой цифрой
Используя полученные результаты попробуем найти последние цифры степени по остатку от деления её показателя на 4
|
24: 4=5(остаток 0) |
1 |
|
|
48:4=12(остаток 0) |
1 |
|
|
2016:4=504(остаток0) |
6 |
|
|
28:4=7(остаток0) |
6 |
Если остаток равен 0 и основание нечетное, то число будет оканчиваться на 1(кроме чисел оканчивающихся на цифру 5), если основание четное (кроме круглых чисел), то числа будут оканчиваться на цифру 6.
Теперь будем подбирать такие числа, что при делении показателя степени на 4 будут давать остатки 1, 2, 3
|
45:4=11 (остаток 1) |
7 |
|
|
37:4=9 (остаток 1) |
2 |
|
|
18:4=4 (остаток 2) |
1 |
|
|
102:4=25 (остаток 2) |
6 |
|
|
31:4=7(остаток3) |
2 |
|
|
1199:4=299(остаток3) |
9 |
Если остаток равен 1, то последняя цифра степени будет равна последней цифре в записи основания степени;
Если остаток равен 2, то последняя цифра степени будет равна последней цифре в записи квадрата основания;
Если остаток равен 3, то последняя цифра степени будет равна последней цифре в записи куба основания.
Значит чтобы найти последнюю цифру степени натурального числа с натуральным показателем, нужно найти остаток от деления показателя степени на 4.
Последние цифры степеней чисел 2 , 12, 22 и т. д. (3, 13, 23 и т.д.) и т. д. будут совпадать.
4. Последние две цифры степени
Мы видим, что последняя цифра рано или поздно будет повторяться, а как будет обстоять дело с 2-мя и 3-мя последними цифрами ? Вероятно, они тоже будут повторяться. Для наглядности составим таблицу, где будут записаны две цифры, которыми оканчиваются записи натуральных чисел:
|
N n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
2 |
2 |
4 |
8 |
16 |
32 |
64 |
28 |
56 |
12 |
24 |
48 |
96 |
92 |
84 |
68 |
36 |
72 |
44 |
88 |
76 |
52 |
04 |
08 |
16 |
|
3 |
3 |
9 |
27 |
81 |
43 |
29 |
87 |
61 |
83 |
49 |
47 |
41 |
23 |
69 |
07 |
21 |
63 |
89 |
67 |
01 |
03 |
09 |
27 |
81 |
|
4 |
4 |
16 |
64 |
56 |
24 |
96 |
84 |
36 |
44 |
76 |
04 |
16 |
64 |
56 |
24 |
96 |
84 |
36 |
44 |
76 |
04 |
16 |
64 |
56 |
|
5 |
5 |
25 |
25 |
25 |
25 |
25 |
25 |
25 |
25 |
25 |
25 |
25 |
25 |
25 |
25 |
25 |
25 |
25 |
25 |
25 |
25 |
25 |
25 |
25 |
|
6 |
6 |
36 |
16 |
96 |
76 |
56 |
36 |
16 |
96 |
76 |
56 |
36 |
16 |
96 |
76 |
56 |
36 |
16 |
96 |
76 |
56 |
36 |
16 |
96 |
|
7 |
7 |
49 |
43 |
01 |
07 |
49 |
43 |
01 |
07 |
49 |
43 |
01 |
07 |
49 |
43 |
01 |
07 |
49 |
43 |
01 |
07 |
49 |
43 |
01 |
|
8 |
8 |
64 |
12 |
96 |
68 |
44 |
52 |
16 |
28 |
24 |
92 |
36 |
88 |
04 |
32 |
56 |
48 |
84 |
72 |
76 |
08 |
64 |
12 |
96 |
|
9 |
9 |
81 |
29 |
61 |
49 |
41 |
69 |
21 |
89 |
01 |
09 |
81 |
29 |
61 |
49 |
41 |
69 |
21 |
89 |
01 |
09 |
81 |
29 |
61 |
|
10 |
10 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
|
11 |
11 |
21 |
31 |
41 |
51 |
61 |
71 |
81 |
91 |
01 |
11 |
21 |
31 |
41 |
51 |
61 |
71 |
81 |
91 |
01 |
11 |
21 |
31 |
41 |
|
12 |
12 |
44 |
28 |
36 |
32 |
84 |
08 |
96 |
52 |
24 |
88 |
56 |
72 |
64 |
68 |
16 |
92 |
04 |
48 |
76 |
12 |
44 |
28 |
36 |
|
13 |
13 |
69 |
97 |
61 |
93 |
09 |
17 |
21 |
73 |
49 |
37 |
81 |
53 |
89 |
57 |
41 |
33 |
29 |
77 |
01 |
13 |
69 |
97 |
61 |
|
14 |
14 |
96 |
44 |
16 |
24 |
36 |
04 |
56 |
84 |
76 |
64 |
96 |
44 |
16 |
24 |
36 |
04 |
56 |
84 |
76 |
64 |
96 |
44 |
16 |
|
15 |
15 |
25 |
75 |
25 |
75 |
25 |
75 |
25 |
75 |
25 |
75 |
25 |
75 |
25 |
75 |
25 |
75 |
25 |
75 |
25 |
75 |
25 |
75 |
25 |
|
16 |
16 |
56 |
96 |
36 |
76 |
16 |
56 |
96 |
36 |
76 |
16 |
56 |
96 |
36 |
76 |
16 |
56 |
96 |
36 |
76 |
16 |
56 |
96 |
36 |
|
17 |
17 |
89 |
13 |
21 |
57 |
69 |
73 |
41 |
97 |
49 |
33 |
61 |
37 |
29 |
93 |
81 |
77 |
09 |
53 |
01 |
17 |
89 |
13 |
21 |
|
18 |
18 |
24 |
32 |
76 |
68 |
24 |
32 |
76 |
68 |
24 |
32 |
76 |
68 |
24 |
32 |
76 |
68 |
24 |
32 |
76 |
24 |
24 |
32 |
76 |
|
19 |
19 |
61 |
59 |
21 |
99 |
81 |
39 |
41 |
79 |
01 |
19 |
61 |
59 |
21 |
99 |
81 |
39 |
41 |
76 |
01 |
19 |
61 |
59 |
21 |
|
20 |
20 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
|
21 |
21 |
41 |
61 |
81 |
01 |
21 |
41 |
61 |
81 |
01 |
21 |
41 |
61 |
81 |
01 |
21 |
41 |
61 |
81 |
01 |
21 |
41 |
61 |
81 |
Глядя на таблицу, замечаем что последние две цифры тоже повторяются, только период повторения увеличивается, кроме того у некоторых чисел 1-е не входит в период, так например:
Но начиная с 21 степени по 40 последние две цифры будут повторяться.
Последние цифры чисел 3,13 и 8 тоже будут повторятся с периодом 20, но последние две цифры чисел 3 и 13 совпадать не будут, не будут совпадать последние две цифры для степеней чисел 4 и 14 и т.д.
Последние цифры чисел 4 и 9 будут повторяться с периодом 10,последние цифры числа 6 будут повторятся с периодом 5, но число 6 не входит в период, последние цифры числа 7 будут повторятся с периодом – 4. Любая степень числа 5 (начиная со 2 –ой) и 25 будет оканчиваться на 25, а число 15 в четной степени будет оканчиваться на 25, а в нечетной на 75. Период чисел 11, тоже будет равен 10, но здесь есть еще одна закономерность:
Для числа 11 в степени – число десятков будет равно показателю степени
Для числа 21 – период равен 4, а число десятков будет равно числу, полученному , если число 2 умножить на показатель степени
.
5. Заключение
Заключение
Определить последнюю цифру степени числа не сложно, мы легко составили алгоритм, для двух последних цифр степени числа такой алгоритм уже не составишь, закономерности есть , но их меньше. Считаю, что таблицу с тремя последними цифрами составлять не имеет смысла – не рационально.
Мы провели большую работу: составили таблицы для последней и двух последних цифр степеней и получили интересные с нашей точки зрения выводы. Результаты работы могут быть использованы на занятиях математического кружка и факультативах в 5- 7 классах для развития интереса к математике у учащихся, а так же для индивидуальной работы с теми учениками, кто интересуется математикой. Кроме того, данными выводами можно воспользоваться при подготовке к различным олимпиадам и конкурсам. Кроме того сам процесс проведённого исследования позволил нам ещё раз убедиться в своих возможностях.
6. Задачи
-
Определите последнюю цифру в записи числа (ответ 8)
-
Найдите последнюю цифру числа 2017 в степени 4207.
 41 .
41 .
(8+3=11, последняя цифра 1)
-
Найдите последнюю цифру суммы степеней числа 2 с показателями, равными 32, 69, 469, 1995, 19951995.
(6+2+2+8+8=26 последняя цифра 6)
-
В книге рекордов Гиннеса написано, что наибольшее известное простое число равно (− 1). Не опечатка ли это?
(опечатка. Число 23021337 оканчивается единицей Поэтому последняя цифра числа (23021337 − 1) равна 0, а значит, это число делится на 10 и потому составное.)
-
Делится ли число+ на 10 ?
(Число 4730 оканчивается цифрой 9, а число 3950 — цифрой 1 Значит, их сумма оканчивается на 0 и потому делится на 10.)
-
Найдите последнюю цифру числа . Степени считаются сверху вниз: =
Последние две цифры числа 77 образуют число 43 (это можно вычислить непосредственно, отбрасывая при каждом умножении все цифры результата, кроме последних двух). Значит, число 77 делится на 4 с остатком 3. Степени семёрки могут оканчиваться на 7, 9, 3 или 1 (в зависимости от того, с каким остатком делится на 4 показатель степени). В нашем случае 43 делится на 4 с остатком 3, значит, и 77 делится на 4 с остатком 3 (согласно признаку делимости на 4). А у всех степеней семёрки, показатели которых делятся на 4 с остатком 3, последняя цифра равна 3).
Значит, число 77 делится на 4 с остатком 3. Степени семёрки могут оканчиваться на 7, 9, 3 или 1 (в зависимости от того, с каким остатком делится на 4 показатель степени). В нашем случае 43 делится на 4 с остатком 3, значит, и 77 делится на 4 с остатком 3 (согласно признаку делимости на 4). А у всех степеней семёрки, показатели которых делятся на 4 с остатком 3, последняя цифра равна 3).
-
Найдите 2 последние цифры числа 81989 .
В таблице 2-х последних цифр, у числа 8 период 20, (1989:20=99 остаток 9 , число 8 в 9 степени оканчивается цифрами 28, последние 2 цифры числа 81989 – 28).
-
На контрольной работе по перекрашиванию юный хамелеон перекрашивается по очереди из красного -> в желтый -> зелёный -> синий -> фиолетовый -> красный -> жёлтый -> зелёный и т.д. перекрасился он 2010 раз и начав с красного он в конце стал синим, но известно что он допустил ошибку, покраснел в тот момент, когда должен был приобрести другой цвет.
 Какого он был цвета перед этим покраснением?
Какого он был цвета перед этим покраснением?
(Заметим, что здесь период повторения цветов равен 5. Красный цвет будет встречаться на числах оканчивающихся на 0 и 5. Значит и должен он был закончить снова на красном. Поэтому чтобы найти ошибку перейдём сразу к 2005 перекрашиванию. Теперь просто будем считать по очереди меняя цвета до 2010-го. Сразу же смотрим что он сделал ошибку допустим после жёлтого, тогда получается 2005-красный, 2006 – жёлтый 2007- снова красный (это его ошибка), 2008 — жёлтый, 2009 -зелёный, 2010 – синий, перед ошибочным покраснением хамелеон был жёлтым).
-
Сейчас на часах 10:00. Какое время они будут показывать через 102938475 часов?
(У часов период повторения равен 24, значит число 102938475 разделить на 24 = 4289103,12… 102938475 — (4289103 * 24) = 3. Значит время которое часы будут показывать через 102938475 часов равно 10+3 = 13 часов, через 102938475 часы будут показывать 13:00).
11. Доказать, что число кратно 2.
12. Доказать, что -1 кратно 5 (при натуральном n).
13. Верно ли, что 1,6*( -1 ) – целое число при любом (натуральном) n. 14. Какой цифрой оканчивается произведение всех двузначных чисел, каждое из которых оканчивается на 7?
7. Использованная литература
1. «Все задачи «Кенгуру» 1994-2008- Санкт-Петербург, 2008.
2. «Задачи для подготовки к олимпиадам. Математика 5-8 классы» сост. Н.В. Заболотнева. – Волгоград: Учитель, 2007.- 99с.
3. Лихтарников Л.М. Занимательные логические задачи. (Для учащихся начальной школы) Оформление С. Григорьева — СПб.: Лань, МИК, 1996.- 125с.
4. Л.М.Лоповок 1000 проблемных задач по математике. Книга для учащихся Москва : Просвещение, 1995
5. Пичурин Л.Ф. За страницами учебника алгебры: Книга для учащихся 7-9 кл. средней школы — М.: Просвещение, 1990.- 224 с.: ил.
Пичурин Л.Ф. За страницами учебника алгебры: Книга для учащихся 7-9 кл. средней школы — М.: Просвещение, 1990.- 224 с.: ил.
6. Чулков П.В. Математика. Школьные олимпиады: методическое пособие. 5- кл./ П.В. Чулков.- М.: Издательство НЦ ЭНАС, 2007.- 88с. (Портфель учителя).
7. Шуба М.Ю. Занимательные задачи в обучении математике: Книга для учителя. — 2-е изд.-М.: Просвещение, 1995.- 22с.
4
Просмотров работы: 43957
Аденоиды у ребенка — откуда берутся, признаки и симптомы
“Кажется, у нашего ребёнка аденоиды!”– с такими сомнениями чаще всего приходят родители с малышом на прием к оториноларингологу, начитавшись статей в интернете, или после разговора с «всезнающими» мамами в песочнице/садике/школе. В этой статье мы постараемся разобрать наиболее частые вопросы об аденоидных вегетациях и попробуем понять, настолько ли все страшно.
Что такое аденоиды и откуда они берутся
Аденоидные вегетации (носоглоточная миндалина) – это лимфоидная ткань в своде носоглотки. Она имеется у всех без исключения детей и является периферическим органом иммунной системы, частью лимфоидного глоточного кольца. Главной функцией данного анатомического образования является борьба с проникающими в организм ребёнка бактериями или вирусами. Главное ее отличие от остальных миндалин — поверхность покрыта особым эпителием, который продуцирует слизь. Увеличение (гипертрофию) аденоидной ткани провоцируют частые аллергические и респираторные заболевания вирусной или бактериальной этиологии. Поэтому пик гипертрофии аденоидной ткани приходится как раз на возраст 3-7 лет. Затем лимфоидная ткань постепенно редуцируется в возрасте 10–12 лет. К 17 годам нередко остаются только фрагменты ткани, у здоровых же взрослых людей аденоидная ткань отсутствует. Гипертрофию аденоидной ткани принято делить на несколько степеней по ее объёму в носоглотке от первой, где аденоиды закрывают носовые ходы (хоаны) на 1/3 , до третьей-четвертой степени, когда происходит полная обтурация носоглотки с невозможностью носового дыхания.
Клинические проявления
Воспаление аденоидной ткани называется аденоидит. Течение его бывает острым, подострым и хроническим. Коснемся кратко основных симптомов, на которые стоит обращать внимание родителям:
1. Насморк, чаще всего он имеет затяжное течение.
2. Преимущественное дыхание через рот. Обусловлено затрудненным носовым дыханием. Степень затруднения напрямую зависит от степени гипертрофии аденоидной ткани. Часто появляется гнусавость. При длительном течении хронического аденоидита и дыхании через рот, возможно изменение лицевого скелета, что в дальнейшем проявляется стойким нарушением произношения речи.
3. Ночной храп, беспокойный сон.
4. Утренний кашель, обусловленный поперхиванием слизью, стекающей из носоглотки за ночь.
5. Снижение слуха, рецидивирующие отиты из-за механической обтурации слуховых труб аденоидными вегетациями. При этом гипертрофия может быть и 1-2 степени, при расположении аденоидов возле устьев слуховых труб, которые отвечают за вентиляцию среднего уха через слуховую трубу. Ребенок начинает постоянно переспрашивать или смотреть мультики слишком громко.
При этом гипертрофия может быть и 1-2 степени, при расположении аденоидов возле устьев слуховых труб, которые отвечают за вентиляцию среднего уха через слуховую трубу. Ребенок начинает постоянно переспрашивать или смотреть мультики слишком громко.
6. Быстрая утомляемость, апатия. Обусловлены постоянным кислородным голоданием головного мозга, особенно при хроническом аденоидите. Возможно отставание от сверстников в умственном и физическом развитии.
Методы исследования аденоидных вегетаций
В обычном состоянии без дополнительных оптических приспособлений эту миндалину увидеть невозможно. Существует ряд исследований, которые помогают установить степень аденоидных вегетаций: пальцевое исследование, задняя риноскопия зеркалом, рентгенография носоглотки, эндоскопия носоглотки, трёхмерное рентгенологическое исследование или КТ носоглотки. Наиболее современными методами на сегодняшний день являются:
-
эндоскопия носоглотки и полости носа.
 Процедура выполняется в нашей клинике под местной анестезией на приеме ЛОР врача. Полностью безболезненна, позволяет оценить не только степень аденоидных вегетаций, но и характер воспаления, состояние устьев слуховых труб, а также осмотреть задние отделы полости носа.
Процедура выполняется в нашей клинике под местной анестезией на приеме ЛОР врача. Полностью безболезненна, позволяет оценить не только степень аденоидных вегетаций, но и характер воспаления, состояние устьев слуховых труб, а также осмотреть задние отделы полости носа. - трёхмерное рентгенологическое исследование / КТ носоглотки. Методы по информативности значительно превосходят обычный рентген носоглотки, так как позволяют определить не только размер, но и соотношение аденоидных вегетаций к остальным структурам носоглотки (устья слуховых труб, хоаны и др). Лучевая нагрузка практически в 3 раза меньше (0,009м3в), а длительность исследования не более 2 мин. Пройти данное исследование можно в клинике на Усачева.
Лечение аденоидита
Лечение аденоидита принято разделять на консервативное и оперативное. Консервативное лечение требует от родителей, в первую очередь, большого терпения (надо научить малыша правильно высмаркиваться, проводить с ним туалет полости носа иногда несколько раз в день!), посещения процедур (промывание носа ЛОР врачом, физиолечение и др. ), четкого выполнения всех назначений врача. Это далеко не быстрый процесс, но если родители и врач заодно, и действуют сплоченной командой, то результат не заставляет себя ждать! Но бывают случаи, когда консервативное лечение неэффективно, тогда врач принимает решение об оперативном вмешательстве, и не всегда это зависит только от степени аденоидов. Чаще всего показаниями к оперативному лечению являются: полное отсутствие носового дыхания, рецидивирующие отиты (тубоотиты), ночное апное, стойкое снижение слуха.
), четкого выполнения всех назначений врача. Это далеко не быстрый процесс, но если родители и врач заодно, и действуют сплоченной командой, то результат не заставляет себя ждать! Но бывают случаи, когда консервативное лечение неэффективно, тогда врач принимает решение об оперативном вмешательстве, и не всегда это зависит только от степени аденоидов. Чаще всего показаниями к оперативному лечению являются: полное отсутствие носового дыхания, рецидивирующие отиты (тубоотиты), ночное апное, стойкое снижение слуха.
«Если они участвуют в иммунном ответе, зачем их удалять? Ничего лишнего в организме нет!»
Действительно, аденоидная ткань является частью лимфоидного кольца глотки, как было сказано выше, но только частью! Здесь важно оценивать соотношение вреда и пользы для организма. В случае хронического аденоидита сама миндалина становится местом обитания и размножения патогенных микроорганизмов, что явно не приносит пользы ребёнку, а частые обострения приводят к увеличению аденоидной ткани в размере, вызывая параллельно заболевание ушей, с последующим стойким снижением слуха.
«Если их удалить — они вырастут заново!»
На данном этапе развития медицины это мнение является ошибочным. Операция аденотомия выполняется под общим наркозом, с использованием эндоскопической техники. Современное оснащение позволяет удалять аденоидную ткань полностью под визуальным контролем, тем самым гарантируя отсутствие рецидивов. При аденотомии под местной анестезией, как выполнялось ранее повсеместно, действительно высок риск повторных аденотомий, так как чаще всего часть миндалины не удаляется с первого раза, что и вызывает рецидив.
Совет от доктора
Как обобщение, хочу сказать, что всем известная шутка про лечение насморка за 7 дней и за неделю с детьми не работает! Те, кто относятся к насморку ребенка как к «обычным соплям, которые и сами пройдут», сталкиваются чаще всего в дальнейшем с целой кипой осложнений. Поэтому, чем раньше вы обратитесь к ЛОР врачу и начнете грамотное лечение, тем выше вероятность, что проблема аденоидов обойдет вас стороной!
Запишитесь к детскому врачу-оториноларингологу по телефону единого контакт-центра в Москве +7 (495) 775 75 66, заполните форму on-line записи или обратитесь в регистратуру клиники «Семейный доктор».
Здоровья вам и вашим малышам!
Калькулятор экспоненты
Калькулятор экспоненты вычислит значение любого основания, возведенного в любую степень. На этой странице будут рассмотрены все связанные темы, включая отрицательный показатель степени. Начнем с основ.
Что такое показатель степени?
Показатель степени — это способ представить, сколько раз число, известное как основание, умножается само на себя. Он представлен в виде небольшого числа в правом верхнем углу основания. Например: x² означает, что вы умножаете x на себя два раза, что составляет x * x .Аналогично, 4² = 4 * 4 и т. Д. Если показатель степени равен 3, в примере 5³ , то результат будет 5 * 5 * 5 .
Это легко с маленькими числами, но для оснований, которые являются большими числами, десятичными знаками или когда они возведены в очень большую или отрицательную степень, используйте наш инструмент. Если вы хотите произвести возведение в степень вручную, сделайте следующее:
Если вы хотите произвести возведение в степень вручную, сделайте следующее:
- Определите базу и мощность, до которой она повышена, например
3⁵. - Запишите основание столько же раз, сколько и экспоненту.
3 3 3 3 3 - Поместите символ умножения между каждым основанием.
3 * 3 * 3 * 3 * 3. - Умножить!
3 * 3 * 3 * 3 * 3 = 243.
Калькулятор отрицательной экспоненты
Идея довольно проста, когда экспонента положительна, но что происходит, когда экспонента отрицательна? По определению, если оно равно -2, мы умножим само основание на на отрицательные два раза. На самом деле, что здесь происходит, мы берем величину, обратную основанию, меняем отрицательный показатель степени на положительный и действуем как обычно.Если вы хотите решить это вручную, сделайте следующее:
- Определите основание и показатель степени.
- Запишите величину, обратную основанию, и измените знак экспоненты на положительный
- Напишите обратную величину основания столько же раз, сколько экспоненту.

- Поместите между ними символ умножения.
- Умножаем и получаем результат.
Вот быстрый пример: 5⁻⁴ = (1/5) ⁴ = (1/5) * (1/5) * (1/5) * (1/5) = 1/625 = 0.0016
Возведение числа в квадрат (возведение числа в степень 2) и извлечение квадратного корня — схожие концепции, многие люди считают одно противоположным или отменяют другое. Если вы хотите возвести число 6 в квадрат, возьмите 6 * 6 = 36 . Теперь, если вы хотите найти, какие два одинаковых числа умножаются, чтобы получить 36, вы извлекаете квадратный корень из 36. Этот квадратный корень дает значение 6. Также можно отметить, что возведение квадратного корня в квадрат удаляет корень.
Если вам нужно вычислить кубический корень, вы можете использовать наш калькулятор кубического корня, который является отличным инструментом для вычисления кубического корня любого числа.
Кроме того, вы можете проверить наш калькулятор логарифмов, который является обратной функцией экспоненты.
Любое число, возведенное в степень 0, равно 1. Калькулятор отрицательной экспоненты полезен при работе с экспоненциальным убыванием, формула которого имеет отрицательный показатель степени.
Что такое 4 в 7-й степени?
Итак, вы хотите знать, какое у вас 4 в 7-й степени? В этой статье мы объясним, как именно выполнить математическую операцию, называемую «возведение 4 в степень 7».Это может показаться фантастическим, но мы объясним это без жаргона! Давай сделаем это.
Что такое возведение в степень?
Давайте сначала определим наши термины, а затем посмотрим, как вычислить, что такое 4 в 7-й степени.
Когда мы говорим о возведении в степень, все, что мы на самом деле имеем в виду, это то, что мы умножаем число, которое мы называем основанием (в данном случае 4) само на себя определенное количество раз. Показатель экспонента — это количество раз умножить 4 на себя, что в данном случае составляет 7 раз. ) для обозначения экспоненты. Каретка полезна в ситуациях, когда вам может не понадобиться или не нужно использовать надстрочный индекс.
) для обозначения экспоненты. Каретка полезна в ситуациях, когда вам может не понадобиться или не нужно использовать надстрочный индекс.
Итак, мы упомянули, что возведение в степень означает умножение основного числа на себя на показатель степени. Давайте посмотрим на это немного визуально:
4 в 7 степени = 4 x … x 4 (7 раз)
Итак, каков ответ?
Теперь, когда мы объяснили теорию, лежащую в основе этого, давайте проанализируем числа и выясним, что такое 4 в 7-й степени:
4 в степени 7 = 4 7 = 16,384
Почему мы вообще используем возведение в степень, например, 4 7 ? Что ж, нам намного проще писать умножения и проводить математические операции как с большими, так и с маленькими числами, когда вы работаете с числами с большим количеством конечных нулей или большим количеством десятичных знаков.
Надеюсь, эта статья помогла вам понять, как и почему мы используем возведение в степень, и дала вам ответ, который вы изначально искали. Теперь, когда вы знаете, что такое 4 в 7-й степени, вы можете продолжить свой веселый путь.
Не стесняйтесь поделиться этой статьей с другом, если вы думаете, что она им поможет, или продолжайте читать дальше, чтобы найти еще несколько примеров.
Цитируйте, дайте ссылку или ссылайтесь на эту страницу
Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большую услугу и используйте инструмент ниже, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали.Мы очень ценим вашу поддержку!
«Что такое 4 в 7-й степени?». VisualFractions.com .
 По состоянию на 15 июня 2021 г. https://visualfractions.com/calculator/exponent/what-is-4-to-the-7th-power/.
По состоянию на 15 июня 2021 г. https://visualfractions.com/calculator/exponent/what-is-4-to-the-7th-power/.«Что такое 4 в 7-й степени?». VisualFractions.com , https: // visualfractions.ru / Calculator / exponent / what-is-4-to-the-7-power /. По состоянию на 15 июня 2021 г.
Что такое 4 в 7-й степени ?. VisualFractions.com. Получено с https://visualfractions.com/calculator/exponent/what-is-4-to-the-7th-power/.
Калькулятор возведения в степень
Хотите найти ответ на другую проблему? Введите свой номер и мощность ниже и нажмите рассчитать.
Случайный список примеров возведения в степень
Если вы зашли так далеко, вы должны ДЕЙСТВИТЕЛЬНО любить возведение в степень! Вот несколько случайных вычислений для вас:
Цифра единиц числа, возведенного в степень
Здесь мы увидим, как найти цифру единиц числа в форме $ {x ^ y} $. Сначала мы попытаемся понять, что такое цифра единиц, затем мы рассмотрим методику нахождения цифры единиц большой степени, а затем, используя эту технику, мы решим некоторые проблемы с цифрой единиц числа, возведенного в степень.
Сначала мы попытаемся понять, что такое цифра единиц, затем мы рассмотрим методику нахождения цифры единиц большой степени, а затем, используя эту технику, мы решим некоторые проблемы с цифрой единиц числа, возведенного в степень.
В конце, пожалуйста, возьмите QUIZ , чтобы проверить свое понимание.
Видео:
Это старая версия нашего видео с закадровым голосом.
Что такое цифра единиц измерения?
Цифра единиц в числе — это цифра, стоящая на месте единицы.т.е. это крайняя правая цифра числа. Например, цифра единиц 243 равна 3, цифра единиц 39 — 9.
Но тогда какова цифра единиц больших чисел, например 23 в степени 46, или какая цифра единиц 2014 года в степени 2014 ? Здесь непросто вычислить цифру единиц этих чисел. {142}} $ и т. Д.
ПОСЛЕДНИЕ ДВЕ ЦИФРЫ БОЛЬШИХ ЧИСЕЛ
4 силовой стол
4 силовой столВы ищете другие числовые диаграммы, воспользуйтесь этим калькулятором Число Поднятый силой Равно
- 4 1 = 4
- 4 2 = 16
- 4 3 = 64
- 4 4 = 256
- 4 5 = 1024
- 4 6 = 4096
- 4 7 = 16384
- 4 8 = 65536
- 4 9 = 262144
- 4 10 = 1048576
от 1 до 10
- 4 11 = 4194304
- 4 12 = 16777216
- 4 13 = 67108864
- 4 14 = 268435456
- 4 15 = 1073741824
- 4 16 = 4294967296
- 4 17 = 1717982169184 4 18 = 68719476736
- 4 19 = 2748774
- 4 20 = 1099511627776
11-20
- 4 21 = 4398046511104
- 4 22 4 = 175921860 900 24
- 4 23 = 70368744177664
- 4 24 = 281474976710656
- 4 25 = 1125899
- 2624
- 4 26 = 4503599627370496
- 4 27 = 1801439824509
21-30
- 4 31 = 4611686018427388000
- 4 32 = 184467440737095520008000
4
- 9992998 = 2951479352830000
- 4 35 = 1.1805916207174113e + 21
- 4 36 = 4,722366482869645e + 21
- 4 37 = 1.888946593147858e + 22
- 4 38 = 7,5557863725e + 22
- 4 514 3954 24 = 3,0732235 40 = 1.2089258196146292e + 24
от 31 до 40
- 4 41 = 4.835703278458517e + 24
- 4 42 = 1.9342813113834067e + 25
- 4
- 99 43 = 7.7371252455 4 44 = 3.094850098213451e + 26
- 4 45 = 1,2379400392853803e + 27
- 4 46 = 4,951760157141521e + 27
- 4 47 = 1,9807040628566084e + 28
- 4 48 14 = 7,9242134816 49 = 3,16005705735e + 29
- 4 50 = 1,2676506002282294e + 30
от 41 до 50
- 4 51 = 5,0706024008e + 30
- 4 52 = 2,02824096036516 4 53 = 8.112963841460668e + 31
- 4 54 = 3,2451855365842673e + 32
- 4 55 = 1,298074214633707e + 33
- 4 56 = 5,192296858534828e + 33
- 4 5718 24 2,0 58 = 8,307674973655724e + 34
- 4 59 = 3,32306998946229e + 35
- 4 60 = 1,329227995784916e + 36
51 до 60
- 4 61 = 5,316
324 - 4 62 = 2.1267647932558654e + 37
- 4 63 = 8,507059173023462e + 37
- 4 64 = 3,402823669209385e + 38
- 4 65 = 1,361129467683754e + 39
- 4 66 70 = 5,45021 67 = 2,1778071482940062e + 40
- 4 68 = 8,711228593176025e + 40
- 4 69 = 3,4844
27041e + 41
- 4 70 = 1,393796574
4e + 42
- до 9 4 71 = 5.575186299632656e + 42
- 4 72 = 2.2300745198530623e + 43
- 4 73 = 8.92029807941225e + 43
- 4 74 = 3.5681192317649e + 44
- 4 75 = 1.42724769 76 = 5,7089
- 82384e + 45
- 4 77 = 2,283596308329536e + 46
- 4 78 = 9,134385233318143e + 46
- 4 79 = 3,6537540933272573e + 47 33 = 1,953 +48
- 4 81 = 5.846006549323612e + 48
- 4 82 = 2,3384026197294447e + 49
- 4 83 = 9,353610478917779e + 49
- 4 84 = 3,74144411115e + 50
- 4 85 2 = 1,49246577 900 86 = 5.986310706507379e + 51
- 4 87 = 2.3945242826029513e + 52
- 4 88 = 9,578097130411805e + 52
- 4 89 = 3,831238852164722e + 53
- 9055 = 3,831238852164722e + 53
- +54
81 до 90
- 4 91 = 6.129982163463556e + 54
- 4 92 = 2,4519928653854222e + 55
- 4 93 = 9,807971461541689e + 55
- 4 94 = 3,9231885846166755e + 56
- 4 9547533 = 1,5692 9004 9002 4
- 4 97 = 2,5108406941546723e + 58
- 4 98 = 1,004336277661869e + 59
- 4 99 = 4,017345110647476e + 59 021 = 4,017345110647476e + 59 021 4,99 +60
от 91 до 100
Powerball — Играйте и проверяйте выигрышные числа
Powerball будет расширен в августе 2021 года! По мере того, как мы готовимся к этим изменениям, возможности многоабонентского розыгрыша, будущей игры и автоматического продления для Powerball будут ограничены онлайн и в розницу.
Мощные джекпоты — это море удовольствия.
Если вам нравится играть на крупные денежные призы, то Powerball — это игра для вас! Powerball может сделать вас следующим мультимиллионером, и есть несколько разных способов играть.
Как играть в Powerball
После розыгрыша 8 апреля 2020 года гарантированные начальные суммы джекпота и минимальное увеличение джекпота будут отменены, а будущие увеличения джекпота будут определены и объявлены группой продуктов перед каждым розыгрышем.В апреле 2020 года Powerball объявил об изменении стартовой суммы джекпота. Больше информации здесь.
Подумайте, как играть в Powerball, используя цвета и числа. Вы должны выбрать числа для пяти белых шаров и одного красного шара (Powerball), всего шесть чисел. Щелкните для более детального просмотра игрового листа, чтобы узнать больше.
Вот способы играть в Powerball:
- Выберите свои собственные числа на листке. Выберите пять разных чисел от 1 до 69; затем выберите один номер Powerball от 1 до 26.
- Или вы можете выбрать Easy Pick и позволить компьютеру выбирать ваши числа
- Вы также можете использовать комбинацию этих методов игры: выберите несколько ваших любимых чисел и позвольте компьютеру подставить остальные.
- Каждая игра (шесть номеров) стоит 2 доллара. Розыгрыши
- Powerball проводятся каждую среду и субботу в 23:00.
Сделайте игру еще более яркой с Power Play
®Power Play® — это дополнительная функция, которая позволяет выиграть еще больше денег всего за 1 доллар за игру.Power Play® может увеличить ваш выигрыш до 2 миллионов долларов! Если вы выиграете с помощью Power Play®, ваш приз, не связанный с джекпотом, увеличивается в 2, 3, 4, 5 или 10 раз в зависимости от номера Power Play®, выпавшего в розыгрыше. Ознакомьтесь с таблицей выше, чтобы увидеть, как добавление Power Play® увеличивает любой приз, кроме джекпота. Добавьте Power Play® и угадайте пять чисел без Powerball, и вы автоматически выиграете 2 миллиона долларов!
Победа в игре Powerball
Есть девять способов выиграть в Powerball, и вот несколько:
- Если вы угадаете только номер Powerball, вы можете выиграть минимум 4 доллара.
- Угадайте первые пять чисел, и вы выиграете 1 миллион долларов.
- Угадайте все пять чисел и число Powerball, и вы получите джекпот Powerball!
Два шанса на победу в неделю
Вы можете играть в Powerball дважды в неделю! Розыгрыши Powerball проводятся каждую среду и субботу в 23:00.
- Мы прекращаем продажу билетов Powerball в 22:00. в розыгрыши, так что покупайте билеты пораньше! Билеты на лотерею
- Вирджиния Powerball не могут быть отменены, и все продажи окончательны.Мы рекомендуем использовать игровой лист, чтобы убедиться, что ваши числа верны.
- При использовании дополнительных розыгрышей не забудьте сообщить своему клерку, какой вариант (-ы) вы предпочитаете — Multi-Draw, Future или Repeat.
- Все выигрышные билеты, купленные в Вирджинии, должны быть погашены в Вирджинии.
Варианты воспроизведения
Всегда здорово иметь варианты, поэтому отметьте поле ДОПОЛНИТЕЛЬНЫЕ ИГРЫ на своем игровом листе для любого из следующего.
- Хотите сыграть одними и теми же числами более чем в одном розыгрыше одного билета? Билет с несколькими розыгрышами позволяет вам сыграть до 26 розыгрышей подряд на одном билете.Помните, что цена билета увеличивается с каждым добавляемым вами розыгрышем.
- Думаете о особой дате? Вы можете купить билет на одну дату розыгрыша в будущем. Это называется розыгрышем будущего. Отметьте поле «Необязательные игры» на своем игровом листе и сообщите секретарю, какую будущую дату розыгрыша вы имеете в виду.
- Вам так нравятся эти числа, что вы хотите, чтобы они присутствовали более чем на одном билете? Вы можете повторить игру и напечатать одни и те же числа на нескольких билетах до 20 раз.
- Сообщите своему клерку, какой вариант вы хотите, когда вы предъявляете свой листок.Имейте в виду, что игра в более чем один розыгрыш увеличивает цену билета на количество розыгрышей, которое вы выберете.
Вы можете найти различные розничные точки VA Lottery Powerball в приложении Virginia Lottery или с помощью инструмента «Найти продавца». Загрузите приложение, чтобы сканировать свои невыигрышные билеты, а также посмотрите наши новейшие скретчеры!
Покупайте онлайн и никогда не пропустите розыгрыши!
Вы можете покупать и играть в Powerball в любое время и в любом месте Вирджинии на своем мобильном телефоне, планшете или компьютере.Приобретите сразу несколько розыгрышей, чтобы оставаться в игре столько, сколько захотите, и выберите функцию автоматического продления, чтобы не беспокоиться о том, что вы пропустите розыгрыш.
Посмотреть розыгрыш
Вы можете смотреть розыгрыши Powerball в прямом эфире каждую среду и субботу в 23:00. щелкнув вкладку «Выигрышные числа» вверху страницы. Вы даже можете посмотреть их позже. Розыгрыши остаются на нашем сайте!
Получите информацию об игре от Alexa!
Если вы загрузите навык Alexa Lottery в Вирджинии, вы можете запросить у Alexa информацию об этой игре, включая недавние выигрышные номера и многое другое.
Юридические вопросы
После розыгрыша 8 апреля 2020 года гарантированные начальные суммы джекпота и минимальное увеличение джекпота будут отменены, а будущие увеличения джекпота будут определены и объявлены группой продуктов перед каждым розыгрышем.
Нужна дополнительная информация? Вот наши официальные правила Powerball.Прибыль от лотереи в пользу государственного образования
С 1999 года вся прибыль от лотереи Вирджинии пошла в государственные школы K-12 в Вирджинии. В 2020 финансовом году лотерея принесла более 595 миллионов долларов государственным школам K-12 в Вирджинии.Каждый раз, когда вы играете в лотерею Вирджинии, вы помогаете детям иметь светлое будущее.
§ 17-4-25 — Право производить аресты в любом графстве; задержанные лица доставлены к судебному исполнителю; транспортные расходы; владение в графстве, отличном от того, в котором совершено преступление; транспортировка в региональную тюрьму :: Кодекс Джорджии 2010 года :: Кодексы и законы США :: Законодательство США :: Justia
О.C.G.A. 17-4-25 (2010)
17-4-25. Право производить аресты в любом графстве; задержанные лица доставлены к судебному исполнителю; транспортные расходы; владение в графстве, отличном от того, в котором было совершено правонарушение; транспортировка в региональную тюрьму(a) В соответствии с ордером, выданным судебным должностным лицом, производящий арест офицер может арестовать любое лицо, обвиняемое в совершении преступления, в любом округе, независимо от места проживания производившего арест офицера. Офицер, производящий арест, обязан доставить обвиняемого с ордером, на основании которого он был арестован, в округ, в котором предположительно было совершено преступление, для допроса перед любым судебным должностным лицом этого округа.
(b) Округ, где предположительно было совершено преступление, должен оплатить расходы офицера, производившего арест, по доставке арестованного в округ. Офицер, производящий арест, может задержать или заключить арестованного в тюрьму в округе, отличном от округа, в котором преступление предположительно было совершено, достаточно долго, чтобы он мог подготовиться к доставке арестованного в округ, в котором преступление предположительно было совершено. совершено.
(c) Если округ, в котором предположительно было совершено правонарушение, входил в состав регионального тюремного управления, созданного в соответствии со статьей 5 главы 4 раздела 42, известного как «Закон о региональных тюремных властях», должностным лицом, производившим арест. перевезет заключенного в районную тюрьму.Судья округа, в котором предположительно было совершено преступление, может проводить допрос обвиняемого, требуемый подразделом (а) настоящего раздела Кодекса, в округе, в котором предположительно было совершено преступление, или в доступных учреждениях. в региональной тюрьме или посредством аудиовизуальной связи между двумя местами и между обвиняемым, судом, адвокатами и свидетелями.
Заявление об отказе от ответственности: Эти коды могут быть не самой последней версией.Грузия может располагать более актуальной или точной информацией. Мы не даем никаких гарантий или гарантий относительно точности, полноты или адекватности информации, содержащейся на этом сайте, или информации, на которую есть ссылки на государственном сайте. Пожалуйста, проверьте официальные источники.
Приложение A к Части 50 — Общие критерии проектирования атомных электростанций
Содержание
КРИТЕРИИ
Номер I.Общие требования: Стандарты и протоколы качества 1 Основы проектирования для защиты от природных явлений 2 Противопожарная защита 3 Основы проектирования для воздействия на окружающую среду и динамику Совместное использование структур, систем и компонентов 5 II. Защита с помощью барьеров множественных продуктов деления: Конструкция реактора 10 Собственная защита реактора 11 Подавление колебаний мощности реактора 12 Граница давления теплоносителя реактора 14 Конструкция системы теплоносителя реактора 15 Конструкция защитной оболочки 16 Электроэнергетические системы 17 18 Диспетчерская 19 III.Системы защиты и контроля реактивности: Функции системы защиты 20 Надежность и тестируемость системы защиты 21 Независимость системы защиты 22 Режимы отказа системы защиты Разделение систем защиты и управления 24 Требования к системе защиты при сбоях в управлении реактивностью 25 Резервирование системы управления реактивностью и ее возможности 26 Комбинированная система управления мощностью Пределы реактивности 28 Защита от ожидаемых нарушений в работе 29 IV.Жидкостные системы: Качество границы давления охлаждающей жидкости реактора 30 Предотвращение разрушения границы давления теплоносителя реактора 31 Проверка границы давления теплоносителя реактора Подпитка 33 Отвод остаточного тепла 34 Аварийное охлаждение активной зоны 35 Проверка системы аварийного охлаждения активной зоны 36 Тестирование системы аварийного охлаждения Отвод тепла защитной оболочки 38 Проверка системы отвода тепла защитной оболочки 39 Испытание системы отвода тепла защитной оболочки 40 Очистка защитной атмосферы 9088 41886 5 Инспекция систем очистки защитной атмосферы 42 Испытание систем очистки защитной атмосферы 43 Охлаждающая вода 44 Система проверки охлаждающей воды 45880 Испытания системы водяного охлаждения 46 V.Защитная оболочка реактора: Основы проектирования защитной оболочки 50 Предотвращение разрушения границы давления защитной оболочки 51 Возможность проведения проверки скорости утечки из защитной оболочки 52 53 Системы, проникающие через защитную оболочку 54 Граничная проникающая защитная оболочка под давлением охлаждающей жидкости реактора 55 Изоляция первичной защитной оболочки 56 9088 Закрытые клапаныVI.Контроль топлива и радиоактивности: Контроль выбросов радиоактивных материалов в окружающую среду 60 Хранение и обращение с топливом и контроль радиоактивности 61 Предотвращение критичности при хранении и обращении с топливом 62 Мониторинг хранения топлива и отходов 63 Мониторинг радиоактивных выбросов 64 Введение
В соответствии с положениями § 50.34, заявка на получение разрешения на строительство должна включать основные критерии проектирования предлагаемого объекта. Согласно положениям 10 CFR 52.47, 52.79, 52.137 и 52.157, заявка на сертификацию конструкции, комбинированную лицензию, утверждение конструкции или лицензию на производство, соответственно, должна включать основные критерии проектирования для предлагаемого объекта. Основные критерии проектирования устанавливают необходимые требования к проектированию, изготовлению, строительству, испытаниям и рабочим характеристикам для конструкций, систем и компонентов, важных для безопасности; то есть конструкции, системы и компоненты, которые обеспечивают разумную уверенность в том, что установка может эксплуатироваться без чрезмерного риска для здоровья и безопасности населения.
Эти Общие критерии проектирования устанавливают минимальные требования к основным критериям проектирования для атомных электростанций с водяным охлаждением, аналогичных по конструкции и расположению станциям, для которых Комиссией выданы разрешения на строительство. Общие критерии проектирования также считаются применимыми к другим типам ядерных энергоблоков и предназначены для обеспечения руководства при установлении основных критериев проектирования для таких других энергоблоков.
Разработка этих общих критериев проектирования еще не завершена.Например, некоторые определения нуждаются в дальнейшем расширении. Кроме того, некоторые из конкретных требований к проектированию конструкций, систем и компонентов, важных для безопасности, еще должным образом не определены. Их упущение не освобождает заявителя от рассмотрения этих вопросов при проектировании конкретного объекта и соблюдения необходимых требований безопасности. Эти вопросы включают:
(1) Рассмотрение необходимости проектирования с учетом единичных отказов пассивных компонентов в жидкостных системах, важных для безопасности.(См. Определение единичного отказа.)
(2) Учет требований к избыточности и разнообразию для жидкостных систем, важных для безопасности. «Система» может состоять из ряда подсистем, каждая из которых по отдельности способна выполнять заданную функцию безопасности системы. Минимально допустимая избыточность и разнообразие подсистем и компонентов внутри подсистемы, а также требуемая взаимосвязь и независимость подсистем еще не разработаны и не определены. (См. Критерии 34, 35, 38, 41 и 44.)
(3) Рассмотрение типа, размера и ориентации возможных разрывов в компонентах границы давления теплоносителя реактора при определении проектных требований для надлежащей защиты от постулируемых аварий с потерей теплоносителя. (См. Определение аварий с потерей теплоносителя.)
(4) Рассмотрение возможности систематических, неслучайных, одновременных отказов резервных элементов при проектировании систем защиты и систем контроля реактивности. (См. Критерии 22, 24, 26 и 29.)
Ожидается, что критерии будут время от времени расширяться и изменяться по мере разработки важных новых требований для этих и других функций.
Будет несколько АЭС с водяным охлаждением, для которых общие критерии проектирования недостаточны и для которых необходимо определить и удовлетворить дополнительные критерии в интересах общественной безопасности. В частности, ожидается, что потребуются дополнительные или иные критерии для учета необычных площадок и условий окружающей среды, а также для ядерных энергоблоков с водяным охлаждением усовершенствованной конструкции.Кроме того, могут существовать атомные энергоблоки с водяным охлаждением, для которых выполнение некоторых общих критериев проектирования может быть необязательным или целесообразным. Для таких заводов отклонения от общих критериев проектирования должны быть идентифицированы и обоснованы.
Определения и пояснения
Атомный энергоблок . Ядерный энергетический блок означает ядерный энергетический реактор и связанное с ним оборудование, необходимое для выработки электроэнергии, и включает те конструкции, системы и компоненты, которые необходимы для обеспечения разумной уверенности в том, что установка может эксплуатироваться без чрезмерного риска для здоровья и безопасности населения.
Аварии с потерей охлаждающей жидкости . Аварии с потерей теплоносителя означают те постулируемые аварии, которые возникают в результате потери теплоносителя реактора со скоростью, превышающей возможности системы подпитки теплоносителя реактора, из-за разрывов границы давления теплоносителя реактора, вплоть до разрыва, эквивалентного размеру двухсторонний разрыв наибольшего патрубка системы теплоносителя реактора. 1
Единичный отказ . Единичный отказ означает событие, которое приводит к потере способности компонента выполнять предусмотренные функции безопасности.Множественные отказы, возникающие в результате одного события, считаются единичным отказом. Считается, что гидравлические и электрические системы спроектированы с учетом предполагаемого единичного отказа, если ни (1) единичный отказ любого активного компонента (при условии, что пассивные компоненты функционируют должным образом), ни (2) единичный отказ пассивного компонента (при условии, что активные компоненты функционируют должным образом). ), приводит к потере способности системы выполнять свои функции безопасности. 2
Ожидаемые нарушения нормальной эксплуатации .Ожидаемые при эксплуатации события означают те условия нормальной эксплуатации, которые, как ожидается, произойдут один или несколько раз в течение срока службы атомной энергоблока, и включают, помимо прочего, потерю мощности всех рециркуляционных насосов, отключение турбогенератора, отключение главный конденсатор, и отключение всего внешнего питания.
Критерии
I. Общие требования
Критерий 1 — Стандарты качества и записи . Конструкции, системы и компоненты, важные для безопасности, должны быть спроектированы, изготовлены, возведены и испытаны в соответствии со стандартами качества, соразмерными важности выполняемых функций безопасности.При использовании общепризнанных кодексов и стандартов они должны быть идентифицированы и оценены для определения их применимости, адекватности и достаточности, а также должны быть дополнены или изменены по мере необходимости, чтобы гарантировать соответствие качественной продукции требуемой функции безопасности. Должна быть разработана и внедрена программа обеспечения качества, чтобы обеспечить адекватную уверенность в том, что эти конструкции, системы и элементы будут удовлетворительно выполнять свои функции безопасности. Соответствующие записи о проектировании, изготовлении, возведении и испытании конструкций, систем и компонентов, важных для безопасности, должны поддерживаться лицензиатом атомной электростанции или под его контролем в течение всего срока службы энергоблока.
Критерий 2 — Расчетные основы защиты от природных явлений . Конструкции, системы и компоненты, важные для безопасности, должны быть спроектированы таким образом, чтобы выдерживать воздействие природных явлений, таких как землетрясения, торнадо, ураганы, наводнения, цунами и сейши, без потери способности выполнять свои функции безопасности. Основы проектирования для этих конструкций, систем и компонентов должны отражать: (1) Соответствующее рассмотрение наиболее серьезных природных явлений, о которых исторически сообщалось для участка и окружающей территории, с достаточным запасом для ограниченной точности, количества и период времени, в течение которого были накоплены исторические данные, (2) соответствующие сочетания эффектов нормальных и аварийных условий с последствиями природных явлений и (3) важность выполняемых функций безопасности.
Критерий 3 — Противопожарная защита . Конструкции, системы и компоненты, важные для безопасности, должны быть спроектированы и размещены таким образом, чтобы в соответствии с другими требованиями безопасности минимизировать вероятность и воздействие пожаров и взрывов. По возможности во всей установке должны использоваться негорючие и термостойкие материалы, особенно в таких местах, как защитная оболочка и диспетчерская. Должны быть предусмотрены и спроектированы системы обнаружения и тушения пожара соответствующей мощности и возможностей, чтобы минимизировать неблагоприятное воздействие пожаров на конструкции, системы и компоненты, важные для безопасности.Системы пожаротушения должны быть спроектированы таким образом, чтобы гарантировать, что их разрыв или непреднамеренное срабатывание не приведет к значительному снижению безопасности этих конструкций, систем и компонентов.
Критерий 4 — Основы расчета экологических и динамических эффектов . Конструкции, системы и компоненты, важные для безопасности, должны быть спроектированы таким образом, чтобы учитывать последствия и быть совместимыми с условиями окружающей среды, связанными с нормальной эксплуатацией, техническим обслуживанием, испытаниями и постулируемыми авариями, включая аварии с потерей теплоносителя.Эти конструкции, системы и компоненты должны быть надлежащим образом защищены от динамических воздействий, в том числе от ударов ракет, ударов труб и сброса жидкостей, которые могут возникнуть в результате отказов оборудования, а также событий и условий за пределами АЭС. Однако динамические эффекты, связанные с предполагаемыми разрывами труб в атомных энергоблоках, могут быть исключены из проектных основ, если анализы, рассмотренные и утвержденные Комиссией, демонстрируют, что вероятность разрыва трубопровода жидкостной системы чрезвычайно мала в условиях, соответствующих проектным основам для трубопровода. .
Критерий 5 — Совместное использование конструкций, систем и компонентов . Структуры, системы и компоненты, важные для безопасности, не должны совместно использоваться атомными энергоблоками, если не будет продемонстрировано, что такое совместное использование не приведет к значительному ухудшению их способности выполнять свои функции безопасности, включая, в случае аварии на одном энергоблоке, упорядоченное отключение и охлаждение остальных агрегатов.
II. Защита барьерами множественных продуктов деления
Критерий 10 — Конструкция реактора .Активная зона реактора и связанные с ней системы теплоносителя, управления и защиты должны быть спроектированы с соответствующим запасом, чтобы гарантировать, что указанные допустимые проектные пределы топлива не превышаются при любых условиях нормальной эксплуатации, включая последствия ожидаемых при эксплуатации событий.
Критерий 11 — Собственная защита реактора . Активная зона реактора и связанные с ней системы теплоносителя должны быть спроектированы таким образом, чтобы в рабочем диапазоне мощности результирующий эффект быстрых внутренних характеристик ядерной обратной связи имел тенденцию компенсировать быстрое увеличение реактивности.
Критерий 12 — Подавление колебаний мощности реактора . Активная зона реактора и связанные с ней системы теплоносителя, управления и защиты должны быть спроектированы так, чтобы гарантировать, что колебания мощности, которые могут привести к условиям, превышающим установленные допустимые проектные пределы топлива, невозможны или могут быть надежно и легко обнаружены и подавлены.
Критерий 13 — КИП . Должны быть предусмотрены приборы для контроля переменных и систем в ожидаемых диапазонах для нормальной эксплуатации, ожидаемых при эксплуатации событий и аварийных условий, в зависимости от обстоятельств, для обеспечения адекватной безопасности, включая те переменные и системы, которые могут влиять на процесс деления, целостность реактора. активная зона, граница давления теплоносителя реактора, защитная оболочка и связанные с ней системы.Должны быть предусмотрены соответствующие средства управления для поддержания этих переменных и систем в установленных рабочих диапазонах.
Критерий 14 — Граница давления теплоносителя реактора . Граница давления теплоносителя реактора должна быть спроектирована, изготовлена, смонтирована и испытана таким образом, чтобы иметь чрезвычайно низкую вероятность аномальной утечки, быстро распространяющегося отказа и крупного разрушения.
Критерий 15 — Конструкция системы теплоносителя реактора . Система теплоносителя реактора и связанные с ней вспомогательные системы, системы управления и защиты должны быть спроектированы с достаточным запасом, чтобы гарантировать, что расчетные условия границы давления теплоносителя реактора не будут превышены при любых условиях нормальной эксплуатации, включая ожидаемые при эксплуатации события.
Критерий 16 — Конструкция защитной оболочки . Должна быть предусмотрена защитная оболочка реактора и связанные с ней системы для создания по существу герметичного барьера против неконтролируемого выброса радиоактивности в окружающую среду и для обеспечения того, чтобы проектные условия защитной оболочки, важные для безопасности, не превышались до тех пор, пока этого требуют постулируемые аварийные условия.
Критерий 17 — Электроэнергетические системы . Для обеспечения функционирования конструкций, систем и компонентов, важных для безопасности, должны быть предусмотрены локальная система электроснабжения и внешняя система электроснабжения.Функция безопасности для каждой системы (при условии, что другая система не функционирует) должна обеспечивать достаточную мощность и способность гарантировать, что (1) указанные допустимые проектные пределы топлива и расчетные условия границы давления теплоносителя реактора не превышаются в результате: ожидаемые при эксплуатации события и (2) активная зона охлаждается, а целостность защитной оболочки и другие жизненно важные функции поддерживаются в случае постулируемых аварий.
Местные источники электропитания, включая батареи, и местная система распределения электроэнергии должны обладать достаточной независимостью, резервированием и тестируемостью для выполнения своих функций безопасности в случае единичного отказа.
Электроэнергия от передающей сети к местной системе распределения электроэнергии должна подаваться двумя физически независимыми цепями (не обязательно на отдельных полосах проезда), спроектированными и расположенными таким образом, чтобы минимизировать, насколько это практически возможно, вероятность их одновременного отказа в процессе эксплуатации. и постулируемая авария и условия окружающей среды. Допускается распределительное устройство, общее для обеих цепей. Каждый из этих контуров должен быть спроектирован таким образом, чтобы он был доступен в течение достаточного времени после выхода из строя всех местных источников питания переменного тока и других внешних электрических цепей, чтобы гарантировать, что указанные допустимые проектные пределы топлива и расчетные условия границы давления теплоносителя реактора не соответствуют. превышено.Один из этих контуров должен быть спроектирован таким образом, чтобы он был доступен в течение нескольких секунд после аварии с потерей теплоносителя, чтобы обеспечить поддержание охлаждения активной зоны, целостности защитной оболочки и других жизненно важных функций безопасности.
Должны быть включены положения для сведения к минимуму вероятности потери электроэнергии от любого из оставшихся источников в результате или одновременно с потерей мощности, генерируемой ядерным энергоблоком, потерей мощности в сети передачи или потеря мощности от локальных источников электропитания.
Критерий 18 — Обследование и испытание электроэнергетических систем . Электроэнергетические системы, важные для безопасности, должны быть спроектированы таким образом, чтобы позволять проводить соответствующие периодические проверки и испытания важных участков и функций, таких как проводка, изоляция, соединения и распределительные щиты, для оценки непрерывности систем и состояния их компонентов. Системы должны быть спроектированы с возможностью периодического тестирования (1) работоспособности и функциональных характеристик компонентов систем, таких как местные источники питания, реле, переключатели и шины, и (2) работоспособность систем как в целом и, в условиях, максимально приближенных к проектным, полную последовательность операций, которая приводит системы в действие, включая работу соответствующих частей системы защиты и передачу энергии между атомным энергоблоком, внешней энергосистемой и локальная энергосистема.
Критерий 19 — БЩУ. Должен быть предусмотрен диспетчерский пункт, из которого можно предпринимать действия для безопасной эксплуатации АЭС в нормальных условиях и поддержания его в безопасном состоянии в аварийных условиях, включая аварии с потерей теплоносителя. Должна быть обеспечена надлежащая радиационная защита, позволяющая доступ и использование поста управления в аварийных условиях без облучения персонала, превышающего 5 бэр, на все тело или его эквивалент на любую часть тела на время аварии.Оборудование в соответствующих местах за пределами диспетчерской должно быть обеспечено (1) проектной возможностью для быстрого горячего останова реактора, включая необходимые контрольно-измерительные приборы и средства управления для поддержания блока в безопасном состоянии во время горячего останова, и (2) возможность возможность последующего холодного останова реактора с помощью соответствующих процедур.
Претенденты и держатели разрешений на строительство и эксплуатационных лицензий в соответствии с этой частью, которые подают заявление не позднее 10 января 1997 г., заявители на одобрение конструкции или сертификаты в соответствии с частью 52 настоящей главы, которые подают заявки 10 января 1997 г. или позднее, заявители и держатели комбинированных лицензий или производственных лицензий в соответствии с частью 52 настоящей главы, которые не ссылаются на стандартное одобрение или сертификацию конструкции, или держатели операционных лицензий, использующие альтернативный источник в соответствии с § 50.67, должны соответствовать требованиям этого критерия, за исключением того, что в отношении доступа и занятости диспетчерской должна быть обеспечена адекватная радиационная защита, чтобы гарантировать, что радиационное облучение не должно превышать 0,05 Зв (5 бэр) суммарного эффективного эквивалента дозы (TEDE), как определено. в § 50.2 на время аварии.
III. Системы защиты и контроля реактивности
Критерий 20 — Функции системы защиты . Система защиты должна быть спроектирована (1) так, чтобы автоматически запускать работу соответствующих систем, включая системы управления реактивностью, чтобы гарантировать, что указанные допустимые проектные пределы топлива не превышаются в результате ожидаемых при эксплуатации событий, и (2) для определения аварийных условий и запускать работу систем и компонентов, важных для безопасности.
Критерий 21 — Надежность и тестируемость системы защиты . Система защиты должна быть спроектирована так, чтобы обеспечивать высокую функциональную надежность и возможность тестирования в процессе эксплуатации, соизмеримые с выполняемыми функциями безопасности. Резервирование и независимость, заложенные в систему защиты, должны быть достаточными, чтобы гарантировать, что (1) ни один единичный отказ не приведет к потере функции защиты и (2) отключение любого компонента или канала не приведет к потере требуемого минимального резервирования, если только иным образом можно продемонстрировать приемлемую надежность работы системы защиты.Система защиты должна быть спроектирована так, чтобы позволять периодические испытания ее функционирования, когда реактор находится в эксплуатации, включая возможность независимого испытания каналов для определения отказов и потерь избыточности, которые могли произойти.
Критерий 22 — Независимость системы защиты . Система защиты должна быть спроектирована таким образом, чтобы гарантировать, что эффекты природных явлений и нормальной эксплуатации, технического обслуживания, испытаний и постулируемых аварийных условий на резервных каналах не приводят к потере функции защиты или должны быть продемонстрированы как приемлемые для некоторых другая определенная основа.Методы проектирования, такие как функциональное разнообразие или разнообразие конструкции компонентов и принципов работы, должны использоваться, насколько это практически возможно, для предотвращения потери функции защиты.
Критерий 23 — Виды отказа системы защиты . Система защиты должна быть спроектирована так, чтобы переходить в безопасное состояние или в состояние, приемлемое на каком-либо другом определенном основании, если такие условия, как отключение системы, потеря энергии (например, электроэнергии, воздуха КИП) или постулируемые неблагоприятные условия. среды (например,ж., сильная жара или холод, огонь, давление, пар, вода и радиация).
Критерий 24 — Разделение систем защиты и управления . Система защиты должна быть отделена от систем управления в той степени, в которой отказ любого отдельного компонента или канала системы управления, отказ или снятие с эксплуатации любого отдельного компонента или канала системы защиты, который является общим для систем управления и защиты, не повреждает систему. удовлетворяющие всем требованиям надежности, избыточности и независимости системы защиты.Взаимосвязь систем защиты и управления должна быть ограничена, чтобы гарантировать, что безопасность не будет значительно снижена.
Критерий 25 — Требования к системе защиты от сбоев регулирования реактивности . Система защиты должна быть спроектирована таким образом, чтобы гарантировать, что указанные допустимые проектные пределы топлива не превышаются при любой единственной неисправности систем управления реактивностью, такой как случайное извлечение (не выброс или выпадение) управляющих стержней.
Критерий 26 — Резервирование и возможности системы управления реактивностью .Должны быть предусмотрены две независимые системы управления реактивностью с разными принципами проектирования. Одна из систем должна использовать управляющие стержни, предпочтительно включающие положительные средства для вставки стержней, и должна быть способна надежно контролировать изменения реактивности, чтобы гарантировать, что в условиях нормальной работы, включая ожидаемые при эксплуатации события, и с соответствующим запасом на неисправности, такие как заклинило стержни, не превышены указанные допустимые проектные пределы топлива. Вторая система управления реактивностью должна быть способна надежно контролировать скорость изменений реактивности в результате запланированных нормальных изменений мощности (включая выгорание ксенона), чтобы гарантировать, что допустимые проектные пределы топлива не превышаются.Одна из систем должна быть способна поддерживать активную зону реактора в докритическом состоянии в холодных условиях.
Критерий 27 — Возможности комбинированных систем контроля реактивности . Системы управления реактивностью должны быть спроектированы так, чтобы иметь комбинированную способность, в сочетании с добавлением яда системой аварийного охлаждения активной зоны, надежного управления изменениями реактивности, чтобы гарантировать, что в постулируемых аварийных условиях и с соответствующим запасом для прихвата стержней способность охлаждать активную зону. поддерживается.
Критерий 28 — Пределы реактивности . Системы управления реактивностью должны быть спроектированы с соответствующими ограничениями на потенциальную величину и скорость увеличения реактивности, чтобы гарантировать, что эффекты постулируемых аварий реактивности не могут ни (1) привести к повреждению границы давления теплоносителя реактора, превышающей ограниченную локальную текучесть, ни (2) ) достаточно возмущать активную зону, ее опорные конструкции или другие внутренние устройства корпуса реактора, чтобы значительно ухудшить способность охлаждения активной зоны.Эти постулируемые аварии реактивности должны включать рассмотрение выброса стержня (если не предотвращено положительными средствами), выпадения стержня, разрыва паропровода, изменений температуры и давления теплоносителя реактора, а также добавления холодной воды.
Критерий 29 — Защита от ожидаемых нарушений нормальной работы . Системы защиты и управления реактивностью должны быть спроектированы таким образом, чтобы обеспечивать чрезвычайно высокую вероятность выполнения своих функций безопасности в случае ожидаемых при эксплуатации событий.
IV. Жидкостные системы
Критерий 30 — Качество границы давления теплоносителя реактора . Компоненты, которые являются частью границы давления теплоносителя реактора, должны быть спроектированы, изготовлены, смонтированы и испытаны в соответствии с самыми высокими практическими стандартами качества. Должны быть предусмотрены средства для обнаружения и, насколько это практически возможно, определения местоположения источника утечки теплоносителя реактора.
Критерий 31 — Предотвращение разрушения границы давления теплоносителя реактора .Граница давления теплоносителя реактора должна быть спроектирована с достаточным запасом, чтобы гарантировать, что при напряжении в условиях эксплуатации, технического обслуживания, испытаний и постулируемых аварийных условий (1) граница ведет себя нехрупким образом и (2) минимизируется вероятность быстро распространяющейся трещины. Проект должен отражать учет рабочих температур и других условий граничного материала при эксплуатации, техническом обслуживании, испытаниях и постулируемых аварийных условиях, а также неопределенности при определении (1) свойств материала, (2) влияния облучения на свойства материала, (3) ) остаточные, установившиеся и переходные напряжения; (4) размер дефектов.
Критерий 32 — Контроль границы давления теплоносителя реактора . Компоненты, которые являются частью границы давления теплоносителя реактора, должны быть спроектированы таким образом, чтобы позволять (1) периодические проверки и испытания важных участков и элементов для оценки их конструкционной и герметичной целостности, и (2) соответствующую программу наблюдения за материалами корпуса высокого давления реактора.
Критерий 33 — Состав теплоносителя реактора . Должна быть предусмотрена система подпитки теплоносителя реактора для защиты от небольших разрывов границы давления теплоносителя реактора.Функция безопасности системы должна гарантировать, что указанные допустимые проектные пределы топлива не превышаются в результате потери теплоносителя реактора из-за утечки через границу давления теплоносителя реактора и разрыва небольших трубопроводов или других мелких компонентов, которые являются частью границы. Система должна быть спроектирована таким образом, чтобы гарантировать, что для работы системы электроснабжения на объекте (при условии отсутствия электроэнергии за пределами площадки) и для работы системы электроснабжения за пределами объекта (при условии отсутствия электроэнергии на объекте) функция безопасности системы может быть выполнена с использованием трубопроводов, насосов и др. и клапаны, используемые для поддержания запаса теплоносителя во время нормальной работы реактора.
Критерий 34 — отвод остаточного тепла . Должна быть предусмотрена система отвода остаточного тепла. Функция безопасности системы должна заключаться в передаче тепла распада продуктов деления и другого остаточного тепла от активной зоны реактора с такой скоростью, чтобы не превышались указанные допустимые проектные пределы топлива и расчетные условия границы давления теплоносителя реактора.
Должно быть обеспечено подходящее резервирование компонентов и функций, а также подходящие соединения, возможности обнаружения утечек и изоляции, чтобы гарантировать, что для работы системы электроснабжения на объекте (при условии, что внешнее питание недоступно) и для работы системы электроснабжения за пределами объекта (при условии наличия электроэнергии на объекте). недоступен) функция безопасности системы может быть выполнена при условии единичного отказа.
Критерий 35 — Аварийное охлаждение активной зоны . Должна быть предусмотрена система обильного аварийного охлаждения активной зоны. Функция безопасности системы должна заключаться в передаче тепла от активной зоны реактора после любой потери теплоносителя в реакторе с такой скоростью, чтобы (1) предотвращалось повреждение топлива и оболочки, которое могло бы помешать непрерывному эффективному охлаждению активной зоны, и (2) реакция металлической оболочки с водой. ограничено незначительными суммами.
Должно быть обеспечено подходящее резервирование компонентов и функций, а также подходящие межсоединения, возможности обнаружения утечек, изоляции и локализации, чтобы гарантировать, что для работы системы электроснабжения на объекте (при условии, что внешнее питание недоступно) и для работы системы электроснабжения за пределами объекта (при условии Электроэнергия на объекте отсутствует) функция безопасности системы может быть выполнена при условии единичного отказа.
Критерий 36 — Проверка системы аварийного охлаждения активной зоны . Система аварийного охлаждения активной зоны должна быть спроектирована таким образом, чтобы позволять проводить соответствующие периодические проверки важных компонентов, таких как распылительные кольца в корпусе реактора, форсунки для нагнетания воды и трубопроводы, чтобы гарантировать целостность и работоспособность системы.
Критерий 37 — Испытание системы аварийного охлаждения активной зоны . Система аварийного охлаждения активной зоны должна быть спроектирована так, чтобы позволять проводить соответствующие периодические испытания под давлением и функциональные испытания, чтобы гарантировать (1) конструктивную целостность и герметичность ее компонентов, (2) работоспособность и характеристики активных компонентов системы и (3) надежность работоспособность системы в целом и, в условиях, максимально приближенных к проектным, выполнение полного рабочего цикла, который приводит систему в действие, включая работу соответствующих частей системы защиты, переключение между обычным и аварийным источниками питания , и работу связанной системы охлаждающей воды.
Критерий 38 — отвод тепла из защитной оболочки . Должна быть предусмотрена система отвода тепла от защитной оболочки реактора. Функция безопасности системы должна заключаться в быстром снижении в соответствии с функционированием других связанных систем давления и температуры в защитной оболочке после любой аварии с потерей теплоносителя и поддержании их на приемлемо низких уровнях.
Должно быть обеспечено подходящее резервирование компонентов и функций, а также подходящие межсоединения, возможности обнаружения утечек, изоляции и локализации, чтобы гарантировать, что для работы системы электроснабжения на объекте (при условии, что внешнее питание недоступно) и для работы системы электроснабжения за пределами объекта (при условии Электроэнергия на объекте отсутствует) функция безопасности системы может быть выполнена при условии единичного отказа.
Критерий 39 — Проверка системы отвода тепла из защитной оболочки . Система отвода тепла от защитной оболочки должна быть спроектирована так, чтобы позволять проводить соответствующие периодические проверки важных компонентов, таких как тор, отстойники, распылительные форсунки и трубопроводы, чтобы гарантировать целостность и работоспособность системы.
Критерий 40 — Испытание системы отвода тепла из защитной оболочки . Система отвода тепла от защитной оболочки должна быть спроектирована таким образом, чтобы позволять проводить соответствующие периодические испытания под давлением и функциональные испытания, чтобы гарантировать (1) конструктивную целостность и герметичность ее компонентов, (2) работоспособность и характеристики активных компонентов системы и (3) надежность работоспособность системы в целом и в условиях, максимально приближенных к проектным, выполнение полного рабочего цикла, который приводит систему в действие, включая работу соответствующих частей системы защиты, переключение между обычным и аварийным источниками питания , и работу связанной системы охлаждающей воды.
Критерий 41 — Очистка защитной атмосферы . При необходимости должны быть предусмотрены системы контроля продуктов деления, водорода, кислорода и других веществ, которые могут быть выброшены в защитную оболочку реактора для снижения, в соответствии с функционированием других связанных систем, концентрации и качества продуктов деления, выбрасываемых в окружающую среду после постулируемых аварий, а также для контроля концентрации водорода или кислорода и других веществ в атмосфере защитной оболочки после постулируемых аварий, чтобы гарантировать сохранение целостности защитной оболочки.
Каждая система должна иметь соответствующее резервирование компонентов и функций, а также подходящие соединения, возможности обнаружения утечек, изоляции и локализации, чтобы гарантировать, что для работы системы электроснабжения на объекте (при условии, что внешнее питание недоступно) и для работы системы электроснабжения за пределами площадки ( при отсутствии электричества на месте) его функция безопасности может быть выполнена при условии единичного отказа.
Критерий 42 — Инспекция систем очистки защитной атмосферы .Системы очистки защитной атмосферы должны быть спроектированы таким образом, чтобы позволять проводить соответствующие периодические проверки важных компонентов, таких как рамы фильтров, воздуховоды и трубопроводы, чтобы гарантировать целостность и работоспособность систем.
Критерий 43 — Испытания систем очистки защитной атмосферы . Системы очистки защитной атмосферы должны быть спроектированы таким образом, чтобы позволять проводить соответствующие периодические испытания под давлением и функциональные испытания, чтобы гарантировать (1) конструктивную целостность и герметичность ее компонентов, (2) работоспособность и производительность активных компонентов систем, таких как вентиляторы, фильтры, демпферы, насосы и клапаны и (3) работоспособность систем в целом и, в условиях, максимально приближенных к проектным, выполнение полного рабочего цикла, который приводит системы в действие, включая работу соответствующих частей система защиты, переключение между штатными и аварийными источниками питания и работа связанных систем.
Критерий 44 — охлаждающая вода . Должна быть предусмотрена система передачи тепла от конструкций, систем и компонентов, важных для безопасности, к конечному поглотителю тепла. Функция безопасности системы должна заключаться в передаче комбинированной тепловой нагрузки этих конструкций, систем и компонентов в нормальных рабочих и аварийных условиях.
Должно быть обеспечено подходящее резервирование компонентов и функций, а также подходящие соединения, возможности обнаружения утечек и изоляции, чтобы гарантировать, что для работы системы электроснабжения на объекте (при условии, что внешнее питание недоступно) и для работы системы электроснабжения за пределами объекта (при условии наличия электроэнергии на объекте). недоступен) функция безопасности системы может быть выполнена при условии единичного отказа.
Критерий 45 — Проверка системы водяного охлаждения . Система охлаждающей воды должна быть спроектирована так, чтобы позволять проводить соответствующие периодические проверки важных компонентов, таких как теплообменники и трубопроводы, чтобы гарантировать целостность и работоспособность системы.
Критерий 46 — Испытания системы водяного охлаждения . Система охлаждающей воды должна быть спроектирована так, чтобы позволять проводить соответствующие периодические испытания под давлением и функциональные испытания, чтобы гарантировать (1) конструктивную целостность и герметичность ее компонентов, (2) работоспособность и рабочие характеристики активных компонентов системы, и (3) надежность работоспособность системы в целом и, в условиях, максимально приближенных к проектным, выполнение полного рабочего цикла, который приводит систему в действие для остановки реактора и аварий с потерей теплоносителя, включая работу соответствующих частей система защиты и переключение между штатным и аварийным источниками питания.
V. Защитная оболочка реактора
Критерий 50 — Проектные основы защитной оболочки . Конструкция защитной оболочки реактора, включая отверстия для доступа, проходки и систему отвода тепла защитной оболочки, должна быть спроектирована таким образом, чтобы конструкция защитной оболочки и ее внутренние отсеки могли выдерживать, без превышения проектной скорости утечки и с достаточным запасом, расчетные условия давления и температуры, которые возникают от любой аварии с потерей охлаждающей жидкости. Этот запас должен отражать учет (1) влияния потенциальных источников энергии, которые не были включены в определение пиковых условий, таких как энергия в парогенераторах, и в соответствии с требованиями § 50.44 энергии от металла с водой и других химических реакций, которые могут быть результатом деградации, но не полного отказа функционирования аварийного охлаждения активной зоны, (2) ограниченный опыт и экспериментальные данные, доступные для определения аварийных явлений и реакции защитной оболочки, и (3) консерватизм расчетная модель и входные параметры.
Критерий 51 — Предотвращение разрушения границы давления защитной оболочки . Граница защитной оболочки реактора должна быть спроектирована с достаточным запасом, чтобы гарантировать, что в условиях эксплуатации, технического обслуживания, испытаний и постулируемых аварийных условий (1) его ферритные материалы ведут себя нехрупким образом и (2) вероятность быстро распространяющегося разрушения сводится к минимуму.Проект должен отражать учет рабочих температур и других условий материала границы защитной оболочки во время эксплуатации, технического обслуживания, испытаний и постулируемых аварийных условий, а также неопределенности в определении (1) свойств материала, (2) остаточных, установившихся и переходных напряжений. и (3) размер дефектов.
Критерий 52 — Возможность проведения испытаний на скорость утечки из защитной оболочки . Защитная оболочка реактора и другое оборудование, которое может подвергаться условиям испытаний защитной оболочки, должны быть спроектированы таким образом, чтобы можно было проводить периодические комплексные испытания скорости утечки при проектном давлении защитной оболочки.
Критерий 53 — Положения об испытаниях и проверках защитной оболочки . Защитная оболочка реактора должна быть спроектирована так, чтобы позволять (1) соответствующую периодическую проверку всех важных зон, таких как проходки, (2) соответствующую программу наблюдения и (3) периодические испытания герметичности проходов, имеющих упругие уплотнения, при расчетном давлении защитной оболочки. и компенсирующие сильфоны.
Критерий 54 — Системы трубопроводов, проникающие через защитную оболочку . Системы трубопроводов, проходящие через первичную защитную оболочку реактора, должны быть обеспечены средствами обнаружения утечек, изоляции и локализации, имеющими возможности резервирования, надежности и производительности, которые отражают важность изоляции этих систем трубопроводов для безопасности.Такие системы трубопроводов должны быть спроектированы с возможностью периодического тестирования работоспособности запорных клапанов и связанного с ними оборудования и определения того, находится ли утечка клапана в допустимых пределах.
Критерий 55 — Граница давления теплоносителя реактора, проходящая через защитную оболочку . Каждая линия, которая является частью границы давления теплоносителя реактора и которая проходит через первичную защитную оболочку реактора, должна быть снабжена изолирующими клапанами защитной оболочки, как указано ниже, если не может быть продемонстрировано, что положения об изоляции защитной оболочки для конкретного класса линий, таких как измерительные линии, выполняются. приемлемо на некоторой другой определенной основе:
(1) Один запертый закрытый запорный клапан внутри и один запертый закрытый запорный клапан снаружи защитной оболочки; или
(2) Один автоматический запорный клапан внутри и один запертый закрытый запорный клапан снаружи защитной оболочки; или
(3) Один запертый закрытый стопорный клапан внутри и один автоматический стопорный клапан снаружи защитной оболочки.Запрещается использовать простой обратный клапан в качестве автоматического запорного клапана вне защитной оболочки; или
(4) Один автоматический стопорный клапан внутри и один автоматический стопорный клапан снаружи защитной оболочки. Запрещается использовать простой обратный клапан в качестве автоматического запорного клапана вне защитной оболочки.
Запорные клапаны за пределами защитной оболочки должны располагаться как можно ближе к защитной оболочке, а в случае потери исполнительной мощности автоматические отсечные клапаны должны быть сконструированы таким образом, чтобы они занимали положение, обеспечивающее большую безопасность.
Другие соответствующие требования для сведения к минимуму вероятности или последствий случайного разрыва этих линий или линий, подключенных к ним, должны быть предусмотрены по мере необходимости для обеспечения надлежащей безопасности. Определение соответствия этих требований, таких как более высокое качество при проектировании, изготовлении и испытаниях, дополнительные меры для технического осмотра, защита от более суровых природных явлений, а также дополнительные запорные клапаны и защитная оболочка, должны включать учет плотности населения, характеристик использования. , и физические характеристики окрестностей участка.
Критерий 56 — Изоляция первичной защитной оболочки . Каждая линия, которая соединяется непосредственно с атмосферой защитной оболочки и проходит через защитную оболочку первичного реактора, должна быть снабжена изолирующими клапанами защитной оболочки, как указано ниже, если только не может быть продемонстрировано, что положения об изоляции защитной оболочки для конкретного класса линий, таких как измерительные линии, приемлемы для некоторых другое установленное основание:
(1) Один запертый закрытый запорный клапан внутри и один запертый закрытый запорный клапан снаружи защитной оболочки; или
(2) Один автоматический запорный клапан внутри и один запертый закрытый запорный клапан снаружи защитной оболочки; или
(3) Один запертый закрытый стопорный клапан внутри и один автоматический стопорный клапан снаружи защитной оболочки.Запрещается использовать простой обратный клапан в качестве автоматического запорного клапана вне защитной оболочки; или
(4) Один автоматический стопорный клапан внутри и один автоматический стопорный клапан снаружи защитной оболочки. Запрещается использовать простой обратный клапан в качестве автоматического запорного клапана вне защитной оболочки.
Запорные клапаны за пределами защитной оболочки должны располагаться как можно ближе к защитной оболочке, а в случае потери исполнительной мощности автоматические отсечные клапаны должны быть сконструированы таким образом, чтобы они занимали положение, обеспечивающее большую безопасность.
Критерий 57 — Запорные клапаны закрытой системы . Каждая линия, которая проходит через первичную защитную оболочку реактора и не является частью границы давления теплоносителя реактора и не связана напрямую с атмосферой защитной оболочки, должна иметь по крайней мере один изолирующий клапан защитной оболочки, который должен быть либо автоматическим, либо заблокированным, либо с возможностью дистанционного ручного управления. Этот клапан должен находиться вне защитной оболочки и располагаться как можно ближе к защитной оболочке. Простой обратный клапан нельзя использовать в качестве автоматического запорного клапана.
VI. Контроль топлива и радиоактивности
Критерий 60 — Контроль выбросов радиоактивных материалов в окружающую среду . В проект ядерной энергоблока должны входить средства для надлежащего управления выбросом радиоактивных материалов в газообразных и жидких отходящих потоках и для обращения с твердыми радиоактивными отходами, образующимися при нормальной эксплуатации реактора, включая ожидаемые при эксплуатации события. Должна быть обеспечена достаточная задерживающая способность для удержания газообразных и жидких стоков, содержащих радиоактивные материалы, особенно в тех случаях, когда можно ожидать, что неблагоприятные условия окружающей среды на площадке наложат необычные эксплуатационные ограничения на выброс таких стоков в окружающую среду.
Критерий 61 — Хранение и обращение с топливом и контроль радиоактивности . Хранение и обращение с топливом, радиоактивными отходами и другие системы, которые могут содержать радиоактивность, должны быть спроектированы таким образом, чтобы обеспечивать адекватную безопасность в нормальных и предполагаемых аварийных условиях. Эти системы должны быть спроектированы (1) с возможностью проведения соответствующих периодических проверок и испытаний компонентов, важных для безопасности, (2) с подходящей защитой для радиационной защиты, (3) с соответствующими системами герметизации, локализации и фильтрации, (4) с возможностью отвода остаточного тепла, имеющей надежность и тестируемость, что отражает важность для безопасности отвода остаточного тепла и другого остаточного тепла, и (5) для предотвращения значительного сокращения запасов теплоносителя в хранилище топлива в аварийных условиях.
Критерий 62 — Предотвращение критичности при хранении и обращении с топливом . Критичность системы хранения и обращения с топливом должна быть предотвращена с помощью физических систем или процессов, предпочтительно путем использования геометрически безопасных конфигураций.
Критерий 63 — Контроль хранения топлива и отходов . Соответствующие системы должны быть предусмотрены в системах хранения топлива и радиоактивных отходов и связанных с ними зонах обращения (1) для обнаружения условий, которые могут привести к потере способности отвода остаточного тепла и чрезмерным уровням излучения, и (2) для инициирования соответствующих мер безопасности.
Критерий 64 — Мониторинг радиоактивных выбросов . Должны быть предусмотрены средства для контроля атмосферы защитной оболочки реактора, пространств, содержащих компоненты для рециркуляции аварийных жидкостей с потерей теплоносителя, путей сброса сточных вод и окружающей среды станции на предмет радиоактивности, которая может высвободиться при нормальной эксплуатации, включая ожидаемые при эксплуатации события, и постулируемые несчастные случаи.
1 Дальнейшие подробности, касающиеся типа, размера и ориентации постулируемых разрывов в конкретных компонентах границы давления теплоносителя реактора, находятся в стадии разработки.
2 Единичные отказы пассивных компонентов в электрических системах должны учитываться при проектировании против единичного отказа. Условия, при которых следует учитывать единичный отказ пассивного компонента в гидравлической системе при проектировании системы против единичного отказа, находятся в стадии разработки.
[36 FR 3256, 20 февраля 1971 г., с поправками, внесенными в 36 FR 12733, 7 июля 1971 г .; 41 FR 6258, 12 февраля 1976 г .; 43 FR 50163, 27 октября 1978 г .; 51 FR 12505, 11 апреля 1986 г .; 52 FR 41294, окт.27, 1987; 64 FR 72002, 23 декабря 1999 г .; 72 FR 49505, 28 августа 2007 г.]
Страница Последняя редакция / обновление Среда, 24 марта 2021 г.
.

 41 .
41 .
 Какого он был цвета перед этим покраснением?
Какого он был цвета перед этим покраснением?
 Процедура выполняется в нашей клинике под местной анестезией на приеме ЛОР врача. Полностью безболезненна, позволяет оценить не только степень аденоидных вегетаций, но и характер воспаления, состояние устьев слуховых труб, а также осмотреть задние отделы полости носа.
Процедура выполняется в нашей клинике под местной анестезией на приеме ЛОР врача. Полностью безболезненна, позволяет оценить не только степень аденоидных вегетаций, но и характер воспаления, состояние устьев слуховых труб, а также осмотреть задние отделы полости носа.
 По состоянию на 15 июня 2021 г. https://visualfractions.com/calculator/exponent/what-is-4-to-the-7th-power/.
По состоянию на 15 июня 2021 г. https://visualfractions.com/calculator/exponent/what-is-4-to-the-7th-power/.
Leave A Comment