Географическая долгота. Географические координаты — Ответы, рабочая тетрадь 6 класс (Карташева, Курчина)
1. На каком из рисунков стрелкой показано, как определяется географическая долгота?
Ответ: на рисунке Б
2. Отметьте на карте точки:
А – имеет северную широту и восточную долготу
Б – имеет северную широту и западную долготу
В – имеет южную широту и западную долготу
Г – имеет южную широту и восточную долготу
Определите координаты этих точек:
А — 40° с.ш., 60° в.д.
Б — 40° с.ш., 60° з.д.
В — 40° ю.ш., 60° з.д.
Г — 40° ю.ш., 120° в.д.
3. Укажите, какие точки, отмеченные на карте (с. 44-45), имеют западную долготу, а какие – восточную
Западная долгота: Б, В
Восточная долгота: А
Какая из точек расположена западнее? —
Б Какая – восточнее? — А
Почему вы так решили?
Точка А расположена на 180-ом меридиане — самая восточная точка.
Точка Б западнее точки В — западнее других точек
Точка Б западнее точки В — западнее других точек4. Определите географическую долготу точек, отмеченных буквами на карте на стр. 44-45
Точка Географическая широта А 180° з.д. Б 100° з.д. В 40° з.д. Г 10° в.д. Д 70° в.д. Е 130° в.д.
5. Город А имеет координаты 20° с.ш. и 30° в.д. Координаты города Б — 10° ю.ш. и 70° з.д.
а) Нанесите эти города на контурную карту
б) На территории каких материков, и в каких полушариях расположен каждый из этих городов?
Город А Африка; Северное и Восточное полушария
Город Б Южная Америка; Южное и Западное полушария
в) Какой из городов – А или Б – расположен южнее? Свой ответ аргументируйте.
Город Б расположен южнее, т.к. находится в Южном полушарии.
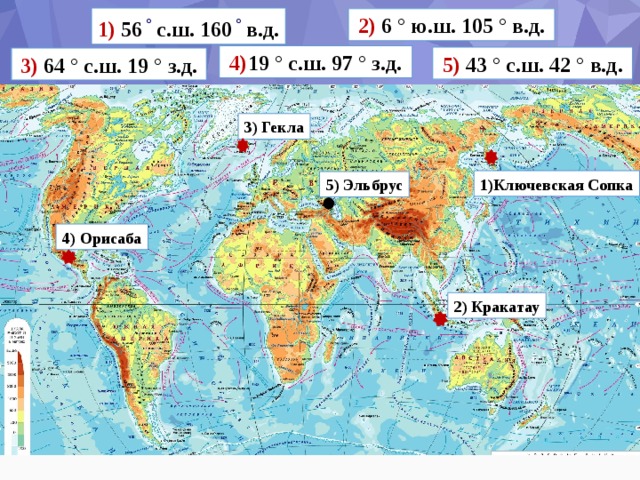
6. Какая из точек, отмеченных на карте, имеет географические координаты:
50° ю.ш., 70° в.д. — А
40° ю.ш., 50° в.д. — Ж
18° с.ш., 8° з.д. — Е
8° ю.ш., 16° з.д. — Г
43° с.ш., 115° з.д. — Д
46° с.ш., 115° в.д. — Б
Определите географические координаты оставшейся точки
23° ю.ш., 90° в.д.
Какая из точек расположена южнее остальных?
А
Какая – севернее?
Б
7. Капитан корабля решил совершить плавание из Евразии в Новую Зеландию. Помогите капитану заполнить судовой журнал, определив местоположение и географические координаты точек, где находился корабль.
Порт Пасположение Географические координаты Мыс Рока Евразия 38° с. Рио-де-Жанейро Южная Америка 22° ю.ш., 43° з.д. Мыс Горн Южная Америка 55° ю.ш., 67° з.д. Остров Пасхи Южная Америка 27° ю.ш., 109° з.д. Веллингтон Океания (рядом с Австралией) 41° ю.ш., 174° в.д.
ш., 9° з.д.8. Определите, в каком направлении следует двигаться туристам, если они перемещаются из точки с координатами 19° с.ш., 73° в.д. в точку с координатами 28° с.ш., 87° в.д. Откуда и куда они совершают путешествие?
На северо-восток. Из города Мумбаи к горе Эверест
10. С помощью политической карты полушарий определите самые крупные страны на каждом из материков Земли. Выпишите их названия и столицы. Определите географические координаты столиц
Материк Страна Столица Географические координаты Евразия Российская Федерация Москва 55° с. Африка Алжир Алжир 36° с.ш., 3° в.д. Северная Америка Канада Оттава 45° с.ш., 75° з.д. Южная Америка Бразилия Бразилиа 15° ю.ш., 47° з.д. Австралия Австралия Канберра 35° ю.ш., 149° в.д.
ш., 37° в.д.§ 18. Градусная сетка. Географические координаты
§ 18.Градусная сетка. Географические координаты
Вы узнаете
•Что такое географическая широта и долгота.
•Как определять географические координаты точки по градусной сетке.
Вспомните
•Одинаковую ли длину имеют параллели и меридианы?
•В каких единицах измеряют углы и дуги окружностей?
Обратитесь к электронному приложению
Рис. 53.
Градусная сетка.
Пересекающиеся параллели и меридианы образуют на глобусах и картах сетку (рис. 53). Каждая «ячейка» сетки состоит из дуг окружностей. Дуги окружностей, как и углы, можно измерять в градусах, поэтому систему параллелей и меридианов называют градусной сеткой. Градусная мера окружности составляет 360°. (Вспомните компас!) Полуокружность — это дуга величиной 180°.
Градусная сетка — это система пересекающихся линий — параллелей и меридианов, которые нанесены на глобус или географическую карту.
С помощью градусной сетки определяют географические координаты точек на земной поверхности: географическую широту и географическую долготу.
Рис. 54. Географическая широта
Географическая широта. Все параллели, нанесённые на глобус и карты, имеют обозначения в градусах (0°, 10°, 20° и т. д.). На глобусе они подписаны вдоль начального меридиана, на карте полушарий — на круглой рамке карты. Эти числа указывают географическую широту параллелей (рис. 54).
Географическая широта — это величина дуги меридиана в градусах от экватора до заданной точки.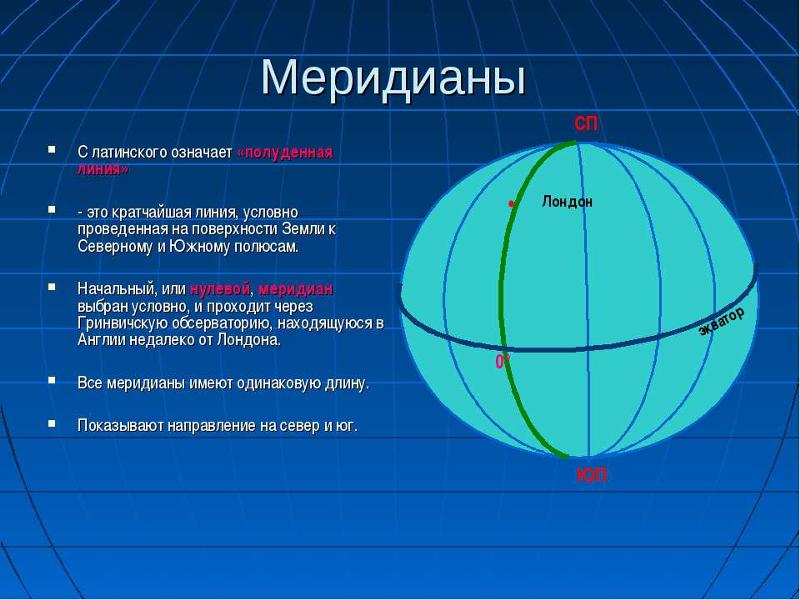
Все точки, лежащие на одной параллели, имеют одинаковую широту. Поскольку географическую широту отсчитывают от экватора, его широта — 0° ш. Значения широты на полюсах — 90° ш.
Рис. 55. Географическая долгота
Все точки, лежащиев Северном полушарии, имеют северную широту (с. ш.), а точки, лежащие в Южном полушарии, — южную широту (ю. ш.).
Географическая долгота. Чтобы определить местоположение какого-либо пункта, недостаточно знать только его широту. Ведь на одной и той же параллели много разных объектов! Поэтому приходится определять географическую долготу (рис. 55).
Географическая долгота — это величина дуги параллели в градусах от начального меридиана до заданной точки.
Все точки, лежащие на одном меридиане, имеют одинаковую долготу. Поскольку географическую долготу отсчитывают от начального (Гринвичского) меридиана, его долгота — 0° д. Поэтому этот меридиан часто называют нулевым. Значения долготы изменяются от 0 до 180°.
Все точки, находящиеся к востоку от начального (нулевого) меридиана, имеют восточную долготу (в.
д.), а точки, лежащие к западу от него, — западную долготу (з. д.). Значения долготы в градусах на глобусе и карте полушарий подписывают вдоль экватора у его пересечения с меридианами.
Определение географических координат. Чтобы определить географическую широту объекта, нужно определить параллель, на которой он находится. Например, Санкт-Петербург расположен в Северном полушарии на параллели 60°, поэтому его широта 60° с. ш. А как определить широту, если объект расположен между параллелями? Для этого нужно определить широту ближайшей к объекту параллели со стороны экватора и к ней прибавить число градусов дуги меридиана от этой параллели до объекта. Например, Москва располагается севернее параллели 50°. Число градусов по меридиану между этой параллелью и Москвой равно шести. Значит, географическая широта Москвы будет 56° с. ш.
Так же нужно поступать при определении географической долготы объекта. Если он располагается между двумя меридианами, то сначала узнают долготу ближайшего к объекту меридиана со стороны Гринвича.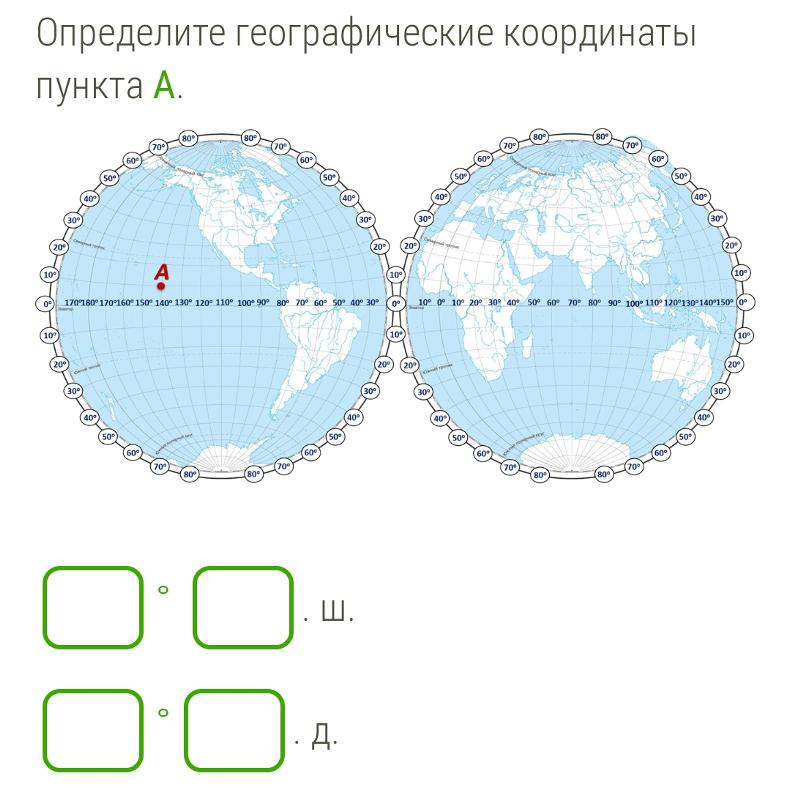
Определение расстояний по градусной сетке. С помощью градусной сетки на географической карте можно определять расстояния. Все меридианы имеют одинаковую длину. Поэтому длины дуг меридианов величиной 1° равны примерно 111 км. А вот длины дуг величиной 1° для разных параллелей неодинаковы — они уменьшаются по направлению от экватора к полюсам. Поэтому для расчётов расстояний используют таблицу значений длин дуг 1° параллелей для разных широт.
Широта, ° | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
Длина 1°, км | 111,4 | 109,6 | 104,6 | 96,4 | 85,4 | 71,6 | 55,8 | 38,2 | 19,4 |
ВОПРОСЫ И ЗАДАНИЯ
1.
Какие линии составляют градусную сетку? Для чего она служит?
2.Что такое географическая широта; географическая долгота?
3.По рисункам 54 и 55 определите географические координаты Владивостока и Лондона.
4.Определите по карте:
— какие горы протягиваются в Евразии вдоль параллели 30° с. ш.; вдоль меридиана 60° в. д.;
— какие объекты имеют географические координаты 78° с. ш. и 104° в. д.; 35° ю. ш. и 20° в. д.; 66° с. ш. и 170° з. д.; 52° с. ш. и 0° д.; 5° с. ш. и 10° в. д. Нанесите эти объекты на контурную карту;
— географические координаты Лондона, Нью-Йорка, Рио-де-Жанейро.
5.С помощью градусной сетки по карте полушарий определите:
— расстояние (в градусах и километрах) от экватора до места впадения реки Нил в Средиземное море;
— ширину Южной Америки (в градусах и километрах) по параллели 20° ю. ш.
Пеленги
Компас показан ниже. Он используется для поиска направление или азимут. Четыре основных направления компаса известны как стороны света .
Это север (N), восток (E), юг (S) и запад (W). Иногда
половины сторон света северо-восток (СВ), северо-запад (СЗ), юго-восток (ЮВ)
и юго-запад (ЮЗ) показаны на компасе. Приведенный выше компас показывает
градусные измерения от 0 до 360 в 10 интервалах с:
- север, представляющий 0 или 360
- восток представляет 90
- юг представляет 180
- запад представляет 270
При использовании компаса держите его так, чтобы точка отмеченные северные точки прямо от вас. Обратите внимание, что магнитный стрелка всегда указывает на север.
Подшипник
Истинный пеленг на точку — это угол, измеренный в степени в по часовой стрелке от северной линии. Мы будем ссылаться на истинное подшипник просто как подшипник .
Например, азимут точки P равен 065, что является номером
градусов по углу, измеренному в
по часовой стрелке от северной линии до линии, соединяющей
центр компаса в точке O с точкой P (т.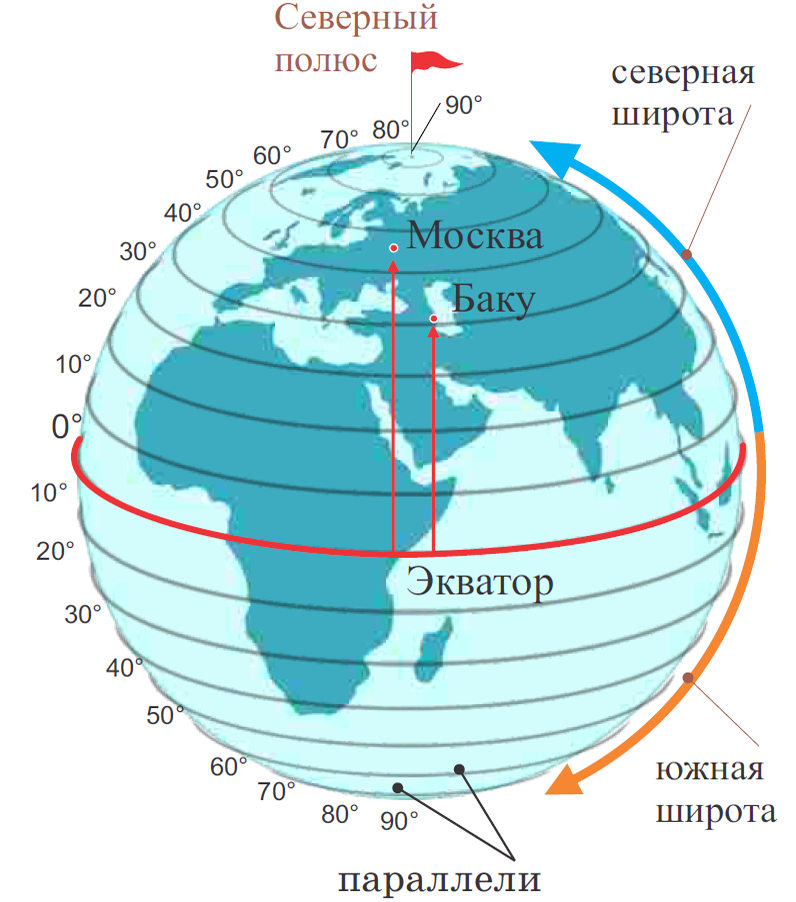
е. OP ).
Азимут точки Q равен 300, что является числом градусов в угол, измеренный в по часовой стрелке от северной линии до линии, соединяющей центр компас на O с точкой Q (т.е. OQ ).
Примечание:
Азимут точки – это количество градусов угла, измеренного в по часовой стрелке от северной линии до линии, соединяющей центр компаса с точкой.
Азимут используется для обозначения направления одной точки относительно
другой момент.
Например, подшипник A из B равен 065. подшипник B из A 245.
Примечание:
- Три цифры используются для обозначения подшипников.
- Все подшипники измеряются в горизонтальной плоскости.
Пример 10
Укажите пеленг точки P на каждой из следующих диаграмм:
Решение:
а.
Отметьте угол в
по часовой стрелке, указав поворот между северной линией и
линия, соединяющая центр компаса с точкой Р .
Азимут точки P 048.
б. Отметьте угол в
по часовой стрелке, указав поворот между северной линией и
линия, соединяющая центр компаса с точкой P .
Сторона света S соответствует 180. Это видно из диаграмме, требуемый угол на 60 больше, чем 180. Итак, угол, измеренный в по часовой стрелке от северной линии до линии, соединяющей центр компаса к пункту P равно 180 + 60 = 240.
Итак, пеленг точки P равен 240.
в. Отметьте угол в
по часовой стрелке, указав поворот между северной линией и
линия, соединяющая центр компаса с точкой P .
Сторона света S соответствует 180. Это видно из
диаграмме, требуемый угол на 40 меньше 180. Итак, угол, измеренный в
по часовой стрелке от линии севера до линии, соединяющей центр компаса с
пункт P равно 180 40 = 140.
Итак, пеленг точки P равен 140.
д. Отметьте угол в
по часовой стрелке, указав поворот между северной линией и
линия, соединяющая центр компаса с точкой P .
Сторона света W соответствует 270. Это видно из диаграмме, требуемый угол на 20 больше, чем 270. Итак, угол, измеренный в по часовой стрелке от северной линии до линии, соединяющей центр компаса к пункту P равно 270 + 20 = 290.
Итак, пеленг точки P равен 290.
Направление
Условный пеленг точки указан как количество градусов к востоку или западу от линии север-юг. Мы будем ссылаться на обычный подшипник просто как направление .
Чтобы указать направление точки, напишите:
- С или Ю, определяемая углом измеряется
- угол между северной или южной линией и точкой, измеряется в градусах
- E или W в зависимости от местоположения точки относительно линии север-юг
напр.
На приведенной выше диаграмме направление:
- A из O — N30E.
- B из O — N60W.
- C из O это S70E.
- D из O — S80W.
Примечание:
N30E означает направление на 30° к востоку от севера.
Пример 11
Опишите каждый из следующих подшипников как направления.
а. 076
б. 150
г. 225
д. 290
Решение:
а. Положение точки P на азимуте 076 показано на следующую схему.
Положение точки P — 76 к востоку от севера. Итак направление N76E.
б. Положение точки P на азимуте 150 показано на
следующую схему.
Положение точки P равно 180 150 = 30° в.д. юга. Итак, направление S30E.
в. Положение точки P на азимуте 225 показано на
следующую схему.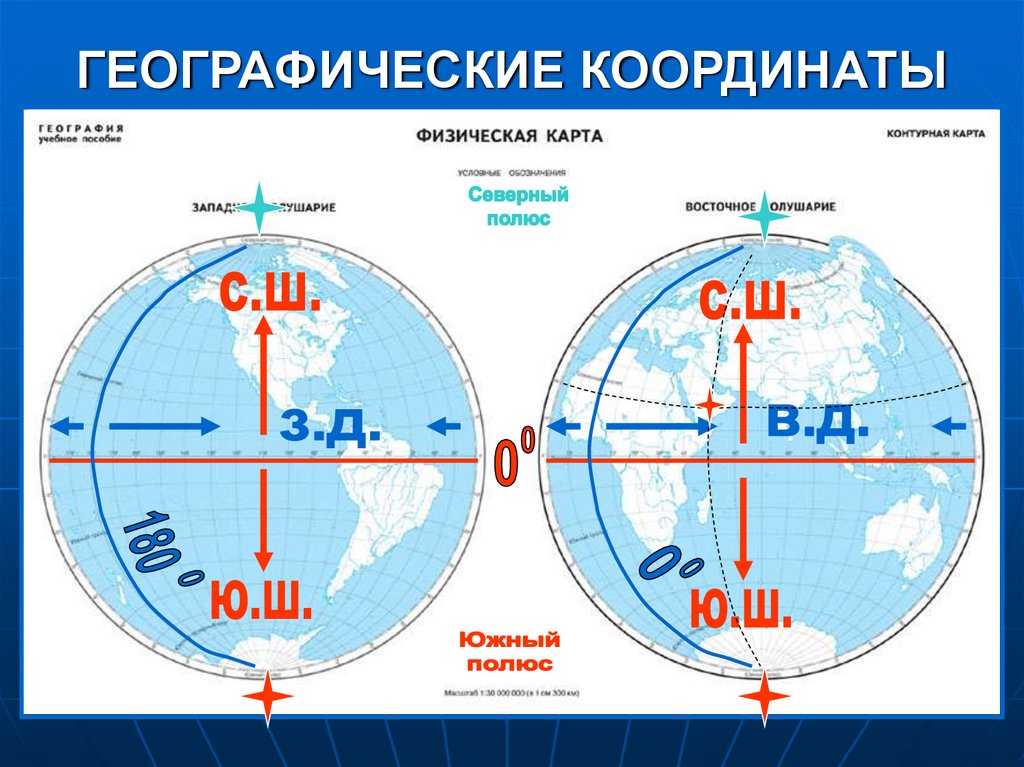
Положение точки P равно 225 180 = 45 з.д. юга. Итак, направление S45W.
д. Положение точки P на азимуте 290 показано на
следующую схему.
Положение точки P равно 360 290 = 70 з.д. севера. Итак, направление N70W.
Основные термины
компас, стороны света точки, истинный пеленг, пеленг, направление, обычный подшипник
Измерение углов
Измерение угловКонцепция угла
Понятие угла — одно из важнейших понятий геометрии. Понятия равенства, суммы и разности углов важны и используются во всей геометрии, но предмет тригонометрии основан на измерении углов. Существуют две широко используемые единицы измерения углов. Более привычной единицей измерения являются градусы. Окружность разделена на 360 равных градусов, так что прямой угол равен 90°. Пока мы будем рассматривать только углы от 0° до 360°, но позже, в разделе о тригонометрических функциях, мы рассмотрим углы больше 360° и отрицательные углы. Градусы могут быть далее разделены на минуты и секунды, но это деление уже не так универсально, как раньше. Каждый градус делится на 60 равных частей, называемых минуты. Итак, семь с половиной градусов можно назвать 7 градусов и 30 минут, записав 7° 30′. Каждая минута далее делится на 60 равных частей, называемых 9.0034 секунды, и, например, 2 градуса 5 минут 30 секунд записывается как 2° 5′ 30″. Деление градусов на минуты и угловые секунды аналогично делению часов на минуты и секунды времени. |
Части градуса теперь обычно указываются в десятичном виде. Например, семь с половиной градусов теперь обычно записывают как 7,5°.
Когда для анализа нарисован один угол на плоскости xy , мы нарисуем его за стандартная позиция с вершиной в начале координат (0,0), одна сторона угла вдоль оси x , а другая сторона над осью x .
Радиан
Другой распространенной единицей измерения углов являются радианы. и Большинство калькуляторов можно настроить на использование углов, измеряемых в градусах или радианах. Убедитесь, что вы знаете, какой режим использует ваш калькулятор. |
Для этого измерения рассмотрим единичную окружность (окружность радиуса 1), центр которой является вершиной рассматриваемого угла. Тогда угол отсекает дугу окружности, и длина этой дуги является мерой угла в радианах. Легко конвертировать между измерением в градусах и измерением в радианах. Длина окружности всего круга 2 π , отсюда следует, что 360° равняется 2 π радиан. Следовательно,Краткая заметка об истории радианов
Хотя слово «радиан» было придумано Томасом Мьюиром и/или Джеймсом Томпсоном примерно в 1870 году, математики давно измеряли углы таким способом. Например, Леонард Эйлер (1707–1783) в своей книге « Элементы алгебры » прямо сказал, что углы измеряются длиной дуги, отсеченной на единичной окружности.
Это было необходимо, чтобы дать его знаменитую формулу с комплексными числами, которая связывает функции знака и косинуса с показательной функцией.где θ — это то, что позже было названо измерением угла в радианах. К сожалению, объяснение этой формулы выходит далеко за рамки этих заметок. Но для получения дополнительной информации о комплексных числах см. мой Краткий курс комплексных чисел.
Радианы и длина дуги
Альтернативное определение радианов иногда дается как отношение. Вместо того, чтобы взять единичную окружность с центром в вершине угла θ , возьмем любую окружность с центром в вершине угла. Тогда радианной мерой угла является отношение длины стягиваемой дуги к радиусу r окружности. Например, если длина дуги равна 3, а радиус окружности равен 2, то мера радиана равна 1,5. Причина, по которой это определение работает, заключается в том, что длина стягиваемой дуги пропорциональна радиусу окружности.
В частности, определение в терминах отношения дает ту же цифру, что и приведенная выше, с использованием единичного круга. Однако это альтернативное определение более полезно, поскольку его можно использовать для связи длин дуг с углами. Длина дуги равна радиусу r , умноженное на угол θ , где угол измеряется в радианах.
Например, дуга θ = 0,3 радиана в окружности радиусом r = 4 имеет длину 0,3 умножить на 4, то есть 1,2.
Радианы и площадь сектора
Сектором окружности называется та часть окружности, которая ограничена двумя радиусами и дугой окружности, соединяющей их концы. Площадь этого сектора легко вычислить по радиусу r окружности и угол θ между радиусами, если он измеряется в радианах. Поскольку площадь всего круга равна πr 2 , а сектор ко всему кругу относится как угол θ к 2 π , поэтомуУглы общие
Ниже приведена таблица общих углов как в градусах, так и в радианах.
Обратите внимание, что измерение в радианах дается как π . Его, конечно, можно было бы представить десятичным числом, но радианное измерение часто появляется с коэффициентом 9.0034 № .| Уголок | градусов | радиан |
|---|---|---|
| 90° | № /2 | |
| 60° | № /3 | |
| 45° | № /4 | |
| 30° | № /6 |
Упражнения
Эдвин С. Кроули написал книгу «Тысяча упражнений в плоской и сферической тригонометрии», Университет Пенсильвании, Филадельфия, 1914 г. Задачи этого краткого курса взяты из этого текста (но не все 1000 из них!) Он дал свои задачи с точностью до пяти знаков, поэтому учащимся пришлось поработать над их решением, и они использовали таблицы логарифмов, чтобы помочь в умножении и делении.
Студенты должны были уметь пользоваться таблицей синусов-косинусов, тангенсов, логарифмов, логарифмических синусоидальных и логарифмических таблиц. Теперь мы можем использовать калькуляторы! Это означает, что вы можете сосредоточиться на концепциях, а не на трудоемких вычислениях.Кроули использовал не десятичную запись для долей градуса, а минуты и секунды.
Каждый набор упражнений включает, во-первых, формулировки упражнений, во-вторых, несколько советов по решению упражнений и, в-третьих, ответы на упражнения.
1. Выразите следующие углы в радианах.
(а). 12 градусов 28 минут, то есть 12° 28′.
(б). 36° 12′.
2. Сократите следующие числа радианов до градусов, минут и секунд.
(а). 0,47623.
(б). 0,25412.
3. Зная угол a и радиус r, найти длину стягивающей дуги.
(а). a = 0° 17′ 48″, r = 6,2935.
(б). a = 121° 6′ 18″, r = 0,2163.
4. Зная длину дуги l и радиус r, найти угол, опирающийся на центр.
(а). l = 0,16296, r = 12,587.
(б). l = 1,3672, r = 1,2978.
5. Зная длину дуги l и угол a , на который она опирается в центре, найти радиус.
(а). a = 0° 44′ 30″, l = 0,032592.
(б). a = 60° 21′ 6″, l = .4572.
6. Найдите длину с точностью до дюйма дуги окружности 11 градусов 48,3 минуты, если радиус равен 3200 футов.
7. Железнодорожная кривая образует дугу окружности 9 градусов 36,7 минут, радиус от центральной линии пути составляет 2100 футов. Если ширина колеи 5 футов, найдите разницу в длине двух рельсов с точностью до полдюйма.
9. На сколько человек изменит широту, пройдя на север одну милю, если предположить, что Земля представляет собой сферу радиусом 3956 миль?
10.
Вычислите длину одной угловой минуты в футах по большому кругу Земли. Какова длина одной угловой секунды?
14. На окружности радиусом 5,782 метра длина дуги 1,742 метра. На какой угол он сужается в центре?
23. Известный воздушный шар диаметром 50 футов вытягивается из глаза под углом 8 1/2 минут. Как далеко это?
Подсказки
1. Чтобы преобразовать градусы в радианы, сначала преобразуйте количество градусов, минут и секунд в десятичную форму. Разделите количество минут на 60 и прибавьте к количеству градусов. Так, например, 12 ° 28 ‘это 12 + 28/60, что равно 12,467°. Далее умножить на π и разделите на 180, чтобы получить угол в радианах.
2. И наоборот, чтобы преобразовать радианы в градусы, разделите π и умножьте на 180. Таким образом, 0,47623, деленное на π и умноженное на 180, дает 27,286°. Вы можете преобразовать доли градуса в минуты и секунды следующим образом.
Умножьте дробь на 60, чтобы получить количество минут. Здесь 0,286 умножить на 60 равно 17,16, поэтому угол можно записать как 27° 17,16′. Затем возьмите любую оставшуюся долю минуты и снова умножьте на 60, чтобы получить количество секунд. Здесь 0,16 умножить на 60 примерно равно 10, поэтому угол можно также записать как 27° 17′ 10″.
3. Чтобы найти длину дуги, сначала переведите угол в радианы. Для 3(a) 0°17’48» составляет 0,0051778 радиан. Затем умножьте на радиус, чтобы найти длину дуги.
4. Чтобы найти угол, разделите его на радиус. Это дает вам угол в радианах. Это можно преобразовать в градусы, чтобы получить ответы Кроули.
5. Как упоминалось выше, радиан умножить на радиус = длине дуги, поэтому, используя буквы для этой задачи, ar = l, , но a необходимо сначала преобразовать из градусов в радианы. Итак, чтобы найти радиус r, сначала преобразуйте угол a в радианы, а затем разделите его на длину l дуги.
6. Длина дуги равна произведению радиуса на угол в радианах.
7. Помогает нарисовать фигуру. Радиус внешней направляющей равен 2102,5, а радиус внутренней направляющей равен 209.7.5.
9. У вас есть окружность радиусом 3956 миль и дуга этой окружности длиной 1 миля. Какой угол в градусах? (Средний радиус Земли был известен довольно точно в 1914 году. Посмотрите, сможете ли вы узнать, каким Эратосфен считал радиус Земли еще в третьем веке до нашей эры.)
10. Угловая минута равна 1/60 градуса. Преобразовать в радианы. Радиус равен 3956. Какова длина дуги?
14. Поскольку длина дуги равна радиусу, умноженному на угол в радианах, отсюда следует, что угол в радианах равен длине дуги, деленной на радиус. Радианы легко перевести в градусы.
23. Представьте, что диаметр воздушного шара является частью дуги окружности, в центре которой вы находитесь. (Это не совсем часть дуги, но довольно близко.
) Эта дуга имеет длину 50 футов. Вы знаете угол, так каков радиус этого круга?
Ответы
1. (а). 0,2176. (б). 0,6318.2. (а). 27° 17′ 10 дюймов (б). 14,56 ° = 14 °33,6′ = 14°33’36».
3. (а). 0,03259 (б). 2,1137 умножить на 0,2163 равно 0,4572.
4. (а). 0,16296/12,587 = 0,012947 радиан = 0° 44′ 30″.
(б). 1,3672/1,2978 = 1,0535
радианы = 60,360° = 60° 21,6′ = 60° 21′ 35″.
5. (а). л/год = 0,032592/0,01294 = 2,518.
(б). л/год = 0,4572/1,0533 = 0,4340.
6. ra = (3200′) (0,20604) = 659,31′ = 659′ 4 дюйма.
7. Угол a = 0,16776 радиан. Разница в длинах есть 2102.5 a – 1997.5 a , что равно 5 a. Таким образом, ответ равен 0,84 фута, что с точностью до дюйма равно 10 дюймам.
9. Угол = 1/3956 = 0,0002528 радиан = 0,01448° = 0,8690′ = 52,14″.
10.
Одна минута = 0,0002909 радиан. 1,15075 мили = 6076 футов. Поэтому одна секунда будет соответствовать 101,3 фута.
14. a = л/об = 1,742/5,782 = 0,3013 радиан = 17,26° = 17°16′.
23. Угол a равен 8,5′, что составляет 0,00247 радиана. Значит радиус равен r = л/год = 50/0,00247 = 20222′ = 3,83 мили, почти четыре мили.
О разрядах точности.
Кроули старается давать свои ответы примерно с той же точностью, что и данные в вопросах. Это важно, особенно сейчас, когда у нас есть калькуляторы. Например, в задаче 1 исходная точка равна 12°28′, что имеет точность около четырех знаков, поэтому ответ 0,2176 также должен быть дан с точностью только до четырех знаков. (Обратите внимание, что начальные нули не учитываются при подсчете цифр точности.) Ответ 0,21758438 предполагает восемь цифр точности, и это может ввести в заблуждение, поскольку данная информация не была такой точной. Другой пример см.
Leave A Comment