2+n-72)=1/(n+9)Тригонометрический круг(окружность): синус, косинус, тангенс в таблице
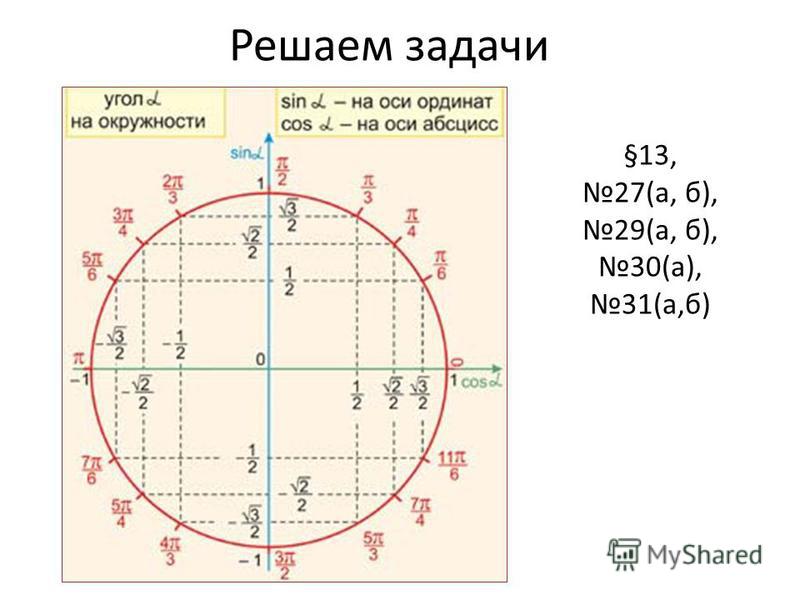
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.
Вот что мы видим на этом рисунке:
- Перевод градусов в радианы и наоборот. Полный круг содержит градусов, или радиан.
- Значения синусов и косинусов основных углов. Помним, что значение косинуса угла мы находим на оси , а значение синуса — на оси .
- И синус, и косинус принимают значения от до .
- Значение тангенса угла тоже легко найти — поделив на . А чтобы найти котангенс — наоборот, косинус делим на синус.
- Знаки синуса, косинуса, тангенса и котангенса.
- Синус — функция нечётная, косинус — чётная.
- Тригонометрический круг поможет увидеть, что синус и косинус — функции периодические. Период равен .
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси против часовой стрелки.
Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .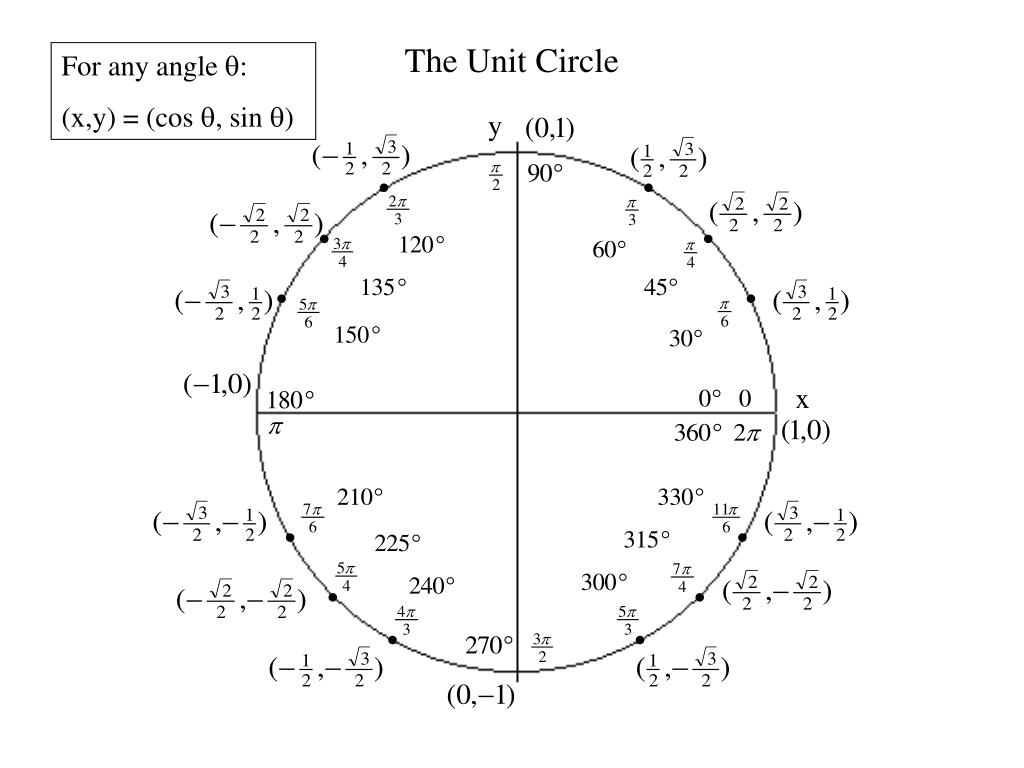
Например:
Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:
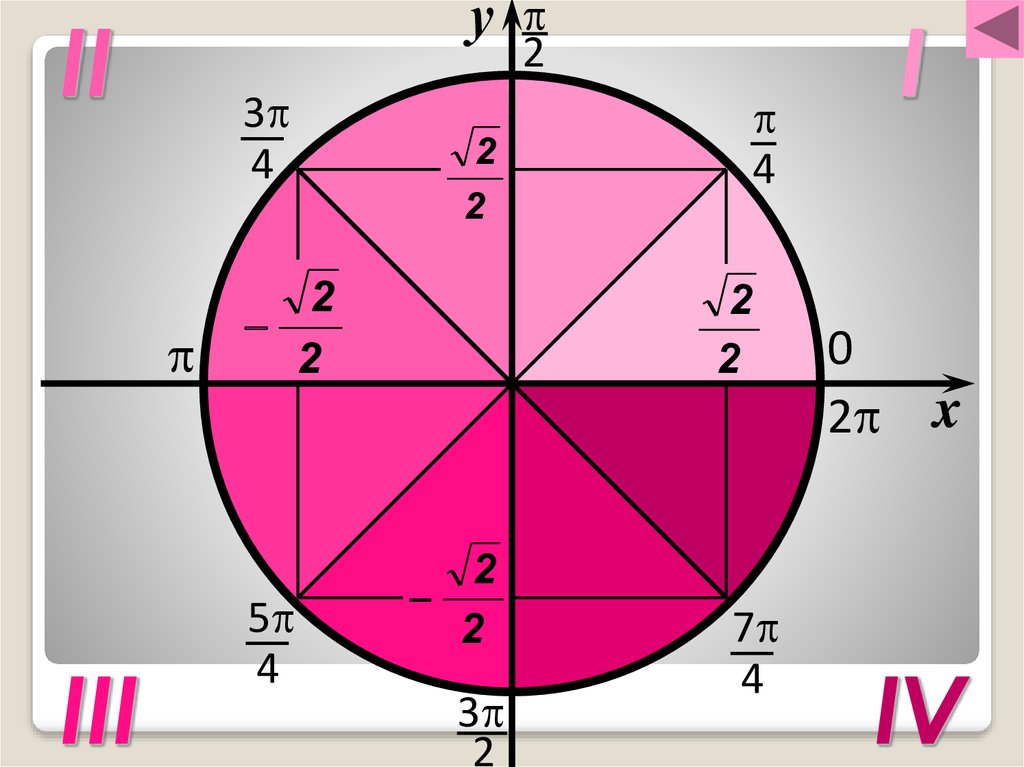
Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный.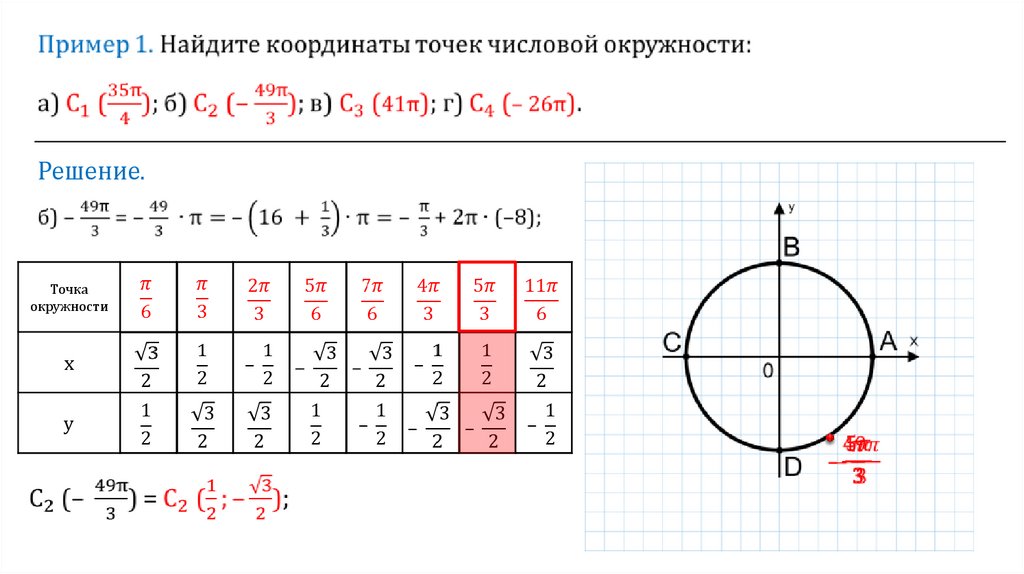
Легко заметить, что
,
.
Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:
,
,
где — целое число.
То же самое можно записать в радианах:
,
.
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения.
По определению:
В результате получим следующую таблицу.
| 0 | |||||||||
| 0 | не существует | 0 | |||||||
| не существует | 0 | не существует |
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Тригонометрический круг: вся тригонометрия на одном рисунке» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена: 09.03.2023
Sin 3pi — Найдите значение Sin 3pi
LearnPracticeDownload
Значение sin 3pi равно 0 . Sin 3pi радиан в градусах записывается как sin ((3π) × 180°/π), то есть sin (540°). В этой статье мы обсудим методы определения значения sin 3pi на примерах.
- Sin 3pi: 0
- Sin (-3pi): 0
-
Каково значение Sin 3pi?
Значение sin 3pi равно 0.
Sin 3pi также можно выразить с помощью эквивалента заданного угла (3pi) в градусах (540°).
Мы знаем, используя преобразование радиан в градусы, θ в градусах = θ в радианах × (180°/pi)
⇒ 3pi радиан = 3pi × (180°/pi) = 540° или 540 градусов
∴ sin 3pi = sin 3π = sin(540°) = 0
Объяснение:
Для sin 3pi угол 3pi > 2pi. Мы можем представить sin 3pi как sin(3pi mod 2pi) = sin(pi). Для sin 3pi угол 3pi лежит на отрицательной оси x. Таким образом, значение sin 3pi = 0
⇒ sin 3pi = sin 5pi = sin 7pi и так далее.
Примечание: Поскольку синус является нечетной функцией, значение sin(-3pi) = -sin(3pi) = 0. , Мы можем найти значение sin 3pi по:
- Используя Unit Circle
- Использование тригонометрических функций
Sin 3pi с использованием единичного круга
Чтобы найти значение sin 3π с помощью единичного круга, представьте 3pi в форме (1 × 2pi) + pi [∵ 3pi>2pi] ∵ синус — периодическая функция, sin 3pi = sin Пи.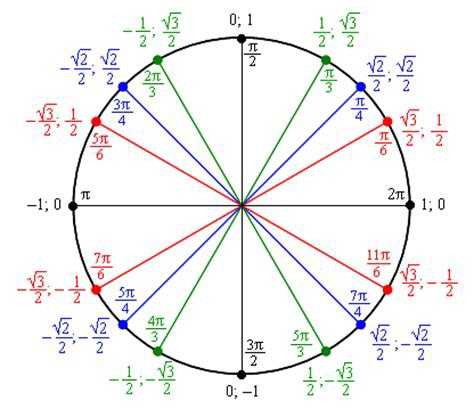
- Поверните «r» против часовой стрелки, чтобы сформировать угол пи или 3 пи с положительной осью x.
- Синус 3pi равен координате y(0) точки пересечения (-1, 0) единичной окружности и r.
Отсюда значение sin 3pi = y = 0
Sin 3pi в терминах тригонометрических функций
Используя формулы тригонометрии, мы можем представить sin 3pi как:
- ± √(1-cos²(3pi))
- ± тангенс(3pi)/√(1 + тангенс²(3pi))
- ± 1/√(1 + раскладушка²(3pi))
- ± √(сек²(3pi) — 1)/сек(3pi)
- 1/косек(3pi)
Примечание: Поскольку 3pi лежит на отрицательной оси x, окончательное значение sin 3pi равно 0.
Мы можем использовать тригонометрические тождества для представления sin 3pi в виде
- sin(pi — 3pi) = sin( -2пи)
- -sin(pi + 3pi) = -sin 4pi
- cos(pi/2 — 3pi) = cos(-5pi/2)
- -cos(pi/2 + 3pi) = -cos 7pi/2
☛ Также проверьте:
- кроватка 4pi/3
- рыжевато-коричневый 5pi/4
- cos 11pi/4
- , потому что 13pi/12
- кроватка пи/2
- потому что 7pi/6
Примеры использования Sin 3pi
Пример 1: Используя значение sin 3pi, найдите: (1-cos²(3pi)).
Решение:
⇒ (1-cos²(3pi)) = 0Пример 2. Найдите значение sin(3pi), если cos(3pi) равно -1 и tan 3pi = 0.
Решение:
Так как tan 3pi = sin 3pi/cos 3pi
⇒ sin 3pi = 0Пример 3. Найдите значение 2 × (sin(3pi/2) cos(3pi/2)). [Подсказка: используйте sin 3pi = 0]
Решение:
Используя формулу sin 2a,
2 sin(3pi/2) cos(3pi/2) = sin(2 × 3pi/2) = sin 3pi
∵ sin 3pi = 0
⇒ 2 × (sin(3pi/2) cos(3pi/2)) = 0
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.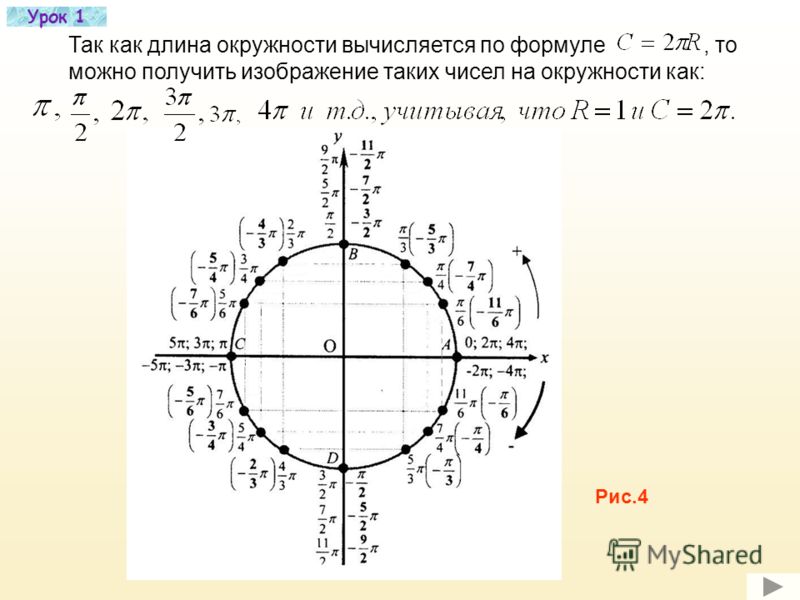
Запишитесь на бесплатный пробный урок
Часто задаваемые вопросы о Sin 3pi
Что такое Sin 3pi?
Sin 3pi — это значение тригонометрической функции синуса для угла, равного 3pi в радианах. Значение sin 3pi равно 0.
Каково значение Sin 3pi в пересчете на Cos 3pi?
Используя тригонометрические тождества, мы можем записать sin 3pi через cos 3pi как sin(3pi) = √(1-cos²(3pi)). Здесь значение cos 3pi равно -1.
Как найти Sin 3pi с точки зрения других тригонометрических функций?
Используя формулу тригонометрии, значение sin 3π может быть выражено через другие тригонометрические функции следующим образом:
- ± √(1-cos²(3pi))
- ± тангенс(3pi)/√(1 + тангенс²(3pi))
- ± 1/√(1 + раскладушка²(3pi))
- ± √(сек²(3pi) — 1)/сек(3pi)
- 1/косек(3pi)
☛ Также проверьте: таблицу тригонометрии
Каково точное значение sin 3pi?
Точное значение sin 3pi равно 0.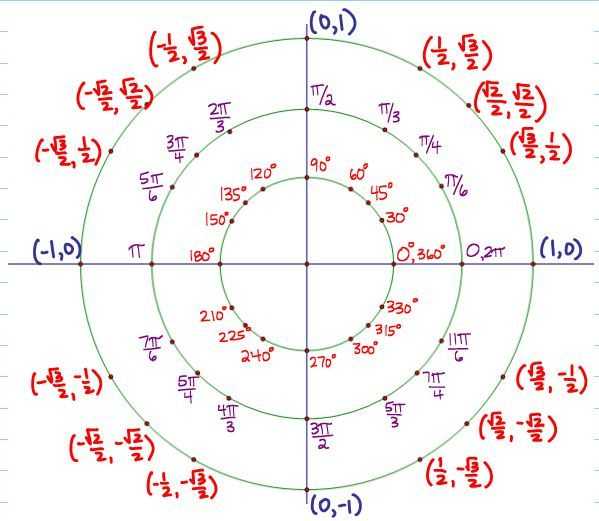
Как найти значение Sin 3pi?
Значение sin 3pi можно вычислить, построив угол 3π радиан с осью x и затем найдя координаты соответствующей точки (-1, 0) на единичной окружности. Значение sin 3pi равно координате y (0). ∴ sin 3pi = 0.
Скачать БЕСПЛАТНО учебные материалы
Тригонометрия
Рабочие листы по математике и
визуальные учебные программы
)/3
Leave A Comment