Mathway | Популярные задачи

1 Найти точное значение sin(30)
2 Найти точное значение sin(45)
3 Найти точное значение sin(60)
4 Найти точное значение sin(30 град. )
5 Найти точное значение sin(60 град. )
6 Найти точное значение tan(30 град. )
7 Найти точное значение arcsin(-1)
8 Найти точное значение sin(pi/6)
9 Найти точное значение cos(pi/4)
10 Найти точное значение sin(45 град. )
11 Найти точное значение sin(pi/3)
12 Найти точное значение arctan(-1)
13 Найти точное значение cos(45 град. )
14 Найти точное значение cos(30 град. )
15 Найти точное значение tan(60)
16 Найти точное значение csc(45 град. )
17 Найти точное значение tan(60 град. )
18 Найти точное значение sec(30 град. )
19 Преобразовать из радианов в градусы (3pi)/4
20 График y=sin(x)
21 Преобразовать из радианов в градусы pi/6
22 Найти точное значение cos(60 град. )
23 Найти точное значение cos(150)
24 Найти точное значение tan(45)
25 Найти точное значение sin(30)
26 Найти точное значение sin(60)
27 Найти точное значение cos(pi/2)
28 Найти точное значение tan(45 град. )
29 График y=sin(x)
30 Найти точное значение arctan(- квадратный корень 3)
31 Найти точное значение csc(60 град. )
32 Найти точное значение sec(45 град. )
33 Найти точное значение csc(30 град. )
34 Найти точное значение sin(0)
35 Найти точное значение sin(120)
36 Найти точное значение cos(90)
37 Преобразовать из радианов в градусы pi/3
38 Найти точное значение sin(45)
39 Найти точное значение tan(30)
40 Преобразовать из градусов в радианы 45
41 Найти точное значение tan(60)
42 Упростить квадратный корень x^2
43 Найти точное значение cos(45)
44 Упростить sin(theta)^2+cos(theta)^2
45 Преобразовать из радианов в градусы pi/6
46 Найти точное значение cot(30 град. 4)
56 Найти точное значение sin((3pi)/4)
57 Найти точное значение tan(pi/2)
58 Найти точное значение sin(300)
59 Найти точное значение cos(30)
60 Найти точное значение cos(60)
61 Найти точное значение cos(0)
62 Найти точное значение arctan( квадратный корень 3)
63 Найти точное значение cos(135)
64 Найти точное значение cos((5pi)/3)
65 Найти точное значение cos(210)
66 Найти точное значение sec(60 град. )
67 Найти точное значение sin(300 град. )
68 Преобразовать из градусов в радианы 135
69 Преобразовать из градусов в радианы 150
70 Преобразовать из радианов в градусы (5pi)/6
71 Преобразовать из радианов в градусы (5pi)/3
72 Преобразовать из градусов в радианы 89 град.
73 Преобразовать из градусов в радианы 60
74 Найти точное значение sin(135 град. 8)
80 Найти точное значение sin(225)
81 Найти точное значение sin(240)
82 Найти точное значение cos(150 град. )
83 Найти точное значение tan(45)
84 Вычислить sin(30 град. )
85 Найти точное значение sec(0)
86 Упростить arcsin(-( квадратный корень 2)/2)
87 Найти точное значение cos((5pi)/6)
88 Найти точное значение csc(30)
89 Найти точное значение arcsin(( квадратный корень 2)/2)
90 Найти точное значение tan((5pi)/3)
91 Найти точное значение tan(0)
92 Вычислить sin(60 град. )
93 Найти точное значение arctan(-( квадратный корень 3)/3)
94 Преобразовать из радианов в градусы (3pi)/4
95 Вычислить arcsin(-1)
96 Найти точное значение sin((7pi)/4)
97 Найти точное значение arcsin(-1/2)
98 Найти точное значение sin((4pi)/3)
99 Найти точное значение csc(45)
100 Найти точное значение cos((4pi)/3)

Уравнения в целых числах (диофантовы уравнения) / math5school.

ru

 

 

Немного теории

Уравнения в целых числах – это алгебраические уравнения с двумя или более неизвестными переменными и целыми коэффициентами. Решениями такого уравнения являются все целочисленные (иногда натуральные или рациональные) наборы значений неизвестных переменных, удовлетворяющих этому уравнению. Такие уравнения ещё называют диофантовыми, в честь древнегреческого математика Диофанта Александрийского, который исследовал некоторые типы таких уравнений ещё до нашей эры.

Современной постановкой диофантовых задач мы обязаны французскому математику Ферма. Именно он поставил перед европейскими математиками вопрос о решении неопределённых уравнений только в целых числах. Наиболее известное уравнение в целых числах – великая теорема Ферма: уравнение

xn + yn = zn

не имеет ненулевых рациональных решений для всех натуральных n > 2.

Теоретический интерес к уравнениям в целых числах достаточно велик, так как эти уравнения тесно связаны со многими проблемами теории чисел.

В 1970 году ленинградский математик Юрий Владимирович Матиясевич доказал, что общего способа, позволяющего за конечное число шагов решать в целых числах произвольные диофантовы уравнения, не существует и быть не может. Поэтому следует для разных типов уравнений выбирать собственные методы решения.

При решении уравнений в целых и натуральных числах можно условно выделить следующие методы:

  • способ перебора вариантов;

  • применение алгоритма Евклида;

  • представление чисел в виде непрерывных (цепных) дробей;

  • разложения на множители;

  • решение уравнений в целых числах как квадратных (или иных) относительно какой-либо переменной;

  • метод остатков;

  • метод бесконечного спуска.

 

Задачи с решениями

1. Решить в целых числах уравнение x2 – xy – 2y2 = 7.

Решение

Запишем уравнение в виде (x – 2y)(x + y) = 7.

Так как х, у – целые числа, то находим решения исходного уравнения, как решения следующих четырёх систем:

1) x – 2y = 7, x + y = 1;

2) x – 2y = 1, x + y = 7;

3) x – 2y = –7, x + y = –1;

4) x – 2y = –1, x + y = –7.

Решив эти системы, получаем решения уравнения: (3; –2), (5; 2), (–3; 2) и (–5; –2).

Ответ: (3; –2), (5; 2), (–3; 2), (–5; –2).

 

2. Решить в целых числах уравнение:

а) 20х + 12у = 2013;

б) 5х + 7у = 19;

в) 201х – 1999у = 12.

Решение

а) Поскольку при любых целых значениях х и у левая часть уравнения делится на два, а правая является нечётным числом, то уравнение не имеет решений в целых числах.

Ответ: решений нет.

 

б) Подберём сначала некоторое конкретное решение. В данном случае, это просто, например,

x0 = 1, y0 = 2.

Тогда

5x0 + 7y0 = 19,

откуда

5(х – x0) + 7(у – y0) = 0,

5(х – x0) = –7(у – y0).

Поскольку числа 5 и 7 взаимно простые, то

х – x0 = 7k, у – y0 = –5k.

Значит, общее решение:

х = 1 + 7k, у = 2 – 5k,

где k – произвольное целое число.

Ответ: (1+7k; 2–5k), где k – целое число.

 

в) Найти некоторое конкретное решение подбором в данном случае достаточно сложно. Воспользуемся алгоритмом Евклида для чисел 1999 и 201:

НОД(1999, 201) = НОД(201, 190) = НОД(190, 11) = НОД(11, 3) = НОД(3 , 2) = НОД(2, 1) = 1.

Запишем этот процесс в обратном порядке:

1 = 2 – 1 = 2 – (3 – 2) = 2·2 – 3 = 2· (11 – 3·3) – 3 = 2·11 – 7·3 = 2·11 – 7(190 – 11·17) =

= 121·11 – 7·190 = 121(201 – 190) – 7·190 = 121·201 – 128·190 =

= 121·201 – 128(1999 – 9·201) = 1273·201 – 128·1999.

Значит, пара (1273, 128) является решением уравнения 201х – 1999у = 1. Тогда пара чисел

x0

= 1273·12 = 15276, y0 = 128·12 = 1536

является решением уравнения 201х – 1999у = 12.

Общее решение этого уравнения запишется в виде

х = 15276 + 1999k, у = 1536 + 201k, где k – целое число,

или, после переобозначения (используем, что 15276 = 1283 + 7·1999, 1536 = 129 + 7·201),

х = 1283 + 1999n, у = 129 + 201n, где n – целое число.

Ответ: (1283+1999n, 129+201n), где n – целое число.

 

3. Решить в целых числах уравнение:

а) x3 + y3 = 3333333;

б) x3 + y3 = 4(x2y + xy2 + 1).

Решение

а) Так как x3 и y3 при делении на 9 могут давать только остатки 0, 1 и 8 (смотрите таблицу в разделе «Делимость целых чисел и остатки»), то x

3 + y3 может давать только остатки 0, 1, 2, 7 и 8. Но число 3333333 при делении на 9 даёт остаток 3. Поэтому исходное уравнение не имеет решений в целых числах.

Ответ: целочисленных решений нет.

 

б) Перепишем исходное уравнение в виде (x + y)3 = 7(x2y + xy2) + 4. Так как кубы целых чисел при делении на 7 дают остатки 0, 1 и 6, но не 4, то уравнение не имеет решений в целых числах.

Ответ: целочисленных решений нет.

 

4. Решить

а) в простых числах уравнение х2 – 7х – 144 = у2 – 25у;

б) в целых числах уравнение x + y = x2 – xy + y2.

Решение

а) Решим данное уравнение как квадратное относительно переменной у. Получим

у = х + 9 или у = 16 – х.

Поскольку при нечётном х число х + 9 является чётным, то единственной парой простых чисел, которая удовлетворяет первому равенству, является (2; 11).

Так как х, у – простые, то из равенства у = 16 – х имеем

2 х 16, 2 у 16.

С помощью перебора вариантов находим остальные решения: (3; 13), (5; 11), (11; 5), (13; 3).

Ответ: (2; 11), (3; 13), (5; 11), (11; 5), (13; 3).

 

б) Рассмотрим данное уравнение как квадратное уравнение относительно x:

x2 – (y + 1)x + y2 – y = 0. 

Дискриминант этого уравнения равен –3y2 + 6y + 1. Он положителен лишь для следующих значений у: 0, 1, 2. Для каждого из этих значений из исходного уравнения получаем квадратное уравнение относительно х, которое легко решается.

Ответ: (0; 0), (0; 1), (1; 0), (1; 2), (2; 1), (2; 2).

 

5. Существует ли бесконечное число троек целых чисел x, y, z таких, что x2 + y2 + z2 = x3 + y3 + z3 ?

Решение

Попробуем подбирать такие тройки, где у = –z. Тогда y3 и z3 будут всегда взаимно уничтожаться, и наше уравнение будет иметь вид

x2 + 2y2 = x3

или, иначе,

x2(x–1) = 2y2.

Чтобы пара целых чисел (x; y) удовлетворяла этому условию, достаточно, чтобы число x–1 было удвоенным квадратом целого числа. Таких чисел бесконечно много, а именно, это все числа вида 2n2+1. Подставляя в x2(x–1) = 2y2 такое число, после несложных преобразований получаем:

y = xn = n(2n2+1) = 2n3+n.

Все тройки, полученные таким образом, имеют вид (2n2+1; 2n3+n; –2n3– n).

Ответ: существует.

 

6. Найдите такие целые числа x, y, z, u, что x2 + y2 + z2 + u2 = 2xyzu.

Решение

Число x2 + y2 + z2 + u2 чётно, поэтому среди чисел x, y, z, u чётное число нечётных чисел.

Если все четыре числа x, y, z, u нечётны, то x2 + y2 + z2 + u2 делится на 4, но при этом 2xyzu не делится на 4 – несоответствие.

Если ровно два из чисел x, y, z, u нечётны, то x2 + y2 + z2 + u2 не делится на 4, а 2xyzu делится на 4 – опять несоответствие.

Поэтому все числа x, y, z, u чётны. Тогда можно записать, что

x = 2x1, y = 2y1, z = 2z1, u = 2u1,

и исходное уравнение примет вид

x12 + y12 + z12 + u12 = 8x1y1z1u1.

Теперь заметим, что (2k + 1)2 = 4k(k + 1) + 1 при делении на 8 даёт остаток 1. Поэтому если все числа x1, y1, z1, u1 нечётны, то x12 + y12 + z12 + u12 не делится на 8. А если ровно два из этих чисел нечётно, то x12 + y12 + z12 + u12 не делится даже на 4. Значит,

x1 = 2x2, y1 = 2y2, z1 = 2z2, u1 = 2u2,

и мы получаем уравнение

x22 + y22 + z22 + u22 = 32x2y2z2u2.

Снова повторив те же самые рассуждения, получим, что x, y, z, u делятся на 2n при всех натуральных n, что возможно лишь при x = y = z = u = 0.

Ответ: (0; 0; 0; 0).

 

7. Докажите, что уравнение

(х – у)3 + (y – z)3 + (z – x)3 = 30

не имеет решений в целых числах.

Решение

Воспользуемся следующим тождеством:

(х – у)3 + (y – z)3 + (z – x)3 = 3(х – у)(y – z)(z – x).

Тогда исходное уравнение можно записать в виде

(х – у)(y – z)(z – x) = 10.

Обозначим a = x – y, b = y – z, c = z – x и запишем полученное равенство в виде

abc = 10.

Кроме того очевидно, a + b + c = 0. Легко убедиться, что с точностью до перестановки из равенства abc = 10 следует, что числа |a|, |b|, |c| равны либо 1, 2, 5, либо 1, 1, 10. Но во всех этих случаях при любом выборе знаков a, b, c сумма a + b + c отлична от нуля. Таким образом, исходное уравнение не имеет решений в целых числах.

 

8. Решить в целых числах уравнение 1! + 2! + . . . + х! = у2.

Решение

Очевидно, что

если х = 1, то у2 = 1,

если х = 3, то у2 = 9.

Этим случаям соответствуют следующие пары чисел:

х1 = 1, у1 = 1;

х2 = 1, у2 = –1;

х3 = 3, у3 = 3;

х4 = 3, у4 = –3.

Заметим, что при х = 2 имеем 1! + 2! = 3, при х = 4 имеем 1! + 2! + 3! + 4! = 33 и ни 3, ни 33 не являются квадратами целых чисел. Если же х > 5, то, так как

5! + 6! + .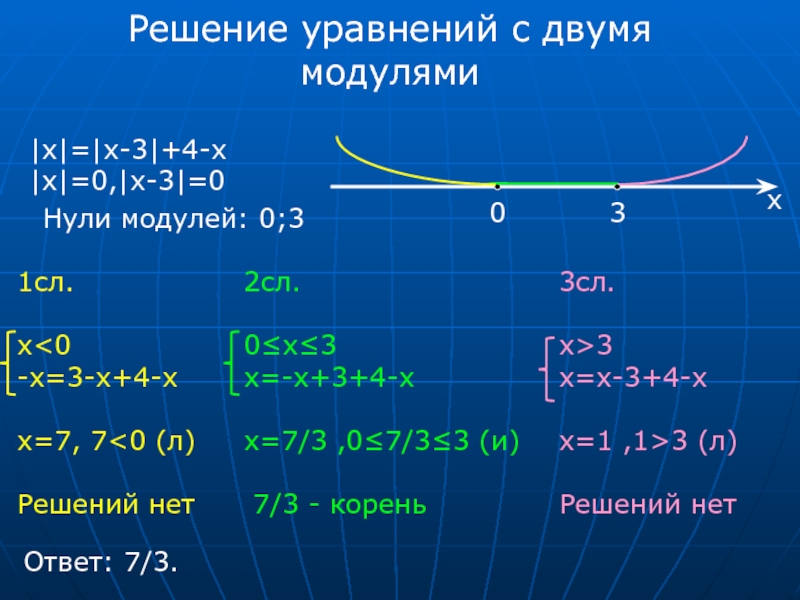 . . + х! = 10n,

можем записать, что

1! + 2! + 3! + 4! + 5! + . . . + х! = 33 + 10n.

Так как 33 + 10n – число, оканчивающееся цифрой 3, то оно не является квадратом целого числа.

Ответ: (1; 1), (1; –1), (3; 3), (3; –3).

 

9. Решите следующую систему уравнений в натуральных числах:

a3 – b3 – c3 = 3abc,  a2 = 2(b + c).

Решение

Так как

3abc > 0, то a3 > b3 + c3;

таким образом имеем

b

Складывая эти неравенства, получим, что

b + c

С учётом последнего неравенства, из второго уравнения системы получаем, что

a2

Но второе уравнение системы также показывает, что а – чётное число. Таким образом, а = 2, b = c = 1.

Ответ: (2; 1; 1)

 

10. Найти все пары целых чисел х и у, удовлетворяющих уравнению х2 + х = у4 + у3 + у2 + у.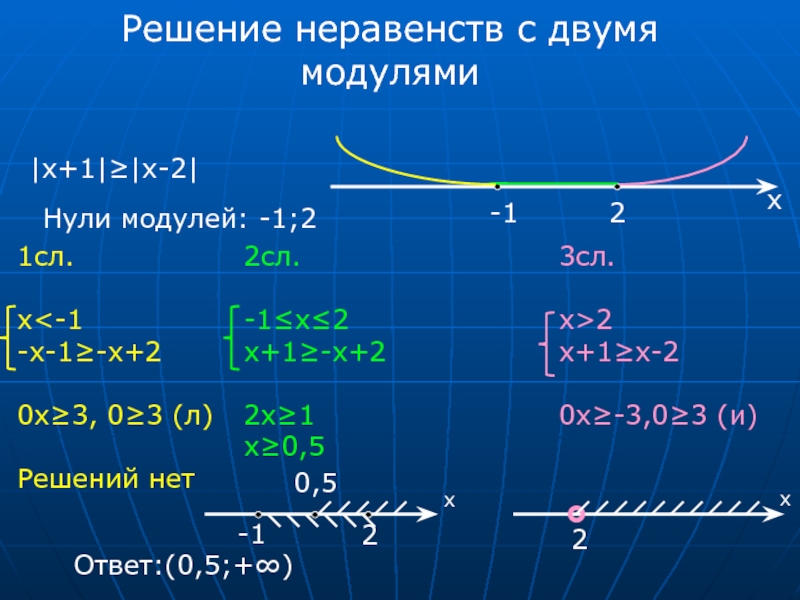

Решение

Разложив на множители обе части данного уравнения, получим:

х(х + 1) = у(у + 1)(у2 + 1),

или

х(х + 1) = (у2 + у)(у2 + 1)

Такое равенство возможно, если левая и правая части равны нулю, или представляют собой произведение двух последовательных целых чисел. Поэтому, приравнивая к нулю те или иные множители, получим 4 пары искомых значений переменных:

х1 = 0, у1 = 0;

х2 = 0, у2 = –1;

х3 = –1, у3 = 0;

х4 = –1, у4 = –1.

Произведение (у2 + у)(у2 + 1) можно рассматривать как произведение двух последовательных целых чисел, отличных от нуля, только при у = 2. Поэтому х(х + 1) = 30, откуда х5 = 5, х6 = –6. Значит, существуют ещё две пары целых чисел, удовлетворяющих исходному уравнению:

х5 = 5, у5 = 2;

х6 = –6, у6 = 2.

Ответ: (0; 0), (0; –1), (–1; 0), (–1; –1), (5; 2), (–6; 2.)

 

Задачи без решений

1. Решить в целых числах уравнение:

а) ху = х + у + 3;

б) х2 + у2 = х + у + 2.

 

2. Решить в целых числах уравнение:

а) х3 + 21у2 + 5 = 0;

б) 15х2 – 7у2 = 9.

 

3. Решить в натуральных числах уравнение:

а) 2х + 1 = у2;

б) 3·2х + 1 = у2.

 

4. Доказать, что уравнение х3 + 3у3 + 9z3 = 9xyz в рациональных числах имеет единственное решение

x = y = z = 0.

 

5. Доказать, что уравнение х2 + 5 = у3 в целых числах не имеет решений.

 

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

      Существует ряд уравнений, которые удается решить при помощи сведения их к квадратным уравнениям.

      К таким уравнениям, в частности, относятся уравнения следующих типов:

      Замечание. Уравнения, носящие название «Биквадратные уравнения», относятся к типу «Трехчленные уравнения».

Возвратные (симметричные) уравнения 3-ей степени

      Возвратным уравнением 3-ей степени называют уравнение вида

ax3 + bx2 + bx + a = 0,(1)

где a, b – заданные числа.

      Решение уравнения (1) осуществляется при помощи разложения левой части уравнения (1) на множители:

      Для завершения решения уравнения (1) остаётся лишь решить квадратное уравнение

ax2 + (b – a) x + a = 0.

      Пример 1. Решить уравнение

2x3 + 7x2 + 7x + 2 = 0.(2)

      Решение. Разложим левую часть уравнения (2) на множители:

      Ответ:.

Возвратные (симметричные) уравнения 4-ой степени

      Возвратными (симметричными) уравнениями 4-ой степени называют уравнения вида

ax4 + bx3 + cx2 +
+ bx + a = 0,		(3)

а также уравнения вида

ax4 + bx3 + cx2–
– bx + a = 0,		(4)

где a, b, c – заданные числа.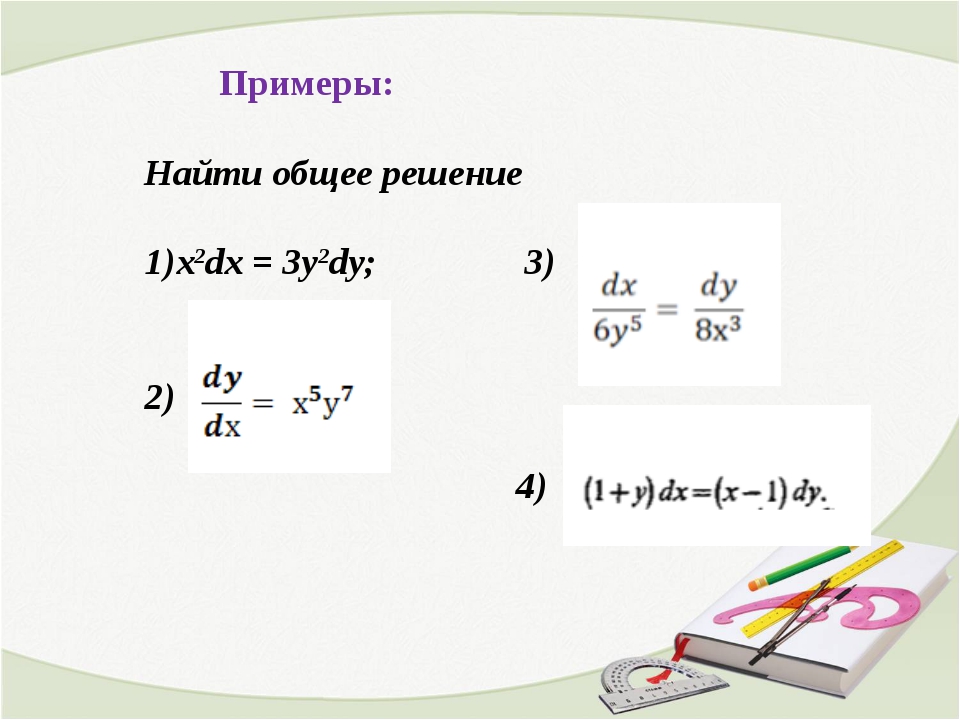

      Для того, чтобы решить возвратное уравнение (3), разделим его на  x2. В результате получится уравнение

(5)

      Преобразуем левую часть уравнения (5):

      В результате этого преобразования уравнение (5) принимает вид

(6)

      Если теперь обозначить

(7)

то уравнение (6) станет квадратным уравнением:

ay2 + by + c – 2a = 0.(8)

     Найдем корни уравнения (8), а после этого, подставив каждый из найденных корней в равенство (7), решим полученное уравнение относительно  x.

      Описание метода решения уравнений вида (3) завершено.

      Для того, чтобы решить возвратное уравнение (4), разделим его на  x2. В результате получится уравнение

(9)

      Преобразуем левую часть уравнения (9):

      В результате этого преобразования уравнение (9) принимает вид

(10)

      Если теперь обозначить

(11)

то уравнение (10) станет квадратным уравнением:

ay2 + by + c + 2a = 0.(12)

      Найдем корни уравнения (13), а после этого, подставив каждый из найденных корней в равенство (11), решим полученное уравнение относительно  x.

      Описание метода решения уравнений вида (4) завершено.

      Пример 2. Решить уравнение

2x4 – 3x3 – x2 –
– 3x + 2 = 0.		(13)

      Решение. Уравнение (13) является возвратным и относится к виду (3). Разделим его на  x2. В результате получится уравнение

(14)

      Преобразуем левую часть уравнения (14):

      В результате этого преобразования уравнение (14) принимает вид

(15)

      Если теперь обозначить

(16)

то уравнение (15) станет квадратным уравнением:

2y2 – 3y – 5 = 0.(17)

      Решим уравнение (17):

(18)

      В первом случае из равенства (16) получаем уравнение:

которое решений не имеет.

      Во втором случае из равенства (16) получаем:

      Ответ:

      Пример 3. Решить уравнение

6x4 – 25x3 + 12x2 +
+ 25x + 6 = 0.		(19)

      Решение. Уравнение (19) является возвратным и относится к виду (4). Разделим его на  x2. В результате получится уравнение

(20)

      Преобразуем левую часть уравнения (20):

      В результате этого преобразования уравнение (20) принимает вид

(21)

      Если теперь обозначить

(22)

то уравнение (21) станет квадратным уравнением:

6y2 – 25y + 24 = 0.(23)

      Решим уравнение (23):

(24)

      В первом случае из равенства (22) получаем:

      Во втором случае из равенства (22) получаем:

      Ответ:

Обобщенные возвратные уравнения 4-ой степени

      Обобщенным возвратным уравнением 4-ой степени назовём уравнение вида

(25)

где  a, b, c, d  – заданные числа.

      Для того, чтобы решить уравнение (25), разделим его на  x2. В результате получится уравнение

(26)

      Преобразуем левую часть уравнения (26):

      В результате этого преобразования уравнение (26) принимает вид

      Если теперь обозначить

(28)

то уравнение (27) станет квадратным уравнением:

(29)

      Найдем корни уравнения (29), а после этого, подставив каждый из найденных корней в равенство (28), решим полученное уравнение относительно  x.

      Описание метода решения уравнений вида (25) завершено.

      Пример 4. Решить уравнение

2x4 – 15x3 + 35x2 –
– 30 x + 8 = 0.		(30)

      Решение. Введем для коэффициентов уравнения (30) следующие обозначения

a = 2 ,      b =– 15,      
c = 35,       d = – 30,

и найдем значение выражения

      Поскольку

то уравнение (30) является обобщенным возвратным уравнением 4-ой степени. В соответствии с изложенным выше, разделим его на x2. В результате получится уравнение

(31)

      Преобразуем левую часть уравнения (31):

      В результате этого преобразования уравнение (31) принимает вид

(32)

      Если теперь обозначить

(33)

то уравнение (32) станет квадратным уравнением:

2y2 – 15y + 27 = 0. 2-7x+4)=0

Решите уравнение

1. Найдём область определения уравнения, то есть все значения х, при которых выражения в уравнении будут иметь смысл.

Известно, что подкоренное выражение должно иметь неотрицательное значение, значит:

*Обратите внимание, что 1 и 4/3 это радианы.

В градусах — учитывая, что 1 радиан  ≈ 57,30 получим:

 

То есть можем записать область определения в виде:

То есть из всей области определения «выпадает» только интервал (57,30; 76,40).

2. Решаем уравнение.

Произведение двух выражений равно нулю, если хотя бы одно из них равно нулю, а другое при этом не теряет смысла, значит:

 

Решением квадратного уравнения будут корни 1 и 4/3. Они принадлежат области определения х и являются решением.

Рассмотрим корни:

Мы установили, что корни принадлежащие интервалу  57,30<х<76,40 не являются решением уравнения.

Такой корень существует только один:

Получается он при n = 0.

*Обратите внимание, что существует он только для

Для второго корня  n может быть равно нулю, получится:

Корень равный 120 градусам принадлежит области определения. Поэтому ответ нужно записывать внимательно. Если запишем в виде:

То корень 1200 получится исключённым, а это ошибка.

Ответ:

*Результат второго корня записали с коэффициентом k. Это допустимо и правильно. Так  мы исключили путаницу и ошибку при записи ответа.

Например при такой записи корень равный 120 градусам будет потерян:

Или можно записать в такой форме:

*Смысл простой. Нужно не допустить того, чтобы у нас  выпал даже один корень.

Вопрос! Если мы решая уравнение с синусом используем объёдинённую формулу вида:

То тогда как можно записать ответ?

Ответ будет записан в виде:  

В данном случае через n≠0 исключается корень  х = 600.

Общий ответ в таком случае запишем так:

Уравнение с тремя неизвестными | Математика

62. Одно уравнение с тремя неизвестными. Пусть имеем уравнение

3x + 4y – 2z = 11.

На это уравнение можно смотреть, как на запись задачи: найти числовые значения для x, y и z, чтобы трехчлен 3x + 4y – 2z оказался равен числу 11. Таким образом это уравнение является уравнением с тремя неизвестными. Так как мы можем решить одно уравнение с одним неизвестным, то уже с первого взгляда возникает мысль, что 2 неизвестных здесь являются как бы лишними, и им можно давать произвольные значения. И действительно, если, например, взять для y число 3 и для z число 5, то получим уравнение с одним неизвестным:

3x + 12 – 10 = 11,

откуда

3x = 9 и x = 3.

Возьмем другие числа для y и z. Например, пусть

y = –1 и z = 0.

Тогда получим уравнение:

3x – 4 = 11,

откуда

3x = 15 и x = 5.

Продолжая эту работу дальше, мы придем к заключению:

Одно уравнение с тремя неизвестными имеет бесконечно много решений, и для получения их надо двум неизвестным давать произвольные значения.

Результаты этой работы можно записать в таблице (мы, кроме двух уже найденных решений, записали в ней еще одно, которое получится, если положить y = –1 и z = –2):

Так как для y и для z мы берем произвольные значения, то они являются независимыми переменными, а x является зависимым (от них) переменным. Другими словами: x является функциею от y и z.

Чтобы удобнее получать решения этого уравнения, можно определить из него x через y и z. Получим:

3x + 4y – 2z = 11; 3x = 11 – 4y + 2z;
x = (11 – 4y + 2z) / 3.

Дадим, напр., значения: y = 5 и z = 1; получим: x = (11 – 20 + 2) / 3 = –2(1/3) и т. д.

Возьмем еще уравнение

3x – 5y – 2z = 7.

Примем x и y за независимые переменные, а z — за зависимое и определим z через x и y

–2z = 7 – 3x + 5y; 2z = 3x – 5y – 7; z = (3x – 5y – 7) / 2

Теперь легко составить таблицу решений:

 

Точка доступа Aruba Instant On AP12 (Япония), 3 x 3 11ac Wave2, для установки в помещениях

Точка доступа Aruba Instant On AP12 (Япония), 3 x 3 11ac Wave2, для установки в помещениях | HPE Store Russia

s2048. t.eloqua.com/visitor/v200/svrGP

50

2048

d6547807cf984896b000ad5232552b28

etrack.ext.hpe.com

secure.p01.eloqua.com/visitor/v200/svrGP

50

2048

10831b2db3a34b9ea5863b752a46bfad

C_EmailAddress,C_FirstName,C_LastName,C_BusPhone,C_Company,C_Address1,C_Address2,C_City,C_Zip_Postal,C_State_Prov,C_Country,C_Number_of_Employees1,C_Email_Opt_In1,C_Estimated_Budget1,C_Industry1,C_Language1,C_Lead_Source___Most_Recent1,C_Mail_Opt_in1,C_Mobile_Opt_in1,C_Phone_Opt_in1,C_MobilePhone,C_Timeframe_to_Buy1,C_Response_Type1,C_Purchase_Role1,C_Contact_Me_Request1,ContactIDExt

2

price.disclaimer.pten Цены, предлагаемые местными реселлерами, могут отличаться. Развернуть Свернуть

https://s2048.t.eloqua.com/e/f2?nocache

ru

Наша система не смогла подтвердить правильность вашего адреса и не может найти его альтернативный вариант. Настоятельно рекомендуем изменить адрес и повторить попытку. Можно также продолжить с введенным вами адресом, если вы уверены в его правильности.

true

addalertattachmentbookmarkbrand markcalculatorcalendardownnextcaret-nextcartchatcheckmarkplaycloseconfigurecontactcost savingscredit card securitycriticalcycledeliverdirectionsadd documentPDF documentdownduplicateeditexpansionfast forwardfilterfoldergridhost maintenanceinternal storageIT transformationlanguagelikedownnextnextpreviouslistlockmailmanagement softwarelocationmarket growthmemorymoneynextnotificationokoperating systemperformanceGoogleGooglepower supplypreviousprintprocessor + memoryprocessorresetreturnsavescorecardsearchdownserviceFacebookLinkedinLinkedinTwitterYoutubespinnerstandardssubtractsupporttrashtreeupuservirtual machinewarning

Реальный продукт может отличаться от представленного на изображении

Точки доступа Aruba Instant On AP12 для установки в помещениях обеспечивают доступную эксплуатацию сетей Wi-Fi бизнес-класса по стандарту Wave 2 802. 11ac для сред в компаниях малого бизнеса с низкой и средней плотностью. Возможности бизнес-класса предназначены для удовлетворения потребностей в мобильных технологиях, Интернете вещей и безопасности, которые возникают у небольших бутиков, новых технологических проектов и розничных магазинов, по привлекательной цене. Благодаря своим компактным размерам точки доступа Aruba Instant On AP12 для установки в помещениях обеспечивают многопользовательские возможности и совокупную максимальную скорость передачи данных на уровне 1,6 Гбит/с для поддержки видеотрансляций с высоким разрешением и потребностей облачных приложений. В такие точки доступа также встроен контроллер для упрощения развертывания, благодаря чему можно легко установить и управлять несколькими точками доступа без привлечения специалистов ИТ, дополнительного оборудования и приложений.

Развернуть Свернуть

QuickSpecs

QuickSpecs

QuickSpecs (PDF)

QuickSpecs (HTML)

№ артикула R2X04A

{«baseProduct»:{«productID»:»R2X04A»,»productName»:»Точка доступа Aruba Instant On AP12 (Япония), 3 x 3 11ac Wave2, для установки в помещениях»},»navigationList»:[«Сеть»,»Беспроводные устройства»,»Точки доступа WLAN»,»Точки доступа Aruba Instant On AP12 для установки в помещениях»,»Точка доступа Aruba Instant On AP12 (Япония), 3 x 3 11ac Wave2, для установки в помещениях»],»cartDetail»:{},»productInfo»:[{«productInfo»:{«quantity»:»1″,»productID»:»R2X04A»,»productName»:»Точка доступа Aruba Instant On AP12 (Япония), 3 x 3 11ac Wave2, для установки в помещениях»}}]}

Дополнительные сведения

Новинки

  • Беспроводные точки доступа начального уровня для небольших и развивающихся компаний по доступной цене.
  • В комплект поставки входит интегрированный виртуальный контроллер для простого развертывания нескольких точек доступа.
  • Поддержка защищенного входа в систему для сотрудников и гостей по протоколу WPA2/WPA3 с использованием технологии Enhanced Open для гостевого доступа на каждого пользователя.

Основные характеристики

Точки доступа 802.11ac Wave 2 для быстрых соединений

Точки доступа Aruba Instant On AP12 для установки в помещениях предоставляют простой в использовании веб-интерфейс пользователя и шаблоны, благодаря чему их можно легко развернуть и подготовить к работе за считанные минуты.

В функции 802.11ac Wave 2 входят режим 3×3:3SS и пропускная способность канала до 80 МГц.

Двухдиапазонная беспроводная связь (2,4 ГГц и 5 ГГц) с суммарной скоростью до 1,6 Гбит/с поддерживает решения, для которых требуется высокая пропускная способность, например обработка видео, голосовая связь и проведение конференций.

Точки доступа Aruba Instant On AP12 для установки в помещениях допускают любые изменения основной конфигурации, которые можно автоматически передавать на каждую точку доступа в одном кластере.

Чтобы обеспечить постоянную доступность сети Wi-Fi в случае сбоя в работе основной точки доступа, выполняется автоматическое переключение на дополнительную точку доступа.

Полномасштабный охват беспроводной ячеистой сетью устраняет необходимость в прокладке дорогостоящих кабелей

Точки доступа Aruba Instant On AP12 для установки в помещениях обладают встроенными функциями беспроводной ячеистой сети, позволяющими экономично расширять подключения Wi-Fi без дополнительных кабелей.

Удобное расширение сети с захватом областей, где прокладывать кабели проблематично, при этом можно практически полностью избавиться от нестабильных соединений и «мертвых» зон, предоставив Wi-Fi в требуемых местах.

Технологии WPA2/WPA3 и Enhanced Open помогут защитить важные данные

В точках доступа Aruba Instant On AP12 для установки в помещениях реализованы стандарт безопасности Wi-Fi Alliance WPA2/WPA3 и поддержка Enhanced Open для организации защищенного беспроводного доступа.

Создавайте до восьми разных SSID под одним сетевым именем, чтобы сохранять данные в безопасности при выполнении любых задач, будь то просмотр веб-страниц или проверка информации отдела кадров.

Простота — залог безупречной работы сетей Wi-Fi

Точки доступа Aruba Instant On AP12 для установки в помещениях отличаются первоклассным качеством аппаратного и программного обеспечения с уровнем надежности, соответствующим проверенному поставщику.

Беспроблемная настройка сразу после установки — всегда под рукой.

Ассортимент продукции Aruba Instant On включает в себя гибкие настройки управления, позволяющие выбрать: Мобильное приложение Aruba Instant On предоставляет поэтапные инструкции на весь период эксплуатации: от первоначальной настройки до текущего управления.

Идеальный вариант для небольших и развивающихся компаний, таких как кафе, розничные магазины или офисы, предоставляющие профессиональные услуги, а также прочих точек доступа Wi-Fi.

Благодаря простому созданию целевой страницы можно настроить страницу гостевого доступа, разместив на ней логотип, фирменную символику и поддержку используемого языка.

Краткие характеристики

Связанные ссылки

Чем мы можем помочь?

Получите советы, ответы на вопросы и решения, когда они необходимы. По общим вопросам пишите на [email protected]

Нашли то, что искали?

Нужна помощь в поиске оптимального продукта для вашего бизнеса?

Наши специалисты с удовольствием пообщаются с вами и помогут найти продукты и услуги, которые откроют новые возможности и решат проблемы вашего бизнеса.

Продолжить покупки

{«baseProduct»:{«productID»:»R2X04A»,»productName»:»Точка доступа Aruba Instant On AP12 (Япония), 3 x 3 11ac Wave2, для установки в помещениях»},»navigationList»:[«Сеть»,»Беспроводные устройства»,»Точки доступа WLAN»,»Точки доступа Aruba Instant On AP12 для установки в помещениях»,»Точка доступа Aruba Instant On AP12 (Япония), 3 x 3 11ac Wave2, для установки в помещениях»],»cartDetail»:{},»productInfo»:[{«productInfo»:{«quantity»:»1″,»productID»:»R2X04A»,»productName»:»Точка доступа Aruba Instant On AP12 (Япония), 3 x 3 11ac Wave2, для установки в помещениях»}}]}

R2X04A

Для сравнения можно добавить до 4 товаров.

Уравнения по математике 3 класс

  • х + 19 = 42
  • x = 42 — 19
  • x = 23
  • 54 + х = 82
  • x = 82 — 54
  • x = 28
  • 9 + у = 15
  • y = 15 — 9
  • y = 6
  • 7 — у = 3
  • y = 7 — 3
  • y = 4
  • с + 6 = 9
  • c = 9 — 6
  • c = 3
  • k + 10 = 30
  • k = 30 — 10
  • k = 20
  • х + 50 = 96
  • x = 96 — 50
  • x = 46
  • х — 25 = 27
  • x = 27 + 25
  • x = 52
  • 42 — х = 18
  • x = 42 — 18
  • x = 24
  • 27 + х = 50
  • x = 50 — 27
  • x = 23
  • х — 28 = 70
  • x = 70 + 28
  • x = 98
  • 63 + х = 90
  • x = 90 — 63
  • x = 27
  • 76 — k = 40
  • k = 76 — 40
  • k = 30
  • х — 16 = 30
  • x = 30 + 16
  • x = 46
  • с + 9 = 12
  • c = 12 — 9
  • c = 3
  • х + 35 = 67
  • x = 67 — 35
  • x = 32

Решение линейных уравнений: с пареном; «All x», «No x» Soln’s

Purplemath

В этом уроке мы сначала попрактикуемся в решении линейных уравнений, содержащих скобки. Их решение потребует умножения и упрощения, прежде чем приступить к фактическому процессу решения. Если вам неудобны скобки, сначала займитесь изучением. Тогда вернись сюда.

Затем мы рассмотрим два странных типа решений: «нет решения» и решение «все x ». В первом случае процесс решения заканчивается бессмыслицей, а во втором — тривиально верным утверждением. Поскольку учащиеся нечасто сталкиваются с такими решениями, их легко забыть, а значит, легко запутать. Но я бы поставил хорошие деньги на то, что в следующем тесте будет хотя бы одно из этих уравнений, а в финале, вероятно, будет еще одно.Так что изучите и сделайте пометку, чтобы просмотреть уравнения «без решения» и «все уравнения — x » перед следующим экзаменом.

MathHelp.com

После того, как вы изучите основы решения линейных уравнений, ваш учебник и инструктор начнут предлагать вам упражнения, содержащие скобки, которые обычно необходимо сначала упростить (или «расширить», что означает, что вы умножили, а затем упростил результат).

Во-первых, я должен умножить скобки в правой части. Затем я могу продолжить как обычно:

Тогда мое решение:

  • Решить 6
    x — (3 x + 8) = 16

Сначала я упрощу левую часть; тогда решу обычным способом.Я хочу быть осторожным, когда пишу негатив в скобках. Если у меня возникают проблемы с отслеживанием знаков «минус», я ставлю «1» перед круглыми скобками.

Тогда мое решение:

  • Решите 7 (5
    x — 2) = 6 (6 x — 1)

Это уравнение заключено в скобки с обеих сторон уравнения. Я должен обязательно взять 7 и 6 до их соответствующих скобок.

После того, как я упростил любую сторону, я переместил меньший из двух членов переменной («35 x » с левой стороны), чтобы убедиться, что у полученного в результате члена переменной не было знака «минус». Это не «правило», но, безусловно, облегчает мою жизнь. И мой окончательный ответ:

Для уравнений с скобками, не торопитесь и выпишите все ваших шагов, как я сделал выше.Не пытайтесь делать все в своей голове.

Во-первых, мне нужно умножить в левой части, взяв 3 через —

Подождите … В этом уравнении я действительно могу избавиться от 3, разделив его, потому что 6 в правой части делится на 3. На самом деле мне не нужно распределять для этого конкретного уравнения. Вместо:

3 (х — 2) = 6
——— —
3 3

х — 2 = 2
+2 +2
———-
х = 4

Тогда мое решение:

Если бы я не заметил, что могу начать с разделения, я все равно получил бы правильный ответ. Но если есть возможность разделить, давая себе меньшие числа для работы, я бы хотел этим воспользоваться. Это упрощение происходит нечасто, но постарайтесь не закрывать глаза на то, что несколько раз оно появляется.

  • Решить 13 — (2
    x + 2) = 2 ( x + 2) + 3 x

Я начну с умножения на каждую скобку (знак «минус» слева и 2 справа).Затем я объединю похожие термины, упрощу и решу:

Тогда мой ответ:

Не забывайте: никогда не бывает причин быть неуверенным в своем решении линейного уравнения, потому что вы всегда можете проверить свой ответ. Значение значения решения состоит в том, что это значение x , которое делает уравнение истинным. Итак, чтобы проверить свой ответ, вы вставляете значение решения обратно в исходное уравнение и убеждаетесь, что уравнение «работает» с этим значением. Например, в последнем упражнении, приведенном выше, мое решение было x = 1. Чтобы проверить свое решение, я подставлю свое значение в левую (LHS) и правую (RHS) части исходного уравнения. и убедитесь, что обе стороны оценивают одно и то же число.

13 — (2 x + 2) = 2 ( x + 2) + 3 x

слева: 13 — (2 [1] + 2)

= 13 — (2 + 2) = 13-4 = 9

ПРА: 2 ([1] + 2) + 3 [1]

Обе стороны уравнения дают одно и то же значение, поэтому решение «проверяет», и теперь я знаю , что мой ответ правильный

Кстати, если есть возможность, попробуйте проверить свои ответы при сдаче тестов.После того, как вы ответили на все вопросы (при условии, что у вас осталось немного времени), вернитесь и вставьте свои решения обратно в исходный вопрос. Если ваше решение вопроса «проверяет», значит, вы знаете, что ответили правильно. Если проверка не выполняется, то у вас есть шанс исправить свою ошибку до того, как вы сдадите тест.

Вам также может потребоваться решить линейные уравнения с вложенными скобками .

  • Решите 2 [3
    x + 4 (3 — x )] = 3 (5 — 4 x ) — 11

Прежде чем я смогу решить, мне нужно упростить.Сначала я упрощу левую часть:

2 [3 x + 4 (3 — x )]

2 [3 x + 4 (3) + 4 (- x )]

2 [3 x + 12–4 x ]

2 [12 — x ]

24-2 х

Тогда упрощу правую часть:

3 (5 — 4 x ) — 11

3 (5) + 3 (–4 x ) — 11

15 — 12 x — 11

4–12 x

Теперь, когда я упростил обе стороны уравнения, я могу перейти к решению.

24 — 2x = 4 — 12x
+ 12x + 12x
——————-
24 + 10x = 4
-24-24
—————
10x = -20
— —
10 10

х = -2

Итак, мой окончательный ответ:

  • Решите 3 [
    x — 2 (3 x — 4)] + 15 = 5 — [2 x — (3 + x )] — 11

Моим первым шагом будет упростить каждую часть этого уравнения, работая изнутри.Начну с левой стороны:

3 [ x — 2 (3 x — 4)] + 15

3 [ x — 6 x + 8] + 15

3 [–5 x + 8] + 15

–15 x + 24 + 15

–15 x + 39

Тогда упрощу правую часть:

5 — [2 x — (3 + x )] — 11

5 — [2 x — 3 — x ] — 11

5 — [ x — 3] — 11

5 — х + 3 — 11

— х — 3

После упрощения каждой стороны могу перейти к решению. Мое упрощенное уравнение:

Я перемещаю меньший член переменной (равный –15 x в левую часть), а затем перемещаю числа, чтобы завершить решение.

-15x + 39 = -x — 3
+ 15x + 15x
——————-
39 = 14x — 3
+3 +3
————
42 = 14x
— —
14 14

3 = х

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в решении линейных уравнений с вложенными круглыми скобками.Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку и выберите «Решить для x», чтобы сравнить свой ответ с ответом Матвея. (Или пропустите виджет и перейдите к следующей странице.)

(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления. )

URL: https: //www.purplemath.com / modules / solvelin4.htm

Решение уравнения | Encyclopedia.com

Методы решения простых уравнений

Решение более сложных уравнений

Решение многомерных уравнений

Решение уравнений второй и более высокой степени

Ресурсы

Решение уравнения представляет собой набор всех значений, которые при замене на неизвестных, сделайте уравнение истинным.Для уравнений с одним неизвестным, возведенным в единственную степень, для определения его решений используются два фундаментальных правила алгебры, включая свойство аддитивности и свойство мультипликативности. Решения для уравнений с несколькими неизвестными переменными находятся с использованием принципов для системы уравнений. Уравнения с членами в степени, большей единицы, могут быть решены путем факторизации, а в некоторых конкретных случаях — с помощью квадратного уравнения.

Идея решения уравнений существовала со времен древних египтян и вавилонян.В то время они использовали простые алгебраические методы для поиска решений практических проблем, связанных с их повседневной жизнью. Методы, используемые древними, были сохранены в трактате, написанном арабским математиком Аль-Коваризми 825 г. н.э.). В эту работу он включает методы решения линейных уравнений, а также уравнений второй степени. Решения для некоторых уравнений высшей степени были разработаны в шестнадцатом веке итальянским математиком Джероламо Кардано (1501–1576).

Уравнение — это алгебраическое выражение, которое обычно связывает неизвестные переменные с другими переменными или константами.Например, x + 2 = 15 — это уравнение, как и y 2 = 4. Решение или корень уравнения — это любое значение или набор значений, которые можно подставить в уравнение, чтобы сделать его истинным. . Для первого примера решение для x равно 13. Во втором примере есть два значения, которые делают утверждение истинным, а именно 2 и –2. Эти значения составляют набор решений уравнения.

Используя два основных правила алгебры, можно получить решения многих простых уравнений.Первое правило гласит, что одна и та же величина может быть добавлена ​​к обеим сторонам уравнения, не изменяя решение уравнения. Например, уравнение x + 4 = 7 имеет решение x = 3. Согласно первому правилу, можно добавить любое число к обеим сторонам уравнения и при этом получить то же решение. При добавлении 4 к обеим частям уравнение становится x + 8 = 11, но решение остается x = 3. Это правило известно как аддитивное свойство равенства. Чтобы использовать это свойство для поиска решения уравнения, все, что требуется, — это выбрать правильное число для добавления.Решение предыдущего примера x + 4 = 7 можно найти, прибавив –4 к обеим сторонам уравнения. Если это сделано, уравнение упрощается до x + 4 — 4 = 7 — 4 или x = 3, и уравнение решается.

Второе фундаментальное правило, известное как мультипликативное свойство равенства, гласит, что каждый член в обеих частях уравнения можно умножить или разделить на одно и то же число, не изменяя решение уравнения. Например, решение уравнения y — 2 = 10 — y = 12.Используя мультипликативное правило, можно получить эквивалентное уравнение с тем же множеством решений, умножив обе части на любое число, например 2. Таким образом, уравнение принимает вид 2y– 4 = 20, но решение остается y = 12. Это свойство может также может использоваться для решения алгебраических уравнений. В случае уравнения 2x = 14 решение получается делением обеих частей на 2. Когда это делается 2x / 2 = 14/2, уравнение упрощается до x = 7.

Часто оба этих правила должны быть используется для решения одного уравнения, такого как уравнение 4x + 7 = 23.В этом уравнении к обеим сторонам уравнения добавляется –7, и оно упрощается до 4x = 16. Обе части этого уравнения затем делятся на 4, и это упрощает решение, x = 4.

Большинство уравнений приведены в более сложная форма, которую можно упростить. Рассмотрим уравнение 4x — x — 5 = 2x + 7. Первым шагом в решении этого уравнения является объединение одинаковых членов с каждой стороны уравнения. В правой части нет одинаковых терминов, но 4x и –x в левой части похожи на термины.Это уравнение в упрощенном виде становится 3x — 5 = 2x + 7. Следующим шагом является устранение неизвестного из одной части уравнения. В этом примере это достигается добавлением –2x к обеим сторонам уравнения, что дает x — 5 = 7. Используя свойство аддитивности, решение получается добавлением 5 к обеим сторонам уравнения, поэтому x = 12.

Весь процесс решения алгебраических уравнений с одной переменной можно описать следующими шагами. Во-первых, удалите скобки, умножив множители.Во-вторых, добавьте одинаковые термины с каждой стороны. В-третьих, удалите неизвестное с одной стороны уравнения, используя мультипликативные или аддитивные свойства. В-четвертых, удалите постоянный член со стороны неизвестного, используя аддитивное свойство. Наконец, исключите любой коэффициент при неизвестном, используя свойство мультипликативности.

Многие алгебраические уравнения содержат более одной переменной, поэтому полный набор решений нельзя найти с помощью методов, описанных до сих пор. Уравнения с двумя неизвестными называются линейными уравнениями и могут быть представлены общей формулой ax + by = c; где a, b и c — константы, а x и y — переменные.Решением этого типа уравнения будет упорядоченная пара x и y, которая делает уравнение истинным. Например, набор решений для уравнения x + y = 7 будет содержать все пары значений x и y, которые удовлетворяют уравнению, такие как (2,5), (3,4), (4,3), и т. д. Как правило, для определения решения линейного уравнения с двумя переменными уравнение переписывается и решается в терминах одной переменной. Решением уравнения x + y = 7 становится любая пара значений, которая делает x = 7 — y истинным.

Часто существует несколько линейных уравнений, связывающих две переменные в одной системе. Все уравнения, связанные с переменными, известны как система уравнений, а их решение — это упорядоченная пара, которая делает каждое уравнение истинным. Эти уравнения решаются методами построения графиков, замены и исключения.

Уравнения, содержащие неизвестные в степени единицы, известны как уравнения первой степени. Также существуют уравнения второй степени, которые включают:

КЛЮЧЕВЫЕ УСЛОВИЯ

Аддитивное свойство — Свойство уравнения, в котором указано число, может быть добавлено к обеим сторонам уравнения, не влияя на его решение.

Факторинг — метод сведения уравнения более высокой степени к продукту уравнений более низкой степени.

Уравнение первой степени —Алгебраическое выражение, содержащее неизвестное в первой степени.

Мультипликативное свойство — Свойство уравнения, которое устанавливает все члены в уравнении, можно умножить на то же число, не влияя на окончательное решение.

Уравнение второй степени —Алгебраическое выражение, содержащее неизвестное во второй степени.

как минимум одна переменная, возведенная в квадрат или возведенная в степень двойки. Уравнения также могут быть третьей, четвертой и т. Д. Самым известным уравнением второй степени является квадратное уравнение, которое имеет общий вид ax 2 + bx + c = 0; где a, b и c — константы, а a не равно 0. Решение этого типа уравнения часто можно найти с помощью метода, известного как факторинг.

Поскольку квадратное уравнение является произведением двух уравнений первой степени, оно может быть включено в эти уравнения.Например, произведение двух выражений (x + 2) (x — 3) дает одно квадратичное выражение x 2 — x — 6. Два выражения (x + 2) и (x — 3) называются коэффициенты квадратного выражения x 2 — x — 6. Приняв каждый коэффициент квадратного уравнения равным нулю, можно получить решения. В этом квадратном уравнении решениями являются x = –2 и x = 3.

Нахождение множителей квадратного уравнения не всегда легко. Для решения этой задачи была изобретена квадратная формула, позволяющая решить любое квадратное уравнение.Квадратное уравнение для общего уравнения формулируется следующим образом: ax 2 + bx + c = 0

Чтобы использовать квадратную формулу, числа для a, b и c подставляются в уравнение, и определяются решения для x .

См. Также Системы уравнений.

КНИГИ

Биттингер, Марвин Л. и Давик Элленбоген. Промежуточная алгебра: концепции и приложения . 7-е изд. Ридинг, Массачусетс: Addison-Wesley Publishing, 2006.

Ларсон, Рон. Precalculus . 7-е изд. Бостон, Массачусетс: Houghton Mifflin, 2007.

Lorenz, Falko. Алгебра. Нью-Йорк: Springer, 2006.

Сетек, Уильям М. Основы математики . Верхняя Сэдл Ривер, Нью-Джерси: Pearson Prentice Hall, 2005.

Perry Romanowski

Как найти общее решение с помощью корней

Введение
Пример
Простое решение
Креативное решение
Другой пример
Действительно простое решение
Использование кувалды
Последний пример
Нет простого решения
Кардано спешит на помощь
Квадратное уравнение
Кубическое уравнение
Номенклатура
Обратная связь

Я всегда думал, что объяснения, которые я прочитал решения Кардано общей кубики были излишне сложно.

Всякий раз, когда я спрашиваю кого-то, кто был разоблачен методу объяснения, обычный ответ таков: они не помнят, как это было. Это моя попытка объясните это так, чтобы у него было больше шансов быть запомненным. Если ничего другого, я запомню это лучше!

Поскольку большинство подходов очень быстро становятся общими, Вместо этого я займусь чем-нибудь другим. Я начну с прогрессии тщательно подобранных конкретных примеров. Тогда я обобщу. Я собираюсь использовать следующие примеры:

х 3 — 3х + 2 = 0
х 3 — 3х = 0
х 3 — 3х + 1 = 0

Попутно посмотрю в квадратном уравнении и завершая квадрат, описывая эту технику таким образом, чтобы решение кубической.

В первом примере комплексные числа не потребуются, но скоро после того, как они будут интенсивно использоваться. Если вы не знакомы с комплексные числа, вы можете попробовать прочитать это эссе, но скоро за этим станет действительно трудно уследить. Вас предупредили!

Я хотел бы начать с примера: х 3 — 3х + 2 = 0.

Стандартный способ решить эту проблему — попробовать несколько простых значения: 1, -1, 2, -2. Оказывается, 1 — это решение! Это означает, что (x-1) является фактором х 3 — 3х + 2 = 0.Полиномиальное деление дает

x 3 -3x + 2 можно разложить на множители как (x-1) (x 2 + x — 2).

Это говорит нам о том, что решения x 3 — 3x + 2 = 0 даются решениями x-1 = 0 и x 2 + x-2 = 0.

Решение квадратичного множителя может быть выполнено разными способами. В этом случае очевидна факторизация х 2 + х — 2 = (х-1) (х + 2). Итак, x 3 — 3x + 2 = (x-1) 2 (x + 2).

Корни равны -2 и 1 (кратность 2).

Единственная проблема с этим методом решения — что это зависит от некоторого интуитивного линейного фактора. Когда вы можете это сделать, вы в деле. Когда ты не можешь, ты застрял. Техника Кардано — это больше работы, но он всегда даст вам ответ.

Вот как этот пример решается с использованием техники Кардано.

Решающий творческий шаг (на мой взгляд) — заменить x с (w + 1 / w) и решить относительно w. Это приводит к уравнение шестого порядка по w, НО, это шестой порядок уравнение, которое легко решить.Вот подробности:

х 3 — 3 х + 2 =
(ш + 1 / ш) 3 — 3 (ш + 1 / ш) + 2 =
w 3 + 3 w 2 (1 / w) + 3 w (1 / w) 2 + (1 / w) 3 — 3 (w + 1 / w) + 2 =
w 3 + 3 w + 3 (1 / w) + (1 / w 3 ) — 3 (w + 1 / w) + 2 =
w 3 + (1 / w 3 ) + 2.

Таким образом, x 3 -3x + 2 = 0 становится ш 3 + 1 / ш 3 +2 = 0

Это уравнение шестого порядка по w.Уловка для ее решения состоит в том, чтобы понять, что это действительно квадратичный в ш 3 . Заменяя w 3 на z, получаем:

г + 1 / г + 2 = 0

то есть z 2 + 1 + 2z = 0.

Решение квадратичной любой из техник, которые вам нравятся (Мне нравится z 2 + 1 + 2z = (z + 1) 2 ) вы получите z = -1.

Итак, w 3 = -1.

Решение этого — w = -1, что дает решение х = ш + 1 / ш = -1 + 1 / -1 = -2.

Полиномиальное деление теперь дает

x 3 -3x + 2 можно разложить на множители как (x + 2) (x 2 — 2x + 1).

x 2 — 2x + 1 = (x-1) 2 , поэтому мы получаем, что решения x = -2 и 1 (с кратностью 2).

Если вы что-то знаете о комплексных числах, вы могли заметить что я мог бы использовать другие решения для w 3 = -1. Три решения:

ш = -1, 1/2 + я √3 / 2, 1/2 — я √3 / 2

Выбирая w = 1/2 + i √3 / 2, получаем решение

x = w + 1 / w = (1/2 + i √3 / 2) + (1/2 — i √3 / 2) = (1/2) + (1/2) = 1

Здесь следует отметить то, что нам удалось получить реальное решение для кубическая с помощью комплексных чисел!

Кроме того, в этом конкретном примере использование комплексных чисел необязательно.Выбирая решение w = -1 для w 3 = -1, мы успешно избегал иметь с ними дело. Так бывает не всегда! Когда я написал что этот пример был тщательно выбран, я имел ввиду.

Чтобы еще немного разогреться, рассмотрим х 3 — 3х = 0.

Это очень легко решить без техники Кардано. Поскольку нет постоянного члена, x является фактором.

x 3 -3x можно разложить на множители как x (x 2 — 3).

Это говорит нам о том, что решения х = 0, √3, -√3.

Заменить x на (w + 1 / w)

х 3 — 3 х =
(ш + 1 / ш) 3 — 3 (ш + 1 / ш) =
w 3 + 3 w 2 (1 / w) + 3 w (1 / w) 2 + (1 / w) 3 — 3 (w + 1 / w) =
w 3 + 3 w + 3 (1 / w) + (1 / w 3 ) — 3 (w + 1 / w) =
w 3 + (1 / w 3 ).

Заменяя w 3 на z, получаем:

г + 1 / г = 0

г 2 = -1

На этот раз от комплексных чисел никуда не деться!

г = я, -i.

Переходя к решению i, теперь нам нужно решить

w 3 = i

Что ж, одно из решений — w = -i. Это дает нам x = w + 1 / w = -i + 1 / -i = -i + i = 0.

Это говорит нам, что (x-0) множитель x 3 -3x, а остальное — рутина: x 3 -3x = x (x 2 -3) дает решения х = 0, √3, -√3.

Теперь рассмотрим х 3 — 3х + 1 = 0.

Насколько я знаю, простого способа решить эту проблему нет.

Заменить x на (w + 1 / w)

х 3 — 3 х + 1 =
(ш + 1 / ш) 3 — 3 (ш + 1 / ш) + 1 =
w 3 + 3 w 2 (1 / w) + 3 w (1 / w) 2 + (1 / w) 3 — 3 (w + 1 / w) + 1 =
w 3 + 3 w + 3 (1 / w) + (1 / w 3 ) — 3 (w + 1 / w) + 1 =
w 3 + (1 / w 3 ) + 1.

Заменяя w 3 на z, получаем:

г + 1 / г + 1 = 0

г 2 + 1 + г = 0

г = -1/2 + я √3 / 2, -1/2 — я √3 / 2

Используя решение 1/2 + i √3 / 2, теперь нам нужно решить

ш 3 = -1/2 + я √3 / 2

т. е. w 3 = cos (120 °) + i sin (120 °)

Это означает, что решения следующие: w = cos (40 °) + i sin (40 °), cos (160 °) + i sin (160 °), cos (280 °) + i sin (280 °)

Это дает нам x = w + 1 / w = 2cos (40 °), 2 cos (160 °), 2cos (280 °)

Общее квадратное уравнение:

а х 2 + б х + с = 0.

Идея состоит в том, чтобы уменьшить его до другого квадратичного

y 2 = Т.

Мы знаем, как это решить: y = √T, −√T.

Примечание: если a, b, c действительны в общем уравнении, тогда T будет действительным в редуцированном уравнении. Я подчеркиваю это, потому что соответствующие Утверждение для кубического уравнения НЕ верно.

Обычные шаги:

Разделите на , чтобы получить уравнение вида

x 2 + B x + C = 0 (здесь B = b / a, C = c / a).

Теперь заменим x на y + k, где k выбрано так что уравнение имеет вид

у 2 + D = 0.

Это делается путем выбора k так, чтобы 2k = -B, т. е. k = -B / 2.

Взяв T = -D, теперь имеем y 2 = Т.

Были сделаны!

Общее кубическое уравнение:

а х 3 + б х 2 + в х + г = 0

Идея состоит в том, чтобы уменьшить его до другого кубического

w 3 = Т.

Мы знаем, как это решить.

Примечание: даже если a, b, c, d действительны в общем уравнении, это НЕ означает, что T будет реальным. Это могло быть любое комплексное значение.

Это не намного больше.

Все важные шаги рассмотрены в примерах. Остальные идеи присутствуют в квадратичном случае.

Вот что вы делаете:

Отметим, что первые два шага имеют прямые аналоги в квадратичном случае.

Сначала разделите на a, чтобы получить уравнение вида

х 3 + В х 2 + С х + D = 0.

Теперь заменим x на y + k, где k выбрано так что уравнение имеет вид

у 3 + р у + д знак равно 0.

Это делается путем выбора k так, чтобы 3k = −B, т.е. k = -B ⁄ 3.

Теперь заменим y на w + m / w, где m выбрано так, чтобы члены w и 1 / w исчезают. Это делается путем выбора m, чтобы удовлетворить p = -3m, т.е. m = — p / 3. Вот почему я выбрал p = -3 в приведенных выше примерах.

Теперь у нас есть уравнение шестого порядка по w в виде

w 3 + R (1 / w 3 ) + S = 0.

(или, если хотите, w 6 + S w 3 + R = 0)

Взяв z = w 3 , мы имеем квадратичную систему с двумя решениями, и то, и другое может быть сложным. Выбери один. Назовите это Т.

Общая кубика сведена к кубической

w 3 = T

Решите эту проблему и отмените указанные выше замены.

Замена x = w + m / w иногда называется заменой Виета .

Уравнение шестого порядка вида

ш 6 + ш ш 3 + R = 0

иногда называют трехквадратичным уравнением

Выражение третьего порядка формы

y 3 + p y + q

иногда называют депрессивной кубической

4 декабря 2003 г. {\ displaystyle 3})}} {3-3}

долл. США

$ = \ dfrac {\ log_ {2} {(9-8)}} {0}

$

$ = \ dfrac {\ log_ {2} {(1)}} {0}

$

$ = \ dfrac {0} {0}

$

Следовательно, значение выражения в левой части неопределенно при $ x $ равно $ 3 $.Следовательно, $ x \ ne 3 $, но $ x = 0 $ является только решением логарифмического уравнения и математически является необходимым решением этой логарифмической задачи.


Промежуточная алгебра
Урок 20: Решение систем линейных уравнений
в трех переменных

WTAMU > Виртуальная математическая лаборатория> Алгебра среднего уровня

Цели обучения

После изучения этого руководства вы сможете:
  1. Решите систему линейных уравнений с тремя переменными с помощью устранение метод.

Введение


Учебник



Система линейных уравнений

Система линейных уравнений состоит из двух или более линейных уравнения, которые решаются одновременно.

В этом руководстве мы рассмотрим системы, которые иметь три линейных уравнения и три неизвестных.

Урок 19: Решение системы линейных уравнений с двумя переменными рассмотрел три способа решать линейные уравнения с двумя переменными.




В общем, решение системы из трех переменные — это упорядоченный тройной ( x , y , z ) это делает ВСЕ ТРИ уравнения истинными.

Другими словами, это то, что есть у всех троих. общий. Так что если упорядоченная тройка является решением одного уравнения, но не другого, тогда это НЕ решение системы.

Обратите внимание, что линейные уравнения с двумя переменными, найденные в Урок 19: Решение системы линейных уравнений с двумя переменными, изображенных на графике линия в двумерной декартовой системе координат.Если бы вы были график (который вас не попросят делать здесь) линейное уравнение в трех переменных, вы получите фигуру самолета в трех размерный система координат. Пример того, как будет выглядеть самолет: пол или столешница.

Вспомните следующее из
Урок 19: Решение системы линейных уравнений с двумя переменными:

Согласованная система — это система, в которой хотя бы одно решение.

Несогласованная система — это система, которая имеет нет решения .

Уравнения системы зависимы , если ВСЕ решения одного уравнения являются решениями двух других уравнений. В другими словами, они заканчиваются тем, что совпадают с строкой .

Уравнения системы независимы , если они не делятся ВСЕ решения .У них может быть одна общая черта, только не все их.




Одно решение
Если система с тремя переменными имеет одно решение, это заказанный тройной ( x , y , z ) это решение ВСЕХ ТРЕХ уравнений. Другими словами, когда вы подставляете значения упорядоченной тройки, получается ВСЕ ТРИ уравнения ИСТИННЫЙ.

Если у вас есть одно решение для окончательного ответа, будет эта система непротиворечива или непоследовательна?
Если вы сказали «последовательный», похлопайте себя по плечу!

Если вы получите одно решение для окончательного ответа, будет уравнения быть зависимыми или независимыми?
Если вы сказали независимый, вы правы!


Нет решения
Если три плоскости параллельны друг другу, они никогда пересекаются. Это означает, что у них нет точек в общий. В этой ситуации у вас не будет решения.

Если окончательного ответа нет, — это эта система непротиворечива или непоследовательна?
Если вы сказали непоследовательно, вы правы!

Если вы не получите окончательного ответа, будет уравнения быть зависимыми или независимыми?
Если вы сказали независимый, вы правы!


Бесконечный Решения
Если три плоскости в конечном итоге лежат друг на друге, то есть — бесконечное количество решений. В этой ситуации они бы в конечном итоге окажутся в одной плоскости, поэтому любое решение, которое будет работать в одном уравнение будет работать в другом.

Если вы получите бесконечное количество решений для ваш окончательный ответ, это эта система непротиворечива или непоследовательна?
Если вы сказали «последовательный», вы правы!

Если вы получите бесконечное количество решений для ваш окончательный ответ, уравнения быть зависимыми или независимыми?
Если вы сказали иждивенец, вы правы!


Решение систем линейных
Уравнений с тремя переменными
Использование метода исключения

Обратите внимание, что существует более одного способа решения Этот тип система. Метод исключения (или добавления) — один из наиболее общий способы сделать это. Поэтому я предпочитаю показать это так.

Если у вас есть другой способ сделать это, непременно сделайте это твой путь, тогда вы можете проверить свои окончательные ответы с моими. Независимо от того, в какую сторону ты выбрать сделать это, если вы делаете это правильно, ответ будет имеют быть таким же.


Шаг 1. Упростите и поместите все три уравнения в при необходимости сформируйте A x + B y + C z = D.


Это может включать в себя такие вещи, как удаление () и удаление фракций.

Чтобы удалить (): просто используйте свойство distributive.

Чтобы удалить дроби: поскольку дроби — это еще один способ написать деление, а обратное деление — умножение, дробь удаляется на умножение обе стороны ЖК-дисплеем всех ваших фракций.


Шаг 2: Выберите для удаления любого переменных из любой пары уравнений.


На данный момент вы только работа с двумя ваших уравнений. На следующем этапе вы добавите в третьих уравнение в смесь.

Забегая вперед, вы добавите эти два уравнения вместе . В этом процессе вам нужно убедиться, что одна из переменных падает из, оставив одно уравнение и два неизвестных. Единственный способ вы можете гарантия то есть если вы добавляете противоположности . Сумма противоположностей равно 0.

Неважно, какую переменную вы выберете для удаления из. Вы хотите, чтобы это было как можно проще. Если переменная уже имеет противоположные коэффициенты, чем при добавлении двух уравнений вместе. В противном случае вам нужно умножить одно или оба уравнения на число. который создаст противоположные коэффициенты в одной из ваших переменных. Ты может думайте об этом как о ЖК-дисплее. Подумайте, какой номер оригинал коэффициенты оба входят и соответственно умножают каждое отдельное уравнение. Делать убедитесь, что одна переменная положительна, а другая отрицательна, прежде чем вы Добавить.

Например, если у вас есть 2 x в одном уравнении и 3 x в другом уравнении, вы могли бы умножать первое уравнение на 3 и получаем 6 x и то второе уравнение на -2, чтобы получить -6 x . Так когда вы собираетесь сложить эти два вместе, они выпадут.


Шаг 3: Удалите ЖЕ переменная, выбранная в шаг 2 из любой другой пары уравнений, создавая систему из двух уравнения и 2 неизвестных.





Шаг 5: Решите для третьего Переменная.


Если вы придумали значение для двух переменных в шаг 4, что означает, что три уравнения имеют одно решение. Вставьте значения найденное на шаге 4 в любое из уравнений задачи, которые имеют отсутствующая переменная в нем и решите третью переменную.



Предлагаемое решение можно подключить ко ВСЕМ ТРИ уравнения. Если он делает ВСЕ ТРИ уравнения истинными, то у вас есть решение система.

Если хотя бы один из них окажется ложным, вам нужно перейти назад и повторить проблема.




Пример 1 : Решите систему.


Обратите внимание, что числа в () Являются уравнением числа.Они будут использоваться в задачах для справки. целей.

По сути, мы сделаем то же самое, что и с системами двух уравнений, просто больше. Другими словами, у нас будет к выполните исключение дважды, чтобы перейти к одной переменной, поскольку мы на этот раз начав с трех переменных.



Здесь не требуется никаких упрощений.Перейдем к следующий шаг.




Давайте начнем с выбора нашей первой переменной для Устранить. Я иду выбрать y исключить. я нуждаюсь сделать это с ЛЮБОЙ парой уравнений.

Давайте сначала удалим y , используя первую и вторые уравнения. Этот процесс идентичен тому, как мы подошел это с системами, найденными в Tutorial 19: Решение системы линейных уравнений с двумя переменными.

Если я умножу 2 раза второе уравнение, то члены на будут противоположны друг другу и в конечном итоге выпадут.

Умножаем второе уравнение на 2 и затем добавив это к первое уравнение получаем:



* Мног.экв. (2) по 2

* y х иметь противоположное коэффициенты
* y ‘s выпал


Теперь мы не можем останавливаться на достигнутом по двум причинам. Во-первых, мы бы застрять, потому что у нас есть одно уравнение и два неизвестных.Второй, когда мы решаем систему, она должна быть решением ВСЕХ участвующих уравнений и мы еще не включили третье уравнение. Давайте сделаем это сейчас же.




Мы продолжаем устранять y , на этот раз я хочу использовать второе и третье уравнения.я мог используйте первый и третий, если я не использовал оба одинаковых те используется на шаге 2 выше.

В этом примере я выбрал второй и третий, потому что члены и уже противоположны, поэтому нам не нужно умножать на что-либо, мы можем сразу перейти к их сложению:



* y х иметь противоположное коэффициенты

* y х выпал




Соединяя два найденных нами уравнения, теперь у нас есть система двух уравнений и двух неизвестных, которую мы можем решить просто подобно те, которые показаны в Уроке 19: Решение системы линейных уравнений в Две переменные. Вы можете использовать либо устранение, либо подмена. Я собираюсь продолжить и придерживаться метода исключения, чтобы завершить это.

Давайте сначала соединим эти уравнения:


* Поместите уравнения, найденные в шагах 2 и 3
вместе в одну систему


Теперь я собираюсь выбрать x , чтобы исключить . Мы можем либо умножьте первое уравнение на -1, либо второе, в любом случае создайте противоположности перед членами x .

Я умножу уравнение (5) на -1. а затем добавить уравнения вместе:


* Мног. экв. (5) по -1

* x ‘s иметь противоположное коэффициенты

* x х выпал




* Инверсная к мульт.на 4 — div. по 4


Если вернуться на один шаг назад к системе, в которой было два уравнения и две переменные и введите 1 для z в каком является обозначенное уравнение 4, получим:


* Ур. (4)
* Вставить 1 для z
* Добавление 5 обратное. 5

* Инверсная по отношению к мульт. на 5 дел. по 5




Теперь нам нужно вернуться к исходной системе и выбрать любое уравнение чтобы подключить две известные переменные и решить для нашей последней переменной.

Я выбираю уравнение (1) для вставки нашего 2 для x и 1 для z , что мы нашли:


* Ур. (1)
* Вставка 2 для x и 1 для z

* Прибавление 3 — это под. 3

* Инверсная по отношению к мульт. на 2 — div. по 2




Вы обнаружите, что если вы подключите заказанный тройной (2, 0, 1) во ВСЕ ТРИ уравнения исходной системы, это решение ВСЕХ ТРИ их.

(2, 0, 1) — это решение нашей системы.




Пример 2 : Решите систему.

Обратите внимание, что числа в () Являются уравнением числа. Они будут использоваться в задачах для справки. целей.



К сожалению, мы имеем дело с некоторыми дробями в уравнение (3).
Мы можем позаботиться о них точно так же, как и с ними. перед в уравнениях на , умножив обе части уравнения (3) на это LCD, что составляет 4.




* Мног.экв. (3) по LCD 4







Давайте начнем с выбора нашей первой переменной для Устранить. Я иду выбрать z для нас, чтобы устранить. Мы необходимость сделать это с ЛЮБОЙ парой уравнений.

Давайте сначала удалим z , используя первый и вторые уравнения. Этот процесс идентичен тому, как мы подошел это с системами, найденными в Tutorial 19: Решение системы линейных уравнений с двумя переменными. Если мы умножим -1 на второе уравнение, то члены z будут противоположны друг другу и в конечном итоге выпадут.

Умножение второго уравнения на -1 и затем добавляя это к первое уравнение получаем:



* Мног. уравнение (2) по -1

* z ‘s иметь противоположное коэффициенты

* z ‘s выпал




Мы все еще продолжаем устранять z , на этот раз мы хотим использовать второе и третье уравнения. Мы мог используйте первый и третий, пока мы не использовали оба одинаковых те используется на шаге 2 выше.

Похоже, нам придется умножить первую уравнение на 2, чтобы получить противоположности на z .

Умножение первого уравнения на 2 и последующее добавление уравнения (1) и (3) вместе получаем:


* Мног.экв. (2) по 2

* z ‘s иметь противоположное коэффициенты

* Выпадают все три переменные И
у нас есть ЛОЖНЫЙ оператор




Привет всем нашим переменным исчез. Что случилось??? Так же, как с двумя уравнениями и двумя неизвестными показано в Уроке 19 (Решение системы линейных уравнений с двумя переменными), , когда все ваши переменные выпадают в любой момент, И у вас есть ложное утверждение, у вас нет решения для вашего ответа.




Поскольку у нас нет решения, нет значения, которое нужно найдено для третья переменная.




Нет заказанных троек для проверки.

Окончательный ответ — нет решения.





Пример 3 : Решите систему.

Обратите внимание, что числа в () Являются уравнением числа. Они будут использоваться в задачах для справки. целей.



Здесь не требуется никаких упрощений. Перейдем к следующий шаг.




Обратите внимание, что в каждом уравнении отсутствует переменная. Например уравнение (1) отсутствует z. Мы можем использовать это в наших интересах. Мы можем использовать это уравнение в исходном виде как уравнение с переменной устранено.

Я решил исключить z .

Так как z уже исключен из первого уравнения мы будем использовать первое уравнение в исходной форме для этого шага:


* z уже исключенная форма ур. (1)




Мы все еще продолжаем устранять z , на этот раз я хочу использовать второе и третье уравнения.

Похоже, z ‘ s в второй и у третьих уравнений уже есть противоположности, поэтому нам просто нужно их сложить вместе:



* z ‘s иметь противоположное коэффициенты

* z ‘s выпал




Соединение двух найденных нами уравнений вместе теперь у нас есть система двух уравнений и двух неизвестных.

Вы можете использовать метод исключения или замены для Найди решение. Я собираюсь продолжить и придерживаться метода исключения, чтобы завершить это.

Давайте сначала соединим эти уравнения:


* Поместите уравнения, найденные в шагах 2 и 3
вместе в одну систему


Обратите внимание, как мы получили точно такие же два уравнения.Это похоже, что все снова выпадет, но на этот раз мы в конечном итоге 0 = 0.

Давайте продолжим и покажем этот шаг, умножив уравнение (4) по -1, чтобы получить противоположные коэффициенты для x и затем сложите два уравнения.



* Мног.экв. (4) по -1

* x ‘s иметь противоположное коэффициенты

* Все переменные выпали И
у нас есть ИСТИНА


Как и предполагалось, все переменные выпали И мы имеем верное заявление.Это означает, что существует бесконечное количество решений.




Как упоминалось выше, существует бесконечное количество решения. Таким образом, третьей переменной нет.




Нет заказанной тройки для проверки.

Вы можете написать свой ответ разными способами:
{( x, y, z ) | x + y = 9} OR {( x, y, z ) | y + z = 7} ИЛИ {( x, y, z ) | x — z = 2}



Практические задачи

Это практические задачи, которые помогут вам следующий уровень. Это позволит вам проверить и понять, понимаете ли вы эти типы проблем. Math работает так же, как что-либо иначе, если вы хотите добиться успеха в этом, вам нужно практиковаться Это. Даже лучшим спортсменам и музыкантам помогали на протяжении всего пути. практиковаться, практиковаться, практиковаться, чтобы стать лучше в своем виде спорта или инструменте. На самом деле не бывает слишком много практики.

Чтобы получить от них максимальную отдачу, вы должны работать проблема на свой, а затем проверьте свой ответ, щелкнув ссылку для ответ / обсуждение для этой проблемы . По ссылке вы найдете ответ а также любые шаги, которые привели к поиску этого ответа.

Практика Проблемы 1a — 1b: Решите систему.


Нужна дополнительная помощь по этим темам?



Последнее обновление 10 июля 2011 г. Ким Сьюард.
Авторские права на все содержимое (C) 2001 — 2011, WTAMU и Kim Seward. Все права защищены.

Многоступенчатые уравнения — наименьшее (или наибольшее) решение

Просмотр по стандартам Common Core State

Просмотр по общим основным государственным стандартам Выберите категорию Расчет (12) Информатика (2) 1 класс (24) Геометрия (3) Измерения и данные (4) Числа и операции по основанию десяти (7) Операции и алгебраическое мышление (10) 2 класс ( 18) Геометрия (3) Измерение и данные (3) Число и операции в десятичной системе (11) Операции и алгебраическое мышление (1) Уровень 3 (25) Измерения и данные (14) Число и операции в десятичной системе (7) Число и Операции — дроби (2) Операции и алгебраическое мышление (2) 4 класс (52) Измерения и данные (10) Число и операции в десятичной системе (18) Числа и операции — дроби (18) Операции и алгебраическое мышление (6) 5 класс (68) Геометрия (1) Измерения и данные (2) Числа и операции в базе десяти (26) Числа и операции — дроби (33) Операции и алгебраическое мышление (7) 6 класс (70) Выражения и уравнения (21) Геометрия ( 8) Соотношения и пропорциональные отношения (10) Статистика и вероятность (6) Числовая система em (26) 7 класс (55) Выражения и уравнения (10) Геометрия (19) Отношения и пропорциональные отношения (4) Статистика и вероятность (4) Система счисления (18) 8 класс (85) Выражения и уравнения (38) Функции (13) Геометрия (20) Статистика и вероятность (2) Система счисления (13) Высшая школа: Алгебра (32) Арифметика с многочленами и рациональными выражениями (5) Создание уравнений (4) Рассуждение с помощью уравнений и неравенств (22) Видение Структура в выражениях (6) Старшая школа: функции (30) Построение функций (5) Функции интерпретации (13) Линейные, квадратичные и экспоненциальные модели (5) Тригонометрические функции (7) Старшая школа: геометрия (39) Круги (3) Конгруэнтность (8) Выражение геометрических свойств уравнениями (22) Геометрические измерения и размерность (3) Сходство, прямоугольные треугольники и тригонометрия (5) Средняя школа: число и количество (16) Система комплексных чисел (5) Система действительных чисел (9) ) Вектор и мат rix Количества (2) Средняя школа: статистика и вероятность (4) Условная вероятность и правила вероятности (2) Интерпретация категориальных и количественных данных (2) Детский сад (13) Подсчет и количество элементов (3) Геометрия (3) Число и операции в База десять (1) Операции и алгебраическое мышление (6)

Обсудить природу решений линейных уравнений с тремя переменными

Каждое уравнение в системе представляет собой плоскость в трехмерном пространстве, и решение системы уравнений — это в точности точка пересечения трех плоскостей, определяемых тремя линейными уравнениями системы.

Система может иметь только одно решение, бесконечно много решений или ни одного решения в зависимости от того, как плоскости пересекают друг друга.

  • Решая линейные уравнения, если мы получаем разные значения для x, y и z, то мы можем решить, что они имеют уникальные решения.
  • Если вы получите ложное уравнение, такое как 0 = 1, на любом из шагов система не имеет решения.
  • Если вы не получите ложное решение, а получите тождество, например 0 = 0, то система имеет бесконечно много решений.

Вопрос 1:

Обсудите природу решений следующей системы уравнений.

х + 2у — z = 6; −3x — 2y + 5z = −12; x −2z = 3

Решение:

x + 2y — z = 6 —— (1)

-3x — 2y + 5z = −12 —— (2)

x −2z = 3 —— (3)

(1) + (2)

x + 2y — z = 6

-3x — 2y + 5z = −12

——- —————

-2x + 4z = -6 —— (4)

Из (3),

x = 3 + 2z

Применяя значение x в (4)

-2 (3 + 2z) + 4z = -6

-6 — 4z + 4z = -6

-6 + 6 = 0

0 = 0

Итак, система имеет бесконечно много решений.

Вопрос 2:

Обсудите природу решений следующей системы уравнений.

2y + z = 3 (−x +1); −x + 3y −z = −4; 3x + 2y + z = -1/2

Решение:

2y + z = 3 (−x +1)

2y + z = -3x + 3

3x + 2y + z = 3 — —- (1)

−x + 3y −z = −4 —— (2)

3x + 2y + z = -1/2

2 (3x + 2y + z) = -1

6x + 4y + 2z = -1 —— (3)

(1) + (2)

3x + 2y + z = 3

−x + 3y −z = −4

——————— —

2x + 5y = -1 — (4)

2 (2) + (3)

−2x + 6y — 2z = −8

6x + 4y + 2z = -1

—————— —-

4x + 10y = -9 — (5)

2 (4) — (5)

4x + 10y = -2

4x + 10y = -9

(-) (-) (+)

———— ——

0 = 7

Следовательно, у системы нет решения.

Вопрос 3:

Обсудите природу решений следующей системы уравнений.

(y + z) / 4 = (z + x) / 3 = (x + y) / 2; x + y + z = 27

Решение:

(y + z) / 4 = (z + x) / 3

3 (y + z) = 4 (z + x)

3y + 3z = 4z + 4x

4x — 3y + 4z — 3z = 0

4x — 3y + z = 0 — (1)

(z + x) / 3 = (x + y) / 2

2 (z + x) = 3 (x + y)

2z + 2x = 3x + 3y

3x — 2x + 3y — 2z = 0

x + 3y — 2z = 0 —- (2)

x + y + z = 27 —- (3)

(1) + (2)

4x — 3y + z = 0

x + 3y — 2z = 0

—— —————

5x — z = 0 —- (4)

(1) — 3 (3)

4x — 3y + z = 0

3x + 3y + 3z = 81

———————

7x + 4z = 81 — (5)

4 (4) + (5)

20x — 4z = 0

7x + 4z = 81

—————

27x = 81

x = 81/27 = 3

Следовательно, уравнения будут иметь единственное решение.

Дальнейшие поиски решения дают

(4) ==> 7x + 4z = 81

7 (3) + 4z = 81

21 + 4z = 81

4z = 81 — 21

4z = 60

z = 15

(1) ==> 4x — 3y + z = 0

4 (3) — 3y + 15 = 0

12 + 15 — 3y = 0

-3y = 27

y = -9

Помимо вышеперечисленного, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.

Если у вас есть какие-либо отзывы о наших математических материалах, напишите нам:

[email protected]

Мы всегда ценим ваши отзывы.

Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.

ЗАДАЧИ СО СЛОВАМИ

Задачи со словами HCF и LCM

Задачи со словами на простых уравнениях

Задачи со словами на линейных уравнениях

Задачи со словами на квадратных уравнениях

Проблемы со словами

Проблемы со словами в поездах

Проблемы со словами по площади и периметру

Проблемы со словами по прямому и обратному изменению

Проблемы со словами по цене за единицу

Проблемы со словами по количеству слов

задачи по сравнению ставок

Преобразование обычных единиц в текстовые задачи

Преобразование метрических единиц в текстовые задачи

Word задачи по простому проценту

Word по сложным процентам

ngles

Проблемы с дополнительными и дополнительными углами в словах

Проблемы со словами с двойными фактами

Проблемы со словами в тригонометрии

Проблемы со словами в процентах

Проблемы со словами о прибылях и убытках 9336 Задачи со словами

Задачи с десятичными словами

Задачи со словами на дроби

Задачи со словами на смешанные дроби

Одношаговые задачи со словами с уравнениями

Проблемы со словами с линейным неравенством и соотношением слов90 Задачи со словами

Проблемы со временем и рабочими словами

Задачи со словами на множествах и диаграммах Венна

Задачи со словами на возрастах

Проблемы со словами по теореме Пифагора

Процент числового слова проблемы

Проблемы со словами при постоянной скорости

Проблемы со словами при средней скорости

Проблемы со словами на сумме углов треугольника 180 градусов

ДРУГИЕ ТЕМЫ

Сокращения прибыли и убытков

Сокращение в процентах

Сокращение в таблице времен

Сокращение времени, скорости и расстояния

Сокращение соотношения и пропорции

Домен и диапазон рациональных функций 9336 функции с отверстиями

Графики рациональных функций

Графики рациональных функций с отверстиями

Преобразование повторяющихся десятичных знаков в дроби

Десятичное представление рациональных чисел

Поиск корня из длинного квадрата видение

Л. Метод CM для решения временных и рабочих задач

Преобразование задач со словами в алгебраические выражения

Остаток при делении 2 в степени 256 на 17

Остаток при делении в степени 17 на 16

Сумма всех трехзначных чисел, делимых на 6

Сумма всех трехзначных чисел, делимых на 7

Сумма всех трехзначных чисел, делящихся на 8

Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4

Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами

Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3

Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6

.

Related Posts

Leave A Comment