2

Как решать линейные уравнения — формулы и примеры решения простейших уравнений

Научим решать линейные уравнения быстрее всех в классе

Начать учиться

440.5K

Сначала мы решаем уравнения в школе в тетрадях, а потом в уме на совещаниях. В статье расскажем, как решать самые простые уравнения быстро и легко.

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.

Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.

Решить уравнение значит найти все возможные корни или убедиться, что их нет.

Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Какие бывают виды уравнений

Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.

Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.

Линейное уравнение выглядят так: ах + b = 0, где a и b — действительные числа. Вот, что поможет в решении:

  • если а ≠ 0 — уравнение имеет единственный корень: х = -b : а;

  • если а = 0 — уравнение корней не имеет;

  • если

    а и b равны нулю, то корнем уравнения является любое число.

Квадратное уравнение выглядит так: ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Числовой коэффициент — число, которое стоит при неизвестной переменной.

Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:

  • кубические,
  • уравнения четвертой степени,
  • иррациональные и рациональные,
  • системы линейных алгебраических уравнений и другие.

Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.

Как решать простые уравнения

Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.

1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.

Для примера рассмотрим простейшее уравнение: x+3=5.

Начнем с того, что в каждом уравнении есть левая и правая часть.

Перенесем 3 из левой части в правую и меняем знак на противоположный.

Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.

Решим еще один пример: 6x = 5x + 10.

Как решаем:

  1. Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.

    6x — 5x = 10

  2. Приведем подобные и завершим решение.

    x = 10

Ответ: x = 10.

2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.

Применим правило при решении примера: 4x=8.

При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.

Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.

Разделим каждую часть на 4. Как это выглядит:

Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:

Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: -4x = 12

Как решаем:

  1. Разделим обе части на -4, чтобы коэффициент при неизвестной стал равен единице.

    -4x = 12 | : (-4)
    x = −3

Ответ: x = −3.

Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.

Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.

Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.

Алгоритм решения простого линейного уравнения
  1. Раскрываем скобки, если они есть.
  2. Группируем члены, которые содержат неизвестную переменную в одну часть уравнения, остальные члены — в другую.
  3. Приводим подобные члены в каждой части уравнения.
  4. Решаем уравнение, которое получилось: aх = b. Делим обе части на коэффициент при неизвестном.

Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.

Примеры линейных уравнений

Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!

Пример 1. Как правильно решить уравнение: 6х + 1 = 19.

Решаем так:

  1. ЮПеренести 1 из левой части в правую со знаком минус.

    6х = 19 − 1

  2. Выполнить вычитание.

    6х = 18

  3. Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.

    х = 3

Ответ: 3.

Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3(х − 4) + 2х − 1.

Решаем так:

  1. Раскрыть скобки

    5х − 15 + 2 = 3х − 12 + 2х − 1

  2. Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены.

    Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.

    5х − 3х − 2х = −12 − 1 + 15 − 2

  3. Приведем подобные члены.

    0х = 0

Ответ: х — любое число.

Пример 3. Решить: 4х = 1/8.

Решаем так:

  1. Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.

    х = 1/8 : 4

    х = 1/32

Ответ: 1/32.

Пример 4. Решить: 4(х + 2) = 6 − 7х.

Решаем так:

  1. 4х + 8 = 6 − 7х

  2. 4х + 7х = 6 − 8

  3. 11х = −2

  4. х = −2 : 11

  5. х = −2/11

Ответ: −2/11 или −(0,18). О десятичных дробях можно почитать в другой нашей статье.

Пример 5. Решить:

Решаем так:

  2. 3(3х — 4) = 4 · 7х + 24

  3. 9х — 12 = 28х + 24

  4. 9х — 28х = 24 + 12

  5. -19х = 36

  6. х = 36 : (-19)

  7. х = — 36/19

Ответ: 1 17/19.

Пример 6. Как решить линейное уравнение: х + 7 = х + 4.

Решаем так:

  1. Сгруппировать в левой части неизвестные члены, в правой — свободные члены:

    х – х = 4 — 7

  2. Приведем подобные члены.

    0 * х = — 3

Ответ: нет решений.

Пример 7. Решить: 2(х + 3) = 5 − 7х.

Решаем так:

  1. 2х + 6 = 5 − 7х

  2. 2х + 7х = 5 − 6

  3. 9х = −1

  4. х = −1/9

Ответ: −1/9.

 

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Лидия Казанцева

Автор Skysmart

К предыдущей статье

470.3K

Решение уравнений с дробями

К следующей статье

396. 7K

Натуральные числа

Получите план обучения, который поможет понять и полюбить математику

Премиум

На вводном уроке с методистом

  1. Проверим знание линейной алгебры и других разделов математики, выявим пробелы

  2. Подберём курс

  3. Познакомим с интерактивной платформой

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Системы линейных уравнений

Системы линейных уравнений

Часто приходится рассматривать несколько функций одного и того же независимого переменная. Рассмотрим предыдущий пример, где x — количество произведенных изделий. и продано, была независимой переменной в трех функциях, функции затрат, функция дохода и функция прибыли.

            В целом может быть:

n уравнений

v переменные

            Есть четыре метода решения систем линейных уравнений:

а. графическое решение

б. алгебраическое решение

в. метод исключения

д. метод замены

Графическое решение

Пример 1

            данные два следующих линейных уравнения:

f(x) = y = 1 + 0,5x

f(x) = y = 11 — 2x

Постройте график первого уравнения , найдя две точки данных. Установив сначала x, а затем y равными нулю, можно найти точку пересечения y на вертикальная ось и точка пересечения x с горизонтальной осью.

            Если x = 0, тогда f(0) = 1 + 0,5(0) = 1

            Если y = 0, тогда f(x) = 0 = 1 + 0,5x

-. 5x = 1

х  = -2

            Результирующий точки данных: (0,1) и (-2,0) 90 908.

Постройте график второго уравнения  , найдя две точки данных. К установив сначала x, а затем y равными нулю, можно найти точку пересечения y по вертикальной оси и точку пересечения x по горизонтальной оси.

            Если x = 0, тогда f(0) = 11 — 2(0) = 11

            Если y = 0, тогда f(x) = 0 = 11 — 2x

2x = 11

х =  5,5 90 908

            Результирующий точки данных: (0,11) и (5,5,0) 90 908.

В точке пересечения двух уравнений x и y имеют одинаковые значения. Из графика эти значения можно прочитать как x = 4 и y = 3,

 

Пример 2

            данные два следующих линейных уравнения:

f(x) = y = 15 —  5x

f(x) = y = 25 — 5x

Постройте график первого уравнения , найдя две точки данных. Установив сначала x, а затем y равными нулю, можно найти точку пересечения y на вертикальная ось и точка пересечения x с горизонтальной осью.

            Если x = 0, тогда f(0) = 15 — 5(0) = 15

            Если y = 0, тогда f(x) = 0 = 15 — 5x

5x = 15

х =  3

            Результирующий точки данных: (0,15) и (3,0) 90 908.

Постройте график второго уравнения  , найдя две точки данных. К установив сначала x, а затем y равными нулю, можно найти точку пересечения y по вертикальной оси и точку пересечения x по горизонтальной оси.

            Если x = 0, тогда f(0) = 25 — 5(0) = 25

            Если y = 0, тогда f(x) = 0 = 25 — 5x

5x = 25

х =  5

            Результирующий точки данных: (0,25) и (5,0) 90 908.

Из графика видно, что эти линии не пересекаются. Они параллельны. У них одинаковый наклон. Уникального решения нет.

 

Пример 3

            данные два следующих линейных уравнения:

21x — 7y = 14

-15x + 5y = -10

            Переписать уравнения, поместив их в форму пересечения наклона.

            Первый уравнение становится

7 лет = -14 + 21 x 90 908

у = -2 + 3x

            Второй уравнение становится

5 лет = -10 + 15 x 90 908

у  = -2 + 3 x 90 908

Постройте график любого уравнения, найдя две точки данных. Установив сначала x и тогда y равны нулю, можно найти точку пересечения y на вертикали ось и точка пересечения x на горизонтальной оси.

            Если x = 0, тогда f(0) = -2 +3(0) = -2

            Если y = 0, тогда f(x) = 0 = -2 + 3x

3x = 2

х =  2/3 90 908

            Результирующий точки данных: (0,-2) и (2/3,0)

Из графика видно, что эти уравнения эквивалентны. Там являются бесконечным числом решений.

 

Алгебраическое решение

Этот метод будет проиллюстрирован с помощью анализа спроса и предложения. Этот тип анализа заимствован из работ великого английского экономиста Альфреда Маршалл.

Q  = количество     и  P  =  цена

P (s) = функция предложения   и P (d)  = функция спроса

При построении графика цена располагается по вертикальной оси. Таким образом, цена является зависимая переменная. Было бы логичнее рассматривать количество как зависимая переменная, и именно этот подход использовал великий французский экономист, Леон Вальрас. Однако по соглашению экономисты продолжают строить графики, используя Анализ Маршалла, который называют маршаллианским крестом.

Цель состоит в том, чтобы найти равновесную цену и количество, т.е. решение где цена и количество будут иметь одинаковые значения в обеих функциях предложения и функция цены.

            Q E = равновесное количество P E   = равновесная цена

            Для равновесия 
предложение = спрос
или Р(с) = Р(д)

Учитывая следующие функции

            P (с) = 3Q + 10 и P (d) = -1/2Q + 80

Приравняйте уравнения друг к другу и найдите Q.

            П (с) =  3Q + 10  =   -1/2Q + 80  = P (d)

3,5Q =  70

Q =  20 Равновесное количество равно 20.

Подставьте это значение вместо Q в любое уравнение и найдите P.

            П (с) = 3(20) + 10

            P (с) = 70

            P (г) = -1/2(20) + 80 90 908

            P (г) =  70 Равновесная цена равна 70,

.


Метод исключения

Этот метод включает удаление переменных из уравнений. Переменные удаляются последовательно до тех пор, пока не останется только одна последняя переменная, т. е. пока не останется одно уравнение с одним неизвестным. Затем это уравнение решается для одного неизвестного. Затем решение используется для нахождения второго последняя переменная. Процедура повторяется путем добавления обратных переменных в качестве их решений. найдены.

Пример 1

2x + 3y = 5

-5x   — 2y  = 4 

Процедура: устранить y. Коэффициенты y неодинаковы в два уравнения, но если бы они были, можно было бы добавить два уравнения и члены y сократятся. Однако можно через умножение каждого уравнения, чтобы заставить члены y иметь одинаковые коэффициенты в каждом уравнении.

            Шаг 1: Умножьте первое уравнение на 2, а второе уравнение умножьте на 3. Это дает

4x + 6y = 10

-15x   — 6y = 12 

            Шаг 2: Сложите два уравнения. Это дает

-11x     =     22

х          = -2

            Шаг 3: Найдите y в любом из исходных уравнений

2(-2) + 3 года = 5

3 года  =  9

г =  3 или

-5(-2) — 2г = 4

10 – 2 года  =     4

2 года  =     6

г  =  3

Альтернативная процедура: исключить x. Коэффициенты при х не совпадают в двух уравнениях, но если бы они были, можно было бы добавить два уравнения и члены y сокращаются. Однако это возможно путем умножения каждого уравнения, чтобы заставить члены x имеют одинаковые коэффициенты в каждом уравнении.

            Шаг 1: Умножьте первое уравнение на 5, а второе уравнение умножьте на 2. Это дает

10x + 15y = 25

-10x   — 4y     = 8

            Шаг 2: Сложите два уравнения. Это дает

11 лет      =     33

у          = 3

            Шаг 3: Найдите x в любом из исходных уравнений

2x + 3(3) = 5

2x = -4

 х = -2 или

-5x     — 2(3)  = 4

           — 5x = 10

х  =     -2

 

Пример 2

2x 1   + 5x 2   +  7x 3   = 2

4x 1  — 4x 2  —  3x 3  = 7

3x 1   — 3x 2   —  2x 3   = 5

В этом примере есть три переменные: x 1 , x 2 и х 3 . Одна из возможных процедур — исключить первые x 1 , , чтобы исключить следующие x 2 , а затем найти x 3 . Значение, полученное для x 3 , используется для решения x 2 и наконец, значения, полученные для x 3 и x 2 , используются для найти х 1 .

Процедура     Часть A  Первое устранение x 1 .

            Шаг 1. Умножение первое уравнение на 2 и вычесть второе уравнение из первого уравнение. Это дает

4x 1   + 10x 2   +  14x 3   = 4 первое уравнение

4x 1 — 4x 2 — — 3x 3 =  7 второе уравнение

14x 2    + 17x 3 = -3 второе уравнение вычитается из первого

            Шаг 2. Умножение первое уравнение на 3, третье уравнение умножить на 2 и вычесть третье уравнение из первого уравнения. Это дает

6x 1   + 15x 2   +  21x 3   = 6 первое уравнение

6x 1   — 6x 2   —  4x 3        = 10 третье уравнение

21x 2    + 25x 3 = -4 третье уравнение вычитается из первого

Процедура     Часть B  Второе устранение x 2 . Из части А осталось два уравнения. Из этих двух уравнений исключить х 2 .

14x 2    + 17x 3      = -3 первое уравнение

21x 2    + 25x 3      = -4 второе уравнение

            Шаг 1. Умножение первое уравнение на 21, второе уравнение умножить на 14. и вычесть второе уравнение из первого уравнения. Это дает

294x 2    + 357x 3      = -63 первое уравнение

294x 2    + 350x 3      = -56 второе уравнение

7x 3   =   -7 второе уравнение вычитается из первого

                                                 x 3 =   -1

Часть С Найдите x 2 , вставив значение, полученное для x 3 , в любое уравнение из части B.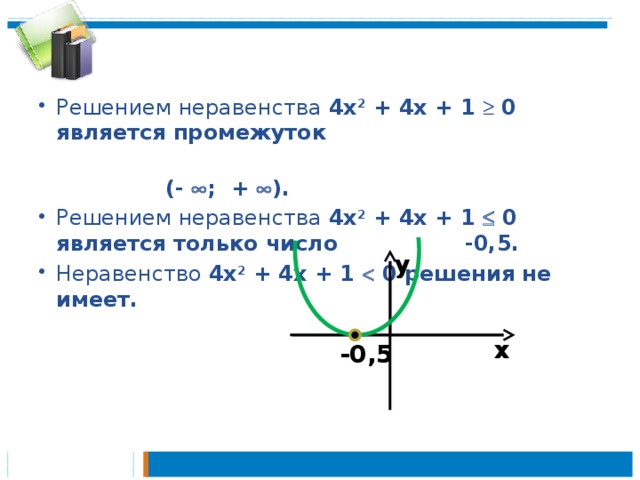

14x 2    + 17(-1)     = -3

1 4x 2    =     14

х 2    =     1 или

21x 2    + 25(-1)    = -4

21x 2 =   21

х 2 =     1  

Часть D Найдите x 1 , подставив полученные значения x 2 andx 3 в любом из трех исходных уравнений.

2x 1   + 5x 2 + 7x 3   =  2 первое исходное уравнение

2x 1   + 5(1) +  7(-1) =  2

2x 1     =  4

x 1     =  2                    или

4x 1 — 4x 2   —  3x 3   =   7                    секунда исходное уравнение

4x 1  — 4(1) —  3(-1) =  7

4x 1     =  8

х 1     =  2 или

3x 1 — 3x 2   —  2x 3   =  5 третье исходное уравнение

3x 1  — 3(1) -2(-1) = 5

3x 1 =  6

х 1     =  2

Метод замены

Это включает в себя выражение одной переменной через другую до тех пор, пока не будет одно уравнение с одним неизвестным.