Сумма цифр трехзначного числа. Решение задачи на Python
Вводится трехзначное число. Написать программу, которая вычисляет сумму его цифр.
(Это задача на линейные алгоритмы, если требуется найти сумму цифр числа произвольной длины с помощью цикла см. задачу «Сумма и произведение цифр числа».)
Например, если было введено 349, программа должна вывести на экран число 16, так как 3 + 4 + 9 = 16.
Как извлечь отдельные цифры из числа? Если число разделить нацело на десять, в остатке будет последняя цифра этого числа. Например, если 349 разделить нацело на 10, то получится частное 34 и остаток 9. Если потом 34 разделить также, получится частное 3 и остаток 4; далее при делении 3 на 10 получим частное 0 и остаток 3.
В языках программирования почти всегда есть две операции:
1) нахождение целого при делении нацело,
2) нахождение остатка при делении нацело.
В языке программирования Python первая операция обозначается % (знаком процента).
Например:
>>> 34 // 10 3 >>> 34 % 10 4
Примечание. Операции деления нацело и нахождения остатка с точки зрения арифметики применимы только к целым числам. Но в Python их можно использовать и по отношению к дробным числам:
>>> 34.5 % 10 4.5 >>> 34.5 // 10 3.0 >>> 34.5 // 12.9 2.0
Алгоритм нахождения суммы цифр трехзначного числа abc (где a — сотни, b — десятки и c — единицы) можно описать так:
- Найти остаток от деления abc на 10, записать его в переменную d1. Это будет цифра
- Избавиться от цифры c в числе abc, разделив его нацело на 10.
- Найти остаток от деления ab на 10, записать его в переменную d2. Это будет цифра b.
- Избавиться от цифры b в числе ab, разделив его нацело на 10.
- Число a однозначное. Это еще одна цифра исходного числа.
- Сложить оставшееся число a со значениями переменных d1 и d2.
n = input("Введите трехзначное число: ")
n = int(n)
d1 = n % 10
n = n // 10
d2 = n % 10
n = n // 10
print("Сумма цифр числа:", n + d2 + d3)Пример выполнения программы:
Введите трехзначное число: 742 Сумма цифр числа: 13
Однако, если нам известно, что число состоит из трех разрядов (цифр), есть немного другой способ извлечения цифр из числа:
- Остаток от деления на 10 исходного числа дает последнюю цифру числа.
- Если найти остаток от деления на 100 исходного числа, то мы получи последние две цифры числа. Далее следует разделить полученное двухзначное число нацело на 10, и у нас окажется вторая цифра числа.
- Если исходное трехзначное число разделить нацело на 100, то получится первая цифра числа.
n = input("Введите трехзначное число: ")
n = int(n)
d1 = n % 10
d2 = n % 100 // 10
d3 = n // 100
print("Сумма цифр числа:", d1 + d2 + d3)В Python данную задачу можно решить без использования арифметических действий, а путем извлечения из исходной строки отдельных символов с последующим их преобразованием к целому.
n = input("Введите трехзначное число: ")
# Извлекается первый[0] символ строки,
# преобразуется к целому.
# Аналогично второй[1] и третий[2].
a = int(n[0])
b = int(n[1])
c = int(n[2])
print("Сумма цифр числа:", a + b + c)Задача может быть усложнена тем, что число вводится не пользователем с клавиатуры, а должно быть сгенерировано случайно. Причем обязательно трехзначное число.
В этом случае надо воспользоваться функциями randint(), randrange() или random() из модуля random. Первым двум функциям передаются диапазоны: randint(100, 999), randrange(100, 1000). Получить трехзначное число, используя random() немного сложнее:
# Функция random генерирует # случайное дробное число от 0 до 1 from random import random # При умножении на 900 получается случайное # число от 0 до 899.(9). # Если прибавить 100, то получится # от 100 до 999.(9). n = random() * 900 + 100 # Отбрасывается дробная часть, # число выводится на экран n = int(n) print(n) # Извлекается старший разряд числа # путем деления нацело на 100 a = n // 100 # Деление нацело на 10 удаляет # последнюю цифру числа.# Затем нахождение остатка при # делении на 10 извлекает последнюю цифру, # которая в исходном числе была средней. b = (n // 10) % 10 # Младший разряд числа находится # как остаток при делении нацело на 10. c = n % 10 print(a+b+c)
Больше задач в PDF
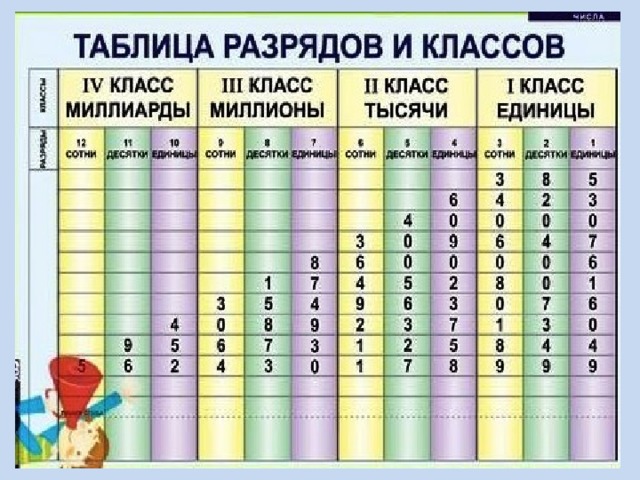
Таблица разрядов и классов чисел в математике
Научим называть и записывать многозначные числа без ошибок
Начать учиться
345.6K
Хорошо, когда все на своих местах: кастрюли в шкафу, зубная щетка — в ванной. У цифр при записи чисел тоже есть свое место. В этой статье раскроем тему разрядов и классов.
Числа и цифры
Числа — это единицы счета. С помощью чисел можно сосчитать количество предметов и определить различные величины.
Для записи чисел используются специальные знаки — цифры.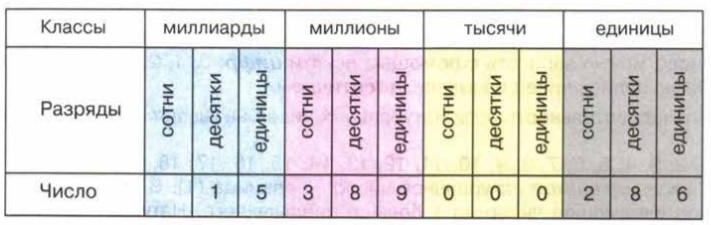
Всего их десять: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Натуральные числа — это числа, которые мы используем при счете. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …
- Единица (1) — самое маленькое число, а самого большого числа не существует.
- Ноль (0) означает, что предмета нет. Ноль не является натуральным числом.
От количества цифр в числе зависит его название.
Число, которое состоит из одного знака, называется однозначным. Наименьшее однозначное — 1, наибольшее — 9.
Число, которое состоит из двух знаков цифр, называется двузначным. Наименьшее двузначное — 10, наибольшее — 99.
Числа, которые записаны с помощью двух, трех, четырех и более цифр, называются двузначными, трехзначными, четырехзначными
Наименьшее трехзначное — 100, наибольшее — 999.Каждая цифра в записи многозначного числа занимает определенное место — позицию.
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Классы чисел
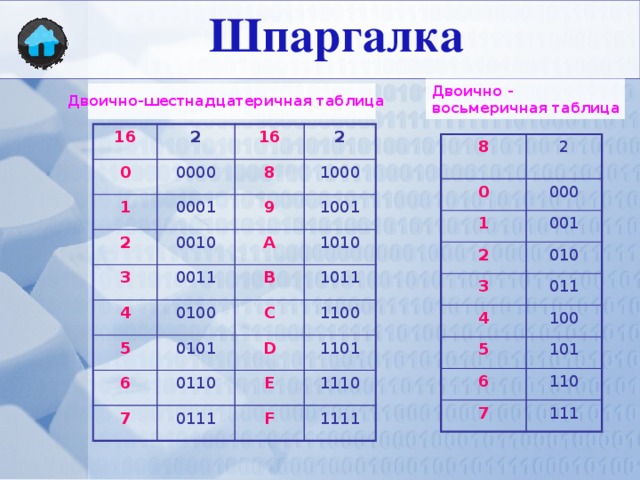
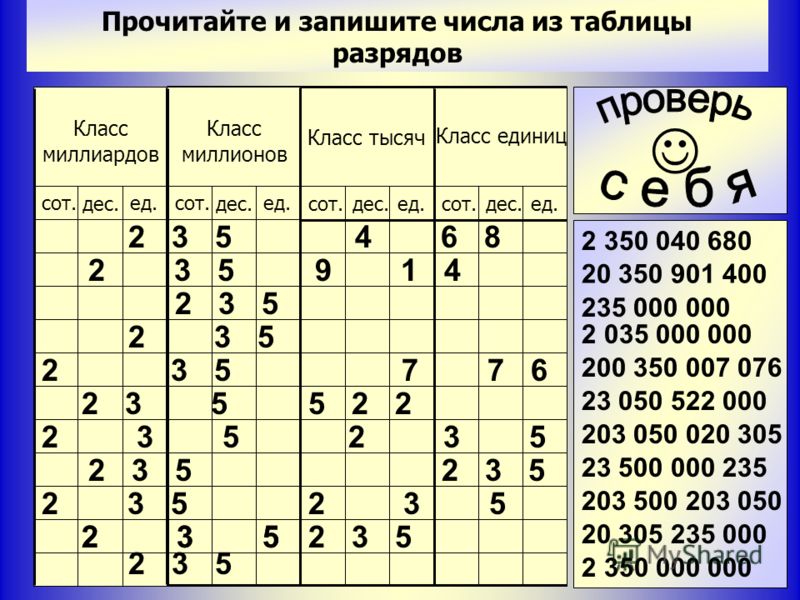
Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса.
Таблица классов:
Названия классов многозначных чисел справа налево:
- первый — класс единиц,
- второй — класс тысяч,
- третий — класс миллионов,
- четвертый — класс миллиардов,
- пятый — класс триллионов,
- шестой — класс квадриллионов,
- седьмой — класс квинтиллионов,
- восьмой — класс секстиллионов.
Чтобы читать запись многозначного числа было удобно, между классами оставляют небольшой пробел. Например, чтобы прочитать число 125911723296, удобно сначала выделить в нем классы:
- 125 911 723 296.
А теперь прочитаем число единиц каждого класса слева направо:
- 125 миллиардов 911 миллионов 723 тысячи 296.
Когда читаем класс единиц, добавлять слово «единиц» в конце не нужно.
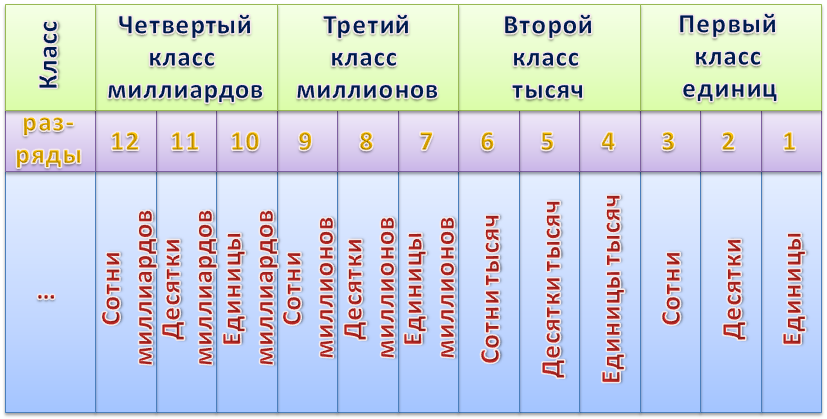
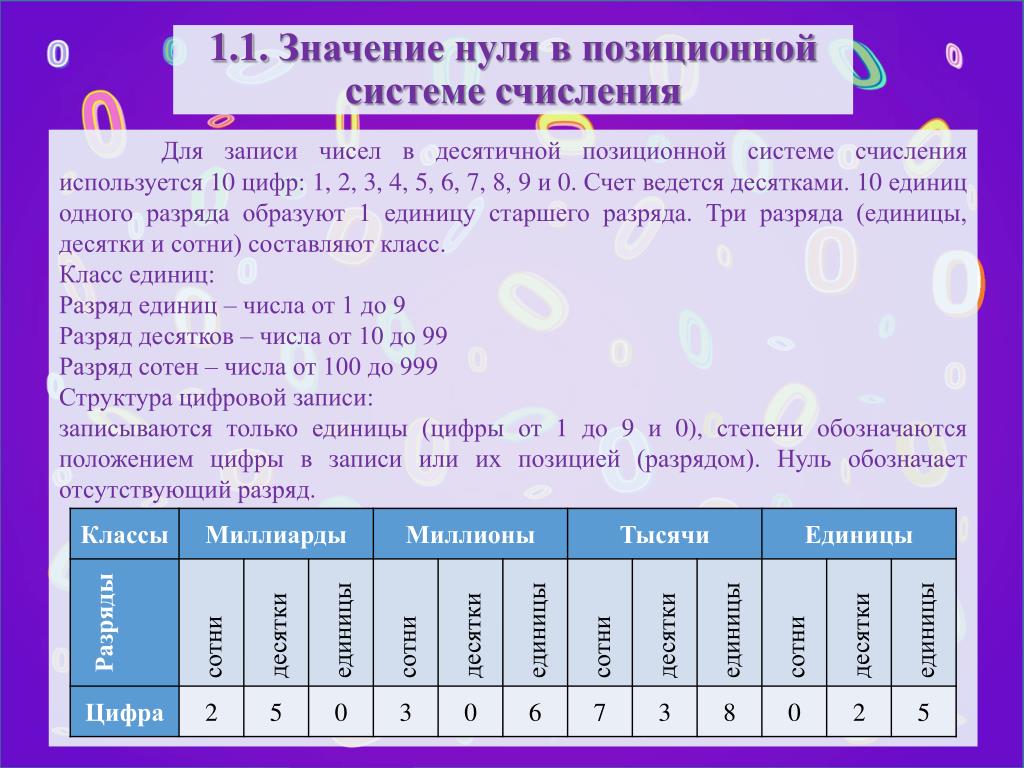
Разряды чисел
От позиции, на которой стоит цифра в записи числа, зависит ее значение. Например:
- 1 123 содержит в себе: 3 единицы, 2 десятка, 1 сотню, 1 тысячу.
Можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен, а 1 служит значением разряда тысяч.
Проясним, что такое разряд в математике.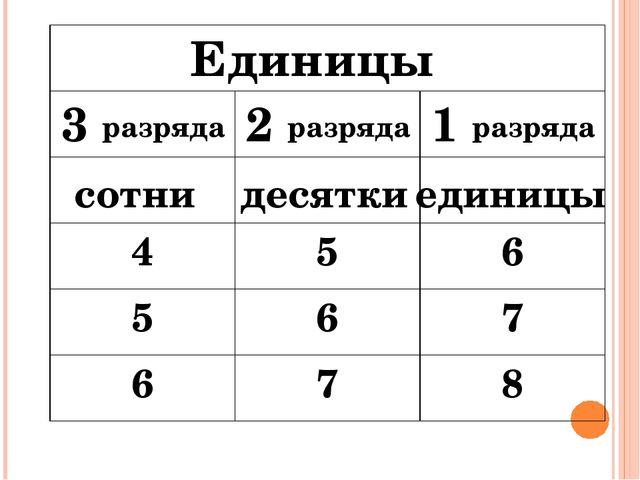
Разряд — это позиция или место расположения цифры в записи натурального числа.
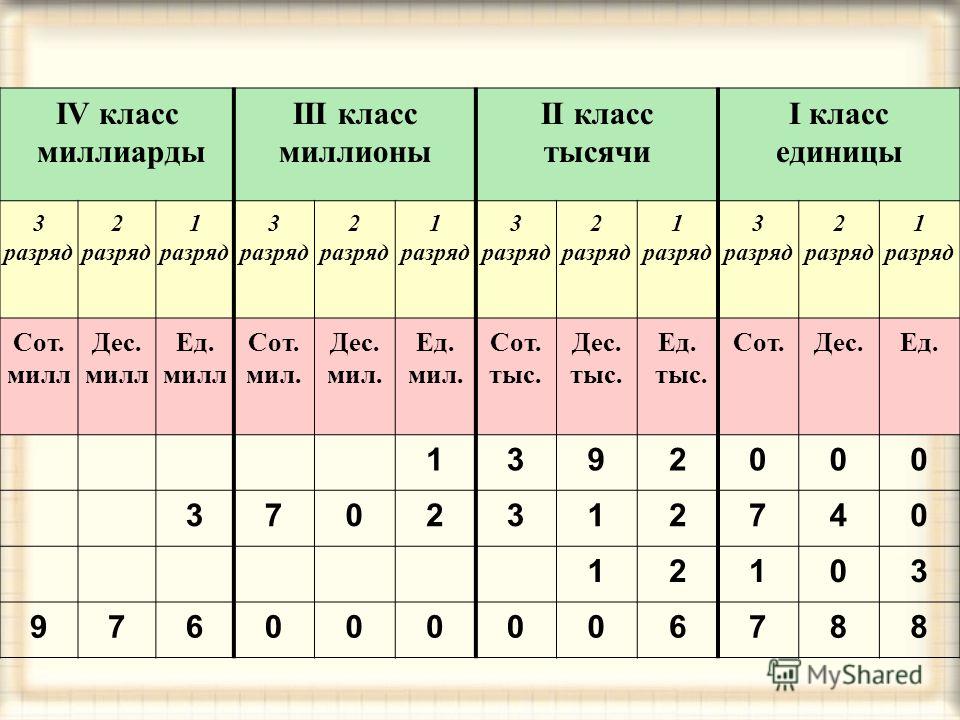
У каждого разряда есть свое название. Слева всегда живут старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Разрядные единицы обозначают так:
- Единицы — единицами первого разряда (или простыми единицами) и пишут на первом месте справа.
- Десятки — единицами второго разряда и записывают в числе на втором месте справа.
- Сотни — единицами третьего разряда и записывают на третьем месте справа.
- Единицы тысяч — единицами четвертого разряда и записывают на четвертом месте справа.
- Десятки тысяч — единицами пятого разряда и записывают на пятом месте справа.
- Сотни тысяч — единицами шестого разряда и записывают в числе на шестом месте справа и так далее.
Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.
Чтобы легче понимать математику — записывайтесь на наши курсы по математике! |
Потренируемся
Пример 1.
Записать цифрами число, в котором содержится:
- 55 единиц второго класса и 100 единиц первого класса;
- 110 единиц второго класса и 5 единиц первого класса;
- 7 единиц второго класса и 13 единиц первого класса.
Ответ:
- 55 100;
- 110 005;
- 7 013.
Все разрядные единицы, кроме простых единиц, называют составными единицами. Каждые десять единиц любого разряда составляют одну единицу следующего более высокого разряда:
- 10 единиц равны 1 десятку;
- 10 десятков равны 1 сотне;
- 10 сотен равны 1 тысяче;
- 10 тысяч равны 1 десятку тысяч;
- 10 десятков тысяч равны 1 сотне тысяч;
- 10 сотен тысяч равны 1 миллиону.
Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, нужно отбросить все цифры, обозначающие единицы низших разрядов и прочитать число, которое выражено оставшимися цифрами.
Пример 2. Сколько сотен содержится в числе 6284?
Как рассуждаем:
В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит, в числе есть две сотни.
Следующая цифра слева — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60.
Значит, в данном числе содержится 62 сотни.
Цифра 0 в любом разряде означает отсутствие единиц в данном разряде.
Проще говоря, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:
- 11 627 — одиннадцать тысяч шестьсот двадцать семь.
- 31 502 — тридцать одна тысяча пятьсот два.
Чтобы проще освоить эту тему, можно распечатать таблицу классов и разрядов для учащихся 4 класса и обращаться к ней, если возникнут сложности.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
Многочлен стандартного вида
К следующей статье
137.8K
Теорема синусов
Получите план обучения, который поможет понять и полюбить математику
ПремиумНа вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Определим уровень и подберём курс
Расскажем, как
проходят занятия
2.
5: Значимые цифры в расчетах- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 136184
Цели обучения
- Правильно использовать значащие цифры в арифметических операциях.
Округление
Прежде чем разбираться с особенностями правил определения значащих цифр в вычисляемом результате, нужно уметь правильно округлять числа. Чтобы округлить число, сначала решите, сколько значащих цифр должно быть в числе. Как только вы это узнаете, округлите до указанного количества цифр, начиная слева. Если число непосредственно справа от последней значащей цифры меньше 5, оно отбрасывается, а значение последней значащей цифры остается прежним.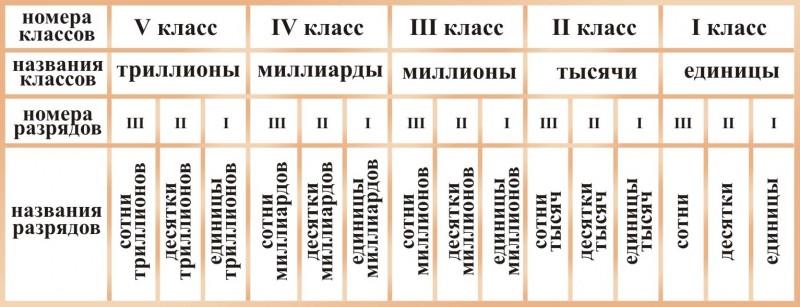
Если число непосредственно справа от последней значащей цифры больше или равно 5, последняя значащая цифра увеличивается на 1.
Рассмотрим измерение \(207,518 \: \text{m}\). Прямо сейчас измерение содержит шесть значащих цифр. Как бы мы последовательно округляли его до все меньшего и меньшего числа значащих цифр? Следуйте процессу, указанному в таблице \(\PageIndex{1}\).
| Количество значащих цифр | Округленное значение | Рассуждение |
|---|---|---|
| 6 | 207,518 | Все цифры значащие |
| 5 | 207,52 | 8 раундов от 1 до 2 |
| 4 | 207,5 | 2 выпадает |
| 3 | 208 | 5 раундов от 7 до 8 |
| 2 | 210 | 8 заменяется на 0 и округляет 0 до 1 |
| 1 | 200 | 1 заменяется на 0 |
Обратите внимание, что чем больше округление сделано, тем менее надежна цифра.
Приблизительного значения может быть достаточно для некоторых целей, но научная работа требует гораздо более высокого уровня детализации.
При математических операциях с числами важно помнить о значащих цифрах. Например, деление 125 на 307 на калькуляторе дает 0,4071661238… с бесконечным числом цифр. Но имеют ли цифры в этом ответе какое-либо практическое значение, особенно когда вы начинаете с чисел, каждое из которых имеет только три значащих цифры? При выполнении математических операций существует два правила ограничения количества значащих цифр в ответе: одно правило для сложения и вычитания, а другое правило для умножения и деления.
В операциях со значащими цифрами ответ сообщается таким образом, чтобы он отражал надежность наименее точной операции. Ответ не более точен, чем наименее точное число, использованное для получения ответа.
Умножение и деление
Для умножения или деления правило состоит в том, чтобы подсчитать количество значащих цифр в каждом умножаемом или делимом числе, а затем ограничить значащие цифры в ответе до наименьшего количества.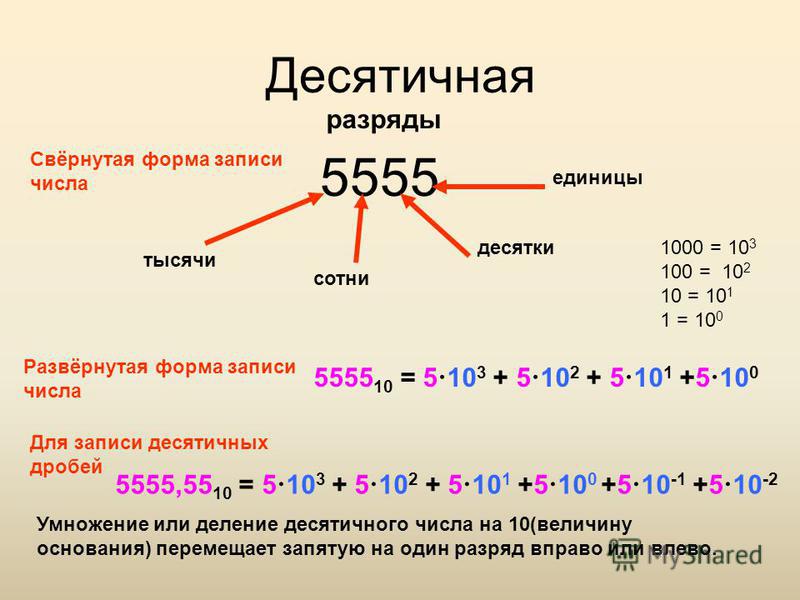
Например:
Окончательный ответ, ограниченный четырьмя значащими цифрами, равен 4094. Первая отброшенная цифра — 1, поэтому мы не округляем.
Экспертная запись обеспечивает способ передачи значащих цифр без двусмысленности. Вы просто включаете все значащие цифры в начальное число. Например, число 450 имеет две значащие цифры и будет записано в экспоненциальном представлении как 4,5 × 10 2 , тогда как число 450,0 имеет четыре значащих цифры и будет записано как 4,500 × 10 9 .0124 2 . В экспоненциальном представлении все значащие цифры указаны явно.
Пример \(\PageIndex{1}\)
Запишите ответ для каждого выражения в экспоненциальном представлении с соответствующим количеством значащих цифр.
- 23,096 × 90,300
- 125 × 9.000
Решение
a
Второй столбец помечен как «Ответ», а под ним в строке находится ответ. 93\)b
| Пояснение | Ответить |
|---|---|
| Калькулятор дает ответ 1125, но мы ограничиваем его тремя значащими цифрами. 93\) |
Сложение и вычитание
Как обрабатываются значащие числа в вычислениях? Это зависит от того, какой тип расчета выполняется. Если вычисление представляет собой сложение или вычитание, правило следующее: ограничьте сообщаемый ответ крайним правым столбцом, в котором все числа имеют общие значащие цифры. Например, если вы должны сложить 1,2 и 4,71, мы заметим, что первое число останавливает свои значащие цифры в столбце десятых, а второе число останавливает свои значащие цифры в столбце сотых.
Поэтому мы ограничиваем наш ответ десятым столбцом.
Мы опускаем последнюю цифру — 1 — потому что она не имеет значения для окончательного ответа.
Отбрасывание позиций в суммах и разностях поднимает тему округления. Несмотря на некоторые соглашения, в этом тексте мы примем следующее правило: окончательный ответ следует округлить в большую сторону, если первая пропущенная цифра 5 или больше, и округлить в меньшую сторону, если первая пропущенная цифра меньше 5.
Пример \(\PageIndex{2}\)
- 13,77 + 908.226
- 1027 + 611 + 363,06
Решение
a
| Пояснение | Ответить |
|---|---|
| Ответ калькулятора: 92\) |
b
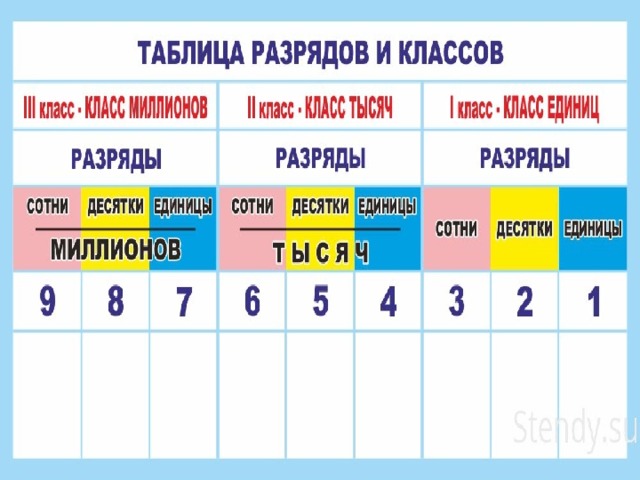Первый столбец слева помечен как «Объяснение», а под ним в строке находится объяснение. Второй столбец помечен как «Ответ», а под ним в строке находится ответ.
Поскольку последовательное округление может усугубить неточности, промежуточное округление должно выполняться правильно. При работе на бумаге всегда округляйте промежуточный результат, чтобы сохранить по крайней мере на одну цифру больше, чем можно оправдать, и перенести это число на следующий шаг в расчетах. Затем окончательный ответ округляется до правильного количества значащих цифр в самом конце.
Эта процедура предназначена для закрепления правил определения количества значащих цифр, но в некоторых случаях она может давать окончательный ответ, отличающийся последней цифрой от полученного с помощью калькулятора, где все цифры переносятся на последний шаг.
Первый столбец слева помечен как «Объяснение», а под ним в строке находится объяснение первого деления. Второй столбец помечен как «Ответ», а под ним в строке находится ответ.
На этот раз я хочу более подробно рассмотреть, почему они определены такими, какие они есть, что потребует рассмотрения некоторых особых случаев.
4, мы понимаем, что это означает, что даже если вы запишете это как 23400, 9(-3) = 0,006643, а затем округлить до требуемых двух значащих цифр, что даст число «0,0». Что здесь не так? 
Если я не ошибаюсь, значащие цифры в числе это цифры, которые были точно измерены , поэтому я бы сказал, что два нуля в 0,024 также являются значащими цифрами. (?) 
Нули слева , я полагаю, говорят вам, что эти цифры не что иное, как ноль, но вы не изменили бы их, если бы сделали более точное измерение . Изменение с 0,012 на 0,112 — это не просто повышение точности, а полное изменение значения.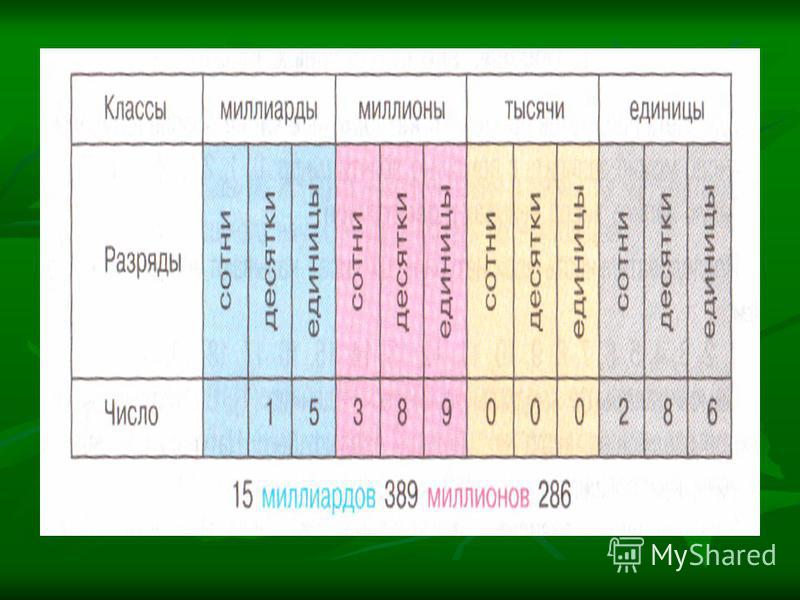 
Таким образом, значащие цифры — это все цифры, начинающиеся с первой ненулевой цифры и заканчивающиеся последней цифрой, которая будет записана в экспоненциальном представлении — последней ненулевой цифрой или, возможно, последним нулем, который написано, потому что оно представляет собой точное измерение. 
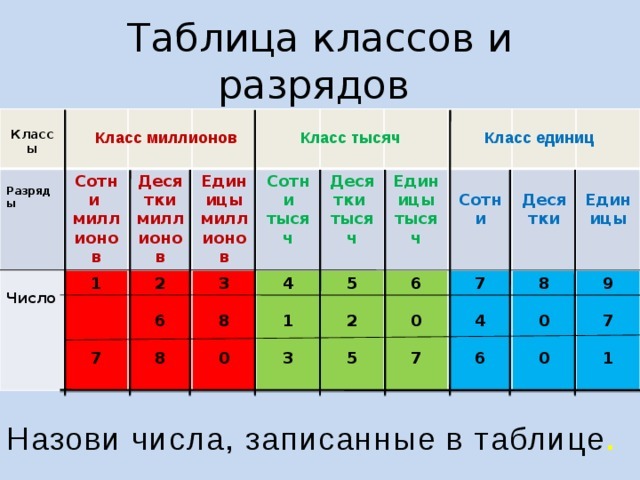Спасибо за вашу помощь. 
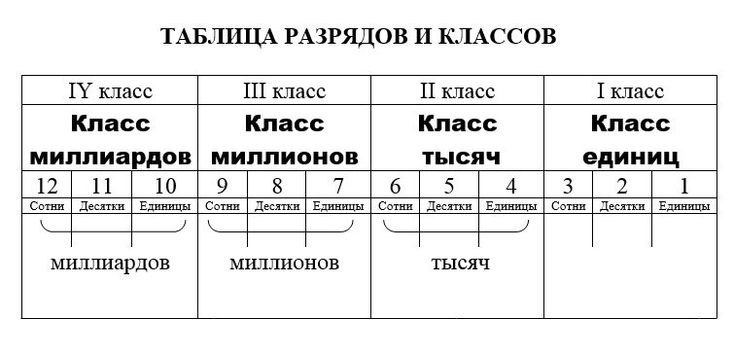Число с четырьмя значащими цифрами будет иметь примерно одну десятую этой относительной ошибки. Мы можем более точно определить «количество значащих цифр» как отрицательный десятичный логарифм этой относительной ошибки, в данном случае 2,39:
9{2.39}}\) значения числа; округление результата в большую сторону дает нам 3 значащих цифры, что согласуется с тем, как записывается 1,23. Тот факт, что нам приходится округлять, отражает тот факт, что это лишь приблизительная оценка. При подсчете значащих цифр мы делаем быструю оценку относительной ошибки, которая хороша с практической точки зрения, но недостаточна, если вам нужно быть очень осторожным с точностью. 
Если мы применим мое определение, то получим -log(0,0005/0) = -бесконечность, а не 0. Так что я рад, что сказал "без значащих цифр", а не "ноль", потому что правильный ответ таков: количество значащих цифр в этом случае НЕОПРЕДЕЛЕНО ! 
Дальнейшее похоже на то, что я сказал в своих примерах, но теперь я округляю в меньшую сторону:
Если бы вы умножили на 0,000, результат был бы 0,00000, который по-прежнему будет иметь неопределенное количество значащих цифр, так что все согласовано. 
Можете ли вы привести какие-то похожие вопросы, в ответах на которые вы уверены, и рассказать мне о контексте? Были ли вам даны какие-либо определения или правила, которым вы должны следовать?
Значащие цифры просто эмпирическое правило , а числа, близкие к десятичной степени, во многих ситуациях проблематичны. Так что здесь может не быть «правильного» ответа . Но если вопрос перефразировать, его можно изменить на менее двусмысленный. Я думаю, что именно это вы и ваш коллега-учитель в конечном счете сделали: каждый из вас ответил по-своему, переформулировав вопрос. 
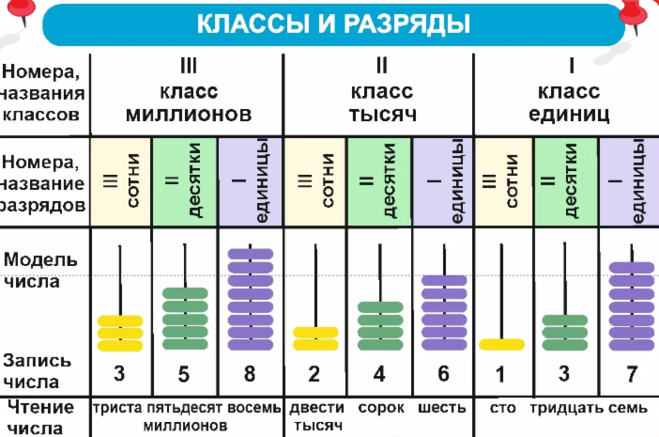
.. потому что, в конечном счете, детали правил sigfig произвольны и являются лишь грубым приближением правильных соображений распространения ошибок.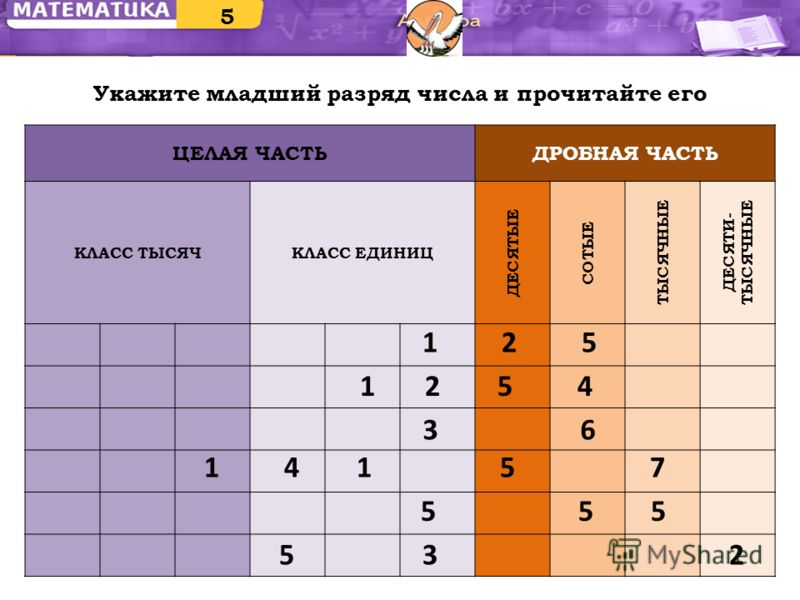 
Leave A Comment