Ответ: 2.
2.5. Количество значащих нулей в двоичной записи десятичного числа 126 равно:
1)1 2)2 3)3 4)0
Решение
Способ I. Преобразуем число 126 в двоичную систему:
Число | Неполное частное | Остаток | ||
126 | :2 | = | 63 | 0 |
:2 | = | 31 | 1 | |
31 | :2 | = | 15 | 1 |
15 | :2 | = | 7 | 1 |
7 | :2 | = | 3 | 1 |
3 | :2 | = | 1 | |
I | :2 | = | 0 | 1 |
Выписав
остатки от деления, получим: 126 = 11111102.
Способ2. Число 126 можно представить как разность чисел 128 = 27 и 2, для которых легко найти двоичные представления, после чего останется вычислить полученную разность в двоичной системе:
126 = 128 — 2 = 10000000, — 102 = 1111110.
Ответ: 1.
2.6. Перевести число 15FC16 в десятичную систему счисления.
Решение
15FCI6= 1 ∙163 + 5∙162+ 15∙161 + 12∙16° = = 4096 + 1280 + 240+ 12 = 5628 Ответ: 5628.
2.7. Перевести число 10111012 в десятичную систему счисления.
Решение
1011012 = 1∙25‘+0∙24 + 1∙23+ 1∙22+ 0∙21 + 1∙20 = 32 + 8 + 4 + 1 = 45
Ответ: 45.
2.8. Перевести
число 101,11
Решение
1011112 = 1∙ 22 + 0∙21 + 1∙20+ 1∙2-1+ 1∙2-2 = 4+ 1 + 1/2+ 1/4 = 5,75
Ответ: 5,75.
2.9. Перевести десятичную дробь 0.1875 в двоичную и восьмеричную системы счисления.
Решение
Перевод в двоичную систему
0,1875 х 2 | |
0 | ,3750 х 2 |
0 | ,7500 х 2 |
1 | ,5000 х 2 |
1 | ,0000 |
Перевод в восьмеричную систему
0,1875 х 8 | |
1 | ,5000 х 8 |
4 | ,0000 |
Ответ:
0,00112,
0,148 .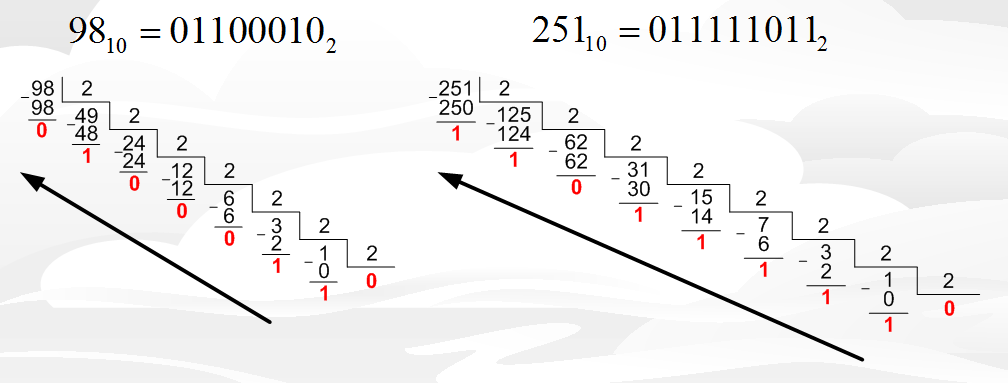
2.10. Перевести двоичное число 110111101011101111, в шестнадцатеричную систему счисления.
Решение
Разделим данное число на группы по четыре цифры, начиная справа. Поскольку при этом в крайней левой группе окажется меньше четырех цифр, дополним слева эту группу нулями: 0011 0111 1010 1110 1111.
Теперь, глядя на
двоично-шестнадцатеричную таблицу (см.
пункт «Системы счисления с основанием
2
Ответ: 37AEF]6.
2.11. Дано а = D716, b = 33l8. Какое из чисел с, записанных в двоичной системе, отвечает условию а<с<b?
1)110110012 2)110111002 3)110101112 4)110110002
Решение
Вначале
следует записать числа а
и в двоичной
системе счисления.
Получаем а = D716 = 110101112, b = 3318 = 110110012. Осталось сравнить найденные двоичные числа с предложенными вариантами. Числа из вариантов 1 и 3 совпадают с числами b и а соответственно, число из варианта 2 больше числа b, и только число из варианта 4 находится между a и b:
110101112< 110110002 < 110110012
Ответ: 4.
2.12.
1)7 2)8 3)9 4)10
Решение
Заметим,
что целое число, имеющее вид 22,
в двоичной записи представляется
одной единицей и п нулями,
приписанными справа. В нашем примере
все слагаемые являются степенями двойки
и встречаются только по
одному разу.
2 = 21= 102
8 = 23 = 10002
16 = 24= 100002
128 = 27 = 100000002
256 = 28 = 1000000002
512 = 29= 10000000002
Следовательно, сумма будет содержать столько же цифр, сколько и самое большое слагаемое: 512 = 29 = 10000000002. Итак, количество цифр равно 10.
Ответ: 4.
2.13. Укажите через запятую в порядке возрастания все числа, не превосходящие 25. запись которых в двоичной системе счисления оканчивается на 101. Ответ запишите в десятичной системе счисления.
Решение
Воспользуемся развернутой формой записи числа в двоичной системе счисления для чисел, не превышающих 25:
Аq= an-1qn-1 + an-2

Поскольку 25 < 25. такие числа должны иметь представление
а424 + a323 + 1·22 + 0·21 + 1·2°.
Рассмотрев вес варианты значений для a4 и а3 получим искомые значения Аq :
a4 | a3 | Aq |
0 | 0 | 5 |
0 | 1 | 13 |
1 | 0 | 21 |
1 | 1 | 29 |
Последнее найденное
число превосходит 25, поэтому в ответ
его включать не следует.
Ответ: 5, 13,21.
B13 — Двоичная система счисления
1. Переведите число 126 из десятичной системы счисления в двоичную систему счисления. В ответе укажите двоичное число. Основание системы счисления указывать не нужно. |
| Ответ: |
2. Переведите число 120 из десятичной системы счисления в двоичную систему счисления. Сколько единиц содержит полученное число? |
| Ответ: |
3. Переведите число 101110 из двоичной системы счисления в десятичную систему счисления. В ответе запишите полученное число. |
| Ответ: |
4. Переведите число 259 из десятичной системы счисления в двоичную систему счисления. Сколько единиц содержит полученное число? |
| Ответ: |
5. Переведите число 189 из десятичной системы счисления в двоичную систему счисления. В ответе укажите двоичное число. |
| Ответ: |
6. Переведите число 1110110 из двоичной системы счисления в десятичную систему счисления. В ответе запишите полученное число. |
| Ответ: |
7. Переведите число 147 из десятичной системы счисления в двоичную систему счисления. Сколько значащих нулей содержит полученное число? |
| Ответ: |
8. Переведите число 1100011 из двоичной системы счисления в десятичную систему счисления. В ответе запишите полученное число. |
| Ответ: |
9. Переведите число 41 из десятичной системы счисления в двоичную систему счисления. В ответе напишите полученное число. |
| Ответ: |
10. Переведите число 62 из десятичной системы счисления в двоичную систему счисления. В ответе напишите полученное число. |
| Ответ: |
11. |
| Ответ: |
12. Переведите число 222 из десятичной системы счисления в двоичную систему счисления. Сколько единиц содержит полученное число? |
| Ответ: |
13. Переведите число 10100110 из двоичной системы счисления в десятичную систему счисления. В ответе запишите полученное число. |
| Ответ: |
14. Переведите число 111 из десятичной системы счисления в двоичную систему счисления. Сколько единиц содержит полученное число? |
| Ответ: |
15. Переведите число 156 из десятичной системы счисления в двоичную систему счисления. Сколько единиц содержит полученное число? |
| Ответ: |
16. Переведите число 146 из десятичной системы счисления в двоичную систему счисления. |
| Ответ: |
17. Переведите число 10101001 из двоичной системы счисления в десятичную систему счисления. В ответе запишите полученное число. |
| Ответ: |
18. Переведите число 1101011 из двоичной системы счисления в десятичную систему счисления. В ответе запишите полученное число. |
| Ответ: |
19. Переведите число 245 из десятичной системы счисления в двоичную систему счисления. Сколько единиц содержит полученное число? |
| Ответ: |
20. Переведите число 143 из десятичной системы счисления в двоичную систему счисления. Сколько значащих нулей содержит полученное число? |
| Ответ: |
21. Переведите число 138 из десятичной системы счисления в двоичную систему счисления. В ответе напишите полученное число. |
| Ответ: |
22. Переведите число 10111001 из двоичной системы счисления в десятичную систему счисления. В ответе запишите полученное число. |
| Ответ: |
126 в двоичном формате — Как преобразовать 126 из десятичного в двоичный?
126 в двоичном формате равно 1111110. В отличие от десятичной системы счисления, где мы используем цифры от 0 до 9 для представления числа, в двоичной системе мы используем только 2 цифры, которые равны 0 и 1 (биты). Мы использовали 7 бит для представления 126 в двоичном виде. В этой статье давайте узнаем, как преобразовать десятичное число 126 в двоичное.
Как преобразовать 126 в двоичный код?
Шаг 1: Разделите 126 на 2. Используйте целое частное, полученное на этом шаге, в качестве делимого для следующего шага. Повторяйте процесс, пока частное не станет равным 0,9.0005
| Дивиденд | Остаток |
|---|---|
| 126/2 = 63 | 0 |
| 63/2 = 31 | 1 |
| 31/2 = 15 | 1 |
| 15/2 = 7 | 1 |
| 7/2 = 3 | 1 |
| 3/2 = 1 | 1 |
| 1/2 = 0 | 1 |
Шаг 2: Запишите остаток снизу вверх, т. е. в обратном хронологическом порядке. Это даст двоичный эквивалент числа 126.
е. в обратном хронологическом порядке. Это даст двоичный эквивалент числа 126.
Следовательно, двоичный эквивалент десятичного числа 126 равен 1111110.
☛ Калькулятор десятичного числа в двоичный
Давайте посмотрим на значение десятичного числа 126 в различных системы счисления.
- 126 в двоичном формате: 126₁₀ = 1111110₂
- 126 в восьмеричном: 126₁₀ = 176₈
- 126 в шестнадцатеричном формате: 126₁₀ = 7E₁₆
- 1111110₂ в десятичном формате: 126₁₀
Описание проблемы:
Часто задаваемые вопросы о 126 в двоичном формате
Что такое 126 в двоичном формате?
126 в двоичном виде равно 1111110. Чтобы найти десятичный эквивалент в двоичном, разделите 126 последовательно на 2, пока частное не станет равным 0. Двоичный эквивалент можно получить, записывая остаток на каждом шаге деления снизу вверх.
☛ Двоичное преобразование в десятичное
Найдите значение 3 × 126 в двоичной форме.
Мы знаем, что 126 в двоичном формате равно 1111110, а 3 равно 11. Используя правила двоичного умножения (0 × 0 = 0; 0 × 1 = 0, 1 × 0 = 0 и 1 × 1 = 1), мы можем умножить 1111110 × 11 = 101111010, что равно 378 в десятичной системе счисления. [126 × 3 = 378]
Сколько бит имеет число 126 в двоичном формате?
Мы можем подсчитать количество нулей и единиц, чтобы увидеть, сколько битов используется для представления 126 в двоичном формате, т. е. 1111110. Таким образом, мы использовали 7 бит для представления 126 в двоичном формате.
Как преобразовать 126 в двоичный эквивалент?
Мы можем разделить 126 на 2 и продолжать деление, пока не получим 0. Записывайте остаток на каждом шаге.
- 126 mod 2 = 0 — LSB (младший значащий бит)
- 63 модуль 2 = 1
- 31 модуль 2 = 1
- 15 мод 2 = 1
- 7 мод 2 = 1
- 3 мод 2 = 1
- 1 mod 2 = 1 — MSB (старший бит)
Записать остатки от MSB до LSB. Следовательно, десятичное число 126 в двоичном виде можно представить как 1111110.
Следовательно, десятичное число 126 в двоичном виде можно представить как 1111110.
Что такое двоичный эквивалент числа 126 + 74?
126 в двоичной системе счисления равно 1111110, а 74 равно 1001010. Мы можем сложить двоичный эквивалент 126 и 74, используя правила двоичного сложения [0 + 0 = 0, 0 + 1 = 1, 1 + 1 = 10, обратите внимание, что 1 равно перенос на следующий бит]. Следовательно, (1111110)₂ + (1001010)₂ = (11001000)₂, что есть не что иное, как 200.
☛ Калькулятор двоично-десятичного преобразования
☛ Также проверьте:
- 2 2 084
- 38 в двоичном формате — 100110
- 63 в двоичном формате — 111111
- 205 в двоичном формате — 11001101
- 34 в двоичном формате — 100010
- 109 в двоичном формате — 1101101
- 192 в двоичном формате — 11000000
Рабочие листы по математике и
наглядный учебный план
преобразовать десятичное число 126 в двоичное
Как записать 126 в двоичном формате (с основанием 2)?
126 равно 1111110 в двоичной форме
| ||||||||||||||||
Преобразование из/в десятичные, шестнадцатеричные, восьмеричные и двоичные числа. Калькулятор преобразования десятичной базы.
Здесь вы можете найти ответ на такие вопросы, как: преобразовать десятичное число 126 в двоичное или преобразовать десятичное число в двоичное.
Калькулятор преобразования десятичной базы.
Здесь вы можете найти ответ на такие вопросы, как: преобразовать десятичное число 126 в двоичное или преобразовать десятичное число в двоичное.
| Декабрь | Шестнадцатеричный | Октябрь | Бин | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 609022 60 9025 | ||||||||||||||||||||
| 1 | 1 | 1 | 1 | |||||||||||||||||||
| 2 | 2 | 2 | 10 | |||||||||||||||||||
| 3 | 3 | 3 | 11 | 6 | 4 26 | 4 | 100 | |||||||||||||||
| 5 | 5 | 5 | 101 | |||||||||||||||||||
| 6 | 6 | 6 | 110 | 7 | ||||||||||||||||||
| 7 | 111 | |||||||||||||||||||||
| 8 | 8 | 10 | 1000 | |||||||||||||||||||
| 9 | 9 | 11 | 1001 | |||||||||||||||||||
| 10 | А | 12 201656
11 | Б | 13 | 1011 | 12 | С | 14 | 1100 | 13 | D | 6 10 | 15 | 14 | E | 16 | 1110 | 15 | F | 17 | 1111 | |
| Дек | Шестнадцатер 0026 | 10 | 20 | 10000 | ||
|---|---|---|---|---|---|---|
| 17 | 11 | 21 | 10001 | |||
| 18 | 12 | 10025 26 22|||||
| 19 | 13 | 23 | 10011 | |||
| 20 | 14 | 24 | 10100 | |||
| 21 | 15 | 25 | 10101 | |||
| 5 | 26 | 10110 | ||||
| 23 | 17 | 27 | 10111 | |||
| 24 | 18 | 30 | 11000 25 25 | 19 | 31 | 11001 |
| 26 | 1A | 32 | 11010 | |||
| 27 | 1Б | 33 | 11011 | |||
| 28 | 50 61С | 11100 | ||||
| 29 | 1D | 35 | 11101 | |||
| 30 | 1E | 36 | 11110 | 3 9 002513 25 1F | 37 | 11111 |
| Декабрь | Шестнадцатеричный | Октябрь | Корзина | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 32 | 20 | 40 | 100000 | ||||||
| 33 | 504 261 21 26100001 | ||||||||
| 34 | 22 | 42 | 100010 | ||||||
| 35 | 23 | 43 | 9 1000256 | 0025 36 | 24 | 44 | 100100 | | ||
| 37 | 25 | 45 | 100101 | ||||||
| 38 | 26 | 46 | 100110 | ||||||
| 39 | 709 267 267 26100111 | ||||||||
| 40 | 28 | 50 | 101000 | ||||||
| 41 | 29 | 51 | 101001 | 2||||||
| 52 | 101010 | ||||||||
| 43 | 2B | 53 | 101011 | ||||||
| 44 | 2C | 54 | 101100 | ||||||
| 45 | 2D | 15 55 26||||||||
| 46 | 2Е | 56 | 101110 | ||||||
| 47 | 2F | 57 | 101111 |

 Основание системы счисления указывать не нужно.
Основание системы счисления указывать не нужно. Переведите число 211 из десятичной системы счисления в двоичную систему счисления. Сколько единиц содержит полученное число?
Переведите число 211 из десятичной системы счисления в двоичную систему счисления. Сколько единиц содержит полученное число?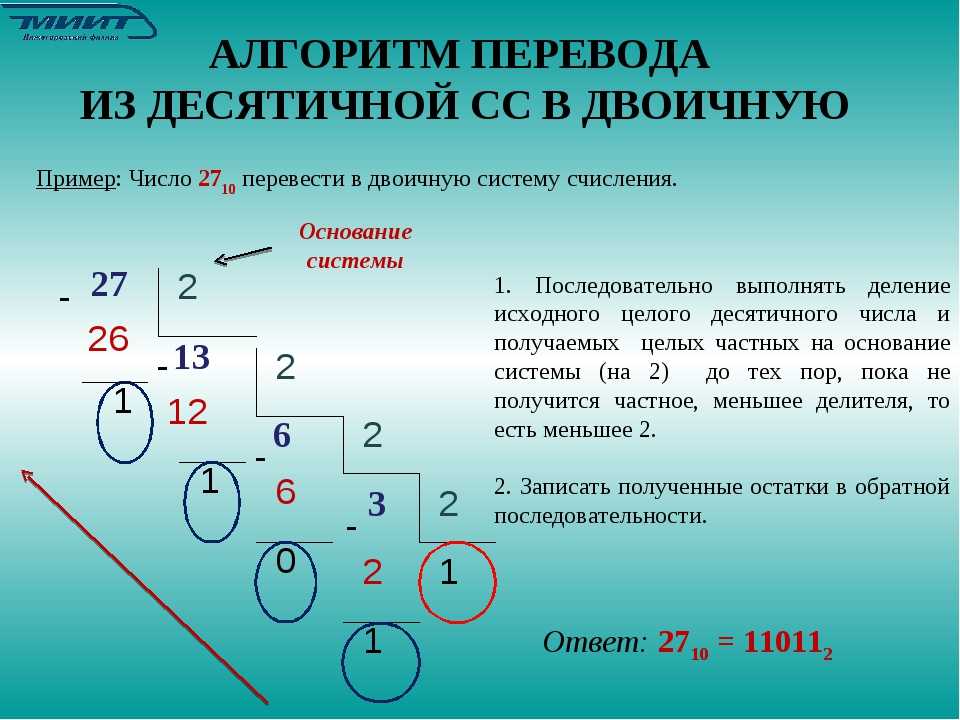 Сколько значащих нулей содержит полученное число?
Сколько значащих нулей содержит полученное число?



Leave A Comment