1 в степени 9 5: Mathway | Популярные задачи

Степень с натуральным показателем / Алгебра / Справочник по математике 5-9 класс

Главная
Справочники
Справочник по математике 5-9 класс
Алгебра
Степень с натуральным показателем

Мы помним, что степенью числа «» с натуральным показателем «», большим 1, называется произведение «» одинаковых множителей, каждый из которых равен числу «».

Выражение «» читают так: » в степени » или » — ая степень числа «, и называют степенью. При этом в этой записи число «» называют основанием степени, а число «», которое показывает число множителей в произведении, — показателем степени.

Квадрат числа — это вторая степень числа. Квадрат числа записывают так: . Читают: » в квадрате» или » во второй степени».

Куб числа — это третья степень числа. Куб числа записывают так: . Читают: » в кубе» или » в третьей степени».

В определении степени на показатель наложено ограничение 1, так как не принято рассматривать произведение, которое состоит из одного множителя. Но стоит запомнить, что степенью числа «» с показателем = 1 является само это число, то есть .

Ноль в любой степени — это ноль, единица — это единица.

Возведение рациональных чисел в степень:

При возведении неотрицательного числа в степень получаем неотрицательное число.
При возведении отрицательного

числа в степень с чётным показателем получаем положительное число, а при возведении отрицательного числа в степень с нечётным показателем получаем отрицательное число.

Пример 1: Найдите значение выражения 10³2⁴.

Решение. 10³ = 101010 = 1 000;

2⁴ = 2222 = 16;

Значит получаем: 10³2⁴ = 1 00016 = 984.

Пример 2: Докажите, что значение выражения 100

n + 8 делится нацело на 9.

Решение. Запись значения выражения 100ⁿсостоит из цифры 1 и из 2n цифр 0, а запись значения выражения 100ⁿ + 8 — из цифры 1, цифры 8 и (2n1) цифр 0. Следовательно, сумма цифр числа, являющегося значением данного выражения, равна 9. Значит, само это число делится нацело на 9.

Советуем посмотреть:

Введение в алгебру

Линейное уравнение с одной переменной

Решение задач с помощью уравнений

Тождественно равные выражения. Тождества

Свойства степени с натуральным показателем

Одночлены

Многочлены

Сложение и вычитание многочленов

Умножение одночлена на многочлен

Умножение многочлена на многочлен

Разложение многочленов на множители

Формулы сокращенного умножения

Функции

Системы линейных уравнений с двумя переменными

Алгебра

Правило встречается в следующих упражнениях:

7 класс

Номер 224, Мерзляк, Полонский, Якир, Учебник

Номер 232, Мерзляк, Полонский, Якир, Учебник

Номер 467, Мерзляк, Полонский, Якир, Учебник

Номер 523, Мерзляк, Полонский, Якир, Учебник

Номер 585, Мерзляк, Полонский, Якир, Учебник

Номер 606, Мерзляк, Полонский, Якир, Учебник

Номер 679, Мерзляк, Полонский, Якир, Учебник

Номер 687, Мерзляк, Полонский, Якир, Учебник

Номер 725, Мерзляк, Полонский, Якир, Учебник

Номер 906, Мерзляк, Полонский, Якир, Учебник

8 класс

Номер 36, Мерзляк, Полонский, Якир, Учебник

Номер 46, Мерзляк, Полонский, Якир, Учебник

Номер 48, Мерзляк, Полонский, Якир, Учебник

Номер 4, Мерзляк, Полонский, Якир, Учебник

Номер 215, Мерзляк, Полонский, Якир, Учебник

Номер 229, Мерзляк, Полонский, Якир, Учебник

Номер 233, Мерзляк, Полонский, Якир, Учебник

Номер 239, Мерзляк, Полонский, Якир, Учебник

Номер 350, Мерзляк, Полонский, Якир, Учебник

Номер 374, Мерзляк, Полонский, Якир, Учебник

Таблицы экспонент и шаблоны

Горячая математика

В таблицах степеней целых чисел можно найти много интересных закономерностей.

Полномочия 2	Полномочия 3	Полномочия 4
2 1 «=» 2	3 1 «=» 3	4 1 «=» 4
2 2 «=» 4	3 2 «=» 9	4 2 «=» 16
2 3 «=» 8	3 3 «=» 27	4 3 «=» 64
2 4 «=» 16	3 4 «=» 81	4 4 «=» 256
2 5 «=» 32	3 5 «=» 243	4 5 «=» 1024
2 6 «=» 64	3 6 «=» 729	4 6 «=» 4096
2 7 «=» 128	3 7 «=» 2187	4 7 «=» 16384
2 8 «=» 256	3 8 «=» 6561	4 8 «=» 65536
2 9 «=» 512	3 9 «=» 19683	4 9 «=» 262144
2 10 «=» 1024	3 10 «=» 59049	4 10 «=» 1048576

Одна вещь, которую вы можете заметить, это закономерности в цифрах. В полномочиях 2 таблица, единичные цифры образуют повторяющийся шаблон 2 , 4 , 8 , 6 , 2 , 4 , 8 , 6 , … . В полномочиях 3 таблица, единичные цифры образуют повторяющийся шаблон 3 , 9, 7 , 1 , 3 , 9 , 7 , 1 , … . Мы оставляем это вам, чтобы выяснить, почему это происходит!

В полномочиях 4 таблица, чередуются единичные цифры: 4 , 6 , 4 , 6 . На самом деле, вы можете видеть, что силы 4 совпадают с четными степенями 2 :

4 1 «=» 2 2 4 2 «=» 2 4 4 3 «=» 2 6 и т. д.

Такие же отношения существуют между силы 3 и силы 9 :

Полномочия 3	Полномочия 9
3 1 «=» 3	91 «=» 9
3 2 «=» 9	9 2 «=» 81
3 3 «=» 27	9 3 «=» 729
3 4 «=» 81	9 4 «=» 6561
3 5 «=» 243	9 5 «=» 59 049
3 6 «=» 729	9 6 «=» 531 441
3 7 «=» 2187	9 7 «=» 4 782 969
3 8 «=» 6561	9 8 «=» 43 046 721
3 9 «=» 19,683	9 9 «=» 387 420 489
3 10 «=» 59 049	9 10 «=» 3 486 784 401

силы 10 легко, потому что мы используем база 10 : для 10 н просто напишите » 1 » с н нули после него.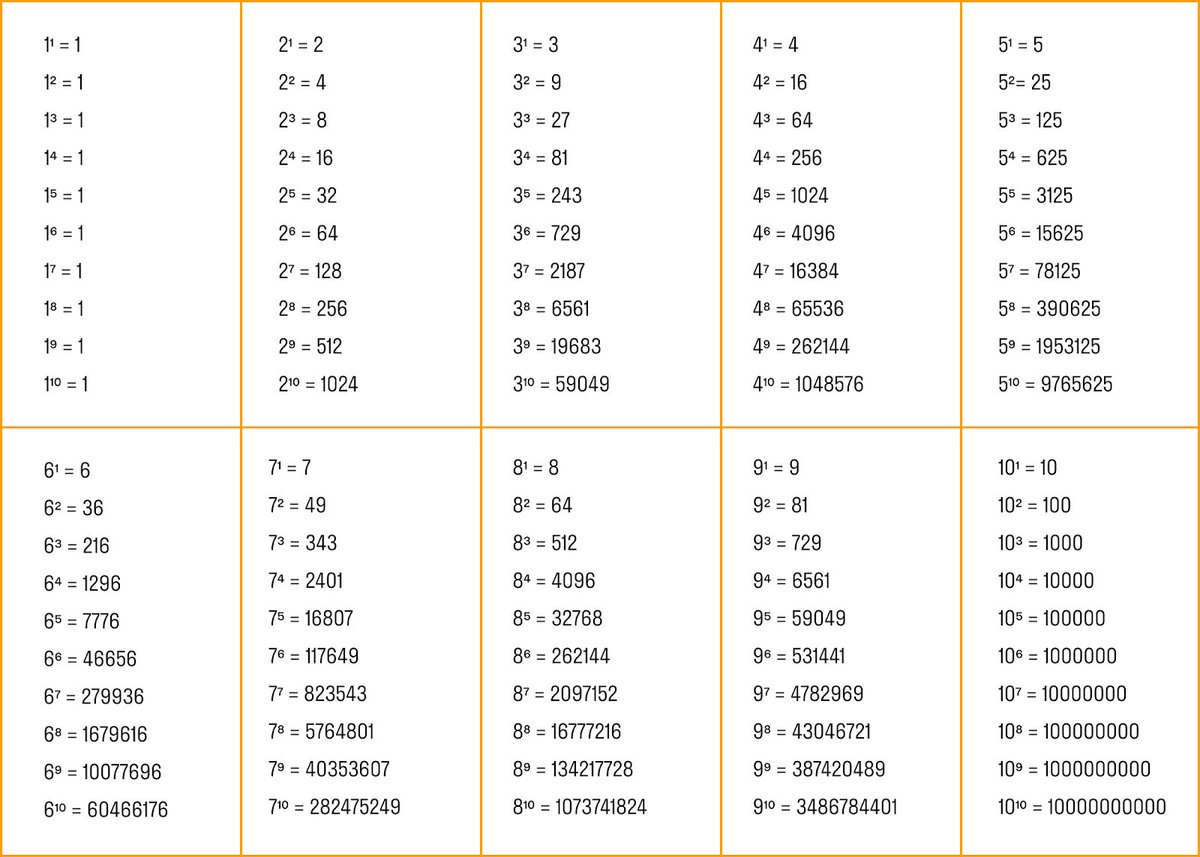 Для отрицательные силы 10 − н , писать » 0. » с последующим н − 1 нули, а затем 1 . Полномочия 10 широко используются в научная нотация , так что это хорошая идея, чтобы освоиться с ними.

Полномочия 10

10 1 «=» 10

10 0 «=» 1

10 2 «=» 100

10 − 1 «=» 0,1

10 3 «=» 1000

10 − 2 «=» 0,01

10 4 «=» 10 000

10 − 3 «=» 0,001

10 5 «=» 100 000

(сто тысяч)

10 − 4 «=» 0,0001

(одна десятитысячная)

10 6 «=» 1 000 000

(один миллион)

10 − 5 «=» 0,00001

(стотысячный)

10 7 «=» 10 000 000

(десять миллионов)

10 − 6 «=» 0,000001

(одна миллионная)

10 8 «=» 100 000 000

(сто миллионов)

10 − 7 «=» 0,0000001

(одна десятимиллионная)

10 9 «=» 1 000 000 000

(один миллиард)

10 − 8 «=» 0,00000001

(стомиллионный)

10 10 «=» 10 000 000 000

(десять миллиардов)

10 − 9 «=» 0,000000001

(одна миллиардная)

Нажмите здесь для большего количества имен для очень большие и очень маленькие числа .

Еще одно следствие нашего использования база 10 хороший образец между отрицательными степенями 2 и полномочия 5 .

Полномочия 2	Полномочия 5
2 − 5 «=» 1 32 «=» 0,03125	5 − 5 «=» 1 3125 «=» 0,00032
2 − 4 «=» 1 16 «=» 0,0625	5 − 4 «=» 1 625 «=» 0,0016
2 − 3 «=» 1 8 «=» 0,125	5 − 3 «=» 1 125 «=» 0,008
2 − 2 «=» 1 4 «=» 0,25	5 − 2 «=» 1 25 «=» 0,04
2 − 1 «=» 1 2 «=» 0,5	5 − 1 «=» 1 5 «=» 0,2
2 0 «=» 1	5 0 «=» 1

Калькулятор показателей степени

Калькулятор экспоненты Калькулятор логарифмов

Калькулятор показателей степени с отрицательными числами и шагами.

Введите Базовый	Введите Показатель степени

Результат

Расчет

* Используйте e для научной записи. Например: 5e3, 4e-8, 1.45e12

** Чтобы найти показатель степени по основанию и результат возведения в степень, используйте калькулятор логарифмов: 9показатель:

Выражение

Результат

Калькулятор логарифмов

Примеры вычисления экспоненты

2 ⁵ = ? , 2 ^-5 = ? , -2 ⁵ = ? , -2 ^-5 = ?

Законы и правила экспоненты

Формула экспоненты:

a ⁿ = a × a × … × a

n раз

Основание a, возведенное в степень n, равно n-кратному умножению числа a.

For example:

2 ⁵ = 2×2×2×2×2 = 32

Multiplying exponents

a ⁿ ⋅ a ^m = a ^{n + m}

Example: 2 ³ ⋅ 2 ⁴ = 2 ⁽³⁺⁴⁾ = 2 ⁷ = 128

a ^н ⋅ б ^н ^{= ( a ⋅ B ) ^N}

Пример: 3 ² ⋅ 4 ² = (3 %). ⁿ a ^m

= a ^{n — m}

Example:

2 ⁵ 2 ³

= 2 ^{(5 -3)} = 2 ² = 4

a ⁿ b ⁿ

= ( a / b ) ⁿ

Example:

8 ² 2 ²

= (8/2) ² = 4 ² = 16

ЭКСПОРИЯ

( A ^{N 4428) ^{N 44428) ^{N 44428) ^{N 4428) ^{N 4428) ^{N 4428) ^{. п ⋅ м}}}}}}}

Пример: (2 ³) ⁴ = 2 ^{(3 ⋅ 4)} = 2 ¹² = 4096