Огэ математика задание: ОГЭ Математика 2023. Открытый банк заданий с ответами. — math100.ru

Как решать задание 11 ОГЭ по математике в 2023 году

Вы успешно справитесь с заданием 11 ОГЭ по математике в 2023 году при условии, что

1. Владеете понятием функция и связанными с ним основными понятиями, такими как область определения функции и область значений функции.

2. Знаете уравнения, свойства и графики функций, которые изучали в курсе алгебры.

3. Умеете читать графики известных функций: по виду графика определять свойства функции.

Функция — это соответствие f (зависимость, правило) между двумя множествами X и Y, при котором каждому элементу множества X соответствует

единственный элемент множества Y.

На рисунке изображены три соответствия: f , h и g . Определим, какое из них является функцией, а какое – нет.

Соответствие f – функция. Обозначают f: X илиy=f( x).

X

– область определения функции, обозначают D (f).

Y – область значений функции, обозначают E(f ).

Соответствие h не является функцией, так как не каждому элементу множества X соответствует элемент множества Y.

Соответствие g не является функцией так как элементу a множества X соответствует два элемента (

не единственный!) множества Y.

Рассмотрим несколько примеров того, как решать 11 задания ОГЭ по математике 2023.

Пример 1. Найдите область определения и область значений функции y=

Решение. Дробь имеет смысл, когда её знаменатель не равен нулю, значит при этом подкоренное выражение может быть только положительным, то естьx-2>0. Итак, область определения функции (2; + . При x>2 y>0, значит область значений — (0; +

Напомним свойства функций, которые применяются в задании 11.

Пример 2.

На рисунках изображены графики функций вида y=kx+b. Установите соответствие между знаками коэффициентов k и b и графиками функций. В таблице под каждой буквой запишите соответствующий номер.

Решение. На каждом из трёх рисунков обозначим угол a, который прямая составляет с положительным направлением оси Ox, а также точку пересечения прямой с осью Oy (см. рис.__). Рисунку 1 соответствует А (k<0, b<0), рисунку 2 — В (k<0,b>0), рисунку 3 – Б (k>0, b<0).

Заполняем таблицу

A	Б	В
1	3	2

Ответ. 132.

Пример 3. Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ

ФОРМУЛЫ

1) y= – x²– 2x+1 2) y= x²+2x– 1 3) y=x²– 2x– 1

Решение.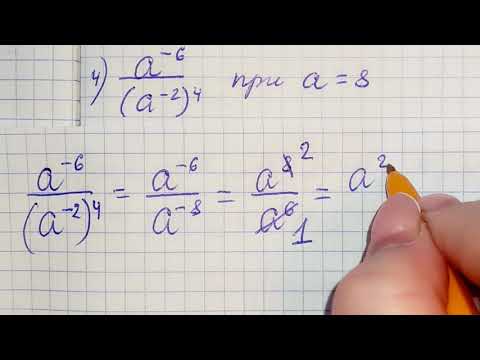 Из трёх формул 1) — 3) только в формуле 3 старший коэффициент отрицательный, а из графиков только у графика В ветви параболы направлены вниз, значит В соответствует 1. В формуле 2 а в формуле 3 значит А соответствует 3, а Б – 2.

Ответ. 321

ГРАФИКИ

Решение. Графиком квадратичной функции А является парабола, значит А соответствует 3. График обратной пропорциональности Б гипербола 1, а графиком линейной функции В является прямая 2.

Ответ. 312

Вернуться

Поделиться

Задание 10 ОГЭ по математике. Вероятность и статистика.

Джамиля Агишева

Задание 10 ОГЭ по математике – это задача по теории вероятностей.

Теория вероятностей рассматривает случайные действия, явления, процессы, исход которых заранее неизвестен. Например, высаживая семена огурцов, мы проводим эксперимент. В результате из десяти семечек может взойти от 0 до 10 ростков, т.е. случайное количество.

Событие – результат некоторого действия. Случайное событие – событие, которое может произойти или не произойти в данном эксперименте. Например, проигрыш или выигрыш нашей любимой футбольной команды заранее предсказать невозможно – это стечение обстоятельств, а сам исход игры мы узнаем по её окончании.

События принято обозначать заглавными латинскими буквами: A, B, C  и т.д.

Пример: A – взошло ровно 9 ростков из десяти посаженных семян огурцов. Оно может произойти или не произойти.

Вероятность события P(A) – это отношение числа  исходов, благоприятствующих событию , к числу всех исходов , возможных в данном эксперименте. Итак,

Имейте в виду, что числитель такой дроби не может быть больше знаменателя, а значит, вероятность всегда меньше либо равна 1.

Приступим к решению задач.

Пример 1. Бабушка испекла одинаковые на вид пирожки: 7 с мясом, 8 с капустой и 5 с яблоками. Внучка Даша наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с мясом.

Выбор пирожка – несомненно, испытание для Даши. А вдруг попадётся нелюбимый, с капустой?

Решение. Событие A – достался пирожок с мясом. Найдём m и n.

m – число исходов, благоприятствующих событию A.

n – число всех исходов, возможных в данном эксперименте.

Давайте перефразируем на языке пирожков: m – количество пирожков с мясом, т.е. m=7, n  – количество всех испечённых пирожков, т.е.

Осталось найти вероятность. Вспомним формулу и вычислим. Итак,

Замечание: не забудьте ответ представить в виде десятичной дроби!

Ответ: 0,35.

Давайте рассмотрим задачу посложнее.

Пример 2. В коробке хранятся жетоны с номерами от 5 до 54 включительно. Какова вероятность того, что на извлечённом наугад из коробки жетоне написано двузначное число?

Решение. Событие A – извлечённый наугад жетон содержит двузначное число. Найдём m и n.

m – число жетонов с двузначным номером,  n – число всех жетонов.

Сначала определимся с n. Типичная ошибка считать так: . На самом деле когда-то были жетоны от 1 до 54. Но номера 1, 2, 3 и 4 со временем потерялись, т.е. пропало четыре штуки. Тогда,  .

Сколько жетонов с двузначными номерами? Всего 50, номера 5, 6, 7, 8, 9 (их пять штук) – однозначные. Тогда, .

Итак,

Ответ: 0,9.

Пример 3. В лыжных гонках участвуют 10 спортсменов из России, 8 спортсменов из Швеции и 7 спортсменов из Норвегии. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что спортсмен из Швеции будет стартовать последним.

Решение. Событие A – спортсмен из Швеции будет стартовать последним.

– число спортсменов из Швеции,  – число всех спортсменов.

Т.к. старт определяется жребием, то не важно, под каким стартовым номером будет выступать тот или иной лыжник, под вторым или последним.

Итак,

Ответ: 0,32.

Пример 4. Оля наугад выбирает трёхзначное число. Найдите вероятность того, что оно делится на 51.

Решение. Событие A – выбранное число делится на 51. Найдём m и n.

m – количество трёхзначных чисел, кратных 51, n – число всех трёхзначных чисел.

Последнее трёхзначное число 999. Найдём все числа, кратные 51 среди чисел от 1 до 999 (их даже можно попробовать пересчитать непосредственно: 51, 102, 153, …, 969). Разделим 999 на 51. Получим  , т.е. ровно 19 чисел, кратных 51. Но среди этого количества окажется двузначное число 51, которое не учитывается в задаче, значит, .

Теперь определим n. Чисел от 1 до 999 ровно 999, исключим из них однозначные и двузначные числа от 1 до 99. Таким образом,  .

Итак,

Ответ: 0,02.

Пример 5. Фабрика выпускает сумки. В среднем на 200 качественных сумок приходится двадцать сумок с дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.

Обратите внимание на условие задачи. Здесь не говорится, что из 200 сумок двадцать – с дефектами. В тексте чётко обозначено, что качественных – 200 штук, а некачественных – 20 штук.

Решение. Событие A – купленная сумка окажется качественной. Найдём m и n.

Всё просто, , .

Итак,

Что-то пошло не так? Полученный результат невозможно будет записать в бланк ответов, т.к. ответом может быть либо целое число, либо конечная десятичная дробь. Ещё раз внимательно перечитываем задачу, а точнее, вопрос задачи. Там сказано: результат округлите до сотых. Помним, калькулятор использовать нельзя. Честно делим в столбик. Т.к. округлить нужно до сотых, то мы найдём три цифры после запятой и только потом запишем результат.

Ответ: 0,91.

 

Больше задач по теории вероятностей: https://ege-study.ru/teoriya-veroyatnostej/ и  https://ege-study.ru/teoriya-veroyatnostej-na-ege-po-matematike/

Благодарим за то, что пользуйтесь нашими материалами. Информация на странице «Задание 10 ОГЭ по математике. Вероятность и статистика.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена: 07.02.2023

Mathigon – математическая игровая площадка

Бесплатные инструменты, курсы и манипуляции, которые сделают онлайн-обучение более интерактивным и увлекательным, чем когда-либо прежде.

Polypad

Раскройте свой творческий потенциал с лучшими в мире манипуляторами ! Занимайтесь решением проблем , изучайте закономерности и сотрудничайте с другими.

Запуск учебных планов Polypad

Фракталы

Флэш-карты

Хронология

Последовательности

Теория графов

Factris

Оригами

Симметрия

Будьте любопытны и изобретательны. Научитесь решать проблемы и критическому мышлению. Откройте для себя великую силу и неожиданную красоту математики.

Любим педагогами всего мира.

Наши уникальные и мощные инструменты работают с любыми учебными программами и устройствами, которые вы используете. Чтобы узнать больше, подпишитесь на наши еженедельные мероприятия или изучите наши бесплатные ресурсы для учителей!

Планы уроков Мероприятия и учебные пособия

Тим Бжезински

@TimBrzezinski

Это потрясающее обновление Mathigon открывает двери для множества новых возможностей для исследования и деятельности учащихся в области геометрии!

Марк Лабуда

@MrMLabuda

Бесспорно лучший виртуальный манипулятивный сайт, который я когда-либо встречал. Вы можете манипулировать инструментами, чтобы удовлетворить потребности вашего урока и получить доступ ко многим урокам. Удивительные вещи

Сунил Сингх

@Mathgarden

Polypad быстро становится волшебным центром для большинства учеников/учителей и их интерактивного взаимодействия с математикой, а результат – радостными переживаниями!

Грант Сандерсон

@3blue1brown

Mathigon, без сомнения, является одним из лучших математических ресурсов в Интернете.

Guardian

theguardian.com

Один из самых доступных и увлекательных математических ресурсов в Интернете, настоящая математическая страна чудес.

Джеймс Тэнтон

@jamestanton

Компания Mathigon находится на пути к революционному изменению преподавания математики в том виде, в каком мы ее знаем, и какая честь иметь в своем арсенале взрывающиеся точки!

Андреа Биро

@mrsbistro

Не могу смириться с тем, насколько изменил правила игры Polypad. Я могу манипулировать плитками и писать/печатать на экране, когда мы вместе проходим урок. Ss практикуются на своих полотнах, и я вижу их работы. Красивый.

Адина Р

@adinam225

Если вы еще не проверили Polypad и не нашли время, чтобы изучить все его функции, вы многое упускаете!

Келли Холден

@KelliHolden

На этой неделе я работаю с областью и мне нравится, как Mathigon упрощает работу для моих онлайн-учеников. Их комментарий? «Каждый день использования Mathigon похож на мой день рождения!» Так благодарна за этот мощный инструмент.

Хантер П.

@professorpatton

Polypad изменил правила игры для виртуального обучения (и личного обучения).

Брэд Водден

@MrVodden

Если вы ищете онлайн математические манипуляции, Mathigon изменит правила игры! Мои ученики любят все инструменты для представления и демонстрации своего мышления. Вы также можете сохранить шаблон, чтобы начать Ss.

Mark Kaercher

@shskaercher

Polypad быстро становится мощным инструментом для ВСЕХ областей контента!

Джин Хьюм

@HumieJ

Вау. Mathigon Polypad меняет правила игры! Он идеально подходит для математики среднего возраста и задач PAA. Я не могу дождаться, чтобы попробовать это со своими детьми в этом году! Спасибо за этот удивительный ресурс!

Джейн Бретон

@JBretonmath

Только что услышала, как ребенок с энтузиазмом воскликнул: «БАМ! Polypad baby…”

Пип – Математика

@AccomplishEdu

Прекрасная реакция учителя, с которым я работал сегодня, когда я поделился заданием с использованием плиток Mathigon: «Я должен сообщить остальной команде об этом сайте». !! Настоятельно рекомендую вам взглянуть на

Geoff Krall

@geoffkrall

Polypad полностью меняет правила игры, и я узнал о нем всего несколько месяцев назад.

Кружки учителей математики

@MathsCirclesOz

Математическая игра. С какой частью Polypad вам больше всего нравится играть? Эта игровая площадка Mathigon использовалась во время исследований кружков учителей математики.

Maine Math & Science Alliance

@mmsa_org

В этом учебном году в сотрудничестве с учителями мы использовали Polypad в классах K-8 для моделирования новой игры, дизайна и проектов изображений для математических выступлений и многого другого.

Кэтрин Тан

@EduScribblings

Открывая для себя все эти удивительные вещи на Polypad. Эта манипулятивная полоска дроби помогает сделать эквивалентные дроби очень четкими!

RenieMc

@reniemck

Проверьте это потрясающее математическое приложение для средней школы. Нравится график! Так много вариантов для изучения запросов.

Новое слово в образовании.

Наша беспрецедентная интерактивность позволяет учащимся исследовать, делать открытия, учиться решать проблемы и проявлять творческий подход. Увлекательное повествование и реальные приложения делают абстрактные темы более привлекательными, чем когда-либо прежде.

Узнать больше

Для школьного округа

Мы работаем со школами и округами по всему миру. Пожалуйста, напишите нам, если вам нужно подписать соглашение о конфиденциальности данных.

Партнер с нами

Мы лицензируем наши технологии и контент другим организациям. Пожалуйста, свяжитесь с нами, если вы заинтересованы в сотрудничестве с нами.

Еще больше математики!

Mathigon является частью Amplify, одного из ведущих поставщиков учебных программ и программ оценивания в США. Узнать больше…

победитель

Winner

Gold Winner

Финалист

Top Pick

Honouree

Gold Winner

ALA Примечание

Assure

Сертифицированные

. , Предложения, которые должны иметь (*): 1. (Oge xa ​​ika) 2. * (Ye amu vo oge) 3. * (Ika oge xa ​​ye) 4. (Oge ye vo ika ye) 5.

F. Предложения, которые должны иметь (*): Аму ха оге) 6.

Конец предварительного просмотра

Загрузите свои учебные документы или станьте участником.

Недавно загруженные документы

Рабочая M4A1.docx

Рабочая M4A1.docx

эссе

Большинство респондентов были из организаций США, которые представляли 92 из ответов

903 респондентов из 92 организаций, которые были из США документ

2 Эта формула усиления или потери мощности потери или усиления дБspl 10 x Log Power of

2 Эта формула прироста или потери мощности Потеря или усиление дБspl 10 x Log Мощность

документ

11 12 23 34 Основная часть массы атома состоит из Определите

11 12 23 34 Основная часть атома масса состоит из Определить

документ

44 Влияние кадрового обеспечения и продвижения по службе как компонентов отношений с работниками

44 Влияние кадрового обеспечения и продвижения по службе как компонентов отношений с работниками

документ

быков, груженных пшеницей В провинции Татта также было много пшеницы в течение

быков, груженных пшеницей В провинции Татта также было много пшеницы в течение

document

ПОЛИТИКА РАВНЫХ ВОЗМОЖНОСТЕЙ ЖИЛЬЯ Мы предоставляем аренду жилья на равных

РАВНОЕ ЖИЛЬЕ ПОЛИТИКА ВОЗМОЖНОСТЕЙ Мы предоставляем арендное жилье на равных условиях.

Revison B.pdf

Revison B.pdf

временная декомпозиция ² стоимость ресурсов Дуализм методов декомпозиции

временная декомпозиция ² стоимость ресурсов Дуализм методов декомпозиции

документ

мужская сила и

Модели спортивной социализации в боксе натурализовать и материализовать мужскую силу и

документ

Управление пожизненной ценностью клиента 18 Проблемы динамики рынка были

Управление пожизненной ценностью клиента 18 Проблемы динамики рынка были

документ

Ванесса Ривера — Лаборатория сепарации — Откройте лабораторию, нажав Мой документ — 10034166.pdf

Ванесса Ривера — Лаборатория сепарации — Откройте лабораторию, нажав My doc — 10034166.pdf

Днем солнечный свет активирует молекулы, замедляющие рост Если растение

Днем солнечный свет активирует молекулы, замедляющие рост Если растение

документ

В баньяновом коммутаторе на 8 входов и 8 выходов у нас есть микропереключатели на каждом

В баньяновом коммутаторе на 8 входов и 8 выходов у нас есть микровыключатели на каждом

документ

Применить сервисный аккаунт и привязку с kubectl применить и указать ваш rbac

Применить сервисный аккаунт и привязку с kubectl применить и указать ваш rbac

документ

ответы на задание 30(1).