Егэ профиль математика 4 задание: 4 задание ЕГЭ по математике профильного уровня 2023: теория и практика

4 задание ЕГЭ по математике профильного уровня 2023: теория и практика

Русский язык Математика (профиль) Математика (база) Обществознание История Биология Физика Химия Английский язык Информатика Литература

Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 10 Задание 11 Задание 12 Задание 13 Задание 14 Задание 15 Задание 16 Задание 17 Задание 18

За это задание ты можешь получить

1 балл. На решение дается около 5 минут. Уровень сложности: повышенный.
Средний процент выполнения: 86.9%
Ответом к заданию 4 по математике (профильной) может быть целое число или конечная десятичная дробь.

Разбор сложных заданий в тг-канале

Посмотреть

Задачи для практики

Задача 1

Чтобы поступить в институт на специальность «Комплексное использование и охрана водных ресурсов», абитуриент должен набрать на ЕГЭ не менее $70$ баллов по каждому из трёх предметов — математике, русскому языку и физике. Чтобы поступить на специальность «Безопасность жизнедеятельности в техносфере», нужно набрать не менее $70$ баллов по каждому из трёх предметов — математике, русскому языку и химии. Вероятность того, что абитуриент Э. получит не менее $70$ баллов по математике, равна $0{,}5$, по русскому языку — $0{,}7$, по физике — $0{,}6$ и по химии — $0{,}3$. Найдите вероятность того, что Э. сможет поступить хотя бы на одну из двух упомянутых специальностей.

Решение

Чтобы поступить хотя бы на одну специальность, абитуриенту Э. надо набрать не менее 70 баллов по математике, русскому языку и хотя бы по одному из предметов химия и физика.

Найдём вероятность того, что абитуриент Э. наберёт не менее 70 баллов хотя бы по одному из предметов химия и физика. Сначала отыщем вероятность противоположного события, то есть вероятность того, что абитуриент Э. по обоим этим предметам не наберёт 70 баллов. Результаты экзаменов не зависят друг от друга, вероятность не набрать 70 баллов по физике равна 1 — 0.6 = 0.4, а вероятность не набрать 70 баллов по химия равна 1 — 0.3 = 0.7. Отсюда вероятность того, что абитуриент Э. по обоим этим предметам не наберёт 70 баллов, равна 0.4 · 0.7 = 0.28. Следовательно, вероятность того, что абитуриент Э. наберёт не менее 70 баллов хотя бы по одному из предметов химия и физика, равна 1 — 0.28 = 0.72.

Таким образом, вероятность того, что абитуриент Э.

наберёт не менее 70 баллов по математике, русскому языку и хотя бы по одному из предметов химия и физика, равна 0.5 · 0.7 · 0.72 = 0.252.

Ответ: 0.252

Показать решение

Бесплатный интенсив

Задача 2

Биатлонист Алексей Антонов пять раз стреляет по мишеням. Вероятность попадания при одном выстреле равна $0{,}7$. Найдите вероятность того, что биатлонист Алексей Антонов один раз попал по мишени, а четыре — промахнулся. Результат округлите до сотых.

Решение

Вероятность промахнуться при одном выстреле равна $1 — 0.7 = 0.3$. Обозначим события.

1. $A_1$ — «Алексей попал по мишени при первом выстреле».

2. $A_2$ — «Алексей попал по мишени при втором выстреле».

3. $A_3$ — «Алексей попал по мишени при третьем выстреле».

4. $A_4$ — «Алексей попал по мишени при четвёртом выстреле».

5. $A_5$ — «Алексей попал по мишени при пятом выстреле».

События ${A_1}↖{-}, {A_2}↖{-}, {A_3}↖{-}, {A_4}↖{-}$ и ${A_5}↖{-}$ — означают, что Алексей промахнулся при соответствующем выстреле.

Событие «Алексей Антонов первый раз попал по мишени, а последние четыре промахнулся» означает одновременное наступление (пересечение) независимых событий ${A_1}, {A_2}↖{-}, {A_3}↖{-}, {A_4}↖{-}$ и ${A_5}↖{-}$.

$P (A_1 ∩ {A_2}↖{-} ∩ {A_3}↖{-} ∩ {A_4}↖{-} ∩ {A_5}↖{-}) = P (A_1) · P ({A_2}↖{-}) · P ({A_3}↖{-}) · P ({A_4}↖{-}) · P ({A_5}↖{-}) = 0.7 · 0.3 · 0.3 · 0.3 · 0.3 = 0.00567$.

По условию Алексей мог попасть единожды, но это попадание могло прийтись на любой из пяти выстрелов, не обязательно на первый.

Тогда, аналогично, $P ({A_1}↖{-} ∩ A_2 ∩ {A_3}↖{-} ∩ {A_4}↖{-} ∩ {A_5}↖{-}) = P ({A_1}↖{-}∩ {A_2}↖{-} ∩ A_3 ∩ {A_4}↖{-} ∩ {A_5}↖{-}) =$

$= P ({A_1}↖{-} ∩ {A_2}↖{-} ∩ {A_3}↖{-} ∩ A_4 ∩ {A_5}↖{-}) = P ({A_1}↖{-} ∩ {A_2}↖{-} ∩ {A_3}↖{-} ∩ {A_4}↖{-} ∩ A_5) =$

$= P (A_1 ∩ {A_2}↖{-} ∩ {A_3}↖{-} ∩ {A_4}↖{-} ∩ {A_5}↖{-}) = (0.

4 · 0.7 = 0.00567$.

Следовательно, искомая вероятность равна $0.00567 · 5 = 0.02835 ≈0.03$.

Ответ: 0.03

Показать решение

Бесплатный интенсив

Задача 3

Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы $4$ очка в двух играх. Если команда выигрывает, она получает $3$ очка, в случае ничьей — $1$ очко, если проигрывает — $0$ очков. Найдите вероятность того, что команде «Ветерок» удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны $0{,}3$.

Решение

Вероятность ничьей в каждой игре равна 1 — 0.3 — 0.3 = 0.4 (из единицы вычитаем вероятность выигрыша и вероятность проигрыша). «Ветерок» выйдет в следующий круг в одном из трёх следующих случаев.

1. «Ветерок» выиграет обе игры. Вероятность этого равна 0.3 · 0.3 = 0.09.

2. «Ветерок» выиграет первую игру и сыграет вничью вторую. Вероятность этого равна 0.3 · 0.4 = 0.12.

3. «Ветерок» сыграет вничью первую игру и выиграет вторую. Вероятность этого равна 0.4 · 0.3 = 0.12.

Искомая вероятность равна 0.09 + 0.12 + 0.12 = 0.33.

Ответ: 0.33

Показать решение

Бесплатный интенсив

Задача 4

Помещение торгового дома «Светлый» освещается фонарём с двумя лампами. Вероятность перегорания одной лампы в течение года равна $0{,}6$. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.

Решение

Найдём вероятность события «перегорели обе лампы», а затем искомую вероятность.

Вероятность события «перегорела первая лампа» равна вероятности события «перегорела вторая лампа» и равна 0.6. Эти два события независимы, значит, вероятность того, что они наступили оба, равна произведению их вероятностей, то есть равна 0.6 · 0.6 = 0.36. Это вероятность события «перегорели обе лампы».

События «перегорели обе лампы» и «хотя бы одна лампа не перегорела» противоположны, следовательно, сумма их вероятностей равна 1. Значит, вероятность события «хотя бы одна лампа не перегорела» равна 1 — 0.36 = 0.64.

Ответ: 0.64

Показать решение

Бесплатный интенсив

Задача 5

В ларьке на улице Счастья стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью $0{,}1$ независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.

Решение

Найдём вероятность события «оба автомата неисправны», а затем искомую вероятность.

Вероятность события «неисправен первый автомат» равна вероятности события «неcисправен второй автомат» и равна 0,1. Эти два события независимы, значит, вероятность того, что они наступят оба, равна произведению их вероятностей, то есть равна 0.1 · 0.1 = 0.01. Таким образом, мы нашли вероятность события «оба автомата неисправны».

События «оба автомата неисправны» и «хотя бы один автомат исправен» противоположны, следовательно, сумма их вероятностей равна 1. Значит, вероятность события «хотя бы один автомат исправен» равна 1 — 0.01 = 0.99.

Ответ:

0.99

Показать решение

Бесплатный интенсив

Задача 6

Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью $0{,}72$. Если А. играет чёрными, то А. выигрывает у Б. с вероятностью $0{,}6$. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.

Решение

По условию вероятность события «шахматист А. выиграет белыми» равна $0{,}72$, вероятность события «шахматист А. выиграет чёрными» равна $0{,}6$. Эти события независимы. Значит, вероятность того, что оба этих события наступят (А. выиграет оба раза) равна произведению вероятностей, то есть равна $0{,}72⋅ 0{,}6=0{,}432$.

Ответ: 0.432

Показать решение

Бесплатный интенсив

Задача 7

На железнодорожном вокзале $3$ кассира. Каждый из них занят с клиентом с вероятностью $0{,}2$ независимо от других кассиров. Найдите вероятность того, что в случайный момент времени все три кассира заняты одновременно.

Решение

События «первый кассир занят», «второй кассир занят» и «третий кассир занят» по условию независимы. Тогда вероятность их одновременного наступления (вероятность пересечения событий) равна произведению вероятностей этих событий, то есть равна 0.2 · 0.2 · 0.2 = 0.008.

Ответ: 0.008

Показать решение

Бесплатный интенсив

Задача 8

В магазине сантехники три продавца. Каждый из них занят с клиентом с вероятностью $0{,}7$ независимо от других продавцов. Найдите вероятность того, что в случайный момент времени все три продавца заняты одновременно.

Решение

События «первый продавец занят», «второй продавец занят» и «третий продавец занят» по условию независимы.

Тогда вероятность их одновременного наступления (вероятность пересечения событий) равна произведению вероятностей этих событий

То есть равна $0.7 · 0.7 · 0.7 = 0.343$

Ответ: 0.343

Показать решение

Бесплатный интенсив

Задача 9

Вероятность того, что новый электрический чайник прослужит больше года, равна $0{,}93$. Вероятность того, что он прослужит больше двух лет, равна $0{,}84$. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.

Решение

Заметим, что из событий «чайник прослужит меньше года», «чайник прослужит от 1 до 2 лет» и «чайник прослужит больше двух лет» произойдёт обязательно ровно одно, то есть, говоря математическим языком, они попарно несовместны, а их объединение — достоверное событие. Следовательно, сумма вероятностей этих событий равна 1.

При этом события «чайник прослужит меньше года» и «чайник прослужит больше года» противоположны, поэтому вероятность события «чайник прослужит меньше года» равна 1 — 0.93 = 0.07. Заполним таблицу.

Событие	Прослужит меньше года	Прослужит от 1 до 2 лет	Прослужит больше двух лет
Вероятность	0.07	?	0.84

Отсюда искомая вероятность равна 1 — 0.07 — 0.84 = 0.09.

Ответ: 0.09

Показать решение

Бесплатный интенсив

Задача 10

На экзамене по биологии студент отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Млекопитающие», равна $0{,}36$. Вероятность того, что это вопрос по теме «Бактерии», равна $0{,}18$. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене студенту достанется вопрос по одной из этих двух тем.

Решение

Из условия следует, что события A = «достанется вопрос по теме Млекопитающие» и B = «достанется вопрос по теме Бактерии» несовместны. Действительно, нет билетов, относящихся к обоим этим темам одновременно. Событие «достанется вопрос по одной из этих двух тем» — это объединение событий A и B (A $∪$ B). По формуле вероятности объединения несовместных событий получим, что искомая вероятность равна P(A $∪$ B) = P(A) + P(B) = 0.36 + 0.18 = 0.54.

Ответ: 0.54

Показать решение

Бесплатный интенсив

Задача 11

В торговом центре два одинаковых автомата продают лимонад. Вероятность того, что к концу дня в автомате закончится лимонад, равна $0{,}2$. Вероятность того, что лимонад закончится в обоих автоматах, равна $0{,}09$. Найдите вероятность того, что к концу дня лимонад останется в обоих автоматах.

Решение

По условию вероятность события A =«лимонад закончится в первом автомате» равна вероятности события B =«лимонад закончится во втором автомате» и равна $0.2$. Эти два события зависимые.

В этом случае воспользуемся формулой $P (A + B) = P (A) + P (B) — P (A B)$.

$P (A + B) = 0.2 + 0.2 — 0.09 = 0.31$. Событие $A + B$ — это событие «лимонад закончилась хотя бы в одном автомате». Указанное событие противоположно искомому. Отсюда вероятность события «лимонад останется в обоих автоматах» равна $1 — 0.31 = 0.69$.

Ответ: 0.69

Показать решение

Бесплатный интенсив

Задача 12

Предприниматель закупает для продажи на рынке куриные яйца в двух хозяйствах. $50%$ яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — $40%$ яиц высшей категории. При продаже яиц на рынке оказалось, что всего получилось $42%$ яиц высшей категории. Найдите вероятность того, что яйцо, купленное у предпринимателя, окажется из второго хозяйства.

Решение

Ответ: 0.8

Показать решение

Бесплатный интенсив

Задача 13

Робин Гуд подошел к столу, на котором лежали 3 его старых лука и 2 новых. Он решил сбить стрелой яблоко с дерева. Робин попадает в цель из своего старого лука с вероятностью $0{,}8$, а из нового — с вероятностью $0{,}3$. Робин случайным образом выбирает один лук. Найдите вероятность того, что Робин промахнётся при стрельбе.

Решение

Ответ: 0.4

Показать решение

Бесплатный интенсив

Показать еще

Для доступа к решениям необходимо включить уведомления от группы Турбо в вк — это займет буквально 10 секунд. Никакого спама, только самое важное и полезное для тебя. Ты всегда можешь запретить уведомления.

Включить уведомления

Бесплатный интенсив по математике (профильной)

3 огненных вебинара, домашние задания, беседа курса, личный кабинет, связь с преподавателем и многое другое.

Курс стартует 28 марта. Бесплатный интенсив

Как сдать ЕГЭ по математике на 80+ баллов

Математика — обязательный для сдачи на ЕГЭ предмет, без которого не получишь аттестат. Это также один из самых сложных экзаменов для выпускников. Почти 8% сдающих в 2021 году не прошли минимальный порог, а количество высокобалльников составило лишь 2,4%. 

Как повысить свои шансы на успешную сдачу ЕГЭ по математике и на каких заданиях легче набрать баллы, разбираем в этой статье вместе с преподавателем онлайн-школы Вебиум. 

ЕГЭ по математике — обязательный предмет 

ЕГЭ по математике — обязательный для сдачи предмет. В 2015 году его разделили на два уровня сложности — базовый и профильный. Это упростило жизнь выпускникам, которым не нужна математика для поступления в вуз. В основном, ЕГЭ по базовой математике сдают те, кто идёт в медицинские вузы или на некоторые гуманитарные специальности: рекламу, юриспруденцию, издательское дело, остальные сдают профиль.  

Чтобы получить аттестат, нужно успешно сдать ЕГЭ либо по профильной математике, либо по базовой. Но выбрать профиль и базу «для подстраховки» нельзя: с 2018 года запретили сдавать оба уровня.

В 2022 году в ЕГЭ по математике также появились изменения, о них подробно рассказали в нашей статье. 

Базовая математика: структура экзамена

В базовой математике всего 21 задание, из них 16  — по алгебре и началам анализа, пять — по геометрии. За каждое можно получить 1 балл. Этот ЕГЭ пишут  3 часа. 

Это единственный экзамен, результат которого переводится не в 100-балльную систему, а в оценки по 5-балльной шкале. Для получения аттестата нужно набрать семь баллов. 

Подготовьтесь к базовой математике на 5 за шесть недель с нашим спецкурсом. 

Профильная математика: структура экзамена

Количество заданий в ЕГЭ по профильной математике — 18. Их делят на три блока: восемь заданий по алгебре и началам анализа, четыре — по геометрии и шесть — по реальной математике.  

При этом номеров базового уровня сложности шесть, повышенного — десять, высокого — два. Время на их выполнение — 3 часа 55 минут. 

Список тем, которые нужно знать для экзамена, собрали в нашей шпаргалке. Также рекомендуем посмотреть разбор демоверсии ЕГЭ 2022 по профильной математике. 

Для получения аттестата нужно преодолеть минимальный порог в 27 вторичных баллов — то есть решить шесть заданий тестовой части. 

Есть и особенности: сдать ЕГЭ по профильной математике на 100 баллов вы можете, даже если допустите ошибку. Дело в том, что первичный балл, которому соответствуют 100 вторичных баллов, — 30. Но максимальное количество вторичных баллов, которое вы можете получить, — 31, то есть у вас есть запас в 1 балл.

Перевод баллов: сколько я получу, если решу N заданий

Если вы решите всю первую часть без единой ошибки, то получите 11 первичных баллов. Согласно шкале перевода, это соответствует 56 вторичным баллам по 100-балльной системе.  

Чтобы получить 60+ баллов (62–68), вам нужно суммарно с верно решённой тестовой частью набрать ещё 1–2 первичных балла соответственно. Набор задач может быть таким: вся первая часть + 12 или 14 задание. 

Вы можете решить первую часть с двумя ошибками — тогда нужно будет выполнить 12 и 14 номер на максимальный балл или суммарно потерять в них не более одного балла.  

Если вы решите верно всю первую часть, а также 12 и 14 задания, то сдадите ЕГЭ по профилю на 72 вторичных балла. Добавив к этому набору задачу по финансовой математике, вы получите 76 вторичных баллов. 

Решив верно тестовую часть, 12,14,15 задания и задачу с параметром вы получите 80+ баллов. Вместо полностью правильной 17 задачи можно решить пункты а) и б) в 13 задании и пункт а) в 18 задании.   

Простые задания в ЕГЭ по профильной математике

Несмотря на то, что профиль — достаточно сложный экзамен, к которому нужно долго и упорно готовиться, в нём есть лёгкие задания. Это задачи из первой части КИМа.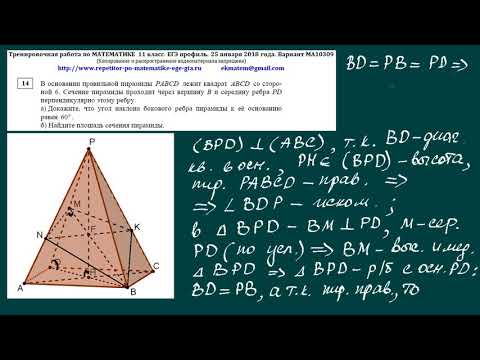  

Задание 1

Это задание на решение простейших уравнений. Здесь нужны базовые знания в работе с линейными, квадратными, показательными, логарифмическими уравнениями. Если повезёт, то нужно будет всего лишь разделить одно число на другое.

Задание 2

Здесь встречаются простейшие задачи на теорию вероятности, для решения которых нужна одна формула: число благоприятных событий разделить на количество всех событий. Подробнее об этом — в шпаргалке по теории вероятности. Также можно пройти бесплатный курс по этой теме. 

Задание 4

Задача проверяет ваше умение выполнять простейшие вычисления и преобразования. Вы должны понимать, как работать с дробями, иррациональными, степенными, логарифмическими, тригонометрическими выражениями, а потом вычислять их значение, подставив числа.

Освежить в памяти тему логарифмов и степеней поможет наша шпаргалка, а тему тригонометрических преобразований — статья с основными формулами.

Задание 7

Это задача с прикладным содержанием. Здесь от вас требуется лишь умение верно считать и подставлять значение в формулу, которая даётся в условии. 

Задания по геометрии из первой части

Планиметрия и стереометрия — достаточно пугающие разделы для большинства выпускников, но подождите паниковать: справиться с задачами первой части под силу каждому. Вы должны знать лишь основные свойства и формулы площадей плоских фигур — треугольников, параллелограммов, трапеций, разбираться в центральных и вписанных углах и знать основные свойства и формулы площадей объёмных тел — параллелепипедов, призм, конусов, шаров, цилиндров, пирамид.

Основные лайфхаки по решению тестовой части мы собрали в этой статье.

Самые сложные задания в ЕГЭ по профильной математике

Чтобы гарантированно сдать ЕГЭ по профильной математике на 80+ баллов, необходимо решать не только первую часть, уравнение из 12 задания и неравенство из 14, но и более сложные задания: стереометрию, планиметрию, задачу с параметром и олимпиадную задачу на свойства чисел.  

Забудьте про «Либо всё, либо ничего» — на ЕГЭ по математике так не работает. Вы должны бороться за каждый балл: записать половину решения с идеей, которая пришла вам в голову за пять минут до конца и кажется вам глупой, или сделать только пункт А) в задаче. Возможно, именно эти драгоценные баллы помогут вам с поступлением. 

Сложная стереометрия (13 задание)

Это задача даётся, как правило, легче, чем задание на сложную планиметрию, но не всё так просто. Не стоит сразу решать задания ЕГЭ, если у вас есть пробелы в стереометрии. Перед этим повторите необходимый объём теоретического материала — свойства объёмных фигур, теоремы, научитесь строить сечения, находить расстояние между прямыми и плоскостями или от точки до прямой и до плоскости, находить углы: между плоскостями, между прямой и плоскостью, между скрещивающимися прямыми. И только потом приступайте к задачам, начиная с самых простых. Постепенно вы научитесь применять теорию и будете видеть случаи, когда можно использовать ту или иную теорему.  

Ключ к успеху в том, чтобы перестать думать, что геометрия вам не по силам. Начните с простых заданий, дайте себе время, чтобы подумать над задачей — вы можете вернуться к ней даже через день. Поверьте, регулярный труд даст свои плоды через некоторое время. 

Сложная планиметрия (16 задание)

В этой задаче, как и в предыдущей, не стоит сразу открывать типовые варианты — скорее всего, вы подумаете, что это очень сложно, и запал пропадёт. Помимо базовых свойств и теорем, обратите внимания на «экзотику» — теоремы, которые вы, скорее всего, не встречали в школьных учебниках. Это, например, теоремы Менелая или Чевы. Больше теорем вы найдёте в нашей шпаргалке. 

Не игнорируйте пункт на доказательство: он может быть простым и подарить драгоценный балл. Однако если вы решили пункт б), но не притронулись к а) — вы все равно получите балл за него. 

Задача с параметром (17 задание)

То, что пугает выпускников больше, чем геометрия. За это задание дают четыре первичных балла — столько же вы получите только за последнюю олимпиадную задачу, но решают его только 2% сдающих ЕГЭ по профильной математике.  

К сожалению, в школе это задание зачастую не объясняют, поэтому вам придётся изучать это самому или на курсах.

Начните с повторения элементарных функций, далее — с равносильных преобразований неравенств и их систем. Поймите, при каких ограничениях параметра вы можете выполнить определённое преобразование. Идеальный вариант для практики — начать с заданий вида «Для каждого значения параметра решить…»

После этого начните подробнее знакомиться с аналитическим методом решения задач с параметром: познакомьтесь с заданиями вида, например, «При каких значениях параметра уравнение (неравенство, система) имеет N решений».

Теперь приступайте к изучению графического метода решения. Для этого обязательно повторите графики, уравнение прямой и окружности, области определения и значения функции, чётность, периодичность, параллельный перенос.

Пройдите спецкурс по параметрам от Вебиума, чтобы разложить эту тему по полочкам

Олимпиадная задача на свойства чисел (18 задание) 

За верное решение этого номера вы получите четыре первичных балла. Но здесь нужно пробовать ухватить и один балл — иногда это может быть достаточно легко. 

Что нужно знать? Теорию чисел, их свойства, признаки делимости чисел, прогрессии — арифметическую и геометрическую, среднее арифметическое. Когда вы освоите более простые задания, можно изучить метод кругов Эйлера, метод математической индукции и принцип Дирихле. 

Как получить 1 балл? Традиционно этот номер содержит в себе три пункта — а), б) и в). В первом пункте обычно предлагается решить несложную задачу, где вы должны привести пример. Обычно их существует несколько, но вы можете привести только один. Если пример будет верным, то вы получите желанный балл. Вот, как может выглядеть задание:

На доске написано несколько различных натуральных чисел, каждое из которых делится на 3 и оканчивается на 7.

а) Может ли сумма этих чисел быть равна 231?

Решение:

а) Да, может. Числа 27, 57 и 147 дают в сумме 231.

Как видите, ничего сверхъестественного от вас в первом пункте не требуют, и получить 1 первичный балл достаточно легко.  

Пункт б) тоже стоит 1 первичный балл, но решить его будет немного сложнее. Зачастую вопрос этого пункта очень похож на вопрос пункта а), но есть исключение: чаще всего пример привести невозможно, и это нужно доказать. Делают это обычно «от противного»

За верное решение пункта в) вы получите 2 первичных балла, но это уже достаточно высокий уровень сложности. Чаще всего в задании требуют найти минимальное значение какой-нибудь величины. К решению пункта в) стоит приступать, когда предыдущие начнут стабильно получаться.

Как готовиться, если осталось два месяца

Начинать подготовку нужно с составления плана занятий. Самостоятельно сделать это достаточно сложно, но вот основные рекомендации:

• Нарешайте тестовую часть так, чтобы стабильно не допускать в ней ошибок. Её верное решение даст вам 56 вторичных баллов, в то время как потерю придётся компенсировать сложными заданиями второй части.
• Вы должны уметь решать все виды 12 и 14 заданий, а также задачи на финансовую математику. Не стоит забывать про 2018 год: составители добавили новую задачу на кредиты, и её смогли решить только те, кто понимал суть, а не следовал алгоритму. 
• Когда вы перейдёте к подготовке ко второй части, рекомендуем раз в 3–5 дней прорешивать полный вариант. Иначе вы рискуете забыть что-нибудь простое, уделяя время только сложному.
• Используйте сборники и пособия для подготовки к ЕГЭ по профильной математике. Анализ ресурсов и подборку лучших мы сделали в этой статье. 
• Изучите типичные ошибки, которые допускают участники ЕГЭ, — вы научитесь видеть недочёты и совершите их с меньшей вероятностью. 

Подготовка будет эффективной, если ваши работы будет проверять человек с опытом — иногда верный ответ не даёт максимальный балл за задание. Именно поэтому мы запустили спецкурсы с проверкой от наставников по заданию 14 и по заданию 12. 

На курсах Вебиума мы поможем вам подготовиться к ЕГЭ на максимальный балл: разберём актуальные задания, ты получишь обратную связь и ответы на вопросы по домашкам и закроешь пробелы во всех темах.   

Какие задания реже всего выполняют на ЕГЭ по профилю

Мы проанализировали статистику с официального сайта ФИПИ за 2021 год и составили рейтинг заданий в соответствии со средним процентов выполнения. Номера заданий приведены согласно новой демоверсии ЕГЭ по профильной математике.

Номер задания	Тема	Средний процент выполнения, %
1	Простейшие уравнения и неравенства	95,0%
2	Теория вероятности	92,9%
7	Задачи с прикладным содержанием	78,3%
3	Планиметрия	70,6%
4	Вычисления и преобразования	68,8%
5	Стереометрия	66,3%
6	Производная и первообразная	58,8%
11	Наибольшее и наименьшее значение функции	55,5%
8	Текстовые задачи	53,8%
12	Уравнения	36,1%
14	Неравенства	22,3%
16	Экономическая задача	19,0%
18	Задача на теорию чисел	11,4%
13	Сложная стереометрия	7,20%
15	Сложная планиметрия	3,50%
17	Задача с параметром	2,00%

 

Как сдать ЕГЭ по математике на 80+ баллов: советы от Эйджея Гаусса

Преподаватель математики в Вебиуме Эйджей Гаусс поделился советами, как правильно готовиться к ЕГЭ по профилю.  

• Внимательно изучите критерии заданий второй части, особенно связанные с оформлением! Даже если вам кто-то сказал, что именно в вашей области «вот это можно не писать», — это не гарантия того, что эксперт, проверяющий вашу работу, закроет глаза на мелкие нарушения.
• Запаситесь терпением и готовьте свои нервы к атмосфере экзамена. Советую заранее спланировать, в каком порядке вы будете решать задания: это поможет избежать паники в стрессовой ситуации. 
• Не забывайте решать пробники. Так вы поймёте, сколько времени вам требуется для решения определённого типа заданий, что вызывает наибольшие трудности и какие номера вы точно должны успеть решить. В стрессовых ситуациях время течёт иначе, поэтому будьте готовы к любому развитию событий — в этом поможет регулярная практика. 

Решайте бесплатные варианты ЕГЭ по профильной математике на сайте Вебиума, чтобы набить руку.

• Осознайте важную вещь: прорешать все задания, пробники, просмотреть все видео-разборы, которые вы сохранили на будущее, не получится! Сколько бы вы ни готовились, не опирайтесь на паттерны заданий и внимательно читайте условия. Даже в таком экзамене, как ЕГЭ, важна изворотливость ума и умение применять все свои знания. Шаблонно решать номера не получится, и пытаться не стоит — кто знает, что взбредёт составителям в голову. Именно поэтому нужно понимать логику решения, а не заучивать алгоритм.  
• Сохраните здравомыслие. Можно каждый месяц говорить себе: «О ужас! Осталось N дней до экзамена, а я ничего не знаю и ничего не сдам!» Однако задайте себе вопрос: чем паника и необоснованное недовольство собой помогут вам сдать ЕГЭ по профильной математике? Каждый день времени становится меньше, но ведь в сутках целых 24 часа! Стоит ли расстраиваться и накручивать себя из-за потерянной минуты? Конечно же, нет. Подготовиться с нуля можно, даже начав в апреле. Главное — верить в себя, в свои силы и прилагать усилия, чтобы достичь результата. 
• Не доводите себя до изнеможения! Находясь в постоянном напряжении, ваш мозг будет перегружаться. Это может привести к сильной усталости, нежеланию что-либо делать и даже к эмоциональному выгоранию. О том, как с этим справиться, рассказывали в этой статье. 
• Когда вы находитесь на пике стрессовой активности, у вас снижаются концентрация и внимание: даже простые задания перестанут получаться. А это ещё больше способствует самобичеванию. Так что не забывайте отдыхать и проводить время не только с учебниками. 

Для тех, кто сдаёт ЕГЭ по профильной математике и не знает, куда поступать, мы сделали подборки из десяти топовых технических вузов России и пяти лучших социально-экономических вузов России.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!

DOE: ILEARN

Когда проводится оценка ILEARN?

В течение учебного года предусмотрено три окна тестирования ILEARN Biology ECA, одно окно тестирования ILEARN 3-8 и одно окно тестирования ILEARN U.S. Government. ILEARN Biology ECA проводится осенью, зимой и весной для учащихся по триместровому расписанию, ILEARN 3-8 проводится каждую весну, а ILEARN US Government ECA предлагается в качестве дополнительной оценки весной. Просмотрите окна оценки этого года на веб-странице оценки Департамента образования штата Индиана (IDOE).

Какова схема тестирования ILEARN?

Каждое онлайн-тестирование ILEARN состоит из компьютерно-адаптивного тестового сегмента и тестового задания, а также тестовых сегментов фиксированной формы по общественным наукам и правительству США. Тесты фиксированной формы не являются адаптивными и доступны только в качестве адаптации для студентов с формальной адаптацией.

ILEARN измеряет широту академических стандартов штата Индиана. Это означает, что в планах тестов представлены все стандарты, включая грамотность в области содержания, грамотность в средствах массовой информации, стандарты аудирования и информатики, а также спецификации предметов. Педагогические комитеты Индианы сотрудничали с экспертами по контенту, чтобы создать схемы тестов ILEARN и спецификации предметов.

Кто участвует в ILEARN?

	ELA	Math	Science	Social Studies	Biology*	U. S. Government
Класс 3	x	x
Grade 4	x	x	x
Grade 5	x	x		x
Grade 6	x	x	x
Grade 7	x	x			x
Grade 8	x	x			x
High School					x	Optional

*Students will participate in ILEARN Biology ECA по окончании курса биологии в средней или старшей школе.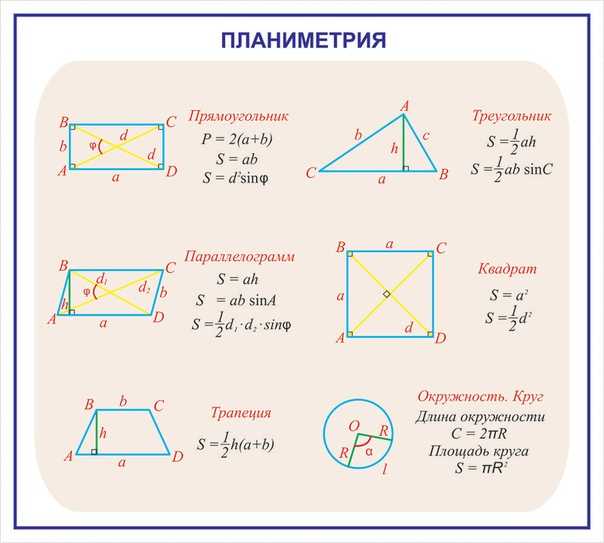

Как студенты будут получать баллы?

Результаты будут доступны соответствующим пользователям через централизованную систему отчетности Cambium Assessment, Inc. (CAI). Школы будут предоставлять результаты учащимся и их семьям на местном уровне, используя Индивидуальный отчет учащегося (ISR).

Библиотека примеров заданий для оценки PPAT

Библиотека примеров представляет собой набор фактических письменных ответов, представленных участниками теста PPAT. Ответы различаются по стилю написания и представлению, но наиболее важным фактором является то, насколько хорошо доказательства соответствуют направляющим подсказкам и рубрикам.

Примеры показывают, как другие кандидаты в вашей предметной области реагировали на направляющие подсказки, и дают более сильный и слабый ответ на одно и то же текстовое поле. Сравните свои ответы, чтобы определить, содержит ли ваша работа достаточные доказательства для полного выполнения каждой направляющей подсказки.

Помните, что примеры следует использовать только для целей сравнения. Работа, которую вы отправляете, должна быть вашей и только вашей. ETS использует программное обеспечение для сканирования всех ответов на совпадение с материалами, отправленными тестируемыми из всех окон подачи и из библиотеки примеров. Любое совпадение может быть расследовано, и ваши результаты могут быть аннулированы. См. Политики оценки.

Задача 1 состоит из двух этапов:

• Этап 1: Факторы, ресурсы и протоколы
• Шаг 2: Знание учащихся

Ниже приведены примеры для всех текстовых полей на каждом шаге.

• Арт (молния)
• Раннее детство (молния)
• Начальное образование (zip)
• Искусство английского языка (zip)
• Математика (zip)
• Музыка (zip)
• Физкультура (zip)
• Наука (zip)
• Социальные науки (zip)
• Специальное образование (zip)

Задача 2 состоит из трех шагов:

• Шаг 1: Планирование оценки
• Шаг 2: администрирование оценки и анализ данных
• Шаг 3: отражение

Ниже приведены примеры для всех текстовых полей на каждом шаге.

• Сельское хозяйство (zip)
• Арт (молния)
• Бизнес и промышленное/техническое образование (zip)
• Раннее детство (молния)
• Начальное образование (zip)
• Искусство английского языка (zip)
• Семейные и потребительские науки (zip)
• Математика (zip)
• Музыка (zip)
• Физкультура (zip)
• Наука (zip)
• Социальные науки (zip)
• Испанский (zip)
• Специальное образование (zip)

Задание 3 состоит из четырех шагов:

• Шаг 1: Планирование урока
• Шаг 2: Ученики в центре внимания
• Шаг 3. Анализ инструкции
• Шаг 4: отражение

Ниже приведены примеры для всех текстовых полей на каждом шаге.

• Сельское хозяйство (zip)
• Арт (молния)
• Бизнес и промышленное/техническое образование (zip)
• Раннее детство (молния)
• Начальное образование (zip)
• Искусство английского языка (zip)
• Семейные и потребительские науки (zip)
• Математика (zip)
• Музыка (zip)
• Физкультура (zip)
• Наука (zip)
• Социальные науки (zip)
• Испанский (zip)
• Специальное образование (zip)

Задача 4 состоит из четырех шагов:

• Шаг 1: Планирование
• Шаг 2: Реализация плана
• Шаг 3: Понимание студентов двух направлений
• Шаг 4: отражение

Ниже приведены примеры для всех текстовых полей на каждом шаге по предметным областям, а также ответы виртуальной среды обучения.