Задачи 14 ЕГЭ профильная математика



Задачи 14 ЕГЭ профильная математика

MATHM >> ЕГЭ >> ЕГЭ профиль >>

задача 14

ЗАДАЧА 14
сортировка
по сложности

СПИСОК ТЕМ

Тема 1: Реальные задачи ЕГЭ последних лет
Тема 2: Рациональные неравенства
Тема 3: Иррациональные неравенства
Тема 4: Неравенства с модулем
Тема 5: Показательные неравенства
Тема 6: Логарифмические неравенства
Тема 7: Логарифмические неравенства с переменным основанием
Тема 8: Смешанные неравенства

Задачи разделены на темы. Задачи из любой темы вполне реально встретить на настоящем экзамене ЕГЭ.

Внутри каждой темы задачи мы постарались расположить по возрастанию сложности.

Тема 1: Реальные задачи ЕГЭ последних лет

    2. посмотреть ответ

    посмотреть решение

    3. посмотреть ответ

    посмотреть решение

    4. посмотреть ответ

    посмотреть решение

    5. посмотреть ответ

    посмотреть решение

    6. посмотреть ответ

    посмотреть решение

    7. посмотреть ответ

    посмотреть решение

    8. посмотреть ответ

    посмотреть решение

    9. посмотреть ответ

    посмотреть решение

    10. посмотреть ответ

    посмотреть решение

    11. посмотреть ответ

    посмотреть решение

    12. посмотреть ответ

    посмотреть решение

    13. посмотреть ответ

    посмотреть решение

    14. посмотреть ответ

    посмотреть решение

    15. посмотреть ответ

    посмотреть решение

    16. посмотреть ответ

    посмотреть решение

    17. посмотреть ответ

    посмотреть решение

    18. посмотреть ответ

    посмотреть решение

    19. посмотреть ответ

    посмотреть решение

    20. посмотреть ответ

    посмотреть решение

    21. посмотреть ответ

    посмотреть решение

    22. посмотреть ответ

    посмотреть решение

    23. посмотреть ответ

    посмотреть решение

    24. посмотреть ответ

    посмотреть решение

    25. посмотреть ответ

    посмотреть решение

    26. посмотреть ответ

    посмотреть решение

    27. посмотреть ответ

    посмотреть решение

    28. посмотреть ответ

    посмотреть решение

    29. посмотреть ответ

    посмотреть решение

    30. посмотреть ответ

    посмотреть решение

    31. посмотреть ответ

    посмотреть решение

    32. посмотреть ответ

    посмотреть решение

    33. посмотреть ответ

    посмотреть решение

    34. посмотреть ответ

    посмотреть решение

    35. посмотреть ответ

    посмотреть решение

    36. посмотреть ответ

    посмотреть решение

    37. посмотреть ответ

    посмотреть решение

    38. посмотреть ответ

    посмотреть решение

    39. посмотреть ответ

    посмотреть решение

    40. посмотреть ответ

    посмотреть решение

    41. посмотреть ответ

    посмотреть решение

    42. посмотреть ответ

    посмотреть решение

Тема 2: Рациональные неравенства

    2. посмотреть ответ

    посмотреть решение

    3. посмотреть ответ

    посмотреть решение

    4. посмотреть ответ

    посмотреть решение

    5. посмотреть ответ

    посмотреть решение

    6. посмотреть ответ

    посмотреть решение

    7. посмотреть ответ

    посмотреть решение

    8. посмотреть ответ

    посмотреть решение

    9. посмотреть ответ

    посмотреть решение

    10. посмотреть ответ

    посмотреть решение

    11. посмотреть ответ

    посмотреть решение

Тема 3: Иррациональные неравенства

    2. посмотреть ответ

    посмотреть решение

    3. посмотреть ответ

    посмотреть решение

    4. посмотреть ответ

    посмотреть решение

    5. посмотреть ответ

    посмотреть решение

    6. посмотреть ответ

    посмотреть решение

    7. посмотреть ответ

    посмотреть решение

    8. посмотреть ответ

    посмотреть решение

    9. посмотреть ответ

    посмотреть решение

    10. посмотреть ответ

    посмотреть решение

Тема 4: Неравенства с модулем

    2. посмотреть ответ

    посмотреть решение

    3. посмотреть ответ

    посмотреть решение

    4. посмотреть ответ

    посмотреть решение

    5. посмотреть ответ

    посмотреть решение

    6. посмотреть ответ

    посмотреть решение

    7. посмотреть ответ

    посмотреть решение

    8. посмотреть ответ

    посмотреть решение

Тема 5: Показательные неравенства

    2. посмотреть ответ

    посмотреть решение

    3. посмотреть ответ

    посмотреть решение

    4. посмотреть ответ

    посмотреть решение

    5. посмотреть ответ

    посмотреть решение

    6. посмотреть ответ

    посмотреть решение

    7. посмотреть ответ

    посмотреть решение

    8. посмотреть ответ

    посмотреть решение

    9. посмотреть ответ

    посмотреть решение

    10. посмотреть ответ

    посмотреть решение

    11. посмотреть ответ

    посмотреть решение

    12. посмотреть ответ

    посмотреть решение

    13. посмотреть ответ

    посмотреть решение

    14. посмотреть ответ

    посмотреть решение

Тема 6: Логарифмические неравенства

    2. посмотреть ответ

    посмотреть решение

    3. посмотреть ответ

    посмотреть решение

    4. посмотреть ответ

    посмотреть решение

    5. посмотреть ответ

    посмотреть решение

    6. посмотреть ответ

    посмотреть решение

    7. посмотреть ответ

    посмотреть решение

    8. посмотреть ответ

    посмотреть решение

    9. посмотреть ответ

    посмотреть решение

Тема 7: Логарифмические неравенства с переменным основанием

    2. посмотреть ответ

    посмотреть решение

    3. посмотреть ответ

    посмотреть решение

    4. посмотреть ответ

    посмотреть решение

    5. посмотреть ответ

    посмотреть решение

    6. посмотреть ответ

    посмотреть решение

    7. посмотреть ответ

    посмотреть решение

    8. посмотреть ответ

    посмотреть решение

    9. посмотреть ответ

    посмотреть решение

    10. посмотреть ответ

    посмотреть решение

    11. посмотреть ответ

    посмотреть решение

Тема 8: Смешанные неравенства

    2. посмотреть ответ

    посмотреть решение

    3. посмотреть ответ

    посмотреть решение

    4. посмотреть ответ

    посмотреть решение

    5. посмотреть ответ

    посмотреть решение

    6. посмотреть ответ

    посмотреть решение

    7. посмотреть ответ

    посмотреть решение

    8. посмотреть ответ

    посмотреть решение

Задача 12 ЕГЭ математика профиль, сортировка по темам



Задача 12 ЕГЭ математика профиль, сортировка по темам

MATHM >> ЕГЭ >> ЕГЭ профиль >>

задача 12

ЗАДАЧА 12
сортировка
по сложности

ЗАДАЧА 12
сортировка
по темам

СПИСОК ТЕМ

Тема 1: Реальные задачи ЕГЭ последних лет
Тема 2: Тригонометрические уравнения
Тема 3: Тригонометрические уравнения с ОДЗ
Тема 4: Показательные уравнения (с тригонометрией и без)
Тема 5: Логарифмические уравнения (с тригонометрией и без)
Тема 6: Рациональные и иррациональные уравнения
Тема 7: Ответы с arcsin или arccos или arctg

Задачи разделены на темы.

Задачи из любой темы вполне реально встретить на настоящем экзамене ЕГЭ. Внутри каждой темы задачи мы постарались расположить по возрастанию сложности.
Тема 1: Реальные задачи ЕГЭ последних лет

    2. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    3. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    4. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    5. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    6. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    7. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    8. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    9. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    10. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    11. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    12. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    13. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    14. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    15. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    16. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    17. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    18. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    19. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    20. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    21. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    22. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    23. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    24. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    25. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    26. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    27. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    28. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    29. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    30. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    31. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    32. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    33. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    34. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    35. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    36. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    37. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    38. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    39. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    40. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    41. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

Тема 2: Тригонометрические уравнения

    2. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    3. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    4. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    5. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    6. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    7. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    8. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    9. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    10. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    11. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    12. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    13. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    14. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    15. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    16. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    17. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    18. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    19. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    20. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    21. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    22. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    23. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    24. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    25. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    26. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    27. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    28. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    29. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

Тема 3: Тригонометрические уравнения с ОДЗ

    2. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    3. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    4. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    5. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

  5. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    7. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    8. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    9. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    10. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    11. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    12. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    13. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    14. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    15. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

Тема 4: Показательные уравнения (с тригонометрией и без)

    2. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    3. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    4. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    5. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    6. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    7. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    8. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    9. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    10. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    11. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

Тема 5: Логарифмические уравнения (с тригонометрией и без)

    2. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    3. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    4. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    5. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    6. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    7. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    8. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

Тема 6: Рациональные и иррациональные уравнения

    2. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

Тема 7: Ответы с arcsin или arccos или arctg

    2. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    3. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

    4. посмотреть ответ

    посмотреть решение а)

    посмотреть решение б)

Анализ и профили решений бегущей волны для жидкости Дарси-Форхгеймера, сформулированной с нелинейной диффузией с нелинейной диффузией.

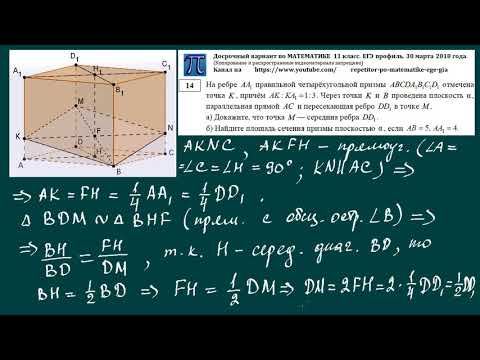Такая формулировка является основным новшеством настоящего исследования и требует введения соответствующей математической обработки для учета введенной вырожденной диффузии. Во-первых, анализ на существование, регулярность и единственность показан при определении соответствующей тестовой функции. После этого задача формулируется в области бегущей волны и анализируется вблизи критических точек с помощью геометрической теории возмущений. На основе этой теории получены точные и асимптотические профили бегущей волны. Кроме того, геометрическая теория возмущений используется для получения доказательств нормальной гиперболичности вовлеченных многообразий, которые используются для получения соответствующих решений бегущей волны. Основной вывод, нетривиальный в случае нелинейной диффузии, связан с существованием экспоненциального профиля вдоль бегущей системы отсчета. В конце концов, численное упражнение вводится для проверки полученных аналитических решений.

[1] P. Forchheimer, Wasserbewegung durch Boden, Z. Ver. Дтч. Инж. , 45 (1901), 1782–1788.
[2] М. Джавад, З. Шах, С. Ислам, Э. Бонья, А. З. Хан, Течение Дарси-Форхгеймера тонкопленочного течения МГД-наножидкости с диссипацией Джоуля и частичным скольжением Навье, J. Phys. коммун. , 2 (2018), 115014.
[3] С. Деро, Х. Шайх, Г. Х. Талпур, И. Хан, С. О. Альхарбим, М. Андуалем, Влияние пористой среды Дарси-Форхгеймера на течение радиационно намагниченной вращающейся гибридной наножидкости по сжимающейся поверхности, Sci. Респ. , 11 (2021), 24257. https://doi.org/10.1038/s41598-021-03470-x doi: 10.1038/s41598-021-03470-x
[4] В. Аль-Куз, А. Айсса, А. Кулали, В. Джамшед, Х. Мориа, К.С. Нисар и др., МГД-поток наножидкости Дарси-Форхгеймера и оптимизация энтропии в корпусе странной формы, заполненном (МУНТ- Fe3O4/вода) с использованием галёркинского анализа конечных элементов, Sci. Отчет , 11 (2021), 22635. https://doi.org/10.1038/s41598-021-02047-y doi: 10.1038/s41598-021-02047-y
[5] C. Soulaine, M. Quintard, Об использовании модели, подобной Дарси-Форххаймеру, для макромасштабного описания турбулентности в пористой среде и ее применении к структурированным упаковкам, Int. J. Heat Mass Tran. , 74 (2014), 88–100. https://doi.org/10.1016/j.ijheatmasstransfer.2014.02.069 doi: 10.1016/j.ijheatmasstransfer.2014.02.069
[6] Г. Расул, Т. Чжан, А. Дж. Чамха, А. Шафик, И. Тлили, Г. Шахзади, Генерация энтропии и последствия бинарной химической реакции на МГД поток наножидкости Дарси-Форхгеймера Вильямсона по нелинейно растягивающейся поверхности, Энтропия , 22 (2020), 18. https://doi.org/10.3390/e22010018 doi: 10.3390/e22010018
[7] Р. С. Саиф, Т. Мухаммед, Х. Садиа, Значение наклонного магнитного поля в потоке Дарси-Форхгеймера с переменной пористостью и теплопроводностью, Phys. А: Стат. мех. заявл. , 551 (2020), 124067. https://doi.org/10.1016/j.physa.2019.124067 doi: 10.1016/j.physa.2019.124067
[8] Г. Расул, А. Шафик, И. Хан, Д. Балеану, К. С. Нисар, Г. Шахзади, Генерация энтропии и последствия МГД в потоке наножидкости Дарси-Форхгеймера, ограниченном нелинейно растягивающейся поверхностью, Симметрия , 12 (2020), 652. https://doi.org/10.3390/sym12040652 doi: 10.3390/sym12040652
[9] М. А. Садик, Т. Хаят, Течение Дарси-Форхгеймера магнито-максвелловской жидкости, ограниченной конвективно нагретым листом, Results Phys. , 6 (2016), 884–890. https://doi.org/10.1016/j.rinp.2016.10.019doi: 10.1016/j.rinp.2016.10.019
[10] Т. Саджид, М. Сахир, С. Хуссейн, М. Билал, Дарси-Форхгеймер поток наножидкости Максвелла с нелинейным тепловым излучением и энергией активации, AIP Adv. , 8 (2018), 035102. https://doi.org/10.1063/1.5019218 doi: 10.1063/1.5019218
[11] Т. Хаят, К. Рафик, Т. Мухаммед, А. Алсаеди, М. Аюб, Значение углеродных нанотрубок в потоке Дарси-Форхгеймера, результатов Phys. , 8 (2018), 26–33. https://doi.org/10.1016/j.rinp.2017.11.022 doi: 10.1016/j.rinp.2017.11.022
[12] Т. Хаят, Ф. Хайдер, Т. Мухаммад, А. Алсаеди, О течении Дарси-Форхгеймера углеродных нанотрубок из-за вращающегося диска, Int. J. Heat Mass Tran. , 112 (2017), 248–254. https://doi.org/10.1016/j.ijheatmasstransfer.2017.04.123 doi: 10.1016/j.ijheatmasstransfer.2017.04.123
[13] Р. С. Саиф, Т. Хаят, Р. Эллахи, Т. Мухаммад, А. Алсаеди, Течение Дарси-Форххаймера наножидкости из-за искривленной поверхности растяжения, Int. Дж. Нумер. Методы Heat Fluid Flow , 29 (2019), 2–20. https://doi.org/10.1108/HFF-08-2017-0301 doi: 10.1108/HFF-08-2017-0301
[14] Т. Киу, Существование решения для обобщенного течения Форхгеймера в пористой среде с минимальными условиями регулярности, Дж. Матем. физ. , 61 (2020), 013507. https://doi.org/10.1063/1.5085004 doi: 10.1063/1.5085004
[15] Дж. Мюррей, Математическая биология , Springer, 2013. https://doi.org/10.1007/b98869
[16] Дж. Смолл, Ударные волны и уравнения реакции-диффузии , Нью-Йорк: Springer, 1983. https://doi.org/10.1007/978-1-4684-0152-3
[17] Х. Энрайт, П. Х. Мьюир, Решатель ОДУ с граничными значениями типа Рунге-Кутты с контролем дефектов, Comp. науч. Тех. Респ. , д. 1993, 93–267.
[18] А. Р. Чампни, Г. В. Хант, Дж. М. Т. Томпсон, Локализация и уединенные волны в механике твердого тела , World Scientific, 1999.
[19] А. де Пабло, Х. Л. Васкес, Бегущие волны и конечное распространение в уравнении реакции-диффузии, Ж. Дифференц. Уравнения , 93 (1991), 19–61. https://doi.org/10.1016/0022-0396(91)-Z doi: 10.1016/0022-0396(91)-Z
[20] Н. Фенихель, Стойкость и гладкость инвариантных многообразий для потоков, Indiana Univ. Мат. J. , 21 (1971), 193–226.
[21] ME Akveld, J. Hulshof, Решения бегущей волны полулинейного уравнения диффузии четвертого порядка, Appl. Мат. лат. , 11 (1998), 115–120. https://doi.org/10.1016/S0893-9659(98)00042-1 doi: 10.1016/S0893-9659(98)00042-1
[22] А. Де Пабло, Estudio de una ecuación de reacción-difusión , докторская диссертация, Автономный университет Мадрида, 1989.
[23] CKRT Jones, Геометрическая сингулярная теория возмущений, In: Dynamical systems , Lecture Notes in Mathematics, Springer, 1609 (1995), 44–118. https://doi.org/10.1007/BFb0095239
[24] Э. Чо, Ю. Дж. Ким, Распространение, вызванное голодом, как стратегия выживания биологических организмов, Bull. Мат. биол. , 75 (2013), 845–870. https://doi.org/10.1007/s11538-013-9838-1 doi: 10.1007/s11538-013-9838-1
[25] Э. Ф. Келлер, Л. А. Сегель, Перемещающиеся полосы хемотаксических бактерий: теоретический анализ, J. Theor. биол. , 30 (1971), 235–248. https://doi.org/10.1016/0022-5193(71)-8 doi: 10.1016/0022-5193(71)-8
[26] Ю. Тао, М. Винклер, Эффекты сигнал-зависимой подвижности в системе реакции-диффузии типа Келлера-Сегеля, Math. Мод. Мет. заявл. науч. , 27 (2017), 1645–1683. https://doi.org/10.1142/S0218202517500282 doi: 10.1142/S0218202517500282
[27] К. Юн, Ю. Дж. Ким, Глобальное существование и агрегация в модели Келлера-Сегеля с диффузией Фоккера-Планка, Acta Appl. Мат. , 149 (2016), 101–123. https://doi.org/10.1007/s10440-016-0089-7 doi: 10.1007/s10440-016-0089-7
[28] Дж. Ан, К. Юн, Глобальная корректность и стабильность постоянных равновесий в параболо-эллиптической системе хемотаксиса без определения градиента, Нелинейность , 32 (2019), 1327–1351.
[29] А. Шахид, Х. Хуанг, М. Бхатти, Л. Чжан, Р. Эллахи, Численное исследование плавания гиротактических микроорганизмов в наножидкостях через пористую среду по растянутой поверхности, Математика , 8 (2020), 380 https://doi.org/10.3390/math8030380 doi: 10. 3390/математика8030380
[30] Л. Хайин, Бифуркация Хопфа модели хищник-жертва, зависящая от плотности, с задержкой, Acta Math. науч. сер. А , 39 (2019), 358–371.
[31] М. М. Бхатти, А. Зишан, Р. Эллахи, О. Анвар Бег, А. Кадир, Влияние коагуляции на двухфазную перистальтическую прокачку намагниченной биожидкости Прандтля через эндоскопическую кольцевую геометрию, содержащую пористую среду, Подбородок. Дж. Физ. , 58 (2019), 222–234. https://doi.org/10.1016/j.cjph.2019.02.004 doi: 10.1016/j.cjph.2019.02.004

Ли Л. Лоури-младший — Просто еще один сайт CoE WordPress

 

ПРОФЕССОР
Техасский университет A&M
Zachry Факультет гражданского и экологического проектирования
ИНЖЕНЕР-ИССЛЕДОВАТЕЛЬ
Техасский исследовательский фонд A&M
Техасская инженерная экспериментальная станция
Техасский институт транспорта

 

 

Эл.
Телефон: 979-775-5401

Общая информация для работодателей и студентов:

  • Мое резюме
  • Собираетесь перейти к опции «Структуры»? Планирование ваших курсов на ранней стадии имеет решающее значение.
  • Запрос на перевод только в класс CVEN
  • Департамент стипендий и финансовой помощи
  • В нашей компании проходит стажировка, которую мы хотели бы зарегистрировать в Департаменте CE
  • Наша компания заинтересована в том, чтобы связаться с вашими студентами по поводу трудоустройства. Как мы это делаем?
  • Материалы проверки технической регистрации Проверка FE Расширенная проверка FE
  • Уровень сдачи экзамена 9 по основам инженерного дела Департамента гражданского строительства Техаса A&M0342
  • Инженерная этика
  • Вакансии — студенты, ищущие работу, или работодатели, ищущие лучших выпускников
  • Рекомендательные письма для моих студентов
  • Возможности для волонтеров для инженеров — И здесь (общий вариант) – Дополните свое резюме значимой работой
  • Как работодатели могут связаться с нашими студентами и встретиться с ними для получения информации, возможностей трудоустройства и т. д.
  • Зарегистрируйте свою корпоративную стажировку в отделе CE TAMU
  • Проблемы с психическим здоровьем в ТАМУ
  • Краткая история инженерно-строительного факультета
  • Личный бред (Добро пожаловать сюда. Только общий бред, юмор, песни и т.д.)
  • Общая информация для классов Лоури
  • Истории успеха
  • Отличные публикации по инженерии для новых инженеров
  • Точное время (с точностью до наносекунды)
  • Старые фотографии моих учеников 1983 года
  • Зум
  • ENGR 385 – Информация для студентов, изучающих гражданское строительство

Классы Лоури

  • Текущие классы
    • CVEN 305/301 – Сопротивление материалов – Летняя программа 2021 г. 
    • CVEN 305/301 Класс Лекции ВИДЕОЗАПИСИ на ЛЕТО 2021 ГОДА
    • ENGR 385 – Информация для студентов, изучающих гражданское строительство, – лето 2021 г.
  • Классы, заменяемые другими
    • CVEN 686 — Джон Нидзвеки — Весенний семестр 2019 г. — Анализ забивки свай с помощью волнового уравнения
    • CVEN 686 — Джон Нидзвеки — Весенний семестр 2018 г. — Анализ забивки свай по волновому уравнению
    • CVEN 345 ​​— Рэй Джеймс — 14.09.15
  • Курсы предыдущего семестра
    • CVEN 345/503 — Теория структур — осень 2020 г.
    • ENGR 484 – Международная инженерная стажировка
    • ENGR 385 – Информация для студентов, изучающих гражданское строительство, – весна 2019 г.
    • CVEN 207 – Компонент регистрации профессиональных инженеров CVEN 207
    • CVEN 221 – Статика – Весенняя программа 2021 г.
    • ВИДЕОЗАПИСИ Лекции класса CVEN 221 на ВЕСНУ 2021
    • CVEN 221 – Статика – Осень 2017 г.
    • CVEN 221 – Статика – Осень 2016 г.
    • CVEN 221 – Статика – Осень 2011 – Возрожденный
    • CVEN 305/301 – Гражданские инженерные системы – лето 2020 г.
    • CVEN 305/301 – Механика материалов – лето 2019 г.
    • CVEN 305 – Механика материалов – весна 2018 г.