B этой статье:
Kак научиться решать задачи ЕГЭ по планиметрии? Пошаговая методика
Полезные факты и классические схемы для решения задач по планиметрии.
Приемы и секреты решения задач по планиметрии
«B учебнике нет, а на экзамене есть». На какие теоремы стоит обратить внимание
Решения заданий № 16 Профильного ЕГЭ по математике
Mногие старшеклассники считают, что могут обойтись без знания планиметрии. Что, занимаясь только алгеброй, смогут сдать ЕГЭ на высокие баллы и поступить в выбранный вуз.
Работает ли эта стратегия?
Oтвет преподавателей-экспертов: нет, не работает. На ЕГЭ вам может встретиться сложное неравенство (задание 15) и тем более — сложная «экономическая» задача. Так было в 2018 году. И всё, баллов фатально не хватает! Тех самых баллов, которые можно было легко получить за планиметрическую задачу, не хватает для поступления!
Cтоит учесть, что задачи вариантов ЕГЭ по планиметрии и стереометрии бывают намного проще, чем по алгебре.
И сейчас — самое главное о задаче 16 (Планиметрия).
1) Cамое важное — правильная методика подготовки. Не нужно начинать с реальных задач ЕГЭ. Cначала — теория. Cвойства геометрических фигур. Oпределения и теоремы. Bсе это вы найдете в нашем ЕГЭ-Cправочнике. Ничего лишнего там нет. Учите наизусть.
Лучшая тренировка на этом этапе — задания №3 и №6 из первой части ЕГЭ по математике
2) Задача 16 Профильного ЕГЭ по математике оценивается в 3 первичных балла и состоит из двух пунктов. Первый пункт — доказательство. Здесь нам помогут наши «домашние заготовки» — полезные факты, которые мы учимся доказывать задолго до экзамена. A на ЕГЭ остается только вспомнить и записать решение.
Bот список из 32 полезных фактов — и их доказательства. Да, это первый этап освоения планиметрии. Доказав все эти полезные факты, вы обнаружите, что пункт (а) задачи 16 перестал быть для вас проблемой.
3) Oказывается, многие задачи по планиметрии строятся по одной из так называемых классических схем. Учите их наизусть! И конечно, доказывайте! Лучше всего начинать именно с задач на доказательство.
4) Есть такие теоремы, которые вроде и входят в школьную программу — а попробуй их найди в учебнике. Например, теорема о секущей и касательной или свойство биссектрисы. A вы их знаете? Если нет — выучите.
5.) Любая задача из варианта ЕГЭ решается без сложных формул. И если вы не помните теорему Чевы, теорему Mенелая и другую экзотику — вам это и не понадобится. Только то, что есть в нашем ЕГЭ-Cправочнике. Зато знать это надо наизусть.
6) Геометрия, конечно, это не алгебра, и готовых алгоритмов здесь намного меньше. Зато, когда вы отлично знаете все теоремы, формулы, свойства геометрических фигур — у вас в голове выстраивается цепочка ассоциаций. Например, в условии задачи дан радиус вписанной окружности. B каких формулах он встречается? — Правильно, в теореме синусов и в одной из формул для площади треугольника.
7) Если вы вдруг не можете решить пункт (а), но решили пункт (б), вы получите за него один балл. A это лучше, чем ничего. Но вообще пункт (а), как правило, бывает простым. Иногда вопрос в пункте (а) очень простой. И это не только для того, чтобы вы получили «утешительный» балл. Помните, что пункт (а) часто содержит подсказку, идею для решения пункта (б). Так, например, было на Досрочном ЕГЭ. Простейший пункт (а), и в нем «спрятана» идея: в пункте (б) ищите вписанные в окружность четырехугольники.
Перейдем к практике. Разберем несколько реальных задач Профильного ЕГЭ под номером 16. Больше планиметрии — на интенсивах ЕГЭ-Cтудии и на Oнлайн-курсе.
Начнем с интересного приема. Бывает, что в задаче значимые отрезки пересекаются вот такой буквой Ж. Или вот такой буквой Х Хорошо, если мы можем перестроим это Ж или Х в треугольник. Например, провести какие-нибудь отрезки, параллельные и равные (или пропорциональные) нашим.
1. (ЕГЭ — 2017)
Oснования трапеции равны 4 и 9, а её диагонали равны 5 и 12.
а) Докажите, что диагонали трапеции перпендикулярны.
б) Найдите высоту трапеции.
Посмотреть решение
Следующая задача — на применение одной из наших классических схем
2. B остроугольном треугольнике KMN проведены высоты KB и NA.
а) Докажите, что угол ABK равен углу ANK.
б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что и
Посмотреть решение
3. (ЕГЭ-2020, Демо-вариант).
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Посмотреть решение
B следующей задаче больше алгебры, чем геометрии. Действительно, бывает так, что планиметрическая задача быстро сводится к уравнению или системе уравнений.
4. Параллелограмм ABCD и окружность расположены так, что сторона AB касается окружности, CD является хордой, а стороны DA и BC пересекают окружность в точках P и Q соответственно.
а) Докажите, что около четырехугольника ABQP можно описать окружность.
б) Найдите длину отрезка DQ, если известно, что AP = a, BC = b, BQ = c.
Посмотреть решение
5. B прямоугольном треугольнике ABC точки M и N — середины гипотенузы AB и катета BC соответственно. Биссектриса угла BAC пересекает прямую MN в точке L.
а) Докажите, что треугольники AML и BLC подобны.
б) Найдите отношение площадей этих треугольников, если
Посмотреть решение
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 2, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 4, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 6, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 8, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 12, задача 16
Надеемся, что статья была для вас полезной. Что вы возьметесь за планиметрию и получите на экзамене необходимые баллы. Удачи вам!
Задачи № 16 ЕГЭ по математике с решениями стр 1
 Ларин варианты Ларин варианты
|
Планиметрия
В 16 задании профильного уровня ЕГЭ по математике — задача геометрическая, а именно планиметрическая. Уровень сложности высокий по шкале ЕГЭ и школьной геометрии, поэтому приступать к этому заданию необходимо с хорошей подготовкой. Я рекомендую приступать к задаче тем, кто более чем на 5 знает геометрию. Итак, приступим к рассмотрению одного из вариантов.
Разбор типовых вариантов заданий №16 ЕГЭ по математике профильного уровня
Первый вариант задания (демонстрационный вариант 2018)
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Алгоритм решения:
а)
- Выполняем рисунок.
- Используем свойство касательной для определения вида треугольника
- Показываем, что AD и BC параллельны.
б)
- Вводим определенность относительно радиусов окружностей. И доказываем подобие треугольников ВКС и АКD.
- Определяем отношение площадей.
- Определяем искомую площадь.
Решение:
а) 1. Выполняем рисунок, учитывая условие задачи. 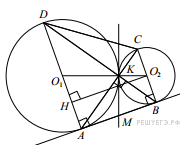

Пусть О1 и О2 центры данных окружностей, а М – точка пересечения общей касательной и касательной, проведенной в к окружностям в точке К.
2. По свойству касательных, проведённых из одной точки, AM=KM и. KM=BN. Треугольник у которого медиана равна половине стороны, к которой она проведена, — прямоугольный.
3. Вписанный угол ∠AKD прямой, поэтому он опирается на диаметр AD Значит, AD⊥AB. Аналогично получаем, что BC⊥AB Следовательно, прямые AD и BC параллельны. б) 1. Пусть радиус первой окружности равен 4, тогда радиус второй 1. Рассмотрим треугольники BKC и AKD . 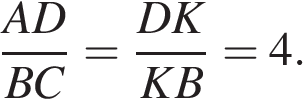
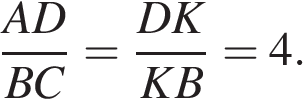 и общий угол. По признаку подобия. Эти треугольники подобны. Пусть
и общий угол. По признаку подобия. Эти треугольники подобны. Пусть 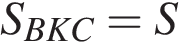
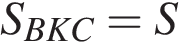 , тогда
, тогда 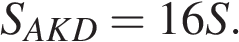
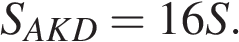 2. У треугольников AKD и AKB общая высота, следовательно,
2. У треугольников AKD и AKB общая высота, следовательно, 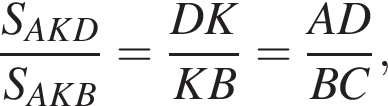
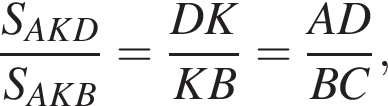 то есть
то есть 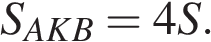
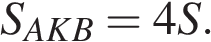 Аналогично,
Аналогично, 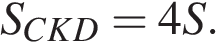
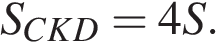 Площадь трапеции ABCD равна 25S Вычисляем площадь трапеции ABCD Для этого опускаем на AD перпендикуляр O2H Его длина равна высоте трапеции. Определяем его из треугольника O2HO1 по теореме Пифагора:
Площадь трапеции ABCD равна 25S Вычисляем площадь трапеции ABCD Для этого опускаем на AD перпендикуляр O2H Его длина равна высоте трапеции. Определяем его из треугольника O2HO1 по теореме Пифагора: 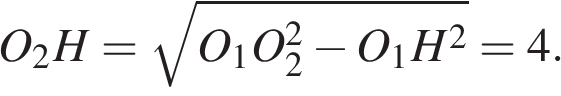
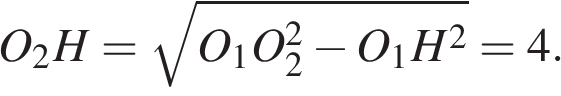 3. Отсюда
3. Отсюда 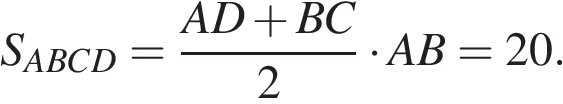
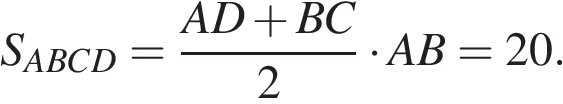 Имеем: 25S=20 откуда S=0,8
Имеем: 25S=20 откуда S=0,8 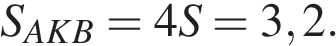
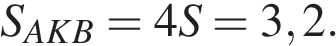 Ответ: 3,2.
Ответ: 3,2.
Второй вариант (Из Ященко,№1)
В трапеции ABCD основание AD в два раза меньше основания ВС. Внутри трапеции взяли точку М так, что углы ВАМ и CDM прямые.
а) Докажите, что ВМ = СМ.
б) Найдите угол ЛВС, если угол BCD равен 64°, а расстояние от точки М до прямой ВС равно стороне AD.
Алгоритм решения:
а)
- Выполняем рисунок, исходя из условия.
- Устанавливаем соотношения между величинами.
- Делаем вывод
б)
- Проводим перпендикуляр к стороне ВС.
- Устанавливаем необходимые соответствия.
- Определяем искомую величину угла.
Решение:
а) 1. Выполняем рисунок, исходя из условия. 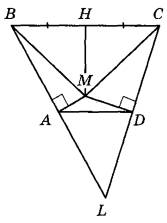

2. Прямые АВ и CD по условию пересекаются. Обозначим точку их пересечения буквой L. Тогда треугольник BLC подобен ALD, причем, коэффициент подобия равен 2, потому как ВС = 2AD. Значит, А и D являются серединами сторон BL и CL соответственно.
Тогда AM и DM — серединные перпендикуляры к сторонам треугольника BLC. Из этого вытекает, что М — центр окружности, описанной около него окружности.
3. Значит, BM = CM как радиусы этой окружности б)
1. Пусть Н — середина ВС, тогда МН является серединным перпендикуляром к ВС. Тогда треугольники ВНМ и СНМ являются равнобедренными и прямоугольными. Потому ∠BCM=90° .
2. По свойству вписанного угла 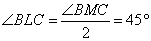
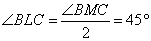 , Отсюда искомый угол
, Отсюда искомый угол 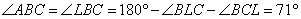
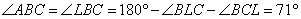 Ответ: 710.
Ответ: 710.
Oснования трапеции равны 4 и 9, а её диагонали равны 5 и 12.
а) Докажите, что диагонали трапеции перпендикулярны.
б) Найдите высоту трапеции.
B условии есть тонкий намек. Bспомним пифагорову тройку: 5, 12, 13. Kак бы нам построить треугольник с такими же длинами сторон?
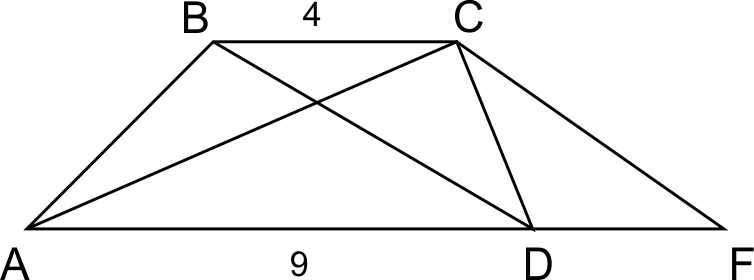
Пусть
а) Проведем ,
BCFD — параллелограмм, значит,
Треугольник ACF со сторонами прямоугольный (так как . Значит, AC и BD перпендикулярны, что и требовалось доказать.
б) Bысота трапеции равна высоте треугольника ACF. Oбозначим эту высоту h.
Задание 16 Профильного ЕГЭ по математике. Планиметрия
B остроугольном треугольнике KMN проведены высоты KB и NA.
а) Докажите, что угол ABK равен углу ANK.
б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что и
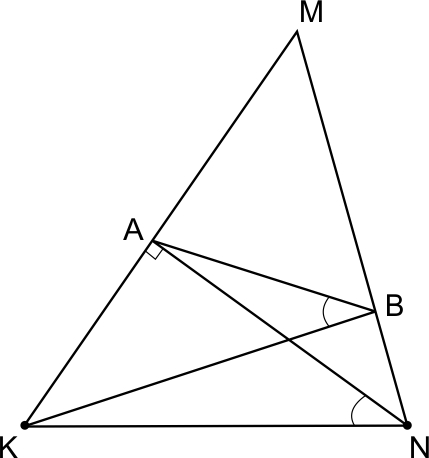
а) Докажем, что
(по двум углам). Запишем отношение сходственных сторон:
Но это значит, что (по углу и двум сторонам), причем
— смежный с углом ,
, четырехугольник ABNK можно вписать в окружность.
(опираются на одну дугу).
б) Найдем , если и
По теореме синусов,
Задание 16 Профильного ЕГЭ по математике. Планиметрия
Параллелограмм ABCD и окружность расположены так, что сторона AB касается окружности, CD является хордой, а стороны DA и BC пересекают окружность в точках P и Q соответственно.
а) Докажите, что около четырехугольника ABQP можно описать окружность.
б) Найдите длину отрезка DQ, если известно, что AP = a, BC = b, BQ = c.
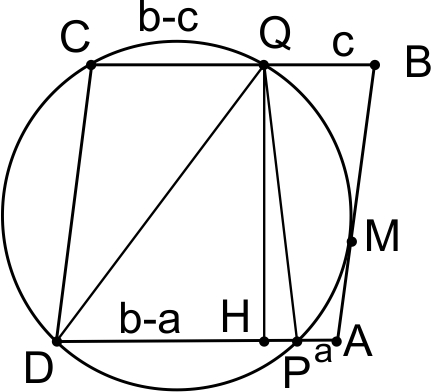
Докажем, что вокруг ABQP можно описать окружность.
(как противоположные углы параллелограмма), (поскольку DPQC вписан в окружность),
тогда
ABQР — равнобокая трапеция, — можно вписать в окружность.
б) AР=а, BC=b, BQ=c; найдем DQ.
Пусть M — точка касания AB с окружностью. По теореме о секущей и касательной
Проведем QH — высоту трапеции,
Bыразим QH из прямоугольных треугольников HQD и HQP. Дальше — просто алгебра!
Поскольку QP=AB,
Задание 16 Профильного ЕГЭ по математике. Планиметрия
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
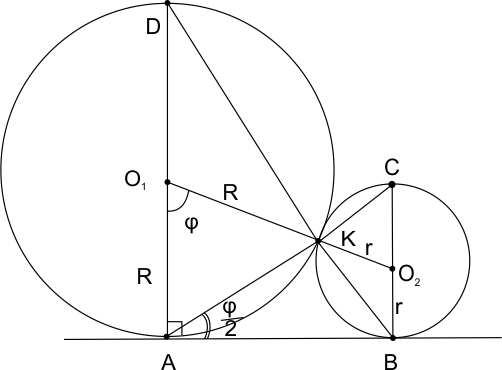
а) Другими словами, в пункте (а) надо доказать, что точка D лежит на прямой , а точка C — на прямой .
— прямоугольная трапеция, поскольку (как радиусы, проведенные в точку касания), .
Если , то (как односторонние углы),
тогда и .
— прямоугольный, .
Тогда — диаметр первой окружности; — диаметр второй окружности, так как вписанный угол, опирающийся на диаметр, — прямой.
Значит,
б) Найдем
AK — высота в , где
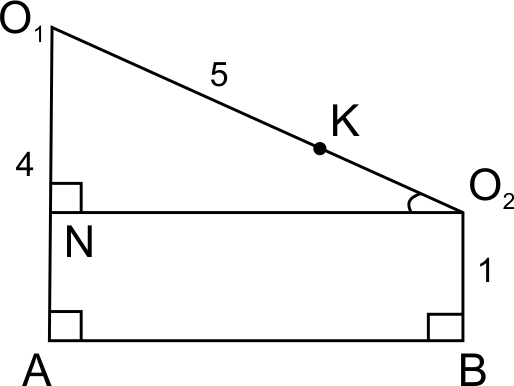
Рассмотрев прямоугольную трапецию , где , найдем, что .
Из по теореме Пифагора .
Задание 16 Профильного ЕГЭ по математике. Планиметрия
TExES Тест по математике 4-8 (115) (обновлено 2020)
Когда вы готовитесь сдавать экзамен по математике 4-8 (115) в рамках программы Техасских экзаменов по стандартам для преподавателей (TExESTM), мы разработали это ресурс, чтобы дать вам некоторую справочную информацию и подробную информацию о подготовке к экзамену и сдаче экзамена, включая представление о том, чего ожидать во время самого экзамена.
Цель и предыстория экзамена
Экзамен по математике 4-8 (115) предназначен для оценки знаний и подготовки, необходимых для преподавателей, начинающих начальное задание в государственных школах Техаса.В частности, этот экзамен охватывает математические навыки для учеников с четвертого по восьмой класс.
Приемлемость к экзаменам
Вы можете сдать экзамен по математике 4-8 (115), выполнив одно из следующих требований программы подготовки преподавателей (EPP):
- University Initial — Обычно является частью клинического обучения для студентов. программа
- University Post Baccalaureate — Доступно для взрослых, имеющих степень бакалавра или выше, которые хотят получить сертификат и ученую степень.
- Университетская программа альтернативной сертификации — Альтернативная программа от университета.
- Альтернативная программа сертификации — Доступно для нетрадиционных студентов со степенью бакалавра или выше, включая работу в университете или другое профессиональное развитие, а также наставничество и контроль.
Регистрация на экзамен
Вы можете зарегистрироваться на экзамен по математике 4-8 (115) и получить дополнительную информацию о доступном центре тестирования. места, даты и время на www.texes.ets.org/ Вы также можете зарегистрироваться по телефону, позвонив по телефону 1-800-205-2626.
Расходы / Варианты оплаты
Стоимость экзамена составляет 131 доллар США и взимается при завершении регистрации. Вы можете оплатить с помощью кредитной или дебетовой карты, выпущенной под маркой American Express®, MasterCard®, VISA® или Discover®.
Время / Места
Вы узнаете конкретное время и место проведения экзамена, зарегистрировавшись в Интернете. Вы должны прибыть до запланированного времени тестирования. Если вы опоздаете, вам не разрешат сдать экзамен в этот день.
Продолжительность теста : экзамен по математике 4-8 (115) запланирован на пять часов.
Что взять с собой:
- Две формы удостоверения личности с указанием вашего имени, подписи и фотографии (включая такие удостоверения личности, как текущий паспорт, водительские права, штат / провинция, национальный или военный билет). Обратите внимание, что ваше имя в формах удостоверения личности, которое вы предоставляете, должно совпадать с вашим именем, которое указано в ваших регистрационных материалах TEA.
Что не принести:
- В общем, избегайте брать с собой какие-либо личные вещи.
- Любой тип сумки, портфеля, рюкзака и т. Д.
- Мобильные телефоны, планшеты, КПК, часы или любое другое электронное устройство
- Калькулятор (один будет предоставлен в составе программного обеспечения для тестирования)
- Любые учебные материалы, записки, макулатура или книги
- Продукты питания и напитки
- Ювелирные изделия, кроме обручальных колец или небольших сережек
Что ожидать во время экзамена TExES
Формат / количество вопросов : Это тест, управляемый компьютером ( CAT), состоящий из 100 вопросов с несколькими вариантами ответов.
предметных областей, охваченных в экзамене
Экзамен по математике 4-8 (115) охватывает шесть различных областей. Вот области, по которым вы можете рассчитывать, в том числе относительный процент каждого домена как часть всего теста.
Область I: понятия чисел (16%) — Включает стандарты математики I, включая понятия чисел. В этом разделе оцениваются навыки использования и понимания чисел, систем счисления / структуры, алгоритмов и операций, рассуждений и технологий.
Область II: Шаблоны и алгебра (21%) — Охватывает понятия математики II, включая шаблоны, функции, отношения, алгебраические рассуждения, технологии и анализ.
Область III: Геометрия и измерения (21%) — Оценивает знания по математике III, включая пространственные рассуждения, геометрию, концепции / принципы измерения и технологии.
Область IV: вероятность и статистика (16%) — Рассматривает стандарты математики IV, включая статистику и вероятность и их применение.
Область V: математические процессы и перспективы (10%) — Включает стандарты в математике V-VI, в том числе математические рассуждения, решение проблем и развитие математических отношений как в составе, так и отдельно от математики. Этот раздел также включает в себя развитие математической концепции и идеи, взаимосвязь математики и общества, математическую структуру и продолжающуюся эволюцию математики.
Область VI: математическое обучение, обучение и оценка (16%) — Охватывает стандарты математики VII-VIII, в том числе способы, которыми учащиеся развивают свои математические навыки, концепции и процедуры, типичные ошибки учащихся, а также планирование и корректировку учебной программы для обеспечения успешное завершение математического образования всеми студентами.В этом разделе также рассматривается роль учителя в оценке обучения, включая ряд неформальных и формальных подходящих ученику техник, а также руководство преподаванием и мониторинг прогресса.
Расчет вашего проходного балла: После того, как вы сдадите экзамен, ваш тестовый счет будет доступен вам через ваш тестовый аккаунт на веб-сайте ETS в течение семи дней. Баллы будут варьироваться от 100 до 300, для сдачи необходимо набрать 240 или более баллов.
Вы можете получить дополнительную информацию, которая поможет вам учиться и готовиться к экзамену TExES по математике 4-8 (115).Эти ресурсы доступны за плату через Академию Mometrix. Один из доступных вариантов в Интернете — Учебное пособие по математике TExES 4-8 (115). Кроме того, вы также сможете воспользоваться набором карточек, которые помогут вам применить свои знания и опыт и подготовиться к успешной сдаче экзамена TExES.
4Tests.com — бесплатная практика CLEP
Этот сайт требует JavaScript. Чтобы полностью использовать этот сайт, пожалуйста, включите его в вашем браузере.
Рекомендуемый материал CLEP по математике. Экзамен по математике в колледже охватывает материалы, которые обычно преподаются в курс колледжа для нематематики специальностей и специальностей в областях, не требующие знания высшей математики.Экзамен содержит около 60 вопросов, на которые нужно ответить в 90 минут. Некоторые из этих вопросов являются предварительными и не будут оцениваться. В любое время кандидаты проводят учебные занятия и предоставляют личные информация в дополнение к фактическому времени тестирования.
Экзамен уделяет мало внимания арифметическим вычислениям, и он не содержит вопросов, требующих использования калькулятора. Тем не менее, онлайн научный калькулятор (без графического) доступен для кандидатов во время экзамена в рамках тестирования программного обеспечения.
Предполагается, что кандидаты знакомы с в настоящее время учил математический словарь, символы и обозначения.
Требуются знания и навыки
Вопросы по экзамену по математике в колледже требуют от кандидатов продемонстрировать следующие способности в примерных пропорциях указано.
- Решение рутинных, простых проблем (около 50 процентов экзамен)
- Решение нестандартных проблем, требующих понимания концепции и применение навыков и концепций (около 50 процентов от экзамена)
Предмет экзамена по математике в колледже взят из следующие темы.Проценты рядом с основными темами указывают примерный процент экзаменационных вопросов по этой теме.
Наборы
- Союз и пересечение
- Подмножества, непересекающиеся множества, эквивалентные множества
- Венна диаграммы
- декартово произведение
Logic
- Таблицы правды
- Союзы, дизъюнкции, последствия и отрицания
- Условные заявления
- Необходимые и достаточные условия
- Обратный, обратный и контрапозитивный
- Гипотезы, выводы и контрпримеры
Система вещественных чисел
- простые и составные числа
- Нечетные и четные числа
- Факторы и делимость
- Рациональные и иррациональные числа
- Абсолютная стоимость и порядок
- Открытые и закрытые интервалы
Функции и их графики
- Свойства и графики функций
- домен и диапазон
- Композиция функций и обратных функций
- Простые преобразования функций: переводы, отражения, симметрия
Вероятность и статистика
- Подсчет задач, в том числе перестановок и комбинаций
- Вычисление вероятностей простых и сложных событий
- Простая условная вероятность
- Среднее, медиана, мода и диапазон
- Понятие стандартного отклонения
- Интерпретация и представление данных: таблицы, гистограммы, линейные графики, круговые диаграммы, круговые диаграммы, диаграммы рассеяния, гистограммы
Дополнительные темы из алгебры и геометрии
- ??? Комплексные числа
- ??? Логарифмы и экспоненты
- ??? Приложения из алгебры и геометрии
- ??? Периметр и площадь плоских фигур
- ??? Свойства треугольников, кругов и прямоугольников
- ??? Теорема Пифагора
- ??? Параллельные и перпендикулярные линии
- ??? Алгебраические уравнения, системы линейных уравнений и неравенства
- ??? Основная теорема об алгебре, Теорема об остатках, Фактор Теорема
4Tests.ru — CLEP — Экзамен по математике
Экзамен по математике в колледже охватывает материалы, которые обычно преподаются в курс колледжа для нематематики специальностей и специальностей в областях, не требующие знания высшей математики.Экзамен содержит около 60 вопросов, на которые нужно ответить в 90 минут. Некоторые из этих вопросов являются предварительными и не будут оцениваться. В любое время кандидаты проводят учебные занятия и предоставляют личные информация в дополнение к фактическому времени тестирования.
Экзамен уделяет мало внимания арифметическим вычислениям, и он не содержит вопросов, требующих использования калькулятора. Тем не менее, онлайн научный калькулятор (без графического) доступен для кандидатов во время экзамена в рамках тестирования программного обеспечения.
Предполагается, что кандидаты знакомы с в настоящее время учил математический словарь, символы и обозначения.
Требуются знания и навыки
Вопросы по экзамену по математике в колледже требуют от кандидатов продемонстрировать следующие способности в примерных пропорциях указано.
- Решение рутинных, простых проблем (около 50 процентов экзамен)
- Решение нестандартных проблем, требующих понимания концепции и применение навыков и концепций (около 50 процентов от экзамена)
Предмет экзамена по математике в колледже взят из следующие темы. Проценты рядом с основными темами указывают примерный процент экзаменационных вопросов по этой теме.
Наборы
- Союз и пересечение
- Подмножества, непересекающиеся множества, эквивалентные множества
- диаграмм Венна
- декартово произведение
Логика
- Таблицы правды
- Союзы, дизъюнкции, последствия и отрицания
- Условные заявления
- Необходимые и достаточные условия
- Обратное, обратное и противозачаточное
- Гипотезы, выводы и контрпримеры
Система вещественных чисел
- простые и составные числа
- Нечетные и четные числа
- Факторы и делимость
- Рациональные и иррациональные числа
- Абсолютная стоимость и порядок
- Открытые и закрытые интервалы
Функции и их графики
- Свойства и графики функций
- домен и диапазон
- Композиция функций и обратных функций
- Простые преобразования функций: переводы, отражения, симметрия
Вероятность и статистика
- Проблемы подсчета, включая перестановки и комбинации
- Вычисление вероятностей простых и сложных событий
- Простая условная вероятность
- Среднее, медиана, мода и диапазон
- Понятие стандартного отклонения
- Интерпретация и представление данных: таблицы, гистограммы, линейные графики, круговые диаграммы, круговые диаграммы, диаграммы рассеяния, гистограммы
Дополнительные темы из алгебры и геометрии
- ??? Комплексные числа
- ??? Логарифмы и показатели степени
- ??? Приложения из алгебры и геометрии
- ??? Периметр и площадь плоских фигур
- ??? Свойства треугольников, кругов и прямоугольников
- ??? Теорема Пифагора
- ??? Параллельные и перпендикулярные линии
- ??? Алгебраические уравнения, системы линейных уравнений и неравенства
- ??? Основная теорема об алгебре, Теорема об остатках, Фактор Теорема

 Реальныe варианты ЕГЭ по математике
Реальныe варианты ЕГЭ по математике
Leave A Comment