Базовый уровень ЕГЭ по математике: полезные советы
В ЕГЭ по математике базового уровня – 20 заданий. Они не требуют развернутой записи решения, достаточно найти ответ и правильно записать его в графу.
Один верный ответ — 1 балл. 20 верных ответов — 20 баллов.
На выполнение заданий даётся 3 часа. Этого достаточно, чтобы все решить, перепроверить и аккуратно перенести на черновик.
Нужно правильно понять, что именно спрашивают, а это не всегда очевидно.
Задание 7: чтение диаграммТипичный ответ
Очень часто школьники упускают из виду часть условия «с февраля по конец мая» и дают неправильный ответ на простейшую задачу – «Февраль, март, ноябрь, декабрь».
Хотя правильный ответ
«Февраль и март».
Для решения задачи часто нужно составить уравнение, а для этого важно не упустить ни одного элемента условия и правильно записать его математическим языком.
Иногда для решения задачи можно и даже нужно использовать элемент, который прямо не прописан в условии.
Задание 16: текстовая задачаВводим неизвестное: х – количество винограда. Чтобы составить уравнение, нам необходимо равенство. Что мы можем в данном случае уравнять? Сухое вещество, ведь оно остается одинаковым и в винограде, и в изюме. Если в винограде 82% воды, значит сухого вещества – 18%. Точно так же находим сухое вещество в изюме: 100 – 19 = 81%.
Получается, что 18% от неизвестного нам количество винограда – это то же самое, что 81% от 42 килограммов изюма. Составляем уравнение и решаем его:
х ∙ 18% = 42 ∙ 81%
Ответ: х = 189.
В некоторых заданиях быстрее и проще не проводить долгих вычислений, а прикинуть или догадаться, каков верный ответ. Но после этого, разумеется, надо выполнить проверку. Так вы экономите время и развиваете математическое мышление и эрудицию.
Но после этого, разумеется, надо выполнить проверку. Так вы экономите время и развиваете математическое мышление и эрудицию.
Для начала мы вводим неизвестное: х деталей в час делает второй рабочий. Тогда х+4 детали в час делает первый рабочий. Известно, что 140 деталей первый рабочий делает на 4 часа быстрее, чем второй. Составляем уравнение:
Решаем и получаем выражение х(x+4)=140. Внимательно присмотритесь к этому равенству. Вам необходимо найти такое значение х, при котором произведение двух чисел, отличающихся на 4, будет равно 140. Не обязательно считать, можно просто увидеть, что это 10 и 14.
Ответ на задачу: х=10.
Чтобы развить в себе подобное математическое видение, достаточно решать как можно больше задач и не обращаться к калькулятору сразу же, как только надо что-то посчитать.
Здесь тоже гораздо быстрее не делить с остатком, а прикинуть, сколько автобусов может понадобиться, а затем выполнить простую операцию умножения.
В данном случае нам надо перевести 274 человека, а в автобус влезает 46. Возьмем для начала цифру 6 и умножим на 46, получилось 276 человек. Это значит, что мы нашли правильный ответ, не углубляясь в сложные расчеты.
Помните о том, что большинство задач можно решить не одним, а несколькими способами. Это поможет вам избежать ошибок, в том числе связанных с выполнением вычислений или обычной невнимательностью.
Если вы решили задачу двумя способами и получили один и тот же ответ, значит, он точно правильный.
При этом выбирайте более простые пути решения, а вот громоздких решений, наоборот, избегайте. Чем проще решение, тем меньше вероятность ошибиться.
Задание 9: клетчатая бумагаСпособ 1. Делим трапецию на два треугольника по краям и прямоугольник в центре. Считаем площадь по клеточкам. Площадь прямоугольника – 12 см2
Треугольники для удобства продолжаем до прямоугольников, считаем площадь этих прямоугольников (она получается 6 и 9 см2) и делим ее пополам. Таким образом, получается, что площадь первого треугольника – 3 см2, а второго – 4,5 см2. Складываем 3 + 12 + 4,5 и находим площадь трапеции = 19,5 см2.
Таким образом, получается, что площадь первого треугольника – 3 см2, а второго – 4,5 см2. Складываем 3 + 12 + 4,5 и находим площадь трапеции = 19,5 см2.
Способ 2. Используем формулу для нахождения площади трапеции.
S=1/2 ∙h(a+b), где h – высота трапеции, a и b – основания.
S=123(9+4) = 19,5 см
Ответ сошёлся, значит он верен.
Многие задания на экзамене проще, чем кажутся. Правильно считайте, применяйте знание формул, будьте внимательны, и у вас все получится.
Любой нормально развитый человек способен понять математику, и вы — не исключение.
Задача 12: простейший анализ
Чтобы решить эту задачу, нужно знать одну единственную формулу — Ньютона-Лейбница.
S=F(b) – F(а).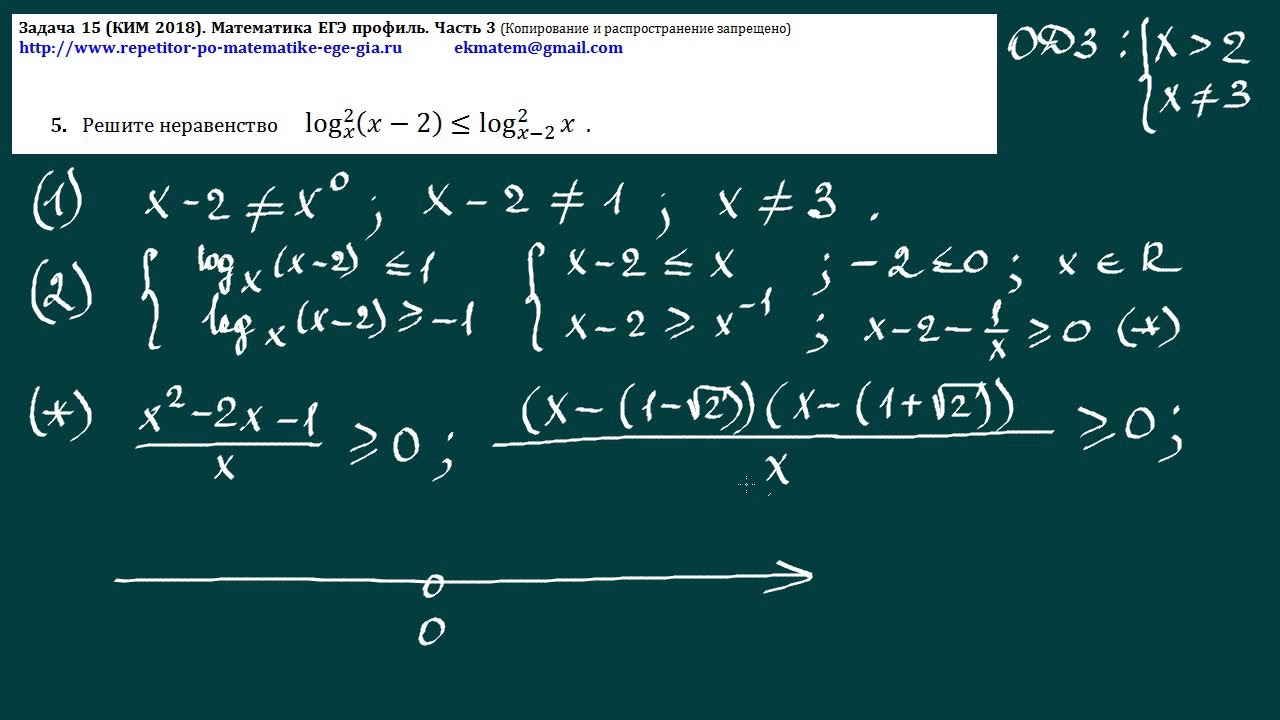 Подставляем значения х в функцию, указанную в условии, находим F(–1) и F(–3), подставляем в формулу и получаем S=5–3=2.
Подставляем значения х в функцию, указанную в условии, находим F(–1) и F(–3), подставляем в формулу и получаем S=5–3=2.
Это одна из самых простых задач с точки зрения математики, хотя и стоит ближе к концу списка заданий. Здесь нужно всего лишь взять формулу, подставить в нее величины и правильно подсчитать.
Обращайте внимание на то, чтобы все упомянутые в задаче числа были указаны в одной системе измерений. При необходимости нужно перевести всё в одну систему, но в данном примере и этого не требуется.
m(t)=31,25
M(0)=250
T=3 мин
Вычисляем и получаем ответ: t=9.
Восемь советов от разработчиков заданий — Российская газета
Какие ошибки — самые «популярные» на ЕГЭ? Почему нельзя считать в уме? И зачем выпускнику — учебник пятого класса? Советы по подготовке к экзаменам дает руководитель федеральной группы разработчиков ЕГЭ по математике, научный руководитель Центра педагогического мастерства Иван Ященко.
1. Занимайтесь математикой регулярно. Даже если вы сдаете не профильный экзамен, а базовый. Советую выделить на это хотя бы 10-15 минут в день. Закреплять, в первую очередь, базовые умения. Новую теорию учить уже бесполезно.
2. Решайте задачи, где есть текст. К сожалению, до 40 процентов ошибок на экзаменах связаны именно с тем, что ученик не так прочитал, неправильно понял условие. Каждый год десятки тысяч ребят решают, казалось бы, «правильно», но вовсе не ту задачу, которая дана. И получают за нее в итоге «законный» ноль… Поэтому внимательно читайте условия. И когда у вас получился какой-то ответ, сверьте его с условием.
3. Не спешите и не считайте в уме. Если торопиться, даже базовые арифметические навыки могут подвести. Огромное количество ошибок связано с дробями, процентами и с отрицательными числами. Особенно с отрицательными числами! Обиднее всего, когда за задачу на теорию вероятностей получаешь ноль баллов из-за простейшей вычислительной ошибки. Поэтому и при подготовке, и на самом экзамене избегайте вычислений в уме: обязательно пишите промежуточные выкладки. Как только вы совершаете два действия в уме, это сразу повышает риск ошибки.
Как только вы совершаете два действия в уме, это сразу повышает риск ошибки.
4. Советую обратить внимание на задачи по геометрии, по теории вероятностей, и задачи с реальными статистическими данными. Например, связанными с выбором оптимального тарифного плана сотовой связи. Такие задачи придется решать каждому в жизни.
5. Решать многочисленные варианты, похожие на демоверсию — самый неэффективный способ подготовки. Повторение должно быть тематическое. И если уж прорешиваете варианты, то делайте это тематическими блоками. Делайте акцент, во-первых, на те задачи, которые получаются, и на те, которые вы точно планируете решить на экзамене. Некоторые задачи, возможно, стоит сразу заранее пропускать и особо их не разбирать.
6. Не получаются первые задачи ЕГЭ? Регулярно подводят дроби, проценты и отрицательные числа? Не надо стесняться — можно взять учебник пятого-шестого класса и повторить базу.
7. Сдать профильную математику на максимальный балл сможет далеко не каждый выпускник. Поэтому нужно реально рассчитывать свои силы. Нужно понимать, что хороший результат ЕГЭ — это не 100 баллов. А тот балл, который ты реально можешь получить, или чуть-чуть выше. Выберите несколько вузов, посмотрите, с какими баллами туда поступали в прошлом году. Прикиньте свои оценки по другим предметам — и составьте «вилку»: вот сюда я смогу поступить, если наберу, допустим, 80 баллов. А вот этот вуз будет запасным: здесь хватит и 65.
Поэтому нужно реально рассчитывать свои силы. Нужно понимать, что хороший результат ЕГЭ — это не 100 баллов. А тот балл, который ты реально можешь получить, или чуть-чуть выше. Выберите несколько вузов, посмотрите, с какими баллами туда поступали в прошлом году. Прикиньте свои оценки по другим предметам — и составьте «вилку»: вот сюда я смогу поступить, если наберу, допустим, 80 баллов. А вот этот вуз будет запасным: здесь хватит и 65.
8. Используйте все возможности дистанционки. Сроки ЕГЭ сдвигаются — и это оправданная мера, потому что нужно в первую очередь заботится о здоровье ребят. Они, конечно, нервничают, — хочется уже быстрее сдать экзамены. Но теперь появилось дополнительное время. Если потратить его с умом, можно не просто получить больше баллов, но и лучше подготовиться к обучению в выбранном вузе.
По инициативе министерства просвещения открыт телеканал для подготовки к ЕГЭ «Моя школа online». На сайте Федерального института педагогических измерений (ФИПИ) размещены реальные варианты досрочного ЕГЭ 2020 года, есть даже ответы к ним для самопроверки, методические материалы. По инициативе правительства Москвы и при поддержке Рособрнадзора мы сделали цикл уроков по подготовке ЕГЭ — с разбором всех задач, автоматическими домашними заданиями от лучших педагогов, в том числе членов комиссии разработчиков ЕГЭ. Они открыты бесплатно абсолютно для всех школьников на сайте московского Центра педагогического мастерства.
По инициативе правительства Москвы и при поддержке Рособрнадзора мы сделали цикл уроков по подготовке ЕГЭ — с разбором всех задач, автоматическими домашними заданиями от лучших педагогов, в том числе членов комиссии разработчиков ЕГЭ. Они открыты бесплатно абсолютно для всех школьников на сайте московского Центра педагогического мастерства.
Для родителей будущих выпускников
— Наши исследования показывают, что огромное количество проблем в математике — это проблемы, которые накопились у ребенка уже к пятому-шестому классу. Те же дроби дети начинают изучать еще в началке, и продолжают делать на них ошибки даже в одиннадцатом классе.
И проблема не в том, что такие ребята не способны к математике. Когда ты учишься, ты делаешь ошибки, не все получается с первого раза, это совершенно естественно. Но важно, чтобы учитель эти проблемы вовремя заметил и постарался решить их вместе с ребенком, а не просто поставил «троечку». В последнем случае проблемы накапливаются как снежный ком, и уже в средних и старших классах уроки математики фактически проходят зря.
Мы очень рады, что в последние годы и родители и школьники стали понимать: экзамен по математике — это не скучная «обязаловка», а инструмент, который готовит ребят к реальным задачам, с которыми они столкнутся в жизни. Базовый ЕГЭ по математике — на обычном, бытовом уровне. Профильный — позволяет человеку показать, что он готов обучаться в вузе.
Задача 11 — текстовые задачи
Для текстовых задач не существует единого алгоритма решения — в этом вся их сложность. Фактически, каждую задачу приходится решать «с нуля». Зубрить их тоже бесполезно, потому что текстовых задач слишком много.
Тем не менее, существуют типовые задачи, которые вполне стандартно решаются и постоянно встречаются на ЕГЭ по математике. Ими мы и займемся.
- § 1.
- Вебинар по задачам B14: движение, работа, смеси и сплавы
- Глава 1.
- Классические задачи на движение
- § 1.
- Особенности решения текстовых задач
- § 2.
- Задача B14: движение навстречу
- § 3.

- Движение вдогонку и сравнение времени
- § 4.
- Тест по задачам B14: легкий уровень, 1 вариант
- § 5.
- Тест по задачам B14: легкий уровень, 2 вариант
- § 6.
- B14 и эскалаторы: считаем скорость
- § 7.
- Задача B14 про эскалаторы: считаем ступеньки
- Глава 2.
- Работа и производительность труда
- § 1.
- Производительность совместного труда
- § 2.
- B14: количество вопросов в тесте
- § 3.
- Трубы и резервуары: одинаковый объем
- § 4.
- Трубы и резервуары: разный объем
- § 5.
- Более сложные задачи на производительность
- Глава 3.
- Движение по воде
- § 1.
- Решение задач на движение по воде
- § 2.
- Тест по задачам B14: средний уровень, 1 вариант
- § 3.
- Тест по задачам B14: средний уровень, 2 вариант
- Глава 4.
- Смеси и сплавы
- § 1.
- Как решать задачи про смеси и сплавы
- § 2.

- Простая задача B14 на смеси и сплавы
- § 3.
- Сложная задача B14 на смеси и сплавы
- § 4.
- Смеси и сплавы в задаче B14: неизвестна масса
- Проценты и нестандартные задачи
- § 1.
- Задача B14: сложные проценты
- § 2.
- Семья из трех человек (нестандартная задача)
- § 3.
- Сложная задача B14: работа трех исполнителей
- § 4.
- Изюм и виноград (смеси и сплавы)
Подготовка школьников к ЕГЭ-21 по математике (базовый уровень)
Единый государственный экзамен по математике базового уровня ориентирован на проверку фундаментальных знаний, умений и навыков учащихся, формируемых на уроках математики (алгебры и геометрии) на протяжении всех лет обучения в школе. Так, например, есть задания на проверку умения считать, сравнивать величины, пользоваться процентами, решать уравнения, пользоваться математическими формулами.
Для подготовки к ЕГЭ по математике ВГСПУ запускает онлайн-класс, который явлется инновационной формой дополнительного образования. Онлайн-класс рассчитан на учащихся одиннадцатых классов, но часть учебного материала будет понятна даже для девятиклассников. Некоторые темы школьного курса математики разбираются в ходе занятий. Поэтому онлайн-класс может стать базой, отправной точкой для улучшения понимания материала школьной программы и отработки навыков решения задач.
Также онлайн-класс будет полезен и учителям-предметникам, занимающимся подготовкой обучающихся к ЕГЭ по математике. Существует довольно много подходов к подготовке школьников к сдаче ЕГЭ по математике. У каждого преподавателя есть свой взгляд на данный процесс. Этот онлайн-класс позволит Вам познакомиться с методом, практикуемым преподавателем с более чем 20-летним опытом работы со школьниками, из которых около 15 лет были посвящены подготовке к ЕГЭ.
Все зачисленные на обучение в онлайн-классе получают доступ к одноименному онлайн-курсу, содержащему все необходимые для обучения материалы: видеолекции, автоматизированные проверочные задания, дополнительные материалы. Учителя получают дополнительные организационно-методические рекомендации по организации обучения по методике автора. Открытое обсуждение занятий, общение с автором курса, другими обучающимися проходит в группе в социальной сети Вконтакте.
ПРОГРАММА КУРСА
Курс состоит из уроков, каждый из которых посвящен изучению методов решения основных типов задач, предлагаемых организаторами экзамена (ФИПИ) к решению в текущем учебном году. Для каждого типа задач приводится и разбирается пример решения, после чего учащимся предоставляется возможность отработать навык самостоятельного решения задач. При этом по необходимости можно воспользоваться подсказками, рассчитанными на восстановление полного хода решения задачи.
Факультативный курс по математике «Практикум решения задач по подготовке к ЕГЭ»
Пояснительная записка.
Данный курс предназначен для учащихся 11 класса, выбравшие сдавать ЕГЭ по математике на профильном уровне и рассчитан на 68 часов. Разработка программы данного курса отвечает как требованиям стандарта математического образования, так и требованиям контрольно-измерительных материалов ЕГЭ на профильном уровне. Программа включает повторение, обобщение некоторых вопросов содержания курса математики, а также дополнительных вопросов, расширяющих и углубляющих его по основным идейным линиям.
Цели курса:
— практическая помощь обучающимся 11 класса при подготовке к ЕГЭ по математике на профильном уровне;
— повторение, систематизация, расширение и углубление знаний за курс математики основной и средней школы;
— интеллектуальное развитие обучающихся, формирование качеств мышления, характерных для математической деятельности и необходимых человеку для жизни в современном обществе, для общей социальной ориентации и решения практических проблем. Задачи курса:
Задачи курса:
— подготовить обучающихся к успешной сдаче ЕГЭ по математике на профильном уровне;
— активизировать познавательную деятельность обучающихся;
— расширить знания и умения в решении различных математических задач, подробно рассмотрев возможные или более приемлемые методы их решения;
— формировать общие умения и навыки по решению задач 2 и 3 части работы КИМ на профильном уровне;
— повысить информационную и коммуникативную компетентность обучающихся; — помочь учащимся оценить свой потенциал с точки зрения образовательной перспективы.
Курсу отводится 2 часа в неделю. Всего 68 часов.
Особенности курса:
— интеграция разных тем;
— расширение и углубление базового курса математики;
— практическая значимость для обучающихся.
Содержание курса.
1. Стереометрия (задача 14). 9ч.
Нахождение расстояний, длин и периметров.
Нахождение углов.
Нахождение площадей и объёмов.
2. Планиметрия (задача 16). 8ч.
Окружности и треугольники.
Окружности и четырёхугольники.
3. Финансовая математика (задача 17). 8ч Банки, вклады, кредиты.
4. Неравенства (задача 15). 10ч.
Рациональные и иррациональные неравенства.
Показательные неравенства.
Логарифмические неравенства.
Неравенства с модулем.
Смешанные неравенства.
5. Задача с параметром (задача 18). 8ч.
Расположение корней квадратного трёхчлена.
Использование симметрий, оценок, монотонности.
Уравнения с параметром.
Функции, зависящие от параметра.
6. Уравнения (задача 13). 8ч.
Логарифмические и показательные уравнения.
Тригонометрические уравнения.
Уравнения смешанного типа.
7. Текстовые задачи (задача 11). 8ч.
Задачи на проценты, смеси и сплавы.
Задачи на движение.
Задачи на работу.
Разные задачи.
8. Задачи с прикладным содержанием (задача 10). 4ч. Задачи с прикладным содержанием.
9. Производная и первообразная (задачи 7 и 12). 5ч. Физический и механический смысл производной.
Применение производной к исследованию функций.
Первообразная. Итого: 68 часов.
Требования к уровню подготовки обучающихся.
В результате изучения курса, обучающиеся должны уметь решать задачи второй части ЕГЭ профильного уровня, иметь представление о методах и приёмах решения задач повышенного и высокого уровней сложности. В записи решений к заданиям с развернутым ответом особое внимание обращать на построение чертежей и рисунков, лаконичность пояснений, доказательность рассуждений. Уметь вычислять значения корня, степени. Находить значения тригонометрических выражений. Выполнять тождественные преобразования тригонометрических, рациональных и иррациональных выражений. Решать тригонометрические, рациональные, иррациональные уравнения и неравенства и их системы, включая с параметром и модулем, а также комбинирование типов аналитическими и функционально-графическими методами. Знать приёмы решения различных типов текстовых задач с практическим содержанием на проценты, движение, работу. Знать широту применения процентных вычислений в жизни, решать основные задачи на проценты, применять формулу сложных процентов, задачи на вклады и кредиты. Решать некоторые типы стереометрических задач, содержащие разный уровень необходимых для решения обоснований и количество шагов в решении задач, включенных в часть I и часть II экзаменационной работы, часто требующие построения вспомогательных элементов и сечений, сопровождаемых необходимыми доказательствами. Производить прикидку и оценку результатов вычислений. При вычислениях сочетать устные и письменные приёмы, использовать приёмы, рационализирующие вычисления.
Знать широту применения процентных вычислений в жизни, решать основные задачи на проценты, применять формулу сложных процентов, задачи на вклады и кредиты. Решать некоторые типы стереометрических задач, содержащие разный уровень необходимых для решения обоснований и количество шагов в решении задач, включенных в часть I и часть II экзаменационной работы, часто требующие построения вспомогательных элементов и сечений, сопровождаемых необходимыми доказательствами. Производить прикидку и оценку результатов вычислений. При вычислениях сочетать устные и письменные приёмы, использовать приёмы, рационализирующие вычисления.
Уровень достижений учащихся определяется в результате:
• наблюдения активности на практикумах;
• беседы с учащимися;
• решения задач самостоятельно;
• самостоятельно решённых домашних диагностических работ.
Основные формы организации учебных занятий:
• лекция;
• объяснение;
• выполнение тренировочных упражнений; работа в малых группах.
Формы контроля:
• проверка самостоятельно выполненных заданий;
• групповая и индивидуальная работа над решением заданий; выполнение домашних диагностических работ в формате ЕГЭ профильного уровня.
Тематическое планирование по курсу
«Практикум решения задач по подготовке к ЕГЭ по математике». 11 класс (профиль).
|
№ урока |
Раздел, название урока |
Кол-во часов |
Дата |
Корректировка |
|
1. |
9ч |
|
|
|
|
№1 №2 №3 №4 №5 №6 №7 №8 №9 |
Нахождение расстояний, длин и периметров. Нахождение расстояний, длин и периметров. Нахождение расстояний, длин и периметров. Нахождение углов. Нахождение углов. Нахождение углов. Нахождение площадей и объёмов. Нахождение площадей и объёмов. Нахождение площадей и объёмов. |
1 1 1 1 1 1 1 1 1 |
03.09. 03.09. 10.09 10.09 17.09 17.09 24.09 24.09 01. |
|
|
2. Планиметрия (задача 16). |
8ч |
|
|
|
|
№10 №11 №12 №13 №14 №15 №16 №17 |
Окружности и треугольники. Окружности и треугольники. Окружности и треугольники. Окружности и треугольники. Окружности и четырёхугольники. Окружности и четырёхугольники. Окружности и четырёхугольники. Окружности и четырёхугольники. |
1 1 1 1 1 1 1 1 |
01.10 08.10 08.10 15.10 15.10 22.10 22.10 29.10 |
|
|
3. |
8ч |
|
|
|
|
№18 №19 №20 №21 №22 |
Банки, вклады, кредиты. Банки, вклады, кредиты. Банки, вклады, кредиты. Банки, вклады, кредиты. Банки, вклады, кредиты. |
1 1 1 1 1 |
29. 19.11 |
|
|
№23 №24 №25 |
Банки, вклады, кредиты. Банки, вклады, кредиты. Банки, вклады, кредиты. |
1 1 1 |
26.11 26.11 03.12 |
|
|
4. |
10ч |
|
|
|
|
№26 №27 №28 №29 №30 №31 №32 №33 №34 №35 |
Рациональные и иррациональные неравенства. Рациональные и иррациональные неравенства. Показательные неравенства. Показательные неравенства. Логарифмические неравенства. Логарифмические неравенства. Неравенства с модулем. Неравенства с модулем. Смешанные неравенства. Смешанные неравенства. |
1 1 1 1 1 1 1 1 1 1 |
03. 21.01 |
|
|
5. Задача с параметром (задача 18). |
8ч |
|
|
|
|
№36 №37 №38 №39 №40 №41 №42 №43 |
Расположение корней квадратного трёхчлена. Расположение корней квадратного трёхчлена. Использование симметрий, оценок, монотонности. Использование симметрий, оценок, монотонности. Уравнения с параметром. Уравнения с параметром. Функции, зависящие от параметра. Функции, зависящие от параметра. |
1 1 1 1 1 1 1 1 |
21.01 28.01 28.01 04.02 04.02 11.02 11.02 18. |
|
|
6. Уравнения (задача 13). |
8ч |
|
|
|
|
№44 №45 №46 №47 №48 №49 |
Логарифмические и показательные уравнения. Логарифмические и показательные уравнения. Тригонометрические уравнения. Тригонометрические уравнения Тригонометрические уравнения Уравнения смешанного типа. |
1 1 1 1 1 1 |
18.02 25.02 25.02 03.03 03.03 10.03 |
|
|
№50 №51 |
Уравнения смешанного типа. |
|
1 1 |
10.03 17.03 |
|
||
|
7. Текстовые задачи (задача 11). |
|
8ч |
|
|
|||
|
№52 №53 №54 №55 №56 №57 №58 №59 |
Задачи на проценты, смеси и сплавы. Задачи на проценты, смеси и сплавы. Задачи на движение Задачи на движение. Задачи на работу. Задачи на работу. Разные задачи. Разные задачи. |
|
1 1 1 1 1 1 1 1 |
17.03 24.03 24.03 07.04 07.04 14.04 14.04 21.04 |
|
||
|
8. |
|
4ч |
|
|
|||
|
№60 №61 №62 №63 |
Задачи с прикладным содержанием (задача 10). Задачи с прикладным содержанием (задача 10). Задачи с прикладным содержанием (задача 10). Задачи с прикладным содержанием (задача 10). |
|
1 1 1 1 |
21.04 28.04 28.04 12.05. |
|
||
|
9. Производная и первообразная (задачи 7 и 12). |
|
5ч |
|
|
|||
|
№64 №65 №66 №67 №68 |
Физический и механический смысл производной. Физический и механический смысл производной. Применение производной к исследованию функций. Применение производной к исследованию функций. Первообразная. |
|
1 1 1 1 1 |
12.05 19.05 19.05 21.05 21.05 |
|
||
|
|
|
Итого: |
68ч. |
|
|
||
|
|
|
|
|
||||
Учебно-методическое и материально-техническое обеспечение.
Литература.
1. Вольфсон Г.И. и др. ЕГЭ 2019. Математика. Арифметика и алгебра. Задача 19 (профильный уровень) / Под ред. И. В. Ященко.—М.: МЦНМО, 2019.
2. Гордин Р.К. ЕГЭ 2019. Математика. Геометрия. Планиметрия. Задача 16 (профильный уровень) / Под ред. И. В. Ященко. — М.: МЦНМО, 2019.
3. Гордин Р.К. ЕГЭ 2019. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень) / Под ред. И. В. Ященко. — М.: МЦНМО, 2019.
4. Гущин Д.Д., Малышев А. В. ЕГЭ 2018. Математика. Задачи прикладного содержания. Задача 10 (профильный уровень). Рабочая тетрадь / Под ред. И. В. Ященко.- М.: МЦНМО, 2018.
5. Лысенко Ф.Ф., Кулабухова С.Ю. Математика. Подготовка к ЕГЭ — 2018. Профильный уровень.
40 тренировочных тестов по демоверсии на 2018 года: учебно-методическое пособие. — Ростовна-Дону: Легион, 2017. 6. Сергеев И.Н. ЕГЭ. Математика. 1000 задач с ответами и решениями. Все задания части 2 / И.Н. Сергеев, В.С. Панферов.– М.: Экзамен, 2019.
Математика. 1000 задач с ответами и решениями. Все задания части 2 / И.Н. Сергеев, В.С. Панферов.– М.: Экзамен, 2019.
7. Садовничий Ю.В. ЕГЭ 2018. Математика. Решение уравнений и неравенств / Ю. В. Садовничий. – М.: УЧПЕДГИЗ, 2019.
8. Садовничий Ю.В. ЕГЭ 2019. 100 баллов. Математика. Профильный уровень. Задачи с параметром /Ю.В. Садовничий. – М.: УЧПЕДГИЗ, 2019.
9. Шестаков С. А. ЕГЭ 2019. Математика. Задачи на составление уравнений. Задача 11 (профильный уровень). Рабочая тетрадь / Под ред. И. В. Ященко.- М.: МЦНМО, 2019.
10. Шестаков С. А. ЕГЭ 2019. Математика. Задачи с параметром. Задача 18 (профильный уровень) / Под ред. И. В. Ященко. — М.: МЦНМО, 2019.
11. Шестаков С. А. ЕГЭ 2019. Математика. Задачи с экономическим содержанием. Задача 17 (профильный уровень) / Под ред. И. В. Ященко — М.: МЦНМО, 2019.
12. Шестаков С. А. ЕГЭ 2019. Математика. Неравенства и системы неравенств. Задача 15 (профильный уровень). — М.: МЦНМО, 2019.
— М.: МЦНМО, 2019.
13. Шестаков С. А. ЕГЭ 2019. Математика. Производная и первообразная. Исследование функций. Задача 12 (профильный уровень). Рабочая тетрадь / Под ред. И. В. Ященко — М.:
МЦНМО, 2019.
14. Шестаков С. А., Захаров П.И. ЕГЭ 2019. Математика. Уравнения и системы уравнений. Задача 13 (профильный уровень) / Под ред. И. В. Ященко. — М.: МЦНМО, 2019.
15. Ященко И.В., Шестаков С.А. Подготовка к ЕГЭ по математике в 2019 году. Профильный уровень. Методические указания. – М.: МЦНМО, 2019.
16. Ященко И.В. ЕГЭ: 4000 задач с ответами по математике. Все задания «Закрытый сегмент».
Базовый и профильный уровни/ И.В. Ященко, И.Р. Высоцкий, А.В. Забелин и др.; под ред. И.В.
Ященко. – М.: Экзамен, 2019.
17. Математика. Подготовка к ЕГЭ в 2019 году. Профильный уровень. Диагностические работы. — М.: МЦНМО, 2019.
18. Ященко И.В., Захаров П.И. ЕГЭ 2019. Математика. Геометрический смысл производной.
Задача 7 (профильный уровень). Задача 14 (базовый уровень). Рабочая тетрадь / Под ред. И. В.
Ященко. — М.: МЦНМО, 2019.
19. ЕГЭ 2019: Математика: 30 тренировочных вариантов экзаменационных работ для подготовки к единому государственному экзамену: профильный уровень /под ред. И. В. Ященко. – Москва: АСТ, 2019.
Программно-педагогические средства, реализуемые с помощью компьютера.
1. CD «1С: Репетитор. Математика» (КИМ).
2. CD «Математика. 5-11 классы. Практикум».
Цифровые образовательные ресурсы (ЦОР) для поддержки подготовки школьников.
1. Открытый банк заданий по математике. Базовый уровень. Профильный уровень. Режим доступа: http://mathege.ru/or/ege/Main. 2. ФИПИ. Открытый банк заданий ЕГЭ. Базовый уровень. Профильный уровень. Режим доступа:
Базовый уровень. Профильный уровень. Режим доступа:
http://www.fipi.ru/content/otkrytyy-bank-zadaniy-ege 3. Образовательные ресурсы Интернета – математика. – Режим доступа:
http://www.alleng.ru/edu/math4.htm.
4. Образовательные ресурсы Интернета. ЕГЭ. Математика. – Режим доступа: http://alexlarin.net/.
5. Интернет-портал Всероссийской олимпиады школьников. — Режим доступа: http://www. rusolymp.ru
6. Образовательный портал для подготовки к экзаменам. – Режим доступа: РЕШУ ЕГЭ. РФ.
7. Информационно-поисковая система «Задачи». — Режим доступа: http://zadachi.mccme. ru/easy
8. Задачи: информационно-поисковая система задач по математике. — Режим доступа: http:// zadachi.mccme.ru
9. Конкурсные задачи по математике: справочник и методы решения. — Режим доступа: http://mschool.kubsu.ru/cdo/shabitur/kniga/tit.htm
10. Материалы (полные тексты) свободно распространяемых книг по математике. — Режим доступа: http://www.mccme.ru/firee-books
— Режим доступа: http://www.mccme.ru/firee-books
11. Математика для поступающих в вузы. — Режим доступ: http://www.matematika.agava.ru
12. Экзамены по математике: варианты, методика.-Р.Д.http://www.mathnet.spb.ru
13. Олимп. задачи по математике: база данных.- Р.Д.: http://zaba.Tu
14. Виртуальная школа юного математика.-Р.Д.: http://math.ournet.md/indexr.htm
15. Библиотека эл. уч. пособий по математике.-Р.Д.: http:// mschool.kubsu.ru
16. Образов. портал «Мир алгебры».- Р.Д: http://www.algmir.org/ ifidex.html
17. Словари БСЭ различных авторов. — Режим доступа: http://slovari.yandex.ru
18. Этюды, выполненные с использованием современной компьютерной ЗБ-графики, увлекательно и интересно рассказывающие о математике и ее приложениях. — Режим доступа: http:// www.etudesju
19. Тестирование on-line. 5-11 классы. – Р.Д.: http://www.kokch.kts.ru/cdo
– Р.Д.: http://www.kokch.kts.ru/cdo
20. Архив уч. программ инф. Обр. портала «RusEdu!».-Р.Д: http://www.rusedu.ru
21. Мегаэнциклопедия Кирилла и Мефодия. — Режим доступа: http://mega.km.ru
22. Сайты энцик. – Р. Д: http://www.rubricon.ru; http://www.encyclopedia.ru
23. Вся элементарная математика. — Режим доступа: http://www.bymath.net
24. ЕГЭ по математике. — Режим доступа: http://uztest.ru
8
Калькулятор на ЕГЭ по математике
Насколько объективно ЕГЭ по математике показывает уровень знаний учеников и можно ли считать, что сдавшие на высокие баллы экзамен выпускники смогут хорошо учиться в технических вузах?
Рособрнадзор ежегодно публикует новости об улучшающихся результатах школьников на ЕГЭ по математике. Не стал исключением и 2019: средний балл за профильную математику вырос на 6 пунктов, а количество двоечников сократилось на 5 тысяч человек. Однако эксперты обращают внимание на то, что общий уровень заданий стал слабее, а процент не сдавших экзамен базового уровня (с учетом обязательного разделения математики на общую и профильную) даже увеличился.
Не стал исключением и 2019: средний балл за профильную математику вырос на 6 пунктов, а количество двоечников сократилось на 5 тысяч человек. Однако эксперты обращают внимание на то, что общий уровень заданий стал слабее, а процент не сдавших экзамен базового уровня (с учетом обязательного разделения математики на общую и профильную) даже увеличился.
В качестве одной из причин можно назвать запрет графических калькуляторов на экзаменах. Это фактически исключает их использование и в рамках уроков, поскольку вся программа изучения математики в школах построена на достижение высоких показателей на ЕГЭ.
Как сдали ЕГЭ по математике в 2019 году
Согласно данным Рособрнадзора, этим летом экзамен по профильной математике сдавали более 400 тысяч человек, базовую — 316 тысяч человек. При этом, по заявлению заместителя главы Рособрнадзора Анзора Мусаева, не смогли набрать минимальный балл по базовой математике на 5 тысяч человек меньше, чем в 2018.
Статистика кажется положительной, пока не сравнишь количество сдававших экзамен. Так, в 2018 году его выбрали 567 тысяч человек, при этом процент двоечников составил 3,1% (приблизительно 17,5 тысяч человек). В этом году сдавало экзамен существенно меньше выпускников, и если учесть, что двойки получили 12,5 тысяч человек, получится — процент несдавших возрос до 4%!
Так, в 2018 году его выбрали 567 тысяч человек, при этом процент двоечников составил 3,1% (приблизительно 17,5 тысяч человек). В этом году сдавало экзамен существенно меньше выпускников, и если учесть, что двойки получили 12,5 тысяч человек, получится — процент несдавших возрос до 4%!
Рост среднего балла за профильную математику (+ 6 пунктов), на который также обращает внимание Рособрнадзор, отчасти связан с тем фактом, что в 2019 году впервые были разделены экзамены по базовой и профильной математике: можно было сдать или один, или другой. Выпускники, которые не были уверены в своих силах, сдавали базовый экзамен. Кстати, чтобы набрать баллов на тройку (необходимый минимум для получения аттестата), нужно было решить всего семь заданий. Некоторые настолько простые (вычисление процентов, расчет пройденного человеком расстояния с использованием одной формулы), что справиться с ними может даже семиклассник.
Если копнуть глубже, то можно наблюдать снижение качества образования и процента успешно сдающих экзамен по математике школьников, начиная с 2006 года. Уже по статистике за 2008 год видно, насколько ниже стал процент сдавших экзамен неудовлетворительно и удовлетворительно. Получается, что несмотря на позитивные новости от Рособрнадзора, уровень знаний выпускников падает. Возможно, в этом одна из причин, почему статистика по сдаче ЕГЭ стала закрытой информацией.
Уже по статистике за 2008 год видно, насколько ниже стал процент сдавших экзамен неудовлетворительно и удовлетворительно. Получается, что несмотря на позитивные новости от Рособрнадзора, уровень знаний выпускников падает. Возможно, в этом одна из причин, почему статистика по сдаче ЕГЭ стала закрытой информацией.
Доверять или нет? Как относятся к результатам ЕГЭ вузы
Система ЕГЭ была введена отчасти для того, чтобы упростить жизнь выпускников школ: им нужно сдавать экзамены только один раз, а не дважды: для получения аттестата о среднем образовании и поступления в вуз. Однако лучшие университеты России не на 100% доверяют результатам тестирования. «ЕГЭ не улавливает талантливых и способных», — сказал в одном из интервью ректор МГУ Виктор Садовничий.
Ежегодно Правительство РФ составляет списки вузов, которые имеют право проводить внутренние вступительные экзамены в дополнение к ЕГЭ. В их числе МГИМО, МГУ им. Ломоносова, Московская государственная юридическая академия, РГГУ, Московская медицинская академия им. Сеченова и др. Всего заявку в этом году подавало более 50 учебных заведений, но одобрили ее не для всех.
Сеченова и др. Всего заявку в этом году подавало более 50 учебных заведений, но одобрили ее не для всех.
Еще один способ «отсеять» действительно талантливых учеников — при помощи олимпиад и собственных вузовских конкурсов. Так, например, МГТУ имени Баумана для специализированного отбора проводит конкурс «Шаг в будущее». Физтех ежегодно публикует списки олимпиад, которые дают особые права при поступлении: например, «Турнир городов», «Высшая проба» и др.
К слову, и уровень неодобрения ЕГЭ гражданами также растет. По сравнению с 2014 годом число людей, которые не довольны едиными госэкзаменами, увеличилось на 15% и составило 64%. При этом 71% респондентов считают, что прежняя система, до введения ЕГЭ, более объективно оценивала уровень знаний выпускников школ (по результатам опроса, предоставленного фондом «Общественное мнение»).
Калькулятор на ЕГЭ по математике: смерть системы образования или отражение современных реалий?
В 2019-м году калькуляторы были под запретом на ЕГЭ по математике: согласно приказу Министерства просвещения РФ, выпускникам разрешалось использовать только линейку, не содержащую справочной информации. В 2020 году ситуация никак не изменилась.
В 2020 году ситуация никак не изменилась.
Специалисты сайта Calculators-Online.ru — эксперта в области вычислительных технологий — уже не раз обращали внимание на ошибочность такой политики. Достаточно провести сравнение с международными системами проверки знаний — экзаменами SAT, AP, PSAT/NMQT, ACT, IB Diploma, Advanced Placement Test, Praxi. На них допускается использовать калькуляторы — с некоторыми оговорками. Так, не разрешается приносить программируемые устройства и подключаться при помощи калькуляторов к интернету (обе задачи у современных моделей решаются включением экзаменационного режима). Кроме того, некоторые экзамены разделены на две части: первая выполняется при помощи калькулятора, вторая — без его использования.
Чего удается добиться благодаря калькуляторам на экзаменах?
- Составители тестов могут давать сложные задания и просить выпускников решить большее их количество. Задания на экзаменах SAT, IB Diploma, ACT требуют объемных вычислений. Школьники без труда работают с цифрами при помощи калькуляторов, выдавая правильные ответы.
 За счет большего количества заданий экзамены становятся объективнее.
За счет большего количества заданий экзамены становятся объективнее. - Выпускники чувствуют меньший стресс из-за экзаменов. Они привыкли решать задачи в классе с помощью калькуляторов и могут пользоваться ими и во время тестирования.
- В разы уменьшается число вычислительных ошибок. К сожалению, если школьник правильно решает задание, но допускает ошибку в вычислениях, ответ не засчитывается. Кстати, именно вычислительные ошибки — одни из самых частых на ЕГЭ. Согласитесь, несправедливо, когда ребенок знает правильное решение и может дать нужный ответ, но спотыкается на элементарных вещах из-за волнения и недополучает баллы.
Математика в школе XXI века
Устного счета катастрофически недостаточно для той математики, которая нужна современным выпускникам. С каждым годом технологии, с которыми приходится работать специалистам, становятся сложнее, и невозможно представить себе успешного инженера, программиста, экономиста, который бы практиковал вычисления в уме.
У оппонентов разрешения калькуляторов на экзаменах есть еще один аргумент: ведь ничто не мешает использовать устройства на обычных занятиях. Можно запретить их только во время проверочных работ. К сожалению, в нынешних условиях это невозможно. Дело в том, что вся программа, начиная с 9-го (а зачастую даже с 8-го) класса построена на успешную сдачу ОГЭ/ЕГЭ. Ни учителя, ни ученики не имеют возможности отвлекаться от программы и изучать современные технологии, которые дети все равно не смогут использовать в рамках подготовки к госэкзаменам. Таким образом, запрет использования калькуляторов на ЕГЭ автоматически исключает их из системы школьного образования.
Это приводит нас еще к двум фундаментальным проблемам обучения математике в школе.
Первая — для поколения, выросшего с гаджетами в руках, математика становится сложной и скучной наукой. Вместо наглядного отображения графиков функций на экранах калькуляторов — абстрактные примеры. Вместо решения интересных, творческих задач с минимальной тратой времени на вычисления — многоступенчатые операции с цифрами и таблицами Брадиса. Растущий процент выпускников, которые не могут сдать даже общую математику, показывает, что программа далека от совершенства.
Растущий процент выпускников, которые не могут сдать даже общую математику, показывает, что программа далека от совершенства.
Вторая проблема — оторванность математики от других наук и реальности. Из-за ограниченных возможностей устного счета и использования пособий и примеров, составленных 20-30 лет назад, школьники не используют знания, полученные на уроках, в реальной жизни.
Зачем калькуляторы в школе? Чтобы растить успешных специалистов
Давайте мыслить шире. Именно в школе закладываются базовые знания, на основе которых будет строиться и высшее образование. Школьники, не умеющие пользоваться современными научными калькуляторами, придут в вуз. У студентов два варианта: в срочном порядке осваивать программируемые модели самостоятельно или по старинке выполнять все вычисления на бумаге или с использованием простейших калькуляторов, как в школе. В итоге многие выпускники экономических, инженерных, IT-специальностей даже после окончания вуза не используют калькуляторы в профессиональной сфере. Это увеличивает время выполнения базовых задач, повышает вероятность вычислительных ошибок.
Это увеличивает время выполнения базовых задач, повышает вероятность вычислительных ошибок.
Отвечает ли запрет на использование калькуляторов на ЕГЭ реалиям XXI века? Эксперты сайта Calculators-Online.ru считают, что нет. В условиях дефицита времени специалисты не могут позволить себе долгие вычисления в столбик или исправление арифметических ошибок. Калькуляторы, учитывающие профессиональные нужды, есть сегодня для практически каждой технической или экономической специальности: экономистов, бухгалтеров, инженеров, строителей. К сожалению, в России некоторые специалисты даже не слышали о программируемых калькуляторах с возможностями расчета налогов, нахождения уклона, регрессионного анализа и т.д. И первопричина именно в том, что научные калькуляторы исключены из школьной программы.
ЕГЭ математика (профильный уровень)
Единый государственный экзамен (ЕГЭ) — это форма государственной итоговой аттестации (ГИА) по образовательным программам среднего общего образования.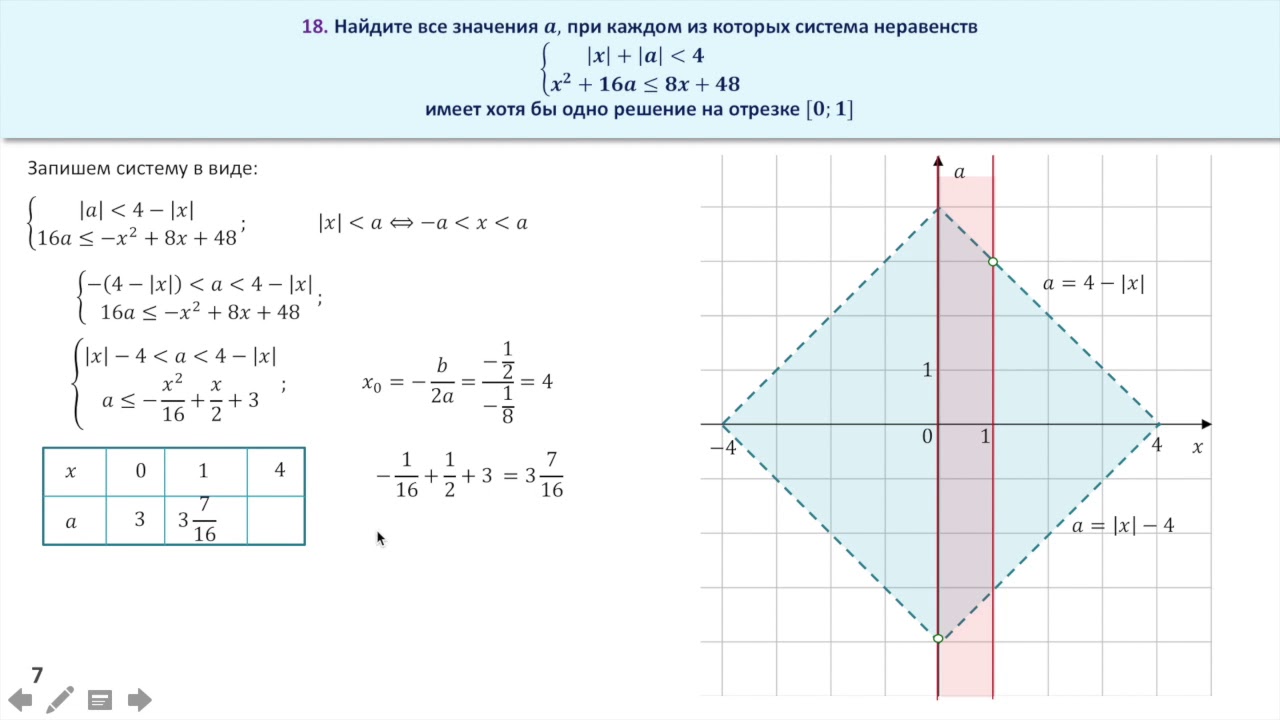
При проведении ЕГЭ используются контрольные измерительные материалы (КИМ), представляющие собой комплексы заданий стандартизированной формы, а также специальные бланки для оформления ответов на задания.
ЕГЭ по математике является обязательным экзаменом для всех учащихся, заканчивающих 11 класс. Школьники могут выбрать базовый или профильный уровень экзамена. Профильный ЕГЭ нужен тем учащимся, которым при поступлении в ВУЗ понадобятся результаты ЕГЭ по математике, остальным подойдет базовый ЕГЭ по математике.
Профильный ЕГЭ по математике длится 235 мин и состоит из 12 заданий с кратким ответом, которым является целое число, или конечная десятичная дробь, или последовательность цифр и 7 заданий второй части к которым нужно привести полные решения.
Дальневосточный центр математики предлагает учащимся 10-х и 11-х классов пройти программу подготовки к профильному ЕГЭ по математике. Наш центр реализуются две программы подготовки к профильному ЕГЭ по математике:
- профильный уровень,
- ЕГЭ по математике 70+.

Первая программа подойдет для большинства школьников и позволит при должном уровне упорства набрать не менее 60 баллов. Данная программа предусматривает развитие общематематической грамотности, совершенствование навыков быстрого счета и развитие уверенности при решении тестовых задач. Основной акцент в данной программе сделан на подготовку к решению первых 12 заданий профильного экзамена. Кроме того, будут рассматриваться задачи 13, 15 и 17 из второй части, как наиболее простые из второй части экзамена.
Вторая программа подойдет для тех школьников, кто уже уверенно справляется с первыми 12 заданиями профильного экзамена. Для зачисления на курс учащиеся должны сдать входной тест не менее чем на 62 балла. Упор в данной программе сделан на подготовку к решению задач второй части профильного ЕГЭ.
Занятие длится 80 минут. На занятии учащиеся разбирают теоретический и практический материал, и большую часть времени решают задачи самостоятельно, закрепляя полученные знания.
GRE Стратегии решения проблем (для тестируемых)
Вопросов по критерию количественного мышления Общего теста GRE® просят вас смоделировать и решить проблемы, используя количественные или математические методы. Как правило, решение математической задачи состоит из трех основных шагов:
- Шаг 1. Разберитесь в проблеме
- Шаг 2: Реализуйте стратегию решения проблемы
- Шаг 3. Проверьте свой ответ
Вот описание трех шагов, за которым следует список полезных стратегий для решения математических задач.
Шаг 1. Понять проблему
Первый шаг — внимательно прочитать формулировку проблемы, чтобы убедиться, что вы понимаете предоставленную информацию и проблему, которую вас просят решить.
Некоторая информация может описывать определенные количества. Количественная информация может быть дана словами или математическими выражениями, или их комбинацией. Кроме того, в некоторых задачах вам может потребоваться прочитать и понять количественную информацию в представлениях данных, геометрических фигурах или системах координат. Другая информация может иметь форму формул, определений или условий, которым должны соответствовать количества. Например, условия могут быть уравнениями или неравенствами или могут быть словами, которые могут быть переведены в уравнения или неравенства.
Другая информация может иметь форму формул, определений или условий, которым должны соответствовать количества. Например, условия могут быть уравнениями или неравенствами или могут быть словами, которые могут быть переведены в уравнения или неравенства.
Помимо понимания информации, которую вам дают, важно понимать, что вам нужно сделать, чтобы решить проблему. Например, какие неизвестные количества нужно найти? В какой форме они должны быть выражены?
Шаг 2: Реализация стратегии решения проблемы
Решение математической задачи требует большего, чем понимание описания проблемы, то есть больше, чем понимание величин, данных, условий, неизвестных и всех других математических фактов, связанных с проблемой.Требуется определить, какие математические факты использовать, когда и как использовать эти факты для разработки решения проблемы. Это требует стратегии.
Математические задачи решаются с использованием самых разных стратегий. Также могут быть разные способы решения данной проблемы. Следовательно, вам следует разработать репертуар стратегий решения проблем, а также представление о том, какие стратегии могут лучше всего работать при решении конкретных проблем. Попытка решить проблему без стратегии может привести к большому объему работы без получения правильного решения.
Следовательно, вам следует разработать репертуар стратегий решения проблем, а также представление о том, какие стратегии могут лучше всего работать при решении конкретных проблем. Попытка решить проблему без стратегии может привести к большому объему работы без получения правильного решения.
После того, как вы определились со стратегией, вы должны ее реализовать. Если вы застряли, проверьте свою работу, чтобы увидеть, не допустили ли вы ошибки в своем решении. Важно иметь гибкий и непредвзятый настрой. Если вы проверяете свое решение и не можете найти ошибку или ваша стратегия решения просто не работает, поищите другую стратегию.
Шаг 3. Проверьте свой ответ
Когда вы получите ответ, вы должны проверить его разумность и правильность с точки зрения вычислений.
- Вы ответили на заданный вопрос?
- Разумен ли ваш ответ в контексте вопроса? Проверить разумность ответа можно так же просто, как вспомнить основной математический факт и проверить, соответствует ли ваш ответ этому факту.
 Например, вероятность события должна быть от 0 до 1 включительно, а площадь геометрической фигуры должна быть положительной. В других случаях вы можете использовать оценку, чтобы проверить разумность вашего ответа. Например, если ваше решение включает сложение трех чисел, каждое из которых находится в диапазоне от 100 до 200, оценка суммы говорит вам, что сумма должна быть между 300 и 600.
Например, вероятность события должна быть от 0 до 1 включительно, а площадь геометрической фигуры должна быть положительной. В других случаях вы можете использовать оценку, чтобы проверить разумность вашего ответа. Например, если ваше решение включает сложение трех чисел, каждое из которых находится в диапазоне от 100 до 200, оценка суммы говорит вам, что сумма должна быть между 300 и 600. - Вы допустили ошибку в вычислениях при получении ответа? Ошибка ввода ключа с помощью калькулятора? Вы можете проверять наличие ошибок на каждом этапе вашего решения.Или вы можете напрямую проверить правильность вашего решения. Например, если вы решили уравнение для x и получили ответ, вы можете проверить свой ответ, подставив его в уравнение, чтобы увидеть это.
Стратегии
Нет установленных правил — применимых ко всем математическим задачам — для определения наилучшей стратегии. Способность определять стратегию, которая будет работать, растет по мере того, как вы решаете все больше и больше проблем. Далее следует краткое описание полезных стратегий.Вместе с каждой стратегией даются один или два типовых вопроса, на которые вы можете ответить с помощью стратегии. Эти стратегии не составляют полный список, и, кроме объединения первых четырех стратегий вместе, они не представлены в каком-либо определенном порядке.
Далее следует краткое описание полезных стратегий.Вместе с каждой стратегией даются один или два типовых вопроса, на которые вы можете ответить с помощью стратегии. Эти стратегии не составляют полный список, и, кроме объединения первых четырех стратегий вместе, они не представлены в каком-либо определенном порядке.
Первые четыре стратегии — это стратегии трансляции, когда одно представление математической задачи переводится в другое.
Как решать сложные математические задачи
Как решать сложные математические задачи
17 ноября 2017 Ричард Рушик
Родитель одного из наших студентов написал сегодня о том, что его дочь время от времени разочаровывалась в сложности некоторых проблем на наших курсах.Она отлично справляется с работой на наших курсах и легко входила в число самых лучших учеников в классе, который она брала со мной, и все же она до сих пор иногда сталкивается с проблемами, которые не может решить. Более того, у нее есть доступ к прекрасному учителю математики в ее школе, который иногда также не может помочь ей решить эти проблемы.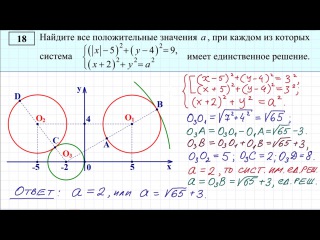 (Для него это не пренебрежительно — студенты приносят мне проблемы, которые я тоже не могу решить!) Ее вопрос: «Почему это должно быть так сложно?»
(Для него это не пренебрежительно — студенты приносят мне проблемы, которые я тоже не могу решить!) Ее вопрос: «Почему это должно быть так сложно?»
Мы задаем сложные вопросы, потому что многие проблемы, которые стоит решать в жизни, являются сложными.Если бы они были простыми, кто-то другой решил бы их, прежде чем вы добрались до них. Вот почему в классах колледжей в ведущих университетах есть тесты, по которым почти никто не сдает 70%, не говоря уже о наивысшем балле. Они обучают будущих исследователей, и весь смысл исследования состоит в том, чтобы найти и ответить на вопросы, которые никогда не были решены. Вы не можете научиться делать это, не борясь с проблемами, которые не можете решить. Если вы постоянно решаете каждую задачу в классе, вы не должны быть слишком счастливы — это означает, что вы недостаточно эффективно учитесь.Вам нужно найти класс посложнее.
Проблема отсутствия достаточного количества вызовов выходит далеко за рамки того, что вы не выучите математику (или что-то еще) так быстро, как вы можете.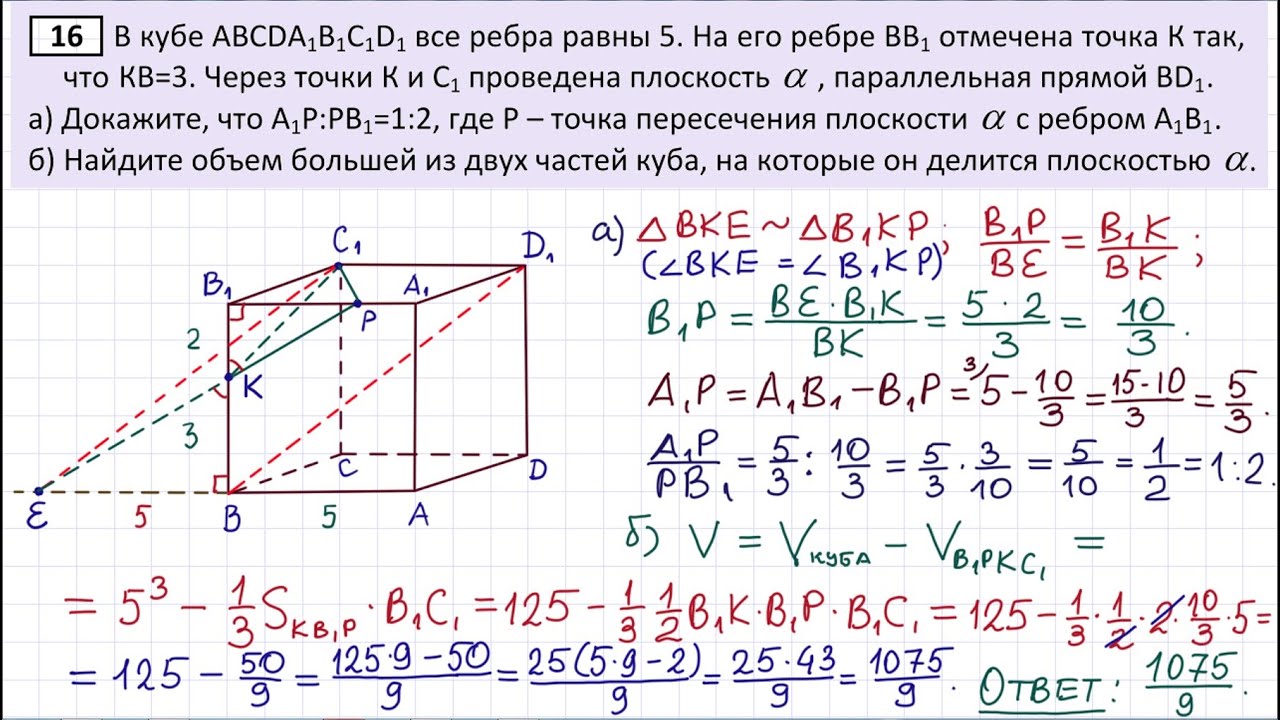 Я думаю, что многое из того, что мы делаем в AoPS, готовит учащихся к задачам, выходящим далеко за рамки математики. Стратегии того же типа, которые используются при решении очень сложных математических задач, могут использоваться для решения очень многих задач. Я считаю, что мы учим студентов думать, как решать сложные задачи, и что математика оказывается для многих лучшим способом сделать это.
Я думаю, что многое из того, что мы делаем в AoPS, готовит учащихся к задачам, выходящим далеко за рамки математики. Стратегии того же типа, которые используются при решении очень сложных математических задач, могут использоваться для решения очень многих задач. Я считаю, что мы учим студентов думать, как решать сложные задачи, и что математика оказывается для многих лучшим способом сделать это.
Первый шаг в решении сложных проблем — это принять и понять их важность. Не уклоняйся от них. Они научат вас гораздо большему, чем просто рабочий лист с простыми задачами. Блестящий «Ага!» момента почти всегда возникают из умов, культивируемых долгими периодами разочарования. Но без этого разочарования никогда не появятся эти блестящие идеи.
Вот несколько стратегий решения сложных проблем и связанных с ними разочарований:
Сделай что-нибудь .Да, проблема сложная. Да, вы не представляете, что делать, чтобы решить эту проблему. В какой-то момент вам нужно перестать пялиться и начать пробовать что-то. Большинство из них не сработает. Примите тот факт, что многие ваши усилия будут потрачены впустую. Но есть шанс, что один из ваших ударов поразит что-то, и даже если этого не произойдет, усилия могут подготовить ваш разум к победной идее, когда придет время. Мы начали разрабатывать программу начальной школы за несколько месяцев до того, как у нас появилась идея, которая стала Академией зверей.Наш ведущий разработчик учебной программы написал 100–200 страниц содержания, придумав множество различных стилей и подходов, которые мы могли бы использовать. Ни одной из этих страниц не будет в финальной версии, но они породили множество идей для контента, который мы будем использовать. Возможно, что более важно, это подготовило нас к тому, что, когда мы, наконец, натолкнулись на идею Академии Зверей, мы были достаточно уверены, чтобы ее реализовать.
Большинство из них не сработает. Примите тот факт, что многие ваши усилия будут потрачены впустую. Но есть шанс, что один из ваших ударов поразит что-то, и даже если этого не произойдет, усилия могут подготовить ваш разум к победной идее, когда придет время. Мы начали разрабатывать программу начальной школы за несколько месяцев до того, как у нас появилась идея, которая стала Академией зверей.Наш ведущий разработчик учебной программы написал 100–200 страниц содержания, придумав множество различных стилей и подходов, которые мы могли бы использовать. Ни одной из этих страниц не будет в финальной версии, но они породили множество идей для контента, который мы будем использовать. Возможно, что более важно, это подготовило нас к тому, что, когда мы, наконец, натолкнулись на идею Академии Зверей, мы были достаточно уверены, чтобы ее реализовать.
Упростите проблему . Попробуйте меньшие числа и особые случаи. Снимите ограничения. Или добавьте ограничения.Установите прицел чуть ниже, а затем поднимите его, когда решите более простую задачу.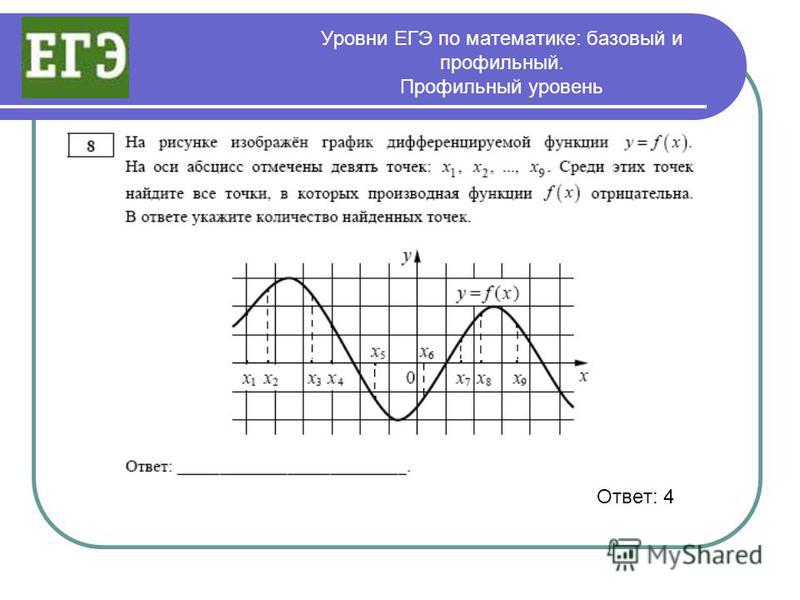
Размышляйте об успехах . Вы решили много проблем. Некоторые из них были даже тяжелыми! Как ты сделал это? Начните с проблем, похожих на ту, с которой вы столкнулись, но даже подумайте о других, которые не имеют ничего общего с вашей текущей проблемой. Подумайте о стратегиях, которые вы использовали для решения этих проблем, и вы можете наткнуться на решение. Несколько месяцев назад я играл с некоторыми проблемами Project Euler и столкнулся с проблемой, которая (в конечном итоге) сводилась к генерации целочисленных решений для c ² = a ² + b ² + ab эффективно.Теория чисел — не моя сильная сторона, но мой путь к решению состоял в том, чтобы сначала вспомнить метод генерации пифагоровых троек. Затем я подумал, как создать этот метод, и путь к решению стал ясен. (Я предполагаю, что некоторые из наших более опытных в математике читателей настолько усвоили процесс решения этого типа диофантова уравнения, что вам не нужно путешествовать с Пифагором, чтобы добраться туда!)
Сосредоточьтесь на том, что вы еще не использовали . Многие проблемы (особенно геометрические) имеют много движущихся частей.Оглянитесь на проблему и на свои открытия и спросите себя: «Что я еще не использовал конструктивно?» Ответ на этот вопрос часто является ключом к вашему следующему шагу.
Многие проблемы (особенно геометрические) имеют много движущихся частей.Оглянитесь на проблему и на свои открытия и спросите себя: «Что я еще не использовал конструктивно?» Ответ на этот вопрос часто является ключом к вашему следующему шагу.
Назад . Это особенно полезно при поиске доказательств. Вместо того, чтобы начинать с того, что вы знаете, и работать над тем, что вы хотите, начните с того, что вы хотите, и спросите себя, что вам нужно для этого.
Обратиться за помощью . Для многих выдающихся учеников это сложно.Вы так привыкли все делать правильно, быть тем, кого все просят, что трудно признать, что вам нужна помощь. Когда я впервые попал в MOP на втором курсе, я был не в себе. Я очень мало понимал, что происходило в классе. Однажды я попросил помощи у профессора — очень тяжело было набраться смелости. Я не понимал ничего из того, что он мне рассказывал, за те 15 минут, что работал со мной наедине. Я просто не мог признаться в этом и попросить помощи, поэтому перестал спрашивать. Я мог бы узнать гораздо больше, если бы просто был более готов признаться людям, которых просто не понимал. (Это одна из причин, почему в наших классах теперь есть функция, которая позволяет студентам задавать вопросы анонимно.) Преодолейте это. Вы застрянете. Вам понадобится помощь. И если вы попросите об этом, вы пойдете намного дальше, чем если бы вы этого не сделали.
Я мог бы узнать гораздо больше, если бы просто был более готов признаться людям, которых просто не понимал. (Это одна из причин, почему в наших классах теперь есть функция, которая позволяет студентам задавать вопросы анонимно.) Преодолейте это. Вы застрянете. Вам понадобится помощь. И если вы попросите об этом, вы пойдете намного дальше, чем если бы вы этого не сделали.
Начало раннего . Это не очень помогает с тестами по расписанию, но с более долгими заданиями, которые являются частью учебы и жизни, это очень важно.Не ждите до последней минуты — сложные задачи достаточно сложны, и вам не нужно иметь дело с нехваткой времени. Более того, для полного понимания сложных идей требуется много времени. Люди, которых вы знаете, которые кажутся безумно умными и которые, кажется, придумывают идеи намного быстрее, чем вы, возможно, — это часто люди, которые просто думали о проблемах намного дольше, чем вы. Я использовал эту стратегию на протяжении всего колледжа с большим успехом — в первые несколько недель каждого семестра я работал далеко вперед во всех моих классах. Поэтому к концу семестра я размышлял над ключевыми идеями намного дольше, чем большинство моих одноклассников, что значительно упростило экзамены и тому подобное в конце курса.
Поэтому к концу семестра я размышлял над ключевыми идеями намного дольше, чем большинство моих одноклассников, что значительно упростило экзамены и тому подобное в конце курса.
Сделайте перерыв . Отойдите ненадолго от проблемы. Когда вы вернетесь к этому, вы можете обнаружить, что совсем не ушли от проблемы полностью — фоновые процессы в вашем мозгу продолжали отключаться, и вы окажетесь намного ближе к решению. Конечно, намного проще сделать перерыв, если вы начнете раньше.
Начать более . Отложите всю свою предыдущую работу, возьмите новый лист бумаги и попробуйте начать с нуля. Другая ваша работа все еще будет там, если вы захотите извлечь из нее позже, и, возможно, она подготовила вас к тому, чтобы воспользоваться идеями, которые вы сделаете во время второго раунда.
Сдаться . Вы не решите их всех. В какой-то момент пришло время сократить свои потери и двигаться дальше. Это особенно верно, когда вы тренируетесь и пытаетесь научиться чему-то новому. Одна трудная задача обычно научит вас большему в первые час или два, чем за следующие шесть, и есть гораздо больше проблем, на которых можно учиться. Итак, установите себе ограничение по времени, и если вы все еще безнадежно застряли в конце, прочтите решения и двигайтесь дальше.
Одна трудная задача обычно научит вас большему в первые час или два, чем за следующие шесть, и есть гораздо больше проблем, на которых можно учиться. Итак, установите себе ограничение по времени, и если вы все еще безнадежно застряли в конце, прочтите решения и двигайтесь дальше.
Будьте самоанализом . Если вы сдадитесь и прочитаете решение, то читайте его активно, а не пассивно. Читая его, подумайте, какие ключи к разгадке проблемы могли привести вас к этому решению.Подумайте, что вы сделали неправильно в своем расследовании. Если в решении есть математические факты, которых вы не понимаете, приступайте к исследованию. Я был совершенно сбит с толку, когда впервые увидел кучу материалов о «модах» в решении олимпиады — тогда у нас не было Интернета, поэтому я не мог легко понять, насколько проста модульная арифметика! Теперь у вас есть Интернет, так что вам нет оправдания. Если вы все же решили проблему, не похлопывайте себя по спине. Подумайте о ключевых шагах, которые вы сделали, и о знаках, по которым можно их попробовать. Подумайте о тупиках, которые вы исследовали на пути к решению, и о том, как вы могли бы их избежать. Эти уроки пригодятся вам позже.
Подумайте о тупиках, которые вы исследовали на пути к решению, и о том, как вы могли бы их избежать. Эти уроки пригодятся вам позже.
Вернись . Если вы сдались и посмотрели на решения, вернитесь и попробуйте снова решить проблему через несколько недель. Если у вас нет никаких решений, оставьте проблему в живых. Храните это на бумаге или в уме. Ричард Фейнман однажды написал, что в глубине души он будет держать четыре или пять проблем активными. Всякий раз, когда он слышал новую стратегию или технику, он быстро перебирал свои проблемы и смотрел, сможет ли он использовать их для решения одной из своих проблем.Он считает, что эта практика стала причиной некоторых анекдотов, которые дали Фейнману такую репутацию гения. Это еще одно свидетельство того, что быть гением — значит очень много усилий, подготовки и уверенности в себе.
Вот секрет успешных результатов всех ваших тестов по математике
Обновлено 21 февраля 2020 г.
Ли Джонсон
Для многих экзамен по математике — это просто кошмар. Вспоминая формулы, готовясь к решению проблем, с которыми вы никогда раньше не сталкивались, и необходимость понимать абстрактные определения слов, которые вы едва помните для начала.Но это не значит, что вы можете просто , а не , пересмотреть — экзамен на горизонте, нравится вам это или нет.
Вспоминая формулы, готовясь к решению проблем, с которыми вы никогда раньше не сталкивались, и необходимость понимать абстрактные определения слов, которые вы едва помните для начала.Но это не значит, что вы можете просто , а не , пересмотреть — экзамен на горизонте, нравится вам это или нет.
Хорошая новость в том, что пересматривать математику — это не так уж плохо, как кажется. Проблема в том, что это отличается от пересмотра большинства других тем, когда вам обычно просто нужно запомнить некоторые ключевые факты или интерпретации текста. Математика — это примерно практика, больше, чем что-либо еще, и если вы адаптируете к ней свою стратегию пересмотра, вы сможете сдать экзамен и получить отличную оценку.
Практика, практика, практика
Совет № 1 для повторного изучения математики — это работа над практическими задачами. Дело в том, что даже если вы не полностью понимаете, , все, что происходит, вы можете ответить на вопросы и сдать экзамен, если вы проходили один и тот же базовый процесс дома достаточно много раз. Просмотрите вопросы в учебнике, повторите некоторые из ваших домашних заданий и найдите все соответствующие вопросы в Интернете. Если большую часть времени вы тратите на решение проблем, у вас все получится лучше, чем если бы вы большую часть времени читали заметки, не отвечая на вопросы.
Просмотрите вопросы в учебнике, повторите некоторые из ваших домашних заданий и найдите все соответствующие вопросы в Интернете. Если большую часть времени вы тратите на решение проблем, у вас все получится лучше, чем если бы вы большую часть времени читали заметки, не отвечая на вопросы.
И всякий раз, когда вы ошибаетесь, внимательно просмотрите решение и посмотрите, что пошло не так. Ошибки — нормальное явление, поэтому не огорчайтесь, но убедитесь, что вы знаете, что именно произошло, чтобы избежать этого в будущем.
Прошлые работы — ваш друг
Лучшим источником практических проблем являются прошлые экзамены по тому же курсу. В них указывается уровень вопросов, на которые вы должны будете ответить, и вы часто можете получить хорошее представление о том, что будет включено в ваш экзамен, просмотрев многие из них.По правде говоря, учителя часто не , а креативные, и иногда вы можете увидеть повторение вопроса из предыдущего экзамена на своей бумаге.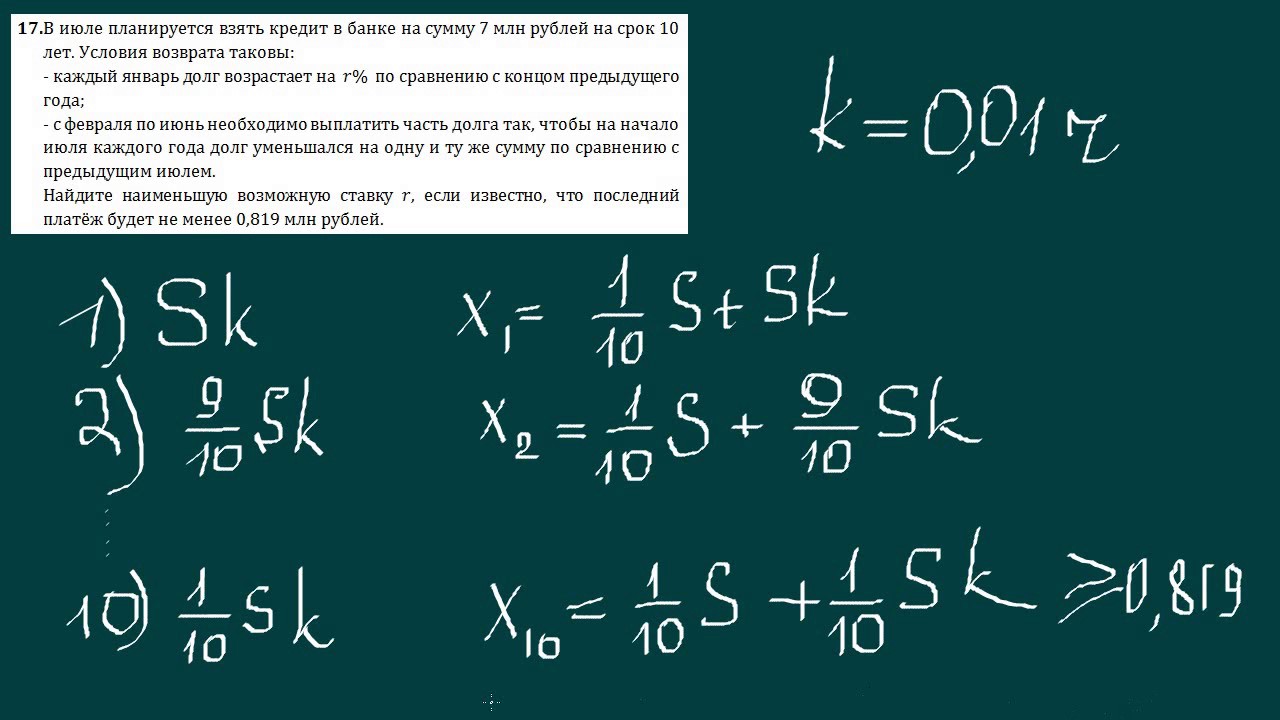 Но даже если вам не повезет, если вы знакомы с прошлыми экзаменационными работами, у вас будет гораздо больше шансов успешно сдать тест.
Но даже если вам не повезет, если вы знакомы с прошлыми экзаменационными работами, у вас будет гораздо больше шансов успешно сдать тест.
Вы можете работать по-своему, но лично я стараюсь сохранить один или два прошлых экзамена, чтобы сдать их в реальных условиях за несколько дней до теста.
Понять концепции
Запоминать формулы сложно, но вы улучшите свои шансы, если действительно поймете , что делает каждая формула и откуда она взялась.Здесь ваши заметки и учебник неоценимы: объяснения на простом языке каждой формулы дадут вам базовое понимание, необходимое для того, чтобы вспомнить и использовать формулы, которые вам нужны на экзамене. Если у вас есть таблица с уравнениями, на которую нужно ссылаться на экзамене, сосредоточьтесь на понимании этих формул, но если у вас их нет или есть дополнительные, которые нужно запомнить, понимание основного смысла и концепций имеет решающее значение.
Работа в группах
Работа в группах не кажется самым естественным подходом к математике, но она может быть действительно полезной. У всех разные сильные стороны, поэтому ваши одноклассники смогут помочь вам, и вы сможете им помочь. Вы можете научиться новым техникам решения проблем, изучить полезную мнемонику или просто получить хорошее объяснение концепции, с которой вы боретесь.
У всех разные сильные стороны, поэтому ваши одноклассники смогут помочь вам, и вы сможете им помочь. Вы можете научиться новым техникам решения проблем, изучить полезную мнемонику или просто получить хорошее объяснение концепции, с которой вы боретесь.
Выпишите пошаговые решения / шпаргалки
Часто в математике есть «рецепт», которому нужно следовать для определенного типа задачи. Решение дифференциального уравнения второго порядка может показаться вашим личным адом, но есть четкий пошаговый подход, который вы можете использовать в подавляющем большинстве ситуаций.Вам следует, , записать это (даже если вы его помните) и попрактиковаться в использовании рецепта на реальных задачах. К концу вы запомните процесс и научитесь его использовать.
Создание подобных «шпаргалок» по целому ряду проблем — действительно эффективный способ закрепить процесс решения проблем в вашем мозгу.
Используйте флеш-карты / стикеры
Если есть, в частности, большой компонент запоминания, флеш-карты и стикеры являются бесценными инструментами для редактирования. Многие люди развешивают их вокруг своих комнат или дома, поэтому вам постоянно напоминают самые важные факты, но самое главное — регулярно их проверять. Есть также приложения, с помощью которых вы можете провести небольшую интерактивную викторину.
Многие люди развешивают их вокруг своих комнат или дома, поэтому вам постоянно напоминают самые важные факты, но самое главное — регулярно их проверять. Есть также приложения, с помощью которых вы можете провести небольшую интерактивную викторину.
Общие советы по редактированию
Конечно, есть много других более общих советов, которые вы должны помнить. Не забывайте делать перерывы, и не решает не спать всю ночь и учиться. Вам нужно хорошо спать, хорошо питаться, пить воду и в целом заботиться о себе, если вы собираетесь работать с максимальной эффективностью.
Вы не нуждаетесь в том, чтобы я проходил все это за вас, но имеет значение . Следуйте советам по математике из этого поста, не пренебрегайте собой в процессе, и вы выбьете экзамен из парка.
Мои варианты колледжа — Задачи со словом
Многие задачи в математическом разделе будут представлены в виде текстовых задач. Иногда формулировки настолько плотные, что легко забыть, что вы вообще занимаетесь математикой! Действительно, для решения многих из этих задач самое сложное — это перевести их в математику.Фактические вычисления часто довольно просты. Эти вопросы проверяют вашу способность составить уравнение на основе информации, содержащейся в словесной задаче, тем самым применяя математические навыки в повседневных ситуациях.
Иногда формулировки настолько плотные, что легко забыть, что вы вообще занимаетесь математикой! Действительно, для решения многих из этих задач самое сложное — это перевести их в математику.Фактические вычисления часто довольно просты. Эти вопросы проверяют вашу способность составить уравнение на основе информации, содержащейся в словесной задаче, тем самым применяя математические навыки в повседневных ситуациях.
Ключевые моменты, которые следует запомнить:
- Прочтите всю задачу! Не пытайтесь ничего решить, пока не прочувствуете весь вопрос.
- Сориентируйтесь, записывая информацию, содержащуюся в задаче.
- Обозначьте переменные тем, что они обозначают.
- Определите, в чем именно заключается проблема (и затем подчеркните это).
- Разработайте ответ.
- Перепроверьте, чтобы убедиться, что ваш ответ имеет смысл. Сравните свой ответ с исходной задачей, а не с уравнением!
Перевод словесных описаний математических отношений в реальные математические термины требует практики. Вот несколько примеров:
Вот несколько примеров:
Примеры
- Произведение двух последовательных отрицательных четных целых чисел равно 24.Какое из двух чисел меньше?
- Стиральная машина Глории сломана. Поскольку ее машина довольно старая, она не хочет тратить на ремонт больше 100 долларов. Сервисный вызов будет стоить 35 долларов, а оплата труда — 20 долларов в час. Других сборов нет. Какое максимальное количество часов может проработать ремонтник, общая стоимость которого не превышает 100 долларов?
Ответы и пояснения
- Правильный ответ — А. Сначала оцените вопрос. Поскольку два числа являются отрицательными и непоследовательными, вы знаете, что они будут разделены на два (например, -2 и -4), и в результате одно число будет на два больше другого. (Подсказка: имея под рукой эту информацию, вы также можете исключить вариант E, который даже не является отрицательным. Вы также можете исключить вариант B, учитывая, что он не четный, еще одно требование вашего ответа.
 ) Итак, мы можем позвонить по первому номеру n и второй номер n + 2.Вопрос гласит, что произведение двух чисел равно 24. Таким образом, ( n ) ( n + 2) = 24. Теперь мы решаем для n : Таким образом, n = -6 или 4. Поскольку в вопросе указано, что числа были отрицательными, ответ не может быть n = 4. Если n = -6, n + 2 = -4 и два числа -6 и -4. Вопрос касается меньшего из двух чисел, а именно -6.
) Итак, мы можем позвонить по первому номеру n и второй номер n + 2.Вопрос гласит, что произведение двух чисел равно 24. Таким образом, ( n ) ( n + 2) = 24. Теперь мы решаем для n : Таким образом, n = -6 или 4. Поскольку в вопросе указано, что числа были отрицательными, ответ не может быть n = 4. Если n = -6, n + 2 = -4 и два числа -6 и -4. Вопрос касается меньшего из двух чисел, а именно -6. - Правильный ответ — D. Пусть h равно максимальному количеству часов, которое может занять ремонт. Запишите уравнение на основе предоставленной информации (35 долларов плюс 20 долларов за час для ч часов равняются 100 долларам): Таким образом, ответ должен быть D. Обратите внимание: если вы забыли о 35 долларах за звонок в службу поддержки, у вас может возникнуть соблазн выбрать E.
 Однако важно помнить, что эта плата должна быть оплачена независимо от того, сколько времени длится звонок.
Однако важно помнить, что эта плата должна быть оплачена независимо от того, сколько времени длится звонок.
Другие проблемы
лучших бесплатных приложений, которые решают математические задачи за вас
Многие справочники и учебники по математике, используемые в школах, предоставляют учащимся пошаговые инструкции по решению различных математических задач.Однако с незапамятных времен мы видели, что этих пошаговых руководств никогда не бывает достаточно, чтобы студенты влюбились в математику. Хорошо то, что теперь есть лучший способ решать математические задачи.
Технологии оказались более чем полезными в разных сферах и в разных отраслях, и, к счастью, образование не осталось позади. Сегодня у нас есть приложения для смартфонов, которые могут решать математические задачи. Щелкая по телефонам, вы можете получить ответы на некоторые из самых сложных математических задач по разным темам.Помимо решения математических задач и предоставления решений на золотом блюде, некоторые из этих приложений также могут научить вас различным методам и инструкциям о том, как решить проблему и прийти к правильному ответу.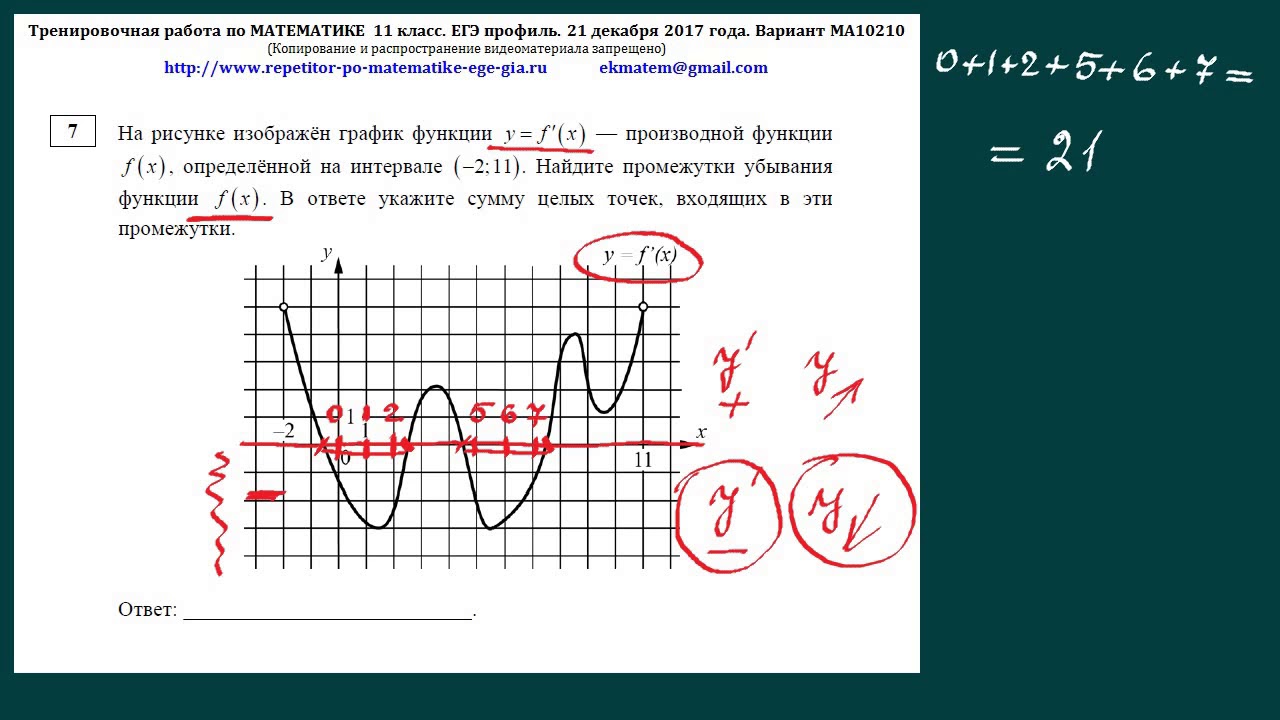 Это намного более простой способ выучить математику, и вы очень быстро влюбитесь в математику.
Это намного более простой способ выучить математику, и вы очень быстро влюбитесь в математику.
Мы просмотрели некоторые приложения, помогающие выполнять задания по математике, и составили список лучших бесплатных приложений, которые помогут вам решать математические задачи.
Photomath Приложение Photomath, несомненно, является одним из лучших приложений, с которыми вы столкнетесь, чтобы помочь вам с математическими задачами.Это приложение использует камеру вашего телефона в сочетании с дополненной реальностью. Все, что вам нужно сделать, это направить камеру своего телефона на лист с уравнением или математической задачей, которую вы хотите решить, и он даст вам ответ. Он считывает проблему и мгновенно ее решает, а все, что вам нужно, — это камера вашего устройства. Современная технология Photomath позволяет ему прочитать проблему и дать ответ, а также показать вам пошаговые объяснения для получения правильного ответа. Неважно, насколько это просто или сложно, будь то простая арифметика или сложное исчисление. Photomath — это приложение, которое одинаково полезно как для учителей, так и для студентов при преподавании и изучении математики. Это помогает понять и интерпретировать проблему, а также изучить основные математические концепции. Это приложение для решения математических задач особенно полезно для решения алгебраических уравнений и фундаментальных арифметических задач. Некоторые из математических материалов, поддерживаемых Photomath, включают числа, десятичные дроби, дроби, корни и степени, алгебраические выражения, комплексные числа, квадратные уравнения / неравенства. Другие — линейные уравнения / неравенства, абсолютные уравнения / неравенства, исчисление, биномиальная теорема и тригонометрические уравнения.
Photomath — это приложение, которое одинаково полезно как для учителей, так и для студентов при преподавании и изучении математики. Это помогает понять и интерпретировать проблему, а также изучить основные математические концепции. Это приложение для решения математических задач особенно полезно для решения алгебраических уравнений и фундаментальных арифметических задач. Некоторые из математических материалов, поддерживаемых Photomath, включают числа, десятичные дроби, дроби, корни и степени, алгебраические выражения, комплексные числа, квадратные уравнения / неравенства. Другие — линейные уравнения / неравенства, абсолютные уравнения / неравенства, исчисление, биномиальная теорема и тригонометрические уравнения.
Solve4x — еще одно интересное приложение для решения математических задач. В этом приложении есть программа для решения уравнений, которая позволяет вам ввести уравнение вручную и решить его за вас. Другой способ — сделать снимок уравнения или проверить фотографию, уже сохраненную в вашей галерее. Он обработает изображение и автоматически решит уравнение. Это приложение работает с печатным текстом, но некоторые тексты все равно могут быть искажены, поэтому вам может потребоваться слегка отредактировать текст после съемки.
Он обработает изображение и автоматически решит уравнение. Это приложение работает с печатным текстом, но некоторые тексты все равно могут быть искажены, поэтому вам может потребоваться слегка отредактировать текст после съемки.
Хотя это приложение не требует большого количества эссе, одним из его ограничений является то, что оно не поддерживает математические задачи, в которых используются скобки. Идея этого приложения заключается в том, чтобы родители могли подтверждать результаты заданий своих детей, не сталкиваясь со сложной алгеброй и другими математическими задачами. Если это так, вы можете держать смартфоны подальше от ваших детей, когда они выполняют их задания.
Mathway
Приложение для решения математических задач Pathway работает как калькулятор алгебры, предлагая мгновенные ответы на самые сложные математические задачи.Это приложение может помочь вам с любой математической задачей, от простых математических задач до более сложных, исчисления, тригонометрии, алгебры, геометрии и т. Д.
Д.
Приложение Pathway поставляется с бесплатной и платной версией или версией по подписке. В бесплатной версии все, что вы получаете, — это просто ответ на поставленную математическую задачу, а в платной версии вы получите пошаговые решения различных математических задач по разным темам. Это приложение настоятельно рекомендуется всем ученикам, которые борются с математикой.Он также очень прост с интуитивно понятным интерфейсом и отличным тематическим глоссарием.
Cymath Cymath — это приложение для решения математических задач, которое предлагает помощь в диссертациях по различным математическим темам в математике. Некоторые из этих тем — алгебра, арифметика, статистика, исчисление, тригонометрия и другие темы с расширенным средством решения математических задач с искусственным интеллектом. Приложение Cymath решает ваши математические задачи в режиме реального времени по нескольким темам.Это приложение также дает вам бесплатный доступ к решению вашей математической задачи. Поэтому, когда вам нужна помощь или вы застряли над математической задачей, у вас есть доступ к приложению Cymath. С помощью этого приложения вы можете получить всю необходимую поддержку при выполнении домашнего задания по математике по различным темам, алгебре, построению графиков, исчислению и т. Д. Калькулятор алгебры в этом приложении имеет различные функции, от экспоненциальных функций до логарифмов и тригонометрии.
Поэтому, когда вам нужна помощь или вы застряли над математической задачей, у вас есть доступ к приложению Cymath. С помощью этого приложения вы можете получить всю необходимую поддержку при выполнении домашнего задания по математике по различным темам, алгебре, построению графиков, исчислению и т. Д. Калькулятор алгебры в этом приложении имеет различные функции, от экспоненциальных функций до логарифмов и тригонометрии.
Калькулятор MyScript
Это математическое приложение распознает ваш почерк.Это означает, что вы получите ответы на свою математическую задачу, просто написав вопрос на экране. Это приложение поддерживает основную арифметику с квадратными корнями и кубическими корнями, но не поддерживает тригонометрию, проценты и логарифмы.
Хотя это приложение удобно в использовании, оно имеет свои ограничения, поскольку оно не всегда может правильно распознавать ваш почерк. Например, у вас может возникнуть проблема с его вычислением кубического корня, если он не распознает то, что вы написали правильно. Однако, когда он распознает ваш почерк и имеет правильное уравнение, это фантастическое приложение, которое можно положить в шкаф, и оно вам очень пригодится.
Однако, когда он распознает ваш почерк и имеет правильное уравнение, это фантастическое приложение, которое можно положить в шкаф, и оно вам очень пригодится.
Существует множество приложений для решения математических задач, которые можно использовать бесплатно. Те, которые обсуждаются в этой статье, — одни из лучших, которые вы можете получить бесплатно. Тем не менее, многие другие аналогичные бесплатные приложения помогут вам решить математическую задачу, не напрягая себя излишне.
Помимо быстрых ответов по математике, некоторые из этих приложений также предлагают обучающие программы и простые пошаговые инструкции, которые помогут вам изучить, понять и полюбить решение математики.
Биография автора Эшли Симмонс — профессиональный журналист и редактор отдела написания статей в колледже. В течение четырех лет она работала рецензентом эссе, написав лучшую диссертацию в газете Солт-Лейк-Сити. Она также является экспертом по написанию контента по таким темам, как психология, современное образование, бизнес и маркетинговые инновации. Она мастер своего дела.
Она также является экспертом по написанию контента по таким темам, как психология, современное образование, бизнес и маркетинговые инновации. Она мастер своего дела.
Реза — опытный инструктор по математике и специалист по подготовке к экзаменам, который занимается со студентами с 2008 года.Он помог многим студентам поднять результаты стандартизированных тестов и поступить в колледжи своей мечты. Он работает со студентами индивидуально и в группах, преподает как живые, так и онлайн-курсы по математике и математическую часть стандартизированных тестов. Он предлагает индивидуальный индивидуальный план обучения и индивидуальное внимание, которое влияет на то, как учащиеся относятся к математике.
Примеры вопросов по SAT Math | College Board
Указания и номера вопросов ниже отражают то, с чем студенты столкнутся в день экзамена. Некоторые математические разделы позволяют использовать калькулятор, а другие — нет, как указано в инструкциях.
Некоторые математические разделы позволяют использовать калькулятор, а другие — нет, как указано в инструкциях.
Откройте Раздел 3 своего листа для ответов, чтобы ответить на вопросы этого раздела.
Для вопросов 1–15 решите каждую задачу, выберите лучший ответ из предложенных вариантов и закрасьте соответствующий кружок на листе для ответов. Для вопросов 16–20 решите проблему и введите свой ответ в сетку на листе ответов. Пожалуйста, ознакомьтесь с инструкциями перед вопросом 16 о том, как ввести свои ответы в сетку.Вы можете использовать любое доступное место в вашем тестовом буклете для черновой работы.
- Использование калькулятора [разрешено] / [запрещено].
- Все используемые переменные и выражения представляют собой действительные числа, если не указано иное.
- Рисунки, представленные в этом испытании, нарисованы в масштабе, если не указано иное.
- Все фигуры лежат на одной плоскости, если не указано иное.
- Если не указано иное, область заданной функции f представляет собой набор всех действительных чисел x , для которых является действительным числом.

Номер ссылки
Число градусов дуги в окружности 360.
Число радианов дуги в окружности
Сумма углов треугольника в градусах равна 180.
Для вопросов, задаваемых студентами, студенты также увидят следующие направления:
Для вопросов 16–20 решите проблему и введите свой ответ в сетку, как описано ниже, на листе для ответов.
- Хотя это и не обязательно, рекомендуется написать свой ответ в квадратах вверху столбцов, чтобы помочь вам правильно заполнить кружки. Вы получите кредит, только если кружки заполнены правильно.
- Отметьте не более одного кружка в любом столбце.
- Ни один вопрос не имеет отрицательного ответа.
- Для некоторых задач может быть несколько правильных ответов. В таких случаях сетка только один ответ.
- Смешанные числа, например, должны быть разделены на 3.5 или
(если ввести в сетку как, оно будет интерпретировано как не - Десятичные ответы: если вы получаете десятичный ответ с большим количеством цифр, чем может вместить сетка, он может быть либо округлен, либо усечен, но он должен заполнять всю сетку.

Если вы будете запрашивать (или были одобрены) для размещения формата, совместимого со вспомогательными технологиями (цифровое тестирование для использования с программой чтения с экрана или другой вспомогательной технологией) для SAT, вы можете также просмотреть примеры математических заданий в их полностью отформатированные версии, которые отсортированы как вопросы, разрешающие использование калькулятора, и вопросы, которые не позволяют использовать калькулятор.
Обратите внимание, что все условия тестирования, в том числе запросы на вспомогательные технологии и специальные форматы, должны быть одобрены Службой Совета колледжей для студентов с ограниченными возможностями до начала экзамена.
(PDF) Что учителя говорят о трудностях учащихся при решении словесных математических задач в 2–5 классах
ЧТО УЧИТЕЛЯ ГОВОРЯТ О ТРУДНОСТЯХ УЧАЩИХСЯ
Эдвардс, С., Малой, Р. В., и Андерсон, Г. (2009). Обучение чтению по математическим задачам.
Информационный центр по обучению грамоте. Получено 12 января 2010 г. с номера
http://www.literacycoachingonline.org/briefs/Reading_Coach_for_Math.pdf.
Fuchs, L. S., Fuchs, D., & Prentice, K. (2004). Отзывчивость к математической задаче —
инструкция по решению: сравнение учащихся с риском инвалидности по математике и
без риска потери способности читать. Журнал нарушений обучаемости, 37, 293-306.
Гриффин, К.К., и Джитендра А. К. (2009). Обучение решению словесных задач в инклюзивных классах математики
класса включительно. Журнал образовательных исследований, 102, 187-202.
Гутштейн, Э. (2006). Чтение и письмо мира с помощью математики: К педагогике
для социальной справедливости. Нью-Йорк, Нью-Йорк: Рутледж.
Харт, Дж. (1996). Эффекты персонализированных текстовых задач. Обучение детей математике,
2 (8), 504-505.
Хембри Р. (1992).Эксперименты и исследования отношений в решении проблем: метаанализ.
Журнал исследований в области математического образования, 23, 242-273.
Герман Дж. Л. (1998). Состояние оценок производительности. Директора школы,
55 (11), 17-22.
Хиггинс, К. М. (1997). Влияние годичного обучения решению математических задач
на отношения, убеждения и способности учащихся средней школы. Журнал экспериментальных
Образование, 66 (1), 5-28.
Хофф, Д. Дж. (2001) Мастерство чтения — новый критерий для решения математических задач. Неделя образования,
21 (14), 1-2.
Хайд, А. (2006). Понимание математики: адаптация стратегий чтения для обучения математике,
K-6. Портсмут, Нью-Хэмпшир: Хайнеманн.
Иммергут Б. (2003). Мастер математики: Решение задач со словами. Франклин Лейкс, Нью-Джерси: Карьера.
Джитендра, А.К., Щесняк, Э., и Дитлайн-Бухман, А. (2005). Исследовательская проверка
математических задач по решению словесных задач на основе учебной программы в качестве показателей уровня владения математикой
для третьеклассников. Обзор школьной психологии, 34, 358-371.
Обзор школьной психологии, 34, 358-371.
Джонсон Б. и Кристенсен Л. (2012). Образовательные исследования: количественный, качественный и
смешанных подходов (4-е изд.). Таузенд-Оукс, Калифорния: Сейдж.
Йонассен, Д. Х. (2003) Разработка основанных на исследованиях инструкций для решения сюжетных задач. Образовательный
Обзор психологии, 15, 267-296.
Кон, А. (2001). Борьба с испытаниями: практическое руководство по спасению наших школ. Дельта Пхи
Каппан, 82 (5), 348-357.
Коско, К. В., и Уилкинс, Дж. Л. М. (2010). Математическая коммуникация и ее отношение к
частоте манипулятивного использования. Международный электронный журнал математики
Образование, 5 (2), 79-90.
Леппанен, У., Ниеми, П., Аунола, К., и Нурми, Дж. (2006). Развитие чтения и правописания
финский язык от дошкольного до 1 и 2 класса. Научные занятия по чтению, 10,
3-30.
Леркканен, М.К., Раску-Путтонен, Х., Аунола, К.



 Стереометрия (задача 14).
Стереометрия (задача 14).
 10
10
 Финансовая математика (задача 17).
Финансовая математика (задача 17). 10 12.11 12.11 19.11
10 12.11 12.11 19.11 Неравенства (задача 15).
Неравенства (задача 15).
 12 10.12 10.12 17.12 17.12 24.12 24.12 14.01 14.01
12 10.12 10.12 17.12 17.12 24.12 24.12 14.01 14.01
 02
02
 Уравнения смешанного типа.
Уравнения смешанного типа.
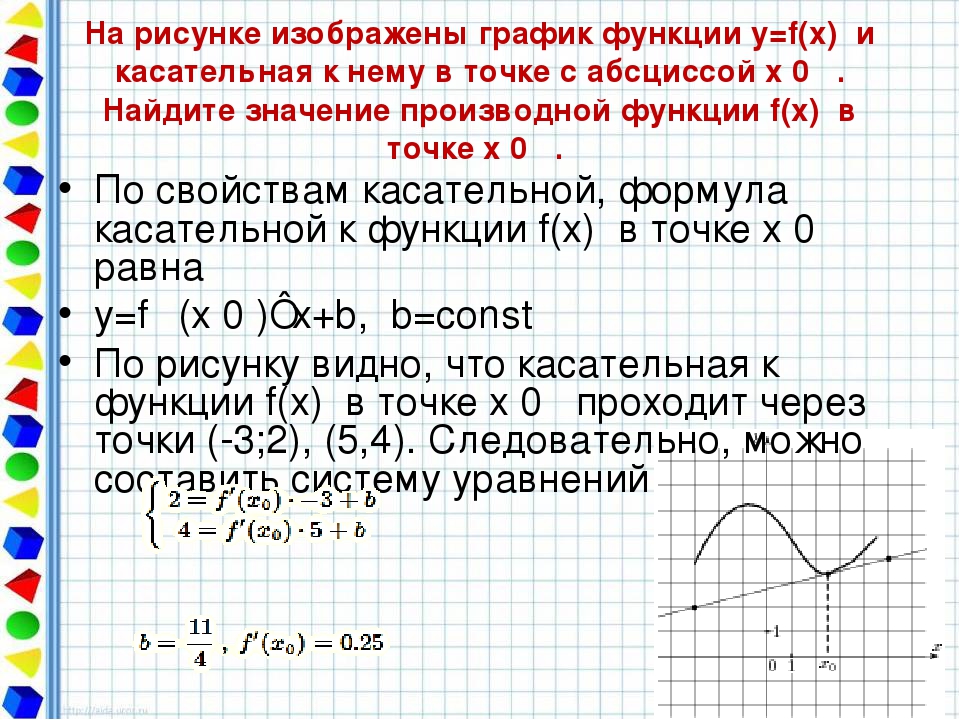 Задачи с прикладным содержанием (задача 10).
Задачи с прикладным содержанием (задача 10).

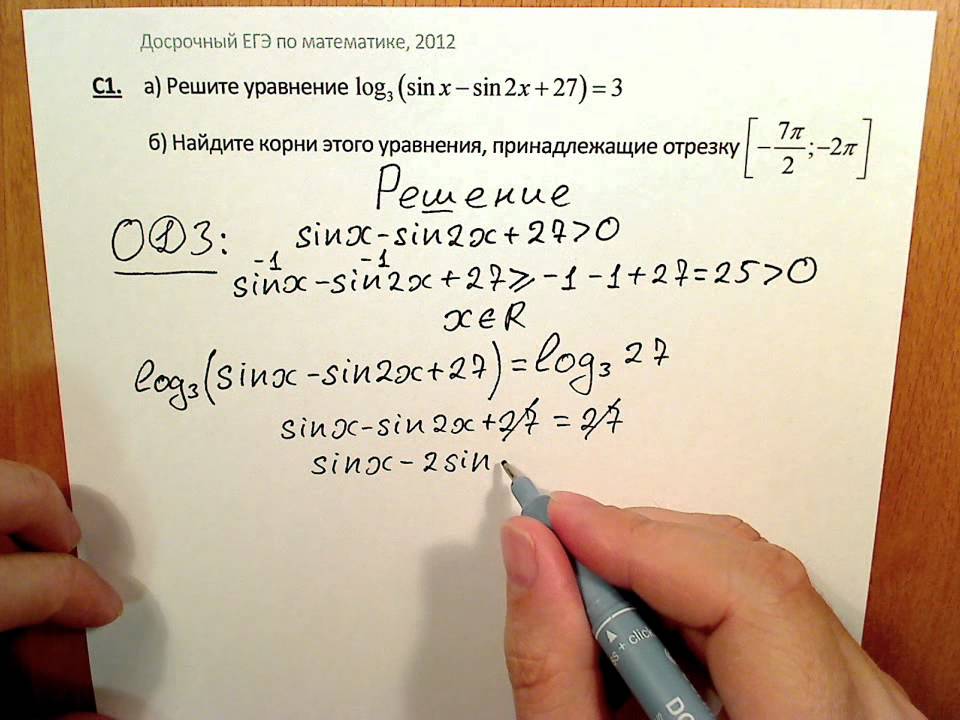
 За счет большего количества заданий экзамены становятся объективнее.
За счет большего количества заданий экзамены становятся объективнее.
 Например, вероятность события должна быть от 0 до 1 включительно, а площадь геометрической фигуры должна быть положительной. В других случаях вы можете использовать оценку, чтобы проверить разумность вашего ответа. Например, если ваше решение включает сложение трех чисел, каждое из которых находится в диапазоне от 100 до 200, оценка суммы говорит вам, что сумма должна быть между 300 и 600.
Например, вероятность события должна быть от 0 до 1 включительно, а площадь геометрической фигуры должна быть положительной. В других случаях вы можете использовать оценку, чтобы проверить разумность вашего ответа. Например, если ваше решение включает сложение трех чисел, каждое из которых находится в диапазоне от 100 до 200, оценка суммы говорит вам, что сумма должна быть между 300 и 600.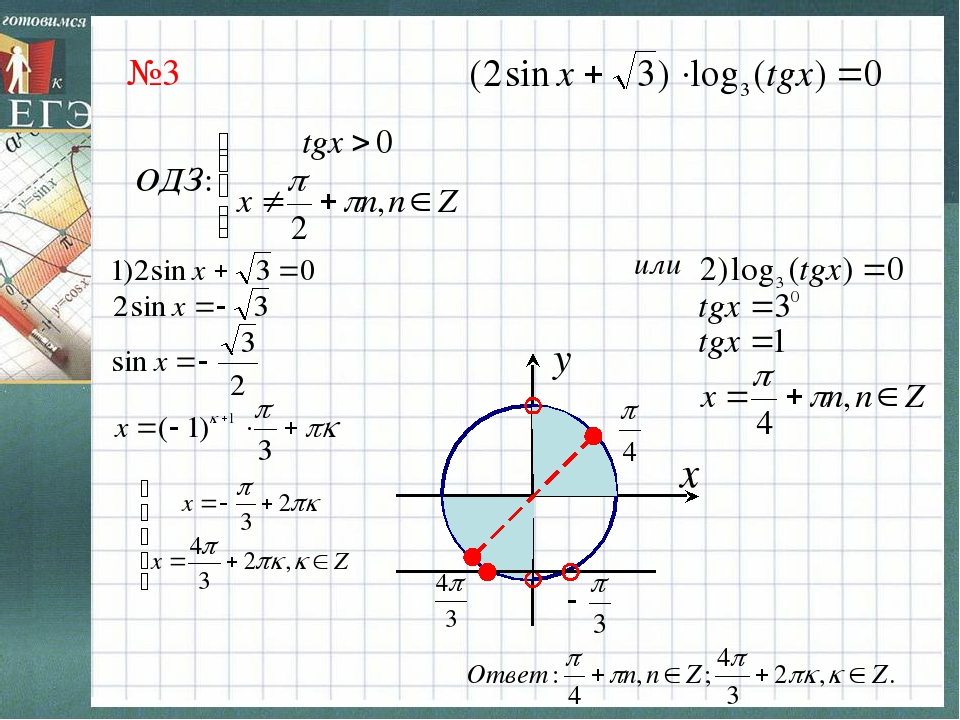 ) Итак, мы можем позвонить по первому номеру n и второй номер n + 2.Вопрос гласит, что произведение двух чисел равно 24. Таким образом, ( n ) ( n + 2) = 24. Теперь мы решаем для n : Таким образом, n = -6 или 4. Поскольку в вопросе указано, что числа были отрицательными, ответ не может быть n = 4. Если n = -6, n + 2 = -4 и два числа -6 и -4. Вопрос касается меньшего из двух чисел, а именно -6.
) Итак, мы можем позвонить по первому номеру n и второй номер n + 2.Вопрос гласит, что произведение двух чисел равно 24. Таким образом, ( n ) ( n + 2) = 24. Теперь мы решаем для n : Таким образом, n = -6 или 4. Поскольку в вопросе указано, что числа были отрицательными, ответ не может быть n = 4. Если n = -6, n + 2 = -4 и два числа -6 и -4. Вопрос касается меньшего из двух чисел, а именно -6.  Однако важно помнить, что эта плата должна быть оплачена независимо от того, сколько времени длится звонок.
Однако важно помнить, что эта плата должна быть оплачена независимо от того, сколько времени длится звонок.

Leave A Comment