Все про баллы ЕГЭ 2021 по математике

— Сколько баллов можно получить за первую часть профильной математики?

— Сколько баллов дают за каждое задание ЕГЭ 2021 по математике (профильный уровень)?

— Перевод баллов ЕГЭ 2021 по профильной математике?

Вопросы с которыми давайте разберемся.

Сколько баллов дается за каждое задание по профильной математике на ЕГЭ 2021 можно узнать в демоверсии.

Распределение баллов ЕГЭ 2021 по заданиям — математика профиль

№ задания Первичные баллы
1 1
2 1
3 1
4 1
5 1
6
1
7 1
8 1
9 1
10 1
11 1
12 1
13 2
14 2
15 2
16
 3
17 3
18 4
19 4
Всего 32

Математика профиль:

1 балл —  за 1-12 задания.

2 балла —  13-15. 

З балла —  16, 17.

4 балла — 18, 19.

Всего: 32 балла

Соответствие первичных баллов тестовым

Первичный балл Тестовый балл Примечание
1 5  
2 9  
3 14  
4 18  
5 23  
6 27
 Порог для получения аттестата
7 33  
8 39  
9 45  
10 50  
11 56  
12 62  
13 68 Минимальный балл для ВУЗА
14 70  
15 72  
16 74  
17 76  
18 78  
19 80  
20 82  
21
 84  
22 86  
23 88  
24 90  
25 92  
26 94  
27 96  
28 98  
29
 99  
30 100  
31 100  
32 100  

 

Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и количеству заданий:

– часть 1 содержит 8 заданий (задания 1–8) с кратким ответом в виде целого числа или конечной десятичной дроби;

– часть 2 содержит 4 задания (задания 9–12) с кратким ответом в виде целого числа или конечной десятичной дроби и 7 заданий (задания 13–19) с развернутым ответом (полная запись решения с обоснованием выполненных действий).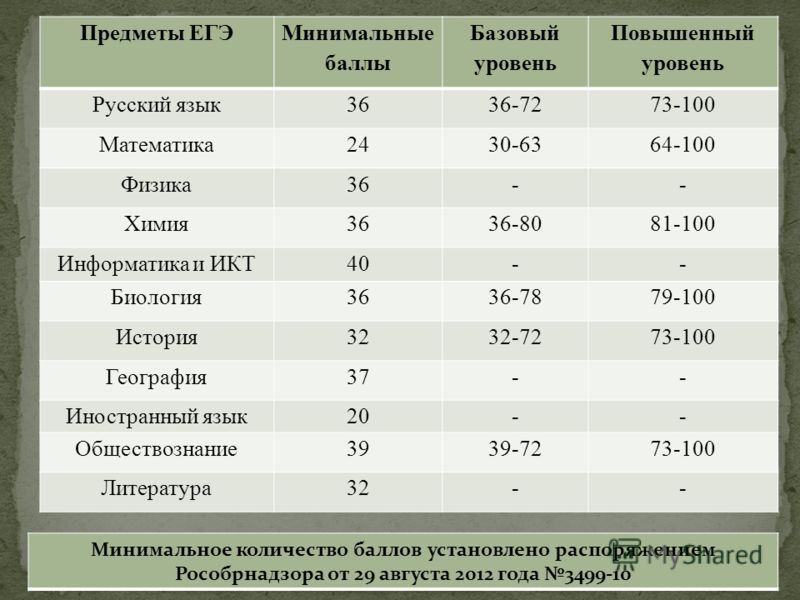

 

Таким образом, за решение первой части можно набрать 8 первичных баллов → 39 тестовых.

Связанные страницы:

Тренировочные варианты ЕГЭ 2021 по математике базового уровня

Тренировочные варианты ЕГЭ 2021 по математике профильного уровня

Решение задания № 14 ЕГЭ по математике

Разбор задания 2 ЕГЭ математика профильный уровень

Решение задачи №19 ЕГЭ по профильной математике

шкала перевода баллов в таблицах

https://ria.ru/20210601/ege-1734978741.html

Баллы ЕГЭ по математике 2022: шкала перевода баллов в таблицах

Баллы ЕГЭ по математике 2022: шкала перевода баллов в таблицах

Баллы ЕГЭ по математике 2022: шкала перевода баллов в таблицах

Баллы ЕГЭ по математике — мера оценки знаний выпускника по одному из обязательных предметов. Шкала перевода баллов в таблицах в 2022 году, отличие первичного и… РИА Новости, 20.05.2022

2021-06-01T17:08

2021-06-01T17:08

2022-05-20T18:01

образование — общество

единый государственный экзамен (егэ)

/html/head/meta[@name=’og:title’]/@content

/html/head/meta[@name=’og:description’]/@content

https://cdnn21. img.ria.ru/images/152436/98/1524369808_0:104:2000:1229_1920x0_80_0_0_0c805c9b1fc600bb6b9b88643f7d3928.jpg

МОСКВА, 1 июня – РИА Новости. Баллы ЕГЭ по математике — мера оценки знаний выпускника по одному из обязательных предметов. Шкала перевода баллов в таблицах в 2022 году, отличие первичного и тестового баллов — в материале РИА Новости. Перевод баллов по математике в оценкиЕсть два уровня ЕГЭ по математике: базовый и профильный. Сдать базовый экзамен для получения аттестата достаточно тем, кто не планирует поступление в вуз или поступает на специальности, где математика не является одним из вступительных испытаний. Профильный уровень более сложный и требует изучения предмета на углубленном уровне. Он дает возможность участвовать в конкурсе на поступление в вузы, где среди вступительных испытаний есть “Математика”. Для получения аттестата на ЕГЭ по профильной математике необходимо набрать не менее 27 тестовых баллов. Экзаменационная работа состоит из заданий базового, повышенного и высокого уровней сложности.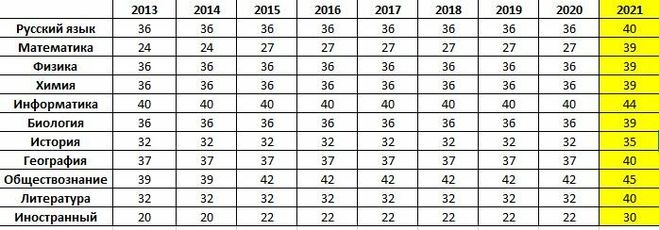 Базовый уровеньНа базовом уровне можно получить не более 21 первичного балла. Они переводятся в отметки по пятибалльной шкале, а не в 100-балльную шкалу.Профильный уровеньПеревод баллов профильного уровня в оценки не осуществляется с 2008 года, однако условно их можно сопоставить. Распределение баллов за каждое задание по математикеВсего на ЕГЭ по математике можно получить 31 первичный балл, которые потом переведут в 100-балльную шкалу. По заданиями они распределяются так:Профильный уровень включает в себя 11 заданий с кратким ответом и 7 с развернутым.Минимальные и максимальные баллы по математикеДля профильного уровня минимальный балл для поступления в вуз и получения аттестата устанавливается Рособрнадзором. В 2022 году он составляет 27 тестовых баллов. Министерства сами могут устанавливать минимальные пороги баллов для подведомственных им вузов. Большинство вузов находится в ведении Минобрнауки РФ, для них минимальный порог по профильной математике на этот год установлен на уровне 39 баллов. Максимальный балл экзамена — 100, однако свыше 80 тестовых баллов показывают, что выпускник имеет высокий уровень подготовки.

https://ria.ru/20210531/apellyatsiya-1734980175.html

https://radiosputnik.ria.ru/20210531/ege-1734915765.html

РИА Новости

1

5

4.7

96

[email protected]

7 495 645-6601

ФГУП МИА «Россия сегодня»

https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/

2021

РИА Новости

1

5

4.7

96

[email protected]

7 495 645-6601

ФГУП МИА «Россия сегодня»

https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/

Новости

ru-RU

https://ria.ru/docs/about/copyright.html

https://xn--c1acbl2abdlkab1og.xn--p1ai/

РИА Новости

1

5

4.7

96

[email protected]

7 495 645-6601

ФГУП МИА «Россия сегодня»

https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/

1920

1080

true

1920

1440

true

https://cdnn21. img.ria.ru/images/152436/98/1524369808_112:0:1888:1332_1920x0_80_0_0_946c2f5ef74b61f9b65607b2116dd464.jpg

1920

1920

true

РИА Новости

1

5

4.7

96

[email protected]

7 495 645-6601

ФГУП МИА «Россия сегодня»

https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/

РИА Новости

1

5

4.7

96

[email protected]

7 495 645-6601

ФГУП МИА «Россия сегодня»

https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/

образование — общество, единый государственный экзамен (егэ)

Образование — Общество, Единый государственный экзамен (ЕГЭ)

МОСКВА, 1 июня – РИА Новости. Баллы ЕГЭ по математике — мера оценки знаний выпускника по одному из обязательных предметов. Шкала перевода баллов в таблицах в 2022 году, отличие первичного и тестового баллов — в материале РИА Новости.

Перевод первичных баллов в тестовые

Первичные баллы

Тестовые баллы

1

6

2

11

3

17

4

22

5

27

6

34

7

40

8

46

9

52

10

58

11

56

12

62

Первичные баллы

Тестовые баллы

11

56

12

62

13

68

14

70

15

72

16

74

17

76

18

78

19

80

20

82

21

84

22

86

Первичный балл

Тестовый балл

21

84

22

86

23

88

24

90

25

92

26

94

27

96

28

98

29

100

30

100

31

100

Перевод баллов по математике в оценки

Есть два уровня ЕГЭ по математике: базовый и профильный. Сдать базовый экзамен для получения аттестата достаточно тем, кто не планирует поступление в вуз или поступает на специальности, где математика не является одним из вступительных испытаний. Профильный уровень более сложный и требует изучения предмета на углубленном уровне. Он дает возможность участвовать в конкурсе на поступление в вузы, где среди вступительных испытаний есть “Математика”. Для получения аттестата на ЕГЭ по профильной математике необходимо набрать не менее 27 тестовых баллов. Экзаменационная работа состоит из заданий базового, повышенного и высокого уровней сложности.

Апелляция ЕГЭ: ее виды, сроки и порядок подачи жалобы

31 мая 2021, 17:56

Базовый уровень

На базовом уровне можно получить не более 21 первичного балла. Они переводятся в отметки по пятибалльной шкале, а не в 100-балльную шкалу.

Количество баллов

Оценка по пятибалльной шкале

0-6

2

7-11

3

12-16

4

17-21

5

Профильный уровень

Перевод баллов профильного уровня в оценки не осуществляется с 2008 года, однако условно их можно сопоставить.

Количество тестовых баллов

Оценка по пятибалльной шкале

0-26

2

27-46

3

47-64

4

65-100

5

Распределение баллов за каждое задание по математике

Всего на ЕГЭ по математике можно получить 31 первичный балл, которые потом переведут в 100-балльную шкалу. По заданиями они распределяются так:

  • 1 балл — 1-11 задания;
  • 2 балла — 12, 14, 15 задания;
  • З балла — 13, 16 задания;
  • 4 балла — 17, 18.

Профильный уровень включает в себя 11 заданий с кратким ответом и 7 с развернутым.

Эксперт оценила возможность дистанционной сдачи ЕГЭ

31 мая 2021, 13:14

Минимальные и максимальные баллы по математике

Для профильного уровня минимальный балл для поступления в вуз и получения аттестата устанавливается Рособрнадзором. В 2022 году он составляет 27 тестовых баллов. Министерства сами могут устанавливать минимальные пороги баллов для подведомственных им вузов. Большинство вузов находится в ведении Минобрнауки РФ, для них минимальный порог по профильной математике на этот год установлен на уровне 39 баллов. Максимальный балл экзамена — 100, однако свыше 80 тестовых баллов показывают, что выпускник имеет высокий уровень подготовки.

ЕГЭ по математике

6.2 Использование нормального распределения

Введение Расчеты вероятностей

Введение

Заштрихованная область на следующем графике обозначает область слева от x . Эта область может представлять процент учащихся, набравших меньше определенного балла на выпускном экзамене. Эта область представлена ​​вероятностью P ( X x). Обычные таблицы, компьютеры и калькуляторы используются для получения или расчета вероятности Р ( х х).

Рисунок 6.4

Площадь справа равна

P ( X > x ) = 1 – P ( X x). Помните, P ( X x) = Площадь слева от вертикальной линии, проходящей через x . P ( X x) = 1 – P ( X x) = Площадь справа от вертикальной линии, проходящей через x . Р ( Х x) то же самое, что
P ( x ≤ x ), и P ( x > x ) то же самое, что P ( x ≥ x ) для непрерывного дистрибутивы.

Предположим, что приведенный выше график представляет процент учащихся, набравших менее 75 баллов на выпускном экзамене, с вероятностью, равной 0,39. Это также указывало бы на то, что процент учащихся, набравших более 75 баллов, был равен 1 минус 0,39 или 0,61.

Расчеты вероятностей

Вероятности рассчитываются с помощью технологии. Приведены необходимые инструкции для калькуляторов ТИ-83+ и ТИ-84.

ПРИМЕЧАНИЕ

Для расчета вероятности используйте таблицы вероятностей, представленные на рисунке G1, без использования технологии. Таблицы содержат инструкции по их использованию.

Вероятность представлена ​​площадью под нормальной кривой. Чтобы найти вероятность, вычислите z -score и найдите z -score в таблице z под столбцом z . Большинство таблиц z показывают площадь под нормальной кривой слева от z . Другие показывают среднее значение для области z . Используемый метод будет указан в таблице.

Мы обсудим таблицу z , которая представляет площадь под кривой нормали слева от z . После того, как вы нашли счет z , найдите соответствующую область. Это будет площадь под нормальной кривой слева от z — счет. Эту площадь можно использовать для нахождения площади справа от z -счета или путем вычитания из 1 или общей площади под нормальной кривой. Эти площади также можно использовать для определения площади между двумя z -оценками.

Пример 6.7

Если площадь слева равна 0,0228, то площадь справа равна 1 – 0,0228 = 0,9772.

Пример 6.8

Итоговые баллы за экзамен по статистике были нормально распределены со средним значением 63 и стандартным отклонением, равным пяти.

 

а. Найти вероятность того, что случайно выбранный студент наберет на экзамене более 65 баллов.

Раствор 6.8

а. Пусть X = балл на выпускном экзамене. X ~ N (63, 5), где μ = 63 и σ = 5.

Нарисуйте график.

Рассчитайте z -значение:

z=x−μσ=65−635=25=.40z=x−μσ=65−635=25=.40

Таблица z показывает, что область слева от z равно 0,6554. Вычитание этой площади из 1 дает 0,3446.

Затем найдите P ( x > 65).

P(x > 65) = 0,3446P(x > 65) = 0,3446

Рис. 6.5

Вероятность того, что любой выбранный наугад учащийся наберет больше 65 баллов, равна 0,3446.

Историческая заметка

Программа вероятности TI вычисляет z -оценку, а затем вероятность на основе z -оценки. До технологий z -показатель искали в стандартной таблице нормальных вероятностей, также известной как Z-таблица — математика, используемая для определения вероятности, громоздка. В этом примере использовалась стандартная нормальная таблица с областью слева от z баллов. Вы вычисляете z -значение и ищете область слева. Вероятность – это площадь справа.

б. Найти вероятность того, что случайно выбранный студент наберет меньше 85 баллов.

Решение 6.8

b. Нарисуйте график.

Затем найдите P ( x

С помощью компьютера или калькулятора найдите P ( x

normalcdf(0,85,63,5) = 1 (округляется до единицы)

Вероятность того, что один учащийся наберет меньше 85 баллов, приблизительно равна единице, или 100 процентам.

 

в. Найдите процентиль 90 th , то есть найдите результат k , который имеет 90 процентов значений ниже k и 10 процентов значений выше 9. 0007 к .

Раствор 6.8

c. Найдите процентиль 90 90 205 90 206. Для каждой проблемы или части проблемы нарисуйте новый график. Нарисуйте ось x . Заштрихуйте область, соответствующую 90 90 205 th 90 206 процентилю. На этот раз мы ищем оценку, которая соответствует заданной области под кривой.

Пусть k = 90 -й -й процентиль. Переменная k расположена на оси x . С ( x k) — это область слева от k . 90 й процентиль k разделяет экзаменационные баллы на те, которые равны или ниже k , и такие же или выше. Девяносто процентов результатов тестов равны или ниже k , а 10 процентов равны или выше. Переменную k часто называют критическим значением.

Мы знаем среднее значение, стандартное отклонение и площадь под нормальной кривой. Нам нужно найти z -оценка, которая соответствует площади 0,9, а затем замените ее средним значением и стандартным отклонением в нашу формулу z -оценка. Таблица z показывает z-значение приблизительно 1,28 для площади под нормальной кривой слева от z (большая часть) приблизительно 0,9. Таким образом, мы можем написать следующее:

1,28=x−6351,28=x−63,5

Умножив каждую часть уравнения на 5, получим

6,4=x−636,4=x−63

уравнение дает

69,4=х,69,4=х.

Таким образом, наш счет k равен 69,4.

к = 69,4 к = 69,4

Рисунок 6.6

90 90 205 й 90 206 процентиль равен 69,4. Это означает, что 90 процентов результатов тестов находятся на уровне 69,4 или ниже, а 10 процентов — на уровне или выше. Чтобы получить этот ответ на калькуляторе, выполните следующий шаг.

д. Найдите 70 й процентиль, то есть найдите число k такое, что 70% баллов меньше k и 30 процентов баллов выше k .

Раствор 6.8

d. Найдите процентиль 70 90 205 90 206.

Нарисуйте новый график и подпишите его соответствующим образом. k = 65,6

70 -й процентиль равен 65,6. Это означает, что 70 % результатов тестов находятся на уровне 65,5 или ниже, а 30 % — на уровне или выше.

инвНорма(0,70,63,5) = 65,6

Пример 6.9

Персональный компьютер используется для офисной работы дома, исследований, общения, личных финансов, образования, развлечений, общения в социальных сетях и множества других целей. Предположим, что среднее количество часов, в течение которых домашний персональный компьютер используется для развлечения, составляет два часа в день. Предположим, что время развлечений распределено нормально, а стандартное отклонение времени составляет полчаса.

 

а. Найти вероятность того, что домашний персональный компьютер используется для развлечения от 1,8 до 2,75 часов в день.

Раствор 6.9

а. Пусть X = количество времени в часах, в течение которого домашний персональный компьютер используется для развлечения. X ~ N (2, 0,5), где μ = 2 и σ = 0,5.

Найти P (1,8 x

Сначала подсчитайте z -оценки для каждого x -значение.

z=1,8−20,5=−0,20,5=−0,40z=2,75−20,5=0,750,5=1,5z=1,8−20,5=−0,20,5=−0,40z=2,75−20,5=0,750,5=1,5

Теперь используйте таблицу Z , чтобы найти площадь под кривой нормали слева от каждой из этих z -оценок.

Площадь слева от z -значения -0,40 равна 0,3446. Площадь слева от z с показателем 1,5 составляет 0,9332. Площадь между этими показателями будет разницей между двумя областями, или 0,9332−0,34460,9.332−0,3446, что равно 0,5886.

Рисунок 6.7

normalcdf(1,8,2,75,2,0,5) = 0,5886

Вероятность того, что домашний персональный компьютер используется для развлечения от 1,8 до 2,75 часов в день, равна 0,5886.

 

б. Найдите максимальное количество часов в день, в течение которых нижний квартиль домохозяйств использует персональный компьютер для развлечения.

Раствор 6.9

б. Чтобы найти максимальное количество часов в день, в течение которых нижний квартиль домохозяйств использует персональный компьютер для развлечения, найти 25 й процентиль, k , где P ( x k) = 0,25.

Рисунок 6.8

invNorm(0.25,2,0.5) = 1,66

Мы используем invNorm, потому что ищем значение k .

Максимальное количество часов в день, в течение которых нижний квартиль домохозяйств использует персональный компьютер для развлечения, составляет 1,66 часа.

Пример 6.10

В США пользователи смартфонов в возрасте от 13 до 55+ примерно следуют нормальному распределению с приблизительным средним значением и стандартным отклонением 36,9.лет и 13,9 лет соответственно.

 

а. Определите вероятность того, что случайному пользователю смартфона в возрасте от 13 до 55+ лет будет от 23 до 64,7 лет.

Раствор 6.10

а. normalcdf(23,64,7,36,9,13,9) = 0,8186

z -оценки рассчитываются как =2z=23−36,913,9=−13,913,9=−1z=64,7−36,913,9=27,813,9=2

Таблица Z показывает область слева от z — оценка с абсолютным значением 1 должна быть 0,1587. Он показывает, что площадь слева от z — оценка 2 равна 0,9772. Разница в двух областях составляет 0,8185.

Это немного отличается от площади, указанной калькулятором, из-за округления.

б. Определите вероятность того, что случайно выбранному пользователю смартфона в возрасте от 13 до 55+ лет будет не более 50,8 лет.

Раствор 6.10

b. normalcdf(–10 99 ,50,8,36,9,13,9) = 0,8413

 

в. Найдите 80 90 205-й 90 206-й процентиль этого распределения и интерпретируйте его в виде полного предложения.

Раствор 6.10

c.

  • инвНорма(0,80,36,9,13,9) = 48,6
  • 80 й процентиль равен 48,6 годам.
  • 80 процентов пользователей смартфонов в возрасте от 13 до 55 лет старше 48,6 лет.

Пример 6.11

В США пользователи смартфонов в возрасте от 13 до 55+ примерно следуют нормальному распределению с приблизительным средним значением и стандартным отклонением 36,9.лет и 13,9 лет соответственно. Используя эту информацию, ответьте на следующие вопросы, округлив ответы до одного знака после запятой:

 

a. Рассчитайте межквартильный размах ( IQR ).

Раствор 6.11

а.

  • IQR = Q 3 – Q 1
  • Вычислить Q 3 = 75 th процентиль и Q 1 = 25 th процентиль.
  • Вспомните, что мы можем использовать invNorm, чтобы найти k -значение. Мы можем использовать это, чтобы найти значения квартилей.
  • invNorm(0,75,36,9,13,9) = Q 3 = 46,2754
  • invNorm(0,25,36,9,13,9) = Q 1 = 27,5246
  • IQR = Q 3 – Q 1 = 18,8

 

 

б. 40% людей в возрасте от 13 до 55+ относятся к какому возрасту?

Решение 6.11

б.

  • Найдите k , где P ( x ≥ k ) = 0,40. По крайней мере преобразуется в больше или равно .
  • 0,40 = площадь справа
  • Площадь слева = 1 – 0,40 = 0,60.
  • Площадь слева от k = 0,60
  • инвНорма(0,60,36,9,13,9) = 40,4215
  • к = 40,4.
  • Сорок процентов лиц в возрасте от 13 до 55 лет и старше составляют по крайней мере 40,4 года.

Пример 6.12

Фермер, выращивающий цитрусовые, который выращивает мандарины, обнаружил, что диаметры мандаринов, собранных на его ферме, подчиняются нормальному распределению со средним диаметром 5,85 см и стандартным отклонением 0,24 см.

 

а. Найти вероятность того, что случайно выбранный мандарин с этой фермы будет иметь диаметр больше 6,0 см. Нарисуйте график. 999,5,85,0,24) = 0,2660

Рисунок 6.9

б. Средние 20 процентов мандаринов с этой фермы имеют диаметр от ______ до ______.

Раствор 6.12

b.

  • 1 – 0,20 = 0,80. За пределами средних 20 процентов будет 80 процентов значений.
  • Каждый хвост графика нормального распределения имеет площадь 0,40.
  • Найти k 1 , 40 -й -й процентиль и k 2 , 60 th процентиль (0,40 + 0,20 = 0,60). Это оставляет средние 20 процентов в середине распределения.
  • k 1 = invNorm(0,40,5,85,0,24) = 5,79 см
  • k 2 = invNorm(0,60,5,85,0,24) = 5,91 см

 

 

Итак, средние 20 процентов мандаринов имеют диаметр от 5,79 см до 5,91 см.

в. Найдите 90 -й -й процентиль диаметра мандаринов и интерпретировать его в виде полного предложения.

Раствор 6.12

c. 6.16: Девяносто процентов диаметра мандаринов составляет не более 6,16 см.

 

  • Печать
  • Поделиться

2.

4: Нормальное распределение — Математика LibreTexts
  1. Последнее обновление
  2. Сохранить как PDF
  • Идентификатор страницы
    22313
    • Макси Иниго, Дженнифер Джеймсон, Кэтрин Козак, Майя Ланзетта и Ким Сонье Сообщество Колледж 9
    • Cocon0438

    Существует множество различных типов распределений (форм) количественных данных. В разделе 1.5 мы рассмотрели различные гистограммы и описали их формы как симметричные, скошенные влево и скошенные вправо. Существует специальное симметричное распределение, называемое нормальным распределением. Он высокий в середине, а затем быстро и одинаково опускается на обоих концах. Она похожа на колокол, поэтому иногда ее называют колоколообразной кривой. Одним из свойств нормального распределения является то, что оно симметрично относительно среднего. Другое свойство связано с тем, какой процент данных попадает в определенные стандартные отклонения от среднего значения. Это свойство определяется как эмпирическое правило.

    Эмпирическое правило: Учитывая набор данных, который приблизительно нормально распределен:

    Приблизительно 68% данных находятся в пределах одного стандартного отклонения от среднего значения.

    Приблизительно 95 % данных находятся в пределах двух стандартных отклонений от среднего значения.

    Приблизительно 99,7% данных находятся в пределах трех стандартных отклонений от среднего значения.

    Чтобы увидеть эти проценты, см. следующий рисунок.

    Рисунок \(\PageIndex{1}\): Эмпирическое правило

    Примечание: эмпирическое правило справедливо только для приблизительно нормальных распределений.

    Пример \(\PageIndex{1}\): использование эмпирического правила

    Предположим, что ваш класс прошел тест, средний балл составил 75 %, а стандартное отклонение — 5 %. Если результаты теста подчиняются примерно нормальному распределению, ответьте на следующие вопросы:

    1. Какой процент учащихся набрал от 65 до 85 баллов?
    2. Какой процент учащихся набрал от 65 до 75 баллов?
    3. Какой процент учащихся набрал от 70 до 80 баллов?
    4. Какой процент учащихся набрал больше 85 баллов?

    Чтобы решить каждую из них, было бы полезно нарисовать нормальную кривую, соответствующую этой ситуации. Среднее значение равно 75, поэтому центр равен 75. Стандартное отклонение равно 5, поэтому для каждой строки выше среднего прибавьте 5, а для каждой строки ниже среднего вычтите 5. График выглядит следующим образом:

    Рисунок \(\PageIndex{2}\): Эмпирическое правило для примера \(\PageIndex{1}\)
    1. Из графика видно, что 95% учащихся имеют баллы от 65 до 85.
    2. Показатели от 65 до 75 составляют половину площади графика от 65 до 85. Из-за симметрии это означает, что процент от 65 до 85 составляет ½ от 95%, что составляет 47,5%.
    3. Из графика видно, что 68% учащихся набрали от 70 до 80 баллов.
    4. Для этой задачи нам понадобится немного математики. Если бы вы посмотрели на всю кривую, вы бы сказали, что 100% всех результатов тестов попадают под нее. Таким образом, из-за симметрии 50 % результатов теста попадают в область выше среднего, а 50 % результатов теста попадают в область ниже среднего. Из части б мы знаем, что процент от 65 до 75 составляет 47,5%. Из-за симметрии процент от 75 до 85 также составляет 47,5%. Таким образом, процент выше 85 составляет 50% — 47,5% = 2,5%.

    Глядя на пример \(\PageIndex{1}\), мы понимаем, что цифры на шкале не так важны, как количество стандартных отклонений числа от среднего. Например, число 80 — это одно стандартное отклонение от среднего. Число 65 — это 2 стандартных отклонения от среднего. Однако 80 выше среднего, а 65 ниже среднего. Предположим, мы хотим узнать, сколько стандартных отклонений составляет число 82 от среднего. Как бы мы это сделали? С другими числами было проще, потому что они представляли собой целое число стандартных отклонений от среднего. Нам нужен способ количественной оценки этого. Мы будем использовать z-оценку (также известную как z-значение или стандартизированная оценка), чтобы измерить, сколько стандартных отклонений значения данных от среднего. Это определяется как:

    z-значение: \(z = \dfrac{x-\mu}{\sigma}\)

    , где \(x\) = значение данных (необработанная оценка)

    \(z\) = стандартизированное значение (z-оценка или z-значение)

    \(\mu\) = среднее значение населения

    \(\сигма\) = стандартное отклонение населения

    Примечание. Помните, что z-оценка всегда представляет собой количество стандартных отклонений значения данных от среднего значения распределения.

    Предположим, что значение данных имеет z-показатель 2,13. Это говорит нам о двух вещах. Во-первых, это говорит о том, что значение данных выше среднего, поскольку оно положительное. Во-вторых, это говорит нам о том, что вам нужно добавить более двух стандартных отклонений к среднему значению, чтобы получить это значение. Поскольку большинство данных (95%) находится в пределах двух стандартных отклонений, то все, что находится за пределами этого диапазона, будет считаться странным или необычным значением. Z-значение 2,13 находится за пределами этого диапазона, поэтому это необычное значение. В качестве другого примера предположим, что значение данных имеет z-показатель -1,34. Это значение данных должно быть ниже среднего, так как z-оценка отрицательна, и вам нужно вычесть более одного стандартного отклонения от среднего, чтобы получить это значение. Поскольку это находится в пределах двух стандартных отклонений, это обычное значение.

    Ан необычное значение имеет z-показатель < или z-показатель > 2

    Обычное значение имеет z-оценку от 2, то есть \(-2 < z-оценка < 2\).

    Вы можете столкнуться со стандартными оценками в отчетах по стандартизированным тестам или поведенческим тестам, как упоминалось ранее.

    Пример \(\PageIndex{2}\): расчет Z-показателей

    Предположим, что ваш класс прошел тест со средним баллом 75% и стандартным отклонением 5%. Если результаты теста подчиняются примерно нормальному распределению, ответьте на следующие вопросы:

    1. Если учащийся набрал 87 баллов за тест, каков его z-балл и что он означает?

    \(\mu = 75\), \(\sigma = 5\) и \(x = 87\)

    \(z = \dfrac{x-\mu}{\sigma}\)

    \( = \dfrac{87-75}{5}\)

    \(=2,40\)

    Это означает, что оценка 87 более чем на два стандартных отклонения превышает среднее значение, и поэтому считается необычной оценкой.

    1. Если учащийся набрал 73 балла за тест, каков его z-балл и что он означает?

    \(\mu = 75\), \(\sigma = 5\) и \(x = 73\)

    \(z = \dfrac{x-\mu}{\sigma}\)

    \(= \dfrac{73-75}{5}\)

    \(=-0,40\)

    Это означает, что оценка 73 менее чем на половину стандартного отклонения ниже среднего. Он считается обычным или рядовым счетом.

    1. Если учащийся набрал 54 балла за тест, каков его z-показатель и что он означает?

    \(\mu = 75\), \(\sigma = 5\) и \(x = 54\)

    \(z = \dfrac{x-\mu}{\sigma}\)

    \( = \dfrac{54-75}{5}\)

    \(=-4. 20\)

    Означает, что оценка 54 более чем на четыре стандартных отклонения ниже среднего значения, и поэтому считается необычной оценкой.

    1. Если учащийся имеет z-показатель 1,43, какой фактический балл он получил на тесте?

    \(\mu = 75\), \(\sigma = 5\) и \(z = 1,43\)

    Эта задача требует немного алгебры. Не волнуйтесь, это не так сложно. Поскольку теперь вы ищете x вместо z, измените решение уравнения для x следующим образом:

    \(z = \dfrac{x-\mu}{\sigma}\)

    \(z \cdot \sigma= \dfrac{x-\mu}{\cancel{\sigma}} \cdot \cancel{\sigma}\)

    \(z \sigma= x — \mu\)

    \(z\sigma + \mu = x — \cancel{\mu} + \cancel{\mu}\)

    \(х = г\сигма + \мю\)

    Теперь вы можете использовать эту формулу, чтобы найти x, когда вам известно z.

    \(х = г\сигма + \мю\)

    \(х = 1,43 \cdot 5 + 75 \)

    \(х = 7,15 + 75 \)

    \(х = 82,15 \)

    Таким образом, z-показатель 1,43 соответствует фактическому результату теста 82,15%.

    1. Если у учащегося z-показатель -2,34, какой фактический балл он получил за тест?

    \(\mu = 75\), \(\sigma = 5\) и \(z = -2,34\)

    Используйте формулу для x из части d этой задачи:

    \(х = г\сигма + \мю\)

    \(х = -2,34 \cdot 5 + 75 \)

    \(х = -11,7 + 75 \)

    \(х = 63,3 \)

    Таким образом, z-показатель -2,34 соответствует фактическому результату теста 63,3%.

    Пятизначная сводка для нормального распределения

    Глядя на эмпирическое правило, 99,7% всех данных находятся в пределах трех стандартных отклонений от среднего значения. Это означает, что аппроксимация минимального значения в нормальном распределении представляет собой среднее значение минус трехкратное стандартное отклонение, а максимальное — среднее значение плюс трехкратное стандартное отклонение. В нормальном распределении среднее и медиана совпадают. Наконец, первый квартиль может быть аппроксимирован путем вычитания 0,67448-кратного стандартного отклонения от среднего значения, а третий квартиль может быть аппроксимирован путем добавления 0,67448-кратного стандартного отклонения к среднему значению. Все это вместе дает сводку из пяти чисел.

    В математической нотации сводка из пяти чисел для нормального распределения со средним значением и стандартным отклонением выглядит следующим образом:

    Пятизначная сводка для нормального распределения

    \(мин = \мю — 3\сигма\)

    \(Q_{1} = \мю — 0,67448\сигма\)

    \(мед = \му \)

    \(Q_{3} = \мю + 0,67448\сигма\)

    \(макс. = \мю + 3\сигма\)

    Пример \(\PageIndex{3}\): вычисление сводки пяти чисел для нормального распределения

    Предположим, что ваш класс прошел тест, средний балл составил 75 %, а стандартное отклонение — 5 %. Если результаты теста следуют примерно нормальному распределению, найдите сводку из пяти чисел.

    Среднее значение равно \(\mu = 75 \%\), а стандартное отклонение равно \(\sigma = 5 \%\). Таким образом, сводка из пяти чисел для этой задачи:

    .

    \(мин = 75 — 3(5) = 60 \%\)

    \(Q_{1} = 75 — 0,67448(5)\приблизительно 71,6 \%\)

    \(средн.