Задание 17 Экономические задачи ЕГЭ 2021 Практика.
Задание 17 Экономические задачи ЕГЭ 2021 Практика. | Университет СИНЕРГИЯВ задание 17 ЕГЭ математика профильный уровень предлагается решить задачу с экономическим содержанием. Раздел содержит 36 заданий. В задачах требуется найти процентную ставку, исходную сумму кредита, суммарные выплаты по кредиту и т. п. Задачи требуют оригинального подхода и отличаются от стандартных задач на простые и сложные проценты, поскольку не предполагают постоянного начисления процентов в конце периода. В заданиях 17−24 нужно определить выпуск продукции, который обеспечит максимальную прибыль. Задания 29−36 содержат задачи на формулу суммы бесконечно убывающей геометрической прогрессии. Даны решения всех задач.
Этот документ можно скачать по ссылке
Курс подготовки к ЕГЭ и ОГЭ. Идёт набор!
Я даю согласие на обработку персональных данных, согласен на получение информационных рассылок от Университета «Синергия» и соглашаюсь c политикой конфиденциальности.
Какую профессию можно получить, сдав обществознание и английский
25.10.2022
Из чего складывается проходной балл
30.06.2022
Что значит первичный балл в ЕГЭ
14.06.2022
Самые высокооплачиваемые профессии, связанные с биологией
14.06.2022
Распределение баллов ЕГЭ по русскому языку
14.04.2022
Куда можно поступить после 9 класса с обществознанием и информатикой
28.03.2022
Смотреть все
Всё нужное в твоём телефоне
Скачай приложение и узнавай самую актуальную информацию
ПОДБЕРИ КУРС ЕГЭ И ОГЭ
Ответь на пять вопросов и узнай, где будешь учиться!
Подобрать программуОбразование для карьеры
К каким профессиям вы более склонны?
ТехническимГуманитарнымТворческимМедицинским
Какой у вас уровень образования?
Без образованияШкола 9-11 классКолледжБакалавриатМагистратураАспирантура
Какой формат обучения вам подходит?
ОчноЗаочноОнлайнПо выходным дням
Вас интересуют бюджетные места?
ДаНет
И последний вопрос. Вы из Москвы?
Вы из Москвы?
ДаНет
Мы подобрали вам программу обучения
Заполните форму, чтобы узнать больше о программе и наших предложениях
Я даю согласие на обработку персональных данных, согласен на получение информационных рассылок от Университета «Синергия» и соглашаюсь c политикой конфиденциальности
Уважаемый посетитель!
Если у вас есть вопрос, предложение или жалоба, пожалуйста, заполните короткую форму и изложите суть обращения в текстовом поле ниже. Мы обязательно с ним ознакомимся и в 30-дневный срок ответим на указанный вами адрес электронной почты
Статус Абитуриент Студент Родитель Соискатель Сотрудник Другое
Филиал Абакан Актобе Алагир Алматы Алушта Анапа Ангарск Архангельск Армавир Асбест Астана Астрахань Атырау Баку Балхаш Барановичи Барнаул Белая Калитва Белгород Бельцы Берлин Бишкек Благовещенск Бобров Бобруйск Борисов Боровичи Бронницы Брянск Бузулук Чехов Челябинск Череповец Черкесск Дамаск Дербент Димитровград Дмитров Долгопрудный Домодедово Дубай Дубна Душанбе Екатеринбург Электросталь Елец Элиста Ереван Евпатория Гана Гомель Гродно Грозный Хабаровск Ханты-Мансийск Хива Худжанд Иркутск Истра Иваново Ижевск Калининград Карабулак Караганда Каракол Кашира Казань Кемерово Киев Кинешма Киров Кизляр Королев Кострома Красноармейск Краснодар Красногорск Красноярск Краснознаменск Курган Курск Кызыл Липецк Лобня Магадан Махачкала Майкоп Минеральные Воды Минск Могилев Москва Моздок Мозырь Мурманск Набережные Челны Нальчик Наро-Фоминск Нижневартовск Нижний Новгород Нижний Тагил Ногинск Норильск Новокузнецк Новосибирск Новоуральск Ноябрьск Обнинск Одинцово Омск Орехово-Зуево Орел Оренбург Ош Озёры Павлодар Пенза Пермь Петропавловск Подольск Полоцк Псков Пушкино Пятигорск Радужный Ростов-на-Дону Рязань Рыбинск Ржев Сальск Самара Самарканд Санкт-Петербург Саратов Сергиев Посад Серпухов Севастополь Северодвинск Щербинка Шымкент Симферополь Слоним Смоленск Солигорск Солнечногорск Ставрополь Сургут Светлогорск Сыктывкар Сызрань Тамбов Ташкент Тбилиси Терек Тихорецк Тобольск Тольятти Томск Троицк Тула Тверь Тюмень Уфа Ухта Улан-Удэ Ульяновск Ургенч Усть-Каменогорск Вёшенская Видное Владимир Владивосток Волгодонск Волгоград Волжск Воркута Воронеж Якутск Ярославль Юдино Жлобин Жуковский Златоуст Зубова Поляна Звенигород
Тип обращения Вопрос Предложение Благодарность Жалоба
Тема обращения Поступление Трудоустройство Обучение Оплата Кадровый резерв Внеучебная деятельность Работа автоматических сервисов университета Другое
* Все поля обязательны для заполнения
Я даю согласие на обработку персональных данных, согласен на получение информационных рассылок от Университета «Синергия» и соглашаюсь c политикой конфиденциальности
Экономическая задача при подготовке к ЕГЭ по математике профильного уровня | Статья по алгебре (11 класс):
УДК 378
ПАВЛОВА Т. А.
А.
кандидат технических наук, доцент, ФГКОУ Московское суворовское военное училище Министерства обороны Российской Федерации
Е-mail: [email protected]
UDC 378
PAVLOVA T. A.
candidate of technical Sciences, associate Professor, FSCI Moscow Suvorov military school of the Ministry of defence of the Russian Federation
E-mail: [email protected]
Экономическая задача при подготовке к ЕГЭ по математике профильного уровня
В статье анализируются экономические задачи по математике профильного уровня, методы их решения. Особое внимание уделяется взаимосвязи различных разделов математики при решении прикладных задач. Проанализрованы предлагаемые задания и рассмотрены основные ошибки.
Ключевые слова: ЕГЭ, экономические задачи, проценты, дисконтированный доход, оптимизация.
The article analyzes economic problems in mathematics of the profile level, methods of their solution. Special attention is paid to the relationship of various sections of mathematics in solving applied problems. The proposed tasks are analyzed and the main errors are considered.
The proposed tasks are analyzed and the main errors are considered.
Keywords: unified state exam, economic tasks, interest, discounted income, optimization
Анализ контрольно-измерительных материалов показывает, что не все разделы школьного курса математики изучены должным образом, особые трудности вызывают те задания, где наряду с применением знакомых формул требуется понять практическую составляющую задачи. К таким заданиям можно отнести задание 17 (экономические задачи) [1,2,3]. Особенностью экономических задач является составление уравнения или системы уравнений, связанных между собой определенными ограничениями, которые в дальнейшем необходимо исследовать на экстремум с использованием понятия производной или в ряде задач нахождения вершины параболы (если исследуемая функция является квадратичной). [5,6] К другому типу задач можно отнести задачи на кредиты, при решении которых использую понятие «процент», «сложный процент», дифференцированные и аннуитетные платежи. При решении используют формулу
, где S –конечная сумма, S0 – первоначальная сумма вклада, n –срок вклада, р-процентная ставка.
Задачи на кредитование являются наиболее часто встречающимися и поэтому учащиеся к ним привыкли, трудности возникают, когда встречаются так называемые нетипичные задачи. Разберем две из них. Особенностью их решения является то, что используются знания не только в области теории функций и построения графиков, но и основы линейного программирования, когда по рисунку необходимо найти оптимальные точки. [1, 2]
На свой день рождения Пятачок испек большой пирог массой 10 кг и пригласил 100 гостей, среди которых Винни-Пух, неравнодушный к сладостям. Именинник огласил правило деления пирога: первый гость отрезает себе кусок пирога размером 1%, второй гость отрезает себе кусок пирога размером 2% оставшейся части, третий гость отрезает себе кусок пирога размером 3% оставшейся части и так далее. Какое место по счету в очереди нужно занять Винни-Пуху, чтобы получить наибольший кусок пирога? [1]
Предложим самое очевидное и легкодоступное пониманию абитуриента решение.
Составим таблицу вычислений.
Номер гостя | Получил | Осталось |
1 | 0,01*10= 0,1 | 9,9 |
2 | 0,02*9,9=0,198 | 9,702 |
3 | 0,03*9,702=0,29106 | 9,41094 |
4 | 0,04*9,41094=0,3764376 | 9,0429624 |
5 | 0,05*9,0429624=0,4521481 | 8,5908143 |
6 | 0,06*8,5908143=0,5154488 | 8,0753655 |
7 | 0,07*8,0753655=0,5652755 | 7,52009 |
8 | 0,08*7,52009=0,6008072 | 6,9192828 |
9 | 0,09*6,9192828=0,6227354 | 6,2965474 |
10 | 0,1*6,2965474=0,6296547 | 5,6668927 |
11 | 0,11*5,6668927=0,6233581 | 5,0435346 |
… |
Заметим, что кусок пирога 11-го гостя меньше куска 10-го. Каждый следующий гость будет получать кусок пирога все меньше и меньше. Следовательно, Винни-Пуху надо становиться в очередь на 10-м месте.
Каждый следующий гость будет получать кусок пирога все меньше и меньше. Следовательно, Винни-Пуху надо становиться в очередь на 10-м месте.
Минус такого решения состоит в том, что приходится довольно много вычислять. Скорее всего, обучающийся будет вести вычисления в столбик и очень велик шанс допустить вычислительную ошибку. Кроме того, есть риск недосчитать до момента, когда достающаяся часть пирога уменьшается. Поэтому предложим другой способ решения, который вытекает из первого.
Будем рассматривать гостей, стоящих в очереди под номерами n-2, n-1, n. Пусть, после того как гостю под номером n-2 достался свой кусок пирога, остался кусок весом m кг. Тогда гостю под номером n-1 достанется (n-1)% от m кг, т.е. . После этого осталось .
Гостю под номером n достанется кусок пирога равный .
При оформлении задачи удобно составить таблицу:
Номер гостя | Получил | Осталось |
n-2 | m | |
n-1 | ||
n |
Разность между кусками пирога n-го и n-1-го гостя должны быть положительной, тогда
.
Следовательно, при .
Наибольшее натуральное значение в этом интервале n=10. Значит, 10-й по счету гость получит наибольший кусок пирога.
Следующий пример 17-й задачи показывает, что вопреки ожиданиям абитуриента он сталкивается не с экономической моделью и не с оптимизационной задачей, а с задачей 8-9-го класса, решение которой сводится к составлению уравнения прямой.
Авиарадар отслеживает рейс в текущий момент на карте мира. Самолет, который движется прямолинейно, во время первого измерения находился в 24 км к северу и 5 км к западу от радара, а во время второго измерения находился в 20 км к северу и км к западу от радара. Определите наименьшее расстояние, на которое самолет приблизится к радару.
Если задано уравнение прямой Ax+ By+ C = 0, то расстояние от точки (x0, y0) до прямой можно найти, используя следующую формулу
.
Отметим указанные точки в прямоугольной системе координат. Пусть начала координат совпадают с координатами метеостанции, как точка отсчета. Положительное направление оси Ох показывает направление на восток, отрицательное – на запад. Положительное направление оси Oy показывает направление на север, соответственно отрицательное – на юг. Таким образом, первое измерение дает нам координаты точки (-5;24), а второе измерение — точку с координатами (-3,5;20).
Положительное направление оси Ох показывает направление на восток, отрицательное – на запад. Положительное направление оси Oy показывает направление на север, соответственно отрицательное – на юг. Таким образом, первое измерение дает нам координаты точки (-5;24), а второе измерение — точку с координатами (-3,5;20).
Так как в задаче сказано, что самолет летит прямолинейно, то уравнение прямолинейного движения следует искать в виде уравнения с угловым коэффициентом Чтобы найти коэффициенты этого уравнения, подставим в него координаты точек (-5;24) и (-3,5;20), получим систему уравнений:
Подставляя найденные коэффициенты в уравнение получим
.
Следовательно, наименьшее расстояние, на которое самолет приблизится к радару, будет равно расстоянию от точки (0;0) до прямой
Ответ: км.
Анализ результатов решения экономических задач с достаточно высокой степенью вероятности позволяет судить о том, что основными трудностями при решении является построение математической модели задачи с учетом всех ограничений и применения различных разделов школьного курса математики (таких, например, как арифметическая и геометрическая прогрессия, теория функций, графическое изображение функций), не достаточно высокая математическая культура (допускались арифметические ошибки при решении). Следует отметить, что в целом результаты по заданию №17 оказались выше в сравнении с предыдущими годами, многие выпускники научились решать задачи такого уровня, особенно если условие было схожим с «эталонным».
Следует отметить, что в целом результаты по заданию №17 оказались выше в сравнении с предыдущими годами, многие выпускники научились решать задачи такого уровня, особенно если условие было схожим с «эталонным».
Библиографический список
- Лысенко, Ф.Ф. Математика. Подготовка к ЕГЭ-2020. Профильный уровень. 40 тренировочных вариантов по демоверсии 2020 года: учебно-методическое пособие /Ф.Ф. Лысенко, С.Ю. Кулабухов// Ростов-на-Дону: Легион, 2019. – 416 с.
- Попова, Р.В. Анализ выполнения заданий по математике с учетом результатов по административно-территориальным единицам./В.Р. Попова// Педагогические измерения. 2017. №1. С.56-65.
- Павлова, Т.А. Актуальные проблемы развития и качества образования в высшей школе на примере Орловской области. / Т.А. Павлова, М.Н. Уварова// Инновации в образовании. 2018. №3. С. 42-49.
- Павлова, Т.А. Олимпиада по математике в вузе. / Т.А. Павлова, М.Н. Уварова// Ученые записки Орловского государственного университета.
 Серия: Естественные, технические и медицинские науки. 2015. №4. С. 67-70.
Серия: Естественные, технические и медицинские науки. 2015. №4. С. 67-70. - Семенченко, М.А. Плюсы и минусы единого государственного экзамена по математике и пути их решения./М.А. Семенченко// В сборнике: Наука и образование: сохраняя прошлое, создаем будущее. Сборник статей XIII Международной научно-практической конференции: в 3 ч. 2017. С.14-17.
Математическая экономика: определение, использование и критика
Что такое математическая экономика?
Математическая экономика — это метод экономики, который использует математические принципы и инструменты для создания экономических теорий и исследования экономических затруднений. Математика позволяет экономистам создавать точно определенные модели, из которых с помощью математической логики могут быть получены точные выводы, которые затем могут быть проверены с использованием статистических данных и использованы для количественного прогнозирования будущей экономической деятельности.
Сочетание статистических методов, математики и экономических принципов позволило разработать эконометрику. Достижения в области вычислительной мощности, методов работы с большими данными и других передовых математических приложений сыграли большую роль в превращении количественных методов в стандартный элемент экономики.
Достижения в области вычислительной мощности, методов работы с большими данными и других передовых математических приложений сыграли большую роль в превращении количественных методов в стандартный элемент экономики.
Ключевые выводы
- Математическая экономика — это форма экономики, которая опирается на количественные методы для описания экономических явлений.
- Хотя на экономическую дисциплину сильно влияет предвзятость исследователя, математика позволяет экономистам точно определять и проверять экономические теории на реальных данных.
- Решения по экономической политике редко принимаются без математического моделирования для оценки их воздействия, а новые статьи по экономике редко публикуются без математических расчетов.
Понимание математической экономики
Математическая экономика опирается на определение всех соответствующих допущений, условий и причинно-следственных структур экономических теорий в математических терминах.
До конца 19 века экономическая наука в значительной степени полагалась на словесные, логические аргументы, ситуационные объяснения и выводы, основанные на неофициальных данных, чтобы попытаться понять экономический феномен. Экономисты часто боролись с конкурирующими моделями, способными объяснить одну и ту же повторяющуюся взаимосвязь, называемую эмпирической закономерностью, но не могли окончательно определить степень связи между центральными экономическими переменными.
В то время математическая экономика была отклонением в том смысле, что она предлагала формулы для количественной оценки изменений в экономике. Это вернулось в экономику в целом, и теперь большинство экономических теорий имеют те или иные математические доказательства.
От Мейн-стрит до Уолл-стрит и Вашингтона лица, принимающие решения, привыкли к жестким количественным прогнозам экономики из-за влияния математической экономики. Например, при определении денежно-кредитной политики центральные банки хотят знать вероятное влияние изменений официальных процентных ставок на инфляцию и темпы роста экономики. Именно в таких случаях экономисты обращаются к эконометрике и математической экономике.
Эконометрика
Эконометрика пытается превратить абстрактные экономические теории в полезные инструменты для ежедневного принятия экономических решений, сочетая математическую экономику со статистическими методами. Цель эконометрики в целом состоит в преобразовании качественных утверждений, таких как «отношение между двумя или более переменными является положительным», в количественные утверждения, такие как «потребительские расходы увеличиваются на 95 центов на каждый доллар увеличения располагаемого дохода».
Смотреть сейчас: что такое эконометрика?
Эконометрика особенно полезна при решении задач оптимизации, когда, например, лицо, определяющее политику, ищет наилучшую корректировку из ряда корректировок, чтобы повлиять на конкретный результат.
Поскольку мы наводнены все большим количеством информации, эконометрические методы стали повсеместными в экономике. Как сказано в книге Сток и Уотсон
Решения в области экономической политики редко принимаются без эконометрического моделирования для оценки их воздействия, а статьи по эмпирической экономике редко публикуются без какого-либо эконометрического содержания.
Критика математической экономики
Критики предупреждают, что математическая экономика может затемнить, а не прояснить экономическую теорию, и создать ложный вид точности, уверенности как в теоретической, так и в эмпирической экономике.
К сожалению, из-за того неизбежного факта, что экономические явления всегда включают в себя субъективные и ненаблюдаемые элементы, которые имеют место в человеческом сознании изучаемых экономических агентов, такое точное определение никогда не бывает полностью возможным в экономической науке. Это неизбежно приводит к двусмысленности интерпретации и искажению факторов, которые не могут быть легко вписаны в математическую или эконометрическую модель.
Именно такой двусмысленности и подтасовок стремится избежать практика математической экономики в своем стремлении дать жесткие и точные ответы на вопросы лиц, принимающих решения, и политиков. В лучшем случае это резко ограничивает уровень уверенности в выводах, полученных таким образом, а в худшем случае сложная математика может использоваться для сокрытия принципиально вводящих в заблуждение результатов и выводов.
В результате экономисты и те, кто полагаются на них как на экспертов и авторитетов, как правило, замалчивают эти вопросы в интересах уверенности и уверенности в продвижении предпочитаемых ими экономических объяснений и политических предписаний.
Экзамены по программе | Центрально-европейский университет
- Домашний
- Прием
- Программы для выпускников
- После подачи заявки
- Экзамены по программе
В некоторых случаях академические программы имеют дополнительные вступительные требования (тесты, экзамены, собеседования и т. д.) в дополнение к общим требованиям CEU. Подробнее см. на веб-сайте соответствующей программы.
Индивидуальные собеседования
Некоторые факультеты или школы CEU могут проводить собеседования с некоторыми из предварительно отобранных кандидатов в рамках процесса отбора. Индивидуальные собеседования начинаются вскоре после первого рассмотрения файлов заявки и продолжаются до соответствующей даты уведомления. Каждое подразделение свяжется с подходящими кандидатами для принятия необходимых мер. В случае интервью по скайпу или телефону могут быть приняты меры для приглашения кандидатов в место, где их личность может быть проверена.
Каждое подразделение свяжется с подходящими кандидатами для принятия необходимых мер. В случае интервью по скайпу или телефону могут быть приняты меры для приглашения кандидатов в место, где их личность может быть проверена.
Магистр экономики: экзамен по математике или GRE
Если вы подаете заявление на получение степени магистра экономики, вы должны сдать экзамен по математике (или представить общие баллы GRE вместе с заявлением). Экзамен по математике предназначен для проверки кандидатов по базовому исчислению, теории вероятностей и линейной алгебре и организован CEU 17 февраля 2023 г. .
Кандидат экономических наук: GRE
Кандидаты на получение степени кандидата экономических наук должны представить результаты теста GRE вместе с заявкой.
Кандидатская степень в области делового администрирования: GMAT или GRE
Кандидаты на получение степени доктора наук в области делового администрирования должны предоставить результаты теста GMAT или GRE вместе с заявкой.
MS в области бизнес-аналитики и MS в области финансов: экзамен по математике GMAT или GRE или CEU
Общий тест GMAT или GRE может быть заменен тестом по математике CEU: формат, длина и сложность теста сопоставимы с количественным раздел GMAT. Если вы хорошо подготовлены к GMAT, вы также успешно сдадите тест CEU по математике. См. образец теста здесь. Тест CEU по математике организован CEU онлайн 10 февраля 2023 г. для кандидатов , подавших заявку до 1 февраля 2023 г.
Мы не отменяем это требование для кандидатов с опытом работы.
Степень магистра в области социальных данных: экзамен по математике GMAT или GRE или CEU
Если вы не получили степень бакалавра или магистра в области науки о данных, математики, статистики, экономики, физики, информатики или других количественных областях, отправьте сертификат GMAT с баллом не менее 600 (или эквивалентом GRE ; пожалуйста, проверьте эквивалент GMAT вашего балла GRE в инструменте сравнения GRE®).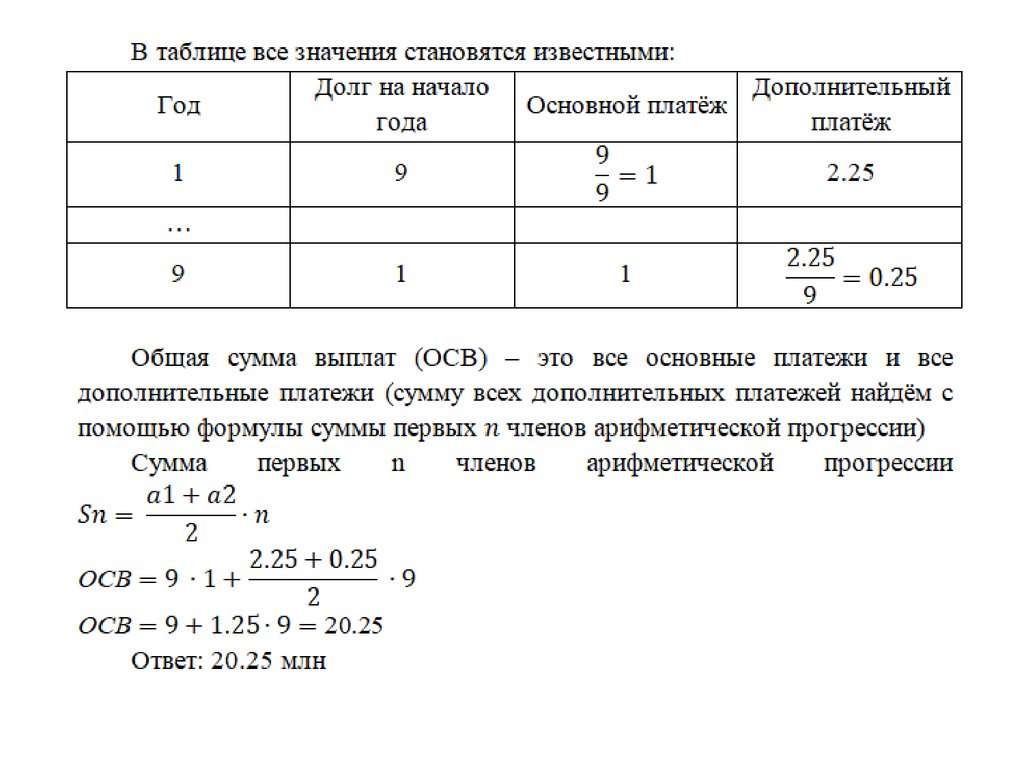

 Серия: Естественные, технические и медицинские науки. 2015. №4. С. 67-70.
Серия: Естественные, технические и медицинские науки. 2015. №4. С. 67-70.
Leave A Comment