Задания с выбором ответа.
1. Координата тела меняется с течением времени согласно закону x=5−2,5t, где все величины выражены в СИ. Какой из графиков отражает зависимость проекции скорости движения тела от времени?
1) 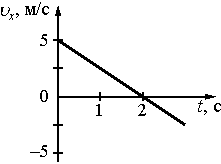
2) 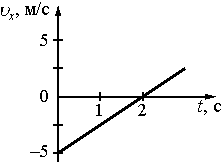
3) 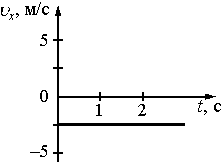
4) 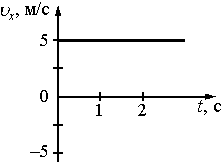
2. На рисунке приведён график зависимости координаты тела от времени при его прямолинейном движении по оси
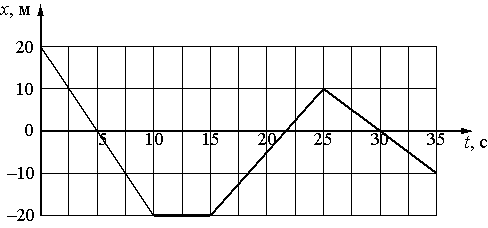
Какой из графиков соответствует зависимости от времени проекции υx скорости тела в промежутке времени от 25 до 30 с?
1) 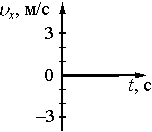
2) 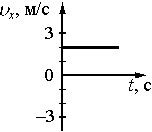
3) 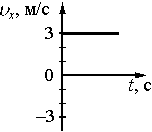
4) 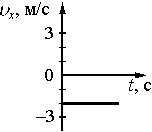
3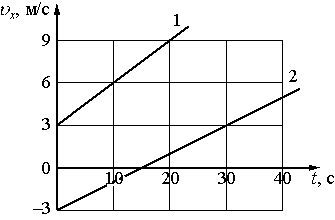 ) Два тела движутся по оси Ox. На рисунке приведены графики зависимости проекций их скоростей υx от времени t. На основании графиков выберите два верных утверждения о движении тел.
) Два тела движутся по оси Ox. На рисунке приведены графики зависимости проекций их скоростей υx от времени t. На основании графиков выберите два верных утверждения о движении тел.
1)Проекция ax ускорения тела 1 меньше проекции ax ускорения тела 2.
2)Проекция ax
3) Тело 2 в момент времени 15 с находилось в начале отсчёта.
4) Первые 15 с тела двигались в разные стороны.
5) Проекция ax ускорения тела 2 равна 0,1 м/с2.
4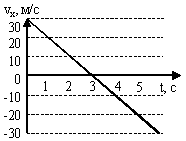 . Стрела пущена вертикально вверх. Проекция ее скорости на вертикальное направление меняется со временем согласно графику на рисунке. В какой момент времени стрела достигла максимальной высоты?
. Стрела пущена вертикально вверх. Проекция ее скорости на вертикальное направление меняется со временем согласно графику на рисунке. В какой момент времени стрела достигла максимальной высоты?
1)
1,5 с
2)
3 с
3)
4,5 с
4)
6 с
5. Зависимость координаты от времени для некоторого тела описывается уравнением x=8t−t2 , где все величины выражены в СИ. В какой момент времени скорость тела равна нулю?
1)
8 с
2)
4 с
3)
3 с
4)
0 с
6. От высокой скалы откололся и стал свободно падать камень. Какую скорость он будет иметь через 3 с от начала падения?
1)
30 м/с
2)
10 м/с
3)
3 м/с
4)
2 м/с
7. Тело брошено вертикально вверх с начальной скоростью 20 м/с. Каков модуль скорости тела через 0,5 с после начала движения? Сопротивление воздуха не учитывать.
1)
5 м/с
2)
10 м/с
3)
15 м/с
4)
20 м/с
8. При прямолинейном равноускоренном движении с нулевой начальной скоростью путь, пройденный телом за две секунды с начала движения, больше пути, пройденного за первую секунду, в
1)
2 раза
2)
3 раза
3)
4 раза
4)
5 раз
9. Камень, брошенный вертикально вверх с поверхности Земли со скоростью 20 м/с, упал обратно на Землю. Сопротивление воздуха мало. Камень находился в полете примерно
1)
1 с
2)
2 с
3)
4 с
4)
8 с
10. Зависимость пути от времени прямолинейно движущегося тела имеет вид: s(t) = 2t + 3t
1)
1 м/с2
2)
2 м/с2
3)
3 м/с2
4)
6 м/с2
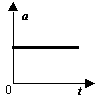
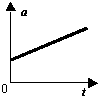
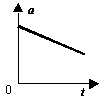
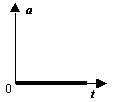
11 На рисунках изображены графики зависимости модуля ускорения от времени для разных видов движения. Какой график соответствует равномерному движению?
1) 
2) 
3) 
4) 
12. Скорость пули при вылете из ствола пистолета равна 250 м/с. Длина ствола 0,1 м. Каково примерно ускорение пули внутри ствола, если считать ее движение равноускоренным?
1)
312 км/с2
2)
114 км/с2
3)
1248 км/с2
4)
100 м/с2
13. Одной из характеристик автомобиля является время t его разгона с места до скорости 100 км/ч. Два автомобиля имеют такие времена разгона, что
t1 = 2t2. Ускорение первого автомобиля по отношению к ускорению второго автомобиля
1)
меньше в 2 раза
2)
больше в 2√2 раз
3)
больше в 2 раза
4)
больше в 4 раза
14. Мотоциклист и велосипедист одновременно начинают равноускоренное движение из состояния покоя. Ускорение мотоциклиста в 3 раза больше, чем у велосипедиста. Во сколько раз больше времени понадобится велосипедисту, чтобы достичь скорости 50 км/ч?
1)
в 1/3 раза
2)
в 3√3 раза
3)
в 3 раза
4)
в 9 раз
15. К.Э. Циолковский в книге «Вне Земли», описывая полет ракеты, отмечал, что через 10 с после старта ракета находилась на расстоянии 5 км от поверхности Земли. С каким ускорением двигалась ракета?
1)
1000 м/с2
2)
500 м/с2
3)
100 м/с2
4)
50 м/с2
16. Ускорение велосипедиста на одном из спусков трассы равно 1,2 м/с2. На этом спуске его скорость увеличивается на 18 м/с. Велосипедист заканчивает свой спуск после его начала через
1)
0,07 с
2)
7,5 с
3)
15 с
4)
21,6 с
1) 
2) 
3) 
4) 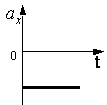
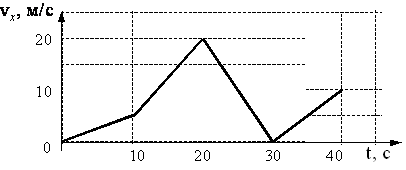
18. Автомобиль движется по прямой улице. На графике представлена зависимость скорости автомобиля от времени. Модуль ускорения максимален на интервале времени
1)
от 0 с до 10 с
2)
от 10 с до 20 с
3)
от 20 с до 30 с
4)
от 30 с до 40 с

19. На рисунке представлен график зависимости пути S велосипедиста от времени t. В каком интервале времени после начала движения велосипедист не двигался?
1)
от 0 с до 1 с
2)
от 1 с до 3с
3)
от 3 с до 5с
4)
от 5 с и далее
2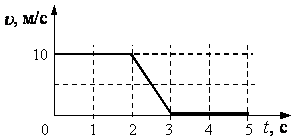 0. На рисунке представлен график зависимости скорости u автомобиля от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от 0 до 3 с.
0. На рисунке представлен график зависимости скорости u автомобиля от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от 0 до 3 с.
1)
20 м
2)
10 м
3)
15 м
4)
25 м
2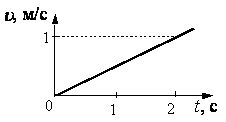
1)
0 м/с2
2)
0,5 м/с2
3)
1 м/с2
4)
2 м/с2
22. Тело упало с некоторой высоты с нулевой начальной скоростью и при ударе о землю имело скорость 40 м/с. Чему равно время падения? Сопротивлением воздуха пренебречь.
1)
0,25 с
2)
4 с
3)
40 с
4)
400 с
23. Автомобиль движется по закруглению дороги радиусом 20 м с центростремительным ускорением 5 м/с2. Скорость автомобиля равна
1)
12,5 м/с
2)
10 м/с
3)
5 м/с
4)
4 м/с
24. Две материальные точки движутся по окружностям радиусами R1 и R2, причем R2 = 2R1. При условии равенства линейных скоростей точек их центростремительные ускорения связаны соотношением
1)
a1 = 2a2
2)
a1 = a2
3)
a1 = ½ a2
4)
a1 = 4a2
25. Точка движется с постоянной по модулю скоростью v по окружности радиуса R. Как изменится центростремительное ускорение точки, если ее скорость увеличить вдвое, а радиус окружности вдвое уменьшить?
1)
уменьшится в 2 раза
2)
увеличится в 2 раза
3)
увеличится в 4 раза
4)
увеличится в 8 раза
26. Точка движется по окружности радиуса R со скоростью v. Как изменится центростремительное ускорение точки, если скорость уменьшить в 2 раза, а радиус окружности в 2 раза увеличить?
1)
уменьшится в 2 раза
2)
увеличится в 2 раза
3)
уменьшится в 8 раз
4)
не изменится
27. Материальная точка равномерно движется со скоростью по окружности радиусом r. Если скорость точки будет вдвое больше, то модуль ее центростремительного ускорения
1)
не изменится
2)
уменьшится в 2 раза
3)
увеличится в 2 раза
4)
увеличится в 4 раза
28. Шарик движется по окружности радиусом r со скоростью . Как изменится его центростремительное ускорение, если радиус окружности увеличить в 3 раза, оставив скорость шарика прежней?
1)
увеличится в 3 раза
2)
уменьшится в 3 раза
3)
увеличится в 9 раза
4)
уменьшится в 9 раза
Задания с кратким ответом.
1. Мимо остановки по прямой улице проезжает грузовик со скоростью 10 м/с. Через 5 с от остановки вдогонку грузовику отъезжает мотоциклист, движущийся с ускорением 3 м/с2. На каком расстоянии от остановки мотоциклист догонит грузовик?
2. Материальная точка, двигаясь равноускоренно по прямой, за время t увеличила скорость в 3 раза, пройдя путь 20 м. Найдите t, если ускорение точки равно 5 м/с2.
3. За 2 с прямолинейного равноускоренного движения тело прошло 20 м, увеличив свою скорость в 3 раза. Определите начальную скорость тела.
4. На последнем километре тормозного пути скорость поезда уменьшилась на 10 м/с. Определите скорость в начале торможения, если общий тормозной путь поезда составил 4 км, а торможение было равнозамедленным.
5. Небольшой камень, брошенный с ровной горизонтальной поверхности земли под углом к горизонту, упал обратно на землю в 20 м от места броска. Сколько времени прошло от броска до того момента, когда его скорость была направлена горизонтально и равна 10 м/с?
6 . Две шестерни, сцепленные друг с другом, вращаются вокруг неподвижных осей (см. рисунок). Бóльшая шестерня радиусом 10 см делает 20 оборотов за 10 с, а частота обращения меньшей шестерни равна 5 с–1. Каков радиус меньшей шестерни? Ответ укажите в сантиметрах.
. Две шестерни, сцепленные друг с другом, вращаются вокруг неподвижных осей (см. рисунок). Бóльшая шестерня радиусом 10 см делает 20 оборотов за 10 с, а частота обращения меньшей шестерни равна 5 с–1. Каков радиус меньшей шестерни? Ответ укажите в сантиметрах.
Задания с развернутым ответом.
1. Тело, свободно падающее с некоторой высоты без начальной скорости, за время = 1 с после начала движения проходит путь в n = 5 раз меньший, чем за такой же промежуток времени в конце движения. Найдите полное время движения.
2. Тело, свободно падающее с некоторой высоты, первый участок пути проходит за время τ = 1 с, а такой же последний – за время ½ τ. Найдите полное время падения t, если начальная скорость равна нулю.
3. Маленький шарик падает сверху на наклонную плоскость и упруго отражается от неё. Угол наклона плоскости к горизонту равен 30°. На какое расстояние по горизонтали перемещается шарик между первым и вторым ударами о плоскость? Скорость шарика в момент первого удара направлена вертикально вниз и равна 1 м/с.
Кинематика Движение по окружности Страница из
Кинематика 2 вариант
ГРАФИКИ
Определение вида движения по графику
- На рисунках изображены графики зависимости модуля ускорения от времени для разных видов движения. Какой график соответствует равномерному движению?
1) 1 2) 2 3) 3 4) 4
- Какой из графиков зависимости проекции скорости от времени (рис.) соответствует движению тела, брошенного вертикально вверх с некоторой скоростью (ось Y направлена вертикально вверх)?
1) 1 2) 2 3) 3 4) 4
Определение и сравнение характеристик движения по графику
- На рисунке изображен график зависимости скорости движения тел от времени. Чему равно ускорение тела?
- 1 м/с2
- 2 м/с2
- 3 м/с2
- 18 м/с2
- На рисунке представлен график движения автобуса из пункта А в пункт Б и обратно. Пункт А находится в точке х = 0, а пункт Б в точке х = 30 км. Чему равна скорость автобуса на пути из А в Б?
- 40 км/ч
- 50 км/ч
- 60 км/ч
- 75 км/ч
- Автомобиль движется по прямой улице. На графике представлена зависимость скорости автомобиля от времени. Модуль ускорения максимален в интервале времени
- от 0 с до 10 с
2) от 10 с до 20 с
3) от 20 с до 30 с
4) от 30 с до 40 с
- На рисунке представлен график зависимости пути S велосипедиста от времени t. Определите интервал времени, когда велосипедист двигался со скоростью 2,5 м/с.
- от 5 с до 7 с
- от 3 с до 5 с
- от 1 с до 3 с
- от 0 до 1 с
7.Материальная точка движется прямолинейно с ускорением, зависимость от времени которого приведена на рисунке. Начальная скорость точки равна 0. Какая точка на графике соответствует максимальной скорости материальной точки:
- 2
- 3
- 4
- 5
Составление кинематических зависимостей (функций зависимости кинематических величин от времени) по графику
8.На рис. изображен график зависимости координаты тела от времени. Определите кинематический закон движения этого тела
- x(t) = — 2 + 2t
- x(t) = – 2 – 2t
- x(t) = 2 – 2t
- x(t) = 2 + 2t
Определение перемещения и пути по графику
9.Камень брошен вертикально вверх. Проекция его скорости на вертикальное направление изменяется со временем согласно графику на рисунке. Чему равен путь, пройденный камнем за первые 3 с?
- 30 м
- 45 м
- 60 м
- 90 м
10.Камень брошен вертикально вверх. Проекция его скорости на вертикальное направление изменяется со временем согласно графику на рисунке к заданию 9. Чему равно перемещение камня за 6 с?
- 0 м
- 30 м
- 45 м
- 60 м
- На рисунке дан график зависимости проекции скорости тела, движущегося вдоль оси Ох, от времени. Чему равен путь, пройденный телом к моменту времени t = 10 с?
- 1м 2) 6м 3) 7м 4) 13м
УРАВНЕНИЯ
- Движение самолета при разбеге задано уравнением: x = 100 + 0,85t2, м Чему равно ускорение самолета?
- 0 м/с2
- 0,85 м/с2
- 1,7 м/с2
- 100 м/с2
13.Уравнение зависимости проекции скорости движущегося тела от времени: vx = 5 — 3t (м/с). Каково соответствующее уравнение проекции перемещения тела?
1) Sx = 5t — 3t2 2) Sx = — 3t + 10t2
3) Sx = 5t — 6t2 4) Sx = 5t — 1,5t2
14.Зависимость координаты от времени для некоторого тела описывается уравнением х = 8t – t2 . В какой момент времени скорость тела равна нулю?
- 8 с
- 4 с
- 3 с
- 0 c
ТАБЛИЦЫ
15.Четыре тела двигались по оси Ох. В таблице представлена зависимость их координат от времени.
t, с | 0 | 1 | 2 | 3 | 4 | 5 |
x1 м | 6 | 4 | 2 | 0 | -2 | -4 |
х2, м | 3 | 3 | 3 | 3 | 3 | 3 |
х3, м | 0 | 1 | 4 | 9 | 16 | 25 |
х4, м | 0 | 2 | 0 | -2 | 0 | 2 |
У какого из тел скорость могла быть постоянна и отлична от нуля?
1) 1 2) 2 3) 3 4) 4
Движение по окружности
1.При равномерном движении по окружности модуль вектора изменения скорости при перемещении из точки А в точку В (см. рис.) равен
l) 0 2) v 3) v 4) 2v
2.Какая из физических величин не изменяется при равномерном движении по окружности?
- Перемещение
- Ускорение
- Скорость
- Все перечисленные выше величины изменяются
3.Автомобиль движется по закруглению дороги радиусом 20 м с центростремительным ускорением 5 м/с2. Скорость автомобиля равна
- 12,5 м/с
- 10 м/с
- 5 м/с
- 4 м/с
4.Материальная точка, двигаясь равномерно по окружности против часовой стрелки, через 3 секунды первый раз попала из точки А в точку В (см. рисунок). Частота обращения точки равна
- 1/12 с-1
- 1/4 с-1
- 1/3 с-1
- 1/2 с-1
5.На рисунке изображены положения шарика, равномерно движущегося по окружности радиусом 1 м в горизонтальной плоскости. Положения шарика зафиксированы через каждые 0,1 с. Каков модуль скорости шарика?
1) 1,07 м/с 2) 3,14 м/с 3) 6,28 м/с 4) 31,4 м/с
6.Точка движется с постоянной по модулю скоростью v по окружности радиуса R. Как изменится центростремительное ускорение точки, если ее скорость увеличить вдвое, а радиус окружности вдвое уменьшить?
1)уменьшится в 2 раза
3)увеличится в 4 раза
2)увеличится в 2 раза
4)увеличится в 8 раз
- Две материальные точки движутся по окружностям радиусами R1 и R2 = 3R1 с одинаковой угловой скоростью. Отношение модулей их центростремительных ускорений a2 / a1 равно
- 9
- 3
- 1
Блок В
Тело брошено под углом к горизонту. Как меняются в ходе полета до верхней точки траектории модуль его скорости, проекция скорости на горизонтальную ось и ускорение?
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами. Цифры могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ИХ ИЗМЕНЕНИЕ | ||
А) | модуль скорости тела | 1) | Не изменяется |
Б) | проекция скорости тела на горизонтальную ось | 2) | Увеличивается |
В) | модуль ускорения тела | 3) | Уменьшается |
Модуль скорости тела | Проекция скорости тела на горизонтальную ось | Модуль ускорения тела |
ЕГЭ Решение задач по физике. Механика 11-20
24 июня, 2019| Админ|
ЕГЭ Решение задач по физике. Механика 11-20
ЕГЭ Решение задач по физике. Глава 1. МЕХАНИКА (кинематика, динамика, статика, колебания и волны). Задачи ЕГЭ по физике М11 — М20 с указаниями, подсказками, ответами и решениями (ГДЗ по ЕГЭ). Материал для подготовки к ЕГЭ по физике может быть использован репетиторами, учителями и самими учащимися.
Вернуться к Списку заданий тренинга по физике.
Задачи по физике. Механика 11-20
Задача 1.11. Тело массой m = 400 г брошено с некоторой высоты по направлению к земле под углом α = 30° к горизонту. Начальная скорость тела ʋ0 = 20 м/с. Определите, через сколько времени скорость тела будет направлена под углом β = 60° к горизонту. Определите изменение потенциальной энергии тела за это время. Ускорение свободного падения g ≈ 10 м/с2.Указания (подсказка)
Покажите на рисунке направление горизонтальной, вертикальной и полной скоростей тела в начальный момент времени и в искомый момент времени. Учтите, что горизонтальная составляющая скорости не изменяется, а вертикальная увеличивается с течением времени. Вспомните определение тангенса угла и из треугольника скоростей получите уравнение для времени. Изменение потенциальной энергии определите из закона сохранения энергии или как работу силы тяжести за указанный промежуток времени.
Решение и ответ
Задача 1.12. Тело массой m = 0,5 кг брошено со скоростью ʋ0 = 20 м/с под углом α = 30° к горизонту. Определите наибольшую высоту полета н изменение импульса за время полета. Сопротивлением воздуха можно пренебречь. Примите g ≈ 10 м/с2.Указания (подсказка)
Наибольшую высоту подъема определите или из уравнения движения, или из закона сохранения энергии (см. задачу 1.10). Изменение импульса определите как разность векторов конечного и начального импульсов. Внимание! Не забывайте о векторном характере импульса. Можно воспользоваться вторым законом Ньютона. Изменение импульса системы равно импульсу внешней силы. Этой силой является сила тяжести.
Решение и ответ
Задача 1.13. Катер пересекает реку шириной l = 360 м. Скорость течения ʋ = 2 м/с. Рулевой держит курс перпендикулярно течению. Двигатель обеспечивает постоянное ускорение а = 0,1 м/с2. Начальная скорость катера равна нулю. Определите, через сколько времени катер пересечет реку. На какое расстояние он будет снесен течением?Указания (подсказка)
Катер участвует в двух движениях: по течению реки он движется равномерно, а перпендикулярно течению относительно воды его движение равноускоренное.
Решение и ответ
Задача 1.14. Из окна вагона поезда, движущегося по горизонтальной дороге со скоростью ʋ = 54 км/ч, бросают в горизонтальном направлении предмет. Предмет падает на землю на расстоянии s = 12,1 м от места, над которым он находился в момент бросания. Определите скорость ʋ0 предмета относительно вагона сразу после бросания, если она была направлена перпендикулярно скорости движения поезда. Высота окна над поверхностью земли H = 2,5 м. Сопротивлением воздуха можно пренебречь.Указания (подсказка)
Необходимо воспользоваться принципом относительности движения, рассматривая движение одного тела относительно другого или относительно Земли. Вспомните правило сложения скоростей: скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости этой подвижной системы относительно неподвижной. Помните о векторном характере скоростей. Если вам трудно запомнить такие «сложные» закономерности, вспомните простое правило сложения скоростей для лодки, переплывающей реку: течение ее сносит вдоль берега, а рулевой стремится переправиться на противоположный берег. И тогда любая задача, связанная с относительностью движения, будет вами решена.
Решение и ответ
Задача 1.15. Тело 1 бросают вертикально вверх с начальной скоростью ʋ0 = 30 м/с. Тело 2, находящееся на высоте Н = 40 м по вертикали и на расстоянии l = 20 м по горизонтали от точки бросания тела 1, бросают горизонтально со скоростью ʋ1 =20 м/с. Определите, с каким запаздыванием или опережением т надо бросить тело 2, чтобы тела столкнулись в полете. Ускорение свободного падения g ≈ 10 м/с2.Указания (подсказка)
Необходимо воспользоваться принципом относительности движения, рассматривая движение одного тела относительно другого или относительно Земли. Вспомните правило сложения скоростей: скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости этой подвижной системы относительно неподвижной. Помните о векторном характере скоростей. Если вам трудно запомнить такие «сложные» закономерности, вспомните простое правило сложения скоростей для лодки, переплывающей реку: течение ее сносит вдоль берега, а рулевой стремится переправиться на противоположный берег.
Решение и ответ
Задача 1.16. Человек начинает подниматься по движущемуся вверх эскалатору метро с ускорением а = 0,21 м/с2. Добежав до середины эскалатора, он останавливается, поворачивает и начинает спускаться вниз с тем же ускорением. Определите, сколько времени человек находится на эскалаторе. Длина эскалатора l = 100 м, а скорость его движения ʋ = 2 м/с.Указания (подсказка)
Смотрите указание к задаче 1.14
Решение и ответ
Задача 1.17. Самолет, пролетая над зенитной батареей на высоте H = 1 км, начинает пикировать с выключенным двигателем на цель со скоростью ʋ1 = 540 км/ч, направленной под углом а = 60° к горизонту. Самолет сбивают выстрелом из орудия, произведенным в тот момент времени, когда он находился над батареей. Определите, на каком расстоянии от батареи, считая по горизонтальному направлению, снаряд попал в сaмолет. Скорость снаряда при вылете из ствола орудия ʋ2 = 600 м/с. Сопротивлением воздуха можно пренебречь.Указания (подсказка)
Смотрите указание к задаче 1.14. Выберите систему отсчета, связанную с Землей, и составьте уравнения движения для снаряда и самолета. Равенство соответствующих координат и означает момент столкновения.
Решение и ответ
Задача 1.18. Две лодки переплывают реку, отправляясь одновременно из пунктов A и В, расположенных на противоположных берегах реки против друг друга. Скорость течения реки ʋp = 20 м/мин, ширина реки l = 200 м. Скорости лодок относительно воды равны ʋ1 = 15 м/мин, ʋ2 = 20 м/мин. Первая лодка начала движение перпендикулярно течению, а вторая держит курс под углом α = 150° к скорости течения реки. Определите, на каком расстоянии от пункта А будет находиться первая лодка, когда расстояние между лодками будет наименьшим.Указания (подсказка)
После построения векторов скоростей учтите, что наименьшее расстояние между лодками будет определяться перпендикуляром из точки А на направление относительной скорости для лодки, выходящей из пункта В. Для того чтобы это понять, мысленно остановите лодку в пункте А, тогда вторая лодка должна двигаться в направлении относительной скорости, это ее перемещение, а наименьшее расстояние есть перпендикуляр, опущенный из точки на выбранное направление!
Решение и ответ
Задача 1.19. Лодочник отплывает из пункта А, держа курс перпендикулярно берегу. Скорость течения реки ʋp = 2 м/с, ее ширина h = 144 м. Лодка в течение времени t1 движется равноускоренно с ускорением а = 1 м/с2, а затем в течение промежутка времени t2 движется равномерно и, наконец, в течение промежутка времени t3 – равнозамедленно с тем же ускорением а. Определите промежутки времени t1 и t2, если известно, что лодка пришла в пункт В, расположенный на противоположном берегу реки на расстоянии l = 80 м вниз по течению. Постройте траекторию движения лодки в системе координат (XOY), связанной с берегом.Указания (подсказка)
Выберите оси координат по течению реки и в перпендикулярном направлении. Запишите уравнения движения по обеим осям. Решите полученную систему.
Решение и ответ
Задача 1.20. Из танка, движущегося со скоростью ʋ = 70 км/ч, стреляют по горизонтально летящему на высоте Н = 6 км самолету. Скорость самолета ʋ = 790 км/ч, а ее направление совпадает с направлением движения танка. Определите угол вылета α снаряда относительно горизонта. Известно, что в момент выстрела самолет находился над танком, а снаряд попал в самолет в высшей точке траектории.Указания (подсказка)
Выберите систему отсчета, связанную с Землей, и составьте уравнения движения для снаряда и самолета. Равенство соответствующих координат и означает момент столкновения.
Решение и ответ
Вы смотрели «ЕГЭ Решение задач по физике. Механика 11-20». Задачи ЕГЭ по физике с указаниями, подсказками, ответами и решениями (ГДЗ по ЕГЭ). Материал для подготовки к ЕГЭ по физике.
Вернуться к Списку заданий тренинга по физике.
Просмотров: 2 948
Метки: задачиНавигация по записям
Кинематика. Теория и формулы для ЕГЭ + шпаргалка
КИНЕМАТИКА.
Теория и формулы (кратко и сжато)
Кинематика – раздел физики, изучающий способы математического описания движения без выяснения его причин.

Механическое движение – изменение положения тела относительно других тел с течением времени. Способы описания: словесный, табличный, графический, формулами.
Материальная точка – тело, собственными размерами которого в данных условиях можно пренебречь.
Траектория – линия, которую описывает материальная точка при своём движении в пространстве. По виду траектории все движения делятся на прямолинейные и криволинейные.
Система отсчёта – часы и система координат, связанные с условно выбираемым телом отсчёта (наблюдателем).

Относительность движения – различие скорости, направления и траектории движения в различных системах отсчёта.
Перемещение – вектор, проведённый из начального положения материальной точки в её конечное положение.

Типы движений
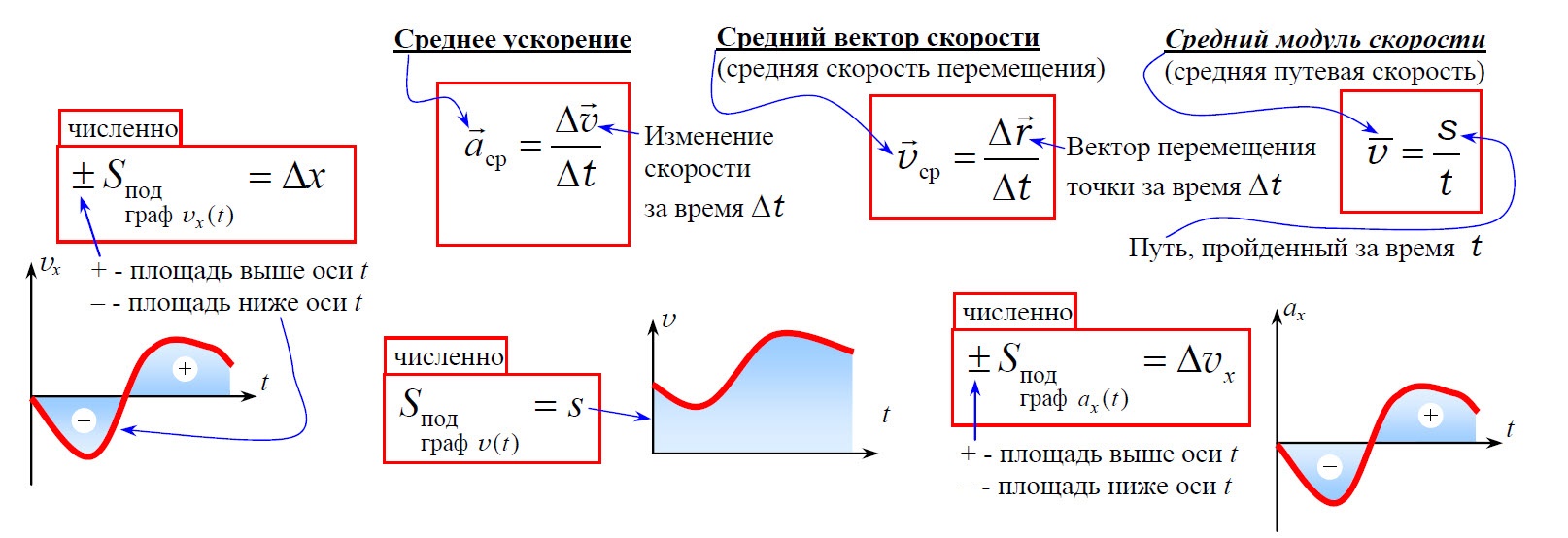
1. Равномерное движение
1.1. Равномерное прямолинейное движение
Равномерное движение – движение тела, при котором за равные интервалы времени оно преодолевает равные части пути.
Скорость равномерного движения равна отношению пройденного пути к интервалу времени, за который этот путь пройден.
Скорость равномерного прямолинейного движения равна отношению перемещения к интервалу времени его совершения.
Уравнение равно-прямолинейного движения x = xo + υoxt показывает, что координата линейно зависит от времени.
Мгновенная скорость равна отношению перемещения к бесконечно малому интервалу времени, за который оно произошло.
1.2 Равномерное движение по окружности (равномерное вращение)
Равномерное движение по окружности — это движение, при котором материальная точка за равные промежутки времени проходит равные по длине дуги окружности.
Равномерное движение тела по окружности — это частный и наиболее простой случай криволинейного движения. Хотя при таком движении модуль скорости остается постоянным, это движение с ускорением, которое является следствием изменения направления вектора скорости.
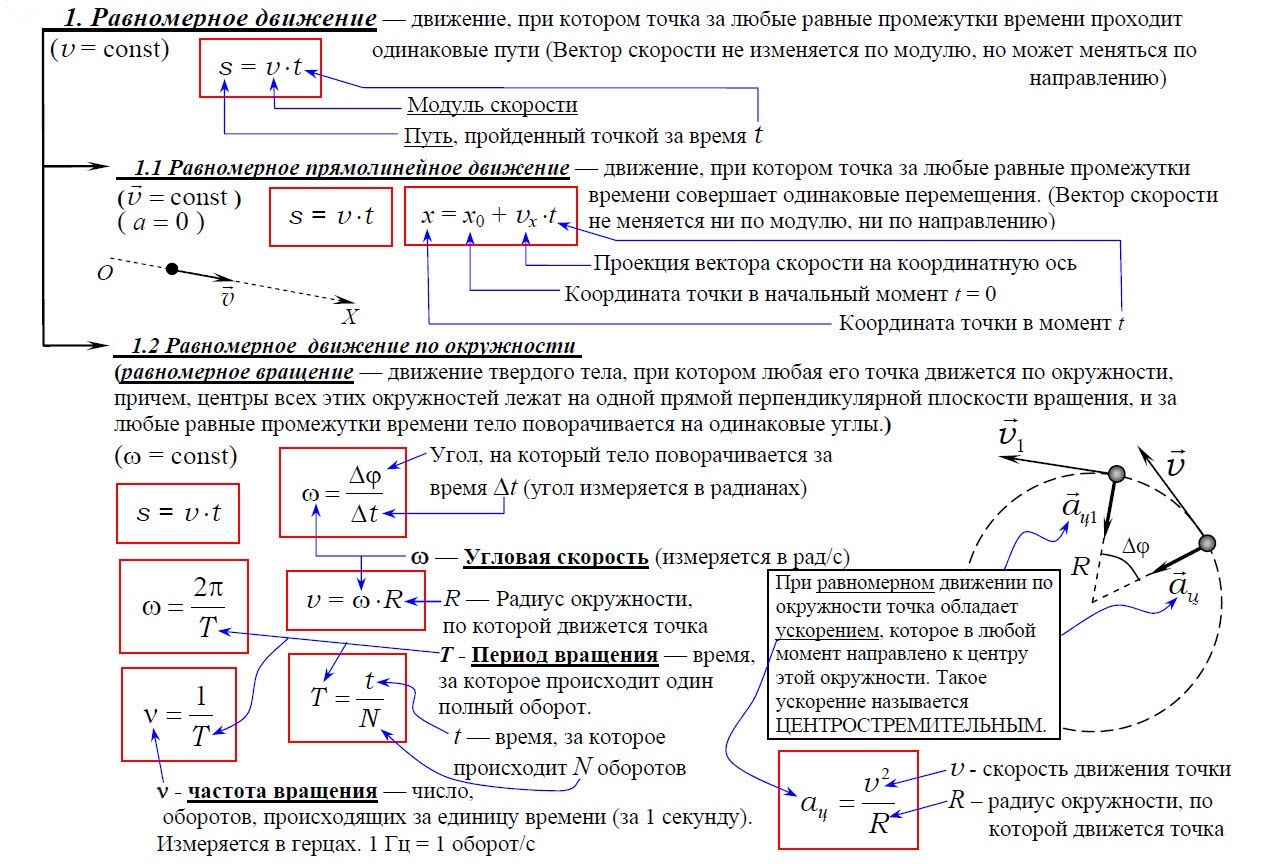
2. Движение с постоянным ускорением
Равноускоренное движение – движение, при котором мгновенная скорость за любые равные интервалы времени меняется одинаково.
Мгновенное ускорение равно отношению изменения мгновенной скорости тела к бесконечно малому интервалу времени, за который это изменение произошло.
Ускорение равноускоренного движения равно отношению изменения мгновенной скорости тела к интервалу времени, за который это изменение произошло.
Уравнение равноускоренного движения y = yo + υoyt + ½ayt² показывает, что координата квадратично зависит от времени. Уравнение υy = υoy + ayt показывает, что скорость линейно зависит от времени.
Центростремительное ускорение – ускорение, всегда направленное к центру окружности при равномерном движении по ней материальной точки. Модуль центростремительного ускорения равен отношению квадрата модуля скорости равномерного движения по окружности к её радиусу.
3. Гармоническое движение

Виды движений
Прямолинейное движение

Криволинейное движение

Частные случаи равноускоренного движения под действием силы тяжести

Частные случаи решения задач

Дополнительные материалы по кинематике
Кинематика. Таблица кратко.


Это конспект по физике «Кинематика. Теория и формулы для ЕГЭ» + шпаргалка.
Еще конспекты для 10-11 классов:
Оглавление:
Основные теоретические сведения
Система СИ
К оглавлению…
Основные единицы измерения величин в системе СИ таковы:
- единица измерения длины — метр (1 м),
- времени — секунда (1 с),
- массы — килограмм (1 кг),
- количества вещества — моль (1 моль),
- температуры — кельвин (1 К),
- силы электрического тока — ампер (1 А),
- Справочно: силы света — кандела (1 кд, фактически не используется при решении школьных задач).
При выполнении расчетов в системе СИ углы измеряются в радианах.
Если в задаче по физике не указано, в каких единицах нужно дать ответ, его нужно дать в единицах системы СИ или в производных от них величинах, соответствующих той физической величине, о которой спрашивается в задаче. Например, если в задаче требуется найти скорость, и не сказано в чем ее нужно выразить, то ответ нужно дать в м/с.
Для удобства в задачах по физике часто приходится использовать дольные (уменьшающие) и кратные (увеличивающие) приставки. их можно применять к любой физической величине. Например, мм – миллиметр, кт – килотонна, нс – наносекунда, Мг – мегаграмм, ммоль – миллимоль, мкА – микроампер. Запомните, что в физике не существует двойных приставок. Например, мкг – это микрограмм, а не милликилограмм. Учтите, что при сложении и вычитании величин Вы можете оперировать только величинами одинаковой размерности. Например, килограммы можно складывать только с килограммами, из миллиметров можно вычитать только миллиметры, и так далее. При переводе величин пользуйтесь следующей таблицей.
Таблица дольных и кратных приставок в физике:

Путь и перемещение
К оглавлению…
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин этого движения.
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.
Всякое тело имеет определенные размеры. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать материальной точкой. Так при движении автомобиля на большие расстояния можно пренебречь его длиной, так как длина автомобиля мала по сравнению с расстояниями, которое он проходит.
Интуитивно понятно, что характеристики движения (скорость, траектория и т.д.) зависят от того, откуда мы на него смотрим. Поэтому для описания движения вводится понятие системы отсчета. Система отсчета (СО) – совокупность тела отсчета (оно считается абсолютно твердым), привязанной к нему системой координат, линейки (прибора, измеряющего расстояния), часов и синхронизатора времени.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает в данной СО некоторую линию, которую называют траекторией движения тела.
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его конечным положением. Перемещение есть векторная величина. Перемещение может в процессе движения увеличиваться, уменьшаться и становиться равным нулю.
Пройденный путь равен длине траектории, пройденной телом за некоторое время. Путь – скалярная величина. Путь не может уменьшаться. Путь только возрастает либо остается постоянным (если тело не движется). При движении тела по криволинейной траектории модуль (длина) вектора перемещения всегда меньше пройденного пути.
При равномерном (с постоянной скоростью) движении путь L может быть найден по формуле:
где: v – скорость тела, t – время в течении которого оно двигалось. При решении задач по кинематике перемещение обычно находится из геометрических соображений. Часто геометрические соображения для нахождения перемещения требуют знания теоремы Пифагора.
Средняя скорость
К оглавлению…
Скорость – векторная величина, характеризующая быстроту перемещения тела в пространстве. Скорость бывает средней и мгновенной. Мгновенная скорость описывает движение в данный конкретный момент времени в данной конкретной точке пространства, а средняя скорость характеризует все движение в целом, в общем, не описывая подробности движения на каждом конкретном участке.
Средняя скорость пути – это отношение всего пути ко всему времени движения:

где: Lполн – весь путь, который прошло тело, tполн – все время движения.
Средняя скорость перемещения – это отношение всего перемещения ко всему времени движения:

Эта величина направлена так же, как и полное перемещение тела (то есть из начальной точки движения в конечную точку). При этом не забывайте, что полное перемещение не всегда равно алгебраической сумме перемещений на определённых этапах движения. Вектор полного перемещения равен векторной сумме перемещений на отдельных этапах движения.
- При решении задач по кинематике не совершайте очень распространенную ошибку. Средняя скорость, как правило, не равна среднему арифметическому скоростей тела на каждом этапе движения. Среднее арифметическое получается только в некоторых частных случаях.
- И уж тем более средняя скорость не равна одной из скоростей, с которыми двигалось тело в процессе движения, даже если эта скорость имела примерно промежуточное значение относительно других скоростей, с которыми двигалось тело.
Равноускоренное прямолинейное движение
К оглавлению…
Ускорение – векторная физическая величина, определяющая быстроту изменения скорости тела. Ускорением тела называют отношение изменения скорости к промежутку времени, в течение которого происходило изменение скорости:

где: v0 – начальная скорость тела, v – конечная скорость тела (то есть спустя промежуток времени t).
Далее, если иное не указано в условии задачи, мы считаем, что если тело движется с ускорением, то это ускорение остается постоянным. Такое движение тела называется равноускоренным (или равнопеременным). При равноускоренном движении скорость тела изменяется на одинаковую величину за любые равные промежутки времени.
Равноускоренное движение бывает собственно ускоренным, когда тело увеличивает скорость движения, и замедленным, когда скорость уменьшается. Для простоты решения задач удобно для замедленного движения брать ускорение со знаком «–».
Из предыдущей формулы, следует другая более распространённая формула, описывающая изменение скорости со временем при равноускоренном движении:

Перемещение (но не путь) при равноускоренном движении рассчитывается по формулам:



В последней формуле использована одна особенность равноускоренного движения. При равноускоренном движении среднюю скорость можно рассчитывать, как среднее арифметическое начальной и конечной скоростей (этим свойством очень удобно пользоваться при решении некоторых задач):

С расчетом пути все сложнее. Если тело не меняло направления движения, то при равноускоренном прямолинейном движении путь численно равен перемещению. А если меняло – надо отдельно считать путь до остановки (момента разворота) и путь после остановки (момента разворота). А просто подстановка времени в формулы для перемещения в этом случае приведет к типичной ошибке.
Координата при равноускоренном движении изменяется по закону:

Проекция скорости при равноускоренном движении изменяется по такому закону:

Аналогичные формулы получаются для остальных координатных осей. Формула для тормозного пути тела:

Свободное падение по вертикали
К оглавлению…
На все тела, находящиеся в поле тяготения Земли, действует сила тяжести. В отсутствие опоры или подвеса эта сила заставляет тела падать к поверхности Земли. Если пренебречь сопротивлением воздуха, то движение тел только под действием силы тяжести называется свободным падением. Сила тяжести сообщает любым телам, независимо от их формы, массы и размеров, одинаковое ускорение, называемое ускорением свободного падения. Вблизи поверхности Земли ускорение свободного падения составляет:

Это значит, что свободное падение всех тел вблизи поверхности Земли является равноускоренным (но не обязательно прямолинейным) движением. Вначале рассмотрим простейший случай свободного падения, когда тело движется строго по вертикали. Такое движение является равноускоренным прямолинейным движением, поэтому все изученные ранее закономерности и фокусы такого движения подходят и для свободного падения. Только ускорение всегда равно ускорению свободного падения.
Традиционно при свободном падении используют направленную вертикально ось OY. Ничего страшного здесь нет. Просто надо во всех формулах вместо индекса «х» писать «у». Смысл этого индекса и правило определения знаков сохраняется. Куда направлять ось OY – Ваш выбор, зависящий от удобства решения задачи. Вариантов 2: вверх или вниз.
Приведем несколько формул, которые являются решением некоторых конкретных задач по кинематике на свободное падение по вертикали. Например, скорость, с которой упадет тело падающее с высоты h без начальной скорости:

Время падения тела с высоты h без начальной скорости:
Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v0, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):


Горизонтальный бросок
К оглавлению…
При горизонтальном броске с начальной скоростью v0 движение тела удобно рассматривать как два движения: равномерное вдоль оси ОХ (вдоль оси ОХ нет никаких сил препятствующих или помогающих движению) и равноускоренного движения вдоль оси OY.
Скорость в любой момент времени направлена по касательной к траектории. Ее можно разложить на две составляющие: горизонтальную и вертикальную. Горизонтальная составляющая всегда остается неизменной и равна vx = v0. А вертикальная возрастает по законам ускоренного движения vy = gt. При этом полная скорость тела может быть найдена по формулам:


При этом важно понять, что время падения тела на землю никоим образом не зависит от того, с какой горизонтальной скоростью его бросили, а определяется только высотой, с которой было брошено тело. Время падения тела на землю находится по формуле:

Пока тело падает, оно одновременно движется вдоль горизонтальной оси. Следовательно, дальность полета тела или расстояние, которое тело сможет пролететь вдоль оси ОХ, будет равно:

Угол между горизонтом и скоростью тела легко найти из соотношения:

Также иногда в задачах могут спросить о моменте времени, при котором полная скорость тела будет наклонена под определенным углом к вертикали. Тогда этот угол будет находиться из соотношения:

Важно понять, какой именно угол фигурирует в задаче (с вертикалью или с горизонталью). Это и поможет вам выбрать правильную формулу. Если же решать эту задачу координатным методом, то общая формула для закона изменения координаты при равноускоренном движении:

Преобразуется в следующий закон движения по оси OY для тела брошенного горизонтально:

При ее помощи мы можем найти высоту на которой будет находится тело в любой момент времени. При этом в момент падения тела на землю координата тела по оси OY будет равна нулю. Очевидно, что вдоль оси OХ тело движется равномерно, поэтому в рамках координатного метода горизонтальная координата изменятся по закону:
Бросок под углом к горизонту (с земли на землю)
К оглавлению…
Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):

Время подъема до максимальной высоты при броске под углом к горизонту:

Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т.е. тело бросали, например, с земли на землю):


Минимальная скорость тела брошенного под углом к горизонту – в наивысшей точке подъёма, и равна:

Максимальная скорость тела брошенного под углом к горизонту – в моменты броска и падения на землю, и равна начальной. Это утверждение верно только для броска с земли на землю. Если тело продолжает лететь ниже того уровня, с которого его бросали, то оно будет там приобретать все большую и большую скорость.
Сложение скоростей
К оглавлению…
Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными. Таким образом, покой и движение тела относительны. Классический закон сложения скоростей:

Таким образом, абсолютная скорость тела равна векторной сумме его скорости относительно подвижной системы координат и скорости самой подвижной системы отсчета. Или, другими словами, скорость тела в неподвижной системе отсчета равна векторной сумме скорости тела в подвижной системе отсчета и скорости подвижной системы отсчета относительно неподвижной.
Равномерное движение по окружности
К оглавлению…
Движение тела по окружности является частным случаем криволинейного движения. Такой вид движения также рассматривается в кинематике. При криволинейном движении вектор скорости тела всегда направлен по касательной к траектории. То же самое происходит и при движении по окружности (см. рисунок). Равномерное движение тела по окружности характеризуется рядом величин.

Период – время, за которое тело, двигаясь по окружности, совершает один полный оборот. Единица измерения – 1 с. Период рассчитывается по формуле:

Частота – количество оборотов, которое совершило тело, двигаясь по окружности, в единицу времени. Единица измерения – 1 об/с или 1 Гц. Частота рассчитывается по формуле:

В обеих формулах: N – количество оборотов за время t. Как видно из вышеприведенных формул, период и частота величины взаимообратные:

При равномерном вращении скорость тела будет определяется следующим образом:

где: l – длина окружности или путь, пройденный телом за время равное периоду T. При движении тела по окружности удобно рассматривать угловое перемещение φ (или угол поворота), измеряемое в радианах. Угловой скоростью ω тела в данной точке называют отношение малого углового перемещения Δφ к малому промежутку времени Δt. Очевидно, что за время равное периоду T тело пройдет угол равный 2π, следовательно при равномерном движении по окружности выполняются формулы:

Угловая скорость измеряется в рад/с. Не забывайте переводить углы из градусов в радианы. Длина дуги l связана с углом поворота соотношением:

Связь между модулем линейной скорости v и угловой скоростью ω:

При движении тела по окружности с постоянной по модулю скоростью изменяется только направление вектора скорости, поэтому движение тела по окружности с постоянной по модулю скоростью является движением с ускорением (но не равноускоренным), так как меняется направление скорости. В этом случае ускорение направлено по радиусу к центру окружности. Его называют нормальным, или центростремительным ускорением, так как вектор ускорения в любой точке окружности направлен к ее центру (см. рисунок).

Модуль центростремительного ускорения связан с линейной v и угловой ω скоростями соотношениями:

Обратите внимание, что если тела (точки) находятся на вращающемся диске, шаре, стержне и так далее, одним словом на одном и том же вращающемся объекте, то у всех тел одинаковые период вращения, угловая скорость и частота.
Kinematics -Изучающий материал для IIT JEE

- Полный курс физики — 11 класс
Предлагаемая цена: рупий2968
- Подробнее

Kinematics - одна из самых простых и важных глав механики в программе IIT JEE, AIEEE и других инженерных экзаменов.Начинающим также легко, и им очень интересно решать численные задачи на них. Эта глава также важна с точки зрения того, что она является обязательным условием для всех других глав Механики. Более того, концепция этой главы полезна в других разделах физики. Эту главу можно назвать одной из самых простых, так как в ней очень мало поворотов.
При изучении движения тел мы должны помнить две вещи. Мы должны изучить различные характеристики, связанные с движущимися телами, в то время как мы должны изучить и детально изучить причину возникновения движения.Соответственно мы разделили исследование на две категории. Один - это кинематика, а другой - динамика.
Это раздел физики, который занимается только описанием движения тел. В этой ветви мы изучим некоторые характеристики, связанные с движущимися телами, например, смещение, скорость, ускорение и т. Д. Мы также изучим различные связи, связывающие их друг с другом. Но мы не будем концентрироваться на причине движения. В этой главе рассматриваются фундаментальные понятия о движении частицы в одном и двух измерениях.Различные виды движения могут быть симметрично сгруппированы в несколько широких категорий. Различие проводится на основе вектора скорости. На этом основании движение может быть одномерным, двухмерным или трехмерным. В этой главе мы рассмотрим часть механики, которая занимается только движением тела, а не причиной движения.

Помимо прочего, мы научимся описывать тела, движущиеся по прямой линии, равномерное круговое движение, движение снарядов - и это лишь некоторые из них.
Эти описания составляют основу нашего изучения физики. Решенные примеры, как обычно, очень полезны, так как они могут появиться на экзамене с небольшими изменениями.
Кинематика охватывает следующие темы: -
Кинематика важна с точки зрения получения высоких баллов в IIT JEE, так как есть несколько концепций, которые необходимо понять, на которых сформулировано множество Вопросов с множественным выбором.Если мы рассмотрим главы «Кинематика», «Законы движения Ньютона» и «Рабочая сила и энергия» вместе, мы можем сказать, что хорошее понимание концепции может помочь студенту набрать 20-30 баллов, варьирующихся от одного экзамена к другому.
Связанные ресурсы: —
Чтобы узнать больше, купите учебные материалы по кинематике, включающие в себя учебные заметки, заметки о пересмотре, видео-лекции, вопросы, решенные за предыдущий год и т. Д. Также см. Другие учебные материалы по физике здесь.

Особенности курса
- 101 видео лекций
- Редакция Примечания
- Документы за предыдущий год
- Mind Map
- Планировщик исследования
- NCERT Solutions
- Дискуссионный форум
- Тестовая бумага с Video Solution
,
Замечания по пересмотру кинематики | AskIITians

- Инерциальная система отсчета: — Система отсчета, в которой действует ньютоновская механика, называется инерциальной системой отсчета или инерциальной системой отсчета.Система отсчета, в которой не работает ньютоновская механика, называется неинерциальной системой отсчета или неинерциальной системой отсчета.
- Средняя скорость v av и средняя скорость
 тела в течение интервала времени? т определяется как,
тела в течение интервала времени? т определяется как,
v av = средняя скорость
=? с /? т


Примечание:
(a) Изменение скорости или направления движения приводит к изменению скорости
(b) Говорят, что частица, которая совершает один оборот по круговой траектории с одинаковой скоростью, обладает нулевой скоростью и ненулевой скоростью.
(c) Частица не может иметь нулевую скорость с ненулевой скоростью.
- Среднее ускорение определяется как изменение скорости
 за промежуток времени? т .
за промежуток времени? т .

Мгновенное ускорение частицы — это скорость, с которой ее скорость изменяется в этот момент.

- Три уравнения движения для объекта с постоянным ускорением приведены ниже.
(a) v = u + при
(b) s = ut + 1/2 при 2
(с) v 2 = u 2 + 2as
Здесь u — начальная скорость, v — конечная скорость, a — ускорение, с — смещение, пройденное телом, и t — время.
Примечание. Примите знак «+ ve», когда тело ускоряется, и знак «-ve», когда тело замедляется.
- Смещение телом в n th секунды задается,
с n = u + a /2 (2 n -1)
- График времени-позиции ( x против т ), график скорости-времени ( против против т ) и график времени ускорения ( против против т ) для движения в одномерном пространстве:
(i) Изменение смещения (x), скорости (v) и ускорения (a) по времени для различных типов движения.
| Водоизмещение (x) | Скорость (V) | Ускорение (а) |
(а) В состоянии покоя | | | |
(б) Движение с постоянной скоростью | | | |
(с) Движение с постоянным ускорением | | | |
(d) Движение с постоянным замедлением | | | |
Скалярные величины: — Скалярные величины — это те величины, которые требуют только величины для их полной спецификации.(например, масса, длина, объем, плотность)
Векторные величины: — Векторные величины — это те величины, которые требуют величины, а также направления для их полной спецификации. (например, смещение, скорость, ускорение, сила)
Нулевой вектор (нулевые векторы): — Это вектор нулевой величины и произвольного направления.
Когда нулевой вектор добавляется или вычитается из заданного вектора, результирующий вектор совпадает с заданным вектором.
Точечное произведение нулевого вектора на любое произвольное всегда равно нулю. Перекрестное произведение нулевого вектора с любым другим вектором также является нулевым вектором.
- Коллинеарный вектор: — Векторы, имеющие общую линию действия, называются коллинеарным вектором. Есть два типа.
Параллельный вектор ( θ = 0 °): — Два вектора, действующих в одном направлении, называются параллельными векторами.
Антипараллельный вектор ( θ = 180 °): — Два вектора, которые направлены в противоположных направлениях, называются антипараллельными векторами.
копланарные векторы- Векторы, расположенные в одной плоскости, независимо от их направлений, известны как копланарные векторы.
Добавление вектора: —
векторное дополнение коммутативно — 
Добавление вектора ассоциативно — 
векторное дополнение дистрибутивное — 
- Закон сложения треугольников по закону вектора: — Если два вектора представлены двумя сторонами треугольника, взятыми в одном и том же порядке, то их результирующее представление представлено третьей стороной треугольника, взятой в противоположном порядке.


Величина результирующего вектора  : —
: —
R = √ ( A 2 + B 2 +2 AB cos θ )
Здесь θ — угол между  и
и  .
.
Если β — угол между  и
и  ,
,
,

- Если три вектора, действующих одновременно на частицу, могут быть представлены тремя сторонами треугольника, взятыми в одном и том же порядке, то частица останется в равновесии.
Итак, 
- Закон сложения параллелограмма вектора: —

R = √ ( A 2 + B 2 +2 AB cos θ ),

Случаи 1: — Когда, θ = 0 °, то
R = A + B (максимум), β = 0 °
Случаи 2: — Когда, θ = 180 °, то
R = A — B (минимум), β = 0 °
Случаи 3: — Когда, θ = 90 °, то
R = √ ( A 2 + B 2 ), β = загар -1 (B / A)
- Процесс вычитания одного вектора из другого эквивалентен добавлению вектора отрицательного вектора, который необходимо вычесть.
Итак,


(a) Точечный или скалярный продукт: —
 ,
,

Здесь A — величина  , B — величина
, B — величина  , а θ — угол между
, а θ — угол между  и
и  .
.
(i) Перпендикулярный вектор: —

(ii) Коллинеарный вектор: —
Когда, Параллельный вектор (θ = 0 °), 
Когда, Анти параллельный вектор (θ = 180 °), 
(b) Перекрестное произведение или векторное произведение: —

или

Здесь A — это величина  , B — это величина
, B — это величина  , θ — это угол между
, θ — это угол между  и
и  , а
, а  — это единичный вектор в направлении, перпендикулярном плоскости, содержащей
— это единичный вектор в направлении, перпендикулярном плоскости, содержащей  и
и  .
.
(i) Перпендикулярный вектор (θ = 90 °): —

(ii) Коллинеарный вектор: —
Когда, Параллельный вектор (θ = 0 °),  (нулевой вектор)
(нулевой вектор)
Когда, θ = 180 °,  (нулевой вектор)
(нулевой вектор)
В трех измерениях,

Площадь треугольника: — 
Площадь параллелограмма: — 
Объем параллелепипеда: — 
 (i) Перпендикулярный вектор: — В верхней части наклонной плоскости ( t = 0, u = 0 и a = g sin q ), уравнение движения будет,
(i) Перпендикулярный вектор: — В верхней части наклонной плоскости ( t = 0, u = 0 и a = g sin q ), уравнение движения будет,
(a) v = (g sinθ) t
(b) s = ½ (g sinθ) t 2
(с) v 2 = 2 (g sinθ) с
(ii) Если время, необходимое организму для достижения дна, составляет т , то с = ½ ( г грех θ ) т 2
т = √ (2 с / г грех θ )
Но грех θ = ч / с или с = ч / грех θ
Итак, т = (1 / грех θ ) √ (2 ч / г )
(iii) Скорость тела на дне
v = г (sin θ ) т
= √2 гц
- Относительная скорость объекта A по отношению к объекту B задается как
В AB = В A — В B
Здесь, V В называется ссылкой скорость объекта.
- Изменение массы: — В соответствии с формулой изменения массы Эйнштейна, релятивистская масса тела определяется как,
м = м 0 / √ (1- v 2 / c 2 )
Здесь м 0 — масса покоя тела, v — скорость тела, а c — скорость света.
- Движение снаряда в плоскости: — Если частица с начальной скоростью u проецируется под углом θ (угол проекции) с осью x , то

Time of Flight, T = (2 u sin α ) / г
Горизонтальный диапазон, R = u 2 sin2 α / г
Максимальная высота, H = u 2 sin 2 α /2 г
Уравнение траектории, y = x tan α — ( gx 2 /2 u 2 cos 2 α )
(a) При падении: — Период времени, t = √ (2 часа / г) и скорость, v = √ (2 часа
)(b) При подбрасывании: — период времени, t = u / г и высота, h = u 2 / 2g
- Состояние равновесия: —
(а) 
(b) | F 1 + F 2 | ≥ | F 3 | ≥ | F 1 -F 2 |

Особенности курса
- 728 видео лекций
- Редакция Примечания
- Предыдущие документы года
- Mind Map
- Планировщик исследования
- NCERT Solutions
- Дискуссионный форум
- Тестовая бумага с Video Solution
,
Кинематика | физика | Britannica
Kinematics , раздел физики и подразделение классической механики, занимающееся геометрически возможным движением тела или системы тел без учета задействованных сил (т.е. , то есть причин и следствий движений).
Британика Викторина
Все о физике викторины
Какая единица измерения для циклов в секунду?
Краткая обработка кинематики следует.Для полной обработки см. механика.
Кинематика имеет целью дать описание пространственного положения тел или систем материальных частиц, скорости, с которой частицы движутся (скорость), и скорости, с которой их скорость изменяется (ускорение). Когда причинные силы не учитываются, описания движения возможны только для частиц с ограниченным движением — , то есть , движущихся по определенным путям. В неограниченном или свободном движении силы определяют форму пути.
Для частицы, движущейся по прямой траектории, список позиций и соответствующие времена будут представлять собой подходящую схему для описания движения частицы. Непрерывное описание потребовало бы математической формулы, выражающей положение в терминах времени.
Получите эксклюзивный доступ к контенту из нашего первого издания 1768 года с вашей подпиской. Подпишитесь сегодняКогда частица движется по искривленной траектории, описание ее положения становится более сложным и требует двух или трех измерений.В таких случаях непрерывные описания в виде одного графика или математической формулы неосуществимы. Например, положение частицы, движущейся по кругу, можно описать радиусом вращения круга, подобным спице колеса, один конец которого зафиксирован в центре круга, а другой конец прикреплен к частице. Радиус вращения известен как вектор положения частицы, и, если угол между ним и фиксированным радиусом известен как функция времени, можно рассчитать величину скорости и ускорения частицы.Скорость и ускорение, однако, имеют направление и величину; скорость всегда касается траектории, в то время как ускорение имеет две составляющие: одну касательную к траектории, а другую перпендикулярную касательной.



 тела в течение интервала времени? т определяется как,
тела в течение интервала времени? т определяется как, за промежуток времени? т .
за промежуток времени? т .











Leave A Comment