Призма. Формулы и свойства призмы
Навигация по странице: Определение призмы Элементы призмы Прямая призма Наклонная призма Правильная призма Усечённая призма Объём призмы Площадь поверхности призмы Основные свойства призмы
Определение.
Призма — это многогранная объемная фигура, которая состоит из двух одинаковых плоских многоугольников (основ), находящихся в двух параллельных плоскостях, а другие грани (боковые грани) — параллелограммы, что имеют общие стороны с этими многоугольниками.
| Рис.1 | Рис.2 |
Определение. Основы призмы — две грани, которые являются равными параллельными плоскими многоугольниками (ABCEF, GMNJK).
Определение.
Определение. Боковая поверхность призмы — совокупность всех боковых граней призмы.
Определение. Поверхность призмы — это совокупность поверхностей двух оснований и боковой поверхности.
Определение. Боковое ребро призмы — общая сторона двух боковых граней.
Определение. Высота — это перпендикуляр, который соединяет две основы призмы под прямым углом.
Определение. Диагональ основания призмы — это отрезок, соединяющий две не соседние вершины, принадлежащие этой же основе.
Определение. Диагональ боковой грани призмы
Определение. Диагональ призмы (AN) — это отрезок, соединяющий две вершины, лежащие на разных основаниях, но не лежат на одной боковой стороне.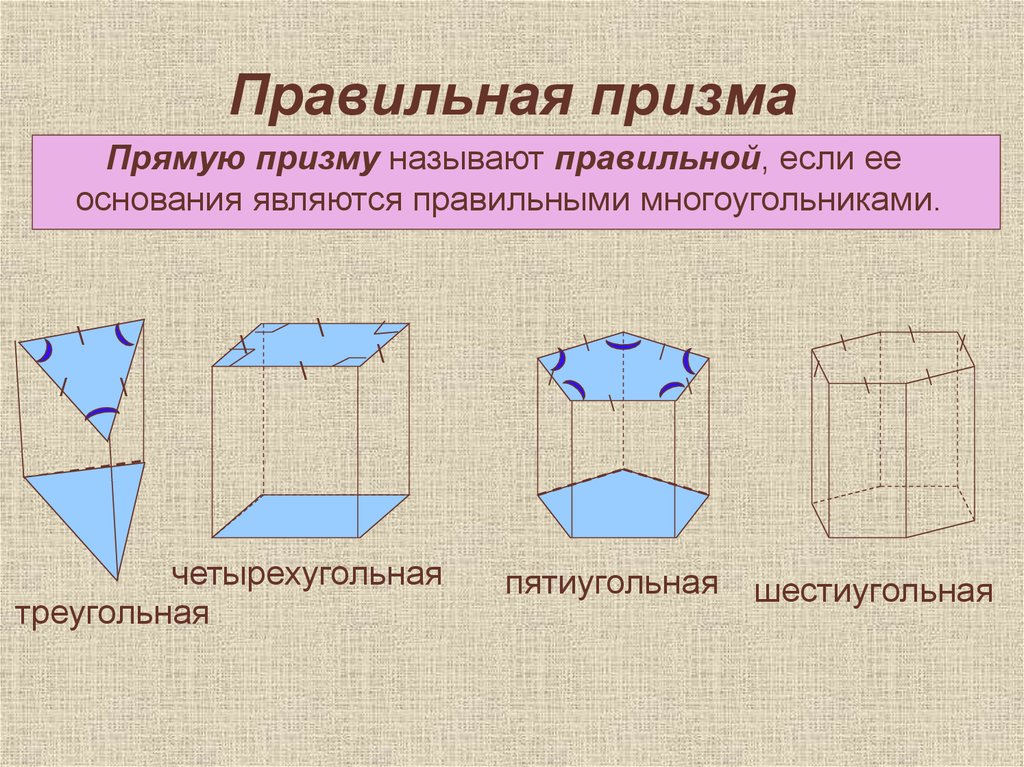
Определение. Диагональное сечение — это пересечение призмы плоскостью, проходящей через диагональ основания призмы и боковое ребро. Треугольная призма (в основе призмы треугольники) не имеет диагональных сечений.
Определение.
Определение. Прямая призма — это призма, в которой все боковые грани перпендикулярны к основанию. Высота равна длине бокового ребра.
Определение. Наклонная призма — это призма, в которой боковые грани не перпендикулярны к основанию.
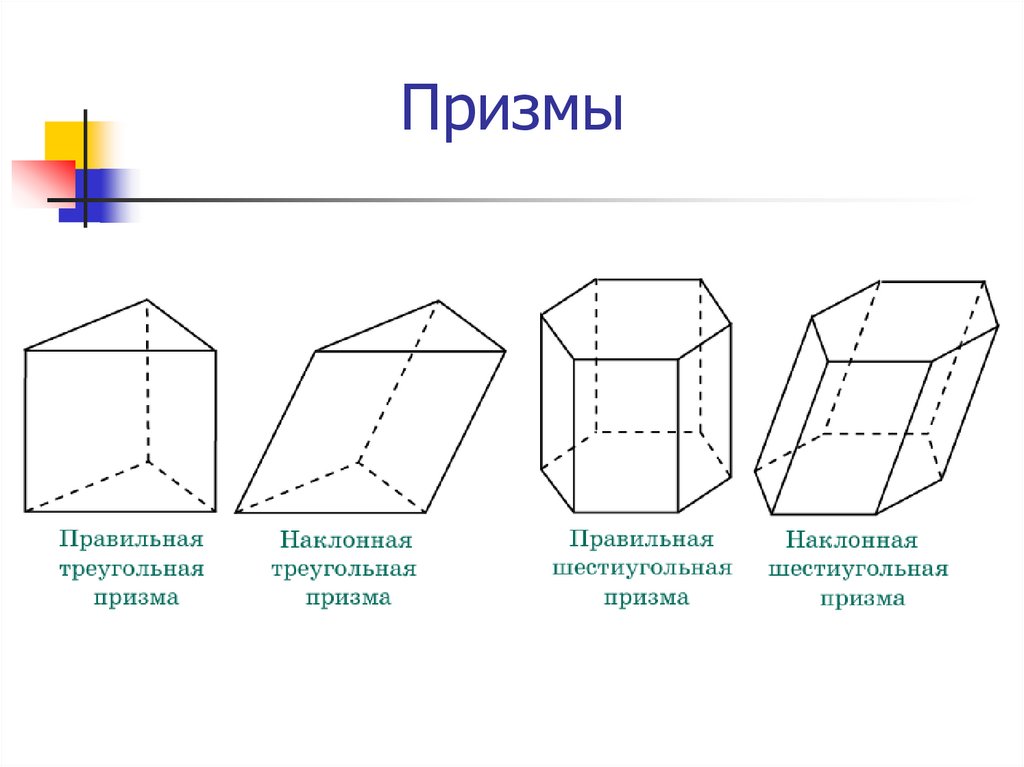
Определение. Правильная призма — это призма, в которой основы являются правильными многоугольниками. Правильная призма может быть, как прямой, так и наклонной.
Определение. Усечённая призма — это призма, в которой две основы не параллельны (рис. 2). Усечённая призма может быть, как прямой, так наклонной.
Объём призмы
Формула. Объём призмы через площадь основания и высоту:
V = SоснH
Формула. Объём наклонной призмы через площадь перпендикулярного сечения и длину бокового ребра:
V = SпL
Формула. Объём правильной прямой призмы через высоту (h), длину стороны (a) и количество сторон (n):
| V = | n | π | |
| 4 | n |
Площадь поверхности призмы
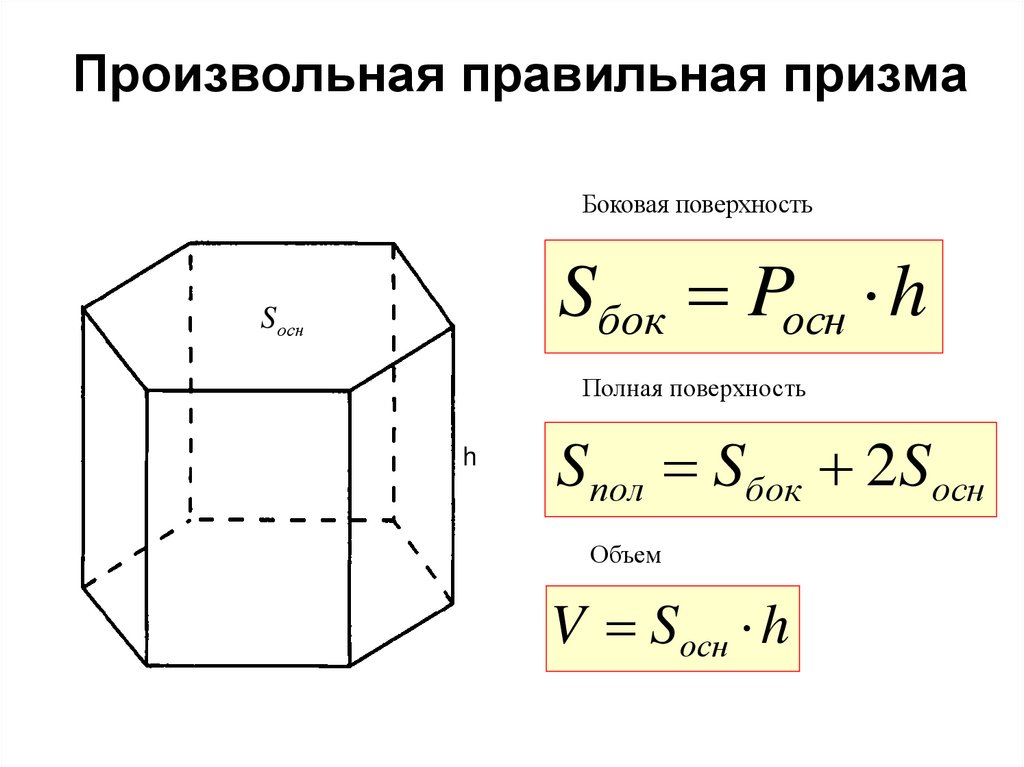
Формула. Площадь боковой поверхности призмы через периметр основания и высоту:
Sb = P·h
Формула. Площадь поверхности призмы через площадь основания, периметр основания и высоту:
S = 2Soсн + P·h
Формула.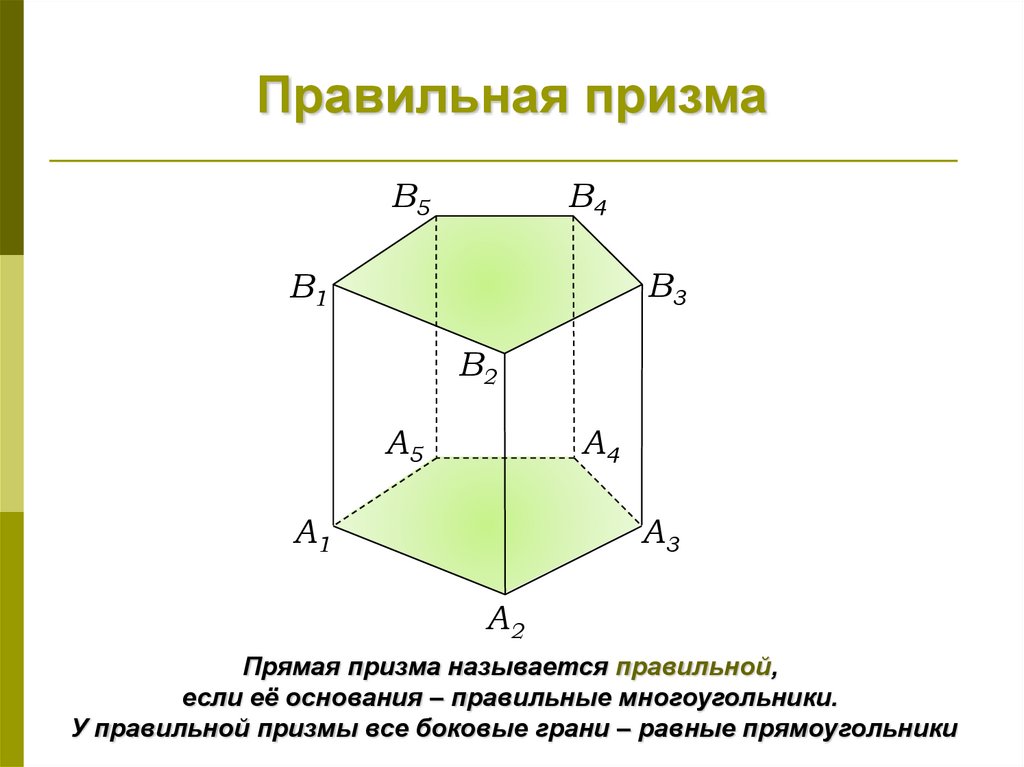 Площадь поверхности правильной призмы через высоту (h), длину стороны (a) и количество сторон (n):
Площадь поверхности правильной призмы через высоту (h), длину стороны (a) и количество сторон (n):
| S = | n | a2ctg | π | + nah |
| 2 | n |
Основные свойства призмы
Основы призмы — равные многоугольники.
Боковые грани призмы — параллелограммы.
Боковые ребра призмы параллельны и равны между собой.
Перпендикулярное сечение перпендикулярно всем боковым ребрам и боковым граням.
Высота прямой призмы равна длине бокового ребра.
Высота наклонной призмы всегда меньше длины ребра.
В прямой призме гранями могут быть прямоугольниками или квадратами.
Все таблицы и формулы
Призма — Умскул Учебник
На этой странице вы узнаете- Чем упаковка стикеров похожа на призму?
- Как можно попасть в призму в реальной жизни?
- Как сложить игральные кости из листа бумаги?
- Как найти объем воды в аквариуме?
Слышали такое выражение «смотреть сквозь призму чего-либо»? Оно значит ситуацию, в которой мы воспринимаем что-либо под влиянием каких-то убеждений или представлений. Замысловато, конечно… Возможно, потому что и сама призма — непростое понятие. Давайте разберемся с ней с точки зрения математики.
Замысловато, конечно… Возможно, потому что и сама призма — непростое понятие. Давайте разберемся с ней с точки зрения математики.
Многие из нас пользуются стикерами. Для записи своих дел, для закладок, для пометок при ведении конспектов. Даже если мы ими не пользуемся, то наверняка видели их в магазинах или у родственников и друзей.
Один такой стикер можно принять за плоскость. Теперь вспомним, как выглядит упаковка с ними. Много-много стикеров накладываются друг на друга и получается небольшая объемная фигура, сверху и снизу которой лежат два абсолютно одинаковых листа. При этом сразу заметим, что нижний и верхний стикеры будут параллельны друг другу.
На самом деле, упаковка со стикерами является не чем иным, как призмой!
Призма — это многогранник, в котором две грани являются равными многоугольниками и лежат в параллельных плоскостях, а все остальные — параллелограммами.
| Чем упаковка стикеров похожа на призму? Упаковка стикеров является объемной фигурой, в основаниях которой лежат равные прямоугольники. |
Определение может показаться немного запутанным, но в нем нет ничего страшного. Разберемся, поближе взглянув на составные призмы.
Строение призмыПредставим себе обычную коробку. Ее дно и крышка равны между собой и лежат в параллельных плоскостях. Это и есть равные многоугольники. Также их называют основаниями призмы.
Посмотрим на стенки коробки. Они являются параллелограммами, просто с прямыми углами. Подробнее про параллелограммы можно прочитать в статье «Параллелограмм». Эти параллелограммы называются боковыми гранями призмы.
Возьмем линейку и измерим расстояние между основаниями призмы. Для этого из любой точки одного основания проведем перпендикуляр к другому.
Подробнее про расстояния между плоскостями можно узнать в статьях «Углы в пространстве» и «Расстояния между фигурами».
Может возникнуть вопрос, что мы сейчас нашли? Мы нашли высоту призмы.
Высота призмы — перпендикуляр, опущенный из любой точки одного основания на другое основание призмы.
В задачах намного удобнее опускать перпендикуляр не из произвольной точки, а из вершины призмы.
Рассмотрим элементы призмы.
Ребро — это линия пересечения двух плоскостей.
Представим, что вместо картонных стенок в нашей коробке ткань, которую нам нужно натянуть на каркас так, чтобы коробка не изменилась. В этом случае все прямые этого каркаса и будут ребрами.
Ребра бывают двух видов:
- ребра оснований,
- боковые ребра.
Отличить их также легко: ребра основания являются стороной многоугольника, который в нем лежит, в то время как боковые ребра не принадлежат основаниям.
У боковых ребер есть одно очень важное свойство: они равны между собой и параллельны.
Диагональ призмы — отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.
Например, мы можем взять клетку попугая и от угла до угла сделать ему жердочку, чтобы птичке было весело жить. Эта жердочка и будет диагональю призмы.
Виды призмВернемся к рассуждениям о том, чем упаковка стикеров похожа на призму. Например, куб и параллелепипед будут отличаться. А если в основании призмы будет лежать треугольник или шестиугольник? Или двадцатиугольник? Разделим призмы на несколько видов.
Мы рассмотрим две классификации.
В первом случае будем рассматривать призмы по фигурам, которые лежат в основании. В многоугольнике может быть множество сторон, а значит, и в основании призмы может быть треугольник, четырехугольник, шестиугольник, десятиугольник и так далее.
В зависимости от фигуры в основании призмы могут называться по-разному. Вот три основных, которые чаще всего встречаются при решении заданий:
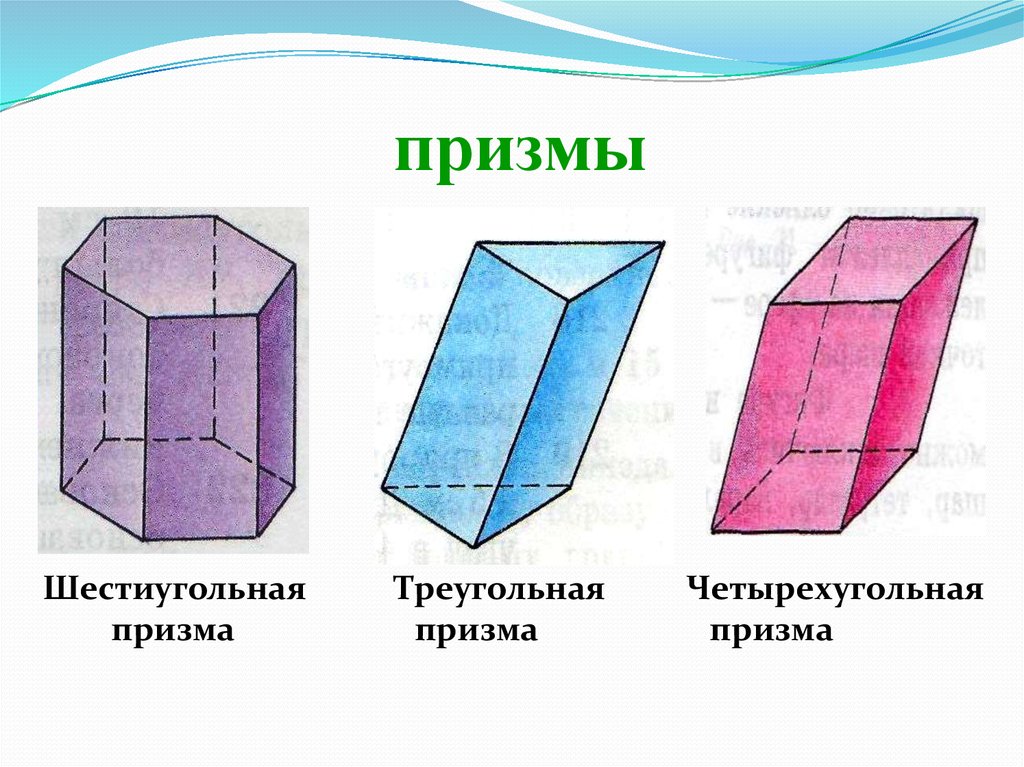
- треугольная призма,
- четырехугольная призма,
- шестиугольная призма.

Аналогичным образом можно дать название любой призме, например, десятиугольная призма или стоугольная призма.
В определении призмы сказано, что в боковых гранях лежат параллелограммы. До этого мы чертили только прямоугольники, но в боковых гранях могут лежать не только они.
С этим связана вторая классификация призм. По этому признаку призмы делятся всего на два вида:
- прямые,
- наклонные.
Разберемся в них чуть подробнее.
Прямая призма — призма, боковые ребра которой перпендикулярны основаниям.
В этом случае боковые ребра и ребра оснований действительно образовывают прямоугольник.
Наклонная призма — призма, боковые ребра которой находятся под углом к основаниям.
Где мы можем найти прямые и наклонные призмы? Оказывается, в архитектуре. Обычный жилой дом типовой застройки будет прямой призмой. А вот примером наклонной призмы может служить комплекс зданий “Ворота Европы” в Мадриде.
Чуть подробнее остановимся на прямых призмах. Они встречаются достаточно часто и обладают несколькими важными свойствами.
Посмотрите на свою комнату. Если по плану квартиры она будет многоугольником, то вы как бы сидите в призме. Теперь ответим на вопрос: как найти высоту комнаты?
Простой ответ: померить по стене. А если посмотреть на угол, то можно заметить, что ребро призмы совпадает с высотой. Таким образом, мы получаем первое свойство прямых призм.
Свойство 1. Высота прямой призмы совпадает с её боковым ребром.
Посмотрим на стены комнаты, на их форму. Они все являются прямоугольниками, верно?
Свойство 2. Все боковые грани прямой призмы — прямоугольники.
| Как можно попасть в призму в реальной жизни? Многие комнаты и помещения, особенно в типовой застройке, обладают формой призмы. Сидя в комнате, в классе, в столовой, даже в автобусе — мы как бы находимся внутри большой призмы. |
Если мы в основании прямой призмы разместим правильный многоугольник, у нас получится правильная призма.
Правильная призма — прямая призма, в основании которой лежит правильный многоугольник.
Например, в правильной треугольной призме будет лежать равносторонний треугольник, а в правильной шестиугольной призме — правильный шестиугольник.
Определение параллелепипедаЕще одной разновидностью прямоугольной призмы является параллелепипед.
Параллелепипед — это четырехугольная призма, все грани которой являются параллелограммами.
Параллелепипеды встречаются повсюду: коробки, мебель, комнаты, здания, склады, магазины. Поэтому изучить их не составит труда.
Свойство параллелепипеда, видимое невооруженным глазом: противоположные грани параллелепипеда равны. Как пример, вспомним ту же комнату: потолок и пол равны, так же как и стены, находящиеся напротив друг друга.
Нельзя не упомянуть про одно очень важное свойство параллелепипеда:
- Все его диагонали пересекаются в одной точке и этой точкой делятся пополам. Это свойство справедливо для всех видов параллелепипеда.
Какие бывают параллелепипеды?
Параллелепипеды также бывают прямыми и наклонными. В этих случаях все определения такие же, как и для всех остальных призм.
Прямой параллелепипедРассмотрим несколько интересных свойств прямого параллелепипеда.
1 свойство. Боковые ребра прямого параллелепипеда перпендикулярны основаниям.
2 свойство. Высота прямоугольного параллелепипеда равна длине его бокового ребра.
3 свойство. Боковые грани, которые лежат напротив друг друга, равны между собой и являются прямоугольниками.
Прямые параллелепипеды можно разделить еще на два вида:
- Прямой параллелепипед: в основании лежит параллелограмм;
- Прямоугольный параллелепипед: в основании лежит прямоугольник.
 2\)
2\)
225 = 35 + 46 + x2
x2 = 144
x = 12Ответ: 12.
У прямоугольного параллелепипеда существует еще несколько видов. Прямоугольные параллелепипеды делятся на:
- Произвольный прямоугольный параллелепипед. В основании может лежать прямоугольник.
- Правильный прямоугольный параллелепипед. В основании лежит правильный четырехугольник, то есть квадрат.
При этом боковые ребра не равны ребрам основания. Следовательно, в основаниях будут лежать квадраты, а в боковых гранях прямоугольники.
- Куб. В основании лежит квадрат, а боковые ребра равны ребрам основания.
В кубе все ребра равны, а все его грани будут квадратом.
Таким образом, мы рассмотрели все виды параллелепипеда.
Формулы для призмыОднако ни одна задача не может быть решена без формул. Поэтому необходимо рассмотреть несколько основных формул, которые могут встретиться не только в задачах, но и в жизни.

Немного вспомним моделирование, а именно развертку кубика. Мы знаем, что из листа бумаги без труда можно сложить кубик, если правильно его вычертить.
Как сложить игральные кости из листа бумаги? Задумали вы вечером сыграть с семьей или друзьями в настольную игру. Но вот незадача: игральные кости опять куда-то запропастились. Не беда.Достаточно вычертить на листе бумаги несколько квадратов, вырезать получившуюся фигуру, согнуть по ребрам и склеить между собой с помощью клея. В итоге получатся кубики для игры.
На рисунке оранжевым показаны основания, а желтым боковые грани нашего будущего кубика. А теперь представим, что нам нужно найти площадь боковой поверхности. Как это сделать?
Нужно найти площади желтых квадратиков и сложить их.
Площадь боковой поверхности призмы — сумма площадей всех боковых ее граней.
Единой формулы тут нет, поскольку призмы могут очень сильно отличаться друг от друга.
 В произвольных призмах придется считать площадь каждой боковой грани, а уже после их складывать.
В произвольных призмах придется считать площадь каждой боковой грани, а уже после их складывать. Но есть один фокус! Правда, он работает только для прямой призмы. Если по условию дана прямая призма, то можно воспользоваться формулой
Sбок. = P * h
В этой формуле Р — периметр основания, h — высота призмы, которая совпадает с высотой боковой грани.
Пример 1. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равняется 2, а высота 10.
Решение.
Шаг 1. Поскольку правильная призма по определению прямая, мы можем воспользоваться формулой S = Ph.
Шаг 2. В основании правильной призмы лежит правильный шестиугольник, следовательно, периметр основания будет равен 6 * 2 = 12.
Шаг 3. Осталось найти только площадь боковой поверхности. Подставляем данные в формулу и получаем: S = 12 * 10 = 120.
 2} = \sqrt{144 + 25} = \sqrt{169} = 13\).
2} = \sqrt{144 + 25} = \sqrt{169} = 13\). Шаг 3. Найдем периметр основания: P = 12 + 5 + 13 = 30.
Шаг 4. Осталось найти только площадь боковой поверхности. Подставляем данные в формулу и получаем: S = 30 * 13 = 390.
Ответ: 390.
Мы научились находить площадь боковой поверхности. А как найти всю площадь призмы? Вспомним нашу развертку с кубиком. Чтобы найти всю площадь кубика, нужно найти площадь всех квадратов, из которых он состоит. То есть и площадь боковой поверхности, и площадь оснований.
Площадь полной поверхности призмы — сумма площадей всех граней.
Следовательно, нам нужно сложить площади всех боковых граней и дважды площадь основания. Получаем следующую формулу.
S = Sбок + 2Sосн
Вспомним обычный хлеб, черный или белый. Его форма очень приближена к параллелепипеду. Тогда его корочка будет площадью полной поверхности параллелепипеда.
 2} = \sqrt{36 + 64} = \sqrt{100} = 10\).
2} = \sqrt{36 + 64} = \sqrt{100} = 10\).Шаг 3. Периметр ромба будет равен 4 * 10 = 40. Тогда площадь боковой поверхности равна 40 * 25 = 1000.
Шаг 4. Площадь полной поверхности будет равняться 1000 + 2 * 96 = 1000 + 192 = 1192.
Ответ: 1192
Пример 4. Площадь поверхности правильной четырехугольной призмы равняется 1980. Сторона основания равна 5. Найдите боковое ребро этой призмы.
Решение.
Шаг 1. Воспользуемся формулой S = Sбок + 2Sосн. Площадь основания будет равняться площади квадрата, то есть 5 * 5 = 25.
Шаг 2. Подставим известные величины в формулу:
1980 = Sбок + 2 * 25
Sбок = 1930Шаг 3. Площадь боковой поверхности равна произведению периметра основания на высоту призмы. Периметр равен 5 * 4 = 20. Тогда получаем уравнение:
20h = 1930
h = 96,5Шаг 4.
 Поскольку по условию дана правильная призма, то высота совпадает с боковым ребром. Следовательно, боковое ребро равняется 96,5.
Поскольку по условию дана правильная призма, то высота совпадает с боковым ребром. Следовательно, боковое ребро равняется 96,5.Ответ: 96,5.
Теперь рассмотрим, как найти объем призмы. Допустим, мы налили в прямоугольный аквариум немного воды. Как определить, сколько воды мы налили?
Для этого достаточно воспользоваться формулой объема призмы.
V = Sосн. * h
Эта формула общая, однако для каждой призмы она может принять свой вид в зависимости от того, какую формулу нужно использовать для поиска площади основания или высоты.
Например, чтобы найти объем воды в аквариуме, необходимо длину умножить на ширину и на высоту, а значит формула принимает вид V = abh.
Как найти объем воды в аквариуме? Для этого достаточно перемножить ширину, длину аквариума и высоту воды. Тем самым мы найдем объем призмы, форму которой принимает вода в аквариуме.
Пример 5.
 Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 12 и 15. Боковое ребро призмы равно 4. Найдите объем этой призмы.
Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 12 и 15. Боковое ребро призмы равно 4. Найдите объем этой призмы. Решение.
Шаг 1. Для начала найдем площадь основания. В этом случае мы можем воспользоваться формулой \(\frac{1}{2}ab\). Площадь равна \(\frac{1}{2} * 12 * 15 = 90\).
Шаг 2. Воспользуемся формулой объема призмы и подставим известные величины:
V = 90 * 4 = 360.
Ответ: 360.
Пример 6. Дан сосуд, в основании которого лежит правильный треугольник. В этот сосуд налили 3000 см3 воды. Высота жидкости оказалась равной 10 см. После этого в сосуд опустили шарик и высота изменилась с 10 см на 14 см. Найдите объем шарика.
Решение. Немного вспомним физику, а именно тот факт, что объем вытесненной жидкости равен объему тела. Значит, чтобы найти объем шарика, необходимо найти насколько изменился объем воды.

Шаг 1. Найдем площадь основания сосуда. Для этого немного преобразуем формулу объема:
\(S = \frac{V}{h}\)
Тогда:
\(S = \frac{3000}{10} = 300\)Шаг 2. А теперь найдем объем после того, как в воду погрузили шарик. Он будет равен 300 * 14 = 4200.
Шаг 3. Объем вытесненной жидкости равен 4200 — 3000 = 1200.
Ответ: 1200.
Мы рассмотрели основные формулы, которые применяются для решения задач. Стоит заметить, что они универсальны, и в каждой задаче их рационально преобразовывать под ситуацию.
Фактчек- Призма — это многогранник, в котором две грани являются равными многоугольниками и лежат в параллельных плоскостях, а все остальные — параллелограммами. Равные многоугольники называются основаниями призмы, а остальные стороны — боковыми гранями. В призме есть ребра — линии пересечения двух ее граней.
 Ребра как бы образуют каркас призмы.
Ребра как бы образуют каркас призмы. - Призмы можно разделить на несколько видов по тому, какая фигура лежит в основании: треугольник, четырехугольник, шестиугольник или любой другой многоугольник. Призмы бывают прямые и наклонные. В прямых призмах боковые ребра перпендикулярны основанию, а в наклонных — нет. Правильная призма — прямая призма, в основании которой лежит правильный многоугольник.
- Параллелепипед — это четырехугольная призма, все грани которой являются параллелограммами. Параллелепипеды бывают наклонными и прямыми. Прямые параллелепипеды включают в себя прямоугольные параллелепипеды, которые, в свою очередь, делятся на произвольные, правильные и кубы.
- В призме можно найти площадь боковой поверхности, площадь полной поверхности и объем. Для каждого из этих случаев необходимо пользоваться формулами.
Задание 1.
Что такое диагональ призмы?- Отрезок, соединяющий две соседние вершины в призме.

- Отрезок, соединяющий противоположные углы в боковой грани призмы.
- Отрезок, соединяющий противоположные углы в основании призмы.
- Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.
Задание 2.
Что такое прямая призма?- Призма, боковые ребра которой перпендикулярны основаниям.
- Призма, боковые ребра которой расположены под острым углом относительно основания.
- Призма, боковые ребра которой расположены под тупым углом относительно основания.
- Призма, в основании которой лежит прямоугольник.
Задание 3.
Как найти высоту прямой призмы?- Высоту нужно найти с помощью оснований.
- Высота совпадает с боковым ребром.
- Необходимо найти расстояние между двумя вершинами, не принадлежащими одной грани.
- В прямой призме невозможно найти высоту.
Задание 4.
Какая фигура лежит в основании прямоугольного параллелепипеда?- Параллелограмм с острыми углами.

- Ромб с острыми углами.
- Трапеция.
- Прямоугольник.
Задание 5.
Как найти площадь полной поверхности призмы?- Нужно найти сумму площадей всех боковых граней.
- Нужно сложить площадь боковой поверхности и площадь основания.
- Нужно сложить площадь боковой поверхности и удвоенную площадь основания.
- Нужно сложить площади оснований.
Ответы: 1. — 4 2. — 1 3. — 2 4. — 4 5. — 3
Что такое призменная коррекция в очках?
Призматическая коррекция используется в очках для некоторых людей с диплопией или двоением в глазах. Это когда кто-то видит два отдельных изображения одного объекта. Призма помогает совместить два изображения, чтобы было видно только одно изображение.
Почему у людей двоится в глазах?
Обычно мы видим одно изображение двумя глазами, потому что свет падает на одну и ту же часть сетчатки в каждом глазу.
 При двойном зрении видны два изображения, потому что свет падает на разные части сетчатки.
При двойном зрении видны два изображения, потому что свет падает на разные части сетчатки.Как Prism устраняет двоение в глазах?
Призма, добавленная к очкам, преломляет свет до того, как он пройдет через глаз. Свет перенаправляется в нужное место на сетчатке каждого глаза. Затем мозг объединяет два изображения вместе, чтобы создать одно четкое изображение.
Призма исправит мое двоение в глазах?
Призма может устранить двоение в глазах из-за смещения глаз, если оно вызвано:
- проблемами глазных мышц , такими как тяжелая миастения, болезнь Грейвса или косоглазие (косоглазие или косоглазие)
- Неврологические (связанные с головным мозгом) проблемы , такие как травмы головы, инсульт, мигрень или опухоль.
- Заболевания нервной системы , такие как рассеянный склероз или сахарный диабет
Двоение в глазах может быть вызвано многими причинами, и призма помогает не для всех видов двоения.
 Поскольку это может быть признаком серьезного заболевания, важно выяснить, что вызывает двоение в глазах.
Поскольку это может быть признаком серьезного заболевания, важно выяснить, что вызывает двоение в глазах.Немедленно обратитесь к врачу, если у вас двоение в глазах:
- новый
- вызвано смещением глаз
- или происходит по неизвестным причинам
Как вставить призму в очки?
Как и в случае с обычными очками, для проверки зрения необходимо пройти личный осмотр. Это единственный способ получить правильный рецепт.
Во время осмотра ваш офтальмолог может провести один или несколько из следующих тестов, чтобы определить, нужна ли вам призма:
Тест Хиршберга . Этот базовый тест помогает проверить наличие косоглазия. Свет ручки направлен на глаза. Отражение света должно появиться в центре зрачка каждого глаза. Если отражение не по центру в одном или обоих глазах, может быть косоглазие.
Смещенное от центра отражение света роговицей левого глаза, показывающее возможное косоглазие
Проба Крымского .
 Этот тест помогает измерить степень несоосности. Это как тест Хиршберга, но с призмой. При взгляде на перьевой свет перед глазами помещаются призмы разной силы. Когда призма сводит отражение в каждом глазу к центру, правильное измерение призмы найдено.
Этот тест помогает измерить степень несоосности. Это как тест Хиршберга, но с призмой. При взгляде на перьевой свет перед глазами помещаются призмы разной силы. Когда призма сводит отражение в каждом глазу к центру, правильное измерение призмы найдено.Проверка покрытия . Существует три типа тестов покрытия. С тест с закрытием/раскрытием , один глаз закрыт, а другой остается открытым. Врач ищет любые движения в открытом глазу. Тест призмы и альтернативного покрытия чередует покрытие обоих глаз, в то время как призма помещается перед одним глазом. Это измеряет смещение (разницу) между двумя глазами, чтобы найти правильную призму, чтобы устранить двоение в глазах. С помощью теста Maddox Rod каждый глаз видит вертикальную или горизонтальную линию. Смещение этих изображений позволяет врачу определить, какой у вас тип двоения в глазах. Призмы также используются для измерения расстояния между двумя изображениями и получения предписанного значения.

Как выглядит рецепт на Призму?
Рецепт на призму обычно имеет два номера:
- Призма . Как и обычные очки, диоптрии измеряют величину призменной коррекции (от 0,5 PD, 1,0 PD, 1,5 PD и т. д.) и показывают, насколько смещены ваши глаза.
- Основание . В зависимости от вашего двоения в глазах призма размещается вертикально, горизонтально или по диагонали в одной или обеих линзах ваших очков. «Основание» — это самый толстый край призмы, который говорит вам, куда перенаправляется свет. Это может быть внешний край линзы (Base Out, BO), внутренний край (Base In, BI), верхний (Base Up, BU) или нижний край (Base Down, BD).
Как выглядят призматические очки?
Иногда на переднюю или заднюю часть очков наклеивают временную призму Френеля (тонкая виниловая наклейка). При использовании линзы с призмой Френеля призма немного видна. Это не идеально для длительного использования, но позволяет протестировать призму и посмотреть, как она работает.
 Призмы Френеля также используются, когда рецепт призмы нестабилен и может скоро измениться.
Призмы Френеля также используются, когда рецепт призмы нестабилен и может скоро измениться.Очки с временной призмой Френеля на левой линзе.
Если призменная коррекция необходима в течение более длительного периода времени, ее можно втереть (сделать частью) в линзу ваших очков. Очки с призмой выглядят как любые другие очки без призмы, хотя линза с одной стороны может быть толще и заметнее. Если вас это беспокоит, подумайте о более толстой оправе, чтобы скрыть эту часть линзы.
Очки со встроенной в линзу призмой.
Вызывают ли очки Prism побочные эффекты?
Может потребоваться несколько дней, чтобы привыкнуть к новым призматическим очкам или очкам с обновленным рецептом. В это время у вас может быть некоторое напряжение глаз.
К редким симптомам относятся:
- двоение в глазах
- головная боль
- тошнота
- боль в глазах
Если у вас есть какие-либо из этих симптомов, позвоните своему офтальмологу, который выписал вам очки.
 Вам может понадобиться замена рамы или новый рецепт.
Вам может понадобиться замена рамы или новый рецепт.Как работают призматические очки | Нейролинза
Врачи-офтальмологи обычно рекомендуют призматические очки пациентам, которые борются с двоением в глазах, нечеткостью зрения, головными болями или другими симптомами, вызванными небольшим смещением глаз. Призменная коррекция помогает скорректировать положение глаз, чтобы вы могли видеть только одно четкое изображение. Призма, добавленная к вашим очкам, преломляет свет до того, как он достигает вашего глаза. Затем свет перенаправляется в нужное место на сетчатке каждого глаза. По сути, ваш мозг объединяет два изображения, чтобы создать одно четкое изображение.
Почему вам может быть полезна призменная коррекция
Диплопия может быть вызвана несколькими причинами. Призма не всегда является решением для всех случаев двоения в глазах. Поскольку эта проблема со зрением может быть симптомом серьезного заболевания, вы должны проконсультироваться со своим глазным врачом, чтобы определить, что именно вызывает ее.

Во многих случаях двоение в глазах возникает из-за смещения глаз. Призматические очки могут помочь исправить двоение в глазах, если смещение вызвано проблемами глазных мышц, такими как косоглазие, или проблемами, связанными с нервами, такими как сахарный диабет. Призматическая коррекция также может помочь вам, если диплопия вызвана неврологической или связанной с мозгом проблемой, такой как мигрень, травма головы или инсульт.
Neurolenses: передовое решение для очков
Знаете ли вы, что около двух третей людей в Соединенных Штатах борются с симптомами, связанными с неправильным положением глаз? Симптомы обычно включают головные боли, напряжение глаз, сухость глаз, усталость глаз, боль в шее, боль в плече и укачивание.
До того, как эксперты поняли связь между глазами и мозгом, врачи-офтальмологи повышали зрительный комфорт своих пациентов, добавляя небольшое количество призм к своим очкам, отпускаемым по рецепту.
 Но пара стандартных очков с призмой может устранить смещение глаз только на одном расстоянии. Нейролинзы, с другой стороны, могут решить проблемы смещения на всех расстояниях. Эта передовая технология использует контурную призму для медленного увеличения призмы от дальнего до ближнего. Это помогает обеспечить правильное выравнивание во всех точках. В результате нейролинзы выравнивают ваши глаза, облегчая симптомы, связанные с дисфорией тройничного нерва.
Но пара стандартных очков с призмой может устранить смещение глаз только на одном расстоянии. Нейролинзы, с другой стороны, могут решить проблемы смещения на всех расстояниях. Эта передовая технология использует контурную призму для медленного увеличения призмы от дальнего до ближнего. Это помогает обеспечить правильное выравнивание во всех точках. В результате нейролинзы выравнивают ваши глаза, облегчая симптомы, связанные с дисфорией тройничного нерва.Что такое дисфория тройничного нерва
Дисфория тройничного нерва — это общий термин, который врачи используют для описания распространенных проблем со зрением, с которыми сегодня сталкиваются люди. Это особенно актуально для тех, кто часами пользуется цифровыми устройствами. Симптомы, упомянутые выше, не новы. Фактически, дисфория тройничного нерва в прошлом упоминалась под многими другими названиями, включая, среди прочего, несоответствие фиксации или недостаточность конвергенции.


 А боковые стороны упаковки являются параллелограммом. Таким образом, упаковка стикеров полностью соответствует определению призмы.
А боковые стороны упаковки являются параллелограммом. Таким образом, упаковка стикеров полностью соответствует определению призмы. 

 2\)
2\)
 В произвольных призмах придется считать площадь каждой боковой грани, а уже после их складывать.
В произвольных призмах придется считать площадь каждой боковой грани, а уже после их складывать. 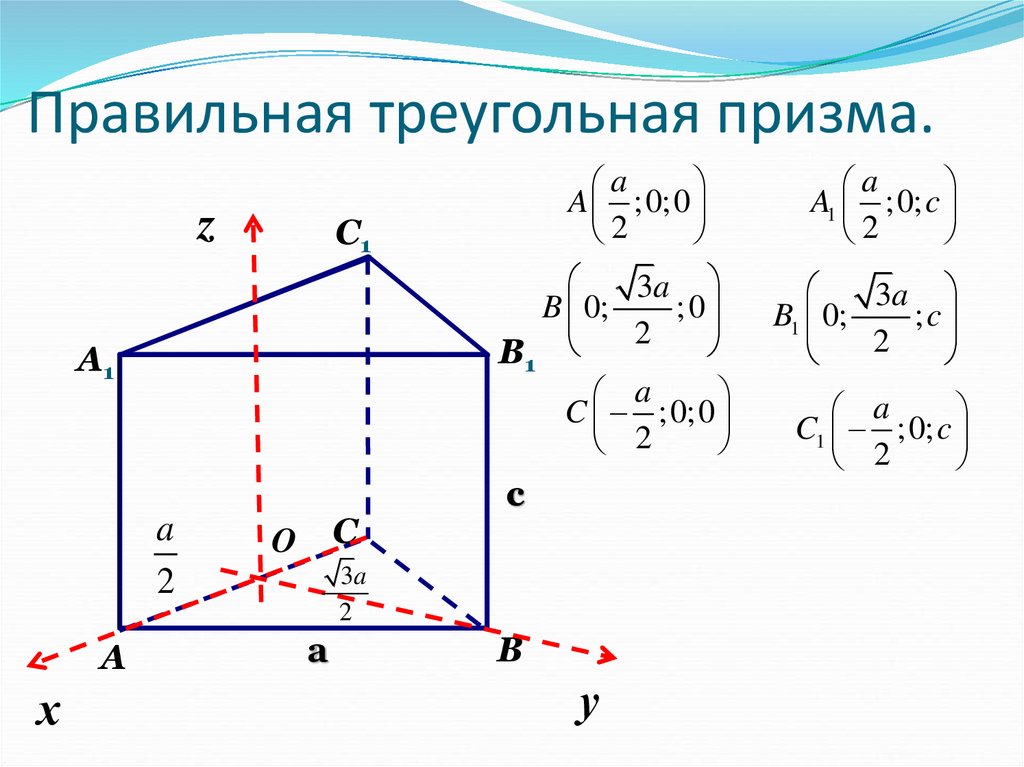 2} = \sqrt{144 + 25} = \sqrt{169} = 13\).
2} = \sqrt{144 + 25} = \sqrt{169} = 13\). 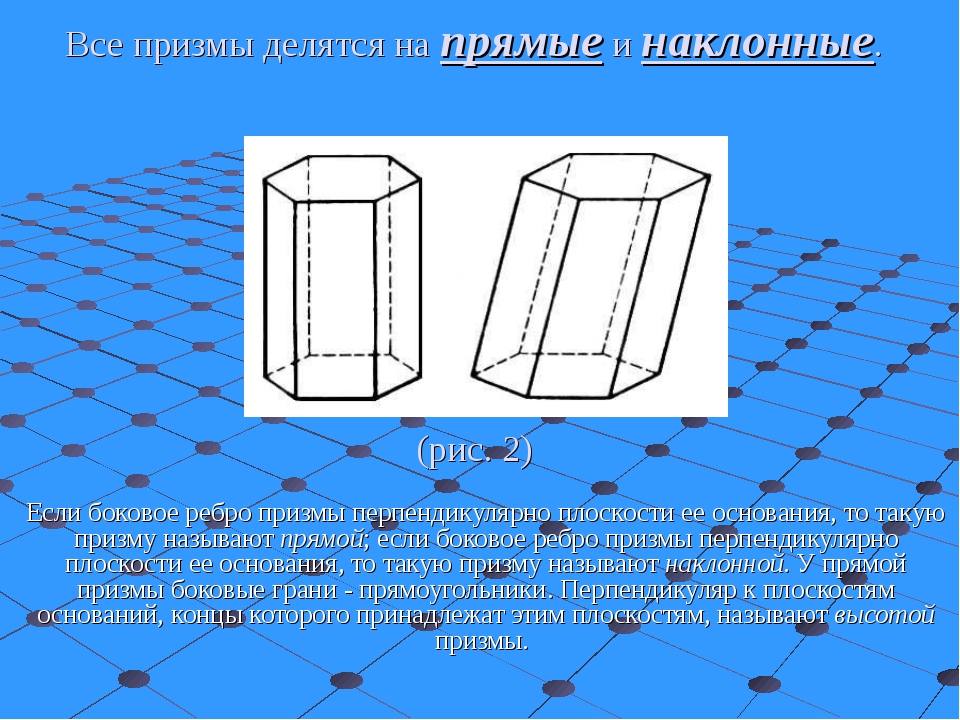 2} = \sqrt{36 + 64} = \sqrt{100} = 10\).
2} = \sqrt{36 + 64} = \sqrt{100} = 10\).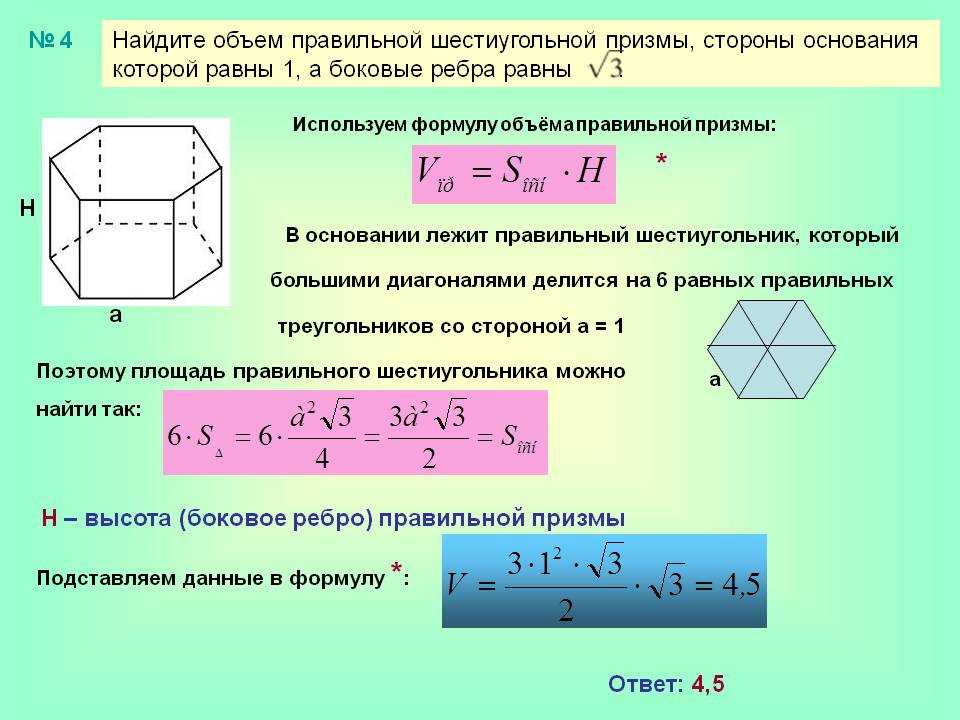 Поскольку по условию дана правильная призма, то высота совпадает с боковым ребром. Следовательно, боковое ребро равняется 96,5.
Поскольку по условию дана правильная призма, то высота совпадает с боковым ребром. Следовательно, боковое ребро равняется 96,5. Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 12 и 15. Боковое ребро призмы равно 4. Найдите объем этой призмы.
Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 12 и 15. Боковое ребро призмы равно 4. Найдите объем этой призмы. 
 Ребра как бы образуют каркас призмы.
Ребра как бы образуют каркас призмы. 
 При двойном зрении видны два изображения, потому что свет падает на разные части сетчатки.
При двойном зрении видны два изображения, потому что свет падает на разные части сетчатки. Поскольку это может быть признаком серьезного заболевания, важно выяснить, что вызывает двоение в глазах.
Поскольку это может быть признаком серьезного заболевания, важно выяснить, что вызывает двоение в глазах.
Leave A Comment