Ответ: $0.25$
Практика: решай 9 задание и тренировочные варианты ЕГЭ по математике (профильной)
Тождественные преобразования показательных и логарифмических выражений
3.
Тождественные преобразования показательных и логарифмических выражений
Комментарий. Для выполнения заданий этой группы требуется хорошо знать свойства логарифмов и уметь их применять. Эта работа очень полезна для подготовки к решению логарифмических и показательных уравнений и неравенств. Рассмотрим далее задания, связанные с упрощением показательных и логарифмических выражений.
Формулы для справок
Вспомним основные свойства логарифмов.
-
.
Комментарий. Логарифм единицы по любому основанию равен нулю. Для того, чтобы убедиться в истинности данной формулы, достаточно вспомнить, что любое число (кроме нуля) в нулевой степени равно единице.
-
.
Комментарий.
 Логарифм равен единице в случае равенства чисел (выражений) — основания логарифма и выражения, стоящего под логарифмом.
Логарифм равен единице в случае равенства чисел (выражений) — основания логарифма и выражения, стоящего под логарифмом. -
.
Комментарий. Представленная формула является одним из вариантов записи определения логарифма.
-
.
-
.
-
.
-
.
-
.
Комментарий.
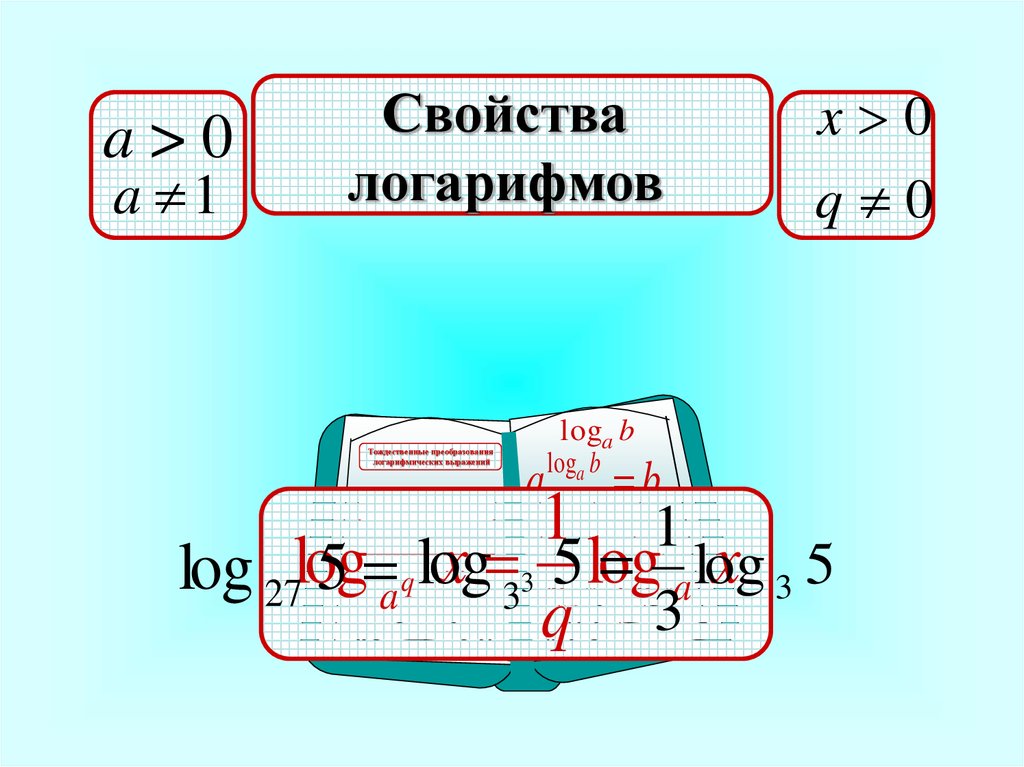
Данная формула называемая формулой перехода к новому основанию, имеет два важных следствия. Приравняем в формуле , тогда . Рассмотрим числитель полученной дроби. Поставим вопрос: в какую степень следует возвести число b, чтобы получить число b. Ответ — в первую степень, т.е. числитель рассматриваемой дроби равен единице. Таким образом, . В ряде задач полезно бывает полученную формулу записать в преобразованном виде: .
-
.

Комментарий. Предполагается, что во всех представленных формулах параметры принимают допустимые значения.
Пример 3.1
Вычислить
Решение
Представим в виде степени числа 5, тогда
Далее воспользуемся правилом умножения степеней одинаковым основанием (при умножении степеней с одинаковым основанием показатели складываются):
.
Преобразуем полученную в процессе решения разность логарифмов (по одному основанию) и применим определение логарифма (зададим вопрос: В какую степень следует возвести основание логарифма 3, чтобы получить число, стоящее под логарифмом — 9?):
Ответ: 25.
Пример 3.2.
Упростить выражение
Решение
Упростим показатель степени подкоренного выражения:
Тогда
Ответ: 27.
Пример 3.3.
Упростить выражение:
Решение
Вначале упростим логарифмируемое выражение. Если Вы уже занимались упрощением алгебраических выражений, то вид первого множителя в знаменателе вызовет предположение, что перед нами полный квадрат.
Следовательно,
Ответ: 1/2.
Пример 3.4.
Найти значение выражения
Решение
Разделим на знаменатель каждое слагаемое числителя по отдельности:
Переходя далее в каждом слагаемом к новому основанию 18, получаем, что:
Преобразуем далее сумму логарифмов с одинаковым основанием в логарифм произведения и используем определение логарифма:
Ответ: 1.
Пример 3.5.
Вычислить
Решение
Для преобразования данного выражения перейдем во всех логарифмах к основанию 4:
.
Тогда выражение принимает вид:
Далее разложим на множители логарифмируемые выражения, выделяя в каждом из них множитель вида 4n :
28 = 4 ∙ 7, 112 = 16 ∙ 7 = 42 ∙ 7, 448 = 64 ∙ 7 = 43 ∙ 7.
Продолжим преобразование выражения, используя свойства логарифмов:
Ответ: 2.
Пример 3.6.
Вычислить
Решение
Представим числа 2 и 1 в виде: Тогда
Ответ: 2.
Пример 3.7.
Найти если
Решение
Обратим внимание на то, что в каждом логарифме (либо в основании, либо в аргументе) присутствует множитель 7. Поэтому перейдем к основанию 7 во всех логарифмах:
Обратим внимание, что , тогда:
Следовательно, для вычисления этого логарифма нужно знать значения и Воспользуемся формулами перехода к новому основанию:
Подставим далее найденные значения в преобразованное исходное выражение:
Ответ:
Пример 3.8.
Известно, что лежит между числами 8 и 13, а принимает целые значения. Найти количество этих значений.
Решение
Перейдем в обоих логарифмах к основанию b.
Для этого воспользуемся сначала формулой «логарифм частного»: . Обратим далее внимание, что .
Получаем, что
Решим методом интервалов неравенство: .
Для этого перейдем к систем нестрогих неравенств: .
Рассматривая каждое из записанных неравенств отдельно и впоследствии находя решение как пересечение множеств (решений первого и второго неравенств), получаем:
Выполним преобразования полученного двойного неравенства.
Прибавим 1 ко всем частям неравенства: Поскольку его значения задаются неравенством:
или
Следовательно, может принимать 6 целых значений – от 11 до 16.
Ответ: 6.
8.2- Преобразования логарифмических функций
Графические логарифмические функции и уравнения Существуют два основных метода, которые можно использовать в порядке, чтобы точно график. output’, подставьте значения одной переменной (например: x), чтобы получить значения другой переменной (например: y). Затем нанесите точки на график и соедините точки. ☆Примечание. Помните, что при построении графиков логарифмических функций вручную значения x обычных журналов больше нуля и не определены при нуле. Следовательно, все значения x общей логарифмической функции должны быть больше нуля. ~ Использование графических калькуляторов, таких как Texas Instruments TI-84 или 🌟 desmos Общий логарифмический график: y = log 10 (x) Домен и диапазон Logarithms 010 • Домен: все возможные значения x, которыми может быть функция. • Диапазон: все возможные значения y, которыми может быть функция. В общих логарифмических уравнениях y — все действительные числа, {yER} Правила преобразования Стандартное уравнение преобразования выглядит следующим образом: Логарифмическое: ]+сЭкспонента: y=a b (k(x-d)) +c Где a = вертикальное растяжение/сжатие; если a<0, функция претерпела вертикальное отражение по оси x. Где c = вертикальное смещение (вверх или вниз) Где k = горизонтальное растяжение/сжатие; если k<0, функции претерпели горизонтальное отражение по оси y. Где d =the horizontal shift (left or right) y=log 10 (x): Therefore…Logarithmic transformation rules are as followed:
🌟 Видео-трансформации логарифмических функций Разнообразные преобразования: . функции, содержащие одновременно несколько различных преобразований (вертикальное растяжение и сжатие + отражение), всегда делают это по пунктам; преобразование преобразованиями, чтобы успешно применить преобразования к родительской функции!
Написание и описание алгебраических представлений в соответствии с геометрическими описаниями. Пример 1: Родительская функция: y=log10 x была растянута по горизонтали в 5 раз и смещена на 2 единицы влево. Функция также была сжата по вертикали в ⅓ раза, смещена на 6 единиц вниз и отражена по оси x. Напишите новое уравнение логарифмической функции в соответствии с указанными преобразованиями, а также областью определения и областью значений. Шаг 1: Запишите родительскую функцию y=log10 x Шаг 2: Запишите логарифмическое уравнение в общем виде y= a log 10 (k(x-d)) +c 9004 3: Вставьте значения в общую форму в соответствии с описаниями:• Поскольку функция была растянута по горизонтали в 5 раз, k=⅕ • Поскольку функция была смещена по горизонтали на 2 единицы влево, d=-2 • Поскольку функция была сжата по вертикали в ⅓ раз, a=⅓ • Поскольку функция была смещена по вертикали на 6 единиц вниз, c=-6 • Из-за того, что функция была отражена по оси x, a будет отрицательным значением, таким образом, a теперь будет равно — ⅓. Шаг 4: Подставьте известные значения в общую форму логарифмического уравнения -2))]+(-6) ∴ уравнение преобразованной функции будет y=-⅓ log 10 [⅕ (x+2)]-6 Шаг 5: Запишите домен и диапазон • В логарифмических функциях диапазон преобразованной функции будет таким же, как диапазон преобразованной функции. Таким образом, диапазон y=-⅓ log 10 (⅕(x+2))-6 равен {yER} • Поскольку кривая находится справа от асимптоты (где x=-2), домен будет больше чем х=-2. Таким образом, домен y=-⅓ log 10 (⅕(x+2))-6 равен {xR│x>-2} ∴ D: {xER│x>-2}; R: {yER} Графики логарифмических функций согласно заданному уравнению Пример 2: Используя y=log10(x), s , найдите функцию 3log 10(x+9)-8 с помощью преобразований и укажите домен и диапазон. Шаг 1: Постройте график родительской функции (y=log10(x)) и извлеките несколько точек выборки: Шаг 2: Примените преобразование, одно преобразование за раз! ~1.
~2. Примените сдвиг по вертикали (8 единиц вниз) – таким образом вычтите все значения y на 8
~3.
∴ Новые точки преобразованной функции 89/10, -11), (-8, -8), (1, -5) и (23, -7/2) Шаг 3: График новой функции с использованием новых преобразованных точек Шаг 4: Укажите домен и диапазон ~ Поскольку диапазон остается таким же, как у родительской функции, диапазон преобразованной функции будет {yER} ~ Как видно из графика, поскольку кривая находится справа от асимптоты (где x=-9), график будет больше, чем x=-9. ∴ D: {xER│x>-9}; R:{yER} Так как y=logax эквивалентно x=ay, где a>0 и a≠1, те же правила применяются к логарифмическим функциям в форме x=ay или y=a x 🌟 Видео- Графики преобразований логарифмических функций 🌟 Видео- Графики логарифмических функций |
Интерпретация логарифмических преобразований в линейной модели
Логарифмические преобразования часто рекомендуются для искаженных данных, таких как денежные показатели или определенные биологические и демографические показатели.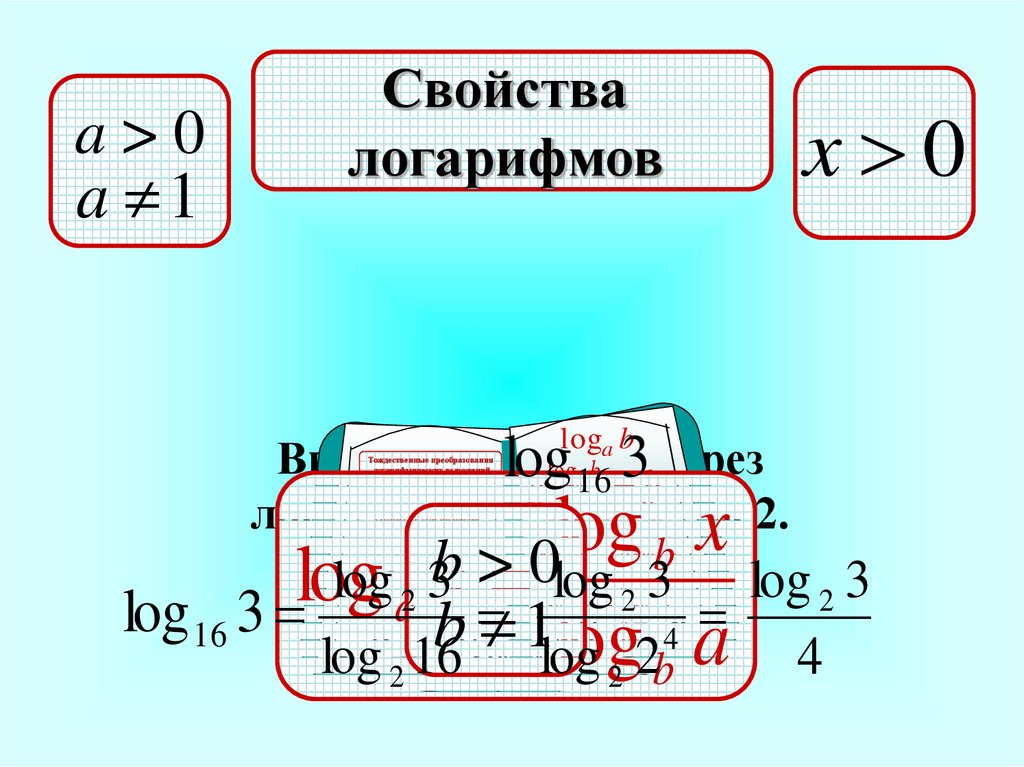
история(государство.область)
После преобразования журнала обратите внимание, что гистограмма более или менее симметрична. Мы сдвинули большие штаты ближе друг к другу и разнесли меньшие штаты.
история (журнал (состояние. область))
Зачем это делать? Одна из причин — сделать данные более «нормальными» или симметричными. Если мы выполняем статистический анализ, который предполагает нормальность, логарифмическое преобразование может помочь нам удовлетворить это предположение. Другая причина состоит в том, чтобы помочь удовлетворить предположение о постоянной дисперсии в контексте линейного моделирования. Еще одна — помочь сделать нелинейные отношения более линейными. Но хотя реализовать логарифмическое преобразование легко, оно может усложнить интерпретацию.
Сначала мы дадим рецепт интерпретации для тех, кому просто нужна быстрая помощь. Затем мы немного углубимся в то, что мы говорим о нашей модели, когда мы логируем наши данные.
Правила интерпретации
Хорошо, вы запустили регрессию/подгонку линейной модели, и некоторые из ваших переменных были логарифмически преобразованы.
- Только зависимая переменная/переменная отклика подвергается логарифмическому преобразованию . Возведите коэффициент в степень, вычтите из этого числа единицу и умножьте на 100. Это дает процент увеличения (или уменьшения) отклика на каждое увеличение независимой переменной на одну единицу. Пример: коэффициент 0,198. (ехр(0,198) – 1) * 100 = 21,9. При увеличении независимой переменной на одну единицу наша зависимая переменная увеличивается примерно на 22%.

- Только независимые переменные/переменные-предикторы подвергаются логарифмическому преобразованию . Разделите коэффициент на 100. Это говорит нам о том, что увеличение независимой переменной на 1% увеличивает (или уменьшает) зависимую переменную на (коэффициент/100) единиц. Пример: коэффициент равен 0,198. 0,198/100 = 0,00198. На каждый 1% увеличения независимой переменной наша зависимая переменная увеличивается примерно на 0,002. Для увеличения на x процентов умножьте коэффициент на log(1.x). Пример: на каждые 10% увеличения независимой переменной наша зависимая переменная увеличивается примерно на 0,19.8 * log(1,10) = 0,02.
- И зависимая переменная/переменная-отклик, и независимая/переменная-предиктор(ы) подвергаются логарифмическому преобразованию . Интерпретируйте коэффициент как процент увеличения зависимой переменной на каждый 1% увеличения независимой переменной. Пример: коэффициент равен 0,198. На каждый 1% увеличения независимой переменной наша зависимая переменная увеличивается примерно на 0,20%.

Что на самом деле означают логарифмические преобразования для ваших моделей
Приятно знать, как правильно интерпретировать коэффициенты для логарифмически преобразованных данных, но важно знать, что именно подразумевает ваша модель, когда она включает логарифмически преобразованные данные. Чтобы лучше понять, давайте воспользуемся R для моделирования некоторых данных, которые потребуют логарифмических преобразований для правильного анализа. Мы упростим задачу с одной независимой переменной и нормально распределенными ошибками. Сначала мы рассмотрим логарифмически преобразованную зависимую переменную.
x <- seq(0.1,5,length.out = 100) set.seed(1) e <- rnorm(100, среднее = 0, sd = 0,2)
Первая строка генерирует последовательность из 100 значений от 0,1 до 5 и присваивает ее x. Следующая строка устанавливает начальное число генератора случайных чисел в 1. Если вы сделаете то же самое, вы получите те же случайно сгенерированные данные, которые мы получили при запуске следующей строки. Код
Следующая строка устанавливает начальное число генератора случайных чисел в 1. Если вы сделаете то же самое, вы получите те же случайно сгенерированные данные, которые мы получили при запуске следующей строки. Код rnorm(100, mean = 0, sd = 0,2) генерирует 100 значений из нормального распределения со средним значением 0 и стандартным отклонением 0,2. Это будет наша «ошибка». Это одно из предположений простой линейной регрессии: наши данные могут быть смоделированы с помощью прямой линии, но будут отклоняться на некоторую случайную величину, которая, как мы предполагаем, исходит из нормального распределения со средним значением 0 и некоторым стандартным отклонением. Мы присваиваем нашу ошибку e.
Теперь мы готовы создать нашу зависимую переменную с логарифмическим преобразованием. Мы выбираем точку пересечения (1.2) и наклон (0.2), которые мы умножаем на x, а затем добавляем нашу случайную ошибку, т.е. Наконец возводим в степень.
у <- ехр(1,2 + 0,2 * х + е)
Чтобы понять, почему мы возводим в степень, обратите внимание на следующее:
$$\text{log}(y) = \beta_0 + \beta_1x$$
$$\text{exp}(\text{log}(y)) = \text{exp}(\beta_0 + \beta_1x)$$
$$y = \text{exp}(\beta_0 + \beta_1x)$$
Таким образом, логарифмически преобразованная зависимая переменная означает, что наша простая линейная модель была возведена в степень. Напомним из правила произведения показателей, что мы можем переписать последнюю строку выше как
Напомним из правила произведения показателей, что мы можем переписать последнюю строку выше как
$$y = \text{exp}(\beta_0) \text{exp}(\beta_1x)$$
Это также означает, что наша независимая переменная имеет мультипликативную связь с нашей зависимой переменной вместо обычной аддитивной связи. Отсюда необходимость выражать влияние изменения x на y на одну единицу в процентах.
Если мы подгоним правильную модель к данным, обратите внимание, что мы довольно хорошо восстанавливаем истинные значения параметров, которые мы использовали для создания данных.
lm1 <- lm(log(y) ~ x)
резюме(lm1)
Вызов:
лм (формула = журнал (у) ~ х)
Остатки:
Мин. 1 кв. Медиана 3 кв. Макс.
-0,4680 -0,1212 0,0031 0,1170 0,4595
Коэффициенты:
Оценка стд. Значение ошибки t Pr(>|t|)
(Перехват) 1,22643 0,03693 33,20 <2е-16***
х 0,19818 0,01264 15,68 <2е-16***
---
Сигн. коды: 0 «***» 0,001 «**» 0,01 «*» 0,05 «.» 0,1 « » 1
Остаточная стандартная ошибка: 0,1805 при 98 степенях свободы. Множественный R-квадрат: 0,7151, скорректированный R-квадрат: 0,7122
F-статистика: 246 на 1 и 98 DF, p-значение: <2,2e-16
Множественный R-квадрат: 0,7151, скорректированный R-квадрат: 0,7122
F-статистика: 246 на 1 и 98 DF, p-значение: <2,2e-16
Расчетное значение пересечения 1,226 близко к истинному значению 1,2. Расчетный наклон 0,198 очень близок к истинному значению 0,2. Наконец, расчетная остаточная стандартная ошибка 0,1805 не слишком далека от истинного значения 0,2.
Напомним, что для интерпретации значения наклона нам необходимо возвести его в степень.
exp(коэффициент(lm1)["x"])
Икс
1.219179
Здесь говорится, что каждое увеличение x на одну единицу умножается примерно на 1,22. Или, другими словами, при каждом увеличении x на одну единицу y увеличивается примерно на 22%. Чтобы получить 22%, вычтите 1 и умножьте на 100.
(exp(coef(lm1)["x"]) - 1) * 100
Икс
21.91786
Что, если мы подгоним только y вместо log(y)? Как мы можем понять, что нам следует рассмотреть преобразование журнала? Просто просмотр коэффициентов мало что вам скажет.
lm2 <- lm(y ~ x)
резюме(lm2)
Вызов:
лм (формула = у ~ х)
Остатки:
Мин. 1 кв. Медиана 3 кв. Макс.
-2,3868 -0,6886 -0,1060 0,5298 3,3383
Коэффициенты:
Оценка стд. Значение ошибки t Pr(>|t|)
(Пересечение) 3,00947 0,23643 12,73 <2e-16 ***
х 1,16277 0,08089 14,38 <2е-16***
---
Сигн. коды: 0 «***» 0,001 «**» 0,01 «*» 0,05 «.» 0,1 « » 1
Остаточная стандартная ошибка: 1,156 на 98 степеней свободы
Множественный R-квадрат: 0,6783, скорректированный R-квадрат: 0,675
F-статистика: 206,6 на 1 и 98 DF, p-значение: <2,2e-16
Конечно, поскольку мы сгенерировали данные, мы видим, что коэффициенты далеко не совпадают, а остаточная стандартная ошибка слишком высока. Но в реальной жизни вы этого не узнаете! Именно поэтому мы проводим регрессионную диагностику. Ключевым предположением для проверки является постоянная дисперсия ошибок. Мы можем сделать это с помощью графика Scale-Location. Вот график для модели, которую мы только что запустили без логарифмического преобразования y.
plot(lm2, which = 3) # 3 = график Scale-Location
Обратите внимание, что стандартизированные остатки имеют тенденцию к увеличению. Это признак того, что предположение о постоянной дисперсии было нарушено. Сравните этот график с тем же графиком для правильной модели.
сюжет (lm1, который = 3)
Линия тренда ровная, а остатки равномерно разбросаны.
Означает ли это, что вы должны всегда преобразовывать вашу зависимую переменную в журнал, если вы подозреваете, что предположение о постоянной дисперсии было нарушено? Не обязательно. Непостоянная дисперсия может быть связана с другими неверными спецификациями вашей модели. Также подумайте о том, что означает моделирование логарифмически преобразованной зависимой переменной. Он говорит, что имеет мультипликативную связь с предикторами. Это кажется правильным? Используйте свое суждение и предметный опыт.
Теперь давайте рассмотрим данные с логарифмически преобразованной независимой переменной-предиктором. Это проще сгенерировать. Мы просто лог-преобразуем x.
Это проще сгенерировать. Мы просто лог-преобразуем x.
у <- 1,2 + 0,2 * log (х) + е
И снова мы сначала подбираем правильную модель и замечаем, что она отлично справляется с восстановлением истинных значений, которые мы использовали для создания данных:
lm3 <- lm(y ~ log(x))
резюме(lm3)
Вызов:
лм (формула = у ~ журнал (х))
Остатки:
Мин. 1 кв. Медиана 3 кв. Макс.
-0,46492 -0,12063 0,00112 0,11661 0,45864
Коэффициенты:
Оценка стд. Значение ошибки t Pr(>|t|)
(Пересечение) 1,22192 0,02308 52,938 < 2e-16 ***
log(x) 0,19979 0,02119 9,427 2,12e-15 ***
---
Сигн. коды: 0 «***» 0,001 «**» 0,01 «*» 0,05 «.» 0,1 « » 1
Остаточная стандартная ошибка: 0,1806 при 98 степенях свободы.
Множественный R-квадрат: 0,4756, скорректированный R-квадрат: 0,4702
F-статистика: 88,87 на 1 и 98 DF, p-значение: 2,121e-15
Для интерпретации коэффициента наклона мы делим его на 100.
коэф(лм3)["журнал(х)"]/100
журнал (х)
0. 001997892
001997892
Это говорит нам о том, что увеличение x на 1% увеличивает зависимую переменную примерно на 0,002. Почему это говорит нам об этом? Давайте займемся математикой. Ниже мы вычисляем изменение y при изменении x от 1 до 1,01 (т. е. увеличение на 1%).
$$(\beta_0 + \beta_1\text{log}1.01) – (\beta_0 + \beta_1\text{log}1)$$
$$\beta_1\text{log}1.01 – \beta_1\text{ журнал}1$$
$$\beta_1(\text{log}1.01 – \text{log}1)$$
$$\beta_1\text{log}\frac{1.01}{1} = \beta_1\text{log}1.01$ $
В результате коэффициент наклона умножается на log(1,01), что приблизительно равно 0,01, или \(\frac{1}{100}\). Отсюда интерпретация, согласно которой увеличение x на 1% увеличивает зависимую переменную на коэффициент /100.
Еще раз давайте подгоним неправильную модель, не указав логарифмическое преобразование для x в синтаксисе модели.
lm4 <- lm(y ~ x)
Просмотр сводки модели покажет, что оценки коэффициентов сильно отличаются от истинных значений. Но на практике мы никогда не знаем истинных значений. И снова диагностика предназначена для оценки адекватности модели. Полезной диагностикой в этом случае является график частичного остатка, который может выявить отклонения от линейности. Напомним, что линейные модели предполагают, что предикторы являются аддитивными и имеют линейную связь с переменной отклика. Пакет car предоставляет функцию crPlot для быстрого создания графиков частичного остатка. Просто дайте ему объект модели и укажите, для какой переменной вы хотите создать график частичного остатка.
Но на практике мы никогда не знаем истинных значений. И снова диагностика предназначена для оценки адекватности модели. Полезной диагностикой в этом случае является график частичного остатка, который может выявить отклонения от линейности. Напомним, что линейные модели предполагают, что предикторы являются аддитивными и имеют линейную связь с переменной отклика. Пакет car предоставляет функцию crPlot для быстрого создания графиков частичного остатка. Просто дайте ему объект модели и укажите, для какой переменной вы хотите создать график частичного остатка.
библиотека (машина) crPlot(lm4, переменная = "x")
Прямая линия представляет указанное соотношение между x и y. Изогнутая линия представляет собой гладкую линию тренда, которая суммирует наблюдаемую взаимосвязь между x и y. Мы можем сказать, что наблюдаемая зависимость нелинейна. Сравните этот график с графиком частичного остатка для правильной модели.
crPlot(lm3, переменная = "log(x)")
Гладкие и облегающие линии точно накладываются друг на друга, не обнаруживая серьезных отклонений от линейности.
Это не означает, что если вы видите отклонение от линейности, вы должны немедленно предположить, что логарифмическое преобразование является единственным исправлением! Нелинейная зависимость может быть сложной, и ее не так легко объяснить с помощью простого преобразования. Но в таких случаях может подойти логарифмическое преобразование, и его, безусловно, следует учитывать.
Наконец, давайте рассмотрим данные, в которых как зависимая, так и независимая переменные логарифмически преобразованы.
y <- exp(1,2 + 0,2 * log(x) + e)
Посмотрите внимательно на приведенный выше код. Отношения между x и y теперь мультипликативны и нелинейны!
Как обычно, мы можем подобрать правильную модель и заметить, что она отлично справляется с восстановлением истинных значений, которые мы использовали для создания данных:
lm5 <- lm(log(y)~ log(x))
резюме (lm5)
Вызов:
лм (формула = журнал (у) ~ журнал (х))
Остатки:
Мин. 1 кв. Медиана 3 кв. Макс.
-0,46492 -0,12063 0,00112 0,11661 0,45864
Коэффициенты:
Оценка стд. Значение ошибки t Pr(>|t|)
(Перехват) 1.22192 0,02308 52,938 < 2е-16***
log(x) 0,19979 0,02119 9,427 2,12e-15 ***
---
Сигн. коды: 0 «***» 0,001 «**» 0,01 «*» 0,05 «.» 0,1 « » 1
Остаточная стандартная ошибка: 0,1806 при 98 степенях свободы.
Множественный R-квадрат: 0,4756, скорректированный R-квадрат: 0,4702
F-статистика: 88,87 на 1 и 98 DF, p-значение: 2,121e-15
Макс.
-0,46492 -0,12063 0,00112 0,11661 0,45864
Коэффициенты:
Оценка стд. Значение ошибки t Pr(>|t|)
(Перехват) 1.22192 0,02308 52,938 < 2е-16***
log(x) 0,19979 0,02119 9,427 2,12e-15 ***
---
Сигн. коды: 0 «***» 0,001 «**» 0,01 «*» 0,05 «.» 0,1 « » 1
Остаточная стандартная ошибка: 0,1806 при 98 степенях свободы.
Множественный R-квадрат: 0,4756, скорректированный R-квадрат: 0,4702
F-статистика: 88,87 на 1 и 98 DF, p-значение: 2,121e-15
Интерпретируйте коэффициент x как процентное увеличение y на каждый 1% увеличения x. В данном случае это увеличение y примерно на 0,2% на каждый 1% увеличения x.
Подгонка неправильной модели снова дает оценки коэффициента и остаточной стандартной ошибки, которые сильно отличаются от целевых.
lm6 <- lm(y ~ x) резюме (lm6)
Графики Scale-Location и Partial-Residual свидетельствуют о том, что с нашей моделью что-то не так. График Scale-Location показывает кривую линию тренда, а график Partial-Residual показывает линейные и гладкие линии, которые не совпадают.

 Логарифм равен единице в случае равенства чисел (выражений) — основания логарифма и выражения, стоящего под логарифмом.
Логарифм равен единице в случае равенства чисел (выражений) — основания логарифма и выражения, стоящего под логарифмом.
 Поскольку x должен быть больше нуля, как правило, областью определения десятичных логарифмических функций является {x>0}.
Поскольку x должен быть больше нуля, как правило, областью определения десятичных логарифмических функций является {x>0}. x отражение через
x отражение через

 Примените вертикальное растяжение (с коэффициентом 3) — таким образом, умножьте (растяните) все значения y на коэффициент 3.
Примените вертикальное растяжение (с коэффициентом 3) — таким образом, умножьте (растяните) все значения y на коэффициент 3.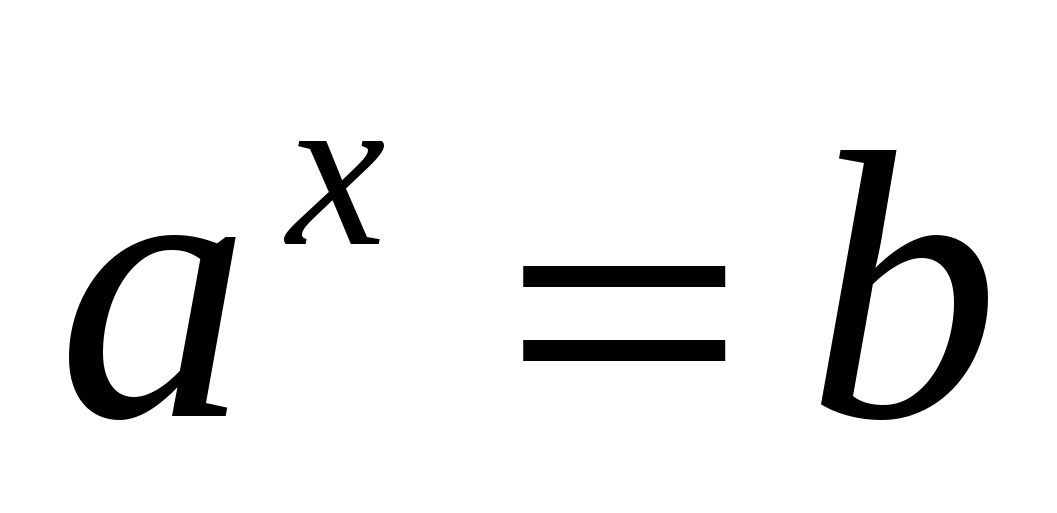 Примените сдвиг по горизонтали (осталось 9 единиц) — таким образом, вычтите все значения x на 9
Примените сдвиг по горизонтали (осталось 9 единиц) — таким образом, вычтите все значения x на 9 Таким образом, домен будет {xER│x>-9}
Таким образом, домен будет {xER│x>-9}
 Множественный R-квадрат: 0,7151, скорректированный R-квадрат: 0,7122
F-статистика: 246 на 1 и 98 DF, p-значение: <2,2e-16
Множественный R-квадрат: 0,7151, скорректированный R-квадрат: 0,7122
F-статистика: 246 на 1 и 98 DF, p-значение: <2,2e-16
 001997892
001997892
 Макс.
-0,46492 -0,12063 0,00112 0,11661 0,45864
Коэффициенты:
Оценка стд. Значение ошибки t Pr(>|t|)
(Перехват) 1.22192 0,02308 52,938 < 2е-16***
log(x) 0,19979 0,02119 9,427 2,12e-15 ***
---
Сигн. коды: 0 «***» 0,001 «**» 0,01 «*» 0,05 «.» 0,1 « » 1
Остаточная стандартная ошибка: 0,1806 при 98 степенях свободы.
Множественный R-квадрат: 0,4756, скорректированный R-квадрат: 0,4702
F-статистика: 88,87 на 1 и 98 DF, p-значение: 2,121e-15
Макс.
-0,46492 -0,12063 0,00112 0,11661 0,45864
Коэффициенты:
Оценка стд. Значение ошибки t Pr(>|t|)
(Перехват) 1.22192 0,02308 52,938 < 2е-16***
log(x) 0,19979 0,02119 9,427 2,12e-15 ***
---
Сигн. коды: 0 «***» 0,001 «**» 0,01 «*» 0,05 «.» 0,1 « » 1
Остаточная стандартная ошибка: 0,1806 при 98 степенях свободы.
Множественный R-квадрат: 0,4756, скорректированный R-квадрат: 0,4702
F-статистика: 88,87 на 1 и 98 DF, p-значение: 2,121e-15
Leave A Comment